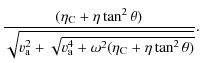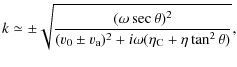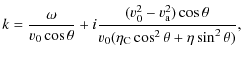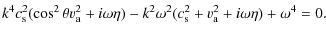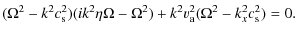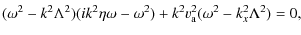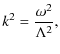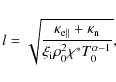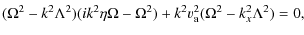| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913024 | |
| Published online | 11 June 2010 | |
The spatial damping of magnetohydrodynamic waves in a flowing partially ionised prominence plasma
M. Carbonell1 - P. Forteza2 - R. Oliver2 - J. L. Ballester2
1 - Departament de Matemàtiques i Informàtica, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
2 - Departament de Física, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
Received 30 July 2009 / Accepted 1 February 2010
Abstract
Context. Solar prominences are partially ionised plasmas
displaying flows and oscillations. These oscillations exhibit time and
spatial damping and have commonly been explained in terms of
magnetohydrodynamic (MHD) waves.
Aims. We study the spatial damping of linear non-adiabatic MHD
waves in a flowing partially ionised plasma with prominence-like
physical properties.
Methods. We consider single fluid equations for a partially
ionised hydrogen plasma by including in the energy equation optically
thin radiation, thermal conduction by electrons and neutrals, and
heating. By keeping ![]() real and fixed, we solved the dispersion relations obtained for the complex wavenumber, k,
and analysed the behaviour of the damping length, wavelength and the
ratio of the damping length to the wavelength, versus period, for
Alfvén, fast, slow, and thermal waves.
real and fixed, we solved the dispersion relations obtained for the complex wavenumber, k,
and analysed the behaviour of the damping length, wavelength and the
ratio of the damping length to the wavelength, versus period, for
Alfvén, fast, slow, and thermal waves.
Results. In the presence of a background flow, the results
indicate that new strongly damped fast and Alfvén waves appear that
depend on the joint action of flow and resistivity. The damping lengths
of adiabatic fast and slow waves are strongly affected by partial
ionisation, which also modifies the ratio between damping lengths and
wavelengths. The behaviour of adiabatic fast waves also resembles that
of Alfvén waves. For non-adiabatic slow waves, the unfolding in both
wavelength and damping length induced by the flow allows efficient
damping to be found for periods compatible with those observed in
prominence oscillations. This effect is enhanced when low ionised
plasmas are considered.
Conclusions. Since flows are ubiquitous in prominences, in the
case of non-adiabatic slow waves and within the range of periods of
interest for prominence oscillations, the joint effect of both flow and
partial ionisation leads to a ratio of damping length to wavelength
denoting a very efficient spatial damping. For fast and Alfvén waves,
the most efficient damping occurs at very short periods not compatible
with those observed in prominence oscillations.
Key words: Sun: oscillations - magnetic fields - Sun: filaments, prominences
1 Introduction
A solar prominence is a cool (
![]() K) and dense (
K) and dense (
![]() kg/m3) mass of gas located in the much
denser and hotter solar corona. Although it is poorly understood
how this structure persists for a long time within the solar corona,
it is thought that its support and thermal isolation are of magnetic
origin. Thanks to ground and space-based observations, small-amplitude oscillations in prominences
and filaments have been detected and details about their
properties can be found in Oliver and Ballester (2002), Banerjee et al. (2007), Oliver (2009), and Mackay et al. (2010). The
oscillations are mainly detected by the periodic Doppler shifts of
spectral lines, with periods from a few minutes to hours, and the
observations have shown that they are local in origin, that they can
be coherent over large regions of prominences/filaments, that
simultaneously flowing and oscillating features are present, and
that oscillations display time and spatial damping (Terradas et al.
2002). These small-amplitude oscillations have been commonly
interpreted in terms of linear magnetohydrodynamic (MHD) waves and
the damping of oscillations has been studied by considering
different dissipative mechanisms. For instance, in the case of
fully ionised plasmas, the time damping of prominence oscillations
has been studied by considering non-adiabatic MHD waves, including
the effects of optically thin radiation, thermal conduction, and
heating, in unbounded and bounded prominence plasmas (Carbonell et al. 2004; Terradas et al. 2005). By assuming that the threads of
which the solar filaments consist can be modeled as cylindrical flux
tubes, the time damping of homogeneous and inhomogeneous cylindrical
flux tubes, with prominence physical conditions, has been modeled
using thermal mechanisms and resonant absorption, respectively
(Soler et al. 2008; Arregui et al. 2008; Soler et al. 2009b).
kg/m3) mass of gas located in the much
denser and hotter solar corona. Although it is poorly understood
how this structure persists for a long time within the solar corona,
it is thought that its support and thermal isolation are of magnetic
origin. Thanks to ground and space-based observations, small-amplitude oscillations in prominences
and filaments have been detected and details about their
properties can be found in Oliver and Ballester (2002), Banerjee et al. (2007), Oliver (2009), and Mackay et al. (2010). The
oscillations are mainly detected by the periodic Doppler shifts of
spectral lines, with periods from a few minutes to hours, and the
observations have shown that they are local in origin, that they can
be coherent over large regions of prominences/filaments, that
simultaneously flowing and oscillating features are present, and
that oscillations display time and spatial damping (Terradas et al.
2002). These small-amplitude oscillations have been commonly
interpreted in terms of linear magnetohydrodynamic (MHD) waves and
the damping of oscillations has been studied by considering
different dissipative mechanisms. For instance, in the case of
fully ionised plasmas, the time damping of prominence oscillations
has been studied by considering non-adiabatic MHD waves, including
the effects of optically thin radiation, thermal conduction, and
heating, in unbounded and bounded prominence plasmas (Carbonell et al. 2004; Terradas et al. 2005). By assuming that the threads of
which the solar filaments consist can be modeled as cylindrical flux
tubes, the time damping of homogeneous and inhomogeneous cylindrical
flux tubes, with prominence physical conditions, has been modeled
using thermal mechanisms and resonant absorption, respectively
(Soler et al. 2008; Arregui et al. 2008; Soler et al. 2009b).
A typical feature in prominence oscillations are flows observed in H![]() ,
UV, and EUV lines (Labrosse et al. 2010). In H
,
UV, and EUV lines (Labrosse et al. 2010). In H![]() quiescent filaments, the observed velocities range from 5 to 20 km s-1 (Zirker et al. 1998; Lin et al. 2003, 2007) and, because of
the physical conditions in filament plasma, they seem to be
field-aligned. In the case of active region prominences, flow
speeds can be higher. Observations made with
Hinode/SOT by Okamoto et al. (2007) detected
synchronous vertical oscillatory motions in the threads of an active
region prominence, and flows along the
same threads. However, in limb prominences different kinds of flows
are observed and, for instance, observations made by Berger et al.
(2008) with Hinode/SOT uncovered a complex dynamics with vertical
downflows and upflows. Taking all this into account, Carbonell et al.
(2009) explored the time damping of non-adiabatic slow and thermal waves in an unbounded prominence medium with a background flow,
while Soler et al. (2008, 2009a)
investigated the time damping of the oscillations of an individual
prominence thread and of a threaded prominence when both mass flows and
non-adiabatic processes are considered.
quiescent filaments, the observed velocities range from 5 to 20 km s-1 (Zirker et al. 1998; Lin et al. 2003, 2007) and, because of
the physical conditions in filament plasma, they seem to be
field-aligned. In the case of active region prominences, flow
speeds can be higher. Observations made with
Hinode/SOT by Okamoto et al. (2007) detected
synchronous vertical oscillatory motions in the threads of an active
region prominence, and flows along the
same threads. However, in limb prominences different kinds of flows
are observed and, for instance, observations made by Berger et al.
(2008) with Hinode/SOT uncovered a complex dynamics with vertical
downflows and upflows. Taking all this into account, Carbonell et al.
(2009) explored the time damping of non-adiabatic slow and thermal waves in an unbounded prominence medium with a background flow,
while Soler et al. (2008, 2009a)
investigated the time damping of the oscillations of an individual
prominence thread and of a threaded prominence when both mass flows and
non-adiabatic processes are considered.
Although there is a large amount of observational evidence about the time damping of MHD waves propagating in coronal structures such as coronal loops or prominences, current observational information about the spatial damping of MHD waves in coronal structures remains scarce. Time damping is usually produced when an impulsive perturbation excites a medium and waves begin to propagate, then, the wave amplitude decreases as time goes by. Alternatively, if the medium is excited by a continuous driver with a fixed frequency, the spatial damping is detected by the decrease in the amplitude as the wave propagates. Since, probably, most of the phenomena exciting waves in solar structures are impulsive in origin rather than produced by continuous drivers, time damping of waves is more often observed.
Using thermal conduction,
compressive viscosity, gravitational stratification, and field line
divergence, De Moortel et al. (2002) and De Moortel & Hood (2003,
2004) studied the spatial damping of driven and non-driven slow MHD
waves in coronal conditions and applied the results obtained to the
case of standing and propagating slow waves in coronal loops
observed with SOHO and TRACE. In the case of prominences, Terradas
et al. (2002) analysed small amplitude oscillations in a polar
crown prominence detecting both a plane propagating wave and a
standing wave. The plane wave propagates in opposite directions
with wavelengths of 67 500 and 50 000 km and phase speeds of
15 km s-1 and 12 km s-1, while in the case of the
standing wave, the estimated wavelength is 44 000 km and the
phase speed 12 km s-1. These authors also reported that for
the propagating wave, which was interpreted as a slow MHD wave, the
amplitude of the oscillations spatially decreases significantly over
a distance of
![]() km from the location where wave
motion was being generated. This distance can be considered as a
typical spatial damping length,
km from the location where wave
motion was being generated. This distance can be considered as a
typical spatial damping length, ![]() ,
of the oscillations.
,
of the oscillations.
From the theoretical point of view and assuming a fully ionised plasma, Ballai (2003) qualitatively studied the spatial damping of linear compressional waves in solar prominences by considering different dissipative mechanisms, such as isotropic and anisotropic viscosity, isotropic magnetic diffusivity, isotropic radiative damping (Newton's law), and anisotropic thermal conduction. The conclusions were that thermal radiation can damp compressional waves and that waves can also be damped by anisotropic thermal conduction provided that they have short enough wavelengths. Using linear non-adiabatic MHD waves including optically thin radiation, thermal conduction, and heating, Carbonell et al. (2006) quantitatively studied the spatial damping of slow, fast, and thermal waves in a fully ionised unbounded prominence medium. In the frequency space, they determined the regions where radiation or thermal conduction are the dominant damping mechanisms, the critical frequencies at which the dominance changes from one mechanism to another, and that different heating mechanisms do not strongly affect the damping. The most important conclusions were that the thermal wave propagates but is strongly damped, and that slow waves are efficiently damped by thermal effects, which does not happen for fast waves. Singh et al. (2006) performed a similar study but considering only Newtonian radiation and, later, Singh et al. (2007) considered again the same problem including Newtonian radiation and turbulent viscosity.
The typical composition of solar prominences is ![]() hydrogen and
hydrogen and
![]() helium. They constitute partially ionised plasmas since
hydrogen lines are observed (Labrosse et al. 2010). The exact
ionisation degree of prominences is unknown and the ratio of
electron density to neutral hydrogen density seems to be in the
interval 0.1-10 (Patsourakos & Vial 2002). From a
theoretical point of view, partial ionisation was considered by
Mercier and Heyvaerts (1977) when they studied the difusion of
neutral atoms by gravity. Gilbert et al. (2002) studied the
diffusion of neutral atoms in a partially ionized prominence plasma,
concluding that the loss timescale is much longer for hydrogen than
for helium. Gilbert et al. (2007) investigated the temporal and
spatial variations in the relative abundance of helium with respect
to hydrogen in a sample of filaments. They found that a majority of
filaments show a deficit of helium in the top part, while in the
bottom part there is an excess. This seems to be due to the shorter
loss timescale of neutral helium compared to that of neutral
hydrogen. The consideration of prominences as partially
ionised plasma is extremely important for the physics of
prominences, and the effects on MHD waves in prominences need to be
taken into account. From the theoretical point of view, and in the
framework of laboratory plasma physics, there is an extensive amount
of literature about wave propagation in a partially ionized
multifluid plasma (Watanabe 1961a,b; Tanenbaum 1961; Tanenbaum &
Mintzer 1962; Woods 1962; Kulsrud & Pearce 1969; Watts &
Hanna 2004). In astrophysical plasmas, the typical frequency of MHD
waves is much lower than the collisional frequencies between
species. In this case, the single fluid approach is usually adopted
and has been applied to wave damping in the solar atmosphere (De Pontieu et al. 2001; Khodachenko et al. 2004; Leake et al. 2005).
In the case of solar prominences, Forteza et al. (2007) derived the
full set of MHD equations for a partially ionized, single-fluid
plasma and applied them to study the time damping of linear,
adiabatic waves in an unbounded prominence medium. This study was
later extended to the non-adiabatic case by including thermal
conduction by neutrals and electrons, radiative losses, and heating
(Forteza et al. 2008). Because of the effect of neutrals, in
particular that of ion-neutral collisions, a generalized Ohm's law
has to be considered, which causes some additional terms to appear
in the resistive magnetic induction equation relative to the fully
ionized case. Among these additional terms, the dominant one in the
linear regime is the so-called ambipolar magnetic diffusion, which
enhances magnetic diffusion across magnetic field lines.
Furthermore, one of the interesting effects produced by the
consideration of partial ionisation and ion-neutral collisions is
that Alfvén waves can be damped, which cannot be obtained by means
of thermal mechanisms, and Singh & Krishnan (2010) studied the time
damping of Alfvén-like waves in a partially ionised plasma
representing a particular model of the solar atmosphere. For
bounded media, Soler et al. (2009c) applied this formalism to the
study of the time damping of fast, Alfvén, and slow waves in a
partially ionised filament thread modeled as a cylinder, and Soler
et al. (2009d) used a cylindrical filament thread, having an
inhomogeneous transition layer between prominence and coronal
material, to study the influence of partial ionisation on the time
damping of fast kink waves caused by resonant absorption in the
inhomogeneous layer.
helium. They constitute partially ionised plasmas since
hydrogen lines are observed (Labrosse et al. 2010). The exact
ionisation degree of prominences is unknown and the ratio of
electron density to neutral hydrogen density seems to be in the
interval 0.1-10 (Patsourakos & Vial 2002). From a
theoretical point of view, partial ionisation was considered by
Mercier and Heyvaerts (1977) when they studied the difusion of
neutral atoms by gravity. Gilbert et al. (2002) studied the
diffusion of neutral atoms in a partially ionized prominence plasma,
concluding that the loss timescale is much longer for hydrogen than
for helium. Gilbert et al. (2007) investigated the temporal and
spatial variations in the relative abundance of helium with respect
to hydrogen in a sample of filaments. They found that a majority of
filaments show a deficit of helium in the top part, while in the
bottom part there is an excess. This seems to be due to the shorter
loss timescale of neutral helium compared to that of neutral
hydrogen. The consideration of prominences as partially
ionised plasma is extremely important for the physics of
prominences, and the effects on MHD waves in prominences need to be
taken into account. From the theoretical point of view, and in the
framework of laboratory plasma physics, there is an extensive amount
of literature about wave propagation in a partially ionized
multifluid plasma (Watanabe 1961a,b; Tanenbaum 1961; Tanenbaum &
Mintzer 1962; Woods 1962; Kulsrud & Pearce 1969; Watts &
Hanna 2004). In astrophysical plasmas, the typical frequency of MHD
waves is much lower than the collisional frequencies between
species. In this case, the single fluid approach is usually adopted
and has been applied to wave damping in the solar atmosphere (De Pontieu et al. 2001; Khodachenko et al. 2004; Leake et al. 2005).
In the case of solar prominences, Forteza et al. (2007) derived the
full set of MHD equations for a partially ionized, single-fluid
plasma and applied them to study the time damping of linear,
adiabatic waves in an unbounded prominence medium. This study was
later extended to the non-adiabatic case by including thermal
conduction by neutrals and electrons, radiative losses, and heating
(Forteza et al. 2008). Because of the effect of neutrals, in
particular that of ion-neutral collisions, a generalized Ohm's law
has to be considered, which causes some additional terms to appear
in the resistive magnetic induction equation relative to the fully
ionized case. Among these additional terms, the dominant one in the
linear regime is the so-called ambipolar magnetic diffusion, which
enhances magnetic diffusion across magnetic field lines.
Furthermore, one of the interesting effects produced by the
consideration of partial ionisation and ion-neutral collisions is
that Alfvén waves can be damped, which cannot be obtained by means
of thermal mechanisms, and Singh & Krishnan (2010) studied the time
damping of Alfvén-like waves in a partially ionised plasma
representing a particular model of the solar atmosphere. For
bounded media, Soler et al. (2009c) applied this formalism to the
study of the time damping of fast, Alfvén, and slow waves in a
partially ionised filament thread modeled as a cylinder, and Soler
et al. (2009d) used a cylindrical filament thread, having an
inhomogeneous transition layer between prominence and coronal
material, to study the influence of partial ionisation on the time
damping of fast kink waves caused by resonant absorption in the
inhomogeneous layer.
To our knowledge, no study of the spatial damping of MHD waves in a partially ionised plasma has been performed. Therefore, since solar prominences are partially ionised plasmas in which material flows and oscillations are present and these oscillations are commonly interpreted in terms of MHD waves, our main aim here is to explore the theoretical and observational effects associated with the spatial damping of non-adiabatic MHD waves in an unbounded and partially ionised plasma, with prominence-like physical conditions, when a background flow is present. The layout of the paper is as follows. In Sect. 2, the equilibrium model and some theoretical considerations are presented; in Sect. 3, the spatial damping of Alfvén waves is studied; in Sect. 4, we consider the spatial damping of magnetoacoustic waves; finally, in Sect. 5, we present our conclusions.
2 Model and methods
2.1 Equilibrium properties
As a background model, we use a homogeneous unbounded medium threaded
by a uniform magnetic field along the x-direction, and with a
field-aligned background flow. The equilibrium magnitudes of the
medium are given by
where B0 and v0 are constants, and the effect of gravity has been ignored. Since we consider a medium with physical properties akin to those of a solar prominence, the density is
2.2 Basic and linearised equations
The derivation of the single-fluid MHD equations for a partially
ionised hydrogen plasma can be found in Forteza et al. (2007). These equations were later modified to include non-adiabatic processes in
the energy equation (Forteza et al. 2008), and the physical meaning
of all the terms and quantities used in the following can be found
in those papers. When a background flow is considered, the single
fluid basic equations for the study of non-adiabatic MHD waves in a
partially ionised plasma originate from Forteza et al. (2007, 2008) and Carbonell et al. (2009). The most important difference with
respect to the non-adiabatic case without a background flow is that
instead of the operator
![]() ,
we have
,
we have
![]() in the MHD
equations (Goedbloed & Poedts 2004).
Before proceeding, some remarks are in order. We consider a partially
ionised hydrogen plasma characterized by a plasma density,
in the MHD
equations (Goedbloed & Poedts 2004).
Before proceeding, some remarks are in order. We consider a partially
ionised hydrogen plasma characterized by a plasma density,
![]() ,
temperature, T0, and number densities of neutrals,
,
temperature, T0, and number densities of neutrals, ![]() ,
ions,
,
ions, ![]() ,
and electrons
,
and electrons ![]() ,
with
,
with
![]() .
Thus, the gas pressure is
.
Thus, the gas pressure is
![]() ,
where
,
where ![]() is Boltzmann's constant. The relative densities of neutrals,
is Boltzmann's constant. The relative densities of neutrals,
![]() ,
and ions,
,
and ions,
![]() ,
are given by
,
are given by
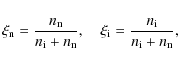
|
(1) |
where we have neglected the contribution of electrons. We can now define a ionization fraction,
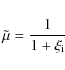
|
(2) |
and the quantity
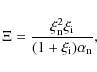
|
(3) |
where
- (1)
- A fully ionised ideal plasma (FIIP), where
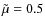 ,
,
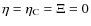 ;
;
- (2)
- A fully ionised resistive plasma (FIRP), where
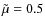 ,
,
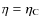 and
and 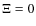 ;
;
- (3)
- A partially ionised plasma (PIP), where
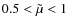 ,
,
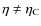 and
and
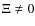 .
.
To obtain the dispersion relation for linear MHD waves, we next
consider small perturbations from equilibrium of the form
and linearise the single fluid basic equations. Since the medium is unbounded, we perform a Fourier analysis in terms of plane waves and assume that perturbations behave as
| (4) |
and with no loss of generality, we choose the z-axis so that the wavevector
After the Fourier analysis, we obtain the linearised scalar equations
2.3 Dispersion relation for Alfvén waves
Equations (8) and (12) are decoupled
from the remainder and from them we can obtain a dispersion relation
for Alfvén waves in a partially ionised plasma with a background
flow, which is,
where
where
which was introduced by Forteza et al. (2008). In the case of a fully ionised ideal plasma without a background flow, Eq. (16) reduces to the well known expression for Alfvén waves.
2.4 Dispersion relation for magnetoacoustic waves
From the remaining linearised equations, assumimg that the
determinant of the algebraic system is zero, we obtain our general
dispersion relation for thermal and magnetoacoustic waves in
presence of a background flow, which is given by
where
where A and H, including the effects of optically thin radiative losses, thermal conduction by electrons and neutrals, and a constant heating per unit volume, are defined in Forteza et al. (2008). When Eq. (19) is expanded, it becomes a seventh degree polynomial in the wavenumber k. By setting the appropriate values to the corresponding quantities, the dispersion relation (19) is consistent with the case of an adiabatic and partially ionised plasma without flow (Forteza et al. 2007), the case of a non-adiabatic and partially ionised plasma without flow (Forteza et al. 2008) and the case of a non-adiabatic, fully ionised plasma with a background flow (Carbonell et al. 2009).
3 Spatial damping of Alfvén waves in a partially ionised plasma
Since we are interested in the spatial damping of MHD waves, we
consider the frequency, ![]() ,
to be real and seek for complex
solutions of the wavenumber k expressed as
,
to be real and seek for complex
solutions of the wavenumber k expressed as
![]() .
The wavelength of the waves is given by
.
The wavelength of the waves is given by
![]() ,
the damping length by
,
the damping length by
![]() ,
the damping length per wavelength is
,
the damping length per wavelength is
![]() ,
and, in general, we consider a
propagation angle
,
and, in general, we consider a
propagation angle
![]()
3.1 Spatial damping of Alfvén waves without background flow
In this case, our governing dispersion relation is given by
Eq. (17) and the wavenumbers are

|
(21) |
representing two Alfvén waves propagating in opposite directions. The real part (
while the imaginary part (
Figure 1 (left panels) shows a plot of the damping length, wavelength, and the ratio of the damping length to wavelength versus the period for Alfvén waves. The plots have been made for four different ionisation fractions and the shaded region corresponds to the interval of observed periods in prominence oscillations. When a period within the shaded region is considered, we observe that the damping length decreases substantially when the amount of neutrals in the plasma increases. Then, when ion-neutral collisions are present the spatial damping of Alfvén waves is enhanced for periods longer than 1 s. We can also observe that for a FIRP the behaviour of the damping length, wavelength and their ratio versus period is linear, except for periods below 10-6 s. However, when a PIP is considered, a deviation from the linear behaviour appears for periods below 1 s. This is because of the joint effect of the terms including frequency and resistivities in the real
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{13024fg1.eps}\includegraphics[width=3.8cm,clip]{13024fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg99.png)
|
Figure 1:
Left panels: damping length, wavelength, and ratio of the damping length to the wavelength versus the period
for Alfvén waves in a FIRP (solid) and in PIP with
|
| Open with DEXTER | |
3.2 Spatial damping of Alfvén waves with background flow
Our dispersion relation is given by Eq. (16), which
once expanded becomes a cubic polynomial in the wavenumber k, such as
With respect to the case without flow, the increase in the degree of the dispersion relation is produced by the joint presence of flow and resistivities. In this case, we obtain three propagating Alfvén waves; therefore, Fig. 1 (right panels) shows the numerical solution of the dispersion relation given by Eq. (24) for the three Alfvén waves in a partially ionised plasma with a background flow. For all the interval of periods considered, a strongly damped third Alfvén wave appears, while in contrast, as in Sect. 3.1, the other two Alfvén waves are very efficiently damped for periods below 1 s. However, within the interval of periods typically observed in prominence oscillations, these waves are only efficiently attenuated when almost neutral plasmas are considered. Furthermore, approximations for the different wavenumbers corresponding to two of the expected Alfvén waves can be calculated to be
whose real part (
| |
![$\displaystyle \frac{ \sqrt{(v_{\rm0} \pm v_{\rm a})^{2}+\sqrt{(v_{\rm0} \pm v_{...
... \pm v_{\rm a})^{4} + \omega^{2} (\eta_{\rm C} +\eta \tan ^{2} \theta)\right]}}$](/articles/aa/full_html/2010/07/aa13024-09/img106.png)
|
||
| (26) |
while its imaginary part (
| |
![$\displaystyle \frac{-\omega^{2} \sec \theta}{\sqrt{2 \left[(v_{\rm0} \pm v_{\rm a})^{4} + \omega^{2}
(\eta_{\rm C} +\eta \tan ^{2} \theta)\right]}}$](/articles/aa/full_html/2010/07/aa13024-09/img108.png)
|
||
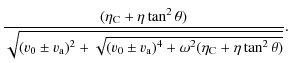
|
(27) |
From the above expressions, if we consider a FIIP we recover the dispersion relation for Alfvén waves with a background flow (Carbonell et al. 2009), and if we remove the flow, the well-known dispersion relation for Alfvén waves is recovered. Since the flow speed is much lower than the Alfvén speed, the effect of the flow on the real and imaginary parts of the wavenumber is very small and, the wavelengths and damping lengths are then similar to those in Sect. 3.1. The third remaining wavenumber of Eq. (24) can be approximated by
corresponding to the third Alfvén wave. All the above analytical approximations display excellent agreement with the numerical results, and the presence of the third Alfvén wave, given by Eq. (28), fully depends on the join presence of a flow and resistivities since, otherwise, the dispersion relation given by Eq. (24) would be quadratic. For an external observer to the flowing plasma, this additional wave could be detectable, although its strong spatial damping would make its detection very difficult. For an observer linked to the flow inertial rest frame, only the two usual Alfvén waves, modified by resistivities, would be detected.
4 Spatial damping of magnetoacoustic waves in a partially ionised plasma
Our general dispersion relation for non-adiabatic magnetoacoustic waves in a background flow is given by Eq. (19). Because of the complexity of this dispersion relation and to help us to understand our results, we divided our study into a sequence of four different cases with dispersion relations of increasing complexity. In the first two cases, the behaviour of adiabatic magnetoacoustic waves in a non-flowing (Sect. 4.1) and flowing plasma (Sect. 4.2) is considered; in the last two cases, the behaviour of non-adiabatic waves in a non-flowing (Sect. 4.3) and flowing plasma (Sect. 4.4) is studied.
4.1 Adiabatic magnetoacoustic waves without background flow
Setting A = H = 0 in Eq. (20),
![]() in
Eq. (5), and substituting into Eq. (19), we
obtain the dispersion relation for adiabatic magnetoacoustic waves
in a PIP without a background flow, which is
in
Eq. (5), and substituting into Eq. (19), we
obtain the dispersion relation for adiabatic magnetoacoustic waves
in a PIP without a background flow, which is
as previously found by Forteza et al. (2007)
4.1.1 Fully ionised resistive plasma
Imposing FIRP conditions from Sect. 2.2, the dispersion relation given by Eq. (30) simplifies to
which once expanded gives a fourth degree polynomial in the wavenumber k
Furthermore, when only longitudinal propagation is allowed (
producing two undamped slow waves with a dispersion relation given by
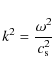
and since for longitudinal propagation, fast waves become Alfvén waves, we obtain two Alfvén waves, damped by resistivity, whose dispersion relation is
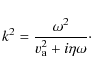
For these Alfvén waves, the real
| |
= | 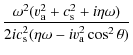
|
|
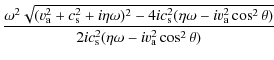
|
(34) |
and
| |
= | 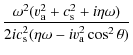
|
|
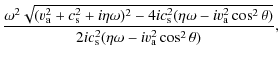
|
(35) |
where
![\begin{figure}
\par\includegraphics[width=4cm,clip]{13024fg3.eps}\includegraphics[width=4cm,clip]{13024fg4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg130.png)
|
Figure 2:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the adiabatic fast ( left panels) and slow ( right panels) waves in a FIIP (solid), a FIRP
(dashed) and a PIP with
|
| Open with DEXTER | |
4.1.2 Partially ionised plasma
The dispersion relation is given by Eq. (30), and considering
only longitudinal propagation we obtain
which could suggest that the consideration of longitudinal propagation in either a FIRP or a PIP leads to the same dispersion relation. However, there is an important difference: while for FIRP both resistivities have the same numerical value, for PIP the numerical value of the Cowling's resistivity is much greater than that of the Spitzer's resistivity. Furthermore, for longitudinal propagation the slow waves are not influenced by Cowling's resistivity. Once expanded, Eq. (36) gives the following fourth degree polynomial in the wavenumber k
After solving this biquadratic dispersion relation, we obtain
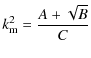
|
(38) | |
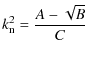
|
(39) |
with
| A | = | ||
| B | = | ||
| C | = |
and the wavenumbers are,
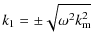
|
(40) | |
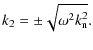
|
(41) |
Figure 2 displays the behaviour of damping length, wavelength, and the ratio of damping length to wavelength versus period for fast and slow waves in a PIP, respectively. The damping length of both slow and fast waves is severely influenced by ion-neutral collisions, exhibiting a strong dependence on period for periods longer than 1 s, while for shorter periods the dependence becomes weaker. This figure also shows that with respect to a FIIP the wavelength of the fast waves is affected slightly by the partial ionisation, deviating from the linear behaviour for periods below 1 s, while the wavelength of slow waves is not affected at all. Within the interval of observed periods in prominence oscillations, when ionisation decreases the ratio of the damping length to the wavelength also decreases for both waves and the spatial damping becomes more efficient. The maximum efficiency of the spatial damping for fast waves is attained for periods below 1 s, while for slow waves the maximum of efficiency is attained at a period that depends on the ionisation fraction. The location of this maximum moves towards long periods when the ionisation of the plasma decreases, but when almost neutral plasmas are considered it is still located at a period slightly longer than 1 s, which is beyond the region of interest. Finally, comparing Figs. 1 and 2 it becomes obvious that the behaviour of Alfvén and fast waves is quite similar.
4.2 Adiabatic magnetoacoustic waves with background flow
Setting A = H = 0 in Eq. (20) and substituting this into Eq. (19), we obtain the dispersion relation for adiabatic magnetoacoustic waves in a PIP with a background flow, which is
4.2.1 Fully ionised resistive plasma
Considering FIRP conditions from Sect. 2.2, the dispersion relation given by Eq. (42) becomes,
The dispersion relation is a fifth degree polynomial of the wavenumber k, and we therefore expect two slow waves and two fast waves that, for the flow speed considered, propagate in opposite directions, plus an additional wave. When only longitudinal propagation is considered, the above dispersion relation becomes
and slow waves are decoupled from fast waves propagating undamped, while fast waves are damped by resistivity. The wavenumbers corresponding to the undamped slow waves are given by
| (45) |
For the fast waves, which become Alfvén waves because of longitudinal propagation, the corresponding dispersion relation, given by the second factor in Eq. (44), is equivalent to Eq. (24) when
![\begin{figure}
\par\includegraphics[width=4cm,clip]{13024fg5.eps}\includegraphics[width=4cm,clip]{13024fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg148.png)
|
Figure 3:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the adiabatic fast ( left panels) and slow ( right panels) waves in a FIIP (solid) and in a PIP with
|
| Open with DEXTER | |
4.2.2 Partially ionised plasma
Our dispersion relation is given by Eq. (42), which is a fifth degree polynomial in k, and when longitudinal propagation is considered we recover the results of Sect. 4.2.1 with slight differences due to the different numerical value of Cowling's resistivity adopted. As shown in Fig. 3, at periods longer than 0.1 s, the damping lengths of both slow and fast waves increase linearly with period. However, for periods below 0.1 s the damping length slowly decreases in the case of fast waves and becomes constant for slow waves. Furthermore, the wavelength of fast waves for periods below 0.1 s increases relatively to the FIRP case, while the wavelengths corresponding to slow waves are only slightly modified. For the ratio of the damping length to the wavelength, the unfolding in wavelength caused by the flow and the change in the damping length due to the partial ionisation produces fast waves that are far more efficiently attenuated than in a FIRP, for any period, but especially at periods below 0.1 s. In contrast the peak of maximum efficiency for slow waves is displaced towards long periods when ionisation decreases, and for almost neutral plasmas would approach the region of periods usually observed in prominence oscillations. The behaviour of the remaining third fast wave is again very similar to that found for the third Alfvén wave discussed in Sect. 3.2.
In the absence of flow, the dispersion relation given by Eq. (43) becomes a fourth degree polynomial in k and the third fast wave disappears. As happens for Alfvén waves with a background flow, this third fast wave is produced by the joint action of flow and resistivity, since when a FIIP with a background flow is considered, the dispersion relation also becomes a fourth degree polynomial in k and the third fast wave is absent.
4.3 Non-adiabatic magnetoacoustic waves in a prominence plasma without background flow
Setting
![]() in Eq. (5) and substituting this
into Eq. (19), we obtain the dispersion relation for
non-adiabatic magnetoacoustic waves in a PIP without a background
flow, which is
in Eq. (5) and substituting this
into Eq. (19), we obtain the dispersion relation for
non-adiabatic magnetoacoustic waves in a PIP without a background
flow, which is
4.3.1 Fully ionised resistive plasma
After imposing the conditions corresponding to a FIRP, the following dispersion relation, a sixth degree polynomial in the
wavenumber k, is obtained
which describes coupled fast, slow, and thermal waves. When only longitudinal propagation is allowed, the above dispersion relation becomes
As in Sect. 3.1, we then obtain two decoupled Alfvén waves, damped by resistivity, whose dispersion relation is given by
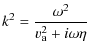
|
(49) |
and another dispersion relation
which is a fourth degree polynomial in k describing coupled propagating thermal and slow waves, damped only by thermal effects. The dispersion relation given by Eq. (47) was solved numerically, and Figs. 4 and 5 present the damping length, wavelength, and ratio of the damping length to the wavelength versus period for the fast, slow, and thermal waves. Starting with Fig. 4, we only considered an interval of periods between 10-2 and 107 s, since for periods shorter than 10-2 s, much shorter than those of interest, the curves become very entangled. When an FIIP is considered, the spatial damping of the fast wave is governed by radiative losses and thermal conduction (Carbonell et al. 2006) in the interval of periods from 10-2 to 107 s. However, in a FIRP we observe a slight change in the damping length of fast waves around a period of 1 s. This change tells us that the dominance of thermal conduction appears slightly earlier in time than for the ideal case. For the ratio of the damping length to the wavelength, we observe that the efficiency of the damping for fast waves is higher than for a FIIP, for periods below 1 s. For slow waves, no differences appear between the behaviours of FIIP and FIRP. The behaviour of thermal waves (Fig. 5) is exactly the same in FIIP and FIRP.
4.3.2 Partially ionised plasma
In this case, our dispersion relation is given by Eq. (46)
and when only longitudinal propagation is allowed the expression is
similar to that of Sect. 4.3.1, although the numerical value of the
Cowling's resistivity is different and the results for fast waves
would differ. When oblique propagation is considered,
Eq. (46) is solved numerically and a strong distortion of
the damping length and wavelength curves corresponding to fast waves
(Fig. 4, left panels) appears. The changes affect the
radiative plateau, between periods 103 and 10-2 s, and
partial ionisation decreases the damping length of fast waves in
this region. For slow waves (Fig. 4, right panels), a
similar behaviour is found in the same regions, although the
distortion is not so important since a very short radiative plateau,
between 102 and 103 s, remains, together with a region,
between 1 and 102 s, where thermal conduction is dominant.
Compared to a FIRP, the ratio
![]() for fast waves
decreases substantially for periods below 103 s, although for
the periods of interest in prominences, this ratio remains very
large. For slow waves, partial ionisation causes the ratio
for fast waves
decreases substantially for periods below 103 s, although for
the periods of interest in prominences, this ratio remains very
large. For slow waves, partial ionisation causes the ratio
![]() to reach a maximum efficiency of
to reach a maximum efficiency of ![]() 1 for
periods similar to those involved in prominence oscillations, and
this maximum is displaced towards longer periods when ionisation is
decreased. The changes in the wavelengths of slow and fast waves
are similar to those shown in the adiabatic case (Sect. 4.1.2).
In the case of thermal waves (Fig. 5), partial ionisation
increases both the damping length and wavelength of these waves,
although the behaviour of the ratio
1 for
periods similar to those involved in prominence oscillations, and
this maximum is displaced towards longer periods when ionisation is
decreased. The changes in the wavelengths of slow and fast waves
are similar to those shown in the adiabatic case (Sect. 4.1.2).
In the case of thermal waves (Fig. 5), partial ionisation
increases both the damping length and wavelength of these waves,
although the behaviour of the ratio
![]() is
similar to previous cases. Since a thermal wave is always strongly
damped, which makes its detection very difficult, in the following
we avoid additional comments on it.
is
similar to previous cases. Since a thermal wave is always strongly
damped, which makes its detection very difficult, in the following
we avoid additional comments on it.
To understand the effects of radiation and thermal conduction by neutrals and electrons, in Fig. 6 we represent, for fast and slow waves, the same quantities but with optically thin radiation and heating removed, i.e., only thermal conduction is at work, and we can observe that the most efficient damping for both waves occurs for partially ionised plasmas, which suggests that the inclusion of the isotropic thermal conduction due to neutrals plays a very important role for all the periods considered. However, we must take into account that when the ionisation fraction decreases, radiation also decreases and that, because of neutrals, thermal conduction is favoured, which makes it difficult to establish meaningful comparisons between plasmas with different degrees of ionisation.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{13024fg7.eps}\includegraphics[width=4cm,clip]{13024fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg156.png)
|
Figure 4:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast ( left panels), slow ( right panels) waves in a FIIP (solid), a FIRP
(dashed), and a PIP with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13024fg9.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg157.png)
|
Figure 5: Damping length,
wavelength, and ratio of the damping length to the wavelength versus
period for the non-adiabatic thermal wave in a FIIP (solid), a FIRP
(dashed), and a PIP with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{13024fg10.eps}\includegraphics[width=4.3cm,clip]{13024fg11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg158.png)
|
Figure 6:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast ( left panels), slow ( right panels) waves, without radiation, in a FIIP (dashed), a FIRP (dotted), and a PIP with
|
| Open with DEXTER | |
In Fig. 7, we plot the behaviour of fast and slow waves, when thermal conduction has been removed, i.e., only radiation and heating remain. When thermal conduction by electrons and neutrals is removed, the behaviour of fast waves in a FIIP and in FIRP is similar and, within the interval of periods of interest, the behaviour of the different quantities corresponding to the different types of plasma is the same. However, when periods below 100 s are considered, FIIP and FIRP are strongly affected by the lack of thermal conduction. For slow waves, a similar behaviour appears and the most important conclusion after comparing Figs. 6 and 7, within the interval of periods of interest, is that very efficient damping is caused by optically thin radiation.
On the other hand, when non-adiabatic magnetoacoustic waves are
considered, the importance of radiation and thermal conduction can
also be quantified in terms of two dimensionless parameters (De Moortel & Hood 2004), namely, the thermal ratio, which modified
for the case of partial ionisation becomes
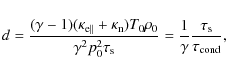
|
(51) |
which is
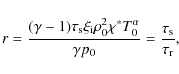
|
(52) |
which is the ratio of the sound travel time to the radiation timescale
where
4.4 Non-adiabatic magnetoacoustic waves in a prominence plasma with background flow
4.4.1 Fully ionised ideal plasma
Setting in Eq. (19) conditions corresponding to FIIP, we obtain
which is a sixth degree polynomial in the wavenumber k. When only longitudinal propagation is allowed, we obtain two undamped Alfvén waves given by
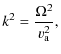
|
(55) |
whose solutions for the wavenumbers are
| (56) |
as in Carbonell et al. (2009), while the dispersion relation
| (57) |
describes coupled slow and thermal waves modified by the flow and damped by thermal effects. In the case of oblique propagation, Eq. (54) is solved numerically and the behaviour of fast and slow waves is shown in Fig. 8. When a flow is present the unfolding of wavelengths and damping lengths appears. Since the considered flow speed is much lower than Alfvén speed, the separation of the curves corresponding to the fast wave is very small, while, since flow speed and sound speed are comparable, the curves corresponding to slow waves separate substantially. This effect strongly affects the behaviour of the damping length versus wavelength for slow waves, since one of them has a very efficient spatial damping for periods observed in prominence oscillations. In the case considered in this section, the damping of fast and slow waves is strictly due to thermal effects.
4.4.2 Fully ionised resistive plasma
In this case, considering FIRP conditions, the dispersion relation becomes
which is a seventh degree polynomial in the wavenumber k. Considering only longitudinal propagation, again we find coupled slow and thermal waves modified by the flow and damped by thermal effects, and three Alfvén waves given by the dispersion relation (24), with
4.4.3 Partially ionised plasma
The dispersion relation is now given by Eq. (19) and
Fig. 9 displays the behaviour of the damping length,
wavelength, and ratio of damping length to wavelength for fast and
slow waves. The most interesting results are those related to the
ratio
![]() .
For fast waves, this ratio decreases
with the period becoming small for periods below 10-2 s, while
for one of the slow waves, the ratio becomes very small for periods typically observed in prominence oscillations.
When ionisation
is decreased, slight changes in the above described behaviour occur,
the most important being the displacement towards longer periods of
the peak for the most efficient damping corresponding to slow waves.
As pointed out before, a third fast wave is, again, produced by the
joint action of flow and resistivity. In the absence of flow or
resistivity, the dispersion relation would become a sixth order
polynomial of the wavenumber and this wave would be absent.
.
For fast waves, this ratio decreases
with the period becoming small for periods below 10-2 s, while
for one of the slow waves, the ratio becomes very small for periods typically observed in prominence oscillations.
When ionisation
is decreased, slight changes in the above described behaviour occur,
the most important being the displacement towards longer periods of
the peak for the most efficient damping corresponding to slow waves.
As pointed out before, a third fast wave is, again, produced by the
joint action of flow and resistivity. In the absence of flow or
resistivity, the dispersion relation would become a sixth order
polynomial of the wavenumber and this wave would be absent.
5 Conclusions
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{13024fg12.eps}\includegraphics[width=4cm,clip]{13024fg13.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg176.png)
|
Figure 7:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast ( left panels), slow ( right panels) waves in a PIP (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{13024fg14.eps}\includegraphics[width=4cm,clip]{13024fg15.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg177.png)
|
Figure 8: Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast (left panels), slow (right panels) waves in a FIIP (solid), and in a FIRP (dashed). The flow speed is 10 km s-1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.05cm,clip]{13024fg16.eps}\includegraphics[width=4cm,clip]{13024fg17.eps} \end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg178.png)
|
Figure 9:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast (left panels), slow (right panels) waves in a PIP with
|
| Open with DEXTER | |
Quiescent solar prominences and filaments are partially ionised plasmas and some of their main characteristics are material flows and oscillations. While the time damping of these oscillations has been thoroughly studied, their spatial damping has not been in detail. Interpreting the observed oscillations in terms of MHD waves, we have analysed the spatial damping of Alfvén and non-adiabatic magnetoacoustic waves in a flowing partially ionised prominence plasma. Several different cases, with dispersion relations of increasing complexity, have been considered, and we summarize our main conclusions below.
As is well known, Alfvén waves are difficult to damp because they are insensitive to non-adiabatic effects. However, when Alfvén waves in a partially ionised plasma are considered, they can be spatially damped and analytical expressions describing their spatial damping can be obtained. When the ionisation decreases, the damping length of these waves also decreases and the efficiency of their spatial damping in the range of periods of interest is improved, although the most efficient damping is attained for periods below 1 s. A new feature is that when a flow is present a new third Alfvén wave, strongly attenuated, appears. This wave depends on the joint action of flow and resistivities, since in the absence of a flow, or for a FIIP, the dispersion relation becomes quadratic producing the two well-known Alfvén waves. Furthermore, this third wave could only be detected by an observer not moving with the flow.
When adiabatic magnetoacoustic waves are considered and the effect of partial ionisation is taken into account, some new features appear. When a FIRP is considered and only longitudinal propagation is allowed, slow waves are decoupled from fast waves, propagating undamped, while fast waves propagate with a modified Alfvén speed and are damped by resistivity. When a PIP plasma is studied and only longitudinal propagation is allowed, the same occurs but then the numerical value of Cowling's resistivity is greater than before, enhancing the damping. The behaviour of slow waves is then only influenced by partial ionisation when oblique propagation is allowed. Furthermore, when a PIP is considered the behaviour of fast waves is very similar to that of Alfvén waves and the damping becomes very efficient for periods below 1 s, while for slow waves the peak denoting the most efficient damping moves towards higher periods as the plasma ionisation decreases. When a flow is considered in the adiabatic case, the main difference is the unfolding of the damping-length, wavelength and damping-length to wavelength curves, and the apparition of a third fast wave, strongly damped, caused by the join presence of flow and resistivities.
For non-adiabatic magnetoacoustic waves, when partial ionisation
is
present the behaviour of fast, slow, and thermal waves is strongly
modified. Comparing with non-adiabatic fast waves in a FIIP, which
are damped by electronic thermal conduction and radiation, the
damping length of a fast wave in a PIP is strongly diminished by
neutrals thermal conduction for periods between 0.01 and 100 s,
and, at the same time, the radiative plateau present in FIIP and
FIRP disappears. The behaviour of slow waves is not so strongly
modified as for fast waves, although thermal conduction by neutrals
also diminishes the damping length for periods below 10 s, and a
short radiative plateau remains for periods between 10 and
1000 s. Finally, thermal waves are only slightly modified,
although the
effect of partial ionisation is to increase the damping length of
these waves, the converse of what happens for the other waves. When
a background flow is included, a new third fast wave appears, which
is again, due to the joint action of flow and resistivities. As we
already know, wavelengths and damping lengths are modified by the
flow, and since, for slow waves, sound speed and observed flow
speeds are comparable, the change in wavelength and
damping length are important leading to an improvement in the
efficiency of the damping. The maximum of efficiency is also
displaced towards long periods when the ionisation decreases, and
for ionisation fractions from 0.8 to 0.95, it is clearly
located
within the range of periods typically observed in prominence
oscillations with a value of
![]() smaller than 1. This means that for a typical period of 103 s, the
damping length would be between 102 and 103 km, the
wavelength around 103 km and, as a consequence, in a distance
smaller than a wavelength the slow wave would be strongly
attenuated. On the other hand, during our calculations, we have
found that the different heating mechanisms usually considered
(Carbonell et al. 2004) do not affect the results.
smaller than 1. This means that for a typical period of 103 s, the
damping length would be between 102 and 103 km, the
wavelength around 103 km and, as a consequence, in a distance
smaller than a wavelength the slow wave would be strongly
attenuated. On the other hand, during our calculations, we have
found that the different heating mechanisms usually considered
(Carbonell et al. 2004) do not affect the results.
In conclusion, the joint effect of non-adiabaticity, flows, and partial ionisation allows slow waves to damp in an efficient way within the interval of periods typically observed in prominences. Thermal waves are attenuated very efficiently within the interval of interest but their observational detection is probably very difficult, and fast waves are very unefficiently attenuated within the considered interval. Furthermore, since Alfvén and fast waves display similar behaviours, the observational differentiation between them should be based on the detection of their associated perturbations. We also note that the new fast and Alfvén waves are only detectable in a reference system external to the flow, although their short damping length should make their detection very difficult. As we have seen, even in the most simple case of an unbounded medium threaded by a uniform magnetic field, the inclusion of non-adiabatic effects, partial ionisation, and flows complicates the study of the spatial damping of prominence oscillations because of the apparition of new waves and the difficulty in distinguishing between the different effects. From observations, this implies that because of the entanglement of the different effects, it is extremely difficult to properly interpret the observed oscillations in terms of MHD waves.
The present study represents a first step in investigating the behaviour of the spatial damping of MHD waves in partially ionised prominence plasmas. Forthcoming studies must focus on investigating the behaviour of this type of damping in threads, which seem to be the basic constituents of quiescent prominences.
AcknowledgementsThe authors acknowledge the financial support provided by MICINN and FEDER funds under grant AYA2006-07637. P. Forteza acknowledges a FPU fellowship from MECyT. Also, the Conselleria d'Economia, Hisenda i Innovació of the Government of the Balearic Islands is gratefully acknowledged for the funding provided under grant PCTIB2005GC3-03.
References
- Arregui, A., Terradas, J., Oliver, R., et al. 2008, ApJ, 682, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, D., Erdélyi, R., Oliver, R., et al. 2007, Sol. Phys., 246, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. E., Shine, R. A., Slater, G. L., et al. 2008, ApJ, 676, L89 [Google Scholar]
- Braginskii, S. I. 1965, Rev. Plasma Phys., 1, 205 [NASA ADS] [Google Scholar]
- Carbonell, M., Oliver, R., & Ballester, J. L. 2004, A&A, 415, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carbonell, M., Terradas, J., Oliver, R., et al. 2006, A&A, 460, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carbonell, M., Oliver, R., & Ballester, J. L. 2009, New A., 14, 277 [Google Scholar]
- De Moortel, I., Hood, A. W., Ireland, J., et al. 2002, Sol. Phys., 209, 89 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Hood, A. W. 2003, A&A, 408, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Hood, A. W. 2004, A&A, 415, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pontieu, B., Martens, P. C. H., & Hudson, H. S. 2001, ApJ, 558, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Forteza, P., Oliver, R., Ballester, J. L., et al. 2007, A&A, 461, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forteza, P., Oliver, R., & Ballester, J. L. 2008, A&A, 492, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilbert, H. R., Hansteen, V. H., & Holzer, T. E. 2002, A&A, 577, 464 [Google Scholar]
- Gilbert, H., Kilper, G., & Alexander, D. 2007, ApJ, 671, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Goedbloed, H., & Poedts, S. 2004, Principles of Magnetohydrodynamics (Cambridge University Press) [Google Scholar]
- Kulsrud, R., & Pearce, W. P. 1969, ApJ, 156, 445 [Google Scholar]
- Khodachenko, M. L., Arber, T. D., Rucker, H. O., et al. 2004, A&A, 422, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J. V., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Leake, J. E., Arber, T. D., & Khodachenko, M. L. 2005, A&A, 442, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, Y., Engvold, O., & Wiik, J. E. 2003, Sol. Phys., 216, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L. H. M., et al. 2007, Sol. Phys., 246, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D., Karpen, J., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev. [Google Scholar]
- Mercier, C., & Heyvaerts, J. 1977, A&A, 61, 685 [NASA ADS] [Google Scholar]
- Okamoto, T.J, Tsuneta, S., Berger, TE, et al. 2007, Sciences, 318, 1577 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Oliver, R. 2009, Space Sci. Rev., in press [Google Scholar]
- Oliver, R., & Ballester, J. L. 2002, Sol. Phys., 206, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Patsourakos, S., & Vial, J.-C. 2002, Sol. Phys., 208, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, K. A. P. 2006, JApA, 27, 321 [NASA ADS] [Google Scholar]
- Singh, K. A. P., Dwivedi, B. N., & Hasan, S. S. 2007, A&A, 473, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singh, K. A. P., & Krishan, V. 2010, New A., 15, 119 [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2008, ApJ, 684, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2009a, ApJ, 693, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2009b, ApJ, 695, L166 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2009c, ApJ, 699, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2009d, ApJ, 707, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Tanenbaum, B. S. 1961, Phys. Fluids, 4, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Tanenbaum, B. S., & Mintzer, D. 1962, Phys. Fluids, 5, 1226 [Google Scholar]
- Terradas, J., Molowny-Horas, R., Wiehr, E., et al. 2002, A&A, 393, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., Carbonell, M., Oliver, R., et al. 2005, A&A, 434, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watanabe, T. 1961a, Can. J. Phys., 39, 1044 [NASA ADS] [Google Scholar]
- Watanabe, T. 1961b, Can. J. Phys., 39, 1197 [NASA ADS] [Google Scholar]
- Watts, C., & Hanna, J. 2004, Phys. Plasmas, 11, 1358 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, L. C. 1962, J. Fluid Mechanics, 13, 570 [Google Scholar]
- Zirker, J. B., Engvold, O., & Martin, S. F. 1998, Nature, 434, 741 [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{13024fg1.eps}\includegraphics[width=3.8cm,clip]{13024fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg99.png)
|
Figure 1:
Left panels: damping length, wavelength, and ratio of the damping length to the wavelength versus the period
for Alfvén waves in a FIRP (solid) and in PIP with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{13024fg3.eps}\includegraphics[width=4cm,clip]{13024fg4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg130.png)
|
Figure 2:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the adiabatic fast ( left panels) and slow ( right panels) waves in a FIIP (solid), a FIRP
(dashed) and a PIP with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{13024fg5.eps}\includegraphics[width=4cm,clip]{13024fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg148.png)
|
Figure 3:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the adiabatic fast ( left panels) and slow ( right panels) waves in a FIIP (solid) and in a PIP with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{13024fg7.eps}\includegraphics[width=4cm,clip]{13024fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg156.png)
|
Figure 4:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast ( left panels), slow ( right panels) waves in a FIIP (solid), a FIRP
(dashed), and a PIP with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13024fg9.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg157.png)
|
Figure 5: Damping length,
wavelength, and ratio of the damping length to the wavelength versus
period for the non-adiabatic thermal wave in a FIIP (solid), a FIRP
(dashed), and a PIP with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{13024fg10.eps}\includegraphics[width=4.3cm,clip]{13024fg11.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg158.png)
|
Figure 6:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast ( left panels), slow ( right panels) waves, without radiation, in a FIIP (dashed), a FIRP (dotted), and a PIP with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{13024fg12.eps}\includegraphics[width=4cm,clip]{13024fg13.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg176.png)
|
Figure 7:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast ( left panels), slow ( right panels) waves in a PIP (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{13024fg14.eps}\includegraphics[width=4cm,clip]{13024fg15.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg177.png)
|
Figure 8: Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast (left panels), slow (right panels) waves in a FIIP (solid), and in a FIRP (dashed). The flow speed is 10 km s-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.05cm,clip]{13024fg16.eps}\includegraphics[width=4cm,clip]{13024fg17.eps} \end{figure}](/articles/aa/full_html/2010/07/aa13024-09/Timg178.png)
|
Figure 9:
Damping length, wavelength, and ratio of the damping length to the wavelength versus period for the non-adiabatic fast (left panels), slow (right panels) waves in a PIP with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



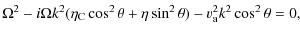
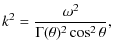
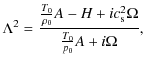
![$\displaystyle k_{\rm r} = \omega \sec \theta \frac{
\sqrt{v_{\rm a}^{2}+\sqrt{v...
...left[v_{\rm a}^{4} + \omega^{2} (\eta_{\rm C} +\eta \tan
^{2} \theta)\right]}},$](/articles/aa/full_html/2010/07/aa13024-09/img88.png)
![$\displaystyle \frac{-\omega^{2} \sec \theta}{\sqrt{2 \left[v_{\rm a}^{4} + \omega^{2} (\eta_{\rm C} +\eta \tan
^{2} \theta)\right]}}$](/articles/aa/full_html/2010/07/aa13024-09/img91.png)