The triple system AO Monocerotis

M. Wolf; H. Kučáková; T. Hynek; L. Šmelcer

doi:10.1051/0004-6361/201014181

Free Access

Issue		A&A Volume 514, May 2010


Article Number		A75
Number of page(s)		5
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/201014181
Published online		26 May 2010

A&A 514, A75 (2010)

The triple system AO Monocerotis
(Research Note)

M. Wolf¹ - H. Kucáková² - T. Hynek² - L. Smelcer³

1 - Astronomical Institute, Faculty of Mathematics and Physics, Charles University Prague, 180 00 Praha 8, V Holesovickách 2, Czech Republic
2 - Johann Palisa Observatory and Planetarium, Technical University Ostrava, 17. listopadu 15, 708 33 Ostrava, Czech Republic
3 - Observatory Valasské Mezirící, Vsetínská 78, 757 01 Valasské Mezirící, Czech Republic

Received 2 February 2010 / Accepted 26 February 2010

Abstract
The variable star AO Mon is a relatively bright but seldom investigated early-type eccentric eclipsing binary. Thirty new eclipses were measured as a part of our long-term observational project or derived from previous measurements. Based on a new solution of the current O-C diagram, we found for the first time a rapid apsidal advance superimposed with a light-time effect caused by a third unseen body in the system. Their short periods are 33.8 years and 3.6 years for the apsidal motion and the third-body circular orbit, respectively. The observed internal structure constant was derived to be $\log k_{\rm 2,~obs} = -2.23$ , which is close to the theoretically expected value. The relativistic as well as the third-body effects on the apsidal advance are negligible, as they are only about 3% of the total apsidal motion rate.

Key words: binaries: eclipsing - binaries: close - stars: individual: AO Mon - stars: fundamental parameters

1 Introduction

The detached and double-lined eclipsing binary AO Monocerotis (HD 53883, BD $-4^\circ1822$ , HIP 34299, FL 740, Sp. B3+B5, $V_{\max} = 9.6$ mag) is a seldom studied early-type binary with a slightly eccentric orbit and a short orbital period of about 1.88 days. It was discovered to be a variable star by Hoffmeister (1931). The first photographic light curve was presented by Lause (1933) with an incorrect period of 0.9423 days. The first spectroscopic analysis was presented by Struve (1945), who obtained the radial velocity curve and spectroscopic elements. The next photographic light curve was obtained by Gaposchkin (1953). The photoelectric photometry and photometric elements was published by Kandpal (1976), who also found that the orbit of AO Mon is slightly eccentric ( $e \simeq 0.05$ ) and derived the absolute dimensions of components. Later, Giuricin et al. (1980) recalculated the photometric elements by means of the Wood's WINK code. To our knowledge, no modern period, photometric or spectroscopic study of this early-type eclipsing binary exists so far.

2 Observations

Our photoelectric and CCD photometry of AO Mon was obtained at four observatories:

: $\bullet$ Ondrejov Observatory, Czech Republic: the 0.65-m (f/3.6) reflecting telescope with the CCD camera SBIG ST-8 or Apogee AP7 and Johnson's VR filters,
: $\bullet$ South African Astronomical Observatory (hereafter SAAO), Sutherland, South Africa: the 0.50-m Cassegrain reflector (f/18) equipped with modular photometer utilizing a Hamamatsu EA1516 photomultiplier and Johnson UBV filters; during two weeks in April 2004.
: $\bullet$ Johann Palisa Observatory and Planetarium Ostrava, Czech Republic: 0.2-m or 0.3-m telescopes with the CCD camera SBIG ST-8XME and R filter,
: $\bullet$ Observatory Valasské Mezirící, Czech Republic: the 0.3-m Celestron Ultima telescope with the CCD camera SBIG ST-7 and R filter.

The new CCD observations were reduced in a standard way. The A PHOT, synthetic aperture photometry software developed by M. Velen and P. Pravec at the Ondrejov observatory and C-M UNIPACK were routinely used for reduction of these CCD images. The data were dark-subtracted and flat-fielded and the heliocentric correction was applied. The new times of primary and secondary minima and their errors were determined by the well-known Kwee-van Woerden (1956) algorithm.

Photoelectric measurements at SAAO were done with the Johnson photometric system UBV filters with a 10 s integration time. The nearby star HD 296318 (spectral type A2, V = 10.5 mag) - used also in our CCD photometry - served as a primary comparison star. All observations were carefully reduced to the Cousins E-region standard system (Menzies et al. 1989) and corrected for differential extinction with the reduction program HEC 22 rel. 16.1. The standard errors of these measurements were about 0.009, 0.007 and 0.005 magnitude in U, B and V filters respectively.

The original photometric data of Kandpal (1976) were recalculated and three new times of minima in B and V filters were obtained. Using the Hipparcos photometry (ESA 1997) and the ASAS-3 photometric database (Pojmanski 2002) we were able to derive numerous additional times of minimum light with lower accuracy. The light-curve profile fitting method was used. All these new times are collected in Table A.1, where the epochs were calculated according to the linear light elements given in the GCVS catalogue:

$\begin{displaymath}\rm Pri.~ Min. = HJD ~2~440~588.3272 + 1\hbox{$.\!\!^{\rm d}$ }884660 \cdot {\it E}. \end{displaymath}$

3 Apsidal motion and light-time effect

$\begin{figure} \par\includegraphics[width=8cm,clip]{14181fg1.eps} \end{figure}$	Figure 1: Complete O-C graph for AO Mon. The individual primary and secondary minima are denoted by circles and triangles, respectively. Larger symbols correspond to the photoelectric or CCD measurements, which were used in our calculations. Visual timings between epochs 0 and 1000 with large negative deviations were omitted.
Open with DEXTER

As was mentioned in the previous section, AO Mon has a small but significant orbital eccentricity. Both the classical theory of tides and the General Relativity predict that a close system like this should show a certain degree of periastron advance.

Analysing the preliminary O-C diagram in Fig. 1, we tried to solve the apsidal motion and the light-time effect (hereafter LITE) simultaneously. In this case the deviation of the observed values (O-C) $_{\rm obs}$ from the linear ephemeris is given by a superposition of the apsidal advance of the eccentric orbit and by the LITE caused by a third star:

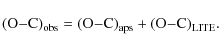
$\begin{displaymath}\rm (O{-}C)_{obs} = (O{-}C)_{aps} + (O{-}C)_{LITE}. \end{displaymath}$

For the apsidal motion the method described by Giménez & García-Pelayo (1983), which is a weighted least-squares iterative procedure, including terms in the eccentricity up to the fifth order, was routinely used. The periastron position $\omega$ at epoch E is defined by the linear equation

$\begin{displaymath}\omega = \omega_0 + \dot{\omega}\ E , \end{displaymath}$

where $\dot{\omega}$ is the rate of the periastron advance, and the position of periastron for the zero epoch T₀ is denoted as $\omega_0$ . The relation between the sidereal and the anomalistic period, $P_{\rm s}$ and $P_{\rm a}$ , is given by

$\begin{displaymath}P_{\rm s} = P_{\rm a} ~(1 - \dot{\omega}/360^\circ), \end{displaymath}$

and the period of apsidal motion by

$\begin{displaymath}U = 360^\circ P_{\rm s}/\dot{\omega}. \end{displaymath}$

The theory of the third body motion and the LITE analysis in eclipsing binaries was reviewed several times in the literature, see e.g. Mayer (1990). The light travel time is given by

$\begin{displaymath}{\rm O{-}C} = \frac{A}{\sqrt{1-e_3^2 \cos^2 \omega_3}} \bigg... ...+e_3 \cos v} \sin(v + \omega_3) + e_3 \sin \omega_3 \biggl] , \end{displaymath}$

where e₃ is the eccentricity of the third-body orbit, $\omega_3$ the longitude of periastron and v the mean anomaly. The observed semi-amplitude A of the light-time curve (in days) is

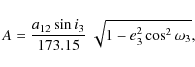
$\begin{displaymath}A = \frac{a_{12}\sin i_3} {173.15} ~ \sqrt{1-e_3^2 \cos^2 \omega_3}, \end{displaymath}$

where a₁₂ is semi-major axis of the relative orbit of the eclipsing pair around the common centre of mass (in AU), i₃ is the inclination of the third-body orbit, e₃ is the eccentricity and $\omega_3$ the longitude of periastron of the third-body orbit. There are ten independent variables to be determined in this procedure:

$\begin{eqnarray*}\hspace*{-3mm}&&(T_0, P_{\rm s}, e, \dot{\omega}, \omega_0), ~\... ...ace*{-3mm}&& (A,T_3, P_3, e_3, \omega_3) ~\textrm{for the LITE}. \end{eqnarray*}$

The orbital eccentricity of the eclipsing pair was taken as a free parameter in our calculations. The resulting values of e have smaller intrinsic errors compared to those determined independently from the light curve analysis. This procedure gives us a better result for this important element.

Many eclipse timings for AO Mon have been reported in the literature using a variety of techniques, photoelectric or CCD measurements have greater precision and were used in this study. Besides the minima given in Table A.1, we have also added the minima obtained by Zejda (2004), Nakajima (2006, 2007), Dvorak (2006), and Hübscher et al. (2006, 2009, 2010).

Table 1: Apsidal motion and LITE elements of AO Mon.

A total of 42 reliable times of minimum light were used in our dataset, with 17 secondary eclipses among them. The old visual timings of Lause (1933, 1936, 1949) and those of BBSAG observers were not used due to large scatter. The orbital inclination was assumed to be $i = 86\hbox{$.\!\!^\circ$ }2$ as a mean value of the B and V light-curve solution of the last photometric analysis of Giuricin et al. (1980). We minimized a quality function, which describes the difference between the observed and calculated times of minima:

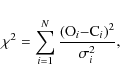
$\begin{displaymath}\chi^2 = \sum_{i=1}^N \frac{({\rm O}_i{-}{\rm C}_i)^2}{\sigma^2_i}, \end{displaymath}$

where $\sigma_i$ is the corresponding error of a minimum estimation. The computed apsidal motion and LITE parameters and their internal errors of the least-squares fit (in brackets) are given in Table 1, the O-C diagram illustrating the apsidal advance is shown in Fig. 2. The detailed O-C diagram in Fig. 3 is the resulting combination of the apsidal motion and LITE with the very short orbital period of the third body. The value of $\chi^2 \simeq 150$ is substantially higher than the number of degrees of freedom N = 42-10 = 32.

Assuming a coplanar orbit ( $i_3 = 90^{\circ}$ ) and the total mass of the eclipsing pair M₁ + M₂ = 10.7 $M_{\odot}$ , we can obtain a lower limit for the mass of the third component $M_{\rm 3,~ min}$ . This value, as well as the mass function f(m), and the amplitude of the systemic radial velocity K are also given in Table 1. The third component may be a main-sequence star of a spectral type B9 with a bolometric magnitude of about +0.4 mag (Harmanec 1988) producing the third light of $L_3 \simeq 3\%$ .

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{14181fg2.eps}\vspace*{2mm} \end{figure}$	Figure 2: Rapid apsidal motion in AO Mon with period of about 34 years. The continuous and dashed curves represent predictions for the primary and secondary eclipses, respectively. For clarity, the LITE terms were subtracted and error bars of individual times are indicated.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{14181fg3.eps} \end{figure}$	Figure 3: O-C diagram of AO Mon in detail since the Hipparcos mission. The continuous and dashed curves represent the combination of the apsidal motion and LITE with the period of 3.6 years. The dash-dotted curves illustrate the apsidal motion (see Fig. 2). Symbols are as in Fig. 1.
Open with DEXTER

4 Internal structure constant

Observations of eccentric binary systems allow us to determine the internal structure constant (ISC), k₂, which is related to the variation in density within the star and is an important parameter of stellar evolution models. It is best studied in binary systems with eccentric orbits that show apsidal motion. The observed average value of $\overline k_{2,\rm obs}$ is given by

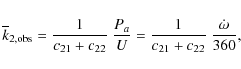
$\begin{displaymath}\overline k_{\rm 2, obs} = \frac{1}{c_{21} + c_{22}} ~ \frac{P_a}{U} = \frac{1}{c_{21} + c_{22}} ~ \frac{\dot{\omega}}{360} , \end{displaymath}$

where c₂₁ and c₂₂ are functions of the orbital eccentricity, fractional radii, the masses of the components, and the ratio between rotational velocity of the stars and Keplerian velocity (Kopal 1978). The rotation of the stars was assumed to be synchronized with the maximum angular orbital velocity achieved at periastron.

Table 2: Astrophysical parameters of AO Mon.

Taking the value of the eccentricity and the masses of the components into account, a relativistic correction $\dot{\omega}_{\rm rel}$ (Giménez 1985) is subtracted

$\begin{displaymath}\dot{\omega}_{\rm rel} = \; 5.45 \times 10^{-4} \: \frac{1}{1-e^2} \:\Biggl( \frac{M_1 + M_2}{P} \Biggr) ^{2/3}, \end{displaymath}$

where M_i denotes the individual masses of the components in solar units and P is the orbital period in days. The values of $\dot{\omega}_{\rm rel}$ and the resulting mean internal structure constants $\overline k_{\rm 2,obs}$ are given in Table 2. The theoretical value $k_{\rm 2,theo}$ was taken as a mean value from the tables of the Granada stellar models (Claret 2004) according to the adopted masses ( $\log m = 0.7{-}0.8$ ) and chemical composition (X,Z) = (0.70, 0.02).

The acceleration of the rate of the apsidal motion $\dot{\omega}_3$ could also be caused by the third body in the system (Brown 1936; Martynov 1971)

$\begin{displaymath}\dot{\omega}_3 = \frac{3}{4} \lambda ~ m^2 + \frac{225}{32} \lambda^2 ~ m^3 + \dots , \end{displaymath}$

where

$\begin{displaymath}\lambda = \frac{M_3}{M_1 + M_2 + M_3} , {\rm ~~~~~and~~~~~} m = \frac{P_{\rm s}}{P_3}\cdot \end{displaymath}$

The resulting value of $\dot{\omega}_3$ for the derived minimal mass $M_{3, \min}$ and the third-body orbital period P₃ is also given in Table 2. This correction for the apsidal motion rate is also negligible, as it is only 0.2% of the observed apsidal motion rate.

5 Summary

We completed a new apsidal motion study of AO Mon by performing an O-C diagram analysis and adopting a complete list of published and observed times of minimum light. Our results indicate that AO Mon is an interesting triple and eccentric eclipsing system showing the rapid apsidal motion as well as the LITE caused by a third body orbiting with the short period of 3.6 years. The combination of the apsidal advance with a LITE in this multiple system serves as an excellent laboratory of celestial mechanics for other effects (e.g. precession of orbital planes, Söderhjelm 1975). We also calculated the internal structure constant of AO Mon and found that it is close to its theoretical value. The slight difference will probably be removed in the future with more precise masses. Moreover, AO Mon probably belongs to the important group of other early-type and triple eclipsing systems with a very short third-body orbital period (e.g. IM Aur, IU Aur, FZ CMa).

New high-accuracy timings of this eclipsing binary are necessary to improve the LITE parameters derived in this paper. It is also highly desirable to obtain new, high-dispersion and high-S/N spectroscopic observations for this system and to apply modern disentangling methods to obtain the radial-velocity curves of all components and, therefore, derive accurate masses for this important system. This massive system with its relatively short orbital period could be attractive for spectroscopists. The radial velocity curve should have a semi-amplitude of more than 200 km s^-1.

Acknowledgements

This investigation was supported by the Research Program MSM0021620860 of the Ministry of Education of the Czech Republic and partially by the Czech Science Foundation, grants 205/04/2063, 205/06/0217, and in its final stage by the grant P205/10/0715. We also acknowledge allocation of SAAO observing time. The authors thank Bc. Lenka Kotková, Ondrejov Observatory, Mr. Robert Uhlár, Jílové u Prahy, and Dr. Miloslav Zejda, Masaryk University Brno, for their important help with the photometric observations. The following internet-based resources were used in research for this paper: the SIMBAD database and the VizieR service operated at CDS, Strasbourg, France; the NASA's Astrophysics Data System Bibliographic Services; the O-C Gateway of the Czech Astronomical Society (http://var.astro.cz/ocgate/); the BAV, BBSAG and VSOLJ Bulletins.

Appendix A: Table of minima

Table A.1: Times of minimum light of AO Mon.

References

Brát, L., Trnka, J., Lehký, M., et al. 2009, OEJV, 107, 1 [NASA ADS] [Google Scholar]
Brown, E. W. 1936, MNRAS, 97, 56 [NASA ADS] [Google Scholar]
Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dvorak, S. W. 2006, IBVS, 5677 [Google Scholar]
ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200, ESA, Noordwijk [Google Scholar]
Gaposchkin, S. 1953, Harvard Ann., 113, 67 [NASA ADS] [Google Scholar]
Giménez, A. 1985, ApJ, 297, 405 [NASA ADS] [CrossRef] [Google Scholar]
Giménez, A., & García-Pelayo, J. M. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
Giuricin, G., Mardirossian, F., & Mezzetti, M. 1980, A&ASS, 39, 255 [NASA ADS] [Google Scholar]
Harmanec, P. 1988, Bull. Astr. Inst. Czech., 39, 329 [NASA ADS] [Google Scholar]
Hoffmeister, C. 1931, Astron. Nachr., 242, 129 [NASA ADS] [CrossRef] [Google Scholar]
Hübscher, J., Lehmann, P. B., Monninger, G., et al. 2010, IBVS, 5918 [Google Scholar]
Hübscher, J., Paschke, A., & Walter, F. 2006, IBVS, 5731 [Google Scholar]
Hübscher, J., Steinbach, H.-M., & Walter, F. 2009, IBVS, 5874 [Google Scholar]
Kandpal, C. D. 1976, Ap&SS, 40, 3 [NASA ADS] [CrossRef] [Google Scholar]
Kopal, Z. 1978, Dynamics of Close Binary Systems (Dordrecht, Holland: Reidel) [Google Scholar]
Kwee, K. K., & van Woerden, H. 1956, Bull. Astron. Inst. Netherlands, 12, 327 [NASA ADS] [Google Scholar]
Lause, F. 1933, Astron. Nachr., 250, 9 [NASA ADS] [CrossRef] [Google Scholar]
Lause, F. 1936, Astron. Nachr., 260, 292 [NASA ADS] [Google Scholar]
Lause, F. 1949, Astron. Nachr., 277, 40 [NASA ADS] [CrossRef] [Google Scholar]
Mayer, P. 1990, Bull. Astr. Inst. Czech., 41, 231 [NASA ADS] [Google Scholar]
Nakajima, K. 2006, Variable Star Bulletin, 44, 6 [Google Scholar]
Nakajima, K. 2007, Variable Star Bulletin, 45, 5 [Google Scholar]
Martynov, D. Ya. 1971, in Eclipsing Variable Stars, ed. V. P. Tsesevich, Nauka, Moscow [Google Scholar]
Menzies, J. W., Cousins, A. W., Banfield, R. M., & Laing, J. D. 1989, SAAO Circ., 13, 1 [NASA ADS] [Google Scholar]
Pojmanski, G. 2002, Acta Astron., 52, 397 [NASA ADS] [Google Scholar]
Söderhjelm, S. 1975, A&A, 42, 229 [NASA ADS] [Google Scholar]
Struve, O. 1945, ApJ, 102, 74 [NASA ADS] [CrossRef] [Google Scholar]
Zejda, M. 2004, IBVS, 5583 [Google Scholar]

Footnotes

... Monocerotis: Partly based on observations secured at the South African Astronomical Observatory, Sutherland, South Africa, in April 2004.
... UNIPACK: http://c-munipack.sourceforge.net/
... 16.1: http://astro.troja.mff.cuni.cz/ftp/hec/HEC22/
... catalogue: GCVS: http://www.sai.msu.su/groups/cluster/gcvs/
...2007): http://vsolj.cetus-net.org/

All Tables