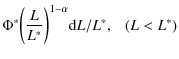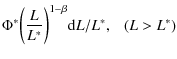EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 514 (May 2010) A&A, 514 (2010) A7 Full HTML
Science with AKARI
Free Access
Issue
A&A
Volume 514, May 2010
Science with AKARI
Article Number A7
Number of page(s) 5
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200913473
Published online 03 May 2010
A&A 514, A7 (2010)

Science with AKARI

Environmental dependence of 8 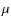 $\mu $m luminosity functions of galaxies at z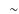$~\sim $ 0.8

Comparison between RXJ1716.4+6708 and the AKARI NEP-deep field[*],[*]

T. Goto1,2,[*] - Y. Koyama3 - T. Wada4 - C. Pearson5,6,7 - H. Matsuhara4 - T. Takagi4 - H. Shim8 - M. Im8 - M. G. Lee8 - H. Inami4,9,10 - M. Malkan11 - S. Okamura3 - T. T. Takeuchi12 - S. Serjeant7 - T. Kodama2 - T. Nakagawa4 - S. Oyabu4 - Y. Ohyama13 - H. M. Lee8 - N. Hwang2 - H. Hanami14 - K. Imai15 - T. Ishigaki16

1 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA e-mail: tomo@ifa.hawaii.edu
2 - National Astronomical Observatory, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
3 - Department of Astronomy, School of Science, The University of Tokyo, Tokyo 113-0033, Japan
4 - Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, Sagamihara, Kanagawa 229-8510, Japan
5 - Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire OX11 0QX, UK
6 - Department of Physics, University of Lethbridge, 4401 University Drive, Lethbridge, Alberta T1J 1B1, Canada
7 - Astrophysics Group, Department of Physics, The Open University, Milton Keynes, MK7 6AA, UK
8 - Department of Physics & Astronomy, FPRD, Seoul National University, Shillim-Dong, Kwanak-Gu, Seoul 151-742, Korea
9 - Spitzer Science Center, California Institute of Technology, Pasadena, CA 91125, USA
10 - Department of Astronomical Science, The Graduate University for Advanced Studies
11 - Department of Physics and Astronomy, UCLA, Los Angeles, CA 90095-1547, USA
12 - Institute for Advanced Research, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8601, Japan
13 - Academia Sinica, Institute of Astronomy and Astrophysics, Taiwan
14 - Physics Section, Faculty of Humanities and Social Sciences, Iwate University, Morioka 020-8550, Japan
15 - TOME R&D Inc. Kawasaki, Kanagawa 213 0012, Japan
16 - Asahikawa National College of Technology, 2-1-6 2-jo Shunkohdai, Asahikawa-shi, Hokkaido 071-8142, Japan

Received 14 October 2009 / Accepted 22 December 2009

Abstract
Aims. We aim to reveal environmental dependence of infrared luminosity functions (IR LFs) of galaxies at $z\sim 0.8$ using the AKARI satellite. AKARI's wide field of view and unique mid-IR filters help us to construct restframe 8 $\mu $m LFs directly without relying on SED models.
Methods. We construct restframe 8 $\mu $m IR LFs in the cluster region RXJ1716.4+6708 at z=0.81, and compare them with a blank field using the AKARI north ecliptic pole deep field data at the same redshift. AKARI's wide field of view ( $10'\times 10'$) is suitable to investigate wide range of galaxy environments. AKARI's 15 $\mu $m filter is advantageous here since it directly probes restframe 8 $\mu $m at $z\sim 0.8$, without relying on a large extrapolation based on a SED fit, which was the largest uncertainty in previous work.
Results. We have found that cluster IR LFs at restframe 8 $\mu $m have a factor of 2.4 smaller L* and a steeper faint-end slope than that of the field. Confirming this trend, we also found that faint-end slopes of the cluster LFs becomes flatter and flatter with decreasing local galaxy density. These changes in LFs cannot be explained by a simple infall of field galaxy population into a cluster. Physics that can preferentially suppress IR luminous galaxies in high density regions is required to explain the observed results.

Key words: galaxies: evolution - galaxies: interactions - galaxies: starburst - galaxies: peculiar - galaxies: formation - infrared: galaxies

1 Introduction

It has been observed that galaxy properties change as a function of galaxy environment. The morphology-density relation reports that a fraction of elliptical galaxies is larger at higher galaxy density (Goto et al. 2003a). The star formation rate (SFR) is higher at lower galaxy density (Gómez et al. 2003; Tanaka et al. 2004). Despite accumulating observational evidence, we still do not fully understand the underlying physics governing the environmental-dependent evolution of galaxies.

Infrared (IR) emission of galaxies is an important probe of galaxy activity, since at higher redshift, a significant fraction of star formation is obscured by dust (Takeuchi et al. 2005; Goto et al. 2010). Although there are low-z cluster studies (Tran et al. 2009; Bai et al. 2006; Shim et al. 2010), not much attention has been paid to the infrared properties of high-z cluster galaxies, mainly due to the lack of sensitivity in previous IR satellites such as ISO and IRAS. The superb sensitivity of recently launched Spitzer and AKARI satellites can revolutionise the infrared view of the environmental dependence of galaxy evolution.

In this work, we compare restframe 8 $\mu $m LFs between cluster and field regions at z=0.8 using data from the AKARI. Monochromatic restframe 8 $\mu $m luminosity ( $L_{8~\mu {\rm m}}$) is important since it is known to correlate well with the total IR luminosity (Huang et al. 2007; Babbedge et al. 2006), hence, with the SFR of galaxies (Kennicutt 1998). This is especially true for star-forming galaxies because the rest-frame 8 $\mu $m flux are dominated by prominent PAH features such as at 6.2, 7.7, and 8.6 $\mu $m (Desert et al. 1990).

Significant advantages brought by the AKARI are as follows. (i) At z=0.8, AKARI's 15 $\mu $m filter (L15) covers the redshifted restframe 8 $\mu $m, thus we can estimate 8 $\mu $m LFs without using a large extrapolation based on SED models, which were the largest uncertainty in previous work. (ii) The large field of view of the AKARI's mid-IR camera (IRC, $10'\times 10'$) allows us to study wider area including cluster outskirts, where important evolutionary mechanisms are suggested to be at work (Kodama et al. 2004; Goto et al. 2004). For example, passive spiral galaxies have been observed in such an environment (Goto et al. 2003b). Unless otherwise stated, we adopt a cosmology with $(h,\Omega_{\rm m},\Omega_\Lambda) = (0.7,0.3,0.7)$ (Komatsu et al. 2009).

2 Data and analysis

2.1 LFs of cluster RXJ1716.4+6708

The AKARI is a Japanese infrared satellite (Murakami et al. 2007), which has continuous filter coverage in the mid IR wavelengths ( N2,N3,N4,S7,S9W,S11,L15,L18W and L24). The AKARI has observed a massive galaxy cluster, RXJ1716.4+6708, in N3, S7 and L15 (Koyama et al. 2008). RXJ1716.4+6708 is at z=0.81 and has $\sigma=1522^{+215}_{-150}$ km s-1, $L_{\rm X_{\rm bol}}=13.86\pm1.04\times 10^{44}$ erg s-1, kT=6.8+1.0-0.6 keV. The mass estimates from weak lensing and X-ray are $3.7\pm 1.3 \times 10^{14}~M_{\odot}$ and $4.35\pm 0.83\times 10^{14}~M_{\odot}$, respectively (see Koyama et al. 2007, for references).

A significant advantage of the AKARI observation is its L15 filter, which corresponds to a restframe wavelength of 8 $\mu $m at z=0.81. With 15 (3) pointings, L15 reaches 66.5 (96.5) $\mu $Jy in deep (shallow) regions at 5$\sigma $. Here flux is measured in an 11'' aperture, and converted to total flux using AKARI's IRC correction table (2009.5.1) [*]. Cluster studies with the Spitzer are often performed in 24 $\mu $m and thus needed a large extrapolation to estimate either $L_{8~\mu {\rm m}}$ or total infrared luminosity ( $L_{\rm TIR},8{-}1000~\mu $m). We do not claim that $L_{8~\mu {\rm m}}$ is a better indicator of the total IR luminosity than other indicators (Rieke et al. 2009; Calzetti et al. 2007; Brandl et al. 2006), but it is important that the AKARI can meausure redshifted 8 $\mu $m flux directly in one of the filters.

\begin{figure} \par\includegraphics[width=6.5cm,clip]{13473fig1.ps} \end{figure} Figure 1:

Restframe 8 $\mu $m LFs of cluster RXJ1716.4+6708 at z=0.81 in the squares, and those of the AKARI NEP-deep field in the triangles. For RXJ1716.4+6708, only photometric and spectroscopic cluster member galaxies are used. For the NEP-deep field, galaxies with photo-z/specz in the range of 0.65< z<0.9 are used. The dot-dashed lines are 8 $\mu $m LFs of RXJ1716.4+6708, but scaled down for easier comparison. The thin dotted lines are the best-fit double power laws. Vertical arrows show the 5$\sigma $ flux limits of deep/shallow regions of the cluster (red) and the NEP-deep field (blue) in terms of $L_{8~\mu {\rm m}}$ at z=0.81.

Open with DEXTER

Thanks to the AKARI's wide field of view ( $10'\times 10'$), the total area coverage around the cluster is 200 arcmin2, a larger area than previous cluster studies with Spitzer, allowing us to study IR sources in the outskirts, where dramatic galaxy evolution takes place (e.g., Goto et al. 2003a). Previously, Koyama et al. (2008) report a high fraction of L15 sources in the intermediate density region in the cluster, suggesting an environmental effect in the intermediate density environment.

This same region was imaged with Suprime-Cam in VRi'z' and led to a good photometric redshift estimate (Koyama et al. 2007). Used in this work are 54 L15-detected galaxies that are identified with optical sources with $0.76\leq z_{\rm photo}\leq 0.83$.

With the L15 filter covering the restframe 8 $\mu $m, we simply converted the observed flux to 8 $\mu $m monochromatic luminosity ( $L_{8~\mu {\rm m}}$) using a standard cosmology. Completeness was measured by distributing artificial point sources with varying flux within the field and by examining those recovered as a function of input flux. Since we have deeper coverage at the center of the cluster, the completeness was measured separately in the central deep region and the outer regions of the field. More detail on the method is found in Wada et al. (2008).

Once the flux is converted to luminosity and completeness is taken into account, it is straightforward to construct $L_{8~\mu {\rm m}}$ LFs, which we show in Fig. 1. Errors of the LFs are assumed to follow Poisson distribution. Here, we take an angular distance of the most distant source from the cluster center as a cluster radius ( $R_{\rm max}=6.2$ Mpc). We assumed $\frac{4}{3}\pi R_{\max}^3$ as the volume of the cluster to obtain galaxy density ($\phi$). This is only one of many ways to define a cluster volume, and thus, caution must be taken to compare absolute values of our LFs to other works, such as Shim et al. (2010). Since this cluster is elongated in an angular direction (Koyama et al. 2007), the volume might not be spherical, and yet, comparison of the shape of the LFs is valid.

Table 1:   Best double power-law fit parameters for LFs.

2.2 Luminosity functions in the AKARI NEP-deep field

Our field LFs are based on the AKARI NEP-deep field data. The AKARI performed deep imaging in the north ecliptic pole region (NEP) from 2-24 $\mu $m, with 4 pointings in each field over 0.4 deg2 (Matsuhara et al. 2007,2006; Wada et al. 2008). The 5$\sigma $ sensitivity in the AKARI IR filters ( N2,N3,N4,S7,S9W,S11,L15,L18W, and L24) are 14.2, 11.0, 8.0, 48, 58, 71, 117, 121, and 275 $\mu $Jy (Wada et al. 2008). Flux is measured in 3 pix radius aperture (=7''), then corrected to total flux.

A subregion of the NEP-deep field (0.25 deg2) has ancillary data from Subaru BVRi'z' (Imai et al. 2007; Wada et al. 2008), CFHT u' (Serjeant et al. in prep.), KPNO2m/FLAMINGOs J and Ks (Imai et al. 2007), and GALEX FUV and NUV (Malkan et al. in prep.). For the optical identification of MIR sources, we adopted the likelihood ratio method (Sutherland & Saunders 1992). Using these data, we estimated a photometric redshift of L15 detected sources in the region with the LePhare (Arnouts et al. 2007; Ilbert et al. 2006). The measured errors on the photo-z against 293 spec-z galaxies from Keck/DEIMOS (Takagi et al. in prep.) are $\frac{\Delta z}{1+z}=0.036$ at $z\leq0.8$. We excluded those sources that are better fit with QSO templates from the LFs.

To construct field LFs, we selected L15 sources at $0.65<z_{\rm photoz}<0.9$. This gives 289 IR galaxies with a median redshift of 0.76. L15 flux is converted to $L_{8~\mu {\rm m}}$ using the photometric redshift of each galaxy. LFs are computed using the $1/V_{\max}$ method. We used the SED templates (Lagache et al. 2003) for k-corrections to obtain the maximum observable redshift from the flux limit. Completeness of the L15 detection is corrected using Pearson et al. (2009). This correction is 25% at maximum, since we only used the sample where the completeness is greater than 80%.

The resulting field LFs are shown in Fig. 1. Errors of the LFs were computed using a 1000 Monte Caro simulation with varying z and flux within their errors. These estimated errors were added to the Poisson errors in each LF bin in quadrature.

We performed a detaild comparison of restframe 8 $\mu $m LFs to those in the literature in Goto et al. (2010). Briefly, there is an order of difference between Caputi et al. (2007) and Babbedge et al. (2006), reflecting difficulty in estimating $L_{8~\mu {\rm m}}$ dominated by PAH emissions using Spitzer 24 $\mu $m flux. Our field 8 $\mu $m LF lies between Caputi et al. (2007) and Babbedge et al. (2006). Compared with these works, we have directly observed restframe 8 $\mu $m using the AKARI L15 filter, eliminating the uncertainty in flux conversion based on SED models. More details on the evolution of field IR LFs are given in Goto et al. (2010).

3 Results and discussion

3.1 8 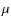$\mu $m IR LFs

In Fig. 1, we show restframe 8 $\mu $m LFs of cluster RXJ1716.4+6708, and the LFs of the field region. First of all, cluster LFs have higher density by a factor of $\sim$700 than the field LFs, reflecting that the galaxy cluster is indeed a high density region in terms of infrared sources.

\begin{figure} \par\includegraphics[width=6.5cm,clip]{13473fig2.ps}\vspace*{3mm} \end{figure} Figure 2:

Restframe 8 $\mu $m LFs of cluster RXJ1716.4+6708 at z=0.81, divided according to the local galaxy density ( $\Sigma _{\rm 5th}$). The stars, circles, and squares indicate galaxies with $\log{\Sigma_{\rm 5th}}\geq 2 $, $1.6\leq \log{\Sigma_{\rm 5th}}<2$, and $\log{\Sigma_{\rm 5th}}< 1.6$, respectively.

Open with DEXTER

Next, to compare the shape of the LFs, we normalized the cluster LF to match the field LFs at the faintest end. In contrast to the field LFs, which show flattening of the slope at $\log L_{8~\mu {\rm m}}<10.8~L_{\odot}$, the cluster LF maintains the steep slope in the range of $10.0~L_{\odot}<\log L_{8~\mu {\rm m}}<10.6~L_{\odot}$. The difference is significant, considering the size of errors on each LF.

We fit a double-power law to both cluster and field LFs using the following formulae:

              $\displaystyle \Phi(L){\rm d}L/L^{*}$ = $\displaystyle \Phi^{*}\bigg(\frac {L}{L^{*}}\bigg)^{1-\alpha}{\rm d}L/L^{*}, ~~~ (L<L^{*})$ (1)
$\displaystyle \Phi(L){\rm d}L/L^{*}$ = $\displaystyle \Phi^{*}\bigg(\frac {L}{L^{*}}\bigg)^{1-\beta}{\rm d}L/L^{*}, ~~~ (L>L^{*})$ (2)

Free parameters are L* (characteristic luminosity, $L_{\odot}$), $\phi^*$ (normalization, Mpc-3), $\alpha$, and $\beta$ (faint and bright end slopes), respectively. The best-fit values for field and cluster LFs are summarized in Table 1 and shown in Fig. 1. The bright-end slopes are not very different, but the L* of the cluster LF is smaller than the field by a factor of 2.4, and the faint-end tail of cluster LF is steeper than for field LF.

To further examine the difference at the faint end of the LFs, we divide the cluster LF using the local galaxy density ( $\Sigma _{\rm 5th}$) measured by Koyama et al. (2008). This density is based on the distance to the 5th nearest neighbor in the transverse direction using all the optical photo-z members, making it a surface galaxy density. We separated LFs using similar criteria, $\log{\Sigma_{\rm 5th}}\geq 2 $ (dense), $1.6\leq \log{\Sigma_{\rm 5th}}<2$ (intermediate), and $\log{\Sigma_{\rm 5th}}< 1.6$ (sparse), then plotted LFs of each region in Fig. 2. A fraction of the total volume of the cluster is assigned to each density group, inversely proportional to the sum of $\Sigma_{\rm 5th}^{3/2}$ of each group.

Interestingly, the faint-end slope becomes flatter and flatter with decreasing local galaxy density. This result is consistent with our comparison to the field in Fig. 1. In fact, the lowest density LF has a flat faint-end tail similar to the one in the field LF. Since these LFs are based on the same data, changes in the faint-end slope are not likely to be caused by the errors in completeness correction or by calibration problems. The completeness of the deep and shallow regions of the cluster are measured separately. The changes in the slope is much larger than the maximum completeness correction of 25%. We also checked the cluster LFs as a function of cluster centric radius, to find no significant difference, perhaps thanks to the elongated morphology of this cluster. At the same time, assuming the same cluster volume, Fig. 2 shows that a possible contamination from the field galaxies to cluster LFs is only $\sim$0.1% in the dense region and $\sim$1% even in the sparse region.

It is interesting that there is not just the change in the scale of the LFs, but also a change in the L* and the faint-end slope ($\alpha$) of the LFs, resulting in the deficit in the $10.2~L_{\odot}<\log L_{8~\mu {\rm m}}<10.8~L_{\odot}$ for cluster LFs. One might imagine that a change just in L* might explain the difference in Fig. 1. However, in Fig. 2, there clearly is a change in the slope as a function of $\Sigma _{\rm 5th}$.

However, interpretation is rather complicated, because a shape of LF would not change if field galaxies fall into a cluster uniformly without changing their star-formation activity. Although in a cluster environment, a fraction of MIR luminous galaxies is smaller than the field (Koyama et al. 2008), the uniform and instant quenching of star-formation activity of field galaxies can only shift a LF, but cannot account for a change in L* and $\alpha$ of the LFs.

Two important findings in this work are (i) L* is smaller in the cluster, (ii) the faint-end slopes become steeper toward higher density regions. To explain these changes in LFs, IR-luminous galaxies need to be reduced, with a relative increase in IR-faint galaxies. However, an environmentally-driven physical process, such as ram-pressure stripping or galaxy-merging would quench star formation not only in massive galaxies but also in less massive galaxies, and thus it is unable to explain the observed changes in LFs.

On the other hand, it has been frequently observed that more massive galaxies were formed earlier in the Universe. This downsizing scenario also depends on the environment, in that galaxies with the same mass are more evolved in higher density environments than galaxies in less dense environments (Goto et al. 2005; Tanaka et al. 2005,2008). Statistically, a good correlation has been found between $L_{\rm TIR}$ and stellar mass (Elbaz et al. 2007). Our finding that there is a relative lack of IR-luminous galaxies in the cluster environment may be consistent with the downsizing scenario, where higher density regions have more evolved galaxies and lack massive star-forming galaxies. In contrast, more massive galaxies still form stars in lower density regions. However, since the data we have shown is in IR luminosity, we need good stellar mass estimate based on deeper near-IR data to reach a conclusion.

Although a specific mechanism is unclear, the steep faint end could also result from the enhanced star-formation in less massive galaxies. In the above scenario, massive galaxies have already ceased their star formation in the cluster, but less massive galaxies are still forming stars. These less massive galaxies may stop star formation soon to join the faint end of the red sequence (Koyama et al. 2007).

3.2 Total IR LFs

\begin{figure} \par\includegraphics[width=7cm,clip]{13473fig3.ps} \end{figure} Figure 3:

Total infrared LFs of cluster RXJ1716.4+6708 at z=0.81 in the solid line, and those of the AKARI NEP-deep field in the dashed line. Overplotted are the LFs of MS1054 from Bai et al. (2007).

Open with DEXTER

To compare the $L_{8~\mu {\rm m}}$ LF in Fig. 1 to those in the literature, we need to convert $L_{8~\mu {\rm m}}$ to $L_{\rm TIR}$. We use the following relation by Caputi et al. (2007);

$\displaystyle L_{\rm TIR}=1.91\times (\nu L_{\nu_{8~\mu {\rm m}}})^{1.06} (\pm 55\%).$   (3)

This is better tuned for a similar luminosity range to the one used here than the original relation by Bavouzet et al. (2008). The conversion, however, has been the main source of errors in estimating $L_{\rm TIR}$ from $L_{8~\mu {\rm m}}$. Caputi et al. (2007) report 55% dispersion around the relation. It should be kept in mind that the restframe 8 $\mu $m is sensitive to the star-formation activity, but at the same time, it is where the SED models have the strongest discrepancies due to the complicated PAH emission lines (see Fig. 12 of Goto et al. 2010; Caputi et al. 2007).

The estimated $L_{\rm TIR}$ can then be converted to SFR using the following relation for a Salpeter IMF, $\phi$ (m) $\propto m^{-2.35}$ between $0.1{-}100~ M_{\odot}$ (Kennicutt 1998):

$\displaystyle {\it SFR} (M_{\odot} ~{\rm yr}^{-1}) =1.72 \times 10^{-10} L_{\rm TIR} (L_{\odot}).$   (4)

In Fig. 3, we show the $L_{\rm TIR}$ LFs. Symbols are the same as in Fig. 1. In the top axis, we show corresponding SFR. Overplotted asterisks are cluster LF of MS1054 at z=0.83 with $\times$2 higher mass by Bai et al. (2007), which shows good agreement with our LFs of RXJ1716.4+6708. Bai et al. (2007) cover only the central region of MS1054 due to the smaller field of view of the Spitzer. The shape of their LF looks more like our LFs in the highest density bin in Fig. 2. A shift in scale is perhaps the result of the difference in esimating cluster volumes.

A major difference of our work to that of Bai et al. (2007) is that they were not able to compare the shape of the LFs in detail between field and cluster regions, mainly because of a smaller field coverage and larger errors on LFs. They had to fix the faint-end slope with a local value. The largest source of errors is when converting Spitzer 24 $\mu $m flux into 8 $\mu $m. Both cluster and field LFs of this work use L15 filter, which measures restframe 8 $\mu $m flux directly, eliminating the main source of errors. In addition, both cluster and filed LFs are measured with essentially the same methodology, allowing us a fair comparison of LFs.

4 Summary

We constructed restframe 8 $\mu $m LFs of a massive galaxy cluster (RXJ1716.4+6708) and a rarefied field region (the NEP-deep field) at $z\sim 0.8$ using essentially the same method and data from the AKARI telescope. AKARI's 15 $\mu $m filter nicely covers restframe 8 $\mu $m at $z\sim 0.8$, so we do not need a large interpolation based on SED models. AKARI's wide field of view allows us to investigate a variety of cluster environments with 2 orders of difference in local galaxy density.

We found that L* of the cluster 8 $\mu $m LF is smaller than the field by a factor of 2.4, and the faint-end tail of cluster IR LFs becomes steeper and steeper with increasing local galaxy density. This difference cannot be explained by a simple infall of field galaxies into a cluster. Physics that preferentially supresses IR luminous galaxes in higher density regions is needed to explain the observed results.

Acknowledgements
We thank the anonymous referee for many insightful comments, which significantly improved the paper. We are grateful to Masayuki Tanaka for useful discussions. We thank L.Bai for providing data for comparison. T.G., Y.K., and H.I. acknowledge financial support from the Japan Society for the Promotion of Science (JSPS) through JSPS Research Fellowships for Young Scientists. M.I. was supported by the Korea Science and Engineering Foundation(KOSEF) grant No. 2009-0063616, funded by the Korea government (MEST). H.M.L. acknowledges the support from KASI through its cooperative fund in 2008. This research is based on the observations with AKARI, a JAXA project with the participation of ESA. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this sacred mountain.

References

  1. Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Babbedge, T. S. R., Rowan-Robinson, M., Vaccari, M., et al. 2006, MNRAS, 370, 1159 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bai, L., Rieke, G. H., Rieke, M. J., et al. 2006, ApJ, 639, 827 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bai, L., Rieke, G. H., Rieke, M. J., Christlein, D., & Zabludoff, A. I. 2009, ApJ, 693, 1840 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bai, L., Marcillac, D., Rieke, G. H., et al. 2007, ApJ, 664, 181 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bavouzet, N., Dole, H., Le Floc'h, E., et al. 2008, A&A, 479, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Brandl, B. R., Bernard-Salas, J., Spoon, H. W. W., et al. 2006, ApJ, 653, 1129 [NASA ADS] [CrossRef] [Google Scholar]
  8. Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [NASA ADS] [CrossRef] [Google Scholar]
  9. Caputi, K. I., Lagache, G., Yan, Lin, Dole, H., et al. 2007, ApJ, 660, 97 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
  11. Desert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
  12. Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Gómez, P. L., Nichol, R. C., Miller, C. J., et al. 2003, ApJ, 584, 210 [NASA ADS] [CrossRef] [Google Scholar]
  14. Goto, T. 2005, MNRAS, 360, 322 [NASA ADS] [CrossRef] [Google Scholar]
  15. Goto, T., Yamauchi, C., Fujita, Y., et al. 2003a, MNRAS, 346, 601 [NASA ADS] [CrossRef] [Google Scholar]
  16. Goto, T., Okamura, S., Sekiguchi, M., et al. 2003b, PASJ, 55, 757 [NASA ADS] [CrossRef] [Google Scholar]
  17. Goto, T., Yagi, M., Tanaka, M., & Okamura, S. 2004, MNRAS, 348, 515 [NASA ADS] [CrossRef] [Google Scholar]
  18. Goto, T., Postman, M., Cross, N. J. G., et al. 2005, ApJ, 621, 188 [NASA ADS] [CrossRef] [Google Scholar]
  19. Goto, T., Takagi, T., Matsuhara, H., et al. 2010, A&A, 514, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Huang, J.-S., Ashby, M. L. N., Barmby, P., et al. 2007, ApJ, 664, 840 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Imai, K., Matsuhara, H., Oyabu, S., et al. 2007, AJ, 133, 2418 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
  24. Kodama, T., Balogh, M. L., Smail, I., Bower, R. G., & Nakata, F. 2004, MNRAS, 354, 1103 [NASA ADS] [CrossRef] [Google Scholar]
  25. Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
  26. Koyama, Y., Kodama, T., Tanaka M., Shimasaku, K., & Okamura, S. 2007, MNRAS, 382, 1719 [NASA ADS] [CrossRef] [Google Scholar]
  27. Koyama, Y., Kodama, T., Shimasaku, K., et al. 2008, MNRAS, 391, 1758 [NASA ADS] [CrossRef] [Google Scholar]
  28. Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]
  29. Matsuhara, H., Wada, T., Matsuura, S., et al. 2006, PASJ, 58, 673 [NASA ADS] [Google Scholar]
  30. Matsuhara, H., Wada, T., Pearson, C. P., et al. 2007, PASJ, 59, 543 [NASA ADS] [Google Scholar]
  31. Murakami, H., Baba, H., Barthel, P., et al. 2007, PASJ, 59, 369 [Google Scholar]
  32. Pearson, C., Oyabu, S., Wada, T., et al. 2010, A&A, 514, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
  34. Shim, H., et al. 2010, ApJ, submitted [Google Scholar]
  35. Sutherland, W., & Saunders, W. 1992, MNRAS, 259, 413 [NASA ADS] [CrossRef] [Google Scholar]
  36. Takeuchi, T. T., Buat, V., & Burgarella, D. 2005, A&A, 440, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Tanaka, M., Goto, T., Okamura, S., Shimasaku, K., & Brinkmann, J. 2004, AJ, 128, 2677 [NASA ADS] [CrossRef] [Google Scholar]
  38. Tanaka, M., Kodama, T., Arimoto, N., et al. 2005, MNRAS, 362, 268 [NASA ADS] [CrossRef] [Google Scholar]
  39. Tanaka, M., Finoguenov, A., Kodama, T., et al. 2008, A&A, 489, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Tran, K.-V. H., Saintonge, A., Moustakas, J., et al. 2009, ApJ, 705, 809 [NASA ADS] [CrossRef] [Google Scholar]
  41. Wada, T., Matsuhara, H., Oyabu, S., et al. 2008, PASJ, 60, 517 [NASA ADS] [Google Scholar]

Footnotes

... field[*]
This research is based on the observations with AKARI, a JAXA project with the participation of ESA.
...[*]
Based on data collected at Subaru Telescope, which is operated by the National Astronomical Observatory of Japan.
...1,2,[*]
JSPS SPD fellow
... (2009.5.1)[*]
http://www.ir.isas.jaxa.jp/ASTRO-F/Observation/DataReduction/IRC/ApertureCorrection_090501.html

All Tables

Table 1:   Best double power-law fit parameters for LFs.

All Figures

  \begin{figure} \par\includegraphics[width=6.5cm,clip]{13473fig1.ps} \end{figure} Figure 1:

Restframe 8 $\mu $m LFs of cluster RXJ1716.4+6708 at z=0.81 in the squares, and those of the AKARI NEP-deep field in the triangles. For RXJ1716.4+6708, only photometric and spectroscopic cluster member galaxies are used. For the NEP-deep field, galaxies with photo-z/specz in the range of 0.65< z<0.9 are used. The dot-dashed lines are 8 $\mu $m LFs of RXJ1716.4+6708, but scaled down for easier comparison. The thin dotted lines are the best-fit double power laws. Vertical arrows show the 5$\sigma $ flux limits of deep/shallow regions of the cluster (red) and the NEP-deep field (blue) in terms of $L_{8~\mu {\rm m}}$ at z=0.81.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.5cm,clip]{13473fig2.ps}\vspace*{3mm} \end{figure} Figure 2:

Restframe 8 $\mu $m LFs of cluster RXJ1716.4+6708 at z=0.81, divided according to the local galaxy density ( $\Sigma _{\rm 5th}$). The stars, circles, and squares indicate galaxies with $\log{\Sigma_{\rm 5th}}\geq 2 $, $1.6\leq \log{\Sigma_{\rm 5th}}<2$, and $\log{\Sigma_{\rm 5th}}< 1.6$, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13473fig3.ps} \end{figure} Figure 3:

Total infrared LFs of cluster RXJ1716.4+6708 at z=0.81 in the solid line, and those of the AKARI NEP-deep field in the dashed line. Overplotted are the LFs of MS1054 from Bai et al. (2007).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.