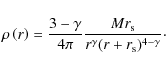| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913240 | |
| Published online | 12 May 2010 | |
Isolated dwarf galaxies: from cuspy to flat dark matter density profiles and metalicity gradients
S. Pasetto1,2 - E. K. Grebel1 - P. Berczik1,3,4 - R. Spurzem3,5,1 - W. Dehnen6
1 - Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Germany
2 - Max-Planck-Institut für Astronomie, Heidelberg, Germany
3 - National Astronomical Observatories of China (NAOC), Chinese
Academy of Sciences (CAS), Datun Lu 20A, Chaoyang District, Beijing
100012, PR China
4 - Main Astronomical Observatory (MAO), National Academy of
Sciences of Ukraine (NASU), Akademika Zabolotnoho 27, 03680 Kyiv,
Ukraine
5 - Kavli Institute of Astronomy and Astrophysics, Peking University, Beijing, PR China
6 - Department of Physics & Astronomy, University of Leicester, Leicester, LE1 7RH, UK
Received 3 September 2009 / Accepted 28 January 2010
Abstract
The chemodynamical evolution of spherical multi-component
self-gravitating models for isolated dwarf galaxies is studied. We
compared their evolution with and without feedback effects from star
formation processes. We found that initially cuspy dark matter profiles
flatten with time without any special tuning conditions as a result of
star formation. Thus the seemingly flattened profiles found in many
dwarfs do not contradict the cuspy profiles predicted by cosmological
models. We also calculated the chemical evolution of stars and gas,
to permit comparisons with observational data.
Key words: galaxies: dwarf - galaxies: formation - galaxies: evolution - galaxies: kinematics and dynamics - galaxies: abundances
1 Introduction
Dwarf galaxies are the most common galaxies in the Universe (e.g. Marzke & da Costa 1997) and the Local Group sample is an excellent laboratory where to study these systems and their properties (Grebel 1999; Mateo 1998).
Our interest in these structures is related to many important mutually
related topics: the growth of structure, the nature of the dark matter
and dynamical interactions. In the last decades, new observational
data have become available for many dwarf galaxies (in particular
in our Local Group) especially regarding the velocity dispersion
profiles of stars and the rotation curves of gas, providing clean
measures of the dynamical mass at all radii where baryonic matter can
be found. This is gradually permitting a deeper investigation of the
equilibrium and stability of the dark matter profiles. Such studies
revealed a discrepancy between the prediction of the
![]() models by numerical simulations, which require power law density profiles with cusps
models by numerical simulations, which require power law density profiles with cusps
![]() where
where
![]() or 1.5 (e.g. Moore et al. 1999a; Navarro et al. 2004,1997), and the more flattened profiles derived from observations (e.g. Burkert 1995; de Blok 2005; de Blok & Bosma 2002; Gentile et al. 2005).
Other problems strictly related to the nature of the dark matter and
its clustering properties are, e.g., the missing satellites
problem (e.g. Moore et al. 1999b,a; Klypin et al. 1999b,a), the triaxiality of the halos for clusters of galaxies inferred from gravitational lensing (e.g. Tyson et al. 1998) and the angular momentum problem (e.g. Navarro & Steinmetz 2000). Despite the many successes of the
or 1.5 (e.g. Moore et al. 1999a; Navarro et al. 2004,1997), and the more flattened profiles derived from observations (e.g. Burkert 1995; de Blok 2005; de Blok & Bosma 2002; Gentile et al. 2005).
Other problems strictly related to the nature of the dark matter and
its clustering properties are, e.g., the missing satellites
problem (e.g. Moore et al. 1999b,a; Klypin et al. 1999b,a), the triaxiality of the halos for clusters of galaxies inferred from gravitational lensing (e.g. Tyson et al. 1998) and the angular momentum problem (e.g. Navarro & Steinmetz 2000). Despite the many successes of the
![]() paradigm,
a large number of open questions remain. Among the large body of
literature on the nature of dark matter and tests of different
formulations of gravity, the work of e.g., Bode et al. (2001); Spergel & Steinhardt (2000) and Bekenstein (2004)
provide classical results. Our goal in this paper is to extend
these studies by examining the interplay between dynamics and star
formation in the evolution of dwarf galaxies. Although including star
formation makes the modeling more complex, it also allows for
comparisons with dwarf galaxies in the Local Group.
paradigm,
a large number of open questions remain. Among the large body of
literature on the nature of dark matter and tests of different
formulations of gravity, the work of e.g., Bode et al. (2001); Spergel & Steinhardt (2000) and Bekenstein (2004)
provide classical results. Our goal in this paper is to extend
these studies by examining the interplay between dynamics and star
formation in the evolution of dwarf galaxies. Although including star
formation makes the modeling more complex, it also allows for
comparisons with dwarf galaxies in the Local Group.
Chemodynamical modeling of this type has been productive in the
past, particularly in investigations of the effects of winds from
high-mass stars and supernova explosions in the ISM (e.g. de Avillez & Breitschwerdt 2005; Pelupessy et al. 2004; Slyz et al. 2005).
Given the small dynamical mass inferred for dwarf galaxies, it is
surprising that the ISM can remain bound long enough to permit star
formation episodes that last for a few Gyr (as found by,
e.g., Dolphin 2002; Grebel et al. 2003; Mateo 1998; Carney & Seitzer 1986; Babusiaux et al. 2005) giving a typical baryonic matter![]() binding energy of
binding energy of
![]() with a total expected number of SN events of
with a total expected number of SN events of
![]() .
.
We will focus our attention in this paper on the dwarf spheroidal
(dSph) galaxies. These systems are the least massive galaxies known,
but their velocity dispersions suggest a mass-to-light ratio of up to
![]() ,
making them some of the most dark matter dominated objects in the universe (e.g., Gilmore et al. 2007).
For these galaxies, the star formation history and chemical
composition are very environment-dependent, making the realization of a
consistent theory of their origin and evolution that combines dynamics,
star formation and chemical enrichment more difficult. High-resolution
spectroscopy of several dSphs shows a large spread in metallicity
(e.g. Shetrone et al. 2001) corroborated by photometric studies (e.g. Bellazzini et al. 2002; Harbeck et al. 2001; Aparicio et al. 2001). Several authors suggested that the ISM of dSph systems could be entirely removed by SNe explosions (Mac Low & Ferrara 1999; Murakami & Babul 1999; Hensler et al. 2004; Mori et al. 2002,2004; Lanfranchi & Matteucci 2004; Dekel & Silk 1986; Mori et al. 1997).
,
making them some of the most dark matter dominated objects in the universe (e.g., Gilmore et al. 2007).
For these galaxies, the star formation history and chemical
composition are very environment-dependent, making the realization of a
consistent theory of their origin and evolution that combines dynamics,
star formation and chemical enrichment more difficult. High-resolution
spectroscopy of several dSphs shows a large spread in metallicity
(e.g. Shetrone et al. 2001) corroborated by photometric studies (e.g. Bellazzini et al. 2002; Harbeck et al. 2001; Aparicio et al. 2001). Several authors suggested that the ISM of dSph systems could be entirely removed by SNe explosions (Mac Low & Ferrara 1999; Murakami & Babul 1999; Hensler et al. 2004; Mori et al. 2002,2004; Lanfranchi & Matteucci 2004; Dekel & Silk 1986; Mori et al. 1997).
Mashchenko et al. (2006) discuss how star formation processes can successfully act as flattener for the central density cusps within very short timescales (more details will be given below). Read & Gilmore (2005) obtain the same result as effect of an external impulsive mass loss event. Gnedin & Zhao (2002) investigate the influence of winds. Navarro et al. (1996) were one of the first to point out the possibility that feedback mechanisms can turn the central dark-matter cusp into a cored one.
We start our analysis by demonstrating the gravitational stability of the isolated model. Then, once the stellar processes are included, we combine the dynamical and chemical analysis. In Sect. 2 we outline our research approach. In Sect. 3 we set up the initial model, in Sect. 3 we present the evolution of the models with and without stellar processes, in Sect. 5 we add the chemistry analysis and in Sect. 6, we discuss our results.
2 The modeling approach
We are trying to address the problem of the dark matter profiles in the dwarf galaxies introduced in the previous section. Despite the complicated processes acting on the true physical systems, different tools have been developed and presented in the literature to follow the chemodynamical evolution of an isolated spherical multi-component self-gravitating model of a dwarf galaxy system. Briefly, we will base our arguments on a chemodynamical code. Our code can follow the time evolution of dynamically interacting smoothed-particles that represent stars, gas and dark matter components of a dwarf galaxy. The code takes stellar evolution and chemical enrichment of the stellar populations and of the gas into account. A full description of the code used can be found in Spurzem et al. (2009); Berczik (1999), to which we refer the reader for details on codification and the implementation. We will use observational constraints in order to tune our models and simulations. We will proceed as follows:
- 1.
- We first realize multi-component self-gravitating models of a dwarf galaxy composed of a cuspy dark matter density profile, a stellar density distribution and a gas component.
- 2.
- We evolve these models in isolation to check their gravitational stability.
- 3.
- We activate the star formation (SF) processes to see the changes in the dark matter profiles (if any) and vary the physical parameters.
- 4.
- We compare the results to understand the interplay of SF processes and dynamics.
- 5.
- We turn off the stellar evolution processes to check again the dynamical equilibrium of the resulting system.
The same approach will be tested on an initially cored dark matted density profile (see later sections.)
Our focus on isolated systems is the first hypothesis that makes our modeling not immediately comparable with observations since completely isolated galaxies probably do not exist in nature.
Our first hypothesis leads to the following corollaries:
- 1.
- We can assume a ``
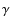 -profile''
(see below) that represents quite well both cored and cusped dark
matter profiles in the inner part of the dwarf galaxies. The inner
slope of a
-profile''
(see below) that represents quite well both cored and cusped dark
matter profiles in the inner part of the dwarf galaxies. The inner
slope of a 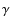 -profile has the advantage of depending on just one single parameter, i.e.
-profile has the advantage of depending on just one single parameter, i.e. 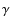 .
For the gas and stellar density profiles adopted in the starting models
we can again assume gamma profiles as good representation of the
projected luminosity profile of the dwarf galaxies in the
de-Vaucouleurs form (e.g. Dehnen 1993; Tremaine et al. 1994)
.
For the gas and stellar density profiles adopted in the starting models
we can again assume gamma profiles as good representation of the
projected luminosity profile of the dwarf galaxies in the
de-Vaucouleurs form (e.g. Dehnen 1993; Tremaine et al. 1994)
- 2.
- The outer part of the true dwarf galaxy is not expected to drop off like the
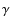 -models.
However, we are considering a synthetic spherical isolated model, so
that for Newton's first theorem at any given radius
-models.
However, we are considering a synthetic spherical isolated model, so
that for Newton's first theorem at any given radius 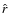 the dynamics within
the dynamics within 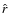 are not affected by the mass distribution exterior to
are not affected by the mass distribution exterior to 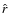 .
As a consequence we expect a priori no differences in
the evolution of isolated models regardless of the slope by which our
dark matter profile falls off, in particular in the outskirts of the
galaxy whenever spherical symmetry is assumed. This permits us to work
consistently with the
.
As a consequence we expect a priori no differences in
the evolution of isolated models regardless of the slope by which our
dark matter profile falls off, in particular in the outskirts of the
galaxy whenever spherical symmetry is assumed. This permits us to work
consistently with the 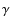 -models.
-models.
We point out that these two corollaries are not true if the first hypothesis is not assumed. Nonetheless different dark matter profiles are used often in the literature, especially from the family of the King profiles and the Plummer spheres. But, even if the gravitational force at a given radius is not dependent on the matter distribution outside of that radius, this is not true for the tidal forces. Therefore we expect that in real systems the tidal influence of external galaxies is relevant for the determination of both the shape of the DM density profile and its inner slope (except in the unlikely case of a dwarf galaxy evolved at rest exactly at the center of a spherical cluster of galaxies). The tidal effects are expected to act both by truncating the dark matter profile by tidal compression and by stretching the outer part of the dwarfs when evolved as satellite systems of a primary. Thus, changes in the dark matter profiles in the directions of the leading and trailing tails are also expected, or shallower profiles in the outer part of the dwarfs have to be used if we want to introduce our isolated system in the cosmological framework, e.g., Navarro et al. (1997, hereafter NFW). However, that is not our objective here (but see the comment in Sect. 4).
3 Isolated galaxy
3.1 The model
Our goal is to provide a self-gravitating three-component model of a dwarf galaxy. The evolution proceeds initially without any astrophysical process other than gravity. This is done in order to check the consistency of the model and to permit us to isolate the different effects in the evolution of a true astrophysical system due to gravitation or stellar evolution.
In order to choose realistic parameters for our model of a dwarf galaxy, we looked at a system that in the literature has been the subject of extensive investigation, i.e. the Carina dwarf galaxy. Our target is not to realize a specific model of the Carina dwarf galaxy, but first to use observationally motivated input physics and then extend our analysis to the dwarf galaxies class of systems (but see Pasetto et al. 2010). The wealth of literature data available on this galaxy starts already in 1983 with studies of the stellar populations of Carina (Mould & Aaronson 1983). Color magnitude diagrams were used to derive the star formation history (Monelli et al. 2004b; Mighell 1992; Monelli et al. 2003a,2004a; Mighell 1990b,a; Monelli et al. 2004c,2006b; Rizzi et al. 2004; Monelli et al. 2003b; Rizzi et al. 2003; Mighell 1997; Monelli et al. 2006a; Hurley-Keller et al. 1998). Spectroscopic measurements yielded chemical abundances, e.g., Koch et al. (2008,2006), the M/L ratio, e.g., Gilmore et al. (2007) and the dark matter distribution, e.g., Gilmore et al. (2007); Hayashi et al. (2003). Proper motion determinations were obtained by Piatek et al. (2003) (see also Piatek et al. 2004). Dynamical considerations are available for the orbit from timing arguments in Muñoz et al. (2008) and for Carina's tidal tails in Muñoz et al. (2006), which make this system well-suited for further orbit investigations (Pasetto et al. 2010).
We adopted the following density distribution profile
From the analysis of the CMD of Carina (e.g. Hurley-Keller et al. 1998)
we infered that the oldest stellar population contributes no more
than 15% of the stellar mass. Moreover from the work of Mateo et al. (1993) we got a mass to light ratio in the V band of
![]() .
Thus from Table 3 of Hayashi et al. (2003) we got L = 0.43
.
Thus from Table 3 of Hayashi et al. (2003) we got L = 0.43 ![]()
![]() ,
which leads to a stellar mass estimate of
,
which leads to a stellar mass estimate of
![]()
![]() 0.43
0.43 ![]()
![]() = 9.89
= 9.89 ![]()
![]() .
If we now assume that the mass lost by tidal interactions could reach an order of 95%, following e.g., Hayashi et al. (2003) we get
.
If we now assume that the mass lost by tidal interactions could reach an order of 95%, following e.g., Hayashi et al. (2003) we get
![]()
![]()
![]() .
From this initial mass only 1/50 is assumed to be observable. This
baryonic material consists of 15% stars, 85% gas. We thus
adopted a starting value of
.
From this initial mass only 1/50 is assumed to be observable. This
baryonic material consists of 15% stars, 85% gas. We thus
adopted a starting value of
![]() = 3.3
= 3.3 ![]()
![]() and
and
![]() =
=
![]()
![]()
![]() for our reference model. These numbers can be considered as starting values for an orbiting dwarf galaxy (Pasetto et al. 2010),
but here we will work only on an isolated system, thus for us the gas
amount retained by the dwarf galaxy after its oldest stellar population
is formed will be considered as a free parameter. This approach
was assumed because the present-day dSphs contain little or no gas,
possibly because a large fraction of gas was expelled by the initial
SNII component, by tidal interaction with a host galaxy or in
general photoevaporation, rampressure, by star formation
processes. Depending on its own individual evolution and on its orbital
parameters, each dwarf ultimately evolves under different conditions
depending on its orbital peri-center passages, and a general study
cannot be included in the present work.
for our reference model. These numbers can be considered as starting values for an orbiting dwarf galaxy (Pasetto et al. 2010),
but here we will work only on an isolated system, thus for us the gas
amount retained by the dwarf galaxy after its oldest stellar population
is formed will be considered as a free parameter. This approach
was assumed because the present-day dSphs contain little or no gas,
possibly because a large fraction of gas was expelled by the initial
SNII component, by tidal interaction with a host galaxy or in
general photoevaporation, rampressure, by star formation
processes. Depending on its own individual evolution and on its orbital
parameters, each dwarf ultimately evolves under different conditions
depending on its orbital peri-center passages, and a general study
cannot be included in the present work.
The initial temperature for the gas can be inferred assuming a
spherical collapse model for the initial dark matter model and a matter
power spectrum P(k) at redshift zero compatible with studies from the SDSS, e.g., Tegmark et al. (2004) or work on the analysis of the Lyman-![]() forest, e.g., Gnedin & Hamilton (2002). In this case the typical rms internal velocity of a halo within
forest, e.g., Gnedin & Hamilton (2002). In this case the typical rms internal velocity of a halo within
![]() is less than
is less than
![]() .
This implies that e.g., hydrogen with a sound speed higher than
.
This implies that e.g., hydrogen with a sound speed higher than
![]() has a velocity
has a velocity ![]() higher than the escape velocity of the potential well in which it has
to collapse. This gas is hence not in the condition to be retained by
the dwarf. Therefore we assumed an initial sound speed in hydrogen of
roughly around
higher than the escape velocity of the potential well in which it has
to collapse. This gas is hence not in the condition to be retained by
the dwarf. Therefore we assumed an initial sound speed in hydrogen of
roughly around
![]() corresponding to a temperature of
corresponding to a temperature of
![]() .
.
The evolution of the reference model presented here will be used as normalization case for the realization of a Carina-like dwarf galaxy model that is discussed in more detail in Paper II (Pasetto et al. 2010). Carina is one of the few dSph galaxies in the Local Group that shows long-lasting star formation and pronounced intermediate-age populations. This mean Carina resembles much more isolated, low-mass dwarf irregulars and is one of the reasons why we chose it as a reference for the approximate masses of the different galactic components. We emphasize that it is not the intent of this paper to reproduce the star formation history of the actual orbiting Carina dSph. That is the subject of a separate paper. Indeed, we explore a larger range of stellar, gas and dark matter masses (Table 1) in our simulations in order to bracket the classical dwarf spheroidal galaxies given in Mateo (1998) or Grebel (1997).
Another parameter on which Eq. (1) depends, is the scale radius ![]() .
It is interesting that in the analysis of Hayashi et al. (2003) of the possible extension of the dark matter halo, they deduce that the tidal radius
.
It is interesting that in the analysis of Hayashi et al. (2003) of the possible extension of the dark matter halo, they deduce that the tidal radius ![]() of the assumed NFW shaped halos can greatly exceed the surface brightness cut-off
of the assumed NFW shaped halos can greatly exceed the surface brightness cut-off
![]() by an order of
by an order of
![]() and that the mass loss rate can vary from 5% to 95% depending
on the specific orbit chosen. We proceeded by tuning the outer profiles
for our dwarf model as follows. We can express the radius
containing 90% of the mass, r90, as a function of the scale radius for the profiles of Eq. (1) with
and that the mass loss rate can vary from 5% to 95% depending
on the specific orbit chosen. We proceeded by tuning the outer profiles
for our dwarf model as follows. We can express the radius
containing 90% of the mass, r90, as a function of the scale radius for the profiles of Eq. (1) with
![]() by solving the simple equation
by solving the simple equation
![]() =
=
![]() ,
which yields
,
which yields

For our model we adopted
Since we are not interested in the external radial dependence of the
profile, as previously remarked, we could produce the same outer
radial dependence for the dark matter profile by modifying the scale
length to obtain the same r90 radius
containing the 90% of the mass as used for the baryonic profile.
But the approximation adopted for massive particles with Plummer
spheres imposes a natural limit on the inner resolution radius we are
going to analyze. The assumed smoothing length for our model
(see below) is roughly
![]() depending on the specific model. We will not attempt an analysis within the limiting radius
depending on the specific model. We will not attempt an analysis within the limiting radius
![]() below. Nonetheless we need to be able to discriminate between a dark matter profile with
below. Nonetheless we need to be able to discriminate between a dark matter profile with
![]() or
or
![]() for radii
for radii
![]() .
.
![]() -models with an assumed total mass of
-models with an assumed total mass of
![]()
![]()
![]() are almost indiscernible for
are almost indiscernible for
![]() for
for
![]() at our particle resolution.
at our particle resolution.
4 Evolution
We focus our attention here only on the properties of interest for dwarf galaxy systems, for which the following results hold. The
role of the triaxiality and the extension to the more general class of
elliptical galaxies is not investigated in the present paper. A table with the range of masses considered here is presented in Table 1. Within this range we mostly sampled models with an
![]() .
This range of ratios partially excludes very massive ``dwarfs'', e.g.
Large-Magellanic-Cloud-sized proto-systems (unrealistic for the scale
radius adopted here, but see Pasetto et al., in prep.), and
we completely excluded system with initial
.
This range of ratios partially excludes very massive ``dwarfs'', e.g.
Large-Magellanic-Cloud-sized proto-systems (unrealistic for the scale
radius adopted here, but see Pasetto et al., in prep.), and
we completely excluded system with initial
![]() .
.
The age of the Universe is 13.7 Gyr, or if expressed as lookback time,
![]() Gyr.
We started our simulations much later, namely at a time when the dwarf
galaxies we wanted to analyze have already formed their old
populations. Our final goal is to study the influence of star formation
on the dark matter density profiles. In oder to more clearly isolate
this effect we needed to neglect the Hubble flow and all
heating/cooling processes that influenced the star formation at hight
redshift. Hence, by starting at lookback time of T0=-9 Gyr
we follow the phase-space description of our models in a simpler way
and could implement the star formation processes and their feedback on
the interstellar medium with higher numerical resolution. Nevertheless,
this approach forced us to introduce a preexisting stellar
population to take the gas evolution from
Gyr.
We started our simulations much later, namely at a time when the dwarf
galaxies we wanted to analyze have already formed their old
populations. Our final goal is to study the influence of star formation
on the dark matter density profiles. In oder to more clearly isolate
this effect we needed to neglect the Hubble flow and all
heating/cooling processes that influenced the star formation at hight
redshift. Hence, by starting at lookback time of T0=-9 Gyr
we follow the phase-space description of our models in a simpler way
and could implement the star formation processes and their feedback on
the interstellar medium with higher numerical resolution. Nevertheless,
this approach forced us to introduce a preexisting stellar
population to take the gas evolution from
![]() to T0 into account. In this initial time the
to T0 into account. In this initial time the
![]() paradigm
predicts that the dwarf galaxies are the first structures to form as
scale invariant perturbations having masses greater than the Jeans mass
of isothermal perturbations at the time of recombination
(masses of
paradigm
predicts that the dwarf galaxies are the first structures to form as
scale invariant perturbations having masses greater than the Jeans mass
of isothermal perturbations at the time of recombination
(masses of
![]() ).
Hence, in this scenario we needed to consider the time to
violently relax the dark halo component within which the proto-cloud
will congregate and produce the first stars. It is clear that
these complicated phases, treated in cosmological simulations, make it
more difficult to clearly evidence and disentangle the single stellar
evolution influence on the whole gravitational potential of a single
system because two fundamental conditions we want to use are missing: equilibrium and isolation. After this initial phase and after an equilibrium configuration has been reached, say at T0=-9 Gyr, we expected that an old stellar population has already formed.
).
Hence, in this scenario we needed to consider the time to
violently relax the dark halo component within which the proto-cloud
will congregate and produce the first stars. It is clear that
these complicated phases, treated in cosmological simulations, make it
more difficult to clearly evidence and disentangle the single stellar
evolution influence on the whole gravitational potential of a single
system because two fundamental conditions we want to use are missing: equilibrium and isolation. After this initial phase and after an equilibrium configuration has been reached, say at T0=-9 Gyr, we expected that an old stellar population has already formed.
Table 1: Range of masses within which the simulations are run.
4.1 The evolution without the star formation processes
Once the model was realized we evolved the system in isolation to test
the equilibrium of the system's density profiles. The critical
parameter was of course the smoothing length of the particles, although
in the treecodes the gravitational force estimation is largely
performed through cell-cell interactions. Different studies in the
literature can be found on the best-fit tuning of the smoothing length
parameter (e.g. Dehnen 2001; Athanassoula et al. 2000; Zhan 2006,
and references therein). We mention here that different codes require
to be tuned on different softening lengths to grant the stability of
the starting model depending on the implementation of the code. The
initial conditions evolved on a special purposed hardware (GRAPE) reach
stability with
![]() .
.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13240fg3.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg80.png)
|
Figure 1:
( Left panel)
Density profile temporal evolution for the model evolved in isolation
under the action of gravity alone. The blue lines represent the dark
matter profile at the beginning (solid) of the simulation and at the
end (dashed). The red lines show the stellar profile. The baryonic
component remains exactly the same as the starting profile, hence the
red dashed line is not visible here since it coincides with the solid
red line. ( Right panel) Density temporal evolution for the same model as the right panel, evolved in isolation and
considering the most relevant star formation processes. The blue solid
line represents the dark matter profile at the beginning of the
simulation T=T0. The final profile is the
blue dashed line. The same line types are used for the stellar profile
(red lines). Intermediate thinner lines refer to intermediate
evolutionary stages:
|
| Open with DEXTER | |
As can be seen in Fig. 1
(left panel), stability is achieved within the resolution used here.
The figure represents a simulation with 35 000 particles
![]()
![]() 104. The same stability is obtained with slightly different values for the smoothing length
104. The same stability is obtained with slightly different values for the smoothing length
![]() of the dark matter, stars, and gas with a larger number of particles
of the dark matter, stars, and gas with a larger number of particles
![]()
![]() 104 and
104 and
![]()
![]() 105 for a total amount of 350 000 particles in the beginning
of the highest resolution simulation. Even if the higher resolution
would permit us to analyze regions closest to the core of the dwarf
galaxy, we will see that our chosen distance of
105 for a total amount of 350 000 particles in the beginning
of the highest resolution simulation. Even if the higher resolution
would permit us to analyze regions closest to the core of the dwarf
galaxy, we will see that our chosen distance of
![]() from the core, to which we limited our consideration due to the
smoothing length resolution of the dark matter particles,
is enough to confirm our results. In Fig. 1 (left panel), the overlapping lines represent the evolution of the system at T = T0, i.e. 9 Gyr ago, and after
from the core, to which we limited our consideration due to the
smoothing length resolution of the dark matter particles,
is enough to confirm our results. In Fig. 1 (left panel), the overlapping lines represent the evolution of the system at T = T0, i.e. 9 Gyr ago, and after
![]() ,
i.e. now (
T=T0+9=-9+9=0 Gyr), respectively. The
density profile of the model hardly changes with time as is desired,
both for dark matter profile as for the stellar component, thus
confirming that the initial conditions of our model are reasonable.
,
i.e. now (
T=T0+9=-9+9=0 Gyr), respectively. The
density profile of the model hardly changes with time as is desired,
both for dark matter profile as for the stellar component, thus
confirming that the initial conditions of our model are reasonable.
4.2 The evolution with the star formation processes
Once the equilibrium of the density profile was confirmed under the effect of gravity alone, we activated the star formation processes.
The understanding of the star formation processes was a primary task of astronomy during the second half of the last century (e.g., Silk 1987; Larson 1969) but, despite the great improvement of knowledge acquired, the micro-physics description still represents a challenge of modern astrophysics. Great improvement was made within the framework of the smooth particles hydrodynamics star formation algorithms (Katz 1992; Navarro & White 1993) which we adopt in our description in its more updated recipe as explained in Berczik (1999).
We emphasize again that we started our simulation after the old stellar populations were already formed. For instance, if it took the dwarf galaxy
![]() or 4 Gyr to accrete gas, to have it collapse and to
experience its first measurable episode of star formation, then we
assumed this equilibrium stage as our initial time of evolution, from
which we began to analyze the system (T=T0) 3 to 4 Gyr after the Big Bang.
or 4 Gyr to accrete gas, to have it collapse and to
experience its first measurable episode of star formation, then we
assumed this equilibrium stage as our initial time of evolution, from
which we began to analyze the system (T=T0) 3 to 4 Gyr after the Big Bang.
The assumed dynamical equilibrium of the model is as previously described in Sect. 4.1 for the old stellar component, the gas and the dark matter, under the effect of gravity alone. The system evolves from an initial time T0 until the present time. Since we are interested in systems with cuspy dark matter density profiles, we only present their evolution here. Further considerations on flat dark matter profile systems can be found in Sect. 6.
Depending on the initial amount of gas and on the total mass of the system, the general behavior of the system is to expel part of the gas due to the effect of SNII that gradually eject the gas to the outer part of the galaxy. Some of the gas is nevertheless conserved in the inner part of the system thanks to the steep potential well. The dwarf galaxy starts as an extremely dark matter dominated system especially in the inner part of the galaxy, where the density profile is very cuspy (M/L>200 within 5 kpc from the center). In this sense, the steepness of the dark matter profile seems to be a necessity in the initial phase of the dwarf galaxy where just a few percent of the stellar population are formed after the primordial collapse. There are at least three reasons for this:
- 1.
- If the initial dark matter density profile is not cuspy but flat, the possibility for the dwarf galaxy to survive several pericenter passages as expected for a dwarf like Sagittarius (e.g. Helmi & White 2001) becomes more problematic.
- 2.
- If the initial dark matter profile is not cuspy but flat, the efficiency of the SNII to expel the gas is expected to be higher (e.g. Bradamante et al. 1998; Read & Gilmore 2005) thus increasing the amount of primordial gas necessary to reproduce tidally triggered bursts of star formation in galaxies like e.g., Carina (see Paper II). However, this result is strictly dependent on the initial environment in which the gas collapses, and we started our simulations only after a time T0 where all these effects have already taken place.
- 3.
- Cosmological N-body simulations predict cuspy profiles (e.g. Navarro et al. 1997) with an inner slope proportional to
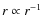 .
The asymptotic behavior for the
.
The asymptotic behavior for the 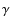 models in the inner zones predicts in the acceptable range studied here
models in the inner zones predicts in the acceptable range studied here
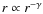 ,
including incidentally the NFW inner slope.
,
including incidentally the NFW inner slope.
It is difficult to constrain this residual fraction of gas. It seems to be a free parameter that can play a role in the periodic bursts of star formation recently suggested by Pelupessy et al. (2004) or may play a role in the dwarf evolving in an orbit where the SFR can be activated by strong tidal interactions.
As we can see from Fig. 1 for the reference model of Sect. 3, we experienced a stellar density profile evolution with the same time scale
![]() as the dark matter density profile time scale
as the dark matter density profile time scale
![]() .
The system evolves slowly over timescales of a few Gyr,
modifying its stellar profile thanks to stellar evolution: new stars
born and die interacting with the small fraction of gas to reach new
configurations of dynamical equilibrium each time
.
The system evolves slowly over timescales of a few Gyr,
modifying its stellar profile thanks to stellar evolution: new stars
born and die interacting with the small fraction of gas to reach new
configurations of dynamical equilibrium each time![]() .
We point out here that not all the literature recipes for the SF are
able to efficiently follow the gravitational changes of the baryonic
component. The code really has to ``make'' the stars in a way that the
number of particles increases regardless of the substantially
increasing computational time required. Only these prescriptions, see
e.g. Fig. 2 and Berczik & Petrov (2001); Berczik (1999); Berczik & Kravchuk (2000),
together with the correct gravitational treatment (here provided by a
devoted GRAPE hardware) permit one to correctly follow this slow change
of the gravitational potential. In Fig. 2
we plot the range of particles used to test our results and their time
evolution. The thick lines refer to the reference models and the
thinner ones to the test models as defined in Sect. 4.1.
The test model was developed to confirm the particle number
independence of our results. The slight variation on the number of dark
matter particles is due to a small evaporation in the outer part of the
dwarf that occurs at distances out of 10 kpc from the center of
the system. The number of particles for the stellar and gas components
changes depending on the star formation processes (Sect. 5.1)
as well as on the evaporation in the outer part of all the components
(gas, stars and also dark matter). The similarity of the
evolutionary trend is remarkably good from the reference model up to
the test model with the highest particle number.
.
We point out here that not all the literature recipes for the SF are
able to efficiently follow the gravitational changes of the baryonic
component. The code really has to ``make'' the stars in a way that the
number of particles increases regardless of the substantially
increasing computational time required. Only these prescriptions, see
e.g. Fig. 2 and Berczik & Petrov (2001); Berczik (1999); Berczik & Kravchuk (2000),
together with the correct gravitational treatment (here provided by a
devoted GRAPE hardware) permit one to correctly follow this slow change
of the gravitational potential. In Fig. 2
we plot the range of particles used to test our results and their time
evolution. The thick lines refer to the reference models and the
thinner ones to the test models as defined in Sect. 4.1.
The test model was developed to confirm the particle number
independence of our results. The slight variation on the number of dark
matter particles is due to a small evaporation in the outer part of the
dwarf that occurs at distances out of 10 kpc from the center of
the system. The number of particles for the stellar and gas components
changes depending on the star formation processes (Sect. 5.1)
as well as on the evaporation in the outer part of all the components
(gas, stars and also dark matter). The similarity of the
evolutionary trend is remarkably good from the reference model up to
the test model with the highest particle number.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg7.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg92.png)
|
Figure 2: Variation of the number of particles for the reference models and higher resolution test models. Black solid lines refer to the total number of particles, green dashed lines refer to the gas, red dotted lines refer the stars and blue dot-dashed lines refer to the dark matter. The reference model is marked with a thicker line. |
| Open with DEXTER | |
Once new stars are added to the stellar component, they contribute to
reshape the mass distribution (the density profile), and as a
consequence the dark matter reacts, with the same scale time
![]() by passing through several states of dynamical equilibrium. This
can be proven by simply stopping all the star formation processes and
evolving the new equilibrium configuration under the influence of
gravity alone. The phase-space configuration seems to be stable with
respect to the simple dynamical evolution
by passing through several states of dynamical equilibrium. This
can be proven by simply stopping all the star formation processes and
evolving the new equilibrium configuration under the influence of
gravity alone. The phase-space configuration seems to be stable with
respect to the simple dynamical evolution![]() .
.
We observed that the inner flattening of the dark matter halo was
accompanied by a simultaneous decrease of the density profile of the
baryonic component (Fig. 1). That is simply an indication that the final density profile has to depend at least on two parameters (other than the total mass or the central density). As an example, the family of ![]() models
or King models permits this kind of metamorphosis: we can obtain this
result by simply fixing the radius containing 90% of the mass
models
or King models permits this kind of metamorphosis: we can obtain this
result by simply fixing the radius containing 90% of the mass
![]() and expressing in this way the scale radius as a function of r90 and
and expressing in this way the scale radius as a function of r90 and ![]() .
At fixed r90 and total mass M in Eq. (1), one can easily obtain central densities that differ by a few orders of magnitude.
.
At fixed r90 and total mass M in Eq. (1), one can easily obtain central densities that differ by a few orders of magnitude.
More intuitive is the explanation of the evolution of the stellar density profile because it changed both the central density and the scale length due to the increasing number of particles and mass, while nonetheless roughly preserving the projected surface brightness.
In Fig. 3 we plotted the rotation curve
![]() of the dark matter component at the starting time T = T0 and at the end of the simulation
of the dark matter component at the starting time T = T0 and at the end of the simulation
![]() (the intermediate-time snapshots have been omitted for the sake of
clarity). The general trend expected as a consequence of the flattening
of the profile is exactly the decrease of the central part of the
rotation curve, as shown in Fig. 3.
We can however observe the small overlap of the rotation curve, which
in a two parameter density-potential pair is an indication that the
matter distribution at
(the intermediate-time snapshots have been omitted for the sake of
clarity). The general trend expected as a consequence of the flattening
of the profile is exactly the decrease of the central part of the
rotation curve, as shown in Fig. 3.
We can however observe the small overlap of the rotation curve, which
in a two parameter density-potential pair is an indication that the
matter distribution at
![]() is slightly more concentrated. A fit of the dark matter profile
showed that the outer homoeoids for the dark matter profile had
slightly contracted. The trend is generally present in our simulations
even though the effect here is minimal. Nevertheless, this is a further
indication that a good dark matter density profile has to be at least a
2-parameter model.
is slightly more concentrated. A fit of the dark matter profile
showed that the outer homoeoids for the dark matter profile had
slightly contracted. The trend is generally present in our simulations
even though the effect here is minimal. Nevertheless, this is a further
indication that a good dark matter density profile has to be at least a
2-parameter model.
The cumulative mass density profile
![]() shows this trend as well (Fig. 4). The theoretical expectation for the curves in Fig. 4
indicates that the flatter density profile curve asymptotically
converges under the cuspier density curve profile (once we
assumed the same total mass). Considering the asymptotic behavior, the
overlapping part of the final cumulative mass profile is an indication
of a slightly reduced final scale radius: the same amount of matter is
reached in inner homoeoids and starting from a central lower value as
shown in Fig. 4.
shows this trend as well (Fig. 4). The theoretical expectation for the curves in Fig. 4
indicates that the flatter density profile curve asymptotically
converges under the cuspier density curve profile (once we
assumed the same total mass). Considering the asymptotic behavior, the
overlapping part of the final cumulative mass profile is an indication
of a slightly reduced final scale radius: the same amount of matter is
reached in inner homoeoids and starting from a central lower value as
shown in Fig. 4.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg12.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg98.png)
|
Figure 3:
Rotation curve for the dark matter profile (and the stellar component)
of the reference model. The solid line represents the starting profile
at T=T0 and the dashed line the profile after
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg6.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg99.png)
|
Figure 4:
( Upper panel) Cumulative mass profile for the dark component (blue) and the stellar component (red). The starting profile is at T=T0 (solid lines) and mostly lower than the profile for time
|
| Open with DEXTER | |
Before discussing the kinematics we point out the limits of our simulations. Our finding that a two parameter dark matter density profile is favored is based on
- the flattening of the density profile at a constant total amount of mass;
- the analysis of the rotation curve and cumulative mass profile.
But only the first point is conclusive evidence for the
necessity of the two free parameters model in the dark matter component
(in addition to the total mass), while the second point comes with
an intrinsic theoretical bias and cannot be used to claim the
necessity to add a further parameter to the NFW profile. The low
reactivity of the outer homoeoids to the changes of the inner mass
distribution is expected as direct consequence ofNewton's second
theorem. This theorem describes how the total force acting on the
matter distribution out to e.g., r90,
is the same as it would be if the shells' matter were concentrated
into a point at the center of the dwarf galaxy, despite the different
radial distribution it shows in spherical approximation. Thus the
finding that the stable dark matter profile has to be at least a
two-parameter density profile is just an indication that comes from the
baryonic/non-baryonic interaction analysis and does not necessarily
rule out the one-parameter density profiles as in Navarro et al. (1997). Moreover, as already explained in Sect. 3,
a model evolved in isolation is expected to show a sharper decline of
the external profile as compared to the one resulting from the
cosmological collapse of a cube (as we effectively see by
comparing a ![]() -model with a NFW model).
-model with a NFW model).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg1.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg101.png)
|
Figure 5:
Anisotropy parameter (light green) and radial velocity dispersion (red) for the stellar component. The left scale on the y axis
is for the anisotropy parameter, the right scale for the radial
velocity dispersion parameter. The thick solid lines show the starting
stellar profile, here at T0=196 Myr, and the dotted lines show the resulting profile at
|
| Open with DEXTER | |
To investigate these processes further in detail we present below also
some chemical considerations that will help us to improve the present
theory on dwarf galaxy evolution. The idea to include some chemical
considerations emerged from the analysis of the anisotropy parameter,
defined as
![]() ,
where
,
where
![]() is the radial velocity dispersion and
is the radial velocity dispersion and
![]() is the tangential component in a suitable spherical coordinate reference system
is the tangential component in a suitable spherical coordinate reference system
![]() .
It is evident from this definition and from assuming that as for every reasonable Galactic potential
.
It is evident from this definition and from assuming that as for every reasonable Galactic potential
![]() that the anisotropy parameter
that the anisotropy parameter
![]() ,
where
,
where
![]() ,
corresponds to a system dominated by pure circular orbits
,
corresponds to a system dominated by pure circular orbits
![]() ,
in contrast to a system with
,
in contrast to a system with
![]() with pure radial orbits. As seen in Fig. 5 the system develops within the timescale
with pure radial orbits. As seen in Fig. 5 the system develops within the timescale
![]() of the flattening of the dark matter cusp a zone of increasing circular orbits fraction, roughly out to a radius
of the flattening of the dark matter cusp a zone of increasing circular orbits fraction, roughly out to a radius
![]() kpc in radial distance. The kinematics in the outer part of the galaxy are left unchanged in this isolated model
kpc in radial distance. The kinematics in the outer part of the galaxy are left unchanged in this isolated model![]() and the radial dispersion velocity profile remains basically unchanged beyond
and the radial dispersion velocity profile remains basically unchanged beyond
![]() .
Similarly the anisotropy parameter approaches unity at larger radii, getting closer to unity after
.
Similarly the anisotropy parameter approaches unity at larger radii, getting closer to unity after
![]() kpc.
This indicates how circular orbits tend to become more and more
relevant in the inner part of the galaxy when the dark matter cusp
becomes flatter. This will leave some observable traces in the radial
gradient of the chemical composition that we are now going
to explain.
kpc.
This indicates how circular orbits tend to become more and more
relevant in the inner part of the galaxy when the dark matter cusp
becomes flatter. This will leave some observable traces in the radial
gradient of the chemical composition that we are now going
to explain.
5 Chemo-dynamical evolution
5.1 Star formation recipes
The coding of the star formation processes is not the subject of our analysis. A more extended description can be found in the works by Berczik et al. (2002,2003a); Berczik (2000); Berczik & Petrov (2001); Berczik (1999); Berczik et al. (2003b). Nevertheless the robustness of our evolution was tested against the different star formation criteria that are discussed in the literature. We found that there are several physical conditions that we have to take into account to obtain the evolution of the dark matter profiles:
- A fluid element has to be instable, e.g., it has to satisfy the Jeans instability criteria
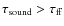 between sound speed timescale and free fall timescale.
between sound speed timescale and free fall timescale.
- For the gas particles
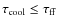 ,
the cooling timescale has to be lower than the free fall timescale
(this is also often expressed in terms of the over-density criterion
,
the cooling timescale has to be lower than the free fall timescale
(this is also often expressed in terms of the over-density criterion
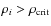 ,
i.e., the density of the gas particle i,
,
i.e., the density of the gas particle i, 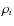 , has to be higher than a critical density
, has to be higher than a critical density
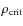 ).
).
- The efficiency of the energy that heats the ISM in a dwarf galaxy can be reduced to a few percent
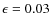 ,
say
,
say
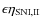 where
where
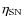 is the standard energy injection per SN explosion. This is a
result that was derived by the chemical modeling approach already
presented in the literature by e.g., Bradamante et al. (1998).
is the standard energy injection per SN explosion. This is a
result that was derived by the chemical modeling approach already
presented in the literature by e.g., Bradamante et al. (1998).
- A radius limit of the sphere of influence of a SNII event can be assumed when the sound speed of the front shock is cooled at the sound speed of the ISM. Simulations by Cioffi & Shull (1991) showed that a reasonable value is on the order of a few hundred parsec.
These are sufficient although not necessary conditions. There
are other studies that correctly reproduce the observed dynamical
effects e.g., when using dynamical times
![]() instead of the free fall time in the first criterion (e.g., Navarro & White 1993), or when using convergent fluxes with the criterion of the divergence of the velocity
instead of the free fall time in the first criterion (e.g., Navarro & White 1993), or when using convergent fluxes with the criterion of the divergence of the velocity
![]() (e.g., Carraro et al. 1998), or even applying higher values of SN efficiency (e.g., Recchi et al. 2001).
The first two criteria are universally accepted and do not require any
particular fine-tuning in our dwarf galaxy simulations to reproduce our
results
(e.g., Carraro et al. 1998), or even applying higher values of SN efficiency (e.g., Recchi et al. 2001).
The first two criteria are universally accepted and do not require any
particular fine-tuning in our dwarf galaxy simulations to reproduce our
results![]() (see Fig. 6). The last two criteria are not
tuning parameters. They are results that were already presented in the
literature many years ago. They basically act as SN-``shock absorbers''
in the dwarf galaxy environment. Thus the result we presented for the
dark matter evolution is not dependent on any physical tuned
mechanism acting on the baryonic component, nor does it require any
``special'' mechanism to explain the change of the baryonic density
profile and in turn the resulting gravitational effect it produces (the
conversion of a cuspy dark matter profile into a flat DM profile).
(see Fig. 6). The last two criteria are not
tuning parameters. They are results that were already presented in the
literature many years ago. They basically act as SN-``shock absorbers''
in the dwarf galaxy environment. Thus the result we presented for the
dark matter evolution is not dependent on any physical tuned
mechanism acting on the baryonic component, nor does it require any
``special'' mechanism to explain the change of the baryonic density
profile and in turn the resulting gravitational effect it produces (the
conversion of a cuspy dark matter profile into a flat DM profile).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg9.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg127.png)
|
Figure 6: Evolution of the star formation rate with time for the reference model. |
| Open with DEXTER | |
5.2 Chemical evolution
In our simulations we assumed that the first episode of star formation and its associated SN explosions led to gas ejection to the outer regions of the dwarf galaxy as described in e.g., Mac Low & Ferrara (1999); Lanfranchi & Matteucci (2004); Marcolini et al. (2006). This is not a direct result of our simulation because, as mentioned, we consider the evolution of a dwarf galaxy after its initial star formation episode to better control the gas fraction present at the initial stage T=T0 in our simulations.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg4.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg128.png)
|
Figure 7: The evolution of the stellar [Fe/H] over time. The contour plot shows the metalicity spread distribution with time. |
| Open with DEXTER | |
In Fig. 7 we consider the metalicity evolution with time, without considering its spatial dependence (see Fig. 11), by plotting the trend of iron enrichment. Newly formed stars peak above the mean value of iron,
![]() which in turn increases with time and is strongly dependent on the
initial chemical composition assumed for the ISM and for the stellar
component. We are actually not interested to reproduce any specific
observed trend, but wish to understand the expected rate of enrichment.
Starting with a rather metal-poor population (
which in turn increases with time and is strongly dependent on the
initial chemical composition assumed for the ISM and for the stellar
component. We are actually not interested to reproduce any specific
observed trend, but wish to understand the expected rate of enrichment.
Starting with a rather metal-poor population (
![]() dex),
we were able to see the general rate of enrichment independent from the
specific initial conditions that differ from galaxy to galaxy in the
true Universe. It is evident that a mean range of
dex),
we were able to see the general rate of enrichment independent from the
specific initial conditions that differ from galaxy to galaxy in the
true Universe. It is evident that a mean range of
![]() can be covered in
can be covered in
![]() of isolated evolution, provided that the system has an initial range of
rather low metalicity and then undergoes rapid early enrichment in the
initial star formation episodes that need to have taken place during
the first, say, 3 Gyr (e.g. Lanfranchi & Matteucci 2004; Mac Low & Ferrara 1999). We note that observationally such a rapid initial increase does seem to take place, see e.g., Koch et al. (2007b,a),
but we point out that a direct comparison with any real dwarf galaxy
cannot be carried out here. With the trend here evidenced we wish to
reproduce an ``upper-limit'' to the observed chemical enrichment. Thus
the results presented here are a reference model that can be used to
impose an upper limit constraint.
of isolated evolution, provided that the system has an initial range of
rather low metalicity and then undergoes rapid early enrichment in the
initial star formation episodes that need to have taken place during
the first, say, 3 Gyr (e.g. Lanfranchi & Matteucci 2004; Mac Low & Ferrara 1999). We note that observationally such a rapid initial increase does seem to take place, see e.g., Koch et al. (2007b,a),
but we point out that a direct comparison with any real dwarf galaxy
cannot be carried out here. With the trend here evidenced we wish to
reproduce an ``upper-limit'' to the observed chemical enrichment. Thus
the results presented here are a reference model that can be used to
impose an upper limit constraint.
In Fig. 8 we plot the
number of SN events and PN as a function of time. This helps to explain
how the spread in the previous figures originates. In line with
the arguments of different authors (e.g. Marcolini et al. 2006) we see how the SNIa, mainly responsible for the iron enrichment of the ISM, operate to fill gradually the tail of the
![]() diagram, even though their number is only a few percent of the SNII. This can indeed be deduced from Fig. 8,
where the number evolution of SN events is presented as a function
of time. Depending on the chemical enrichment we assumed for the oldest
stellar population, at the end of the 8 to 9 Gyr of evolution
we obtained a mean present day metalicity of
diagram, even though their number is only a few percent of the SNII. This can indeed be deduced from Fig. 8,
where the number evolution of SN events is presented as a function
of time. Depending on the chemical enrichment we assumed for the oldest
stellar population, at the end of the 8 to 9 Gyr of evolution
we obtained a mean present day metalicity of
![]() integrated along the radial direction (cf. Lanfranchi & Matteucci 2004; Marcolini et al. 2006).
integrated along the radial direction (cf. Lanfranchi & Matteucci 2004; Marcolini et al. 2006).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg11.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg135.png)
|
Figure 8: Cumulative number of SNII events in red, SNIa in magenta and planetary nebulae in gray. |
| Open with DEXTER | |
The initial dominance of SNII is partially suppressed in this model
because the ad-hoc conditions avoid the initial bursts of star
formation (see Fig. 9) and the SNIa rate decrease with time as e.g., predicted in Matteucci & Recchi 2001). The reason is that in the collapse of the proto-cloud the star formation is enhanced by the increasing density (
![]() ),
thus favoring the SN events, while in our simulation this phase
was neglected and a starting Population II sample is always
initially present at T=T0.
),
thus favoring the SN events, while in our simulation this phase
was neglected and a starting Population II sample is always
initially present at T=T0.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg8.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg137.png)
|
Figure 9: Here the SNIa rate is presented. We find agreement with the literature prediction (e.g. Greggio & Renzini 1983) of a decreasing SNIa rate with time (see also Matteucci & Recchi 2001). |
| Open with DEXTER | |
Prior to the onset of contributions of SNIa, stellar metallicities (
![]() )
tend to increase while the
)
tend to increase while the
![]() ratio remains rougly constant. This leads to a flat, plateau-like feature at low metallicities when plotting
ratio remains rougly constant. This leads to a flat, plateau-like feature at low metallicities when plotting
![]() vs.
vs.
![]() (Lanfranchi & Matteucci 2004; Marcolini et al. 2006). Since our simulations only start after the formation of the old stellar population, our Fig. 10 does not show such a plateau. Instead we see the characteristic decline of
(Lanfranchi & Matteucci 2004; Marcolini et al. 2006). Since our simulations only start after the formation of the old stellar population, our Fig. 10 does not show such a plateau. Instead we see the characteristic decline of
![]() with increasing
with increasing
![]() due to the combined action of Fe production in SNIa and
due to the combined action of Fe production in SNIa and ![]() element production in SNII.
element production in SNII.
Moreover, differences in the initial gas fractions affect the
metallicities reached during the first episodes of star formation.
Lower gas fractions imply less enrichment. Figure 10 shows the results for different initial gas fractions of ![]() ,
,
![]() and
and ![]() as an example. These result in differences in the amount of gas that
the galaxy is able to retain at a fixed dark matter amount. Of course,
the true behavior of a dwarf galaxy depends on its intrinsic
properties, but also on the tidal interaction that may activate
SF processes.
as an example. These result in differences in the amount of gas that
the galaxy is able to retain at a fixed dark matter amount. Of course,
the true behavior of a dwarf galaxy depends on its intrinsic
properties, but also on the tidal interaction that may activate
SF processes.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg2.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg142.png)
|
Figure 10:
The evolution of the |
| Open with DEXTER | |
5.3 Radial chemical gradients
We now turn to the radial dependence of the chemical composition. The spatial distribution of stellar populations of different ages and metalicities is a matter of debate in different studies (see below). Here we want to show what is expected from the simple evolution of our isolated synthetic model. Observationally one tends to find gradients that show that the younger and/or more metal-rich populations are more centrally concentrated (e.g. Harbeck et al. 2001; Koch et al. 2006). The general expectation is that the SNe generate local enrichment at the beginning of the evolution and that then diffusion tends to erase any radial gradient with time. This affects both iron and oxygen, but on different time scales. While oxygen is produced by SNII and so distributed across the entire dwarf galaxy quite fast, iron is expected to be more concentrated in the central regions where the SNIa are more densely located (e.g. Marcolini et al. 2006). As result the gradient is expected to be steeper and longer lasting for iron, while flatter and shorter in duration for oxygen.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13240fg5.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg143.png)
|
Figure 11:
Radial dependence of the mean
|
| Open with DEXTER | |
We suggest a possible link between the timescale of the change of the
dark matter density profiles and of the formation of chemical gradients
that also involve the evolution of the stellar orbit families.
If we consider Fig. 11 together with the evolution of the anisotropy parameter in Fig. 5,
we see how the progressive growth of the number of stars and the
resulting changes of the stellar density profile cause a change in the
overall gravitational potential, leading to a new equilibrium
configuration for the dark matter, which changes its profile from cuspy
to flat. For the stellar component we can study the evolution of the
orbits, which helps us to interpret the gradient and the link with the
dark matter. As can be seen in Fig. 11,
in the first few Gyr the gradient is present only in the central
zones where the star formation is more intense due to the higher
density. The spatial extent of the gradient encompasses up to
1 kpc after 1 Gyr, up to 2 kpc after
3 Gyr etc. This effect is initially due to the higher
fraction of radial orbits (Fig. 5)
which mix the inner and outer regions of the system with high
efficiency. As time passes the new density profile generated by the
newly born stars gives rise to a growing fraction of circular orbits
(preferred when a system is slowly evolving, because they are closer to
the equilibrium and at lower energy). This can also be inferred from
the slow decrease of the radial velocity dispersion, which leads to a
decrease of the anisotropy parameter. This is happening within the
limiting radius
![]() ,
within which the chemical gradient and the anisotropy parameter develop
for the 9 Gyr of our simulation. While the fraction of circular
orbits is increased (corresponding to the decrease of the anisotropy
parameter seen in Fig. 5)
the mixing efficiency decreases, because there are fewer orbits that
extend to the galaxy outskirts. This together with the gradual decrease
of the gas fraction acts to slow the radial expansion of the zones
where the chemical gradient can be evidenced: as seen in Fig. 11, the lines for T=7 Gyr, T=8 Gyr, T=9 Gyr lie closer and closer to the dotted line (T=T0+9 Gyr) for r<5 kpc. Evidence of such a radial gradient is already present in the literature on N-body simulations, see e.g. Chiosi & Carraro (2002), where the massive spectrum of the elliptical galaxy and the role of the stellar winds are further investigated.
,
within which the chemical gradient and the anisotropy parameter develop
for the 9 Gyr of our simulation. While the fraction of circular
orbits is increased (corresponding to the decrease of the anisotropy
parameter seen in Fig. 5)
the mixing efficiency decreases, because there are fewer orbits that
extend to the galaxy outskirts. This together with the gradual decrease
of the gas fraction acts to slow the radial expansion of the zones
where the chemical gradient can be evidenced: as seen in Fig. 11, the lines for T=7 Gyr, T=8 Gyr, T=9 Gyr lie closer and closer to the dotted line (T=T0+9 Gyr) for r<5 kpc. Evidence of such a radial gradient is already present in the literature on N-body simulations, see e.g. Chiosi & Carraro (2002), where the massive spectrum of the elliptical galaxy and the role of the stellar winds are further investigated.
We did not include galactic winds, thus excluding them as a possible
explanation of the chemical mixing and consequently a faster
disappearance of the
![]() gradient.
We point out that recently the same result was found with a different
mechanism, but still avoiding stellar winds, by Marcolini et al. (2008).
We agree with the general result presented in their paper and extend it
by showing that the reshaping of the dark matter profile seems to work
on the same time scale of the metalicity gradient formation. The
overlap of the shells of the SNII is also evidenced in Fig. 12. In this figure an especially intense episode in the time evolution around
T0+T=0.730 Myr is plotted where two
SN events are clearly visible (in red) and the remnants of at
least other two other ones are still evident (in orange/yellow).
Different spots of higher temperature/sound velocity are shown in the
velocity surface cut arbitrary tilted by 45 degrees w.r.t. the
vertical axis Z. This is a convenient representation of the velocity (or temperature) map that is partially comparable with Fig. 3 of Cioffi & Shull (1991), but here in a full 3D description. We clearly see how two green shells of irregular shape (sound speed contour of
gradient.
We point out that recently the same result was found with a different
mechanism, but still avoiding stellar winds, by Marcolini et al. (2008).
We agree with the general result presented in their paper and extend it
by showing that the reshaping of the dark matter profile seems to work
on the same time scale of the metalicity gradient formation. The
overlap of the shells of the SNII is also evidenced in Fig. 12. In this figure an especially intense episode in the time evolution around
T0+T=0.730 Myr is plotted where two
SN events are clearly visible (in red) and the remnants of at
least other two other ones are still evident (in orange/yellow).
Different spots of higher temperature/sound velocity are shown in the
velocity surface cut arbitrary tilted by 45 degrees w.r.t. the
vertical axis Z. This is a convenient representation of the velocity (or temperature) map that is partially comparable with Fig. 3 of Cioffi & Shull (1991), but here in a full 3D description. We clearly see how two green shells of irregular shape (sound speed contour of
![]() )
from two different SN remnants are overlapping.
)
from two different SN remnants are overlapping.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13240fg10.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg145.png)
|
Figure 12: Shells of isovelocity for the sound speed of the gas component. The sketch shows a cut tilted by 45 degrees w.r.t. the vertical axis Z to show the overlapping shells of isovelocity (see text for details). |
| Open with DEXTER | |
On the one hand, we are able to follow the behavior of the orbits and
the evolution of the density profiles. On the other hand we cannot
reach the resolution of the chemical codes used by Marcolini et al. (2006)
and are thus prevented from confirming the general efficiency of the
mechanism invoked by these authors. Nevertheless we sustain their
complementary picture, because we also find the possibility of
overlapping polluted regions of the SNII (see e.g. Fig. 12).
In this figure the isocontours of the sound speed velocity of the gas
component are shown. A limiting radius for the sphere of influence
of the SNII event feedback on the ISM is assumed when the sound
speed of the front shock is cooled at the sound speed of the ISM, here
![]() (see Sect. 3 and Cioffi & Shull 1991). This permits it to have overlapping phenomena of the shock fronts in the dwarf galaxies as proposed by Marcolini et al. (2008).
(see Sect. 3 and Cioffi & Shull 1991). This permits it to have overlapping phenomena of the shock fronts in the dwarf galaxies as proposed by Marcolini et al. (2008).
6 Conclusions, discussion and limits of the approach
We focused our attention on the problem of the dark matter density profiles by investigating the apparent incongruence between dynamical theoretical predictions of a cuspy dark matter profile and the observations that indicate a flatter profile. With our simple description based on the ``classical'' approach of smoothed particles hydrodynamics (e.g. Hernquist & Katz 1989) we obtained the results that we briefly summarize here.
The classical description of the star formation processes seems to be
sufficient to change a cuspy profile into a flatter one. This is shown
with the classical smoothed particles approach to the hydrodynamic
equations of motion completed with the star formation criteria based on
the Jeans theory. The evolution of dark matter profiles could offer a
natural explanation for the apparent flat density profiles found in
observations (Burkert 1995; de Blok 2005; de Blok & Bosma 2002; Gentile et al. 2005)
once applied in a realistic context. If we introduce our theory in
the context of the cosmological hierarchical merging picture, where the
dwarf galaxies are the first stellar population systems that form, the
theory developed here predicts that today the star formation processes
should have flatten all the initially cuspy dark matter density
profiles (for the range in masses explored). Any dwarf galaxy that
contains a stellar population older than, say 8 Gyr,
is expected to have a flat dark matter profile, because either the
tidal gravitational effect has changed the dark matter profile,
or because internal star formation processes acted on the dwarf in
isolation as presented here. The combination of both effects is
expected to accelerate the profile flattening by tidally activating and
enhancing the star formation processes. We point out here that the dark
matter density profile change happens as soon as the star formation
processes act to modify the gravitational equilibrium of the stellar
component and, in turn, the gravitational equilibrium of the dark
matter. Once the star formation efficiency is reduced, i.e. the
stellar over gas fraction exceeds the smaller value predicted in
Table 1,
the effect is minor. An initially very gas deficient dwarf galaxy
cannot experience this profile change. On the other hand, galaxies
which reach dynamical equilibrium with a high amount of gas still bound
to the system (say
![]() at T>T0) do not have observational counterparts because they produce a dwarf system with super-solar
at T>T0) do not have observational counterparts because they produce a dwarf system with super-solar
![]() (see e.g. Fig. 10). Nevertheless dwarf galaxies with an initial old stellar population of less than
(see e.g. Fig. 10). Nevertheless dwarf galaxies with an initial old stellar population of less than
![]() probably belong to a different dynamical regime that is not of interest for us here.
probably belong to a different dynamical regime that is not of interest for us here.
By analyzing the time evolution of the dark matter profiles, we extensively investigated their dynamical properties and showed the necessity for at least a two free parameter density model (in addition to the total mass) to correctly represent the shape resulting from the baryonic/non baryonic interaction. This is a result partially dependent on the isolation of the model and does necessarily rule out NFW profiles, which are obtained only in a baryon-free simulations.
We used an extremely strongly peaked cuspy DM profile in
our simulations to study the effect expected for a very deep potential
well for the dark matter profile. As a consequence these
phenomena act even on smaller time scales for a central shallower dark
matter density peak or for small M/L ratios. The same effect, in a different cosmological context, was described by Mashchenko et al. (2006), although they derived a very short timescale for the effect (
![]() Myr). The most plausible explanation for their extremely short timescale
Myr). The most plausible explanation for their extremely short timescale
![]() is an ``overheating'' by SN of the interstellar medium. The role
of the SN feedback (especially the SNII sphere of influence
and the
is an ``overheating'' by SN of the interstellar medium. The role
of the SN feedback (especially the SNII sphere of influence
and the
![]() )
is more carefully taken in consideration in our present study compared
to earlier work by other authors. This leads us in a natural way to a
longer
)
is more carefully taken in consideration in our present study compared
to earlier work by other authors. This leads us in a natural way to a
longer
![]() ,
which presents attractive advantages. In the context of dwarf
galaxies tidally perturbed by the gravitational field of a primary host
(i.e., a major galaxy, or a cluster of galaxies) the
existence of deeply embedded systems (e.g. Sagittarius in
our MW) could become more problematic whenever the orbital
pericenter lies close to the center of the hosting system if
,
which presents attractive advantages. In the context of dwarf
galaxies tidally perturbed by the gravitational field of a primary host
(i.e., a major galaxy, or a cluster of galaxies) the
existence of deeply embedded systems (e.g. Sagittarius in
our MW) could become more problematic whenever the orbital
pericenter lies close to the center of the hosting system if
![]() is as short as predicted by Mashchenko et al. (2006).
Our models do not suffer this problem, because the cuspy profile in our
case is lasting several Gyr and is gradually flattened.
As a result we are easily able to save the bulk of the
orbiting dwarf galaxy around a primary system (Pasetto et al. 2010). A second difference is that we treat completely isolated models, while Mashchenko et al. (2006)
have to work with interacting objects. This offers us the advantage to
eliminate spurious perturbations and to have a clean determination of
the role of star formation alone. The peculiar orbital path of every
different dwarf galaxy when evolved in interaction has a determining
role on its SFH and on the density profile evolution. Our modeling of
isolated system offers an easier analysis and theoretical
interpretation of the results.
is as short as predicted by Mashchenko et al. (2006).
Our models do not suffer this problem, because the cuspy profile in our
case is lasting several Gyr and is gradually flattened.
As a result we are easily able to save the bulk of the
orbiting dwarf galaxy around a primary system (Pasetto et al. 2010). A second difference is that we treat completely isolated models, while Mashchenko et al. (2006)
have to work with interacting objects. This offers us the advantage to
eliminate spurious perturbations and to have a clean determination of
the role of star formation alone. The peculiar orbital path of every
different dwarf galaxy when evolved in interaction has a determining
role on its SFH and on the density profile evolution. Our modeling of
isolated system offers an easier analysis and theoretical
interpretation of the results.
We tried to link the dark matter profile change with an
observable property. A suggested indication in the paper is the
chemical radial gradient of metalicity. We performed an experiment that
shows how a
![]() radial
gradient may originate, in absence of galactic winds,
as simply a result of the baryonic reshaping of the density
profiles on a timescale compatible with the dark matter profile
reshaping. Thus in this model the presence of a radial gradient is
always expected in the evolved dwarf as consequence of a smaller
anisotropy parameter and a flat dark matter profile shape. Finally, we
want to point out a few general caveats:
radial
gradient may originate, in absence of galactic winds,
as simply a result of the baryonic reshaping of the density
profiles on a timescale compatible with the dark matter profile
reshaping. Thus in this model the presence of a radial gradient is
always expected in the evolved dwarf as consequence of a smaller
anisotropy parameter and a flat dark matter profile shape. Finally, we
want to point out a few general caveats:
- The fraction of gas has generally to be assumed as a free parameter (within the range indicated in Table 1) both in isolated and orbiting dwarf galaxies. We expect that different contents of gas left in the primordial dwarf galaxy can cause different star formation histories especially when the system evolves in orbit around a more massive host (e.g. Mayer et al. 2001b; Pasetto et al. 2003), leading to differences in the baryonic and dark matter phase space re-filling. We started with an already present stellar population formed in isolation. We will show in Pasetto et al. (2010) that the gas consumption is mostly led by the orbit evolution.
- Another type of observed SFH is the one presented by local systems as Dra and UMi. These systems show long-lasting early star formation episodes that led to considerable chemical enrichment. Obviously a substantial amount of the gas must thus have been retained in this early period (of, say, 13-10 Gyr). When this type of system lies within the well of an hosting system, the major role in the density profiles evolution is surely played by the external environment. Even in an absence of gas, the tidal stripping is able to smooth system irregularities and to convert them in dSph (e.g., Mayer et al. 2001a). This effect is shown to be efficient also in the MW dwarf companions (e.g., Pasetto et al. 2003) by morphologically evolving their density profiles. By extending these arguments to the more crowded cluster of galaxies (as Coma or Virgo), we enter the galaxy harassment regime (Moore et al. 1996) that is a pure gravitational effect and on which the literature has still put too few constraints from the star formation and chemical point of view.
- While the trend that leads to the chemical radial gradient
is universally evident across the range of masses explored
(and also generally present in the more extended sample of the
elliptical galaxies, see, e.g. Chiosi & Carraro 2002), its gradient slope is not.
![$\frac{{{\rm d}\left[ {\rm Fe/H} \right]}}{{{\rm d}r}}$](/articles/aa/full_html/2010/06/aa13240-09/img152.png) shows a strong dependence on the initial fraction of gas and stars that is not studied here.
shows a strong dependence on the initial fraction of gas and stars that is not studied here.
- The possible role of the triaxiality of the system is not
investigated here. This is expected to play a minor role for the range
of masses here investigated. Nevertheless the link between the
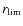 as defined in this paper and the scale length of the model
as defined in this paper and the scale length of the model 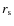 for
the models here adopted has still to be investigated even for the more
general class of elliptical galaxies and is the subject of a
forthcoming study (Pasetto et al., in prep.).
for
the models here adopted has still to be investigated even for the more
general class of elliptical galaxies and is the subject of a
forthcoming study (Pasetto et al., in prep.).
We thank C. Chiappini, F. Matteucci and C. Chiosi for useful discussions. We thank the referee G. Lanfranchi for useful comments. Simulations were performed on the GRACE supercomputer (grants I/80 041-043 of the Volkswagen Foundation and 823.219-439/30 and /36 of the Ministry of Science, Research and the Arts of Baden-Württemberg). P.B. acknowledges the special support by the NAS Ukraine under the Main Astronomical Observatory GRAPE/GRID computing cluster project. P.B.'s studies are also partially supported by the program Cosmomicrophysics of NAS Ukraine. R.S. is supported by the Chinese Academy of Sciences Visiting Professorship for Senior International Scientists, Grant Number 2009S1-5 (The Silk Road Project).
References
- Aparicio, A., Carrera, R., & Martínez-Delgado, D. 2001, AJ, 122, 2524 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Fady, E., Lambert, J. C., & Bosma, A. 2000, MNRAS, 314, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Gilmore, G., & Irwin, M. 2005, MNRAS, 359, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J. D. 2004, Phys. Rev. D, 70, 083509 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Ferraro, F. R., Origlia, L., et al. 2002, AJ, 124, 3222 [NASA ADS] [CrossRef] [Google Scholar]
- Berczik, P. 1999, A&A, 348, 371 [NASA ADS] [Google Scholar]
- Berczik, P. 2000, Kinematika i Fizika Nebesnykh Tel Supplement, 3, 91 [NASA ADS] [Google Scholar]
- Berczik, P., & Kravchuk, S. G. 2000, Astron. Astrophys. Trans., 18, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Berczik, P. P., & Petrov, M. I. 2001, Kinematika i Fizika Nebesnykh Tel, 17, 213 [NASA ADS] [Google Scholar]
- Berczik, P., Hensler, G., Theis, C., & Spurzem, R. 2002, Ap&SS, 281, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Berczik, P., Hensler, G., Theis, C., & Spurzem, R. 2003a, Ap&SS, 284, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Berczik, P., Hensler, G., Theis, C., & Spurzem, R. 2003b, Commmunications of the Konkoly Observatory Hungary, 103, 155 [NASA ADS] [Google Scholar]
- Berczik, P., Hensler, G., Theis, C., & Spurzem, R. 2006, in Presentation from the 1st SPHERIC Workshop, Rome, Italy, May 2006 [Google Scholar]
- Berczik, P., Nakasato, N., Berentzen, I., Spurzem, R., & Marcus, G. 2007, in SPHERIC - Smoothed Particle Hydrodynamics European Research Interest Community, 5 [Google Scholar]
- Bode, P., Ostriker, J. P., & Turok, N. 2001, ApJ, 556, 93 [Google Scholar]
- Bradamante, F., Matteucci, F., & D'Ercole, A. 1998, A&A, 337, 338 [NASA ADS] [Google Scholar]
- Burkert, A. 1995, ApJ, 447, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Carney, B. W., & Seitzer, P. 1986, AJ, 92, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G., Lia, C., & Chiosi, C. 1998, MNRAS, 297, 1021 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chiosi, C., & Carraro, G. 2002, MNRAS, 335, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Cioffi, D. F., & Shull, J. M. 1991, ApJ, 367, 96 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2005, A&A, 436, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Blok, W. J. G. 2005, ApJ, 634, 227 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., & Bosma, A. 2002, A&A, 385, 816 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dehnen, W. 1993, MNRAS, 265, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 2001, MNRAS, 324, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Dolphin, A. E. 2002, MNRAS, 332, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Burkert, A., Salucci, P., Klein, U., & Walter, F. 2005, ApJ, 634, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Wilkinson, M. I., Wyse, R. F. G., et al. 2007, ApJ, 663, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y., & Hamilton, A. J. S. 2002, MNRAS, 334, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, O. Y., & Zhao, H. 2002, MNRAS, 333, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Grebel, E. K. 1997, in Rev. Mod. Astron. 10, ed. R. E. Schielicke, 29 [Google Scholar]
- Grebel, E. K. 1999, in The Stellar Content of Local Group Galaxies, ed. P. Whitelock, & R. Cannon, IAU Symp., 192, 17 [Google Scholar]
- Grebel, E. K., Gallagher, III, J. S., & Harbeck, D. 2003, AJ, 125, 1926 [NASA ADS] [CrossRef] [Google Scholar]
- Greggio, L., & Renzini, A. 1983, A&A, 118, 217 [NASA ADS] [Google Scholar]
- Harbeck, D., Grebel, E. K., Holtzman, J., et al. 2001, AJ, 122, 3092 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, E., Navarro, J. F., Taylor, J. E., Stadel, J., & Quinn, T. 2003, ApJ, 584, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., & White, S. D. M. 2001, MNRAS, 323, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Hensler, G., Theis, C., & Gallagher, J. S., I. 2004, A&A, 426, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernquist, L., & Katz, N. 1989, ApJS, 70, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley-Keller, D., Mateo, M., & Nemec, J. 1998, AJ, 115, 1840 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M., & Hatzidimitriou, D. 1995, MNRAS, 277, 1354 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, N. 1992, ApJ, 391, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Gottlöber, S., Kravtsov, A. V., & Khokhlov, A. M. 1999a, ApJ, 516, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Kravtsov, A. V., Valenzuela, O., & Prada, F. 1999b, ApJ, 522, 82 [Google Scholar]
- Koch, A., Grebel, E. K., Wyse, R. F. G., et al. 2006, AJ, 131, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Grebel, E. K., Kleyna, J. T., et al. 2007a, AJ, 133, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Wilkinson, M. I., Kleyna, J. T., et al. 2007b, ApJ, 657, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Grebel, E. K., Gilmore, G. F., et al. 2008, AJ, 135, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Lanfranchi, G. A., & Matteucci, F. 2004, MNRAS, 351, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 405 [NASA ADS] [Google Scholar]
- Mac Low, M., & Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Marcolini, A., D'Ercole, A., Brighenti, F., & Recchi, S. 2006, MNRAS, 371, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Marcolini, A., D'Ercole, A., Battaglia, G., & Gibson, B. K. 2008, MNRAS, 386, 2173 [NASA ADS] [CrossRef] [Google Scholar]
- Marzke, R. O., & da Costa, L. N. 1997, AJ, 113, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Mashchenko, S., Couchman, H. M. P., & Wadsley, J. 2006, Nature, 442, 539 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mateo, M. L. 1998, ARA&A, 36, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Mateo, M., Olszewski, E. W., Pryor, C., Welch, D. L., & Fischer, P. 1993, AJ, 105, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Recchi, S. 2001, ApJ, 558, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L., Governato, F., Colpi, M., et al. 2001a, ApJ, 559, 754 [Google Scholar]
- Mayer, L., Governato, F., Colpi, M., et al. 2001b, Ap&SS, 276, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Mighell, K. J. 1990a, A&AS, 82, 1 [NASA ADS] [Google Scholar]
- Mighell, K. J. 1990b, A&AS, 82, 207 [NASA ADS] [Google Scholar]
- Mighell, K. J. 1992, Proc. Astron. Soc. Aust., 10, 83 [NASA ADS] [Google Scholar]
- Mighell, K. J. 1997, AJ, 114, 1458 [NASA ADS] [CrossRef] [Google Scholar]
- Monelli, M., Pulone, L., Corsi, C. E., et al. 2003a, AJ, 126, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Monelli, M., Walker, A. R., Bono, G., et al. 2003b, Mem. Soc. Astron. Ital., 74, 909 [NASA ADS] [Google Scholar]
- Monelli, M., Walker, A. R., Bono, G., et al. 2004a, Mem. Soc. Astron. Ital. Suppl., 5, 65 [NASA ADS] [Google Scholar]
- Monelli, M., Walker, A. R., Bono, G., et al. 2004b, in Variable Stars in the Local Group, ed. D. W. Kurtz, & K. R. Pollard, IAU Colloq., 193, ASP Conf. Ser., 310, 133 [Google Scholar]
- Monelli, M., Walker, A. W., Bono, G., et al. 2004c, Mem. Soc. Astron. Ital., 75, 114 [NASA ADS] [Google Scholar]
- Monelli, M., Bono, G., Nonino, M., et al. 2006a, Photometry and Spectroscopy of Bright Stars in the Carina dSph Galaxy, ed. S. Randich, & L. Pasquini, 272 [Google Scholar]
- Monelli, M., Nonino, M., Bono, G., et al. 2006b, Mem. Soc. Astron. Ital., 77, 270 [NASA ADS] [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999a, ApJ, 524, L19 [Google Scholar]
- Moore, B., Quinn, T., Governato, F., Stadel, J., & Lake, G. 1999b, MNRAS, 310, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M., Yoshii, Y., Tsujimoto, T., & Nomoto, K. 1997, ApJ, 478, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M., Ferrara, A., & Madau, P. 2002, ApJ, 571, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M., Umemura, M., & Ferrara, A. 2004, ApJ, 613, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Mould, J., & Aaronson, M. 1983, ApJ, 273, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, R. R., Majewski, S. R., Zaggia, S., et al. 2006, ApJ, 649, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, R. R., Majewski, S. R., & Johnston, K. V. 2008, ApJ, 679, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Murakami, I., & Babul, A. 1999, MNRAS, 309, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., & White, S. D. M. 1993, MNRAS, 265, 271 [NASA ADS] [Google Scholar]
- Navarro, J. F., & Steinmetz, M. 2000, ApJ, 538, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Eke, V. R., & Frenk, C. S. 1996, MNRAS, 283, L72 [NASA ADS] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Hayashi, E., Power, C., et al. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Pasetto, S., Chiosi, C., & Carraro, G. 2003, A&A, 405, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasetto, S., Grebel, E., Berczik, P., Spurzem, R., & Chiosi, C. 2010, A&A, submitted [Google Scholar]
- Pelupessy, F. I., van der Werf, P. P., & Icke, V. 2004, A&A, 422, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piatek, S., Pryor, C., Olszewski, E. W., et al. 2003, AJ, 126, 2346 [Google Scholar]
- Piatek, S., Pryor, C., Olszewski, E. W., et al. 2004, AJ, 128, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. I., & Gilmore, G. 2005, MNRAS, 356, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Matteucci, F., & D'Ercole, A. 2001, MNRAS, 322, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzi, L., Held, E. V., Bertelli, G., & Saviane, I. 2003, ApJ, 589, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzi, L., Held, E. V., Bertelli, G., & Saviane, I. 2004, Mem. Soc. Astron. Ital., 75, 110 [Google Scholar]
- Shetrone, M. D., Côté, P., & Sargent, W. L. W. 2001, ApJ, 548, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 1987, in Star Forming Regions, ed. M. Peimbert, & J. Jugaku, IAU Symp., 115, 663 [Google Scholar]
- Slyz, A. D., Devriendt, J. E. G., Bryan, G., & Silk, J. 2005, MNRAS, 356, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., & Steinhardt, P. J. 2000, Phys. Rev. Lett., 84, 3760 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Spurzem, R., Berczik, P., Marcus, G., et al. 2009, Comput. Sci., 23, 231 [Google Scholar]
- Tegmark, M., Blanton, M. R., & Strauss, M. A. 2004, ApJ, 606, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S., Richstone, D. O., Byun, Y.-I., et al. 1994, AJ, 107, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Tyson, J. A., Kochanski, G. P., & dell'Antonio, I. P. 1998, ApJ, 498, L107 [Google Scholar]
- Zhan, H. 2006, ApJ, 639, 617 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... matter
![[*]](/icons/foot_motif.png)
- Hereafter we identify baryonic matter with the stellar component; the dark matter will generally be called not-baryonic matter even if its nature could be baryonic as for baryonic-dark-matter objects like MACHOs or brown dwarfs.
- ... simulations
![[*]](/icons/foot_motif.png)
- The definition of T0 is provided in the following section.
- ... time
![[*]](/icons/foot_motif.png)
- This is obtained whenever the cell opening parameter of the
treecode keeps a conservative value, say
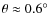 to grant a better energy conservation, or when a more extensive use of
the GRAPE hardware is adopted (e.g., Berczik et al. 2007,2006).
to grant a better energy conservation, or when a more extensive use of
the GRAPE hardware is adopted (e.g., Berczik et al. 2007,2006).
- ... evolution
![[*]](/icons/foot_motif.png)
- This might seem a numerical test on the stability of the equilibrium configuration, but it is not, because it is model dependent. The treecode approach prefers the cell-cell force computation, for distant interactions by reducing the role played by the softening length (which is, on the other hand, dependent on the growing number of particles used in the systems). The stability of the equilibrium configurations will not be the subject of further investigation here.
- ... model
![[*]](/icons/foot_motif.png)
- Any further investigation of the link between the scale
length of the starting model
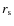 and this limiting distance is not the subject of this paper.
Nevertheless, when evolving this isolated system in an orbit around a
host system, we expect that the external tidal force can perturb any
relation that may exist between this limiting radius
and this limiting distance is not the subject of this paper.
Nevertheless, when evolving this isolated system in an orbit around a
host system, we expect that the external tidal force can perturb any
relation that may exist between this limiting radius
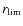 and the scale length
and the scale length 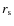 .
.
- ... results
![[*]](/icons/foot_motif.png)
- The only slight modification of the Jeans instability
criterion is for of the presence of magnetic fields. In this situation
also the first criterion can be slightly modified in favor of a
critical mass depending on the Alfv
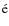 n and the sound speeds. Despite
their relevance in the collapse and fragmentation of cold clouds,
magnetic considerations were not investigated in our simulations.
n and the sound speeds. Despite
their relevance in the collapse and fragmentation of cold clouds,
magnetic considerations were not investigated in our simulations.
All Tables
Table 1: Range of masses within which the simulations are run.
All Figures
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13240fg3.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg80.png)
|
Figure 1:
( Left panel)
Density profile temporal evolution for the model evolved in isolation
under the action of gravity alone. The blue lines represent the dark
matter profile at the beginning (solid) of the simulation and at the
end (dashed). The red lines show the stellar profile. The baryonic
component remains exactly the same as the starting profile, hence the
red dashed line is not visible here since it coincides with the solid
red line. ( Right panel) Density temporal evolution for the same model as the right panel, evolved in isolation and
considering the most relevant star formation processes. The blue solid
line represents the dark matter profile at the beginning of the
simulation T=T0. The final profile is the
blue dashed line. The same line types are used for the stellar profile
(red lines). Intermediate thinner lines refer to intermediate
evolutionary stages:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg7.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg92.png)
|
Figure 2: Variation of the number of particles for the reference models and higher resolution test models. Black solid lines refer to the total number of particles, green dashed lines refer to the gas, red dotted lines refer the stars and blue dot-dashed lines refer to the dark matter. The reference model is marked with a thicker line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg12.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg98.png)
|
Figure 3:
Rotation curve for the dark matter profile (and the stellar component)
of the reference model. The solid line represents the starting profile
at T=T0 and the dashed line the profile after
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg6.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg99.png)
|
Figure 4:
( Upper panel) Cumulative mass profile for the dark component (blue) and the stellar component (red). The starting profile is at T=T0 (solid lines) and mostly lower than the profile for time
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg1.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg101.png)
|
Figure 5:
Anisotropy parameter (light green) and radial velocity dispersion (red) for the stellar component. The left scale on the y axis
is for the anisotropy parameter, the right scale for the radial
velocity dispersion parameter. The thick solid lines show the starting
stellar profile, here at T0=196 Myr, and the dotted lines show the resulting profile at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg9.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg127.png)
|
Figure 6: Evolution of the star formation rate with time for the reference model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg4.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg128.png)
|
Figure 7: The evolution of the stellar [Fe/H] over time. The contour plot shows the metalicity spread distribution with time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg11.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg135.png)
|
Figure 8: Cumulative number of SNII events in red, SNIa in magenta and planetary nebulae in gray. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg8.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg137.png)
|
Figure 9: Here the SNIa rate is presented. We find agreement with the literature prediction (e.g. Greggio & Renzini 1983) of a decreasing SNIa rate with time (see also Matteucci & Recchi 2001). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13240fg2.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg142.png)
|
Figure 10:
The evolution of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13240fg5.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg143.png)
|
Figure 11:
Radial dependence of the mean
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13240fg10.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13240-09/Timg145.png)
|
Figure 12: Shells of isovelocity for the sound speed of the gas component. The sketch shows a cut tilted by 45 degrees w.r.t. the vertical axis Z to show the overlapping shells of isovelocity (see text for details). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.