| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 24 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200913210 | |
| Published online | 20 May 2010 | |
What ignites on the neutron star of 4U 0614+091?
E. Kuulkers1 - J. J. M. in 't Zand2 - J.-L. Atteia3 - A. M. Levine4 - S. Brandt5 - D. A. Smith6 - M. Linares7 - M. Falanga8 - C. Sánchez-Fernández1 - C. B. Markwardt9 - T. E. Strohmayer10 - A. Cumming11 - M. Suzuki12
1 - ISOC, ESA, European Space Astronomy Centre (ESAC), PO Box 78, 28691 Villanueva de la Cañada (Madrid), Spain
2 -
SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
3
- Laboratoire d'Astrophysique de Toulouse-Tarbes, Observatoire
Midi-Pyrénées (CNRS-UMR5572/Université Paul Sabatier Toulouse III), 14
avenue Édouard Belin, 31400 Toulouse, France
4 -
Kavli Institute for Astrophysics and Space Research,
Massachusetts Institute of Technology, Cambridge, MA 02139, USA
5 -
National Space Institute, DTU, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
6 -
Guilford College, Physics Department, 5800 West Friendly Ave., Greensboro, NC 27410, USA
7
- Astronomical Institute ``Anton Pannekoek'', University of Amsterdam
and Center for High-Energy Astrophysics, PO Box 94249, 1090 GE,
Amsterdam, The Netherlands
8 -
International Space Science Institute, Hallerstrasse 6, 3012 Bern, Switzerland
9 -
UMD/CRESST/GSFC, Greenbelt, MD 20771, USA
10 -
Astrophysics Science Division, NASA/GSFC, Greenbelt, MD 20771, USA
11 -
Physics Department, McGill University, 3600 rue University, Montreal, QC, H3A 2T8, Canada
12 -
ISS Science Project Office ISAS, JAXA, 2-1-1 Sengen, Tsukuba, Ibaraki 305-8505, Japan
Received 31 August 2009 / Accepted 4 February 2010
Abstract
The low-mass X-ray binary 4U 0614+091 is a source of sporadic
thermonuclear (type I) X-ray bursts. We find bursts with a wide
variety of characteristics in serendipitous wide-field X-ray
observations by the WATCH on EURECA, the ASM on RXTE, the WFCs on BeppoSAX, the FREGATE on HETE-2, the IBIS/ISGRI on INTEGRAL, and the BAT on Swift, as well as pointed observations with the PCA and HEXTE on RXTE.
Most of the bursts are bright, i.e., they reach a peak flux of about
15 Crab, but a few are weak and only reach a peak flux below
a Crab. One of the bursts shows a very strong photospheric
radius-expansion phase. This allows us to evaluate the distance to the
source, which we estimate to be 3.2 kpc. The burst durations vary
generally from about 10 s to 5 min. However, after
one of the intermediate-duration bursts, a faint tail is seen to at
least about 2.4 h after the start of the burst. One very long
burst was observed, which lasted for several hours. This superburst
candidate was followed by a normal type-I burst only 19 days
later. This is, to our knowledge, the shortest burst-quench
time among the superbursters. The observation of a superburst in this
system is difficult to reconcile if the system is accreting at
about 1% of the Eddington limit. We describe the burst properties
in relation to the persistent emission. No strong correlations are
apparent, except that the intermediate-duration bursts occurred when
4U 0614+091's persistent emission was lowest and calm, and when
bursts were infrequent (on average roughly one every month to
3 months). The average burst rate increased significantly after
this period. The maximum average burst recurrence rate is about once
every week to 2 weeks. The burst behaviour may be partly
understood if there is at least an appreciable amount of helium present
in the accreted material from the donor star. If the system is an
ultra-compact X-ray binary with a CO white-dwarf donor, as has been
suggested, this is unexpected. If the bursts are powered by helium, we
find that the energy production per accumulated mass is about
2.5 times less than expected for pure helium matter.
Key words: accretion, accretion disks - binaries: close - stars: individual: 4U 0614+091 - stars: neutron - X-rays: binaries - X-rays: bursts
1 Introduction
Type I X-ray bursts (Grindlay et al. 1975; Belian et al. 1976; Hoffman et al. 1978,
hereafter bursts) result from thermonuclear shell flashes on a neutron
star, which is caused by the ignition of either He and/or H-rich
material supplied by a binary companion star (Hansen & van Horn 1975; Woosley & Taam 1976; Maraschi & Cavaliere 1977; Lamb & Lamb 1978; for reviews see Lewin et al. 1993; Strohmayer & Bildsten 2006).
Bursts generally appear as short transient events wherein the X-ray
intensity rises rapidly on a time scale of seconds, and decays in an
exponential fashion
back to the pre-burst level. The decay lasts almost always longer than
the rise. Burst durations range from several seconds up to half
an hour. The burst spectra generally harden during the rise and
soften during the decay. This has been attributed to the heating and
cooling of the uppermost layers of the neutron star. The spectra can be
satisfactorily described by black-body emission from spherical regions
with radii of around 10 km at inferred temperatures up to kT ![]() 3 keV.
The burst-to-burst time intervals are typically of the order of hours
to days. They are thought to be determined by the time for the neutron
star to accumulate enough fuel to power another burst.
3 keV.
The burst-to-burst time intervals are typically of the order of hours
to days. They are thought to be determined by the time for the neutron
star to accumulate enough fuel to power another burst.
Under certain conditions, the local luminosity may reach or exceed the Eddington limit and matter may be pushed outward. As a result, the neutron star photosphere also moves outward. Consequently, the emitting area increases and the observed inferred black-body temperature drops. When the surge of energy release is over, the photosphere gradually returns to its pre-burst radius. During this phase, the emitting area decreases and the inferred temperature increases. During the expansion and contraction phase, the luminosity is expected to be close to the Eddington limit. After the photosphere recedes to its pre-burst radius (called ``touch-down'') cooling is typically observed. Such bursts are referred to as photospheric radius-expansion type I X-ray bursts (e.g., Lewin et al. 1984; Tawara et al. 1984, hereafter radius-expansion bursts).
A few bursts last hours to half a day (Cornelisse et al. 2000; Strohmayer & Brown 2002; for a review see, e.g., Kuulkers 2004). Such bursts show the same characteristics as the typical bursts described above, except that the energy output is about a thousand times higher. They recur on time scales of months to years. Their origin is different from the typical bursts, because they are thought to be due to unstable burning of C deeper in the neutron star envelope (Cumming & Bildsten 2001; Strohmayer & Brown 2002). These long events are called superbursts (Wijnands 2001). Typical bursts are seen up to the time of the superbursts. However, they cease to occur after the superburst, for up to about a month (see, e.g., Cornelisse et al. 2002a; Kuulkers et al. 2002a). This is thought to be due to the superburst heating up the surface layer, and therefore preventing the unstable ignition of H and/or He (Cumming & Macbeth 2004).
There are also bursts that have durations and energy releases
intermediate between typical bursts and superbursts. They are referred
to as intermediate-duration X-ray bursts (Cumming et al. 2006;
hereafter intermediate-duration bursts). They show decay times ranging
from several to tens of minutes and energy outputs of about 1041 erg. Most of these events occur in sources with low persistent luminosity (
![]()
![]() 0.01
0.01
![]() ,
where
,
where
![]() represents the Eddington luminosity) and are thought to be due to
flashes of relatively thick He layers in ultra-compact X-ray
binaries (UCXBs; i.e., low-mass X-ray binaries with an orbital period
less than an hour), see in 't Zand et al. (2005), Cumming
et al. (2006), Falanga et al. (2008),
and references therein. The intermediate-duration bursts in the H-rich and luminous system GX 17+2 (Kuulkers et al. 2002b) probably have a different origin.
represents the Eddington luminosity) and are thought to be due to
flashes of relatively thick He layers in ultra-compact X-ray
binaries (UCXBs; i.e., low-mass X-ray binaries with an orbital period
less than an hour), see in 't Zand et al. (2005), Cumming
et al. (2006), Falanga et al. (2008),
and references therein. The intermediate-duration bursts in the H-rich and luminous system GX 17+2 (Kuulkers et al. 2002b) probably have a different origin.
The low-mass X-ray binary 4U 0614+091 has long been known to be a
source of bursts, but this identification was based on the detections
of only several of them, with relatively poor, ![]() 1
1
![]() ,
position determinations
,
position determinations![]() , as well as coarse timing and/or X-ray spectral information (Lewin 1976; Swank et al. 1978; Brandt et al. 1992, 1993a,b; Brandt 1994; Brandt & Lund 1995). More recently, an hours-long flare was reported, which showed characteristics resembling superbursts (Kuulkers 2005; see Sect. 3.2). Brandt et al. (1992) used the observation with GRANAT/WATCH of a peak burst flux of
, as well as coarse timing and/or X-ray spectral information (Lewin 1976; Swank et al. 1978; Brandt et al. 1992, 1993a,b; Brandt 1994; Brandt & Lund 1995). More recently, an hours-long flare was reported, which showed characteristics resembling superbursts (Kuulkers 2005; see Sect. 3.2). Brandt et al. (1992) used the observation with GRANAT/WATCH of a peak burst flux of ![]() 10 Crab (6-20 keV) to infer,
assuming this peak flux does not exceed the Eddington limit for a 1.4
10 Crab (6-20 keV) to infer,
assuming this peak flux does not exceed the Eddington limit for a 1.4 ![]() neutron star with a He-rich atmosphere, that the source distance must
be about 3.2 kpc. 4U 0614+091 is, therefore, one of the
closest to Earth of the known actively bursting systems
(see, e.g., Jonker & Nelemans 2004; Galloway et al. 2008).
neutron star with a He-rich atmosphere, that the source distance must
be about 3.2 kpc. 4U 0614+091 is, therefore, one of the
closest to Earth of the known actively bursting systems
(see, e.g., Jonker & Nelemans 2004; Galloway et al. 2008).
In the last decade, HETE-2 triggered thirteen times on bursts from 4U 0614+091. Moreover, three strong bursts from 4U 0614+091 triggered the ![]() -ray burst monitors on board INTEGRAL (see Chelovekov et al. 2007) and Swift. Strohmayer et al. (2008) discovered burst oscillations near 415 Hz in one of the brightest Swift/BAT bursts.
-ray burst monitors on board INTEGRAL (see Chelovekov et al. 2007) and Swift. Strohmayer et al. (2008) discovered burst oscillations near 415 Hz in one of the brightest Swift/BAT bursts.
It is difficult to understand 4U 0614+091 as the origin of bursts. Since it is thought to be an UCXB (in 't Zand et al. 2007; Shahbaz et al. 2008, and references therein), it is supposed to be so compact that the donor star can only be a non-degenerate H-deficient star or a white dwarf. Evolutionary models suggest that the accreted material could be rich in C/O or He (Nelemans et al. 2010). However, no evidence of He (or H) has been found so far in optical spectra, with rather stringent upper limits: He and/or H are at most present at the 10% level (Werner et al. 2006). These spectra suggest the donor star to be a C/O white dwarf (Nelemans et al. 2003, 2006; Werner et al. 2006). This seems to be at odds (see Juett et al. 2001; Juett & Chakrabarty 2003) with the fact that we see bursts in 4U 0614+091, which are usually understood as being due to unstable ignition of He or H. Moreover, 4U 0614+091 is an interesting case among the sources showing superbursts. Superbursts are expected to occur only in systems with accretion rates in excess of about 10% of the Eddington rate, i.e., the rate which yields emission at the Eddington limit (Cumming & Bildsten 2001; Strohmayer & Brown 2002). However, the low persistent X-ray luminosity of 4U 0614+091 indicates an accretion rate which is an order of magnitude lower (e.g., Ford et al. 2000).
In this paper we report on the detection of bursts from 4U 0614+091 made with various instruments. In Sects. 2.1 and 2.2 we describe the instruments and the data analyses of the bursts seen between 1992 and 2007, as well as the analysis of the persistent emission. We complement this with information extracted for the bursts seen before 1992 (Sect. 2.3). An overview of all the typical and intermediate-duration bursts seen appears in Sect. 3.1. We collectively refer to both types of bursts as normal bursts. One of them is a radius-expansion burst; it is discussed in Sect. 3.1.2. We then describe the results of our analysis of the superburst (Sect. 3.2), our burst oscillation search (Sect. 3.3), and the characteristics of the persistent emission of the source (Sect. 3.4). Finally, we show the long-term X-ray behaviour of 4U 0614+091 (Sect. 3.5) and close the paper with a discussion of our results (Sect. 4).
2 Observations and data analysis
Almost all the observations between 1992 and 2007 described in this paper were serendipitously obtained using six different X-ray instruments on just as many space-borne observatories, see Table 1. Only the observations with the RXTE/PCA and RXTE/HEXTE were purposely dedicated to 4U 0614+091. In the next subsections we describe these instruments and the analysis of the data in more detail. We usually refer to the instruments by acronyms only. In Table 1 we also give the total time of exposure for observations with 4U 0614+091 in the field of view and the total number of bursts detected from this source in these observations.
Table 1: Overview of instruments that have detected bursts from 4U 0614+091 between 1992 and 2007.
2.1 Observations and instrument-specific data analysis issues
2.1.1 EURECA WATCH
EURECA (EUropean REtrievable CArrier) carried the Wide Angle Telescope for Cosmic Hard X-rays (WATCH; Lund 1985; Brandt et al. 1990).
WATCH operated from August 1992 to June 1993.
It comprised a rotating modulation collimator (RMC) and yielded
images through a cross-correlation method. It viewed a circular
field with a radius of about 65
![]() ,
was sensitive between 6 and 150 keV, and had an effective area of about 45 cm2. For events with a duration longer than the rotation period of the RMC (
,
was sensitive between 6 and 150 keV, and had an effective area of about 45 cm2. For events with a duration longer than the rotation period of the RMC (![]() 1 s), the relative position accuracy was better than 1
1 s), the relative position accuracy was better than 1
![]() ,
and, in favourable cases, was as good as about 0.1
,
and, in favourable cases, was as good as about 0.1
![]() .
The flux sensitivity was about 100 mCrab in one day.
.
The flux sensitivity was about 100 mCrab in one day.
4U 0614+091 was located in the ![]() 1 steradian
field of view from mid January 1993 until the end of
April 1993, with an observing efficiency of a little more
than 40%. EURECA/WATCH observed a total of three bursts
during that time. Preliminary reports of these events can be found in
Brandt et al. (1993a,b), Brandt (1994) and Brandt & Lund (1995).
1 steradian
field of view from mid January 1993 until the end of
April 1993, with an observing efficiency of a little more
than 40%. EURECA/WATCH observed a total of three bursts
during that time. Preliminary reports of these events can be found in
Brandt et al. (1993a,b), Brandt (1994) and Brandt & Lund (1995).
For our analysis, we used count rates as a function of time along with
vignetting estimates for the source. Background rates were determined
by polynomial fits to the count rates outside the intervals of each
burst. We define the 3![]() confidence
level above which we regard a signal as significant as 3 times the
square root of the number of background counts in each time bin.
confidence
level above which we regard a signal as significant as 3 times the
square root of the number of background counts in each time bin.
2.1.2 RXTE All-Sky Monitor
2.1.2.1 Scanning Shadow Cameras.
The Rossi X-ray Timing Explorer (RXTE; launched December 1995) All-Sky Monitor (ASM) consists of three Scanning Shadow Cameras (SSCs, hereafter called SSC0, SSC1 and SSC2; Levine et al. 1996). Each SSC views a 12For each dwell, histograms of counts (``raw'' counts, i.e., not
corrected for transmission, sources
in the field of view, background, etc.) as a function of
position in each detector are recorded for three energy bands
(roughly 1.5-3, 3-5, 5-12 keV). Also, the total number
of counts registered in each SSC are recorded in 1/8 s time-series
bins in the same energy bands. For observations done before
March 2001 (MJD 51 970), there is imaging data
integrated over entire dwells, and count rate data with no imaging
information. Since March 2001 event-by-event data are telemetered
so that both temporal and imaging information can be extracted for
portions of dwells. For sources away from bright sources, the
sensitivity is roughly 10-15 mCrab (![]() in
the 1.5-12 keV band) for a reliable single-dwell source detection;
multi-day averaging improves the sensitivity down to about
a few mCrab. The average intensity of each known source
in the field of view is determined by the instrument team through an
analysis of the coded-aperture data and is made available via the
internet, on a dwell by dwell basis as well as 1-day averages
in
the 1.5-12 keV band) for a reliable single-dwell source detection;
multi-day averaging improves the sensitivity down to about
a few mCrab. The average intensity of each known source
in the field of view is determined by the instrument team through an
analysis of the coded-aperture data and is made available via the
internet, on a dwell by dwell basis as well as 1-day averages![]() .
.
The intensity history of 4U 0614+091 up to September 2007 was obtained from each of 62 720 dwells, more or less evenly spread over the years (see also Sect. 3.5.1). We used the following method to search for bursts: 1) identify candidate dwells in which the source intensity minus its uncertainty was larger than the overall mean intensity of 4U 0614+091 by 4 times the rms uncertainty in the overall mean intensity; 2) visually inspect raw count rates at 1-s time resolution within the candidate dwells for evidence of burst-like temporal behaviour; 3) use the hardness ratios, defined as the time-bin-wise ratios of the count rates in the 5-12 keV band to those in the 1.5-5 keV band, to verify the typical hard-to-soft behaviour of bursts. Note that this technique is not suitable for bursts that last substantially longer than a dwell or for bursts that do not start within a dwell. Our search yielded 6 bursts and one superburst.
2.1.2.2 (Time-resolved) X-ray spectral analysis of ASM data.
The 3-channel ASM data can constrain simple spectral models like power laws and black-body radiation (see, e.g., Ford et al. 1996; Kuulkers 2002; Keek et al. 2008). In our spectral analyses we employed the same method as in Keek et al. (2008). This includes calibrations of the source flux with average ASM data of the Crab over 200-day intervals around each data point.The spectral analysis can also be satisfactorily applied to raw
ASM data when dealing with bursts. If one assumes that the
burst emission is not influenced by persistent emission
(see, e.g., Kuulkers et al. 2002b),
net-burst count rates can be obtained by subtracting the average raw
pre-burst count rates from the raw burst count rates. If one also
knows the celestial position of the burst, the effective
mask/collimator transmission can be computed. This allows the
estimation of equivalent on-axis net burst count rates for the given
energy bands and these, after renormalization with the Crab as
described above, can be fit with a black-body spectrum model. Whenever
a burst was simultaneously observed by two SSCs we combined the
renormalized net count rate information from
the two cameras. We derived the three-channel transmission-corrected
net-burst spectra from the 1-s raw count rates. We calculated the
errors by taking square roots of the numbers of counts per each
time bin. We started with a spectral time bin size of 1 s
(2S 0918-549, see below) or 2 s (4U 0614+091). Each time
the net-burst rates following the peak decreased by a factor of ![]() ,
we doubled the spectral time-bin size.
,
we doubled the spectral time-bin size.
Since all the corrections may introduce errors in our analysis of the
raw ASM data, we first applied our method to bursts from
2S 0918-549 that, like 4U 0614+091, lies in a relatively
empty field in the sky (spatially the closest bursters to
2S 0918-549 are EXO 0748-676 at ![]() 16
16
![]() away and the transient GS 0836-429 at
away and the transient GS 0836-429 at ![]() 14
14
![]() away). 2S 0918-549 is similar to 4U 0614+091 in that it is
also thought to be an UCXB which shows low persistent accretion and
infrequent bursts (see, e.g., in 't Zand et al. 2005). Most
of the 2S 0918-549 bursts show a radius-expansion phase.
By comparing the ASM time-resolved X-ray
burst spectral analysis to that derived from high-quality X-ray spectra
observed with well-calibrated detectors, one can verify our ASM
burst-spectral analysis method.
away). 2S 0918-549 is similar to 4U 0614+091 in that it is
also thought to be an UCXB which shows low persistent accretion and
infrequent bursts (see, e.g., in 't Zand et al. 2005). Most
of the 2S 0918-549 bursts show a radius-expansion phase.
By comparing the ASM time-resolved X-ray
burst spectral analysis to that derived from high-quality X-ray spectra
observed with well-calibrated detectors, one can verify our ASM
burst-spectral analysis method.
We searched the ASM data on 2S 0918-549 for bursts using the same
algorithm as that used for 4U 0614+091. We found 5 bursts
(see Table A.1) over the more than ![]() 11 year
time span of observations, with a net effective exposure time of
47.8 days between 1996 January and 2007 August. Three of
them were already noted by in 't Zand et al. (2005); our third
X-ray
burst, which occurred on UT 2002 August 23, was not
noted by them probably due of its weakness (because of relatively low
transmission, see Table A.1).
By comparing our ASM time-resolved spectral fit results with those
for the bursts seen with the WFC (see in 't Zand et al. 2005)
and PCA (see Galloway et al. 2008),
we find comparable values for all spectral parameters. The
ASM spectral fits show similar kind of radius expansion phases
which reach similar derived peak fluxes as the other instruments. We,
therefore, conclude that our time resolved X-ray spectral analysis of
the raw ASM data gives consistent results with that seen from
other instruments, and therefore our method can be trusted.
11 year
time span of observations, with a net effective exposure time of
47.8 days between 1996 January and 2007 August. Three of
them were already noted by in 't Zand et al. (2005); our third
X-ray
burst, which occurred on UT 2002 August 23, was not
noted by them probably due of its weakness (because of relatively low
transmission, see Table A.1).
By comparing our ASM time-resolved spectral fit results with those
for the bursts seen with the WFC (see in 't Zand et al. 2005)
and PCA (see Galloway et al. 2008),
we find comparable values for all spectral parameters. The
ASM spectral fits show similar kind of radius expansion phases
which reach similar derived peak fluxes as the other instruments. We,
therefore, conclude that our time resolved X-ray spectral analysis of
the raw ASM data gives consistent results with that seen from
other instruments, and therefore our method can be trusted.
2.1.3 RXTE PCA and HEXTE
The Proportional Counter Array (PCA; Bradt et al. 1993; Jahoda et al. 2006) onboard RXTE provides a large collecting area (maximum net geometric area of about 8000 cm2) and high time resolution (down to ![]() s). It consists of 5 proportional counter units (PCUs) behind 1
s). It consists of 5 proportional counter units (PCUs) behind 1
![]() (full-width at half maximum, FWHM) collimators. It is sensitive in the 2-60 keV range down to
(full-width at half maximum, FWHM) collimators. It is sensitive in the 2-60 keV range down to ![]() 0.2 mCrab.
0.2 mCrab.
The High-Energy X-ray Timing Experiment (15-250 keV; Rothschild et al. 1998) onboard the same satellite consists of 8 detectors with a total area of about 1600 cm2.
The 8 detectors are split up in two clusters
of 4 each. During normal operations, each cluster is
alternately pointed on and off the source generally every 16
or 32 s, to provide near real-time background
measurements (note that at the end of 2006 cluster A was fixed to
always view the source). HEXTE can measure a typical X-ray source down
(at the 3![]() level) to about 1 mCrab up to
level) to about 1 mCrab up to ![]() 100 keV in 105 s.
100 keV in 105 s.
We first inspected the light curves at 1 s time resolution of all the publicly available PCA data up to September 2007 on 4U 0614+091 that was collected in the Standard 1 mode. A couple of strong burst-like events were seen; all except one were due to detector-related events. The one celestial event occurred simultaneously with the burst seen by FREGATE, on UT 2001 February 4 (MJD 51 944; see Sect. 2.1.5). Only the first 30 s of the event were covered, after which the PCA was shut off because the count rate (>55 kct s-1) exceeded the ``High Rate Monitor'' safety threshold. Apart from the first 30 s of the burst, the PCA also observed the tail of the burst. In observations taken on UT 2000 September 2 (MJD 51 789) we found the tail of another burst for which the onset was missed.
We used version 6.5 of the HEASOFT software suite for our RXTE
data analysis. For the time-resolved analysis of the prompt burst on
MJD 51 944 we used the PCA data from either Event
mode or Burst Catcher mode when available (the high count rates
reached during the maximum of the burst resulted in data losses near
the ends of the 1 s buffers of the Event mode). These modes
provided numbers of counts in 64 channels covering the
PCA energy range at time resolutions of 122 ![]() s
and 8 ms, respectively. At the time the prompt burst
occurred, 4 PCUs (PCU 0-3) were on; the data from
all layers and all PCUs were automatically combined in these modes.
During the spike (see Sect. 3.1.2)
we created time-resolved spectra at 2 ms resolution. During
the rest of the prompt burst, we used a time resolution
of 0.125 s. Although the majority of the prompt burst was
observed by HEXTE, we do not use the HEXTE data for the burst
spectral analysis because data from a broader energy range
(7-400 keV) was obtained by FREGATE (see Sect. 2.1.5).
For the tail of the bursts on MJD 51 789 and
MJD 51 944 we used the PCA data from the Standard 2
mode; this mode provides counts in 129 channels covering the
PCA energy range with a time resolution of 16 s. We
formed spectra averaged over 112 s intervals from the events
occurring in all layers of the PCUs which were on during and before or
after the burst; this was PCU 3 on MJD 51 944 and
PCUs 2, 3 on MJD 51 789.
s
and 8 ms, respectively. At the time the prompt burst
occurred, 4 PCUs (PCU 0-3) were on; the data from
all layers and all PCUs were automatically combined in these modes.
During the spike (see Sect. 3.1.2)
we created time-resolved spectra at 2 ms resolution. During
the rest of the prompt burst, we used a time resolution
of 0.125 s. Although the majority of the prompt burst was
observed by HEXTE, we do not use the HEXTE data for the burst
spectral analysis because data from a broader energy range
(7-400 keV) was obtained by FREGATE (see Sect. 2.1.5).
For the tail of the bursts on MJD 51 789 and
MJD 51 944 we used the PCA data from the Standard 2
mode; this mode provides counts in 129 channels covering the
PCA energy range with a time resolution of 16 s. We
formed spectra averaged over 112 s intervals from the events
occurring in all layers of the PCUs which were on during and before or
after the burst; this was PCU 3 on MJD 51 944 and
PCUs 2, 3 on MJD 51 789.
Dead-time correction is only possible for all spectra with a time resolution equal or higher than 0.125 s. We subtracted the pre-burst persistent emission from the burst emission. Our time-resolved burst spectral fits of PCA data covered the 3 to 20 keV energy band. We included a 1% systematic uncertainty in each spectral bin in addition to the usual statistical uncertainties.
We extracted information on the persistent emission only when RXTE data was available within 1 day of a burst (see Sect. 3.4).
We did this for data from both the PCA and HEXTE by applying standard
criteria, i.e., by filtering out data taken at elevations less
than 10
![]() or with an offset from the source greater than 0.02
or with an offset from the source greater than 0.02
![]() .
Also, we created instrument response and background files following the
standard analysis threads using the latest information available
.
Also, we created instrument response and background files following the
standard analysis threads using the latest information available![]() . We corrected the count-rate spectra for dead-time losses. For the PCA we only used PCU 2 data (across the RXTE mission
this PCU has the highest duty cycle) obtained with the Standard 2
mode. Pulse-height spectra were formed from the events from all layers
and we included a 1% systematic uncertainty in each
spectral bin. We performed fits to the persistent emission in the
3-30 keV and 17-100 keV bands for the PCA and HEXTE,
respectively. A multiplicative constant was applied to the
HEXTE spectra to account for the uncertainty in the relative
normalizations of the instruments,
i.e., both HEXTE Cluster A and B were allowed to vary with
respect to the PCA. This multiplicative factor was found to be
between 0.6 and 0.8.
. We corrected the count-rate spectra for dead-time losses. For the PCA we only used PCU 2 data (across the RXTE mission
this PCU has the highest duty cycle) obtained with the Standard 2
mode. Pulse-height spectra were formed from the events from all layers
and we included a 1% systematic uncertainty in each
spectral bin. We performed fits to the persistent emission in the
3-30 keV and 17-100 keV bands for the PCA and HEXTE,
respectively. A multiplicative constant was applied to the
HEXTE spectra to account for the uncertainty in the relative
normalizations of the instruments,
i.e., both HEXTE Cluster A and B were allowed to vary with
respect to the PCA. This multiplicative factor was found to be
between 0.6 and 0.8.
For the comparison (see Sect. 3.1.2) of the burst observed on MJD 51 944 with that of the superbursts of 4U 1820-303 (Strohmayer & Brown 2002) and 4U 1636-536 (Strohmayer & Markwardt 2002)
at hard X-ray energies, we extracted light curves from data obtained by
HEXTE
in the 15-60 keV band. In this process we applied the same
standard filtering criteria as those described above. We corrected the
light curves for dead time and background following the standard
procedures![]() , and normalized them to the Crab count rate in the same energy band. For this analysis we only used the
Standard Modes (Archive Spectral Bin, 64-bin spectra produced every 16 s) data from Cluster A.
, and normalized them to the Crab count rate in the same energy band. For this analysis we only used the
Standard Modes (Archive Spectral Bin, 64-bin spectra produced every 16 s) data from Cluster A.
To characterise the overall spectral behaviour of 4U 0614+ 091 we
created so-called colour-colour and hardness-intensity diagrams
(CD and HID, respectively). All publicly available pointed
PCA observations of 4U 0614+091 up to September 2007
were used. We extracted background and dead-time corrected count rates
from the Standard 2 data using the same standard procedures and
filtering criteria as applied to the spectral data, with 16 s time
resolution. We used the following energy bands:
2.0-3.5 keV (A),
3.5-6.0 keV (B), 6.0-9.7 keV (C),
and 9.7-16.0 keV (D). We define the soft and hard
colours (SC, HC) as the ratios of the count rates in the
various bands: SC = B/A and HC = D/C; the
intensity (Int) is defined as the sum of the count rates in the
four energy bands:
![]() .
We normalized both the colours and intensity to the Crab values nearest
in time to account for changes in detector gas gain (see, e.g.,
Kuulkers et al. 1994; van Straaten et al. 2003).
Since the values do not change significantly within an observation
(i.e., on time scales of order an hour), they were averaged
over one observation.
.
We normalized both the colours and intensity to the Crab values nearest
in time to account for changes in detector gas gain (see, e.g.,
Kuulkers et al. 1994; van Straaten et al. 2003).
Since the values do not change significantly within an observation
(i.e., on time scales of order an hour), they were averaged
over one observation.
2.1.4 BeppoSAX Wide-Field Cameras
The Wide-Field Cameras (WFCs; Jager et al. 1997) were two identical coded-aperture instruments onboard the BeppoSAX satellite (Satellite per Astronomia X; Boella et al. 1997), which were operated between April 1996 and April 2002. The field of view was 40
![]()
![]() 40
40
![]() (FWZR), the angular resolution 5
(FWZR), the angular resolution 5
![]() (FWHM) and the source-location accuracy was generally better than 1
(FWHM) and the source-location accuracy was generally better than 1
![]() (99% confidence).
The detectors were sensitive to the energy range 2
to 28 keV and had a net collecting area of 140 cm2. The on-axis detection
threshold was of the order of 0.3 Crab for a 1 s observation and a few mCrab for a 105 s observation.
(99% confidence).
The detectors were sensitive to the energy range 2
to 28 keV and had a net collecting area of 140 cm2. The on-axis detection
threshold was of the order of 0.3 Crab for a 1 s observation and a few mCrab for a 105 s observation.
The WFCs pointed in opposite directions with respect to each other and perpendicular to the Narrow-Field Instruments (NFIs) on the same satellite. Since the pointing directions of the WFCs were usually governed by the observations of the NFIs, the WFC sky coverage was not uniform. 4U 0614+091 was mostly seen at large off-axis angles.
We extracted the reconstructed source flux in the 2-25 keV bandpass with a time resolution of 2 s whenever 4U 0614+091 was in the field of view. We also extracted information on all photons detected on the appropriate detector with varying time resolutions between 0.5 and 8 s. Light curves were formed from both the fluxes and the photon rate data. Bursts were searched for by eye as well using an automatic algorithm (see Cornelisse et al. 2003). We found only one burst.
For the generation of WFC X-ray spectra we first cross-correlated the detector data with the expected imaging response of WFC unit 2 for 4U 0614+091 (see in 't Zand 1992, for more detail). Background radiation is then automatically subtracted. We then extracted 2-28 keV spectra from the resulting imaging data. Burst time bins were defined such that the significance of the source (i.e., the photon flux divided by the standard deviation expected from all other photon sources) is at least 10. Experience shows that spectra are ill defined for lower significances. The X-ray spectrum of the persistent emission around the burst was determined from the whole observation in which the burst occurred (with an exposure time of 14.3 ks). This spectrum was subtracted from the burst emission in our time-resolved burst spectral analysis. The burst and persistent spectra were fit in the 2-28 keV band.
Table 2: Burst and persistent emission properties for all bursts from 4U 0614+091.
2.1.5 HETE-2 FREGATE
One of the instruments onboard the High Energy Transient Explorer satellite (HETE-2; Ricker et al. 2003) that operated between 2000 and 2007, was the omnidirectional ![]() -ray
spectrometer named French Gamma Telescope (FREGATE; Atteia et al. 2003).
FREGATE consisted of 4 detectors, mounted in two pairs.
It was sensitive in the 6-400 keV range, with a maximum
effective area of 158 cm2. The field of view was 70
-ray
spectrometer named French Gamma Telescope (FREGATE; Atteia et al. 2003).
FREGATE consisted of 4 detectors, mounted in two pairs.
It was sensitive in the 6-400 keV range, with a maximum
effective area of 158 cm2. The field of view was 70
![]() (half-width at zero response, HWZR),
but it had no imaging capacities. It provided continuous 128
channel energy spectra with 5 s time resolution (except in the
beginning of the mission when it was 10 s), as well as
continuous four-channel energy spectra with 0.164 s time
resolution (0.327 s in the beginning).
(half-width at zero response, HWZR),
but it had no imaging capacities. It provided continuous 128
channel energy spectra with 5 s time resolution (except in the
beginning of the mission when it was 10 s), as well as
continuous four-channel energy spectra with 0.164 s time
resolution (0.327 s in the beginning).
A burst trigger occurred when there were two coincident 6![]() or higher excesses on two of the FREGATE detectors within a time bin;
this corresponds to an increase by 1.2 Crab or higher in
5.24 s for a burst observed on-axis in a source-free region. When
this happened, 256 000 individual photons were time- and
energy-tagged. FREGATE triggered 13 times on bursts coming from
the direction of 4U 0614+091 (see Table 2).
Three of them were weak and exhibited low signal to noise
(on MJD 52 961, MJD 53 074 and
MJD 53 740). The first two FREGATE events
(MJD 51 944 and MJD 52 322) were already reported
by Barraud (2002); they occurred when the Wide Field X-ray Monitor (WXM, imager onboard HETE-2, 2-25 keV; Shirasaki et al. 2003)
was not operating. The remaining bursts were detected by the WXM, and
some of these were also detected by the Soft X-ray Camera (SXC,
CCD-based imager onboard HETE-2, 0.5-2 keV; Villasenor et al. 2003). The WXM and SXC, when operating, were able to get precise burst localizations (see, e.g., Suzuki et al. 2004).
Two additional bursts were seen by the WXM, but FREGATE was not
operating at those times (MJD 53 041 and
MJD 54 101). Due to the anti-solar pointing of HETE-2,
4U 0614+091 was within the field-of-view of FREGATE during nearly
4 months every year. We estimate the total exposure on
4U 0614+091 from 2001 to 2006 to be about 194 days.
or higher excesses on two of the FREGATE detectors within a time bin;
this corresponds to an increase by 1.2 Crab or higher in
5.24 s for a burst observed on-axis in a source-free region. When
this happened, 256 000 individual photons were time- and
energy-tagged. FREGATE triggered 13 times on bursts coming from
the direction of 4U 0614+091 (see Table 2).
Three of them were weak and exhibited low signal to noise
(on MJD 52 961, MJD 53 074 and
MJD 53 740). The first two FREGATE events
(MJD 51 944 and MJD 52 322) were already reported
by Barraud (2002); they occurred when the Wide Field X-ray Monitor (WXM, imager onboard HETE-2, 2-25 keV; Shirasaki et al. 2003)
was not operating. The remaining bursts were detected by the WXM, and
some of these were also detected by the Soft X-ray Camera (SXC,
CCD-based imager onboard HETE-2, 0.5-2 keV; Villasenor et al. 2003). The WXM and SXC, when operating, were able to get precise burst localizations (see, e.g., Suzuki et al. 2004).
Two additional bursts were seen by the WXM, but FREGATE was not
operating at those times (MJD 53 041 and
MJD 54 101). Due to the anti-solar pointing of HETE-2,
4U 0614+091 was within the field-of-view of FREGATE during nearly
4 months every year. We estimate the total exposure on
4U 0614+091 from 2001 to 2006 to be about 194 days.
The extraction of burst spectra relies on a quadratic fit of the ``background'' (i.e., true background plus any emission from sources in the field of view) during tens of seconds before and after a burst in all the 128 energy channels. The availability of this simple background spectrum allows for the subtraction of the background channel by channel. We used the counts above the fitted background to build the count spectrum of the burst, which we then deconvolved using the response matrix constructed with the known gain and angular response of the detector. We performed the X-ray spectral fits to the integrated and time-resolved (10 s resolution for the burst on MJD 51 944, 5 s for the rest) burst emission in the well-calibrated 7-40 keV range. For several of the bursts we also extracted spectral information at a higher time resolution in a similar way.
2.1.6 INTEGRAL IBIS/ISGRI and JEM-X
One of the two main instruments onboard INTEGRAL (International Gamma-Ray Astrophysics Laboratory; Winkler et al. 2003; launched October 2002) is IBIS (Imager on Board the INTEGRAL Satellite; Ubertini et al. 2003). It comprises two detector planes that view the sky through a coded mask. The field of view is 29
![]()
![]() 29
29
![]() (FWZR) and the angular resolution is 12
(FWZR) and the angular resolution is 12
![]() (FWHM). We use data collected with one of its detectors: the INTEGRAL Soft Gamma-Ray Imager (ISGRI) which is sensitive in the
(FWHM). We use data collected with one of its detectors: the INTEGRAL Soft Gamma-Ray Imager (ISGRI) which is sensitive in the ![]() 15 keV to 1 MeV range with a total effective area of about 2600 cm2 (Lebrun et al. 2003).
15 keV to 1 MeV range with a total effective area of about 2600 cm2 (Lebrun et al. 2003).
One of the two supplementing monitors onboard INTEGRAL is the Joint European X-ray Monitor (JEM-X; Lund et al. 2003).
JEM-X consists of 2 identical units, which are both sensitive in
the 3-35 keV band. Most of the time only one unit is operating.
The angular resolution is 3
![]() (FWHM); one single unit has a detector area of about 500 cm2. The units have a circular view with diameter of about 13
(FWHM); one single unit has a detector area of about 500 cm2. The units have a circular view with diameter of about 13
![]() (FWZR), i.e., narrower than ISGRI. In practice, the transmission of the collimator beyond an off-axis angle of 5
(FWZR), i.e., narrower than ISGRI. In practice, the transmission of the collimator beyond an off-axis angle of 5
![]() is
so low that only the brightest sources can be observed at larger
angles. JEM-X is sensitive to X-ray bursts seen on-axis down to about
0.1 Crab at the 5
is
so low that only the brightest sources can be observed at larger
angles. JEM-X is sensitive to X-ray bursts seen on-axis down to about
0.1 Crab at the 5![]() level in 5 s.
level in 5 s.
The INTEGRAL Burst Alert System (IBAS; Mereghetti et al. 2003)![]() is the automatic on-ground software that in near-real time searches for
is the automatic on-ground software that in near-real time searches for ![]() -ray
bursts in IBIS data and promptly publicly distributes results. For a
trigger time interval of 1 s and a certain threshold value
(currently about 8
-ray
bursts in IBIS data and promptly publicly distributes results. For a
trigger time interval of 1 s and a certain threshold value
(currently about 8![]() ), a minimum flux of about 0.5-0.75 Crab (20-200 keV) is required to trigger a typical
), a minimum flux of about 0.5-0.75 Crab (20-200 keV) is required to trigger a typical ![]() -ray
burst (and to produce enough counts to locate the position in the
deconvolved image). One burst from 4U 0614+091 triggered IBAS on
UT 2005 March 31 (nr. 2441 on MJD 53 460).
-ray
burst (and to produce enough counts to locate the position in the
deconvolved image). One burst from 4U 0614+091 triggered IBAS on
UT 2005 March 31 (nr. 2441 on MJD 53 460).
To search offline for bursts and to study the hard X-ray long-term persistent behaviour of
4U 0614+091, we analysed all public INTEGRAL pointing data in the ISOC Science Data Archive![]() . Up to September 2007 there were
. Up to September 2007 there were ![]() 840 pointings
available where 4U 0614+091 was within the ISGRI field of
view with a total exposure time of about 25 days. Since most of
these observations were taken with the prime objective of instrument
calibration on the Crab, many pointings (about 200) were carried
out in non-standard modes. The total exposure time of all ISGRI
standard pointings is about 22 days. All public JEM-X data
whenever 4U 0614+091 was in the field of view (i.e., <6
840 pointings
available where 4U 0614+091 was within the ISGRI field of
view with a total exposure time of about 25 days. Since most of
these observations were taken with the prime objective of instrument
calibration on the Crab, many pointings (about 200) were carried
out in non-standard modes. The total exposure time of all ISGRI
standard pointings is about 22 days. All public JEM-X data
whenever 4U 0614+091 was in the field of view (i.e., <6
![]() off-axis)
amounts to a total exposure of only about 70 ks. In our
analysis we use the high-energy source ISDC reference catalog (see
Ebisawa et al. 2003;
v. 27) as input source catalog. We processed the ISGRI and
JEM-X data using the latest available Off-line Scientific Analysis
software (OSA; see Courvoisier et al. 2003),
v. 7.0. The description of the algorithms used in the ISGRI and
JEM-X scientific analyses can be found in Goldwurm et al. (2003) and Westergaard et al. (2003), respectively.
off-axis)
amounts to a total exposure of only about 70 ks. In our
analysis we use the high-energy source ISDC reference catalog (see
Ebisawa et al. 2003;
v. 27) as input source catalog. We processed the ISGRI and
JEM-X data using the latest available Off-line Scientific Analysis
software (OSA; see Courvoisier et al. 2003),
v. 7.0. The description of the algorithms used in the ISGRI and
JEM-X scientific analyses can be found in Goldwurm et al. (2003) and Westergaard et al. (2003), respectively.
We 1) processed the ISGRI 15-20 keV band data using OSA with default parameters; 2) analysed
the data through to the imaging step; and 3) extracted light curves for all detected sources with 10 s time resolution![]() .
Next, a potential onset of a burst was flagged when, in a
time bin, the difference between the source count rate and the average
source count rate in the whole pointing exceeded four times the
standard deviation of the count rates in the whole pointing. The count
rate versus time was then examined around each flagged time to check
for the presence of a shape consistent with that of a type I
X-ray burst. If this was the case, we generated reconstructed
images within the good-time interval covering the whole burst, and
checked them visually to verify that the event indeed originated from
4U 0614+091.
.
Next, a potential onset of a burst was flagged when, in a
time bin, the difference between the source count rate and the average
source count rate in the whole pointing exceeded four times the
standard deviation of the count rates in the whole pointing. The count
rate versus time was then examined around each flagged time to check
for the presence of a shape consistent with that of a type I
X-ray burst. If this was the case, we generated reconstructed
images within the good-time interval covering the whole burst, and
checked them visually to verify that the event indeed originated from
4U 0614+091.
Using the above described procedure we confirmed the burst
which triggered IBAS in 2005 (see above). We also detected
another burst from 4U 0614+091 on UT 2003 August 16
(MJD 52 867). Unfortunately, the latter burst was seen far
off-axis, about 16.5
![]() ,
near the edge of the detector (see Fig. A.3), and thus again outside the field of view of JEM-X. We found no bursts from 4U 0614+091 in the JEM-X data.
,
near the edge of the detector (see Fig. A.3), and thus again outside the field of view of JEM-X. We found no bursts from 4U 0614+091 in the JEM-X data.
For the time-resolved spectral analysis of the 2005 burst we
divided the burst only in three parts so that the rise, the top and the
decay were covered with satisfactorily spectral quality,
in 5 spectral energy bins covering 17 to 40 keV.
The statistical quality of the 2003 burst precludes a
time-resolved analysis. The ISGRI spectrum of the persistent emission
around the 2005 burst
is derived from the 1800 s single pointing during which the burst
occurred. The net-burst spectra were calculated by subtracting the
persistent spectrum from the burst spectra. X-ray spectral fits to the
burst and persistent ISGRI spectra were performed in the 17-40 keV
and 20-200 keV bands, respectively. During the INTEGRAL
observations around the 2003 burst 4U 0614+091 was always far
off-axis (>10
![]() ), and therefore we did not include these ISGRI data in our analysis of the persistent emission.
), and therefore we did not include these ISGRI data in our analysis of the persistent emission.
For the long-term light curves we used OSA through the
production of ISGRI images per single pointing in the 15-50 keV
range. This energy band was chosen to supplement the ISGRI light curves
with the publicly available BAT long-term light curves
(see Sect. 2.1.7).
We force the flux extraction of each of the catalog sources, regardless
of the detection significance of the source (see, e.g., Kuulkers
et al. 2007). The correction for off-axis response is generally good up to ![]() 10
10
![]() from the centre of the field of view. We therefore selected only those pointings where 4U 0614+091 was less than 10
from the centre of the field of view. We therefore selected only those pointings where 4U 0614+091 was less than 10
![]() off axis. This led to a total of 115 pointings with different
exposure times spanning the time interval from
2003 February 18 to 2006 April 18.
off axis. This led to a total of 115 pointings with different
exposure times spanning the time interval from
2003 February 18 to 2006 April 18.
2.1.7 Swift BAT
The Burst Alert Telescope (BAT; Barthelmy et al. 2005) onboard Swift (launched November 2004; Gehrels et al. 2004)
is a coded-aperture imager with a very wide field of view of about
2 steradians, which operates in the 15-150 keV band. The
detector plane covers a net collecting area of 5200 cm2; the BAT angular resolution is 22
![]() (FWHM).
(FWHM).
As soon as the BAT triggers on a ![]() -ray burst, Swift automatically slews to the
-ray burst, Swift automatically slews to the ![]() -ray
burst position and starts to observe the source with its more sensitive
instruments. However, strong type I X-ray bursts may also trigger
the BAT (but do not lead to automatic slews if
they come from a known source). Assuming a black-body source with kT
-ray
burst position and starts to observe the source with its more sensitive
instruments. However, strong type I X-ray bursts may also trigger
the BAT (but do not lead to automatic slews if
they come from a known source). Assuming a black-body source with kT ![]() 2.5 keV, the 5
2.5 keV, the 5![]() detection limit for the BAT in 5 s is approximately 0.7 Crab in the 15-25 keV band.
detection limit for the BAT in 5 s is approximately 0.7 Crab in the 15-25 keV band.
Two bursts from 4U 0614+091 triggered the BAT into a ![]() -ray
burst data collecting mode but did not result in automated slews. The
triggers occurred on UT 2006 October 21 (nr. 234849 on
MJD 54 029) and 2007 March 31 (nr. 273106 on
MJD 54 189). For these triggers, about 45 s of BAT
event data were produced. A first account of these bursts has been
given by Strohmayer et al. (2008). We ran the standard complete
-ray
burst data collecting mode but did not result in automated slews. The
triggers occurred on UT 2006 October 21 (nr. 234849 on
MJD 54 029) and 2007 March 31 (nr. 273106 on
MJD 54 189). For these triggers, about 45 s of BAT
event data were produced. A first account of these bursts has been
given by Strohmayer et al. (2008). We ran the standard complete ![]() -ray
burst processing script on the BAT burst products of the two triggers
to obtain a first impression of the burst behaviour, and to derive an
updated position of the origin of the burst (see Appendix A).
We then applied the latest calibration available (as of
August 2007) to these data (energy calibration, detector quality
map, mask weighting), following the analysis threads provided by the Swift Science Center
-ray
burst processing script on the BAT burst products of the two triggers
to obtain a first impression of the burst behaviour, and to derive an
updated position of the origin of the burst (see Appendix A).
We then applied the latest calibration available (as of
August 2007) to these data (energy calibration, detector quality
map, mask weighting), following the analysis threads provided by the Swift Science Center![]() .
From these calibrated data we produced light curves, images and
spectra. The first burst is strong enough to support a detailed
time-resolved spectral analysis in the 15-30 keV band, starting
with a time resolution of 1 s. For the second, weaker burst
we started with a time resolution of 2 s. We doubled the
spectral time bin
size, whenever the net-burst rates following the peak decreased by a
factor of
.
From these calibrated data we produced light curves, images and
spectra. The first burst is strong enough to support a detailed
time-resolved spectral analysis in the 15-30 keV band, starting
with a time resolution of 1 s. For the second, weaker burst
we started with a time resolution of 2 s. We doubled the
spectral time bin
size, whenever the net-burst rates following the peak decreased by a
factor of ![]() .
.
The BAT continually monitors the sky; more than about 70% of the
sky is observed on a daily basis. Results from this survey mode are
publicly available in the form of light curves covering the
15-50 keV energy band on two time scales: a single Swift
pointing (![]() 20 min) and the weighted average for each day
20 min) and the weighted average for each day![]() . In the latter a 6 mCrab source typically can be detected at the 3
. In the latter a 6 mCrab source typically can be detected at the 3![]() level (Krimm et al. 2006). We used the daily average light curve for 4U 0614+091 to study its long-term hard X-ray behaviour.
level (Krimm et al. 2006). We used the daily average light curve for 4U 0614+091 to study its long-term hard X-ray behaviour.
2.2 Further data analysis issues
2.2.1 X-ray burst properties
The band passes we used for the investigation of the burst light curves and extraction of some of the burst properties (see below) are 6-15 keV, 2-28 keV, 1.5-12 keV, 2-60 keV, 7-40 keV, and 15-30 keV for the EURECA/WATCH, WFC, ASM, PCA, FREGATE, and both the ISGRI and BAT, respectively.
For each of the ASM bursts, we derived the start time by taking the time when the count rate rose more than 5![]() above the pre-burst level, while, for each FREGATE burst, the
start time is the actual trigger time. For the other bursts we
determined the start times by eye, because most of these bursts
rise more slowly at higher energies. We define the burst rise
time,
above the pre-burst level, while, for each FREGATE burst, the
start time is the actual trigger time. For the other bursts we
determined the start times by eye, because most of these bursts
rise more slowly at higher energies. We define the burst rise
time,
![]() ,
as the difference between the time of the start and the time of the
peak of the burst; the derived values were verified by visual
inspection of the light curves. We estimate the error on the rise time
to be about half a second (except during the spike of the burst
observed on MJD 51 944, see
Sect. 3.1.2). The decay times,
,
as the difference between the time of the start and the time of the
peak of the burst; the derived values were verified by visual
inspection of the light curves. We estimate the error on the rise time
to be about half a second (except during the spike of the burst
observed on MJD 51 944, see
Sect. 3.1.2). The decay times,
![]() ,
are derived from fits of an exponential function plus a constant to the
light curves. We fit from the maximum of the burst up to
about 100 s after burst onset, if possible. For the
longer bursts a longer time base was used when possible. When no
post-burst information is available, we first fit the pre-burst rate
with a constant and fix
that when fitting the decay portion of the burst light curve. The range
of values for which
,
are derived from fits of an exponential function plus a constant to the
light curves. We fit from the maximum of the burst up to
about 100 s after burst onset, if possible. For the
longer bursts a longer time base was used when possible. When no
post-burst information is available, we first fit the pre-burst rate
with a constant and fix
that when fitting the decay portion of the burst light curve. The range
of values for which ![]() remains within 1 of the minimum value (i.e.,
remains within 1 of the minimum value (i.e.,
![]() = 1) is used to set the uncertainties of the decay times (assuming the fit parameters are uncorrelated).
= 1) is used to set the uncertainties of the decay times (assuming the fit parameters are uncorrelated).
![\begin{figure}
\par\includegraphics[angle=-90,width=16.2cm,clip]{13210f1a.ps}\par\includegraphics[angle=-90,width=15.8cm,clip]{13210f1b.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg110.png)
|
Figure 1: Time profiles of raw full-bandpass photon rates ( top panels), bolometric black-body flux (2nd panels), black-body temperature (3rd panels), black-body radius for 3 kpc distance (4th panels) and goodness of fit ( bottom panels). The unit of intensity ( top panels) is cts s-1 for the 6 ASM bursts, cts s-1 bin-1 for the ISGRI burst, kcts s-1 bin-1 for the 2 BAT bursts, kcts s-1 for the 10 FREGATE bursts and cts s-1 for the WFC burst. The bursts are denoted by instrument (FR = FREGATE) and MJD (see Table 2). For the ASM bursts which occurred on MJD 50 200 and MJD 51 164 we show the light curves from SSC1 and SSC0 data, respectively (see Table A.1). |
| Open with DEXTER | |
Further burst properties include the bolometric fluence (![]() )
and bolometric black-body peak flux (
)
and bolometric black-body peak flux (
![]() ),
where the underlying assumption is that the burst emission is on top of
unchanged persistent emission (see, e.g., Kuulkers et al. 2002b), as well as information on the out-of-burst, i.e., persistent, emission (see below). Estimates of
),
where the underlying assumption is that the burst emission is on top of
unchanged persistent emission (see, e.g., Kuulkers et al. 2002b), as well as information on the out-of-burst, i.e., persistent, emission (see below). Estimates of ![]() were obtained by integrating the fitted black-body models of the
time-resolved spectra over photon energy and time (i.e., we do not
take into account any residual burst emission outside the time range in
which we did the time-resolved spectral fits). Since bursts decay more
rapidly at higher energies, i.e.,
were obtained by integrating the fitted black-body models of the
time-resolved spectra over photon energy and time (i.e., we do not
take into account any residual burst emission outside the time range in
which we did the time-resolved spectral fits). Since bursts decay more
rapidly at higher energies, i.e.,
![]() depends on the bandpass used, we also determine the characteristic decay time
depends on the bandpass used, we also determine the characteristic decay time ![]() =
=
![]() which is not dependent on bandpass. Uncertainties in
which is not dependent on bandpass. Uncertainties in ![]() and
and ![]() were
estimated by propagating the errors derived from the individual
time-resolved burst spectral fits and by assuming that these errors are
symmetric. For the WATCH bursts and the 3 weak bursts
observed by FREGATE, time-resolved X-ray spectral analysis is not
possible. Instead,
we derive
were
estimated by propagating the errors derived from the individual
time-resolved burst spectral fits and by assuming that these errors are
symmetric. For the WATCH bursts and the 3 weak bursts
observed by FREGATE, time-resolved X-ray spectral analysis is not
possible. Instead,
we derive
![]() from the peak count rates by scaling from the count rates and fluxes of the Crab. The Crab flux is taken to be 1.03
from the peak count rates by scaling from the count rates and fluxes of the Crab. The Crab flux is taken to be 1.03 ![]() 10-8 erg cm-2 s-1 in the 6-15 keV WATCH band and 1.89
10-8 erg cm-2 s-1 in the 6-15 keV WATCH band and 1.89 ![]() 10-8 erg cm-2 s-1
in the 7-40 keV FREGATE band. We then converted these values
to estimated bolometric values assuming the emission comes from
a 3 keV black body (which is fine for a large part of a burst
seen at hard energies, see, e.g., Fig. 1). For the 3 weak FREGATE bursts we derived
10-8 erg cm-2 s-1
in the 7-40 keV FREGATE band. We then converted these values
to estimated bolometric values assuming the emission comes from
a 3 keV black body (which is fine for a large part of a burst
seen at hard energies, see, e.g., Fig. 1). For the 3 weak FREGATE bursts we derived ![]() from the average burst-integrated spectra; for the WATCH bursts we derived
from the average burst-integrated spectra; for the WATCH bursts we derived ![]() from the burst integrated number of counts and by performing a correction similar to that described above for
from the burst integrated number of counts and by performing a correction similar to that described above for
![]() .
We define the duration of the burst (
.
We define the duration of the burst (
![]() )
as
)
as
![]() ,
since not all bursts are fully covered. Inspection of the light curves
show that these values are consistent with the total durations
determined by eye.
,
since not all bursts are fully covered. Inspection of the light curves
show that these values are consistent with the total durations
determined by eye.
Burst oscillations at 414.7 Hz were present during a 5 s
time interval in the brightest BAT burst cooling tail at the 4![]() significance level (Strohmayer et al. 2008).
We verified the presence of burst oscillations during this burst and
searched for burst oscillations during the FREGATE and the 2005 ISGRI
bursts where data were available at a high time resolution. We selected
the 13-20 keV band for BAT, 15-30 keV for ISGRI and
7-40 keV for FREGATE, mainly to have the highest possible
signal-to-noise ratio to search for a timing signature. We applied the Z21-statistic (standard Rayleigh statistic, see Buccheri et al. 1983)
to the photon event distributions for trial frequencies in a narrow
window centred on the expected frequency of 414.7 Hz
(i.e., 413-416 Hz). The dynamical power spectra were computed
using the same method as in Strohmayer et al. (2008).
We employed intervals of 4 s or 8 s, stepping
through the BAT, FREGATE and ISGRI bursts with intervals of
0.25 s; for the calculation of upper limits we used intervals
of 10 s.
significance level (Strohmayer et al. 2008).
We verified the presence of burst oscillations during this burst and
searched for burst oscillations during the FREGATE and the 2005 ISGRI
bursts where data were available at a high time resolution. We selected
the 13-20 keV band for BAT, 15-30 keV for ISGRI and
7-40 keV for FREGATE, mainly to have the highest possible
signal-to-noise ratio to search for a timing signature. We applied the Z21-statistic (standard Rayleigh statistic, see Buccheri et al. 1983)
to the photon event distributions for trial frequencies in a narrow
window centred on the expected frequency of 414.7 Hz
(i.e., 413-416 Hz). The dynamical power spectra were computed
using the same method as in Strohmayer et al. (2008).
We employed intervals of 4 s or 8 s, stepping
through the BAT, FREGATE and ISGRI bursts with intervals of
0.25 s; for the calculation of upper limits we used intervals
of 10 s.
We searched data from both the PCA and HEXTE for oscillations
during the prompt burst seen on MJD 51 944 using fast Fourier
transforms (FFTs). We used the single bit mode data available (full
2-60 keV PCA energy range taken at 122 ![]() s
time resolution). FFTs of data from 4 s-long intervals within
the burst were performed keeping the original time resolution. For
HEXTE we computed FFTs of 1 s-long sets of 15-40 keV band
data with 122
s
time resolution). FFTs of data from 4 s-long intervals within
the burst were performed keeping the original time resolution. For
HEXTE we computed FFTs of 1 s-long sets of 15-40 keV band
data with 122 ![]() s time resolution. For the oscillation search in the long-lasting faint tails we employed the PCA data only.
s time resolution. For the oscillation search in the long-lasting faint tails we employed the PCA data only.
2.2.2 X-ray spectral fits
In all our spectral fits (using XSPEC 11.3.0) we fix the
low-energy absorption equivalent to a hydrogen column density of ![]() = 3
= 3 ![]() 1021 cm-2 (e.g., Piraino et al. 1999; Méndez et al. 2002) for a composition of the absorbing matter as given by Wilms et al. (2000), employing absorption cross sections as provided by Verner et al. (1996). We derived errors in the fit parameters by using
1021 cm-2 (e.g., Piraino et al. 1999; Méndez et al. 2002) for a composition of the absorbing matter as given by Wilms et al. (2000), employing absorption cross sections as provided by Verner et al. (1996). We derived errors in the fit parameters by using
![]() (assuming the fit parameters are uncorrelated). We use a distance of 3 kpc (see Sect. 3.1.2) when reporting black-body radii or emission areas, X-ray luminosities and absolute fluences.
(assuming the fit parameters are uncorrelated). We use a distance of 3 kpc (see Sect. 3.1.2) when reporting black-body radii or emission areas, X-ray luminosities and absolute fluences.
To describe the persistent emission we used ASM spectra around the ASM,
FREGATE, 2003 ISGRI and BAT bursts, ASM plus ISGRI spectra around the
2005 ISGRI burst and WFC spectra around the WFC burst. We
also used PCA+HEXTE spectra, whenever available within about 1 day
of a burst. All spectra, except the PCA+HEXTE spectra, could
be well modelled by an absorbed power-law (power-law parameters:
index,
![]() and normalization at 1 keV,
and normalization at 1 keV,
![]() ).
For the PCA+HEXTE spectral fits a soft component had to be included (we
used a black body), as well as an Fe K line in the form of a
Gaussian (line parameters: line energy,
).
For the PCA+HEXTE spectral fits a soft component had to be included (we
used a black body), as well as an Fe K line in the form of a
Gaussian (line parameters: line energy,
![]() (keV), and photon flux,
(keV), and photon flux,
![]() (photons cm-2 s-1);
line width arbitrarily fixed at 0.1 keV). The time ranges over
which the persistent ASM or WFC emission was integrated are given
in Table 2. For the ASM spectra we generally used all data from about 1.5 days before the burst up to the
last dwell before the start of the burst. This leads to reasonably good spectra except for a few cases.
(photons cm-2 s-1);
line width arbitrarily fixed at 0.1 keV). The time ranges over
which the persistent ASM or WFC emission was integrated are given
in Table 2. For the ASM spectra we generally used all data from about 1.5 days before the burst up to the
last dwell before the start of the burst. This leads to reasonably good spectra except for a few cases.
To get an estimate of the bolometric (unabsorbed) persistent
luminosity, we extrapolate the
spectral fit results to the 0.1-200 keV band (arbitrarily chosen).
Note that these values should be taken with some caution: power-law
emission can contribute significantly to the total spectrum, at the
lowest energies for high power-spectral indices (about 80%
and 8% of the 0.1-200 keV emission is at 0.1-2 keV
and 10-200 keV, respectively, for
![]() = 2.5),
and at the highest energies for low power-spectral indices
(about 8% and 80%, respectively, for
= 2.5),
and at the highest energies for low power-spectral indices
(about 8% and 80%, respectively, for
![]() = 1.5).
= 1.5).
XSPEC cannot provide errors on the integrated flux in an energy
band. We therefore randomized the spectral parameters using the fit
values and the derived 1![]() -errors;
this was done 10 000 times and we recorded the resulting
integrated 2-10 keV and 0.1-200 keV fluxes. The flux
distributions are significantly skewed towards larger fluxes. We
therefore fitted the flux distributions below and above the peak of the
distribution with Gaussians with different widths. The plus and minus
errors in the integrated flux derived from the spectral fits were then
taken as the 1
-errors;
this was done 10 000 times and we recorded the resulting
integrated 2-10 keV and 0.1-200 keV fluxes. The flux
distributions are significantly skewed towards larger fluxes. We
therefore fitted the flux distributions below and above the peak of the
distribution with Gaussians with different widths. The plus and minus
errors in the integrated flux derived from the spectral fits were then
taken as the 1![]() widths.
widths.
2.3 Data and properties of previously reported bursts
We complete the information on the properties of the bursts seen after 1992 with that of the bursts reported by Lewin (1976), Swank et al. (1978) and Brandt et al. (1992). We digitized the 2-60 keV light curve of the OSO-8/GCXSE burst from Fig. 2 in Swank et al. (1978) and also obtained further information on the event from that paper. Data on the GRANAT/WATCH burst (6-20 keV; Brandt et al. 1992) is available in a form similar to that of the EURECA/WATCH bursts (see Sect. 2.1.1). We analysed this GRANAT/WATCH burst in a way similar to our analysis of the EURECA/WATCH bursts. Further information on the burst seen with the Horizontal Tube collimator (see Lewin et al. 1976) onboard SAS-3 was taken from Lewin (1976). Information about the persistent emission around the times of all these bursts, including those seen by EURECA/WATCH, were extracted from other literature (see Table 2).
3 Results
We report on 33 bursts from 4U 0614+091, including the bursts previously reported and the superburst. They are listed in Table 2. Figures 1 (top panels) and 2 present the raw light curves (for a perspective on the short time-scale behaviour of the bursts) of, respectively, 20 unpublished bursts, and the 3 previously reported EURECA/WATCH and the 2003 ISGRI bursts. Time-resolved spectroscopy for the 20 bursts is also presented separately in Fig. 1. An overview of the normal bursts is given in Sect. 3.1. The burst that occurred on MJD 51 944 and that shows evidence of radius expansion as well as a long-lasting faint tail is described in detail in Sect. 3.1.2. Our analysis of the superburst is presented in Sect. 3.2.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{13210f2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg117.png)
|
Figure 2:
From left to right: the 3 bursts observed with EURECA/WATCH in the 6-15 keV ( top) and 15-150 keV ( bottom) bands, and the burst observed with ISGRI in 2003 in the 15-30 keV ( top) and 30-200 keV ( bottom) bands.
Zero time corresponds to the start of each burst (see Table 2). For EURECA/WATCH detector count rates (in cts bin-1)
are shown, i.e., no correction has been made for background and
vignetting. The dashed line indicates the background level and the
dotted line marks the 3 |
| Open with DEXTER | |
3.1 Overview of all normal bursts
Apart from the fact that 4U 0614+091 is not bursting as seldomly as previously thought, Table 2 shows that the recurrence time between bursts can be on the order of a week, when burst active (see also Sect. 3.5.1). The bursts generally last between about 10 s and 10 min (ignoring long-lasting faint tails, see below). Based on the FREGATE bursts, we designate bursts as short bursts if the burst duration is less than about 100 s, and intermediate-duration bursts if they last between about 5 and 10 min. The intermediate-duration bursts thus refer to the two bursts that were seen by FREGATE in 2001 and 2002. The short bursts will be discussed in Sect. 3.1.1 and the intermediate-duration bursts in Sect. 3.1.2.
Based on the facts that for all bursts the emission can be well described by black-body emission with canonical type I X-ray burst parameter values, that their profiles generally show an initial fast rise (at low energies) with a final slower decay which is exponential-like, and that the effective black-body temperature decreases during the decay for most of the bursts, we infer that the events are indeed type I X-ray bursts.
3.1.1 Short bursts
For the short bursts the rise times to maximum of the bursts as
recorded by ASM, WFC and FREGATE are relatively fast, i.e., about
1-10 s. For the bursts seen by WATCH, ISGRI and BAT the rise times
tend to be a bit longer, i.e., about 5-20 s; this can be
attributed to these instruments being sensitive primarily at higher
energies than the former instruments. Also, many of the bursts from
these hard X-ray instruments show a two-stage rise, i.e., first a
fast rise within
seconds, then a slower rise to the peak intensity. The slow rise may be
attributed to the slow increase in
![]() (see, e.g., Fig. 1), and therefore to the peak of the X-ray spectrum shifting towards the centre of the instrument bandpass.
(see, e.g., Fig. 1), and therefore to the peak of the X-ray spectrum shifting towards the centre of the instrument bandpass.
The short bursts have e-folding decay times
between 2 and 20 s; the shortest decay times are seen at the
highest energies (ISGRI and BAT), as expected if the burst
spectrum softens during the decay. The characteristic decay time, ![]() ,
is in the range 6-42 s.
,
is in the range 6-42 s.
![\begin{figure}
\par\includegraphics[angle=-90,width=17.5cm,clip]{13210f3.ps}
\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg119.png)
|
Figure 3: Light curves ( top row) and time-resolved spectral fit results (lower four rows) for selected bursts shown with higher time resolution than in Fig. 1. See the caption to Fig. 1 for brief explanations of the spectral parameters. The date (MJD) of each burst and the instrumental origin (FR = FREGATE) of the data are indicated. Left: FREGATE light curve and time-resolved spectroscopy for the burst on MJD 52 997 with a time resolution of 0.16 s. The unit of intensity is kcts s-1. Middle left: ( top) PCA full band-pass light curve of the MJD 51 944 burst with a time resolution of 0.001 s (from t = 0-0.05 s), 0.01 s (from t = 0.05-2.25 s), 0.125 s (from t = 2.25-30 s), and 16 s (from t = 4000-8000 s). The unit of intensity is 104 c s-1 per 4 PCUs. The PCA (PCU3) rates after t = 4000 s have been multiplied by four. The ASM data are indicated with open squares; they have been scaled to the PCA rates using the Crab as a reference. Time t = 0 s corresponds to UT 2001 Feb. 4 21:52:42.8. (rest) Time-resolved spectral fit results using the data from the PCA (filled circles), ASM (open squares) and FREGATE (open triangles). Middle right: PCA full band-pass light curve ( top) and time resolved spectroscopy of the long-lasting faint tail of a possible burst observed on MJD 51 789. For this burst we do not have an exact start time, so t = 0 s corresponds to the start of the data sequence (UT 2000 Sep. 2 at 01:19:47). Intensity is in units of c s-1 for PCUs 2 and 3 combined. Right: ASM full-bandpass light curve of the superburst on MJD 53 441 from 4U 0614+091 ( top) and time resolved spectroscopy. Time is given in hours since UT 2005 March 12, 0h, and the intensity is given in cts s-1. |
| Open with DEXTER | |
The WFC burst (on MJD 51 073) and two FREGATE bursts (on
MJD 52 961 and MJD 53 740) are intrinsically weak;
they reach peak intensities of less than a few Crab. The WFC event
showed peak temperatures of about 1.5 keV, markedly below that
seen during maximum of most of the other bursts
(![]() 3 keV). These weak events may be similar to the burst reported from OSO-8, which reached a peak of
3 keV). These weak events may be similar to the burst reported from OSO-8, which reached a peak of ![]() 0.36 Crab and showed
0.36 Crab and showed
![]() = 0.8
= 0.8 ![]() 0.1 keV during the first 20 s (Swank et al. 1978; see also Table 2). The event seen by SAS-3 (Lewin 1976) was rather weak too (see Table 2), but only part of a burst was seen, so one cannot infer its true peak intensity.
0.1 keV during the first 20 s (Swank et al. 1978; see also Table 2). The event seen by SAS-3 (Lewin 1976) was rather weak too (see Table 2), but only part of a burst was seen, so one cannot infer its true peak intensity.
The fluxes of the strongest bursts (including the intermediate-duration
bursts) reach peak values of about 15 Crab. Both this and the
properties of the time-resolved spectral fits (see Fig. 1 and Table 2) suggest they reach a limiting bolometric flux between about 21 and 32 ![]() 10-8 erg cm-2 s-1. When taking into
account only those bursts which reached a peak flux of more than 15
10-8 erg cm-2 s-1. When taking into
account only those bursts which reached a peak flux of more than 15 ![]() 10-8 erg cm-2 s-1, the average peak value is about 27
10-8 erg cm-2 s-1, the average peak value is about 27 ![]() 10-8 erg cm-2 s-1 (fitting the observed values with a constant results, however, in a very high value of
10-8 erg cm-2 s-1 (fitting the observed values with a constant results, however, in a very high value of
![]() ,
i.e., 23, for 14 d.o.f.
,
i.e., 23, for 14 d.o.f.![]() ). The highest bolometric peak flux measured is 31.5
). The highest bolometric peak flux measured is 31.5 ![]() 0.5
0.5 ![]() 10-8 erg cm-2 s-1.
10-8 erg cm-2 s-1.
The observed fluences, ![]() ,
of the intrinsically weak bursts are between 7 and 13
,
of the intrinsically weak bursts are between 7 and 13 ![]() 10-7 erg cm-2. The values for the other short bursts range from about 16 to about 124
10-7 erg cm-2. The values for the other short bursts range from about 16 to about 124 ![]() 10-7 erg cm-2. For a source distance of 3 kpc we derive absolute fluences from the above quoted values between 0.8 and 13
10-7 erg cm-2. For a source distance of 3 kpc we derive absolute fluences from the above quoted values between 0.8 and 13 ![]() 1039 erg.
1039 erg.
We also inspected the burst light curves at higher time resolutions.
One of the FREGATE bursts (MJD 52 997) showed an interesting
spike at the start of the burst. The high-time resolution
light curve is shown in Fig. 3
(top left). The spike lasts for about 0.3 s; after that the
flux slowly rises to maximum for about 4 s. Double peaked
light curves are typically seen in hard X-ray light curves when
photospheric radius expansion is important (see, e.g., Lewin
et al. 1984; Tawara et al. 1984; Cocchi et al. 2000).
We performed time-resolved X-ray spectral fits at higher time
resolution, to follow in more detail the evolution of the burst,
especially the spike (Fig. 3,
left, bottom panels). During the spike, the spectrum is quite hard
compared to that generally observed near maximum of type I X-ray
bursts
(
![]() = 4.3
+0.6-0.5 keV versus
= 4.3
+0.6-0.5 keV versus ![]() 3 keV), and
3 keV), and
![]() is quite small.
During the first few seconds
is quite small.
During the first few seconds
![]() rises, after which it drops slightly and then levels off.
rises, after which it drops slightly and then levels off.
![]() quickly drops after the spike, but then it increases up to
quickly drops after the spike, but then it increases up to ![]() 3 keV
at the peak of the burst. This may be a hint of a short
radius-expansion phase, but the statistics are somewhat poor. Note
that
3 keV
at the peak of the burst. This may be a hint of a short
radius-expansion phase, but the statistics are somewhat poor. Note
that
![]() does not stay constant but slowly rises during that phase,
casting some doubt on the radius-expansion interpretation.
does not stay constant but slowly rises during that phase,
casting some doubt on the radius-expansion interpretation.
3.1.2 Intermediate-duration bursts and evidence of photospheric radius expansion
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{13210f4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg122.png)
|
Figure 4: PCA 2-60 keV light curve centred around the burst onset on MJD 51 944 at a 10 ms time resolution. The intensity is as measured by 4 PCUs combined. Time t = 0 s corresponds to UT 2001 Feb. 4 21:52:42.8. |
| Open with DEXTER | |
The PCA light curve around the time of the start of burst MJD 51 944 is shown in Fig. 4.
One may see a strong, very short, spike followed by a large drop in the
flux, and then the onset of the main burst. In the top part of
Fig. 3 (middle
left), the first part of the burst is plotted again, but the spike is
shown at higher time resolution. During the spike the intensity reaches
maximum within 5 ms. Then, within 0.04 s,
the intensity drops to a level consistent with the background and
certainly below that seen before the spike. About 1.1 s later
emission reappears again and continues as the main burst![]() .
A local maximum is then reached within 2 s. In the
spike, higher count rates are observed than during the first 30 s
of the main burst.
.
A local maximum is then reached within 2 s. In the
spike, higher count rates are observed than during the first 30 s
of the main burst.
The spike, drop below pre-burst levels and main burst indicate strong radius-expansion (see, e.g., Molkov et al. 2000; Strohmayer & Brown 2002;
see also in 't Zand & Weinberg, in preparation). The results
of the PCA time-resolved spectral fits are shown in the bottom panels
of Fig. 3
(middle left), together with spectral fits to the average of the
ASM measurements about 0.3 h after the start of the burst. We
also overlaid the spectral fit results from FREGATE (see Fig. 1,
most left of bottom panels). Indeed, the inferred emitting area clearly
increases during the spike and decreases during the very first part of
the main burst. The expansion is more than 3 orders of magnitude.
The peak of the emission (as parametrized by
![]() )
therefore shifts outside the PCA observable energy band, causing the dramatic drop in intensity.
)
therefore shifts outside the PCA observable energy band, causing the dramatic drop in intensity.
After the fast contraction, it takes about 100 s for the
burst to reach a maximum inferred temperature. During that time the
emission area slowly decreases further (the end of this phase is
usually referred to as ``touch-down''). During the maximum of the main
burst, between about 5 and 100 s after the start, the
flux varies only slightly between about 18 and 26 ![]() 10-8 erg s-1 cm-2. This is consistent with the peak flux values reached during the other strong bursts (see Sect. 3.1.1).
If we assume that during that time the flux is close to the
Eddington value, the distance to the source may be inferred.
By using the highest measured peak flux (Sect. 3.1.1) and the empirically derived Eddington luminosity of
3.79
10-8 erg s-1 cm-2. This is consistent with the peak flux values reached during the other strong bursts (see Sect. 3.1.1).
If we assume that during that time the flux is close to the
Eddington value, the distance to the source may be inferred.
By using the highest measured peak flux (Sect. 3.1.1) and the empirically derived Eddington luminosity of
3.79 ![]() 1038 erg s-1 appropriate for a pure He accretor (Kuulkers et al. 2003),
we infer a distance to the source of 3.2 kpc. Since the
estimated uncertainty in the empirically derived Eddington luminosity
is about 15% (see Kuulkers et al. 2003),
we use for simplicity a distance value of 3 kpc in all our
calculations. We note that during the strong expansion and contraction
phase the apparent flux increases by more than an order of magnitude
with respect to that described above. This would mean that
super-Eddington fluxes are reached; however, since most of the emission
is outside the PCA sensitive energy band and the spectra in this
phase are highly non-Planckian (see below), these flux values must
be regarded with caution.
1038 erg s-1 appropriate for a pure He accretor (Kuulkers et al. 2003),
we infer a distance to the source of 3.2 kpc. Since the
estimated uncertainty in the empirically derived Eddington luminosity
is about 15% (see Kuulkers et al. 2003),
we use for simplicity a distance value of 3 kpc in all our
calculations. We note that during the strong expansion and contraction
phase the apparent flux increases by more than an order of magnitude
with respect to that described above. This would mean that
super-Eddington fluxes are reached; however, since most of the emission
is outside the PCA sensitive energy band and the spectra in this
phase are highly non-Planckian (see below), these flux values must
be regarded with caution.
Because of the very high count rates, the spectra constructed
from the PCA data have small statistical errors, and this often means
that simple spectral models are not sufficient to fit the spectra
within the uncertainties. We find
![]() values as high as 20, especially
during the first part of the contraction phase (see bottom panel of Fig. 3, middle left). Deviations from a pure black body are seen frequently during radius-expansion bursts
(see, e.g., Kuulkers et al. 2002b, 2003,
and references therein). Since the temperature changes are fast during
the expansion/contraction phase, a single black body may not be
adequate in the time bins used. However, 10-20 s after the start
of the bursts the temperature stays more or less constant, while still
the spectra fits are not ideal. The deviations are thus intrinsic to
the source.
values as high as 20, especially
during the first part of the contraction phase (see bottom panel of Fig. 3, middle left). Deviations from a pure black body are seen frequently during radius-expansion bursts
(see, e.g., Kuulkers et al. 2002b, 2003,
and references therein). Since the temperature changes are fast during
the expansion/contraction phase, a single black body may not be
adequate in the time bins used. However, 10-20 s after the start
of the bursts the temperature stays more or less constant, while still
the spectra fits are not ideal. The deviations are thus intrinsic to
the source.
Both intermediate-duration bursts show very long rise times during the main burst part, i.e.,
![]() 70 s and
70 s and ![]() 140 s,
on MJD 51 944 and MJD 52 322, respectively. They
also have long exponential and characteristic decay times, i.e.,
140 s,
on MJD 51 944 and MJD 52 322, respectively. They
also have long exponential and characteristic decay times, i.e.,
![]()
![]() 40 s and
40 s and ![]() 90 s, respectively, and
90 s, respectively, and ![]()
![]() 119 s and
119 s and ![]() 216 s, respectively.
216 s, respectively.
The burst on MJD 51 944 showed a long and faint tail, lasting
for hours: after the main burst, during the next pass of PCA
observations (between about 1.2 and 2.2 h after the start of
the burst), the intensity was still slowly decaying but had not yet
reached pre-burst levels. Serendipitously, the ASM scanned over
4U 0614+091 about 0.3 h (i.e., in between the two
above described PCA passes) and 1.9 h after the start of the
burst. The trend seen in the ASM data points is consistent with that
seen in the second PCA pass (see Fig. 3, top middle left).
The e-folding decay as measured from the bolometric black-body flux,
![]() ,
light
curves,
,
light
curves,
![]() ,
is 1143
+2119-492 s, i.e., a factor of
about 35 longer than that measured during the first part of the
decline from maximum of the main burst (
,
is 1143
+2119-492 s, i.e., a factor of
about 35 longer than that measured during the first part of the
decline from maximum of the main burst (
![]() = 33
+7-5 s). During the first part of the decline
= 33
+7-5 s). During the first part of the decline
![]() drops quickly (see Fig. 1), but after the flux has dropped by more than an order of magnitude,
drops quickly (see Fig. 1), but after the flux has dropped by more than an order of magnitude,
![]() does
not decrease anymore, but stays more or less constant near 1 keV;
the decrease in flux is then due to an inferred decrease in emitting
area. About 5.2 h after the start of the burst the flux still
had not yet reached pre-burst levels; the steady flux decay suggests
that it is still due to remaining burst emission. However, at that low
flux level we cannot be certain whether this is indeed remaining burst
emission or due to a slight change in the persistent flux.
does
not decrease anymore, but stays more or less constant near 1 keV;
the decrease in flux is then due to an inferred decrease in emitting
area. About 5.2 h after the start of the burst the flux still
had not yet reached pre-burst levels; the steady flux decay suggests
that it is still due to remaining burst emission. However, at that low
flux level we cannot be certain whether this is indeed remaining burst
emission or due to a slight change in the persistent flux.
We found one other clear example of a long and faint tail in
the PCA data, on MJD 51 789, between UT 01:19:34 and
02:10:35 (see Fig. 3, top, middle right). In the bottom panels of Fig. 3
(middle right) we show the results of the time-resolved fits. The
behaviour is similar to that seen in the long-lasting faint tail of the
burst on MJD 51 944, albeit at a slightly higher flux level:
![]() stays constant near
stays constant near ![]() 1 keV,
while the inferred emitting area decreases by a factor of about 2.
The exponential decay time as measured from the bolometric black-body
flux light curves is
1 keV,
while the inferred emitting area decreases by a factor of about 2.
The exponential decay time as measured from the bolometric black-body
flux light curves is
![]() = 868
= 868 ![]() 32 s. No RXTE
observations of 4U 0614+091 were obtained for about 5 h
prior to the start of the observation at UT 01:19:47 and none for
about 2.5 h following the end of this observation. Therefore,
an intermediate-duration burst like that seen on MJD 51 944
may have preceded the tail here.
32 s. No RXTE
observations of 4U 0614+091 were obtained for about 5 h
prior to the start of the observation at UT 01:19:47 and none for
about 2.5 h following the end of this observation. Therefore,
an intermediate-duration burst like that seen on MJD 51 944
may have preceded the tail here.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{13210f5.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg124.png)
|
Figure 5: HEXTE hard X-ray (15-60 keV, cluster A) light curve of the burst on MJD 51 944 of 4U 0614+091 (filled circles), as well as the superburst light curves of 4U 1820-303 (filled triangles) and 4U 1636-536 (open squares). The time resolution is 16 s for 4U 0614+091 and 32 s for 4U 1820-303 and 4U 1636-536. Time = 0 s corresponds to UT 2001-02-04 21:52:43, 1999-09-09 01:46:54 and 2001-02-22 16:52:11, for 4U 0614+091, 4U 1820-303 and 4U 1636-536, respectively. |
| Open with DEXTER | |
Although the long-lasting faint tails last as long as various superbursts, their properties are different. Superbursts still show evidence of cooling, hours after they started. We show this in Fig. 5 by comparing the hard X-ray (15-60 keV) emission during the intermediate-duration burst with that seen during the two superbursts observed from 4U 1820-303 (Strohmayer & Brown 2002) and 4U 1636-536 (Strohmayer & Markwardt 2002). Clearly, hard X-ray persists during most of the superburst, while it only lasts for minutes during the intermediate-duration burst.
For the two intermediate-duration bursts the observed fluences are approximately 320 ![]() 10-7 erg cm-2 (MJD 51 944) and 610
10-7 erg cm-2 (MJD 51 944) and 610 ![]() 10-7 erg cm-2 (MJD 52 322), corresponding to absolute fluences of 34
10-7 erg cm-2 (MJD 52 322), corresponding to absolute fluences of 34 ![]() 1039 erg s-1 and 67
1039 erg s-1 and 67 ![]() 1039 erg s-1,
respectively, at 3 kpc. We have ignored here any long-lasting
faint tails; we expect that corrections for contributions from the
tails would change the above values by only a few per cent
(see Table 2).
1039 erg s-1,
respectively, at 3 kpc. We have ignored here any long-lasting
faint tails; we expect that corrections for contributions from the
tails would change the above values by only a few per cent
(see Table 2).
3.2 Superburst
Inspection of the ASM light curve of 4U 0614+091 revealed a long
flare on March 12, 2005 (MJD 53 441; see top right
of Figs. 3 and 6, see also Kuulkers 2005).
Between about UT 10:38 and 16:53 the ASM flux increased by a
factor of 9.5 up to 0.3 Crab. About 1.5 h later the
flux had dropped to 0.17 Crab; ![]() 9.5 h later it was still a factor of about 2 above the pre-flare flux level. The exponential decay time,
9.5 h later it was still a factor of about 2 above the pre-flare flux level. The exponential decay time,
![]() ,
of
the flare is
,
of
the flare is ![]() 2.1 h.
We calculated the hardness ratio using various energy bands. We found
the most significant results when we used the ratio of count rates in
the 3-12 keV to 1.5-3 keV bands, as shown in Fig. 6.
The hardness was higher during the flare than in the pre- or post-flare
measurements; it softened during the decay. We investigated the
raw dwell light curves during the flare, and found no evidence of
strong variability, anomalous features such as normal bursts, or for
instrumental artifacts. We, therefore, confidently attribute the high
fluxes to the source.
2.1 h.
We calculated the hardness ratio using various energy bands. We found
the most significant results when we used the ratio of count rates in
the 3-12 keV to 1.5-3 keV bands, as shown in Fig. 6.
The hardness was higher during the flare than in the pre- or post-flare
measurements; it softened during the decay. We investigated the
raw dwell light curves during the flare, and found no evidence of
strong variability, anomalous features such as normal bursts, or for
instrumental artifacts. We, therefore, confidently attribute the high
fluxes to the source.
We grouped the flare into three time bins, and performed a
time-resolved spectral analysis of the average ASM spectra in
these time bins. The spectra of the first two time bins are
inconsistent with an absorbed power law (
![]() /d.o.f. of 6.1/1 and 16.2/1, respectively; for the third time bin
/d.o.f. of 6.1/1 and 16.2/1, respectively; for the third time bin
![]() /d.o.f. = 0.7/1).
The net-flare spectra can best be modelled by absorbed black-body
spectra. The results of this time resolved spectral analysis are
displayed in Fig. 3 (right). The peak flux is rather low, about 0.7
/d.o.f. = 0.7/1).
The net-flare spectra can best be modelled by absorbed black-body
spectra. The results of this time resolved spectral analysis are
displayed in Fig. 3 (right). The peak flux is rather low, about 0.7 ![]() 10-8 erg s-1 cm-2, and the maximum value for
10-8 erg s-1 cm-2, and the maximum value for
![]() black-body
temperature only about 1.5 keV. However, we may not have seen
the true peak intensity or black-body temperature due to the sparse
coverage by the ASM. The inferred emission areas are rather low
(2-4 km). They are similar to those inferred for the long-lasting
faint tails of the bursts observed by the PCA (Sect. 3.1.2). However,
black-body
temperature only about 1.5 keV. However, we may not have seen
the true peak intensity or black-body temperature due to the sparse
coverage by the ASM. The inferred emission areas are rather low
(2-4 km). They are similar to those inferred for the long-lasting
faint tails of the bursts observed by the PCA (Sect. 3.1.2). However,
![]() is
somewhat higher, and the time scales
involved about a factor of 7 longer, than those seen in these
tails. Note that the inferred radii are not inconsistent with those
seen during some of the superbursts from other LMXB burst sources
(e.g., Kuulkers et al. 2002a). Since our observed flare resembles other superbursts,
we suggest the flare to be a superburst.
is
somewhat higher, and the time scales
involved about a factor of 7 longer, than those seen in these
tails. Note that the inferred radii are not inconsistent with those
seen during some of the superbursts from other LMXB burst sources
(e.g., Kuulkers et al. 2002a). Since our observed flare resembles other superbursts,
we suggest the flare to be a superburst.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{13210f6.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg125.png)
|
Figure 6: ASM individual dwell intensity measurements (1.5-12 keV) and average hardness ratios around the time of the superburst from 4U 0614+091. Hardness is defined as the ratio of the intensity in the 3-12 keV band to that in the 1.5-3 keV band. |
| Open with DEXTER | |
3.3 Search for burst oscillations
Table 3: Results of spectral fits of PCA+HEXTE data taken outside of but within one day of bursts, i.e., representing persistent emission only.
We confirm the presence of burst oscillations during the brightest BAT
burst, but do not detect any
significant signal in any of the other bursts. This is no surprise:
compared to the bright burst BAT light curve, the 2005 ISGRI burst
light curve has a factor 6 lower signal-to-noise ratio, and the
FREGATE light curves have a factor 1.6 to 2 lower
signal-to-noise ratio. Therefore, a 4![]() detection
by BAT would correspond to non-detection by both ISGRI and FREGATE,
assuming that the fractional amplitude was equal to that measured in
the BAT data. We derive 3
detection
by BAT would correspond to non-detection by both ISGRI and FREGATE,
assuming that the fractional amplitude was equal to that measured in
the BAT data. We derive 3![]() upper limits on the fractional rms (e.g., van der Klis 1995)
in the 413-416 Hz range of about 4-6% at the peaks of the
bursts observed by FREGATE, while they are about 9-12% in the
burst tails.
upper limits on the fractional rms (e.g., van der Klis 1995)
in the 413-416 Hz range of about 4-6% at the peaks of the
bursts observed by FREGATE, while they are about 9-12% in the
burst tails.
The 3![]() upper
limits on the fractional rms amplitude of burst oscillations during the
prompt burst on MJD 51 944 are about 0.3% and 2% in
the 100-1000 Hz range as measured by the PCA and HEXTE,
respectively. Thus, if there were oscillations during the prompt
burst on MJD 51 944 they were much weaker than those observed
during the brightest BAT burst on MJD 54 029.
No evidence of oscillations was found during the faint
long-lasting tails either, with 3
upper
limits on the fractional rms amplitude of burst oscillations during the
prompt burst on MJD 51 944 are about 0.3% and 2% in
the 100-1000 Hz range as measured by the PCA and HEXTE,
respectively. Thus, if there were oscillations during the prompt
burst on MJD 51 944 they were much weaker than those observed
during the brightest BAT burst on MJD 54 029.
No evidence of oscillations was found during the faint
long-lasting tails either, with 3![]() upper limits of about 1.2%.
upper limits of about 1.2%.
3.4 Persistent emission
Moderate resolution X-ray spectra of the persistent emission from
4U 0614+091 above typically 1 keV have been satisfactorily
fit by a soft component plus a hard, power-law component, both
subjected to interstellar absorption. Generally, for 4U 0614+091
photon indices for the power-law component are found to be
between 2 and 3 and temperatures for the soft black-body
component are between kT = 0.5 and 1.5 keV. Total fluxes (1-20 keV) are typically between 1 and 5 ![]() 10-9 erg s-1 cm-2 (Barret & Grindlay 1995; Ford et al. 1996, 1997; see also Piraino et al. 1999; Fiocchi et al. 2008). Our four most accurate measurements for these components are provided in Table 3. Our other lower-quality measurements based on power-law fits only are provided in Table 2. Our derived values of the power-law index,
10-9 erg s-1 cm-2 (Barret & Grindlay 1995; Ford et al. 1996, 1997; see also Piraino et al. 1999; Fiocchi et al. 2008). Our four most accurate measurements for these components are provided in Table 3. Our other lower-quality measurements based on power-law fits only are provided in Table 2. Our derived values of the power-law index, ![]() ,
vary between
,
vary between ![]() 1.6 and
1.6 and ![]() 2.5. The persistent 2-10 keV flux is around 0.5-2
2.5. The persistent 2-10 keV flux is around 0.5-2 ![]() 10-9 erg s-1 cm-2, with an average of 0.66
10-9 erg s-1 cm-2, with an average of 0.66 ![]() 0.06
0.06 ![]() 10-9 erg s-1 cm-2. Our spectral fits are consistent with that derived previously.
10-9 erg s-1 cm-2. Our spectral fits are consistent with that derived previously.
The unabsorbed bolometric flux (as estimated from the 0.1-200 keV flux estimates in Table 2, see Sect. 2.2.2) is about a factor of 5 higher than the 2-10 keV flux, i.e., on average 3.4 ![]() 0.2
0.2 ![]() 10-9 erg s-1 cm-2.
The best estimates of the bolometric correction factor from the
2-10 keV flux are obtained from a joint analysis of the PCA and
HEXTE spectra, because of the quality and broad-band coverage.
They are between 4.0 and 4.3 with an average of 4.16
10-9 erg s-1 cm-2.
The best estimates of the bolometric correction factor from the
2-10 keV flux are obtained from a joint analysis of the PCA and
HEXTE spectra, because of the quality and broad-band coverage.
They are between 4.0 and 4.3 with an average of 4.16 ![]() 0.05 (see Table 3), which is consistent with that derived from the ASM plus ISGRI spectra (4.4
0.05 (see Table 3), which is consistent with that derived from the ASM plus ISGRI spectra (4.4 ![]() 1.3, see Table 2). These factors are compatible with that derived by in 't Zand et al. (2007) from a broad sample of LMXBs, i.e., a factor 2.9
1.3, see Table 2). These factors are compatible with that derived by in 't Zand et al. (2007) from a broad sample of LMXBs, i.e., a factor 2.9 ![]() 1.4
between the 2-10 keV flux and the bolometric flux as estimated
from the extrapolated 0.1-100 keV flux, but are a bit higher than
the value estimated by Migliari & Fender (2006)
for an atoll source in the hard state, i.e., 2.5. Our bolometric
fluxes derived from the ASM spectral fits are consistent
with the fluxes derived from the broad-band PCA plus HEXTE spectral
fits. Also, our fluxes are comparable to that measured using broad-band
BeppoSAX data on 4U 0614+091 in the 0.1-200 keV band (Piraino et al. 1999; see also Fiocchi et al. 2008), as well as simultaneous
Swift/XRT and PCA plus HEXTE data in the 0.6-100 keV band (Migliari et al. 2010).
This lends confidence to the bolometric correction and the
interpretation that the extrapolated 0.1-200 keV flux represents
the bolometric flux.
1.4
between the 2-10 keV flux and the bolometric flux as estimated
from the extrapolated 0.1-100 keV flux, but are a bit higher than
the value estimated by Migliari & Fender (2006)
for an atoll source in the hard state, i.e., 2.5. Our bolometric
fluxes derived from the ASM spectral fits are consistent
with the fluxes derived from the broad-band PCA plus HEXTE spectral
fits. Also, our fluxes are comparable to that measured using broad-band
BeppoSAX data on 4U 0614+091 in the 0.1-200 keV band (Piraino et al. 1999; see also Fiocchi et al. 2008), as well as simultaneous
Swift/XRT and PCA plus HEXTE data in the 0.6-100 keV band (Migliari et al. 2010).
This lends confidence to the bolometric correction and the
interpretation that the extrapolated 0.1-200 keV flux represents
the bolometric flux.
If the source emits isotropically during and between bursts, and if the peak flux during the bursts
![]() represents emission at the Eddington limit, then the parameter
represents emission at the Eddington limit, then the parameter ![]() (
(![]()
![]() ,
where both fluxes are bolometric) gives the source persistent
luminosity in terms of the Eddington limit (see, e.g., Cornelisse
et al. 2002b). Using the
values from Table 2 and using only those bursts where
,
where both fluxes are bolometric) gives the source persistent
luminosity in terms of the Eddington limit (see, e.g., Cornelisse
et al. 2002b). Using the
values from Table 2 and using only those bursts where
![]() > 15
> 15 ![]() 10-8 erg s-1 cm-2 (see Sect. 3.1.1), we find values for
10-8 erg s-1 cm-2 (see Sect. 3.1.1), we find values for ![]() between about 0.0032 and 0.016, with an average of
between about 0.0032 and 0.016, with an average of ![]() = 0.013
= 0.013 ![]() 0.001. This is consistent with the estimates by, e.g., Ford et al. (2000) and in 't Zand et al. (2007).
0.001. This is consistent with the estimates by, e.g., Ford et al. (2000) and in 't Zand et al. (2007).
3.5 Long-term X-ray behaviour
![\begin{figure}
\par\includegraphics[angle=-90,width=12cm,clip]{13210f7a.ps}\includegraphics[angle=-90,width=6cm,clip]{13210f7b.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg130.png)
|
Figure 7: Left: daily averaged ASM light curve (1.5-12 keV). The times of the normal bursts (see Table 2) are indicated with arrows at the top. The superburst occurrence is marked with an ``S''. Right: the yearly averaged ASM light curve (1.5-12 keV; filled circles) and the measure of the variability (rms) in the yearly time bins (filled triangles). |
| Open with DEXTER | |
We investigated the long-term X-ray behaviour of 4U 0614+091 to see whether it affected its bursting behaviour using results from the RXTE/ASM (Sect. 3.5.1) and instruments on a number of other spacecrafts (Sect. 3.5.2).
3.5.1 ASM long-term persistent flux and burst recurrence times
Table 4: Average burst recurrence time estimates for various instruments during three periods.
The ASM data provide a uniquely long and homogeneous history of the persistent flux. In Fig. 7 (left) we show the ASM (1.5-12 keV) long-term light curves as daily averages. The corresponding average flux and variability (rms) per year are shown in Fig. 7 (right). From 1996 to mid 2000 the source was flaring on time scales of days to weeks from about 25-50 mCrab up to about 100-125 mCrab, with yearly averages above 30-35 mCrab. Then the source stayed at a relatively quiet level near 30 mCrab for about two and a half years (mid 2000 to 2003). Flaring behaviour similar to before mid 2000 was seen from 2003 to mid 2005. From mid 2005 to mid 2007 4U 0614+091 was still flaring, but less intensely, i.e., it varied from 25-50 mCrab up to about 75-100 mCrab and the yearly averages were again above 30-35 mCrab. The figure suggests that the degree of flaring and the long-term average (months to years) intensity seem to be related; a high degree of flaring is seen when the yearly average persistent flux is above about 30-35 mCrab and a low degree of flaring is seen otherwise. A flux of 30-35 mCrab (1.5-12 keV) corresponds to about 1% of the Eddington limit (see Sect. 3.4). For the following discussion we roughly divide the ASM history of 4U 0614+091 into three periods: (I) 1996-2000 flaring period, (II) 2001-2002 calm period, and (III) 2003-2007 flaring period.
In Fig. 7 (left) we mark the times of the normal bursts, as well as the superburst. The timing of burst detections is related, in part, to the times of year when the Sun is not near the source and the latter is more easily observed. Moreover, bursts could have occurred during many of the data gaps. It is also possible that with the ASM we missed the bursts which last significantly longer than the dwell duration (like the two intermediate-duration bursts). Also, weak bursts like that seen by the WFC may have been gone unnoticed with the other instruments; moreover, FREGATE, ISGRI and BAT operate in a higher bandpass than the ASM and WFC, and have to cope with higher backgrounds and so tend to trigger on brighter bursts. Therefore, we cannot rule out that we did not see all bursts which happened in our time frame of interest.
Figure 7 (left)
suggests, however, that bursts appear more frequently during the
2003-2007 flaring period with respect to the previous periods. This is
especially apparent if we take into account that during the 2000-2002
period there were 3 surveying X-ray instruments active (WFC, ASM
and FREGATE). To support this suggestion, we determined the
average burst recurrence times
during the three above described periods for each instrument,
as well as all together.
We excluded results from the BAT (we only have information on triggered
bursts, i.e., we did not perform a systematic search through the BAT
archive) and JEM-X (very low source exposure time).
We also did not take into account either the tail of a possible burst
on MJD 51 789 or the superburst. When considering all
instruments, we assumed that the exposure intervals did not overlap,
and that they have the same efficiency in detecting bursts. We also
assumed that the exposure time of a particular instrument is randomly
distributed in each of the three periods. If n is the number of bursts seen during a certain period, then the average burst recurrence time
is defined as
![]() divided by n, where
divided by n, where
![]() is the total exposure time on the source in question in that period
(note that this does not necessarily mean that the bursts recur
periodically). Since we are dealing with relatively low number of
observed bursts, Poisson statistics apply. For the expected range in
average burst recurrence times (
is the total exposure time on the source in question in that period
(note that this does not necessarily mean that the bursts recur
periodically). Since we are dealing with relatively low number of
observed bursts, Poisson statistics apply. For the expected range in
average burst recurrence times (
![]() )
we use the Poisson likelihood 1
)
we use the Poisson likelihood 1![]() lower and upper limits on the expected number of events when n events are observed (where n =
0, 1, 2, 3, ...). We verified our method by doing
Monte Carlo simulations. The net source exposure times, number of
bursts observed, and resulting average burst recurrence times per
period of interest are shown in Table 4.
For the individual instruments, the ASM and FREGATE give the best
constraints on the average burst recurrence times, mainly because of
the number of bursts observed. The estimates of the PCA average burst
recurrence times differ significantly from those for the other
instruments; we attribute this is to the fact that the data are not
taken serendipitously, as well as to the relatively low exposure times.
lower and upper limits on the expected number of events when n events are observed (where n =
0, 1, 2, 3, ...). We verified our method by doing
Monte Carlo simulations. The net source exposure times, number of
bursts observed, and resulting average burst recurrence times per
period of interest are shown in Table 4.
For the individual instruments, the ASM and FREGATE give the best
constraints on the average burst recurrence times, mainly because of
the number of bursts observed. The estimates of the PCA average burst
recurrence times differ significantly from those for the other
instruments; we attribute this is to the fact that the data are not
taken serendipitously, as well as to the relatively low exposure times.
The average burst recurrence times in periods I and II are
not significantly different; the average over the two periods combined
is 29
+17-10 days (taking into account all
considered instruments). Period III shows a significant change in
the average burst recurrence time with
respect to the previous period: 11
+3-2 days (taking into account all
considered instruments); it is just consistent with period I.
The lower limit on the average burst recurrence time in period III
is close to the shortest observed value of ![]() in that period (7 days, see Table 2). During the EURECA/WATCH period in 1993 the burst average recurrence time is 17
+15-7 days, consistent with values of
in that period (7 days, see Table 2). During the EURECA/WATCH period in 1993 the burst average recurrence time is 17
+15-7 days, consistent with values of ![]() in that period (see Table 2). It is consistent also with the values of all three ASM periods I-III.
in that period (see Table 2). It is consistent also with the values of all three ASM periods I-III.
Interestingly, the only two bursts that were observed in 2001 and 2002 are both intermediate-duration bursts. They thus occurred during a period when 4U 0614+091 was not only less burst active, but also when the persistent emission was rather calm and had the lowest averaged values. All other bursts (22, including the BAT bursts) are shorter and occurred during the two flaring periods. The burst duration, therefore, seems to be related to the level of the persistent emission, and possibly to the degree of flaring.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{13210f8.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg132.png)
|
Figure 8: Zoom in on the long-term hard X-ray (15-50 keV) light curve ( top) and soft X-ray (1.5-12 keV) light curve ( bottom), of 4U 0614+091. Shown are the 1-day and 10-day averages for ISGRI (filled circles) and Swift/BAT (grey filled triangles), respectively ( top), and 10-day averages for the ASM. Time in years is given above the plot. The occurrence times of the normal bursts are indicated by arrows at the top. The superburst occurrence is marked with an ``S''. |
| Open with DEXTER | |
3.5.2 Further long-term broad-band X-ray behaviour
4U 0614+091 was discovered by UHURU with variable flux levels between about 15 and 70 mCrab (2-6 keV; Giacconi et al. 1972). Other early measurements of the flux, besides those from UHURU, may be found in, e.g., Mason et al. (1976), Swank et al. (1978), Parsignault & Grindlay (1978), Markert et al. (1979), and Warwick et al. (1981). In that time it was always seen at a flux of about 10-100 mCrab in roughly the ![]() 2 to
2 to ![]() 10 keV band. During sporadic measurements by the Ginga/All
Sky Monitor between February 1987 and November 1991
4U 0614+091 was never detected in the 1-20 keV band, with an
upper limit on the source flux of about 100 mCrab
(S. Kitamoto, private communication).
10 keV band. During sporadic measurements by the Ginga/All
Sky Monitor between February 1987 and November 1991
4U 0614+091 was never detected in the 1-20 keV band, with an
upper limit on the source flux of about 100 mCrab
(S. Kitamoto, private communication).
4U 0614+091 was too weak to be detected by EURECA/WATCH on a daily basis, but data from the entire observation period can be combined. By adding the skymaps (see Brandt 1994, for a description of the technique), 4U 0614+091 was detected at an average persistent flux of 25 ![]() 10 mCrab in the 6-12 keV energy band (see also Fig. A.1, right).
10 mCrab in the 6-12 keV energy band (see also Fig. A.1, right).
We investigated the CGRO/BATSE occultation measurements (see, e.g., Harmon et al. 2004)
in the period April 1991 and November 2000; they show 10-day
average 20-100 keV fluxes from non-detections (with typical 10-day
3![]() upper limits between about 50-70 mCrab) up to about 150 mCrab. During the period of the EURECA/WATCH observations when 4U 0614+091 was in the field of view, the 20-100 keV flux was on average 57
upper limits between about 50-70 mCrab) up to about 150 mCrab. During the period of the EURECA/WATCH observations when 4U 0614+091 was in the field of view, the 20-100 keV flux was on average 57 ![]() 6 mCrab; close to the time of the bursts seen by EURECA/WATCH it was around 100 mCrab.
6 mCrab; close to the time of the bursts seen by EURECA/WATCH it was around 100 mCrab.
The BAT and ISGRI 15-50 keV long-term light curves are consistent
with each other. The 15-50 keV flux in the February 2003 to
September 2007 time frame ranges from a few mCrab to
50 mCrab, but is most frequently around 20 mCrab. A zoom
in on the 15-50 keV light curve and the corresponding part of the
ASM light curve is shown in Fig. 8.
Three interesting features may be seen in this figure. First, there is
a rapid increase to about 50 mCrab for about a month, followed by
a drop within weeks to about 10 mCrab at MJD 53 500.
After about 2 months it goes back up again to the average level.
Second, whenever the hard X-ray flux drops below roughly 10 mCrab,
the soft X-ray intensity increases, up to a factor of 2
or so. Such an anti-correlation between soft and hard X-rays on
these long time scales was previously discussed by Barret &
Grindlay (1995) and Ford et al. (1996). On the other hand, hard X-ray flares are not
accompanied by changes in the soft
X-ray emission. Third, the superburst occurred around the time when the
15-50 keV flux was at its highest level (unfortunately no
simultaneous BAT measurements exist at the time of the
superburst). Just after the superburst the 10-day average
15-50 keV flux is low, while the 1.5-12 keV flux is at high
levels. The ASM data show that this high average flux is not only
due to the superburst itself, but also to a somewhat increased
persistent level just after the superburst (see Fig. 6): before the superburst the 1.5-12 keV flux was 31 ![]() 1 mCrab, whereas for several days after the superburst it was at an elevated level of 53
1 mCrab, whereas for several days after the superburst it was at an elevated level of 53 ![]() 2 mCrab. About
10 days after the superburst it was back at the pre-superburst
level. A normal burst (MJD 53 460) was seen only
19 days after the superburst (see Table 2);
note that this
is only slightly longer than the typical average burst recurrence time
when 4U 0614+091 is burst active (see Sect. 3.5).
2 mCrab. About
10 days after the superburst it was back at the pre-superburst
level. A normal burst (MJD 53 460) was seen only
19 days after the superburst (see Table 2);
note that this
is only slightly longer than the typical average burst recurrence time
when 4U 0614+091 is burst active (see Sect. 3.5).
| Figure 9:
PCA colour-colour diagram ( Left) and hardness-intensity diagram ( Right)
of all public data of 4U 0614+091. Plotted are all persistent data
points averaged per observation, and normalised using the Crab (see
Sect. 2.1.3). Data taken close to a burst are marked with a black filled triangle ( |
|
| Open with DEXTER | |
The CD and HID (Fig. 9) are qualitatively similar to those presented for the PCA data obtained in 1996-1998 by van Straaten et al. (2000). The colours often change on a daily time scale, as is typical for atoll sources (e.g., Hasinger & van der Klis 1989). For a wide range in hard colour, the soft colour does not change noticeably. Only near the lowest hard colours does the soft colour start to change; then there is an anti-correlation between hard and soft colour. When the hard colours are lowest, however, the soft colour changes are large while the hard colour changes are small. This is in line with the broad-band behaviour on longer time scales of the fluxes in the 1.5-12 keV and 15-50 keV bands described in the previous paragraph. In the HID higher intensities correspond to lower hard colours. Again, at the highest intensities (above about 50 mCrab), however, the hard colour changes only very little. The part of the diagram where the soft colour and intensity increases at constant hard colour (value of about 0.5) is referred to as the soft state or ``banana'' branch (see van Straaten et al. 2000). The rest is referred to as the intermediate state or ``island'' branch.
For 4 bursts (i.e., those that occurred on MJD 51 789,
MJD 51 944, 53 040 and 54 188) we have information
about the persistent emission within about 1 day of the burst (see
Table 3). In Fig. 9
we indicate the position the persistent source was in at these times.
All 4 bursts occurred when the persistent emission was
hardest and when the intensity was below ![]() 40 mCrab, i.e., when the source was in the intermediate or hard state
(``island'' or extreme ``island'').
40 mCrab, i.e., when the source was in the intermediate or hard state
(``island'' or extreme ``island'').
4 Discussion
4.1 Observational summary
We have expanded the number of observed bursts that can be attributed to 4U 0614+091 from a
handful to 33. These include a superburst. Most of the newly-found bursts are localized within 1
![]() 5
of the optical position of 4U 0614+091. This confirms the
type I X-ray
burster nature of this low-mass X-ray binary. We find a significant
change in the average burst recurrence time in a decade of
observations, i.e., from roughly a month before mid-2003 to about one
to two weeks afterwards. When burst active, the bursts have peak
luminosities of about 3
5
of the optical position of 4U 0614+091. This confirms the
type I X-ray
burster nature of this low-mass X-ray binary. We find a significant
change in the average burst recurrence time in a decade of
observations, i.e., from roughly a month before mid-2003 to about one
to two weeks afterwards. When burst active, the bursts have peak
luminosities of about 3 ![]() 1038 erg s-1, last for up to about a minute, and release energies of about 1039-1040 erg.
The larger set of bursts shows a wide variety of characteristics, with
dynamic ranges of a factor of 40 in peak flux, 100 in
duration, and 230 in absolute fluence.
1038 erg s-1, last for up to about a minute, and release energies of about 1039-1040 erg.
The larger set of bursts shows a wide variety of characteristics, with
dynamic ranges of a factor of 40 in peak flux, 100 in
duration, and 230 in absolute fluence.
We found three long-duration bursts. Two of them have initial decay time scales of about 100 s and resemble intermediate-duration bursts seen from other sources (thought to be due to deep He flashes; see in 't Zand et al. 2005; Cumming et al. 2006). The third has an initial decay time of about 8000 s, comparable to the decay times of superbursts (due to an even deeper C flash contained in the ocean of the NS envelope; see Cumming & Bildsten 2001; Strohmayer & Brown 2002). It lasts a factor of 10 longer than the longest known intermediate-duration burst (for example, see in 't Zand et al. 2007; Keek & in 't Zand 2009). Unfortunately, the coverage of this burst is incomplete. This prevents a measurement of the true peak flux and a check for the occurrence of radius expansion. The average burst recurrence time when the two intermediate-duration bursts were seen, is notably longer than when the shorter bursts were seen (40 +49-18 days during a two-year period versus 11 +3-2 days for other bursts in the subsequent 4.7-year period).
One of the intermediate-duration bursts shows clear signs of strong radius expansion within the first few seconds of the event. The flux seen at the end of this episode of radius expansion must correspond to a luminosity near the Eddington limit, and we thereby confirm the distance to be close to 3 kpc. The average accretion rate suggested by the broad-band non-burst flux is 0.32-1.6% of the Eddington rate.
The two intermediate-duration bursts occur in a two-year time
interval when the accretion flux lacks the otherwise so typical flaring
behaviour and is on average about 30% lower than at other times.
Similar effects are seen in other (candidate) UCXBs. A calm component
is present which changes on time scales of a year, while flaring occurs
with a time scale of a week (see in 't Zand et al. 2007). Also, bursts are shorter when a source shows more flaring activity (e.g., A 1246-58; in 't Zand et al. 2008).
Moreover, UCXBs accreting above 1% of the Eddington limit show
burst recurrence times on the order of days; those accreting
below 1% of the
Eddington limit show recurrence times on the order of weeks (in 't Zand
et al. 2007).
In this respect it is interesting to note that during
4U 0614+091's high flux and flaring period it was detected in the
radio (0.34 ![]() 0.02 mJy at 4.86 GHz), while it was not detected during the low flux and calm period (3
0.02 mJy at 4.86 GHz), while it was not detected during the low flux and calm period (3![]() upper
limit of about 0.1 mJy at 4.86 GHz). This supports the
existence of different states and suggests a connection between the
radio and X-ray emission mechanisms (Migliari et al. 2010).
upper
limit of about 0.1 mJy at 4.86 GHz). This supports the
existence of different states and suggests a connection between the
radio and X-ray emission mechanisms (Migliari et al. 2010).
The wide range of peak fluxes is not unprecedented. Galloway et al. (2008) find that roughly 2% of bursts have bolometric peak fluxes less than 0.1 times the maximum for the same source. Three
sources exhibit dynamic ranges in excess of 100: EXO 0748-676 (236 ![]() 36), 4U 1608-522 (446
36), 4U 1608-522 (446 ![]() 115), and 4U 1636-536 (151
115), and 4U 1636-536 (151 ![]() 25),
although it should be mentioned that the high value in the last source
is due to a weak secondary burst in a double burst (excluding that
diminishes the dynamic range to 23
25),
although it should be mentioned that the high value in the last source
is due to a weak secondary burst in a double burst (excluding that
diminishes the dynamic range to 23 ![]() 1).
These three sources are not UCXBs, implying that the wide dynamic range
in 4U 0614+091 is not necessarily due to extraordinary abundances
of H,
He, C or O.
1).
These three sources are not UCXBs, implying that the wide dynamic range
in 4U 0614+091 is not necessarily due to extraordinary abundances
of H,
He, C or O.
We found two long-lasting faint tails wherein the flux decays exponentially with a time constant in the range of 1000 to 2000 s. One of them is the remainder of the intermediate-duration radius-expansion burst. The tail is seen clearly up to at least 2.5 h after the start of the burst, possibly even up to 5 h. During the tail no cooling is seen; the inferred temperature stays constant near about 1 keV, while the apparent emitting area decreases. Similar faint tails have been seen in various other bursters (Linares et al. 2009; Falanga et al. 2009; in 't Zand et al. 2009), but they were not as long lasting as those seen in 4U 0614+091. A hot underlying neutron star (with temperatures between 0.5-1 keV, i.e., slightly lower than that found in the burst tail) can explain the fact that in the tails the inferred temperatures are effectively constant (van Paradijs & Lewin 1986; in 't Zand et al. 2009). In this regard, we note that a soft component in our persistent PCA spectral fits is present, perhaps coming from the neutron star and/or the inner parts of the accretion disk; when the soft component is modelled by a black-body we infer temperatures of about 1 keV, i.e., close to that found in the long-lasting tails. As noted by in 't Zand et al. (2009), neutron stars in UCXBs accrete at lower rates and lack the CNO burning of H in their surface layers, compared to those in other, ordinary, bursters. This may result in a cooler neutron star in the former systems, leading to a different behaviour in the long-lasting tails during their bursts. However, the temperature reached in the long-lasting faint tail of 4U 0614+091 (and that of the transient XTE J1701-407, see Linares et al. 2009; Falanga et al. 2009, presumably also containing a cool neutron star due to its long off-states) is similar to that seen in ordinary persistent bursters, which may indicate that a different explanation is required for the constant temperature in the tail.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13210f10.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg135.png)
|
Figure 10: Models of the burst
light curves for the superburst (SB), the intermediate-duration
burst on MJD 51 944 (H1488), and the short burst on
MJD 53 718 (H3982). For the superburst, the model parameters
are E17 = 5, y11 = 2 (solid curve) and E17 = 2, y11 = 3 (dotted curve). For the intermediate-duration burst, the model parameters are E17 = 7, y9 = 8 (solid curve) and E17 = 5, y9 = 10 (dotted curve). For the short burst, the model parameters are E17 = 6, y9 = 2 (solid curve) and E17 = 4, y9 = 3 (dotted curve). Here E = E17 |
| Open with DEXTER | |
4.2 The burst light curves and energetics
In an attempt to constrain the energy release and ignition depth of the
bursts, we made some models of the light curves following the approach
of Cumming & Macbeth (2004) for superbursts. We deposit an energy per unit mass E = E17 ![]() 1017 erg g-1 uniformly in the layer down to a particular column depth y.
The cooling of the layer is then followed by integrating the thermal
diffusion equation. We set the composition after burning to be 56Fe. Our models assume neutron star parameters of 1.4
1017 erg g-1 uniformly in the layer down to a particular column depth y.
The cooling of the layer is then followed by integrating the thermal
diffusion equation. We set the composition after burning to be 56Fe. Our models assume neutron star parameters of 1.4 ![]() ,
R = 10 km, giving a redshift factor 1+z=1.31 and g = 2.44
,
R = 10 km, giving a redshift factor 1+z=1.31 and g = 2.44 ![]() 1014 cm s-2.
To avoid following the expansion of the outer layers that occurs
when the luminosity approaches the Eddington limit, we set the top of
our grid to y = 108 g cm-2,
and choose our outer boundary condition such that the maximum flux at
that point is the Eddington flux at the surface of the star for pure He
composition, i.e.,
1014 cm s-2.
To avoid following the expansion of the outer layers that occurs
when the luminosity approaches the Eddington limit, we set the top of
our grid to y = 108 g cm-2,
and choose our outer boundary condition such that the maximum flux at
that point is the Eddington flux at the surface of the star for pure He
composition, i.e.,
![]() =
= ![]() with
with ![]() = 0.2 cm2 g-1 (Thomson scattering for pure He), giving
= 0.2 cm2 g-1 (Thomson scattering for pure He), giving
![]() =
=
![]() = 2.1
= 2.1 ![]() 1025 erg cm-2 s-1.
Because of this crude treatment of the outer layers, and the simplistic
way in which the energy is initially deposited, our models are not
valid for early times,
1025 erg cm-2 s-1.
Because of this crude treatment of the outer layers, and the simplistic
way in which the energy is initially deposited, our models are not
valid for early times, ![]() 10 s (the thermal time scale at a depth of 108 g cm-2).
10 s (the thermal time scale at a depth of 108 g cm-2).
We varied the two parameters E17 and y to find values that agree well with the observed light curves. Note that the values of E17 and y are taken to be independent parameters of the model, which allows us to investigate the ignition depth and energy release without assuming a particular fuel for the burst. The model light curves are compared with the observed light curves for the superburst, the intermediate-duration burst on MJD 51 944, and the short burst on MJD 53 718, in Fig. 10. We assume a distance to the source of d = 3 kpc and a neutron star radius R = 10 km to convert the observed fluxes into flux at the surface of the neutron star; these values give good agreement with the maximum flux from the model.
The best fitting column depths for the three bursts in order of decreasing duration are y ![]() 2
2 ![]() 1011 g cm-2,
1011 g cm-2, ![]() 8
8 ![]() 109 g cm-2, and
109 g cm-2, and ![]() 2
2 ![]() 109 g cm-2.
For the intermediate-duration and short bursts, the column
depths inferred from the light curves are consistent with accretion at
about 1% Eddington for the observed times since the previous
burst,
109 g cm-2.
For the intermediate-duration and short bursts, the column
depths inferred from the light curves are consistent with accretion at
about 1% Eddington for the observed times since the previous
burst, ![]() = 155 and 16 days, respectively (see Table 2).
This can be derived as follows. The local Eddington accretion rate
(accretion rate per unit area) at the surface of the neutron star is
= 155 and 16 days, respectively (see Table 2).
This can be derived as follows. The local Eddington accretion rate
(accretion rate per unit area) at the surface of the neutron star is
![]() =
= ![]() .
We define the Eddington rate as the value corresponding to R = 10 km and
.
We define the Eddington rate as the value corresponding to R = 10 km and
![]() = 0.2 cm2 g-1, giving
= 0.2 cm2 g-1, giving
![]()
![]() 1.5
1.5 ![]() 105 g cm-2 s-1, or 1%
105 g cm-2 s-1, or 1%
![]() = 1500 g cm-2 s-1.
Accretion at
= 1500 g cm-2 s-1.
Accretion at ![]() = 1%
= 1%
![]() then gives a column y =
then gives a column y =
![]() = 1.6
= 1.6 ![]() 109 g cm-2 (
109 g cm-2 (
![]() %
%
![]() .
Matching the column depths inferred from the light curves assuming that
.
Matching the column depths inferred from the light curves assuming that ![]() is the recurrence time implies
is the recurrence time implies ![]() = 0.52%, and 1.3%
= 0.52%, and 1.3%
![]() for the intermediate-duration and short burst, respectively.
for the intermediate-duration and short burst, respectively.
The time span between the superburst and the previous observed burst is 367 days (i.e., ![]() = 367 days, see Table 2), in which time the accumulated column is
= 367 days, see Table 2), in which time the accumulated column is
![]()
![]() 1010 g cm-2
1010 g cm-2
![]() %
%
![]() .
Therefore, we require the accretion rate to be
.
Therefore, we require the accretion rate to be ![]()
![]() 5%
5%
![]() for the column inferred from the superburst light curve to be accreted
in the 367 days leading up to the superburst (assuming no bursts
occurred in between). An alternative explanation is that the
superburst involves a different fuel layer (e.g., He for the short
and intermediate-duration bursts, C for the superburst) in which case
the column for the superburst could accumulate over a
longer time scale than
for the column inferred from the superburst light curve to be accreted
in the 367 days leading up to the superburst (assuming no bursts
occurred in between). An alternative explanation is that the
superburst involves a different fuel layer (e.g., He for the short
and intermediate-duration bursts, C for the superburst) in which case
the column for the superburst could accumulate over a
longer time scale than ![]() .
At 1% Eddington, the accumulation time would then be about 5 yr.
.
At 1% Eddington, the accumulation time would then be about 5 yr.
The best fitting values for the energy release are E17 ![]() 5-7 (see Fig. 10).
In addition, the fact that the light curves reach the Eddington flux
implies a minimum energy release. For the intermediate-duration burst,
we find that the flux does not reach
the Eddington flux for E17
5-7 (see Fig. 10).
In addition, the fact that the light curves reach the Eddington flux
implies a minimum energy release. For the intermediate-duration burst,
we find that the flux does not reach
the Eddington flux for E17 ![]() 4. These values of energy release are smaller than the values E17
4. These values of energy release are smaller than the values E17 ![]() 16 for complete burning of He to Fe group or E17
16 for complete burning of He to Fe group or E17 ![]() 10 for complete
burning of C to Fe group. This implies that the energy release is about a factor of 3 lower
than expected for complete burning of pure He.
10 for complete
burning of C to Fe group. This implies that the energy release is about a factor of 3 lower
than expected for complete burning of pure He.
The low energies of the bursts can also be seen in the overall
energetics. If all the matter accreted since the previous burst were
completely burned during each burst, one would expect the ratio, ![]() ,
of the average luminosity in the persistent emission to the
time-averaged
luminosity emitted in type-I X-ray bursts to have a value in the range
25-200, depending on the composition of the burning material. If one
assumes that both the persistent and burst emission are
isotropic, that the persistent emission has not varied since the
previous burst, and that
,
of the average luminosity in the persistent emission to the
time-averaged
luminosity emitted in type-I X-ray bursts to have a value in the range
25-200, depending on the composition of the burning material. If one
assumes that both the persistent and burst emission are
isotropic, that the persistent emission has not varied since the
previous burst, and that
![]() is the bolometric persistent flux, then this statement relating the persistent and burst
luminosities is equivalent to
is the bolometric persistent flux, then this statement relating the persistent and burst
luminosities is equivalent to ![]()
![]()
![]()
![]() .
If we take that the minimum average burst recurrence time is the lowest observed value for
.
If we take that the minimum average burst recurrence time is the lowest observed value for ![]() ,
i.e., 7 days, then the corresponding values for
,
i.e., 7 days, then the corresponding values for ![]() are in fact lower limits, which are between 125 and 5525 for the short bursts and around 30-70 for the intermediate-duration
bursts. Calculating an
are in fact lower limits, which are between 125 and 5525 for the short bursts and around 30-70 for the intermediate-duration
bursts. Calculating an ![]() value by assuming that no bursts were missed between observed bursts (that is
value by assuming that no bursts were missed between observed bursts (that is ![]() is
the average burst recurrence time) gives a range from 500 to 5000,
larger than the canonical value of 100-200 for pure He burning.
Another way to look at this is presented in Fig. 11 which shows the burst energy against time since the last burst
is
the average burst recurrence time) gives a range from 500 to 5000,
larger than the canonical value of 100-200 for pure He burning.
Another way to look at this is presented in Fig. 11 which shows the burst energy against time since the last burst ![]() from Table 2.
The solid lines show the expected burst energy as a function of
recurrence time for accretion at 1% of the Eddington rate, for two
different values of the nuclear energy release per nucleon
from Table 2.
The solid lines show the expected burst energy as a function of
recurrence time for accretion at 1% of the Eddington rate, for two
different values of the nuclear energy release per nucleon
![]() = 1.6 and 0.6 MeV per nucleon (where E17
= 1.6 and 0.6 MeV per nucleon (where E17 ![]()
![]() ). The curves at the top left are pure He ignition models from Cumming et al. (2006) that assume complete burning. The observed bursts lie well
below the expected energies assuming complete burning.
). The curves at the top left are pure He ignition models from Cumming et al. (2006) that assume complete burning. The observed bursts lie well
below the expected energies assuming complete burning.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13210f11.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg154.png)
|
Figure 11:
The observed burst energies (assuming d = 3 kpc) versus the time since the last observed burst |
| Open with DEXTER | |
Figure 10 shows also that for the intermediate-duration burst on MJD 51 944, the model light curve nicely connects the early decay from the peak luminosity to the long tail lasting thousands of seconds. Therefore the long tail is naturally explained by the cooling of deep layers heated by the burst as proposed for tails seen in other sources by in 't Zand et al. (2009). The theoretical expectation is that the luminosity should decay as a power law in the cooling tail. This is confirmed by our observations (e.g., Fig. 10).
4.3 He as a fuel for the bursts
In Sect. 4.2, we found that the short and intermediate-duration burst light curves could be explained by ignition depths of y ![]() 2 and 8
2 and 8 ![]() 109 g cm-2, respectively, and that these depths are compatible with the amount of mass accreted at an accretion rate close to
109 g cm-2, respectively, and that these depths are compatible with the amount of mass accreted at an accretion rate close to ![]()
![]() 1%
1%
![]() in the observed time between bursts,
in the observed time between bursts, ![]() .
These
ignition depths would be naturally explained if the neutron star
accreted a substantial amount of He. At low accretion rates, most of
the energy released by pycnonuclear and electron capture reactions in
the crust flows outwards, because the neutron star core is too cold for
significant neutrino emission. This results in an outward flux from the
crust of F =
.
These
ignition depths would be naturally explained if the neutron star
accreted a substantial amount of He. At low accretion rates, most of
the energy released by pycnonuclear and electron capture reactions in
the crust flows outwards, because the neutron star core is too cold for
significant neutrino emission. This results in an outward flux from the
crust of F =
![]() with
with ![]()
![]() 1 MeV per nucleon (Brown 2000; Cumming et al. 2006: their Fig. 18, top panel). For this value of
1 MeV per nucleon (Brown 2000; Cumming et al. 2006: their Fig. 18, top panel). For this value of ![]() ,
Fig. 22 of Cumming et al. (2006) shows that pure He accretion gives ignition at y
,
Fig. 22 of Cumming et al. (2006) shows that pure He accretion gives ignition at y ![]() 109-1010 g cm-2 at
109-1010 g cm-2 at ![]()
![]() 1%
1%
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13210f12.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg156.png)
|
Figure 12:
The mass fraction of He needed to achieve unstable He ignition as
a function of accretion rate, for accretion of He and an equal mixture
of C and O. The different curves are for
different values of |
| Open with DEXTER | |
However, as we noted in the introduction, the lack of He lines in
the optical spectrum of the source implies that the accreted material
is not significantly enriched in He. To investigate whether a
small amount of He in the accreted material could still explain the
observed bursts, we constructed ignition models for type I X-ray
bursts following Cumming & Bildsten (2000). We assume that the
accreted material consists of He and a 50/50 C-O mixture. We find
that for small He mass fractions, the He burns away stably
before reaching the conditions required for a thermal runaway. In
Fig. 12 we plot the He mass fraction required to achieve unstable ignition as a function of ![]() and
and ![]() .
It shows that the amount of He inferred from the fits of disk spectra by Werner et al. (2006), i.e., Y
.
It shows that the amount of He inferred from the fits of disk spectra by Werner et al. (2006), i.e., Y ![]() 10%, do not lead to unstable ignition at any accretion rate unless the neutron star is cold,
10%, do not lead to unstable ignition at any accretion rate unless the neutron star is cold, ![]()
![]() 0.1 MeV
per nucleon, and even then the recurrence times are extremely long. We,
therefore, conclude that matching the observations requires a
significant amount of He in the accreted material.
0.1 MeV
per nucleon, and even then the recurrence times are extremely long. We,
therefore, conclude that matching the observations requires a
significant amount of He in the accreted material.
If we allow a large enough He fraction, we can match the
inferred ignition depth for the short and intermediate-duration bursts.
For example, taking a He mass fraction Y = 0.5, ![]() = 0.3 MeV per nucleon, and local accretion rates
= 0.3 MeV per nucleon, and local accretion rates ![]() = 3000 and 5000 g cm-2 s-1 (2% and 3.3% of the Eddington rate) gives ignition depths of y=2 and 8
= 3000 and 5000 g cm-2 s-1 (2% and 3.3% of the Eddington rate) gives ignition depths of y=2 and 8 ![]() 109 g cm-2, respectively. The corresponding recurrence times are 7 days and 46 days,
respectively. For pure He and
109 g cm-2, respectively. The corresponding recurrence times are 7 days and 46 days,
respectively. For pure He and ![]() = 1 MeV per nucleon, the correct ignition depths are obtained for
= 1 MeV per nucleon, the correct ignition depths are obtained for ![]() = 1% and 1.7%
= 1% and 1.7%
![]() ,
with recurrence times of 81 days and 11 days for the
intermediate-duration and short burst, respectively. These recurrence
time estimates are consistent with the observed values.
,
with recurrence times of 81 days and 11 days for the
intermediate-duration and short burst, respectively. These recurrence
time estimates are consistent with the observed values.
For each of these examples, a decrease in accretion rate of
only 40% is required to change the ignition column depth by a factor
of 4 from 2 to 8 ![]() 109 g cm-2.
This is because of the steep dependence of the ignition column on
temperature - only a small decrease in temperature, and a small
corresponding decrease in
109 g cm-2.
This is because of the steep dependence of the ignition column on
temperature - only a small decrease in temperature, and a small
corresponding decrease in ![]() is needed. The required decrease in
accretion rate is comparable to the observed difference in persistent
flux between the 2001-2002 calm period when the intermediate-duration
bursts occurred and the 2003-2007 flaring period when more regular
bursting resumed: as noted in Sect. 4.1,
the 1-year-averaged ASM fluxes for 4U 0614+091 in 2001 and 2002
are about 30% smaller than for the years after this time interval.
is needed. The required decrease in
accretion rate is comparable to the observed difference in persistent
flux between the 2001-2002 calm period when the intermediate-duration
bursts occurred and the 2003-2007 flaring period when more regular
bursting resumed: as noted in Sect. 4.1,
the 1-year-averaged ASM fluxes for 4U 0614+091 in 2001 and 2002
are about 30% smaller than for the years after this time interval.
It is not clear why unstable He ignition would give a nuclear energy release of only
![]()
![]() 0.6 MeV, as inferred from the burst energetics and light curve fits (see Sect. 4.2). This energy is approximately the energy released in burning He to C. For
a He mass fraction Y, setting the total energy release to be
0.6 MeV, as inferred from the burst energetics and light curve fits (see Sect. 4.2). This energy is approximately the energy released in burning He to C. For
a He mass fraction Y, setting the total energy release to be
![]() = 0.6 MeV per nucleon implies that the energy release from burning beyond C to heavy elements is
= 0.6 MeV per nucleon implies that the energy release from burning beyond C to heavy elements is
![]()
![]() 0.6(1-Y) MeV per nucleon. This is much less than the
0.6(1-Y) MeV per nucleon. This is much less than the ![]() 1 MeV available for complete burning of C to Fe, unless the helium fraction Y is small (however, as noted above, the observations require Y to be large). At a depth of y
1 MeV available for complete burning of C to Fe, unless the helium fraction Y is small (however, as noted above, the observations require Y to be large). At a depth of y ![]() 109 g cm-2, an energy deposition of only
0.03 MeV per nucleon is sufficient to raise the temperature to above 109 K,
at which the nuclear burning would be expected to proceed beyond
C, so a significant energy release from burning beyond C would be
expected. Numerical models of bursts at low accretion rates would be
useful to follow the nucleosynthesis and determine the expected energy
release.
109 g cm-2, an energy deposition of only
0.03 MeV per nucleon is sufficient to raise the temperature to above 109 K,
at which the nuclear burning would be expected to proceed beyond
C, so a significant energy release from burning beyond C would be
expected. Numerical models of bursts at low accretion rates would be
useful to follow the nucleosynthesis and determine the expected energy
release.
Another possibility is that not all of the accreted fuel burns during the burst. For example, the burning may consume only part of the depth of the fuel layer, or may cover only part of the stellar surface. Numerical models of bursts at low accretion rates are needed to follow the nucleosynthesis and burning dynamics, and determine the expected energy release.
4.4 The superburst
In the previous section we argued that the short bursts and intermediate-duration bursts could be explained by a substantial fraction of He in the accreted material, despite the fact that the optical spectrum of 4U 0614+091 suggests that very little He is present in the accreted material. However, the superburst poses a more severe problem.
The superbursts observed in other sources at accretion rates ![]()
![]() 0.1
0.1
![]() have been explained as being due to C ignition (Strohmayer & Brown 2002; Cumming & Bildsten
2001). However, there are problems with this scenario: (1) producing enough C during H/He burning (e.g., Schatz et al. 2003; Woosley et al. 2004), (2) heating the neutron star ocean strongly enough to reach ignition temperature (e.g., Cumming et al. 2006; Keek et al. 2008), and (3) accreting rapidly enough for the C to survive to the ignition depth (Cumming & Bildsten 2001; Cumming et al. 2006).
have been explained as being due to C ignition (Strohmayer & Brown 2002; Cumming & Bildsten
2001). However, there are problems with this scenario: (1) producing enough C during H/He burning (e.g., Schatz et al. 2003; Woosley et al. 2004), (2) heating the neutron star ocean strongly enough to reach ignition temperature (e.g., Cumming et al. 2006; Keek et al. 2008), and (3) accreting rapidly enough for the C to survive to the ignition depth (Cumming & Bildsten 2001; Cumming et al. 2006).
If there is accretion of a significant amount of C from the
CO white dwarf companion in 4U 0614+091, the first problem
would be eased by removing the need to make the C during nuclear
burning of H or He. However, if He flashes are responsible for the
intermediate-duration and short bursts, the C would likely burn away
during these flashes. The last two problems are
more difficult to circumvent. First, the ignition temperature for C at
the column depth inferred from the superburst light curve, y ![]() 2
2 ![]() 1011 g cm-2, is above
6
1011 g cm-2, is above
6 ![]() 108 K. This temperature is much higher than the ignition temperatures of He flashes, i.e., about 1
108 K. This temperature is much higher than the ignition temperatures of He flashes, i.e., about 1 ![]() 108 K.
Achieving this temperature is even more difficult when the accretion
rate and therefore crust heating rate are significantly below those
typical around the times of the superbursts seen in other sources.
Second, we calculated models for C ignition following Cumming
& Bildsten (2001) and extended their Fig. 2 to lower accretion rates, but were not able to find values of
108 K.
Achieving this temperature is even more difficult when the accretion
rate and therefore crust heating rate are significantly below those
typical around the times of the superbursts seen in other sources.
Second, we calculated models for C ignition following Cumming
& Bildsten (2001) and extended their Fig. 2 to lower accretion rates, but were not able to find values of ![]() or C fraction for which the C survives to ignition depth at accretion rates of
or C fraction for which the C survives to ignition depth at accretion rates of ![]() 0.01
0.01
![]() .
.
Another possibility is that ignition of a thick He layer is responsible for the observed superburst. Indeed, for the ![]() = 0.3 MeV per nucleon and Y = 0.5 case considered earlier, we find that reducing the local accretion rate to 1000 g cm-2 s-1,
a factor of 3 below the accretion rate that reproduces the
ignition column of the intermediate-duration burst, gives
He ignition at 2
= 0.3 MeV per nucleon and Y = 0.5 case considered earlier, we find that reducing the local accretion rate to 1000 g cm-2 s-1,
a factor of 3 below the accretion rate that reproduces the
ignition column of the intermediate-duration burst, gives
He ignition at 2 ![]() 1011 g cm-2.
The time scale for He burning is longer
than the accumulation time (although close to it), indicating that
He should survive down to the ignition depth, even for such a low
accretion rate (this is not the case for the Y=1,
1011 g cm-2.
The time scale for He burning is longer
than the accumulation time (although close to it), indicating that
He should survive down to the ignition depth, even for such a low
accretion rate (this is not the case for the Y=1, ![]() =
1 MeV per nucleon model; there we find that the He burns stably
away). However, although the ignition depth can be achieved, the
expected recurrence time is 9.8 yr, an order of magnitude longer
than the observed time between the superburst and the previous burst,
=
1 MeV per nucleon model; there we find that the He burns stably
away). However, although the ignition depth can be achieved, the
expected recurrence time is 9.8 yr, an order of magnitude longer
than the observed time between the superburst and the previous burst, ![]() =
367 days.
On the other hand, this can be reconciled if an appreciable portion of
the accreted He survives the preceding shorter bursts (see previous
section).
=
367 days.
On the other hand, this can be reconciled if an appreciable portion of
the accreted He survives the preceding shorter bursts (see previous
section).
Another constraint on the superburst ignition depth comes from
the quenching time scale for normal bursts following the superburst.
Normal bursting behaviour resumed 19 days following the
superburst, the fastest time scale so far observed (see, e.g., Kuulkers
2004). Cumming & Macbeth (2004) predict that the quench time for normal bursting behaviour after a superburst is
![]() = 1.6
= 1.6
![]() days
(where y = y12
days
(where y = y12 ![]() 1012 g cm-2). The constraint on the quench time
1012 g cm-2). The constraint on the quench time
![]() < 19 days implies for
< 19 days implies for
![]() = 6 and
= 6 and
![]() = 0.016 (at the time of the superburst) that y12 < 0.18.
This is in good agreement with the ignition
column inferred from the superburst light curve, and consistent with
the normal burst observed 19 days after the superburst being the
first burst to occur following the superburst. The dependencies are not
very strong. For
= 0.016 (at the time of the superburst) that y12 < 0.18.
This is in good agreement with the ignition
column inferred from the superburst light curve, and consistent with
the normal burst observed 19 days after the superburst being the
first burst to occur following the superburst. The dependencies are not
very strong. For
![]() = 0.0032-0.016, the ignition depth is between y12 < 0.04-0.18. For E17 = 1-6 this becomes y12 <
0.18-0.44. Therefore, the quench time constraint provides another piece
of evidence that the ignition depth for the superburst was lower than
the depths inferred for all or most previously analysed superbursts in
other sources.
= 0.0032-0.016, the ignition depth is between y12 < 0.04-0.18. For E17 = 1-6 this becomes y12 <
0.18-0.44. Therefore, the quench time constraint provides another piece
of evidence that the ignition depth for the superburst was lower than
the depths inferred for all or most previously analysed superbursts in
other sources.
5 Conclusions
We can understand several aspects of the type I X-ray bursts
observed from 4U 0614+091. The column depths and energy release
per gram in the bursts can be estimated by comparing the observed light
curves with models, and by considering the burst energetics. Both
methods are in good agreement. Helium ignition naturally explains the
observed ignition depths for accretion at ![]()
![]() 1%
1%
![]() .
Furthermore, the sensitive dependence of the He ignition depth on
temperature means that small (factor of two) changes in accretion rate
can lead to an order of magnitude variation among the depths, and can
thereby explain the occurrence of both short bursts and
intermediate-duration bursts. The ignition depth for the superburst
inferred from the light curve is the lowest of the current sample of
superbursts and agrees well with the constraint from the observed
quenching time scale.
.
Furthermore, the sensitive dependence of the He ignition depth on
temperature means that small (factor of two) changes in accretion rate
can lead to an order of magnitude variation among the depths, and can
thereby explain the occurrence of both short bursts and
intermediate-duration bursts. The ignition depth for the superburst
inferred from the light curve is the lowest of the current sample of
superbursts and agrees well with the constraint from the observed
quenching time scale.
However, several puzzles remain. First, the amount of He
required to achieve the required ignition conditions without stably
burning away is significantly larger than the ![]() 10%
limit from the optical spectra. Recently, however, formation studies
using evolutionary calculations indicate that the donor in
4U 0614+091 may be a hybrid white dwarf or very evolved helium
star (Nelemans et al. 2010).
This suggests the donor still to be a possible supplier of a
significant amount
of He to the accretion disk, onto the neutron star. Further
investigations have to be done, why the He does not show up then in the
optical observations.
10%
limit from the optical spectra. Recently, however, formation studies
using evolutionary calculations indicate that the donor in
4U 0614+091 may be a hybrid white dwarf or very evolved helium
star (Nelemans et al. 2010).
This suggests the donor still to be a possible supplier of a
significant amount
of He to the accretion disk, onto the neutron star. Further
investigations have to be done, why the He does not show up then in the
optical observations.
Second, understanding the superburst remains problematic.
Unstable C ignition is not known to be
possible at these low accretion rates: the accumulating layer is too
cold, and even if heated the C burns stably. A superburst powered
by a large He pile is possible, but takes several years to
accumulate if the accretion rate is ![]() 1% Eddington.
Such an accumulation time is much greater than the observed time of one
year. Finally, the reason for the low energy per gram
1% Eddington.
Such an accumulation time is much greater than the observed time of one
year. Finally, the reason for the low energy per gram
![]()
![]() 0.6 MeV per nucleon released in the bursts is not clear.
0.6 MeV per nucleon released in the bursts is not clear.
It is important to emphasize, however, that the ignition models and light curve models used in this paper are simplified. The model light curves assume uniform and instantaneous energy deposition in the fuel layer, and do not follow the detailed nucleosynthesis. These models cannot address the early part of the light curve, for example the interesting ripples in the early light curve of the intermediate duration burst (Fig. 10), nor whether the burning is expected to be incomplete (as we infer from the burst energetics). Incomplete burning, either across the neutron star surface or with depth in the fuel layer, may at least partly solve the above puzzles. Our ignition models rely on a simplified one-zone ignition criterion. Numerical models of accumulating and burning of He/CO mixtures at low accretion rates are needed to confirm our conclusions, for example, regarding the amount of helium needed to avoid stable burning.
It is interesting that at least in principle He can power a
superburst-like event. The requirement is that the accumulating fuel
layer remains cold. Recently, Cooper et al. (2009) ruled out He as
a fuel for superbursts, but their argument assumed an ignition temperature of T = 5 ![]() 108 K that is much larger than the He ignition temperature at superburst columns. Even in the superburst sources with
108 K that is much larger than the He ignition temperature at superburst columns. Even in the superburst sources with ![]()
![]() 0.1
0.1
![]() ,
He-powered superbursts could occur if the accumulating layer is cold
enough. One way to keep the layer cold would be to have direct URCA
neutrino emission in the neutron star core, so that most of the energy
release in the crust flows inwards rather than outwards. Triple alpha
ignition becomes mostly sensitive to density rather than temperature
when the column depth reaches y
,
He-powered superbursts could occur if the accumulating layer is cold
enough. One way to keep the layer cold would be to have direct URCA
neutrino emission in the neutron star core, so that most of the energy
release in the crust flows inwards rather than outwards. Triple alpha
ignition becomes mostly sensitive to density rather than temperature
when the column depth reaches y ![]() 3
3 ![]() 1011 g cm-2,
as the ignition becomes pycnonuclear and therefore temperature
independent. This could potentially explain the narrow range of
superburst ignition columns. Further work on this possibility
is needed.
1011 g cm-2,
as the ignition becomes pycnonuclear and therefore temperature
independent. This could potentially explain the narrow range of
superburst ignition columns. Further work on this possibility
is needed.
Partly based on observations with INTEGRAL, an ESA project with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain), Czech Republic and Poland, and with the participation of Russia and the USA. The RXTE/ASM dwell average results are provided by the ASM/RXTE teams at MIT and at the RXTE SOF and GOF at NASA's GSFC. The Swift/BAT transient monitor results are provided by the Swift/BAT team. We thank Jean Swank and Lucien Kuiper for discussions regarding the bursts seen with OSO-8 and in 2005 with INTEGRAL, respectively. EK thanks Andy Pollock for discussion regarding the burst recurrence times and small-number statistics. S.B. was partly supported by the Danish Space Board. A.C. acknowledges support from an NSERC Discovery Grant and the Canadian Institute for Advanced Research (CIFAR). This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
Appendix A: Localizations of bursts
The three bursts observed by EURECA/WATCH had positional 3![]() error circles of less than 1
error circles of less than 1
![]() radius (taking into account systematic errors and errors due to uncertainties in the
spacecraft pointing). The optical (Davidsen et al. 1974; Murdin et al. 1974), infrared (Migliari et al. 2006) and radio (Migliari et al. 2010)
counterparts to 4U 0614+091 were always within these error
circles. The WATCH imaging results for the event which occurred on
February 17 is shown in Fig. A.1 (left)
radius (taking into account systematic errors and errors due to uncertainties in the
spacecraft pointing). The optical (Davidsen et al. 1974; Murdin et al. 1974), infrared (Migliari et al. 2006) and radio (Migliari et al. 2010)
counterparts to 4U 0614+091 were always within these error
circles. The WATCH imaging results for the event which occurred on
February 17 is shown in Fig. A.1 (left)![]() .
.
At the time of the sole burst seen by the WFC, the satellite attitude
solution was not optimum. However, the position for the burst is the
same to within 0.1 pixel of the position determined for the
persistent emission at times when the attitude solution was optimum,
with an uncertainty of 2
![]() (99% confidence). We conclude that the origin of the burst is coincident within 2
(99% confidence). We conclude that the origin of the burst is coincident within 2
![]() of the position of 4U 0614+091.
of the position of 4U 0614+091.
The first two bursts (in 1996 and 1998) of the six normal ASM bursts were observed by multiple SSCs, either because the burst position was in the region where the fields of view of SSC 0 and SSC 1 overlap, or because the burst was active across two sequential dwells (or both, as in the first case, yielding four independent observations). The four subsequent bursts were only detected in a single SSC for a single dwell, yielding a total of eleven observations of the six bursts (see Table A.1).
| Figure A.1: Left: the cross-correlation map (6-15 keV) containing the burst observed from the direction of 4U 0614+091 on February 17, 1993 by EURECA/WATCH. The burst was contained in a modulation pattern integrated for 56.7 s. The contours are shown in Crab units and the averaged correlation at the position of 4U 0614+091 was 3.6 Crab. Note that the integration time is too short to give a detection of the Crab. Right: detection of the persistent emission from 4U 0614+091 by EURECA/WATCH. The skymap is based on data from the period of February to April 1993 in the energy band 6-12 keV. The contours show the cross correlation in units of mCrab (only positive correlation is shown). The ring-like structure around 4U 0614+091 is an artefact caused by the WATCH RMC detection principle. |
|
| Open with DEXTER | |
Table A.1: Observation log of ASM bursts from 4U 0614+091 (left) and 2S 0918-549 (right).
For each ASM dwell, the intensities of known sources in the field of view are derived via a fit of model slit-mask shadow patterns to counts binned by position along each anode in each detector. The residuals from a successful fit are then cross-correlated with each of the expected shadow patterns corresponding to a set of possible source directions which make up a grid covering the field of view. A peak in the resulting cross-correlation map indicates the possible presence and approximate location of a new, uncatalogued X-ray source (Levine et al. 1996; Smith et al. 1999).
To test the hypothesis that the six ASM bursts were from 4U 0614+091, we removed this source from the catalog used for the fitting procedure described. We fit the eleven observations with this truncated catalog, and we searched the residuals for evidence of a source of emission unaccounted for by the catalog. For bursts that occurred after the ASM began recording in event mode, we omitted from the fit those time bins that did not show evidence of burst activity, to increase the signal to noise ratio. All eleven dwells showed evidence of a ``new'' source in the residuals. If 4U 0614+091 were the source of the burst in each of these dwells, the localization of this new source should be consistent with the location of 4U 0614+091.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13210fA2.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg165.png)
|
Figure A.2: Equatorial (J2000.0) map of ten independent ASM localizations of the source of six bursts. The asterisk marks the location of the optical counterpart to 4U 0614+091 (Davidson et al. 1974; Murdin et al. 1974). |
| Open with DEXTER | |
Ten of the eleven localizations are plotted in Fig. A.2. The boxes are determined by the 95% confidence interval in each of the two dimensions recorded by the SSC, projected onto the sky. Since the two dimensions are independent, the total confidence level of the error box is about 90%. These uncertainties are statistical only. The location of the optical counterpart of 4U 0614+091 is indicated by an asterisk. This location cannot be excluded by any of the error boxes, including an eleventh error box that lies outside the limits of this plot.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13210fA3a.ps}\par\includegraphics[width=8.8cm,clip]{13210fA3b.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg166.png)
|
Figure A.3:
IBIS/ISGRI (15-30 keV) significance images during the bursts detected on 2003 August 16 ( top) and 2005 March 31 ( bottom). Shown is the equatorial J2000.0 grid with 5
|
| Open with DEXTER | |
For ten of the thirteen FREGATE bursts a precise localization was possible using the WXM and/or SXC, and they are consistent with coming from 4U 0614+091 (see Sect. 2.1.5). For the other three bursts we can only suppose they are coming from 4U 0614+091, since the source was the only persistent burster in the FREGATE field of view.
Table A.2: Positions of the bursts seen by ISGRI and BAT.
The reconstructed 15-30 keV images of the field of view around
4U 0614+091 during the bursts seen by ISGRI are shown in Fig. A.3.
The only two detected sources in the 2003 (24 s) and 2005
(15 s) time frames are indeed 4U 0614+091, as well as
the persistently bright Crab source. The data from the two BAT bursts
were subjected to the post ``![]() -ray
burst'' processing script, which led to refined positions for these
bursts. The derived ISGRI and BAT bursts coordinates are given in
Table A.2. They are also consistent with the optical, IR and radio counterparts to 4U 0614+091.
-ray
burst'' processing script, which led to refined positions for these
bursts. The derived ISGRI and BAT bursts coordinates are given in
Table A.2. They are also consistent with the optical, IR and radio counterparts to 4U 0614+091.
We conclude that the 27 bursts seen by EURECA/WATCH, WFC, ASM, FREGATE, ISGRI and BAT indeed originated from 4U 0614+091.
References
- Atteia, J.-L., Boer, M., Cotin, F., et al. 2003, in Gamma-Ray Burst and Afterglow Astronomy 2001, ed. G. Ricker, & R. Vanderspek (New York: AIP), AIP Conf. Proc., 662, 17 [Google Scholar]
- Barraud, C. 2002, presentation given at the AMS Workshop on Sources and GRBs, 6/12/2002, Montpellier, France [Google Scholar]
- Barret, D., & Grindlay, J. E. 1995, ApJ, 440, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, SSRv, 120, 143 [Google Scholar]
- Belian, R. D., Conner, J. P., & Evans, W. D. 1976, ApJ, 206, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Salpeter, E., & Wasserman, I. 1992, ApJ, 384, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Boella, G., Butler, R. C., Perola, G. C., et al. 1997, A&A, 122, 299 [Google Scholar]
- Bradt, H. V., Rothschild, R. E., & Swank, J. H. 1993, A&AS, 97, 355 [NASA ADS] [Google Scholar]
- Brandt, S. 1994, Ph.D. Thesis, DSRI, Denmark [Google Scholar]
- Brandt, S., & Lund, N. 1995, Adv. Space Res., 16(8), 37 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brandt, S., Castro-Tirado, A. J., Lund, N., et al. 1992, A&A, 262, L15 [NASA ADS] [Google Scholar]
- Brandt, S., Lund, N., & Rao, A. R. 1990, Adv. Space Res., 10(2), 239 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, S., Lund, N., & Castro-Tirado, A. J. 1993a, IAU Circ., 5710 [Google Scholar]
- Brandt, S., Lund, N., & Castro-Tirado, A. J. 1993b, IAU Circ., 5717 [Google Scholar]
- Brown, E. F. 2000, ApJ, 531, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, E. F., & Bildsten, L. 1998, ApJ, 496, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Buccheri, R., Bennett, K., Bignami, G. F., et al. 1983, A&A, 128, 245 [NASA ADS] [Google Scholar]
- Chelovekov, I. V., Grebenev, S. A., & Sunyaev, R. A. 2007, Proceedings of the 6th INTEGRAL Workshop, The Obscured Universe, ESA SP-622, 445 [Google Scholar]
- Cocchi, M., Bazzano, A., Natalucci, L., et al. 2000, A&A, 357, 527 [NASA ADS] [Google Scholar]
- Cooper, R. L., Steiner, A. W., & Brown, E. F. 2009, ApJ, 702, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Cornelisse, R., Heise, J., Kuulkers, E., Verbunt, F., & in 't Zand, J. J. M. 2000, A&A, 357, L21 [NASA ADS] [Google Scholar]
- Cornelisse, R., Kuulkers, E., in 't Zand, J. J. M., Verbunt, F., & Heise, J. 2002a, A&A, 382, 174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cornelisse, R., Verbunt, F., in 't Zand, J. J. M., et al. 2002b, A&A, 392, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cornelisse, R., in 't Zand, J. J. M., Verbunt, F., et al. 2003, A&A, 405, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courvoisier, T. J.-L., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cumming, A. 2004, Nuc. Phys. B Proc. Suppl., 132, 435 [Google Scholar]
- Cumming, A., & Bildsten, L. 2001, ApJ, 559, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., & Macbeth, J. 2004, ApJ, 603, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Macbeth, J., in 't Zand, J. J. M., & Page, D. 2006, ApJ, 646, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsen, A., Malina, R., Smith, H., et al. 1974, ApJ, 193, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ebisawa, K., Bourban, G., Bodaghee, A., Mowlavi, N., & Courvoisier, T. J.-L. 2003, A&A, 411, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falanga, M., Chenevez, J., Cumming, A., et al. 2008, A&A, 484, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falanga, M., Cumming, A., Bozzo, E., & Chenevez, J. 2009, A&A, 496, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiocchi, M., Bazzano, A., Ubertini, P., et al. 2008, A&A, 492, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ford, E., Kaaret, P., Tavani, M., et al. 1996, ApJ, 469, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. C., Kaaret, P., Chen, K., et al. 1997, ApJ, 486, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. C., van der Klis, M., Méndez, M., et al. 2000, ApJ, 537, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., et al. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Giacconi, R., Murray, S., Gursky, H., et al. 1972, ApJ, 178, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Goldwurm, A., David, P., Foschini, L., et al. 2003, A&A, 411, L223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grindlay, J., Gursky, H., Schnopper, H., et al. 1975, ApJ, 205, L127 [Google Scholar]
- Hansen, C. J., & van Horn, H. M. 1975, ApJ, 195, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Harmon, B. A., Wilson, C. A., Fishman, G. J., et al. 2004, ApJS, 154, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] [Google Scholar]
- Hoffman, J. A., Marshall, H. L., & Lewin, W. H. G. 1978, Nature, 271, 630 [NASA ADS] [CrossRef] [Google Scholar]
- in Zand, J. J. M. 1992, Ph.D. Thesis, Utrecht University [Google Scholar]
- in 't Zand, J. J. M., Cumming, A., van der Sluys, M. V., Verbunt, F., & Pols, O. R. 2005, A&A, 441, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in 't Zand, J. J. M., Bassa, C. G., Jonker, P. G., et al. 2008, A&A, 485, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in 't Zand, J. J. M., Jonker, P. G., & Markwardt, C. B. 2007, A&A, 465, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in 't Zand, J. J. M., Keek, L., Cumming, A., et al. 2009, A&A, 497, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jager, R., Mels, W. A., Brinkman, A. C., et al. 1997, A&A, 125, 557 [Google Scholar]
- Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., & Nelemans, G. 2004, MNRAS, 354, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Juett, A. M., & Chakrabarty, D. 2003, ApJ, 599, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Juett, A. M., Psaltis, D., & Chakrabarty, D. 2001, ApJ, 560, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Keek, L., & in 't Zand, J. J. M. 2009, in proceedings of the 7th INTEGRAL Workshop, An INTEGRAL View of Compact Objects, PoS(Integral08)032 [Google Scholar]
- Keek, L., in 't Zand, J. J. M., Kuulkers, E., et al. 2008, A&A, 479, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krimm, H., Barbier, L., Barthelmy, S. D., et al. 2006, ATel, #904 [Google Scholar]
- Kuulkers, E. 2002, A&A, 383, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuulkers, E. 2004, Nuc. Phys. B Proc. Suppl., 132, 466 [Google Scholar]
- Kuulkers, E. 2005, ATel, #483 [Google Scholar]
- Kuulkers, E., den Hartog, P. R., in 't Zand, J. J. M., et al. 2003, A&A, 399, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuulkers, E., in 't Zand, J. J. M., van Kerkwijk, M. H., et al. 2002a, A&A, 382, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuulkers, E., Homan, J., van der Klis, M., Lewin, W. H. G., & Méndez, M. 2002b, A&A, 382, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuulkers, E., Shaw, S. E., Paizis, A., et al. 2007, A&A, 466, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuulkers, E., van der Klis, M., Oosterbroek, T., et al. 1994, A&A, 289, 795 [NASA ADS] [Google Scholar]
- Lamb, D. Q., & Lamb, F. K. 1978, ApJ, 220, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levine, A. M., Bradt, H., Cui, W., et al. 1996, ApJ, 469, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G. 1976, IAU Circ., 2914 [Google Scholar]
- Lewin, W. H. G., Vacca, W. D., & Basinska, E. M. 1984, ApJ, 277, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., van Paradijs, J., & Taam, R. E. 1993, SSRv, 62, 223 [NASA ADS] [Google Scholar]
- Linares, M., Watts, A. L., Wijnands, R., et al. 2009, MNRAS, 392, L11 [NASA ADS] [Google Scholar]
- Lund, N. 1985, in X-Ray Instrumentation in Astronomy, ed. J. L. Culhane, Porc. SPIE, 597, 95 [Google Scholar]
- Lund, N., Brandt, S., Budtz-Jørgensen, C., et al. 2003, 411, L231 [Google Scholar]
- Maraschi, L., & Cavaliere, A. 1977, in Highlights in Astronomy, ed. E. A. Müller, 4, 127 [Google Scholar]
- Markert, T. H., Laird, F. N., Clark, G. W., et al. 1979, ApJS, 39, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, K. O., Charles, P. A., White, N. E., et al. 1976, MNRAS, 177, 513 [NASA ADS] [Google Scholar]
- Méndez, M., Cottam, J., & Paerels, F. 2002 [arXiv:astro-ph/0207277] [Google Scholar]
- Mereghetti, S., Götz, D., Borkowski, J., Walter, R., & Pedersen, H. 2003, A&A, 411, L291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Migliari, S., & Fender, R. 2006, MNRAS, 366, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Migliari, S., Tomsick, J. A., Maccarone, T. J., et al. 2006, ApJ, 643, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Migliari, S., Tomsick, J. A., Miller-Jones, J. C. A., et al. 2010, ApJ, 710, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Molkov, S. V., Grebenev, S. A., & Lutovinov, A. A. 2000, 357, L41 [Google Scholar]
- Murdin, P., Penston, M. J., Penston, M. V., et al. 1974, MNRAS, 169, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Jonker, P. G., Marsh, T. R., & van der Klis, M. 2003, MNRAS, 348, L7 [Google Scholar]
- Nelemans, G., Jonker, P. G., & Steeghs, D. 2006, MNRAS, 370, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Yungelson, L. R., van der Sluys, M. V., & Tout, C. A. 2010, MNRAS, 401, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Parsignault, D. R., & Grindlay, J. E. 1978, ApJ, 225, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Piraino, S., Santangelo, A., Ford, E. C., & Kaaret, P. 1999, A&A, 349, L77 [NASA ADS] [Google Scholar]
- Ricker, G. R., Atteia, J.-L., Crew, G. B., et al. 2003, in Gamma-Ray Burst and Afterglow Astronomy 2001: A Workshop Celebrating the First Year of the HETE Mission, ed. G. R. Ricker, & R. K. Vanderspek, AIP Conf. Ser., 662, 3 [Google Scholar]
- Rothschild, R. E., Blanco, P. R., Gruber, D. E., et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Schatz, H., Bildsten, L., & Cumming, A. 2003, ApJ, 583, L87 [Google Scholar]
- Shahbaz, T., Watson, C. A., Zurita, C., Villaver, E., & Hernandez-Peralta, H. 2008, PASP, 120, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Shirasaki, Y., Kawai, N., Yoshida, A., et al. 2003, PASJ, 55, 1033 [NASA ADS] [Google Scholar]
- Smith, D. A., Levine, A. M., Bradt, H. V., et al. 1999, ApJ, 526, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T., & Bildsten, L. 2006, in Compact stellar X-ray sources, ed. W. H. G. Lewin, & M. van der Klis, Cambridge Astrophys. Ser., 39, 113 [Google Scholar]
- Strohmayer, T. E., & Brown, E. F. 2002, ApJ, 566, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., & Markwardt, C. B. 2002, ApJ, 577, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., Markwardt, C. B., & Kuulkers, E. 2008, ApJ, 672, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, M., Sakamoto, T., Takahashi, D., et al. 2004, in Third Rome Workshop on Gamma-Ray Bursts in the Afterglow Era, ed. M. Feroci, F. Frontera, N. Masetti, & L. Piro, ASP Conf. Ser., 312, 138 [Google Scholar]
- Swank, J. H., Becker, R. H., Boldt, E. A., Holt, S. S., & Serlemitsos, P. J. 1978, MNRAS, 182, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Tawara, Y., Kii, T., Hayakawa, S., et al. 1984, ApJ, 276, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Klis, M. 1995, in The Lives of the Neutron Stars, ed. M. A. Alpar, Ü. Kiziloglu, & J. van Paradijs (Kluwer Academic Publishers), NATO ASI Ser. C, 450, 301 [Google Scholar]
- van Paradijs, J., & Lewin, W. H. G. 1986, A&A, 157, L10 [NASA ADS] [Google Scholar]
- van Straaten, S., Ford, E. C., van der Klis, M., Méndez, M., & Kaaret, P. 2000, ApJ, 540, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- van Straaten, S., van der Klis, M., & Méndez, M. 2003, ApJ, 596, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Villasenor, J. N., Dill, R., Doty, J. P., et al. 2003, in Gamma-Ray Burst and Afterglow Astronomy 2001: A Workshop Celebrating the First Year of the HETE Mission, ed. G. R. Ricker, & R. K. Vanderspek, AIP Conf. Ser., 662, 33 [Google Scholar]
- Warwick, R. S., Marshall, N., Fraser, G. W., et al. 1981, MNRAS, 197, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, K., Nagel, T., Rauch, T., Hammer, N. J., & Dreizler, S. 2006, A&A, 450, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westergaard, N. J., Kretschmar, P., Oxborrow, C. A., et al. 2003, A&A, 411, L257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijnands, R. 2001, ApJ, 554, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McGray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Taam, R. E. 1976, Nature, 263, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., Cumming, A., et al. 2004, ApJS, 151, 75 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... determinations
![[*]](/icons/foot_motif.png)
- Note that spatially the closest known X-ray burster to 4U 0614+091 is MXB 0513-40, with a distance of 51
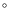 .
.
- ... averages
![[*]](/icons/foot_motif.png)
- http://heasarc.gsfc.nasa.gov/docs/xte/asm_products.html and http://xte.mit.edu/ASM_lc.html
- ... available
![[*]](/icons/foot_motif.png)
- http://heasarc.nasa.gov/docs/xte/data_analysis.html
- ...
procedures
![[*]](/icons/foot_motif.png)
- http://heasarc.gsfc.nasa.gov/docs/xte/recipes/hexte.html
- ...2003)
![[*]](/icons/foot_motif.png)
- http://ibas.iasf-milano.inaf.it/
- ... Archive
![[*]](/icons/foot_motif.png)
- http://integral.esac.esa.int/isda/
- ... resolution
![[*]](/icons/foot_motif.png)
- http://www.isdc.unige.ch/integral/download/osa_doc.
- ... Center
![[*]](/icons/foot_motif.png)
- http://swift.gsfc.nasa.gov/docs/swift/analysis/
- ... day
![[*]](/icons/foot_motif.png)
- http://swift.gsfc.nasa.gov/docs/swift/results/transients/index.html
- ... for 14 d.o.f.
![[*]](/icons/foot_motif.png)
- The goodness of fit is expressed by the reduced chi-squared, or
 .
It is the sum of the weighted square deviations between the data
and the model, divided by the number of degrees of
freedom (d.o.f.).
.
It is the sum of the weighted square deviations between the data
and the model, divided by the number of degrees of
freedom (d.o.f.).
- ... burst
![[*]](/icons/foot_motif.png)
- FREGATE triggered on the main burst.
- ... (left)
![[*]](/icons/foot_motif.png)
- Note that this analysis was done more than 10 years ago. Therefore, the best-fit estimates on the position of the various bursts are not available; also the regeneration of images is not possible anymore.
All Tables
Table 1: Overview of instruments that have detected bursts from 4U 0614+091 between 1992 and 2007.
Table 2: Burst and persistent emission properties for all bursts from 4U 0614+091.
Table 3: Results of spectral fits of PCA+HEXTE data taken outside of but within one day of bursts, i.e., representing persistent emission only.
Table 4: Average burst recurrence time estimates for various instruments during three periods.
Table A.1: Observation log of ASM bursts from 4U 0614+091 (left) and 2S 0918-549 (right).
Table A.2: Positions of the bursts seen by ISGRI and BAT.
All Figures
![\begin{figure}
\par\includegraphics[angle=-90,width=16.2cm,clip]{13210f1a.ps}\par\includegraphics[angle=-90,width=15.8cm,clip]{13210f1b.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg110.png)
|
Figure 1: Time profiles of raw full-bandpass photon rates ( top panels), bolometric black-body flux (2nd panels), black-body temperature (3rd panels), black-body radius for 3 kpc distance (4th panels) and goodness of fit ( bottom panels). The unit of intensity ( top panels) is cts s-1 for the 6 ASM bursts, cts s-1 bin-1 for the ISGRI burst, kcts s-1 bin-1 for the 2 BAT bursts, kcts s-1 for the 10 FREGATE bursts and cts s-1 for the WFC burst. The bursts are denoted by instrument (FR = FREGATE) and MJD (see Table 2). For the ASM bursts which occurred on MJD 50 200 and MJD 51 164 we show the light curves from SSC1 and SSC0 data, respectively (see Table A.1). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{13210f2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg117.png)
|
Figure 2:
From left to right: the 3 bursts observed with EURECA/WATCH in the 6-15 keV ( top) and 15-150 keV ( bottom) bands, and the burst observed with ISGRI in 2003 in the 15-30 keV ( top) and 30-200 keV ( bottom) bands.
Zero time corresponds to the start of each burst (see Table 2). For EURECA/WATCH detector count rates (in cts bin-1)
are shown, i.e., no correction has been made for background and
vignetting. The dashed line indicates the background level and the
dotted line marks the 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=17.5cm,clip]{13210f3.ps}
\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg119.png)
|
Figure 3: Light curves ( top row) and time-resolved spectral fit results (lower four rows) for selected bursts shown with higher time resolution than in Fig. 1. See the caption to Fig. 1 for brief explanations of the spectral parameters. The date (MJD) of each burst and the instrumental origin (FR = FREGATE) of the data are indicated. Left: FREGATE light curve and time-resolved spectroscopy for the burst on MJD 52 997 with a time resolution of 0.16 s. The unit of intensity is kcts s-1. Middle left: ( top) PCA full band-pass light curve of the MJD 51 944 burst with a time resolution of 0.001 s (from t = 0-0.05 s), 0.01 s (from t = 0.05-2.25 s), 0.125 s (from t = 2.25-30 s), and 16 s (from t = 4000-8000 s). The unit of intensity is 104 c s-1 per 4 PCUs. The PCA (PCU3) rates after t = 4000 s have been multiplied by four. The ASM data are indicated with open squares; they have been scaled to the PCA rates using the Crab as a reference. Time t = 0 s corresponds to UT 2001 Feb. 4 21:52:42.8. (rest) Time-resolved spectral fit results using the data from the PCA (filled circles), ASM (open squares) and FREGATE (open triangles). Middle right: PCA full band-pass light curve ( top) and time resolved spectroscopy of the long-lasting faint tail of a possible burst observed on MJD 51 789. For this burst we do not have an exact start time, so t = 0 s corresponds to the start of the data sequence (UT 2000 Sep. 2 at 01:19:47). Intensity is in units of c s-1 for PCUs 2 and 3 combined. Right: ASM full-bandpass light curve of the superburst on MJD 53 441 from 4U 0614+091 ( top) and time resolved spectroscopy. Time is given in hours since UT 2005 March 12, 0h, and the intensity is given in cts s-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{13210f4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg122.png)
|
Figure 4: PCA 2-60 keV light curve centred around the burst onset on MJD 51 944 at a 10 ms time resolution. The intensity is as measured by 4 PCUs combined. Time t = 0 s corresponds to UT 2001 Feb. 4 21:52:42.8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{13210f5.ps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg124.png)
|
Figure 5: HEXTE hard X-ray (15-60 keV, cluster A) light curve of the burst on MJD 51 944 of 4U 0614+091 (filled circles), as well as the superburst light curves of 4U 1820-303 (filled triangles) and 4U 1636-536 (open squares). The time resolution is 16 s for 4U 0614+091 and 32 s for 4U 1820-303 and 4U 1636-536. Time = 0 s corresponds to UT 2001-02-04 21:52:43, 1999-09-09 01:46:54 and 2001-02-22 16:52:11, for 4U 0614+091, 4U 1820-303 and 4U 1636-536, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{13210f6.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg125.png)
|
Figure 6: ASM individual dwell intensity measurements (1.5-12 keV) and average hardness ratios around the time of the superburst from 4U 0614+091. Hardness is defined as the ratio of the intensity in the 3-12 keV band to that in the 1.5-3 keV band. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=12cm,clip]{13210f7a.ps}\includegraphics[angle=-90,width=6cm,clip]{13210f7b.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg130.png)
|
Figure 7: Left: daily averaged ASM light curve (1.5-12 keV). The times of the normal bursts (see Table 2) are indicated with arrows at the top. The superburst occurrence is marked with an ``S''. Right: the yearly averaged ASM light curve (1.5-12 keV; filled circles) and the measure of the variability (rms) in the yearly time bins (filled triangles). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{13210f8.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg132.png)
|
Figure 8: Zoom in on the long-term hard X-ray (15-50 keV) light curve ( top) and soft X-ray (1.5-12 keV) light curve ( bottom), of 4U 0614+091. Shown are the 1-day and 10-day averages for ISGRI (filled circles) and Swift/BAT (grey filled triangles), respectively ( top), and 10-day averages for the ASM. Time in years is given above the plot. The occurrence times of the normal bursts are indicated by arrows at the top. The superburst occurrence is marked with an ``S''. |
| Open with DEXTER | |
| In the text | |
| |
Figure 9:
PCA colour-colour diagram ( Left) and hardness-intensity diagram ( Right)
of all public data of 4U 0614+091. Plotted are all persistent data
points averaged per observation, and normalised using the Crab (see
Sect. 2.1.3). Data taken close to a burst are marked with a black filled triangle ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13210f10.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg135.png)
|
Figure 10: Models of the burst
light curves for the superburst (SB), the intermediate-duration
burst on MJD 51 944 (H1488), and the short burst on
MJD 53 718 (H3982). For the superburst, the model parameters
are E17 = 5, y11 = 2 (solid curve) and E17 = 2, y11 = 3 (dotted curve). For the intermediate-duration burst, the model parameters are E17 = 7, y9 = 8 (solid curve) and E17 = 5, y9 = 10 (dotted curve). For the short burst, the model parameters are E17 = 6, y9 = 2 (solid curve) and E17 = 4, y9 = 3 (dotted curve). Here E = E17 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13210f11.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg154.png)
|
Figure 11:
The observed burst energies (assuming d = 3 kpc) versus the time since the last observed burst |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13210f12.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg156.png)
|
Figure 12:
The mass fraction of He needed to achieve unstable He ignition as
a function of accretion rate, for accretion of He and an equal mixture
of C and O. The different curves are for
different values of |
| Open with DEXTER | |
| In the text | |
| |
Figure A.1: Left: the cross-correlation map (6-15 keV) containing the burst observed from the direction of 4U 0614+091 on February 17, 1993 by EURECA/WATCH. The burst was contained in a modulation pattern integrated for 56.7 s. The contours are shown in Crab units and the averaged correlation at the position of 4U 0614+091 was 3.6 Crab. Note that the integration time is too short to give a detection of the Crab. Right: detection of the persistent emission from 4U 0614+091 by EURECA/WATCH. The skymap is based on data from the period of February to April 1993 in the energy band 6-12 keV. The contours show the cross correlation in units of mCrab (only positive correlation is shown). The ring-like structure around 4U 0614+091 is an artefact caused by the WATCH RMC detection principle. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13210fA2.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg165.png)
|
Figure A.2: Equatorial (J2000.0) map of ten independent ASM localizations of the source of six bursts. The asterisk marks the location of the optical counterpart to 4U 0614+091 (Davidson et al. 1974; Murdin et al. 1974). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13210fA3a.ps}\par\includegraphics[width=8.8cm,clip]{13210fA3b.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa13210-09/Timg166.png)
|
Figure A.3:
IBIS/ISGRI (15-30 keV) significance images during the bursts detected on 2003 August 16 ( top) and 2005 March 31 ( bottom). Shown is the equatorial J2000.0 grid with 5
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


