| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 5 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200912828 | |
| Published online | 19 May 2010 | |
A mass estimate of an intermediate-mass black hole in 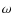 Centauri
Centauri
P. Miocchi
INAF, Osservatorio Astronomico di Bologna, and Dipartimento di Astronomia, Universitá di Bologna, via Ranzani 1, Bologna 40127, Italy
Received 4 July 2009 / Accepted 8 February 2010
Abstract
Context. The problem of the existence of intermediate-mass
black holes (IMBHs) at the centre of globular clusters is a hot and
controversial topic in current astrophysical research with important
implications in stellar and galaxy formation.
Aims. The purpose of this paper is to provide further evidence on the presence of an IMBH in ![]() Centauri and to give an independent estimate of its mass.
Centauri and to give an independent estimate of its mass.
Methods. We employed a self-consistent spherical model with
anisotropic velocity distribution. It consists in a generalisation of
the King model by including the Bahcall-Wolf distribution function in
the IMBH vicinity.
Results. By the parametric fitting of the model to recent
HST/ACS data for the surface brightness profile, we found an IMBH to
cluster total mass ratio of
![]() .
It is also found that the model yields a fit of the line-of-sight
velocity dispersion profile that is better without mass segregation
than in the segregated case. This confirms the current thought of a
non-relaxed status for this peculiar cluster. The best fit model to the
kinematic data leads, moreover, to a cluster total mass estimate of
.
It is also found that the model yields a fit of the line-of-sight
velocity dispersion profile that is better without mass segregation
than in the segregated case. This confirms the current thought of a
non-relaxed status for this peculiar cluster. The best fit model to the
kinematic data leads, moreover, to a cluster total mass estimate of
![]() ,
thus giving an IMBH mass in the range
,
thus giving an IMBH mass in the range
![]() (at 1
(at 1![]() confidence level). A slight degree of radial velocity anisotropy in the outer region (
confidence level). A slight degree of radial velocity anisotropy in the outer region (
![]() )
is required to match the outer surface brightness profile.
)
is required to match the outer surface brightness profile.
Key words: black hole physics - methods: analytical -
methods: numerical - Galaxy: kinematics and dynamics -
globular clusters: individual: ![]() Centauri (NGC 5139) -
stars: kinematics and dynamics
Centauri (NGC 5139) -
stars: kinematics and dynamics
1 Introduction
Intermediate-mass black holes (IMBH) still belong to the class of ``exotic'' objects in the current astrophysical belief. With a massTo date, only the GC G1 (in M 31) exhibits a detected source, seen in both radio (with an 8.4 GHz power of
![]() W Hz-1, see Ulvestad et al. 2007) and X-ray (with a
W Hz-1, see Ulvestad et al. 2007) and X-ray (with a
![]() erg s-1 luminosity at 0.2-10 keV, see Pooley & Rappaport 2006) bands. The observed fluxes, as well as their ratio, are compatible with the claimed presence of a
erg s-1 luminosity at 0.2-10 keV, see Pooley & Rappaport 2006) bands. The observed fluxes, as well as their ratio, are compatible with the claimed presence of a
![]() IMBH (Gebhardt et al. 2005) -
although other kinds of sources cannot be completely ruled out (e.g. Kong et al. 2009).
Another extra-galactic hyperluminous
X-ray source (
IMBH (Gebhardt et al. 2005) -
although other kinds of sources cannot be completely ruled out (e.g. Kong et al. 2009).
Another extra-galactic hyperluminous
X-ray source (
![]() erg s-1 at
0.3 - 10 keV) is
located in the S0-a galaxy ESO243-49
and its features suggest an IMBH emission.
Recently, an unresolved optical counterpart with
brightness comparable to that of a massive GC has been
identified around this source (Soria et al. 2010),
though higher resolution observations are needed.
erg s-1 at
0.3 - 10 keV) is
located in the S0-a galaxy ESO243-49
and its features suggest an IMBH emission.
Recently, an unresolved optical counterpart with
brightness comparable to that of a massive GC has been
identified around this source (Soria et al. 2010),
though higher resolution observations are needed.
In our Galaxy, the central region of NGC 6388 hosts an unresolved set of X-ray sources,
with a total luminosity of
![]() erg s-1 (Nucita et al. 2008), implying an accretion
efficiency compatible with the inferred presence of a
erg s-1 (Nucita et al. 2008), implying an accretion
efficiency compatible with the inferred presence of a
![]() IMBH (Lanzoni et al. 2007).
On the other hand,
no detectable X-ray sources have been found at the centre of mass of NGC 2808,
leading Servillat et al. (2008) to state that
IMBH (Lanzoni et al. 2007).
On the other hand,
no detectable X-ray sources have been found at the centre of mass of NGC 2808,
leading Servillat et al. (2008) to state that
![]() in this cluster.
in this cluster.
In fact, in most cases only upper limits for IMBHs masses can be deduced from
radio observations (see, e.g. Maccarone & Servillat 2008, for NGC 2808 and for a general discussion). These surprisingly low upper limits lead Maccarone & Servillat (2008) to
cast doubts on the fact that the scaling relation
![]() -
- ![]() ,
where
,
where ![]() is the central velocity dispersion
of the host stellar system (with mass M and luminosity L), is the same
is the central velocity dispersion
of the host stellar system (with mass M and luminosity L), is the same
![]() law that has been clearly noted for
super-massive black holes in galaxies (Ferrarese & Merritt 2000; Gebhardt et al. 2000).
It should be emphasised, however,
that the upper limits on IMBH masses drawn from X-ray or radio
observations strongly depend on the assumption that the gas distribution
around the compact object is uniform (isotropic accretion).
It is clear that, if this distribution had any amount of clumpiness, those limits could be largely underestimated.
law that has been clearly noted for
super-massive black holes in galaxies (Ferrarese & Merritt 2000; Gebhardt et al. 2000).
It should be emphasised, however,
that the upper limits on IMBH masses drawn from X-ray or radio
observations strongly depend on the assumption that the gas distribution
around the compact object is uniform (isotropic accretion).
It is clear that, if this distribution had any amount of clumpiness, those limits could be largely underestimated.
Nevertheless, the question of the validity of the extrapolation of the
![]() -
- ![]() scaling relation to IMBHs is still open and
deserves to be discussed briefly here.
In general, this relation can be understood as a consequence of the fundamental
scaling law
scaling relation to IMBHs is still open and
deserves to be discussed briefly here.
In general, this relation can be understood as a consequence of the fundamental
scaling law
![]() (Magorrian et al. 1998).
In galaxies, this scaling law and the two relations
(Magorrian et al. 1998).
In galaxies, this scaling law and the two relations
![]() (Faber et al. 1987) and
(Faber et al. 1987) and
![]() (Faber & Jackson 1976), lead just to
(Faber & Jackson 1976), lead just to
![]() .
In globular clusters, on the other hand, the observed trends are
.
In globular clusters, on the other hand, the observed trends are
![]() and
and
![]() (Meylan & Heggie 1997), which in fact yield
(Meylan & Heggie 1997), which in fact yield
![]() .
This implies a generally lower mass ratio between
the IMBH and the host cluster, as noted by Maccarone & Servillat (2008).
A shallow
.
This implies a generally lower mass ratio between
the IMBH and the host cluster, as noted by Maccarone & Servillat (2008).
A shallow ![]() -
- ![]() relation, namely
relation, namely
![]() ,
was already reported in Miocchi (2007, hereafter M07)
based on
parametric IMBH mass estimates (see below). On the other hand, we must
mention a recent study of this specific topic, in which the low-mass
extrapolation of the galactic
,
was already reported in Miocchi (2007, hereafter M07)
based on
parametric IMBH mass estimates (see below). On the other hand, we must
mention a recent study of this specific topic, in which the low-mass
extrapolation of the galactic
![]() relation seems to fit a sample of 5 reported IMBHs in GCs (Safonova & Shastri 2010).
relation seems to fit a sample of 5 reported IMBHs in GCs (Safonova & Shastri 2010).
In view of all this, the study of possible IMBH fingerprints on either star-count or surface brightness (SB) profiles is a detection route that still deserves to be pursued, especially when kinematic observations close to the IMBH gravitational influence region are available. In this respect, a spherical and self-consistent model of GCs with a central IMBH at rest was presented in M07, both with equal mass stars, i.e. the single-mass (SM) case, and with a multimass (MM) stellar spectrum including mass segregation. This model is an extension of King-Michie models (Michie & Bodenheimer 1963; King 1966; Michie 1963) that is obtained by including the Bahcall-Wolf stellar distribution function within the IMBH gravitational influence region. The latter was shown to solve the Fokker-Planck equation in the vicinity of a central IMBH that formed long before a cluster relaxation time (Bahcall & Wolf 1976; Binney & Tremaine 1987), and its validity was subsequently confirmed by accurate numerical simulations (Freitag & Benz 2002; Baumgardt et al. 2004; Preto et al. 2004).
The typical SB profile that comes out of the model
has, for any reasonable IMBH mass, the appearance of a normal low- or
medium-concentration cluster
(![]() )
and shows a steep cusp only in the very inner region (typically
within a tenth of the core radius) delimited by the ``cusp radius'',
)
and shows a steep cusp only in the very inner region (typically
within a tenth of the core radius) delimited by the ``cusp radius'',
![]() .
In fact, outside
.
In fact, outside
![]() ,
a shallow power-law behaviour - with
a logarithmic slope
,
a shallow power-law behaviour - with
a logarithmic slope ![]() - is the most easily
observable fingerprint in the otherwise flat core profile.
Interestingly, this confirmed the finding of other authors
who - using a completely different approach (accurate N-body simulations) -
also claim that IMBHs most likely reside in non-core-collapsed clusters
showing just a weak rise of the SB in the core region (Baumgardt et al. 2005; Trenti et al. 2007).
Recently, high-resolution Montecarlo simulations have provided another
independent confirmation of these structural features (Umbreit et al. 2009).
On the other hand,
according to other N-body experiments, it is claimed that post-core-collapsed
GCs also exhibit a King-like profile, but with a
- is the most easily
observable fingerprint in the otherwise flat core profile.
Interestingly, this confirmed the finding of other authors
who - using a completely different approach (accurate N-body simulations) -
also claim that IMBHs most likely reside in non-core-collapsed clusters
showing just a weak rise of the SB in the core region (Baumgardt et al. 2005; Trenti et al. 2007).
Recently, high-resolution Montecarlo simulations have provided another
independent confirmation of these structural features (Umbreit et al. 2009).
On the other hand,
according to other N-body experiments, it is claimed that post-core-collapsed
GCs also exhibit a King-like profile, but with a
![]() steep core behaviour (Trenti et al. 2010);
it must be emphasised, however, that M07 models yield core
profiles that are always significantly flatter and unable to fit behaviours with
such a high s.
steep core behaviour (Trenti et al. 2010);
it must be emphasised, however, that M07 models yield core
profiles that are always significantly flatter and unable to fit behaviours with
such a high s.
The shape of the SB profile given by the M07 model depends
on 2 dimensionless parameters![]() .
For the purposes of this study, we use the IMBH to cluster mass ratio,
.
For the purposes of this study, we use the IMBH to cluster mass ratio,
![]() ,
and the dimensionless gravitational potential at the edge of
the IMBH dynamical influence region,
,
and the dimensionless gravitational potential at the edge of
the IMBH dynamical influence region,
![]() .
The latter replaces the usual King model's central dimensionless potential W0,
with the aim of avoiding the singularity at the
cluster centre in the presence of the IMBH (see M07; for further details).
.
The latter replaces the usual King model's central dimensionless potential W0,
with the aim of avoiding the singularity at the
cluster centre in the presence of the IMBH (see M07; for further details).
In M07 it was shown that lower and upper limits of ![]() exist as a function of c and s.
This relationship was then applied to investigate the presence of
IMBHs in the set of GCs, whose SB was accurately measured in Noyola & Gebhardt (2006)
using HST/WFPC2 archive images.
Among the six candidate clusters found, NGC 6388 and M54 have subsequently
been the objects of further
and more detailed studies (through parametric fitting
of star-count profiles) that suggest the presence of an IMBH with
mass
exist as a function of c and s.
This relationship was then applied to investigate the presence of
IMBHs in the set of GCs, whose SB was accurately measured in Noyola & Gebhardt (2006)
using HST/WFPC2 archive images.
Among the six candidate clusters found, NGC 6388 and M54 have subsequently
been the objects of further
and more detailed studies (through parametric fitting
of star-count profiles) that suggest the presence of an IMBH with
mass
![]() in the former (Lanzoni et al. 2007) and
in the former (Lanzoni et al. 2007) and
![]() in the latter
(Ibata et al. 2009, in this case kinematic data were also exploited).
On the other hand, the massive cluster
in the latter
(Ibata et al. 2009, in this case kinematic data were also exploited).
On the other hand, the massive cluster ![]() Cen was
not checked as a possible candidate, because it was not included
in the Noyola & Gebhardt (2006) sample, and moreover,
small slopes in the core region could not be revealed in published
SB profiles (e.g. Ferraro et al. 2006; Meylan 1987).
Cen was
not checked as a possible candidate, because it was not included
in the Noyola & Gebhardt (2006) sample, and moreover,
small slopes in the core region could not be revealed in published
SB profiles (e.g. Ferraro et al. 2006; Meylan 1987).
Nonetheless, a recent and accurate determination of the ![]() Cen centre
and the use of HST/ACS images led Noyola et al. (2008) to detect
a steeper profile in the core region of this peculiar cluster, thus
suggesting the influence of an IMBH. By fitting the high inner peak of
the line-of-sight velocity dispersion
(LOSVD) found from Gemini GMOS/IFU integrated light spectroscopy (
Cen centre
and the use of HST/ACS images led Noyola et al. (2008) to detect
a steeper profile in the core region of this peculiar cluster, thus
suggesting the influence of an IMBH. By fitting the high inner peak of
the line-of-sight velocity dispersion
(LOSVD) found from Gemini GMOS/IFU integrated light spectroscopy (![]() km s-1at an average radius
km s-1at an average radius
![]() )
with non-parametric and orbit-based models
with uniform mass-to-light ratio, Noyola et al. estimate a
)
with non-parametric and orbit-based models
with uniform mass-to-light ratio, Noyola et al. estimate a
![]() object residing at the cluster
centre.
However, by solving the spherical and anisotropic Jeans equation on the
Anderson & van der Marel (2010) projected density and kinematic data,
van der Marel & Anderson (2010) find that the presence of an IMBH is possible
only if
object residing at the cluster
centre.
However, by solving the spherical and anisotropic Jeans equation on the
Anderson & van der Marel (2010) projected density and kinematic data,
van der Marel & Anderson (2010) find that the presence of an IMBH is possible
only if
![]() ,
which corresponds to about half the mass
predicted by Noyola et al.
,
which corresponds to about half the mass
predicted by Noyola et al.
In this paper we would like to provide further evidence on the presence of the IMBH and to give another independent estimate of its mass, by means of a parametric fitting of both the SB and the LOSVD profiles using the M07 model. The results from the best fit of the SB profile are described in Sect. 2, while those coming from the LOSVD fitting are presented in Sect. 3. Concluding remarks are reported in Sect. 4.
2 The fit of the surface brightness
To study theAs is evident from the too low concentration of the dotted profile in Fig. 1
(bottom panel), we notice that the SM isotropic model is unable to
fit the outermost part (
![]() )
of the SB profile, where, however,
the background contamination should be negligible,
for it was shown to only be relevant for
)
of the SB profile, where, however,
the background contamination should be negligible,
for it was shown to only be relevant for
![]() (Leon et al. 2000).
Thus, the discrepancy from the prediction of this model should be due
to the intrinsic dynamical state of the cluster outskirts.
In fact, we find that a good fit of the whole profile can be achieved by including
either a certain degree of radial velocity anisotropy or an MM stellar
population with mass segregation (keeping isotropic velocities).
(Leon et al. 2000).
Thus, the discrepancy from the prediction of this model should be due
to the intrinsic dynamical state of the cluster outskirts.
In fact, we find that a good fit of the whole profile can be achieved by including
either a certain degree of radial velocity anisotropy or an MM stellar
population with mass segregation (keeping isotropic velocities).
Nevertheless, the fit of the inner SB profile with a SM isotropic model
permitted us to determine the
best fit value for
![]() regardless of velocity anisotropy,
because the presence of the latter only influences the outer region
(as happens in normal King-Michie models, see, e.g., Gunn & Griffin 1979;
Miocchi 2006).
Thus, a grid
of SM isotropic models have been generated by sampling
the form parameters
regardless of velocity anisotropy,
because the presence of the latter only influences the outer region
(as happens in normal King-Michie models, see, e.g., Gunn & Griffin 1979;
Miocchi 2006).
Thus, a grid
of SM isotropic models have been generated by sampling
the form parameters
![]() and
and
![]() .
As the model profiles are expressed in dimensionless units,
they have to be scaled in both the radial and the SB dimension.
Thus, for each model of the grid
we found the best fit values for two suitable scale
parameters, namely the ``visual'' core radius
.
As the model profiles are expressed in dimensionless units,
they have to be scaled in both the radial and the SB dimension.
Thus, for each model of the grid
we found the best fit values for two suitable scale
parameters, namely the ``visual'' core radius![]()
![]() and the
normalisation value of the SB,
restricting the fit to data points with
and the
normalisation value of the SB,
restricting the fit to data points with
![]() .
Since the SB measurements uncertainties are known, we minimised the
.
Since the SB measurements uncertainties are known, we minimised the
![]() sum weighted by the width of the error bars.
sum weighted by the width of the error bars.
The calculated ![]() values are
reported in Fig. 2, from which we deduce that
values are
reported in Fig. 2, from which we deduce that
![]() and
and
![]() ,
with a level of confidence (LOC) of 68.3%.
The best fit isotropic model gives
,
with a level of confidence (LOC) of 68.3%.
The best fit isotropic model gives
![]() ,
which confirms both the
more recent observations by Ferraro et al. (2006) and the value listed
in Trager et al. (1995).
,
which confirms both the
more recent observations by Ferraro et al. (2006) and the value listed
in Trager et al. (1995).
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg1.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg58.png)
|
Figure 1:
Bottom panel: surface brightness profile of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg59.png)
|
Figure 2:
Contours of |
| Open with DEXTER | |
Once
![]() and
and
![]() has been determined by fitting the inner SB profile, we
fit the entire data set by including radial velocity anisotropy in the stellar
system outskirts (confirming what was already noted by Meylan 1987),
namely outside an anisotropy radius
has been determined by fitting the inner SB profile, we
fit the entire data set by including radial velocity anisotropy in the stellar
system outskirts (confirming what was already noted by Meylan 1987),
namely outside an anisotropy radius ![]() ;
see, e.g., Miocchi (2006)
for a description of how anisotropic velocities can be efficiently implemented in
King-Michie models.
Thus, a ``sub-grid'' of anisotropic models is generated by sampling
;
see, e.g., Miocchi (2006)
for a description of how anisotropic velocities can be efficiently implemented in
King-Michie models.
Thus, a ``sub-grid'' of anisotropic models is generated by sampling
![]() in the range
in the range
![]() .
The resulting
.
The resulting ![]() behaviour,
this time evaluated over all SB data,
is plotted in Fig. 3 and leads to the estimates
behaviour,
this time evaluated over all SB data,
is plotted in Fig. 3 and leads to the estimates
![]() with an
LOC of 68.3%. From this figure, it can also be noted how the anisotropic
model when ``pushed'' towards the isotropic case (
with an
LOC of 68.3%. From this figure, it can also be noted how the anisotropic
model when ``pushed'' towards the isotropic case (
![]() )
gives unacceptable fits (huge
)
gives unacceptable fits (huge ![]() values).
van de Ven et al. (2006) find that the velocity distribution in
values).
van de Ven et al. (2006) find that the velocity distribution in ![]() Cen
is nearly isotropic inside
Cen
is nearly isotropic inside
![]() ,
in agreement to our best fit
value for
,
in agreement to our best fit
value for ![]() .
On the other hand, these authors reported the presence
of a slight tangential anisotropy in the cluster outskirts which is, however,
below the uncertainty in the velocity dispersion measurements (see their Fig. 8).
.
On the other hand, these authors reported the presence
of a slight tangential anisotropy in the cluster outskirts which is, however,
below the uncertainty in the velocity dispersion measurements (see their Fig. 8).
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg3.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg64.png)
|
Figure 3:
|
| Open with DEXTER | |
The SM anisotropic best fit model reported in Fig. 1
yields a tidal radius
![]() and a
concentration parameter,
and a
concentration parameter,
![]() ,
substantially lower than the 1.6 value quoted in the Harris (1996) catalogue,
but in good agreement with recent results
(van de Ven et al. 2006; Ferraro et al. 2006).
,
substantially lower than the 1.6 value quoted in the Harris (1996) catalogue,
but in good agreement with recent results
(van de Ven et al. 2006; Ferraro et al. 2006).
As we said at the beginning of this section, the entire observed SB profile
can also be fitted fairly well
by an MM isotropic model (see also Meylan 1987) including the IMBH
and stars in the mass range
![]() distributed following
the Salpeter mass function, with central energy equipartition.
In this case, the best fit profile is for
distributed following
the Salpeter mass function, with central energy equipartition.
In this case, the best fit profile is for
![]() (and
(and
![]() ),
and it practically overlaps with that of the anisotropic case (Fig. 1).
Nonetheless, we discarded this MM
model because it underestimates the LOSVD in the central region, as we see in
detail in next section.
),
and it practically overlaps with that of the anisotropic case (Fig. 1).
Nonetheless, we discarded this MM
model because it underestimates the LOSVD in the central region, as we see in
detail in next section.
3 Velocity dispersion profile
To provide an estimate of ![]() ,
we have to quantify the cluster total mass M first.
This can be done by exploiting the most recent kinematic observations of
,
we have to quantify the cluster total mass M first.
This can be done by exploiting the most recent kinematic observations of ![]() Cen.
For this purpose, along with the two innermost points taken from the Gemini
GMOS-IFU measurements in Noyola et al. (2008), we use the LOSVD data employed
by van de Ven et al. (2006, see references therein for the discussion of the various data
sources).
These are based on various independent sets
of measurements, which in most of the radial annuli include values taken in
different apertures (see Fig. 4).
A radial error bar is plotted for the innermost point to indicate
the width of the
Cen.
For this purpose, along with the two innermost points taken from the Gemini
GMOS-IFU measurements in Noyola et al. (2008), we use the LOSVD data employed
by van de Ven et al. (2006, see references therein for the discussion of the various data
sources).
These are based on various independent sets
of measurements, which in most of the radial annuli include values taken in
different apertures (see Fig. 4).
A radial error bar is plotted for the innermost point to indicate
the width of the
![]() GMOS-IFU field of view that was centred on the cluster nucleus to
obtain the integrated spectrum (Noyola et al. 2008).
GMOS-IFU field of view that was centred on the cluster nucleus to
obtain the integrated spectrum (Noyola et al. 2008).
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg72.png)
|
Figure 4:
Best fit LOSVD radial profile in the SM anisotropic (solid line)
and MM isotropic case (dashed line; in this case, it is determined by
weighting the contributions of all the stellar components according to their luminosity).
The best fit total cluster mass is 3.1 and
|
| Open with DEXTER | |
Once the SB profile has been fitted, the form of the LOSVD profile is univocally given by the model and cannot be adapted to the observed behaviour. The best fit can be found by adjusting only the velocity scale factor (corresponding to a vertical shifting of the profile). In turn, this factor depends on the adopted cluster distance and total mass M. We chose to a-priori fix the distance to 4.8 kpc (as from van de Ven et al. 2006), and then to find the M value that gives the best fit to the LOSVD observations. Shown in Fig. 4 are two LOSVD best fit profiles: the one given by the SM anisotropic model and the one produced by the MM isotropic one.
It is evident (see also Fig. 5) that the SM case yields a better fit
to LOSVD data, having
![]() %,
compared with
the MM model that gives
%,
compared with
the MM model that gives
![]() % mainly because, in
the inner region (
% mainly because, in
the inner region (
![]() ), it exhibits too low an LOSVD.
This is naturally expected from the mass distribution in the MM
case being dominated by the lighter (and fainter) stars, which are
much less concentrated than the giants. Thus, the velocity dispersion
of the giants starts to decrease at larger radii, consequently
the best fit tends to give a lower inner LOSVD in the attempt to fit
the outer data.
Interestingly, that the SM model better represents the
dynamical situation of this cluster suggests that mass segregation has not been
efficient in
), it exhibits too low an LOSVD.
This is naturally expected from the mass distribution in the MM
case being dominated by the lighter (and fainter) stars, which are
much less concentrated than the giants. Thus, the velocity dispersion
of the giants starts to decrease at larger radii, consequently
the best fit tends to give a lower inner LOSVD in the attempt to fit
the outer data.
Interestingly, that the SM model better represents the
dynamical situation of this cluster suggests that mass segregation has not been
efficient in ![]() Cen. In this sense, it confirms the current thought that
this cluster is not completely relaxed by collisions, because of its relatively
long relaxation time (see, e.g., Meylan et al. 1995; Meylan 1987). Various
authors, indeed, have found indications of a uniform mass-to-light ratio
(see, e.g., Merritt et al. 1997; van de Ven et al. 2006).
Cen. In this sense, it confirms the current thought that
this cluster is not completely relaxed by collisions, because of its relatively
long relaxation time (see, e.g., Meylan et al. 1995; Meylan 1987). Various
authors, indeed, have found indications of a uniform mass-to-light ratio
(see, e.g., Merritt et al. 1997; van de Ven et al. 2006).
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg5.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg76.png)
|
Figure 5:
|
| Open with DEXTER | |
Considering the relatively large error bars of LOSVD measurements
in crowded regions, from Fig. 4 we note that the model profile
predicts that the central velocity cusp is apparently more centrally
concentrated than Noyola et al. (2008) observations suggest
(it starts to be evident only for
![]() ), though one has to consider
the ``visual effect'' of the logarithmic scale in r.
In fact, a relatively large residual (
), though one has to consider
the ``visual effect'' of the logarithmic scale in r.
In fact, a relatively large residual (![]() km s-1) still remains
for the innermost LOSVD data point, although its radial error bar intersects
the model profile (at
km s-1) still remains
for the innermost LOSVD data point, although its radial error bar intersects
the model profile (at
![]() ).
If the M07 model represents the real cluster
dynamical state well,
this could
indicate the influence of some statistical bias affecting
this bin or too large an average radius chosen for it.
In this respect, it is also worth noting that recent and accurate proper
motion measurements reveal no significant velocity cusp at
the central region of this cluster,
though this study relies on a different dataset and kinematic centre location
and, moreover, the authors do not observe any appreciable cusp in density
(Anderson & van der Marel 2010).
).
If the M07 model represents the real cluster
dynamical state well,
this could
indicate the influence of some statistical bias affecting
this bin or too large an average radius chosen for it.
In this respect, it is also worth noting that recent and accurate proper
motion measurements reveal no significant velocity cusp at
the central region of this cluster,
though this study relies on a different dataset and kinematic centre location
and, moreover, the authors do not observe any appreciable cusp in density
(Anderson & van der Marel 2010).
In Noyola et al. (2008) the innermost bins are fitted quite well (apart from
the measurement at
![]() ,
see their Fig. 4).
However, it must be noticed that in these authors' model the IMBH mass best fit
value depends almost completely on the few innermost LOSVD data points,
while it has practically no effects for
,
see their Fig. 4).
However, it must be noticed that in these authors' model the IMBH mass best fit
value depends almost completely on the few innermost LOSVD data points,
while it has practically no effects for
![]() and plays no role at all on the SB profile.
In our case, on the contrary, the behaviour of the LOSVD given by the model is strongly
dependent on the best fit parameters of the SB profile.
If our model were forced
to fit the entire LOSVD well, then the required
and plays no role at all on the SB profile.
In our case, on the contrary, the behaviour of the LOSVD given by the model is strongly
dependent on the best fit parameters of the SB profile.
If our model were forced
to fit the entire LOSVD well, then the required
![]() IMBH would
produce a much steeper SB core behaviour (along with too low a concentration), which
would be completely different from the observed one.
The disadvantage of our parametric approach is that it is
``less general'', because it is constrained by the theoretical hypothesis
lying behind the assumption of that particular distribution function in phase-space.
IMBH would
produce a much steeper SB core behaviour (along with too low a concentration), which
would be completely different from the observed one.
The disadvantage of our parametric approach is that it is
``less general'', because it is constrained by the theoretical hypothesis
lying behind the assumption of that particular distribution function in phase-space.
The predicted cluster total mass is
![]() with an LOC of 68.3% (Fig. 5).
It is in marginal agreement with the dynamical estimate of
with an LOC of 68.3% (Fig. 5).
It is in marginal agreement with the dynamical estimate of
![]() in van de Ven et al. (2006) - though it would agree well at
in van de Ven et al. (2006) - though it would agree well at ![]() level -
while much lower than the Meylan (1987)
level -
while much lower than the Meylan (1987)
![]() value.
This author used a King-Michie MM model in which an approximated
energy equipartition was imposed (see Miocchi 2006, for a discussion of this approximation). This, together with the assumed presence
of very low-mass stars (down to
value.
This author used a King-Michie MM model in which an approximated
energy equipartition was imposed (see Miocchi 2006, for a discussion of this approximation). This, together with the assumed presence
of very low-mass stars (down to
![]() ), can explain the higher M estimate.
As far as the M/L ratio is concerned, if one assumes a total V-band
luminosity in the ``prudential'' range
), can explain the higher M estimate.
As far as the M/L ratio is concerned, if one assumes a total V-band
luminosity in the ``prudential'' range
![]()
![]() (e.g. Seitzer 1983; Carraro & Lia 2000; Meylan 1987),
one gets
(e.g. Seitzer 1983; Carraro & Lia 2000; Meylan 1987),
one gets
![]() ,
a value compatible with the accurate
,
a value compatible with the accurate
![]() van de Ven et al. (2006) estimate.
Of course, as the model predicts no mass segregation, the mass-to-light ratio
turns out to be uniform.
van de Ven et al. (2006) estimate.
Of course, as the model predicts no mass segregation, the mass-to-light ratio
turns out to be uniform.
The estimate made in Sect. 2 of the ratio
![]() ,
combined with
the uncertainty on the cluster total mass, yields an IMBH mass in the range
,
combined with
the uncertainty on the cluster total mass, yields an IMBH mass in the range
![]() (with a 68.3% LOC),
which spans about one third to a half the mass predicted by Noyola et al. (2008),
but is marginally compatible with the
(with a 68.3% LOC),
which spans about one third to a half the mass predicted by Noyola et al. (2008),
but is marginally compatible with the
![]() van der Marel & Anderson (2010)
estimate. However, it has to be kept in mind that these two estimates rely
on different cluster centre.
Finally, it is worth noting how our estimate range, though still incompatible, gets
closer to the
van der Marel & Anderson (2010)
estimate. However, it has to be kept in mind that these two estimates rely
on different cluster centre.
Finally, it is worth noting how our estimate range, though still incompatible, gets
closer to the
![]() upper limit as constrained by the
upper limit as constrained by the ![]() Cen
radio continuum emission (Maccarone & Servillat 2008).
Cen
radio continuum emission (Maccarone & Servillat 2008).
4 Conclusions
In this paper we have presented a parametric fit of the surface brightness (SB) profile ofFrom this parametric study we deduce the 68.3% confidence intervals
![]() for the cluster total mass and
for the cluster total mass and
![]() for the mass ratio,
leading to an estimate for the IMBH mass in the range
for the mass ratio,
leading to an estimate for the IMBH mass in the range
![]() .
This value is from about one third
to a half the
.
This value is from about one third
to a half the
![]() mass predicted by Noyola et al. (2008),
though it is compatible with the
mass predicted by Noyola et al. (2008),
though it is compatible with the
![]() upper limit provided by the dynamical
analysis in van der Marel & Anderson (2010). Note, however, that these two
published estimates are based on different cluster centre.
upper limit provided by the dynamical
analysis in van der Marel & Anderson (2010). Note, however, that these two
published estimates are based on different cluster centre.
The author is warmly grateful to Dr. B. Lanzoni and Dr. E. Noyola for helpful discussions and suggestions. The paper presentation greatly benefited from the comments of the anonymous referee.
References
- Anderson, J., & van der Marel, R. P. 2010, ApJ, 710, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Wolf, R. A. 1976, ApJ, 209, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Makino, J., & Ebisuzaki, T. 2004, ApJ, 613, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Makino, J., & Hut, P. 2005, ApJ, 620, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. J., & Tremaine, S. 1987, Galactic Dynamics (Princeton, NJ: Princeton Univ. Press) [Google Scholar]
- Carraro, G., & Lia, C. 2000, A&A, 357, 977 [NASA ADS] [Google Scholar]
- Faber, S. M., Dressler, A., Davies, R. L., Burstein, D., & Lynden-Bell, D. 1987, in Nearly Normal Galaxies: From the Planck time to the present, ed. S. M. Faber (New York: Springer), 175 [Google Scholar]
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Sollima, A., Rood, R. T., et al. 2006, ApJ, 638, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Freitag, M., & Benz, W. 2002, A&A, 394, 345 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Rich, R. M., & Ho, L. C. 2005, ApJ, 634, 1093 [Google Scholar]
- Gill, M., Trenti, M., Miller, C. M., et al. 2008, ApJ, 686, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Griffin, R. F. 1979, AJ, 84, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. R. 1966, AJ, 71, 64 [Google Scholar]
- Kong, A. K. H., Heinke, C. O., Di Stefano, R., et al. 2009, ApJL, submitted [arXiv:0910.3944] [Google Scholar]
- Ibata, R. A., Bellazzini, M., Chapman, S. C. et al. 2009, ApJ, 699, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J. A., Brink, T., Bregman, J. N., & Roberts, T. P. 2010, ApJ, 712, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzoni, B., Dalessandro, E., Ferraro, F. R., et al. 2007, ApJ, 668, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Leon, S., Meylan, G., & Combes, F. 2000, A&A, 359, 907 [NASA ADS] [Google Scholar]
- Liu, J., & Di Stefano, R. 2008, 10th HEAD meeting of the American Astronomical Society, 1, 14 [Google Scholar]
- Maccarone, T. J., & Servillat, M. 2008, MNRAS, 389, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Meylan, G. 1987, A&A, 184, 144 [NASA ADS] [Google Scholar]
- Meylan, G., & Heggie, D. C. 1997, A&AR, 8, 1 [Google Scholar]
- Meylan, G., Mayor, M., Duquennoy, A., & Dubath, P. 1995, A&A, 303, 761 [NASA ADS] [Google Scholar]
- Merritt, D., Meylan, G., & Mayor, M. 1997, AJ, 114, 1074 [NASA ADS] [CrossRef] [Google Scholar]
- Michie, R. W. 1963, MNRAS, 125, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Michie, R. W., & Bodenheimer, P. 1963, MNRAS, 126, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, C. M., & Colbert , E. J. M. 2004, Int. J. Mod. Phys. D, 13, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Miocchi, P. 2006, MNRAS, 366, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Miocchi, P. 2007, MNRAS, 381, 103 (M07) [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., & Gebhardt, K. 2006, AJ, 132, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., Gebhardt, K., & Bergmann, M. 2008, ApJ, 676, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Nucita, A. A., De Paolis, F., Ingrosso, G., Carpano, S., & Guainazzi, M. 2008, A&A, 478, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pooley, D., & Rappaport, S. 2006, ApJ, 644, L45, 2006 [NASA ADS] [CrossRef] [Google Scholar]
- Preto, M., Merritt, D., & Spurzem, R. 2004, ApJ, 613, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Safonova, M., & Shastri, P. 2010, Ap&SS, 325, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Seitzer, P. O. 1983, Ph.D. Thesis, Australian National Univ. [Google Scholar]
- Servillat, M., Dieball, A., Webb, N. A., et al. 2008, A&A, 490, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soria, R., Hau, G. K. T., Graham, A. W., et al. 2010, MNRAS, accepted [arXiv:0910.1356] [Google Scholar]
- Strohmayer, T. E., & Mushotzky, R. F. 2009, ApJ, 703, 1386 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., King, I. R., & Djorgovski, S. 1995, AJ, 109, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., Ardi, E., Mineshige, S., & Hut, P. 2007, MNRAS, 374, 857 [NASA ADS] [Google Scholar]
- Trenti, M., Vesperini, E., & Pasquato, M. 2010, ApJ, 708, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- Ulvestad, J. S., Greene, J. E., & Ho, L. C. 2007, ApJ, 661, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Umbreit, S., Fregeau, J. M., & Rasio, F. A. 2009, ApJ, submitted [arXiv:0910.5293] [Google Scholar]
- van de Ven, G., van den Bosch, R. C. E., Verolme, E. K., & de Zeeuw, P. T. 2006, A&A, 445, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, R. P., & Anderson, J. 2010, ApJ, 710, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Zepf, S. E., Stern, D., Maccarone, T. J., et al. 2008, ApJ, 683, L139 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... parameters
![[*]](/icons/foot_motif.png)
- The model can also include velocity anisotropy in the GC outskirts. In this case the outer SB profile shape depends on the anisotropy radius, too.
- ... radius
![[*]](/icons/foot_motif.png)
- Here
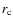 is defined as the radius
at which the SB drops to half its value at
is defined as the radius
at which the SB drops to half its value at 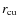 .
In good approximation,
.
In good approximation, 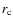 coincides
with the location of the ``turn-off'' of the profile (also called
``break radius''
in Noyola & Gebhardt 2006;
see M07 for more details).
coincides
with the location of the ``turn-off'' of the profile (also called
``break radius''
in Noyola & Gebhardt 2006;
see M07 for more details).
All Figures
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg1.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg58.png)
|
Figure 1:
Bottom panel: surface brightness profile of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg59.png)
|
Figure 2:
Contours of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg3.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg64.png)
|
Figure 3:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg72.png)
|
Figure 4:
Best fit LOSVD radial profile in the SM anisotropic (solid line)
and MM isotropic case (dashed line; in this case, it is determined by
weighting the contributions of all the stellar components according to their luminosity).
The best fit total cluster mass is 3.1 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12828fg5.ps}\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/06/aa12828-09/Timg76.png)
|
Figure 5:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


