| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912544 | |
| Published online | 26 May 2010 | |
Ultraluminous X-ray sources out to z  0.3 in the COSMOS field
0.3 in the COSMOS field
V. Mainieri1 - C. Vignali2,3 - A. Merloni4,5 - F. Civano6 - S. Puccetti7 - M. Brusa5 - R. Gilli3 - M. Bolzonella3 - A. Comastri3 - G. Zamorani3 - M. Aller9 - M. Carollo9 - C. Scarlata9,10 - M. Elvis6 - T. L. Aldcroft6 - N. Cappelluti5 - G. Fabbiano6 - A. Finoguenov5 - F. Fiore8 - A. Fruscione6 - A. M. Koekemoer11 - T. Contini12 - J.-P. Kneib13 - O. Le Fèvre13 - S. Lilly9 - A. Renzini14 - M. Scodeggio15 - S. Bardelli3 - A. Bongiorno5 - K. Caputi9 - G. Coppa3 - O. Cucciati16 - S. de la Torre13 - L. de Ravel13 - P. Franzetti15 - B. Garilli15 - A. Iovino16 - P. Kampczyk9 - C. Knobel9 - K. Kovac9 - F. Lamareille12 - J.-F. Le Borgne12 - V. Le Brun13 - C. Maier9 - M. Mignoli3 - R. Pello12 - Y. Peng9 - E. Perez Montero12 - E. Ricciardelli17 - J. D. Silverman9 - M. Tanaka1 - L. Tasca13 - L. Tresse13 - D. Vergani3 - E. Zucca3 - P. Capak19 - O. Ilbert13 - C. Impey18 - M. Salvato19 - N. Scoville19 - Y. Taniguchi20 - J. Trump18
1 - ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
2 -
Dipartimento di Astronomia, Università degli Studi di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 -
INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
4 -
Excellence Cluster Universe, TUM, Boltzmannstr. 2, 85748 Garching bei München, Germany
5 -
Max-Planck-Institute für Extraterrestrische Physik, Postfach 1312, 85741, Garching bei München, Germany
6 -
Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA
7 -
ASI Science Data Center, via Galileo Galilei, 00044 Frascati Italy
8 -
INAF - Osservatorio astronomico di Roma, via Frascati 33, 00040 Monteporzio Catone, Italy
9 -
Institute of Astronomy, Swiss Federal Institute of Technology (ETH Hönggerberg), 8093, Zürich, Switzerland
10 -
Spitzer Science Center, Pasadena, CA, 91125, USA
11 -
Space Telescope Science Institute, Baltimore, Maryland 21218, USA
12 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 avenue Edouard Belin, 31400 Toulouse, France
13 -
Laboratoire d'Astrophysique de Marseille, Marseille, France
14 -
INAF - Osservatorio astronomico di Padova, Vicolo Dell'Osservatorio 5, 35122 Padova, Italy
15 -
INAF - IASF Milano, Milan, Italy
16 -
INAF Osservatorio Astronomico di Brera, Milan, Italy
17 -
Dipartimento di Astronomia, Universita di Padova, Padova, Italy
18 -
Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721, USA
19 -
California Institute of Technology, MC 105-24, 1200 East California Boulevard, Pasadena, CA 91125, USA
20 -
Research Center for Space and Cosmic Evolution, Ehime University, Bunkyo-cho 2-5, Matsuyama 790-8577, Japan
Received 20 May 2009 / Accepted 22 February 2010
Abstract
Context. Using Chandra observations we identified a sample of seven off-nuclear X-ray sources in the redshift range
z=0.072-0.283, located within optically bright galaxies in the
COSMOS Survey. All of them, if associated with their closest bright
galaxy, would have L[0.5-7 keV
] >1039 erg s-1 and therefore can be classified as ultraluminous X-ray sources (ULXs).
Aims. Using the multi-wavelength coverage available in the
COSMOS field, we studied the properties of the host galaxies of these
ULXs. In detail, we derived their star formation rate from H![]() measurements and their stellar masses using SED fitting techniques with
the aim to compute the probability to have an off-nuclear source based
on the host galaxy properties. We divided the host galaxies in
different morphological classes with the available ACS/HST imaging.
measurements and their stellar masses using SED fitting techniques with
the aim to compute the probability to have an off-nuclear source based
on the host galaxy properties. We divided the host galaxies in
different morphological classes with the available ACS/HST imaging.
Methods. We selected off-nuclear candidates with the following
criteria: 1) the distance between the X-ray and the optical centroid
has to be larger than 0.9
![]() ,
larger than 1.8 times the radius of the Chandra positional error circle
and smaller than the Petrosian radius of the host galaxy; 2) the
optical counterpart is a bright galaxy (
,
larger than 1.8 times the radius of the Chandra positional error circle
and smaller than the Petrosian radius of the host galaxy; 2) the
optical counterpart is a bright galaxy (
![]() ); 3) the redshift of the counterpart is lower than z=0.3; 4) the source has been observed in at least one Chandra pointing at an off-axis angle smaller than 5
); 3) the redshift of the counterpart is lower than z=0.3; 4) the source has been observed in at least one Chandra pointing at an off-axis angle smaller than 5![]() ;
5) the X-ray positional error is smaller than 0.8
;
5) the X-ray positional error is smaller than 0.8
![]() .
We verified each candidate super-imposing the X-ray contours on the
optical/IR images. We expect less than one misidentified AGN due to
astrometric errors and on average 1.3 serendipitous background source
matches.
.
We verified each candidate super-imposing the X-ray contours on the
optical/IR images. We expect less than one misidentified AGN due to
astrometric errors and on average 1.3 serendipitous background source
matches.
Results. We find that our ULXs candidates are located in regions of the SFR versus M![]() plane where one or more off-nuclear detectable sources are expected.
From a morphological analysis of the ACS imaging and the use of
rest-frame colours, we find that our ULXs are hosted both in late and
early type galaxies. Finally, we find that the fraction of galaxies
hosting a ULX ranges from
plane where one or more off-nuclear detectable sources are expected.
From a morphological analysis of the ACS imaging and the use of
rest-frame colours, we find that our ULXs are hosted both in late and
early type galaxies. Finally, we find that the fraction of galaxies
hosting a ULX ranges from ![]() 0.5% to
0.5% to ![]() 0.2% going from
0.2% going from
![]() erg s-1 to
erg s-1 to
![]() erg s-1.
erg s-1.
Key words: X-rays: galaxies - X-rays: binaries - X-rays: general - surveys
1 Introduction
An intriguing class of X-ray objects are the so called ultraluminous
X-ray sources (ULXs). Here an ULX is defined as an X-ray source in an
extra-nuclear region of a galaxy with an observed luminosity in excess
of 1039 erg s-1 in the 0.5-7 keV band. These X-ray
luminosities are higher than expected for spherical Eddington-limited
accretion onto a
![]() black hole. ULXs were known already
from studies with Einstein, ROSAT, and ASCA (e.g. Fabbiano 1989; Colbert & Ptak 2002; Makishima et al. 2000), but it was after the advent of Chandra
with its combination of high angular resolution and moderate spectral
resolution that it has been possible to make significant progress in
their study (e.g. Swartz et al. 2004; Roberts et al. 2004). There is a wide
debate in the literature on the nature of these sources. They may be
powered by accretion onto stellar-mass black holes assuming that there
is relativistic beaming (e.g. Körding et al. 2002), or radiative
anisotropy (e.g. King 2002), or they may be associated with
super-Eddington disks (e.g. Begelman 2002). It has also been
suggested that ULXs represent a new class of intermediate-mass
(
black hole. ULXs were known already
from studies with Einstein, ROSAT, and ASCA (e.g. Fabbiano 1989; Colbert & Ptak 2002; Makishima et al. 2000), but it was after the advent of Chandra
with its combination of high angular resolution and moderate spectral
resolution that it has been possible to make significant progress in
their study (e.g. Swartz et al. 2004; Roberts et al. 2004). There is a wide
debate in the literature on the nature of these sources. They may be
powered by accretion onto stellar-mass black holes assuming that there
is relativistic beaming (e.g. Körding et al. 2002), or radiative
anisotropy (e.g. King 2002), or they may be associated with
super-Eddington disks (e.g. Begelman 2002). It has also been
suggested that ULXs represent a new class of intermediate-mass
(
![]() )
black holes
(e.g. Colbert & Mushotzky 1999; Miller & Colbert 2004). These intermediate-mass black
holes may be fed by Roche lobe overflow from a tidal captured stellar
companion that is not destroyed by tidal heating
(Hopman et al. 2004). Off-nuclear AGN activity could also be a
signature of a recoiling massive black hole: a massive black hole
binary coalesces and causes gravitational waves which can give a kick
to the center of mass of the system. If the recoiling black hole
retains the inner parts of its accretion disk, we could see its
luminous phase as an off-nuclear AGN (see Volonteri & Madau 2008, and
references therein). Finally, ULXs could also be the high-luminosity
extension of supernovae (e.g. Swartz et al. 2004).
)
black holes
(e.g. Colbert & Mushotzky 1999; Miller & Colbert 2004). These intermediate-mass black
holes may be fed by Roche lobe overflow from a tidal captured stellar
companion that is not destroyed by tidal heating
(Hopman et al. 2004). Off-nuclear AGN activity could also be a
signature of a recoiling massive black hole: a massive black hole
binary coalesces and causes gravitational waves which can give a kick
to the center of mass of the system. If the recoiling black hole
retains the inner parts of its accretion disk, we could see its
luminous phase as an off-nuclear AGN (see Volonteri & Madau 2008, and
references therein). Finally, ULXs could also be the high-luminosity
extension of supernovae (e.g. Swartz et al. 2004).
Many of the
previous studies based on Chandra data are focused on local galaxies,
where the Chandra angular resolution allows the detection of several
off-nuclear sources in one single galaxy. In this paper, we select a
sample of ULXs from the Chandra survey in the COSMOS field. We have
here the advantage to combine deep X-ray observation with a wealth of
multiwavelength ancillary data that we will use to put constraints on
the nature of these sources and on the properties of their host
galaxies. The redshift range that we cover is up to
![]() .
A
study of off-nuclear sources in a similar redshift range was performed
by Lehmer et al. (2006) on the Chandra Deep Fields (CDFs).
.
A
study of off-nuclear sources in a similar redshift range was performed
by Lehmer et al. (2006) on the Chandra Deep Fields (CDFs).
We quote in
this paper magnitudes in the AB system and assume a cosmology with
H0 = 70 km s-1 Mpc-1,
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12544fg1.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg20.png)
|
Figure 1: Distribution of the difference between the detected X-ray positions and the input positions in units of the X-ray positional error. |
| Open with DEXTER | |
2 Sample selection
We have selected off-nuclear X-ray candidates from the Chandra COSMOS
Survey (C-COSMOS), which is a recently completed 1.8 Ms Chandra
program to image the central 0.9 deg2 of the COSMOS field with an
effective exposure ranging from ![]() 160 ks to
160 ks to ![]() 80 ks going
from the center to the borders of the field (Elvis et al. 2009). The
limiting source detection depths are
80 ks going
from the center to the borders of the field (Elvis et al. 2009). The
limiting source detection depths are
![]() erg cm-2 s-1 in the [0.5-2 keV] band,
erg cm-2 s-1 in the [0.5-2 keV] band,
![]() erg cm-2 s-1 in the [2-10 keV] band, and
erg cm-2 s-1 in the [2-10 keV] band, and
![]() erg cm-2 s-1 in the [0.5-10 keV] band. We used a point source
catalog including 1761 objects detected in at least one band (0.5-2,
2-7 and 0.5-7 keV) with a maximum likelihood ratio larger than
detml = 10.8, corresponding to a probability of
erg cm-2 s-1 in the [0.5-10 keV] band. We used a point source
catalog including 1761 objects detected in at least one band (0.5-2,
2-7 and 0.5-7 keV) with a maximum likelihood ratio larger than
detml = 10.8, corresponding to a probability of
![]() that a catalog source is instead a background fluctuation
(Puccetti et al. 2009). The optical and infrared identifications of
almost all (99.7%) of the sources are reported in
Civano et al. (2010, in prep.)
that a catalog source is instead a background fluctuation
(Puccetti et al. 2009). The optical and infrared identifications of
almost all (99.7%) of the sources are reported in
Civano et al. (2010, in prep.)![]() .
.
As a first step to select off-nuclear X-ray sources, we verified the
X-ray position accuracy that we have in the C-COSMOS observations
following the procedure presented in Sect. 4.3 of
Puccetti et al. (2009). A set of 49 Chandra ACIS-I pointings has been
simulated with the MARX![]() simulator, adopting the same exposure times, aim points, and
roll-angles as the real C-COSMOS pointings. The detection code
PWDetect (Damiani et al. 1997) was applied to the simulated data. We then
compared the output of the detection algorithm with the input catalog
of the simulation. In Fig. 1 we show the distribution of
the difference between the detection algorithm positions and the
input positions in units of the X-ray positional error. The last was
estimated as the ratio of the PSF at the position of the source and
the square root of the net background subtracted source counts. In
comparison with Fig. 10 of Puccetti et al. (2009), we restricted the
analysis only to sources that were detected at least in one image at
an off-axis angle smaller than 5
simulator, adopting the same exposure times, aim points, and
roll-angles as the real C-COSMOS pointings. The detection code
PWDetect (Damiani et al. 1997) was applied to the simulated data. We then
compared the output of the detection algorithm with the input catalog
of the simulation. In Fig. 1 we show the distribution of
the difference between the detection algorithm positions and the
input positions in units of the X-ray positional error. The last was
estimated as the ratio of the PSF at the position of the source and
the square root of the net background subtracted source counts. In
comparison with Fig. 10 of Puccetti et al. (2009), we restricted the
analysis only to sources that were detected at least in one image at
an off-axis angle smaller than 5![]() to take advantage of an
excellent PSF. From the distribution in Fig. 1, we find
that 94% of the sources have offsets below 1.8 times the
positional error. We will adopt this value as a threshold to select
off-nuclear candidates and therefore we expect that up to 6% of
our sample is contaminated by nuclear X-ray sources with large
astrometric errors. We will shortly come back to this issue. Another
possible source of spurious off-nuclear objects could be a poor
astrometric accuracy of the X-ray images. According to Fig. 6 of
Elvis et al. (2009), 95% of the Chandra sources have an absolute
astrometric accuracy better than 1.4
to take advantage of an
excellent PSF. From the distribution in Fig. 1, we find
that 94% of the sources have offsets below 1.8 times the
positional error. We will adopt this value as a threshold to select
off-nuclear candidates and therefore we expect that up to 6% of
our sample is contaminated by nuclear X-ray sources with large
astrometric errors. We will shortly come back to this issue. Another
possible source of spurious off-nuclear objects could be a poor
astrometric accuracy of the X-ray images. According to Fig. 6 of
Elvis et al. (2009), 95% of the Chandra sources have an absolute
astrometric accuracy better than 1.4
![]() .
For our study we aim at
even better astrometric accuracy, therefore we considered only the
X-ray sources with an X-ray positional error smaller that
0.8
.
For our study we aim at
even better astrometric accuracy, therefore we considered only the
X-ray sources with an X-ray positional error smaller that
0.8
![]() .
We show the comparison between X-ray coordinates and
optical coordinates for sources with a secure identification in
Fig. 2: 95% of the X-ray sources have an absolute
astrometric accuracy better than 0.9
.
We show the comparison between X-ray coordinates and
optical coordinates for sources with a secure identification in
Fig. 2: 95% of the X-ray sources have an absolute
astrometric accuracy better than 0.9
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12544fg2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg25.png)
|
Figure 2:
X-ray to optical offsets in arcsec for X-ray sources with a secure
identification (Civano et al. 2010, in prep.) and with an X-ray
positional error smaller than 0.8
|
| Open with DEXTER | |
Summarizing, the off-nuclear candidates were selected with the following criteria:
- a)
- The distance between the X-ray centroid and the optical centroid has to be larger than 1.8 times the radius of the Chandra positional error circle at that position.
- b)
- The X-ray positional error is smaller than 0.8
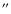 .
.
- c)
- The source was observed in at least one Chandra pointing at
an off-axis angle smaller than 5
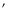 .
.
- d)
- The optical counterpart is a bright galaxy (
 ).
).
- e)
- The redshift of the host galaxy is less than z=0.3. The
projected linear distance corresponding to an average Chandra
positional error is
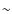 4 kpc at z=0.3. This means we will
consider only off-nuclear candidates that are more than
4 kpc at z=0.3. This means we will
consider only off-nuclear candidates that are more than 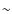 7 kpc
away from the center of the galaxy at z=0.3. At larger redshifts we
would be able to select only off-nuclear candidates that are at
larger distances (>7 kpc) from the host galaxy center, where the
number of observed off-nuclear sources seems to decrease
(Swartz et al. 2004) and we would be more affected by the
contamination of background objects. Therefore we limit our sample
to z<0.3.
7 kpc
away from the center of the galaxy at z=0.3. At larger redshifts we
would be able to select only off-nuclear candidates that are at
larger distances (>7 kpc) from the host galaxy center, where the
number of observed off-nuclear sources seems to decrease
(Swartz et al. 2004) and we would be more affected by the
contamination of background objects. Therefore we limit our sample
to z<0.3.
- f)
- The distance between the X-ray centroid and the optical centroid
is larger than 0.9
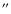 and smaller than the Petrosian radius
(Petrosian 1976,
and smaller than the Petrosian radius
(Petrosian 1976, 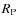
![[*]](/icons/foot_motif.png) ) of
the galaxy, which we use as a measure of the galaxy's extension.
) of
the galaxy, which we use as a measure of the galaxy's extension.
For all the candidates provided by these selection criteria we
verified that no other counterpart closer to the Chandra position was
present in any band from the ![]() (
(
![]() nm)
filter to 24 micron. After this one-by-one check, we were left with
seven off-nuclear source candidates. Cutouts of these objects,
obtained from the COSMOS HST/ACS F814W imaging
(Koekemoer et al. 2007), are shown in Fig. 3, together
with the corresponding Chandra [0.5-7 keV] image.
nm)
filter to 24 micron. After this one-by-one check, we were left with
seven off-nuclear source candidates. Cutouts of these objects,
obtained from the COSMOS HST/ACS F814W imaging
(Koekemoer et al. 2007), are shown in Fig. 3, together
with the corresponding Chandra [0.5-7 keV] image.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12544fg3.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg36.png)
|
Figure 3:
Cutouts in the HST/ACS F814W band (Koekemoer et al. 2007)
of the seven X-ray off-nuclear sources in the C-COSMOS field. The red
cross indicates the position of the X-ray centroid and the red circle
the X-ray positional error (Elvis et al. 2009). We provide for each object the Chandra ID ( top-left), the redshift ( top-right), the logarithm of the X-ray luminosity in the [0.5-7] keV band ( bottom-left), the maximum likelihood ratio for the X-ray detection ( bottom-right), the morphological classification of the host galaxy (bottom-middle; see Sect. 3.1). The images have different sizes for display purposes; the vertical bar in each cutout corresponds to 2
|
| Open with DEXTER | |
Table 1: Properties of ULXs in C-COSMOS.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{12544fg4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg45.png)
|
Figure 4:
Aperture photometry for each off-nuclear candidate. The vertical
dot-dashed line indicates the distance between the X-ray position and
the centroid of the host galaxy; the vertical dashed line is the
Petrosian radius of the host galaxy; the horizontal line corresponds to
the counts estimated by EMLdetect (Puccetti et al. 2009).
For objects XID = 1151, 1388, and 1870, the filled circles represent
the photometry on an area including 90% of the PSF obtained applying an
aperture correction factor to the photometry measured on an aperture of
1
|
| Open with DEXTER | |
Each of our off-nuclear sources has an estimate of the X-ray flux in
the [0.5-7] keV band reported in Elvis et al. (2009). These fluxes are
derived from the counts estimated by
EMLdetect![]() ,
corrected to an area including 90% of the PSF
(Puccetti et al. 2009). In some cases such an area is large enough to
include the whole host galaxy and therefore the X-ray flux could be
the total integrated flux of the host galaxy itself. This would
include the contribution from the population of X-ray binaries in the
host, emission from diffuse gas and a possible weak central AGN. In
order to estimate these possible contaminations on the measured X-ray
fluxes, we performed aperture photometry for each off-nuclear
source. The radii of the apertures were chosen with increasing size
from a minimum of 1
,
corrected to an area including 90% of the PSF
(Puccetti et al. 2009). In some cases such an area is large enough to
include the whole host galaxy and therefore the X-ray flux could be
the total integrated flux of the host galaxy itself. This would
include the contribution from the population of X-ray binaries in the
host, emission from diffuse gas and a possible weak central AGN. In
order to estimate these possible contaminations on the measured X-ray
fluxes, we performed aperture photometry for each off-nuclear
source. The radii of the apertures were chosen with increasing size
from a minimum of 1
![]() up to include the whole galaxy. In
Fig. 4, we plot the net counts in the [0.5-7] keV band
as a function of the aperture radius. For four of our sources (XID =
2418, 3441, 11100, 11938) the counts measured at different apertures
are constant within the uncertainties. Therefore, we assume that the
contribution of the host galaxy is not significant compared with the
uncertainties on the measure. For the remaining three sources (XID =
1151, 1388, 1870) the counts rise with the aperture radius and there
may be a significant contamination due to the integrated flux of the
whole galaxy. In order to minimize this contamination, we considered
the measured counts in the smaller aperture (1
up to include the whole galaxy. In
Fig. 4, we plot the net counts in the [0.5-7] keV band
as a function of the aperture radius. For four of our sources (XID =
2418, 3441, 11100, 11938) the counts measured at different apertures
are constant within the uncertainties. Therefore, we assume that the
contribution of the host galaxy is not significant compared with the
uncertainties on the measure. For the remaining three sources (XID =
1151, 1388, 1870) the counts rise with the aperture radius and there
may be a significant contamination due to the integrated flux of the
whole galaxy. In order to minimize this contamination, we considered
the measured counts in the smaller aperture (1
![]() ). We then used
the known PSF shape at the position of the source to estimate the
expected fraction between the counts measured in an aperture of
1
). We then used
the known PSF shape at the position of the source to estimate the
expected fraction between the counts measured in an aperture of
1
![]() and those over an area corresponding to 90% of the
PSF. We then used this ratio to convert our measured counts on the
1
and those over an area corresponding to 90% of the
PSF. We then used this ratio to convert our measured counts on the
1
![]() aperture into the expected ones on a 90% PSF area. These
corrected counts are indicated with a filled circle in the plots of
Fig. 4, and we used them to estimate the X-ray
fluxes.
aperture into the expected ones on a 90% PSF area. These
corrected counts are indicated with a filled circle in the plots of
Fig. 4, and we used them to estimate the X-ray
fluxes.
Full band 0.5-7 keV fluxes and errors were computed
converting counts rates to fluxes with the formula
Flux =
![]() /(CF
/(CF
![]() ), where
), where
![]() is the count
rate estimated as described above, and CF is the energy conversion
factor. This conversion factor varies with the energy band and the
spectral index
is the count
rate estimated as described above, and CF is the energy conversion
factor. This conversion factor varies with the energy band and the
spectral index ![]() assumed for the power-law spectrum. We used
the correction factor CF = 0.89 counts erg-1 cm2 reported in
Table 4 of Elvis et al. (2009) obtained for the 0.5-7 keV band and
assumed for the power-law spectrum. We used
the correction factor CF = 0.89 counts erg-1 cm2 reported in
Table 4 of Elvis et al. (2009) obtained for the 0.5-7 keV band and
![]() .
We decided for this average value of the spectral index
following the study of Swartz et al. (2004) that has found a mean
power-law index of
.
We decided for this average value of the spectral index
following the study of Swartz et al. (2004) that has found a mean
power-law index of
![]() for a sample of 154 ULX
candidates observed with Chandra. We finally report in Table 1 the 0.5-7 keV luminosities and errors for the seven
off-nuclear sources. All sources have luminosities well in excess of
1039 erg s-1 in the 0.5-7 keV band (the lowest X-ray
luminosity in this band is
for a sample of 154 ULX
candidates observed with Chandra. We finally report in Table 1 the 0.5-7 keV luminosities and errors for the seven
off-nuclear sources. All sources have luminosities well in excess of
1039 erg s-1 in the 0.5-7 keV band (the lowest X-ray
luminosity in this band is
![]() erg s-1)
and are therefore classified as ULX sources, using either
spectroscopic or photometric redshifts.
erg s-1)
and are therefore classified as ULX sources, using either
spectroscopic or photometric redshifts.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{12544fg5.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg52.png)
|
Figure 5: X-ray luminosity in the
0.5-7 keV band vs. redshift of the seven off-nuclear sources. The
different symbols correspond to the host galaxy classification based on
morphology and rest-frame colors: circles are ETGs, while stars are
LTGs (see Sect. 3.1). Squares are the off-nuclear sources from Lehmer et al. (2006); crosses are the collection of local off-nuclear sources by Liu & Mirabel (2005). The dashed line corresponds to the flux limit in the deepest region of the C-COSMOS survey: S
|
| Open with DEXTER | |
We have secure spectroscopic redshifts for four host galaxies from
zCOSMOS VIMOS observations at VLT (Lilly et al. 2009,2007). For the
remaining three objects we used the extremely accurate photometric
redshifts available in the COSMOS field (Ilbert et al. 2009; Salvato et al. 2009)
based on 30 broad, intermediate, and narrow bands from the UV to the
mid-IR. We show in Fig. 5 the X-ray luminosity in the [0.5-7] keV band versus redshift of the seven ULXs. The X-ray luminosities
were computed according to the formula
| (1) |
where
In order to estimate how many background sources we expect to
contaminate our sample, we applied a random shift between 30
![]() and 2
and 2![]() to the C-COSMOS sources and searched for chance
coincidences with
to the C-COSMOS sources and searched for chance
coincidences with
![]() and z<0.3 galaxies. We repeated
this procedure 10,000 times and found that on average the chance
coincidences are
and z<0.3 galaxies. We repeated
this procedure 10,000 times and found that on average the chance
coincidences are ![]() 1.3. Only for 2% of the 10 000 simulations we found more than three chance coincidences. Summarizing, we
expect less than one misidentified AGN due to astrometric errors and
on average 1.3 serendipitous background source matches.
1.3. Only for 2% of the 10 000 simulations we found more than three chance coincidences. Summarizing, we
expect less than one misidentified AGN due to astrometric errors and
on average 1.3 serendipitous background source matches.
3 Host galaxy properties
3.1 Galaxy classification
Studies of local samples of ULXs (e.g. Swartz et al. 2004) have shown that these sources are mainly present in late type galaxies. A visual inspection of Fig. 3 suggests that the ULXs at intermediate redshifts that we are studying are hosted in both early and late type galaxies (ETGs and LTGs, hereafter).
To confirm this impression we classified the host galaxies based on
their morphology and colors (e.g. Mignoli et al. 2009). Taking
advantage of the COSMOS HST/ACS F814W images (Koekemoer et al. 2007),
we used an accurate morphological classification derived by
Scarlata et al. (2007) through the Zurich Estimator of Structural Type
(ZEST). Scarlata et al. (2007) describe in detail the methodology and the
performances of this method. We only recall here that the ZEST
classification is based on a) five non-parametric diagnostics
(asymmetry A, concentration C, Gini coefficient G, 2nd order
moment of the brightest 20% of galaxy pixels M20, ellipticity
![]() ); and b) the exponent n of single Sersic fits to the
two-dimensional surface brightness distributions. ZEST assigns to each
galaxy a morphological type (1 = early type; 2 = disk; 3 = irregular) and a
bulgeness parameter that splits the disk galaxies in four separate
bins, from bulge dominated disks (2.0) to pure disk galaxies
(2.3). For the bulge-dominated galaxies (2.0), we complemented the
morphological information with their rest-frame colors to further
subdivide them: if they have red U-B rest-frame colors, we included
them in the ETGs sample (XID = 1151), otherwise we classified them as
LTGs (XID = 1870). In Fig. 6 we plot the color-mass
diagram for our ULX host galaxies: they can be divided into three ETGs
and four LTGs. We will describe in Sect. 3.2 the method used
to estimate stellar masses.
); and b) the exponent n of single Sersic fits to the
two-dimensional surface brightness distributions. ZEST assigns to each
galaxy a morphological type (1 = early type; 2 = disk; 3 = irregular) and a
bulgeness parameter that splits the disk galaxies in four separate
bins, from bulge dominated disks (2.0) to pure disk galaxies
(2.3). For the bulge-dominated galaxies (2.0), we complemented the
morphological information with their rest-frame colors to further
subdivide them: if they have red U-B rest-frame colors, we included
them in the ETGs sample (XID = 1151), otherwise we classified them as
LTGs (XID = 1870). In Fig. 6 we plot the color-mass
diagram for our ULX host galaxies: they can be divided into three ETGs
and four LTGs. We will describe in Sect. 3.2 the method used
to estimate stellar masses.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12544fg6.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg58.png)
|
Figure 6:
Color-mass diagram: circles and stars are respectively
ULX host galaxies classified as ETGs and LTGs based on their
morphology/colors; the dots are galaxies in the C-COSMOS area
with z<0.3 and
|
| Open with DEXTER | |
The slight preference for ULXs to be hosted in LTGs could be explained
by the different shapes of the X-ray luminosity function (XLF) for
Low-Mass X-ray Binaries (LMXBs) and High-Mass X-ray Binaries (HMXBs)
derived for local galaxies (Gilfanov 2004; Grimm et al. 2003): the former
has an abrupt cut-off at
![]() erg s-1,
while the latter can be described with a power-law with a slope
erg s-1,
while the latter can be described with a power-law with a slope
![]() .
Because early-type stars are the dominant stellar
population of LTGs, we expect X-ray binaries with O or B type
companions, HMXBs, to be common in these objects. This translates into
a higher chance to detect ULXs in LTGs or, in any case, in galaxies
with current star formation activity.
.
Because early-type stars are the dominant stellar
population of LTGs, we expect X-ray binaries with O or B type
companions, HMXBs, to be common in these objects. This translates into
a higher chance to detect ULXs in LTGs or, in any case, in galaxies
with current star formation activity.
3.2 Stellar masses and star formation rates.
Stellar masses (- stellar population synthesis models from the libraries of Bruzual & Charlot (2003);
- eleven ``smooth'' star formation histories for each library: one constant star formation model plus 10
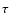 -model with e-folding time-scales
-model with e-folding time-scales
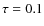 ,
0.3, 0.6, 1, 2, 3, 5, 10, 15, 30 Gyr;
,
0.3, 0.6, 1, 2, 3, 5, 10, 15, 30 Gyr;
- a Chabrier initial mass function;
- a Calzetti extinction law with
 ;
;
- solar metalicity (
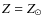 ).
).
From the COSMOS catalog (Ilbert et al. 2009; Capak et al. 2007) we selected a
comparison sample of galaxies inside the area covered by Chandra. We
imposed the same constraints used to select the off-nuclear
candidates: z<0.3 and
![]() .
We also removed all sources
that are best fitted by stellar SED templates (Ilbert et al. 2009). At
the end, the comparison sample consists of 2066 galaxies. For all of
them we derived stellar masses and SFR values as described above.
.
We also removed all sources
that are best fitted by stellar SED templates (Ilbert et al. 2009). At
the end, the comparison sample consists of 2066 galaxies. For all of
them we derived stellar masses and SFR values as described above.
We now estimate the probability to have an off-nuclear source given a host galaxy with a particular stellar mass and SFR. We will consider both LMXBs and HMXBs.
For LMXBs we used the average XLF derived by Gilfanov (2004). This
is described by a power-law with two breaks, from their Eq. (8):
where
We used the best-fitting parameter derived by Gilfanov (2004):
![\begin{figure}
\par\includegraphics[width=8cm]{12544fg7.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg89.png)
|
Figure 7:
SFR versus stellar masses of the galaxies in the comparison sample (see
text). The contours correspond to the region where more than 0.1 (red),
1 (green), 5 (cyan), and 10 (yellow) X-ray off-nuclear sources per
galaxy are expected. The symbols show the location in this plane of the
host galaxies of the ULXs. For the source XID = 1151 the
photometric coverage is limited to few bands and we cannot constrain
its stellar mass. The symbols are the same as in Fig. 5. The dashed line is where we expect the same number of LMXBs and HMXBs with
|
| Open with DEXTER | |
For the HMXBs we used instead the luminosity function derived by
Grimm et al. (2003). In particular, we used the cumulative form of it,
corresponding to their Eq. (7):
| (3) |
where the SFR is in units of
We then calculated the number of X-ray binaries with
![]() erg s-1 that we expect in each galaxy integrating
the XLFs for a given SFR and
erg s-1 that we expect in each galaxy integrating
the XLFs for a given SFR and ![]() .
In Fig. 7 we
show the contours corresponding to regions where we expect more than
0.1 (red), 1 (green), 5 (cyan), 10 (yellow) X-ray sources with
.
In Fig. 7 we
show the contours corresponding to regions where we expect more than
0.1 (red), 1 (green), 5 (cyan), 10 (yellow) X-ray sources with
![]() erg s-1. In reality these numbers have to be
considered upper limits because we have not taken into account the
limited Chandra spatial resolution that does not allow the detection
of off-nuclear sources with small offsets (see Fig. 10 of
Lehmer et al. 2006).
erg s-1. In reality these numbers have to be
considered upper limits because we have not taken into account the
limited Chandra spatial resolution that does not allow the detection
of off-nuclear sources with small offsets (see Fig. 10 of
Lehmer et al. 2006).
From Fig. 7 we find that all our ULX candidates are
hosted in galaxies for which a large number of X-ray binaries is
predicted. The dashed line in Fig. 7 is where we expect
the same number of LMXBs and HMXBs with
![]() erg s-1. This line clearly divides a region (below the line) where
the XLF of LMXBs is dominating and therefore the contours are mainly
defined by the
erg s-1. This line clearly divides a region (below the line) where
the XLF of LMXBs is dominating and therefore the contours are mainly
defined by the ![]() values, from a region (above the line)
where the HMXBs are more numerous and the contours are determined by
the level of the SFR. Our morphological classification is consistent
with this picture: ETGs, characterized by a lower SFR and high stellar
masses, are located in the bottom-right part of the plot, where the
expected number of LMXBs is higher than the number of HMXBs. However,
we note that there are suggestions in the literature that no ULX LMXBs
may actually exist. Irwin et al. (2004) have shown that the number of
ULXs detected in a sample of 28 ellipticals observed with Chandra is
equal to the number of expected foreground/background
objects. Additionally, these ULXs are uniformly distributed and do not
follow the optical light of the galaxies. Irwin et al. (2004) also
verified that the same statements can be made for the ULXs associated
to early-type galaxies presented in Colbert & Ptak (2002).
values, from a region (above the line)
where the HMXBs are more numerous and the contours are determined by
the level of the SFR. Our morphological classification is consistent
with this picture: ETGs, characterized by a lower SFR and high stellar
masses, are located in the bottom-right part of the plot, where the
expected number of LMXBs is higher than the number of HMXBs. However,
we note that there are suggestions in the literature that no ULX LMXBs
may actually exist. Irwin et al. (2004) have shown that the number of
ULXs detected in a sample of 28 ellipticals observed with Chandra is
equal to the number of expected foreground/background
objects. Additionally, these ULXs are uniformly distributed and do not
follow the optical light of the galaxies. Irwin et al. (2004) also
verified that the same statements can be made for the ULXs associated
to early-type galaxies presented in Colbert & Ptak (2002).
It would be interesting to repeat the same computation that generated
Fig. 7 considering only X-ray binaries with
![]() erg s-1, and therefore to be able to verify the
hypothesis that ULXs are the high-luminosity tail of normal X-ray
binaries. Unfortunately, this is not possible due to the poor
knowledge of the high luminosity slope of the XLF for LMXBs and HMXBs.
erg s-1, and therefore to be able to verify the
hypothesis that ULXs are the high-luminosity tail of normal X-ray
binaries. Unfortunately, this is not possible due to the poor
knowledge of the high luminosity slope of the XLF for LMXBs and HMXBs.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12544fg8.ps} \vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg93.png)
|
Figure 8:
Top panel: the
number of galaxies for which we could detect an off-nuclear source
of a given 0.5-2 keV luminosity
|
| Open with DEXTER | |
4 Fraction of galaxies hosting a ULX
As already pointed out by Ptak & Colbert (2004), useful constraints on the
nature of ULXs can be obtained deriving the fraction of galaxies that
harbor a ULX as a function of the X-ray luminosity. For example,
Körding et al. (2002) have compared the luminosity distribution of X-ray
point sources in nearby galaxies with that predicted by X-ray
population synthesis models to check whether microblazars
(microquasars with relativistically beamed jets pointing towards the
observer) may represent an alternative to the intermediate mass black
holes scenario for ULXs. In order to compute this fraction, we used
the comparison sample selected in Sect. 3.2. We derived for
each individual galaxy a 90% upper limit on its X-ray flux in the
[0.5-2] keV band according to the procedure described in Sect. 6.5 of
Puccetti et al. (2009), to which we refer the reader for details. The top
panel of Fig. 8 shows the number of galaxies for which
we could detect an off-nuclear source of 0.5-2 keV luminosity
![]() or larger. The bottom panel of the same figure shows
the observed number of galaxies in each
or larger. The bottom panel of the same figure shows
the observed number of galaxies in each
![]() bin hosting an
ULX of a luminosity
bin hosting an
ULX of a luminosity
![]() or larger. In order to derive the
observed fraction of galaxies with an off-nuclear source, we divided
the values of the histogram in the bottom panel by those in the top
panel of Fig. 8. The result is shown in
Fig. 9. The red points are the result of our analysis,
and the dashed area is the 1
or larger. In order to derive the
observed fraction of galaxies with an off-nuclear source, we divided
the values of the histogram in the bottom panel by those in the top
panel of Fig. 8. The result is shown in
Fig. 9. The red points are the result of our analysis,
and the dashed area is the 1![]() confidence region computed with
the prescriptions for small numbers statistic by
Gehrels (1986). For comparison, we report in the same figure also
the fractions obtained by Lehmer et al. (2006) from the Chandra Deep
Fields (dashed line and 1
confidence region computed with
the prescriptions for small numbers statistic by
Gehrels (1986). For comparison, we report in the same figure also
the fractions obtained by Lehmer et al. (2006) from the Chandra Deep
Fields (dashed line and 1![]() confidence region). These fractions
should be considered as lower limits due to the limited Chandra
spatial resolution that does not allow the detection of off-nuclear
sources with small offsets (see Fig. 10 of Lehmer et al. 2006). The
agreement between our results and the CDFs points is reasonably good
above log(
confidence region). These fractions
should be considered as lower limits due to the limited Chandra
spatial resolution that does not allow the detection of off-nuclear
sources with small offsets (see Fig. 10 of Lehmer et al. 2006). The
agreement between our results and the CDFs points is reasonably good
above log(
![]() ,
although our point and the associated
confidence contours are about a factor of two lower than, but
consistent with, those derived by Lehmer et al. (2006). In the lower
luminosity bins, it seems that the two measures are discrepant;
however, we do not consider this difference highly significant, since
the measured fractions are consistent at the 2
,
although our point and the associated
confidence contours are about a factor of two lower than, but
consistent with, those derived by Lehmer et al. (2006). In the lower
luminosity bins, it seems that the two measures are discrepant;
however, we do not consider this difference highly significant, since
the measured fractions are consistent at the 2![]() level. Also, at
the faintest fluxes the differences between the two X-ray catalogs
used is more severe. For these faint sources the positional
uncertainties affecting our sample are larger than for the same
sources detected in the longer Chandra exposures of the CDFs, and
therefore we may be missing the faintest ULXs in the sample if their
error box is consistent with the position of the nucleus. We also note
that our selection criteria for off-nuclear sources reported in
Sect. 2 are more conservative than those used by
Lehmer et al. (2006). From Fig. 9 we found that
level. Also, at
the faintest fluxes the differences between the two X-ray catalogs
used is more severe. For these faint sources the positional
uncertainties affecting our sample are larger than for the same
sources detected in the longer Chandra exposures of the CDFs, and
therefore we may be missing the faintest ULXs in the sample if their
error box is consistent with the position of the nucleus. We also note
that our selection criteria for off-nuclear sources reported in
Sect. 2 are more conservative than those used by
Lehmer et al. (2006). From Fig. 9 we found that ![]() 0.5% and
0.5% and ![]() 0.2% of the galaxies are hosting a ULX with
0.2% of the galaxies are hosting a ULX with
![]() and
and
![]() erg s-1, respectively.
erg s-1, respectively.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{frac_off.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg97.png)
|
Figure 9:
Observed fraction of galaxies with an off-nuclear source with a luminosty of
|
| Open with DEXTER | |
We now discuss the observed trend of the fraction of ULX as a function
of their X-ray luminosities in the frame of the beaming model of
King (2009). According to this model, ULX are stellar mass black
holes accreting at a super-Eddington rate (
![]() ,
for a typical radiative efficiency
,
for a typical radiative efficiency
![]() and accretion rate
and accretion rate ![]() ). Matter accreting at these rates is
easily blown away close to the inner edge of the accretion disk
(Shakura & Sunyaev 1973); then, the radiative output from the resulting
flow pattern is on the order of
). Matter accreting at these rates is
easily blown away close to the inner edge of the accretion disk
(Shakura & Sunyaev 1973); then, the radiative output from the resulting
flow pattern is on the order of
![]() ,
but emerges collimated by the central funnel with a
beaming
,
but emerges collimated by the central funnel with a
beaming![]() factor
factor
![]() ,
so that an external observer who happens to have its line of
sight within the beaming cone would infer a spherical luminosity:
,
so that an external observer who happens to have its line of
sight within the beaming cone would infer a spherical luminosity:
![]() erg/s (where m7 is
the black hole mass in units of 7 solar masses; see King 2009
for further details). Thus, neglecting the weak logarithmic dependence
on
erg/s (where m7 is
the black hole mass in units of 7 solar masses; see King 2009
for further details). Thus, neglecting the weak logarithmic dependence
on ![]() ,
this model directly links the observed luminosity of a
ULX with its beaming factor b.
,
this model directly links the observed luminosity of a
ULX with its beaming factor b.
Let us now consider a population of ULX with a host galaxy space density
(as a function of distance d):
![]() Mpc-3. The results of
Lehmer et al. (2006) imply an almost linear decline of the cumulative
number of ULX per galaxy with observed luminosity,
Mpc-3. The results of
Lehmer et al. (2006) imply an almost linear decline of the cumulative
number of ULX per galaxy with observed luminosity,
![]() ,
where
,
where
![]() is the observed
fraction of galaxies hosting a ULX with
is the observed
fraction of galaxies hosting a ULX with
![]() .
The
differential fraction
.
The
differential fraction
![]() ,
i.e. the fraction of galaxies
containing a ULX with luminosity
,
i.e. the fraction of galaxies
containing a ULX with luminosity
![]() per unit logarithmic
interval of luminosity can be derived by simply differentiating the
above expression, to obtain
per unit logarithmic
interval of luminosity can be derived by simply differentiating the
above expression, to obtain
![]() ,
where the
last approximate equality was derived neglecting the logarithmic
dependence of
,
where the
last approximate equality was derived neglecting the logarithmic
dependence of
![]() on b.
on b.
We now consider the application of this model to a multi-wavelength
survey like COSMOS. We define the limiting flux of the survey in the
X-ray band as
![]() erg s-1cm-2, so that an object of beaming factor b can be seen out to
a distance of
erg s-1cm-2, so that an object of beaming factor b can be seen out to
a distance of
![]() Mpc, and express, in full
generality, the number density of galaxies as a function of distance
as
Mpc, and express, in full
generality, the number density of galaxies as a function of distance
as
![]() ,
where
,
where
![]() is the number density of possible host galaxies in the survey at the
maximum distance where an un-beamed source (b=1) can be seen. This
expression is a very general form appropriate for power-law luminosity
functions in Euclidean Universes and is adopted here for the sake of
simplicity
is the number density of possible host galaxies in the survey at the
maximum distance where an un-beamed source (b=1) can be seen. This
expression is a very general form appropriate for power-law luminosity
functions in Euclidean Universes and is adopted here for the sake of
simplicity![]() ; the exponent
; the exponent ![]() depends
both on the galaxy luminosity function slope and on the survey
selection function and can in principle be derived empirically for any
given survey: typically we have for flux-limited
depends
both on the galaxy luminosity function slope and on the survey
selection function and can in principle be derived empirically for any
given survey: typically we have for flux-limited ![]() ,
while
volume limited ones have
,
while
volume limited ones have
![]() .
Given the observed
cumulative fraction
.
Given the observed
cumulative fraction
![]()
![]() ,
and the corresponding differential
,
and the corresponding differential
![]() ,
one has
to search through a space volume
,
one has
to search through a space volume
![]() to find a
ULX with beaming factor b (within a unit logarithmic interval of b). From this expression for the volume we derive
to find a
ULX with beaming factor b (within a unit logarithmic interval of b). From this expression for the volume we derive
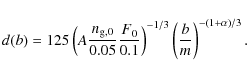
|
(4) |
Thus, the minimum beaming factor (corresponding to the maximal luminosity) of a ULX in a survey of an area A (in units of square degrees) is given by
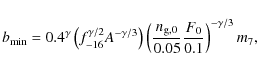
|
(5) |
where
5 Conclusions
We presented a sample of ultraluminous X-ray sources (ULXs) selected from the Chandra survey in the COSMOS area (C-COSMOS). From 1761 X-ray sources detected with a maximum likelihood threshold of detml = 10.8 in at least one detection band, we selected 7 ULX candidates covering the redshift range z=0.072-0.283.
Taking advantage of the excellent ancillary data available in the COSMOS field, we studied the properties of their host galaxies. From a detailed morphological analysis of the ACS images and rest-frame colors, we found that ULXs are hosted both in late and in early type galaxies, with a slight preference for the former.
From the multi-band photometry and from the optical spectral lines, we
measured stellar masses and star formation rates for the host
galaxies. Using literature X-ray luminosity functions for HMXBs and
LMXBs, we defined probability areas for having detectable off-nuclear
sources in the plane SFR versus ![]() .
All our ULXs candidates are
hosted in galaxies for which we expect a large number of X-ray
binaries with
.
All our ULXs candidates are
hosted in galaxies for which we expect a large number of X-ray
binaries with
![]() erg s-1.
erg s-1.
Table 2: Properties of the host galaxies of ULXs in C-COSMOS.
The presence of IMBHs (
![]() )
in some of our ULXs
cannot be excluded with the current data. The best candidates for this
new class of accreting black holes are the ULXs hosted in early type
galaxies (therefore not associated with recent star formation
activity) and with X-ray luminosity above 1041 erg s-1 that
can be difficult to explain with high-mass stellar black holes. The
objects that satisfy these criteria from our sample are XID = 2418
and 11938. Longer X-ray exposures could give us more insights into the
real nature of these sources from a detailed study of the X-ray
spectrum. Similarly, we cannot set constraints on the recoiling
black-hole nature of our sources with the current data, but it is
worth mentioning that recent predictions by Volonteri & Madau (2008) expect
at most one of these objects in the C-COSMOS survey, assuming the most
favorable scenario (spinning black holes, no bulge in the host galaxy,
long active phase).
)
in some of our ULXs
cannot be excluded with the current data. The best candidates for this
new class of accreting black holes are the ULXs hosted in early type
galaxies (therefore not associated with recent star formation
activity) and with X-ray luminosity above 1041 erg s-1 that
can be difficult to explain with high-mass stellar black holes. The
objects that satisfy these criteria from our sample are XID = 2418
and 11938. Longer X-ray exposures could give us more insights into the
real nature of these sources from a detailed study of the X-ray
spectrum. Similarly, we cannot set constraints on the recoiling
black-hole nature of our sources with the current data, but it is
worth mentioning that recent predictions by Volonteri & Madau (2008) expect
at most one of these objects in the C-COSMOS survey, assuming the most
favorable scenario (spinning black holes, no bulge in the host galaxy,
long active phase).
Finally, we derived the fraction of galaxies hosting a ULX as a
function of the X-ray luminosity. We found that ![]() 0.5% and
0.5% and
![]() 0.2% of the galaxies are hosting a ULX with
0.2% of the galaxies are hosting a ULX with
![]() and
and
![]() erg s-1. This agrees reasonably well with the
observed fraction derived in the Chandra Deep Fields by
Lehmer et al. (2006) above log(
erg s-1. This agrees reasonably well with the
observed fraction derived in the Chandra Deep Fields by
Lehmer et al. (2006) above log(
![]() erg s-1. A possible
discrepancy in the lower luminosity bins can be likely attributed to
the differences in the limiting fluxes of the two catalogs and,
therefore, to the different positional uncertainties affecting faint
X-ray sources.
erg s-1. A possible
discrepancy in the lower luminosity bins can be likely attributed to
the differences in the limiting fluxes of the two catalogs and,
therefore, to the different positional uncertainties affecting faint
X-ray sources.
This work is based on observations made with ESO Telescopes at the La Silla or Paranal Observatories under programme ID 175.A-0839. We are grateful to the referee for detailed and extremely useful comments that improved the quality of the paper. We thank Piero Rosati and Bret Lehmer for useful scientific discussions. We are grateful to Bret Lehmer for providing the data points of the CDFs used in Fig. 9. This work has been supported in part by the grants: ASI/COFIS/WP3110 I/026/07/0, ASI/INAF I/023/05/0, ASI I/088/06/0, PRIN/MIUR 2006-02-5203.
References
- Begelman, M. C. 2002, ApJ, 568, 97 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Kovac, K., Pozzetti, L., et al. 2009, A&A, submitted [arXiv:0907.0013] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Colbert, E. J. M., & Mushotzky, R. F. 1999, ApJ, 519, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Colbert, E. J. M., & Ptak, A. F. 2002, ApJS, 143, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Damiani, F. Maggio, A., Micela, G., & Sciortino, S. 1997, ApJ, 483, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Civano, F., Vignali, C., et al. 2009, ApJS, 184, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbiano, G. 1989, ARA&A, 27, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gilfanov, M. 2004, MNRAS, 349, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Grimm, H.-J., Gilfanov, M., & Sunyaev, R. 2003, MNRAS, 339, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Hopman, C., Portegies Zwart, S. F., & Alexander, T. 2004, ApJ, 604, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Humphrey, P. J., & Buote, D. A. 2008, ApJ, 689, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O. Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J. A. Bregman, J. N., & Athey, A. E. 2004, ApJ, 601, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. Jr. 1998, ARA&A, 36,189 [Google Scholar]
- Kim, D.-W., & Fabbiano, G. 2004, ApJ, 611, 846 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R. 2002, MNRAS, 335, L13 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., 2009, MNRAS, 393, L41 [NASA ADS] [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Körding, E., Falke, H., & Markoff, S. 2002, A&A, 382, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehmer, B. D., Brandt, W. N., Hornschemeier, A. E., et al. 2006, AJ, 131, 2394 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Liu, Q. Z., & Mirabel, I. F. 2005, A&A, 429, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Makishima, K., Kubota, A., Mizuno, T., et al. 2000, ApJ, 535, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, C. Lilly, S. J., Carollo, C. M., Stockton, A., & Brodwin, M. 2005, ApJ, 634, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Mignoli, M. Zamorani, G., Scodeggio, M., et al. 2009, A&A, 493, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, M. C., & Colbert, E.J. M. 2004, Int. J. Mod. Phys., D13, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, R. C. Jr., & Tremonti, C. 2006, ApJ, 642, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Ptak, A., & Colbert, E. 2004, ApJ, 606, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V. 1976, ApJ, 209, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Puccetti, S. Vignali, C., Cappelluti, N., et al. 2009, ApJS, 185, 586 [NASA ADS] [CrossRef] [Google Scholar]
- O'Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, T. P., Warwick, R. S., Ward, M. J., & Goad, M. R. 2004, MNRAS, 349, 1193 [CrossRef] [Google Scholar]
- Shakura N., & Sunyaev, R., 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Salvato, M., Hasinger, G., Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Scarlata, C., Carollo, C. M., Lilly, S., et al. 2007, ApJS, 172, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1979, MNRAS, 187, 76P [Google Scholar]
- Swartz, D. A., Ghosh, K. K., Tennant, A. F., & Wu, K. 2004, ApJS, 154, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., & Madau, P., 2008, ApJ, 687, L57 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...(J2000)
![[*]](/icons/foot_motif.png)
- X-ray coordinates of the ULX.
- ... prep.)
![[*]](/icons/foot_motif.png)
- The ULX candidates presented in this paper are flagged as ``off-nuclear'' sources in Civano et al. (2010, in prep.).
- ... MARX
![[*]](/icons/foot_motif.png)
- http://space.mit.edu/CXC/MARX.
- ...
![[*]](/icons/foot_motif.png)
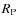 is
defined as the radius at which the ratio (
is
defined as the radius at which the ratio (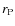 )
of the local surface brightness at that radius and the mean surface
brightness within that radius equals some specified value
)
of the local surface brightness at that radius and the mean surface
brightness within that radius equals some specified value 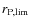 .
For a surface brightness distribution described by a de Vaucouleurs or
an exponential profile, a value
.
For a surface brightness distribution described by a de Vaucouleurs or
an exponential profile, a value 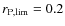 is reached at
is reached at 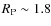
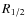 and
and 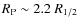 ,
respectively (
,
respectively (
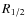 is the half-light radius of the galaxy, see Fig. 17 of Scarlata et al. 2007).
is the half-light radius of the galaxy, see Fig. 17 of Scarlata et al. 2007).
- ... EMLdetect
![[*]](/icons/foot_motif.png)
- http://xmm.esac.esa.int/sas/8.0.0/emldetect
- ...
beaming
![[*]](/icons/foot_motif.png)
- Note that here ``beaming'' simply means geometrical collimation, and not relativistic beaming.
- ...
simplicity
![[*]](/icons/foot_motif.png)
- Although we applied a k-correction to the luminosity values in Eq. (1), we resolved to make the calculations in this paragraph under the assumption of a Euclidean Universe to simplify the derivation of Eq. (5).
- ...
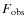
![[*]](/icons/foot_motif.png)
- We assume in this calculation that the fraction of galaxies hosting a ULX does not change as a function of distance. This is an approximation, because the star formation rate varies with redshift, and therefore it is plausible that the fraction of galaxies hosting a ULX varies too.
All Tables
Table 1: Properties of ULXs in C-COSMOS.
Table 2: Properties of the host galaxies of ULXs in C-COSMOS.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12544fg1.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg20.png)
|
Figure 1: Distribution of the difference between the detected X-ray positions and the input positions in units of the X-ray positional error. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12544fg2.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg25.png)
|
Figure 2:
X-ray to optical offsets in arcsec for X-ray sources with a secure
identification (Civano et al. 2010, in prep.) and with an X-ray
positional error smaller than 0.8
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12544fg3.eps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg36.png)
|
Figure 3:
Cutouts in the HST/ACS F814W band (Koekemoer et al. 2007)
of the seven X-ray off-nuclear sources in the C-COSMOS field. The red
cross indicates the position of the X-ray centroid and the red circle
the X-ray positional error (Elvis et al. 2009). We provide for each object the Chandra ID ( top-left), the redshift ( top-right), the logarithm of the X-ray luminosity in the [0.5-7] keV band ( bottom-left), the maximum likelihood ratio for the X-ray detection ( bottom-right), the morphological classification of the host galaxy (bottom-middle; see Sect. 3.1). The images have different sizes for display purposes; the vertical bar in each cutout corresponds to 2
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{12544fg4.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg45.png)
|
Figure 4:
Aperture photometry for each off-nuclear candidate. The vertical
dot-dashed line indicates the distance between the X-ray position and
the centroid of the host galaxy; the vertical dashed line is the
Petrosian radius of the host galaxy; the horizontal line corresponds to
the counts estimated by EMLdetect (Puccetti et al. 2009).
For objects XID = 1151, 1388, and 1870, the filled circles represent
the photometry on an area including 90% of the PSF obtained applying an
aperture correction factor to the photometry measured on an aperture of
1
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{12544fg5.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg52.png)
|
Figure 5: X-ray luminosity in the
0.5-7 keV band vs. redshift of the seven off-nuclear sources. The
different symbols correspond to the host galaxy classification based on
morphology and rest-frame colors: circles are ETGs, while stars are
LTGs (see Sect. 3.1). Squares are the off-nuclear sources from Lehmer et al. (2006); crosses are the collection of local off-nuclear sources by Liu & Mirabel (2005). The dashed line corresponds to the flux limit in the deepest region of the C-COSMOS survey: S
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12544fg6.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg58.png)
|
Figure 6:
Color-mass diagram: circles and stars are respectively
ULX host galaxies classified as ETGs and LTGs based on their
morphology/colors; the dots are galaxies in the C-COSMOS area
with z<0.3 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12544fg7.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg89.png)
|
Figure 7:
SFR versus stellar masses of the galaxies in the comparison sample (see
text). The contours correspond to the region where more than 0.1 (red),
1 (green), 5 (cyan), and 10 (yellow) X-ray off-nuclear sources per
galaxy are expected. The symbols show the location in this plane of the
host galaxies of the ULXs. For the source XID = 1151 the
photometric coverage is limited to few bands and we cannot constrain
its stellar mass. The symbols are the same as in Fig. 5. The dashed line is where we expect the same number of LMXBs and HMXBs with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12544fg8.ps} \vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg93.png)
|
Figure 8:
Top panel: the
number of galaxies for which we could detect an off-nuclear source
of a given 0.5-2 keV luminosity
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{frac_off.ps}
\end{figure}](/articles/aa/full_html/2010/06/aa12544-09/Timg97.png)
|
Figure 9:
Observed fraction of galaxies with an off-nuclear source with a luminosty of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.