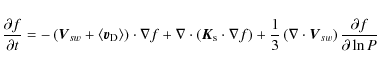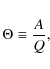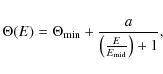EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) A24 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number A24
Number of page(s) 6
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/200913866
Published online 16 April 2010
A&A 513, A24 (2010)

The heliospheric transport and modulation of multiple charged anomalous oxygen revisited

R. D. Strauss - M. S. Potgieter - S. E. S. Ferreira

Unit for Space Physics, North-West University, 2520, Potchefstroom, South Africa

Received 14 December 2009 / Accepted 1 February 2010

Abstract
Context. Since the crossings of the solar wind termination shock by the Voyager 1 and 2 spacecraft, much speculation has surrounded the acceleration mechanism and region where the anomalous cosmic ray component is accelerated. A peculiar, and mostly overlooked feature of the observed anomalous oxygen spectrum near the termination shock, is the power law form of the roll-over (cut-off) at the high energy range of this spectrum.
Aims. We investigate, using a numerical model, why this deviation from the expected exponential form of the cut-off part of the anomalous oxygen spectrum occurs, and if the observed power law form can be explained in terms of the acceleration of multiple charged anomalous oxygen.
Methods. Multiple charged anomalous cosmic rays are incorporated in a numerical model, based on the standard Parker transport equation, including acceleration at the solar wind termination shock. This is done by specifying an energy dependent charge state, constrained by observations.
Results. Comparing computational results with spacecraft observations, it is found that the inclusion of multiply charged anomalous cosmic rays in the modulation model can explain the observed spectrum of anomalous oxygen in the energy range from 10-70 MeV per nucleon. The more effective acceleration of these multiple charge anomalous particles at the solar wind termination shock causes a significant deviation from the usual exponential cut-off spectrum to display instead a power law decrease up to 70 MeV per nucleon where galactic oxygen starts to dominate. In addition, the model reproduces the features of multiple charged oxygen at Earth so that a good comparison is obtained between computations and observations.

Key words: Sun: heliosphere - cosmic rays - acceleration of particles

1 Introduction

Anomalous cosmic ray (ACR) spectra are expected to decrease exponentially above the energy where the acceleration of these particles is getting ineffective. This feature of observed and modelled ACR spectra is usually referred to as the roll-over or cut-off spectrum, the latter indicative of the fact that the acceleration process is progressively becoming less effective with further increases in energy (e.g. Jokipii 1986; Potgieter & Moraal 1988). However, Webber et al. (2007), who studied the temporal and spectral variations of ACR oxygen (O*) nuclei at the Voyager 1 (V1) and 2 (V2) spacecraft in the outer heliosphere from 1990 to 2006, reported that the observed O* spectra exhibited, for both V1 and V2, a clear power-law decrease with intensity $j \sim E^{-3.0\pm 0.2}$ at energies of 10 to 70 MeV nuc-1. This is evidently in the roll-over range (see their Fig. 9). To emphasize this feature of the observations, Fig. 1 shows the observed O* spectra from V1 during its TS crossing and from V2 at about 4 AU from its TS crossing as reported by Webber et al. (2007). For comparison a $j \sim E^{-3}$ decrease is also shown in the figure, clearly illustrating that both spectra decrease in this form. Note that above 50 MeV nuc-1, the O* spectra contain a significant contribution from galactic origin, which is not investigated further in this study as the level of galactic oxygen at these energies is too low.

The spectra below 8 MeV nuc-1 are not shown in Fig. 1, neither investigated in this study because their peculiar behaviour remains a very controversial subject. This seemingly modulated portion of the ACR spectra has already been addressed previously by various authors, offering a wide range of explanations (and speculations). These include adiabatic heating (Langner et al. 2006; Ferreira et al. 2007), second order Fermi acceleration (e.g. Zhang 2006; Ferreira et al. 2007), transient events (e.g. Florinski & Zank 2006), preferred acceleration at the flanks (e.g. McComas & Schwadron 2006) and at the equatorial regions of the heliosphere (e.g. Langner & Potgieter 2006; Ngobeni & Potgieter 2008), energy cascade processes (e.g. Fisk & Gloeckler 2009) and magnetic reconnection occurring near the heliopause (e.g. Lazarian & Opher 2009). The applicability and validity of these processes have remained a topic of further investigation. See also the reviews by Potgieter (2008), Lee et al. (2009) and Florinski et al. (2009).

It is generally accepted that the seed population of ACRs is pick-up ions (PUIs) (Fisk et al. 1974), formed by the ionization of interstellar neutrals, and then getting accelerated to higher energies in the outer heliosphere (Pesses et al. 1981). Because of the singly ionized seed population it is thus expected that ACRs must also be singly ionized. Earlier observations by Biswas et al. (1988), Adams et al. (1991) and Klecker et al. (1995) confirmed that low energy ACRs are indeed mostly singly ionized. Later measurements by Mewaldt et al. (1996b,a) indicated that ACR neon, nitrogen and oxygen contain a large fraction of higher charge states at energies E > 10 MeV nuc-1, and that the fraction of singly ACRs decreases as a function of kinetic energy, as shown in Fig. 2. For O*, the $50\%$ level for singly ionized nuclei (Q=1) occurs at $E \sim 22$ MeV nuc-1, with the higher energy values being dominated by higher charge states.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{13866f0.eps} \end{figure} Figure 1:

Observed O* energy spectra from V1 during its TS crossing (filled circles) and from V2 at 4 AU away from its TS crossing (open circles). For comparison, a  $j \propto E^{-3}$spectral decrease is shown, being the topic of investigation in this study. The observations are adapted from Webber et al. (2007).

Open with DEXTER

These higher charge states can be explained in terms of electron stripping occurring at the TS because of the finite acceleration time of ACRs. Discussed by Jokipii (1996), this is essentially a charge exchange process whereby ACRs lose additional electrons by interacting with solar wind protons. The possibility of charge exchange occurring in other regions of the heliosphere (Chalov et al. 2007) are not investigated here. The importance of these higher charge states lies in the fact that the energy gain $\Delta E$ per TS crossing of ACRs is proportional to their charge Q=Ze,

\begin{displaymath}% \Delta E \approx Ze \Delta \phi, \end{displaymath} (1)

where $\Delta \phi$ is the potential gained when drifting across the shock front (Jokipii 1990). The higher charge states are thus expected to be accelerated more effectively to higher energies at the TS. This aspect, as well as the effect of these higher charge states on computed O* intensities, will be shown in subsequent sections. It will also be shown that the inclusion of an energy dependent ionic states is able to reproduce the observed $j \sim E^{-3}$ power law decrease in O* intensities as reported by Webber et al. (2007).

2 The modulation model

The omni-directional ACR distribution function $f(r,\theta,P,t)$ is obtained numerically by solving the time dependent Parker transport equation (Parker 1965)

\begin{displaymath}% \frac{\partial f}{\partial t}=-\left(\vec{V}_{sw} +\langle ... ...a \cdot \vec{V}_{sw} \right) \frac{\partial f}{\partial \ln P} \end{displaymath} (2)

in terms of radial distance r, co-latitude (polar angle) $\theta$, particle rigidity P and time t. The differential intensity j is related to f by j=P2f.

\begin{figure} \par\includegraphics[width=8cm,clip]{13866f1.eps} \end{figure} Figure 2:

The observed fraction of singly ionized ACR oxygen, neon and nitrogen as a function of kinetic energy. The data set is adapted from Mewaldt (2006). Because this fraction decreases with energy, ACRs are dominated by higher charge states (Q > 1) at higher energies, E > 10 MeV nuc-1.

Open with DEXTER

The PUIs, as source of ACRs, are introduced by specifying the source function as

\begin{displaymath}% S(r,P)=S^* \delta(P-P_{\rm PUI}) \delta(r-r_{\rm TS}). \end{displaymath} (3)

It is assumed that $r_{\rm TS}=90$ AU is the position of the solar wind termination shock (TS) with a compression ratio of s=2 and $P_{\rm PUI}=0.05$ GV. The TS is assumed to be a semi-discontinuous transition, with a shock precursor of 1.2 AU (le Roux et al. 1996). The results are however relatively insensitive to this structure, as the effective radial mean free path of O* is quite large at higher energies. The solutions are also insensitive to the choice of  $P_{\rm PUI}$, as long as this is lower than the ACR cut-off energy. The value of s is in accordance with recent V2 observations (Richardson et al. 2008). Subsequent acceleration is by means of Fermi I (diffusive shock) acceleration. Because S* is of arbitrary magnitude, the modelled ACR intensities must be scaled to observed levels (see also Jokipii 1996), because no absolute measurement of the PUI source function is available. The spatial diffusion tensor  $\vec{K}_{\rm s}$ is according to Burger et al. (2000), changing across the TS according to the results of Zank et al. (1996). The average guiding center drift velocity, including curvature, gradient and neutral sheet drifts, $\langle \vec{v}_{\rm D} \rangle$ is related to the asymmetrical drift tensor  $\vec{K}_{\rm A}$ by $\langle \vec{v}_{\rm D} \rangle = \nabla$ $\times$ $\vec{K}_{\rm A}\vec{e}_B$ with $\vec{e}_B=\vec{B}/B$, where $\vec{B}$ is the Parker spiral magnetic field (Parker 1958). The magnitude of this field is modified in the polar regions of the heliosphere following the approach of Jokipii & Kóta (1989). The drift tensor  $\vec{K}_{\rm A}$ used here is described by Burger et al. (2000). However, drifts are assumed to be only 55% effective according to the work of Potgieter (1989), Langner et al. (2004) and Minnie et al. (2007). For the bulk solar wind flow it is assumed that $\vec{V}_{sw}(r,\theta)=V_{sw}(r,\theta)\vec{e}_r$, with incompressible flow ( $V_{sw} \propto r^{-2}$) in the heliosheath, thus leading to no adiabatic energy losses/gains in this region. The model is restricted to solar minimum conditions with an assumed heliospheric current sheet (HCS) tilt angle of 100, with corresponding HCS drifts. Furthermore, modelling results are later shown for both the qA > 0 (1992-2003) and the qA < 0 (2003 - present) magnetic polarity cycles. The heliopause is assumed to be located at $r_{\rm HP}=120$ AU. For specific details of the numerical modulation model, see Langner et al. (2003).

Useful in modulation studies, the specie value of the ACR population under consideration is defined as

\begin{displaymath}% \Theta \equiv \frac{A}{Q}, \end{displaymath} (4)

where A is the atomic mass and Q is the charge of the particles. With A=16, singly ionized O* thus has a specie value of $\Theta_{\rm max}=16$. When O* is ``contaminated'' by higher charge states (Q>1), the average specie value of the ACR population will decrease accordingly. To incorporate the effect of multiple charged ACRs into the modulation model, the nett specie value (and therefore the nett charge) of the ACR distribution function, which appears in e.g. the drift velocity and diffusion tensor, is scaled as a function of kinetic energy by using the transition

\begin{displaymath}% \Theta (E) =\Theta_{{\rm min}} + \frac{a}{\left( \frac{E}{E_{{\rm mid}}}\right) + 1}, \end{displaymath} (5)

where $E_{{\rm mid}}$ is the energy about which the transition is centered, $\Theta_{{\rm max}} \equiv (\Theta_{{\rm min}} + a)$ is the maximum and  $\Theta _{\rm min}$ is the minimum specie values. Using the observations of Mewaldt et al. (1996b) and Mewaldt et al. (2006) as a guide, the transition function given by Eq. (5) can be constrained. Using the data shown in Fig. 2 gives $E_{\rm mid}=0.022$ GeV nuc-1 for O*. Mewaldt et al. (1996b) reported measuring O* charge states of Q=1,2,3 and also Q=8 (which is believed to be of galactic origin and thus not considered in this study). Using these values, the following transitions are used in this study: $\Theta _{\rm max}=\Theta _{\rm min}=16$, $\Theta_{\rm max}=16\rightarrow \Theta_{\rm min}=8$, $\Theta_{\rm max}=16\rightarrow \Theta_{\rm min}=16/3$ and $\Theta_{\rm max}=16\rightarrow \Theta_{\rm min}=4$ added an extreme case. These four transitions are shown in Fig. 3 as a function of kinetic energy, with the data points indicating the energies where the specie value is sampled in the numerical modulation model. Also note that the $\Theta _{\rm max}=\Theta _{\rm min}=16$ transition, corresponding to a purely singly ionized O* population, will act as a reference solution.

\begin{figure} \par\includegraphics[width=8cm,clip]{13866f2.eps} \end{figure} Figure 3:

The nett charge of the O* distribution function is scaled as a function of kinetic energy using the transition given by Eq. (5). This figure shows the transitions for four different choices of  $\Theta _{\rm min}$, as a function of kinetic energy. The data points indicate the energies at which the specie value is sampled in the numerical model.

Open with DEXTER

3 Modelling results and discussion

Computed energy O* spectra, with the inclusion of multiple charged ACRs, using the energy dependent transition of $\Theta (E)$, are shown in Fig. 4 for the qA > 0 magnetic polarity cycle. Spectra are shown at the TS and at Earth, in the equatorial plane ( $\theta=90^\circ$). The four solutions shown correspond to the different specie transitions discussed previously. The reference solutions (solid lines) illustrate the general characteristics of these acceleration models, which are briefly discussed next: below ${\sim}10$ MeV nuc-1, the TS spectra are dominated by the well known power law form caused by Fermi I acceleration. This spectral index is largely dependent on the TS compression ratio. With increasing energy, intensities eventually start to fall away almost exponentially. The energy at which this deviation in the power law spectrum occurs is referred to as the cut-off or roll-over energy determined by, amongst others, the curvature of the shock front (Steenberg & Moraal 1999; Langner & Potgieter 2007). The spectra at Earth illustrate the corresponding modulated roll-over intensities; below ${\sim}10$ MeV nuc-1 these spectra are dominated by adiabatic cooling giving rise to the well-known $j \propto E$ spectral shapes.

The effect of including additionally charged ACR can readily be seen in Fig. 4. The TS spectra (for all transition of $\Theta (E)$) show a large effect with the roll-over occurring at higher energies the higher the charge state is made. Consequently, the O* intensities in the roll-over energy range are higher for multiple charged ACR at a given energy, leading to a factor ${\sim}100$ difference in intensities at ${\sim}50$ MeV nuc-1 between the reference and $\Theta_{\rm max}=16\rightarrow \Theta_{\rm min}=4$ transitions (dottted line). Below the cut-off energy, the TS spectra remain completely unchanged.

The spectra at Earth exhibit similar behaviour at higher energies, with the intensities being higher in this energy regime for higher charge states. In the adiabatic energy region the intensities are also higher with the inclusion of higher charge states, with a factor ${\sim}2$ difference between results from the different specie transitions.

Figure 5 is similar to Fig. 4 except that the results are shown for the qA < 0 magnetic polarity cycle. The effect of incorporating multiple charged ACRs are qualitatively similar to the results of the qA > 0 polarity cycle, although the effect thereof in this cycle is much more pronounced. Also evident is a clear intensity enhancement (flattening of the power law part of the spectra) of the TS spectra at ${\sim}10$ MeV nuc-1 just above the roll-over energy. This is believed to be caused by drifts for this particular magnetic cycle. See also le Roux et al. (1996), Jokipii & Kóta (1997) and Florinski & Jokipii (2003) for a discussion regarding this interesting phenomenon.

\begin{figure} \par\includegraphics[width=8cm,clip]{13866f3.eps} \end{figure} Figure 4:

The computed O* energy spectra are shown at the TS (top set of curves) and at Earth (bottom set of curves) for the qA > 0 magnetic polarity cycle. Four different spectra are shown, corresponding to the computed solutions for the different transitions of  $\Theta (E)$ used in this study. The $\Theta _{\rm max}=\Theta _{\rm min}=16$ solutions (solid lines) serve as reference solutions for comparison purposes.

Open with DEXTER

A comparison between computed and observed O* spectra at Earth is made in the left panel of Fig. 6. The observational data, measured by the SAMPEX spacecraft during the qA > 0 magnetic polarity cycle from 1993-1995, show both singly ionized (Q=1) and the total (Q=1+Q>1) O* spectra, adapted from Mewaldt (2006). The data set does not represent solar minimum conditions, making quantitative comparison with modelled solutions difficult so that qualitative agreement will have to suffice. The deduction can be made that the lower data points were observed in 1993. Evidently, from Fig. 6, the singly ionized observations and reference model solution (i.e. without introducing higher charge states, $\Theta _{\rm max}=\Theta _{\rm min}=16$) show good agreement, while the total observed spectrum shows very good agreement with the $\Theta_{\rm max}=16\rightarrow \Theta_{\rm min}=8$ transition. This agreement confirms that the method introduced here to incorporate the effect of higher charge states in the modulation model is indeed valid, and able to reproduce O* observations at Earth. We interpret this good agreement as confirmation of the presence of higher charge states in the observed O* population.

The right panel of Fig. 6 shows the modelled O* energy spectra at the TS for the different specie transitions considered throughout. In the range 10-70 MeV nuc-1, a clear $j \propto E^{-3}$ decrease was observed (Webber et al. 2007), as alluded to previously. The reference solution (dashed-dotted line) is for a singly ionized ACR distribution only, resulting in a spectrum falling off exponentially beyond the ACR roll-over energy. The other computed solutions show how this exponential roll-over gradually changes as multiple charge particles are introduced. While the $\Theta_{\rm max}=16\rightarrow \Theta_{\rm min}=8$ transition is similar to the reference case at low energies, deviations from this behaviour begin to occur so that the ACR roll-over spectrum is altered into what appears to be a power-law decrease as the roll-over energy shifts to much higher energies. This solution also shows the best agreement with the observations in reproducing the observed power law roll-over. All the higher charged ACR solutions show a similar behaviour. Clearly, the exponential decay is modified to an almost power law decrease in intensity for energies ${\sim}10{-}70$ MeV nuc-1.

As higher charge states were also observed for ACR neon and nitrogen (Mewaldt 2006), similar looking power law decreases are also expected for these populations at the TS and further investigation is warranted.

\begin{figure} \par\includegraphics[width=8cm,clip]{13866f4.eps} \end{figure} Figure 5:

Similar to Fig. 4, but for the qA < 0 magnetic polarity cycle.

Open with DEXTER

4 Conclusions

\begin{figure} \par\includegraphics[width=8cm,clip]{13866f5.eps}\hspace*{1.5cm} \includegraphics[width=8cm,clip]{13866f6.eps} \end{figure} Figure 6:

The left panel shows the observed and computed O* spectra at Earth. The observations are adapted from Mewaldt (2006), and show both the singly ionized (Q=1) and total (Q=1+Q>1) energy spectra, with the latter including higher charge states. The different lines show model calculations for the different energy dependent charge states as discussed previously. The right panel shows similar results, but now at the TS. The V1 observations from Fig. 1 are also shown for comparison.

Open with DEXTER

We have included the effect of higher charge state in modelling O* intensities, by specifying an appropriate energy dependent charge state as constrained by the observations of Mewaldt et al. (1996a,b). We have showed that the low energy O* spectra (and therefore the intensities) remain relatively unchanged by the inclusion of these higher charge states because this energy region is dominated by the well known Fermi I (diffusive shock) acceleration power law at the TS, which is independent of the particle charge, or ionization state of the ACR population under consideration. The effect on the high energy portion of the O* spectra is more pronounced with the inclusion of the multiple charged ACRs. The ACR roll-over energy moves to higher energies for the higher charge states at the TS, creating an increase in high energy O* intensities throughout the heliosphere. This increase in O* intensities is also reflected in the modulated spectra at Earth, with the low energy portion of these spectra again remaining relatively unaltered.

Introducing an energy dependent charge state, as outlined in this article, we are able to reproduce both the singly ionized (Q=1), as well as the total (with the inclusion of higher charge states, Q=1+Q>1) observed O* spectra at Earth, confirming that O* does consist of a large fraction of higher charge states at high energies, and more importantly, confirming that the effect of multiple charge O* must be included into a modulation model to correctly reproduce the observed high energy O* spectra.

Using the same approach in the outer heliosphere, we are able to reproduce the observed $j \propto E^{-3}$ decrease in intensity (Webber et al. 2007) observed by the V1 spacecraft at the TS for O* in the energy range 10-70 MeV nuc-1. This deviation from the expected exponential form can thus be attributed to multiple charged ACRs being both present and even dominant at high energies. Furthermore it is concluded that this almost power law behaviour is not characteristic of any additional acceleration mechanisms but due to the more efficient acceleration of higher charge states.

The fact that this model can reproduce the power-law form of the observed high energy portion (E > 20 MeV nuc-1) of the O* spectra so well can be interpreted that diffusive shock acceleration of multiple charged O* is indeed occurring near and at the TS, and that this process is primarily responsible for accelerating O* to such high energies. However, it appears that diffusive shock acceleration, as the only acceleration mechanism, cannot account for the modulated form of the low energy ACR spectra ( ${\sim}1{-}10$ MeV nuc-1) at the TS and their subsequent unfolding into the heliosheath. This indicates that the process is indeed very complex, with additional re-acceleration of ACRs in the heliosheath required or that it may be attributed to specific heliospheric geometries, causing more effective acceleration elsewhere at the TS, or that the seed particle distribution for ACRs is less straightforward than previously assumed, as the latest IBEX results may suggest. Clearly, more observations and modelling efforts are needed to constrain these physical processes further, and until then, it will remain a controversial topic.

Acknowledgements
The authors wish to thank W.R. Webber and M.E. Hill for informative research discussions.

References

  1. Adams, J. H., Gracia-Munoz, M., Grigorov, N. L., et al. 1991, Proc. Int. Cosmic Ray Conf., 3, 358 [Google Scholar]
  2. Biswas, S., Durgaprasad, N., Mitra, B., et al. 1988, Astrophys. Space Sci., 149, 357 [NASA ADS] [CrossRef] [Google Scholar]
  3. Burger, R. A., Potgieter, M. S., & Heber, B. 2000, J. Geophys. Res., 105, 27447 [Google Scholar]
  4. Chalov, S. V., Fahr, H. J., & Malama, Y. G. 2007, Ann. Geophys., 25, 575 [Google Scholar]
  5. Ferreira, S. E. S., Potgieter, M. S., & Scherer, K. 2007, J. Geophys. Res., 112, 11101 [Google Scholar]
  6. Fisk, L. A., & Gloeckler, G. 2009, Adv. Space Res., 43, 1471 [NASA ADS] [CrossRef] [Google Scholar]
  7. Fisk, L. A., Kozlovsky, B., & Ramaty, R. 1974, ApJ, 190, L35 [NASA ADS] [CrossRef] [Google Scholar]
  8. Florinski, V., & Jokipii, J. R. 2003, ApJ, 591, 454 [NASA ADS] [CrossRef] [Google Scholar]
  9. Florinksi, V., & Zank, G. P. 2006, Geophys. Res. Lett., 33, 15110 [NASA ADS] [CrossRef] [Google Scholar]
  10. Florinksi, V., Balogh, A., Jokipii, J. R., et al. 2009, Space Sci. Rev., 143, 57 [NASA ADS] [CrossRef] [Google Scholar]
  11. Jokipii, J. R. 1986, J. Geophys. Res., 91, 2929 [NASA ADS] [CrossRef] [Google Scholar]
  12. Jokipii, J. R. 1990, in Physics of the Outer Heliosphere, ed. S. Grzedzielski, & D. E. Page (Oxford: Pergamon Press), 169 [Google Scholar]
  13. Jokipii, J. R. 1996, ApJ, 466, L47 [NASA ADS] [CrossRef] [Google Scholar]
  14. Jokipii, J. R., & Kóta, J. 1989, J. Geophys. Res., 16, 1 [Google Scholar]
  15. Jokipii, J. R., & Kóta. 1997, Proc. Int. Cosmic Ray Conf., 8, 151 [Google Scholar]
  16. Klecker, B., McNab, M. C., Blake, J. B., et al. 1995, ApJ, 442, L69 [NASA ADS] [CrossRef] [Google Scholar]
  17. Langner, U. W., & Potgieter, M. S. 2006, in Acceleration of galactic and anomalous cosmic rays in the heliosheath, ed. J. Heerikhuisen, V. Florinski, G. P. Zank, et al. (New York: AIP), 858, 233 [Google Scholar]
  18. Langner, U. W., & Potgieter, M. S. 2007, Adv. Space Res., 41, 368 [NASA ADS] [CrossRef] [Google Scholar]
  19. Langner, U. W., Potgieter, M. S., & Webber, W. R. 2003, J. Geophys. Res., 108, 8039 [CrossRef] [Google Scholar]
  20. Langner, U. W., Potgieter, M. S., & Webber, W. R. 2004, Adv. Space Res., 34, 138 [NASA ADS] [CrossRef] [Google Scholar]
  21. Langner, U. W., Potgieter, M. S., Fichtner, H., et al. 2006, J. Geophys. Res., 111, A101106 [Google Scholar]
  22. Lazarian, A., & Opher, M. 2009, ApJ, 703, 8 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lee, M. A., Fahr, H. J., & Kucharek, H. 2009, Space Sci. Rev., 146, 275 [NASA ADS] [CrossRef] [Google Scholar]
  24. le Roux, J. A., Potgieter, M. S., & Ptuskin, V. S. 1996, J. Geophys. Res., 101, 4791 [NASA ADS] [CrossRef] [Google Scholar]
  25. McComas, D. J., & Schwadron, N. A. 2006, Geophys. Res. Lett., 33, 4102 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mewaldt, R. A. 2006, in Physics of the Inner Heliosheath, ed. J. Heerikhuisen, V. Florinski, G. P. Zank, et al. (New York: AIP), 858, 92 [Google Scholar]
  27. Mewaldt, R. A., Cummings, J. R., Leske, R. A., et al. 1996a, Geophys. Res. Lett., 23, 617 [NASA ADS] [CrossRef] [Google Scholar]
  28. Mewaldt, R. A., Selesnick, R. S., Cummings, J. R., et al. 1996b, ApJ, 466, L43 [NASA ADS] [CrossRef] [Google Scholar]
  29. Minnie, J., Bieber, J. W., Matthaeus, W. H., et al. 2007, ApJ, 670, 1149 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ngobeni, M. D., & Potgieter, M. S. 2008, Adv. Space Res., 41, 373 [Google Scholar]
  31. Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
  32. Parker, E. N. 1965, Planet. Space. Sci., 13, 9 [NASA ADS] [CrossRef] [Google Scholar]
  33. Pesses, M. E., Eichler, D., & Jokippi, J. R. 1981, ApJ, 246, L85 [NASA ADS] [CrossRef] [Google Scholar]
  34. Potgieter, M. S. 1989, Adv. Space. Res., 9, 1989 [Google Scholar]
  35. Potgieter, M. S. 2008, Adv. Space. Res., 41, 245 [Google Scholar]
  36. Potgieter, M. S., & Moraal, H. 1988, ApJ, 330, 445 [NASA ADS] [CrossRef] [Google Scholar]
  37. Richardson, J. D., Kasper, J. C., Wang, C., et al. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  38. Steenberg, C. D., & Moraal, H. 1999, J. Geophys. Res., 104, 24879 [Google Scholar]
  39. Webber, W. R., Cummings, A. C., McDonald, F. B., et al. 2007, J. Geophys. Res., 112, 6105 [Google Scholar]
  40. Zank, G. P., Matthaeus, W. H., & Smith, C. W. 1996, J. Geophys. Res., 101, 17093 [NASA ADS] [CrossRef] [Google Scholar]
  41. Zhang, M. 2006, in Acceleration of galactic and anomalous cosmic rays in the heliosheath, ed. J. Heerikhuisen, V. Florinski, G. P. Zank, et al. (New York: AIP), 858, 226 [Google Scholar]

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{13866f0.eps} \end{figure} Figure 1:

Observed O* energy spectra from V1 during its TS crossing (filled circles) and from V2 at 4 AU away from its TS crossing (open circles). For comparison, a  $j \propto E^{-3}$spectral decrease is shown, being the topic of investigation in this study. The observations are adapted from Webber et al. (2007).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13866f1.eps} \end{figure} Figure 2:

The observed fraction of singly ionized ACR oxygen, neon and nitrogen as a function of kinetic energy. The data set is adapted from Mewaldt (2006). Because this fraction decreases with energy, ACRs are dominated by higher charge states (Q > 1) at higher energies, E > 10 MeV nuc-1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13866f2.eps} \end{figure} Figure 3:

The nett charge of the O* distribution function is scaled as a function of kinetic energy using the transition given by Eq. (5). This figure shows the transitions for four different choices of  $\Theta _{\rm min}$, as a function of kinetic energy. The data points indicate the energies at which the specie value is sampled in the numerical model.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13866f3.eps} \end{figure} Figure 4:

The computed O* energy spectra are shown at the TS (top set of curves) and at Earth (bottom set of curves) for the qA > 0 magnetic polarity cycle. Four different spectra are shown, corresponding to the computed solutions for the different transitions of  $\Theta (E)$ used in this study. The $\Theta _{\rm max}=\Theta _{\rm min}=16$ solutions (solid lines) serve as reference solutions for comparison purposes.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13866f4.eps} \end{figure} Figure 5:

Similar to Fig. 4, but for the qA < 0 magnetic polarity cycle.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13866f5.eps}\hspace*{1.5cm} \includegraphics[width=8cm,clip]{13866f6.eps} \end{figure} Figure 6:

The left panel shows the observed and computed O* spectra at Earth. The observations are adapted from Mewaldt (2006), and show both the singly ionized (Q=1) and total (Q=1+Q>1) energy spectra, with the latter including higher charge states. The different lines show model calculations for the different energy dependent charge states as discussed previously. The right panel shows similar results, but now at the TS. The V1 observations from Fig. 1 are also shown for comparison.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.