Long period oscillations in sunspots

N. Chorley; B. Hnat; V. M. Nakariakov; A. R. Inglis; I. A. Bakunina

doi:10.1051/0004-6361/200913683

Home

All issues

Volume 513 (April 2010)

A&A, 513 (2010) A27

Full HTML

Free Access

Issue		A&A Volume 513, April 2010


Article Number		A27
Number of page(s)		7
Section		The Sun
DOI		https://doi.org/10.1051/0004-6361/200913683
Published online		16 April 2010

A&A 513, A27 (2010)

Long period oscillations in sunspots

N. Chorley¹ - B. Hnat¹ - V. M. Nakariakov¹ - A. R. Inglis¹ - I. A. Bakunina^2,3

1 - Centre for Fusion, Space and Astrophysics, Physics Department, University of Warwick, Coventry CV4 7AL, UK
2 - Radiophysical Research Institute, 25 B. Pecherskaya Street, Nizhny Novgorod, 603950, Russia
3 - Central Astronomical Observatory at Pulkovo, Russian Academy of Sciences, Pulkovskoe chaussee., 65/1, St. Petersburg, 196140, Russia

Received 17 November 2009 / Accepted 23 January 2010

Abstract
Long period oscillations of the gyroresonant emission from sunspot atmospheres are studied. Time series data generated from the sequences of images obtained by the Nobeyama Radioheliograph operating at a frequency of 17 GHz for three sunspots have been analysed and are found to contain significant periods in the range of several tens of minutes. Wavelet analysis shows that these periods are persistent throughout the observation periods. The presence of the oscillations is confirmed by several methods (periodogram, wavelets, Fisher randomisation and empirical mode decomposition). Spatial analysis using the techniques of period, power, correlation and time lag mapping reveals regions of enhanced oscillatory power in the umbral regions. Also seen are two regions of coherent oscillation of about 25 pixels in size, that oscillate in anti-phase with each other. Possible interpretation of the observed periodicities is discussed, in terms of the shallow sunspot model and the leakage of the solar g-modes.

Key words: Sun: oscillations - sunspots

1 Introduction

Oscillatory processes observed in sunspots have attracted attention for several decades (for a comprehensive review, see, e.g. Bogdan 2000). Such oscillations are usually placed into one of four categories: (a) umbral chromospheric oscillations with a period of 3 minutes, thought to be slow magnetoacoustic waves (e.g. Centeno et al. 2006); (b) umbral photospheric oscillations with a period of 5 minutes, which may be a response to driving by the well known 5 minute photospheric acoustic oscillations (Thomas et al. 1984); (c) long period oscillations (of the order of hours, e.g. Goldvarg et al. 2005; Efremov et al. 2007); (d) ultra-long period (torque or torsional) oscillations of sunspot umbrae, with periods of several days (Gopasyuk 2004).

So far, most of the work on sunspot oscillations has been focused on the first two, short period categories above. However, long period sunspot oscillations are interesting for a number of reasons, in particular because of their possible association with the eigenmodes of the sunspot magnetic flux tube, the dynamical processes in the solar interior, including the generation and transfer of the magnetic field, and the possible role these oscillations play in solar coronal dynamics (see, e.g. Sych et al. 2009).

Observational evidence of the long period sunspot oscillations is abundant in both the optical and radio bands. For example, 30-60 min oscillations have been detected in the intensity difference of two solar radio signals recorded at two close frequencies, 9.67 GHz and 9.87 GHz (Kobrin & Korshunov 1972). Oscillation periods of tens and hundreds of minutes have also been seen as modulation of the microwave emission (Gelfreikh et al. 2006). Recently, oscillations of the line-of-sight velocity with periods from 60 to 80 min have been detected in sunspots (Efremov et al. 2009) in the Doppler shift of lines in the sunspot spectrum formed at different heights. The oscillations were found to be well pronounced at a level of 100-200 km and decreasing rapidly above it.

Theoretical interpretation of long-period radial oscillations in sunspots is in an embryonic state. Possibly, the most advanced approach is the consideration of the oscillations in terms of the shallow'' sunspot model (e.g. Solov'ev & Kirichek 2008, and references therein). According to this model, a sunspot can oscillate, similar to a raft in water, with the frequency determined by the ratio of the sunspot depth to its Alfvén speed, taking the mass density averaged over the depth. For typical sunspot parameters (the surface mass density of $3.19\times 10^{-7}$ g cm^-3, the magnetic field of 2000 G, and the depth of 3000 km), the oscillation period of the global mode was found to be 1.5 h. This mode is localised near the umbra. Lower subharmonics with periods of integer multiples of the period of the global mode can occur too.

$\begin{figure} \par\subfigure[MDI image of AR108 (10-Sep-2002 22:23).]{\includeg... ...Sep-2004 16:28).]{\includegraphics[width=5cm,clip]{13683f1c.eps} }\end{figure}$	Figure 1: White light images of the active regions studied in this paper.
Open with DEXTER

In this paper, we study long period sunspot oscillations in the microwave emission, utilising both time and spatial information. The paper is organised as follows: in Sect. 2, we present the data used; Sect. 3 details our analysis (Sects. 3.1-3.4 describe the analysis of time signals from the sunspots, while Sects. 3.5 and 3.6 describe the analysis of time signals from the quiet Sun and spatial analysis, respectively) and in Sect. 4, we discuss and interpret our results.

2 Observations

We analysed three sunspots that were observed for periods of about 8 h with the Nobeyama Radioheliograph (NoRH, Nakajima et al. 1994), at a frequency of 17 GHz. A cadence of 1 s and a spatial resolution of 10'' per pixel can be obtained with NoRH. The sunspots were the isolated sunspot of active region AR0330 (08 April 2003 22:45-09 April 2003 06:29), the leading sunspot of active region of AR108 (10 September 2002 22:45-11 September 2002 06:44) and the large leading sunspot of active region AR673 (21 September 2004 22:45-22 September 2004 06:44). Fig. 1 shows white light images of active regions AR108, AR0330 (obtained with SOHO/MDI) and AR673 (obtained with the Big Bear Solar Observatory). Table 1 summarises the observational details for these sunspots.

The measured emission is likely to be generated by the gyroresonant mechanism (e.g. Vourlidas et al. 2006; Shibasaki et al. 1994) coming from a narrow layer of plasma over the sunspot, where a low harmonic of the gyrofrequency coincides with the observational frequency of the instrument.

Table 1: Summary of data analysis.

2.1 Data generation

Partial disk images, measuring the radio brightness temperature were obtained from NoRH for the 3 considered sunspots and time series were generated from these by integrating the signal over the field of view (FOV). Figure 2 shows the time series of the emission intensity from the analysed sunspots.

Since the observation periods were quite long, it was necessary to track the sunspots through their passage across the solar disk. First, the sunspots were matched with their active region numbers by obtaining a full disk image for the start of the observing period and then adding the active region numbers to the image using SolarSoft's NOAA active region database and its associated routines (get_nar and oplot_nar). The centre of the radio sunspot was then found (see Table 1) at the start of the observing period, as the position of the maximum of the microwave emission. These coordinates were converted to heliographic longitude and latitude and the change in longitude in one time step (i.e. 10 s) due to differential rotation was found for the given latitude. The position at the next time step was given by $(\lambda, \theta + \Delta\theta)$ , where $\lambda$ is the latitude, $\theta$ is the original longitude and $\Delta\theta$ is the change in longitude. The new coordinates were then converted back to arcseconds. Images were then synthesised using the position as the centre of the field of view. The size of the field of view was chosen so as to minimise the amount of quiet Sun in the images. The Koshix algorithm was used for synthesis for all images, since it is best suited to diffuse sources. Since there were no off-limb flares during the observations, any possible jitter of the radio image was neglected.

$\begin{figure} \par\includegraphics[width=9cm,clip]{13683f2.eps} \end{figure}$	Figure 2: Original time series of microwave intensity generated from partial disk radio images for AR108 (top), AR0330 (middle) and AR673 (bottom), as observed by the Nobeyama Radioheliograph, at a frequency of 17 GHz.
Open with DEXTER

3 Analysis

3.1 Trend removal and filtering

It is evident from Fig. 2 that there is a large scale trend in all the datasets due to the motion of the Sun across the sky during the observing period, long period (e.g. daily variation of the Earth's ionosphere) and other ultra-long period processes. To remove the trend, we fitted a 4th order polynomial to the data and then subtracted it from the original signal. Following this, we filtered out ultra-long period, slow varying dynamics from the Fourier spectrum of the signal.

Also evident in the time series for AR108 is a large spike, which is perhaps artificial or a short flare. Since we were only interested in the long period oscillations in the data, the spike was removed. This was done by finding the mean of 5 points to the left of the region and then replacing the points in the region with this mean.

3.2 Period analysis

In order to investigate the various frequencies present in the datasets, we employed both the periodogram technique and wavelet analysis (see, e.g. Torrence & Compo 1998). Figure 3 shows the Lomb-Scargle periodograms (Scargle 1982) and wavelet power spectra computed from the detrended data. We see that in all three periodograms, there is power above the 99% significance level (calculated according to Horne & Baliunas 1986) around frequencies of 5-6 mHz, corresponding to the well-known 3 min chromospheric umbral oscillations. It is also clear that there are several low frequency peaks in all the datasets. For AR108 and AR673, there is significantly more power in the low frequency oscillations than in the 3 min oscillations. Evidently, much longer periodicities, of about an hour are present too.

For the wavelet analysis, the Morlet wavelet was chosen, because of its good performance in the study of oscillatory signals. The 99% significance level has been estimated using the subroutine provided by Torrence & Compo (1998). In Fig. 3, we have only shown power that is above this level. In addition to computing the wavelet power spectrum for each time signal, the global wavelet spectrum was also computed. In the global wavelet spectrum, the power for each frequency is simply the time averaged wavelet power for that frequency. The global wavelet spectra are shown in Fig. 3, overlaid on the periodograms. These spectra show that AR108 and AR0330 have two low frequency peaks and possibly that the same is true of AR673, but the two peaks blend together and are not resolved clearly.

All three applied techniques (periodogram, wavelet and global wavelet) show the presence of coinciding spectral peaks, corresponding to the 3-min oscillations and longer period peaks (18-80 min). The 3-min peaks have the same spectral position. The long periods we find have different ranges for each sunspot and are as follows: AR108: $P_1 = 57 \pm 12$ min, $P_2 = 31 \pm 6$ min; AR0330: P₁ = 88⁺¹⁶_-21 min, P₂ = 37⁺⁸_-11 min; AR673: $P_1 = 27 \pm 16$ min, $P_2 = 16 \pm 4$ min. The errors have been calculated by using the width of the peaks at half their maximum spectral amplitude.

$\begin{figure} \par\includegraphics[width=9cm,clip]{13683f3.eps} \end{figure}$	Figure 3: The Scargle periodograms and Morlet wavelet power spectra for AR0330 (top row), AR108 (middle row) and AR673 (bottom row) time series. The left panels show the periodograms (thin lines) and global wavelet spectra (thick lines). The dashed lines indicate the 99% significance level for the periodograms.
Open with DEXTER

3.3 Significance testing

The Lomb-Scargle periodogram is a redefinition of the traditional power spectrum, which has at its heart simple statistical behaviour, namely that the power at a given frequency has an exponential distribution (for a pure Gaussian noise signal). The cumulative distribution function then has a simple form (see Scargle 1982, Eq. (13)) and using it, we can determine a power threshold, z₀, such that the probability, p₀, that the highest peak above this threshold is due to chance is small. The expression for z₀ given by Scargle (1982) is

$\begin{displaymath}z_0 = -\ln\left[1 - \left(1 - p_0\right)^{\frac{1}{N}}\right], \end{displaymath}$

(1)

where p₀ is the false alarm probability and N is the number of frequencies over which to search for the highest peak. According to Horne & Baliunas (1986), z₀ has to be normalised to the variance of the signal. According to this estimation, the long period sunspot oscillations are statistically significant.

Also, we make use of a significance test based on Fisher's method of randomisation (see, e.g. Linnell Nemec & Nemec 1985) in order to confirm our results from the periodogram analysis. The main reason for doing this is that the test is distribution independent, whereas other techniques implicitly assume a certain model for the statistical distribution.

We would like to calculate the probability that the highest peak in our power spectrum is due to the presence of harmonic oscillations, i.e. not due to chance. Suppose first that the signal does not contain a periodic component. Then, the measurements $I(t_1), I(t_2), \ldots, I(t_n)$ are independent of the observation times (the t_i). If that is the case, there are n! permutations of the signal, where n is the number of measurements. Typically, n is large and as such, it is impractical to perform all n! permutations. Due to this limitation, we choose to perform $m \ll n!$ such permutations and usually choose $m \geq 100$ . When these permutations are performed, the power spectra of the randomised signals are computed and we count the number of times the largest peak in these power spectra have amplitudes greater than, or equal to, the largest peak in the original spectrum.

The probability, p, of the highest peak in the spectrum occuring by chance is then given by

$\begin{displaymath}p = \frac{m_{\rm p}}{m}, \end{displaymath}$

(2)

where $m_{\rm p}$ is the number of times a peak in the spectrum of a randomised signal was found to have an amplitude greater or equal to that of the highest peak in the spectrum of the original signal. The detection probability is then given by (1 - p). It should be noted that both p and (1 - p) are only estimates of the true probabilities and this is due to the limitation on the number of permutations that can be performed.

The Fisher randomisation method was applied to all three datasets with m = 200. We performed m random permutations 1000 times for each dataset (i.e. 1000 random sets of 200 permutations were performed) and for all 1000 experiments, the estimated value of p was found to be less than 0.1%, i.e. there was almost no chance that the detected periods corresponding to the highest spectral peaks (i.e. 88 min for AR0330, 57 min for AR108 and 27 min for AR673) occurred due to chance.

3.4 Empirical mode decomposition

Fourier analysis, while a commonly used technique, is not without problems. For example, any large scale trend in the signal must be removed before performing Fourier analysis, otherwise the spectrum will be dominated by the trend. Also, it requires that signals contain strictly periodic components. In real signals, this is rarely the case and oscillatory components can be modulated by non-stationary and non-linear effects. Fourier analysis does not give the user any time information and using the windowed Fourier transform can be a solution. However, the size of the window needs to be chosen and in general, several different window sizes need to be tested before an appropriate one is chosen. Wavelets allow the window width to be chosen automatically and allow us to study non-stationary signals and analyse frequency modulation, but one disadvantage of that method is that time resolution is limited by the finite width of the wavelet function. Also, these techniques cannot perform well on periodic but significantly anharmonic signals.

Empirical mode decomposition (EMD, Huang et al. 1998) was designed for use with non-linear and non-stationary signals and assumes that the signal is a sum of intrinsic oscillations (which are usually referred to as intrinsic mode functions, or IMFs) that may have varying amplitude and frequency. As such, it is an excellent method for studying frequency modulation. In addition, it is not necessary to remove a trend component from the data before applying the technique - being an adaptive filter, EMD effectively removes the trend. The intrinsic mode functions found do not need to be harmonic oscillations, which allows the technique to be used to investigate the anharmonicity of oscillations in a signal. Applications of EMD in solar physics can be found in Komm et al. (2001) and Terradas et al. (2004). Here, we use EMD to confirm our results derived from other methods.

The IMFs are found for a signal, x(t), by a sifting process. First, the local maxima are identified and are connected with a cubic spline. This is repeated for the local minima and the mean of the envelope created by the connected maxima and minima, m(t), is found. This mean is subtracted from the signal to give

h₁(t) = x(t) - m(t),

(3)

where h₁(t) will be an IMF, provided that it satisfies the following two conditions:

1.: The number of extrema and number of zero crossings must differ by at most one.
2.: The mean of the upper and lower envelopes must be zero at all times.

The first condition means that the IMFs contain a narrow range of frequencies and the second means that the oscillations have zero mean. Once the mean has been subtracted from the original signal, the residual signal, h₁(t) is used as input to the EMD procedure and the process is repeated until all IMFs are found. Huang et al. (1998) proposed the Hilbert spectrum for the visualisation of these components, but here, we make use of the standard wavelet power spectrum, because it is easier to interpret than the Hilbert spectrum. Thus, in this study, EMD is used as an adaptive filtering technique only.

$\begin{figure} \par\includegraphics[width=9cm,clip]{13683f4.eps} \end{figure}$	Figure 4: Three components derived by the empirical mode decomposition method for the signal from AR108. The wavelet power spectra are shown for the first two of these components. The third component (bottom left) is the trend component. Bottom right: the global wavelet spectrum of the two oscillatory components displayed.
Open with DEXTER

The EMD technique was applied to all three datasets, after filtering the signals to contain only frequencies in the range 0-8 mHz, to include the 3 min oscillations and remove high frequency noise. For AR673, 12 components were found and 10 components were found for both AR108 and AR0330.

Figure 4 shows the three longest period intrinsic modes found by the EMD for AR108, two of which are oscillatory and the third is the trend component. Also shown is the global wavelet spectrum for the two oscillatory components. The two oscillatory components are the most significant components (i.e. they have the largest amplitudes, besides the daily trend) and wavelet power spectra were computed for them. It is clear that the periods are persistent throughout the observations and remain stable. Also, EMD analysis shows that the intrinsic modes of the analysed signals are quasi-monochromatic and harmonic.

These features coincide with those found in the significant components of the other signals, which is consistent with the previous results. The global wavelet spectrum in the bottom right of Fig. 4 shows the same periodicities as those shown in Fig. 3.

3.5 Quiet Sun signals

As a final test to determine whether the long period oscillations seen in the sunspot time series were real, we investigated the same time variations of the signals of the quiet Sun. One region, with a starting location of (-170, -500)'', which did not contain any bright microwave features, was studied for the same observation period as for AR0330 and with the same time cadence.

The signals for AR0330 and the quiet Sun region were filtered to contain only long period spectral components. A gaussian filter was used for both signals, with a bandpass of 0.35-0.60 mHz, keeping typical long periods of interest. The two filtered signals are shown in Fig. 5. The amplitude of the oscillations in the quiet Sun is seen to be two orders of magnitude smaller than those in the sunspot and we conclude that the oscillations of the quiet Sun in this narrowband frequency interval are not significant.

$\begin{figure} \par\includegraphics[width=9cm,clip]{13683f5.eps} \end{figure}$	Figure 5: Time series for AR0330 (top) and a quiet Sun region (bottom), after narrowband filtering to contain only long period oscillations ( $f \approx$ 0.35-0.60 mHz).
Open with DEXTER

3.6 Spatial structure of the oscillations

We apply the method of periodmapping, developed by Nakariakov & King (2007) to investigate the spatial distribution of the oscillations seen in the sunspots. This method has been applied to flaring data from NoRH by Inglis et al. (2008), who used the technique to deduce coherency of quasi-periodic pulsations in different segments of a flaring loop.

$\begin{figure} \par\includegraphics[scale=0.32]{13683f6a.eps}\includegraphics[sc... ...3683f6o.eps}\includegraphics[scale=0.32]{13683f6p.eps}\vspace*{2mm} \end{figure}$

Figure 6:

The left two columns are for the two separate frequency ranges for AR108 (left: $\Delta f_1 = 0.417{-}0.833$ mHz, right: $\Delta f_2 = 0.206{-}0.417$ mHz) and the two right columns are for the two separate frequency ranges for AR0330 (left: $\Delta f_1 = 0.292{-}0.833$ mHz, right: $\Delta f_2 = 0.133{-}0.292$ mHz). First row: periodmaps for each sunspot for the two frequency ranges given above. Second row: power maps normalised to the maximum power in the map. Third row: correlation maps showing the maximum value of the correlation coefficient for the two frequency ranges above. The correlation coefficient has been computed over the range of lags $-\frac{1}{2}P - \frac{1}{2}P$ where P is the period of the maximum power in the global wavelet spectrum for the given frequency range. The values of P used were: AR108: P₁ = 31 min (left), P₂ = 57 min (right); AR0330: P₁ = 37 min (left), P₂ = 88 min (right). Only pixels for which the correlation coefficient, $C_{xy}(\tau )$ , is above a threshold of 0.3 are coloured. Fourth row: the corresponding lag maps, showing the lag at which the correlation coefficient was maximal. Lags have been normalised to P. The contours show the position of the sunspot from the first image in the datacube.

Open with DEXTER

For each pixel in the derotated datacube, we generate the time series (by simply taking the values for that pixel along the time dimension of the datacube) and calculate the power spectrum. The frequency of the highest peak in the spectrum is then assigned to this pixel in the periodmap. The periodmap is then a 2D map of frequencies corresponding to the dominant frequencies for each pixel in the images. Nakariakov & King (2007) used the traditional Fourier spectrum to determine the frequency assigned to each pixel in the periodmap. Here, we use the global wavelet spectrum instead, since it is smoother than the Fourier spectrum. In addition, we also make use of power, correlation and lag maps (see Inglis et al. 2008). The first are 2D maps of the maximum global wavelet power in a prescribed frequency range for the corresponding pixel time series, the second show the correlation coefficient, $C_{xy}(\tau )$ (for a given lag, $\tau$ ) of the time series of each pixel with one particular pixel chosen as a reference pixel and the third show the time lag at which the correlation coefficient was maximal, over a given range of lags (for details, see Inglis et al. 2008).

For active regions AR108 and AR0330, we first took images with a larger field of view than the ones used for generating the FOV-integrated time series studied in Sects. 3.1-3.4. The images for both datasets were $20 \times 20$ pixels and all the other parameters (starting centre, start and end times, time cadence) were the same as those for the smaller images. Signals of all pixels outside the sunspot radio source region were suppressed by setting their values to 0 over all time. The choice of which pixels constituted the source region was made by setting a threshold on the intensity in the first image of the datacube - any pixels with values less than the threshold were suppressed. The threshold values used were as follows: AR0330: $2 \times 10^4$ K, AR108: $2.5 \times 10^4$ K. After suppressing pixels outside the source region, the time series for each pixel in the datacubes were subjected to the same detrending and filtering procedure as was used for the FOV-integrated time series described in Sect. 3.1.

The global wavelet spectra in Fig. 3 show that there are two distinct low frequency peaks present for AR108 and AR0330. It was thus decided to produce period, power, correlation and lag maps for each of these peaks independently, so the datacubes were filtered to contain the peaks separately. The frequency ranges used were: AR108: $\Delta f_1$ = 0.417-0.833 mHz, $\Delta f_2 = 0.206{-}0.417$ mHz; AR0330: $\Delta f_1 = 0.292{-}0.833$ mHz, $\Delta f_2 = 0.133{-}0.292$ mHz. For the correlation maps, the reference pixel was chosen as the one with the highest global wavelet power and for each frequency range, we produced a correlation map showing the maximum value of the correlation coefficient, over the range of lags $-\frac{1}{2}P$ to $\frac{1}{2}P$ , where P is the period of the maximum power in the global wavelet spectrum for the given frequency range. The values of P used were: AR108: P₁ = 31 min, P₂ = 57 min; AR0330: P₁ = 37 min, P₂ = 88 min. In addition, we produced lag maps, showing the lag at which the correlation coefficient of the signal of the current pixel with the signal of the reference pixel was maximal over the same range of lags.

The period, power, correlation and lag maps are shown in Fig. 6 and it is quite evident that besides frequency range $\Delta f_1$ for AR108, the highest power for the coherent oscillations is localised in the centre of the radio source. However, it is also clear that the individual pixels with the highest power are usually offset, with respect to the centre. For the correlation and lag maps, we have only shown pixels for which $C_{xy}(\tau) \geq 0.3$ to suppress the effects of noise. The correlation and lag maps for AR108 and AR0330 show that for both frequency ranges, there are regions that oscillate in phase with the master pixels, but also regions that oscillate in anti-phase with them. However, for AR0330, this is not so pronounced in $\Delta f_1$ . The regions of coherent oscillation are seen to be relatively large, of about 25 pixels. In all examples, the transition between the regions oscillating in phase and those oscillating in anti-phase appears to be sharp.

For frequency range $\Delta f_1$ of AR108, the largest region of coherent oscillation can be seen towards the left-hand side of the lag map in Fig. 6 (fourth row, first image). The master pixel is located in this region and as such, we expect (and indeed see) that this large region oscillates in phase (or coherently). A region of almost equal size that oscillates also coherently, but in anti-phase with the first region is seen towards the right of this image. This region is made up of pixels for which the maximum correlation was found at the time lag of plus or minus about half period - these lags are of course almost equivalent when dealing with the maximum correlation value. The lag map for frequency range $\Delta f_2$ of AR108 shows a region of in-phase oscillation through the middle of the sunspot and this is in between two regions that oscillate in anti-phase with the master pixel.

The lag map for frequency range $\Delta f_1$ of AR0330 shows a region of about a quarter of the sunspot size, that oscillates in anti-phase with the master pixel region and is located in the south-west portion of the sunspot. Two regions of coherent oscillation that oscillate in anti-phase with each other are most clearly seen in the lag map for frequency range $\Delta f_2$ of AR0330 (fourth row, last image of Fig. 6). These regions are each about half of the size of the sunspot and are aligned with the sunspot's ``tilt'' with respect to the vertical. The region oscillating in phase with the master pixel is seen in the northern part of the sunspot and the anti-phase region seen in the southern part.

4 Discussion

In this paper we analysed three eight-hour datasets of the microwave emission generated over three different sunspots, recorded with the Nobeyama Radioheliograph at 17 GHz. The main findings of this study are as follows:

1.: Significant long period ( 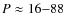$P \approx 16{-}88$ min) oscillatory components are present in the time signals of all three analysed sunspots.
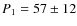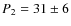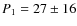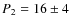2.: In each of the spectra of the sunspots, there are at least two such components. In general, these components are found to have higher power than the three minute oscillations. The periodicities are: AR108: $P_1 = 57 \pm 12$ min, $P_2 = 31 \pm 6$ min; AR0330: P₁ = 88⁺¹⁶_-21 min, P₂ = 37⁺⁸_-11 min; AR673: $P_1 = 27 \pm 16$ min, $P_2 = 16 \pm 4$ min.
3.: The periodicities stay constant during the observing intervals, without any significant drift.
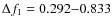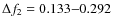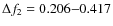4.: The spatial distribution of the oscillations shows, in general, (for both frequency ranges of AR0330 ( $\Delta f_1 = 0.292{-}0.833$ mHz, $\Delta f_2 = 0.133{-}0.292$ mHz) and for frequency range $\Delta f_2 = 0.206{-}0.417$ mHz of AR108) regions of enhanced power in the umbral regions.
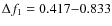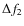5.: There are regions of the sunspots that coherently oscillate both in phase and in anti-phase with the chosen master pixel. The typical size of the coherently oscillating regions is about 25 pixels. For frequency ranges $\Delta f_1 = 0.417{-}0.833$ mHz of AR108 and $\Delta f_2$ of AR0330, there are two regions of almost equal size that oscillate in anti-phase with each other. 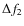For frequency range $\Delta f_2$ of AR108, a region of in-phase oscillation (with the master pixel) is found in the centre of the sunspot and is surrounded by regions oscillating in anti-phase. A sharp spatial transition between the different regions of coherent oscillation is seen in all cases.

The nature of the detected long period oscillations in sunspots is still not revealed. In the following, we discuss possible options.

The observed periodicities are close to the periods of candidate spectral peaks associated with g-modes: e.g. 22-26 min and about 75 min (García et al. 2008) and the sunspot magnetic flux tubes can operate as waveguides, channelling signals of g-modes from deeper regions. Thus, one possible interpretation of the observed periodicities is their association with the leakage of g-modes, but this scenario requires a solid theoretical foundation. Also, the observed anti-phase oscillations in different parts of the sunspots do not seem to support this interpretation.

The observed patterns of fluctuations are also consistent with the shallow sunspot model of Solov'ev & Kirichek (2008). In this model a cylindrical magnetic flux tube has a finite depth of $L \sim$ 3 Mm below the solar surface, where it terminates. The flow around the structure and close to its boundary is mainly vertically downwards for depths smaller than L, and becomes a mostly horizontal flow below the depth L (Zhao et al. 2001). For such a configuration, radially structured fluctuations (that is fluctuations with a certain azimuthal symmetry) could be excited at the bottom of the flux tube and propagate vertically to generate patterns, such as these observed in the last row of Figure 6. It has been shown, using the variational principle, that the periods of such oscillations vary from 40-200 min (Solov'ev & Kirichek 2008), in agreement with periods detected in this work.

Further investigations using numerical modelling will be carried out in order to study the generation of such modes in sunspots. Further work is also needed to investigate the modulation of the 3 min oscillations.

Acknowledgements

N.C. is supported by an EPSRC studentship. N.C. would also like to thank Kiyoto Shibasaki for discussions about this work and financial support for a recent trip to the Nobeyama Solar Radio Observatory. Part of this work was supported by the Royal Society British-Russian Collaboration grant.

References

Bogdan, T. J. 2000, Sol. Phys., 192, 373 [NASA ADS] [CrossRef] [Google Scholar]
Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Efremov, V. I., Parfinenko, L. D., & Solov'ev, A. A. 2007, Ast. Rep., 51, 401 [Google Scholar]
Efremov, V. I., Parfinenko, L. D., & Solov'ev, A. A. 2009, Cosmic Res., 47, 279 [Google Scholar]
García, R. A., Jiménez, A., Mathur, S., et al. 2008, Astron. Nachr., 329, 476 [Google Scholar]
Gelfreikh, G. B., Nagovitsyn, Y. A., & Nagovitsyna, E. Y. 2006, PASJ, 58, 29 [NASA ADS] [Google Scholar]
Goldvarg, T. B., Nagovitsyn, Y. A., & Solov'ev, A. A. 2005, Ast. Lett., 31, 414 [Google Scholar]
Gopasyuk, O. S. 2004, in Multi-Wavelength Investigations of Solar Activity, 223, 249 [Google Scholar]
Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
Huang, N. E., Shen, Z., Long, S. R., et al. 1998, Proc. R. Soc. Lond. A, 454, 903 [CrossRef] [Google Scholar]
Inglis, A. R., Nakariakov, V. M., & Melnikov, V. F. 2008, A&A, 487, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kobrin, M. M., & Korshunov, A. I. 1972, Sol. Phys., 25, 339 [NASA ADS] [CrossRef] [Google Scholar]
Komm, R. W., Hill, F., & Howe, R. 2001, ApJ, 558, 428 [NASA ADS] [CrossRef] [Google Scholar]
Linnell Nemec, A. F., & Nemec, J. M. 1985, AJ, 90, 2317 [NASA ADS] [CrossRef] [Google Scholar]
Nakajima, H., Nishio, M., Enome, S., et al. 1994, IEEE Proceedings, 82, 705 [Google Scholar]
Nakariakov, V. M., & King, D. B. 2007, Sol. Phys., 241, 397 [NASA ADS] [CrossRef] [Google Scholar]
Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
Shibasaki, K., Enome, S., Nakajima, H., et al. 1994, PASJ, 46, L17 [NASA ADS] [Google Scholar]
Solov'ev, A. A., & Kirichek, E. A. 2008, Astrophysical Bulletin, 63, 169 [Google Scholar]
Sych, R., Nakariakov, V. M., Karlicky, M., & Anfinogentov, S. 2009, A&A, 505, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Terradas, J., Oliver, R., & Ballester, J. L. 2004, ApJ, 614, 435 [NASA ADS] [CrossRef] [Google Scholar]
Thomas, J. H., Cram, L. E., & Nye, A. H. 1984, ApJ, 285, 368 [Google Scholar]
Torrence, C., & Compo, G. P. 1998, Bull. Amer. Meteorolog. Soc., 79, 61 [Google Scholar]
Vourlidas, A., Gray, D. E., & Shibasaki, K. 2006, PASJ, 58, 11 [NASA ADS] [CrossRef] [Google Scholar]
Zhao, J., Kosovichev, A. G., & Duvall, T. L. 2001, ApJ, 557, 384 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... analysis: The software used for wavelet analysis was provided by C. Torrence and G. P. Compo and can be found at http://paos.colorado.edu/research/wavelets.

All Tables

Table 1: Summary of data analysis.

All Figures

$\begin{figure} \par\subfigure[MDI image of AR108 (10-Sep-2002 22:23).]{\includeg... ...Sep-2004 16:28).]{\includegraphics[width=5cm,clip]{13683f1c.eps} }\end{figure}$	Figure 1: White light images of the active regions studied in this paper.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{13683f2.eps} \end{figure}$	Figure 2: Original time series of microwave intensity generated from partial disk radio images for AR108 (top), AR0330 (middle) and AR673 (bottom), as observed by the Nobeyama Radioheliograph, at a frequency of 17 GHz.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{13683f3.eps} \end{figure}$	Figure 3: The Scargle periodograms and Morlet wavelet power spectra for AR0330 (top row), AR108 (middle row) and AR673 (bottom row) time series. The left panels show the periodograms (thin lines) and global wavelet spectra (thick lines). The dashed lines indicate the 99% significance level for the periodograms.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{13683f4.eps} \end{figure}$	Figure 4: Three components derived by the empirical mode decomposition method for the signal from AR108. The wavelet power spectra are shown for the first two of these components. The third component (bottom left) is the trend component. Bottom right: the global wavelet spectrum of the two oscillatory components displayed.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{13683f5.eps} \end{figure}$	Figure 5: Time series for AR0330 (top) and a quiet Sun region (bottom), after narrowband filtering to contain only long period oscillations ( $f \approx$ 0.35-0.60 mHz).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[scale=0.32]{13683f6a.eps}\includegraphics[sc... ...3683f6o.eps}\includegraphics[scale=0.32]{13683f6p.eps}\vspace*{2mm} \end{figure}$	Figure 6: The left two columns are for the two separate frequency ranges for AR108 (left: $\Delta f_1 = 0.417{-}0.833$ mHz, right: $\Delta f_2 = 0.206{-}0.417$ mHz) and the two right columns are for the two separate frequency ranges for AR0330 (left: $\Delta f_1 = 0.292{-}0.833$ mHz, right: $\Delta f_2 = 0.133{-}0.292$ mHz). First row: periodmaps for each sunspot for the two frequency ranges given above. Second row: power maps normalised to the maximum power in the map. Third row: correlation maps showing the maximum value of the correlation coefficient for the two frequency ranges above. The correlation coefficient has been computed over the range of lags $-\frac{1}{2}P - \frac{1}{2}P$ where P is the period of the maximum power in the global wavelet spectrum for the given frequency range. The values of P used were: AR108: P₁ = 31 min (left), P₂ = 57 min (right); AR0330: P₁ = 37 min (left), P₂ = 88 min (right). Only pixels for which the correlation coefficient, $C_{xy}(\tau )$ , is above a threshold of 0.3 are coloured. Fourth row: the corresponding lag maps, showing the lag at which the correlation coefficient was maximal. Lags have been normalised to P. The contours show the position of the sunspot from the first image in the datacube.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Bogdan, T. J. 2000, Sol. Phys., 192, 373 [NASA ADS] [CrossRef] [Google Scholar]

[2] Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[3] Efremov, V. I., Parfinenko, L. D., & Solov'ev, A. A. 2007, Ast. Rep., 51, 401 [Google Scholar]

[4] Efremov, V. I., Parfinenko, L. D., & Solov'ev, A. A. 2009, Cosmic Res., 47, 279 [Google Scholar]

[5] García, R. A., Jiménez, A., Mathur, S., et al. 2008, Astron. Nachr., 329, 476 [Google Scholar]

[6] Gelfreikh, G. B., Nagovitsyn, Y. A., & Nagovitsyna, E. Y. 2006, PASJ, 58, 29 [NASA ADS] [Google Scholar]

[7] Goldvarg, T. B., Nagovitsyn, Y. A., & Solov'ev, A. A. 2005, Ast. Lett., 31, 414 [Google Scholar]

[8] Gopasyuk, O. S. 2004, in Multi-Wavelength Investigations of Solar Activity, 223, 249 [Google Scholar]

[9] Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]

[10] Huang, N. E., Shen, Z., Long, S. R., et al. 1998, Proc. R. Soc. Lond. A, 454, 903 [CrossRef] [Google Scholar]

[11] Inglis, A. R., Nakariakov, V. M., & Melnikov, V. F. 2008, A&A, 487, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[12] Kobrin, M. M., & Korshunov, A. I. 1972, Sol. Phys., 25, 339 [NASA ADS] [CrossRef] [Google Scholar]

[13] Komm, R. W., Hill, F., & Howe, R. 2001, ApJ, 558, 428 [NASA ADS] [CrossRef] [Google Scholar]

[14] Linnell Nemec, A. F., & Nemec, J. M. 1985, AJ, 90, 2317 [NASA ADS] [CrossRef] [Google Scholar]

[15] Nakajima, H., Nishio, M., Enome, S., et al. 1994, IEEE Proceedings, 82, 705 [Google Scholar]

[16] Nakariakov, V. M., & King, D. B. 2007, Sol. Phys., 241, 397 [NASA ADS] [CrossRef] [Google Scholar]

[17] Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]

[18] Shibasaki, K., Enome, S., Nakajima, H., et al. 1994, PASJ, 46, L17 [NASA ADS] [Google Scholar]

[19] Solov'ev, A. A., & Kirichek, E. A. 2008, Astrophysical Bulletin, 63, 169 [Google Scholar]

[20] Sych, R., Nakariakov, V. M., Karlicky, M., & Anfinogentov, S. 2009, A&A, 505, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[21] Terradas, J., Oliver, R., & Ballester, J. L. 2004, ApJ, 614, 435 [NASA ADS] [CrossRef] [Google Scholar]

[22] Thomas, J. H., Cram, L. E., & Nye, A. H. 1984, ApJ, 285, 368 [Google Scholar]

[23] Torrence, C., & Compo, G. P. 1998, Bull. Amer. Meteorolog. Soc., 79, 61 [Google Scholar]

[24] Vourlidas, A., Gray, D. E., & Shibasaki, K. 2006, PASJ, 58, 11 [NASA ADS] [CrossRef] [Google Scholar]

[25] Zhao, J., Kosovichev, A. G., & Duvall, T. L. 2001, ApJ, 557, 384 [NASA ADS] [CrossRef] [Google Scholar]