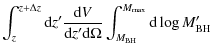EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) A7 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number A7
Number of page(s) 14
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/200913467
Published online 13 April 2010
A&A 513, A7 (2010)

Probing high-redshift quasars with ALMA

I. Expected observables and potential number of sources

D. R. G. Schleicher1,2 - M. Spaans3 - R. S. Klessen4

1 - Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
2 - ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
3 - Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV, Groningen, The Netherlands
4 - Zentrum für Astronomie der Universität Heidelberg, Institut für Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany

Received 14 October 2009 / Accepted 5 January 2010

Abstract
Aims. We explore how ALMA observations can probe high-redshift galaxies in unprecedented detail. We discuss the main observables that are excited by the large-scale starburst, and formulate expectations for the chemistry and the fluxes in the center of active galaxies, in which chemistry may be driven by the absorption of X-rays. We estimate the expected number of sources at high redshift in an ALMA deep field. As a specific example for the complex interpretation of sub-mm line observations, we analyze the recently detected z=6.42 quasar, for which a number of different line fluxes is already available. We note that our diagnostics may also be valuable for future observations in the local universe with space-borne instruments like on SPICA or FIRI.
Methods. To estimate the observables from the starburst, we check which emission from the starburst ring of the nearby Seyfert 2 galaxy NGC 1068 falls into the ALMA bands if the galaxy were placed at z=8. We estimate the sizes of the central X-ray dominated region based on a semi-analytic model, and employ a detailed 1D approach for the chemistry in X-ray irradiated molecular clouds to evaluate the chemistry and the expected line emission under these conditions. We make use of pre-existing chemistry calculations in X-ray dominated regions to show the dependence of different line fluxes on X-ray luminosity, cloud density and cloud column density. We use theoretical models for the high-z black hole population and the local SMBH density to estimate the number of sources at higher redshift.
Results. We show that a number of different fine-structure lines may be used to probe the starburst component of high-redshift quasars in considerable detail, providing specific information on the structure of these galaxies by several independent means. We show that the size of the central X-ray dominated region is of the order of a few hundred parsec, and we provide detailed predictions for the expected fluxes in CO, [CII] and [OI]. While the latter fine-structure lines quickly become optically thick and depend mostly on the strength of the X-ray source, the rotational CO lines have a non-trivial dependence on these parameters. We compare our models to XDRs observed in NGC 1068 and APM 08279 and find that the observed emission can indeed be explained with these models. Depending on the amount of X-ray flux, the CO line intensities may rise continuously up to the (17-16) transition. A measurement of such high-J lines allows one to distinguish observationally between XDRs and PDRs. For the recently observed z=6.42 quasar, we show that the collected fluxes cannot be interpreted in terms of a single gas component. We find indications for the presence of a dense warm component in active star forming regions and a low-density component in more quiescent areas. Near z=6, an ALMA deep field may find roughly one source per arcmin2. At higher redshift, one likely has to rely on other surveys like JWST to find appropriate sources.

Key words: astrochemistry - galaxies: active - galaxies: high-redshift - galaxies: ISM - X-rays: ISM

1 Introduction

The recent detection of kpc-scale star-forming structures at z=6.42 through the detection of [CII] emission (Walter et al. 2009a) and emission in various rotational CO lines (Riechers et al. 2009a) confirms the importance of mm/sub-mm observations to infer gas distribution and dynamics in quasar host galaxies. Emission in CO and the continuum in high-redshift quasars have also been reported by Omont et al. (1996), Carilli et al. (2002), Walter et al. (2004), Klamer et al. (2005), Weiß et al. (2005), Maiolino et al. (2007), Walter et al. (2007), Weiß et al. (2007), Riechers et al. (2008b) and Riechers et al. (2008a).

With the upcoming mm/sub-mm telescope ALMA[*], it will be possible to probe such structures in even more detail, due to its significantly improved sensitivity, angular and spectral resolution. From a theoretical point of view, it is therefore interesting to speculate what ALMA might observe in the center of such host galaxies. Within the next ten years, we further expect the advent of SPICA[*] and FIRI[*], which will probe the universe in the mid- or far-IR regime, respectively. These telescopes will be able to apply in the local universe what we suggest as high-redshift diagnostics for ALMA.

Before speculating what ALMA may see in the centers of high-redshift galaxies, we turn our attention to the properties of molecular clouds in the central molecular zone (CMZ) of the Milky Way. Studies employing H3+ and CO lines indicate the presence of high-temperature ($T\sim250$ K) and low-density ($n\sim100$ cm-3) gas (Oka et al. 2005). NH3 observations by Nagayama et al. (2007) confirm the presence of warm molecular clouds, with temperatures mostly between 20-80 K. The presence of a 120 pc star-forming ring was infered by CO observations, indicating typical densities of 10 3.5-4 cm-3 and kinetic temperatures of 20-35 K (Nagai et al. 2007). These temperatures were derived under the conservative assumption of a beam filling factor 1, while smaller filling factors would give rise to higher temperatures.

In the centers of active galaxies, the supermassive black hole will emit radiation in a broad range of frequencies. Particularly interesting is the emission of X-rays, as those photons can penetrate molecular clouds even at high column densities. The resulting cloud temperatures range from a hundred K up to 1000 K (Meijerink et al. 2007; Meijerink & Spaans 2005; Maloney et al. 1996; Lepp & Dalgarno 1996). Such X-ray dominated regions have been reported for instance in NGC 1068 by Galliano et al. (2003). Due to the high ambient pressure, higher-density clouds may form due to the thermal instability (Wada & Norman 2007).

At high redshift, resolution of present-day telescopes is generally not sufficient to resolve the central regions of quasar host galaxies. Under exceptional circumstances, this is however possible. Indeed, highly excited high-J CO and HCN line emission was found in APM 08279+5255 by Weiß et al. (2007). As this galaxy is gravitationally lensed, it was possible to measure fluxes from the central X-ray dominated region that are usually beam-diluted. While the CO line fluxes usually rise up to the CO (5-4) transition and then decrease, they continue to rise in this system up to the CO (10-9) transition, providing clear evidence for the presence of warm gas in the central region. Similar results have also been obtained for the Cloverleaf quasar (Bradford et al. 2009).

Motivated by these results, we study in more detail the possibility to probe high-redshift quasar host galaxies with ALMA, and in particular their central regions. In Sect. 2, we review the main heating mechanisms that may be present in high-redshift quasars, and discuss their influence on the chemistry. In Sect. 3, we give a brief summary on the main PDR observables, which are already used to probe galaxies at high redshift. As a specific example, we calculate the expected fluxes for the Seyfert 2 galaxy NGC 1068 if it were located at z=8. Our expectations for the central X-ray dominated regions (XDRs) are formulated in Sect. 4 based on detailed chemical models including $\sim$50 species and several thousand reactions. Evidence for X-ray dominated regions at different redshifts is reviewed and discussed in Sect. 5. On this basis, we assess the prospects for finding new sources in an ALMA deep field in Sect. 6. We conclude in Sect. 7. In summary, this paper provides a basic set of predictions concerning observations of high-redshift quasars with ALMA. In a companion paper, we plan to provide diagnostics based on the observed line fluxes that will allow one to infer physical properties such as the star formation rate or the X-ray luminosity based on the observed line emission.

2 Chemistry in high-redshift quasars

Emission from molecular clouds in active galaxies can be excited by a variety of different mechanisms. Mechanical feedback may be important locally, in particular in the presence of shocks or outflows (Papadopoulos et al. 2008; Loenen et al. 2008). In addition, there is radiation in a broad range of frequencies, both from the starburst and the supermassive black hole. UV emission generally gives rise to compact HII regions at temperatures of $\sim$104 K in which molecules are completely dissociated and emission is mostly by Lyman $\alpha$ and various fine-structure lines. Such photons are however absorbed by relatively small column densities, and stellar HII regions never become larger than a few pc, considerably smaller than the scales of interest here.

Soft UV-photons have smaller cross sections and may penetrate larger columns. In the presence of a starburst, they are therefore the dominant driver of the molecular cloud chemistry (Hollenbach & Tielens 1999). While their heating efficiency is low $(0.1{-}0.3\%)$, they are very efficient in dissociating molecules. In such photon-dominated regions (PDRs), one generally expects somewhat enhanced cloud temperatures, with most of the emission in fine-structure lines, as CO is efficiently dissociated. A detailed review of these processes is given by Meijerink & Spaans (2005).

X-ray photons have even smaller cross sections than the soft-UV photons, and can thus penetrate larger columns. Specifically, a 1 keV photon penetrates a typical column of $2\times10^{22}$ cm-2, a 10 keV photon penetrates $4\times10^{25}$ cm-2 and a 100 keV photon $1\times10^{29}$ cm-2. For this reason, X-rays can keep molecular clouds at high temperatures even at high column densities. They have high heating efficiencies of the order of $30\%$, and are inefficient in the dissociation of molecules. A fraction of them may however be reprocessed by the gas and converted in soft-UV photons, which may lead to some molecular dissociation. Detailed reviews are given by Meijerink & Spaans (2005); Maloney et al. (1996); Lepp & Dalgarno (1996). Therefore, X-ray absorption drives a completely different type of chemistry, and may potentially result in temperatures up to 1000 K. The fraction of molecules, in particular CO, can be very high.

To estimate the potential extent of such a central X-ray dominated region, we employ a toy model that takes into account the heat input from the starburst and from the X-ray emission of the supermassive black hole. We assume here an axisymmetric situation with a central supermassive black hole and an extended molecular disk in the host galaxy. The radiation from the SMBH will consist of a soft and a hard component. The soft component is easily absorbed at the edge of the molecular clouds and can be neglected for column densities of 1022 cm-2 and above. The X-ray photons, on the other hand, penetrate deeply into the molecular disk and excite emission there. For the X-ray photons, we adopt a power-law spectrum for frequencies larger than 1 keV and use the cross sections given by Verner & Yakovlev (1995). For soft photons from the starburst, we adopt a typical frequency of 10 eV and a cross section of $2.78\times10^{-22}$ cm-2 (Meijerink & Spaans 2005). Typical heating efficiencies are $30\%$ in XDRs and $0.3\%$ in PDRs. We assume that the radiation field from the starburst is roughly constant within the central region. The X-ray radiation field, on the other hand, will be geometrically diluted and partially shielded by the gas. To calculate the attenuation of X-rays, we introduce an effective density for the central region, which is given as

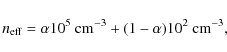
\begin{displaymath}n_{{\rm eff}}=\alpha 10^5~{\rm cm}^{-3}+(1-\alpha) 10^2~{\rm cm}^{-3}, \end{displaymath} (1)

where $\alpha$ is the volume-filling factor of dense clouds, 105 cm-3 is a typical cloud density and 102 cm-3 a typical density of the atomic medium. We adopt now a specific reference case for which we evaluate the heating rates and the expected size of the XDR. The X-ray emission depends essentially on the product of black hole mass $M_{{\rm BH}}$, the Eddington ratio $\lambda_{\rm E}$, and the fraction $f_{\rm X}$ of the total luminosity going into the hard spectrum. We assume a modest black hole mass $M_{\rm BH}=10^7~M_\odot$, an Eddington ratio $\lambda_{\rm E}=30\%$, which lies in the typical range of measured Eddington ratios for high-redshift AGN (Kollmeier et al. 2006; Shankar et al. 2009,2004), and a fraction of $f_{\rm X}=10\%$ of the total luminosity emitted in X-rays. For the X-ray spectrum, we adopt a frequency range between 1 and 100 keV with a spectral slope of -1.

We further assume that the starburst produces a soft UV-radiation field of G0=10 (Habing units) and an effective density of $n_{{\rm eff}}=10^5$ cm-3. Such an effective density corresponds to a volume-filling factor of order 1 and is therefore an upper limit. In real AGN, the effective density may be smaller in the central region, implying less attenuation of the X-rays and therefore a larger X-ray dominated region. On the other hand, the parameter G0 may vary as well and depend on the strength of the ongoing starburst. For this scenario, the expected heating rates per hydrogen atom are given in Fig. 1.

To explore the parameter dependence in more detail, we now consider the effective density and the strength of the starburst radiation field as free parameters and check how they influence the size of the XDR, keeping black hole mass, Eddington ratio and the luminosity fraction in the hard component as specified above. We consider two cases, one with the hard component between 1 and 5 keV (case A), and one with the hard component between 1 and 100 keV (case B). The results for the XDR size are given in Fig. 2. In case A shielding effects can be clearly recognized and the size of the XDR depends more on the effective density than on the strength of the starburst. As typical molecular cloud densities in these environments are $\sim$105 cm-3 and the filling factor is of order $1\%$, we can expect an average density of 103 cm-3. At its largest baseline, ALMA can even resolve spatial scales of $\sim$30 pc at z=5, and should thus resolve the corresponding XDRs.

Simulations by Wada et al. (2009) for the clumpy medium at scales of $\sim30$ pc indicate a volume-filling factor $\alpha\sim0.03$. Models by Galliano et al. (2003) for NGC 1068, on scales of a few hundred parsec, indicate a volume-filling factor of 0.01, which still leads to a surface-filling factor of order 1. For the central 200 pc of our galaxy, values of $\alpha\sim0.1{-}0.01$ have been suggested (Oka et al. 2005; McCall et al. 1999). For a large volume-filling factor, we expect a somewhat smaller XDR due to the attenuation of X-rays. At the same time, however, this region will consist of a large number of clouds that are highly excited. For smaller clumping factors, the number densitiy of clouds will be reduced, but the size of the XDR increased.

Of course, the approach used here is only approximate, as the attenuation may depend on the direction and be stronger in some directions and weaker in others. However, these order-of-magnitude estimates should still be applicable for a broad range of conditions and also hold in cases of spherical rather than flattened structures. An implicit assumption of the model is that we average over sufficiently large scales where the effective density provides a good approximation with respect to X-ray attenuation. For more clumpy structures, the XDR would be more inhomogeneous and reach out further along the low-density regions. In case the large-scale clumpiness is considerable, so that molecular clouds do no longer fill the projected surface area in the beam, our model predictions need to be corrected with the corresponding area-filling factor.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{13467fg1.eps} \end{figure} Figure 1:

The heating rates per hydrogen atom due to X-ray absorption (XDR contribution), absorption of soft UV-photons (PDR contribution) and total heating rate as a function of radius. The calculation assumes a $10^7~M_\odot$ black hole, with $3\%$ of its Eddington luminosity being emitted in a hard spectral component between 1 and 100 keV with a spectral slope of -1. The strength of the soft UV radiation field is taken as G0=10 in Habing units and the effective density $n_{{\rm eff}}=10^5$ cm-3. For such a configuration, the XDR contribution clearly dominates within the central 100 pc.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.5cm,clip]{13467fg2.eps} \end{figure} Figure 2:

The expected size of the X-ray dominated region in pc, for a black hole with $10^7~M_\odot$ with a spectral slope of -1, as a function of the soft UV radiation field G0 in Habing units and the effective number density $n_{{\rm eff}}$. The straight lines assume the power-law between 1 and 5 keV, while the dotted lines assume it between 1 and 100 keV.

Open with DEXTER

3 Observables in the PDR

In photon-dominated regions, soft UV-photons from the starburst provide some heat input for molecular clouds, in particular at low column densities, and are efficient in dissociating molecules like H2 or CO. The main coolants in this regime are therefore fine-structure lines of [CII] and [OI]. Depending on the strength of the radiation field, some flux may also be emitted in molecules like CO or HCN, in particular in the low-lying rotational transitions, and there are further fine-structure lines that may contribute as well. As mentioned in the introduction, there are plenty of observations that studied emission from starburst galaxies with present-day sub-mm telescopes (e.g. Maiolino et al. 2007; Klamer et al. 2005; Walter et al. 2009a; Riechers et al. 2008b,a; Walter et al. 2004; Weiß et al. 2005; Greve et al. 2009; Riechers et al. 2009a; Carilli et al. 2002; Omont et al. 1996; Walter et al. 2007).

Table 1:   The main observables for ALMA in PDRs at high redshift.

With the upcoming sensitivity of ALMA, we expect that such PDRs can be probed in more detail as well. Therefore, bright lines like the [CII] 158 $\mu $m line can be detected at higher significance, allowing higher spectral resolution and probing the velocity structure of the gas in more detail. Also, weaker lines may be detected as well, probing gas at different densities and providing additional information on the chemical conditions.

Table 2:   Frequency range, angular resolution $\theta _{{\rm res}}$ at the largest baseline, line sensitivity $S_{\rm l}$ for a linewidth of 300 km s-1 and continuum sensitivity $S_{\rm c}$ for $3\sigma $ detection in one hour of integration time and primary beam size $\theta _{{\rm beam}}$.

To obtain a rough estimate on the expected PDR fluxes in different lines, we have evaluated the PDR fluxes that we would expect for a system like the Seyfert 2 galaxy NGC 1068, if it were placed at high redshift. We adopt z=8. This system consists of a central X-ray dominated region (Galliano et al. 2003) and a circumnuclear starburst ring of $\sim$3 kpc in size, with a stellar mass of $\sim$ $10^6~M_\odot$ and an age of 5 Myr (Spinoglio et al. 2005). On scales of a few hundred parsecs, one finds a star formation rate of a few times $10~M_\odot$ yr-1 kpc-2 (Davies et al. 2007). This is close to the star formation rate in Eddington-limited starbursts as suggested by Thompson et al. (2005). To understand which of the fluxes emitted in this region would be detectable with ALMA if this system were located at z=8, we went through the spectroscopic sample of Spinoglio et al. (2005) and checked which lines would be redshifted into the ALMA frequency bands, and what would be the expected amount of flux. The fluxes given by Spinoglio et al. (2005) have been measured with a frequency resolution of 1500 km s-1. Correspondingly high velocities can indeed be reached in the presence of fast jets or outflows. However, typical line profiles show that most of the flux is in a range of $\pm$150 km s-1, which we adopt here as a fiducial value. The so obtained observable line transitions are summarized in Table 1, while the expected sensitivity and angular resolution at the largest baselines is given in Table 2. For all the transitions, a $3\sigma $ detection seems possible for an integration time of a few hours. The table does not include CO transitions, as the PDR would only excite the low-lying transitions which would not fall in ALMA's frequency range for z>8. We note that the expected ratio between [NII] and [CII] is comparable to the observational upper limit derived by Walter et al. (2009b).

4 Expectations for the XDR

As ALMA may for the first time detect and resolve emission for the central X-ray dominated regions, we want to assess here in more detail the expected chemical conditions in the central region and the corresponding fluxes in different lines. We start by discussing the implications of X-rays for the conditions in molecular clouds. We then show how ALMA observations can distinguish between X-ray chemistry and an intense burst of star formation on the same spatial scales. Afterwards, we provide a set of systematic model predictions, first assuming an XDR of constant size, but also considering the potential increase of the XDR in case of a higher X-ray luminosity.

4.1 Implications of X-rays for molecular clouds

We follow the chemistry in a one-dimensional molecular cloud complex irradiated by X-rays with the XDR code of Meijerink & Spaans (2005). The model includes more than 50 chemical species and several thousand reactions. For CO, the detailed level populations are solved consistently with the 1D radiation transport equation (Poelman & Spaans 2005,2006). As the low-metallicity case was explored in detail by Spaans & Meijerink (2008), we focus here in particular on situations with about solar metallicity.

The first model we discuss corresponds to the XDR in the Seyfert 2 galaxy NGC 1068 (see Sect. 5.1). We plot chemical abundances and CO emission for cloud column densities between 1020-1024 cm-2 in Fig. 3. Larger column densities correspond to extreme ULIRGs like Arp 220 that is even optically thick around 350 GHz (P. Papadopoulos, private communication). The fiducial gas density of 105 cm-3 has little impact on our results, unless it drops to below 104.5 cm-3. Above this limit, the XDR properties are determined by the ratio of X-ray flux to gas density. For lower densities, emission in the high-J CO lines would not be excited due to the critical densities. However, high-density gas appears to exist in the center of NGC 1068 (Galliano et al. 2003).

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13467fg3.eps} \end{figure} Figure 3:

A model for the X-ray chemistry in NGC 1068. The adopted flux impinging on the cloud is 170 erg s-1 cm-2. The adopted density is 105 cm-3. Top: the abundances of different species as a function of column density. Middle: the low-J CO lines as a function of column density. Bottom: the high-J CO lines as a function of column density.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13467fg4.eps} \end{figure} Figure 4:

The X-ray chemistry in a system with X-ray flux of 1 erg s-1 cm-2 impinging on the cloud. The adopted density is 105 cm-3. Top: the abundances of different species as a function of column density. Middle: the low-J CO lines as a function of column density. Bottom: the high-J CO lines as a function of column density.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13467fg5.eps} \end{figure} Figure 5:

The X-ray chemistry in a system with X-ray flux of 10 erg s-1 cm-2 impinging on the cloud. The adopted density is 105 cm-3. Top: the abundances of different species as a function of column density. Middle: the low-J CO lines as a function of column density. Bottom: the high-J CO lines as a function of column density.

Open with DEXTER

The strong X-ray flux of $\sim$170 erg s-1 cm-2 in NGC 1068 suffices to make the gas essentially atomic and leads to high temperatures of $\sim$3000 K, as well as relatively low CO abundances of the order 10-7 due to photodissociation by soft UV-photons produced after the absorption of X-rays. However, the CO abundance is still higher than in typical PDRs, and the CO intensity is high, due to the strong thermal excitation in the hot gas. For a column of $10^{22}~{\rm cm}^{-2}$, our results appear of the same magnitude as in the model of Galliano et al. (2003). For larger columns, the temperature gradually decreases, the gas becomes molecular and CO gets more abundant, and we find intensities of the order 10-2 erg s-1 cm-2 sr-1 in the high-J CO lines.

To explore the dependence of the chemistry on the X-ray flux, we consider two additional cases. An extreme case with $\sim$1 erg s-1 cm-2 is shown in Fig. 4. In this model, we find lower temperatures of $\sim$70 K, a large fraction of molecular gas and CO abundances of the order of 10-4. While the lower temperature tends to decrease the CO line intensities, they are still enhanced due to the larger CO abundance. Above a column of $10^{23}~{\rm cm}^{-2}$, the intensities increase rather slowly as the lines become optically thick.

As an intermediate scenario, we consider a source with an X-ray flux of $\sim$10 erg s-1 cm-2 (see Fig. 5). In this model, the temperature is increased to $\sim$100 K. The CO abundance is initially of the order $3\times10^{-6}$ and increases to $\sim$10-4 for larger columns. For columns less than $10^{22}~{\rm cm}^{-2}$, the intensities are thus reduced by about an order of magnitude compared to the previous case, while they are increased by an order of magnitude for larger columns.

4.2 Separating the XDR from a nuclear starburst

In the center of an active galaxy, not only the X-ray emission is enhanced, but one may expect the presence of a strong nuclear starburst. For instance, Arp 220 harbors such a starburst on scales of $\sim$300 pc. We therefore compare the expected CO line SED of a strong starburst with G0=105 with the CO line SEDs in X-ray dominated regions, based on the models provided by Meijerink et al. (2007). We normalize them such that the CO (10-9) transition has the same intensity in all models. In this case, the SEDs can hardly be distinguished at the low-J transitions that are typically observed at low redshift (see Fig. 6). At higher-J transitions, the PDR SED drops considerably and flattens on a low level due to the small amount of hot gas in the outer layer of the molecular cloud. We expect that a value of G0=105 is a robust upper limit for the soft-UV flux that can be obtained in a galaxy. In fact, larger values have never been indicated in previous observations, and indeed such a value would require extreme conditions as in the Orion Bar throughout all of the galaxy. In XDRs, a much larger fraction of the gas is at high temperatures, and thus the SED is not expected to drop as rapidly.

If the total amount of energy injected by X-rays and by soft-UV photons is comparable (within a factor of 10), then the presence of X-rays can be clearly inferred using the CO (16-15) transition, if the local X-ray flux is at least 2.8 erg s-1 cm-2. However, as discussed in Sect. 2, we expect X-ray flux to dominate over the soft-UV in the center of the galaxy. Observations at even higher-J transitions may be useful to determine the local amount of X-ray flux from the CO line SED. A potential uncertainty is the presence of cold dust, which may to some degree absorb the CO line emission and thus change the appearance of the SED. Due to the characteristic scaling of dust absorption with wavelength, we expect that such a behavior could be recognized and potentially corrected. For this purpose, it is of course desirable to measure as many high-J CO lines as possible.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13467fg6.eps} \end{figure} Figure 6:

A comparison of the CO line SED in case of an intense starburst with G0=105 with the corresponding SED for molecular clouds under X-ray irradiation, for different X-ray fluxes in erg s-1 cm-2. The spectra are normalized such that they have the same intensity in the 10th transition. If the impinging X-ray flux is at least 2.8 erg s-1 cm-2, observations of the 15th CO rotational transition can clearly discriminate between PDR and XDR chemistry.

Open with DEXTER

4.3 Model predictions for XDRs of constant size

Although we have shown in Sect. 2 that the central XDRs can likely be resolved with ALMA, it is currently not clear how the expected XDR size varies with X-ray luminosity. If the strength of the soft-UV field is independent of this, one should on average expect a larger XDR for higher X-ray luminosities. However, it is also conceivable that the X-ray luminosity is indicative of the system as a whole, and that a higher X-ray luminosity may be accompanied by a stronger soft-UV field. In such a case, one might expect a smaller increase in the XDR size or even a constant size. For this reason, we will consider two extreme cases, assuming that more realistic scenarios should lie in between the two. In this subsection, we will assume that the size of the XDR is always constant, of $\sim$200 pc. Of course, the numbers given here can be easily rescaled for other XDR sizes, or for area-filling factors smaller than 1. In the following subsection, we will then discuss the implications of varying the X-ray luminosity for constant G0.

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg7.eps} \end{figure} Figure 7:

The expected flux in mJy for high-J CO lines, for a central XDR of 200 pc, and molecular clouds of 105 cm-3, as a function of X-ray luminosity and cloud column density. We focus on lines that fall in ALMA band 6, which offers a good compromise between angular resolution and sensitivity. For a source at z=5 (solid line), this corresponds to the (10-9) CO transition, for a source at z=8, it corresponds to the (14-13) CO transition.

Open with DEXTER

For a first estimate, let us consider at source at z=5 with an XDR of at least 100 pc, corresponding to an angular scale of 0.016'', and a typical intensity in the high-J CO lines of 10-3 erg s-1 cm-2 sr-1. As can be seen from the calculations above, such an intensity can be reached in a broad range of systems for column densities of at least 1023 cm-2, and in fact also for column densities of at least 1022 cm-2 in the presence of sufficient X-ray flux. With a fiducial velocity dispersion of 300 km s-1, this corresponds to a flux of 0.03 mJy, which is detectable in a bit more than a day in ALMA band 6.

In a similar way, it is possible to calculate the expected fluxes also in various fine-structure lines. Based on the detailed parameter study provided by Meijerink et al. (2007)[*], which shows the expected fluxes in various lines as a function of X-ray luminosity density and column density, we therefore provide detailed predictions for the fluxes from the central X-ray dominated region, assuming a characteristic size of 200 pc, consistent with the results obtained in Sect. 2.

For the high-J CO lines, we focus on those which are redshifted into ALMA band 6, which offers a good compromise between angular resolution (0.014'' at the largest baseline) and sensitivity ($\sim$0.04 mJy for an integration time of one day, $3\sigma $ detection and a line width of 300 km s-1). At a redshift z=5, this corresponds to the (10-9) CO transition, at z=8 to the (14-13) CO transition. We assume that the projected surface area is homogeneously filled with molecular clouds with central densities of 105 cm-3. Figure 7 shows how the expected flux varies as a function of the cloud column density and the X-ray luminosity[*]. Similar results would be obtained for cloud densities of 104.5 cm-3, while it is more difficult to excite CO emission at lower densities.

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg8.eps} \end{figure} Figure 8:

The expected flux in mJy for the [CII] 158 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 105 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 7, with a sensitivity of 0.08 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 6 with a sensitivity of 0.04 mJy.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg9.eps} \end{figure} Figure 9:

The expected flux in mJy for the [CII] 158 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 104 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 7, with a sensitivity of 0.08 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 6 with a sensitivity of 0.04 mJy.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg10.eps} \end{figure} Figure 10:

The expected flux in mJy for the [OI] 63 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 105 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 10, with a sensitivity of 0.2 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 8 with a sensitivity of 0.13 mJy.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg11.eps}\end{figure} Figure 11:

The expected flux in mJy for the [OI] 63 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 104 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 10, with a sensitivity of 0.2 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 8 with a sensitivity of 0.13 mJy.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg12.eps} \end{figure} Figure 12:

The expected flux in mJy for the [OI] 146 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 105 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 7, with a sensitivity of 0.37 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 6 with a sensitivity of 0.225 mJy.

Open with DEXTER

The figure illustrates that higher fluxes can be obtained for larger column densities, while intermediate X-ray fluxes are ideal for stimulating emission in the CO lines considered here. This is because at very high fluxes, a significant amount of X-rays would be converted into soft UV-photons and dissociate the molecules.

In Figs. 8 and 9, we show the corresponding results for the [CII] 158 $\mu $m line, both for a density of 105 cm-3 and a density of 104 cm-3. For densities of 105 cm-3, low column densities are sufficient to yield a detectable amount of flux, and the flux monotonically increases with the X-ray luminosity. As in the PDR case, this line is therefore valuable to explore the centers of high-redshift quasars, and provides complementary information to the CO lines. For densities of 104 cm-3, we find a stronger dependence on column density, and indeed columns of at least 1023 cm-2 are needed to yield a detectable amount of flux.

The results for the [OI] 63 $\mu $m line are given in Figs. 10 and 11, again for densities of 105 cm-3 and 104 cm-3, respectively. This line quickly becomes optically thick. Therefore, in particular for cloud densities of 105 cm-3, it is insensitive to the column density, but provides a good measure for the X-ray flux. It is very bright. Even for cloud densities of 104 cm-3, it depends more on X-ray luminosity than column density, and is still detectable in the case of high column densities and strong X-ray fluxes. It is thus well-suited to study gas dynamics in the central XDR by resolving the line profile.

We also provide results for the [OI] 146 $\mu $m line in Fig. 12, for a cloud density of 105 cm-3. For lower densities, this line is hard to excite. It can also be very bright and shows a strong dependence on the X-ray flux. The ratio between the [OI] 63 $\mu $m line and the 145 $\mu $m line is generally about 0.1.

Emission from neutral carbon seems more difficult to detect. The intensity of the [CI] 369 $\mu $m line is typically at least an order of magnitude smaller than the intensity in the [CII] 158 $\mu $m line, and only significant in the case of strong X-ray fluxes and high column densities. As discussed in Sect. 5.3, the relatively low ratio between these lines in the recently detected z=6.42 quasar puts a significant constraint on theoretical models. Other carbon lines like [CI] 609 $\mu $m or [CI] 230 $\mu $m are even weaker and should never be visible. Additional lines like [SiII] 35 $\mu $m or [FeII] 26 $\mu $m can be bright as well (Meijerink et al. 2007), but typically have too short wavelengths for ALMA, except at redshifts z>9.

The reader may notice that for the model predictions given in this subsection, we restricted ourselves to a range of X-ray luminosities of about two orders of magnitude, corresponding to the range of X-ray fluxes available in the data by Meijerink et al. (2007). This range of data has been chosen such that it covers the observationally interesting cases. For lower fluxes, or in our case lower X-ray luminosities, we would not expect significant emission driven by X-rays, as can be seen in the corresponding figures. Similarly, it is straightforward to extrapolate the behavior towards higher X-ray fluxes: as shown in Fig. 7, the CO intensities decrease considerably at higher luminosities. This is because part of the X-rays are reprocessed to soft-UV photons that dissociate all the CO. At even higher intensities, the gas temperature would increase up to 104 K and become fully ionized. Molecules would no longer survive under such circumstances. The emission of [CII] may increase a bit further, until a large fraction of carbon is doubly-ionized at temperatures near 104 K. Similar considerations hold for the oxygen line. However, it is not clear whether such scenarios are actually physical, or if the molecular cloud would rather be photo-evaporated at that point. As already mentioned above, the size of the XDR may be more extended in the case of such high luminosities. Then, moderate X-ray fluxes will be present on larger scales.

In summary, we can therefore conclude that the main observables for the central XDR are the high-J CO lines as well as the fine-structure lines of [CII] and [OI]. The [OI] 63 and 146 $\mu $m lines show a strong dependence on X-ray luminosity and may provide a good handle on this quantity. In combination with an observation of the [CII] or high-J CO lines, the X-ray luminosity can be estimated as well. As shown by Meijerink et al. (2007), such line ratios also provide valuable information on gas density and temperature. We also note that it is possible to discriminate such XDRs from regions with strong mechanical heating (Papadopoulos et al. 2008). This can be done for instance on the basis of the observed X-ray luminosity, or by looking at the dust SED. While in XDRs, both dust and gas will be at high temperatures in dense clouds, there should be a clear discrepancy between gas and dust temperature if heating is due to local shocks. We therefore expect that the physical conditions in the central XDRs can be probed in detail with ALMA.

4.4 Model predictions for variable XDR-sizes

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg13.eps} \end{figure} Figure 13:

The expected flux in mJy for the CO (14-13) transition (solid line), [CII] 158 $\mu $m (dotted line), [OI] 63 $\mu $m (dashed line) and [OI] 146 $\mu $m (dot-dashed line) emission for a quasar at z=5, as a function of X-ray luminosity and average density. We assume a typical cloud column density of 1023 cm-2, and a soft-UV field G0=100.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg14.eps}\vspace*{-2mm} \end{figure} Figure 14:

The expected flux in mJy for the CO (14-13) transition (solid line), [CII] 158 $\mu $m (dotted line), [OI] 63 $\mu $m (dashed line) and [OI] 146 $\mu $m (dot-dashed line) emission for a quasar at z=8, as a function of X-ray luminosity and cloud column density. We assume a typical cloud density of 104 cm-3, and a soft-UV field G0=100.

Open with DEXTER

As mentioned above, the size of the XDR may increase considerably for increasing X-ray luminosity. We first explore the dependence on the average density and the X-ray luminosity, assuming a typical cloud column density of 1023 cm-2, and a soft-UV field G0=100. The X-ray spectrum is assumed to range from 1 to 100 keV. As shown in Sect. 2, the size of the XDR then varies as a power-law with density. The same is true for the expected fluxes of CO, [CII] and [OI], as shown in Fig. 13. We estimate those by adopting a typical value in mJy on scales corresponding to the size of the XDR. These should indeed consitute the main contribution. For [CII] and [OI], the total flux may be a bit larger, as the expected amount of emission increases with the X-ray flux (see previous subsection). CO, on the other hand, might be efficiently dissociated in the very inner core. However, we do not expect this to affect our predictions significantly.

We also explore the role of the molecular cloud column density for the expected fluxes. For this purpose, we adopt an average density of 104 cm-3 and a soft-UV field G0=100. In Fig. 14, we show the expected fluxes as a function of X-ray luminosity and column density. As a generic feature, we find that the expected fluxes vary for columns smaller than 1023 cm-2, but level-off for higher values. The fluxes in high-column density systems should thus essentially depend on the X-ray luminosity only.

5 Evidence for XDRs and the interpretation of sub-mm line observations

Although the presence of a central X-ray dominated region seems unavoidable from a theoretical point of view, we want to review current evidence for the presence of central XDRs in active galaxies. Such evidence is present in local galaxies like NGC 1068 that can be studied in great detail, as well as in high-redshift quasars like APM 08279 in which the corresponding fluxes are magnified by a gravitational lens. Similar indications are present also in the Cloverleaf quasar, where CO fluxes up to the (9-8) transition have been measured, and no turnover in the line SED has been found yet (Bradford et al. 2009). These sources will allow a first test for the expectations we have formulated in the previous section once the ALMA telescope becomes available. We also discuss the z=6.42 quasar SDSS J114816.64+525150.3, as it provides a good and interesting example concerning the complex interpretation of sub-mm line observations. We will further discuss how its properties can be understood better if additional data are provided, with particular focus on the role of ALMA.

To distinguish between different excitation mechanisms of molecular clouds, it is very important to have observational diagnostics for the various excitation mechanisms. First efforts for modelling the chemistry in XDRs were performed by Maloney et al. (1996) and Lepp & Dalgarno (1996), while PDR chemistry was originally studied by Hollenbach & Tielens (1999). Recent efforts to discriminate such models have been performed by Pérez-Beaupuits et al. (2009,2007), and new diagnostic diagrams to discriminate AGN- and starburst-dominated galaxies have been provided by Spoon et al. (2007) and Hao et al. (2009).

5.1 NGC 1068

As shown by Galliano et al. (2003), NGC 1068 contains a central XDR. Their analysis is based on the observed intensitiy of the H2 2.12 $\mu $m line (Galliano & Alloin 2002) and the rotational CO lines (Schinnerer et al. 2000), and showed that the observed emission can be consistently explained with the XDR-model of Maloney et al. (1996) under the following assumptions:

  • the central engine is a power-law X-ray source with spectral slope 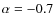$\alpha=-0.7$ and luminosity of 1044 erg s-1 in the 1-100 keV range, consistent with the X-ray luminosity determined from VLBI water maser observations (Greenhill et al. 1996);
  • the emission originates from molecular clouds with a density of 105 cm-3, a column of 1022 cm-2 at a distance of 70 pc and solar metallicity.
They show that the central XDR is indeed inhomogeneous due to a central X-ray absorber that shields the X-rays along the line of sight, while they can stimulate molecular emission in the perpendicular direction. A sketch of such a situation is given in Fig. 15. In the presence of a torus, indeed it seems likely that X-ray emission is preferred in the direction orthogonal to the torus, and the XDR fluxes may therefore be preferentially detectable in situations where the molecular disk is observed face-on.

5.2 APM 08279

In the z=3.9 galaxy APM 08279, the usual geometric effects concerning emission from the central regions are compensated by a gravitational lens. It therefore provides an ideal test case to study the emission we might see when future telescopes like ALMA can observe the central regions with higher sensitivity and higher spatial resolution. As expected for molecular clouds excited by X-rays, they find that the CO line intensity increases up to the (10-9) transition. Significant flux is also detected in the HCN(5-4) line.

Based on brightness temperature arguments, the results from high-resolution mapping and lens models from the literature, Weiß et al. (2007) show that the molecular lines arise from a compact (100-300 pc), highly gravitationally magnified ( m=60-110) region surrounding the central AGN. It is interesting to note that this amount of magnification is comparable to the increase in sensitivity due to ALMA. They can distinguish two components of the gas: a cool component with a density of 105 cm-3 and a temperature of 65 K, on scales larger than 100 pc, and a warm component of gas with 104 cm-3 and temperatures of 220 K on scales smaller than 100 pc. So far, their results do not provide indications for inhomogeneities.

We have compared the turnover for the rotational CO lines found by Weiß et al. (2007) with the grid of PDR and XDR model predictions that were made publicly available by Meijerink et al. (2007). In the PDR case, we find that cloud densities of 105 cm-3 and a radiation field of $G_0\sim10^{4.75}$ with a cloud column of $\sim$ $6\times10^{22}$ cm-2 are required. For the XDR case, the turn-over can be explained with a cloud density of 104.25 cm-3, an X-ray flux of 2.8 erg s-1 cm-2 and a cloud column density of $\sim$ $2.6\times10^{22}$ cm-2. In both cases, we need to require that additional cold gas is present that emits in particular in the low-lying J levels to explain the observed ratio between high-J and low-J rotational CO lines.

The X-ray spectrum of APM 08279 has been observed with Chandra (Chartas et al. 2002), indicating a luminosity of $4\times10^{46}~M^{-1}$ erg s-1. Adopting a lens magnification of $M\sim100$, one expects a flux of $\sim$354 erg s-1 cm-2 at a distance of 100 pc for an optically thin source. However, for a density of 104.25 cm-3, we expect significant attenuation effects that may considerably decrease the flux in the cloud. As shown by Wada et al. (2009), shielding may locally vary by two orders of magnitude due to column density fluctuations in the torus and give rise to a peak optical depth of $\tau\sim5$ for frequencies of 3 keV. A more conservative magnification factor of M=4, as derived by Riechers et al. (2009b), reduces the physical X-ray luminosity and leads to X-ray fluxes closer to the estimates from our XDR model.

With ALMA, it will be possible to probe the distribution of these gas components and their kinematics in even more detail. Due to the higher sensitivity, the error bars in the flux measurement will decrease further and one may probe whether the turnover occurs at the (10-9) transition, as indicated now, or indeed even at higher-J levels. In this case, one could clearly discriminate between PDR and XDR models.

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg15.eps} \end{figure} Figure 15:

A sketch for a situation with an inhomogeneous XDR, motivated by the observations of Galliano et al. (2003) in NGC 1068. While X-rays are shielded by a central absorber along the line of sight, they may stimulate emission in molecular clouds in the perpendicular direction with the typical characteristics of XDRs.

Open with DEXTER

5.3 SDSS J114816.64+525150.3

The recent detection of a kiloparsec-scale hyper-starburst in the source SDSS J114816.64+525150.3 at z=6.42 by Walter et al. (2009a) has stimulated great observational interest that led to a broad collection of data on this source. Recently, Riechers et al. (2009a) provided a table with fluxes in the CO (3-2), (6-5) and (7-6) transitions, fluxes in the CI line and the [CII] line, as well as upper limits on five additional lines. Although the publication of such upper limits is very valuable and can provide important constraints on theoretical models, for simplicity we focus here on those lines that were actually detected. As we shall see, the interpretation of those is already complex, and a more thorough analysis would be beyond the scope of this work. The models and data empoyed here are based on the publicly available grids provided by Meijerink et al. (2007). Due to the large scales of this source, we assume that most of the flux is driven by PDR chemistry, especially because the relevant scales for XDRs are currently unresolved.

To understand the complexity of these data, it is illustrative to check whether a model with one given density and a fixed parameter G0 is able to explain them. For CO, the ratio between the (6-5) and the (3-2) transition is about 3.35, while the ratio between (7-6) and (3-2) is about 3.15. Although it appears that the turnover in the SED may have been reached, this is not fully clear from the data, as the uncertainty in the fluxes is $\sim$$10\%$. The increased intensity in the (6-5) transition requires a significant amount of soft-UV flux, while the almost flat behavior indicates that the gas should be at intermediate densities of about $\sim$104 cm-3. At higher densities, the seventh rotational level would be more easily excited, which would give rise to a significant discrepancy between the (6-5) and the (7-6) transition, even for low values of G0. For lower densities, on the other hand, it becomes difficult to excite these rotational levels. A reasonable fit to the CO SED can thus be obtained with n=104 cm-3 and  G0=101.75.

A problem arises, though, if the observed fluxes in [CII] and CI should result from the same gas component. In this case, our model predicts a flux ratio of [CII] to CI of $\sim$600, and the intensity of [CII] and CI would be much higher than the CO intensities. We note, however, that the fine-structure lines are already optically thick at these densities, while the CO lines are optically thin. Thus, additional clouds may be present that enhance the CO intensities, while the optically thick emission in [CII] and CI is unaffected. Nevertheless, as observations show a corresponding line ratio of 17.7, these lines should originate from a different gas component. Our models require the presence of additional gas clouds with density of $\sim$103 cm-3, $G_0\sim10^{1.75}$ and large columns $N_{\rm H}>10^{21}$ cm-2, at which enough of the soft-UV flux is shielded to yield a low ratio between [CII] and CI. This line ratio is indeed strikingly low, as PDR models generally predict larger numbers for this ratio, and also in this case the match is not perfect, but only within the $20\%$ error of the CI measurement. Although this may be an issue due to uncertain abundance ratios, a more precise determination of the flux in this line is highly desirable.

So far, we have postulated two gas components to explain the CO line SED and the fluxes from [CII] and CI. It is however important to cross-check whether these components may affect the line ratios that the other component should reproduce. For the CO line SED, indeed the intensity in a low-density cloud is smaller by one order of magnitude. The high-density component, however, gives rise to an intensity in [CII] that is smaller than the corresponding intensity from the other component by just a factor of 5. To avoid that this perturbes the [CII] to CI flux ratio, we need to require that the low-density gas is more abundant than the gas at high densities. In this case, it seems however likely that the low-density gas would perturb the CO line SED significantly.

The most probable explanation in terms of a two-component picture is thus that indeed the low-density component is more abundant and explains the observed fine-structure lines. The impinging soft-UV flux must be moderate in order to reconcile the low ratio between these lines. To still explain the observed CO line SED, we need to require that the high-density component is at higher temperatures, due to an increased value of $G_0\sim10^3$. As one generally expects that high-density gas is exposed to a weaker radiation field due to shielding effects, this component should be spatially separated in regions of strong active star formation. Alternative scenarios are however feasible as well. For instance, the observed [CII]/CI ratio may also be produced in the presence of a weak X-ray background rather than a soft-UV field, or if a the cosmic-ray background is enhanced by a factor of 10-100 compared to the Milky Way (see also Meijerink et al. 2006).

Of course, this model is still an oversimplification, as one may indeed expect a variety of different densities in both star-forming and more quiescent parts of the galaxy. In addition, there are theoretical uncertainties concerning the metallicity and the abundance ratios that may affect our results. Nevertheless, this model reproduces the main features in the observed fluxes and illustrates the difficulties in simultaneously modeling observations in different lines. This challenge will become more severe, as the high sensitivity of ALMA will allow us to study even more lines. On the other hand, it is certainly desirable if some of the simplest models can be discarded on such grounds. We note that such models are also predictive. For the scenario described here, we would for instance expect that also the flux in the [OI] 63 $\mu $m line and the [OI] 145 $\mu $m line originates predominantly from the low-density gas component. In this case, the ratio of these fluxes to the flux in [CII] would be 0.06-0.1 and $8\times10^{-4}$, respectively. If the oxygen abundance is enhanced by a factor of 4 compared to the galactic abundance, the flux in the 63 $\mu $m line would be larger by a factor of 2.

With future ALMA measurements, we expect that the CO line SED can be probed in more detail and with higher accuracy at higher-J levels, to check whether the turnover has already been reached. Apart from the observed gas component that indicates a turnover near the J=6 transition, a higher density component may be present that can more easily excite flux at higher-J levels. The increased sensitivity and angular resolution of ALMA may help to detect spatial variations in the different fluxes, which may help to discriminate regions of intense star formation from more quiescent zones. In the center of the galaxy, ALMA can check for the presence of an X-ray dominated region. Significant progress may however be possible in the mean time, for instance by measuring additional high-J CO lines or by a more accurate determination of the [CII] to CI flux ratio.

6 The expected number of sources

As shown in Sect. 3, large-scale PDR fluxes, for instance in the [CII] 158 $\mu $m line or the [OI] 146 $\mu $m line, are sufficiently large for detection in a few hours. Fluxes from the XDR originate from a smaller region, but may also give rise to a significant flux component. With an integration time of a few hours, active galaxies with a comparable brightness as NGC 1068 should be detectable in an ALMA field of view. One might therefore wonder whether a search for active galaxies, based on the before-mentioned fine-structure lines, is feasible. Beyond that, it is of strong interest to know whether there are reasonable chances to find active galaxies with other surveys such as JWST. In such cases, ALMA could perform relevant follow-up studies that probe the central X-ray dominated regions and the gas dynamics within them. If a sufficient number of sources is obtained, ALMA can probe the feeding of black holes between redshift 6 and 10 and thus constrain models concerning the growth of supermassive black holes based on the diagnostics provided here. We therefore conclude this paper with an estimate on the high-redshift black hole population.

To assess this possibility in more detail, we start with some general considerations regarding the black hole population at z>6. Then we discuss estimates on the number of sources and the possibility to detect them with an ALMA deep field.

6.1 Black hole growth at high redshift

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg16.eps} %\end{figure} Figure 16:

The average accretion history of a black hole with $10^7~M_\odot$ at z=5, depending on a coefficient p which is a function of the conversion of rest-mass energy to luminous energy, the Eddington ratio and the duty cycle.

Open with DEXTER

As shown recently by Shankar et al. (2009), a supermassive black hole with $10^9~M_\odot$ today had, on average, $10^7~M_\odot$ at z=5. Therefore, one needs to explain how supermassive black holes have accreted this mass at early times. Indeed, some of them need to accrete even faster, as $10^9~M_\odot$ black holes have already been detected at z>6 (e.g. Fan et al. 2006). We will however focus on the more conservative case of $10^7~M_\odot$ black holes.

We follow Shapiro (2005) and describe black hole growth by accretion using the formula,

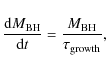
\begin{displaymath}\frac{{\rm d}M_{{\rm BH}}}{{\rm d}t}=\frac{M_{{\rm BH}}}{\tau_{{\rm growth}}}, \end{displaymath} (2)

where
                     $\displaystyle \tau_{{\rm growth}}$ = $\displaystyle 0.0394\frac{(\epsilon_M/0.1)}{1-\epsilon_M}\frac{1}{\lambda_{\rm E}}\frac{1}{f_{{\rm duty}}}~{\rm Gyr}$  
  $\textstyle \equiv$ $\displaystyle 0.0394p~{\rm Gyr},$ (3)

and where $\epsilon_M=L/\dot{M}_0c^2$ is the efficiency of conversion of rest-mass energy to luminous energy, $\lambda_{\rm E}$ the Eddington ratio and $f_{{\rm duty}}$ the duty cycle, i.e. the fraction of quasars active at a time. The parameter p summarizes the complicated dependence on the latter parameters. With the parameters inferred by Shankar et al. (2009) for the observed high-redshift black hole population up to z=6, we obtain $p\sim25$.

The dependence of the black hole mass evolution in this parameter is given in Fig. 16. For p>7, the black hole mass hardly evolves with redshift, implying that black holes would need to form with extremely high masses. There are, however, no theoretical models available that would explain such massive seeds, which would have comparable masses to the first galaxies at high redshift.

It is more likely that the black hole population evolved with redshift, implying that a larger fraction of them was active and had higher Eddington ratios. For instance, a value of p=2.5 requires intermediate mass black holes with $10^4{-}10^5~M_\odot$ to be the progenitors of the first supermassive black holes. Such scenarios have been suggested by Eisenstein & Loeb (1995), Koushiappas et al. (2004), Begelman et al. (2006), Spaans & Silk (2006), Lodato & Natarajan (2006) and Dijkstra et al. (2008). For even smaller values of p, supermassive black holes could even originate from stellar progenitors.

In this respect, it is speculated that so-called dark stars, which would be stars powered by dark matter annihilation rather than nuclear fusion (Spolyar et al. 2008; Freese et al. 2008), could obtain even larger masses than conventional Pop. III stars. However, the high masses suggested in these works are not confirmed by other authors (see also work by Iocco 2008; Iocco et al. 2008) and may be in conflict with the observed reionization optical depth (Schleicher et al. 2009,2008).

In all of these cases, it is evident that the black hole would need to grow considerably by accretion, and that a change in the parameters describing the black hole population is required. In particular, a larger fraction of active quasars and a higher Eddington efficiency are required to obtain the black hole masses that we observe today. As pointed out by Kawakatu & Wada (2009), even super-Eddington accretion may be required to obtain the observed black hole masses.

6.2 Estimates on the number of sources

To estimate the expected number of high-redshift black holes, we will show extrapolations of theoretical models describing the observed high-redshift black hole population, as well as estimates based on the number of $10^9~M_\odot$ black holes in the local universe.

To translate a given black hole number density into the number of sources in a certain field of view, we adopt a similar formalism as Choudhury & Ferrara (2007) and count the number of black holes $N(z,M_{{\rm BH}})$ with masses larger than $M_{{\rm BH}}$ in a redshift interval $[z,z+\Delta z]$ per solid angle. This is given as

                   $\displaystyle N(z,M_{{\rm BH}})$ = $\displaystyle \int_z^{z+\Delta z}{\rm d}z' \frac{{\rm d}V}{{\rm d}z' {\rm d}\Omega}\int_{M_{{\rm BH}}}^{M_{{\rm max}}} {\rm d}\log M'_{{\rm BH}}$  
    $\displaystyle \times f_{\rm a} \frac{{\rm d}n}{{\rm d}\log M_{{\rm BH}}},$ (4)

where ${\rm d}V\ {\rm d}z'^{-1}\ {\rm d}\Omega^{-1}$ denotes the comoving volume element per unit redshift per unit solid angle, which is given as (Peebles 1993)

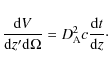
\begin{displaymath}\frac{{\rm d}V}{{\rm d}z' {\rm d}\Omega}=D_{\rm A}^2 c \frac{{\rm d}t}{{\rm d}z}\cdot \end{displaymath} (5)

In this expression, $D_{\rm A}$ is the angular diameter distance, c is the speed of light and ${\rm d}t/{\rm d}z=1/\left (H(z)(1+z)\right )$, where H(z) is the expansion rate as a function of redshift. The term ${\rm d}n/{\rm d}\log M_{\rm h}$ describes the number density of dark matter halos per unit mass, and the maximum black hole mass is taken as $M_{{\rm max}}=10^9~M_\odot$.

As explained above, we focus here on the possibility to search for fine-structure line emission. With a bandwith of 8 GHz, we expect that ALMA could scan a redshift interval of $\delta z=0.2$ at $z\sim8$ in bands 6 and 7 within an integration time of a few hours. We assume here that this process is iterated until a total redshift interval of $\Delta z=0.5$ is covered, which we adopt as a fiducial redshift range in our calculation. Alternatively, one could focus on the detection of continuum flux, which would allow to scan an even larger redshift interval within a given time, but at the same time it would be more difficult to infer the redshift of source.

For our first estimate that extrapolates theoretical models of Shankar et al. (2009) and Treister et al. (2009), we use their results for quasars with luminosities larger than 1044 erg s-1, which can be associated with a black hole mass of $10^7~M_\odot$ for an Eddington ratio of $10\%$, as they find in their calculations. Note that Treister et al. (2009) only provide numbers for Compton-thick quasars, but give a Compton-thick quasar fraction of $\sim$$10\%$, which we use to infer the total population. The results based on this approach are given in Fig. 17 and are only approximate.

\begin{figure} \par\includegraphics[width=8cm,clip]{13467fg17.eps} % \vspace*{-3mm} \end{figure} Figure 17:

Estimates for the number of sources in a redshift interval of $\Delta z=0.5$ within a solid angle of (1')2. We show extrapolations of the results by Shankar et al. (2009) and Treister et al. (2009) to high redshift, for luminosities larger than 1044 erg s-1. In addition, we give an estimate based on the number of high-redshift black holes required in order to produce the present-day $10^9~M_\odot$ black holes. As discussed in the text, the actual number of black holes should lie in between these estimates.

Open with DEXTER

The other approach is based on the number of $10^9~M_\odot$ black holes in the local universe. As noted above, such black holes had an average mass of $10^7~M_\odot$ at z=5 (Shankar et al. 2009). Therefore, the comoving number density of such black holes can be estimated using the number density of today's $10^9~M_\odot$ black holes, which is $\sim$10-3.5 Mpc-3 (Shankar et al. 2009). It may be even higher, as Compton-thick black holes at z=0 are hard to detect (Treister et al. 2009). The expected number of sources based on this estimate is shown in Fig. 17.

One may note that the number of sources obtained in this way is larger than the value from the extrapolation of theoretical models, i.e. by Shankar et al. (2009) and Treister et al. (2009). Such a behavior can be expected from our discussion in Sect. 6.1: as supermassive black holes should have higher duty cycles at z>6, the models by Shankar et al. (2009) and Treister et al. (2009) will naturally underestimate this population. At the same time, the estimate based on the present-day $10^9~M_\odot$ population is also an upper limit, since not all of these black holes will be active at the same time. We therefore expect that these approaches yield an upper and a lower limit and that the actual black hole population will lie in between.

For the expected abundance of $10^7~M_\odot$ black holes at z=5, we therefore adopt a fiducial number of $\sim$0.08 in a solid angle of (1')2, and a number of $\sim$0.03 at z=8. We estimate the uncertainty to be half an order of magnitude. Based on the large fluxes found in Sect. 5.1 and the results of Spaans & Meijerink (2008), we argue that even smaller systems with $10^6~M_\odot$ black holes should be detectable. Calculations by Shankar et al. (2009) show that the cumulative space density of high-redshift quasars increases by almost an order of magnitude if the minimum luminosity is lowered by an order of magnitude. Additional sources may be present as well, such as starburst galaxies or ULIRGS. One may therefore expect one active galaxy in a field of view of one arcmin2 at $z\sim6$.

At higher redshift, this number may however decrease significantly. Therefore, searching for new sources in an ALMA deep field seems difficult for z>6, and it is important that surveys as performed by JWST[*] provide a catalogue of high-redshift sources. Based on the estimates discussed here, we conclude that this may be sufficient to study black hole accretion between redshifts 6 and 10, and perhaps even beyond.

7 Conclusions

In this paper, we have explored how ALMA observations may help to extend our current knowledge concerning the observations of high-redshift quasars. An obvious result is that current observations of the starburst component can be done with higher resolution and higher sensitivity, which may therefore provide detailed local gas kinematics. Due to the higher sensitivity, it seems likely that also a number of the weaker fine-structure lines may be detected, like [NII] 122 $\mu $m for z>2.5, or [SIII] 34 $\mu $m and [SiII] 35 $\mu $m for z>11, providing a valuable independent probe of the gas chemistry.

Due to the combination of high resolution and high sensitivity, ALMA may however go beyond that and try to explore the centers of quasar host galaxies at high redshift. As the models presented here indicate, one may expect that the chemistry in these regions is dominated by X-ray emission from the central engine. In contrast to soft-UV photons, X-rays have high heating efficiencies and low efficiencies for dissociation. They can therefore give rise to an entirely different molecular cloud chemistry, and can excite high-J CO lines well above the (10-9) transition.

Additional probes for the central XDRs are available as well, in particular fine-structure lines like [OI] 63 $\mu $m, [OI] 146 $\mu $m and [CII] 158 $\mu $m. In particular for high X-ray luminosities, the fine-structure lines of [OI] 63 $\mu $m and [CII] 158 $\mu $m may provide a significant amount of flux even for gas densities of 104 cm-3. In general, the fine-structure lines become optically thick more easily than the rotational CO lines, in particular at densities of 105 cm-3. Therefore, they are almost insensitive to the column density, but quite sensitive to the X-ray flux. The CO lines, on the other hand, have a more non-trivial dependence on the X-ray flux and the column density, as in particular for high fluxes some dissociation effects will be present. If ideally both the CO lines and the fine-structure lines are observed, it may thus be possible to derive constraints both on column densities and the local X-ray flux. The line ratios may also provide valuable information on cloud gas density and temperature, as pointed out by Meijerink et al. (2007).

We have applied our models to available data for observed XDRs. For galaxies such as NGC 1068, we expect that the CO line intensity rises continuously up to the (17-16) transition. Such high excitation is not possible in PDR models (Spaans & Meijerink 2008). A detection of such lines therefore provides a unique diagnostic for an XDR.

We consider another example, the lensed galaxy APM 08279. There, the situation is not fully clear and is currently consistent with the presence of an XDR, which should also be expected due to the high X-ray luminosity, but also with the presence of a PDR with a radiation field of G0=104.5. To some degree, this is due to uncertainties in the measured line fluxes. We expect that improved measurements with ALMA may help to distinguish these scenarios further and probe the local gas motions in more detail.

We discussed the chances to find additional sources with ALMA in a survey that scans a few arcmin2. General considerations regarding the average accretion history indicate that quasar duty cycles should be larger at high redshift, so that black holes can grow to the required masses at z=6. We therefore expect more sources compared to what one expects from a naive extrapolation of the observed quasar population. Our estimates indicate that about one source per arcmin2 may be present near $z\sim6$. At larger redshift, the number of sources may decrease significantly and one may need to rely on follow-up observations of sources detected by JWST. Due to the potentially high spatial resolution, the transport of gas to the center of the host galaxy may be probed for the first time in such galaxies even at $z\sim10$.

We finally note that the diagnostics considered in this paper, in particular the high-J CO lines, may not only be important for high-redshift observations with ALMA, but also for future space-borne observations in the local universe with SPICA or FIRI.

Acknowledgements
We thank Robi Banerjee, Max Camenzind, Wilfred Frieswijk, Simon Glover, Edo Loenen, Rowin Meijerink, Padelis Papadopoulos, Dieter Poelman and Fabian Walter for valuable discussions on the topic. The research leading to these results has received funding from the European Community's Seventh Framework Programme (/FP7/2007-2013/) under grant agreement No 229517. RSK thanks the German Science Foundation (DFG) for support via the Emmy Noether grant KL 1358/1. DRGS and RSK also acknowledge subsidies from the DFG SFB 439 Galaxies in the Early Universe, and grant KL 1358/10 under the Priority Programme 1177 ``Witnesses of Cosmic History: formation and evolution of black holes, galaxies and their environment'' of the German Science Foundation, as well as via the FRONTIER program of Heidelberg University. In addition, R.S.K. thanks for subsidies from the German Bundesministerium für Bildung und Forschung via the ASTRONET project STAR FORMAT (grant 05A09VHA) and from the Landesstiftung Baden-Württemberg via their program International Collaboration II. We thank the anonymous referee for valuable comments that helped to improve the manuscript.

References

  1. Begelman, M. C., Volonteri, M., & Rees, M. J. 2006, MNRAS, 370, 289 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bradford, C. M., Aguirre, J. E., Aikin, R., et al. 2009, ApJ, 705, 112 [NASA ADS] [CrossRef] [Google Scholar]
  3. Carilli, C. L., Cox, P., Bertoldi, F., et al. 2002, ApJ, 575, 145 [NASA ADS] [CrossRef] [Google Scholar]
  4. Chartas, G., Brandt, W. N., Gallagher, S. C., & Garmire, G. P. 2002, ApJ, 579, 169 [NASA ADS] [CrossRef] [Google Scholar]
  5. Choudhury, T. R., & Ferrara, A. 2007, MNRAS, 380, L6 [NASA ADS] [Google Scholar]
  6. Davies, R. I., Mueller Sánchez, F., Genzel, R., et al. 2007, ApJ, 671, 1388 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, S. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
  8. Eisenstein, D. J., & Loeb, A. 1995, ApJ, 443, 11 [NASA ADS] [CrossRef] [Google Scholar]
  9. Fan, X., Strauss, M. A., Richards, G. T., et al. 2006, AJ, 131, 1203 [NASA ADS] [CrossRef] [Google Scholar]
  10. Freese, K., Bodenheimer, P., Spolyar, D., & Gondolo, P. 2008, ApJ, 685, L101 [NASA ADS] [CrossRef] [Google Scholar]
  11. Galliano, E., & Alloin, D. 2002, A&A, 393, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Galliano, E., Alloin, D., Granato, G. L., & Villar-Martín, M. 2003, A&A, 412, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Greenhill, L. J., Gwinn, C. R., Antonucci, R., & Barvainis, R. 1996, ApJ, 472, L21 [NASA ADS] [CrossRef] [Google Scholar]
  14. Greve, T. R., Papadopoulos, P. P., Gao, Y., & Radford, S. J. E. 2009, ApJ, 692, 1432 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hao, L., Wu, Y., Charmandaris, V., et al. 2009, ApJ, 704, 1159 [NASA ADS] [CrossRef] [Google Scholar]
  16. Hollenbach, D. J., & Tielens, A. G. G. M. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
  17. Iocco, F. 2008, ApJ, 677, L1 [NASA ADS] [CrossRef] [Google Scholar]
  18. Iocco, F., Bressan, A., Ripamonti, E., et al. 2008, IAU Symp., 255, 61 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kawakatu, N., & Wada, K. 2009, ApJ, 706, 676 [NASA ADS] [CrossRef] [Google Scholar]
  20. Klamer, I. J., Ekers, R. D., Sadler, E. M., et al. 2005, ApJ, 621, L1 [NASA ADS] [CrossRef] [Google Scholar]
  21. Kollmeier, J. A., Onken, C. A., Kochanek, C. S., et al. 2006, ApJ, 648, 128 [NASA ADS] [CrossRef] [Google Scholar]
  22. Koushiappas, S. M., Bullock, J. S., & Dekel, A. 2004, MNRAS, 354, 292 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lepp, S., & Dalgarno, A. 1996, A&A, 306, L21 [NASA ADS] [Google Scholar]
  24. Lodato, G., & Natarajan, P. 2006, MNRAS, 371, 1813 [NASA ADS] [CrossRef] [Google Scholar]
  25. Loenen, A. F., Spaans, M., Baan, W. A., & Meijerink, R. 2008, A&A, 488, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Maiolino, R., Neri, R., Beelen, A., et al. 2007, A&A, 472, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [NASA ADS] [CrossRef] [Google Scholar]
  28. McCall, B. J., Geballe, T. R., Hinkle, K. H., & Oka, T. 1999, ApJ, 522, 338 [NASA ADS] [CrossRef] [Google Scholar]
  29. Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Meijerink, R., Spaans, M., & Israel, F. P. 2006, ApJ, 650, L103 [NASA ADS] [CrossRef] [Google Scholar]
  31. Meijerink, R., Spaans, M., & Israel, F. P. 2007, A&A, 461, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Nagai, M., Tanaka, K., Kamegai, K., & Oka, T. 2007, PASJ, 59, 25 [NASA ADS] [Google Scholar]
  33. Nagayama, T., Omodaka, T., Handa, T., et al. 2007, PASJ, 59, 869 [NASA ADS] [Google Scholar]
  34. Oka, T., Geballe, T. R., Goto, M., Usuda, T., & McCall, B. J. 2005, ApJ, 632, 882 [NASA ADS] [CrossRef] [Google Scholar]
  35. Omont, A., Petitjean, P., Guilloteau, S., et al. 1996, Nature, 382, 428 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  36. Papadopoulos, P. P., Kovacs, A., Evans, A. S., & Barthel, P. 2008, A&A, 491, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Peebles, P. J. E. 1993, Principles of physical cosmology, Princeton Series in Physics (Princeton, NJ: Princeton University Press) [Google Scholar]
  38. Pérez-Beaupuits, J. P., Aalto, S., & Gerebro, H. 2007, A&A, 476, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Pérez-Beaupuits, J. P., Spaans, M., van der Tak, F. F. S., et al. 2009, A&A, 503, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Poelman, D. R., & Spaans, M. 2005, A&A, 440, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Poelman, D. R., & Spaans, M. 2006, A&A, 453, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Riechers, D. A., Walter, F., Brewer, B. J., et al. 2008a, ApJ, 686, 851 [NASA ADS] [CrossRef] [Google Scholar]
  43. Riechers, D. A., Walter, F., Carilli, C. L., Bertoldi, F., & Momjian, E. 2008b, ApJ, 686, L9 [NASA ADS] [CrossRef] [Google Scholar]
  44. Riechers, D. A., Walter, F., Bertoldi, F., et al. 2009a, ApJ, 703, 1338 [NASA ADS] [CrossRef] [Google Scholar]
  45. Riechers, D. A., Walter, F., Carilli, C. L.,& Lewis, G. F. 2009b, ApJ, 690, 463 [NASA ADS] [CrossRef] [Google Scholar]
  46. Schinnerer, E., Eckart, A., Tacconi, L. J., Genzel, R., & Downes, D. 2000, ApJ, 533, 850 [NASA ADS] [CrossRef] [Google Scholar]
  47. Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2008, Phys. Rev. D, 78, 083005 [NASA ADS] [CrossRef] [Google Scholar]
  48. Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2009, Phys. Rev. D, 79, 043510 [NASA ADS] [CrossRef] [Google Scholar]
  49. Shankar, F., Salucci, P., Granato, G. L., De Zotti, G., & Danese, L. 2004, MNRAS, 354, 1020 [NASA ADS] [CrossRef] [Google Scholar]
  50. Shankar, F., Weinberg, D. H., & Miralda-Escudé, J. 2009, ApJ, 690, 20 [NASA ADS] [CrossRef] [Google Scholar]
  51. Shapiro, S. L. 2005, ApJ, 620, 59 [NASA ADS] [CrossRef] [Google Scholar]
  52. Spaans, M., & Meijerink, R. 2008, ApJ, 678, L5 [NASA ADS] [CrossRef] [Google Scholar]
  53. Spaans, M., & Silk, J. 2006, ApJ, 652, 902 [NASA ADS] [CrossRef] [Google Scholar]
  54. Spinoglio, L., Malkan, M. A., Smith, H. A., González-Alfonso, E., & Fischer, J. 2005, ApJ, 623, 123 [NASA ADS] [CrossRef] [Google Scholar]
  55. Spolyar, D., Freese, K., & Gondolo, P. 2008, Phys. Rev. Lett., 100, 051101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  56. Spoon, H. W. W., Marshall, J. A., Houck, J. R., et al. 2007, ApJ, 654, L49 [NASA ADS] [CrossRef] [Google Scholar]
  57. Thompson, T. A., Quataert, E., & Murray, N. 2005, ApJ, 630, 167 [NASA ADS] [CrossRef] [Google Scholar]
  58. Treister, E., Urry, C. M., & Virani, S. 2009, ApJ, 696, 110 [NASA ADS] [CrossRef] [Google Scholar]
  59. Verner, D. A., & Yakovlev, D. G. 1995, A&AS, 109, 125 [NASA ADS] [Google Scholar]
  60. Wada, K., & Norman, C. A. 2007, ApJ, 660, 276 [NASA ADS] [CrossRef] [Google Scholar]
  61. Wada, K., Papadopoulos, P. P., & Spaans, M. 2009, ApJ, 702, 63 [NASA ADS] [CrossRef] [Google Scholar]
  62. Walter, F., Carilli, C., Bertoldi, F., et al. 2004, ApJ, 615, L17 [CrossRef] [Google Scholar]
  63. Walter, F., Riechers, D. A., Carilli, C. L., et al. 2007, From Z-Machines to ALMA: (Sub)Millimeter Spectroscopy of Galaxies, ed. A. J. Baker, J. Glenn, A. I. Harris, J. G. Mangum, & M. S. Yun, ASP Conf. Ser., 375, 182 [Google Scholar]
  64. Walter, F., Riechers, D., Cox, P., et al. 2009a, Nature, 457, 699 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  65. Walter, F., Weiß, A., Riechers, D. A., et al. 2009b, ApJ, 691, L1 [NASA ADS] [CrossRef] [Google Scholar]
  66. Weiß, A., Downes, D., Neri, R., et al. 2007, A&A, 467, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Weiß, A., Downes, D., Walter, F., & Henkel, C. 2005, A&A, 440, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Footnotes

... SPICA[*]
http://www.ir.isas.jaxa.jp/SPICA/index.html
... FIRI[*]
http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=40090
... ALMA[*]
http://www.eso.org/sci/facilities/alma/
...Meijerink et al. (2007)[*]
http://www.strw.leidenuniv.nl/ meijerin/grid/
... luminosity[*]
For the conversion between X-ray luminosity and flux, we assumed optically thin conditions. One may need to correct for further attenuation in case of large filling-factors.
... JWST[*]
http://www.jwst.nasa.gov/

All Tables

Table 1:   The main observables for ALMA in PDRs at high redshift.

Table 2:   Frequency range, angular resolution $\theta _{{\rm res}}$ at the largest baseline, line sensitivity $S_{\rm l}$ for a linewidth of 300 km s-1 and continuum sensitivity $S_{\rm c}$ for $3\sigma $ detection in one hour of integration time and primary beam size $\theta _{{\rm beam}}$.

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{13467fg1.eps} \end{figure} Figure 1:

The heating rates per hydrogen atom due to X-ray absorption (XDR contribution), absorption of soft UV-photons (PDR contribution) and total heating rate as a function of radius. The calculation assumes a $10^7~M_\odot$ black hole, with $3\%$ of its Eddington luminosity being emitted in a hard spectral component between 1 and 100 keV with a spectral slope of -1. The strength of the soft UV radiation field is taken as G0=10 in Habing units and the effective density $n_{{\rm eff}}=10^5$ cm-3. For such a configuration, the XDR contribution clearly dominates within the central 100 pc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{13467fg2.eps} \end{figure} Figure 2:

The expected size of the X-ray dominated region in pc, for a black hole with $10^7~M_\odot$ with a spectral slope of -1, as a function of the soft UV radiation field G0 in Habing units and the effective number density $n_{{\rm eff}}$. The straight lines assume the power-law between 1 and 5 keV, while the dotted lines assume it between 1 and 100 keV.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13467fg3.eps} \end{figure} Figure 3:

A model for the X-ray chemistry in NGC 1068. The adopted flux impinging on the cloud is 170 erg s-1 cm-2. The adopted density is 105 cm-3. Top: the abundances of different species as a function of column density. Middle: the low-J CO lines as a function of column density. Bottom: the high-J CO lines as a function of column density.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13467fg4.eps} \end{figure} Figure 4:

The X-ray chemistry in a system with X-ray flux of 1 erg s-1 cm-2 impinging on the cloud. The adopted density is 105 cm-3. Top: the abundances of different species as a function of column density. Middle: the low-J CO lines as a function of column density. Bottom: the high-J CO lines as a function of column density.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13467fg5.eps} \end{figure} Figure 5:

The X-ray chemistry in a system with X-ray flux of 10 erg s-1 cm-2 impinging on the cloud. The adopted density is 105 cm-3. Top: the abundances of different species as a function of column density. Middle: the low-J CO lines as a function of column density. Bottom: the high-J CO lines as a function of column density.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13467fg6.eps} \end{figure} Figure 6:

A comparison of the CO line SED in case of an intense starburst with G0=105 with the corresponding SED for molecular clouds under X-ray irradiation, for different X-ray fluxes in erg s-1 cm-2. The spectra are normalized such that they have the same intensity in the 10th transition. If the impinging X-ray flux is at least 2.8 erg s-1 cm-2, observations of the 15th CO rotational transition can clearly discriminate between PDR and XDR chemistry.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg7.eps} \end{figure} Figure 7:

The expected flux in mJy for high-J CO lines, for a central XDR of 200 pc, and molecular clouds of 105 cm-3, as a function of X-ray luminosity and cloud column density. We focus on lines that fall in ALMA band 6, which offers a good compromise between angular resolution and sensitivity. For a source at z=5 (solid line), this corresponds to the (10-9) CO transition, for a source at z=8, it corresponds to the (14-13) CO transition.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg8.eps} \end{figure} Figure 8:

The expected flux in mJy for the [CII] 158 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 105 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 7, with a sensitivity of 0.08 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 6 with a sensitivity of 0.04 mJy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg9.eps} \end{figure} Figure 9:

The expected flux in mJy for the [CII] 158 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 104 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 7, with a sensitivity of 0.08 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 6 with a sensitivity of 0.04 mJy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg10.eps} \end{figure} Figure 10:

The expected flux in mJy for the [OI] 63 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 105 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 10, with a sensitivity of 0.2 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 8 with a sensitivity of 0.13 mJy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg11.eps}\end{figure} Figure 11:

The expected flux in mJy for the [OI] 63 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 104 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 10, with a sensitivity of 0.2 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 8 with a sensitivity of 0.13 mJy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg12.eps} \end{figure} Figure 12:

The expected flux in mJy for the [OI] 146 $\mu $m line, for a central XDR of 200 pc, and molecular clouds of 105 cm-3, as a function of X-ray luminosity and cloud column density. The solid line corresponds to a source at z=5, and the dashed line to a source at z=8. At z=5, the line is redshifted into ALMA band 7, with a sensitivity of 0.37 mJy (1 day, $3\sigma $, 300 km s-1). At z=8, it falls into ALMA band 6 with a sensitivity of 0.225 mJy.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg13.eps} \end{figure} Figure 13:

The expected flux in mJy for the CO (14-13) transition (solid line), [CII] 158 $\mu $m (dotted line), [OI] 63 $\mu $m (dashed line) and [OI] 146 $\mu $m (dot-dashed line) emission for a quasar at z=5, as a function of X-ray luminosity and average density. We assume a typical cloud column density of 1023 cm-2, and a soft-UV field G0=100.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg14.eps}\vspace*{-2mm} \end{figure} Figure 14:

The expected flux in mJy for the CO (14-13) transition (solid line), [CII] 158 $\mu $m (dotted line), [OI] 63 $\mu $m (dashed line) and [OI] 146 $\mu $m (dot-dashed line) emission for a quasar at z=8, as a function of X-ray luminosity and cloud column density. We assume a typical cloud density of 104 cm-3, and a soft-UV field G0=100.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg15.eps} \end{figure} Figure 15:

A sketch for a situation with an inhomogeneous XDR, motivated by the observations of Galliano et al. (2003) in NGC 1068. While X-rays are shielded by a central absorber along the line of sight, they may stimulate emission in molecular clouds in the perpendicular direction with the typical characteristics of XDRs.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg16.eps} %\end{figure} Figure 16:

The average accretion history of a black hole with $10^7~M_\odot$ at z=5, depending on a coefficient p which is a function of the conversion of rest-mass energy to luminous energy, the Eddington ratio and the duty cycle.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13467fg17.eps} % \vspace*{-3mm} \end{figure} Figure 17:

Estimates for the number of sources in a redshift interval of $\Delta z=0.5$ within a solid angle of (1')2. We show extrapolations of the results by Shankar et al. (2009) and Treister et al. (2009) to high redshift, for luminosities larger than 1044 erg s-1. In addition, we give an estimate based on the number of high-redshift black holes required in order to produce the present-day $10^9~M_\odot$ black holes. As discussed in the text, the actual number of black holes should lie in between these estimates.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.