EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) A1 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number A1
Number of page(s) 8
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200913379
Published online 09 April 2010
A&A 513, A1 (2010)

Probing quiet Sun magnetism using MURaM simulations and Hinode/SP results: support for a local dynamo

S. Danilovic1,2 - M. Schüssler1 - S. K. Solanki1,3

1 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Straße 2, 37191 Katlenburg-Lindau, Germany
2 - Astronomical Observatory, Volgina 7, 11160 Belgrade 74, Serbia
3 - School of Space Research, Kyung Hee University, Yougin, Gyeonggi 446-701, Korea

Received 30 September 2009 / Accepted 23 December 2009

Abstract
Context. Owing to the limited spatial resolution and the weak polarization signal coming from the quietest regions on the Sun, the organization of the magnetic field on the smallest scales is largely unknown.
Aims. We obtain information about the magnetic flux present in the quiet Sun by comparing radiative MHD simulations with observations, with particular emphasis on the role of surface dynamo action.
Methods. We synthesized Stokes profiles on the basis of the MHD simulation results. The profiles are degraded by taking the properties of the spectropolarimeter (SP) into account onboard the Hinode satellite. We used simulation runs with different magnetic Reynolds numbers ($R_{\rm m}$) and observations at different heliocentric angles with different levels of noise.
Results. Simulations with an imposed mixed-polarity field and $R_{\rm m}$ below the threshold for dynamo action reproduce the observed vertical flux density, but do not display a high enough horizontal flux density. Surface dynamo simulations at the highest $R_{\rm m}$ feasible at the moment yield a ratio of the horizontal and vertical flux density consistent with observational results, but the overall amplitudes are too low. Based on the properties of the local dynamo simulations, a tentative scaling of the magnetic field strength by a factor 2-3 reproduces the signal observed in the internetwork regions.
Conclusions. We find agreement with observations at different heliocentric angles. The mean field strength in internetwork implied by our analysis is roughly 170 G at the optical depth unity. Our study shows that surface dynamo could be responsible for most of the magnetic flux in the quiet Sun outside the network, given that the extrapolation to higher $R_{\rm m}$ is valid.

Key words: Sun: granulation - Sun: photosphere

1 Introduction

The origin of the small-scale magnetic flux found in the quiet Sun is uncertain (de Wijn et al. 2008). The estimated order of magnitude for the magnetic Reynolds number of the granulation flow indicates that a substantial part of the magnetic field in the quiet Sun could be generated locally through dynamo action driven by near-surface convective flows (Petrovay & Szakaly 1993; Vögler & Schüssler 2007; Cattaneo 1999). The simulations suggest that the magnetic field could be organized in mixed-polarity structures down to very small spatial scales. The simulations exhibit a mostly horizontal field in the photospheric layers in the form of low-lying loops connecting nearby opposite polarities (Schüssler & Vögler 2008).

Substantial observational evidence has been gathered showing that internetwork flux is dominated by strongly inclined, almost horizontal magnetic fields (Orozco Suárez et al. 2007a; Lites et al. 2008; Orozco Suárez et al. 2007b). The validity of the deduced properties has been questioned by Asensio Ramos (2009), who argues that the influence of noise has not been adequately taken into account in such studies. Nevertheless, several authors report loop-like horizontal field structures of different sizes (Harvey et al. 2007; Ishikawa et al. 2008; Martínez González et al. 2007; Centeno et al. 2007; Martin 1988). Such structures could be due to local dynamo action, but small-scale flux emergence (Cheung et al. 2008) or flux expulsion of a pre-existing field by granular flows (Steiner et al. 2008) probably also contribute to the horizontal flux.

Another open question concerns the amount of magnetic flux contained in the internetwork. The observations give a wide range of values that vary with the spatial resolution and the diagnostic technique used (e.g, Khomenko et al. (2003); Berdyugina & Fluri (2004); Asensio Ramos et al. (2007); Domínguez Cerdeña et al. (2003)). From the many results (see Solanki 2009; de Wijn et al. 2008, for overviews), we mention here only those that directly concern the work presented in this paper. Comparing the center-to-limb observations of the scattering polarization in the Sr I 4607 Å line with the signal synthesized from the 3D hydrodynamical simulations, Trujillo Bueno et al. (2004) infer that the mean strength of the internetwork field is $\langle B\rangle\sim100$ G, under the assumption that the magnetic field is isotropically tangled at subresolution scales and that it fills the whole resolution element. Khomenko et al. (2005a), on the other hand, compared the observed Stokes V amplitudes of the visible and infrared Fe I lines with the profiles synthesized from 3D radiative MHD simulations, and conclude that $\langle B\rangle\sim20$ G (see also Bello González et al. 2009). Sánchez Almeida et al. (2003) used Boussinesq 3D simulations of local dynamo action to suggest that a snapshot with mean longitudinal magnetic field of 50 G can reproduce both the observed Hanle and Zeeman signals. However, the simulations used by these authors are somewhat idealized and the solar atmospheric structure is arbitrarily introduced for comparison with the observational data.

Table 1:   Details of the three Hinode/SP data sets used.

In this paper, we use 3D radiative MHD simulations of the solar photosphere to obtain an estimate of the true magnetic flux density in the quiet Sun. Our approach differs from that of Khomenko et al. (2005a) by considering also fields produced by a local dynamo action. In addition, the synthesized polarization signals are compared with the higher resolution data, obtained with the spectropolarimeter (Lites et al. 2001) of the Solar Optical telescope (Tsuneta et al. 2008) on board of the Hinode satellite (Kosugi et al. 2007). The comparison with the simulations at the highest $R_{\rm m}$ feasible at the moment allows us to gain insight into the role of the local dynamo action for the quiet Sun magnetism.

2 Observations

We consider three data sets obtained with the spectropolarimeter (SP) onboard Hinode. Details are given in Table 1. Data sets I and II were recorded near disk center, while data set III was obtained closer to the limb. Data sets I and III were obtained in the scan mode of the Hinode/SP, with an exposure time of 9.6 s per slit position. They cover quiet Sun regions at the disk center and a region near the south solar pole, respectively. In the case of data set III, we used a $32\hbox{$^{\prime\prime}$ }$ wide strip perpendicular to the scan direction that corresponds to $\mu=0.4$($\mu $ being the cosine of the heliocentric angle). Corrections for various instrumental effects were made using the procedure sp_prep, included in the SolarSoft[*] package. The procedure gives the longitudinal and transversal magnetic flux density maps (Lites et al. 2008) shown in Fig. 1. The mean values are given in Table 1. The rms continuum contrast values for data sets I and III are 7.5% and 5.1% respectively.

Data set II is a time series recorded with fixed slit position. It consists of 103 scans at solar disk center, each with an exposure time of 9.6 s. After applying a temporal running mean, the effective exposure time becomes 67.2 s, which gives a significantly lower level of noise. This data set has been used previously by Lites et al. (2008) and Orozco Suárez et al. (2007b).

\begin{figure} \par\includegraphics[angle=90,width=15.5cm,clip]{13379fg1.ps} \end{figure} Figure 1:

Maps of longitudinal ( $B_{\rm app}^{\rm L}$) and transversal ( $B_{\rm app}^{\rm T}$) apparent flux density for the observed data sets I ( left) and III ( right) from Table 1. The small squares indicate the sizes of the MHD snapshots. They also mark the position of the regions to which synthesized maps from simulation data are compared (Figs. 4 and 5).

Open with DEXTER

3 Simulation data

We used results from 3D radiative MHD simulations of a layer containing the solar surface, carried out with the MURAM code (Vögler et al. 2005; Vögler 2003). Non-gray LTE radiative transfer and partial ionization are taken into account. We compared snapshots from several simulation runs. The basic properties of the computational domains are given in Table 2. In all runs, the top of the simulation box is located about 500 km above the average height level of optical depth unity. The side boundaries are periodic, whereas the bottom boundary is open, permitting free in and outflow of matter. The magnetic field is vertical at the top and bottom boundaries.

The first run, henceforth referred to as the ``mixed polarity'' run, simulates the decay of the magnetic field in a mixed polarity region. In this run, local dynamo action (Vögler & Schüssler 2007) does not occur since the magnetic Reynolds number is below the threshold for dynamo action. The run starts with a vertical magnetic field of |B| = 200 G, in a checkerboard-like $2\times2$ pattern, with opposite polarities in adjacent parts. The field is concentrated and redistributed by the convective motions, and the opposite polarities are pushed together, which results in flux cancellation and an almost exponential decrease in the mean magnetic field strength. The snapshots with $\langle\vert B\vert\rangle = 35$ G and $\langle\vert B\vert\rangle = 20$ G averaged over the surface $\tau=0.1$ were used in our study. The same snapshots were used by Khomenko et al. (2005b,a).

The second and third groups of snapshots were taken from the runs with a magnetic Reynolds number of the flow sufficiently high for small-scale turbulent dynamo action to take place. A seed field of |B0|=10 mG grows exponentially in time until the saturation level is reached. In the dynamo run C, described in Vögler & Schüssler (2007), the mean magnetic field strength at this phase is $\langle\vert B\vert\rangle =23$ G at $\tau=0.1$. In the case of the dynamo run G, the higher magnetic Reynolds number leads to a saturation level of the magnetic energy that is a factor of 1.7 higher than in run C. Figure 2 shows the mean magnetic field strength (averaged over surfaces of constant $\tau$) as a function of the optical depth for one snapshot from each run. The field from dynamo C run is multiplied by a factor 1.5, to illustrate the similarity of the scaled optical depth profiles in the dynamo runs. This factor differs only by $\sim$15% from $\sqrt{1.7}$, the square root of the corresponding total magnetic energy ratio. This indicates that a tentative scaling of the dynamo-generated field to represent higher Reynolds numbers is not completely unreasonable. Figure 2 shows the optical depth profiles of the horizontal magnetic field, i.e., $\langle B_{\rm hor}\rangle=\langle\!\sqrt{B_{x}^{2} + B_{y}^{2}}\rangle$ and the average vertical field $\langle \vert B_{\rm vert}\vert\rangle$. The dynamo runs have a significantly larger $\langle B_{\rm hor}\rangle$ than $\langle \vert B_{\rm vert}\vert\rangle$. Their ratio reaches values between 2 and 4 in the optical depth interval $-2<\log \tau<-1$. The mixed polarity snapshot, on the other hand, has a $\langle B_{\rm hor}\rangle$ and $\langle \vert B_{\rm vert}\vert\rangle$ of similar magnitude over all heights.

\begin{figure} \par\includegraphics[angle=90,width=8.4cm,clip]{13379fg2.ps} \vspace*{-2mm}\end{figure} Figure 2:

Average total (solid), horizontal (dashed), and vertical (dotted) mean magnetic field strength from MURaM simulations as a function of the optical depth. Snapshots from different runs are indicated by line color: mixed polarity (blue), dynamo G (red), dynamo C multiplied by factor of 1.5 (black), and dynamo C with background unipolar field (green).

Open with DEXTER

The last group of snapshots is taken from a simulation run that continues dynamo run C with a superposed unipolar vertical field. Such a superposition might be a way of describing a weak network region. The mean vertical field strength is thereby increased to around 36 G at $\tau=0.1$ and the strength of the horizontal field to around 50 G at $\tau=0.1$ (Fig. 2).

Table 2:   The simulation parameters with the size of computational domain and vertical ($\delta {z}$) and horizontal ($\delta {x}$) grid spacing.

4 Spectral synthesis

The simulation results have been used as input for the LTE radiative transfer code SPINOR (Frutiger et al. 2000) to synthesize the Stokes profiles for the heliocentric angles  $\theta =0^{\circ }$ and $66^{\circ}$ (corresponding to $\mu=1$ and $\mu=0.4$, respectively). The spectral range that contains the Fe I lines at 630.15 and 630.25 nm is sampled in steps of 7.5 mÅ. The Fe abundance used in the synthesis has been taken from Thevenin (1989) and the values of the oscillator strengths from the VALD database (Piskunov et al. 1995). We then applied a realistic point spread function (PSF, Danilovic et al. 2008) to the maps of synthesized Stokes profiles. The PSF takes the basic optical properties of the Hinode SOT/SP system and a small defocus into account. Applying an ideal PSF without defocus reduces the original rms contrast values of the simulated continuum map from 14.5% to 8.5% ( $\theta =0^{\circ }$) and 11.2% to 5.5% ( $\theta =66^{\circ }$), respectively. For the comparison with the observations at $\theta =0^{\circ }$, we used a defocus of -1.5 mm, which degrades the continuum contrast of the simulation to the observed value of 7.5%. A value of -0.75 mm is used for the synthesized data at $\theta =66^{\circ }$ in order to match the continuum contrast of 5.1% deduced from dataset III. The difference in the focus of the SOT between data sets I and III amounts to approximately 2 steps of the SOT focus mechanism.

\begin{figure} \par\includegraphics[angle=90,width=13.5cm,clip]{13379fg3.ps} \vspace*{2mm}\end{figure} Figure 3:

Histograms of the mean horizontal ( left), the unsigned vertical ( middle) and the signed vertical ( right) magnetic flux density calculated for $7\hbox {$^{\prime \prime }$ }\times 7\hbox {$^{\prime \prime }$ }$ size regions covered by dataset I. The vertical lines mark the mean values for the whole field of view.

Open with DEXTER
Considering that there is an uncertainty of one focus step in the focusing mechanism, the amounts of defocus obtained from reproducing the observed data sets seem plausible.

The appropriate PSF is applied to the 2D maps at each wavelength position for every Stokes parameter. The degraded maps are then rebinned to the pixel size of the Hinode/SP detector. To take the spectral resolution of the spectropolarimeter into account, the profiles are convolved with a Gaussian function of 25 mÅ FWHM and resampled to a wavelength spacing of 21.5 mÅ. Next, a noise level corresponding to the observations is added, and finally the procedure by Lites et al. (2008) is used to calculate the longitudinal and transversal apparent magnetic flux densities, $B^{\rm L}_{\rm app}$ and $B^{\rm T}_{\rm app}$.

5 Results

We present our results in the following sequence: (1) snapshots from the simulation runs are compared with the disk center observations in terms of the mean values of $B^{\rm L}_{\rm app}$ and $B^{\rm T}_{\rm app}$; (2) the spatial distribution of the magnetic features in the observed and in the synthesized maps is compared; (3) a comparison of the probability density functions (PDFs) from the simulations and from the low-noise data set II is presented. Finally, we show how the mean magnetic flux density changes with the heliocentric angle and compare the synthesized and observed signal at a heliocentric angle of $\theta =66^{\circ }$.

5.1 Comparison with the observations at disk center

Table 3:   Mean apparent magnetic flux densities from observations and simulations.

When comparing the observational signals with the ones synthesized from the simulations, one has to take into account that the solar surface area covered by the observations of data set I is much larger than that for the simulations. The small squares in Fig. 1 indicate the actual size of the simulation snapshots. To take this proportion into account, we divided the region covered by the observations into subdomains of $7\hbox {$^{\prime \prime }$ }\times 7\hbox {$^{\prime \prime }$ }$. For each of these, we calculated the mean transversal $\langle B^{\rm T}_{\rm app}\rangle$, the mean unsigned longitudinal $\langle \vert B^{\rm L}_{\rm app}\vert\rangle$ and the mean signed longitudinal $\langle B^{\rm L}_{\rm app}\rangle$ apparent magnetic flux densities. The histograms of these quantities are shown in Fig. 3. By considering the contribution of each subdomain separately, we could exclude the contribution of the network, which extends the wings of the histograms towards higher values of $\langle B^{\rm T}_{\rm app}\rangle$ and $\langle \vert B^{\rm L}_{\rm app}\vert\rangle$. The maxima of the distributions, on the other hand, give an estimate of the typical magnetic flux density value in the internetwork regions. Consequently, when the whole observed region is considered, the mean values (marked by the vertical lines in Fig. 3) are higher than the values retrieved from the maxima. The mean values over the whole FOV agree with the values obtained by Lites et al. (2008) and show a ratio of $\langle B^{\rm T}_{\rm app}\rangle/\langle \vert B^{\rm L}_{\rm app}\vert\rangle=5.8$.

The values retrieved from the distribution maxima are given in the first row of Table 3. The other numbers are the results obtained from the synthesized Stokes profiles from the simulation snapshots, with the values determined from the snapshots at their original resolution given in parenthesis. They roughly correspond to the mean vertical and horizontal field strengths near $\tau=0.1$ (cf. Fig. 2). Thus, the ratio $\langle B^{\rm T}_{\rm app}\rangle/\langle B^{\rm L}_{\rm app}\rangle$obtained from the simulations at the original resolution reflects the ratio of the underlying magnetic fields at $\tau=0.1$. The values are close to unity for the mixed-polarity run and about 3for the dynamo snapshots. For the dynamo snapshots, the values $\langle \vert B^{\rm L}_{\rm app}\vert\rangle$ after spatial smearing and application of noise are considerably reduced compared to the noise-free, unsmeared case owing to the presence of mixed polarities on very small scales. On the other hand, $\langle B^{\rm T}_{\rm app}\rangle$ is increased for all groups of snapshots, except for the dynamo run C with unipolar background field. This is the result of the noise added to the Stokes profiles in order to simulate the Hinode/SP observations. The row labeled ``noise'' in Table 3 gives values determined from pure white noise with a standard deviation corresponding to the noise level of data set I. We give the mean values from 100 realizations. The value of $\langle B^{\rm T}_{\rm app}\rangle$ determined from pure noise is almost as high as the values retrieved from the dynamo snapshots, with the exception of the dynamo run C with a unipolar background field. This means that hardly any signal of $B^{\rm T}_{\rm app}$ remained above the noise after spatial smearing and introduction of noise. Dynamo C run with a unipolar field is a special case because it has a much higher mean field (cf. Fig. 2). The more magnetic flux introduced, the more the field can be tangled by the turbulent flows, so that noticeably more horizontal field is generated.

The last two rows of Table 3 show the results of the attempt to estimate how much field the dynamo simulations would have to contain to reproduce the observed $\langle B^{\rm T}_{\rm app}\rangle$ and $\langle \vert B^{\rm L}_{\rm app}\vert\rangle$ values. Multiplying the magnetic field strengths by factors of 2 and 3(everywhere in the simulation box) in the case of the dynamo run G and dynamo run C, respectively, gives a mean total magnetic field strength of 170 G and 67 G at the levels of $\tau=1$ and $\tau=0.1$, respectively. The strength of the mean vertical magnetic field at the same levels becomes 84 G and 27 G, respectively. These values are consistent with the extrapolation by Pietarila Graham et al. (2009)on the basis of Hinode data. Also, as we have seen in Fig. 2, the average mean field strength distribution of run G can be reproduced by multiplying run C result by a factor roughly corresponding to the square root of the ratio of the total magnetic energies. This suggests that such a simple scaling might extend somewhat into the $R_{\rm m}$regime that is not covered by the simulations. The necessary scaling factor of 2 for run G is not unreasonably large.

Figure 4 shows one snapshot from the dynamo run C with the field multiplied by a factor of 3, before and after spatial smearing, together with an observed region of the same size. Maps of the longitudinal $B^{\rm L}_{\rm app}$ and transversal $B^{\rm T}_{\rm app}$ magnetic flux density are shown. The granular pattern is indicated by white contours of normalized continuum intensity equal to 1.05. Vertical fields with mixed polarities on scales of less than a third of an arcsec are smeared into unipolar ``tube'' or ``sheet''-shaped patches (yellow and blue in the central frame). The bundles of horizontal field, composed of loops of different sizes, are molded into patches with higher $B_{\rm app}^{\rm T}$ values. These can occur on the edges of granules or between patches with vertical field of opposite polarity (see, for instance, the feature at $[4.5\hbox{$^{\prime\prime}$ },2\hbox{$^{\prime\prime}$ }]$). Similar features can be seen in the Hinode maps, e.g. in the two lower frames on the right (see also Lites et al. 2008; Ishikawa et al. 2008)). At the position [ $5\hbox{$^{\prime\prime}$ },3.5\hbox{$^{\prime\prime}$ }$] in the central frame, a vertical field of $B_{\rm app}^{\rm L}\approx20$ Mx/cm2 is located inside a granule. A similar case has been observed by Orozco Suárez et al. (2008).

Figure 5 shows a different region on the Sun, with more vertical flux (outlined by the yellow square in Fig. 1) compared with a snapshot from the dynamo run C with a unipolar background field. No scaling of the dynamo field has been carried out here. The maps based on the simulation show features that are very similar to the structures present in the observed weak network region, although the $B_{\rm app}^{\rm T}$ signal is somewhat weaker than in the observations. Small patches of horizontal field correspond to small loops that are visible between concentrations of the vertical flux at the original resolution of the simulations.

\begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13379fg4.ps} \end{figure} Figure 4:

Comparison of a snapshot from dynamo run C with magnetic field scaled by a factor 3 at original ( left column) and Hinode ( middle column) resolution, with Hinode observations ( right column). From top to bottom: normalized intensity, longitudinal and transversal apparent magnetic flux density. The observed region is outlined by a white square in Fig. 1. White lines outline the contours of normalized continuum intensity equal to 1.05.

Open with DEXTER

5.2 Comparison with the data set II

Pietarila Graham et al. (2009) demonstrated how different effects can influence the probability density function (PDF) of magnetic field derived from Stokes V spectra, such that it differs from the PDF of the underlying magnetic field. In particular, the effect of noise leads to a PDF with a peak at the position that corresponds to the noise level. Here we compare the PDFs of $B^{\rm L}_{\rm app}$(lefthand panels) and $B_{\rm app}^{\rm T}$ (righthand panels) determined from the synthesized Stokes profiles with those from observations. Figure 6 shows, from top to bottom, PDFs computed for the mixed polarity (20 G) snapshot, a snapshot from the dynamo run C without scaling, and from the dynamo run C after scaling by a factor of 3. Overplotted are the results calculated from pure noise with a standard deviation corresponding to the noise level of the observations and the PDFs obtained from data set II.

The figure shows that all the PDFs from the simulation snapshots at Hinode resolution are strongly influenced by the noise at the lowest field strengths, which is also the case for the PDF based on the Hinode data. The noise-induced maxima lie at approximately $B^{\rm L}_{\rm app}\approx 1$ G and $B_{\rm app}^{\rm T}\approx 20$ G. Due to the mixed polarity field on small scales, dynamo run C shows significant loss of stronger signals after spatial smearing. The mixed-polarity simulation snapshot, on the other hand, contains larger unipolar patches so that it retains a considerable amount of the stronger vertical field. Its PDF for $B_{\rm app}^{\rm L}$ has an extended tail of stronger field, which corresponds to the observed distribution. In the observations, this extended tail is a result of the contribution of the network flux concentrations. The $B_{\rm app}^{\rm T}$ distributions of both mixed-polarity and dynamo C run snapshots follow closely the distribution generated from the pure noise, which means that the signature of the horizontal field is mostly lost in the noise. Only a low percentage of the pixels show a $B^{\rm T}_{\rm app}$ signal above the noise level. However, after scaling the original field values by a factor 3, the PDF for $B_{\rm app}^{\rm T}$ (bottom row of the Fig. 6) agrees well with the observed one. Small discrepancies at the weakest signals result from poor sampling (a consequence of the small region covered by the simulations). The corresponding synthesized distribution of $B_{\rm app}^{\rm L}$ follows the observed distribution up to approximately 10 Mx/cm2. Pixels with $B_{\rm app}^{\rm L}$signals higher than 40 Mx/cm2 are very rare for the maps resulting from dynamo run C.

\begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13379fg5.ps} \end{figure} Figure 5:

Same as Fig. 4 but for the dynamo run C with a background unipolar field and a different region from the observed map (outlined by a yellow square in Fig. 1).

Open with DEXTER

\begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13379fg6.ps} \end{figure} Figure 6:

Probability density function (PDFs) for the longitudinal ( left column) and transversal ( right column) apparent magnetic flux density. PDFs from synthetic $B_{\rm app}$ at original (solid) and Hinode (plus signs) resolution are compared with the observed PDFs from data set II (red solid line). From top to bottom: mixed polarity simulation (20 G), dynamo run C and the same snapshot scaled by a factor 3. Also shown are the PDFs derived from Stokes parameters resulting from pure white noise with a standard deviation of $3\times 10^{-4}$(dotted lines).

Open with DEXTER

5.3 Changes with the heliocentric angle

The variation in the apparent magnetic flux density at different heliocentric angles was determined using a snapshot from the dynamo run C. The magnetic field strength was scaled by a factor of 3 in keeping with the findings from the previous sections. The upper panels of Fig. 7 show height profiles of the mean transversal (right) and mean absolute longitudinal (left) field in the simulation at different heliocentric angles. Since the transversal component of the magnetic field becomes increasingly dominant in the layers above optical depth unity, the mean absolute longitudinal (line-of-sight) component of the field increases as the line of sight becomes inclined with respect to the surface normal. However, the polarization signals in spectral lines reflect the component of magnetic field averaged over the line formation heights. The lower left panel of Fig. 7 shows the PDF of $B_{\rm ave}$, the vertical component of magnetic field averaged over the height range that corresponds to $\log \tau = [-3.5,0.1]$ at different heliocentric angles. The PDFs at $\mu<0.8$ follow the PDF at $\mu=1$ closely, with a discrepancy at the strong field end. This discrepancy increases with the heliocentric angle.

As illustrated by Pietarila Graham et al. (2009), $B_{\rm ave}$ and $\vert B_{\rm app}^{\rm L}\vert$ are well correlated, which explains the similar trend of $\vert B_{\rm app}^{\rm L}\vert$ with the heliocentric angle, as shown in the lower right panel of Fig. 7. Plotted are the mean values of $\vert B_{\rm app}^{\rm L}\vert$ and $B_{\rm app}^{\rm T}$ as functions of the heliocentric angle. The mean value of $\vert B_{\rm app}^{\rm L}\vert$ stays roughly constant until $\mu=0.8$ and then gradually decreases when moving further away from disk center. The mean value of $B_{\rm app}^{\rm T}$ decreases monotonically.

5.4 Comparison with observations at 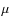$\mu $ = 0.4 (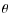$\theta $ = 66$^{\circ }$)

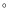\begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13379fg7.ps}\hspace... ...e*{4mm} \includegraphics[angle=90,width=8.8cm,clip]{13379f10.ps} \end{figure} Figure 7:

Simulated change with heliocentric angle retrieved from a dynamo run C snapshot. Upper panels: the mean absolute longitudinal ( left) and transversal ( right) components of the magnetic field as a function of height in the simulation box at different heliocentric angles. Vertical lines indicate the level of optical depth unity. Lower left: PDFs for the signed longitudinal field (averaged over the line formation height) at different heliocentric angles. Lower right: change of the mean absolute longitudinal ( $\vert B_{\rm app}^{\rm L}\vert$) and mean transversal ( $B_{\rm app}^{\rm T}$) apparent flux density as a function of the heliocentric angle. These values are calculated from synthesized Stokes profiles.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13379f11.ps} \end{figure} Figure 8:

PDFs for the longitudinal ( left column) and transversal ( right column) apparent magnetic flux density. Upper row: $B_{\rm app}$ distributions obtained from observations at heliocentric angles $\theta =0^{\circ }$ (red solid line) and $\theta =66^{\circ }$ (green dashed line). The dotted lines in the same colors give the PDFs resulting from the corresponding noise. Bottom row: comparison of observations with the synthetic $B_{\rm app}$ from dynamo run C (scaled with a factor 3) at heliocentric angles $\theta =0^{\circ }$ (black plus signs) and $\theta =66^{\circ }$ (blue plus signs), at Hinode resolution.

Open with DEXTER

In this section, we compare the synthesized signals at Hinode resolution with the observations. The upper panel of Fig. 8 shows PDFs of the field proxies, $B^{\rm L}_{\rm app}$ and $B^{\rm T}_{\rm app}$, retrieved from the observations at disk center and $\theta =66^{\circ }$ (data sets I and III), respectively. The maxima of the PDFs are displaced with respect to each other, because of the difference in the noise level (Table 1) as indicated by the overplotted PDFs resulting from the pure noise. The probability that the $B_{\rm app}^{\rm L}$ signals are stronger than 30 Mx/cm2 decreases at $\theta =66^{\circ }$, while the probability of the $B_{\rm app}^{\rm T}$signals being more than 200 Mx/cm2 increases. This effect results from the strong magnetic concentrations present in the field of view. When a strong magnetic tube-like structure with a vertical field of kG strength is observed under an angle, then the $B_{\rm app}^{\rm L}$ signal decreases, while $B_{\rm app}^{\rm T}$ signal displays a corresponding increase relative to the value at the disk center. This is because, projected onto the line of sight, the strong vertical component of the magnetic field gives rise to a significant transversal component, leading to a strong $B_{\rm app}^{\rm T}$ signal. Note, however that more pixels has values in the range $70<B_{\rm app}^{\rm T}<200$ Mx/cm2 where PDF( $B_{\rm app}^{\rm T}$) decreases towards the limb. Hence the mean value of $B_{\rm app}^{\rm T}$ decreases with heliocentric angle, in agreement with the result obtained from local dynamo simulations at original resolution (shown in lower right frame of Fig. 7).

The lower panels of Fig. 8 show the PDFs retrieved from the dynamo run C snapshot at Hinode resolution. Their trends correspond to the ones at original resolution, showing a small difference only for the strong signals. The PDF of the synthesized $B_{\rm app}^{\rm T}$ signal follows the observations at both heliocentric angles up to $B_{\rm app}^{\rm T}\approx200$ Mx/cm2. The synthesized $B_{\rm app}^{\rm L}$ PDF matches the observations at $\theta =66^{\circ }$up to approximately 20 Mx/cm2.

6 Discussion

We based our comparison between MHD simulations and observational results upon the magnetic proxies, the longitudinal and transversal apparent magnetic flux density introduced by Lites et al. (2008). It was shown that these proxies are prone to the influence of the non-magnetic properties of the atmosphere (Beck & Rezaei 2009) and do not correctly reflect the properties of the underlying field (Pietarila Graham et al. 2009). However, if we take that realistic MHD simulations represent the solar atmosphere properly (supported by numerous studies, e.g., Danilovic et al. (2010); Schüssler et al. (2003); Shelyag et al. (2004,2007)) and that our forward modeling of the instrumental effects and the noise is correct, we introduce the same assumption as in the case of the observations, allowing us to make a relatively unbiased comparison with the findings of Lites et al. (2008).

The magnetic proxies obtained from the synthesized data were compared with observations of the internetwork region. The mixed polarity simulations (which have a magnetic Reynolds number below the threshold for dynamo action) reproduce the observed vertical flux density, as was previously shown by Khomenko et al. (2005a). However, they do not contain enough horizontal field to be consistent with the Hinode data. Simulations of the surface dynamo give a ratio of the horizontal to the vertical flux density consistent with the observational results (Schüssler & Vögler 2008), but the overall amplitudes are too low, at least for the simulations with the magnetic Reynolds number that are feasible at the moment. A simple scaling of the field in the simulation domain by a fixed factor brings the magnetic flux density from the dynamo snapshots at Hinode resolution close to the observed ones. Some justification for this tentative procedure comes from comparing simulations with different magnetic Reynolds numbers. The resulting mean magnetic field strength is $\approx$70 G at $\tau=0.1$ and $\approx$170 G at the solar surface. This is roughly consistent with the estimates given by Trujillo Bueno et al. (2004), since the line they consider samples the middle photosphere, and with extrapolations based on the cancellation coefficient (Pietarila Graham et al. 2009).

The contribution of the surface dynamo dominates in the regions with $\vert B_{\rm app}^{\rm L}\vert<30$ Mx/cm2 and $B_{\rm app}^{\rm T}<200$ Mx/cm2 at Hinode spatial resolution. Everything stronger than that could imply: (1) flux emergence with kG horizontal fields (Cheung et al. 2008) or (2) strong network fields, which have a different source from those in the internetwork, a possibility supported by studies of ephemeral active regions (Harvey 1993; Hagenaar et al. 1999).

The synthesized magnetic proxies exhibit a decrease from the disk center to the limb. This agrees qualitatively with the observations by Lites et al. (2008). The PDFs show little $\mu $ dependence for the low values of the magnetic proxies, in accordance with the results of Martínez González et al. (2008). In contrast, Steiner et al. (2009) could not reproduce the observed simultaneous decrease towards the limb of the longitudinal and transversal field proxies on the basis of MHD simulations assuming a prescribed vertical magnetic flux or a transport of horizontal flux into the computational box from below.

Our results support the presence of local dynamo action in the quiet Sun. They also suggest that the magnetic field is dominantly horizontal. The ratio of the mean horizontal and vertical component of the dynamo-generated magnetic field reaches values between 2 and 4 in the optical depth interval $-2<\log \tau<-1$. This gives the observed ratio of the transversal and longitudinal apparent magnetic flux densities at the Hinode resolution when an adequate noise level is considered.

We note, however, that the conclusions drawn here are based on a simple assumption drawn from the properties of magnetic field in the simulations with different magnetic Reynolds numbers. The increase in the field strength by a factor of 2 or 3 would result in a change of physical parameters, as well as the dynamics of the plasma, since the strong field is much less susceptible to the influence of the turbulent motions. These effects are not considered in our scaling procedure. Thus, we consider our work to be a step towards revealing the role of the surface dynamo in the quiet Sun magnetism until more realistic simulations, as well as higher resolution observation of the solar photosphere become available.

Acknowledgements
We thank Jonathan Pietarila Graham for the valuable help with the PDFs and Anna Pietarila for a critical reading of the paper. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway). This work was partly supported by the Ministry of Science and Technological Development of the Republic of Serbia (Project No 146003 ``Stellar and Solar Physics'') and by WCU grant No. R31-100016 from the Korean Ministry of Education, Science and Technology.

References

  1. Asensio Ramos, A. 2009, ApJ, 701, 1032 [NASA ADS] [CrossRef] [Google Scholar]
  2. Asensio Ramos, A., Martínez González, M. J., López Ariste, A., et al. 2007, ApJ, 659, 829 [NASA ADS] [CrossRef] [Google Scholar]
  3. Beck, C., & Rezaei, R. 2009, A&A, 502, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bello González, N., Yelles Chaouche, L., Okunev, O., & Kneer, F. 2009, A&A, 494, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Berdyugina, S. V., & Fluri, D. M. 2004, A&A, 417, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Cattaneo, F. 1999, ApJ, 515, L39 [NASA ADS] [CrossRef] [Google Scholar]
  7. Centeno, R., Socas-Navarro, H., Lites, B., et al. 2007, ApJ, 666, L137 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cheung, M. C. M., Schüssler, M., Tarbell, T. D., & Title, A. M. 2008, ApJ, 687, 1373 [NASA ADS] [CrossRef] [Google Scholar]
  9. Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Danilovic, S., Schüssler, M., & Solanki, S. K. 2010, A&A, 509, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Domínguez Cerdeña, I., Sánchez Almeida, J., & Kneer, F. 2003, A&A, 407, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 2000, A&A, 358, 1109 [NASA ADS] [Google Scholar]
  13. Hagenaar, H. J., Schrijver, C. J., Title, A. M., & Shine, R. A. 1999, ApJ, 511, 932 [NASA ADS] [CrossRef] [Google Scholar]
  14. Harvey, K. L. 1993, Ph.D. Thesis, Utrecht University [Google Scholar]
  15. Harvey, J. W., Branston, D., Henney, C. J., & Keller, C. U. 2007, ApJ, 659, L177 [NASA ADS] [CrossRef] [Google Scholar]
  16. Ishikawa, R., Tsuneta, S., Ichimoto, K., et al. 2008, A&A, 481, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
  18. Khomenko, E. V., Collados, M., Solanki, S. K., et al. 2003, A&A, 408, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Khomenko, E. V., Martínez González, M. J., Collados, M., et al. 2005a, A&A, 436, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Khomenko, E. V., Shelyag, S., Solanki, S. K., & Vögler, A. 2005b, A&A, 442, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Lites, B. W., Elmore, D. F., & Streander, K. V. 2001, in Advanced Solar Polarimetry - Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 33 [Google Scholar]
  22. Lites, B. W., et al. 2008, ApJ, 672, 1237 [NASA ADS] [CrossRef] [Google Scholar]
  23. Martin, S. F. 1988, Sol. Phys., 117, 243 [NASA ADS] [CrossRef] [Google Scholar]
  24. Martínez González, M. J., Collados, M., Ruiz Cobo, B., & Solanki, S. K. 2007, A&A, 469, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Martínez González, M. J., Asensio Ramos, A., López Ariste, A., & Manso Sainz, R. 2008, A&A, 479, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., et al. 2007a, ApJ, 670, L61 [NASA ADS] [CrossRef] [Google Scholar]
  27. Orozco Suárez, D., Bellot Rubio, L. R., Del Toro Iniesta, J. C., et al. 2007b, PASJ, 59, 837 [Google Scholar]
  28. Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., & Tsuneta, S. 2008, A&A, 481, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Pietarila Graham, J., Danilovic, S., & Schüssler, M. 2009, ApJ, 693, 1728 [Google Scholar]
  30. Petrovay, K., & Szakaly, G. 1993, A&A, 274, 543 [Google Scholar]
  31. Sánchez Almeida, J., Emonet, T., & Cattaneo, F. 2003, ApJ, 585, 536 [NASA ADS] [CrossRef] [Google Scholar]
  32. Schüssler, M., Shelyag, S., Berdyugina, S., et al. 2003, ApJ, 597, L173 [NASA ADS] [CrossRef] [Google Scholar]
  33. Shelyag, S., Schüssler, M., Solanki, S. K., & Vögler, A. 2007, A&A, 469, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Solanki, S. K. 2009, ASP Conf. Ser., 405, 135 [NASA ADS] [Google Scholar]
  35. Shelyag, S., Schüssler, M., Solanki, S. K., et al. 2004, A&A, 427, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Steiner, O., Rezaei, R., Schaffenberger, W., & Wedemeyer-Böhm, S. 2008, ApJ, 680, L85 [NASA ADS] [CrossRef] [Google Scholar]
  37. Steiner, O., Rezaei, R., Schlichenmaier, R., et al. 2009 [arXiv:0904.2030] [Google Scholar]
  38. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., et al. 1995, A&AS, 112, 525 [Google Scholar]
  39. Thevenin, F. 1989, A&AS, 77, 137 [Google Scholar]
  40. Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
  41. Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
  42. Vögler, A. 2003, Ph.D. Thesis, University of Göttingen, Germany, http://webdoc.sub.gwdg.de/diss/2004/voegler [Google Scholar]
  43. Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Schüssler, M., & Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. de Wijn, A. G., Stenflo, J. O. Solanki, S. K., & Tsuneta, S. 2008, Space Sci. Rev., 144, 275 [Google Scholar]

Footnotes

... SolarSoft[*]
http://www.lmsal.com/solarsoft/

All Tables

Table 1:   Details of the three Hinode/SP data sets used.

Table 2:   The simulation parameters with the size of computational domain and vertical ($\delta {z}$) and horizontal ($\delta {x}$) grid spacing.

Table 3:   Mean apparent magnetic flux densities from observations and simulations.

All Figures

  \begin{figure} \par\includegraphics[angle=90,width=15.5cm,clip]{13379fg1.ps} \end{figure} Figure 1:

Maps of longitudinal ( $B_{\rm app}^{\rm L}$) and transversal ( $B_{\rm app}^{\rm T}$) apparent flux density for the observed data sets I ( left) and III ( right) from Table 1. The small squares indicate the sizes of the MHD snapshots. They also mark the position of the regions to which synthesized maps from simulation data are compared (Figs. 4 and 5).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.4cm,clip]{13379fg2.ps} \vspace*{-2mm}\end{figure} Figure 2:

Average total (solid), horizontal (dashed), and vertical (dotted) mean magnetic field strength from MURaM simulations as a function of the optical depth. Snapshots from different runs are indicated by line color: mixed polarity (blue), dynamo G (red), dynamo C multiplied by factor of 1.5 (black), and dynamo C with background unipolar field (green).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=13.5cm,clip]{13379fg3.ps} \vspace*{2mm}\end{figure} Figure 3:

Histograms of the mean horizontal ( left), the unsigned vertical ( middle) and the signed vertical ( right) magnetic flux density calculated for $7\hbox {$^{\prime \prime }$ }\times 7\hbox {$^{\prime \prime }$ }$ size regions covered by dataset I. The vertical lines mark the mean values for the whole field of view.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13379fg4.ps} \end{figure} Figure 4:

Comparison of a snapshot from dynamo run C with magnetic field scaled by a factor 3 at original ( left column) and Hinode ( middle column) resolution, with Hinode observations ( right column). From top to bottom: normalized intensity, longitudinal and transversal apparent magnetic flux density. The observed region is outlined by a white square in Fig. 1. White lines outline the contours of normalized continuum intensity equal to 1.05.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13379fg5.ps} \end{figure} Figure 5:

Same as Fig. 4 but for the dynamo run C with a background unipolar field and a different region from the observed map (outlined by a yellow square in Fig. 1).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8.5cm,clip]{13379fg6.ps} \end{figure} Figure 6:

Probability density function (PDFs) for the longitudinal ( left column) and transversal ( right column) apparent magnetic flux density. PDFs from synthetic $B_{\rm app}$ at original (solid) and Hinode (plus signs) resolution are compared with the observed PDFs from data set II (red solid line). From top to bottom: mixed polarity simulation (20 G), dynamo run C and the same snapshot scaled by a factor 3. Also shown are the PDFs derived from Stokes parameters resulting from pure white noise with a standard deviation of $3\times 10^{-4}$(dotted lines).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13379fg7.ps}\hspace... ...e*{4mm} \includegraphics[angle=90,width=8.8cm,clip]{13379f10.ps} \end{figure} Figure 7:

Simulated change with heliocentric angle retrieved from a dynamo run C snapshot. Upper panels: the mean absolute longitudinal ( left) and transversal ( right) components of the magnetic field as a function of height in the simulation box at different heliocentric angles. Vertical lines indicate the level of optical depth unity. Lower left: PDFs for the signed longitudinal field (averaged over the line formation height) at different heliocentric angles. Lower right: change of the mean absolute longitudinal ( $\vert B_{\rm app}^{\rm L}\vert$) and mean transversal ( $B_{\rm app}^{\rm T}$) apparent flux density as a function of the heliocentric angle. These values are calculated from synthesized Stokes profiles.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{13379f11.ps} \end{figure} Figure 8:

PDFs for the longitudinal ( left column) and transversal ( right column) apparent magnetic flux density. Upper row: $B_{\rm app}$ distributions obtained from observations at heliocentric angles $\theta =0^{\circ }$ (red solid line) and $\theta =66^{\circ }$ (green dashed line). The dotted lines in the same colors give the PDFs resulting from the corresponding noise. Bottom row: comparison of observations with the synthetic $B_{\rm app}$ from dynamo run C (scaled with a factor 3) at heliocentric angles $\theta =0^{\circ }$ (black plus signs) and $\theta =66^{\circ }$ (blue plus signs), at Hinode resolution.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.