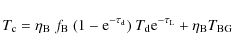EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) A9 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number A9
Number of page(s) 13
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200912241
Published online 14 April 2010
A&A 513, A9 (2010)

A millimeter survey of ultra-compact HII-regions and associated molecular clouds[*]

E. Churchwell1 - A. Sievers2 - C. Thum3

1 - Department of Astronomy, University of Wisconsin-Madison, 475 N. Charter street, Madison, WI 53706, USA
2 - Instituto de Radio Astronomía Milimétrica, Avenida Divina Pastora, 7 Núcleo Central, 18012 Granada, Spain
3 - Institut de Radio Astronomie Millimétrique, Domaine Universitaire de Grenoble, 300 rue de la Piscine, 38406 Saint Martin d'Hères, France

Received 1 April 2009 / Accepted 18 November 2009

Abstract
We report observations, using the IRAM 30 m telescope, of 30 ultracompact and hypercompact HII regions in the lines of HCO+(3-2) and/or HCO+(1-0) and H$30\alpha $ and/or H$39\alpha $. Images are presented in both HCO+(3-2) and H$30\alpha $ toward a subset of regions (16 in HCO+(3-2), 14 in H$30\alpha $) with a resolution of 12''. In addition, H13CO+(3-2) observations are reported toward 13 HII regions where HCO+(3-2) displays complex profiles. It is shown that the absorption dips in the HCO+ profiles are due to HCO+ self-absorption, not absorption of the HII free-free emission or warm dust emission surrounding the HII region or two velocity components along the line of sight. It was found that among the sources with self-absorbed profiles, 8 are contracting and 5 are expanding. Mass fluxes are found to be typically a few times 10-3 $M_\odot$ yr-1, implying time scales for massive star formation <105 yrs. HCO+ and H2 column densities are estimated for a subset of the sources from which masses of the dense central cloud cores were estimated. Implications of the derived column densities, masses, flow velocities, and mass fluxes are discussed.

Key words: surveys - stars: formation - HII regions

1 Introduction

Ultra-compact (UC) HII regions are sites of recent massive star formation. UC HII regions are of special interest because they occupy an important stage in the evolution of young massive stars that is still only understood in broad outline. Identifying the ionizing star(s) and their associated natal cluster of lower mass stars in UC HII regions has proven quite difficult; identifications have been reported for only a few UC HII regions. The immediate regions around the central star(s) of UC HII regions are expected to be very dynamic due to possible infall, outflows, stellar winds, accretion disk rotation, turbulence, and shocks. The dynamics and physical properties of the photo-dissociation regions (PDRs) that surround UC HII regions and the ambient natal molecular gas that surrounds the PDRs must also be included to place UC HII regions in context with their environments. Spectroscopy of the H+, PDR(H0), and molecular envelopes (H2) is essential to understand the interactions of UC HII regions with their environments. Churchwell (2002) has argued, based on the lack of evidence for outflows in high resolution radio continuum images, that by the time young massive stars have formed UC HII regions they have largely ceased the accretion process. This is indirect evidence that has so far not been confirmed by spectroscopic observations. To understand the early evolution of massive stars and how they impact their environments, we must determine at what evolutionary stage young massive stars quench accretion and by what mechanism. Is it because the stars use all the matter in their neighborhood or the central radiation pressure over-powers gravity, or some other reason?

We also need to better understand the extent, morphology, and physical properties of the dense molecular and ionized gas in the immediate neighborhood of UC HII regions. Several papers have been published that address one or more of these issues toward specific UC HII regions (some of which are Baudry et al. (1981); Bourke et al. (1997); Cesaroni et al. (1991, 1994, 1998); Choi et al. (1993); Fey et al. (1992); Garay et al. (2007); Sandell & Sievers (2004); Zhu et al. (2008) and references therein), but a sensitive survey is not available that specifically probes both the dense molecular and ionized gas toward a substantial sample of UC HII regions with the same spatial resolution using a single-dish millimeter-wave telescope (i.e. sensitive to all scale sizes within the mapped area).

Here, we present observations of HCO+(3-2) and/or (1-0) and H$30\alpha $ and/or H$39\alpha $ lines toward 29 UC HII regions. The H$39\alpha $ and/or HCO+(1-0) observations in the 3 mm band were made only toward the central positions of 7 UC HII regions. The HCO+(3-2) and H$30\alpha $ lines in the 1 mm band were mapped toward 23 UC HII regions (see Table 1). The 1 mm observations, we believe, represent a large enough sample to begin to address systematics of the relationship between the ionized gas and the surrounding molecular gas. Among these are: is there systematic evidence for infall of molecular gas toward UC HII regions? Is there evidence for excessive line widths in the molecular or ionized gas and, if so, what is the likely reason? Based on kinematic distance determinations, is there evidence for a temperature gradient with galactocentric radius? That is, are UC HII region temperatures consistent with the observed metallicity gradients (Churchwell & Walmsley 1975; Shaver et al. 1983; Maciel & Köppen 1994; Mezger et al. 1979; Afflerbach et al. 1996; Afflerbach et al. 1997); and, are there any systematics associated with the column densities of HCO+ toward UC HII regions?

In the following we discuss the observations in Sect. 2, the data in Sect. 3, results in Sect. 4, and summary and conclusions in Sect. 5.

Table 1:   Target sources and type of observation made.

2 Observations

Table 2:   Spectral resolution and bandwidth available with the receiver/backend combinations used.

The bulk of the observations were made during the period of 28 March to 02 April 2006 using the IRAM 30 m telescope located at an altitude of 2850 m near Granada (Spain). During most of this period the weather was good enough for observations at 1.3 mm wavelength ( $\tau\leq0.4$). We used the multibeam 1.3 mm receiver HERA (Schuster et al. 2004) whose two orthogonal linearly polarized arrays were tuned to HCO+ at 267.557633 GHz and H$30\alpha $ at 231.900942 GHz. Each array provides 3 $\times$ 3 pixels arranged as a center-filled square. The two arrays are aligned to within ${\sim}2''$, thus permitting precise relative pointing between the two transitions. Each pixel consists of a diffraction-limited beam of 12'' (FWHP), and the pixels are separated by 24''. The observations were made in wobbler-switching mode where the reference positions are offset in azimuth by 30'' to 120''. The array was kept aligned with the equatorial system with the help of a derotator optical assembly that compensates the field rotation due to changes of the parallactic and Nasmyth angles. Maps sampled at 1/2 FWHP intervals of size 66'' $\times$ 66'' size were obtained by stepping the telescope in ${\alpha }$ and $\delta$ by 6, 12, and 18''. The 18 signals generated by HERA were connected to three sets of backends. Their spectral resolutions and bandwidths are listed in Table 2.

During a small fraction of our observing time when the weather was not good enough for 1.3 mm observations, we used the Observatory's 3 mm single pixel receivers A100 and B100 tuned to H$39\alpha $ at 106.737363 GHz and HCO+(1-0) at 89.188526 GHz. respectively. The VESPA correlator set to spectral resolution of 78 kHz (0.26 km s-1 near 100 GHz) and bandwidth of 140 MHz (480 km s-1 near 100 GHz) was connected to both receivers.

During a second session with the 30 m telescope on 03 August 2008 we observed the H13CO+(3-2) line toward a subset of our target list where the main isotope was found to be very optically thick. HC18O+(3-2) was observed in the few cases where even H13CO+(3-2) did not have a clean gaussian profile. We used the Observatory's single pixel receivers A 230 and B 230 tuned to the line frequencis of 260.25548 (H13CO+(3-2)) and 255.479389 (HC18O+(3-2)) GHz. As representative examples of a weak and a strong source, we show the spectra of the 3 HCO+ isotopes obtained toward G28.20-0.04N and G10.62-0.38 in Fig. 1. Note the presence of a weak SO2 emission line redward of HCO+ in G10.68-0.38. The spectrometers and their spectral characteristics are listed in Table 2.

The telescope beam is 12'' (full width at half power) at 1.3 mm. At the 3 mm transitions it is 26'' at 89 GHz and 24'' at 106 GHz. Pointing observations were made every 2-3 h on nearby quasars; pointing errors were found to be ${\leq}3''$. Line and continuum measurements are in units of antenna tempertaure, $T^*_{\rm A}$, calibrated in the usual hot/cold load technique with an estimated precision of 10%. We use $T^*_{\rm A}$ to flux density conversion factors of 6.2, 8.6, and 10 Jy/K at 106, 232, and 268 GHz.

Our target sources were taken from various continuum surveys of ultra-compact HII-regions (Wood & Churchwell 1989; Shepherd & Churchwell 1996; Kurtz et al. 1994). We selected those sources which we estimated to have a 1.3 mm continuum flux density in our 12'' beam of at least 100 mJy. We extrapolated the measured 2 cm flux density to 1.3 mm assuming optically thin emission. Any optically thick emission, unrecognized at cm wavelengths, or a significant extended emission, not imaged by the VLA, of a halo surrounding the UCHII region, would increase the expected 1.3 mm flux density.

The observed sources are listed in Table 1. The last column indicates the type of observations made: either HERA maps of the HCO+ and H$30\alpha $ transitions or pointed observations with the 3 mm single pixel receivers of the transitions H$39\alpha $ and HCO+(1-0). In the case of maps, the given positions refer to map centers.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{12241Fig1.eps} \end{figure} Figure 1:

Spectra of the $3\rightarrow 2$ transitions of the main HCO+ isotopes toward G28.20-0.04N ( left) and G10.62-0.38 ( right). The vertical scales are in degrees K of  $T^*_{\rm A}$.

Open with DEXTER

3 Data

3.1 Ionized gas

We detected recombination lines toward the peaks of 23 out of 30 (77%) of our target sources. Table 3 lists the line parameters derived from Gaussian fits. The line widths are the full widths at half power. The H$30\alpha $ lines are corrected for instrumental broadening of 3 km s-1. The H$39\alpha $ lines which were observed with 0.4 km s-1 spectral resolution do not need any such correction. For the sources where no line was detected we give a $1\sigma$ upper limit for a spectral resolution of 2.6 km s-1. The ${\pm}600$ km s-1 bandwidth used covers the full velocity range of galactic emission.

In most cases, the H$30\alpha $ brightness distribution is only slightly broadened with respect to the beam. As an example, Fig. 2 shows the UC HII-region G10.62-0.38. Maps of the other regions are collected in Fig. 3. Linear baselines have been removed from all spectra in the map, subtracting any free-free emission of the source. Note that the coverage of these maps is slightly incomplete to the east due to one bad pixel.

Table 3:   Recombination line observations.

The H$30\alpha $ line parameters were mostly derived from the HERA raster maps. The four positions nearest to the nominal map center have offsets ${\leq}3''$ and were averaged for the Gaussian fits, corresponding to a beam smoothed to 14''. The H$39\alpha $ parameters refer to a 24'' beam.

\begin{figure} \par\includegraphics[angle=-90,width=8.3cm,clip]{12241Fig2b.eps}\... ...{2mm} \includegraphics[angle=-90,width=8.3cm,clip]{12241Fig2a.eps} \end{figure} Figure 2:

Maps of G10.62-0.38 obtained with HERA at an angular resolution of 12'' (circles at lower left corners) in the transitions of H$30\alpha $ ( left) and HCO+(3-2) ( right). Contours are in K km s-1 and range from 3 to 18 in steps of 3 (H$30\alpha $) and from 15 to 225 in steps of 15 (HCO+(3-2)).

Open with DEXTER

In general, the H$30\alpha $ line is only mildly affected by confusion with molecular lines. The nearest known molecular transitions, an unidentified line and the 132-122 transition of CH3C15N, are -17 and +23 MHz, respectively, away from the recombination line frequency. It is therefore only the line wings which may be affected in a few particularly line-rich sources. These cases are noted in Table 3. The kinematic distances, given in Col. 6 of this table, are based on the H$30\alpha $ LSR velocities assuming an orbital velocity of 220 km s-1. We adopt the IAU standard distance from the Galactic center of 8.5 kpc, even if this distance is somewhat larger than that currently inferred from proper motions (Ghez et al. 2008).

\begin{figure} \par\includegraphics[width=11.6cm,clip]{12241Fig3.eps} \end{figure} Figure 3:

H$30\alpha $ maps obtained with HERA at an angular resolution of 12''. All maps in one row have been plotted using the same contour levels and color scale shown on the right. Contours are in K km s-1, start at and are in steps of 3 (row 1), 2 (rows 2 and 3), and 1 (rows 4 and 5). Note that a broken pixel affects coverage to the left of center.

Open with DEXTER

\begin{figure} \par\includegraphics[width=11.6cm,clip]{12241Fig4.eps} \vspace*{2mm} \end{figure} Figure 4:

HCO+(3-2) maps obtained with HERA at an angular resolution of 12''. All maps in one row have been plotted using the same contour levels and color scale shown on the right. Contours are in K km s-1, start at and are in steps of 30 (row 1), 15 (row 2), 10 (row 3), 8 (row 4), and 4 (row 5).

Open with DEXTER

Table 4:   HCO+ observations. Isotopes are abbreviated as 12 (HCO+), 13 (H13CO+), and 18 (HC18O+).

3.2 Molecular gas

The molecular clouds toward our target UC HII regions were detected toward 24 of 28 sources (86%) observed via their HCO+ emission. We failed to detect HCO+ within 30'' of 5 UC HII regions in our sample (see Table 4). In most cases, the HCO+(3-2) emission is clearly resolved, its extent is in all cases larger than that of H$30\alpha $. As an example, Fig. 2 shows the UC HII region G10.62-0.38. Maps of the other regions are collected in Fig. 4.

Table 4 lists the main properties of the HCO+ line: the antenna temperature and radial velocity of the line peak, the velocity of the self-absorption feature if there is any, and the line width at 10% of the line peak. This quantity, while little affected by self-absorption and still well measurable, gives an indication of the presence of line broadening mechanisms, like supersonic turbulence or high optical depth. In the presence of self-absorption, the peak velocity is the measured H13CO+(3-2) velocity. The measurement errors are typically ${\pm}0.1$ K in $T_{\rm L}$ and ${\pm}0.2$ km s-1 for the weaker sources. We also give in Table 4 an estimate of the size of the HCO+(3-2) core wherever reliable data were obtained. Elliptical gaussians were fitted to the velocity-integrated line intensity. The statistical errors of the major and minor axis are 1'' or less, and less than 5$^\circ$ for the position angle.

As in the case of the recombination lines, the HCO+(3-2) line parameters are derived from the four spectra of the raster maps closest to the nominal map center, and are thus derived for an effective beam of 14''. The HCO+(1-0) parameters refer to a 24'' beam (FWHP).

4 Results

A key goal in the quest to identify protostars that are actually in the process of accreting mass is to find unequivocal evidence for mass infall toward the center of molecular clouds. The period of active accretion is believed to be short, typically ${\leq}10^5$ yr for massive protostars. Consequently, we expect detection of a massive protostar in the act of rapid accretion to be rare. Several surveys have been undertaken to search for infall of molecular gas associated with massive star formation. Among these are Fuller et al. (2005), Purcell et al. (2006), Klassen & Wilson (2007), and Wu et al. (2007). All of these used HCO+ and H13CO+(3-2) observations along with a few other molecular probes. The search for infall, for the most part relied on line profile properties specified in the Myers et al. (1996) ``two-layer'' model and the sample was mostly toward molecular cores in cold dark clouds with no bright continuum source such as UC HII regions. Also, none of the surveys toward massive star formation regions included simultaneous observations of a radio recombination line (RRL) at the same spatial resolution, so the velocities and spatial extent of the molecular gas could not be compared with those of the associated HII region.

4.1 HCO+ and H30${\alpha }$ relative velocities

In this section, we examine the motions of HCO+ relative to H$30\alpha $. The rest frequencies of the lines involved in this comparison are known to a precision of at least 10 kHz, sufficient for deriving velocities to a precision of ${\sim}0.1$ km s-1 as needed here. We assume that the velocity of H$30\alpha $ represents the systemic velocity of the UC HII region. The HCO+ emission distributions are well correlated with positions of the HII regions (see Figs. 2-4). The HCO+ emission is generally more extended than that of the H$30\alpha $ distribution. Also, HCO+ and H$30\alpha $ velocities are similar, within a few km s-1 (Fig. 5). This suggests that the HII regions and HCO+ gas are dynamically connected and that the HII regions are probably embedded in the HCO+ clouds; we assume that this is the case for all the sources in our sample where we have both HCO+ and H$30\alpha $ images.

Here, we will examine the relative velocities of HCO+ and H$30\alpha $ emission to try to determine if the HII regions and molecular clouds are separating from each other, or are at rest with respect to each other. Interpretation of the kinematics from the HCO+ and HII velocities is complicated because it depends on how optically thick the HCO+ line is (i.e. we are mostly seeing only the nearside of the HCO+ cloud) and whether the HCO+ profile has an absorption dip.

Let us now consider the possible scenarios and the implications for expected HCO+ line profiles. If the HCO+ line is optically thin, then we see motions from the entire line of sight. In this case, if $\Delta v$ = $v_{\rm em}{\rm (HCO}^+) - v({\rm RRL}) = 0$, the bulk motions of the HII region and molecular cloud are at rest relative to each other. If  $\Delta v \neq0$, then the molecular cloud and the HII region are in motion relative to each other, the sense of which depends on the sign of $v_{\rm em}{\rm (HCO}^+)$ and v(RRL). However, $\Delta v$ alone cannot tell us if the molecular cloud is contracting or expanding.

As we show in Sect. 4.2 below, the UC HII regions at 1 mm are very optically thin and are too faint to produce detectable absorption in the HCO+ line. This is also supported by the fact that absorption dips in the HCO+ profiles are detected more than a full half-power beam width away from the UC HII positions. Self-absorption, of course, requires that the HCO+ line be optically thick and that its excitation temperature decrease outward.

In the HCO+ optically thick scenario, we see mostly the front face of the HCO+ cloud. So a velocity difference between the H$30\alpha $ and HCO+ lines could imply a relative velocity between the HII region and the HCO+ cloud, or contraction or expansion of the outer HCO+ gas relative to the HII region. That is, we cannot distinguish between relative bulk motions and contraction or expansion of HCO+ about the HII region from comparison of central line velocities. This can be resolved, however, from line profile analysis using techniques outlined by Myers et al. (1996) and generalized by De Vries & Myers (2005).

Figure 5 shows the observed velocity difference between the central velocity of the HCO+ cloud and that of the ionized region for all sources where both velocities were reliably observed. Whenever the HCO+ (3-2 or 1-0) line profile was distorted by an absorption dip within the HCO+ emission profile, the HCO+ central velocity was obtained from H13CO+ profiles. Of the 22 sources toward which both H13CO+(3-2) and H$30\alpha $ or both HCO+(1-0) and H$39\alpha $ were detected, the HII region and HCO+ gas are moving apart at speeds ranging from ${\sim}0.5$ km s-1 up to 9 km s-1; two sources have relative speeds <0.5 km s-1. Thus, ${\sim}90$% of the sample has significant relative motion between the HII region and observed HCO+ gas.

The observed distribution of the velocity differences $\Delta v$ may be compared to that expected in a scenario where the ionized gas is streaming away from the edge of a molecular cloud. Such a scenario was discussed for the Orion Nebula (Zuckeman 1973) where the ionized gas happens to stream toward the observer at $v_{\rm S} = -10$ km s-1. Inasmuch as (i) the streaming directions in our sample sources are random; (ii) $v_{\rm S}$ is the same for all sources; and (iii)  $v_{{\rm HCO}^+}$is a good representation of the velocity of the molecular material, we expect a distribution of velocity differences, projected on the line-of-sight, $\Delta v$ that is flat between $\pm$$v_{\rm S}$. Given the uncertainties due to the small size of our sample, this scenario may well be what we see in Fig. 5. Nevertheless, a small bias toward positive velocity differences is evident from the figure. A departure from this simple scenario, which predicts as many sources with $\vert\Delta v\vert < 5$ km s-1 as with $5 <\vert\Delta v\vert <10$ km s-1, is further supported by the observed imbalance of 14 vs. 8 sources in these two velocity brackets.

Both of these trends may suggest an alternative scenario where the UCHII regions are deeply embedded in their molecular clouds. This geometry tends to reduce $\Delta v$ since any streaming motions are less asymmetric. If the HCO+ line is (partially) optically thick, a small positive bias of $\Delta v$ would result, as observed, if the molecular clouds are mainly contracting. However, as noted above, to determine if the HCO+ cloud is contracting or expanding around the embedded HII region, requires further analysis of the HCO+ profiles.

\begin{figure} \par\includegraphics[angle=-90,width=8.5cm,clip]{12241Fig5.eps} \end{figure} Figure 5:

Histogram of the observed velocity differences between the ionized and molecular gas, as obtained from our H$30\alpha $ and HCO+ data. The weighted mean velocity difference of this sample of 22 sources is +1.45 km s-1.

Open with DEXTER

4.2 Absorption dips in the HCO+ emission profiles

Of the 24 sources where HCO+ was detected, 14 have absorption dips within the emission profile, one of which, NGC 7538 IRS2, appears to have multiple absorption dips within the emission profile. Nine sources have no obvious absorption dip. Among those with observed HCO+ single absorption dips, the ``blue peak'' (i.e. lower velocity) of the double peaked HCO+ profile is brighter than the ``red peak'' toward 8 sources, and the red peak is brighter than the blue peak toward 5 sources (see Table 4). We refer to these profile types as B and R, respectively, in Table 4 and the rest of this paper.

Let us digress for a moment to summarize line profiles in an idealized collapsing molecular cloud. Myers et al. (1996) showed analytically that in the case of an optically thick, centrally condensed, collapsing cloud where the front and back halves have constant excitation temperature and dispersion velocities, the line profile will have two peaks separated by a self-absorption dip. For collapse, the blue peak will be brighter than the red peak (in our nomenclature a B-type profile). Since this analysis is symmetric, an absorption dip that falls in the blue half of the profile (an R-type profile in our nomenclature), would imply expansion. De Vries & Myers (2005) generalized the analytic model results using a Monte Carlo radiative transfer code that incorporated both a constant excitation temperature ``two-layer'' model and one in which excitation temperature increases inward as a function of optical depth. De Vries & Myers (2005) numerically calculated line profiles for collapsing clouds that fit a wide range of observed HCO+ profiles toward low-mass starless cores.

What is the origin of the absorption dips in the HCO+ lines? There are four possibilities: 1) absorption by HCO+ of the radio free-free continuum from the embedded HII region; 2) absorption by HCO+ of warm thermal dust continuum surrounding the HII region (heated by emission from the HII region); 3) self-absorption of HCO+ due to a negative temperature gradient with distance from the HII region; and, 4) two velocity components along the line of sight. Two velocity components along the line of sight can be ruled out by the single peaked H13CO+(3-2) profiles whose peak emission coincides with the velocity of the absorption dip in the H12CO+ profiles.

Let us now address whether the HCO+ absorption dips might be due to absorption of the HII region free-free continuum. In principle, one could test this by observing if the absorption dip is seen only toward the UC HII region but disappears away from the HII region. In this case, one could conclude that the absorption dip in the HCO+ line is due to absorption of the HII continuum emission. However, for a 12'' HPBW at 267 GHz an HII region of temperature 104 K would have a brightness temperature of only $T_{\rm B}$(K) $\sim$ 3 $\times$ 10-9 EM (pc cm-6), where EM is the emission measure. The typical emission measure of UC HII regions are 107 to a few times 108 pc cm-6 (Churchwell 1991). Thus, the main beam brightness temperatures contributed by free-free emission are a few tenths of a degree to perhaps a degree, depending on the flux density of the source. This is substantially less than that needed to produce the observed absorption dips in the HCO+(3-2) lines. This conclusion is strengthened by the fact that the HII continuum distribution traced by the H$30\alpha $ line is a point source or only slightly extended in essentially all of our sample, but absorption dips are detected a full HPBW or more from the HII peak in all the sources in our sample.

What about emission from warm dust surrounding the HII region? Let us take a specific example, say G10.62-0.38. The HCO+ profile shows that at the minimum of the absorption dip, $T^*_{\rm A}$ is about 6.5 K and the maximum $T^*_{\rm A}$ value outside the absorption dip is ${\sim}22$ K. If the HCO+ gas is moderately optically thick, one would expect its excitation temperature to be approximately equal to the kinetic temperature of the gas, implying $T_{\rm ex}$ $\geq$ 22 K. We will also assume that the maximum optical depth in the HCO+ line $\tau_{\rm L}\geq5$ (all sources in Table 7 have HCO+(3-2) optical depths ranging from 260 to 6 with an average value of 77). We will assume that the warm dust shell around the HII region is large enough that it fills the telescope main beam (i.e.  $f_{\rm B}\sim1$). From the radiative transfer equation, we solve for the continuum brightness temperature required to produce the observed antenna temperature  $T^*_{\rm A}$at the absorption dip and find

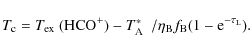
\begin{displaymath}% T_{\rm c} = \hbox {$T_{\rm ex}$ }({\rm HCO^+}) - \hbox {$T^... ...A}$ }\ / \eta_{\rm B} f_{\rm B} (1 - {\rm e}^{-\tau_{\rm L}}). \end{displaymath} (1)

Exploring the range of reasonable values of $T_{\rm ex}$(HCO+) we find that a continuum temperature $T_{\rm C}\sim15$ K is required for $T_{\rm ex}$ = 25 K, $T_{\rm C}\sim25$ K for $T_{\rm ex}$ = 35 K, and $T_{\rm C}\sim35$ K for $T_{\rm ex}$ = 45 K. The continuum temperature is related to the dust temperature $T_{\rm d}$ by the relation

\begin{displaymath}% T_{\rm c} = \eta_{\rm B}~ f_{\rm B}~(1 - {\rm e}^{-\tau_{\r... ...})\ T_{\rm d} {\rm e}^{-\tau_{\rm L}} + \eta_{\rm B}T_{\rm BG} \end{displaymath} (2)

where $\tau_{\rm d}$ is the dust optical depth and $T_{\rm BG}$ is the cosmic background temperature, 2.7 K.

Let us assume that the dust is moderately optically thick, say $\tau_{\rm d} = 0.5$and the beam filling factor of warm dust is unity. Then solving Eq. (2) for $T_{\rm d}$, we find that $T_{\rm d} > 2000$ K for the minimum $T_{\rm c} = 15$ K. The main result of this exercise is that for a reasonable range of  $T_{\rm ex}$(HCO+) and  $\tau_{\rm L}$, the dust temperatures would have to be unreasonably high to produce the observed absorption dips. Although it is possible for dust to achieve temperatures >1000 K within HII regions near a hot star, it is quite unlikely that dust could have such high temperatures a beamwidth or more from the central HII region. We therefore conclude that the absorption dips are most likely produced by HCO+ self-absorption due to high HCO+ optical depths and a negative temperature gradient with distance from the central heat source (i.e. the HII region). The absorption dips are spatially strongest toward the HII regions because this is where the highest $T_{\rm ex}$(HCO+) values are observed.

Two sources in our sample, SgrB2MC and G31.41+0.31, have absorption dips that go below the continuum level. This cannot be due to the source extending into our reference position, since our reference beam shows no evidence for residual emission toward either source. In the case of G31.41, our map of HCO+ shows that the cloud is small relative to the beam throw. We therefore must find another explanation for the subcontinuum absorption dips. Since molecular clouds are effectively bathed in an isotropic radiation field of 2.7 K, the absorption dips cannot go below 2.7 K. Also, scattering and absorption of line photons cannot remove more photons from the line than are produced in the line and therefore cannot account for absorption below the continuum. As we showed above, free-free emission from the HII regions can contribute a few tenths of a degree or so to the continuum and therefore could contribute an equivalent amount of absorption below the contnuuum. Also, as we showed above, thermal dust emission essentially contributes no measurable emission in the HCO+ line because of large line optical depths; however, outside the line frequencies dust could be the main contributor to the continuum emission. In the case where the dust has a negligible temperature gradient (such that it is not apparent in beam-switching mode), scattering and absorption of continuum photons (i.e. free-free and thermal dust) in the line could produce absorption dips below the continuum down to the minimum of 2.7 K if the line optical depths are large enough. Further support for scattering of both line photons and continuum photons at line center is the fact that the widths of the HCO+ lines are substantially broader than other molecular lines along the same line of sight that are presumably optically thin, including the H13CO+(3-2) line (compare the 12C and 13C isotopic line widths in Table 4). For treatments of radiative transfer in very optically thick lines see Auer (1968) and Auer & Mihalas (1972).

Table 5:   Flow velocities, column densities, and mass fluxes

4.3 Infall or outflow mass fluxes

In Fig. 1, we show the spectra of the three HCO+(3-2) isotopes toward two UCHII regions as examples of both a strong and a weak source where HCO+ is strongly self-absorbed. The close correspondence between the velocities of the absorption dips in the HCO+(3-2) and the H13CO+(3-2) profiles with the emission peak of the HC18O+(3-2) line supports the conclusion that the double peaked profiles are due to self-absorption and not to two velocity components along the line of sight. Toward G28.20N, G81.67, and possibly G33.13, the H13CO+(3-2) profiles appear to be weakly self-absorbed but weak enough that the profiles do not appear to be strongly distorted. We use the H13CO+(3-2) profiles to obtain the dispersion velocity of HCO+ and use the H12CO+(3-2) profiles to measure the parameters required to estimate the sign and magnitude of the HCO+ mass flow around each HII region using Eq. (9) in Myers et al. (1996). Results of our analysis of self-absorbed HCO+ profiles are reported in Table 5 where the measured H13CO+(3-2) line full-width at half-maximum intensity, $\Delta V_{\rm r}$, is given in Col. 2. The line dispersion velocity in Eq. (9) of Myers et al. (1996) is given in Col. 3; $\sigma$ is related to  $\Delta V_{\rm r}$by $\sigma = 0.425~ \Delta V_{\rm r}$ (i.e. $\sigma$ is the half-width at 1/e intensity). The temperature of the blue peak above the minimum of the absorption dip T(BD) is given in Col. 4 of Table 5, the temperature at the minimum of the absorption dip T(D) is given in Col. 5, the temperature of the red peak T(RD) is given in Col. 6, the velocity of the red peak $V_{\rm R}$ is given in Col. 7, the velocity of the blue peak $V_{\rm B}$ is given in Col. 8, the derived flow velocities  $v_{\rm flow}$in Col. 9, the half-power radius of the HCO+ emission distribution in Col. 10, the H2 column denisity determined from the H13CO+(3-2) emission toward the HII region in Col. 11, and the mass fluxes are given in Col. 12.

The propagated uncertainties for $v_{\rm flow}$ are based on an ${\sim}10$% error for $\sigma$, ${\pm}0.1$ K for $T_{\rm BD}$, $T_{\rm RD}$, and $T_{\rm D}$, and ${\pm}0.2$ km s-1 for $V_{\rm R}$ and $V_{\rm B}$. The propagated uncertainties for ${\rm d}M/{\rm d}t$ are based on the uncertainties for $v_{\rm flow}$, ${\sim}5$% for R, and 50% for N(H2). The large uncertainties for N(H2) are due to uncertainties in the conversion of NJ=3(H13CO+) to  $N_{\rm tot}$(H13CO+) to N(H2); the uncertainty of N(H2) could be as much as an order of magnitude which would translate to a similar uncertainty in  ${\rm d}M/{\rm d}t$. However, the very large optical depths in the HCO+ lines (ranging from 260 to 6 with an average of 77) require values of N(H2) > 1023 cm-2, which is consistent with the values given in Tables 5 and 7 based on the observed H13CO+(3-2) lines. Thus it seems unlikely that we have over-estimated N(H2) and  ${\rm d}M/{\rm d}t$.

Negative values of flow velocities $v_{\rm flow}$ imply outflow and positive values infall. Five sources apparently have a mass outflow and eight infall. It is clear that the flow velocities in these regions are generally larger than those found in the lower-mass star formation regions studied by Myers et al. (1996) and others. This is not surprising because massive star formation regions are more dynamical due to much larger masses (gravity), radiation fields, and wind luminosities. Presumably those having outflow profiles are more evolved and have had time to reverse infall to an outflow in five of the 13 sources that we are able to analyze. Assuming spherical contraction or expansion, we use the derived flow velocities (Col. 9, Table 5) to estimate the mass flux in each region assuming spherical flow and constant flow velocity with radius

\begin{displaymath}% {\rm d}M/{\rm d}t = 2 \pi~R\ \mu~m_{\rm H}\ N({\rm H}_2)\ {v}_{\rm flow} \end{displaymath} (3)

where $\mu=2.30$ is assumed for the mean molecular weight of the molecular cloud and $m_{\rm H}$ is 1 amu. N(H2) is the H2 column density obtained from the H13CO+(3-2) profiles (see Table 7). The H2 column density N(H2) is obtained from H13CO+(3-2) assuming that the cloud extent along the line of sight is equal to the angular diameter of the HCO+ emission distribution. R is the half-power radius of the HCO+ emission distribution. The mass fluxes range from $\sim$ $2~\times~10^{-2}$to $3.8~\times~10^{-4}$ $M_\odot$ yr-1 with 3 sources having expansion and 5 sources contraction motions. Velusamy et al. (2008) also found about equal numbers of cores in Orion with expansion and contraction motions. These large mass flux rates support star formation model predictions that massive star formation occurs on time scales ${\leq}10^5$ yr. For example, at the infall rates found here it would only require a few times 103 to <105 yr to form a 40 $M_\odot$ star. The mass outflow rates are similar to those of the infall rates with the exception of W51D, which has an unusually large outward mass flux.

Of the 8 sources that have self-absorbed HCO+ profiles, 5 have expansion motions. Exploration of the mechanism by which infall motions are reversed is beyond the scope of this paper. Presumably, these sources are more evolved and have had time to reverse core contraction via radiation pressure or stellar winds or both. It is not known what determines the final mass of massive stars, although much speculation has been given to this question. Detection of expanding young massive cores obviously has important implications for the termination of protostellar accretion and further study of this phase is needed.

Table 6:   Column densities from single peaked HCO+ profiles.

Table 7:   Column densities N and masses M from H13CO+ lines.

It is of interest to compare the flow direction of the molecular gas with that of the ionized gas as discussed in Sect. 4.1. Comparing $v_{\rm flow}$ with $\Delta v$(HCO+ - H$30\alpha $) for each of the 22 sources where both lines are measured does not show any significant trend. Both signs of $\Delta v$(HCO+ - H$30\alpha $) are equally likely for the molecular cores where we see infall or outflow motions. It seems that the large relative velocities of the ionized gas (${\sim}10$ km s-1), directed in random directions away from the molecular cores dominates the small infall or outflow motions (mostly $\la$1 km s-1) of the neutral material, thus masking any possible correlation.

4.4 HCO+ column densities

The column density toward optically thin sources in the upper rotational state of a linear molecule is given by

                                 NJu = 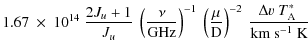$\displaystyle 1.67~\times~10^{14}\ \frac{2J_u+1}{J_u}\ \left(\frac{\nu}{{\rm GH... ...{{\rm D}}\right)^{-2}\ \frac{\Delta{v}~\hbox {$T^*_{\rm A}$ }}{\rm km~s^{-1}~K}$  
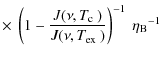
    $\displaystyle \times\ \left(1-\frac{J(\nu,\hbox {$T_{\rm c}$ })}{J(\nu,\hbox {$T_{\rm ex}$ })}\right)^{-1} \ {\eta_{\rm B}}^{-1}$ (4)

where $\nu$ is the frequency in GHz, J($\nu,T$) = $h \nu/k$ (e $^{h\nu/kT} - 1$), $\mu=4.07$ D is the permanent dipole moment of HCO+ in Debye, $\Delta v$ is the line FWHP in km s-1, and  $\eta_{\rm B}$is the main beam efficiency of the 30 m telescope (52% at 267 GHz). For the J=3-2 transition of HCO+ this reduces to

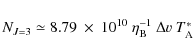
\begin{displaymath}% N_{J=3} \simeq 8.79~\times~10^{10}\ \eta_{\rm B}^{-1}\ \Delta {v}\ \hbox {$T^*_{\rm A}$ } \end{displaymath} (5)

using J($\nu$, $T_{\rm ex}$) $\gg$ J($\nu$, $T_{\rm c}$) and the antenna temperature  $T^*_{\rm A}$in K. Since the lines are seen in emission, the assumption that J($\nu$,  $T_{\rm ex}$) > J($\nu$, $T_{\rm c}$) is reasonable and the fact that a heat source in the form of a UC HII region is embedded at the center of the molecular core makes it likely that J($\nu$,  $T_{\rm ex}$) $\gg$ J($\nu$,  $T_{\rm BG}$). For the J=1-0 transition, we have

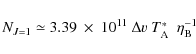
\begin{displaymath}% N_{J=1} \simeq 3.39~\times~10^{11}\ \Delta {v}\ \hbox {$T^*_{\rm A}$ }\ \eta_{\rm B}^{-1} \end{displaymath} (6)

for J($\nu$, $T_{\rm ex}$) $\gg$ J($\nu$, $T_{\rm C}$). The coefficients in Eqs. (5) and (6) are slightly larger for H13CO+ due to its slightly lower corresponding line frequencies.

Applying the appropriate relations to H13CO+(3-2) data toward the peak of the HCO+ distribution, we have estimated the total H2 column densities in Table 5 (Col. 11) and Table 7 (Col. 8) for those sources with double peaked HCO+ profiles. For an optically thick line, a lower limit for the excitation temperature is $T_{\rm ex}$ $\ge$ 2.7 K + $T^*_{\rm A}$/ $\eta_{\rm B}$; this assumes that the line optical depth  $\tau_{\rm L}$is substantially larger than unity ( $\tau_{\rm L}\geq3$). As  $T_{\rm ex}$increases, the line optical depth decreases, so there is a lower limit on $T_{\rm ex}$ set by the maximum line optical depth (i.e. at the minimum of the absorption dip). As  $T_{\rm ex}$increases above this lower limit, the total HCO+ column density will decrease due to dominance of the ${\rm e}^{h\nu/k~T_{\rm ex}}$ term in the partition function. Using the expression for $T_{\rm ex}$ above, the HCO+(3-2) lines all have  $\tau_{\rm L}$well in excess of 3 as expected if the relationship between $T_{\rm ex}$ and $T^*_{\rm A}$ above holds. As noted above, the sources in Table 7 have optical depths in the HCO+(3-2) line ranging from 6 to 260. The column densities of HCO+ and H2 may be somewhat over-estimated, but as we have already noted there does not seem to be a significant additional contribution to $T_{\rm c}$ from free-free emission although emission from extended cool dust may make some contribution. It is unlikely that the molecular column densities are over-estimated by as much as an order of magnitude by an under-estimate of  $T_{\rm ex}$.

Among the sources where HCO+ was detected, 13 are self-absorbed in the HCO+(3-2) line and very optically thick, so we had to use the H13CO+(3-2) line to estimate column densities as described above. Six sources, however, are not self-absorbed and have approximately Gaussian H12CO+(3-2) profiles. They may still suffer some optical depth effects, but we can approximate lower limits for column densities using Eq. (5). Results for the 6 sources with no self-absorption dip and approximate Gaussian profiles are given in Table 6 where the measured peak H12CO+(3-2) line temperature is given in Col. 2, the line full-width at half maximum, FWHM, is in Col. 3, the HCO+ column density in J=3 is in Col. 4, the total HCO+ column density for $T_{\rm ex}$ $\geq$ 2.7 + 1.92  $T^*_{\rm A}$(K) is in Col. 5, and the H2 column density assuming [H2]/[HCO+] = $5~\times~10^{8}$ (see e.g. Fuente et al. 2003) is in Col. 6. For these sources, both N(HCO+) and N(H2) are about an order of magnitude lower than those with self-absorbed profiles, as expected for more optically thin lines. However, we caution that the values reported in Table 6 are lower limits because the HCO+ lines may not satisfy the optical thin assumption even though they do not show evidence of self-absorption.

In Table 7, we report the parameters used to derive total HCO+ and H2 column densities and core masses from the observed H13CO+(3-2) line. The same source size R is assumed as for the main isotope (Table 5). We adopt the kinematic distances given in Table 3 based on the H$30\alpha $ line radial velocities, because the H$30\alpha $ line is likely to be more representative of the systematic velocity of the core than HCO+ which is probably affected by infall/outflow.

In Table 7, Cols. 2 and 3 are the H13CO+(3-2) line FWHM and peak line antenna temperature above the continuum; Col. 4 is the H13CO+ column density in the J=3 level; the lower limit on the excitation temperature ( $T_{\rm ex}$ $\geq$ 2.7 K + 1.92  $T^*_{\rm A}$) is given in Col. 5; the upper limit on the total column density of H13CO+ is given in Col. 6 and the total molecular hydrogen column density assuming [H2]/[HCO+] = $5~\times~10^{8}$ is given in Col. 7. In Col. 8, an upper limit on the core mass is given using M = $\frac{4\pi}{3}$$R^3~\mu$$m_{\rm H}$N(H2)/2R where we assume for the mean molecular weight $\mu=2.30$ and $m_{\rm H}$ = 1 amu. The spherical approximation seems reasonable from the observed HCO+ emission distributions (Figs. 2b and 4). The errors for N(H2) have been discussed in Sect. 4.3 and dominate the estimated errors for the mass M. We assign the lower limits of ${\sim}50$%, but note that the errors could be higher due to uncertainties in the conversions from N(H13CO+) to N(H2). As pointed out in Sect. 4.3, it is more likely that both N(H2) and M are under-estimated rather than over-estimated.

With all the assumptions that have gone into the determinations of total column densities and the masses determined from the column densities, one should view the values as order of magnitude estimates. It is likely that the masses are, in fact, only lower limits on the total mass of the natal H2 cloud since the HCO+ emission probably only traces the dense central cores of more extended clouds. The total mass of the natal clouds are of interest, because it is important to determine the minimum cloud mass required to form a massive O star with its associated cluster of lower mass stars. Typically it has been found that ${\ga}10^3$ $M_\odot$ seem to be required to produce one intermediate mass O-star with its accompanying cluster of lower mass stars (Churchwell 1997). The values found here support thresholds of this magnitude when we take into account that the HCO+ data probably only sample the central cores of substantially larger molecular clouds. G81.68+0.54 may be an exception to this.

4.5 H30${\alpha }$ line widths

The H$30\alpha $ line widths range from 21.5 to over 57 km s-1 in our sample of sources. In terms of the equivalent Doppler temperature (i.e. the kinetic temperature that hydrogen gas would have to have to produce the observed full-width-at-half maximum (FWHM) linewidth, this range corresponds to 5000 K to >35 000 K, respectively. The upper extreme of this range is well outside the values typically found in HII regions; temperatures as low as 5000 K are found in the inner Galaxy where metallicities are substantially greater than at the solar circle. 35 000 K is much hotter than the kinetic temperatures that typical Galactic plane metallicities will permit except in shocks and very near hot stars. A further important point is that the H$30\alpha $ line is unlikely to suffer significant pressure broadening (see Gordon & Sorochenko 2002), even in dense UC HII regions. Sewilo et al. (2008) has successfully separated thermal, turbulent, pressure, and large-scale motions in the hypercompact (HC) HII region G28.20-0.04N and showed that this ultra-dense HII region cannot have significant pressure broadening of the H$30\alpha $ line and accommodate the other broadening components that were independently measured. We therefore will assume that H$30\alpha $ lines with FWHM in excess of ${\sim}30$ km s-1 is not due to pressure broadening, but require large scale motions such as expansion or contraction, bipolar outflows, rotation (of an accretion disk, torus or shell), and/or shocks. Turbulence, although a contributor, was found by Sewilo et al. (2008) to be small relative to large scale motions in G28.20-0.04N. It is no surprise to find bulk motions in UC and HC HII regions, which are expected to be very dynamic especially during the period of rapid accretion that occurs as massive star are built. It is therefore not difficult to understand, in principle, the large linewidths found in our sample (see Sewilo et al. 2008, for a break down of the various line broadening components in G28.20-0.04N).

Electron temperatures of the HII regions could not be measured because the millimeter free-free continuum could not be reliably separated from the dust emission.

5 Summary and conclusions

We have presented observations of 30 ultracompact and hypercompact HII regions in the lines of HCO+(3-2) and/or HCO+(1-0) and H$30\alpha $ and/or H$39\alpha $. Images are presented in HCO+(3-2) and H$30\alpha $ emission regions and sizes are reported with a resolution of 12''. In addition, H13CO+(3-2) observations are reported toward 13 HII regions where HCO+ profiles showed signs of self-absorption. All data have been obtained with the IRAM 30 m telescope, mostly at 1 mm.

It was shown that the HII regions and HCO+ are generally in motion relative to each other at speeds ranging from 0.5 to <9 km s-1. Since the H$30\alpha $ and HCO+ regions coincide almost precisely, the relative velocities may represent a combination of relative bulk motions between the HII region and the molecular cloud plus contraction/expansion of the HCO+ envelope.

We examined four possibilities for the origin of the absorption dips in the HCO+ profiles: HII free-free continuum, warm dust continuum surrounding the HII region, two velocity components along the line of sight, and HCO+ self-absorption. It was shown that UC HII regions at 267 GHz are too optically thin to produce bright enough continuum emission to produce the observed absorption dips. For dust to produce a detectable absorption dip it would have to have temperatures ${\geq}1000$ K, which we rejected because the absorption dips are seen more than one full beam width away from the HII regions where it is highly unlikely that dust could have such high temperatures. The hypothesis of two velocity components along the line of sight was rejected based on H13CO+(3-2) profiles which are not double peaked. Also, the H13CO+ line peaks at the velocities of the absorption dips in the H12CO+ lines. We therefore conclude that the absorption dips are due to HCO+ self-absorption.

Lower limits on HCO+ column densities were determined for sources that have gaussian profiles (i.e. not double peaked) from the intensities of the HCO+ lines. Column densities for sources with self-absorbed profiles were determined using the observed H13CO+ lines; to estimate H2 column densities it was assumed that [HCO+]/[H13CO+] = 40 (see e.g. Langer & Penzias 1990) and [H2]/[HCO+] = $5~\times~10^{8}$. Masses for the dense cloud cores traced by HCO+ were estimated from the observed diameter of the HCO+ emission and the H2 column densities. Due to the uncertain assumptions involved, the column densities and masses should be considered order of magnitude estimates. Evenso, they are useful because they support independently determined threshold masses required to form massive stars along with their associated lower mass stars.

Using the two-layer analytic model of Myers et al. (1996) applied to the 13 sources that have double peaked HCO+ profiles, we derived mass flow velocities and mass flux rates. It was found that 8 sources have infall velocities and 5 have outflow velocities; this is similar to the fractions of expanding and contracting cores found in the Orion molecular cloud by Velusamy et al. (2008). The flow velocities are typically a few tenths of km s-1, although two sources (G10.62 and W51D) have flow velocities $1.0< \vert{v}_{\rm flow}\vert<2.0$ km s-1. Expanding young massive protostellar cores have important implications for the termination of protostellar accretion and the final mass of a massive protostar. An obvious mechanism to reverse infall is the action of stellar radiation and winds; however, this needs to be explored more thoroughly to be put on a more solid theoretical and observational foundation.

Mass flux rates were found to be quite large, typically a few times 10-3 $M_\odot$ yr-1. Both the flow velocities and the mass fluxes found here are consistent with those found by Barnes et al. (2010) in the massive protostellar cluster By 72 in Carina. At these rates, a 40 $M_\odot$ star could be formed in <105 yr. Such short time scales are consistent with massive star formation model predictions and inferences from independent observations. Such short time scales imply that detection of protostars in the rapid accretion phase should be rare. Presumably, the reason we have been successful in detecting 8 such sources out of a sample of 30 is because the sample has been carefully selected for especially young massive star formation regions.

The observed radio recombination lines could not be used to derive electron temperatures of the HII regions because we were unable to reliably detect the free-free continuum emission near 267 GHz.

Acknowledgements
We thank the IRAM Director, Pierre Cox, for granting additional telescope time which permitted us to conclude this project in a timely manner. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). IRAM telescope staff efficiently supported the observations. We also thank an anonymous referee for a very careful reading of the mauscript and for several suggestions that have improved this paper. E.C. acknowledges partial support from NSF grant AST-0808119 and NASA contract No. 1282620.

References

  1. Afflerbach, A., Churchwell, E., Acord, J. M., et al. 1996, ApJS, 106, 423 [NASA ADS] [CrossRef] [Google Scholar]
  2. Afflerbach, A., Churchwell, E., & Werner, M. W. 1997, ApJ, 478, 190 [NASA ADS] [CrossRef] [Google Scholar]
  3. Auer, L. H. 1968, ApJ, 153, 923 [NASA ADS] [CrossRef] [Google Scholar]
  4. Auer, L. H., & Mihalas, D. 1972, ApJS, 24, 193 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barnes, P. J., Yonekura, Y., Ryder, S. D., et al. 2010, ApJ, to be published [Google Scholar]
  6. Baudry, A., Perault, M., del La Noe, J., Despois, D., & Cernicharo, J. 1981, A&A, 104, 101 [NASA ADS] [Google Scholar]
  7. Bourke, T. L., Garay, G., Lehtinen, K. K., et al. 1997, ApJ, 476, 781 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cesaroni, R., Walmsley, C. M., Koempe, C., & Churchwell, E. 1991, A&A, 252, 278 [NASA ADS] [Google Scholar]
  9. Cesaroni, R., Olmi, L., Walmsley, C. M., Churchwell, E., & Hofner, P. 1994, ApJ, 435, 137 [Google Scholar]
  10. Cesaroni, R., Hofner, P., Walmsley, C. M., & Churchwell, E. 1998, A&A, 331, 709 [NASA ADS] [Google Scholar]
  11. Choi, M., Evans, N. J., & Jaffe, D. T. 1993, ApJ, 417, 624 [NASA ADS] [CrossRef] [Google Scholar]
  12. Churchwell, E. 1991, NATO ASI Ser. C, 342, 221 [Google Scholar]
  13. Churchwell, E. 1997, ApJ, 479, L59 [NASA ADS] [CrossRef] [Google Scholar]
  14. Churchwell, E. 2002, ASP Conf. Ser. 267, ed. P. A. Crowther, 3 [Google Scholar]
  15. Churchwell, E., & Walmsley, C. M. 1975, A&A, 38, 451 [NASA ADS] [Google Scholar]
  16. De Vries, C. H., & Myers, P. C. 2005, ApJ, 620, 800 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fey, A. L., Claussen, M. J., Gaume, R. A., et al. 1992, AJ, 103, 234 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fuente, A., Rodriguez-Franco, A., Garcia-Burillo, S., et al. 2003, A&A, 406, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Fuller, G. A., Williams, S. J., & Sridharan, T. K. 2005, A&A, 442, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Garay, G., Mardones, D., Bronfman, L., et al. 2007, A&A, 463, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gordon, M. A., & Sorochenko, R. L. 2002, in Radio Recombination Lines: Their Physics and Astronomical Applications (Dordrecht, Boston, London: Kluwer Academic Pubs.), 28 [Google Scholar]
  23. Klassen, P. D., & Wilson, C. D. 2007, ApJ, 663, 1092 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kurtz, S., Churchwell, E., & Wood, D. O. S. 1994, ApJS, 91, 659 [NASA ADS] [CrossRef] [Google Scholar]
  25. Langer, W. D., & Penzias, A. A. 1990, ApJ, 357, 477 [NASA ADS] [CrossRef] [Google Scholar]
  26. Maciel, W. J., & Köppen, J. 1994, A&A, 282, 436 [NASA ADS] [Google Scholar]
  27. Mezger, P. G., Pankonin, V., Schmid-Burgk, J., Thum, C., & Wink, J. 1979, A&A, 80, L3 [NASA ADS] [Google Scholar]
  28. Myers, P. C., Mardones, D., Tafalla, M., Williams, J. P., & Wilner, D. J. 1996, ApJ, 465, L133 [NASA ADS] [CrossRef] [Google Scholar]
  29. Purcell, C. R., Balasubramanyan, R., Burton, M. B., et al. 2006, MNRAS, 367, 553 [NASA ADS] [CrossRef] [Google Scholar]
  30. Sandell, G., & Sievers, A. 2004, ApJ, 600, 269 [NASA ADS] [CrossRef] [Google Scholar]
  31. Schuster, K.-F., Boucher, C., Brunswig, W., et al. 2004, A&A, 423, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Sewi▯o, M., Churchwell, E., Kurtz, S., Goss, W. M., & Hofner, P. 2008, ApJ, 681, 350 [NASA ADS] [CrossRef] [Google Scholar]
  33. Shaver, P. A., McGee, R. X., Newton, L. M., Danks, A. C., & Pottasch, S. R. 1983, MNRAS, 204, 53 [NASA ADS] [CrossRef] [Google Scholar]
  34. Shepherd, D. S., & Churchwell, E. 1996, ApJ, 472, 225 [NASA ADS] [CrossRef] [Google Scholar]
  35. Velusamy, T., Peng, R., Li, D., Goldsmith, P. F., & Langer, W. D. 2008, ApJ, 688, L97 [Google Scholar]
  36. Wood, D. O. S., & Churchwell, E. 1989, ApJS, 69, 831 [NASA ADS] [CrossRef] [Google Scholar]
  37. Wu, Y., Henkel, C., Xue, R., Guan, X., & Miller, M. 2007, ApJ, 669, L37 [NASA ADS] [CrossRef] [Google Scholar]
  38. Zhu, Q.-F., Lacy, J. H., Jaffe, D. T., Richter, M. J., & Greathouse, Th. K. 2008, ApJS, 177, 584 [NASA ADS] [CrossRef] [Google Scholar]
  39. Zuckerman, B. 1973, ApJ, 183, 863 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... clouds[*]
Maps are available in electronic form from the authors.

All Tables

Table 1:   Target sources and type of observation made.

Table 2:   Spectral resolution and bandwidth available with the receiver/backend combinations used.

Table 3:   Recombination line observations.

Table 4:   HCO+ observations. Isotopes are abbreviated as 12 (HCO+), 13 (H13CO+), and 18 (HC18O+).

Table 5:   Flow velocities, column densities, and mass fluxes

Table 6:   Column densities from single peaked HCO+ profiles.

Table 7:   Column densities N and masses M from H13CO+ lines.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{12241Fig1.eps} \end{figure} Figure 1:

Spectra of the $3\rightarrow 2$ transitions of the main HCO+ isotopes toward G28.20-0.04N ( left) and G10.62-0.38 ( right). The vertical scales are in degrees K of  $T^*_{\rm A}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8.3cm,clip]{12241Fig2b.eps}\... ...{2mm} \includegraphics[angle=-90,width=8.3cm,clip]{12241Fig2a.eps} \end{figure} Figure 2:

Maps of G10.62-0.38 obtained with HERA at an angular resolution of 12'' (circles at lower left corners) in the transitions of H$30\alpha $ ( left) and HCO+(3-2) ( right). Contours are in K km s-1 and range from 3 to 18 in steps of 3 (H$30\alpha $) and from 15 to 225 in steps of 15 (HCO+(3-2)).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=11.6cm,clip]{12241Fig3.eps} \end{figure} Figure 3:

H$30\alpha $ maps obtained with HERA at an angular resolution of 12''. All maps in one row have been plotted using the same contour levels and color scale shown on the right. Contours are in K km s-1, start at and are in steps of 3 (row 1), 2 (rows 2 and 3), and 1 (rows 4 and 5). Note that a broken pixel affects coverage to the left of center.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=11.6cm,clip]{12241Fig4.eps} \vspace*{2mm} \end{figure} Figure 4:

HCO+(3-2) maps obtained with HERA at an angular resolution of 12''. All maps in one row have been plotted using the same contour levels and color scale shown on the right. Contours are in K km s-1, start at and are in steps of 30 (row 1), 15 (row 2), 10 (row 3), 8 (row 4), and 4 (row 5).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8.5cm,clip]{12241Fig5.eps} \end{figure} Figure 5:

Histogram of the observed velocity differences between the ionized and molecular gas, as obtained from our H$30\alpha $ and HCO+ data. The weighted mean velocity difference of this sample of 22 sources is +1.45 km s-1.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.