EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A7 Full HTML
Highlight
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A7
Number of page(s) 15
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200913474
Published online 18 March 2010
A&A 512, A7 (2010)

Observations of the Large Magellanic Cloud with Fermi

A. A. Abdo1,2 - M. Ackermann3 - M. Ajello3 - W. B. Atwood4 - L. Baldini5 - J. Ballet6 - G. Barbiellini7,8 - D. Bastieri9,10 - B. M. Baughman11 - K. Bechtol3 - R. Bellazzini5 - B. Berenji3 - R. D. Blandford3 - E. D. Bloom3 - E. Bonamente12,13 - A. W. Borgland3 - J. Bregeon5 - A. Brez5 - M. Brigida14,15 - P. Bruel16 - T. H. Burnett17 - S. Buson10 - G. A. Caliandro14,15 - R. A. Cameron3 - P. A. Caraveo18 - J. M. Casandjian6 - C. Cecchi12,13 - Ö. Çelik19,20,21 - A. Chekhtman1,22 - C. C. Cheung19 - J. Chiang3 - S. Ciprini12,13 - R. Claus3 - J. Cohen-Tanugi23 - L. R. Cominsky24 - J. Conrad25,26,27 - S. Cutini28 - C. D. Dermer1 - A. de Angelis29 - F. de Palma14,15 - S. W. Digel3 - E. do Couto e Silva3 - P. S. Drell3 - R. Dubois3 - D. Dumora30,31 - C. Farnier23 - C. Favuzzi14,15 - S. J. Fegan16 - W. B. Focke3 - P. Fortin16 - M. Frailis29 - Y. Fukazawa32 - P. Fusco14,15 - F. Gargano15 - D. Gasparrini28 - N. Gehrels19,33 - S. Germani12,13 - G. Giavitto34 - B. Giebels16 - N. Giglietto14,15 - F. Giordano14,15 - T. Glanzman3 - G. Godfrey3 - E. V. Gotthelf35 - I. A. Grenier6 - M.-H. Grondin30,31 - J. E. Grove1 - L. Guillemot30,31 - S. Guiriec36 - Y. Hanabata32 - A. K. Harding19 - M. Hayashida3 - E. Hays19 - D. Horan16 - R. E. Hughes11 - M. S. Jackson25,26,37 - P. Jean41 - G. Jóhannesson3 - A. S. Johnson3 - R. P. Johnson4 - T. J. Johnson19,33 - W. N. Johnson1 - T. Kamae3 - H. Katagiri32 - J. Kataoka38,39 - N. Kawai38,40 - M. Kerr17 - J. Knödlseder41 - M. L. Kocian3 - M. Kuss5 - J. Lande3 - L. Latronico5 - M. Lemoine-Goumard30,31 - F. Longo7,8 - F. Loparco14,15 - B. Lott30,31 - M. N. Lovellette1 - P. Lubrano12,13 - G. M. Madejski3 - A. Makeev1,22 - F. Marshall19 - P. Martin42 - M. N. Mazziotta15 - W. McConville19,33 - J. E. McEnery19 - C. Meurer25,26 - P. F. Michelson3 - W. Mitthumsiri3 - T. Mizuno32 - A. A. Moiseev20,33 - C. Monte14,15 - M. E. Monzani3 - A. Morselli43 - I. V. Moskalenko3 - S. Murgia3 - P. L. Nolan3 - J. P. Norris44 - E. Nuss23 - T. Ohsugi32 - N. Omodei5 - E. Orlando42 - J. F. Ormes44 - D. Paneque3 - D. Parent30,31 - V. Pelassa23 - M. Pepe12,13 - M. Pesce-Rollins5 - F. Piron23 - T. A. Porter4 - S. Rainò14,15 - R. Rando9,10 - M. Razzano5 - A. Reimer45,3 - O. Reimer45,3 - T. Reposeur30,31 - S. Ritz4 - A. Y. Rodriguez46 - R. W. Romani3 - M. Roth17 - F. Ryde37,26 - H. F.-W. Sadrozinski4 - D. Sanchez16 - A. Sander11 - P. M. Saz Parkinson4 - J. D. Scargle47 - A. Sellerholm25,26 - C. Sgrò5 - E. J. Siskind48 - D. A. Smith30,31 - P. D. Smith11 - G. Spandre5 - P. Spinelli14,15 - J.-L. Starck6 - M. S. Strickman1 - A. W. Strong42 - D. J. Suson49 - H. Tajima3 - H. Takahashi32 - T. Tanaka3 - J. B. Thayer3 - J. G. Thayer3 - D. J. Thompson19 - L. Tibaldo9,6,10 - D. F. Torres50,46 - G. Tosti12,13 - A. Tramacere3,51 - Y. Uchiyama52,3 - T. L. Usher3 - V. Vasileiou19,20,21 - C. Venter19,53 - N. Vilchez41 - V. Vitale43,54 - A. P. Waite3 - P. Wang3 - P. Weltevrede55 - B. L. Winer11 - K. S. Wood1 - T. Ylinen37,56,26 - M. Ziegler4

1 - Space Science Division, Naval Research Laboratory, Washington, DC 20375, USA
2 - National Research Council Research Associate, National Academy of Sciences, Washington, DC 20001, USA
3 - W. W. Hansen Experimental Physics Laboratory, Kavli Institute for Particle Astrophysics and Cosmology, Department of Physics and SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94305, USA
4 - Santa Cruz Institute for Particle Physics, Department of Physics and Department of Astronomy and Astrophysics, University of California at Santa Cruz, Santa Cruz, CA 95064, USA
5 - Istituto Nazionale di Fisica Nucleare, Sezione di Pisa, 56127 Pisa, Italy
6 - Laboratoire AIM, CEA-IRFU/CNRS/Université Paris Diderot, Service d'Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette, France
7 - Istituto Nazionale di Fisica Nucleare, Sezione di Trieste, 34127 Trieste, Italy
8 - Dipartimento di Fisica, Università di Trieste, 34127 Trieste, Italy
9 - Istituto Nazionale di Fisica Nucleare, Sezione di Padova, 35131 Padova, Italy
10 - Dipartimento di Fisica ``G. Galilei'', Università di Padova, 35131 Padova, Italy
11 - Department of Physics, Center for Cosmology and Astro-Particle Physics, The Ohio State University, Columbus, OH 43210, USA
12 - Istituto Nazionale di Fisica Nucleare, Sezione di Perugia, 06123 Perugia, Italy
13 - Dipartimento di Fisica, Università degli Studi di Perugia, 06123 Perugia, Italy
14 - Dipartimento di Fisica ``M. Merlin'' dell'Università e del Politecnico di Bari, 70126 Bari, Italy
15 - Istituto Nazionale di Fisica Nucleare, Sezione di Bari, 70126 Bari, Italy
16 - Laboratoire Leprince-Ringuet, École polytechnique, CNRS/IN2P3, Palaiseau, France
17 - Department of Physics, University of Washington, Seattle, WA 98195-1560, USA
18 - INAF-Istituto di Astrofisica Spaziale e Fisica Cosmica, 20133 Milano, Italy
19 - NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
20 - Center for Research and Exploration in Space Science and Technology (CRESST), NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
21 - University of Maryland, Baltimore County, Baltimore, MD 21250, USA
22 - George Mason University, Fairfax, VA 22030, USA
23 - Laboratoire de Physique Théorique et Astroparticules, Université Montpellier 2, CNRS/IN2P3, Montpellier, France
24 - Department of Physics and Astronomy, Sonoma State University, Rohnert Park, CA 94928-3609, USA
25 - Department of Physics, Stockholm University, AlbaNova, 106 91 Stockholm, Sweden
26 - The Oskar Klein Centre for Cosmoparticle Physics, AlbaNova, 106 91 Stockholm, Sweden
27 - Royal Swedish Academy of Sciences Research Fellow, funded by a grant from the K. A. Wallenberg Foundation
28 - Agenzia Spaziale Italiana (ASI) Science Data Center, 00044 Frascati (Roma), Italy
29 - Dipartimento di Fisica, Università di Udine and Istituto Nazionale di Fisica Nucleare, Sezione di Trieste, Gruppo Collegato di Udine, 33100 Udine, Italy
30 - Université de Bordeaux, Centre d'Études Nucléaires Bordeaux Gradignan, UMR 5797, 33175 Gradignan, France
31 - CNRS/IN2P3, Centre d'Études Nucléaires Bordeaux Gradignan, UMR 5797, 33175 Gradignan, France
32 - Department of Physical Sciences, Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan
33 - University of Maryland, College Park, MD 20742, USA
34 - Istituto Nazionale di Fisica Nucleare, Sezione di Trieste, and Università di Trieste, 34127 Trieste, Italy
35 - Columbia Astrophysics Laboratory, Columbia University, New York, NY 10027, USA
36 - University of Alabama in Huntsville, Huntsville, AL 35899, USA
37 - Department of Physics, Royal Institute of Technology (KTH), AlbaNova, 106 91 Stockholm, Sweden
38 - Department of Physics, Tokyo Institute of Technology, Meguro City, Tokyo 152-8551, Japan
39 - Waseda University, 1-104 Totsukamachi, Shinjuku-ku, Tokyo, 169-8050, Japan
40 - Cosmic Radiation Laboratory, Institute of Physical and Chemical Research (RIKEN), Wako, Saitama 351-0198, Japan
41 - Centre d'Étude Spatiale des Rayonnements, CNRS/UPS, BP 44346, 31028 Toulouse Cedex 4, France
42 - Max-Planck Institut für extraterrestrische Physik, 85748 Garching, Germany
43 - Istituto Nazionale di Fisica Nucleare, Sezione di Roma ``Tor Vergata'', 00133 Roma, Italy
44 - Department of Physics and Astronomy, University of Denver, Denver, CO 80208, USA
45 - Institut für Astro- und Teilchenphysik and Institut für Theoretische Physik, Leopold-Franzens-Universität Innsbruck, 6020 Innsbruck, Austria
46 - Institut de Ciencies de l'Espai (IEEC-CSIC), Campus UAB, 08193 Barcelona, Spain
47 - Space Sciences Division, NASA Ames Research Center, Moffett Field, CA 94035-1000, USA
48 - NYCB Real-Time Computing Inc., Lattingtown, NY 11560-1025, USA
49 - Department of Chemistry and Physics, Purdue University Calumet, Hammond, IN 46323-2094, USA
50 - Institució Catalana de Recerca i Estudis Avançats, Barcelona, Spain
51 - Consorzio Interuniversitario per la Fisica Spaziale (CIFS), 10133 Torino, Italy
52 - Institute of Space and Astronautical Science, JAXA, 3-1-1 Yoshinodai, Sagamihara, Kanagawa 229-8510, Japan
53 - North-West University, Potchefstroom Campus, Potchefstroom 2520, South Africa
54 - Dipartimento di Fisica, Università di Roma ``Tor Vergata'', 00133 Roma, Italy
55 - Australia Telescope National Facility, CSIRO, Epping NSW 1710, Australia
56 - School of Pure and Applied Natural Sciences, University of Kalmar, 391 82 Kalmar, Sweden

Received 15 October 2009 / Accepted 22 December 2009

Abstract
Context. The Large Magellanic Cloud (LMC) is to date the only normal external galaxy that has been detected in high-energy gamma rays. High-energy gamma rays trace particle acceleration processes and gamma-ray observations allow the nature and sites of acceleration to be studied.
Aims. We characterise the distribution and sources of cosmic rays in the LMC from analysis of gamma-ray observations.
Methods. We analyse 11 months of continuous sky-survey observations obtained with the Large Area Telescope aboard the Fermi Gamma-Ray Space Telescope and compare it to tracers of the interstellar medium and models of the gamma-ray sources in the LMC.
Results. The LMC is detected at 33$\sigma $ significance. The integrated >100 MeV photon flux of the LMC amounts to $(2.6 \pm 0.2) \times 10^{-7}$ ph cm-2 s-1 which corresponds to an energy flux of $(1.6 \pm 0.1) \times 10^{-10}$ erg cm-2 s-1, with additional systematic uncertainties of $\la$16%. The analysis reveals the massive star forming region 30 Doradus as a bright source of gamma-ray emission in the LMC in addition to fainter emission regions found in the northern part of the galaxy. The gamma-ray emission from the LMC shows very little correlation with gas density and is rather correlated to tracers of massive star forming regions. The close confinement of gamma-ray emission to star forming regions suggests a relatively short GeV cosmic-ray proton diffusion length.
Conclusions. The close correlation between cosmic-ray density and massive star tracers supports the idea that cosmic rays are accelerated in massive star forming regions as a result of the large amounts of kinetic energy that are input by the stellar winds and supernova explosions of massive stars into the interstellar medium.

Key words: acceleration of particles - cosmic rays - Magellanic Clouds - gamma rays: galaxies

1 Introduction

Since the early days of high-energy gamma-ray astronomy, it has been clear that the gamma-ray flux received on Earth is dominated by emission from the Galactic disk (Clark et al. 1968). This emission is believed to arise from cosmic-ray interactions with the interstellar medium, which at gamma-ray energies $\ga$100 MeV are dominated by the decay of $\pi ^0$ produced in collisions between cosmic-ray nuclei and the interstellar medium (Pollack & Fazio 1963). Further contributions are from cosmic-ray electrons undergoing inverse Compton scattering off interstellar soft photons and Bremsstrahlung losses within the interstellar medium. Gamma-ray observations thus have the potential to map cosmic-ray acceleration sites in our Galaxy, which may ultimately help to identify the sources of cosmic-ray acceleration.

Nearby galaxies have some advantages as targets for studies of cosmic-ray physics and have the advantage of being viewed from outside, and so line of sight confusion, which complicates studies of emission from the Galactic disk, is diminished. This advantage is, however, somewhat offset by the limitations by the angular resolution and sensitivity of the instrument. The Large Magellanic Cloud (LMC) is thus an excellent target for studying the link between cosmic-ray acceleration and gamma-ray emission since the galaxy is nearby ( $D\approx50$ kpc; Pietrzynski et al. 2009; Matsunaga et al. 2009), has a large angular extent of $\sim$ $8\ensuremath{^\circ} $, and is seen at a small inclination angle of $i\approx20\ensuremath{^\circ} {-}35\ensuremath{^\circ} $(Van der Marel 2006; Kim et al. 1998), which avoids source confusion. In addition, the LMC is relatively active, housing many supernova remnants, bubbles and superbubbles, and massive star-forming regions that are all potential sites of cosmic-ray acceleration (Cesarsky & Montmerle 1983; Binns et al. 2007; Biermann 2004).

The EGRET telescope aboard the Compton Gamma-Ray Observatory (CGRO, 1991-2000) was the first to detect the LMC (Sreekumar et al. 1992), which has remained the only normal galaxy besides our Milky Way that has been seen in high-energy gamma rays. Due to EGRET's limited angular resolution and limited sensitivity, details of the spatial structure of the gamma-ray emission could not be resolved, yet the observations showed some evidence that the spatial distribution is consistent with the morphology of radio emission. The observations also allowed determining the integral gamma-ray flux from the LMC, which was shown to be consistent with expectations based on a model using the principles of dynamic balance and containment (Fichtel et al. 1991). From the agreement with this model, Sreekumar et al. (1992) conclude that the level of cosmic rays in the LMC is comparable to that in our Galaxy.

The Large Area Telescope (LAT) aboard Fermi is now for the first time providing the capabilities to go well beyond the study of the integrated gamma-ray flux from the LMC (Digel et al. 2000; Weidenspointner et al. 2007). Thanks to its excellent sensitivity and good angular resolution, we are able to spatially resolve the structure of the gamma-ray emission, allowing us to provide a detailed mapping of the cosmic-ray density in the galaxy. In the spectral domain, our data allow for detailed comparisons with cosmic-ray interaction models and can be used to search for spectral variations over the galaxy. In the timing domain, we are able to assess contributions from flaring sources and can search for pulsations from energetic pulsars in the galaxy that may contribute to the total emission (Hartmann et al. 1993; Harding 1981).

In this paper we present our first in-depth analysis of the LMC galaxy based on 11 months of continuous sky survey observations performed with Fermi/LAT. We put particular emphasis on determining the spatial distribution of the gamma-ray emission, which, as we will show, reveals the distribution of cosmic rays in the galaxy. We also search pulsations from energetic pulsars that may contribute to a non-negligible level to the overall emission.

2 Observations

2.1 Data preparation

The characteristics and performance of the LAT aboard Fermi are described in detail by Atwood et al. (2009). The data used in this work amount to 274.3 days of continuous sky survey observations over the period August 8 2008-July 9 2009 during which a total exposure of $\sim$ $2.5 \times 10^{10}$ cm2 s (at 1 GeV) has been obtained for the LMC. Events satisfying the standard low-background event selection (``Diffuse'' events; Atwood et al. 2009) and coming from zenith angles < $105\ensuremath{^\circ} $ (to greatly reduce the contribution by Earth albedo gamma rays) were used. To further reduce the effect of Earth albedo backgrounds, the time intervals when the Earth was appreciably within the field of view (specifically, when the centre of the field of view was more than $47\ensuremath{^\circ} $ from the zenith) were excluded from this analysis. Furthermore, time intervals when the spacecraft was within the South Atlantic Anomaly were also excluded. We further restricted the analysis to photon energies above 200 MeV; below this energy, the effective area in the ``Diffuse class'' is relatively small and strongly dependent on energy.

For the analysis we selected all events within a rectangular region-of-interest (ROI) of size $20\ensuremath{^\circ}\times 20\ensuremath{^\circ} $ centred on $(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}17^{\rm... ...^{\rm s}, -69\ensuremath{^\circ}01\hbox{$^\prime$ }48\hbox{$^{\prime\prime}$ })$[*] and aligned in equatorial coordinates. All analysis was performed using the LAT Science Tools package, which is available from the Fermi Science Support Center, using P6_V3 post-launch instrument response functions (IRFs). These take into account pile-up and accidental coincidence effects in the detector subsystems that were not considered in the definition of the pre-launch IRFs.

2.2 Data selection and background modelling

At the Galactic latitude of the LMC ( $b \approx -33\ensuremath{^\circ} $), the gamma-ray background is a combination of extragalactic and Galactic diffuse emissions and some residual instrumental background. The extragalactic component comprises resolved sources, which often can be associated with known blazars (Abdo et al. 2009b), and a diffuse component, which is attributed to unresolved sources and eventually intrinsically diffuse processes (Dermer 2007; Strong et al. 2004a). The latest LAT collaboration-internal source list that has been derived from 11 months of survey data (comparable to the data volume used in this analysis) contains 542 sources for latitudes $\vert b\vert \ge 30\ensuremath{^\circ} $, corresponding to a source density of 86 sources sr-1. Our ROI covers a solid angle of 0.12 sr, so we expect about 10 resolved background sources in our field. Among those, 1-2 should spatially overlap with the LMC if we assume the galaxy's diameter is between  $8\ensuremath{^\circ} $ and  $10\ensuremath{^\circ} $.

\begin{figure} \par\includegraphics[width=9cm,clip]{13474fg1.eps}\includegraphics[width=9cm,clip]{13474fg2.eps} \end{figure} Figure 1:

Gaussian kernel ( $\sigma =0.2\ensuremath {^\circ } $) smoothed counts maps of the region of interest (ROI) in a true local projection before ( left) and after subtraction of the background model ( right) for the energy range 200 MeV-20 GeV and for a pixel size of $0.1\ensuremath {^\circ }\times 0.1\ensuremath {^\circ } $. Overlaid is the N(H  I) contour of $1\times 10^{21}$ H cm-2 of the LMC to indicate the extent and shape of the galaxy. The boxes show the locations of the 6 point sources that have been included in the background model. The right panel has a true dynamic range from -46 to +248 counts deg-2that has been expanded for display to cover the full dynamic range of the residuals that are shown in Fig. 4.

Open with DEXTER

Within the ROI but outside the boundaries of the LMC we found a total of 6 significant point sources, compatible with expectations (cf. Table 1). For all of them we found counterparts in the CRATES catalogue of flat-spectrum radio sources (Healey et al. 2007) using the procedure described in Abdo et al. (2009a), making them good candidates for being background blazars. Searching for background sources within the LMC boundaries is more difficult due to possible confusion with local emission maxima of the galaxy's diffuse emission. Background blazars may however reveal themselves by their flaring activity, hence we searched for any excess emission above the time averaged level on a monthly basis (cf. Sect. 2.4). We found evidence for a flaring source during month 4 of our dataset (MJD 54777.8-54808.2) near 30 Doradus, and thus we excluded the data within this time interval from our analysis. This results in a dataset that corresponds to 248.7 days of continuous sky survey observations during which a total exposure of $\sim$ $2.3 \times 10^{10}$ cm2 s (at 1 GeV) was obtained for the LMC.

Table 1:   Point sources included in the background model.

We then modelled background gamma-ray emission within the ROI using components for the diffuse Galactic and the extragalactic and residual instrumental backgrounds and the 6 blazars. The Galactic component was based on the LAT standard diffuse background model gll_iem_v02[*] for which we kept the overall normalisation as a free parameter. The extragalactic and residual instrumental backgrounds were combined into a single component which has been taken as being isotropic. The spectrum of this component was determined by fitting an isotropic component together with a model of the Galactic diffuse emission and point sources to the data. Also here we left the overall normalisation of the component as a free parameter. The 6 background blazars were modelled as point sources with power-law spectral shapes. The positions of the blazars were fixed to those given in the CRATES catalogue (Healey et al. 2007) and are given in Table 1. The flux and spectral power-law index of each source were left as free parameters of our background model and their values were determined from likelihood analysis.

2.3 Spatial distribution

2.3.1 Counts map

To investigate the spatial distribution of gamma-ray emission toward the LMC we first binned all photons into a counts map of size $20\ensuremath{^\circ}\times 20\ensuremath{^\circ} $ centred on $(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}17^{\rm... ...^{\rm s}, -69\ensuremath{^\circ}01\hbox{$^\prime$ }48\hbox{$^{\prime\prime}$ })$and aligned in equatorial coordinates. Figure 1 shows the counts map before (left panel) and after (right panel) subtraction of the background model.

The background subtracted map confirms that diffuse Galactic and isotropic backgrounds as well as the 6 background blazars are properly removed by our treatment. The only remaining feature is extended emission that is spatially confined to within the LMC boundaries which we trace by the iso column density contour $N_{\rm H} = 1\times10^{21}$ H cm-2of neutral hydrogen in the LMC (Kim et al. 2003). The total number of excess 200 MeV-20 GeV photons above the background in the LMC area[*] amounts to $\sim$1550 counts whereas the background in the same area amounts to $\sim$2440 counts. With these statistics, the extended gamma-ray emission from the LMC can be resolved into several components. The brightest emission feature is located near $(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ }) \approx (05^{\rm h}40^{\rm m}, -69\ensuremath{^\circ} 15')$, which is close to the massive star-forming region 30 Doradus (30 Dor) that houses the two Crab-like pulsars PSR J0540-6919 and PSR J0537-6910 (Marshall et al. 1998; Seward et al. 1984). Excess gamma-ray emission is also seen toward the north and the west of 30 Dor. These bright regions are embedded into a more extended and diffuse glow that covers an area of approximately $5\ensuremath{^\circ}\times 5\ensuremath{^\circ} $. To further illustrate the emission structure we show profiles of the counts map in Fig. 2 along $\alpha_{\rm J2000}$ (top panel) and $\delta_{\rm J2000}$ (bottom panel) and we provide an adaptively smoothed image of the 30 Dor region in Fig. 3.

\begin{figure} \par\includegraphics[width=9.1cm,clip]{13474fg3.eps} \end{figure} Figure 2:

Profiles of the observed number of counts along Right Ascension ( top) and Declination ( bottom) of the LMC region for the energy range 200 MeV-20 GeV. The solid lines show the corresponding profiles of the background model. The red arrow indicates the location of 30 Dor.

Open with DEXTER

2.3.2 Geometrical models

Out next step was to assess the spatial distribution of the LMC emission using simple parametrised geometrical models of the gamma-ray intensity distribution. We assumed power-law spectral distributions for all models and kept the total flux and power law index as free parameters. We adjusted the spatial and spectral parameters of the models using a binned maximum likelihood analysis with spatial bins of $0.1\ensuremath {^\circ }\times 0.1\ensuremath {^\circ } $ and 60 logarithmically spaced energy bins covering the energy range 200 MeV-20 GeV. For each model we computed the so-called Test Statistic (TS), which is defined as twice the difference between the log-likelihood $\mathcal{L}_1$ that is obtained by fitting the model on top of the background model to the data, and the log-likelihood $\mathcal{L}_0$ that is obtained by fitting the background model only, i.e. ${\rm TS} = 2(\mathcal{L}_1 - \mathcal{L}_0)$. Under the hypothesis that the background model satisfactorily explains our data, TS follows the $\chi^2_p$ distribution with p degrees of freedom, where p is the number of additional free parameters in the maximisation of $\mathcal{L}_1$ with respect to those used in the maximisation of $\mathcal{L}_0$ (Cash 1979). For example, for a single source on top of the background model with free position, flux and spectral power law index we have p=4.

First, we examined whether the gamma-ray emission from the LMC can be explained with a combination of individual point sources. For this purpose we added successive point sources to our model and optimised their locations, fluxes and spectral indices by maximising the likelihood of the model. We stopped this procedure once the TS improvement after adding a further point source dropped below 25. This happened after we added a 6th point source to our model which resulted in a TS improvement of only 21.9, corresponding to a detection significance of $3.7\sigma$for this source. Table 2 provides the maximum likelihood positions and fluxes for the 5 significant point sources, and gives also the TS improvement ($\Delta$TS) that is achieved in each of the successive steps. Adding up $\Delta$TS for all sources provides a total TS of 1089.3 for this model, corresponding to a detection significance of $31.5\sigma$ (p=20). We refer to the point source model as PS.

\begin{figure} \par\includegraphics[width=9.1cm]{13474fg4.eps} \end{figure} Figure 3:

Zoom into a $3\ensuremath {^\circ }\times 3\ensuremath {^\circ } $ large region of the background subtracted counts map around the central star cluster R 136 in 30 Dor. The counts map has been adaptively smoothed (Ebeling et al. 2006) with a signal-to-noise ratio of 5 in order to reveal significant structures at all possible scales while suppressing the noise that arises from photon counting statistics. Stars show the locations of R 136 and of the pulsars PSR J0540-6919 and PSR J0537-6910. The circles show the 95% containment radius of sources S1, S3, and G2 (see text). For G2 we added the Gaussian $\sigma $ of the source to the error radius. We also show the 95% containment radius of a flaring source that appeared during month 4 of the analysed data set. The diamond shows the location of the possible counterpart RX J0546.8-6851 of the flaring source (see Sect. 2.4).

Open with DEXTER

Table 2:   Parameters of the point source model PS.

Second, instead of using point sources we repeated the procedure with 2D Gaussian shaped intensity profiles to build a geometrical model that is more appropriate for extended and diffuse emission structures. We again stopped the successive addition of 2D Gaussian shaped sources once the TS improvement after adding a further source dropped below 25. This occurred after two 2D Gaussian shaped sources have been added to the model. Table 3 lists the maximum likelihood positions, Gaussian widths $\sigma $ and fluxes for the two significant 2D Gaussian sources. Similar to the point sources, the column $\Delta$TS quotes the TS improvements in each of the successive steps. The total TS amounts to 1122.6 for this model, corresponding to a detection significance of $32.7\sigma$ (p=10). We refer to this model from now on as 2DG.

Adding a 3rd 2D Gaussian shaped source improved the TS by only 21.9, corresponding to a detection significance of $3.5\sigma$ for this source (p=5). We note that this 3rd 2D Gaussian source is located at $(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ }) = (05^{\rm h}17.8^{\rm m}, -72\ensuremath{^\circ} 32')$ with a 95% containment radius of $18\hbox{$^\prime$ }$, and that it formally is consistent with a point source ( $\sigma=10\hbox{$^\prime$ }\pm 13\hbox{$^\prime$ }$). Using our standard source association procedure (Abdo et al. 2009a) we found the blazar CRATES J051636-723707 as a possible counterpart of this source, suggesting the presence of a background blazar within the boundaries of the LMC (see also Sect. 2.5).

Table 3:   Parameters of the 2D Gaussian sources model 2DG.

To illustrate how well the models fit the data we show in Fig. 4 the model counts map and the residual counts that are left in the ROI after subtracting the PS or 2DG model from the data. The colour scale and dynamic range of the residual maps has been chosen identical to that of the right panel of Fig. 1 to allow the comparison of the residuals before and after subtraction of the LMC model. Apparently, only very few residual counts are left in the LMC area after subtraction of either of the two models from the data (however a significant negative residual at the position of S1 indicates an overestimation of the flux in the PS model in this area). None of the peaks in the residuals is statistically significant ( $\Delta {\rm TS}<25$) as a point source (for the PS model) or a 2D Gaussian shaped extended source (for the 2DG model).

\begin{figure} \par\includegraphics[width=7.6cm,clip]{13474fg5.eps}\includegraph... ...clip]{13474fg9.eps}\includegraphics[width=7.6cm,clip]{13474fga.eps} \end{figure} Figure 4:

Gaussian kernel ( $\sigma =0.2\ensuremath {^\circ } $) smoothed model counts maps ( left panels) and residual maps ( right panels) of the region of interest (ROI). The model counts maps have been obtained by convolving the model sky maps that were scaled to the fitted flux with the LAT point spread function. The top row shows the PS model, the middle row shows the 2DG model and the bottom row shows the H  II template. The colour scaling and the dynamic range for the residual maps is identical to the right panel of Fig. 1 to allow for comparison.

Open with DEXTER

The PS and 2DG models have in common that they both comprise a strong source located at $(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ }) \approx (05^{\rm h}39^{\rm m}, -69\ensuremath{^\circ} 17')$ in the 30 Dor region (S1 for PS and G2 for 2DG). We indicate the location uncertainties for these sources as circles in Fig. 3. We also show the locations of the powerful star cluster R 136 and of the two Crab-like pulsars PSR J0540-6919 and PSR J0537-6910. From this figure it becomes clear that S1 in the PS model does not coincide with any of these objects. We confirm this observation by moving S1 to the locations of either PSR J0540-6919, PSR J0537-6910 or R 136, which leads to a significant TS reduction of 21.0 ($4.2\sigma$) for the position of PSR J0540-6919, 28.3 ($4.9\sigma$) for the position of PSR J0537-6910, and 31.1 ($5.2\sigma$) for the position of R 136. Thus, none of the 3 sources can explain the observed gamma-ray emission from 30 Dor alone. We come to the same conclusion when we replace G2 in the 2DG model by a point source at any of the 3 locations.

To search for evidence of point source emission from PSR J0540-6919, PSR J0537-6910 or R 136 on top of the diffuse emission, we added point sources at the respective positions to the 2DG model. Adding any of the sources led to only marginal TS improvements of 0.5 ($0.3\sigma$) for PSR J0540-6919, 0 ($0\sigma$) for PSR J0537-6910, and 0.1 ($0.1\sigma$) for R 136. Adding all three sources together marginally improved the TS by 0.5 ( $0.003\sigma$). Thus, we found no evidence for point source emission from any of the 3 sources on top of the diffuse emission that is modelled by G2. When we replaced G2 by a combination of 3 point sources located at the positions of PSR J0540-6919, PSR J0537-6910 and R 136 we obtained a TS of 1113.4, which still is smaller by $\Delta {\rm TS}=9.2$than the TS obtained for the 2DG model. Obviously, the gamma-ray emission from 30 Dor is better described by a single 2D Gaussian shaped extended source than by a combination of point sources situated at the locations of PSR J0540-6919, PSR J0537-6910 and R 136.

2.3.3 Gas templates

To test specific hypotheses about the spatial distribution of the gamma-ray intensity we compared our data to spatial templates that trace the interstellar matter distribution in the LMC. The reasoning behind this comparison is that gamma-rays are expected to primarily arise from interactions between cosmic rays and the interstellar medium (Ozel & Fichtel 1988), and we thus may obtain a measurement of the cosmic-ray density variations from the gamma-ray to gas ratio.

Most of the gas in the LMC is found in form of neutral atomic hydrogen and helium (Staveley-Smith et al. 2003) while $5\%{-}10\%$ in mass is in form of molecular clouds (Fukui et al. 2008) and about $1\%$ in mass is in form of ionized hydrogen (Kennicutt et al. 1995). For the atomic hydrogen component (H  I) we used the map of Kim et al. (2003) that is based on a combination of aperture synthesis and multibeam data from ATCA and Parkes observations. We converted this map into hydrogen column densities assuming optically thin emission or by applying an optical depth correction under the assumption of uniform spin temperature of either 40 K, 60 K or 125 K (Marx-Zimmer et al. 2000). Bernard et al. (2008) suggested the presence of an additional dark gas component in the LMC which correlates well with the distribution of the observed H  I. Thus, if this dark gas component indeed exists it should be morphologically well described by the H  I templates. For the molecular hydrogen component (H2) we used the CO map of the LMC obtained with the NANTEN telescope (Fukui et al. 2008) which we converted into molecular hydrogen column densities using a constant CO intensity to H2 column density conversion factor $X_{\rm CO} = 7\times 10^{20}$ H2 cm-2/(K km s-1) (Fukui et al. 2008). For the ionized hydrogen component we used the full-sky composite H$\alpha$ map of Finkbeiner (2003) which we converted into ionized hydrogen column densities using $N(\mbox{H~{\scriptsize II}}) = 1.37 \times 10^{18} I_{{\rm H}\alpha}$which assumes a gas temperature of 8000 K and an electron density of $n_{\rm e}=1$ cm-3 (cf. Eq. (6) of Bernard et al. 2008). In addition to the individual templates for the interstellar gas phases we also fitted a template of the total gas column density $N({\rm H})$ to the data that we derived by adding together the column densities of H  I, H2, and H  II. Furthermore, we also fitted the linear combination $N(\mbox{H~{\scriptsize I}})+N(\mbox{H$_2$ })+N(\mbox{H~{\scriptsize II}})$ to the data with independent scaling factors and power law indices for each component.

The TS values and detection significances that are obtained by maximum likelihood fitting are summarized in Table 4, where we also give the corresponding results for the geometrical models PS and 2DG for reference. Fitting the optically thin H  I and H2 maps resulted in TS values that are considerably worse than those obtained for the geometrical models. Applying the optical depth correction to the H  I data slightly improved the fit with a maximum TS of $\sim$835 that is reached for spin temperatures of 40 K-60 K, yet still, this TS is considerably worse than that of the geometrical models. Apparently, the H  I and H2 maps provide rather poor fits to the data, indicating that the distribution of gamma rays does not follow the distribution of neutral hydrogen in the LMC.

Table 4:   Comparison of maximum likelihood model fitting results (see text for a description of the models).

Luks & Rohlfs (1992) proposed that the neutral hydrogen in the LMC is confined into two separate structural features (dubbed ``D'' and ``L'' components), and we tested whether gamma-ray emission is possibly only correlated to one of these H  I components. We did this by separating the H  I data of Kim et al. (2003) into two maps covering the heliocentric radial velocity intervals $190<V_{\rm rad}<270$ km s-1 (L) and $270<V_{\rm rad}<386$ km s-1 (D) that roughly separate the two components (see Fig. 4 of Luks & Rohlfs 1992). Fitting both maps simultaneously with independent scaling factors and power law indices to our data only marginally improved the fit upon the $N(\mbox{H~{\scriptsize I}})$ gas map ( $\Delta \rm TS=21.1$). We therefore conclude that the gamma-ray emission does also not follow the distribution of either the D or the L component identified by Luks & Rohlfs (1992).

The H  II map, on the other hand, gave a TS that is very close to that of the PS and 2DG models. Fitting the total hydrogen column densities, i.e. model $N({\rm H})$, gave a rather low TS, close to that obtained for the H  I and H2 templates alone. This result is explained by the preponderance of atomic hydrogen in the LMC which means that the maps of total hydrogen and H  I are very similar. Fitting a linear combination of the three gas phases, i.e. model $N(\mbox{H~{\scriptsize I}})+N(\mbox{H$_2$ })+N(\mbox{H~{\scriptsize II}})$, gave basically the same TS value that is obtained for the H  II template alone. In this case, H  II is in fact the only significant model component in the fit while the maximum likelihood fluxes for the other components are negligible.

The H  II map thus provided the best fit among all of the gas maps to the LAT data. Figure 4 shows the model counts map for the H  II template and the corresponding residual counts map, which apparently is similar to the residual maps that we obtain for the geometrical models. A search for point-like or extended emission on top of the H  II template did not reveal any significant additional signal ( $\Delta {\rm TS}<25$). The H  II map is characterised by a strong emission peak near 30 Dor which is attributed to the intense ionizing radiation of the massive stars in this highly active region. To test whether the fits are mainly driven by this peak of ionizing flux, we repeated the template map analysis by adding the source G2 which describes the emission from 30 Dor in the 2DG model as an additional component to our background model. The flux and spectral index of this component were kept as free parameters. At the same time, we modified the gas maps by setting all pixels within a circular region of $0.5\ensuremath {^\circ } $ around $(\mbox{$\alpha_{\rm J2000}$ },\mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}38^{\rm ... ...^{\rm s}, -69\ensuremath{^\circ}06\hbox{$^\prime$ }03\hbox{$^{\prime\prime}$ })$to zero which removed any peak associated to 30 Dor from the templates (in particular, the bright peak of ionizing flux in 30 Dor is now removed). In that way, we considerably reduced the impact of the gamma-ray emission from 30 Dor on the fit of the gas templates.

Table 5:   Comparison of maximum likelihood model fitting results after inclusion of the source G2 in the background model.

We summarise the results of this analysis in Table 5, where the prime in the model names indicates that the 30 Dor emission has been removed from the gas templates. The TS values are now considerably reduced since $\mathcal{L}_0$ now includes the G2 source that accounts for gamma-ray emission from 30 Dor. Consequently, TS now measures the significance of gamma-ray emission that exists in addition to that seen towards 30 Dor in the LMC. To recognise this change in the definition we label the corresponding column in Table 5 by TS$^\prime$[*]. Globally, however, we found the same trend as before: the H  II template provided the best fit to the data while the H  I and H2 templates resulted in significantly smaller TS$^\prime$ values. We thus conclude that the morphology of the gamma-ray emission from the LMC is not well explained by the distribution of neutral gas in that galaxy, irrespectively of whether the emission from 30 Dor is taken into account. A template based on the distribution of ionized hydrogen as measured by the H$\alpha$ emission describes the spatial distribution of the gamma-ray emission in the LMC considerably better than the distribution of neutral gas.

2.4 Variability

As we noted earlier (cf. Sect. 2.2), our data indicated possible flaring activity within the LMC boundaries during month 4 (MJD 54 777.8-54 808.2) of the observation interval, and we excluded the data of this month from our analysis. Now with reliable spatial templates for the LMC gamma-ray emission at hand (the 2DG model and the H  II gas map), we reconsidered the time variability of the gamma-ray emission in the LMC area.

First, we considered the time-variability of the integrated gamma-ray emission from the LMC. For this purpose we fitted the 2DG model and the H  II gas map to the data on a monthly, 2 weeks and weekly basis using a power law to describe the source spectrum. We fixed the power law spectral index to the average value that we obtain from fitting the 2DG model or the H  II gas map to all data excluding month 4. Figure 5 shows the monthly lightcurve that we obtain using the H  II gas map. Fitting the lightcurve with a constant flux level (solid line) resulted in $\chi^2=25.4$ for 10 degrees of freedom, which corresponds to a probability of $0.2\%$ for the flux being constant. Obviously, the flux measured during month 4 (MJD 54 777.8-54 808.2) from the LMC is significantly larger than the flux measured for the remaining period. Similar results were obtained when we perform the variability analysis on time scales of 2 weeks ( $\chi^2=38.9$ for 23 degrees of freedom, $1.0\%$ probability for constant flux) and 1 week ( $\chi^2=69.9$ for 47 degrees of freedom, $0.8\%$ probability for constant flux). Using the 2DG models instead of the H  II gas map gave comparable results.

\begin{figure} \par\includegraphics[width=9.1cm]{13474fgb.eps} \end{figure} Figure 5:

Monthly lightcurve for gamma-ray emission from the LMC obtained using the H  II gas map. The 4th month of data that was excluded from our analysis is indicated by an open symbol and grey colour. The solid line indicates the average flux over the full 11 months of data that is obtained by assuming a power law spectral shape for the emission.

Open with DEXTER

As next step we tried to localise any flaring source (and in particular the one that occurred during month 4) by fitting a point source with free position, flux and spectral power law index on top of the 2DG model and the H  II gas map to each of the 11 monthly datasets. We fixed the flux and spectral index of the 2DG model and H  II gas map to the values that we obtained from the fit to all data excluding month 4. This analysis revealed that month 4 is the only period where a point source is detected significantly (TS > 25) on top of the LMC models within the galaxy's boundaries. Using the H  II map as template for the LMC, we localised the source at $(\mbox{$\alpha_{\rm J2000}$ },\mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}46.4^{\rm m},-69\ensuremath{^\circ}01\hbox{$^\prime$ })$ with a 95% containment radius of  $29\hbox{$^\prime$ }$and a detection significance of $4.6\sigma$ (TS = 30.1), while with the 2DG model we found $(\mbox{$\alpha_{\rm J2000}$ },\mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}46.2^{\rm m},-69\ensuremath{^\circ}01')$ with a 95% containment radius of $36\hbox{$^\prime$ }$, and a detection significance of $4.5\sigma$ (TS = 29.3). Obviously, the choice of the LMC model had a negligible impact on the maximum likelihood location of the source.

We show the larger localisation error circle obtained with the 2DG model in Fig. 3, which illustrates that the flaring source is located near 30 Dor and that it is close to the maximum gamma-ray intensity observed from the LMC. Independent on the LMC model, we found an integrated >100 MeV photon flux of $(21 \pm 8~({\rm stat}) \pm 4~({\rm sys})) \times 10^{-8}$ ph cm-2 s-1 for the flaring source during month 4 and obtained a maximum likelihood power law spectral index of $\Gamma = 2.8 \pm 0.3~({\rm stat}) \pm 0.1~({\rm sys})$. The spectral index is rather steep and compatible with the softest indices that are typically found for flat-spectrum radio quasars (FSRQs) (Abdo et al. 2009b). FSRQs tend to show also the largest variabilities among all source classes detected by LAT (Abdo et al. 2009a,b) which makes them good candidates for flaring sources. Using the source association procedure described by Abdo et al. (2009a), we searched for plausible counterparts of the flaring source. We did not find a plausible counterpart in any of our standard blazar or AGN catalogues. The only object that fulfilled our association criterion was RX J0546.8-6851 which is listed in the Magellanic Cloud high-mass X-ray binary catalogue of Liu et al. (2005). However, the nature of this source that has been discovered by the Einstein Observatory (Wang et al. 1991) is not yet established. So far, no companion star has been identified for RX J0546.8-6851, and following Kahabka et al. (2001) the source could also be an active galactic nucleus. It is thus conceivable that the flaring source detected by LAT during month 4 is not physically associated with the LMC, but is rather a yet unidentified background blazar that by chance is located near the line of sight toward 30 Dor.

2.5 Blazars in the field of the LMC

As we noted earlier (cf. Sect. 2.2), we expect to find 1-2 gamma-ray blazars within the boundaries of the LMC in our dataset. Identification of these blazars would be possible if they were flaring during the observation period (see the previous section), yet a substantial fraction of the blazars seen by the LAT do not show any significant time variability (Abdo et al. 2009b). Blazars are thus difficult to recognize if they spatially concur with gamma-ray emission from the LMC. Nevertheless, we can try to spot blazar candidates by searching for point source emission that spatially coincides with the locations of blazars.

For this purpose we searched for counterparts for any of the point sources in the PS model. Using our standard source association procedure (Abdo et al. 2009a) we did not find any blazar candidate coincident with any of the sources of the PS model.

As next step, we simultaneously fitted point sources at the positions of all CRATES blazars (Healey et al. 2007) that are found within a radius of  $5\ensuremath{^\circ} $ around the centre of the LMC, which we assumed here to be $(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}17^{\rm... ...^{\rm s}, -69\ensuremath{^\circ}01\hbox{$^\prime$ }48\hbox{$^{\prime\prime}$ })$, in addition to the 2DG model and the H  II template to the data. The fluxes and the spectral power law indices of all sources were left as free parameters of the fit. We found a total of 36 CRATES sources within the selection region of which one (CRATES J060106-703606) was already part of our background model (see Table 1). This left us with 35 CRATES blazars in the field. As expected from our previous searches for significant point sources above the 2DG model and the H  II template (cf. Sects. 2.3.2 and 2.3.3), none of these blazars was significantly detected ($\rm TS>25$). However, two sources had a formal detection significance above $2\sigma$[*]: CRATES J051636-723707 ( $\rm TS=16.7$), and CRATES J053524-673430 (TS =12.4). The locations of these blazars are overplotted together with those of all other CRATES sources in the LMC field over the residual map for the 2DG model in Fig. 6.

CRATES J051636-723707 appeared to be point like and had already been associated in Sect. 2.3.2 as plausible counterpart of the 3rd 2D Gaussian in the 2DG model analysis. Figure 6 clearly shows that this source is associated with a peak in the observed counts maps. CRATES J053524-673430, in contrast, is not associated with any emission peak but is rather situated in the centre of an extended emission feature. Fitting a 2D Gaussian shaped emission profile at the location of CRATES J053524-673430 suggested indeed that the emission is extended ( $\sigma=26\hbox{$^\prime$ }\pm 10\hbox{$^\prime$ }$), making the blazar an unlikely counterpart of the gamma-ray emission in that area. CRATES J051636-723707 seems to be thus the only plausible blazar candidate in the field of the LMC.

We note, however, that although many of the LAT high-latitude sources have counterparts in the CRATES catalogue, there is still a non-negligible population of unassociated high-latitude sources in the LAT source list that may consist of yet unknown (or unidentified) blazars. Some of the residuals seen in Fig. 6 could indeed arise from such blazars, yet their emission does not appear to significantly contribute to the overall emission from the LMC region.

\begin{figure} \par\includegraphics[width=9.1cm]{13474fgc.eps} \end{figure} Figure 6:

Gaussian kernel ( $\sigma =0.2\ensuremath {^\circ } $) smoothed residual map for the 2DG model over which we overplot the CRATES blazars in the field of the LMC as stars. The boxes mark those blazars for which TS > 6.

Open with DEXTER

2.6 Pulsar lightcurves

As we noted earlier (cf. Sect. 2.3 and Fig. 3), the peak of gamma-ray emission that we see toward 30 Dor is spatially close to the locations of the powerful young pulsars PSR J0540-6919 and PSR J0537-6910, which both are potential sources of high-energy gamma rays. By searching for their pulsations in our data we can assess if the pulsars indeed contribute to the observed emission. We used for this search ephemerides that have been obtained from concurrent RXTE observations (Marshall, private communication) and that cover the time intervals MJD 54651-55015 for PSR J0540-6919 and MJD 54710-54714, 54751-54771, and 54885-54897 for PSR J0537-6910. Only data within these time intervals have been used for the analysis. Gamma-ray photon arrival times were referred to the solar-system barycentre and pulse phases were assigned using the standard pulsar timing software TEMPO2 (Hobbs et al. 2006).

Figure 7 shows the lightcurves that we obtained by selecting photons within a radius of  $0.5\ensuremath {^\circ } $ around the nominal pulsar locations for the energy range 200 MeV-20 GeV. For PSR J0540-6919 our data may indicate the presence of pulsations, but the H-test statistic amounts to only 10.1 which corresponds to a detection significance of $2.4\sigma$for the pulsations. For PSR J0537-6910 the lightcurve is featureless and an H-test gives 3.2 corresponding to a detection significance of $1.1\sigma$. Thus, neither pulsar is detected significantly in our data which is in line with our previous finding (cf. Sect. 2.3.2) that the gamma-ray emission from 30 Dor cannot be satisfactorily described by point source emission from the pulsars.

\begin{figure} \par\includegraphics[width=9cm,clip]{13474fgd.eps}\includegraphics[width=9cm,clip]{13474fge.eps} \end{figure} Figure 7:

Lightcurves obtained for PSR J0540-6919 ( left) and PSR J0537-6910 ( right) for the energy range 200 MeV-20 GeV using an event selection radius of $0.5\ensuremath {^\circ } $ around the nominal pulsar positions. The data are binned into 10 phase bins. The dotted lines indicate the sum of the expected contributions from extragalactic and Galactic diffuse emissions and residual instrumental background.

Open with DEXTER

2.7 Spectrum

So far, all analysis has been done by assuming that the spectrum of the LMC emission components is well described by power laws. To determine the spectrum of the gamma-ray emission from the LMC independently of any assumption on the spectral shape, we fitted our data in 6 logarithmically spaced energy bins covering the energy range 200 MeV-20 GeV. We obtained the total spectrum of the LMC by fitting the H  II template to the data. We also obtained separate spectra for the LMC disk and for 30 Dor by fitting the 2DG model to the data. Here, G1 is taken to represent the LMC disk emission while G2 is taken to represent the emission from 30 Dor. The results are shown in Fig. 8. The spectra are relatively flat below a few GeV ( $\Gamma \sim 2$) and show evidence for a break or cut off above that energy.

Table 6:   Maximum likelihood spectral fit results.

To determine the integrated gamma-ray flux of the spectra we fitted exponentially cut off power law spectral models of the form $N(E) = k~(E/E_0)^{-\Gamma} \exp(-E/\mbox{$E_{\rm c}$ })$to the data. We made these fits by means of a binned maximum likelihood analysis over the energy range 200 MeV-20 GeV. This analysis is more reliable than fitting the spectra of Fig. 8 directly since it accounts for the Poissonian statistic of the data. The resulting spectral shapes are shown as lines in Fig. 8 and spectral fit parameters are given in Table 6. Integrated fluxes are derived for energies above 100 MeV and 200 MeV by integrating the spectral model numerically from the lower boundary up to 500 GeV. The >100 MeV fluxes are mainly given for comparison with the former measurements done by EGRET. Since we restricted our analysis to photons >200 MeV the extrapolation down to 100 MeV introduces an additional systematic uncertainty that for the photon flux can reach up to $30\%$(cf. Table 6). We also determined the significance of the spectral cut off by computing the TS difference between fitting a simple power law and fitting an exponentially cut off power law for each component.

3 Discussion

3.1 Comparison to EGRET

Sreekumar et al. (1992) reported the first detection of the LMC in high-energy gamma rays based on 4 weeks of data collected with the EGRET telescope aboard CGRO. They obtained an integrated >100 MeV flux of $(1.9 \pm 0.4) \times 10^{-7}$ ph cm-2 s-1 for the LMC from their data which is in reasonable agreement with our value of $(2.6 \pm 0.2~{\rm (stat)} \pm 0.4~{\rm (sys)}) \times 10^{-7}$ ph cm-2 s-1 that we obtained from spectral model fitting.

The 3rd EGRET catalogue (Hartman et al. 1999) gives positions, fluxes and power law spectral indices for point sources detected during 4 years of EGRET observations and locates the LMC emission at $(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}33^{\rm m}, -69\ensuremath{^\circ} 16\hbox{$^\prime$ })$ with a 95% containment radius of  $32\hbox{$^\prime$ }$, close to our maximum likelihood location for S1 in the PS model or G2 in the 2DG model, and consistent with the location of 30 Dor. The >100 MeV photon flux in the 3rd EGRET catalogue amounts to $(1.4 \pm 0.2) \times 10^{-7}$ ph cm-2 s-1, which is significantly lower than our value. The assumption of a single point source for the EGRET catalogue analysis may have led to an underestimation of the flux from the extended LMC galaxy. On the other hand, our >100 MeV flux is based on power-law extrapolation from our measurement >200 MeV which could lead to overestimation at lower energies. The 3rd EGRET catalogue quotes a power law spectral index of $\Gamma = 2.2 \pm 0.2$for the LMC which is consistent with our value. In particular, fitting the total LMC emission with a simple power law instead of an exponentially cut off power law we obtain $\Gamma = 2.26 \pm 0.04~{\rm (stat)} \pm 0.10~{\rm (sys)}$, consistent with the value obtained from EGRET data.

Thus, globally, our results are in line with those found earlier by EGRET, yet we benefit from a much better photon statistics[*], an improved angular resolution and spectral coverage up to at least $\sim$10 GeV.

3.2 On the origin of gamma rays from 30 Doradus

Although it was already obvious from EGRET observations that the LMC was an extended source, only the Fermi/LAT data allow now for the first time to clearly resolve the LMC and to localise the emission maximum near the 30 Dor massive star forming region. Even if we cannot establish either of the pulsars PSR J0540-6919 or PSR J0537-6910 as the source of the gamma-ray emission toward 30 Dor (cf. Sects. 2.3.2 and 2.6), the indication of possible pulsations from PSR J0540-6919 is a challenging possibility. If further observations of the LMC by Fermi/LAT confirm the detection of pulsations, this would be the first time that a pulsar outside our own Galaxy were detected in gamma rays. We are aware that the H.E.S.S. collaboration has announced[*] the detection of the pulsar wind nebula of PSR J0537-6910 at TeV energies, yet so far we do not find evidence for gamma-ray emission from that source in our data.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13474fgf.eps} \end{figure} Figure 8:

Spectrum of the LMC emission obtained by fitting spatial model maps in 6 logarithmically spaced energy bins covering the energy range 200 MeV-20 GeV. Black dots show the total spectrum obtained by fitting the H  II gas map, red squares and blue triangles show the spectra for the LMC disk and for 30 Dor, respectively, obtained using the 2DG model. Error bars include statistical and systematic uncertainties. The lines show the results obtained by fitting exponentially cut off power law spectral models to the data using maximum likelihood fits.

Open with DEXTER

As the gamma-ray emission from 30 Dor is not dominated by pulsars, cosmic-ray interactions with the ambient interstellar medium and radiation fields are plausibly the origins of the observed emission. In this case, the small size of the emission region puts stringent constraints on the diffusion length of GeV cosmic-ray protons. For source G2 we find an extent of $\sigma=12\hbox{$^\prime$ }\pm4\hbox{$^\prime$ }$ and a $95\%$ confidence level upper limit of $\sigma=19\hbox{$^\prime$ }$, which at the distance of the LMC corresponds to linear dimensions of 170 pc and 270 pc, respectively. This is extremely small compared to expectations. Gamma-ray observations of our own Galaxy suggest in fact a Galactocentric cosmic-ray emissivity gradient that is much smaller than that of the distribution of supernova remnants or pulsars, which has been taken as evidence for large-scale cosmic-ray diffusion in our Galaxy (Strong et al. 1988; Bloemen et al. 1984a; Strong & Mattox 1996; Bloemen et al. 1984b,1986). In addition, the low average gas density that is encountered by cosmic rays as determined from cosmic-ray isotope ratios indicates that the particles spend a considerable fraction of their lifetimes outside the plane of the Galaxy, suggesting a cosmic-ray halo that extends to scale heights of 4-6 kpc above the galactic plane (Moskalenko et al. 2004). On the other hand, Fichtel & Kniffen (1984) have shown that the gamma-ray data are also compatible with a tight coupling of cosmic rays to the matter, and Strong et al. (2004b) suggest that neglecting a possible strong Galactocentric gradient in the CO-to-H2 conversion factor has led in the past to an underestimation of the Galactic cosmic-ray gradient. Thus, observations may also be compatible with a short cosmic-ray diffusion length in our own Galaxy.

Galactic studies are however hampered by our position within the Galactic plane, which does not allow for an unambiguous correlation of the gamma-ray emissivity with Galactic star forming regions, making estimates of cosmic-ray diffusion rather uncertain. Our observations of the LMC provide for the first time a much clearer picture about the link between possible cosmic-ray acceleration sites and gamma-ray emission, and suggest that both are tightly connected. 30 Dor would thus be the most powerful cosmic-ray acceleration site in the LMC, which would be no surprise as it is one of the most active starburst regions in the entire Local Group of galaxies (Pineda et al. 2009).

3.3 Gamma rays from cosmic-ray interactions

The gamma-ray emission from cosmic-ray interactions with the interstellar medium and radiation field is expected to be intrinsically diffuse in nature. Indeed, our analysis suggests that the gamma-ray emission from the LMC does not originate in a small number of individual point sources. By adding successively point sources to our model (cf. Sect. 2.3.2) we formally detected 5 significant point sources (model PS), but we found a model with less components that results in a higher TS value when we allow for the source components to be extended (model 2DG). It is thus more likely that the LMC emission is indeed diffuse in nature, or alternatively, composed of a large number of unresolved and faint sources that can not be detected individually by Fermi/LAT.

From here on we thus make the assumption that the gamma-ray emission from the LMC indeed originates from cosmic-ray interactions with the interstellar gas and the stellar radiation field, and we discuss the implications of this assumption in light of our observations. In particular we test the 2 extreme hypotheses that (1) all gamma-ray emission from the LMC is attributed to diffuse emission from cosmic-ray interactions, and (2) only the emission from component G1 in the 2DG model arises from cosmic-ray interactions, while the gamma rays from 30 Dor (or component G2 in the 2DG model) originate from other sources. Hypothesis 2 is mainly motivated by the particular nature of 30 Dor, and we want to examine how our conclusions are altered when we exclude this source from our considerations. Note that in this case, only $70\%$ of the integrated LMC flux is attributed to cosmic-ray interactions while for hypothesis 1 we assume that $100\%$ of the LMC flux is due to cosmic rays.

Using these two hypotheses (which we call from here on $\mathcal{H}_1$ and $\mathcal{H}_2$) we computed the average integrated >100 MeV gamma-ray emissivity per hydrogen atom of the LMC using

\begin{displaymath}q_{\gamma} = \frac{\Phi_{\gamma}}{\int N_{\rm H}~{\rm d}\Omega} \end{displaymath} (1)

where $\Phi_{\gamma}$ is the integrated >100 MeV photon flux from the LMC under $\mathcal{H}_1$ or $\mathcal{H}_2$, and $\int N_{\rm H}~{\rm d}\Omega$ is the spatially integrated hydrogen column density of the LMC. From the H  I map of Kim et al. (2003) one obtains $\int N_{\rm H}~{\rm d}\Omega = 2.39 \times 10^{19}$ H-atom cm-2 sr for atomic hydrogen, assuming optically thin emission. Including molecular hydrogen increases the value by $5\%$-$10\%$ and applying optical depth corrections for 125 K and 60 K further increases the integral by $12\%$ and $42\%$, respectively. Evidence for some hidden hydrogen (or the presence of substantial optically thick emission) comes from an analysis of infrared data obtained with Spitzer, suggesting an additional component that follows the distribution of the H  I seen in the radio surveys, and that doubles the total gas mass (Bernard et al. 2008). Thus, $\int N_{\rm H}~{\rm d}\Omega$ could be as large as $4.8 \times 10^{19}$ H-atom cm-2 sr and we adopted $\int N_{\rm H}~{\rm d}\Omega = (3.6 \pm 1.2) \times 10^{19}$ H-atom cm-2 sr as a mean value and included the uncertainty of the total hydrogen mass of the LMC in our computation. The resulting emissivities are given in Table 7.

Table 7:   Results of the gamma-ray emissivity analysis of the LMC for hypotheses $\mathcal{H}_1$ and $\mathcal{H}_2$.

Depending on the hypothesis we make, the average gamma-ray emissivity of the LMC is between $\sim$2 to $\sim$4 times smaller than the >100 MeV emissivity of $q_{\gamma} = (1.63 \pm 0.05) \times 10^{-26}$ ph s-1 sr-1 H-atom-1 that has been determined by Fermi/LAT for the local interstellar medium of our own Galaxy (Abdo et al. 2009c). We illustrate this difference in Fig. 9, where we compare the differential gamma-ray emissivity of the local interstellar medium (cf. Fig. 5 of Abdo et al. 2009c) to that of the LMC. Following Eq. (1), we derived the differential gamma-ray emissivity by dividing our spectra by $\int N_{\rm H}~{\rm d}\Omega = (3.6 \pm 1.2) \times 10^{19}$ H-atom cm-2 sr. For $\mathcal{H}_1$ we used the spectrum derived using the H  II gas map for the total emission from the LMC (black dots), while for $\mathcal{H}_2$ we used the LMC disk spectrum obtained using component G1 of model 2DG (red dots)

We compared the differential gamma-ray emissivities to a one-zone model of cosmic-ray interactions with the interstellar medium that takes into account $\pi ^0$ decay following proton-proton interactions, Bremsstrahlung from cosmic-ray electrons and inverse Compton scattering of cosmic-ray electrons on LMC optical and infrared photons and cosmic microwave background photons. We calculated the $\pi ^0$ production by proton-proton interactions following the prescription of Kamae et al. (2006). We used the cosmic-ray proton, electron and positron spectra presented in Abdo et al. (2009c) for the local Galactic environment. The scaling factor ($r_{\rm c}$) of our model with respect to the data, which we refer to as the cosmic-ray enhancement factor, is thus a direct measure of the average LMC cosmic-ray density with respect to that in the vicinity of the Earth. The $\pi ^0$ and Bremsstrahlung emissivities were calculated by assuming the average LMC metallicity to be Z=0.4 $Z_{\odot}$ (Westerlund 1997). We applied a corresponding nuclear enhancement factor of $\epsilon_{\rm M}=1.75$ to the $\pi ^0$emissivities (Mori 2009) and took the total hydrogen mass of the LMC to be $7.2 \times 10^8$ $M_{\odot}$[*]. The inverse Compton component was calculated using the method described by Blumenthal & Gould (1970) using the optical and infrared interstellar radiation fields from Porter et al. (2008) that we rescaled according to the stellar luminosity density and the observed infrared emission (Bernard et al. 2008), respectively.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13474fgh.eps} \end{figure} Figure 9:

Differential average gamma-ray emissivity for $\mathcal{H}_1$ (black dots) and $\mathcal{H}_2$ (red dots) compared to that of the Galactic local interstellar medium determined by Abdo et al. (2009c) (grey data points). The error bars for $\mathcal{H}_1$ and $\mathcal{H}_2$ include statistical and systematic errors and the uncertainties in the total gas mass. The solid line shows the predicted gamma-ray emissivity computed in the framework of a one-zone model for $\mathcal{H}_2$ (see text). The other lines show the contributions of $\pi ^0$-decay (long dashed), Bremsstrahlung (short dashed), and inverse Compton emission (dotted).

Open with DEXTER

Fitting this spectral model to our data using a binned maximum likelihood analysis gave an average cosmic-ray enhancement factor of $r_{\rm c} = 0.31 \pm 0.01$ for $\mathcal{H}_1$, and of $r_{\rm c} = 0.21 \pm 0.01$ for $\mathcal{H}_2$ (cf. Table 7). Systematic errors due to uncertainties in the effective area of the instrument amount to $\pm0.02$. An additional systematic error of $-23\%$ to $+42\%$ comes from the uncertainty in the total gas mass of the LMC, which largely dominates the statistical and systematic measurements errors.

\begin{figure} \par\includegraphics[width=9.1cm,clip]{13474fgi.eps}\includegraphics[width=9.1cm,clip]{13474fgj.eps} \end{figure} Figure 10:

Integrated >100 MeV emissivity maps of the LMC in units of 10-27 ph s-1 sr-1 H-atom-1 for $\mathcal{H}_1$ ( left panel) and $\mathcal{H}_2$ ( right panel). An adaptive smoothing with a signal-to-noise ratio of 5 has been applied to reduce statistical fluctuations. Note that the colour scales are not the same for the two images. As contours we show $N({\rm H})$ column densities convolved with the LAT point spread function that are linearly spaced from $10\%$-$90\%$ of the maximum in steps of $10\%$. Symbols indicate the locations of pulsars (pluses) from ATNF catalogue version 1.36 (Manchester et al. 2005), supernova remnants (diamonds) from Rosa Williams web page http://www.astro.illinois.edu/projects/atlas/index.html, Wolf-Rayet stars (stars) from the fourth catalogue of Breysacher et al. (1999), and supergiant shells (circles) from Staveley-Smith et al. (2003).

Open with DEXTER

Fichtel et al. (1991) estimated the cosmic-ray enhancement factor to be $r_{\rm c}\sim1$ by comparing the synchrotron radiation of the LMC to that of the Milky Way (cf. their Fig. 3). We also computed the synchrotron emission in our model under the assumption that the cosmic-ray proton to electron ratio in the LMC and the electron spectrum are the same than those measured in the local interstellar medium (Abdo et al. 2009c). We further took the thickness of the emitting region to be 2 kpc and assumed a magnetic field of 5 $\mu$G (Pohl 1993). Our predicted synchrotron flux is in good agreement with the observed non-thermal flux quoted by Klein et al. (1989). Fichtel et al. (1991), however, assumed a higher non-thermal flux for the LMC compared to the observations of Klein et al. (1989), which may explain why their $r_{\rm c}$ is in excess of our model.

Pavlidou & Fields (2001) followed another approach and predicted $r_{\rm c}=0.14$ from a comparison of the supernova rate in the LMC to that in our Galaxy, yet they considered also higher values due to the large uncertainties that are inherent to the estimates of supernova rates. Their estimate relies further on the assumption that the cosmic-ray containment in the LMC is similar to that in our own Galaxy, which is not necessarily fulfilled since cosmic rays may escape fairly rapidly into intergalactic space because of the small size of the LMC (Ginzburg & Ptuskin 1985). Our value, which is slightly above the estimate of Pavlidou & Fields (2001), suggests however that cosmic-ray escape from the LMC is not more important than for our own Galaxy. This is in line with the relatively small proton diffusion length that we inferred from the compactness of the 30 Dor source (cf. Sect. 3.2).

3.4 The sites of cosmic-ray acceleration in the LMC

To reveal the sites of cosmic-ray acceleration in the LMC we mapped the cosmic-ray density variations in the galaxy by computing the gamma-ray emissivity  $q_{\gamma}$ as function of position. We did this by generating a background subtracted counts map for $\mathcal{H}_1$, and a background and G2 model subtracted counts map for $\mathcal{H}_2$ that we divided by the  $N({\rm H})$ map after convolution of the latter with the LAT instrumental response function. We normalised  $N({\rm H})$ to a total LMC hydrogen mass of $7.2 \times 10^8$ $M_{\odot}$ that takes into account the possible presence of dark gas that is not seen in radio surveys of H  I (see Sect. 3.3). We adaptively smoothed (Ebeling et al. 2006) the counts maps and used the resulting smoothing kernel distribution to smooth also the convolved  $N({\rm H})$ map before the division to reveal significant structures at all possible scales, while suppressing the noise that arises from the limited photon counting statistics.

The resulting emissivity maps are shown in Fig. 10. We superimpose on the images the interstellar gas distribution, as traced by  $N({\rm H})$, convolved with the LAT instrumental response function, and also show the locations of potential particle acceleration sites, such as pulsars, supernova remnants, Wolf-Rayet stars and supergiant shells.

Figure 10 reveals that the cosmic-ray density varies considerably over the disk of the LMC. The gamma-ray emissivity is highest in 30 Dor and the northern part of the galaxy, while the southern part and in particular the dense ridge of gas south of 30 Dor seems basically devoid of cosmic rays. The large variations in  $q_{\gamma}$ confirm our earlier findings (cf. Sect. 2.3.3) that the gamma-ray emission correlates little with the gas density in the LMC, and this is irrespective of whether we consider 30 Dor to be part of the emission (left panel versus right panel). The most striking variation is found along the gas ridge that runs over $\sim$ $3\ensuremath{^\circ} $ along $\mbox{$\alpha_{\rm J2000}$ }\sim05^{\rm h}40^{\rm m}$ which coincides with the most prominent region of 12CO emission tracing giant molecular clouds in the LMC (Fukui et al. 1999). Roughly $20\%$ of the total gas mass in the LMC is confined into this ridge (Luks & Rohlfs 1992), and if the cosmic-ray density were uniform over the LMC (or at least over the ridge area) the entire ridge should be a source of high-energy gamma rays. This, however, is obviously not the case. Cosmic rays apparently do not penetrate into the southern part of the ridge, which is an additional argument in favour of a short GeV cosmic-ray proton diffusion length in the LMC.

Figure 10 suggests further that the cosmic-ray density correlates with massive star forming tracers, and in particular Wolf-Rayet stars and supergiant shells. This correlation is particularly striking if we assume that the emission from 30 Dor is originating in the same physical process as the rest of the LMC emission ( $\mathcal{H}_1$). If we exclude 30 Dor from the comparison ( $\mathcal{H}_2$) the correlation becomes less striking, yet still, most of the cosmic rays are found in regions that are rich in Wolf-Rayet stars and that are located near supergiant shells. This finding is corroborated by the good fit of the H  II gas map (which is probably the most direct tracer of massive star forming regions within a galaxy), even if the 30 Dor emission is discarded from the analysis (cf. Sect. 2.3.3).

Thus, the gamma-ray emissivity maps of the LMC support the idea that cosmic rays are accelerated in massive star forming regions as a result of the large amounts of kinetic energy that are input by the stellar winds and supernova explosions of massive stars into the interstellar medium. Our data reveal a relatively tight confinement of the gamma-ray emission to star forming regions, which suggests a relatively short diffusion length for GeV protons.

4 Conclusions

Observations of the LMC by Fermi/LAT have for the first time provided a detailed map of high-energy gamma-ray emission from that galaxy. Our analysis revealed the massive star forming region 30 Doradus as bright source of gamma-ray emission in the LMC in addition to fainter emission regions found in the northern part of the galaxy. So far, we could not identify any point source contributions to the emission from the 30 Dor region, and in particular we did not significantly detect pulsations from the energetic Crab-like pulsars PSR J0540-6919 and PSR J0537-6910, although the lightcurve of the former indicates variability at the $2.4\sigma$ level. Cosmic-ray interactions with the interstellar medium and radiation field seem thus the most plausible origin for the observed gamma-ray emission from 30 Dor.

The gamma-ray emission from the LMC shows very little correlation with gas density. A much better correlation is seen between gamma-ray emission and massive star forming regions, as traced by the ionizing gas, Wolf-Rayet stars and supergiant shells, and we take this as evidence for cosmic-ray acceleration in these regions. The close confinement of gamma-ray emission to star forming regions implies a relatively small GeV cosmic-ray protons diffusion length.

Continuing observations of the LMC with Fermi/LAT in the upcoming years will provide the photon statistics to learn more about the origin of the gamma-ray emission from that galaxy. Better statistics will help in identifying more individual emission components and may help to separate true point sources from the more diffuse emission that we expect from cosmic-ray interactions. In particular, 1-2 years of additional exposure should allow the question of the contribution of PSR J0540-6919 to the gamma-ray emission from 30 Dor to be answered, and should also allow clearly establishing the pulsar wind nebulae contributions at higher energies.

Acknowledgements
The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l'Energie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the and the Centre National d'Études Spatiales in France.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJS, 183, 46 [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 700, 597 [Google Scholar]
  3. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009c, ApJ, 703, 1249 [Google Scholar]
  4. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bernard, J.-P., Reach, W. T., Paradis, D., et al. 2008, AJ, 136, 919 [NASA ADS] [CrossRef] [Google Scholar]
  6. Binns, W. R., Wiedenbeck, M. E., Arnould, M., et al. 2007, SSRv, 130, 439 [Google Scholar]
  7. Biermann, P. L. 2004, New Astron. Rev., 48, 41 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bloemen, J. B. G. M., Blitz, L., & Hermsen, W. 1984a, ApJ, 279, 136 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bloemen, J. B. G. M., Bennett, K., Bignami, G. F., et al. 1984b, A&A, 135, 12 [NASA ADS] [Google Scholar]
  10. Bloemen, J. B. G. M., Strong, A. W., Blitz, L., et al. 1986, A&A, 154, 25 [NASA ADS] [Google Scholar]
  11. Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
  12. Breysacher, J., Azzopardi, M., & Testor, G. 1999, A&AS, 137, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cesarsky, C. J., & Montmerle, T. 1983, SSRv, 36, 173 [Google Scholar]
  15. Clark, G. W., Garmire, G. P., & Kraushaar, W. L. 1968, ApJ, 153, 203 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dermer, C. D. 2007, AIPC, 921, 122 [Google Scholar]
  17. Digel, S. W., Moskalenko, I., Ormes, J. F., et al. 2000, AIP, 528, 449 [Google Scholar]
  18. Ebeling, H., White, D. A., & Rangarajan, F. V. N. 2006, MNRAS, 368, 65 [NASA ADS] [Google Scholar]
  19. Fichtel, C. E., & Kniffen, D. A. 1984, A&A, 134, 13 [NASA ADS] [Google Scholar]
  20. Fichtel, C. E., Özel, M. E., Stone, R. G., & Sreekumar, P. 1991, ApJ, 374, 134 [NASA ADS] [CrossRef] [Google Scholar]
  21. Finkbeiner, D. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
  22. Fukui, Y., Mizuno, N., Yamaguchi, R., et al. 1999, PASJ, 51, 745 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fukui, Y., Kawamura, A., & Minamidani, T. 2008, ApJS, 178, 56 [NASA ADS] [CrossRef] [Google Scholar]
  24. Ginzburg, V. L., & Ptuskin, V. S. 1985, Soviet Sci. Rev. E: Astrophys. Space Phys., 4, 161 [Google Scholar]
  25. Harding, A. 1981, ApJ, 247, 639 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hartmann, D. H., Brown, L. E., & Schnepf, N. 1993, ApJ, 408, L13 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hartman, R. C., Chen, A. W., Deines-Jones, P., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] [Google Scholar]
  28. Healey, S. E., Romani, R. W., Taylor, G. B., et al. 2007, ApJS, 171, 61 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hobbs, G., Edwards, R., & Manchester, R. 2006, ChJAS, 6, 198 [Google Scholar]
  30. Kahabka, P., de Boer, K. S., & Brüns, C. 2001, A&A, 371, 816 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kamae, T., Karlsson, N., Mizuno, T., Abe, T., & Koi, T. 2006, ApJ, 647, 692 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kennicutt, R. C., Bresolin, F., Bomans, D. J., Bothun, G. D., & Thompson, I. B. 1995, AJ, 109, 594 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kim, S., Staveley-Smith, L., Dopita, M. A., et al. 1998, ApJ, 503, 674 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kim, S., Staveley-Smith, L., Dopita, M. A., et al. 2003, ApJS, 148, 473 [NASA ADS] [CrossRef] [Google Scholar]
  35. Klein, U., Wielebinski, R., Haynes, R. F., & Malin, D. F. 1989, A&A, 211, 280 [NASA ADS] [Google Scholar]
  36. Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2005, A&A, 442, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Luks, Th., & Rohlfs, K. 1992, A&A, 263, 41 [NASA ADS] [Google Scholar]
  38. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
  39. Marshall, F. E., Gotthelf, E. V., Zhang, W., Middleditch, J., & Wang, Q. D. 1998, ApJ, 499, L179 [NASA ADS] [CrossRef] [Google Scholar]
  40. Marx-Zimmer, M., Herbstmeier, U., Dickey, J. M., et al. 2000, A&A, 354, 787 [NASA ADS] [Google Scholar]
  41. Matsunaga, N., Feast, M. W., & Menzies, J. W. 2009, MNRAS, 397, 933 [NASA ADS] [CrossRef] [Google Scholar]
  42. Mori, M. 2009, Astropart. Phys., 31, 341 [NASA ADS] [CrossRef] [Google Scholar]
  43. Moskalenko, I. V., Strong, A. W., & Reimer, O. 2004, in Cosmic Gamma-Ray Sources, ed. K. S. Cheng, & G. E. Romero (Dordrecht: Kluwer), Astrophys. Space Sci. Libr., 304, 279 [Google Scholar]
  44. Ozel, M. E., & Fichtel, C. E. 1988, ApJ, 335, 135 [NASA ADS] [CrossRef] [Google Scholar]
  45. Pavlidou, V., & Fields, B. D. 2001, ApJ, 558, 63 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pietrzynski, G., Thompson, I. B., Graczyk, D., et al. 2009, ApJ, 697 862 [NASA ADS] [CrossRef] [Google Scholar]
  47. Pineda, J. L., Ott, J., Klein, U., et al. 2009, ApJ, 703, 736 [NASA ADS] [CrossRef] [Google Scholar]
  48. Pohl, M. 1993, A&A, 279, 17 [Google Scholar]
  49. Pollack, J. B., & Fazio, G. G. 1963, Phys. Rev., 131, 2684 [NASA ADS] [CrossRef] [Google Scholar]
  50. Porter, T. A., Moskalenko, I. V., Strong, A. W., Orlando, E., & Bouchet, L. 2008, ApJ, 682, 400 [NASA ADS] [CrossRef] [Google Scholar]
  51. Seward, F. D., Harnden, F. R., & Helfand, D. J. 1984, ApJ, 287, L19 [NASA ADS] [CrossRef] [Google Scholar]
  52. Sreekumar, P., Bertsch, D. L., Dingus, B. L., et al. 1992, ApJ, 400, L67 [NASA ADS] [CrossRef] [Google Scholar]
  53. Staveley-Smith, L., Kim, S., Calabretta, M. R., Haynes, R. F., & Kesteven, M. J. 2003, MNRAS, 339, 87 [NASA ADS] [CrossRef] [Google Scholar]
  54. Strong, A. W., & Mattox, J. R. 1996, A&A, 308, 21 [Google Scholar]
  55. Strong, A. W., Bloemen, J. B. G. M., Dame, T. M., et al. 1988, A&A, 207, 1 [NASA ADS] [Google Scholar]
  56. Strong, A. W., Moskalenko, I., & Reimer, O. 2004a, ApJ, 613, 956 [Google Scholar]
  57. Strong, A. W., Moskalenko, I., Reimer, O., Digel, S., & Diehl, R. 2004b, A&A, 422, L47 [Google Scholar]
  58. Van der Marel, R. P. 2006, in The Local Group as an Astrophysical Laboratory, ed. M. Livio, & T. M. Brown (Cambridge University Press), 47 [Google Scholar]
  59. Wang, Q., Hamilton, T., Helfand, D. J., & Wu, X. 1991, ApJ, 374, 475 [NASA ADS] [CrossRef] [Google Scholar]
  60. Weidenspointner, G., Lonjou, V., & Knödlseder, J. 2007, AIP, 921, 498 [NASA ADS] [CrossRef] [Google Scholar]
  61. Westerlund, B. E. 1997, The Magellanic Clouds, Cambridge Astrophysics, 29 [Google Scholar]

Footnotes

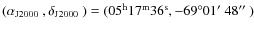
...$(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}17^{\rm... ...^{\rm s}, -69\ensuremath{^\circ}01\hbox{$^\prime$ }48\hbox{$^{\prime\prime}$ })$[*]
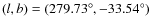Corresponding to $(l,b)=(279.73\ensuremath{^\circ} ,-33.54\ensuremath{^\circ} )$.
... gll_iem_v02[*]
The model can be downloaded from http://fermi.gsfc.nasa.gov/ssc/data/access/lat/BackgroundModels.html
... area[*]
We use a square region $5.5\ensuremath{^\circ}\times 5.5\ensuremath{^\circ} $ centred on $(\mbox{$\alpha_{\rm J2000}$ }, \mbox{$\delta_{\rm J2000}$ })=(05^{\rm h}30^{\rm m}, -68\ensuremath{^\circ} 30\hbox{$^\prime$ })$ to extract these numbers.
...$^\prime$[*]
Fitting the G2 source as the only component to the data resulted in $\rm TS=826.5$. We can thus formally convert TS$^\prime$ into TS using TS =TS  $^\prime+826.5$.
...$2\sigma$[*]
Which corresponds to 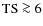$\rm TS\ga6$ for p=2.
... statistics[*]
The total number of counts we attribute to the LMC amounts to 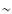$\sim$1550 photons while the 3rd EGRET catalogue quotes a total of 192 counts obtained during 4 years of observations.
... announced[*]
The detection has been announced at the 31${\rm st}$ International Cosmic-Ray Conference in \Lódz 2009, however no details about source flux and spectrum are yet publicly available.
...$M_{\odot}$[*]
For a distance of 50 kpc to the LMC $\int N_{\rm H}~{\rm d}\Omega = (3.6 \pm 1.2) \times 10^{19}$ H-atom cm-2 sr corresponds to a total H  I mass of $(7.2 \pm 2.4) \times 10^8$ $M_{\odot}$.

All Tables

Table 1:   Point sources included in the background model.

Table 2:   Parameters of the point source model PS.

Table 3:   Parameters of the 2D Gaussian sources model 2DG.

Table 4:   Comparison of maximum likelihood model fitting results (see text for a description of the models).

Table 5:   Comparison of maximum likelihood model fitting results after inclusion of the source G2 in the background model.

Table 6:   Maximum likelihood spectral fit results.

Table 7:   Results of the gamma-ray emissivity analysis of the LMC for hypotheses $\mathcal{H}_1$ and $\mathcal{H}_2$.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13474fg1.eps}\includegraphics[width=9cm,clip]{13474fg2.eps} \end{figure} Figure 1:

Gaussian kernel ( $\sigma =0.2\ensuremath {^\circ } $) smoothed counts maps of the region of interest (ROI) in a true local projection before ( left) and after subtraction of the background model ( right) for the energy range 200 MeV-20 GeV and for a pixel size of $0.1\ensuremath {^\circ }\times 0.1\ensuremath {^\circ } $. Overlaid is the N(H  I) contour of $1\times 10^{21}$ H cm-2 of the LMC to indicate the extent and shape of the galaxy. The boxes show the locations of the 6 point sources that have been included in the background model. The right panel has a true dynamic range from -46 to +248 counts deg-2that has been expanded for display to cover the full dynamic range of the residuals that are shown in Fig. 4.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9.1cm,clip]{13474fg3.eps} \end{figure} Figure 2:

Profiles of the observed number of counts along Right Ascension ( top) and Declination ( bottom) of the LMC region for the energy range 200 MeV-20 GeV. The solid lines show the corresponding profiles of the background model. The red arrow indicates the location of 30 Dor.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9.1cm]{13474fg4.eps} \end{figure} Figure 3:

Zoom into a $3\ensuremath {^\circ }\times 3\ensuremath {^\circ } $ large region of the background subtracted counts map around the central star cluster R 136 in 30 Dor. The counts map has been adaptively smoothed (Ebeling et al. 2006) with a signal-to-noise ratio of 5 in order to reveal significant structures at all possible scales while suppressing the noise that arises from photon counting statistics. Stars show the locations of R 136 and of the pulsars PSR J0540-6919 and PSR J0537-6910. The circles show the 95% containment radius of sources S1, S3, and G2 (see text). For G2 we added the Gaussian $\sigma $ of the source to the error radius. We also show the 95% containment radius of a flaring source that appeared during month 4 of the analysed data set. The diamond shows the location of the possible counterpart RX J0546.8-6851 of the flaring source (see Sect. 2.4).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.6cm,clip]{13474fg5.eps}\includegraph... ...clip]{13474fg9.eps}\includegraphics[width=7.6cm,clip]{13474fga.eps} \end{figure} Figure 4:

Gaussian kernel ( $\sigma =0.2\ensuremath {^\circ } $) smoothed model counts maps ( left panels) and residual maps ( right panels) of the region of interest (ROI). The model counts maps have been obtained by convolving the model sky maps that were scaled to the fitted flux with the LAT point spread function. The top row shows the PS model, the middle row shows the 2DG model and the bottom row shows the H  II template. The colour scaling and the dynamic range for the residual maps is identical to the right panel of Fig. 1 to allow for comparison.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9.1cm]{13474fgb.eps} \end{figure} Figure 5:

Monthly lightcurve for gamma-ray emission from the LMC obtained using the H  II gas map. The 4th month of data that was excluded from our analysis is indicated by an open symbol and grey colour. The solid line indicates the average flux over the full 11 months of data that is obtained by assuming a power law spectral shape for the emission.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9.1cm]{13474fgc.eps} \end{figure} Figure 6:

Gaussian kernel ( $\sigma =0.2\ensuremath {^\circ } $) smoothed residual map for the 2DG model over which we overplot the CRATES blazars in the field of the LMC as stars. The boxes mark those blazars for which TS > 6.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13474fgd.eps}\includegraphics[width=9cm,clip]{13474fge.eps} \end{figure} Figure 7:

Lightcurves obtained for PSR J0540-6919 ( left) and PSR J0537-6910 ( right) for the energy range 200 MeV-20 GeV using an event selection radius of $0.5\ensuremath {^\circ } $ around the nominal pulsar positions. The data are binned into 10 phase bins. The dotted lines indicate the sum of the expected contributions from extragalactic and Galactic diffuse emissions and residual instrumental background.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13474fgf.eps} \end{figure} Figure 8:

Spectrum of the LMC emission obtained by fitting spatial model maps in 6 logarithmically spaced energy bins covering the energy range 200 MeV-20 GeV. Black dots show the total spectrum obtained by fitting the H  II gas map, red squares and blue triangles show the spectra for the LMC disk and for 30 Dor, respectively, obtained using the 2DG model. Error bars include statistical and systematic uncertainties. The lines show the results obtained by fitting exponentially cut off power law spectral models to the data using maximum likelihood fits.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13474fgh.eps} \end{figure} Figure 9:

Differential average gamma-ray emissivity for $\mathcal{H}_1$ (black dots) and $\mathcal{H}_2$ (red dots) compared to that of the Galactic local interstellar medium determined by Abdo et al. (2009c) (grey data points). The error bars for $\mathcal{H}_1$ and $\mathcal{H}_2$ include statistical and systematic errors and the uncertainties in the total gas mass. The solid line shows the predicted gamma-ray emissivity computed in the framework of a one-zone model for $\mathcal{H}_2$ (see text). The other lines show the contributions of $\pi ^0$-decay (long dashed), Bremsstrahlung (short dashed), and inverse Compton emission (dotted).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9.1cm,clip]{13474fgi.eps}\includegraphics[width=9.1cm,clip]{13474fgj.eps} \end{figure} Figure 10:

Integrated >100 MeV emissivity maps of the LMC in units of 10-27 ph s-1 sr-1 H-atom-1 for $\mathcal{H}_1$ ( left panel) and $\mathcal{H}_2$ ( right panel). An adaptive smoothing with a signal-to-noise ratio of 5 has been applied to reduce statistical fluctuations. Note that the colour scales are not the same for the two images. As contours we show $N({\rm H})$ column densities convolved with the LAT point spread function that are linearly spaced from $10\%$-$90\%$ of the maximum in steps of $10\%$. Symbols indicate the locations of pulsars (pluses) from ATNF catalogue version 1.36 (Manchester et al. 2005), supernova remnants (diamonds) from Rosa Williams web page http://www.astro.illinois.edu/projects/atlas/index.html, Wolf-Rayet stars (stars) from the fourth catalogue of Breysacher et al. (1999), and supergiant shells (circles) from Staveley-Smith et al. (2003).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.