EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A33 Full HTML
Highlight
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A33
Number of page(s) 5
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/200913400
Published online 25 March 2010
A&A 512, A33 (2010)

Mass fluxes for hot stars

L. B. Lucy

Astrophysics Group, Blackett Laboratory, Imperial College London, Prince Consort Road, London SW7 2AZ, UK

Received 2 October 2009 / Accepted 20 January 2010

Abstract
In an attempt to understand the extraordinarily small mass-loss rates of late-type O dwarfs, mass fluxes in the relevant part of ( $T_{\rm eff},~ g$)-space are derived from first principles using a previously-described code for constructing moving reversing layers. From these mass fluxes, a weak-wind domain is identified within which a star's rate of mass loss by a radiatively-driven wind is less than that due to nuclear burning. The five weak-wind stars recently analysed by Marcolino et al. (2009, A&A, 498, 837) fall within or at the edge of this domain. But although the theoretical mass fluxes for these stars are $\approx$1.4 dex lower than those derived with the formula of Vink et al. (2000), the observed rates are still not matched, a failure that may reflect our poor understanding of low-density supersonic outflows.
Mass fluxes are also computed for two strong-wind O4 stars analysed by Bouret et al. (2005, A&A, 438, 301). The predictions agree with the sharply reduced mass loss rates found when Bouret et al. take wind clumping into account.

Key words: stars: early-type - stars: mass-loss - stars: winds, outflows

1 Introduction

Investigations of late-type O dwarfs in the SMC (Bouret et al. 2003; Martins et al. 2004) and the Galaxy (Marcolino et al. 2009; M09) find that mass-loss rates $\Phi$ determined by spectral modelling are at least an order of magnitude lower than those ($\Phi_{V}$) predicted with the formula of Vink et al. (2000).

Although this weak wind problem is considered to be a major problem for stellar wind theory (Puls et al. 2008), this may not in fact be so since the $\Phi_{V}$'s are semi-empirical estimates based on Monte Carlo (MC) calulations of the deposition rates of radiative energy in the supersonic winds. Accordingly, this conflict might be a consequence of the Vink et al. assumptions concerning physical conditions in these winds. Moreover, the global dynamical constraint imposed by Vink et al. and previously by Abbott & Lucy (1985) does not guarantee that the derived $\Phi$'s are consistent with stationary transonic flows.

In order, therefore, to make a more decisive confrontation between theory and observation, this paper reports an extensive grid of mass fluxes $J = \Phi/4 \pi R^{2}$ for O stars using a code described earlier (Lucy 2007a; L07a). This code, which updates the moving reversing layer (RL) theory of Lucy & Solomon (1970; LS70), uses a MC technique to estimate the J that allows the flow to accelerate continuously from sub- to supersonic velocities. In other words, the eigenvalue J is determined from first principles by imposing a regularity condition at the sonic point.

2 Solution technique

Because the code is unchanged from L07a, details are omitted. However, the search procedure for the adjustable parameters has been revised to facilitate a survey of $(T_{\rm eff}, g)$-space.

2.1 Implicit assumptions

An unstated assumption in L07a is that the subsonic layers of a RL are affected by the exterior supersonic layers only through backscattered radiation. Specifically, therefore, no structural changes occur due to information propagating back into the RL via radiative-acoustic waves (Abbott 1980). This assumption was checked in L07b and found to be justified: for the models from L07a, matching supersonic solutions were constructed and the group velocity of Abbott waves computed. In each case, the direction of information propagation is everywhere outwards towards higher velocities.

However, even without this justification, there are two further reasons for adopting this assumption. First, any conflict with observations would then be possible evidence that structural changes do indeed occur. Second, since such waves have to propagate back into the photosphere through an outflow that, according to most spectroscopists, is chaotic and clumpy, their information content might well be scrambled and lost.

A second unstated assumption is that after achieving supersonic velocities matter continues to be accelerated at least until local escape velocity is reached, so that no matter falls back onto the RL. Again, for the models of L07a, this is confirmed by the matching exterior solutions reported in L07b. But this assumption might well be violated for some late-type O stars (Howk et al. 2000).

In addition, note that these dynamic RL's are constructed without the Sobolev approximation, which, for a microturbulent velocity of 10 km s-1, is not valid for Mach numbers $\la$3 - see Fig. 4 in L07a - and so is inappropriate for the sub- and transonic flows of O stars.

2.2 Adjustable parameters

In addition to J, a model RL as described in L07a has two further adjustable parameters $\delta$ and s. These define the velocity dependence of $g_{\ell}$, the radiative acceleration due to lines, according to the formula

\begin{displaymath}g_{\ell} = g_{*} \max \left[\delta, \left(\frac{v}{a}\right)^{s} \right] \;\;\; {\rm with} \;\;\; g_{*} = g - g_{\rm e} \end{displaymath} (1)

where $g_{\rm e}$ is the radiative acceleration due to electron scattering. With $0 < \delta < 1$ and s > 0, this formula is such that the effective gravity $ g_{\rm eff} = g - g_{\rm e} - g_{\ell} = 0$ at v = a and is negative at supersonic velocities, thus allowing the rapid acceleration of the transonic flow to be accurately modelled - see Fig. 2 in L07a.

2.3 An identity

If the equation of motion for plane-parallel, radiatively-driven isothermal flow - Eq. (2) in L07a - is integrated between heights x1 and x2, we find that $Q_{1,2} \equiv 0$, where

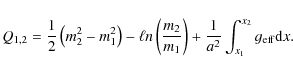
\begin{displaymath}Q_{1,2} = \frac{1}{2} \left(m_{2}^{2} - m_{1}^{2}\right) - \e... ... + \frac{1}{a^{2}} \int_{x_{1}}^{x_{2}} g_{\rm eff} {\rm d}x. \end{displaymath} (2)

Here m = v/a is the flow's Mach number relative to the isothermal speed of sound a.

In physical terms, Q1,2 = 0 implies that the gain in mechanical energy between x1 and x2 is due to the work done by the gradients of gas and radiation pressures. But for a solution generated with the L07a code, the identity will in general be violated because of a non-optimum parameter vector $(J,~\delta,~s)$. Nevertheless, by adjusting this vector as described below, we can find the solution giving Q1,2=0.

The above identity holds for any pair of points (x1, x2). Here, because of our interest in finding a solution representing smooth transonic flow, we choose these points to be where $m_{1} \approx 0.5$ and $m_{2} \approx 2.0$, thus straddling the sonic point. Accordingly, for this MC technique, the constraint Q1,2=0 for the interval (m1, m2) is the analogue of the regularity condition at v = a in conventional investigations of transonic flow.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{13400fg1.ps} \end{figure} Figure 1:

Emergent spectrum of TLUSTY model atmosphere with parameters as indicated. The open circles locate the points used to approximate the continuum.

Open with DEXTER

2.4 Determining the eigenvalue J

The steps followed in obtaining a satisfactory model are:

1)
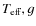For the chosen parameters $T_{\rm eff}, g$, continuum fluxes are extracted from the corresponding TLUSTY model (Lanz & Hubeny 2003) at 26 frequencies $\nu_{k}(Hz)$ from 14.5-16.2 dex. This is illustrated in Fig. 1, with parameters appropriate for a late-type O dwarf. In the MC calculation, fluxes at the base of the RL are obtained by linear logarithmic interpolation in the intervals $(\nu_{k}, \nu_{k+1})$. Note that because the emergent MC flux at the top of the RL is constrained by Eq. (7) of L07a to 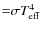${=} \sigma T_{\rm eff}^{4}$, only relative continuum fluxes of the TLUSTY models are used.
2)
For the same TLUSTY model, ground-state departure coefficients are extracted from the point where $T_{\rm e} \approx 0.75 T_{\rm eff}$ in order to compute ionization in the RL from Eq. (6) of L07a.
3)
Initial values are selected for the parameters $(J,~\delta,~s)$, and the resulting stratification of the RL computed as described in Sect. 2.3 of L07a.
4)
The radiation field throughout the RL is then derived with the MC technique described in Sect. 3.2 of L07a. In particular, the MC estimator $\tilde{g_{\ell}}$ for the radiative acceleration due to lines is evaluated.
5)
With these values $\tilde{g_{\ell}}$, the integral in Eq. (2) is approximated as a summation and Q1,2 calculated.
6)
Steps 3) to 6) are repeated for different J's but fixed $(\delta,s)$in order to locate the intersection with Q1,2 = 0 - see Fig. 2. The intersection is derived from a least squares linear fit to 5-12 Q-values closely bracketing Q = 0.
7)
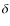From the model thus derived, fits to the variations of $\tilde{g_{\ell}}$in the sub- and supersonic flows suggest improved values of $\delta$and s, respectively. If these differ significantly from the current values, steps 3) to 7) are repeated.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13400fg2.ps} \end{figure} Figure 2:

The search for the eigenvalue J. The atmospheres' parameters are $T_{\rm eff} = 32~500$ K (filled circles) and $T_{\rm eff} = 37~500$ K (open circles) both with $\log g = 4$. For each atmosphere, a sequence of models with varying J but fixed $(\delta,~s)$ is plotted. The values of $\log J$ given by the intersections with Q1,2 = 0 are indicated.

Open with DEXTER

2.5 Dynamical consistency

A qualitative consistency check is the mismatch between $\tilde{g_{\ell}}$, the computed and $g_{\ell} (v; \delta,s)$, the assumed radiative accelerations due to lines. These are plotted for the model with $T_{\rm eff} = 32~500$ K in Fig. 3, which may be compared to the plot for $T_{\rm eff} = 50~000$ K in L07a. This comparison shows that the adopted functional form is here less successful at capturing the structure of the function $g_{\ell } (v)$. Clearly, a more flexible representation is desirable to achieve better dynamical consistency.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13400fg3.ps} \end{figure} Figure 3:

Comparison of assumed and computed radiative accelerations due to lines. The filled circles are the MC estimates and the solid line shows the variation assumed in deriving the RL's stratification. The open circle is the sonic point.

Open with DEXTER

This lack of consistency implies some uncertainty in the predicted J's. A rough estimate of this is derived as follows: 22 of the models in Table 1 were originally computed with $\delta = 0.5$ and s = 2. When $\delta$ and s were optimized, the changes $\vert\Delta\log J\vert$ were $\leq$0.05 in 13 cases and >0.2 in only 3 cases, with the largest difference being 0.42.

This experiment shows that the J's are moderately insensitive to the vector ($\delta,~s$) and thus to deviations from dynamical consistency. The most important step in deriving an accurate J is locating the intersection Q1,2 = 0, thus ensuring that radiative driving makes its mandatory contribution to the gain of mechanical energy as the flow accelerates through the sonic point from m1 to m2.

Given that the disagreement discussed in Sect. 1 is by at least 1.0 dex in $\Phi$, the uncertainties in J are not of present concern.

3 Computed mass fluxes

In this section, J's are calculated for parameter vectors $(T_{\rm eff},~g)$chosen to illustrate the onset of powerful winds for O stars. Results are given in Table 1 for 29 models with a range of g's appropriate for stars in their H-burning main sequence phase. The models' composition is solar with $N_{\rm He}/N_{\rm H} = 0.1$(Grevess & Sauval 1998) and the included metal ions are as in Table 1 of Lanz & Hubeny (2003). The microturbulent velocity vt = 10 km s-1. In cases where dynamical consistency is poor, $\log J$ is followed by a colon. Note that two models from L07a are recomputed in Table 1. The changes in $\log J$ are +0.03 for D-50 and -0.07 for D-40.

Throughout this paper, logarithmic values of J are reported with mass flux unit $\rm gm \:s^{-1}~cm^{-2}$. If the radius of the star is known, its mass-loss rate $\Phi$ in solar masses per year can then be derived from the formula

\begin{displaymath}\log \Phi =\log J + 2 \log \frac{R}{R_{\odot}} + C \end{displaymath} (3)

with C = -3.015.

Table 1:   Computed eigenvalues $J (\rm gm \: s^{-1}~cm^{-2})$.

3.1 Weak-wind domain

In thermal equilibrium, a star's mass loss rate via its wind equals that by nuclear burning when $\Phi = L/c^{2}$, where $L = 4 \pi R^{2} {\cal{F}}$. Accordingly, we can define the weak-wind domain in $(T_{\rm eff},~g)$-space to be where $J < J^{*} \equiv {\cal{F}}/c^{2}$. The locus where J = J* has therefore been derived by interpolating between models in Table 1 and is shown as the bold line in Fig. 4. Also shown is the contour where J/J* has increased to 0.5 dex, illustrating the steepness of the onset of strong winds.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13400fg4.ps} \end{figure} Figure 4:

Weak-wind domain. The bold line is the locus J = J* separating weak from strong winds. Also shown is the locus where J exceeds J*by 0.5 dex. The filled circles are the weak-wind stars investigated in M09, and the asterisks are ZAMS models of Pols et al. (1998) for Z = 0.02 with masses 12(2)34 in solar units.

Open with DEXTER

The five weak-wind stars analysed in M09 are also plotted in Fig. 4. They either fall within the weak-wind domain or have error bars that just overlap the contour J = J*.

In order to determine the transition from weak to strong winds in terms of stellar mass, zero-age main sequence (ZAMS) models from Pols et al. (1998) for Z = 0.02 are also included in Fig. 4. From this sequence, we see that stars on the ZAMS with ${\cal{M/M_{\odot}}} \la 22$ are in the weak-wind domain while stars with ${\cal{M/M_{\odot}}} \ga 28$ are in the strong-wind domain.

The corresponding critical masses can be derived for the mass-loss formula of Vink et al. (2000). From their Eq. (12) with $v_{\infty}/v_{\rm esc} = 2.6$(Lamers et al. 1995) and noting that the formula applies only down to $T_{\rm eff} = 27~500$ K, we find that the upper limit for weak winds drops from 22 to <12, while the lower limit for strong winds drops from 28 to 14 solar masses. These large changes have profound implications for the evolution of massive stars.

3.2 Individual Marcolino stars

Finding that the stars of M09 fall in or at the edge of the weak-wind domain in Fig. 4 appears to suggest that the J's predicted from first principles with the L07a code solve the weak wind problem. But before accepting this conclusion, we must compare observed and predicted mass fluxes for the five stars individually. This is done in Table 2, where the data is as follows:

Table 2:   Mass fluxes for observed stars.

Column 2:
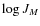$\log J_{M}$ computed from the measured $\log \Phi$'s reported in M09 together with their conservative error estimates.

Column 3:
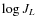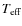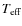$\log J_{L}$ obtained by interpolation in Table 1 for the $T_{\rm eff}$ and g given in Table 3 of M09. The computed errors reflect only the propagation of the errors in $T_{\rm eff}$ and g given in M09 and shown in Fig. 4.

Column 4:
$\log J_{V}$ derived from Eq. (12) in Vink et al. (2000) with parameters from Table 3 in M09.

Column 5:
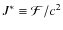$\log J^{*}$, where $J^{*} \equiv {\cal{F}}/c^{2}$.
From Table 2, we see that the JL's are systematically smaller than the JV's by on average 1.4 dex. Nevertheless, this huge reduction is still not enough to explain the measured values JM, which are smaller than the JL's by on average 0.8 dex.

Given the large error bars, the individual differences $\log J_{M} -\log J_{L}$ are barely significant. But with all differences being of the same sign, the data as a whole could be said to reject the hypothesis that the L07a theory correctly predicts observed J's. But this is not purely a question of statistics. The reliability of the diagnostic investigations can be questioned, especially for low $\Phi$'s when often only the C IV doublet is available for analysis, and this line's weak or absent emission component is unexplained (Martins et al. 2004). This latter problem emphasizes how limited is our understanding of the supersonic zones of these stars' low density winds, a problem affecting the Vink et al. (2000) predictions as well as diagnostic codes.

3.3 The matching problem

As noted in Sect. 1, $\Phi$'s derived from a global dynamical constraint may be inconsistent with stationary transonic flow; and the same remark applies to $\Phi$'s derived diagnostically from circumstellar spectra. To illustrate the magnitude of these inconsistencies for the weak-wind stars, the consistency check carried out in Fig. 3 has been repeated in Fig. 5 with JLincreased by 1.4 dex to represent the Vink et al. recipe and decreased by 0.8 dex to represent the Marcolino et al. estimates. In both cases, there are huge differences between $g_{\ell } (v)$ and $\tilde{g_{\ell}}$, indicating gross violations of dynamical consistency. Moreover, searches in ( $\delta,~s$)-space with J fixed at these high or low J's fail to find alternative dynamically-consistent solutions.

Evidently, any estimate of $\Phi$ derived from an analysis of a wind's supersonic flow should ideally be confirmed by matching to a stationary transonic flow, thus exhibiting a successful transition to the quasi-static atmosphere where the star's absorption line spectrum is formed.

\begin{figure} \par\includegraphics[width=7.8cm,clip]{13400fg5.ps} \end{figure} Figure 5:

Departures from dynamical consistency. The solid line shows the variation of $g_{\ell } (v)$ assumed in deriving the stratification of the RL with the indicated parameters, for which $J_{L}(\rm gm \: cm^{-2}~ s^{-1}) = -7.32$ dex - see Fig. 3. The filled circles are the MC estimates $\tilde{g_{\ell}}$ when J is increased to -5.92 dex; and the small open circles are the estimates for J = -8.12 dex. The large open circle is the sonic point.

Open with DEXTER

3.4 Two strong-wind stars

Given the large discrepancies for the weak-wind stars between  JM,  JLand JV, a reader might reasonably conclude that, since no two methods even approximately agree, there is no basis for preferring one estimate over another. The data in Table 1 is therefore now used to compute J's for the two Galactic O4 stars investigated by Bouret et al. (2005). These authors are co-authors of the Marcolino paper, and the same diagnostic codes, TLUSTY and CMFGEN, are used.

For the O4 V star HD 96715, Bouret et al. derive $\Phi = 2.5 \pm 0.5 \times 10^{-7}~ {\cal{M}}_{\odot}~ \rm yr^{-1}$, corresponding to $\log J = -5.74 \pm 0.08$. This is their preferred estimate, derived with the filling factor of clumps as an additional adjustable parameter. For a homogeneous wind, $\Phi$ is 0.86 dex higher, corresponding to $\log J = -4.88$.

The atmospheric parameters derived by Bouret et al. are $T_{\rm eff} = 43~500 \pm 2200$ K and $\log g = 4.0 \pm 0.1$. Interpolation in Table 1 gives $\log J_{L} = -5.54 \pm 0.25$. But note that Table 1 is computed with vt = 10 km s-1, whereas Bouret et al. derive $v_{t} = 15 \pm 5~$km s-1. According to Table 1 in L07a, this increase in vtreduces JL by about 0.30 dex, bringing the prediction to $\log J_{L} = -5.84 \pm 0.36$. This agrees within errors with the clump-corrected value of Bouret et al. but is in strong disagreement with the value for a homogeneous wind.

The second Bouret et al. star is the O4 I supergiant HD 190429A. The clumped-wind analysis gives $\Phi = 1.8 \pm 0.4 \times 10^{-6} ~{\cal{M}}_{\odot}~\rm yr^{-1}$, corresponding to $\log J = -5.31~ \pm~ 0.08$. The atmospheric parameters derived by Bouret et al. are $T_{\rm eff} = 39~000~ \pm ~2000$ K and $\log g = 3.6 \pm 0.1$ giving $\log J_{L} = -5.04 \pm 0.76$, where the large standard error is due to the steep gradient of JL at this star's location in $(T_{\rm eff},~g)$-space. As before, we now apply a correction of -0.30 dex because the measured $v_{t} = 15 \pm 2~$km s-1. The final prediction is therefore $\log J_{L} = -5.34 \pm 0.77$, consistent with the clumped wind analysis but, in this case, also with the value $\log J = -4.78 \pm 0.08$ for a homogeneous wind.

The clumped-wind $\Phi$'s derived by Bouret et al. are lower than the Vink et al. predictions by 0.9 dex for HD 96715 and 0.5 dex for HD 190429A. On this basis, Bouret et al. conclude that our understanding of O-star winds requires fundamental revision. The success here in reproducing their estimates shows that the required revision is simply the inclusion of a dynamically consistent transition to the observed photosphere. In addition, this theoretical confirmation of their low rates reinforces their conclusion that the evolutionary tracks of massive stars need to be recomputed.

3.5 Mechanism

The internal details of the RL models can be investigated in order to understand the sharp rise in J as one moves from late- to early- type O dwarfs. Most illuminating are the fractional contributions of various ions to $\tilde{g_{\ell}}$ in the layer containing the sonic point. Such calculations have been carried out for the models with $\log g = 4$. These reveal that the high J's for $T_{\rm eff} \ga 40~000$ K are due to the ability of high ions to absorb momentum from the emergent flux below the Lyman limit, as has long been understood (Castor et al. 1976; Lamers & Morton 1976). Of dominant importance is the changing ionization balance of iron, resulting in the effective driving ion Fe V replacing the ineffective ion Fe IV (cf. Vink et al. 2000). Thus, in the weak-wind domain at $T_{\rm eff} = 32~500$ K, Fe V lines contribute only 0.7% of $\tilde{g_{\ell}}$ at v = a, but this rises to 44% at 40 000 K and reaches a maximum of 78% at 45 000 K.

These results show that the termination of strong winds in $(T_{\rm eff},~g)$-space is determined by ionization balance in the reversing layer. In these models (L07a, Sect. 2.5), this balance is matched at a representative point to that of the corresponding static TLUSTY atmosphere.

4 Conclusion

The aim of this paper has been to respond to an apparent problem for the theory of radiatively-driven winds arising from the extraordinarily low $\Phi$'s found for late-type Galactic O stars, as exemplified recently by M09. The problem is lessened, though perhaps not entirely resolved, when the observed rates are compared to predictions made from first principles using the theory of dynamic RLs (LS70; L07a) rather than to the semi-empirical estimates of Vink et al. (2000). When this theory is used to define a weak-wind domain in $(T_{\rm eff},~g)$-space, the M09 stars are found to be within or at the edge of this domain. It remains to be seen whether future developments in our understanding of low density supersonic winds will close the remaining gap between predicted and observed rates.

A still outstanding issue is the huge disparity between the $\Phi_{V}$'s and the observed estimates. It would be informative if the Vink et al. code were used to fit the M09 stars individually and the emergent MC spectra compared with the observed spectra, as Abbott & Lucy (1985) did for $\zeta$ Puppis. From experiments reported by M09, this consistency check is expected to fail, revealing that the $\Phi_{V}$'s give rise to unacceptably strong wind lines. Such discrepancies would then provide the basis for revising the Vink et al. assumptions about physical conditions at velocities ${\sim} 0.5 v_{\infty}$ in these stars' winds.

This substantial progress towards resolving the weak-wind problem and the success in reproducing the clumped-wind $\Phi$'s of Bouret et al. (2005) strongly supports the simple picture for the onset of winds presented in LS70: selective radiation pressure expels high atmospheric layers causing a pressure inbalance in the photosphere resulting in an upwelling of matter from deeper layers. The natural steady-state configuration is then the transonic flow described by the theory of moving RL's (LS07; L07a), which merits still further development.

Acknowledgements

I am grateful to J. S. Vink, A. de Koter and T. L. Hoffmann for prompt answers to queries relevant to the refereeing of this paper.

References

  1. Abbott, D. C. 1980, ApJ, 242, 1183 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bouret, J.-C., Lanz, T., Hillier, D. J., et al. 2003, ApJ, 595, 1182 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bouret, J.-C., Lanz, T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Castor, J. I., Abbott, D. C., & Klein, R. I. 1976, in Physique des mouvements dans les atmospheres stellaires, ed. R. Cayrel, & M. Steinberg (Paris: CNRS), 363 [Google Scholar]
  6. Grevess, N., & Sauval, A. J. 1998, Sp. Sci. Rev., 85, 161 [CrossRef] [Google Scholar]
  7. Howk, J. C., Cassinelli, J. P., Bjorkman, J. E., & Lamers, H. J. G. L. M. 2000, ApJ, 534, 348 [NASA ADS] [CrossRef] [Google Scholar]
  8. Lamers, H. J. G. L. M., & Morton, D. C. 1976, ApJS, 32, 715 [NASA ADS] [CrossRef] [Google Scholar]
  9. Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
  10. Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
  11. Lucy, L. B. 2007a, A&A, 468, 649 (L07a) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Lucy, L. B. 2007b, A&A, 474, 701 (L07b) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 (LS70) [NASA ADS] [CrossRef] [Google Scholar]
  14. Marcolino, W. L. F., Bouret, J.-C., Martins, F., et al. 2009, A&A, 498, 837 (M09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Martins, F., Schaerer, D., Hillier, D. J., & Heydari-Malayeri, M. 2004, A&A, 420, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Pols, O. R., Schroder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
  17. Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]

All Tables

Table 1:   Computed eigenvalues $J (\rm gm \: s^{-1}~cm^{-2})$.

Table 2:   Mass fluxes for observed stars.

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{13400fg1.ps} \end{figure} Figure 1:

Emergent spectrum of TLUSTY model atmosphere with parameters as indicated. The open circles locate the points used to approximate the continuum.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13400fg2.ps} \end{figure} Figure 2:

The search for the eigenvalue J. The atmospheres' parameters are $T_{\rm eff} = 32~500$ K (filled circles) and $T_{\rm eff} = 37~500$ K (open circles) both with $\log g = 4$. For each atmosphere, a sequence of models with varying J but fixed $(\delta,~s)$ is plotted. The values of $\log J$ given by the intersections with Q1,2 = 0 are indicated.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13400fg3.ps} \end{figure} Figure 3:

Comparison of assumed and computed radiative accelerations due to lines. The filled circles are the MC estimates and the solid line shows the variation assumed in deriving the RL's stratification. The open circle is the sonic point.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13400fg4.ps} \end{figure} Figure 4:

Weak-wind domain. The bold line is the locus J = J* separating weak from strong winds. Also shown is the locus where J exceeds J*by 0.5 dex. The filled circles are the weak-wind stars investigated in M09, and the asterisks are ZAMS models of Pols et al. (1998) for Z = 0.02 with masses 12(2)34 in solar units.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{13400fg5.ps} \end{figure} Figure 5:

Departures from dynamical consistency. The solid line shows the variation of $g_{\ell } (v)$ assumed in deriving the stratification of the RL with the indicated parameters, for which $J_{L}(\rm gm \: cm^{-2}~ s^{-1}) = -7.32$ dex - see Fig. 3. The filled circles are the MC estimates $\tilde{g_{\ell}}$ when J is increased to -5.92 dex; and the small open circles are the estimates for J = -8.12 dex. The large open circle is the sonic point.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.