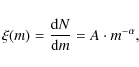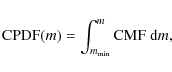| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200912967 | |
| Published online | 08 April 2010 | |
Variations in integrated galactic initial mass functions due to sampling method and cluster mass function
M. R. Haas1 - P. Anders2
1 - Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
2 -
Astronomical Institute, Utrecht University, Princetonplein 5, 3584 CC Utrecht, The Netherlands
Received 23 July 2009 / Accepted 13 January 2010
Abstract
Context. Stars are thought to be formed predominantly in
clusters. The star clusters are formed according to a cluster initial
mass function (CMF) similar to the stellar initial mass function (IMF).
Both the IMF and the CMF can be approximated by (broken) power-laws,
which favour low-mass objects. The numerous low-mass clusters will lack
high mass stars compared to the underlying IMF, since the most massive
star cannot be more massive than its host cluster. If the integrated
galactic initial mass function (IGIMF, i.e. the total stellar mass
function of all stars in a galaxy) originates from stars formed in star
clusters, the IGIMF could be steeper than the IMF in clusters.
Aims. We investigate how well constrained this steepening is and
how it depends on the choice of sampling method and CMF. We investigate
the observability of the IGIMF effect in terms of galaxy photometry and
metallicities.
Methods. We study various ways to sample the stellar IMF within
star clusters and build up the IGIMF from these clusters. We compare
analytic sampling to several implementations of random sampling of the
IMF and different CMFs. We implement different IGIMFs into the GALEV evolutionary synthesis package to obtain colours and metallicities for galaxies.
Results. Choosing different ways of sampling the IMF results in
different IGIMFs. Depending on the lower cluster mass limit and the
slope of the cluster mass function, the steepening varies between very
strong and negligible. We find the size of the effect is continuous as
a function of the power-law slope of the CMF if the CMF extends to
masses smaller than the maximum stellar mass. The number of O-stars
detected by GAIA will, if some uncertain factors are better understood,
help to judge the importance of the IGIMF effect. The impact of
different IGIMFs on integrated galaxy photometry is small, within the
intrinsic scatter of observed galaxies. Observations of gas fractions
and metallicities could rule out at least the most extreme sampling
methods, if other sources of error are sufficiently understood.
Conclusions. As we still do not understand the details of star
formation and the sampling of the stellar IMF in clusters, one sampling
method cannot be favoured over another. Also, the CMF at very low
cluster masses is not well constrained observationally. These
uncertainties therefore need to be taken into account when using an
IGIMF, with severe implications for galaxy evolution models and
interpretations of galaxy observations.
Key words: stars: luminosity function, mass function - Galaxy: stellar content - galaxies: fundamental parameters - methods: numerical - methods: statistical
1 Introduction
A series of papers (Kroupa & Weidner 2003; Weidner & Kroupa 2006, 2005, 2004, the latter WK06 from now on) pointed out that the distribution of initial stellar masses in a galaxy may significantly deviate from the initial mass function (IMF) the stars have when they are born, if the vast majority of stars is born in clusters. These clusters follow a power-law mass function (the cluster mass function, CMF), which means that most stars form in low-mass clusters. In low-mass clusters there is a deficiency of massive stars (as the most massive star cannot exceed the total cluster mass), resulting in an integrated galactic initial mass function (IGIMF) that is, at the high mass end, steeper than the IMF.
The universality of the IMF is still an often debated topic. It is as yet not clear whether the IMF in all Galactic star clusters is the same, whether or not the field stars in the Milky Way follow the same mass distribution as cluster stars, and whether the IMF in other galaxies is the same as here. The IMF is shaped by the very complicated processes which transform molecular cloud cores into stars, processes which would be expected to be environmental-dependent. Therefore, a non-universality of the IMF would intuitively be expected.
As the distribution of stellar masses has a profound impact on many aspects
of the evolution of galaxies, it is important to know to what extent the
IGIMF deviates from the underlying stellar IMF (which is often used as IGIMF
in galaxy evolution studies) and how this affects galaxy properties. For
example, the relation between star formation rate and H![]() luminosity is
shown to be steeper in galaxies with a very low star formation rate
(Skillman et al. 2003), which can be explained by having a steeper IGIMF for low
SFR galaxies (Pflamm-Altenburg et al. 2007) due to the preferential formation of
low-mass clusters. Also, the gradients in galactic disks of SFR and H
luminosity is
shown to be steeper in galaxies with a very low star formation rate
(Skillman et al. 2003), which can be explained by having a steeper IGIMF for low
SFR galaxies (Pflamm-Altenburg et al. 2007) due to the preferential formation of
low-mass clusters. Also, the gradients in galactic disks of SFR and H![]() luminosity are different due to clustered star formation
(Pflamm-Altenburg & Kroupa 2008). The supernova rate per unit stellar mass
formed and the chemical enrichment history of a galaxy are influenced by the
IGIMF as shown by Goodwin & Pagel (2005). In a recent paper
Hakobyan et al. (2009) study the difference in rates of supernovae of type Ib/c
and type II and find that their results can be explained by having a steeper
IMF in the outskirts of galaxies than in their centres, which can be
explained by a different ``IGIMF'' in the outskirts of the galaxy as compared
to the inner regions due to a lower SFR in the outskirts.
luminosity are different due to clustered star formation
(Pflamm-Altenburg & Kroupa 2008). The supernova rate per unit stellar mass
formed and the chemical enrichment history of a galaxy are influenced by the
IGIMF as shown by Goodwin & Pagel (2005). In a recent paper
Hakobyan et al. (2009) study the difference in rates of supernovae of type Ib/c
and type II and find that their results can be explained by having a steeper
IMF in the outskirts of galaxies than in their centres, which can be
explained by a different ``IGIMF'' in the outskirts of the galaxy as compared
to the inner regions due to a lower SFR in the outskirts.
Recently, Recchi et al. (2009) investigated the [![]() Fe] versus
velocity dispersion in early type galaxies and the rates of supernovae
of both type II and Ia in several galaxy types in the light of the
IGIMF framework. They find that if one assumes a constant star
formation rate over a Hubble time, then for all but the irregular
galaxies these numbers agree well with the observed values. Recchi et al. (2009) explained this discrepancy by stating that for
irregular galaxies a constant SFR over the age of the Universe is not
likely to be a good approximation.
Fe] versus
velocity dispersion in early type galaxies and the rates of supernovae
of both type II and Ia in several galaxy types in the light of the
IGIMF framework. They find that if one assumes a constant star
formation rate over a Hubble time, then for all but the irregular
galaxies these numbers agree well with the observed values. Recchi et al. (2009) explained this discrepancy by stating that for
irregular galaxies a constant SFR over the age of the Universe is not
likely to be a good approximation.
However, other studies (see e.g. Sandage 1986) find approximately constant SFR for late-type spiral galaxies (Sd/Irr), and declining SFRs with time for earlier-type galaxies (where the decline time decreases while going from Sc to E galaxies). For Sa-Sc galaxies, the SFR is directly related to the available gas mass, resembling the Kennicutt-Schmidt law (Kennicutt 1998a). Starbursts, superimposed on any of the standard Hubble types, seem to be a common phenomenon. They have the strongest impact on photometry and chemical enrichment for late-type galaxies (which are typically of low mass) and major mergers (due to the triggered extremely high SFRs). Such starbursts might be interpreted as ``recently rising SFR'' as found by Recchi et al. (2009).
WK06 test three different scenarios for sampling stellar masses in a cluster. They conclude that ``sorted sampling'' (see Sect. 3.3.2) best reproduces the observed relation between maximum stellar mass in a cluster and the cluster mass (but see Maschberger & Clarke 2008 for a critical re-evaluation of this relation). The amount of steepening of the IGIMF is found to depend on the sampling method and on the power-law index of the low-mass end of the CMF.
For galaxies as a whole, the low-mass end of the CMF is not well constrained. Even in the Milky Way we can only see low-mass star-forming regions (few to few tens of solar masses) nearby, while for distant galaxies such regions are too faint.
In this work we investigate the dependence of the IGIMF on the
- 1.
- Sampling method: stellar masses in clusters can be sampled in different ways from the stellar IMF. We will show that the specific sampling method is indeed important and that different sampling methods give different results, as was already shown by WK06. We will extend their set of sampling methods;
- 2.
- Cluster mass function: it is to be expected that the effects on the IGIMF depend on the CMF. Sampling issues become more important for low-mass clusters, and therefore a lower minimum cluster mass and/or a steeper CMF will result in a stronger steepening of the IGIMF. We take observed CMFs for high mass clusters and extrapolate them down to the masses of observed star forming regions in the solar neighbourhood. We investigate the impact of different lower mass limits and power-law indices.
We will start by presenting the mass distributions of stars and clusters that we use in Sect. 2 and discuss our sampling methods, including a consistency test of the sampling methods in Sect. 3. The results for the IGIMF are shown in Sect. 4 for several sampling methods with a constant cluster mass function and for one sampling method with a variety of cluster mass functions. In Sect. 5 we calculate the number of O-stars that will be observed by GAIA, under various assumptions, and we compare the results of our IGIMFs with the work on single O-stars by de Wit et al. (2004,2005). Section 6 describes the galaxy evolution models and shows results on the integrated photometry and chemical enrichment of galaxies with various IGIMFs. The conclusions are presented in Sect. 7.
2 The underlying mass functions
Here we discuss our choices for the stellar IMF and the cluster mass function. The methods of sampling these distribution functions are the topic of the next section.
2.1 The stellar initial mass function
For stars we used the Salpeter (1955) IMF:
with
2.2 The cluster mass function
For the star clusters we assumed a power-law mass function similar to
Eq. (1):
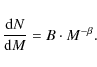
|
(2) |
There exists a debate between different groups who try to obtain the cluster initial mass function (CMF) in distant galaxies. In studies which try to constrain the power-law slope of the CMF from the relation between the SFR of a galaxy and the number of clusters in a galaxy (or, equivalently, the luminosity of the brightest cluster in a galaxy), many groups find values of
Here we took pure power-laws with a slope of
![]() for consistency
with the work of Weidner & Kroupa (2004), and to have a case that is in
between the values found by the two competing camps. In Sect. 4.3 we discuss the specific case
for consistency
with the work of Weidner & Kroupa (2004), and to have a case that is in
between the values found by the two competing camps. In Sect. 4.3 we discuss the specific case
![]() as well as a continuum of slopes in the range
as well as a continuum of slopes in the range
![]() ,
to cover the whole range of slopes found observationally.
,
to cover the whole range of slopes found observationally.
Although the range of cluster masses probed
is wide, the observationally accessible extragalactic star clusters
have masses exceeding 1000 ![]() ,
except for clusters in the Magellanic
Clouds. As minimum mass for star clusters we used a default value of 5
,
except for clusters in the Magellanic
Clouds. As minimum mass for star clusters we used a default value of 5 ![]() ,
as did Weidner & Kroupa (2004). As the value for a
physical lower mass limit for clusters, if any, is unknown, this mass
was taken because it is the lowest mass of groups of stars that is
observed to be forming in the Taurus-Auriga region (Briceño et al. 2002).
This lower limit is far below
the range in which the power-law behaviour is observed. It is an
extrapolation of more than two orders of magnitude. This extrapolation
is assumed in other IGIMF studies as well and the best we can
currently do. The upper mass limit for star clusters was set to infinity.
,
as did Weidner & Kroupa (2004). As the value for a
physical lower mass limit for clusters, if any, is unknown, this mass
was taken because it is the lowest mass of groups of stars that is
observed to be forming in the Taurus-Auriga region (Briceño et al. 2002).
This lower limit is far below
the range in which the power-law behaviour is observed. It is an
extrapolation of more than two orders of magnitude. This extrapolation
is assumed in other IGIMF studies as well and the best we can
currently do. The upper mass limit for star clusters was set to infinity.
We varied both the lower and the upper mass limits to investigate how
sensitive our results are to variations of these values. The minimum
cluster mass is expected to be important, and 5 ![]() is far below
observational limits of any young star cluster that is outside the
solar neighbourhood. Observational indications for an upper cluster
mass limit are found in e.g. the Antennae (Zhang & Fall 1999) and M51
(Gieles et al. 2006b; Haas et al. 2008) and in general from the relation between the
brightest cluster in a galaxy and its star formation rate by
Weidner et al. (2004); Bastian (2008). These upper mass limits are found to be
around
105.5-6.5
is far below
observational limits of any young star cluster that is outside the
solar neighbourhood. Observational indications for an upper cluster
mass limit are found in e.g. the Antennae (Zhang & Fall 1999) and M51
(Gieles et al. 2006b; Haas et al. 2008) and in general from the relation between the
brightest cluster in a galaxy and its star formation rate by
Weidner et al. (2004); Bastian (2008). These upper mass limits are found to be
around
105.5-6.5 ![]() .
See Sect. 4.4 for
an investigation of star formation rate dependent IGIMFs.
.
See Sect. 4.4 for
an investigation of star formation rate dependent IGIMFs.
3 Sampling techniques
In this section we discuss several ways to sample the distribution functions described in the previous section.
3.1 Star formation scenarios and sampling of the IMF
Ideally, one would like to connect sampling methods in numerical experiments like the one conducted here in some way to the astrophysics going on in the studied system. Here this would mean that we construct a method of sampling stellar masses in a cluster, which is based on a scenario about how this cluster forms from its parent molecular cloud. It is expected that the IMF found in star forming regions harbours a wealth of information about the star formation process. A recent paper by Dib et al. (2010) indeed describes several ways of building up an IMF from star formation scenarios.
The problem with constructing sampling methods in this way is that it is not at all guaranteed that the mass function inside clusters follows the same functional form in all clusters. Besides, the mass function of cloud cores is an equally uncertain factor. Likewise, the large number of free parameters and inherent uncertainties of physical star formation scenarios would inhibit us in drawing any conclusions. The point of this paper is to show the effects of different sampling methods, given that the underlying IMF is the same. We chose therefore to use a single underlying IMF and constructed sampling methods that do not necessarily represent physical star formation scenarios.
3.2 Analytic sampling
The first method to sample a distribution function we discuss is
analytic in nature. We use the fact that the total mass of stars inside
a cluster (i.e. the cluster mass) is calculated from
where
The normalisation of the IMF (A in Eq. (1)) is defined by
relation 3. Sampling the distribution function is
done by using
with Ni = N1 = 1 for the most massive star (this star has the mass m1), 2 for the second most massive and so on. For any cluster mass the masses of all stars present in the sample are uniquely determined, see also Weidner & Kroupa (2004).
3.3 Random sampling
In order to introduce stochastic effects, we will mainly sample mass
functions randomly, as it ensures that random fluctuations are present
in the sample of masses. Whereas the analytic way of sampling will never
produce a 80 ![]() star in a 100
star in a 100 ![]() cluster, this will happen
(although rarely) when sampling randomly. There are nevertheless issues,
as described below.
cluster, this will happen
(although rarely) when sampling randomly. There are nevertheless issues,
as described below.
A random number from a distribution function was drawn using a random
number, uniformly distributed between 0 and 1 as many numerical
packages can provide you with, and the normalised cumulative
probability density function, which (in this case) is itself an integral over the
mass function:
normalised to CPDF(
For power-law distribution functions, the inversion can be done analytically, so that the necessity for time consuming numerical integration or the use of look-up tables (constraining the flexibility of our research) is prevented.
3.3.1 The total mass of the cluster
When sampling stars one by one, the chances of them adding up to exactly the cluster mass are marginal. Therefore one has to make a choice about which stars to include. One way is just sampling stellar masses until you first go over the predetermined total cluster mass. Four choices can be made:
- 1.
- stop at that point. The cluster mass will always end up slightly higher than the predetermined value. We will indicate this method by ``stop after'', as we always stop just after passing the cluster mass aimed for;
- 2.
- remove the last star drawn. The cluster mass will now be systematically lower than the masses drawn from the CMF, we will therefore abbreviate it by ``stop before'';
- 3.
- only remove the last drawn star if then the total mass is closer to the desired value. The cluster masses are sometimes slightly lower, sometimes slightly higher than the predetermined value. This will be our default choice, indicated by ``stop nearest'';
- 4.
- like the previous option, but removing the star at 50% probability, regardless of whether it would bring the cluster mass closer to the predetermined mass or not. This will be called ``stop 50/50''.
3.3.2 Sorted sampling à la Weidner & Kroupa (2006)
An alternative treatment was introduced and extensively tested by
WK06, ``sorted sampling'': draw a number of stars (
![]() )
in which
)
in which
![]() is the cluster mass and
is the cluster mass and
![]() is the average stellar mass in the IMF under consideration. Then draw
that many stellar masses from the IMF. Repeat this if the total mass is
not yet the desired
cluster mass by drawing an additional
is the average stellar mass in the IMF under consideration. Then draw
that many stellar masses from the IMF. Repeat this if the total mass is
not yet the desired
cluster mass by drawing an additional
![]() stars (where
stars (where
![]() is the sum of the masses already drawn). When the cluster mass is first
surpassed, sort the masses ascendingly and remove the most massive star
if that brings the total stellar mass closer to the desired cluster
mass. Only the most massive star drawn can be removed. If the first
sample of stars goes over the cluster mass by a large amount, still
only one star can be removed, while the correction upwards in mass can
be with any arbitrary number of stars.
is the sum of the masses already drawn). When the cluster mass is first
surpassed, sort the masses ascendingly and remove the most massive star
if that brings the total stellar mass closer to the desired cluster
mass. Only the most massive star drawn can be removed. If the first
sample of stars goes over the cluster mass by a large amount, still
only one star can be removed, while the correction upwards in mass can
be with any arbitrary number of stars.
3.3.3 Sampling to a total number of stars
Alternatively, one can once draw a predetermined number of stars for a
given cluster from the IMF. The number of stars that is drawn is, as in ``sorted sampling'', given by
![]() .
In this case some clusters may become much
more or much less massive than the mass that was sampled from the
cluster mass function. We will indicate this method simply with ``number''.
.
In this case some clusters may become much
more or much less massive than the mass that was sampled from the
cluster mass function. We will indicate this method simply with ``number''.
3.3.4 Limiting the stellar masses to the cluster mass
By default we limited our maximum possible stellar mass to the mass of the
cluster (so that e.g. a
![]()
![]() cluster can contain only stars at most as massive as
cluster can contain only stars at most as massive as
![]()
![]() ).
Otherwise,
clusters of a predetermined mass may end up with a star that is more
massive than the cluster itself. However, we also tried it without this
constraint, in which case we add ``unlimited'' to the name. Note that
lowering the maximum possible stellar mass heightens the probability
for drawing lower mass stars (per unit mass), as the integral of the
probability density function of stellar masses should still be one.
).
Otherwise,
clusters of a predetermined mass may end up with a star that is more
massive than the cluster itself. However, we also tried it without this
constraint, in which case we add ``unlimited'' to the name. Note that
lowering the maximum possible stellar mass heightens the probability
for drawing lower mass stars (per unit mass), as the integral of the
probability density function of stellar masses should still be one.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f1.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg32.png)
|
Figure 1:
The fraction of clusters per unit |
| Open with DEXTER | |
3.4 The recovered cluster mass function
One consistency test for the sampling methods is to see whether or not the mass function of the clusters after populating them with stars from the IMF recovers the input CMF. For some of the methods mentioned it is obvious that the total mass will always be over- or underestimated (e.g. stopping the sampling always right after or right before you passed the cluster mass, where the mass will be over- or underestimated by on average half an average stellar mass for that IMF). For the high cluster mass end these difference are negligible, but that is not necessarily clear for very low cluster masses, where the recovered CMF could be steeper or shallower than the input CMF.
In Fig. 1 we compare the input CMF (solid black
line, shifted by an arbitrary vertical offset), to several recovered
CMFs after populating the clusters with stars. The default sampling
method is shown in red (dashed), and the preferred method of WK06,
sorted sampling, is shown in dash-dotted blue. The two models for which
discrepancy is expected are shown in the dotted green lines. The
expected under- or overestimate of the total mass is ![]() 0.3
0.3 ![]() ,
which is more than an order of magnitude less than the very lowest
cluster mass. It turned out that even for these models the discrepancy
is marginal. Therefore we cannot rule out one or another sampling
methods based on the recovered CMF.
,
which is more than an order of magnitude less than the very lowest
cluster mass. It turned out that even for these models the discrepancy
is marginal. Therefore we cannot rule out one or another sampling
methods based on the recovered CMF.
4 Integrated galactic initial mass functions
We drew samples of 107 clusters from a cluster mass function with
![]() .
We tested several sample sizes and found
107 to be both computationally feasible and showing only tiny
statistical fluctuations (using e.g. 106 clusters results in IGIMF
scatter nearly as big as the difference between some models we tested). We
constructed the IGIMF by sampling the stars in the clusters in different
ways, as described in the previous section, and summed up all stars from
the individual clusters. In Fig. 2 we show three IGIMFs
from random sampling, together with the Salpeter IMF.
.
We tested several sample sizes and found
107 to be both computationally feasible and showing only tiny
statistical fluctuations (using e.g. 106 clusters results in IGIMF
scatter nearly as big as the difference between some models we tested). We
constructed the IGIMF by sampling the stars in the clusters in different
ways, as described in the previous section, and summed up all stars from
the individual clusters. In Fig. 2 we show three IGIMFs
from random sampling, together with the Salpeter IMF.
4.1 Sampling methods
Figure 2 clearly indicates that the IGIMF steepens for high stellar masses, due to the lack of high-mass stars in low-mass clusters. Also, the impact of using either of the three methods is comprehensible: stopping the sampling one star before the cluster mass filled up biases most against high stellar masses (as the chance of going over the cluster mass is higher for a higher-mass star) and going slightly over the cluster mass biases least against high mass stars. Because the differences are small, from now on we plot the fraction of all stars in a mass bin, divided by the fraction predicted from the input stellar IMF (i.e., Salpeter 1955). The same data as in Fig. 2 are used for Fig. 3, where the differences become clearer.
In Fig. 3 we also compare the analytic method of
sampling as explained in Sect. 3.2 to the random
sampling methods. Both have the stellar masses limited to be at most the
cluster mass, but in the random sampling technique sometimes a
relatively high-mass star does occur in a low-mass cluster. This is not
the case for the analytic sampling, which results in the sharp downturn
at masses close to the upper limit. As noted by WK06, the ``sorted
sampling'' method resembles the shape of analytic sampling, although
less severe. The relation is even steeper (approaching an IGIMF
power-law index of -3) for
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f2.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg35.png)
|
Figure 2: The IGIMF for randomly sampled stars in clusters until (1) the next star would overshoot the cluster mass (dashed), (2) a mass nearest to the cluster mass is reached (dotted), or (3) one star crosses the cluster mass (dot-dashed). The solid line is the input Salpeter IMF. The value on the vertical axis is the fraction of all the stars that are in that particular mass bin. |
| Open with DEXTER | |
Sampling a number of stars equal to the cluster mass divided by the
average stellar mass for the IMF under consideration is also shown in
Fig. 3. If the average mass is calculated with the
upper mass limit in a cluster limited to the cluster mass, the
method gives results rather similar to the default method. When the
average mass is always calculated for a well sampled IMF between 0.1 and
100 ![]() ,
the resultant IGIMF is indistinguishable from the input
IMF. Note that the cluster mass function is still intact.
,
the resultant IGIMF is indistinguishable from the input
IMF. Note that the cluster mass function is still intact.
Using a Kroupa (2001) IMF results in the green dot-dashed line in Fig. 3. The bend again is found at roughly the same stellar mass as for the Salpeter IMF. Deviations from this at lower mass are stronger, though, as the mean mass of a star in the Kroupa IMF is bigger than in a Salpeter IMF. Changing the upper stellar mass limit does not influence any of the results other than that the lines extend to higher stellar masses.
Comparing the calculations to the light grey dotted lines in Fig. 3 shows that all random sampling techniques give high-mass-end power-law indices of the IGIMF very close to -2.60, whereas the analytic sampling technique is slightly steeper, -2.67 and turns completely down close to the physical upper mass limit for stars (i.e. the mass of the cluster needs to become extremely high in order to sample a star with a mass very close to the upper mass limit).
4.2 The cluster mass function
In all randomly sampled realizations, the steepening becomes very
prominent at
m = 100.7 ![]() = 5
= 5 ![]() ,
the lower mass limit
for clusters. The analytically sampled case becomes steeper at lower
masses, as there the most massive stars in these low-mass clusters are
well below the cluster mass. We investigated how the steepening
depends on the imposed lower cluster mass limit and the steepness of the
cluster mass function.
,
the lower mass limit
for clusters. The analytically sampled case becomes steeper at lower
masses, as there the most massive stars in these low-mass clusters are
well below the cluster mass. We investigated how the steepening
depends on the imposed lower cluster mass limit and the steepness of the
cluster mass function.
In Fig. 4 we show the IGIMFs, as obtained with our
default random sampling model, for three different lower cluster mass
limits (1, 5 and 50 ![]() ,
for a CMF slope of -2.2) and three different
cluster mass function slopes (-1.8, -2.2 and -3.2 , for a lower
cluster mass limit of 5
,
for a CMF slope of -2.2) and three different
cluster mass function slopes (-1.8, -2.2 and -3.2 , for a lower
cluster mass limit of 5 ![]() ). The flattest CMF and highest minimum
cluster mass use samples of 106 clusters instead of 107 clusters. The
higher mass in clusters makes the IGIMF less sensitive to errors from
sampling statistics in stars.
). The flattest CMF and highest minimum
cluster mass use samples of 106 clusters instead of 107 clusters. The
higher mass in clusters makes the IGIMF less sensitive to errors from
sampling statistics in stars.
It can be clearly seen that the deviations of the IGIMF from a standard
Salpeter IMF start at the minimum cluster mass. Results therefore are
sensitively dependent on the cluster mass functions at very low cluster
masses. The steepness of the IGIMF depends on the power-law slope of the
cluster mass function. Changing the cluster mass function power-law
index from -2.2 into -3.2 (-4.2, not shown in the figure) makes the IGIMF slope steepen from -2.6
to -3.6 (-4.8). The steepening still occurs at the minimum allowed
cluster mass. A flatter CMF slope of -1.8 results in a much shallower
IGIMF compared to our standard case, with little deviations from the
input Salpeter (1955) IMF. We can also conclude
that as long as the lower mass limit of the CMF is higher than
the upper mass limit of the IMF, IGIMF effects are negligible. We
would like to emphasize that although we used a lower mass limit of the
CMF of 5 ![]() (i.e. considerably lower than the upper mass limit of the IMF), this
value as well as the shape of the CMF at masses below a few hundreds
solar masses is very uncertain due to a lack of observational data, even
in the Milky Way.
(i.e. considerably lower than the upper mass limit of the IMF), this
value as well as the shape of the CMF at masses below a few hundreds
solar masses is very uncertain due to a lack of observational data, even
in the Milky Way.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12967_f3.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg36.png)
|
Figure 3: The same as Fig. 2, but for every mass bin divided by the expected value for the input IMF. The IGIMFs presented in Fig. 2 are represented by the solid lines in various colours. The ``stop 50/50'' model is included as well. We also include the ``analytic sampling'' case (dotted line), the sampling of a specific number of stars based on the expected mean mass, limited by the cluster mass (black dashed) and unlimited (magenta dashed, going around the Salpeter line). The black dot-dashed line is the ``sorted sampling'' method of WK06. The realisation for a Kroupa (2001) IMF is shown in the green dot-dot-dot-dashed line (almost on top of the black solid (default) line). The light grey dotted lines with numbers are lines that would have the indicated power-law index in the IGIMF. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12967_f4.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg37.png)
|
Figure 4:
The same as Fig. 3, but now for variations
of the cluster mass function. We show our default (minimum mass 5 |
| Open with DEXTER | |
4.3 The 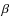 = 2 CMF
= 2 CMF
In Elmegreen (2006) it was claimed that in the case where the CMF is described by a power-law of ![]() ,
IGIMF effects vanish, making this a singular case in between our
,
IGIMF effects vanish, making this a singular case in between our ![]() and
and ![]() cases. In order to validate this result, we ran simulations with values for
cases. In order to validate this result, we ran simulations with values for ![]() close to and including 2. To address the behaviour of the
deviation of the IGIMF from the IMF, we plotted the deviation of the
IGIMF from the underlying IMF at two different stellar masses as a
function of
close to and including 2. To address the behaviour of the
deviation of the IGIMF from the IMF, we plotted the deviation of the
IGIMF from the underlying IMF at two different stellar masses as a
function of ![]() in Fig. 5. We used a minimum mass of 5
in Fig. 5. We used a minimum mass of 5 ![]() for the cluster CMF, no upper mass limit and plotted the results for m* = 10 and 100
for the cluster CMF, no upper mass limit and plotted the results for m* = 10 and 100 ![]() in bins of width
in bins of width
![]() .
We performed the exercise for our default sampling method at 13 different values of
.
We performed the exercise for our default sampling method at 13 different values of ![]() (i.e., with
(i.e., with
![]() ), and for seven different values with the ``sorted sampling'' technique from WK06 (i.e., with
), and for seven different values with the ``sorted sampling'' technique from WK06 (i.e., with
![]() ).
).
We found the results for ![]() to be non-singular and to follow the expected behaviour from its surrounding points. The vanishing effects found by Elmegreen (2006) were not reproduced in our simulations. In the Monte Carlo simulations described in Elmegreen (2006)
a small difference was already visible. In the intuitive analytic
section it is explained why there should be no difference. This
conclusion was based on the crucial statement that ``the probability of
forming a star of a particular mass is independent of cluster mass''.
This is only true for stars in clusters with masses higher than the
upper mass limit for stars. For clusters with lower total masses, the
situation is more complex: stars with masses higher than the total
cluster mass get assigned zero probability (unless one does not impose
a limit to the stellar mass equal to the cluster mass), while stars
with lower masses get higher probabilities to fulfil the IMF
normalisation. For any value of
to be non-singular and to follow the expected behaviour from its surrounding points. The vanishing effects found by Elmegreen (2006) were not reproduced in our simulations. In the Monte Carlo simulations described in Elmegreen (2006)
a small difference was already visible. In the intuitive analytic
section it is explained why there should be no difference. This
conclusion was based on the crucial statement that ``the probability of
forming a star of a particular mass is independent of cluster mass''.
This is only true for stars in clusters with masses higher than the
upper mass limit for stars. For clusters with lower total masses, the
situation is more complex: stars with masses higher than the total
cluster mass get assigned zero probability (unless one does not impose
a limit to the stellar mass equal to the cluster mass), while stars
with lower masses get higher probabilities to fulfil the IMF
normalisation. For any value of ![]() there is some number of clusters which will lack high mass stars, which makes
there is some number of clusters which will lack high mass stars, which makes ![]() a normal case without singular features. The claim by Elmegreen (2006) is correct only if the lower
limit of the CMF is higher than the maximum stellar mass, in agreement with our own findings.
a normal case without singular features. The claim by Elmegreen (2006) is correct only if the lower
limit of the CMF is higher than the maximum stellar mass, in agreement with our own findings.
We learn from Fig. 5
that choosing a value for the power-law index of the CMF of -2.2
instead of -2.0 produces a larger effect, as does the choice of
sampling method made by WK06 compared to our default method. The
observational support for ![]() justifies the use of
justifies the use of ![]() in the rest of this work.
in the rest of this work.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f5.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg42.png)
|
Figure 5:
The deviation at 10 and 100 |
| Open with DEXTER | |
4.4 Star formation rate dependent upper cluster mass limit
On purely statistical grounds a relation between the star formation rate
(SFR) and the mass of the most massive cluster in a galaxy is expected,
as long as the timescale to form a complete population of clusters is
fixed (see Maschberger & Kroupa 2007, they find a timescale of 10 Myr). This relation is expected to be linear.
However, Weidner et al. (2004) have found a relation between the SFR of a
galaxy and the mass of its most massive cluster that is slightly shallower
than linear:
In this section we will show Monte Carlo simulations with upper cluster mass limits which correspond to SFRs of 10-5 to 104
As galaxies with a very low SFR in general also have very low masses
(dwarf galaxies), we can expect to have more statistical (shot) noise in
low SFR samplings. In order to get a handle on the median IGIMF and the
68% (![]()
![]() )
confidence intervals we assumed that the galaxies
have formed stars for 10 Gyr, together with the SFR this gives a total
stellar mass. The CMF (with a lower mass cut-off of 5
)
confidence intervals we assumed that the galaxies
have formed stars for 10 Gyr, together with the SFR this gives a total
stellar mass. The CMF (with a lower mass cut-off of 5 ![]() and a
power-law index of -2.2) then sets the number of clusters drawn. For
the very low SFR runs, there were not so many clusters to be drawn
(10-5
and a
power-law index of -2.2) then sets the number of clusters drawn. For
the very low SFR runs, there were not so many clusters to be drawn
(10-5 ![]() yr
yr
![]() Gyr = 105
Gyr = 105 ![]() total stellar
mass). We ran 500 realizations of the lowest SFRs, gradually reducing
this number, as the 68% confidence intervals are very narrow already
for relatively low SFRs. The corresponding upper cluster mass limits
range from 10
1.08 = 12
total stellar
mass). We ran 500 realizations of the lowest SFRs, gradually reducing
this number, as the 68% confidence intervals are very narrow already
for relatively low SFRs. The corresponding upper cluster mass limits
range from 10
1.08 = 12 ![]() to 107.83
to 107.83 ![]() ,
so extending from extremely (maybe even unphysically) low star
formation rates and corresponding upper cluster mass limits to
extremely high SFR limits. Both limits are far beyond the range in
which the relation between SFR and maximum cluster mass has been
observed. We sampled the IMF with the method which samples up to a
total mass and removes the last drawn star if that brings the total
mass of stars closer to the predetermined cluster mass described
before (i.e., ``stop nearest'').
,
so extending from extremely (maybe even unphysically) low star
formation rates and corresponding upper cluster mass limits to
extremely high SFR limits. Both limits are far beyond the range in
which the relation between SFR and maximum cluster mass has been
observed. We sampled the IMF with the method which samples up to a
total mass and removes the last drawn star if that brings the total
mass of stars closer to the predetermined cluster mass described
before (i.e., ``stop nearest'').
In Fig. 6 we show the IGIMFs for the 19 different SFRs (solid lines). For simulations with a series of runs we show medians (in black) and 68% confidence intervals in colour. It appears that for a given CMF and sampling method the statistical variation around the median IGIMF is very small. Also, the high mass end of the IGIMF is steeper for lower SFRs, due to the lower upper cluster mass limit. With a lower upper cluster mass limit relatively more clusters form with a low mass. As the upper cluster mass limit increases, the variation in the IGIMF becomes smaller. This indicates that our simulations, without an upper limit, are good representatives for high SFR objects (galaxies), whereas for galaxies with a low SFR the IGIMFs are steeper. So for galaxies with a low SFR the effect will in reality be stronger than we indicate.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f6.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg46.png)
|
Figure 6:
SFR dependent IGIMFs, in which the SFR sets an upper cluster mass
limit, given by Eq. (6). We ran the lowest SFR models sufficiently
long to get converged confidence intervals which are shown by the coloured
regions around the solid line medians. For the higher SFR simulations, the
results are very close and the confidence intervals extremely narrow.
Therefore, we only plot the result of one simulation. The order is in a way that
the higher the star formation rate (and hence the upper cluster mass limit),
the shallower the IGIMF. Note that the highest SFR run is 104 |
| Open with DEXTER | |
In Bastian (2008) it was claimed that to reproduce the
relation between SFR and the maximum cluster luminosity, it is preferred
to have a Schechter-like CMF (i.e. a power-law with an exponential
cut-off above some mass) instead of a pure power-law. The typical mass
at which the CMF turns down exponential is a few times 106 ![]() .
As this mass is much higher than the highest stellar mass, the
precise shape of the cut-off is not expected to be important. An
exponential turn-down at that mass has a similar effect on the IGIMF to
truncating the CMF at that mass. For the lower limit to the cut-off
mass found by Bastian (2008) the SFR corresponding to their cut-off
mass, according to Eq. (6), would be 101.6
.
As this mass is much higher than the highest stellar mass, the
precise shape of the cut-off is not expected to be important. An
exponential turn-down at that mass has a similar effect on the IGIMF to
truncating the CMF at that mass. For the lower limit to the cut-off
mass found by Bastian (2008) the SFR corresponding to their cut-off
mass, according to Eq. (6), would be 101.6 ![]() yr-1. In Fig. 6 it can be seen that such IGIMFs are
hardly distinguishable from CMFs without upper cluster mass limits.
yr-1. In Fig. 6 it can be seen that such IGIMFs are
hardly distinguishable from CMFs without upper cluster mass limits.
4.5 Constructing IGIMFs from clustered and non-clustered star formation
The results described above are only valid if all stars are born in
clusters. The fraction of stars formed in clusters is a strongly
debated quantity nowadays. Different authors constrain the fraction of
stars formed in clusters in different and not necessarily comparable
ways. The main hindrance here is the definition of ``a cluster''. Young
clusters often get disrupted (sometimes called ``infant mortality'') on
time scales of about 107 yrs (Tutukov 1978; Kroupa et al. 2001; Lamers et al. 2005).
These young clusters may or may not have a stellar mass distribution
similar to clusters which survive their childhood. Also, stars may form
without ever being part of a ``cluster''. Numbers for the estimate of
the fraction of stars born in clusters vary from ![]()
![]() (Bastian 2008; Miller & Scalo 1978, and references therein) up
to 40% or higher as found in the comparison of cluster mass production for a
particular CMF power-law index by Piskunov et al. (2006).
Different authors used different definitions of what a
cluster/association is and found very different values for the fraction
of stars that is a born in a cluster-like environment (see e.g. also Piskunov et al. 2008; Lada & Lada 2003; Porras et al. 2003; Carpenter 2000; Megeath et al. 2005).
(Bastian 2008; Miller & Scalo 1978, and references therein) up
to 40% or higher as found in the comparison of cluster mass production for a
particular CMF power-law index by Piskunov et al. (2006).
Different authors used different definitions of what a
cluster/association is and found very different values for the fraction
of stars that is a born in a cluster-like environment (see e.g. also Piskunov et al. 2008; Lada & Lada 2003; Porras et al. 2003; Carpenter 2000; Megeath et al. 2005).
The ``real IGIMF'' (i.e. the true distribution of stellar masses at
birth for a whole galaxy) can be straightforwardly estimated from the
IGIMF from clustered star formation (i.e. the results given above), and
the IMF from stars born in isolation. If we denote the distribution of
initial masses in the field as IMF![]() ,
the IGIMF from clustered star formation (i.e. the results obtained above) as IGIMF
,
the IGIMF from clustered star formation (i.e. the results obtained above) as IGIMF![]() and the total IGIMF (the pdf of initial masses of all stars in a galaxy) as IGIMF
and the total IGIMF (the pdf of initial masses of all stars in a galaxy) as IGIMF![]() ,
we can simply write at any given stellar mass
,
we can simply write at any given stellar mass
where f is the fraction of the stellar mass that is born in clusters, assuming that this fraction f is independent of stellar mass and that the mass distributions in the right-hand side of the equation refer to distributions which are both well sampled. In practice, this means that the total IGIMFs will end up in between the IGIMFs described above and the underlying IMF, weighed by the fraction of clustered star formation (so lines in Figs. 3 and 4 will end up in between the horizontal line and the shown IGIMFs).
Note that if the second term in the right-hand side of Eq. (7) is large, IGIMF effects may well become negligible, or at least far less significant than indicated in the rest of this paper.
5 The number of O-stars in the Milky Way
One way to judge between the several IGIMFs (or judging on the importance of the IGIMF effect) would be high mass star counts by upcoming surveys like GAIA (e.g. Perryman et al. 2001).
In order to estimate how many O-stars will be observed by GAIA, we
will here undertake the following exercise, in which we keep things as simple
as possible. We assume that the IGIMFs described earlier are perfectly
sampled (i.e. there are no sampling issues apart from those that make
up the IGIMFs), that the SFR of the Milky Way has been constant for the
last 10 Myr, which we will assume to be the lifetime of O-stars.
Furthermore, we assume that the fraction of all O-stars in the Milky
Way, observed by GAIA, is the same as the fraction of all stars
together (i.e. ![]() 10%). This last number is very uncertain. O-stars
are very bright and would therefore be visible to larger distances (the
GAIA survey will be magnitude limited). If, however, all O-stars form
in the disc, the extinction towards them will be typically higher than
for stars above and below the disk. A fraction of the O-stars may be
runaway stars, launched by multiple body interactions in young star
clusters, which can bring them from the disk into less dusty regions
(O-stars formed in isolation will typically not get far out of the
disk, as with a random velocity of a few times 10 km s-1, they will not
get much further than a few parsecs away from the disc plane they were
formed in). The observed number of O-stars is then given by
10%). This last number is very uncertain. O-stars
are very bright and would therefore be visible to larger distances (the
GAIA survey will be magnitude limited). If, however, all O-stars form
in the disc, the extinction towards them will be typically higher than
for stars above and below the disk. A fraction of the O-stars may be
runaway stars, launched by multiple body interactions in young star
clusters, which can bring them from the disk into less dusty regions
(O-stars formed in isolation will typically not get far out of the
disk, as with a random velocity of a few times 10 km s-1, they will not
get much further than a few parsecs away from the disc plane they were
formed in). The observed number of O-stars is then given by
in which the SFR is that of the Milky Way, averaged over
Table 1:
The factor
![]() from Eq. (8) for Salpeter and all our IGIMFs.
from Eq. (8) for Salpeter and all our IGIMFs.
It is now well established that the real IMF in star forming regions is not Salpeter-like, but bends over towards lower masses (e.g. Chabrier 2003; Kroupa 2001). The difference here mainly lies in the number of very low mass stars, for which our IGIMFs are all indistinguishable from the underlying IMF. The fraction of O-stars in IGIMFs with other underlying IMFs will be different though, as the fraction of very low mass stars is lower than in Salpeter, making the fraction of high mass stars higher. For example, the numbers in a Kroupa or Chabrier IMF will be about 1.6 times higher (the exact values of the ratio depends on the sampling methods and cluster mass functions, but do not vary much). To illustrate this, we ran a selection of our sampling methods also for an underlying Kroupa (2001) IMF, as displayed in the third column of Table 1. The last column gives the ratio between the results for an underlying Kroupa IMF and an underlying Salpeter IMF. From the ratios (for rather ``extreme'' sampling methods) it can be seen that they do not vary much from one sampling method to the other.
From the numbers in Table 1 it is clear that in principle several IGIMFs may be ruled out by the GAIA survey. The difficulty in judging between several IMFs will be in the other numbers quoted in Eq. (8). Some of the extreme IGIMFs can most probably be ruled out with less exact knowledge of the other important parameters. We stress here that the given numbers are only then the number of O-stars observed by GAIA, if the underlying IMF is Salpeter and if the cluster mass functions assumed are the true mass distributions of clumps of forming stars (as here they are heavily extrapolated from the observed mass ranges of young clusters).
5.1 Clusters consisting of one (O-) star
Using our sampling methods we could form clusters that consist of only
one star. The question whether this is important or not was raised by
de Wit et al. (2004,2005). We track here a) the fraction of clusters that
consist of a single star, b) the fraction of clusters that consist of a
single O-star (m>17 ![]() ,
see de Wit et al. 2005) and c) the fraction of
clusters for which the most massive star is an O-star, which contains
more than half the total cluster mass (we call these ``O-star
dominated'' clusters). The results are shown in
Fig. 7. We plot probability distribution
functions (PDFs) for the fraction of clusters that have the indicated
properties in a cluster population. We ran ten thousand realisations of
cluster populations and counted for example how many clusters were
actually single O-stars and divide that number by the total number of
clusters. The distribution of these fractions is what is plotted. So,
the peak of blue dot-dashed line shows that out of all ten thousand cluster
populations about 0.5-0.6% of their clusters are O-star
dominated. PDFs that do not add up to 1, like the fraction of clusters
that consist of exactly one O-star, indicate that the rest of the cluster
populations had zero single O-stars in them.
,
see de Wit et al. 2005) and c) the fraction of
clusters for which the most massive star is an O-star, which contains
more than half the total cluster mass (we call these ``O-star
dominated'' clusters). The results are shown in
Fig. 7. We plot probability distribution
functions (PDFs) for the fraction of clusters that have the indicated
properties in a cluster population. We ran ten thousand realisations of
cluster populations and counted for example how many clusters were
actually single O-stars and divide that number by the total number of
clusters. The distribution of these fractions is what is plotted. So,
the peak of blue dot-dashed line shows that out of all ten thousand cluster
populations about 0.5-0.6% of their clusters are O-star
dominated. PDFs that do not add up to 1, like the fraction of clusters
that consist of exactly one O-star, indicate that the rest of the cluster
populations had zero single O-stars in them.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f7.ps}
\par\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg57.png)
|
Figure 7:
Distribution functions of clusters consisting of single
stars (black solid line), single O-stars (red dashed line), and
clusters dominated by O-stars (i.e. consisting of an O-star that has
more than half of the cluster mass, blue dash-dotted line) in the
default sampling method, in a cluster population with a power-law
CMF with index -2.2 and a lower cluster mass limit of 5 |
| Open with DEXTER | |
For the default sampling method, there are very few
clusters that consist of only one star, only one in ![]() 104. The
number of clusters in which this one single star is an O-star is again
an order of magnitude smaller, with a median of
104. The
number of clusters in which this one single star is an O-star is again
an order of magnitude smaller, with a median of
![]() .
This factor ten in between is less than the ratio of the number of
O-stars
to the number of all other stars, because it is more likely that one is
close to the mass of the cluster if the star is an O-star than
when it is less massive. The fraction of clusters that is dominated by
an O-star (i.e. containing an O-star with at least half the cluster
mass) shows a sharply peaked distribution function around 0.56%.
.
This factor ten in between is less than the ratio of the number of
O-stars
to the number of all other stars, because it is more likely that one is
close to the mass of the cluster if the star is an O-star than
when it is less massive. The fraction of clusters that is dominated by
an O-star (i.e. containing an O-star with at least half the cluster
mass) shows a sharply peaked distribution function around 0.56%.
In the sorted sampling method of WK06, the fraction of clusters
containing a single (O-) star is zero by construction: the first
number of clusters to be drawn is calculated by dividing the total
cluster mass aimed for, divided by the mean stellar mass in that
cluster according to the appropriate IMF. This mean mass is more than
one order of magnitude smaller than the assumed lower cluster mass
limit. Therefore, of the order of ten stars or more are always drawn.
If the cluster mass is exceeded already with the first drawing of
stars (for instance, if there is a really massive O-star drawn, it has on
its own as much mass as the rest of the stars or more), then at
most one star is removed, resulting in a cluster with at least of the
order of ten stars. The number of O-star dominated clusters is
therefore also much lower: the chance of having an O-star with half the
mass of the cluster or more while not going far over the cluster mass
(far enough to let that O-star be removed) is small. Ten stars will
mostly have an average mass that is close to the average mass of stars
according to the IMF. The one dominating O-star then is several solar
masses too massive, making it very likely to be removed. The median
fraction of O-star dominated clusters is
![]() .
.
5.2 The number of single O-stars
In their paper, de Wit et al. (2005) specifically looked at the fraction of
all O-stars which are single, i.e. not part of a detected cluster. They
claimed very low mass clusters can be detected, so that these are
really O-stars without a surrounding cluster. Nevertheless they are
only sensitive to very low mass clusters if these clusters are very
concentrated (i.e. small). Clusters of very low mass are very easily
disrupted, and extrapolating the results of Lamers & Gieles (2006) to
lower mass clusters (by about an order of magnitude), the typical
dissolution time of clusters is given by
![]() Gyr, resulting in O-star lifetimes for
Gyr, resulting in O-star lifetimes for ![]() 10
10 ![]() clusters. Therefore it is very likely that if O-stars
live in very low mass clusters, the clusters are in the process of
being completely dissolved at the time of observation of the cluster.
If not completely disrupted yet, the cluster will have dispersed
already significantly, making it harder to detect the underlying
cluster than assumed by de Wit et al. (2005).
clusters. Therefore it is very likely that if O-stars
live in very low mass clusters, the clusters are in the process of
being completely dissolved at the time of observation of the cluster.
If not completely disrupted yet, the cluster will have dispersed
already significantly, making it harder to detect the underlying
cluster than assumed by de Wit et al. (2005).
We use this argument to claim that our ``O-star dominated'' clusters would also probably be observed as single O-stars. Together with the analysis of the previous section, we can now investigate which fraction of all O-stars would be observed to live outside star clusters (without taking runaway OB stars into account). For the default sampling mechanism 11% of the O-stars would be observed to live outside clusters (if all O-star dominated clusters are detected as single O-stars). For the sorted sampling method this is 0.24%. The difference of course is mainly caused by the different fraction of O-star dominated clusters.
de Wit et al. (2005) found that ![]() % of the O-stars in the Galaxy
cannot be traced back to a formation in a cluster or OB-association.
Although this number is smaller than what we found, taking into
consideration that we did include very low mass (and probably)
dispersed clusters it is legitimate to correct our result by a
factor of a few, bringing the results into nice agreement. Increasing the
number of single O-stars in the ``sorted sampling'' method is much
harder to justify, so we conclude that this method significantly
underproduces single O-stars by a factor of 10-20.
% of the O-stars in the Galaxy
cannot be traced back to a formation in a cluster or OB-association.
Although this number is smaller than what we found, taking into
consideration that we did include very low mass (and probably)
dispersed clusters it is legitimate to correct our result by a
factor of a few, bringing the results into nice agreement. Increasing the
number of single O-stars in the ``sorted sampling'' method is much
harder to justify, so we conclude that this method significantly
underproduces single O-stars by a factor of 10-20.
6 Galaxy evolution models
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[angle=270,width=7cm,cli...
...degraphics[angle=270,width=7cm,clip]{12967_8d.ps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg62.png)
|
Figure 8: The impact of various IGIMFs on the time evolution of integrated Sd galaxy colours. Top row: U-B colour, bottom row: B-V colour. Left column: IGIMFs for various sampling methods, right column: IGIMFs for various CMF parameters. Shown are the differences between models with different IGIMFs and the corresponding model with a Salpeter (1955) IMF. At the highest ages, average colours (and their standard deviation) for Sd galaxies from the HyperLeda database are shown. |
| Open with DEXTER | |
We used models with the following input physics:
- isochrones: from the Padova group (Bertelli et al. 1994 with subsequent updates concerning the TP-AGB phase);
- spectral library: BaSeL 2.2 (Lejeune et al. 1998,1997);
- SFH as a function of Hubble type: following Sandage (1986),
with parameters adjusted to simultaneously reproduce a range of
observations for galaxies of different Hubble types (for details see
Kotulla et al. 2009).
- an Sd galaxy is modelled with a constant SFR;
- an E galaxy with an exponentially declining SFR with a 1/e decline time of 1 Gyr;
- Sa-Sc galaxies are modelled with SFRs depending on the available gas mass at a given time (similar to the Kennicutt-Schmidt law, see Kennicutt 1998b), resulting in approximately exponentially declining SFR with 1/e decline times of 3.5 Gyr (Sa galaxy), 6 Gyr (Sb galaxy) and 10.5 Gyr (Sc galaxy);
- the gas mass-dependence of the Sa-Sc galaxies' SFR results in slight changes between models with Salpeter (1955) IMF and the various IGIMFs, with the IGIMF models having slightly lower SFRs by up to 5% for our standard IGIMF model (``stop nearest'') and up to 10% for extreme cases;
- stellar yields: explosive nucleosynthesis yields are taken from
Woosley & Weaver (1995) for high-mass stars (M > 10
 )
and
from van den Hoek & Groenewegen (1997) for stars with lower masses. In addition,
SN Ia yields from Nomoto et al. (1997) are included (only total metallicity
is traced, not individual elements);
)
and
from van den Hoek & Groenewegen (1997) for stars with lower masses. In addition,
SN Ia yields from Nomoto et al. (1997) are included (only total metallicity
is traced, not individual elements);
- stellar MF: we use the various IGIMFs determined in this work.
- the IGIMF does not change with time or SFR (taking into account the SFR-dependent effects discussed in Sect. 4.4 would only strengthen the deviations, so our results are lower limits for the impact of the IGIMF effect);
- the IGIMF does not change with metallicity (no such dependence is known or expected for Population I or Population II stars and star clusters);
- no infall or outflow of material is used (but also not needed to reproduce a range of galaxy properties correctly, see Kotulla et al. 2009), likewise we neglect galaxy interactions;
- we assume instantaneous mixing and cooling of ejected material with the entire available gas reservoir (however, the SFH parameters are adjusted to reproduce available gas metallicities as a function of the galaxies' Hubble type at the present day);
- we aim at modelling L* galaxies of the respective Hubble type, hence neglect any magnitude-metallicity relation.
6.1 Integrated photometry of galaxies
In Fig. 8 we compare our Sd galaxy models using
various IGIMFs with the standard model using the input
Salpeter (1955) IMF (models for other Hubble types show very similar
behaviour). On the right side (i.e. plotted at old ages) we show
average colours and their standard deviation from data obtained from
the HyperLeda![]() database
(Paturel et al. 2003), subdivided according to their morphological type. In
each of these plots, the intrinsic scatter within the morphological
type class well exceeds the deviations introduced by the different
IGIMFs. Therefore we do not expect that IGIMF variations can be
constrained from integrated photometry of galaxies.
database
(Paturel et al. 2003), subdivided according to their morphological type. In
each of these plots, the intrinsic scatter within the morphological
type class well exceeds the deviations introduced by the different
IGIMFs. Therefore we do not expect that IGIMF variations can be
constrained from integrated photometry of galaxies.
6.2 Chemical enrichment in galaxies from different IGIMFs
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12967f9.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg65.png)
|
Figure 9: The impact of various IGIMFs on the relation between available gas mass and gas metallicity (e.g. chemical enrichment) for Sd galaxies. Top panel: IGIMFs for various sampling methods. Bottom panel: IGIMFs for various CMF parameters. The points mark estimates from observations, see text for details. The red hashed area is the region covered using various individual metallicities instead of the ``chemically consistent'' modelling and a Salpeter (1955) IMF. It represents a worst-case uncertainty range. |
| Open with DEXTER | |
To our best knowledge, there is no study which determines both gas fractions and gas metallicities for a large sample of galaxies in a consistent way. We therefore gathered data on galactic gas masses from Huchtmeier (1989) and Karachentsev et al. (1999), while for the gas metallicities we considered the catalogues by Kewley et al. (2005), Nagao et al. (2006), and Izotov et al. (2007). These catalogues were not only chosen for their (comparably) large sample sizes, but also for their diversity in the galaxy populations they address. Each of these samples has its own intrinsic biases and limitations. Huchtmeier (1989) and Nagao et al. (2006) are more literature compilation papers. The sample by Kewley et al. (2005) intentionally contains galaxies of all Hubble types with a wide range of properties, the Karachentsev et al. (1999) sample is volume-limited, and Izotov et al. (2007) considers specifically low-metallicity H II regions in nearby dwarf galaxies. We supplemented the catalogue information with data from the HyperLeda1 database (Paturel et al. 2003), to have an as uniform as possible determination of Hubble type and absolute luminosity for the sample galaxies. From these data we estimate the average gas fractions and gas metallicities for the galaxy samples. Where multiple observations for a given galaxy were available, we included all of them individually, to access the uncertainties more realistically and to average out metallicity gradients in a single galaxy. In Table 2 we present the derived average values for the individual and the combined samples for five different galaxy types.
Table 2: Average gas properties and integrated galaxy colours for various literature galaxy samples.
From Table 2 one can easily see the non-homogeneity of the samples. The multitude of biases and selection effects hampers a straightforward comparison of these observational data with our models. A dedicated survey of a large number of L* galaxies ( GALEV attempts to model L* galaxies, and therefore neglects galaxy mass-dependent effects!) for the different Hubble types, both in terms of gas fraction and in terms of gas metallicity, with a reliable estimate of the galaxies' Hubble types, will be needed to provide direct calibration values for our (and others) galaxy evolution models.
In Fig. 9 we present gas properties for GALEV models of Sd galaxies, based on the various IGIMFs (equivalent plots for galaxies of other Hubble types appear very similar). We included the data point corresponding to the combined data sets in Table 2. As uncertainties we plotted either the scatter for a given property within the combined sample of Sd galaxies, or the distance to the most deviating mean of any subsample, whichever was larger.
Based on the large spread in the observed gas fractions it is hard to constrain IGIMF models with these data. Future and more homogeneous samples will be helpful, as the spread in observed metallicities is smaller than or at most comparable to the difference arising from different IGIMFs.
7 Conclusions
We have conducted a suite of numerical experiments to investigate how the steepening of the IGIMF depends on the sampling method and the assumed cluster mass function. Hereby we extended the variations already studied by WK06. We found that, unless the maximum occurring stellar mass is not limited by the cluster mass, or the minimum cluster mass is higher than the maximum stellar mass, the IGIMF is always steeper at the high-mass end than the input IMF, assuming that stars all form in clusters and that these clusters follow a power-law CMF which extends down to masses well below the upper mass limit for stars. If there are many stars formed in a non-clustered environment (see Eq. (7)) or the CMF does not extend to these low masses (or turns over and peaks at higher masses), IGIMF effects are much smaller and possibly even become negligible. The amount of steepening and the mass where deviations set in depend on the sampling method and the adopted cluster mass function:
- The numerical method of sampling is important. While all random techniques result in the same high-mass slope (for constant CMF slope), the onset of deviations occurs at different stellar masses, showing a slight steepening already at stellar masses below the lower cluster mass limit.
- The slope of the cluster mass function as well as its lower limit
are very important.
The index of the cluster mass function sets the steepness of the IGIMF
at the high mass end: a steeper cluster mass function results in a
steeper IGIMF. Varying the CMF power-law index in the range
[-1.8, -2.2,
-3.2] results in IGIMF slopes at the high mass end of approximately
[-2.4, -2.6, -3.6].
The observationally ill-constrained lower cluster mass limit sets the mass at which the steepening sets
in, i.e., the IGIMF becomes much steeper from
 .
At slightly lower masses there is a very small deficiency
of stars as compared to the input IMF. The magnitude of this
discrepancy depends on the sampling method. Contrary to results by Elmegreen (2006), we do not find the
.
At slightly lower masses there is a very small deficiency
of stars as compared to the input IMF. The magnitude of this
discrepancy depends on the sampling method. Contrary to results by Elmegreen (2006), we do not find the 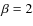 CMF to be singular.
CMF to be singular.
Our default sampling results indicate that ![]() 11% of the
O-stars in the Galaxy will be observed to be separate from any cluster
environment, in nice agreement with results of de Wit et al. (2005). The
sorted sampling method of WK06 strongly underproduces this number.
11% of the
O-stars in the Galaxy will be observed to be separate from any cluster
environment, in nice agreement with results of de Wit et al. (2005). The
sorted sampling method of WK06 strongly underproduces this number.
However, current knowledge, both observationally and theoretically, of the very formation processes of (especially massive) stars in star clusters (see e.g. high-mass star formation from high-mass cloud cores (Krumholz et al. 2005) vs competitive accretion (Bonnell et al. 2004)) prevents us from the conclusion as to which sampling method is favoured by nature.
We conducted numerical experiments using the GALEV evolutionary synthesis package, which self-consistently follows the photometric and chemical history of various idealised isolated galaxy models. The conclusions we draw on photometry and chemical enrichment resulting from our IGIMFs as compared to the standard IMFs can be summarised as follows:
- 1.
- Integrated photometry is likely not a good tracer of IGIMF variations, since differences are smaller than the intrinsic galaxy-to-galaxy scatter for a given morphological type.
- 2.
- Chemical enrichment is a better tracer, as it is directly linked to the number of massive stars, however, observations are rare and cover only small sample sizes. Once the (systematic and random) uncertainties in determining gas mass fractions and metallicities are well understood, these quantities may be able to be the deciding factor between several sampling methods (at least the ones with the most extreme deviations from the underlying IMF).
It is a pleasure to thank the referee, John Scalo, for a very helpful and thorough report that greatly improved the paper. We kindly thank Nate Bastian, Pavel Kroupa, Carsten Weidner and Simon Goodwin for helpful comments on an early version of the manuscript, as well as Ralf Kotulla for reading and discussing details of the GALEV models. We acknowledge the usage of the HyperLeda database (http://leda.univ-lyon1.fr).
References
- Bastian, N. 2008, MNRAS, 390, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS] [Google Scholar]
- Bicker, J., Fritze-v. Alvensleben, U., Möller, C. S., & Fricke, K. J. 2004, A&A, 413, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnell, I. A., Vine, S. G., & Bate, M. R. 2004, MNRAS, 349, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Briceño, C., Luhman, K. L., Hartmann, L., Stauffer, J. R., & Kirkpatrick, J. D. 2002, ApJ, 580, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2000, AJ, 120, 3139 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., Anders, P., Bastian, N., et al. 2003, MNRAS, 343, 1285 [NASA ADS] [CrossRef] [Google Scholar]
- de Wit, W. J., Testi, L., Palla, F., Vanzi, L., & Zinnecker, H. 2004, A&A, 425, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Wit, W. J., Testi, L., Palla, F., & Zinnecker, H. 2005, A&A, 437, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dib, S., Shadmehri, M., Padoan, P., et al. 2010, MNRAS, accepted [arXiv:0908.4522] [Google Scholar]
- Elmegreen, B. G. 2006, ApJ, 648, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Gieles, M., Larsen, S. S., Bastian, N., & Stein, I. T. 2006a, A&A, 450, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieles, M., Larsen, S. S., Scheepmaker, R. A., et al. 2006b, A&A, 446, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodwin, S. P., & Pagel, B. E. J. 2005, MNRAS, 359, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Haas, M. R., Gieles, M., Scheepmaker, R. A., Larsen, S. S., & Lamers, H. J. G. L. M. 2008, A&A, 487, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hakobyan, A. A., Mamon, G. A., Petrosian, A. R., Kunth, D., & Turatto, M. 2009, A&A, 508, 1259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huchtmeier, O.-G., R. W. K. 1989, A General Catalog of HI Observations of Galaxies. The Reference Catalog., ed. O.-G. W. K. Huchtmeier, Richter [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasinska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., & Huchtmeier, W. K. 1999, A&AS, 139, 97 [Google Scholar]
- Kennicutt, Jr., R. C. 1998a, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, Jr., R. C. 1998b, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Jansen, R. A., & Geller, M. J. 2005, PASP, 117, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kotulla, R., Fritze, U., Weilbacher, P., & Anders, P. 2009, MNRAS, 396, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Klein, R. I. 2005, Nature, 438, 332 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., & Gieles, M. 2006, A&A, 455, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamers, H. J. G. L. M., Gieles, M., Bastian, N., et al. 2005, A&A, 441, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsen, S. S. 2002, AJ, 124, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, S. S. 2009, A&A, 494,539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 [Google Scholar]
- Maschberger, T., & Clarke, C. J. 2008, MNRAS, 391, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Maschberger, T., & Kroupa, P. 2007, MNRAS, 379, 34 [NASA ADS] [CrossRef] [Google Scholar]
- McCrady, N., & Graham, J. R. 2007, ApJ, 663, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Flaherty, K. M., Hora, J., et al. 2005, in Massive Star Birth: A Crossroads of Astrophysics, ed. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 383 [Google Scholar]
- Miller, G. E., & Scalo, J. M. 1978, PASP, 90, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Maiolino, R., & Marconi, A. 2006, A&A, 459, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Iwamoto, K., Nakasato, N., et al. 1997, Nuclear Phys. A, 621, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Paturel, G., Petit, C., Prugniel, P., et al. 2003, A&A, 412, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pflamm-Altenburg, J., & Kroupa, P. 2008, Nature, 455, 641 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pflamm-Altenburg, J., Weidner, C., & Kroupa, P. 2007, ApJ, 671, 1550 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, A. E., Kharchenko, N. V., Röser, S., Schilbach, E., & Scholz, R. 2006, A&A, 445, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, A. E., Kharchenko, N. V., Schilbach, E., et al. 2008, A&A, 487, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porras, A., Christopher, M., Allen, L., et al. 2003, AJ, 126, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Calura, F., & Kroupa, P. 2009, A&A, 499, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sandage, A. 1986, A&A, 161, 89 [NASA ADS] [Google Scholar]
- Skillman, E. D., Côté, S., & Miller, B. W. 2003, AJ, 125, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A. V. 1978, A&A, 70, 57 [NASA ADS] [Google Scholar]
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidner, C., & Kroupa, P. 2004, MNRAS, 348, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2005, ApJ, 625, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 (WK06) [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Larsen, S. S. 2004, MNRAS, 350, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Whitmore, B. C. 2003, in A Decade of Hubble Space Telescope Science, 153 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., & Fall, S. M. 1999, ApJ, 527, L81 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Footnotes
- ... HyperLeda
![[*]](/icons/foot_motif.png)
- http://leda.univ-lyon1.fr/
All Tables
Table 1:
The factor
![]() from Eq. (8) for Salpeter and all our IGIMFs.
from Eq. (8) for Salpeter and all our IGIMFs.
Table 2: Average gas properties and integrated galaxy colours for various literature galaxy samples.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f1.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg32.png)
|
Figure 1:
The fraction of clusters per unit |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f2.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg35.png)
|
Figure 2: The IGIMF for randomly sampled stars in clusters until (1) the next star would overshoot the cluster mass (dashed), (2) a mass nearest to the cluster mass is reached (dotted), or (3) one star crosses the cluster mass (dot-dashed). The solid line is the input Salpeter IMF. The value on the vertical axis is the fraction of all the stars that are in that particular mass bin. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12967_f3.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg36.png)
|
Figure 3: The same as Fig. 2, but for every mass bin divided by the expected value for the input IMF. The IGIMFs presented in Fig. 2 are represented by the solid lines in various colours. The ``stop 50/50'' model is included as well. We also include the ``analytic sampling'' case (dotted line), the sampling of a specific number of stars based on the expected mean mass, limited by the cluster mass (black dashed) and unlimited (magenta dashed, going around the Salpeter line). The black dot-dashed line is the ``sorted sampling'' method of WK06. The realisation for a Kroupa (2001) IMF is shown in the green dot-dot-dot-dashed line (almost on top of the black solid (default) line). The light grey dotted lines with numbers are lines that would have the indicated power-law index in the IGIMF. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12967_f4.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg37.png)
|
Figure 4:
The same as Fig. 3, but now for variations
of the cluster mass function. We show our default (minimum mass 5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f5.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg42.png)
|
Figure 5:
The deviation at 10 and 100 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f6.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg46.png)
|
Figure 6:
SFR dependent IGIMFs, in which the SFR sets an upper cluster mass
limit, given by Eq. (6). We ran the lowest SFR models sufficiently
long to get converged confidence intervals which are shown by the coloured
regions around the solid line medians. For the higher SFR simulations, the
results are very close and the confidence intervals extremely narrow.
Therefore, we only plot the result of one simulation. The order is in a way that
the higher the star formation rate (and hence the upper cluster mass limit),
the shallower the IGIMF. Note that the highest SFR run is 104 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12967_f7.ps}
\par\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg57.png)
|
Figure 7:
Distribution functions of clusters consisting of single
stars (black solid line), single O-stars (red dashed line), and
clusters dominated by O-stars (i.e. consisting of an O-star that has
more than half of the cluster mass, blue dash-dotted line) in the
default sampling method, in a cluster population with a power-law
CMF with index -2.2 and a lower cluster mass limit of 5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[angle=270,width=7cm,cli...
...degraphics[angle=270,width=7cm,clip]{12967_8d.ps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg62.png)
|
Figure 8: The impact of various IGIMFs on the time evolution of integrated Sd galaxy colours. Top row: U-B colour, bottom row: B-V colour. Left column: IGIMFs for various sampling methods, right column: IGIMFs for various CMF parameters. Shown are the differences between models with different IGIMFs and the corresponding model with a Salpeter (1955) IMF. At the highest ages, average colours (and their standard deviation) for Sd galaxies from the HyperLeda database are shown. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12967f9.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa12967-09/Timg65.png)
|
Figure 9: The impact of various IGIMFs on the relation between available gas mass and gas metallicity (e.g. chemical enrichment) for Sd galaxies. Top panel: IGIMFs for various sampling methods. Bottom panel: IGIMFs for various CMF parameters. The points mark estimates from observations, see text for details. The red hashed area is the region covered using various individual metallicities instead of the ``chemically consistent'' modelling and a Salpeter (1955) IMF. It represents a worst-case uncertainty range. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.