EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A45 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A45
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/200811000
Published online 30 March 2010
A&A 512, A45 (2010)

Evidence of a massive planet candidate orbiting the young active K5V star BD+20 1790[*],[*]

M. Hernán-Obispo1 - M. C. Gálvez-Ortiz2 - G. Anglada-Escudé3,4 - S. R. Kane5 - J. R. Barnes2 - E. de Castro1 - M. Cornide1

1 - Dpto. de Astrofísica y Ciencias de la Atmósfera, Facultad de Física, Universidad Complutense de Madrid, Avda. Complutense s/n, 28040, Madrid, Spain
2 - Centre for Astrophysics Research, Science & Technology Research Institute, University of Hertfordshire, College Lane, Hatfield, Hertfordshire AL10 9AB, UK
3 - Department of Terrestrial Magnetism, Carnegie Institution of Washington, 5241 Broad Branch Road, NW, Washington, DC 20015-1305, USA
4 - Departament d'Astronomia i Meteorologia. Universitat de Barcelona, Martí i Franqués 1, Barcelona, 08028. Spain
5 - NASA Exoplanet Science Institute, Caltech, MS 100-22, 770 South Wilson Avenue, Pasadena, CA 91125, USA

Received 19 September 2008 / Accepted 4 December 2009

Abstract
Context. BD+20 1790 is a young active, metal-rich, late-type K5Ve star. We have undertaken a study of stellar activity and kinematics for this star over the past few years. Previous results show a high level of stellar activity, with the presence of prominence-like structures, spots on the surface, and strong flare events, despite the moderate rotational velocity of the star. In addition, radial velocity variations with a semi-amplitude of up to 1 km s-1 were detected.
Aims. We investigate the nature of these radial velocity variations, in order to determine whether they are due to stellar activity or the reflex motion of the star induced by a companion.
Methods. We have analysed high-resolution echelle spectra by measuring stellar activity indicators and computing radial velocity (RV) and bisector velocity spans. Two-band photometry was also obtained to produce the light curve and determine the photometric period.
Results. Based upon the analysis of the bisector velocity span, as well as spectroscopic indices of chromospheric indicators, Ca  II H & K, H$\alpha $, and taking the photometric analysis into account, we report that the best explanation for the RV variation is the presence of a substellar companion. The Keplerian fit of the RV data yields a solution for a close-in massive planet with an orbital period of 7.78 days. The presence of the close-in massive planet could also be an interpretation for the high level of stellar activity detected. Since the RV data are not part of a planet search programme, we can consider our results as a serendipitous evidence of a planetary companion. To date, this is the youngest main sequence star for which a planetary candidate has been reported.

Key words: stars: activity - stars: late-type - stars: individual BD+20 1790 - planetary systems

1 Introduction

Since the detection of the first planet orbiting a main sequence star, 51 Peg (Mayor & Queloz 1995), the radial velocity (RV) method has become the most successful technique for detecting exoplanets because the vast majority have thus far been discovered in this way (Udry & Santos 2007). This method is especially efficient for giant planets in close-in orbits owing to the high radial velocities they induce in the host star. The use of the RV technique to detect exoplanets around young and active stars requires, in addition, a careful characterization of stellar activity. An active region on the stellar surface can produce changes in the shape of the spectral lines, thus inducing a subsequent temporal variation of the RVs that may mimic a planetary reflex motion with a period equal to the rotational period of the star (Saar & Donahue 1997). Some cases of false planetary detections are provided by Queloz et al. (2001), Bouvier et al. (2007), Huerta et al. (2008), and Huélamo et al. (2008). Thus the challenge in using the RV technique to detect young planets lies in disentangling the increased levels of stellar activity of young stars from the RV signals of the planets.

There is an absence of planets detected around stars younger than 100 Myr (Setiawan et al. 2007; Setiawan et al. 2008). Most RV searches for planetary companions have focused mainly on stars older than 1 Gyr. Young stars have been omitted from RV surveys until recently. Nevertheless, there has been strong effort by several groups to target young objects in their RV searches of planetary companions. For example, surveys are being carried out to focus on both nearby associations of young stars and moving groups with ages ranging 10-500 Myr. Examples of this include $\beta $ Pic (12 Myr), UMa association (300 Myr), Pleiades (100 Myr), IC 2391 (35 Myr), Hyades (700 Myr), Taurus association (2 Myr), ChaI (2 Myr), TWA (10 Myr) (Paulson et al. 2004; Paulson & Yelda 2007; Esposito et al. 2006; Huerta et al. 2007; Setiawan et al. 2007; Setiawan et al. 2008; Prato et al. 2008). Positive identification of planetary signatures from these efforts are few, with only two candidates to date: HD 70573 (Setiawan et al. 2007) and the controversial TW Hya (Setiawan et al. 2008). Planets orbiting young stars are particularly valuable as they enable us to investigate some of the critical questions about the formation of both stellar and planetary systems. How and at what stage planets form, what the planet formation mechanism is, and how they evolve are important questions and the study of young planetary systems will help answer them. In this paper we report strong evidence of a planetary candidate orbiting the young and active K5V star BD+20 1790. Section 2 is an overview of the properties and our previous studies of this star. The observational strategy and data analysis are presented in Sect.  3. In Sect. 4 the nature of RV variations is investigated. An orbital solution for the data is presented in Sect. 5, and Sect. 6 includes a discussion about planetary parameters, orbital solutions, and the relationship between stellar activity and the planet. Finally, we summarize and offer some concluding remarks in Sect. 7.

Table 1:   Stellar parameters of BD+20 1790.

2 BD+20 1790: an overview

BD+20 1790 was classified by Jeffries (1995) as a K5Ve star, with a magnitude of V = 9.9. Mason et al. (1995) identified this star as the optical counterpart of the 2RE J072343.6+202500 EUV source, located in the ROSAT All-Sky Survey. López-Santiago et al. (2006) propose its membership in the AB Dor kinematic moving group, which has an estimated average age of 50 Myr. By comparing the equivalent width of Li $\lambda$ 6708 Å with the spectral type, López-Santiago et al. (2006) derive an age estimate of 35-80 Myr. The main stellar parameters for BD+20 1790 are compiled in Table 1. We obtained a value for the stellar radius from the measured rotational velocity and photometric period. Our estimated radius agrees with the previous K5V spectral classification (from Carrol & Ostlie 2007, tables). By adopting this spectral type, we used the K5V temperature from the Carrol & Ostlie (2007) tables. In conjunction with the photometric parameters, this enabled us to derive the luminosity, mass, and surface gravity. Errors in the parameters were estimated by following the method of propagation of errors; i.e., the uncertainties were calculated from the errors in the variables involved in the determination of each parameter. No correllation was assumed between the different variables, in principle independent of each other. To test that assuming a fixed value for $T_{\rm eff}$ has a non-negligible effect on the error computation, we investigated whether an error in $T_{\rm eff}$could translate into uncertainties of derived parameters. We have considered an input error in $T_{\rm eff} \sim 10~$K and analysed the propagation of $T_{\rm eff}$ error. Based on this analysis, we noticed that not considering the error in the $T_{\rm eff}$ leads to underestimating the errors in mass and $\log g$, leading to unreliable error bars for these parameters.

The X-ray luminosity was calculated using the count rates and HR1 hardness ratios from the ROSAT All-Sky Survey. By combining the conversion factor Cx, computed by the formula from Fleming (1995), and the distance estimated by Reid et al. (2004), the stellar X-ray luminosity was calculated as $L_{\rm X} = 1.6\pm 0.5 \times 10^{29}$ erg s-1.

We computed a preliminary value of metallicity by using a grid of Kurucz et al. (1993) ATLAS9 atmospheres and the 2002 version of MOOG[*] synthesis code (Sneden 1973). Atmospheric models were constructed with the data given in Table 1. We used 12 Fe I lines selected from González et al. (2001). We also calculated a value of metallicity with the 7 Fe I lines in the MOOG Abfind routine. We find an average value of $A[{\rm Fe}] = 7.82\pm 0.20$ which, when assuming a solar value of $A[{\rm Fe}] = 7.52$, results in a [Fe/H] = $0.30 \pm 0.20$. As mentioned, this is a preliminary value, although compared with the average metallicity of stars of solar neighbourhood, we still could consider the star as metal-rich within the error bars.

In a recent paper, Carpenter et al. (2008) derive the temperature, gravity, and metallicity for BD+20 1790, and their values are $T_{\rm eff} = 4408$ K and $\log g = 4.50$, very close to the corresponding values presented in Table 1. We also point out that the difference between metallicity values may be explained by Carpenter et al. (2008) only assuming a fixed metallicity of [Fe/H] = 0.0, but not actually computing it.

The Li I abundances were analysed in standard local thermodynamic equilibrium (ETL) using MOOG and ATLAS9 in the same way as with the metallicities. Abundances were derived by fitting synthetic spectra to the data. To determine Li abundances, we performed a spectral synthesis around the Li I 6707 Å resonance doublet, fitting all spectra between 6702 and 6712 Å, taking into account the relation between Li6 and Li7 isotopes. We determine an average value of lithium abundance of $\log N({\rm Li}) = 1.03\pm 0.04$ (where $\log N({\rm Li})$ = log (Li/H)+12).

To study the stellar activity and the kinematics, we have carried out both spectroscopic and photometric monitoring over the past few years: high temporal and spectroscopic resolution and two band photometry. The simultaneous study of photospheric and chromospheric active regions is a powerful tool that allows us to trace, reconstruct, and model the puzzle of the magnetic field topology, since these active regions are the fingerprints of magnetic fields (Collier Cameron 2001; Catalano et al. 2002; Frasca et al. 2005; Collier Cameron et al. 2002). Strong chromospheric activity was detected in several observing runs, described by Hernán-Obispo et al. (2005, 2007). In spite of the rotational velocity not being very high, $v \sin i~\sim~10$ km s-1 (López-Santiago et al. 2006), all activity indicators are in emission above continuum, from Ca  II H & K to Ca  II IRT lines (see Fig. 1).

Through studying the profile line asymmetries of H$\alpha $ and H$\beta $ lines, prominence-like structures were detected in the chromosphere of the star (Hernán-Obispo 2005, 2007). These can be observationally detected as transient absorption features superimposed on the line profile that are interpreted as cool material embedded in the surrounding hotter corona and co-rotating with star (Collier Cameron & Robinson 1989a,b; Collier Cameron & Woods 1992; Jeffries et al. 1993; Byrne et al. 1996; Eibe et al. 1998; Barnes et al. 2000; Donati et al. 2001). Several completed prominence-like transients have been detected with durations of a few hours (see Hernán-Obispo 2005, for details). Modelling these chromospheric phenomenae is an important challenge in this case, because of the detection of these prominence-like structures in unstable positions, far from equatorial regions (Ferreira 2000; Jardine et al. 2001; Jardine & van Balegooijen 2006).

In addition, strong large optical flare events were observed. The gradual decay of the flares was observed for up to 5 h. Figure 1 compares the activity indicators for the quiescent and flare states. The energy released is $\sim$1037 erg, while the released energy is $\sim$1029-1032 erg for largest solar flares, thus ranging the flares of BD+20 1790 on the so-called superflare regime (Rubenstein & Schaefer 2000).

The photometric observations yielded a light curve with evidence of rotational modulation, the semi-amplitude of which approaches $\Delta V\sim 0\hbox{$.\!\!^{\rm m}$ }06$ and indicates the presence of spots on the surface. The period analysis of the entire set of observations reveals a photometric period of 2.801 ($\pm$0.001) days, in agreement with the period given by the SuperWASP photometric survey (Norton et al. 2007). A detailed and completed study of the chromospheric and photospheric activity characterization will be published in a forthcoming paper (Hernán-Obispo et al. 2009b, in prep.).

\begin{figure} \par\includegraphics[angle=-90,scale=0.30,clip]{11000f1a.ps}\vspa... ...ce*{0.5mm} \includegraphics[angle=-90,scale=0.30,clip]{11000f1d.ps} \end{figure} Figure 1:

Chromospheric activity indicators. The dashed line indicates quiescent state, while solid line indicates flare state. From top to bottom: He I D3 region, Ca  II K, H$\alpha $, and H$\beta $

Open with DEXTER

Table 2:   Observing runs.

3 Observations and data analysis

To characterize active regions at photospheric and chromospheric levels, we carried out photometric and spectroscopic observations of the target.

3.1 Spectroscopic data

The observational strategy was designed to spectroscopically monitor chromospheric activity indicators with high temporal and spectral resolution. High-resolution echelle spectra were obtained during four observing runs from 2004 to 2007, detailed in Table 2. The exposure times ranged from 900 s to 1200 s, depending on weather conditions, to obtain an S/N typically greater than 140 for SARG runs and 80 for FOCES runs. The spectra in the time series observations were only separated by the CCD readout time, thus enabling us to obtain the highest temporal resolution possible. Our initial temporal cadence was designed to detect prominence-like transient features in the Balmer lines. Spectral types and RV standards were acquired with the same setup and configuration as the target. These standards were reduced and analysed in the same way as the target. The data were bias-subtracted, overscan-corrected, and flat-fielded using the standard routines in the IRAF[*] package.

The wavelength calibration was obtained by taking spectra of a Th-Ar lamp. Using Coudé spectrographs allowed a stable environment for the wavelength calibration, since flexures are not possible. Details about the spectrographs used can be seen in Pfeiffer et al. (1998) for FOCES spectrograph and Gratton et al. (2001) for SARG spectrograph. To enhance the accuracy in calibration, we used about 10-12 lines identified per order, across all orders for SARG spectra and about 80 orders for FOCES spectra. The orders were calibrated simultaneously, and the total fit has an rms value typically lower than 0.003 Å. The spectra were normalized by a polynomial fit to the observed continuum.

Heliocentric radial velocities were determined using a weighted cross-correlation method. The spectra of the star were correlated order by order against spectra of several RV standards with similar spectral types. Orders with chromospheric features and telluric lines were excluded. We calculated the uncertainties based on the cross-correlation peak height and the antisymmetric noise as described by Tonry & Davis (1979). Also, by measuring RVs of the standard stars, we estimated the systematic errors and the accuracy of the RV measurements with our instrumental setup. The accuracy between standards for the same run and between runs is less than 0.05 km s-1.

Additional echelle data were acquired in DDT mode at the FOCES spectrograph in December 2008. The telescope configuration and the setup were identically to previous FOCES runs, except for two nights in which a different CCD was used. Data were taken over 10 consecutive nights, but bad weather conditions meant only five nights were acquired. Because of the time limitation in DDT mode, only one RV standard was observed.

3.2 Photometric data

The purpose of these observations was to determine the photometric period and to look for photometric variability. In addition, the study of both light curve and spectrocopy allowed us to characterize the active regions in the photosphere (Catalano et al. 2002; Frasca et al. 2005; Biazzo et al. 2007). CCD differential aperture photometry was obtained using the 2.0 m fully robotic Liverpool Telescope (Steele et al. 2004) at the Observatorio del Roque de los muchachos in La Palma, Spain. The observations were scheduled in monitoring mode. We obtained 22 photometric epochs during November and December 2007. Our observational strategy permitted us to obtain a photometric epoch every 3 nights on average. Each epoch consisted in alternating $r^\prime$ and ${\it g}^\prime$ exposures[*], thereby obtaining quasi-simultaneous two-band photometry. Custom-made software[*] was used to automatically extract the photometry. By analysing intra-night scatter, we can infer a photometric accuracy of 3 mmag and 4 mmag per exposure ($r^\prime$ and ${g}^\prime$ bands, respectively, see Fig. 2). We fit the best sine-wave model to the photometry by many periods between 0.1 and 50 days, on both bands. Plotting the post-fit residuals as a function of the period, a very strong minimum on the post-fit residuals is found at $2.801 \pm 0.001$days in both bands (see Fig. 3). We note that the period and the amplitude are similar with those given by the SuperWASP survey (Norton et al. 2007).

The different amplitude in each band is consistent with large spot or spot group covering at least $4\%$ of the surface. As can be seen in Fig. 2, the amplitude is greater at shorter wavelength, i.e. at ${g}^\prime$band in this case. This colour variation is correlated with variation in magnitude. The star appears redder when fainter, at minimum light and therefore bluer when brighter, at maximum light. The full analysis of the photometry and its relation to the star activity requires simultaneous discussion with the spectroscopic data, and a more detailed study of the star will be presented elsewhere (Hernán-Obispo et al. 2009b, in prep.)

\begin{figure} \par\includegraphics[width=8.5cm,clip]{11000f2.eps} \end{figure} Figure 2:

Photometry phased to the 2.801 days period. A linear trend and a zero point have been subtracted to both bands The residuals with respect to a simple sine-wave model are shown in the lower panel.

Open with DEXTER

Table 3:   Radial velocity.

\begin{figure} \par\includegraphics[width=8.3cm,clip]{11000f3.eps} \end{figure} Figure 3:

Postfit residuals to the photometry as a function of the period. The sharper minima correspond to the 2.801 day period in both bands. The RVs period is marked in grey to illustrate the absence of related photometric signals.

Open with DEXTER

4 The nature of the RV variations

Variations in the RV peak-to-peak amplitude of up to $\sim$2 km s-1 were observed during all the observing runs. These variations are significantly greater than the individual measurement errors (0.10 to 0.20 km s-1) or the systematic error (0.05 km s-1), even when we consider the scatter between runs with different spectrographs and setups.

4.1 Searching for periodical signals on RV

A Least squares periodogram (see Appendix A) reveals one very significant peak at 7.783 days (see Fig. 4a). The data set contains 91 independent RV measurements. However, many of them are clustered groups of a few hours. The values we used to generate the periodogram and for orbital fitting (shown in Table 3), were averaged on a nightly basis. Figure. 4b shows the empirical false alarm probability (FAP) as a function of the power. The 7.783 days peak has an FAP of 0.35%.

\begin{figure} \par\includegraphics[width=8.2cm,clip]{11000f4a.eps}\par {\hspace... ...m}\includegraphics[width=7.9cm,clip]{11000f4b.eps}\hspace*{1.5mm}}\end{figure} Figure 4:

Up: Least-squares periodogram of the nightly averaged radial velocity measurements. The 7.78 days peak has a FAP of 0.35%. The dotted horizontal line illustrates a FAP lower than 1% and the dashed horizontal line a FAP lower than 5%. Down: Empirical FAP as a function of the power (red line). The grey bars illustrate the distribution of false alarms with an arbitrary normalization used to derive the empirical FAP. The Y axis is on a logarithmic scale.

Open with DEXTER

It is worth noting that the RV period is longer than the photometric period. Nevertheless, to test that the RV period could arise from rotational modulation, we searched for significant frequencies in the data points of the photometry. There is no significant power at the RV period, and no secondary peaks are found in the aliasing frequencies of the RVs or the photometric period after the main signals are removed. To illustrate the absence of related photometric signals, we marked the RV period in Fig. 3, which shows the post-fit residuals of photometric data. In addition to this, there is no signal at photometric period in the RV data, as can be seen in Fig. 4a, which shows the RV periodogram.

4.2 Stellar activity jitter

It is well known that spurious RV variations can be induced by stellar activity, especially because of changes in the profile of spectral lines caused by the presence of active regions, the so-called stellar jitter (Saar & Donahue 1997; Saar 2009). The high level of activity detected in BD+20 1790, induced us at first to relate RV variations with active regions. Since we ruled out the possibility of variations due to systematic errors or any seasonal effect, the main concern was to determine whether stellar activity was responsible.

It is widely accepted that the relationship of bisectors of the cross-correlation function (CCF), and RV is a powerful method of determining whether the RV variation may be caused by stellar activity or a planetary companion (Queloz et al. 2001; Martínez-Fiorenzano et al. 2005). The CCF was determined by the same procedure as for the RV case, computing it for the regions that include the photospheric lines, which are more sensitive to spot being present, while excluding chromospheric lines and telluric lines. The bisector inverse slope (BIS), defined as the difference of the average values of the top and the bottom zones, was computed to quantify the changes in the CCF bisector shape by using the method described by Queloz et al. (2001). In choosing the span zones, we avoided wings and cores of the CCF profiles, where errors from bisector measurements are large. In Fig. 5 it can be seen that there is a lack of correlation between the BIS and RV variation for all the observing runs. This indicates that the RV variations do not come from variations in the asymmetry of the photospheric lines profile, and subsequently not due to stellar activity variations. The least squares periodogram of bisectors shows two tentative peaks around 2.8 days, as shown in Fig. 6.

\begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{11000f5.ps} \end{figure} Figure 5:

Bisector velocity span vs. radial velocity for all the observing runs. Symbols represent the different runs: stars for FOCES 04A, diamonds for SARG 04B, circles for SARG 06A, and triangles for FOCES 07B.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.8cm,clip]{11000f6.eps} \end{figure} Figure 6:

Periodogram for bisectors of all runs.

Open with DEXTER

We estimated the stellar jitter from Santos et al. (2000), which considers the Ca  II H & K index. Assuming an average value for Ca  II H & K index of about -4.2 and by using Eq. (4), we derived a value for the stellar jitter of up to 10 m s-1. This stellar jitter is added in quadrature to the RV error. As an additional test, we investigated the variation of stellar activity indicators, especially those that are ascribed to plage-like structures on the chromosphere, such as Balmer lines, Ca  II H & K, and Ca  II IRT. The emission flux for these lines in active stars usually shows a periodic modulation (and subsequently the spectroscopic indices), which is most likely caused by rotational modulation of plage-like structure emission. As is shown in Sect. 2, all chromospheric activity indicators are in emission above the continuum, indicating a very high level of activity. To avoid the photospheric contribution to the spectral profiles, we applied the spectral subtraction technique described in detail by Montes et al. (1995). This technique makes use of the program STARMOD developed at Penn State University (Barden 1985) and later modificated by Montes et al. (1995). Also, to control the error and minimize the uncertainties, some routines of the astronomical data reduction package RED uc m E [*] developed at the Universidad Complutense de Madrid (Cardiel 1999) were used. In these subtracted spectra, spectroscopic indices have been defined and computed following Saar & Fisher (2000), Küster et al. (2003), and Bonfils et al. (2007). Both Ca  II IRT and Ca  II H & K indices were only determined for FOCES runs, due to the wavelength range coverage of the spectrograph. To avoid contamination from telluric lines, we only considered the 8662 Å Ca  II IRT line. We searched for periodic signals in the spectroscopic indices by computing their least squares periodograms. Figure 7 shows the variation with time (orbital phase folded in this case) for Ca  II IRT, Ca  II H & K, H$\alpha $, and H$\beta $indices. The corresponding computed periodogram shows more noise rather than a clear signal. This result is also seen in the indices figures as a non-modulation of the activity index. As an example, Fig. 8 shows the periodogram for the H$\alpha $ index.

\begin{figure} \par\includegraphics[angle=-90,width=7.4cm,clip]{11000f7a.ps}\par... ...7c.ps}\par\includegraphics[angle=-90,width=7.4cm,clip]{11000f7d.ps} \end{figure} Figure 7:

Spectroscopic index for chromospheric activity indicators, phased folded orbital period. From top to bottom: H$\alpha $ (squares), H$\beta $ (circles), Ca  II IRT (triangles) and Ca  II H & K (stars). The dashed line is indicating the quiescent state. Error bars for indices are about 0.001.

Open with DEXTER

As pointed out by Walter (1994), the rotational modulation of chromospheric lines due to plages is not always detectable in very active stars. Furthermore, in this case the flares could contaminate the data, masking the actual period of variation of the indices. To investigate this possibility we removed the data affected by flare events. Because of the different wavelength range coverage of spectrographs, we considered only H$\alpha $ and H$\beta $ indices. For the H$\alpha $ index, we found a tentative rotational modulation with a period of 2.77 days, similar to the photometric period (see Fig. 9). However, the postfit residuals show in Fig. 10 that this could be a misleading signal, even pure noise. For H$\beta $ index, no clear modulation has been found. The lack of variability of BIS and spectroscopic indices with RV period and the absence of a photometric period larger than 2.8days strongly support the planetary companion hypothesis.

\begin{figure} \par\includegraphics[width=8.4cm,clip]{11000f8.eps} \end{figure} Figure 8:

Periodogram for H$\alpha $ index.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=-90,width=8.2cm,clip]{11000f9.ps} \end{figure} Figure 9:

H$\alpha $ index for the data without flare events, including a modulation with a period of about 2.77 days, similar to the photometric period.

Open with DEXTER

\begin{figure} \par\includegraphics[angle=-90,width=8.2cm,clip]{11000f10.ps} \end{figure} Figure 10:

Postfit residuals to H$\alpha $ index for no-flare data as a function of the period.

Open with DEXTER

4.3 RV wavelength dependence

Desort et al. (2007) (hereafter D07) point out that the colour dependence (with wavelength) of the RV peak-to-peak amplitude with spots can be used as a diagnostic to distinguish between stellar activity or planetary companions. Because the contrast between spots and the surrounding photosphere is greater in the visible than at IR wavelengths, it is expected that an attenuation of RV amplitude would be seen towards red wavelengths. Observationally this effect has been shown by e.g. Martín et al. (2006), Huélamo et al. (2008), and Prato et al. (2008). If the RV variations stem from a planet, the RV amplitude should be the same in every wavelength range. We investigated a possible chromatic dependence by computing the RV in two different ranges of wavelength, one for red and near-IR wavelengths (7650 to 10 000 Å) and the other for blue (4300 to 4800 Å). The resulting RV peak-to-peak amplitude is $2.19 \pm 0.20$ km s-1 for the near-IR range and $2.20 \pm 0.20$ km s-1 for the blue range. The values differ by only 0.5% and agree within the uncertainties. Additional RV infrared follow-up can allow us to confirm this. In a forthcoming paper (Hernán-Obispo et al. 2009d, in prep.), we will present the first results of the study of the RVs of BD+20 1790 in the near-IR range.

4.4 RV variation by empirical spots and plages?

To estimate an order of magnitude of the expected RV amplitude due to spots, we used empirical relations derived by Saar & Donahue 1997 (hereafter SD97) and D07. These relations connect the RV amplitude with the spot filling factor $f_{\rm s}$ and $v \sin i$. We considered both relations by D07 and SD97, because D07 relations take the spectral type and the whole spectral range into account (except telluric and chromospheric lines) to compute the empirical RV, whereas SD97 uses a single line and G5V spectral type. Using Eq. (1) of SD97, we computed an amplitude of up to 575 m s-1 and by using D07 Eq. (5) we similarly estimated an amplitude of up to 600 m s-1. As mentioned, these results are taken as a quantitative estimation. There are more effects that are not taken into account here, such as the spot location at stellar surface given by the colatitude $\theta$ and the spot temperature. SD97 Eq. (1) and D07 Eq. (5) considered the simple case of an equatorial spot, but SD97 assumed a $T_{\rm spot} = 0$ K and D07 assumed a spot temperature 1000 K cooler than the photosphere. The difference between the RV amplitude derived from both equations could be caused by this different spot temperature.

On the other hand, we can estimate the spot filling factor that could produce the RV signal of our data. We considered an average semi-amplitude of 1 km s-1. The $f_{\rm s}$ estimated from SD97 is therefore 23%, while D07 indicates 19%. The $f_{\rm s}$ measured from photometric variation is about 4%. These results indicate that the spot filling factor needed to explain the RV variation purely due to spots does not agree with the photometry.

Saar (2003) and Saar (2009) made significant efforts to model plage-induced RV jitter. Although the models are mostly applicable to solar-like stars, we could estimate the plage filling factor $f_{\rm p}$ that could produce the RV signal by using the Saar (2009) equation that connects the RV amplitude with $v \sin i > 6$ km s-1. This estimated $f_{\rm p}$ is about 70%, which strongly suggests that the RV variation does not come from chromospheric plages.

4.5 The RV signal be without a planet

Empirical relations derived by SD07 and D07 do not take the chromatic effect of spots on the RV signal into account. We therefore investigated how much RV signal would be expected in the absence of a planet and the degree of RV attenuation with wavelength (assuming the RVs come from cool spots). To quantify the attenuation if the cause of variations were spots, we tried to investigate how much spots affect the line profiles. However, BD+20 1790 has a low $v \sin i$ to model the photosphere by generating Doppler imaging spot maps. To carry out a realistic approximation to the problem, we constructed realistic spot maps by using the spectra of another star with similar characteristics, LO Peg, which is widely studied in the literature, and its photospheric activity is well-known (Jeffries & Jewell 1993; Jeffries et al. 1994; Eibe et al. 1998; Eibe et al. 1999; Barnes et al. 2005). LO Peg is a K5V-K7Ve star, identified by Jeffries & Jewell (1993) as a member of the Local Association, with an estimated age of 20-30 Myr. Jeffries et al. (1994) determined the inclination to be $50^{\circ}$. The level of activity is similar to BD+20 1790, but LO Peg is a rapid rotator ( $v \sin i \sim 69$ km s-1). The LO Peg photometry suggests a spot filling factor of up to 1.5%.

Using the Doppler imaging program, DoTS (Collier Cameron 1997), and an input starspot image derived for LO Peg (Barnes et al. 2005), we generated a set of line profiles for a star with $v\sin i = 10$ km s-1 (i.e. matching that of BD+20 1790) over a complete rotation phase. The profiles thus contain asymmetries due to starspots from the observed LO Peg image. We used appropriate temperatures for the BD+20 1790 photosphere and estimated at spots possess temperatures that are up to 1000 K cooler. Profiles were generated for the three different wavelengths of 4000 Å, 6717 Å, and 10 000 Å. The radial velocity variations were then calculated to estimate the relative amplitudes due to spot induced variations at each of the three wavelengths.

The RV attenuation with wavelengths relative to 4000 Å is 16% at 6717 Å and about 30% at 10 000 Å, as illustrated in Fig. 11. When as a first approach assuming the same $f_{\rm s}$ for LO Peg and BD+20 1790, the RV signal for BD+20 1790 should be about 1.5 km s-1 at 10 000 Å. However, in Hernán-Obispo et al. 2009d (in prep.), we find only about 0.5% attenuation in the near-IR region relative to the visible, 6717 Å region. This result is an additional argument favouring support the existence of the planetary companion.

\begin{figure} \par\includegraphics[angle=-90,width=7.8cm,clip]{11000f11.ps} \end{figure} Figure 11:

Radial velocity amplitude variation with wavelength, computed for LO Peg profiles.

Open with DEXTER

4.6 RV jitter from flares

We estimated the rate of the flare's occurrence as the fractional amount of the total observing time (for all runs) where a flare was detected. Thus, we get a flare occurrence frequency of $\sim$40%. This higher rate raises the question of how much RV jitter we should expect from large flares, if any. Saar (2009) presents the first approach to this issue, concluding that RV jitter due to flare occurrence would be non-negligible, although it would probably be a stochastic jitter component. Chromospheric activity indicators exhibited an enhancement at flare state, the broad emission of Balmer lines, and He I D3 in emission being the most notable features (see Fig. 1). As pointed out by Saar (2009), although these lines are excluded when we measure RV, it is possible that a significant core filling in photospheric lines occurs when there is a flare event. The cause could be upper photospheric heating. Results by Houdebine (1992) state that heating is propagated down to low photospheric levels.

A second related problem is the effect of large flares on BIS. While it has not been studied until now, it is expected to be more pronounced, since bisectors are more sensitive to changes in line profiles. To our knowledge it is being reported here for the first time. Figure 12 a shows the relationship of H$\alpha $ index to BIS, and higher values for H$\alpha $ index indicate the occurrence of a flare event. It is seen that the scatter for BIS is higher when a flare occurs. Outliers at quiescent state correspond to a low S/N rate. Similar BIS behaviour is seen in Fig. 12b, which shows the H$\beta $ index vs. BIS.

Table 4:   Orbital parameters of BD+20 1790 b.

\begin{figure} \par\includegraphics[angle=-90,width=7.6cm,clip]{11000f12a.ps}\par\includegraphics[angle=-90,width=7.6cm,clip]{11000f12b.ps} \end{figure} Figure 12:

Up: H$\alpha $ index vs. BIS. The dashed line indicates the quiescent state. Down: H$\beta $ index vs. BIS. Error bars for the indices are about of 0.001.

Open with DEXTER

5 Orbital solution for BD+20 1790 b

\begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{11000f13a.ps}\vs... ...2mm} \par\includegraphics[angle=-90,width=8.8cm,clip]{11000f13b.ps} \end{figure} Figure 13:

Radial velocity variability of BD+20 1790. Up: Circular orbit. Down: Eccentric orbit. Values marked with circle symbol represent FOCES runs except stars that represent DDT FOCES 08B run. Diamond symbols are for SARG runs.

Open with DEXTER

We computed the orbital solution for the RV data using a standard Keplerian fit with the RV period estimated by the least squares periodogram. The fit was obtained first by only considering the FOCES data, averaged by night, in order to avoid intranight scatter. After this, we added the SARG data to improve the fit. The results for the fit considering only FOCES data or all data from the two spectrographs were compatible within uncertainties. With the addition of RVs measured in winter 2008 (DDT FOCES 08b run), the least squares periodogram is strikingly improved, and the 7.78 day peak clearly dominates the power spectrum. Attempts to perform a Keplerian fit using the second and the third highest periodogram peaks produced significantly worse folded curves. We also fitted the RV set computed by López-Santiago (2005). A first fit (see Fig. 13a) derives a close-in massive planet (a =0.066 AU, $M_2 \sin i = 6.54~M_{\rm jup}$) in a circular orbit (e = 0.05) with a rotational period of 7.7834 days and a reduced $\chi^2$ of 1.07. Also we present a second fit (see Fig. 13b) with the same period for an eccentric orbit (a = 0.066 AU, $M_2 \sin i = 6.15~M_{\rm jup}$, e = 0.14, $\chi^2 = 0.997$). Sampling of the data means we cannot discard a possible eccentric orbit. Orbital elements for both solutions are compiled in Table 4 and discussed in the next section.

As an additional test, we computed the orbital solution by removing the data affected by flare events. The fit derives a solution (a =0.066 AU, $M_2 \sin i = 6.54~M_{\rm jup}$, e = 0.01, K = 0.91 km s-1) compatible with the solution when considering all the data. The fit is presented in Fig. 14.

\begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{11000f14.ps}\vspace{-3mm} \end{figure} Figure 14:

Radial velocity variation of BD+20 1790 computed considering only the data that are not affected by flares. Circle symbol represent FOCES runs except that stars represent DDT FOCES 08B run. Diamond symbol are for SARG runs.

Open with DEXTER

6 Discussion

The lack of a relation between the BIS and spectroscopic indices with the RV period, as well as the different RV and photometrical period strongly suggest that the RV variations come from to a planetary companion. However, it is possible that the RV variations actually come from a combination of phenomena (activity and planet).

Stellar magnetic activity may be influenced and enhanced by the presence of a close-in giant planet, as proposed by Cuntz et al. (2000), Cuntz & Shkolnik (2002), and Lanza (2008). Thus, this planetary companion could explain the high level of stellar activity detected. In a recent paper, Lanza (2009) proposes a new model that predicts the formation of prominence-like structures in very highly active stars with close-in giant planets. Also, as presented in Sects. 2 and  4.6, the large flares, with energy releases in the superflare regime, and the high rate of flare ocurrence could find a source in addition to stellar activity in the reconnection of the stellar coronal field as the planet is moving inside the Alfvén radius of the star (Ip et al. 2004). In a forthcoming paper, we explore in detail these possible star-planet interactions (Hernán-Obispo et al. 2009c, in prep).

In addition, as suggested by the statistical analysis by Kashyap et al.(2008), the X-ray flux from stars with close-in giant planets is on average 4 times greater than those with more distant planetary companions. For the ``close-in'' subsample, the X-ray luminosity is $L_{\rm X} = 10^{28.5}$ erg s-1 on average. The X-ray luminosity of BD+20 1790 is 5 times brighter than this average, which is consistent with chromospheric and X-ray emission induced by the massive close-in companion (Lanza 2009).

Even though the stellar activity could swallow the RV signal of a planetary companion, we can detect it for BD+20 1790 b since it is a massive planet. The RV variation is large enough even though the RV accuracy is typically about 150 m s-1.

Because of observational strategy (the data are not part of a planet-search program), the eccentricity is poorly constrained. Indeed there is no ``a priori'' reason to discard an eccentric orbit since the computed circularization time scale reaches several Gyr, but more data is required to properly characterize the eccentricity. RV optical and infrared follow-up over twice the RV period will enable us to constrain the orbital solution, as well as to confirm the presence of the planet. More massive exoplanets $M_2\sin i\sim$5 $M_{\rm jup}$ with orbital periods longer than about 6 days have eccentricities that are significantly higher than lower mass planets (Udry & Santos 2007). Another possibility is that additional undetected, longer period planets are maintaining the eccentricity of BD+20 1790 b. Both situations are discussed in detail by Wu & Murray (2003).

It is worth noting, however, that the star is metal-rich, as presented in Sect. 2. A correlation between stellar metallicity and planet mass is reported by e.g. Santos et al. (2001), Fischer & Valenti (2005), and Guillot et al. (2006). Massive planets tend to form around metal-rich stars; i.e., planets that orbit metal-rich stars also have higher mass cores.

Compared to other planets of similar masses and orbits[*] and considering the statistical results described in recent reviews (Udry & Santos 2007), BD+20 1790 b does not exhibit unusual characteristics, except for its young age and its relatively high mass. We used a complimentary method to determine the stellar age from Mamajek & Hillenbrand (2008) (hereafter MH08), which uses the fractional X-ray luminosity, $R_{\rm X} = L_{\rm X}/L_{\rm bol}$. MH08 demonstrate that $R_{\rm X}$ has the same age-inferring capability as the chromospheric index $R^{\prime}_{\rm HK}$. By using their Eq. (A3), we estimated an age for BD+20 1790 of up to 35 Myr. Considering a value for $\log R^{\prime}_{\rm HK} = -4.2$ on average, we can also estimate the age with the new relation proposed by MH08, by Eq. (3). We computed an age of up to 58 Myr. These values are in agreement with the range estimated by López-Santiago et al. (2006).

Lowrance et al. (2005) include this star BD+20 1790 in a coronographic survey of substellar companions using the coronograph on NICMOS/HST and the 200-inch Hale Telescope (Palomar Osbservatory). No companions were found beyond 10 AU. However, the orbital solutions we find suggest a semi-major axis below 0.1 AU, clearly beyond their resolving capabilities.

Great care must therefore be taken when extrapolating properties of early stellar evolution stages from the characteristics of the later stages, since the current knowledge about planetary system evolution is still somewhat speculative. The diversity exoplanet properties requires that we rethink our ideas on planet formation and migration scenarios. Planets discovered around young stars could be the missing link that reconstructs the scenarios between exoplanets and protoplanetary disks. Indeed, further study of BD+20 1790 b has the potential of improving our understanding of planetary systems at early evolutionary stages.

7 Conclusions

This paper describes the investigation of RV variations for the young and active K5V star BD+20 1790. Based upon the analysis of the BIS of the CCF, as well as activity indicators and photometry, a planetary companion is shown to be the best interpretation. The orbital solution results in a companion with a mass in the planetary regime. No photometric period longer than 2.8 days strongly supports the planetary origin of the observed RV variations. Two solutions for the orbit are computed and discussed. The presence of a close-in massive planet could also be an explanation for the high level of stellar activity. Since the RV data are not part of a planet search programme, we can consider our results as serendipitous evidence of a planetary companion. Indeed additional RV optical and infrared follow-up will enable us to constrain the orbital solution, as well as confirm the presence of the planet. This is thus far the youngest main sequence star for which a planetary candidate has been reported.

Acknowledgements
We thank Calar Alto Observatory for allocation of director's discretionary time to this programme. This work was supported by the Spanish Ministerio de Educación y Ciencia (MEC) under grant AYA2005-02750, Ministerio de Ciencia e Innovacin (MICINN) under grant AYA2008-06423-C03-03, and The Comunidad de Madrid under PRICIT project S-0505/ESP-0237 (ASTROCAM). M.C.G.O. acknowledges financial support from the European Commission in the form of a Marie Curie Intra European Fellowship (PIEF-GA-2008-220679). M.H.O. and G.A.E. thank Dr. Chriss Moss, support astronomer at the LT for his help and patience. Also M.H.O. thanks Dr. Santos Pedraz, support astronomer at the Calar Alto Observatory for his help with DDT run. M.H.O. is grateful to Dr. José Antonio Caballero for valuable discussions, and also Dr. Laurence R. Doyle for his suggestions that was the initial inspiration for this work. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. The authors gratefully acknowledge the valuable comments and suggestions of an anonymous referee that helped to improve the paper.



Appendix A: Periodogram

We use a least squares periodogram approach to identify and visually illustrate the relevant periods in the data. It differs from the more classic Lomb-Scargle periodogram (Scargle 1982) in a few key aspects. For a given period P, a linear model of the form $v_r = \gamma + A\cos 2\pi/P t + B\cos 2\pi/P t$ is fitted using a weighted least square to the data, and the $\chi^2$ of the residuals is obtained. The $\chi^2$ minima reveal the candidate signals of interest. One can represent the root mean square of the residuals (RMS) with respect to the period to show the relevant periods as minima. (This approach is used to illustrate the photometric periods in Fig. 3.) To recover a more familiar view of a periodogram, one can compute the Power of each period P as
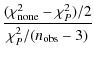
       $\displaystyle {\rm Power}(P)$ = $\displaystyle \frac{(\chi^2_{\rm none}-\chi^2_{P})/2}{\chi^2_{P}/(n_{\rm obs}-3)}$ (A.1)
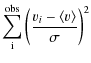
$\displaystyle \chi^2_{\rm none}$ = $\displaystyle \sum_{\rm i}^{\rm obs} \left(\frac{v_i-\left<v\right>}{\sigma}\right)^2$ (A.2)

that follows a Fisher-F Distribution with 2 and $n_{\rm obs}-3$ degrees of freedom and can be used to obtain a first hint of the FAP of a given solution. This definition of the power measures how much the $\chi^2$ of the fit improves when a sinusoid of period P is included (see Cumming 2004, for a more detailed description).

Since analytical approaches tend to give optimistic confidence levels, it is desirable to obtain the FAP of a solution empirically. To make this, we generate a large number of synthetic datasets (105) with the same sampling cadence (same dates) but only containing random noise. Then, for each realization, we compute the least squares periodogram and find the period with higher power, which will be a false alarm. A histogram of false alarms as a function of the Power is obtained and its complementary cumulative distribution gives the FAP of a given peak in our signal. The least squares periodogram of the RVS data and its associated empirical FAP probability distribution are shown in Fig. 4. Compared to the Lomb-Scargle periodogram, this approach allows a proper weighting of each observation and can be easily generalized to include other time-dependent effects in the signal at the period search level.


References

  1. Barden, S. C. 1985, ApJ, 295, 162 [NASA ADS] [CrossRef] [Google Scholar]
  2. Barnes, J. R., Collier Cameron, A., James, D. J., & Donati, J.-F. 2000, MNRAS, 314, 162 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barnes, J. R., Cameron, A. C., Lister, T. A., et al. 2005, MNRAS, 356, 1501 [NASA ADS] [CrossRef] [Google Scholar]
  4. Biazzo, K., Frasca, A., Henry, G. W., et al. 2007, ApJ, 656, 474 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bouvier, J., Alencar, S. H. P., Boutelier, T., et al. 2007, A&A, 463, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Byrne, P. B., Eibe, M. T., & Rolleston, W. R. J. 1996, A&A, 311, 651 [NASA ADS] [Google Scholar]
  8. Cardiel, N. 1999, PhD Thesis, Universidad Complutense de Madrid [Google Scholar]
  9. Carpenter, J. M., Bouwman, J., Silverstone, M. D., et al. 2008, ApJS, 179, 423 [NASA ADS] [CrossRef] [Google Scholar]
  10. Carroll, B. W., & Ostlie, D. A. 2007, An Introduction to Modern Astrophysics, 2nd edn. (Pearson International Edition, Addison Wesley) [Google Scholar]
  11. Catalano, S., Biazzo, K., Frasca, A., et al. 2002, A&A, 394, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Collier Cameron, A. 1997, MNRAS, 287, 556 [NASA ADS] [CrossRef] [Google Scholar]
  13. Collier Cameron, A. 2001, in Recent Insights into the Physics of the Sun and Heliosphere: Highlights from SOHO and Other Space Missions, IAU Symp., 203, 229 [Google Scholar]
  14. Collier Cameron, A., & Robinson, R. D. 1989a, MNRAS, 236, 57 [NASA ADS] [CrossRef] [Google Scholar]
  15. Collier Cameron, A., & Robinson, R. D. 1989b, MNRAS, 238, 657 [NASA ADS] [CrossRef] [Google Scholar]
  16. Collier Cameron, A., & Woods, J. A. 1992, MNRAS, 258, 360 [NASA ADS] [Google Scholar]
  17. Collier Cameron, A., Jardine, M. M., & Donati, J.-F. 2002, in Stellar Coronae in the Chandra and XMM-NEWTON Era, ASP Conf. Ser., 277, 397 [Google Scholar]
  18. Cumming, A. 2004, MNRAS, 354, 1165 [NASA ADS] [CrossRef] [Google Scholar]
  19. Cuntz, M., & Shkolnik, E. 2002, 323, 387 [Google Scholar]
  20. Cuntz, M., Saar, S. H., & Musielak, Z. E. 2000, ApJ, 533, L151 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  21. Desort, M., Lagrange, A.-M., et al. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Donati, J.-F., Mengel, M., Carter, B. D., et al. 2000, MNRAS, 316, 699 [NASA ADS] [CrossRef] [Google Scholar]
  23. Eibe, M. T. 1998, A&A, 337, 757 [NASA ADS] [Google Scholar]
  24. Eibe, M. T., Byrne, P. B., Jeffries, R. D., et al. 1999, A&A, 341, 527 [NASA ADS] [Google Scholar]
  25. Esposito, M., Guenther, E., Hatzes, A. P., et al. 2006, Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies, 127 [Google Scholar]
  26. Ferreira, J. M. 2000, MNRAS, 316, 647 [NASA ADS] [CrossRef] [Google Scholar]
  27. Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fleming, T. A., Schmitt, J. H. M. M., & Giampapa, M. S. 1995, ApJ, 450, 401 [NASA ADS] [CrossRef] [Google Scholar]
  29. Frasca, A., Biazzo, K., Catalano, S., et al. 2005, A&A, 432, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gratton, R. G., Bonanno, G., Bruno, P., et al. 2001, Exp. Ast., 12, 107 [Google Scholar]
  31. Gonzalez, G., Laws, C., Tyagi, S., et al. 2001, AJ, 121, 432 [NASA ADS] [CrossRef] [Google Scholar]
  32. Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Hernán-Obispo, M., de Castro, E., & Cornide, M. 2005, ESA SP, 560, 647 [NASA ADS] [Google Scholar]
  34. Hernán-Obispo, M., de Castro, E., & Gálvez, M. C. 2007, Highlights of Spanish Astrophysics IV (Kluwer Academic Publishers) [Google Scholar]
  35. Houdebine, E. R. 1992, Irish Astron. J., 20, 213 [NASA ADS] [Google Scholar]
  36. Huelamo, N., Figueira, P., Bonfils, X., et al. 2008, A&A, 489, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Huerta, M., Johns-Krull, C. M., Prato, L., et al. 2008, ApJ, 678, 472 [NASA ADS] [CrossRef] [Google Scholar]
  38. Ip, W.-H., Kopp, A., & Hu, J.-H. 2004, ApJ, 602, L53 [NASA ADS] [CrossRef] [Google Scholar]
  39. Jardine, M., & van Ballegooijen, A. A. 2005, MNRAS, 361, 1153 [Google Scholar]
  40. Jardine, M., Collier Cameron, A., Donati, J.-F., et al. 2001, MNRAS, 324, 201 [NASA ADS] [CrossRef] [Google Scholar]
  41. Jeffries, R. D. 1995, MNRAS, 273, 559 [NASA ADS] [Google Scholar]
  42. Jeffries, R. D., & Jewell, S. J. 1993, MNRAS, 264, 106 [NASA ADS] [CrossRef] [Google Scholar]
  43. Jeffries, R. D., Byrne, P. B., Doyle, J. G., et al. 1994, MNRAS, 270, 153 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kashyap, V. L., Drake, J. J., & Saar, S. H. 2008, ApJ, 687, 1339 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kurucz, R. L. 1993, Peculiar versus Normal Phenomena in A-type and Related Stars, IAU Colloq, 138, APCS, 44, 87 [Google Scholar]
  46. Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Lanza, A. F. 2008, A&A, 487, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Lanza, A. F. 2009, A&A, 505, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. López-Santiago, J. 2005, PhD Thesis, Universidad Complutense de Madrid [Google Scholar]
  50. López-Santiago, J., Montes, D., Crespo-Chacón, I., et al. 2006, ApJ, 643, 1160 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lowrance, P. J., Becklin, E. E., Schneider, G., et al. 2005, AJ, 130, 1845 [NASA ADS] [CrossRef] [Google Scholar]
  52. Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
  53. Mason, K. O., Hassall, B. J. M., Bromage, G. E., et al. 1995, MNRAS, 274, 1194 [NASA ADS] [CrossRef] [Google Scholar]
  54. Martín, E. L., Guenther, E., Zapatero Osorio, M., et al. 2006, ApJ, 644, L75 [NASA ADS] [CrossRef] [Google Scholar]
  55. Martínez Fiorenzano, A. F., Gratton, R. G., Desidera, S., et al. 2005, A&A, 442, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
  57. Montes, D., de Castro, E., Fernandez-Figueroa, M. J., et al. 1995, A&AS, 114, 287 [Google Scholar]
  58. Norton, A. J., Wheatley, P. J., West, R. G., et al. 2007, A&A, 467, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Paulson, D. B., & Yelda, S. 2007, PASP, 118, 706 [Google Scholar]
  60. Paulson, D. B., Cochran, W. D., & Hatzes, A. P. 2004, AJ, 124, 3579 [NASA ADS] [CrossRef] [Google Scholar]
  61. Pfeiffer, M. J., Frank, C., Baumueller, D., et al. 1998, A&AS, 130, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Prato, L., Huerta, M., Johns-Krull, C. M., et al. 2008, ApJ, 687, L103 [NASA ADS] [CrossRef] [Google Scholar]
  63. Queloz, D., Henry, G. W., Sivan, J.P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Reid, I. N., Cruz, K. L., Allen, P., et al. 2004, AJ, 128, 463 [NASA ADS] [CrossRef] [Google Scholar]
  65. Rubenstein, E. P., & Schaefer, B. E. 2000, ApJ, 529, 1031 [NASA ADS] [CrossRef] [Google Scholar]
  66. Saar, S. H. 2003, in Scientific Frontiers in Research on Extrasolar Planets, ASP Conf. Ser., 294, 65 [Google Scholar]
  67. Saar, S. H. 2009, AIP Conf. Ser., 1094, 152 [NASA ADS] [CrossRef] [Google Scholar]
  68. Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
  69. Saar, S. H., & Fischer, D. 2000, ApJ, 534, L105 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  70. Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
  71. Santos, N. C., Israelian, G., & Mayor, M. 2001, 373, 1019 [Google Scholar]
  72. Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
  73. Setiawan, J., Weise, P., Henning, T., et al. 2007, ApJ, 660, L145 [NASA ADS] [CrossRef] [Google Scholar]
  74. Setiawan, J., Henning, T., Launhardt, R., et al. 2008, Nature, 451, 38 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  75. Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
  76. Steele, I. A., Smith, R. J., Rees, P. C., et al. 2005, SPIE Conf. Ser., 5489, 679 [NASA ADS] [Google Scholar]
  77. Tonry, J., & Davis, M. 1979, AJ, 84, 1511 [NASA ADS] [CrossRef] [Google Scholar]
  78. Udry, S., & Santos, N. C. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
  79. Walter, F. M. 1994, in Stellar Surface Structure, IAU Symp., 176, 355 [Google Scholar]
  80. Wu, Y., & Murray, N. 2003, ApJ, 589, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Footnotes

... 1790[*]
Based on observations collected at the German-Spanish Astronomical Center, Calar Alto, jointly operated by the Max-Planck-Institut für Astronomie Heidelberg and the Instituto de Astrofísica de Andalucía (CSIC). Based on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Based on observations made with the Liverpool Telescope operated on the island of La Palma by Liverpool John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias with financial support from the UK Science and Technology Facilities Council.
... 1790[*]
Our radial velocity data from Table 3 are available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/512/A45
... MOOG[*]
The source code of MOOG 2002 can be downloaded at http://verdi.as.utexas.edu/moog.html
... IRAF[*]
IRAF is distributed by the National Optical Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under contract with the National Science Foundation.
... exposures[*]
Sloan r' and g' filters were used.
... software[*]
ATP, Automatic TATOOINE Photometry. http://www.am.ub.es/ anglada/atp/atp_testing.htm
... m E[*]
http://www.ucm.es/info/Astrof/software/reduceme/reduceme.html
... orbits[*]
Observational data for the more than 370 exoplanets are compiled on the Extrasolar Planets Encyclopaedia (http://exoplanet.eu), mantained by J. Scheneider

All Tables

Table 1:   Stellar parameters of BD+20 1790.

Table 2:   Observing runs.

Table 3:   Radial velocity.

Table 4:   Orbital parameters of BD+20 1790 b.

All Figures

  \begin{figure} \par\includegraphics[angle=-90,scale=0.30,clip]{11000f1a.ps}\vspa... ...ce*{0.5mm} \includegraphics[angle=-90,scale=0.30,clip]{11000f1d.ps} \end{figure} Figure 1:

Chromospheric activity indicators. The dashed line indicates quiescent state, while solid line indicates flare state. From top to bottom: He I D3 region, Ca  II K, H$\alpha $, and H$\beta $

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{11000f2.eps} \end{figure} Figure 2:

Photometry phased to the 2.801 days period. A linear trend and a zero point have been subtracted to both bands The residuals with respect to a simple sine-wave model are shown in the lower panel.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.3cm,clip]{11000f3.eps} \end{figure} Figure 3:

Postfit residuals to the photometry as a function of the period. The sharper minima correspond to the 2.801 day period in both bands. The RVs period is marked in grey to illustrate the absence of related photometric signals.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.2cm,clip]{11000f4a.eps}\par {\hspace... ...m}\includegraphics[width=7.9cm,clip]{11000f4b.eps}\hspace*{1.5mm}}\end{figure} Figure 4:

Up: Least-squares periodogram of the nightly averaged radial velocity measurements. The 7.78 days peak has a FAP of 0.35%. The dotted horizontal line illustrates a FAP lower than 1% and the dashed horizontal line a FAP lower than 5%. Down: Empirical FAP as a function of the power (red line). The grey bars illustrate the distribution of false alarms with an arbitrary normalization used to derive the empirical FAP. The Y axis is on a logarithmic scale.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{11000f5.ps} \end{figure} Figure 5:

Bisector velocity span vs. radial velocity for all the observing runs. Symbols represent the different runs: stars for FOCES 04A, diamonds for SARG 04B, circles for SARG 06A, and triangles for FOCES 07B.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm,clip]{11000f6.eps} \end{figure} Figure 6:

Periodogram for bisectors of all runs.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=7.4cm,clip]{11000f7a.ps}\par... ...7c.ps}\par\includegraphics[angle=-90,width=7.4cm,clip]{11000f7d.ps} \end{figure} Figure 7:

Spectroscopic index for chromospheric activity indicators, phased folded orbital period. From top to bottom: H$\alpha $ (squares), H$\beta $ (circles), Ca  II IRT (triangles) and Ca  II H & K (stars). The dashed line is indicating the quiescent state. Error bars for indices are about 0.001.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{11000f8.eps} \end{figure} Figure 8:

Periodogram for H$\alpha $ index.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8.2cm,clip]{11000f9.ps} \end{figure} Figure 9:

H$\alpha $ index for the data without flare events, including a modulation with a period of about 2.77 days, similar to the photometric period.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8.2cm,clip]{11000f10.ps} \end{figure} Figure 10:

Postfit residuals to H$\alpha $ index for no-flare data as a function of the period.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=7.8cm,clip]{11000f11.ps} \end{figure} Figure 11:

Radial velocity amplitude variation with wavelength, computed for LO Peg profiles.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=7.6cm,clip]{11000f12a.ps}\par\includegraphics[angle=-90,width=7.6cm,clip]{11000f12b.ps} \end{figure} Figure 12:

Up: H$\alpha $ index vs. BIS. The dashed line indicates the quiescent state. Down: H$\beta $ index vs. BIS. Error bars for the indices are about of 0.001.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{11000f13a.ps}\vs... ...2mm} \par\includegraphics[angle=-90,width=8.8cm,clip]{11000f13b.ps} \end{figure} Figure 13:

Radial velocity variability of BD+20 1790. Up: Circular orbit. Down: Eccentric orbit. Values marked with circle symbol represent FOCES runs except stars that represent DDT FOCES 08B run. Diamond symbols are for SARG runs.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{11000f14.ps}\vspace{-3mm} \end{figure} Figure 14:

Radial velocity variation of BD+20 1790 computed considering only the data that are not affected by flares. Circle symbol represent FOCES runs except that stars represent DDT FOCES 08B run. Diamond symbol are for SARG runs.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.