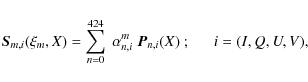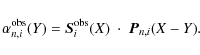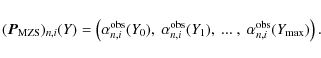EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A6 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A6
Number of page(s) 12
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/200810484
Published online 18 March 2010
A&A 512, A6 (2010)

Spectropolarimetric multi line analysis of stellar magnetic fields

J. C. Ramírez Vélez1,2 - M. Semel2 - M. Stift3,4 - M. J. Martínez González4,5 - P. Petit6 - N. Dunstone7

1 - Instituto de Astronomia - Universidad Nacional Autonoma de Mexico, 04510 Coyoacan, DF, Mexico
2 - LESIA, Observatoire de Paris Meudon, 92195 Meudon, France
3 - Institute for Astronomy, Univ. of Vienna, Türkenschanzstrazze 17, 1180 Wien, Austria
4 - LERMA, Observatoire de Paris Meudon, 92195 Meudon, France
5 - Instituto de Astrofisica de Canarias, via lactea s/n, 38205 Tenerfie, Spain
6 - Laboratoire d'Astrophysique Toulouse-Tarbes, Université de Toulouse, CNRS, France
7 - School of Physics and Astronomy, U. of St Andrews, KY169SS, UK

Received 30 June 2008 / Accepted 20 December 2009

Abstract
Aims. In this paper we study the feasibility of inferring the magnetic field from polarized multi line spectra using two methods: The pseudo line approach and The PCA-ZDI approach.
Methods. We use multi line techniques, meaning that all the lines of a stellar spectrum contribute to obtain a polarization signature. The use of multiple lines dramatically increases the signal-to-noise-ratio of these polarizations signatures. Using one technique, the pseudo line approach, we construct the pseudo line as the mean profile of all the individual lines. The other technique, the PCA-ZDI approach proposed recently by Semel et al. (2006, ASPC, 358, 355) for the detection of polarized signals, combines principle components analysis (PCA) and the Zeeman Doppler imaging technique (ZDI). This new method has a main advantage: the polarized signature is extracted using cross correlations between the stellar spectra and functions containing the polarization properties of each line. These functions are the principal components of a database of synthetic spectra. The synthesis of the spectra of the database are obtained using the radiative transfer equations in LTE. The profiles built with the PCA-ZDI technique are called multi Zeeman signatures.
Results. The construction of the pseudo line as well as the multi Zeeman signatures is a powerful tool in the study of stellar and solar magnetic fields. The information of the physical parameters that governs the line formation is contained in the final polarized profiles. We have shown in particular using inversion codes that the magnetic field vector can be properly inferred with both approaches despite the magnetic field regime.

Key words: magnetic fields - line: profiles - line: formation - radiative transfer - polarization

1 Introduction

The majority of cool stars including our Sun have magnetically confined atmospheres. The study of the magnetic activity is important for understanding 1) the dynamo effect, responsible for generating solar and stellar magnetic fields, and 2) the different states of stellar evolution and the influence of the magnetic field during these stages of evolution.

The development of the Zeeman Doppler imaging technique, described in a series of five papers, is a benchmark in the stellar spectropolarimetry domain and consequently in the study of magnetic stars by observational methods. It opened a new window in the research of magnetic activity in cool stars through the measurement of the circular polarization directly from the spectra. The circular and also the linear polarized signals are detectable through a combination of the Doppler and Zeeman effects (Semel 1989).

A few years after the development of the ZDI technique, Semel & Li (1996) proposed the line addition principle to improve the signal-to-noise ratio and make possible the detection of extremely faint polarization signals in stars. Since then the addition principle has been used in different and more sophisticated techniques, and it has been particularly successful with the least squares deconvolution (LSD) technique (Donati et al. 1997) to construct mean intensity and/or polarization profiles. These mean profiles serve in a secondary step as input for codes that produce magnetic stellar surface maps. Observations at different phases of a star's rotational period are required to produce these maps (Brown et al. 1991; Hussain et al. 2000; Donati & Brown 1997).

\begin{figure} \par\includegraphics[width=9cm,clip]{10484fg1.ps}\includegraphics[width=9cm,clip]{10484fg2.ps}\vspace*{2mm} \end{figure} Figure 1:

The dashed lines represent the Stokes profiles of each of the individual lines listed in Table 1. The solid line represents the pseudo line obtained from the rest of the lines. Left side: stokes profiles considering a moderate field strength of 400 G. Right side: the same as in the left panel, but considering a strong field strength of 4 kG. In both cases the geometry of the magnetic field are the azimuthal and the inclination angles 70 and 45 degrees respectively.

Open with DEXTER

The simplest way to employ the line addition principle is to average the spectral lines. However, this rough line addition technique is currently not used to retrieve the magnetic field vector, not even for solar observations, where the inversion of the Stokes parameters in individual spectral lines is a commonly employed technique. Semel et al. (2009) have recently shown that the signal obtained from the average of multiple spectral lines, the so-called pseudo line, can be employed to estimate the longitudinal magnetic field using the center of the gravity method (e.g. Rees et al. 1979).

In this work we present in Sect. 2 more accurate inversion methods applied to the multi line approach by means of the construction and inversion of the pseudo line, and we extend the study to the linear states of polarization since considering the Stokes parameters (Q, U) is necessary to fully determine the orientation of the magnetic field.

The second part of this work, Sect. 3, is dedicated to another approach of detection of magnetic fields in stars, where all the lines contained in a given spectral range contribute to the final Stokes profiles. We first present the basis of the so-called PCA-ZDI technique. Then we describe the procedure to obtain the final Stokes profiles named multi Zeeman signatures and apply the developed technique to observed spectra of three cool stars. Finally, using synthetic spectra, we will show that the stellar magnetic fields can be correctly retrieved performing direct inversions of the multi Zeeman signature profiles.

The general conclusions are presented in Sect. 4.

2 The pseudo line approach

In this section we concentrate on the line addition technique using the simplest way to combine multiple spectral lines to average them. We called the resulting mean signal pseudo-line (PL) because it does not come from any physical entity, i.e. no intrinsic atomic properties like the Lande factor, potentials of excitation or others are associated with it.

The Stokes vector of the pseudo line, $\vec{S}_{\rm PL}=(I,Q,U,V)$, is obtained averaging each Stokes parameter seperately,

\begin{displaymath}\vec{S}_{\rm PL}=\ \sum_{i=1}^{n_l} \frac{ \left[ I_i(\lambda... ...mbda_{\rm R}), \ \ V_i(\lambda_{\rm R}) \right] } {n_{\rm l}}, \end{displaymath} (1)

where $\lambda_{\rm R} = \lambda - \lambda_{\rm c}$ denotes the reduced wavelength and ${n_{\rm l}}$ is the number of spectral lines.

Table 1:  Central wavelength, transition levels, relative intensities and Lande factors of the spectral lines of the multiplet 816 of the neutral iron.

In Table 1 are listed the individual lines that we have included in this work for the construction of the pseudo line. They have be chosen to be the same lines as in our previous work of Semel et al. (2009), hereafter referred to as Paper I.

Considering the solar case of a single point on the stellar surface, we used the code DIAGONAL (López Ariste & Semel 1999) to compute the Stokes profiles of the lines listed in Table 1 and to obtain the profiles of the pseudo line.

As mentioned in Paper I, we will assume that there is only one magnetic field vector on the stellar surface responsible for the polarized signals and the total radiation comes from this magnetic field. We do not dispute that more sophisticated scenarios can be considered, but we are not interested to simulate real stellar spectra but to show the capabilities of the pseudo line to retrieve the magnetic field vector.

In Fig. 1 we show two examples of the pseudo profiles computed with the same given atmospheric model (see Sect. 2.3), but with a different magnetic strength field. In the left panel, considering a field strength of 400 G, the profiles of all the individual lines are shaped similarly, and consequently the pseudo profiles keep the same shape. In the right panels, considering a field strength of 4 kG, the similarity in the shape of the individuals profiles is not preserved. Note for instance the variety of shape in the I and Q profiles.

The relatively reduced number of individual lines used to construct the pseudo line is a first step for a future generalization where considerably more lines can be included.

Before we continue the inspection of the pseudo line we present the procedure we follow to express the spectral lines as a function of the Doppler coordinates.

2.1 Variable transformation and adequate spectral resolution

In this section we describe a variable transformation from the wavelength coordinate into the velocity one: $\vec S(\lambda) \rightarrow \vec S(X)$.

At present, the typical spectrographes used for stellar spectropolarimetry are of the cross-dispersed type and cover a range of several thousands of Å. We will employ in our analysis a discrete selection of lines, but we present the general procedure as if we were dealing with the complete spectral range.

Consider the transformation equation

\begin{displaymath}X=c \log (\lambda / \lambda_0), \end{displaymath} (2)

where X is expressed in km s-1 and $\lambda $ in Å. c is the speed of light and $\lambda_0$ the minimum wavelength value in a given spectral interval. Deriving the preceding equation,

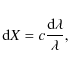
\begin{displaymath}{\rm d}X = c \frac{{\rm d}\lambda }{\lambda}, \end{displaymath} (3)

it is possible to obtain a constant step in km s-1 along the spectra when the velocity are discret values ${\rm d}X \rightarrow \Delta X$.

We have fixed the constant step in $\Delta X$ to 1 km s-1 so that we can invert Eq. (2) to express $\lambda $ as function of X

\begin{displaymath}\lambda=\lambda_0 \exp(X/c), \end{displaymath} (4)

where X=[0, 1, 2, ...].

Let $\lambda_{\rm obs}$ denote the discrete wavelength values obtained in the spectra after the data reduction. By imposing a constant step in $\Delta X$, a problem arises for certain values because the relation $\lambda (X)$ given by Eq. (4) will not necessarily coincide with the values of $\lambda_{\rm obs}$. An interpolation is then applied to determine the exact value at the wavelength of interest. Let $\lambda_n$ be one of the inexact values so that $\lambda_{{\rm obs},i}$ < $\lambda_n$ < $\lambda_{{\rm obs},i+1}$, and let S(Xn) denote any of the Stokes parameters at wavelength $\lambda_n$. The value S(Xn) will then be calculated by

\begin{displaymath}S(X_n) = S(\lambda_i) + \frac{S(\lambda_{i+1})-S(\lambda_i)} {\lambda_{i+1}- \lambda_i } (\lambda_n-\lambda_i ). \end{displaymath} (5)

With this algorithm, the spectra $S(\lambda)$ observed or synthetic will be transformed to a function of the new variable S(X).

2.2 The atmospheric model

In this section we explore the use of accurate inversion methods in their application to the pseudo line, i.e. inversion techniques based on the radiative transfer equation (RTE).

From experience in the solar data analysis we know that some correlation between the atmospheric parameters can generate ambiguities in the determination of the magnetic field when the noise level is close to the polarized signal levels (e.g. del Toro Iniesta & Ruiz Cobos 1996; Bellot Rubio & Collados 2003; Martínez González et al. 2006, and references therein). For simplicity, we initially avoid any possible model parametric degeneration by assuming that the atmospheric model is known and only the magnetic field vector is unknown. With this premise, we test the inference of the magnetic field through the inversion of the pseudo profiles in an ideal scenario where all the variables in the RTE are related to the magnetic field vector: the field strength (B), the azimuthal angle ( $\gamma_{\rm azi}$) and the inclination field ( $\gamma _{\rm incl}$). The atmospheric model we chose to compute the Stokes profiles has the following parameters: we fixed the gradient of the source function ( $\Delta \tau = 10$), the Doppler width to 50 mÅ, the ratio of the line-to-continuum absorption ($\eta$) twice the relative strength of the iron multiplet components and the fixed damping parameter value is 0.01.

The four Stokes parameters for all the individual Fe lines are computed considering the same atmospheric model, and the values of the magnetic field varies randomly in the ranges B=[0, 10] kG, $\gamma_{\rm azi}=[0,~180]$ degrees and $\gamma_{\rm incl}=[0,~90]$ degrees.

Consider now a given combination of the magnetic field parameters $Y^n=(B^n,~\gamma_{\rm azi}^{\ n},~\gamma_{\rm incl}^{\ n}$). From the synthesis of the Fe lines for this combination of parameters we then obtain the respective pseudo line for this Yn model. Note that we are in this way associating a magnetic model to the pseudo line.

\begin{figure} \par\includegraphics[width=17cm,clip]{10484fg3.ps}\vspace*{2mm} \end{figure} Figure 2:

First and second columns: inversions performed using different Stokes parameters (indicated in the Y-axis). Due to the inclusion of the magneto-optical effects in the computation of the profiles, the solutions in the second column contain the correct information in $\gamma _{\rm incl}$ parameters but with wider ranges of errors than in the first column. Third column: all the Stokes parameters are used to retrieve the magnetic field values. Last column: comparison of the error inversions with the discerning criteria (in black) and without them (in gray), more details are given in the text. The better results correspond to the discerned inversions.

Open with DEXTER

2.3 The inversion code

The exercises consist in the determination of the magnetic field supposed point-like and fixed in a known position in the stellar surface. The inversions in each Fe line and in the pseudo line have been done separately, and the goal is to compare the results.

We have developed one inversion code per Fe line and one for the pseudo line. The code works like this: first, we construct a representative synthetic database of a substantial number of profiles (56 600). Then, given a Stokes vector to invert, we find the best-fit solution from the database using the same algorithm as described in Ramírez Vélez et al. (2008).

We inverted a set of 500 profiles for each of the lines listed in Table 1. To compute the sets of profiles to invert, we followed the same procedure as when constructing the database profiles: we fixed the atmospheric model and considered random magnetic field vectors.

While inverting the set of Stokes profiles, we applied and compared different strategies to recover the magnetic field vector. Initially, we considered the four Stokes parameters ( I, Q, U, V) to simultaneously retrieve the solution of the three magnetic parameters (B, $\gamma_{\rm azi}$, $\gamma _{\rm incl}$). We then inverted the same set of profiles with only the I and V Stokes profiles, which is the most common case for stellar observations. Finally we performed the inversions using only the two linear Stokes parameters (Q and U).

The goal of performing different inversion strategies is twofold. On one hand, we compare the degree of accuracy of the inversions using the four Stokes parameters to the most typical case in the data analysis, that is when we only dispose of the intensity and circular polarization spectra.

On the other hand, this procedure permits us to improve the precision of the inversions. Let us call the discerning criteria as the use of different Stokes parameters to retrieve the different components of the magnetic field. Given that the inversion code works finding as solution the best-fit of the profiles in the databases, the employment of the discerning criteria has the advantage that the databases become larger and thus the code reduces the error of the inversions.

We remark however that the results of the analysis of the pseudo line do not depend on the proposed criteria described below, so that some readers may wish to skip the next subsection.

2.3.1 Database extension

To clarify the idea of the extension of the database, let $\vec{P_n}$ denote the Stokes vector for a given set of parameters so that $\vec{P_n} = \vec{P_n} (Y^n) $ and $Y^n=(B^n,~\gamma_{\rm azi}^{\ n},~\gamma_{\rm incl}^{\ n}$).

Let (Bj, $\gamma_{\rm incl}^{\ j}$) denote the associated solution values found with the inversion performed using the I and V Stokes parameters. Now, let $\gamma_{\rm azi}^{\ k}$ be the solution value after inversion of the Q and U Stokes parameters of the same $\vec{P_n}$. Since the values of the parameters were retrieved independently, $j \ne k$ (in more than 90% of the cases). Finally, we use the so-called discerned criteria to construct the final solution with the parameter combination $Y^{\rm sol}=(B^j,~\gamma_{\rm azi}^{\ k},~\gamma_{\rm incl}^{\ j}$). Since $Y^{\rm sol}$ was not originally in the database, we are ``extending'' the database through the use of the discerning criteria.

In Fig. 2, using a set of 500 profiles without any added noise, we show the inversion results following the described criteria. The graphics correspond to the inversions of the Fe I line at 6141 Å, the first line listed in Table 1.

While using only the I and V Stokes profiles to perform the inversions, as is shown in the first column in Fig. 2, more refined inversions are obtained for B and $\gamma _{\rm incl}$ when all the Stokes parameters are included in the inversions (third column). This is so because the number of atmospheric models whom parameters B and $\gamma _{\rm incl}$ are close to the original one gets increased when the $\gamma_{\rm azi}$ is ignored.

In the second column we present the results of the inversions using only the linear Stokes profiles (Q, U). In this case an improvement also happens for the inversions of the parameter $\gamma_{\rm azi}$ compared to the inversions of the third column where the four Stokes parameters are considered.

From the comparison of the inversions, showed in the forth column, we then conclude that the discerning criteria improve the inversion results: in the case of the field strength, the dispersions in the errors diminished considerable and the maximum error value decreased from $\sim$140 G (symbols in gray) to $\sim$25 G (symbols in black). In the case of the geometrical parameters, that is for the angles $\gamma _{\rm incl}$ and $\gamma_{\rm azi}$, the inversions also improve with the adopted criteria.

\begin{figure} \par\includegraphics[width=14.3cm,clip]{10484fg4.ps} \vspace*{2mm} \end{figure} Figure 3:

Percentage histogram inversions of the Fe lines (in gray color) and of the pseudo line (in black color). N represents the percentage number of inversion cases. From left to right are ordered by parameter of the magnetic field configuration: the strength, the azimuthal and, inclination angles. From top to bottom the comparison of the inversion by noise level is shown.

Open with DEXTER

Note that it is expected that the proposed discerning criteria increase the inversion precision only for those codes that employ a large set of profiles (databases) where the solution is found.

2.4 Testing the inversions of the pseudo line

One advantage of the developed inversion codes is the estimation of the typical errors. Thus to quantitatively compare the inversions retrieved from each line, the results are presented in terms of the absolute value of the difference between the original and the inferred parameters

\begin{displaymath} \vec{B}^{\rm ori} - \vec{B}^{\rm sol}=(\vert \Delta B \vert,... ...amma_{\rm azi} \vert, \ \vert \Delta \gamma_{\rm incl}\vert). \end{displaymath} (6)

Additionally, to study the effect of the noise in the determination of the magnetic field, we add three different noise levels to the profiles with the respective values of $ 1 \times 10^{-3}$, $1 \times 10^{-2}$ and $1\times 10^{-1}$ of the continuum level ($I_{\rm c}$).

In Fig.  3 we show the percentage histograms of the inversion's errors for all the Fe lines (in gray) and for the pseudo line (in black).

In the case without any added noise, we can see that all the inverted parameters are well retrieved. The histograms of the errors have a sharp peak at 0 and drop quickly. Note for instance that the field strength is inferred with an error smaller than 10 G with a high probability. The small errors for all the parameters are mainly due to the finiteness of the database, and are identified as the precision errors of the database. In any case, note that the results with the pseudo line are the very same the ones obtained from the inversions of individual spectral lines. We then conclude that the pseudo line encodes the information of the magnetic field vector as the individual spectral lines do!

In the lowest noise case ( $10^{-3} I_{\rm c}$), all parameters are also correctly retrieved, the errors being very close to the precision of the database. However, when increasing the noise levels to 10-2 and to $10^{-1} I_{\rm c}$, the error bars become more important, making the error distributions slightly wider. We remark that for these noisy cases the pseudo line is the one that gives the best results, corroborating that the addition of multiple lines increases the signal-to-noise (S/N) ratio.

2.5 Inversions with an unknown atmospheric model

We continue our inspection of the pseudo line relaxing the constraint that the magnetic field is the only free variable. We have thus included some line formation parameters in the atmospheric model to verify that in a more general case the goodness of the approach remains.

Considering as free variables the Doppler width ($V_{\rm D}$), the absorption line ratio ($\eta_0$), the source function gradient ( $\nabla \tau$) and the magnetic field vector, we repeated the same exercise as before inverting a set of 500 pseudo profiles.

The construction of the pseudo line follows the same principle as before: given a combination of the atmospheric parameters (excepting $\eta_0$) those values are used to compute all the Fe lines and to subsequently obtain the pseudo line. In the case of the $\eta_0$ parameter, a factor (denoted $\eta_{\rm f}$) modifies any of the $\eta_0$ values in the same amount, preserving their relative intensities (i.e. for all Fe lines, $\eta_0$ = $\eta_0 \cdot \eta_{\rm f}$).

In Fig. 4 we show the obtained results. After the inversion of the 500 pseudo profiles we found that the retrieved values in any of the parameters are correct (with an associated error of course). We then conclude that the atmospheric model and the magnetic field can both be deduced from the inversions of the pseudo line. We argue in favor of the results that the method used to invert the pseudo line is the very same as the one used for the construction.

With the present results we then conclude that the multi line approach based in the direct addition of many spectral lines, i.e. in the construction of the pseudo line, is a very useful tool in the study of solar and stellar magnetic fields.

\begin{figure} \par\includegraphics[width=16cm,clip]{10484fg5.ps} \end{figure} Figure 4:

Inversions of a set of 500 pseudo lines performed using the four Stokes parameters. The title in each graphic indicates the atmospheric parameters.

Open with DEXTER

3 The PCA-ZDI approach

Alternatively to the method presented in the last section, instead to make more efforts in this direction considering as many lines as possible in the pseudo line, we prefer to employ a more sophisticated approach recently proposed by Semel et al. (2006), hereafter referred to as Paper II. In this section we focus in this second approach called PCA-ZDI.

The principal idea of the PCA-ZDI technique is to incorporate the computation of the radiative transfer equations for instance with an atmospheric model in local thermodynamic equilibrium (LTE) in combination with a powerful statistical tool, the principal components analysis (PCA), to retrieve reliable detections of the stellar magnetic fields. This is in fact a way to overcome the employment of the weak field approximation used originally in the formulation of the ZDI technique (Semel 1989) and preserved in the LSD technique Donati et al. (1997).

3.1 Detection of stellar magnetic fields with PCA-ZDI

As will be shown, the PCA-ZDI technique is a powerful method for the detection of magnetic fields in stars. To summarize, firstly it is required to have of a representative database composed of stellar spectra at one's disposal. In fact, despite the domain of application, the construction of the database is a key step when it is intended to perform an analysis by principal components (Socas Navarro et al. 2001; Rees et al. 2000). In any case, once the database is defined, however many spectra are assembled in it, it is decomposed into a new basis using the single value algorithm (Golub & Van Loan 1996). The new basis is spanned in terms of eigenvectors which present many interesting properties. For the purposes of this work, we employ the eigenvectors of the new basis as detectors to retrieve the magnetic signature of the Stokes parameters from the spectra. We have called these magnetic signatures as multi Zeeman signature (MZS). The PCA-ZDI technique will thus retrieve always a MZS profile in the polarized Stokes parameters whenever a magnetic field in the stellar atmosphere is present and the signal-to-noise-ratio allows it.

From an observational point of view, the main constraint to retrieve the polarized Stokes parameters in individual spectral lines are the very faint levels expected in the signals.

3.2 Magnetic detectors

Based on the ideas proposed in the first paper of ZDI (Semel 1989), we considered that there is only one magnetic element in the stellar surface at the projected position ($\mu$) and we calculated the local Stokes profiles at this position. From the results already obtained with synthetic and observed spectra, we advance that the employment of the local profiles does not limit the detection in stars with complex magnetic field configurations, be they dipolar, multi-polar and/or multispot. A more detailed inspection of this statement will be presented in a forthcoming paper.

\begin{figure} \par\includegraphics[width=16.5cm,clip]{10484fg6.ps} \end{figure} Figure 5:

Plots of the first three eigenvectors in the four Stokes parameters in a small spectral range of $\lambda $ = [4500, 4503] Å.

Open with DEXTER

The stellar spectra in the four Stokes parameters have been established with the help of COSSAM[*], described in Stift (2000) and in Wade et al. (2001). COSSAM is an LTE line synthesis code in polarized light that calculates the Stokes profiles over arbitrarily large wavelength intervals, both for the Sun and for dipolar field geometries in magnetic stars. Direct opacity sampling is carried out over the $\sigma_{-}$, the $\sigma_{+}$, and the $\pi $ components separately of the (anomalous) Zeeman patterns of the individual lines.

While covering different positions in the stellar surface and at each one considering different field strengths and orientations it is possible to obtain a representative combination of synthetic spectra which will serve to construct the database.

The position of the stellar element is specified through the $\mu=\cos(\theta_{\rm LOS})$, where $\theta_{\rm LOS}$ is the angle between the line-of-sight direction and the normal to surface element. $\mu$ varies from [0.2, 1] with a step size of 0.2. At each $\mu$ position, we have spanned the magnetic field strength B = [0, 250, ..., 3000] G and the inclination angle $\gamma _{\rm incl}$ = [0, 15, ..., 90] $^{\circ}$. For economy in CPU-time we have fixed the azimuthal angle ( $\gamma_{\rm azi}$), but note that this fact does not limit the detection in the linear Stokes parameters since by applying rotations of the reference frame to the calculated spectra it is possible to pass from the Stokes Q to the Stokes U, or to obtain any desired configuration in the linear parameters (e.g. Sect. 6.4 in del Toro Iniesta 2003). Consequently it is justified to consider the approach used in the $\gamma_{\rm azi}$ parameter as the general case. In this way, the combination of parameters produces a database ( $\mathcal M$) with 425 spectra per Stokes parameter.

The spectral range covered from 450 to 750 nm in steps of 10 mÅ produced spectra of 300 000 wavelength points in each of the Stokes parameter. Below we consider the Stokes spectra as vectors $\vec{S}$ of dimension [300 000].

Finally, three different atmospheric models were considered: T=3500, 4750 and 5750 K. For each model we constructed the respective database. In other words, T is fixed to the value T0 in each database. In all cases, we have considered the same atomic solar abundances as in Grevesse & Sauval (1998), leaving out the molecular solar lines.

Let $\xi_{m}$ represent a given combination of the model parameters

\begin{displaymath}\xi_{m} = \xi_{m}(B,\gamma_{\rm incl}, \gamma_{\rm azi}, \mu, T_0)_{m}, \ \ \ m=[0,1,..,424], \end{displaymath} (7)

and let $\vec{S}_m(\xi_m$) denote the mth combination in any of the Stokes parameters calculated with COSSAM. Grouping all the 425 considered spectra models, we obtain an array $\mathcal M$ of the dimensions [300 000, 425] per Stokes parameter.

Applying the single value decomposition (SVD) procedure (Golub & Van Loan 1996), the new basis with a respective set of eigenvectors {$\vec{P}$} = [ $\vec{P}_0, \vec{P}_1,..., \vec{P}_{424}$] that span the database $\mathcal M$ is found.

Consequently, any spectra $\vec{S}_m$can be expressed as a linear combination of the eigenvectors. Considering the change of variables previously described in Sect. 2.1, the correspondent expression for the spectra $\vec{S}_m(X)$ in terms of the eigenvectors is

\begin{displaymath}\vec{S}_{m,i} ({\xi}_m, X) = \sum_{n=0}^{424} \ \alpha_{n,i}^m \ \vec{P}_{n,i}(X) \ ; \ \ \ \ \ \ i=(I,Q,U,V), \end{displaymath} (8)

where X expressed in km s-1 has replaced the wavelength value. Note that any Stokes spectra $\vec{S}_m$ can be already identified by an unique associated set of coefficients, { $\vec{\alpha}^m$} = [ $\alpha^m_0, \alpha^m_1,...,\alpha^m_{424}$].

In Fig. 5 we show a small portion of the first three eigenvectors of the database constructed for T=4750 K.

\begin{figure} \par\includegraphics[width=12cm,clip]{10484fg7.ps} \end{figure} Figure 6:

Percentage contribution of the first ten components from Eq. (8) in a logarithmic scale. Note that the contribution for the 10th component in the reconstruction of the original spectra is already inferior to at least 0.05 percent.

Open with DEXTER

\begin{figure} \par\includegraphics[width=16.2cm,clip]{10484fg8.ps}\par\includegraphics[width=16.2cm,clip]{10484fg9.ps} \end{figure} Figure 7:

Comparison of the MZS for the star IIpeg considered with the absolute value of the eigenvectors ( upper panels) and without it ( lower panels).

Open with DEXTER

3.3 Space dimension reduction

One of the reasons why we employ PCA is its capability of data compression and space dimensions reduction. We maintain that in Eq. (8) the equality is reached only when $n_{\max} = 424$, but in practice $n_{\max}$ could be dramatically reduced so that only the first components are considered. The consequent question is how to determine the number of components wich are really significant i.e., how to determine $n_{\max}$. To answer this question we have reconstructed all the profiles first with one component, then with two, and so on, and we compared the reconstructed spectra with the original ones. The mean percentage contribution per component is plotted in Fig. 6.

From Fig. 6 we can appreciate that the rate of contribution of the components to the original spectra decreases faster than an exponential, permitting us to cut the expansion in Eq. (8) to the first components. Given that the contribution for n=9 is already inferior to 0.001% in the intensity Stokes parameter and inferior to 0.05% in the polarized ones, we decided to keep only the first ten terms in Eq. (8). The same number of components will be used when obtaining the multi Zeeman signatures and inverting them. Moreover, for any star with the same temperature as the one considered in the database, the same ten eigenvectors will be useful to retrieved the MZS.

At this point in the development of the technique we followed a typical approach with PCA. Below we employ the eigenvectors as magnetic detectors so that by combining them with the ZDI principles, the magnetic signature from the spectra will be extracted.

3.4 The multi Zeeman signatures (MZS)

Another of the advantages in employing the PCA apart from the data compression is that it permits us to retrieve a set of coefficients { $\vec{\alpha}^m$ } associated univocally to each one of the spectra $\vec{S}_m$. We will use these coefficients to establish a relation to obtain the multi Zeeman signatures.

Given that the eigenvectors are orthonormals, from Eq. (8) it is trivial to obtain the set of coefficients for any of the synthetic Stokes spectra as

\begin{displaymath}\alpha_{n,i}^m= \vec{S}_{m,i}({\xi}_{m}, X) \cdot \ \vec{P}_{n,i}(X) ; \end{displaymath} (9)

where n = [0, 1, ..., 424] and i=(I, Q, U, V). The relation obtained in Eq. (9) represents the fundamental principle that will be employed to extract the magnetic signature from the observed spectra ( $\vec{S}^{\rm obs}$). To do this, the last step of the procedure is to consider the rotation velocity of the star and the associated Doppler effect, i.e. combine the MZS profiles with the ZDI principles.

It is important to mention that to equalize the spectral resolution of the observations with the one of the eigenvectors, we degraded the resolution of the eigenvectors to the spectral resolution of the observations. This last is done through a linear intrapolation similar to the one described in Sect. 2.1.

We proceed now to apply the same operation expressed in Eq. (9) to the observed spectra $\vec{S}^{\rm obs}$, but when the eigenvectors are Doppler shifted by an amount $Y=\Delta X$

\begin{displaymath}\alpha_{n,i}^{\rm obs} (Y) = \vec{S}_{i}^{\rm obs}(X) \ \cdot \ \vec{P}_{n,i}(X-Y). \end{displaymath} (10)

The vectorial product on the right side of in Eq. (10), wich permits us to retrieve the $ \alpha $-coefficients at each considered Y-value is equivalent to a cross correlation function between the spectra and the magnetic detectors (the eigenvectors).

On the other hand, it is convenient to mention that the expression found in Eq. (10) can be replaced by another one where the eigenvectors {$\vec{P}$} are substituted by the absolute value of the same eigenvectors, denoted by { $\vert\vec{P} \vert$}

\begin{displaymath}\alpha_{n,i}^{\rm obs} (Y) = \vec{S}_{i}^{\rm obs}(X) \ \cdot \ \mid \vec{P}_{n,i} \mid (X-Y) . \end{displaymath} (11)

Considering the whole range of Doppler velocities, Y=[Y0, $Y_1,~...,~Y_{\max}]$, the general expression of the multi Zeeman signature profiles ( $\vec{P}_{\rm MZS}$) is given by

\begin{displaymath}(\vec{P}_{\rm MZS})_{n,i}(Y)= \left( \alpha_{n,i}^{\rm obs} (... ... (Y_{1}),\ ...\ ,\ \alpha_{n,i}^{\rm obs} (Y_{\max}) \right) . \end{displaymath} (12)

Note that for each Stokes parameter ( I, Q, U, V) 425 multi Zeeman signatures are retrieved. Since the eigenvectors are orthonormals, each one of the 425 multi Zeeman signatures are in principle independents, wich makes it possible to perform independent analysis with each one seperately.

\begin{figure} \par\includegraphics[width=8.7cm,clip]{10484fg10.ps}\includegraphics[width=8.7cm,clip]{10484fg11.ps} \end{figure} Figure 8:

Examples of normalized intensity and circular polarization profiles of two solar type stars obtained with the presented PCA-ZDI technique. The left plots show the results for the HD 155555 binary system observed at the the AAT telescope (Australia) in April 2007. The right plots correspond to the results for the HD 190771 star observed at the Bernard Lyot telescope in August 2007.

Open with DEXTER

3.5 Magnetic detections

Now that we have presented the technique, we will apply it to the real observed spectra. We will employ the eigenvectors obtained for the case of single points in the stellar surface, but this does not limit the detection of the global magnetic field.

We will first compare the MZS obtained from Eq. (10) to those retrieved following Eq. (11). Let $v_{\max}$ and $v_{\min}$ denote the maximum and minimum projected rotation velocities of the star $v\sin i$, so that the star velocities span as $V^{\rm rot}=[v_{\min},...,v_{\max}]$. If the considered Doppler velocity Y does not coincide with any of the $V^{\rm rot}$ values, the intensity MZS profile recovers the continuum value and the polarized MZS profile an aleatory sequence of values around zero.

Contrarily, if Y coincides with one of the $V^{\rm rot}$ values, the magnetic signature in the polarized parameters and the total intensity profile are retrieved. In Fig. 7 we compare the first nine MZS considering the absolute value of the eigenvectors (upper panels) to the first nine MZS when the absolute value is not included (lower panels). The data correspond to the IIpeg star observed in August 2007 with the Bernard Lyot telescope at the Pic du Midi Observatory with the NARVAL polarimeter.

From Fig. 7 we appreciate that when the absolute value is included the nine polarized MSZ are clearly detected with a high S/N ratio. If the absolute value is not considered the level of the first polarized MZS is clearly superior to the noise level, but the level of the MZS began to decrease for the rest of eigenvectors.

A discussion about how to take advantage of this multiple multi Zeeman signature detections will be presented in a forthcoming paper. Below we prefer to add the nine individual multi Zeeman signatures to obtain a total profile per Stokes parameter.

In the last subsection we showed that the expansion in Eq. (8) can be reduced to the first ten components. We now add the contribution from these components to find the final expression that will be employed to retrieve the multi Zeeman signature

\begin{displaymath}(\vec{P}_{\rm MZS})_{i}(Y)= \sum_{n=0}^{9} \left( \alpha_{n,i... ...} (Y_{1}),\ ...\ ,\ \alpha_{n,i}^{\rm obs} (Y_{\max}) \right). \end{displaymath} (13)

Considering the absolute value of the eigenvectors and following the procedure of the last equation, we show in Fig. 8 two examples of the MZS profiles obtained in intensity and in circular polarization of two cool stars. The binary system HD 155555, left panels, was observed in April 2007 with the Anglo Australian Telescope at the AAO observatory, using the SEMPOL polarimeter. The solar type star HD 190771, right panels, was observed in August 2007 with the Bernard Lyot telescope at the Pic du Midi Observatory, using the NARVAL polarimeter.

The detection of magnetic fields in these three stars were also found through the LSD method. The MZS profiles from Fig. 8 actually appear to be similar in shape to those retrieved with the LSD method (Dunstone et al. 2008; Petit et al. 2008). Nevertheless a proper comparison has not been done to distinguish possible differences in the profiles and to determine how important those differences could be when retrieving the magnetic field.

In any case the PCA-ZDI technique was for the moment applied with success to retrieve mostly the circular states of polarization in cool stars (Ramírez Vélez et al. 2006). This is partly due to the absence of representative samples of linear data to analyze, so we leave the studies where the linear states of polarization can be incorporated in the detection and measurement of stellar magnetic fields for a future work.

3.6 Inversions of the multi Zeeman signatures

In this section we show that it is possible to infer the magnetic field through the inversion of the MZS profiles. We will use a simple scenario where we consider again local Stokes profiles from different surface elements. We further assume that there is a point-like magnetic field in the surface elements. From now on, the MZS to which we refer will be obtained from the local Stokes profiles through Eq. (13). Given a MZS, the inversion exercise consists in finding the position of the surface element and the magnetic field vector.

The local Stokes profiles are calculated for a small spectral range of [5400, 5500] Å. The parameters of the Stokes profiles and thus those of the MZS vary randomly in the following ranges: the magnetic field strength [0, 10] kG, the inclination field [0, 90]$^{\circ}$, the magnetic azimuthal angle [0, 180]$^{\circ}$ and the projected position of the surface element ($\mu$) [0, 1].

Since the inversions are performed in the space of the MZS, we have produced 6000 MZS that serve as the database where we tested the inversion of a set of 600 MZS.

As mentioned previously there are two alternatives to produce MZS, namely, whit or without considering the the absolute value of the eigenvectors (Eqs. (10) and (11)). We will test both alternatives and will show that whether or not the absolute value is included, the inversions are correct.

We first present the case where the absolute value of the eigenvectors is employed to retrieve the MZS. In the upper panel of Fig. 9 we show an example of a synthetic MZS (in black color) and the respective MZS solution (in gray color). The inversion is correct not only because of the similarity between the MZSs, but because the values of the parameter solution are close to the originals ones (see the title in each panel). Moreover, given that any MZS is associated to a stellar spectrum, in the lower panels of Fig. 9 we corroborate that as expected the Stokes profiles associated to the MZS solution fit the originals one well enough.

\begin{figure} \par\includegraphics[width=8.9cm,clip]{10484fg12.ps}\vspace*{2mm} \includegraphics[width=8.9cm,clip]{10484fg13.ps} \end{figure} Figure 9:

In black the original profiles, in gray the retrieved solution. Upper panels, examples of the MZS when the absolute value of the eigenvectors is considered. Lower panels, a small spectral range of 10 Å of the Stokes profiles associated to the MZSs.

Open with DEXTER

In Fig. 10 we show the MZS associated to the same combination of parameters as before but for the case where the absolute value is not considered. The solution parameters in this case are also close to the original ones (upper panels) and the associated solution Stokes profiles give a good fit to the original Stokes profiles (lower panels).

\begin{figure} \par\includegraphics[width=8.9cm,clip]{10484fg14.ps}\vspace*{2mm} \includegraphics[width=8.9cm,clip]{10484fg15.ps} \end{figure} Figure 10:

Same as in Fig. 9 but when the absolute values of the eigenvectors are not considered to produce the MZS.

Open with DEXTER

Finally, we present the results of the inversions of the 600 MZS. In Fig. 11 the upper panels correspond to the case where the absolute value of the eigenvectors is included to produce the MZS, and the lower panels correspond to the case when it is not included.

These results show that in both cases the magnetic field vector is correctly retrieved despite the position in the stellar surface for all strength fields and orientations.

The final conclusion in this section is that the multi Zeeman signature represents not only an effective tool to detect stellar magnetic fields, but also that inversions in the space of the multi Zeeman signatures can be directly performed.

\begin{figure} \par\includegraphics[width=8.7cm,clip]{10484fg16.ps}\vspace*{2mm} \includegraphics[width=8.7cm,clip]{10484fg17.ps} \end{figure} Figure 11:

Inversion results of the entire set of MZS profiles. The upper (lower) panels are the results for the case when the absolute value of the eigenvectors is (not) included to produce the MZS. In both cases the parameters are properly retrieved.

Open with DEXTER

4 Conclusions

We focused on the multi line analysis of spectropolarimetric data with an emphasis on the detection and inference of stellar magnetic fields. The use of multiple lines is required to increase the signal-to-noise-ratio in those cases where the polarized signals in individual spectral lines are significantly inferior to the noise level, remaining hidden for analysis purposes. This is typically the case for instance in observations of cool stars.

To deal with this observational constraint, we have presented the development of two new approaches that both serve to extract a polarized signal from a mixture of several individual spectral lines. While employing any of the proposed multi-line techniques, namely the pseudo line or the PCA-ZDI approach, we notice three main advantages: (1) the contributions of all the spectral lines to the final polarization signal are included -regardless of the presence of a similarity in the individual shape profile-, (2) it is a valid method for the detection of the circular and the linear states of polarization and (3) it is not limited to weak or to strong magnetic field regimes.

In the case of the pseudo line, we have presented an inversion code that builds a database of pseudo lines where each one is attached to a particular atmospheric model.

Initially, considering an ideal scenario where the magnetic field is the only free variable of the atmospheric model, we found that the results obtained from the inversions of the pseudo line are as good as those obtained from individual spectral lines. We also showed that it is expected that in the case of real observed spectra (with a given noise level), the best results in any of the magnetic components are retrieved with the inversions of the pseudo line. Finally, we showed that the atmospheric model can also be inferred through the inversions of the pseudo line in addition to the magnetic field.

In the case of the multi Zeeman Signatures, we discussed in detail the development of the technique, and we applied it to real observed data to illustrate the type of profile obtained with the PCA-ZDI technique.

The circular polarized MZS profiles, like those in Fig. 8 where the polarized signal level is clearly superior to the noise level, represent in a unambiguous way a detection of the magnetic field present in the stellar object.

By construction, the multi Zeeman signatures contain the information of the magnetic field and atmospheric model. To verify this, we have performed inversions in a synthetic set of MZS profiles. The results obtained after the inversions show that all the considered parameters in the atmospheric model are correctly retrieved.

It is pertinent to mention that some refinements have to be done to the technique to achieve magnetic field measurements through the inversion of the MZS profiles. In particular the Doppler broadening effect due to the rotation of the stars and the case of inversions of continuum field distributions over the stellar surface will be presented in forthcoming papers. For the moment we established that PCA-ZDI is a robust technique for the analysis of stellar magnetic magnetic fields.

The final conclusion of this work is that when the inversion of the magnetic polarized signal is done by the same method used as the one used to construct them, the physical parameters that determine the line formation process can be properly recovered, included in particular, the stellar magnetic field.

References

  1. Allen, C. W. 2000, Astrophysical Quantities (New York: Springer Verlag and AIP press) [Google Scholar]
  2. Brown, S. F., Donati, J. F., Rees, D. E., & Semel, M. 1991, A&A, 250, 463 [NASA ADS] [Google Scholar]
  3. Bellot Rubio, L. R., & Collados, M. 2003, A&A, 406, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. del Toro Iniesta, J. C. 2003, Introduction to spectropolarimetry (Cambridge University Press) [Google Scholar]
  5. del Toro Iniesta, J. C., & Ruiz Cobos, B. 1996, SoPh, 164, 169 [NASA ADS] [Google Scholar]
  6. Donati, J. F., & Brown, S. F. 1997, A&A, 326, 1135 [NASA ADS] [Google Scholar]
  7. Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291,658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  8. Dunstone, N. J., Hussain, G. A. J., Collier Cameron, A., et al. 2008, MNRAS, 387, 481 [NASA ADS] [CrossRef] [Google Scholar]
  9. Golub, G. H., & Van Loan, C. F. 1996, Matrix Computations, 3rd edn. (Baltimore: Johns Hopkins University Press) [Google Scholar]
  10. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
  11. Hussain, G. A. J., Donati, J. F, Collier Cameron, A., & Barnes, J. R. 2000, MNRAS, 318, 961 [NASA ADS] [CrossRef] [Google Scholar]
  12. López Ariste, A., & Semel, M. 1999, A&AS, 139, 417 [Google Scholar]
  13. Martínez González, M. J., Collados, M. J., & Ruiz Cobos, B. 2006, A&A, 456, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  15. Ramírez Vélez, J. C., López Ariste, A., & Semel, M. 2008, A&A, 487, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Rees, D. E., & Semel, M. 1979, A&A, 79, 1 [NASA ADS] [Google Scholar]
  17. Rees, D. E., López Ariste, A., Thatcher, J., & Semel, M. 2000, A&A, 355, 759 [NASA ADS] [Google Scholar]
  18. Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
  19. Semel, M., & Li, J. 1996, SoPh, 164, 417 [Google Scholar]
  20. Semel, M., Ramírez Vélez, J. C., Martínez González, M., et al. 2009, A&A, 504, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Semel, M., Rees, D., Ramírez Vélez, J. C., Stift, M., & Leone, F. 2006, ASPC, 358, 355 [Google Scholar]
  22. Socas Navarro, H., López Ariste, A., & Lites, B. W. 2001, ApJ, 553,949 [NASA ADS] [CrossRef] [Google Scholar]
  23. Wade, G. A., Bagnulo, S., Kochukhov, O. P., et al. 2001, A&A, 374, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Footnotes

... COSSAM[*]
Codice per la Sintesi Spettrale nelle Atmosphere Magnetiche.

All Tables

Table 1:   Central wavelength, transition levels, relative intensities and Lande factors of the spectral lines of the multiplet 816 of the neutral iron.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{10484fg1.ps}\includegraphics[width=9cm,clip]{10484fg2.ps}\vspace*{2mm} \end{figure} Figure 1:

The dashed lines represent the Stokes profiles of each of the individual lines listed in Table 1. The solid line represents the pseudo line obtained from the rest of the lines. Left side: stokes profiles considering a moderate field strength of 400 G. Right side: the same as in the left panel, but considering a strong field strength of 4 kG. In both cases the geometry of the magnetic field are the azimuthal and the inclination angles 70 and 45 degrees respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{10484fg3.ps}\vspace*{2mm} \end{figure} Figure 2:

First and second columns: inversions performed using different Stokes parameters (indicated in the Y-axis). Due to the inclusion of the magneto-optical effects in the computation of the profiles, the solutions in the second column contain the correct information in $\gamma _{\rm incl}$ parameters but with wider ranges of errors than in the first column. Third column: all the Stokes parameters are used to retrieve the magnetic field values. Last column: comparison of the error inversions with the discerning criteria (in black) and without them (in gray), more details are given in the text. The better results correspond to the discerned inversions.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14.3cm,clip]{10484fg4.ps} \vspace*{2mm} \end{figure} Figure 3:

Percentage histogram inversions of the Fe lines (in gray color) and of the pseudo line (in black color). N represents the percentage number of inversion cases. From left to right are ordered by parameter of the magnetic field configuration: the strength, the azimuthal and, inclination angles. From top to bottom the comparison of the inversion by noise level is shown.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{10484fg5.ps} \end{figure} Figure 4:

Inversions of a set of 500 pseudo lines performed using the four Stokes parameters. The title in each graphic indicates the atmospheric parameters.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{10484fg6.ps} \end{figure} Figure 5:

Plots of the first three eigenvectors in the four Stokes parameters in a small spectral range of $\lambda $ = [4500, 4503] Å.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{10484fg7.ps} \end{figure} Figure 6:

Percentage contribution of the first ten components from Eq. (8) in a logarithmic scale. Note that the contribution for the 10th component in the reconstruction of the original spectra is already inferior to at least 0.05 percent.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.2cm,clip]{10484fg8.ps}\par\includegraphics[width=16.2cm,clip]{10484fg9.ps} \end{figure} Figure 7:

Comparison of the MZS for the star IIpeg considered with the absolute value of the eigenvectors ( upper panels) and without it ( lower panels).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.7cm,clip]{10484fg10.ps}\includegraphics[width=8.7cm,clip]{10484fg11.ps} \end{figure} Figure 8:

Examples of normalized intensity and circular polarization profiles of two solar type stars obtained with the presented PCA-ZDI technique. The left plots show the results for the HD 155555 binary system observed at the the AAT telescope (Australia) in April 2007. The right plots correspond to the results for the HD 190771 star observed at the Bernard Lyot telescope in August 2007.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.9cm,clip]{10484fg12.ps}\vspace*{2mm} \includegraphics[width=8.9cm,clip]{10484fg13.ps} \end{figure} Figure 9:

In black the original profiles, in gray the retrieved solution. Upper panels, examples of the MZS when the absolute value of the eigenvectors is considered. Lower panels, a small spectral range of 10 Å of the Stokes profiles associated to the MZSs.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.9cm,clip]{10484fg14.ps}\vspace*{2mm} \includegraphics[width=8.9cm,clip]{10484fg15.ps} \end{figure} Figure 10:

Same as in Fig. 9 but when the absolute values of the eigenvectors are not considered to produce the MZS.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.7cm,clip]{10484fg16.ps}\vspace*{2mm} \includegraphics[width=8.7cm,clip]{10484fg17.ps} \end{figure} Figure 11:

Inversion results of the entire set of MZS profiles. The upper (lower) panels are the results for the case when the absolute value of the eigenvectors is (not) included to produce the MZS. In both cases the parameters are properly retrieved.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.