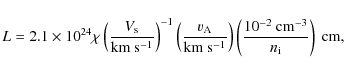EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 511 (February 2010) A&A, 511 (2010) A41 Full HTML
Free Access
Issue
A&A
Volume 511, February 2010
Article Number A41
Number of page(s) 9
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200913277
Published online 04 March 2010
A&A 511, A41 (2010)

Transient evolution of C-type shocks in dusty regions of varying density

I. Ashmore1 - S. Van Loo1 - P. Caselli1 - S. A. E. G. Falle2 - T. W. Hartquist1

1 - School of Physics and Astronomy, University of Leeds, Leeds LS2 9JT, UK
2 - School of Mathematics, University of Leeds, Leeds LS2 9JT, UK

Received 10 September 2009 / Accepted 16 November 2009

Abstract
Context. Outflows of young stars drive shocks into dusty, molecular regions. Most models of such shocks are restricted by the assumptions that they are steady and propagating in directions perpendicular to the magnetic fields. However, the media through which shocks propagate are inhomogeneous and shocks are not steady. Furthermore, only a small fraction of shocks are nearly perpendicular.
Aims. We identify features that develop when a shock encounters a density inhomogeneity and ascertain if any part of the precursor region of a non-steady multifluid shock ever behaves in a quasi-steady fashion. If it does, some time-dependent shocks may be modelled approximately without solving the time-dependent hydromagnetic equations.
Methods. We use the code employed previously to produce the first time-dependent simulations of fast-mode oblique C-type shocks including a self-consistent calculation of the thermal and ionisation balances and a fluid treatment of grains.
Results. Simulations were made for initially steady oblique C-type shocks, each of which encounters one of three types of density inhomogeneities. For a semi-finite inhomogeneity with a density larger than the surrounding medium's, a transmitted shock evolves from being of J-type to a steady C-type shock on a timescale comparable to the ion-flow time through it. A sufficiently upstream part of the precursor of an evolving J-type shock is quasi-steady. The ion-flow timescale is also relevant for the evolution of a shock moving into a region of decreasing density. The models for shocks propagating into regions in which the density increases and then decreases to its initial value cannot be entirely described in terms of the results obtained for monotonically increasing and decreasing densities.
Conclusions. We present the first time-dependent simulations of dusty C-type shocks interacting with density perturbations. We studied the transient evolution of the shock structure and find that the initial interaction always produces a transition to a J-type shock. Furthermore, the long-term evolution back to a C-type shock cannot always be approximated by quasi-steady models.

Key words: magnetohydrodynamics (MHD) - shock waves - dust, extinction - ISM: jets and outflows

1 Introduction

Jets and winds associated with low and high mass proto-stellar objects interact with the molecular clouds surrounding them (e.g. Arce et al. 2007). Shocks are driven into the clouds sweeping up cloud material and producing large scale (0.1-1 pc) molecular outflows with velocities of 10-100 km s-1 (e.g. Bachiller & Tafalla 1999; Santiago-García et al. 2009; Reipurth & Bally 2001). These outflows are often bipolar and are extremely common in young, low-mass stars (Bally & Lada 1983), as well as high-mass stars (Cesaroni 2005; López-Sepulcre et al. 2009; Shepherd 2005).

As the fractional ionisation in molecular clouds is low ( $\chi < 10^{-6}$; Dalgarno 2006, and reference therein), the neutral gas and magnetic field are weakly coupled. This coupling is mediated via ion-neutral and grain-neutral collisions, as the magnetic field forces the charged particles to move through the bulk of neutral particles. When a shock forms, the ion-neutral collisions accelerate, compress and heat the neutral gas upstream of the shock, forming a magnetic precursor. If the shock velocity is low and the postshock cooling efficient, the shock becomes continuous in all fluids and is then referred to as a C-type shock (Mullan 1971; Draine 1980). Observational studies of the velocity widths of SiO emission suggest that most shocks near low mass proto-stellar objects are C-type (e.g. Martin-Pintado et al. 1992).

Previous studies of C-type shocks in dusty plasmas have focused on the shock structure under steady state conditions (e.g. Wardle 1998; Guillet et al. 2007; Pilipp & Hartquist 1994; Pilipp et al. 1990; Draine et al. 1983). However, SiO observations suggest that proto-stellar jets and winds interact with clumpy structures along their propagation axis (Jørgensen et al. 2004; Mikami et al. 1992; Lefloch et al. 1998). Therefore, the steady state assumption must be relaxed. Ciolek & Roberge (2002) were the first[*] to use a time-dependent multifluid magnetohydrodynamics (MHD) code, including dust grains dynamics, to study fast-mode C-type shocks. However, their study is limited to perpendicular shocks. The multifluid approach developed by Falle (2003) overcomes this restriction. Using the Falle method, Van Loo et al. (2009, hereafter Paper I) produced the first time-dependent simulations of fast-mode, oblique C-type shocks that evolve to steady state and include a selfconsistent calculation of the thermal and ionisation balances and a fluid treatment of grain dynamics.

While the time-dependent simulations of Paper I still focus on steady state shock structures, we now extend this work by studying the temporal evolution of fast-mode C-type shocks interacting with regions of inhomogeneous density. In Sect. 2 we describe the numerical model with the initial conditions. We then apply the code to an oblique shock propagating into a region of varying density (Sect. 3) and, in Sect. 4, we discuss these results and give our conclusions.

2 The model

2.1 Numerical code

The numerical code that we use in this paper follows the dynamics of a multifluid plasma consisting of neutrals, ions, electrons and N dust grain species. Here we only consider a single fluid of spherical, large grains with a radius and mass of $a_{\rm g} = 0.4~\mu$m and $8.04 \times 10^{-13}$ g. (The density of the grains is assumed to be 3 g cm-3.) We have included relevant mass transfer processes, such as electron recombination with Mg+and dissociative recombination with HCO+, and radiative cooling by O, CO, H2 and H2O. Also, the mass and charge transfer from ions and electrons to the dust grains is taken into account to calculate the average grain charge. This way we calculate self-consistently the thermal and ionisation balances including appropriate microphysics.

The details of the numerical scheme, which is based on Falle (2003), are given in Paper I. As in Paper I, we advance the scheme explicitly, even though this implies a restriction on the stable time-step, i.e. Falle (2003)

\begin{displaymath}\Delta t \leq \frac{r_{\rm ad}}{\left(r^2_{\rm H} + r^2_{\rm ad}\right)} \Delta x^2, \end{displaymath}

where $r_{\rm ad}$ is the ambipolar resistivity, $r_{\rm H}$ the Hall resistivity and $\Delta x$ the cell spacing. Thus, the time step becomes small for a high numerical resolution, or when the Hall resistivity becomes large compared to the ambipolar resistivity. In our simulations the Hall resistivity is only ever comparable to the ambipolar resistivity implying that the stable time-step is not severely restricted.

The adopted chemistry is based on the network given in Pilipp et al. (1990), and we used the rate coefficients that they did. The code allows the option of incorporating as many advected scalar equations with source terms (i.e. rate equations for fractional abundances) as necessary and solving them with the same methods as those employed to solve the fluid equations. We used rate equations and charge neutrality to obtain the fractional abundances of ions and electrons and the average grain charge. We assumed that cosmic ray induced ionisation leads immediately to the production of heavy molecular ions (e.g. HCO+and H3O+) which involves the justifiable neglect of $\rm {H_3}^+$recombination. The branching ratio between HCO+ and H3O+formation depends on the abundances of simple neutral species like O and CO and the rate coefficients of the reaction rates of $\rm {H_3}^+$ with them. Charge transfer with metals (e.g. Mg) creates metallic ions. All gas phase ions recombine with electrons and on grains. Unlike Pilipp et al. (1990), we did not include the possibility that Mg+ reacts with H2; it does so only in regions with sufficiently high temperatures that the grain charge is high enough and the electron fractional abundance low enough that recombination is dominated by recombination with grains leading to a negligible difference between the rates at which Mg+ and MgH+ are removed. While the abundances of ions and electrons and grain charge can be studied easily with rate equations, the conversion of O to H2O is more problematic as the relevant reaction rates increase by many orders of magnitude as shock gas is heated from several hundred to a thousand degrees. For an H2 number density of 105 cm-3, the timescale for the removal of O in reactions with H2 is $1.4 \times 10^{12}$ s, $1.4 \times 10^9$ s, and $6.7 \times 10^7$ s at 300 K, 600 K, and 1000 K, respectively. The corresponding removal timescale of OH in reactions with H2 are $1.5 \times 10^9$ s, $3.2 \times 10^7$ s, and $4.2 \times 10^6$ s. We could use the code to deal with the O, OH, and H2O chemistry even at temperatures in excess of 103 K if we placed upper limits on the reaction rates; this would still give oxygen chemistry that would be close to the appropriate high temperature equilibrium. However, here we simply assumed that almost all oxygen not in CO is in O until T = 500 K. After it reached 500 K almost all oxygen not in CO was taken to be in H2O. It will remain mostly in H2O for very long times even after the postshock gas has cooled. This approach led to neutral temperatures in the 300-500 K range that are somewhat higher and in the 500-700 K range that are somewhat lower than a more thorough treatment would have. However, this results in a negligible difference in the shock behaviour which is much more strongly influenced by the ionisation structure, which in turn is regulated in this regime primarily by cosmic ray induced ionization and recombination on grains, and grain dynamics than the details of the neutral gas temperature structure.

\begin{figure} \par\includegraphics[width=6.75cm,clip]{13277f1a.eps}\hspace*{1.5cm} \includegraphics[width=6.6cm,clip]{13277f1b.eps} \vspace*{-2.5mm} \end{figure} Figure 1:

Evolution of the shock structure in the shock frame as a 25 km s-1 C-type shock interacts with a inhomogeneity of increasing density (from $n_{\rm H} = 10^4~ {\rm cm^{-3}}$ to $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$). The left panel shows the neutral density and the right panel the grain-neutral relative speed. The profile for the initial C-type shock is given by the thin solid line, while the dashed line shows the shock structure $9.75 \times 10^3$ yr after the shock first interacts with the perturbation, the dotted line after $2.56\times 10^4$ yr, the dash-dotted line after $6.37\times 10^{4}$ yr, and the thick solid line the final steady C-type shock structure (reached after $7.92 \times 10^4$ yr).

Open with DEXTER

2.2 Initial conditions

Unlike the simulations described in Paper I, for which the initial conditions are J-type shocks, each of our simulations starts from a steady C-type shock propagating through a medium with upstream hydrogen nuclei number density of either $n_{\rm H} = 10^4~ {\rm cm^{-3}}$ or $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$. The shock moves parallel to the x-axis with a velocity $V_{\rm s}$ of 25 km s-1. For both cases the initial upstream fluid temperatures are 8.4 K and the upstream magnetic field strengths are B = 10-4 G. The magnetic field lies in the x,y-plane with the angle between the shock normal and the field being 45$^\circ$.

As we are interested in the interaction of a C-type shock with an inhomogeneous medium, we introduce an upstream density perturbation. The shape of the perturbation is chosen so that it reasonably reproduces all or part of the density profile of observed clumps or cores (e.g. Tafalla et al. 2004). Each perturbation is described solely by its width and the density contrast (i.e. a multiple of initial upstream density). Unless otherwise stated, the width and density contrast are 1017 cm and 10 respectively.

2.3 Computational considerations

2.3.1 Computational grid

Some care must be given to the size of the computational grid for models with varying upstream density. This is because a change in the upstream density alters the shock width. For all our simulations, the constraint

\begin{displaymath}\chi < 3 \times 10^{-9} \left(\frac{V_{\rm s}}{\rm km~ s^{-1}}\right) \end{displaymath}

is met (with $\chi$ the fractional ionisation). The shock thickness is then determined by grain-neutral rather than ion-neutral drag (see Paper I) and given approximately by

\begin{displaymath} L = 2.1 \times 10^{24} \chi \left(\frac{V_{\rm s}}{\rm km\ ... ...ft(\frac{10^{-2}~ {\rm cm}^{-3}}{n_{\rm i}} \right) ~{\rm cm}, \end{displaymath} (1)

where $v_{\rm A}$ is the Alfvén speed and $n_{\rm i}$ the ion number density. The shock width in our simulations varies by an order of a magnitude. We need to ensure that the numerical domain is large enough to contain the largest shock width but has enough cells to resolve structures on the finest scale, i.e. the shock width at the highest density. Therefore, we estimate the shock thickness on both densities using Eq. (1). The numerical domain is then set to -10 L < x < 10 L with L the shock width at the lowest density. As the shock width at the highest density is roughly an order of magnitude smaller and we want to resolve it with approximately 10 cells across the shock structure, we adopt a uniform grid of 1200 cells for the numerical domain. We impose a fixed inflow at the upstream boundary and a free-flow boundary condition at the downstream side.

2.3.2 Varying shock speed

When a shock moves through a region of varying density, its propagation speed changes. As we follow the evolution in the initial shock frame, the new shock structures (see Sect. 3) will eventually move off the grid. In order to follow their evolution properly, we adjust the velocity of the initial shock frame with a Lorentz transformation along the x-axis.

2.3.3 Charged fluid inertia

Although our initial conditions are given by a C-type shock, the interaction with a density inhomogeneity produces a neutral subshock (see Sect. 3). Within the subshock, our assumption that the charged fluid inertia is negligible no longer holds. However, the neutral subshock structure can be accurately modelled with our numerical model (see Falle 2003). Furthermore, the inertial phase is expected to be shortlived compared to the timescales of the shock-clump interaction and the subsequent approach to steady state. We can expect that the evolution of the shock shortly after the interaction is modified by charged fluid inertia, but that the changes are modest.

3 Results

Several aspects of the shock interaction with an inhomogeneity are consistent for all our simulations. We discuss these first before commenting on specific models.

In each of our models the initial shock width is larger than or comparable to the length scale of the perturbation. The interaction with the perturbation then leads to a transmitted wave-reflected wave pair separated by a contact discontinuity. Note that, if the perturbation length scale were large compared to the shock width, there would not be a reflected wave. The relative strength of the transmitted and reflected components is determined by both the initial shock speed and the amplitude of the perturbation.

The transmitted shock is initially a J-type shock with a precursor and a subshock. The upstream conditions change faster than information can propagate across the front of the subshock. After some time, collisions between ions and neutrals generate a neutral precursor which then evolves into a C-type shock. The transmitted C-type shock is narrower than the initial shock if the upstream density increases and broader if the upstream density decreases.

While the transmitted wave is always a shock, the reflected wave which propagates into the post-shock flow can either be a rarefaction wave or a shock. As the reflected wave connects the far downstream flow with the downstream flow of the transmitted shock, it is clear that a rarefaction forms when the post-shock density of the transmitted shock is lower than the far downstream density and a shock when it is greater. Similarly to the transmitted shock, the reflected shock evolves from a J-type shock into a C-type shock.

In this paper we focus primarily on the transmitted shocks. We do not follow the long term evolution of the reflected waves. The reflected component thus eventually moves off the grid at the downstream boundary. However, numerical artefacts arise when shocks are reflected from free-flow boundaries (e.g. Hedstrom 1979). Although we can use non-reflecting boundary conditions to overcome this problem, we prefer to simply remove the reflected wave from the computational domain. This can be done because the reflected wave and transmitted shock are separated by a contact discontinuity.

\begin{figure} \par\includegraphics[width =6.1cm,clip]{13277f2a.eps}\par\vspace*... ...\par\vspace*{5mm} \includegraphics[width =6.1cm,clip]{13277f2d.eps} \end{figure} Figure 2:

x component of the neutrals (solid), ions and electrons (dashed) and the grains (dotted) velocity in the upstream frame at different times for a 25 km s-1 C-type shock propagating in a higher density region (from $n_{\rm H} = 10^4~ {\rm cm^{-3}}$ to $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$). a) shows the the initial C-type shock, b) the the shock structure $9.75 \times 10^3$ yr after the first interaction of the shock with the inhomogeneity, c) after $2.56\times 10^4$ yr and d) the final steady C-type shock (after $7.92 \times 10^4$ yr).

Open with DEXTER

\begin{figure} \par\includegraphics[width =6.1cm,clip]{13277f3a.eps}\par\vspace*... ...\par\vspace*{5mm} \includegraphics[width =6.1cm,clip]{13277f3d.eps} \end{figure} Figure 3:

Ion (dashed), electron (dotted) and neutral temperature (solid) and the average grain charge (dash-dotted) in electron charge units for the same shock model as in Fig. 2 at the same times.

Open with DEXTER

3.1 Increasing density

We first follow the evolution of a C-type shock in the molecular outflow from a proto-stellar object moving into a denser region. We consider a 25 km s-1 shock propagating from a region of $n_{\rm H} = 10^4~ {\rm cm^{-3}}$ into a higher density plasma. The initial shock is a strong fast-mode shock with an Alfvénic Mach number of $\approx$11.5.

When the C-type shock encounters the density perturbation, two J-type shocks, a reflected and a transmitted one, form within $3 \times 10^3$ yr. The neutral subshocks can be easily seen in both the velocity and temperature plots of Figs. 1-3, i.e. the discontinuous jump in the neutral velocity along the x-axis and the drastic cooling of the different fluids. The temperature plots also shows that the transmitted shock is considerably stronger than the reflected one, as the maximum temperature in the transmitted shock is roughly 5 times higher. The temperatures of both the transmitted and reflected shocks decrease at later times. This is due to a reduced relative velocity between the neutrals and the charged particles as the energy transfer by collisions heats the gas. The lower temperatures and relative velocities suggest that the higher upstream density regime is less effective for grain sputtering. This agrees with the results of May et al. (2000) who reported that the elemental fraction of Si sputtered from olivine increased with shock velocity, but at a given shock velocity, dropped as the pre-shock density increased.

\begin{figure} \par\includegraphics[width=6.7cm,clip]{13277f4a.eps}\hspace*{1.5cm} \includegraphics[width=6.5cm,clip]{13277f4b.eps}\vspace*{-2mm} \end{figure} Figure 4:

Similar to Fig. 1, but for a shock interacting with a decreasing density perturbation (from $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$ to $n_{\rm H} = 10^4~ {\rm cm^{-3}}$). The thin solid line is the initial C-type shock, the dashed line the shock structure $5\times 10^3$ yr after the shock interacts with the density perturbation, the dotted line after $2.40 \times 10^{4}$ yr, the dash-dotted line after $5.59 \times 10^{4}$ yr and the thick solid line the final steady C-type shock (after $9.8 \times 10^{4}$ yr).

Open with DEXTER

In these early stages of the evolution we can already see the effect of the higher density on the charged particles fluid and the magnetic field. In the high density region the Hall conductivity becomes larger than the Pedersen conductivity (see definition in Paper I). This changes the wave propagation upstream. This is associated with a change of the structure of the evolutionary trajectory in the By-Bz phase space (cf. Wardle 1998). When the Hall conductivity exceeds the Pedersen conductivity, a spiral node develops in the trajectory for those regions corresponding to the flow around and just upstream of the leading part of the shock precursor. The shock structure then contains large oscillations (see Falle 2003, and Paper I) as seen in the x-component of the ion and electron velocities in Fig. 2.

The J-type phase of the shocks is quite short. Within $7.92 \times 10^4$ yr after impact, corresponding to 2 ion shock crossing times, the transmitted shock structure has become a stable C-type shock. For the reflected shock the time for the shock to become a stable C-type shock is somewhat shorter. The transmitted C-type shock is much narrower than the initial shock (roughly 1/8 of the original shock width). It also has a lower propagation speed of 16.3 km s-1 as the shock slows down when moving into a region of higher density and pressure.

The density and velocity plots in Fig. 1 seem to suggest that the neutral flow in sufficiently upstream parts of the precursor is quasi-steady. The precursor shows some small oscillations in both width and gradient, but these are associated with numerical uncertainties. The quasi-steady evolution does not start immediately after the shock interacts with the density perturbation, but only commences after $7 \times 10^3$ yr. We note that this is roughly $(L_{\rm s} + L_{\rm p})/V_{\rm s}$ with $L_{\rm s}$ the initial shock thickness and $L_{\rm p}$ the perturbation width. It is the time needed for the shock and perturbation to cross each other.

Shocks with different propagation speeds or moving into regions with different density contrasts have behaviours similar to that of the model shock described above. Thus, such simulations give us some idea about the relative strengths of the reflected-transmitted shock pairs and the timescales of the J to C-type transitions for cores in which the shock moves into a region of enhanced density.

For instance, for a lower density contrast across the perturbation, the shock does not slow down as much as before. For example, the propagation speed of a shock with an initial speed of 25 km s-1 is 21.1 km s-1 in a region with a density contrast of 3. The transmitted shock is only marginally weaker than the initial C-type shock with peak temperatures of a few times 104 K. The timescale for the transmitted shock to become a steady C-type shock is slightly shorter than before ( $6.02 \times 10^4$ yr or about 1.15 ion shock crossing times). The post-shock density behind the transmitted shock is not much higher than the far downstream density leading to a weak reflected shock. The peak temperature in the reflected shock is only about 300 K, while it is of the order of a few times 103 K for a density contrast of 10. As this temperature is below the threshold for electron cooling to be important, the ion and electron temperatures in the reflected shock are similar. Furthermore, the grain-neutral relative velocity, which roughly scales with the temperature, in the reflected shock is too low for grain sputtering to be important, i.e. $\vert v_{\rm g} - v_n\vert < 2\ {\rm km\ s^{-1}}$(see discussion in Sect. 4).

We also performed a simulation for an initial shock speed of 6 km s-1and a density contrast of 10. In this simulation the shocks were relatively weak. While strong fast-mode shocks considerably heat the incoming gas, weak fast-mode shocks do not. For a shock velocity of 6 km s-1 (or $M_{\rm A} \approx 3$), the gas temperatures are below 103 K. The peak temperature in the transmitted and reflected shock are even less and are about 400 and 80 K respectively. Note that the ratio of the temperatures is similar to the one for the 25 km s-1 shock. Because of the low temperatures in the shock, the grains do not get highly charged and their Hall parameter is of the order of unity. The grains, therefore, move at a speed different from those of the neutrals and of the ions and electrons. As the relative grain-neutral velocity is quite small ($\ll$1 km s-1), grain sputtering will not occur. Variations in the transmitted-shock structure dissappear after $9.20 \times 10^4$ yr (about one ion shock crossing times) when the shock reaches steady state. An interesting difference between this model and the strong fast-mode shock models is that the transmitted shock width is not much smaller than of the width of the initial C-type shock. The ratio of the shock widths is 0.62. This is not surprising as the fractional ionisation does not change much across the density perturbation due to the low temperatures of the shock. Another difference is that, for the weak shock case, the trajectory in the By-Bzphase space has no spiral node. This is because, as the grains are not important charge carriers, the Hall conductivity does not modify the upstream conditions.

3.2 Decreasing density

\begin{figure} \par\includegraphics[width=6.2cm,clip]{13277f5a.eps}\par\vspace*{... ...}\par\vspace*{5mm} \includegraphics[width=6.2cm,clip]{13277f5d.eps} \end{figure} Figure 5:

Similar to Fig. 2, but for a shock interacting with a decreasing density perturbation (from $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$ to $n_{\rm H} = 10^4~ {\rm cm^{-3}}$). a) shows the initial condition, b) the shock structure $5~ \times ~10^3$ yr after the interaction with the density perturbation, c) after $2.40~ \times~ 10^{4}$ yr and d) the final steady state shock (after $9.8 \times 10^{4}$ yr).

Open with DEXTER

\begin{figure} \par\includegraphics[width=6.2cm,clip]{13277f6a.eps}\par\vspace*{... ...}\par\vspace*{5mm} \includegraphics[width=6.2cm,clip]{13277f6d.eps} \end{figure} Figure 6:

Similar to Fig. 3, but for the shock and times shown in Fig. 5.

Open with DEXTER

For this model, a 25 km s-1 C-type shock propagates out of a dense region with $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$ into a more diffuse one with $n_{\rm H} = 10^4~ {\rm cm^{-3}}$. Such a model is representative of a molecular outflow leaving the dense core surrounding a protostellar object.

Note that the final steady shock for the case to which Fig. 1 corresponds, is similar to the initial shock structure here (see Figs. 4-6). Many features of the shock-clump interaction are reversed. As the shock moves into the lower density region, the shock speeds up and broadens (see Fig. 4). Furthermore, the spiral By-Bz feature does not appear. A rarefaction wave propagates into the far downstream gas. In this case, the rarefaction is a slow-mode wave as the magnetic field decreases across the structure. As for multifluid shocks, a multifluid rarefaction wave also introduces an ion-neutral drift (see e.g. Fig. 5b). However, the relative velocities between the charged particles and neutrals is negligible compared to the velocity of the transmitted shock.

\begin{figure} \par\includegraphics[width=6.8cm,clip]{13277f7a.eps}\hspace*{1.5cm} \includegraphics[width=6.6cm,clip]{13277f7b.eps} \end{figure} Figure 7:

Similar to Fig. 1, but for a shock interacting with a clump that has a maximum density of $n_{\rm H} = 2 \times 10^5~ {\rm cm^{-3}}$. The solid line shows the initial and final steady shock (after $1.2 \times 10^5$ yr), the dashed line the shock structure $3.9 \times 10^3$ yr after the shock interacts with the clump, the dotted line after $1.98 \times 10^4$ yr and the dash-dotted line after $1.46 \times 10^5$ yr.

Open with DEXTER

In the transmitted shock a neutral subshock and a precursor are initially present. From the precursor, a C-type shock eventually develops. As in the increasing density, the quasi-steady evolution starts after an initial adaptation phase of the order $1.7\times 10^3$ yr ( ${=}(L_{\rm s} + L_{\rm p})/V_{\rm s}$). The transmitted shock reaches steady state after $9.80 \times 10^4$ yr, which roughly corresponds to 1.2 times the ion flow time through the final shock structure.

As mentioned before, the transmitted shock speeds up to $\approx$28.6 km s-1 or $M_{\rm A} \approx 13$. The shock is thus a strong shock and the gas temperatures are high within the shock. (I.e. the ions have peak temperatures of 105 K.) As the high temperatures are due to collisions between the different fluids, the ion-neutral and grain-neutral relative velocities within the shock structures also remain high (see Fig. 4). Furthermore, the spatial region with high relative velocities is larger than for the case for which results are shown in Fig. 1, which suggests that grain sputtering is going to be more effective than in the initial C-type shock.

3.3 Sinusoidal density perturbation

\begin{figure} \par\includegraphics[width=6.1cm,clip]{13277f8a.eps}\par\vspace*{... ...}\par\vspace*{5mm} \includegraphics[width=6.1cm,clip]{13277f8d.eps} \end{figure} Figure 8:

Similar to Fig. 2, but for a shock interacting with a clump that has a maximum density of $n_{\rm H} = 2 \times 10^5~ {\rm cm^{-3}}$. a) shows the initial and final shock structure (after $1.2 \times 10^5$ yr), b) the shock structure $3.9 \times 10^3$ yr after the shock first interacted with the clump, c) after $1.98 \times 10^4$ yr and d) after $1.46 \times 10^5$ yr.

Open with DEXTER

\begin{figure} \par\includegraphics[width=6.1cm,clip]{13277f9a.eps}\par\vspace*{... ...}\par\vspace*{5mm} \includegraphics[width=6.1cm,clip]{13277f9d.eps} \end{figure} Figure 9:

Similar to Fig. 2, but for the shock and times shown in Fig. 8.

Open with DEXTER

We also study the interaction of a C-type shock with a clump. The shape of the clump is given by a cosine wave with a wavelength ($\lambda$) of $1.46 \times 10^{17}$ cm, or more specifically

\begin{displaymath}n_{\rm H} = \left(\frac{n_{\rm H,max} - n_{\rm H,0}}{2}\right... ...ight] + \left(\frac{n_{\rm H,max} + n_{\rm H,0}}{2}\right), \end{displaymath}

with x0 the start position of the clump. The maximum density in the clump is $n_{\rm H,max} = 2 \times 10^5~{\rm cm^{-3}}$ and is 20 times higher than the background density ( $n_{\rm H,0}$). These values are representative for clump parameters measured by Tafalla et al. (2004).

Unfortunately, the evolution of the shock structure cannot be described by a combination of the previous two models. The behaviour of the shock as it moves up the density gradient is similar to the early evolution shown in Fig. 1. The dashed line in Fig. 7 and in Figs. 8b and 9b show that a reflected shock and a transmitted J-type shock form when propagating up the density gradient. The transmitted shock slows and narrows. A spiral feature develops in the trajectory in By-Bzphase space.

The motion back to the low density region does not resemble the transition of Sect. 3.2. This is because the transmitted shock does not become a steady state C-type shock within a few thousand years. (The time scale for the shock to adapt to the new upstream condition is by itself a few thousand years.) Rather, a J-type shock moves down the density gradient. As the shock reacts to the changing upstream conditions, it broadens and speeds up. The precursor then develops a neutral subshock just as the C-type shock did for the case for which Fig. 4 shows results. This means that the shock structure simultaneously has two neutral subshocks (see Fig. 8c). Interestingly, the neutral and charged flows do not have the same post-shock velocities behind the secondary subshock. However, this is not surprising as the relative velocity of the neutral and charged flow in the original precursor is non-zero.

Although these relative velocities are well below the sputtering thresholds derived in Caselli et al. (1997), other initial parameters may yield relative velocities above this threshold which extend over a spatial region larger than the initial shock width. The relative velocities steadily decrease as both subshocks eventually weaken. The initial one weakens after a few 104 yr. Simultaneously, a steady C-type shock forms from the precursor (see Fig. 7). The timescale for the steady C-type shock to arise is about $1.2 \times 10^5$ yr or 1.2 times the ion flow time through the shock. The final C-type shock is, as expected, identical to the initial one.

4 Summary and discussions

In this paper we present the first time-dependent simulations of oblique C-type shocks in dusty plasmas interacting with density perturbations. We studied the transient evolution of the shock structure for each of several different types of density perturbations, i.e. increasing, decreasing and clump-like, and examined the dependence of this interaction on shock speed and density contrast.

When a steady C-type shock encounters a density perturbation, the shock reacts to the changing upstream condition by breaking up into multiple waves. While a J-type shock moves into or out of a dense region, a shock or rarefaction wave, respectively, is reflected and propagates in the reverse direction. This reflected shock or wave is present because the post-shock flow behind the transmitted shock is different from the post-shock flow of the initial shock. The relative strength of the transmitted and reflected components depends on the initial shock speed and the density contrast of the perturbation, as these control the post-shock properties of the transmitted shock, e.g. a lower density contrasts leads to a smaller difference between the far downstream flow and the transmitted post-shock flow. Hence, a weaker rarefaction wave or shock is needed to adjust this change. For the interaction with a clump, where the density decreases again, the situation gets more complicated as the transmitted J-type shock forms a second subshock in the neutral flow of the precursor. It is thus important to realise that we expect a range of different J- and C-type shocks and multifluid rarefaction waves in inhomogeneous clouds.

In our models, we have focused on the evolution of the transmitted shocks. Such a shock is initially J-type and contains a subshock in the neutral flow. It again becomes a steady C-type shock but with a different shock width and velocity. The timescale for it to become steady is of the same order as the ion-flow time through the final shock structure, i.e. about $0.5{-}1.5 \times 10^5$ yr. An important consequence of these timescales is that, if a shock interacts with density inhomogeneities on timescales shorter than this, no steady C-type shock exists. All shocks are thus J-type, although some shocks will have weak subshocks and are then only marginally distinguishable from C-type shocks.

Our simulations show that the steady dusty C-type shock develops from a shock in which the sufficiently far upstream parts of the precursor are steady. Such an evolution was also observed for multifluid shocks in dustless, weakly-ionised gases (Flower & Pineau des Forêts 1999). Following the Flower & Pineau des Forêts (1999) result, Lesaffre et al. (2004) developed a quasi-steady method to follow the temporal evolution of multifluid shocks. This method involves the treatment of an evolving non-stationary J-type shock as a sequence of truncated C-type shocks each of which has a neutral subshock at the point where the ion-flow time corresponds to the age of the shock. While this approach was only validated for shocks in dustless, weakly ionised gases (Lesaffre et al. 2004), our result confirms quasi-steady models can also be used for dusty shocks and justifies the use of such methods for the temporal evolution of dusty shocks by Gusdorf et al. (2008). However, we also find some limitations of the quasi-steady approach when applied to the interaction of shocks with density perturbations. Firstly, this method can only be used after an early adaptation phase in which the shock adjusts to the changing upstream conditions. Secondly, this approach is only valid for a C-type shock interacting with a density perturbation. For a J-type shock, a second neutral subshock forms in the precursor. Behind this secondary shock, the velocities of the neutral and charged fluids are not the same. Such a situation, which is likely to occur in a clumpy medium, cannot be modelled with a quasi-steady approach.

In quiescent cold clouds, silicon is nearly depleted from the gas phase and stored in the core of dust grains. However, observations of SiO emission near protostellar objects show that some silicon is returned to the gas-phase. It is thought that this is due to sputtering of the dust grains and grain-grain collisions in shocks (Martin-Pintado et al. 1992). Although these processes are not included in the current code, the change of the grain-neutral relative velocity serves as an indication. Grain mantle sputtering requires a grain-neutral relative velocity of $\approx$6 km s-1 whereas core sputtering requires a much higher relative velocity of $\approx$19 km s-1 (Caselli et al. 1997). For our model parameters, with a shock speed of 25 km s-1, the threshold for core sputtering is only just attainable. Therefore, we do not expect much SiO emission from these models. However, grain mantle sputtering occurs in all the initial C-type shocks. Jiménez-Serra et al. (2008) have suggested that if the grain mantle consists of a small fraction of silicon, sputtering by heavy molecules such as CO could erode the mantles even in low velocity shocks and account for the narrow SiO line emission observed in some young outflows (e.g. L1448-mm Jiménez-Serra et al. 2004). Silicon erosion from the mantle would be saturated for shock velocities between 10 and 20 km s-1. This implies that the SiO enhancement from mantle erosion is saturated in all our models. Variations of the SiO emission then arise as the spatial area over which sputtering occurs changes (i.e. the shock width increases/decreases). Furthermore, we expect a small contribution to mantle sputtering from reflected waves. In subsequent papers we will include grain mantle and core sputtering as well as grain-grain collision terms to describe the release of SiO from the grains to the gas phase and use this to calculate the SiO emission (Jiménez-Serra et al. 2008; Caselli et al. 1997).

Acknowledgements
We thank the referee, Pierre Lesaffre, for his constructive comments that improved the paper. The authors thank STFC for the financial support.

References

  1. Arce, H. G., Shepherd, D., Gueth, F., et al. 2007, Protostars and Planets V, 245 [Google Scholar]
  2. Bachiller, R. 1996, ARA&A, 34, 111 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bachiller, R., & Tafalla, M. 1999, The Origin of Stars and Planetary Systems, NATO ASIC Proc., 540, [Google Scholar]
  4. 227 Bally, J., & Lada, C. J. 1983, ApJ, 265, 824 [NASA ADS] [CrossRef] [Google Scholar]
  5. Caselli, P., Hartquist, T. W., & Havnes, O. 1997, A&A, 322, 296 [NASA ADS] [Google Scholar]
  6. Cesaroni, R. 2005, Ap&SS, 295, 5 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chieze, J.-P., Pineau des Forets, G., & Flower, D. R. 1998, MNRAS, 295, 672 [NASA ADS] [CrossRef] [Google Scholar]
  8. Ciolek, G. E., & Roberge, W. G. 2002, ApJ, 567, 947 [Google Scholar]
  9. Dalgarno, A. 2006, Proc. Nat. Acad. Sci., 103, 12269 [NASA ADS] [CrossRef] [Google Scholar]
  10. Draine, B. T. 1980, ApJ, 241, 1021 [NASA ADS] [CrossRef] [Google Scholar]
  11. Draine, B. T., & McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] [CrossRef] [Google Scholar]
  12. Draine, B. T., Roberge, W. G., & Dalgarno, A. 1983, ApJ, 264, 485 [NASA ADS] [CrossRef] [Google Scholar]
  13. Falle, S. A. E. G. 2003, MNRAS, 344, 1210 [NASA ADS] [CrossRef] [Google Scholar]
  14. Flower, D. R., & Pineau des Forêts, G. 1999, MNRAS, 308, 271 [NASA ADS] [CrossRef] [Google Scholar]
  15. Gueth, F., Guilloteau, S., Dutrey, A., & Bachiller, R. 1997, A&A, 323, 943 [NASA ADS] [Google Scholar]
  16. Guillet, V., Pineau Des Forêts, G., & Jones, A. P. 2007, A&A, 476, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gusdorf, A., Pineau Des Forêts, G., Cabrit, S., & Flower, D. R. 2008, A&A, 490, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Hedstrom, G. W. 1979, J. Comp. Phys., 30, 222 [NASA ADS] [CrossRef] [Google Scholar]
  19. Jiménez-Serra, I., Martín-Pintado, J., Rodríguez-Franco, A., & Marcelino, N. 2004, ApJ, 603, L49 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jiménez-Serra, I., Caselli, P., Martín-Pintado, J., & Hartquist, T. W. 2008, A&A, 482, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Jørgensen, J. K., Hogerheijde, M. R., Blake, G. A., et al. 2004, A&A, 415, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Lefloch, B., Castets, A., Cernicharo, J., & Loinard, L. 1998, ApJ, 504, L109 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lesaffre, P., Chièze, J.-P., Cabrit, S., & Pineau des Forêts, G. 2004, A&A, 427, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. López-Sepulcre, A., Codella, C., Cesaroni, R., Marcelino, N., & Walmsley, C. M. 2009, A&A, 499, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Martin-Pintado, J., Bachiller, R., & Fuente, A. 1992, A&A, 254, 315 [NASA ADS] [Google Scholar]
  26. May, P. W., Pineau des Forêts, G., Flower, D. R., et al. 2000, MNRAS, 318, 809 [NASA ADS] [CrossRef] [Google Scholar]
  27. Mikami, H., Umemoto, T., Yamamoto, S., & Saito, S. 1992, ApJ, 392, L87 [NASA ADS] [CrossRef] [Google Scholar]
  28. Mullan, D. J. 1971, MNRAS, 153, 145 [NASA ADS] [Google Scholar]
  29. Pilipp, W., & Hartquist, T. W. 1994, MNRAS, 267, 801 [NASA ADS] [Google Scholar]
  30. Pilipp, W., Hartquist, T. W., & Havnes, O. 1990, MNRAS, 243, 685 [NASA ADS] [Google Scholar]
  31. Reipurth, B., & Bally, J. 2001, ARA&A, 39, 403 [NASA ADS] [CrossRef] [Google Scholar]
  32. Santiago-García, J., Tafalla, M., Johnstone, D., & Bachiller, R. 2009, A&A, 495, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Shepherd, D. 2005, Massive Star Birth: A Crossroads of Astrophysics, 227, 237 [Google Scholar]
  34. Smith, M. D., & Mac Low, M.-M. 1997, A&A, 326, 801 [NASA ADS] [Google Scholar]
  35. Snell, R. L., Loren, R. B., & Plambeck, R. L. 1980, ApJ, 239, L17 [NASA ADS] [CrossRef] [Google Scholar]
  36. Stone, J. M. 1997, ApJ, 487, 271 [NASA ADS] [CrossRef] [Google Scholar]
  37. Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, Ap&SS, 292, 347 [NASA ADS] [CrossRef] [Google Scholar]
  38. Toth, G. 1994, ApJ, 425, 171 [NASA ADS] [CrossRef] [Google Scholar]
  39. Van Loo, S., Ashmore, I., Caselli, P., Falle, S. A. E. G., & Hartquist, T. W. 2009, MNRAS, 395, 319 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
  40. Wardle, M. 1998, MNRAS, 298, 507 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... first[*]
Time-dependent multifluid shock studies prior to Ciolek & Roberge (2002), e.g. those of Toth (1994); Stone (1997); Smith & Mac Low (1997) and Chieze et al. (1998), did not include grain dynamics.
Copyright ESO 2010

All Figures

  \begin{figure} \par\includegraphics[width=6.75cm,clip]{13277f1a.eps}\hspace*{1.5cm} \includegraphics[width=6.6cm,clip]{13277f1b.eps} \vspace*{-2.5mm} \end{figure} Figure 1:

Evolution of the shock structure in the shock frame as a 25 km s-1 C-type shock interacts with a inhomogeneity of increasing density (from $n_{\rm H} = 10^4~ {\rm cm^{-3}}$ to $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$). The left panel shows the neutral density and the right panel the grain-neutral relative speed. The profile for the initial C-type shock is given by the thin solid line, while the dashed line shows the shock structure $9.75 \times 10^3$ yr after the shock first interacts with the perturbation, the dotted line after $2.56\times 10^4$ yr, the dash-dotted line after $6.37\times 10^{4}$ yr, and the thick solid line the final steady C-type shock structure (reached after $7.92 \times 10^4$ yr).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width =6.1cm,clip]{13277f2a.eps}\par\vspace*... ...\par\vspace*{5mm} \includegraphics[width =6.1cm,clip]{13277f2d.eps} \end{figure} Figure 2:

x component of the neutrals (solid), ions and electrons (dashed) and the grains (dotted) velocity in the upstream frame at different times for a 25 km s-1 C-type shock propagating in a higher density region (from $n_{\rm H} = 10^4~ {\rm cm^{-3}}$ to $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$). a) shows the the initial C-type shock, b) the the shock structure $9.75 \times 10^3$ yr after the first interaction of the shock with the inhomogeneity, c) after $2.56\times 10^4$ yr and d) the final steady C-type shock (after $7.92 \times 10^4$ yr).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width =6.1cm,clip]{13277f3a.eps}\par\vspace*... ...\par\vspace*{5mm} \includegraphics[width =6.1cm,clip]{13277f3d.eps} \end{figure} Figure 3:

Ion (dashed), electron (dotted) and neutral temperature (solid) and the average grain charge (dash-dotted) in electron charge units for the same shock model as in Fig. 2 at the same times.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.7cm,clip]{13277f4a.eps}\hspace*{1.5cm} \includegraphics[width=6.5cm,clip]{13277f4b.eps}\vspace*{-2mm} \end{figure} Figure 4:

Similar to Fig. 1, but for a shock interacting with a decreasing density perturbation (from $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$ to $n_{\rm H} = 10^4~ {\rm cm^{-3}}$). The thin solid line is the initial C-type shock, the dashed line the shock structure $5\times 10^3$ yr after the shock interacts with the density perturbation, the dotted line after $2.40 \times 10^{4}$ yr, the dash-dotted line after $5.59 \times 10^{4}$ yr and the thick solid line the final steady C-type shock (after $9.8 \times 10^{4}$ yr).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.2cm,clip]{13277f5a.eps}\par\vspace*{... ...}\par\vspace*{5mm} \includegraphics[width=6.2cm,clip]{13277f5d.eps} \end{figure} Figure 5:

Similar to Fig. 2, but for a shock interacting with a decreasing density perturbation (from $n_{\rm H} = 10^5 ~{\rm cm^{-3}}$ to $n_{\rm H} = 10^4~ {\rm cm^{-3}}$). a) shows the initial condition, b) the shock structure $5~ \times ~10^3$ yr after the interaction with the density perturbation, c) after $2.40~ \times~ 10^{4}$ yr and d) the final steady state shock (after $9.8 \times 10^{4}$ yr).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.2cm,clip]{13277f6a.eps}\par\vspace*{... ...}\par\vspace*{5mm} \includegraphics[width=6.2cm,clip]{13277f6d.eps} \end{figure} Figure 6:

Similar to Fig. 3, but for the shock and times shown in Fig. 5.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.8cm,clip]{13277f7a.eps}\hspace*{1.5cm} \includegraphics[width=6.6cm,clip]{13277f7b.eps} \end{figure} Figure 7:

Similar to Fig. 1, but for a shock interacting with a clump that has a maximum density of $n_{\rm H} = 2 \times 10^5~ {\rm cm^{-3}}$. The solid line shows the initial and final steady shock (after $1.2 \times 10^5$ yr), the dashed line the shock structure $3.9 \times 10^3$ yr after the shock interacts with the clump, the dotted line after $1.98 \times 10^4$ yr and the dash-dotted line after $1.46 \times 10^5$ yr.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.1cm,clip]{13277f8a.eps}\par\vspace*{... ...}\par\vspace*{5mm} \includegraphics[width=6.1cm,clip]{13277f8d.eps} \end{figure} Figure 8:

Similar to Fig. 2, but for a shock interacting with a clump that has a maximum density of $n_{\rm H} = 2 \times 10^5~ {\rm cm^{-3}}$. a) shows the initial and final shock structure (after $1.2 \times 10^5$ yr), b) the shock structure $3.9 \times 10^3$ yr after the shock first interacted with the clump, c) after $1.98 \times 10^4$ yr and d) after $1.46 \times 10^5$ yr.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.1cm,clip]{13277f9a.eps}\par\vspace*{... ...}\par\vspace*{5mm} \includegraphics[width=6.1cm,clip]{13277f9d.eps} \end{figure} Figure 9:

Similar to Fig. 2, but for the shock and times shown in Fig. 8.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.