EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 511 (February 2010) A&A, 511 (2010) A43 Full HTML
Free Access
Issue
A&A
Volume 511, February 2010
Article Number A43
Number of page(s) 11
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/200913134
Published online 05 March 2010
A&A 511, A43 (2010)

Spectral-luminosity relation within individual Fermi gamma rays bursts

G. Ghirlanda1 - L. Nava1,2 - G. Ghisellini1

1 - INAF - Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate, Italy
2 - Università degli Studi dell'Insubria, via Valleggio 11, 22100 Como, Italy

Received 17 August 2009 / Accepted 2 November 2009

Abstract
We study the spectra of all long gamma ray bursts (GRBs) of known redshift detected by the Fermi satellite untill the end of July 2009. Their fluxes and fluences are large enough to allow a time dependent study of their spectral characteristics in the 8 keV-1 MeV energy range. We find that the peak energy $E_{\rm peak}$ of their EL(E) spectrum correlates with the luminosity in a remarkably tight way within individual bursts. This time-resolved $E_{\rm peak}-L_{\rm iso}$ correlation is very similar for all the considered bursts and has a slope and normalisation similar to the analogous $E_{\rm peak}-L_{\rm iso}$ correlation defined by the time-integrated spectra of different bursts detected by several different satellites. For a few of the considered GRBs, we could also study the behaviour of the $E_{\rm peak}-L_{\rm iso}$ correlation during the rising and decaying phases of individual pulses within each burst, finding no differences. Our results indicate the presence of a similar physical mechanism, operating for the duration of different GRBs, tightly linking the burst luminosity with the peak energy of the spectrum emitted at different times. Such a physical mechanism is the same during the rise and decay phase of individual pulses composing a GRB. While calling for a robust physical interpretation, these results strongly indicate that the $E_{\rm peak}-L_{\rm iso}$ spectral energy correlation found considering the time-integrated spectra of different bursts is real and not the result of instrumental selection effects.

Key words: stars: gamma-rays bursts: general

1 Introduction

One of the key properties of the prompt emission of gamma ray bursts (GRBs) that is still poorly understood concerns the spectral-energy correlations found when considering the time-integrated spectra of bursts of known redshift. For these we can define the peak energy of the spectrum, $E_{\rm peak}$, in an EL(E) representation. The peak energy $E_{\rm peak}$ correlates with the isotropic luminosity $L_{\rm iso}$ (Yonetoku et al. 2004), with the isotropic energy $E_{\rm iso}$ (Amati et al. 2002), and more tightly with the collimation-corrected energy $E_{\rm\gamma}$ (Ghirlanda et al. 2004b). There are two very strong motivations for studying these correlations. One is to understand their physical origin, which can disclose a still not understood basic property of GRBs (Yamazaki et al. 2004; Lamb et al. 2005; Rees & Meszaros 2005; Levinson & Eichler 2005; Toma et al. 2005; Eichler & Levinson 2006, 2004; Barbiellini et al. 2006; Thompson 2006; Ryde et al. 2006; Giannios & Spruit 2007; Thompson et al. 2007; Guida et al. 2008; Panaitescu 2009) and the other is the possibility of using these correlations to standardise the GRB energetics, making them cosmological tools (Ghirlanda et al. 2004a, 2006a,b; Firmani et al. 2005, 2006, 2007; Xu et al. 2005; Liang & Zhang 2005, 2006; Wang & Dai 2006; Amati et al. 2008; Kodama et al. 2008; Qi et al. 2008; Li et al. 2008; Liang et al. 2008).

The debate about the reality of these correlations is strong, since some authors have pointed out that they can be the result of observational selection effects (Nakar & Piran 2005; Band & Preece 2005; Butler et al. 2007; Butler et al. 2009; Shahmoradi & Nemiroff 2009), while others argue that selection effects, even if surely present, play a marginal role (Ghirlanda et al. 2005; Bosnjak et al. 2008; Ghirlanda et al. 2008; Nava et al. 2008; Krimm et al. 2009; Amati et al. 2009).

One possibility for some insight into this issue is to study individual, bright bursts to see whether the luminosity and peak energy at different times during the prompt phase correlate. If they do, and furthermore if the slope of this time-resolved correlation (indicated ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ hereafter) is similar to the time-integrated $E_{\rm peak}-L_{\rm iso}$ correlation found among different bursts, then we should conclude that the spectral energy correlations are surely a manifestation of the physics of GRBs and not the result of instrumental selection effects.

Table 1:   Fermi long GRBs with redshift.

Some attempts have already been made. Liang et al. (2004) considered BATSE bursts without known redshifts and show a correlation between the (observer frame) peak energy and the flux within individual bursts, which they interpret as suggestive of a physical origin of the $E_{\rm peak}-L_{\rm iso}$ correlation holding among the GRBs with measured redshift. However, to directly compare the ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlations of individual GRBs with the $E_{\rm peak}-L_{\rm iso}$ correlation defined with time-integrated spectra, it is necessary to know the redshift (which is instead unknown for most of BATSE bursts). Recently, Firmani et al. (2009), have considered Swift bursts of known redshift and find a rather strong ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation within individual GRBs. Having the redshift, they could directly compare the time-resolved correlation of different bursts, finding that the ensemble of data points in the $E_{\rm peak}-L_{\rm iso}$ plane shows a correlation similar to that defined with the time-integrated spectra of the same burst sample. Because of its limited energy range (15-150 keV), however, the Burst Alert Telescope (BAT) onboard Swift is not particularly suited to GRB spectral analysis, especially when dealing with time-resolved spectra. To overcome this limitation, Ohno et al. (2009) combine the Swift-BAT and Suzaku-WAM spectral data to study the spectral evolution of GRB 061007 and investigate the time evolution of the $E_{\rm peak}-L_{\rm iso}$ correlation within the two pulses of this burst. They find that the time-resolved pulses also satisfy the $E_{\rm peak}-L_{\rm iso}$ correlation defined by time-integrated spectra. A more systematic analysis of the time-resolved spectral properties of Swift-Suzaku GRBs (Krimm et al. 2009) shows that individual pulses within a GRB are consistent with the $E_{\rm peak}-E_{\rm iso}$ correlation defined by the time-averaged spectra. They consider the spectra integrated over the duration of individual pulses. In this case $E_{\rm iso}$is computed on different integration timescales. They find that the pulses follow a correlation parallel to the $E_{\rm peak}-E_{\rm iso}$ defined with time-integrated spectra, but with a higher normalisation. Instead, the comparison of time-resolved spectra with the $E_{\rm peak}-L_{\rm iso}$ correlation is independent of the spectral integration time since this correlation involves the luminosity $L_{\rm iso}$ rather than the energy $E_{\rm iso}$. It is therefore important to study the presence of a $E_{\rm peak}-L_{\rm iso}$ correlation (as done by Ohno et al. 2009, for a single event) by concentrating on GRBs with measured redshift, in order to compare their time-resolved ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation with that defined with the time-integrated spectra. In particular we aim at studying how single GRBs evolve in the $E_{\rm peak}-L_{\rm iso}$ plane rather than considering them globally (as in Firmani et al. 2009). Furthermore, we would like to study the rise and decay phases of individual pulses.

Table 2:   The 5 non- Fermi GRBs added in this work to the pre- Fermi list of 90 GRBs from Ghirlanda et al. (2009).

Table 3:   Correlation analysis results.

\begin{figure} \par\includegraphics[width=9cm,clip]{13134fg1.ps}\vspace*{5mm} \end{figure} Figure 1:

The 10 Fermi-GRBs with redshift and $E^{\rm obs}_{\rm peak}$ in the $E_{\rm peak}-E_{\rm iso}$ (top panel) and $E_{\rm peak}-L_{\rm iso}$ (bottom panel) planes. Their position is compared with the correlations defined by the sample of 95 GRBs detected (92 published in Ghirlanda et al. 2009, and updated here) by other instruments (grey filled circles), i.e. pre- Fermi sample. The solid line is the best fit to the pre- Fermi sample, while the dashed lines represent its 3$\sigma $ scatter. The dot-dashed line is the best fit to the 10 Fermi-GRBs. Fermi bursts appear to be fully consistent with both the $E_{\rm peak}-E_{\rm iso}$ and the $E_{\rm peak}-L_{\rm iso}$ correlations.

Open with DEXTER

The Gamma ray Burst Monitor (GBM, Meegan et al. 2009) onboard the Fermi satellite covers a wide energy range (8 keV-30 MeV) and, although slightly less sensitive than Swift/BAT, it is better for studying the spectral properties of the prompt emission of GRBs. In addition, the Large Area Telescope (LAT) sensitive in the 0.1-100 GeV energy range can complement the spectral information for the few bursts it can detect. In one year of operation (up to the end of July 2009), Fermi/GBM detected about 200 bursts and, for about half of them, the (time-integrated) spectral analysis returned a well-defined $E^{\rm obs}_{\rm peak}$.

In this paper we study Fermi GRBs, selecting those of known redshift, to be able to compare their different evolutionary tracks in the $E_{\rm peak}-L_{\rm iso}$ plane with the correlation defined by the time-integrated spectra (see e.g. Ghirlanda et al. 2009, for a recent compilation of the $E_{\rm peak}-L_{\rm iso}$ correlation). For the brightest bursts we study whether the rising and decaying phases of individual pulses behave differently in the $E_{\rm peak}-L_{\rm iso}$ plane, since this can give important clues for a physical understanding of the emission mechanism operating during the GRB prompt phase.

The paper is organised as follows. In Sect. 2 we describe our Fermi GRB sample, whose time-integrated spectral properties are presented in Sect. 3 and compared to the $E_{\rm peak}-E_{\rm iso}$ and $E_{\rm peak}-L_{\rm iso}$ correlation defined by pre-Fermi GRBs. In Sect. 4 we describe the time-resolved spectral analysis whose results are given in Sect. 5. In Sect. 6 we discuss our findings and draw our conclusions. A standard cosmology for a flat universe with $h_{0}=\Omega_{\Lambda}=0.7$ is assumed.

2 The sample

We considered the GRBs detected by the GBM (up to the end of July 2009) of known redshift. They are 13 events. Among these GRB 090510 (z = 0.903, Rau et al. 2009) is a short burst, with an observer frame duration of less than 2 s, so it will not be considered here.

Table 1 lists the 12 long GRBs, their dates and fraction of the day of the burst trigger (Col. 1), their time-integrated spectral parameters (Cols. 3 to 8), the derived isotropic luminosity ( $L_{\rm iso}$, Col. 10) and isotropic energy ( $E_{\rm iso}$, Col. 11), computed in the rest frame 1 keV-10 MeV energy range. The spectral parameters in Table 1 have been collected from the literature (references are given Col. 9), as obtained through the analysis of the time-integrated spectrum extracted from the GBM data. In two cases (GRB 080905 - Bhat et al. 2008b; and GRB 080928 - Paciesas et al. 2008), the time-integrated spectrum is fitted by a single power law and, therefore, the peak energy is unconstrained. In five cases the time-integrated spectrum is modelled with a power law ending with an exponential cutoff at high energies. In the remaining five cases it is modelled by a Band function.

Two of the three GRBs detected by the LAT (in boldface in Table 1) belong to the latter group (i.e. GRB 080916C, Tajima et al. 2008; Abdo et al. 2009; and GRB 090328, Cutini et al. 2009). These bursts show a high-energy power-law component, and their observed peak energies $E^{\rm obs}_{\rm peak}$ are the largest of the sample. Table 1 also lists the most distant burst: GRB 090423, with z=8.2 (Tanvir et al. 2009; Salvaterra et al. 2009).

3 Time-integrated spectra: the 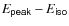$\textit {E}_{\sf peak}-\textit {E}_{\sf iso}$ and the 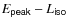$\textit {E}_{\sf peak}-\textit {L}_{\sf iso}$ correlations

First, we check the consistency of Fermi bursts with the $E_{\rm peak}-E_{\rm iso}$ and the $E_{\rm peak}-L_{\rm iso}$ correlations defined by the time-integrated spectra of GRBs detected by other instruments. We start from the recently updated sample of GRBs with known z and $E^{\rm obs}_{\rm peak}$, consisting of 90 pre-Fermi GRBs (from Ghirlanda et al. 2009) detected by different instruments. Here we have updated this sample to 95 objects. The 5 added bursts are reported in Table 2. For each burst we give the redshift, the fluence, the peak flux, and the energy range where they are computed. The isotropic luminosity and isotropic energy and the rest frame peak energy are also reported. All the spectral data are taken from the references listed in the last column of Table 2. If we add the 10 Fermi bursts studied here, our total sample contains 105 GRBs. Therefore, we have three samples: the pre-Fermi bursts (95 objects), the Fermi bursts (10 objects), and the combined sample (105 objects).

Figure 1 shows the pre-Fermi bursts (grey filled circles) in the $E_{\rm peak}-E_{\rm iso}$ and $E_{\rm peak}-L_{\rm iso}$ planes. In both planes they define a strong correlation (the probability that the correlation is by chance is reported in Col. 4 of Table 3), confirming recent analysis (Ghirlanda et al. 2009). The slope and normalisation of the fit of these correlations with a power law are reported in Table 3.

To show where the Fermi bursts lie in these planes we estimated $E_{\rm iso}$ and $L_{\rm iso}$ using the spectral parameters reported in the literature and listed in Table 1, excluding the two GRBs fitted with a single power law (i.e. with an unconstrained $E^{\rm obs}_{\rm peak}$). Figure 1 shows that the position of Fermi bursts is consistent with both correlations (see also Amati et al. 2009). We fitted the 95 pre-Fermi GRBs, the 10 Fermi GRBs, and the combined sample of 105 GRBs with the least square method. The best-fit spectral parameters (normalisation K and slope $\delta$ and their 1$\sigma $ errors) and the probability that the correlation is by chance (P) are reported in Table 3.

4 Time-resolved spectra: data analysis

The data of GRBs detected by the GBM since August 2008 are publicly available at http://fermi.gsfc.nasa.gov/. The GBM consists of 12 NaI and 2 BGO scintillation detectors oriented differently so as to derive the GRB position through the comparison of the count rates of the different detectors. The NaI cover the low-energy spectral domain from 8 keV to $\sim$1 MeV, while the BGO detectors (a factor 10 thicker than the NaI) are sensitive in the 0.2-30 MeV energy range. The GBM uses several trigger algorithms to detect a GRB. These are determined by different choices of the integration timescales and energy range. A trigger algorithm similar to that of BATSE Large Area Detectors (LAD) operates in the 50-300 keV band with a minimum significance of 5.4$\sigma $ for the detection of the GRB over the background (which has typically a rate of 300-350 counts/s in this range - e.g. Meegan et al. 2009) on the 16 ms-4 s timescales. An event is flagged as a burst if at least two NaI detectors are simultaneously triggered.

For our analysis we considered the TTE (time-tagged event) files containing the counts in 128 energy channels relative to the burst period. We considered the TTE files of the two NaI detectors triggered by the GRB. From these we extracted the GRB light curve and the time-resolved spectra with the gtbin tool (as part of the ScienceTools-v9r8p2-fssc-20090225). Light curves were extracted by summing the count rates over the 8 keV-1 MeV energy range of the NaI detectors that were triggered and the 200 keV-30 MeV energy range of the 2 BGO detectors. Time bins of 1 s were adopted for all bursts. Light curves were rescaled in time to the trigger time of the GRB.

Figure 2 shows the burst light curves. In the case of GRB 081007, the data present in the GBM catalogue 081007(224) refer to GRB 081007B, which had very low statistics (Bissaldi et al. 2008). We could not find the data directory of GRB 081007 that triggered Swift (Baumgartner et al. 2008) and Fermi (Bissaldi et al. 2008) 121 s after GRB 081007B. We only report in Table 1 the time-integrated spectral results of GRB 081007 (Bissaldi et al. 2008). We also note that Fermi and Swift both detected a GRB on November 18, 2008. These are, however, two events that coincide neither spatially nor temporally: ${\rm RA}=82.6^{\circ}$ and ${\rm Dec} =-43.3^{\circ}$ is the location (with an uncertainty of 1.6$^\prime$ - Palmer et al. 2008) of the event detected by Swift at 14:56:36 UT (Hoversten et al. 2008) while the Fermi event is located at ${\rm RA} =54^{\circ}$ and ${\rm Dec}=-50.4^{\circ}$ (with an uncertainty of $ 2.9^{\circ}$) and was detected at 21:00:53.5 UT (Bhat et al. 2008a). Only for the Swift GRB is the redshift measured (z=2.58, D'Elia et al. 2008, no $E^{\rm obs}_{\rm peak}$ measured).

\begin{figure} \par\includegraphics[width=18cm,clip]{13134fg2.ps}\vspace*{6mm} \end{figure} Figure 2:

Fermi light curves of the bursts with known redshift detected by the GBM from August 2008 to July 2009. Light curves have a time resolution of 1 s and are not background-subtracted. The vertical dotted lines mark the time intervals selected for the extraction of the time-resolved spectra. The light curve of GRB 081007 is not reported because the data of this burst could not be found.

Open with DEXTER

For the scope of this work, we do not subtract the background count rate from the light curves, they are only used here to show the time intervals within single GRBs selected for the extraction of time-resolved spectra. For 3 GRBs (080905, 080928 and 090423), the count rate is too low to perform a time-resolved spectral analysis. In all the other cases (except GRB 081007), we could divide the light curve into time intervals as indicated in Fig. 2. For GRB 080916C we used the time-resolved spectral analysis results reported by Abdo et al. (2009) who combined the GBM and the LAT data. Spectra of the triggered detectors were extracted over the selected time intervals defined with the gtbindef tool. The spectrum of the background was extracted in a time interval after the burst to limit the GRB contamination. Rebinning (with the grppha(v3.0.1) tool) was applied to each spectrum to have a minimum of 40 counts per energy channel.

The response files corresponding to each detector were used for the spectral fitting. Spectra were analysed with Xspec(v12) in the range 8 keV to $\sim$1 MeV. For most GRBs the spectra of the two (or more) NaI triggered detectors were jointly fitted with a cutoff-power law model (CPL) of the form $F(E)=E^{\alpha}\exp(-E/E_0)$ with a free normalisation constant for the spectra of the two or more detectors jointly fitted. Most of the fits give a value close to 1 for this constant. The CPL has been widely used to fit the spectra of GRBs, in particular the time-resolved spectra (Preece et al. 2000; Ghirlanda et al. 2002; Kaneko et al. 2006). We only analysed the spectra of the NaI detectors because, in most bursts, the inspection of the BGO light curve did not show any evident signal. Morever, the lower sensitivity of the BGO detectors with respect to the NaI ones would lead, in extracting simultaneous spectra for a joint fit, to much fewer time-resolved spectra.

\begin{figure} \par\includegraphics[width=12.5cm,clip]{13134fg3.ps}\vspace*{5mm} \end{figure} Figure 3:

Time-resolved $E_{\rm peak}-L_{\rm iso}$ correlation of Fermi GRBs with known redshift. Small symbols show the evolution of $E_{\rm peak}$ vs. $L_{\rm iso}$. Large symbols are the location in the $E_{\rm peak}-L_{\rm iso}$ plane of the corresponding bursts when the time-integrated spectra (Table 1) are considered. For GRB 081007 and GRB 090423, only the time-integrated spectrum is available. The solid and dotted lines represent the $E_{\rm peak}-L_{\rm iso}$ correlation and its 3$\sigma $ scatter, respectively, as obtained with the pre- Fermi GRBs. The dot-dashed line represents the fit to the 10 Fermi GRBs (time-integrated) and the triple-dot-dashed line is the fit to the 51 time-resolved spectra. The corresponding parameters (slope and normalisation) are reported in Table 2.

Open with DEXTER

We performed a time-resolved spectral analysis for 8 GRBs of Table 1. Note that also the BATSE time-resolved spectra are often fitted with the CPL function (e.g. Kaneko et al. 2006; Nava et al. 2008). For the purpose of comparing the spectral evolution of different bursts in the $E_{\rm peak}-L_{\rm iso}$ plane, the use of the same spectral model ensures that the possible biases, e.g. the overestimate of the peak energy with respect to the Band model (Band et al. 1993), is a common systematic effect of all the analysed spectra (e.g. see Kaneko et al. 2006). In any case, we also verified if our time-resolved spectra could be consistent with the Band model, finding that, in most cases, we could not constrain the high-energy power law slope of this model. This also motivated us to choose the minimal simplest model, i.e. the CPL.

We computed the isotropic luminosity of each time-resolved spectrum by integrating the best fit spectral shape over the rest frame 1 keV-10 MeV energy range. This represents the mean luminosity of each time-resolved spectrum. Table A.1 reports the results of the time-resolved analysis: Cols. 2 and 3 give the start and stop times of the time-resolved spectra, Cols. 4 and 5 give the photon spectral index $\alpha $ and the characteristic energy E0 (with their 90% significance errors), respectively.

5 Results

5.1 Evolutionary tracks

Figure 3 shows the evolutionary tracks of the 8 Fermi GRBs with redshift for which time-resolved spectral analysis was possible. The number of time-resolved spectra extracted per burst depends on its total fluence. Our guideline in defining the time intervals was a trade-off between the need to follow the rise and decay phases of the single pulses within the light curve and to have enough signal in each time-resolved spectrum to constrain its spectral parameters. In two bursts (GRB 090424 and GRB 090618), a denser sampling of the light curve is possible given their large fluence. We limited the number of time bins to have a neater evolutionary track in the $E_{\rm peak}-L_{\rm iso}$ plane, while in the next subsection we discuss their time evolution in full detail. For GRB 090323 the time-resolved spectra up to $\sim$100 s after the trigger are best fitted by a simple power-law model, while only after 100 s can a curved model (CPL) be fitted and the value of the peak energy constrained. Therefore, for GRB 090323 we show in Fig. 3 only the spectral evolution of the final peaks (those after 100 s in the corresponding light curve of Fig. 2).

Figure 3 shows that the prompt spectrum evolves in a well-defined way and that $E_{\rm peak}$ and $L_{\rm iso}$are correlated. The entire evolutionary tracks of all the 8 bursts we studied lie within the 3$\sigma $ stripe of the scatter of the $E_{\rm peak}-L_{\rm iso}$ correlation defined by the time-integrated spectra of different bursts. Figure 3 contains data points that are associated both to the rising or descending parts of the bursts, although they are difficult to distinguish. We show in the next section the results of a finer time-resolved spectral analysis on two of the brightest bursts of our sample, demonstrating that there appears to be no difference between the rising and decaying parts of the pulses.

Since $E_{\rm peak}$ is a derived quantity, as $E_{\rm peak}=E_0 (2+\alpha)$, it is interesting to verify if the ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation is the result of underlying correlations of E0 and/or $\alpha $ with $L_{\rm iso}$. The left panel of Fig. 4 shows the rest frame energy $E_0=E_{\rm peak}/(2+\alpha )$ as a function of the luminosity for the time-resolved spectra and for the corresponding time integrated-spectra (same symbols as in Fig. 3). The right panel of Fig. 4 shows the low-energy spectral index $\alpha $ versus the luminosity $L_{\rm iso}$. We can see that $\alpha $ shows no correlation with $L_{\rm iso}$when considering the ensemble of bursts (but see below the case of the single pulse of GRB 090618), while E0 does. We can conclude that indeed $E_{\rm peak}$ (or E0, i.e. the e-folding energy of the CPL model) is the spectral parameter correlating with $L_{\rm iso}$. From the right panel of Fig. 4 we also see that the low-energy photon index of the time-integrated and time-resolved spectra of the analysed Fermi GRBs are consistent with the -2/3 limit predicted by synchrotron emission, while they violate the -3/2 synchrotron limit for fast cooling electrons (Ghisellini et al. 2000).

We analysed the ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlations obtained with the time-resolved spectra. In Table 3 we report the normalisation and slope (K and $\delta$, respectively) and the chance probability P of the correlation. In total we have 51 time-resolved spectra for the 8 GRBs. They define a correlation in the $E_{\rm peak}-L_{\rm iso}$ plane with a slope $0.37\pm 0.05$ (Fig. 3) consistent with the slope of the correlation defined with the time-integrated spectra (i.e. $0.39\pm0.03$ for the 95 pre-Fermi GRBs - solid line in Fig. 3 - or $0.40\pm0.02$ for the total of 105 GRBs including the Fermi events - dot-dashed line in Fig. 3).

\begin{figure} \par\includegraphics[width=9cm,clip]{13134fg4.ps}\hspace*{1.5mm} \includegraphics[width=9cm,clip]{13134fg5.ps}\vspace*{5mm} \end{figure} Figure 4:

Left panel: the rest frame energy $E_0=E_{\rm peak}/(2+\alpha )$ as a function of luminosity for the time-resolved spectra and for the corresponding time-integrated spectra (same symbols as in Fig. 3). Right panel: the low-energy spectral index $\alpha $ versus the luminosity $L_{\rm iso}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13134fg6.ps}\hspace*{1.5mm} \includegraphics[width=9cm,clip]{13134fg7.ps}\vspace*{5mm} \end{figure} Figure 5:

High time resolution spectral analysis of GRB 090424 (left) and of GRB 090618 (right). Top: light curve (0.1 s resolution) and time intervals of the extracted spectra (vertical dotted lines). The coloured symbols represent the spectra highlighted in the panels below. Spectral evolution panels (from top to bottom): rest frame peak energy $E_{\rm peak}$, rest frame characteristic energy E0 and photon index $\alpha $ versus isotropic luminosity. The filled circles and the open squares identify the first and the second peak of the light curves. The colour code marks the rise/decay phase within each peak.

Open with DEXTER

5.2 Rising and decaying phases of single pulses

GRB 090424 consists of two overlapped peaks. Its total duration is 6 s. GRB 090618 has a complex light curve made of a smooth precursor followed by two intense peaks partially overlapped (see Fig. 2) for a total duration of 150 s. Their high count rates allow a time-resolved spectral analysis with a dense time sampling. These two GRBs are well-suited to studying how the spectrum evolves during the rise and decay phases of their pulses.

We divided the time interval of the duration of GRB 090424 so that each extracted spectrum had a signal-to-noise ratio $S{/}N\geq30$, integrated over the 8 keV-1 MeV energy range. This gives a total of 42 spectra distributed in the $\sim$6 s of duration of GRB 090424. For GRB 090618 we required an S/N ratio of 50 and obtained 34 time-resolved spectra in the 150 s of its duration. These spectra were extracted and analysed as described in Sect. 3. In Fig. 5 the light curve (with 0.1 s time resolution) and the three panels of the correlation between the spectral parameters ( $E_{\rm peak}$, E0 and $\alpha $) and the luminosity $L_{\rm iso}$ are shown for GRB 090424 (left) and GRB 090618 (right). In these plots we have marked the spectral evolution of the different peaks identified in the light curve with different symbols and the rise and decay phase of single pulses with different colours. The different peaks were also fitted individually in the $E_{\rm peak}-L_{\rm iso}$ plane (second panels of Fig. 5) and the results are shown in Table 3. These 4 peaks (two of GRB 090424 and two of GRB 090618) define a very tight $E_{\rm peak}-L_{\rm iso}$ correlation with slope between 0.45 and 0.6.

These plots indicate that the rising and decaying phases are indistinguishable in a $E_{\rm peak}-L_{\rm iso}$ plot. Intriguingly, we also find that there is a correlation between $\alpha $ and $L_{\rm iso}$ for GRB 090618. Since E0 also correlates with $L_{\rm iso}$ (as for the other bursts), this results in an even tighter ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation for the two pulses of this GRB.

6 Discussion and conclusions

The largest sample of long GRBs with measured redshift and $E^{\rm obs}_{\rm peak}$ collected recently (e.g. Ghirlanda et al. 2009) defines a strong correlation $E_{\rm peak}~\propto L_{\rm iso}^{0.4}$ with scatter $\sigma \simeq 0.26$. A similar strong correlation exists between the peak energy and the isotropic energy, i.e. $E_{\rm peak}$ $\propto E_{\rm iso}^{0.5}$. The time-integrated spectra of the 8 Fermi GRBs with measured redshift (open symbols in Fig. 1) are consistent with both the $E_{\rm peak}-E_{\rm iso}$ and the $E_{\rm peak}-L_{\rm iso}$ correlation defined by 95 pre-Fermi bursts. In the $E_{\rm peak}-L_{\rm iso}$ correlation, $E_{\rm peak}$ is that of the time-integrated spectrum and $L_{\rm iso}$ is computed (as done by Yonetoku et al. 2004) using the value of $E_{\rm peak}$ of the time-integrated spectrum and the peak flux of the GRB. From the comparison of the correlation slopes reported in Table 2 we note that the $E_{\rm peak}-E_{\rm iso}$ correlation defined by the 10 Fermi GRBs is consistent with that of the pre-Fermi sample. Also the $E_{\rm peak}-L_{\rm iso}$ correlations found with pre-Fermi and Fermi bursts are consistent within their uncertainties.

6.1 Selection effects

The sample of bursts defining the $E_{\rm peak}-E_{\rm iso}$ and $E_{\rm peak}-L_{\rm iso}$ correlations is heterogeneous: Nava et al. (2008) considered 83 pre-Fermi GRBs detected by different instruments (BATSE, BeppoSAX, Hete-II, Konus-Wind and Swift) since 1997, and a more recent update (Ghirlanda et al. 2009) considers 92 GRBs. Here we have added the 10 Fermi-GRBs with measured redshift and three pre-Fermi GRBs. Adding new GRBs to the above correlations does not represent a secure test of their physical nature, especially when there is a doubt that these correlations are the result of instrumental selection effects. Different instrumental selection effects could be biasing the samples of bursts used to define the $E_{\rm peak}-E_{\rm iso}$ and $E_{\rm peak}-L_{\rm iso}$ correlations. Butler et al. (2007; see also Shahmoradi & Nemiroff 2009) argue that the spectral-energy correlations, in particular the $E_{\rm peak}-E_{\rm iso}$ and the $E_{\rm peak}-L_{\rm iso}$ defined by the time-integrated spectra, are the effect of the trigger threshold, therefore having no physical relevance for the understanding of the GRB emission mechanism. In Ghirlanda et al. (2008), we investigated this issue by studying instrumental selection effects possibly biasing a sample of 76 bursts (updated to Sep. 2007) with measured redshifts. This sample defines strong correlations in the observer frame $E^{\rm obs}_{\rm peak}$-F and $E^{\rm obs}_{\rm peak}$-P planes (F and P are the fluence and peak flux) where the instrumental selection effects can be studied.

Two selection effects were considered for the detectors onboard BATSE, BeppoSAX, and Swift: (i) the trigger threshold, i.e. the minimum flux a burst must have to trigger a given detector; and (ii) the spectral threshold, i.e. the minimum fluence a burst must have to constrain its spectral parameters (in particular the peak energy $E^{\rm obs}_{\rm peak}$). Our results indicate that: (i) both the selection effects are functions of $E^{\rm obs}_{\rm peak}$ but the spectral threshold dominates the trigger threshold, implying that the $E_{\rm peak}-E_{\rm iso}$ or $E_{\rm peak}-L_{\rm iso}$ correlations do not come from the trigger threshold; (ii) the Swift spectral threshold is biasing the Swift GRB sample with redshift added to the $E_{\rm peak}-E_{\rm iso}$ correlation in the last three years; (iii) selection effects are present but do not determine the spectral-energy correlations. Point (ii), in particular, stems from the limited energy range of the BAT instrument onboard Swift, which limits the possibility of a reliable estimate of the burst spectral shape and, particularly, of the peak energy. This limits the use of the Swift burst sample to draw any firm conclusion on the incidence of selection effects on the spectral-energy correlations (see Nava et al. 2008).

Another way to test the incidence of selection effects on the $E_{\rm peak}-E_{\rm iso}$ and $E_{\rm peak}-L_{\rm iso}$ correlation is to verify how much the slope, normalisation, and scatter change by separating the heterogenous sample of GRBs with redshift into subsamples of bursts detected by different instruments (e.g. Butler et al. 2007). Butler et al. (2007) find similar slopes but different normalisations of the $E_{\rm peak}-E_{\rm iso}$ correlation by considering the pre-Swift and the Swift sample (but see Amati et al. 2009). Unfortunately, Swift bursts have a very narrow range of $E^{\rm obs}_{\rm peak}$ limiting the robustness of this test (Nava et al. 2008). Furthermore, different instruments like BATSE and BeppoSAX can have very similar detector thresholds and bias, in a similar way, the GRB samples that they detect.

6.2 Time-resolved 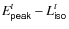$\textit {E}_{\sf peak}^{t}-\textit {L}_{\sf iso}^{t}$ correlation

All the spectral-energy correlations have been derived considering the time-integrated GRB spectral properties. By studying the spectral evolution of the 8 Fermi GRBs with measured redshift, we also find that a correlation ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ between the rest-frame peak energy $E_{\rm peak}$ and the bolometric isotropic luminosity exists within individual bursts (Fig. 3). This ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation can also extend over two orders of magnitude in both $E_{\rm peak}$ and $L_{\rm iso}$ within the duration of a burst. The evolutionary tracks defined by the 8 Fermi GRBs lie in the upper part of the $E_{\rm peak}-L_{\rm iso}$ correlation. This could be caused by a systematic underestimate of the luminosity in time-resolved spectra with respect to time-integrated spectra (which are used to define the $E_{\rm peak}-L_{\rm iso}$ correlation plotted as a solid line in Fig. 3). Indeed, the time-resolved spectra are more frequently fitted with a CPL model that lacks the high-energy power law component of time-integrated spectra.

The finding of a ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation within individual GRBs, consistent with the $E_{\rm peak}-L_{\rm iso}$ correlation defined by time-integrated spectra, is the strongest argument in favour of a physical origin of this correlation and the strongest argument against instrumental selection effects biasing the observed correlations.

6.3 Interpretations of the spectral-energy correlations

A convincing way to ensure the reality of the spectral-energy correlations would be to find a robust physical interpretation. The proposed interpretations of the $E_{\rm peak}-L_{\rm iso}$ and $E_{\rm peak}-E_{\rm iso}$ correlations can be divided into two classes: (a) kinematic interpretations in which the link between $E_{\rm peak}$ and $L_{\rm iso}$ is established by the configuration of the emission region, i.e. a uniform jet observed at different angles (Yamazaki et al. 2004), an inhomogeneous jet model (e.g. Nakamura 2000; Kumar & Piran 2000) made up of multiple sub-jets or emission patches (Toma et al. 2005), or a ring-shaped emission region (Eichler & Levinson 2004); (b) radiative interpretations in which it is the emission mechanism of the prompt phase to link $E_{\rm peak}$ and $L_{\rm iso}$, as in the case of a spectrum dominated by a thermal component (Meszaros & Rees 2007; Ryde et al. 2006; Thompson et al. 2007), in the case of photospheric emission dominated by magnetic reconnection (Giannios & Spruit 2007) or when the emission is synchrotron radiation from the external shock (Panaitescu et al. 2009).

The common feature of the kinematic models in reproducing the $E_{\rm peak}-L_{\rm iso}$ or $E_{\rm peak}-E_{\rm iso}$ correlation is the viewing angle under which different GRBs are observed. Both the off-axis and the sub-jet models need to assume the existence of an on-axis correlation between the peak energy and the luminosity, whose origin could be instead related to the radiative process. Indeed, the kinematical models that (under some assumptions about the typical jet opening angle distribution) succeed in reproducing $E_{\rm peak}$ $\propto$ $L_{\rm iso}^{0.5}$ should still explain a similar correlation within individual GRBs, i.e. a time-dependent correlation ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$, which can extend over 2 orders of magnitude (e.g. Fig. 4).

The simplest way to explain the $E_{\rm peak}-L_{\rm iso}$ correlation is to assume that only the bulk Lorentz factor $\Gamma$ changes. Since $E_{\rm peak}$  $\propto\Gamma$ and $L~\propto \Gamma^2$, we recover $E_{\rm peak}$ $\propto L^{1/2}$. But this assumes that, in the comoving frame, both $E_{\rm peak}$$^\prime$ and $L^\prime$ are the same even if different $\Gamma$-factors are required, and this seems unlikely (both when considering the $E_{\rm peak}-L_{\rm iso}$ correlation defined by different bursts or the ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation holding within individual GRBs).

If the emission comes from the synchrotron process, the peak frequency $E_{\rm peak}$  $\propto B\Gamma\gamma_{\rm p}^2$ (where $\gamma_{\rm p}$ is the random Lorentz factor of the electrons emitting at the peak) and $L~\propto N B^2\Gamma^2 \gamma_{\rm p}^2$, where N is the number of the electrons having $\gamma_{\rm p}$. Therefore a change in the quantity $\Gamma B$, maintaining the same $\gamma_{\rm p}$ and N, would give $E_{\rm peak}$  $\propto L^{1/2}$. But the prompt emission almost surely occurs in the fast cooling regime, implying that the resulting synchrotron spectrum cannot be harder than $L(E)~\propto E^{-1/2}$ (Ghisellini et al. 2000), while we also observe (e.g. Preece et al. 2000; Ghirlanda et al. 2003) in the Fermi GRBs (Fig. 4 right panel) much harder spectra. Furthermore, it seems hard to maintain the same N and $\gamma_{\rm p}$ while changing $\Gamma B$.

Quasi-thermal Comptonization could well explain how both E0 and $\alpha $ correlate with L, as found in GRB 090618. In fact, if the seed photons for Compton scattering remain the same, an increase in the plasma temperature would increase the Comptonization parameter $y\sim 4\tau KT_{\rm e}/ (m_{\rm e} c^2)$, producing both a harder spectrum and a higher $E_{\rm peak}$ ($\tau$ is the optical depth of scattering electrons, and $T_{\rm e}$ their temperature). On the other hand, for likely bulk Lorentz factors $\Gamma\sim 10^2{-}10^3$, the comoving temperature is below 1 keV, implying $\tau>10^3$ to reach the required $y\sim 10$, needed to account for the observed flat spectra. With this value of $\tau$, the resulting spectrum would saturate to a Wien-like spectrum, not to a cutoff power law. A very high value of $\tau$ would also lengthen any variability timescale.

It has been suggested (e.g. Borgonovo & Ryde 2001; Ryde & Petrosian 2002) that the off-latitude emission that follows an abrupt switch-off of the fireball introduces a spectral-energy dependence, since the observer sees progressively less beamed (and less blue-shifted) emission. However, this could explain only the decaying phase of the pulse. We analysed the spectral evolution of two of the most intense bursts in our sample. They allow to make a dense sampling of their light curves in order to extract time-resolved spectra. These are GRB 090424 and GRB 090618 (Fig. 4 right and left panels, respectively). Our findings indicate clearly that there is the same ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation during the rise and the decay phases of different pulses within these two GRBs. The time evolution is such that during the rise phase both $E_{\rm peak}$ and $L_{\rm iso}$ increase to the maximum value and during the decay they decrease along the same evolutionary track that they followed during the rise phase. In the case of GRB 090618, these considerations are also valid for the correlation between $\alpha $ and $L_{\rm iso}$ (bottom right panel of Fig. 4).

In the attempt to explain the $E_{\rm peak}-E_{\rm iso}$ correlation, Thompson Meszaros & Rees (2007) point out the importance of shear layers shocks to extract a large fraction of the bulk kinetic energy of the fireball, leading to a black body spectrum. The same arguments could be used to explain the $E_{\rm peak}-L_{\rm iso}$ correlation, in different bursts and the ${E}_{\rm peak}^{t}-{L}_{\rm iso}^{t}$ correlation within individual bursts as well. The problem with this interpretation is that one of the key assumptions of their scenario is that the value of the bulk Lorentz factor in the dissipation region must be fine-tuned (i.e., of the order of $1/\theta_{\rm j}$, where $\theta_{\rm j}$ is the opening angle of the fireball). This assumption is relaxed in the ``reborn fireball" scenario (Ghisellini et al. 2007), but it remains to be explained why so few bursts have pure black body spectra (Ghirlanda et al. 2003), and, even when adding a power-law component (Ryde et al. 2005), its slope is too soft to explain low-energy data (in the keV band), as shown by Ghirlanda et al. (2007).

We can conclude that new ideas are called for to explain what emerges to be a general and well-defined property of the prompt emission of GRBs.

Acknowledgements

We are grateful to the referee for useful comments. We thank Z. Bosnjak, D. Burlon, A. Celotti, C. Firmani, M. Nardini and F. Tavecchio for stimulating discussion. ASI is thanked for grant I/088/06/0. A PRIN-INAF grant is acknowledged for funding. This research made use of the Fermi-Gamma Burst Monitor data publicly available via the NASA-HEASARC data center.

Appendix A:

Table A.1:   Spectral results of the time-resolved analysis.

Table A.2:   Spectral evolution. Continued.

References

  1. Abdo, A. A., Ackermann, M., Arimoto, M., et al. 2009, Science, 323, 1688 [Google Scholar]
  2. Amati, L., Frontera, F., & Tavani, M. 2002, A&A, 390, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Amati, L., Guidorzi, C., Frontera, F., et al. 2008, A&A, 391, 557 [Google Scholar]
  4. Amati, L., Frontera, F., & Guidorzi, C. 2009, A&A, 508, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Band, D. L., & Preece, R. 2005, ApJ, 627, 319 [NASA ADS] [CrossRef] [Google Scholar]
  6. Band, D. L., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
  7. Barbiellini, G., Long, F., Omodei, N., et al. 2006, NCimB, 121, 1363 [NASA ADS] [Google Scholar]
  8. Barthelmy, S. D., Baumgartner, W. H., Cummings, J. R., et al. 2008, GCN, 8428 [Google Scholar]
  9. Baumgartner, W. H., Cummings, J. R., Evans, P. A., et al. 2008, GCN, 8330 [Google Scholar]
  10. Bhat, P. N., Preece, R. D., & van der Horst, A. J. 2008a, GCN, 8550 [Google Scholar]
  11. Bhat, P. N., Paciesas, W., & van der Horst, A. J. 2008b, GCN, 8205 [Google Scholar]
  12. Bissaldi, E., McBreen, S., & Connaughton, V. 2008, GCN, 8369 [Google Scholar]
  13. Bosnjak, Z., Celotti, A., Longo, F., et al. 2008, 384, 599 [Google Scholar]
  14. Borgonovo, L., & Ryde, F. 2001, ApJ, 548, 770 [NASA ADS] [CrossRef] [Google Scholar]
  15. Butler, N. R., Kocevski, D., Bloom, J. S., & Curtis, J. L. 2007, ApJ, 671, 656 [NASA ADS] [CrossRef] [Google Scholar]
  16. Butler, N. R., Kocevski, D., & Bloom, J. S. 2009, ApJ, 694, 76 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cutini, S., Vasileiou, V., & Chiang, J. 2009, GCN, 9077 [Google Scholar]
  18. D'Elia, V., Thoene, C. C., de Ugarte Postigo, A., et al. 2008, GCN, 8531 [Google Scholar]
  19. Eichler, D., & Levinson, A. 2005, ApJ, 635, 1182 [NASA ADS] [CrossRef] [Google Scholar]
  20. Firmani, C., Ghisellini, G., Ghirlanda, G., et al. 2005, MNRAS, 360, L1 [NASA ADS] [CrossRef] [Google Scholar]
  21. Firmani, C., Avila-Reese, V., Ghisellini, G., et al. 2006, MNRAS, 372, L28 [NASA ADS] [CrossRef] [Google Scholar]
  22. Firmani, C., Avila-Reese, V., Ghisellini, G., et al. 2007, RMxAA, 43, 203 [NASA ADS] [Google Scholar]
  23. Firmani C., Cabrera J. I., Avila-Reese V., et al. 2009, MNRAS, 393, 1209 [Google Scholar]
  24. Ghirlanda, G., Celotti, A., & Ghisellini, G. 2002, A&A, 393, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Ghirlanda G., Celotti A., & Ghisellini G. 2003, A&A, 406, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Ghirlanda, G., Ghisellini, G., Lazzati, D., et al. 2004a, ApJ, 613, L13 [NASA ADS] [CrossRef] [Google Scholar]
  27. Ghirlanda G., Ghisellini G., & Lazzati D. 2004b, ApJ, 616, 331 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ghirlanda, G., Ghisellini, G., Firmani, C., Celotti, A., & Bosnjak, Z. 2005, MNRAS, 360, 45 [Google Scholar]
  29. Ghirlanda, G., Ghisellini, G., Firmani, C., et al. 2006a, A&A, 452, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Ghirlanda, G., Ghisellini, G., & Firmani, C., et al. 2006b, NJPh, 8, 123 [Google Scholar]
  31. Ghirlanda G., Bosnjak Z., Ghisellini G., Tavecchio F., & Firmani C. 2007, MNRAS, 379, 73 [NASA ADS] [CrossRef] [Google Scholar]
  32. Ghirlanda, G., Nava, L., Ghisellini, G., Firmani, C., & Cabrera, J. I. 2008, MNRAS, 387, 319 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ghirlanda, G., Nava, L., Ghisellini, G., et al. 2009, A&A, 496, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Ghisellini, G., Celotti, A., & Lazzati, D. 2000, MNRAS, 313 [Google Scholar]
  35. Giannios, D., & Spruit, H. C. 2007, A&A, 469, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Golenetskii, S., Aptekar, R., Mazets, E., et al. 2008a, GCN, 8258 [Google Scholar]
  37. Golenetskii, S., Aptekar, R., Mazets, E., et al. 2008b, GCN, 8548 [Google Scholar]
  38. Golenetskii, S., Aptekar R., Mazets, E., et al. 2009, GCN, 8776 [Google Scholar]
  39. Guida, R., Bernardini, M. G., & Bianco, L. 2008, A&A, 487, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Guiriec, S., Connaughton, V., & Briggs, M. 2009, GCN, 9336 [Google Scholar]
  41. Hoversten, E. A., Barthelmy, S. D., Baumgartner, W. H., et al. 2008, GCN, 8524 [Google Scholar]
  42. Kaneko, Y., Preece, R. D., Briggs, M. S., et al. 2006, ApJ, 166, 298 [Google Scholar]
  43. Krimm, H. A., Yamaoka, K., Sugita, S., et al. 2009, ApJ, 704, 1405 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kodama, Y., Yonetoku, D., & Murakami, T. 2008, MNRAS, 391, L1 [NASA ADS] [CrossRef] [Google Scholar]
  45. Lamb, D. Q., Donaghy, T. Q., & Graziani, C. 2005, ApJ, 620, 355 [NASA ADS] [CrossRef] [Google Scholar]
  46. Lenvinson, A., & Eichler, D. 2005, ApJ, 629, L13 [NASA ADS] [CrossRef] [Google Scholar]
  47. Li, H., Xia, J.-Q., Liu, J., et al. 2008, ApJ, 680, 92 [NASA ADS] [CrossRef] [Google Scholar]
  48. Liang, E., & Zhang, B. 2005, ApJ, 633, 611 [NASA ADS] [CrossRef] [Google Scholar]
  49. Liang, E. W., Dai, Z. G., & Wu, X. F. 2004, ApJ, 606, L29 [NASA ADS] [CrossRef] [Google Scholar]
  50. Liang, N., Xiao, W.-K., Liu, Y., et al. 2008, ApJ, 685, 354 [NASA ADS] [CrossRef] [Google Scholar]
  51. Meegan C., Lichti G., Bhat P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
  52. Nakar, E., & Piran, T. 2005, MNRAS, 360, L73 [NASA ADS] [CrossRef] [Google Scholar]
  53. Nava, L., Ghirlanda, G., Ghisellini, G., & Firmani, C. 2008, MNRAS, 391, 639 [NASA ADS] [CrossRef] [Google Scholar]
  54. Ohno, M., Ioka, K., Yamaoka, K., et al. 2009, PASJ, 61, 201 [NASA ADS] [Google Scholar]
  55. Omodei, N., Granot, J., Meszaros, P., et al. 2009, GCN, 9350 [Google Scholar]
  56. Paciesas, B., Briggs, M., & Preece, R. 2008, GCN, 8316 [Google Scholar]
  57. Panaitescu, A. 2009, MNRAS, 393, 1010 [NASA ADS] [CrossRef] [Google Scholar]
  58. Palmer, D. M., Barthelmy, S. D., & Baumgartner, W. H. 2008, GCN, 8526 [Google Scholar]
  59. Pal'shin, V., Golenetskii, S., Aptekar, R., et al. 2008, GCN, 8256 [Google Scholar]
  60. Pal'shin, V., Golenetskii, S., Aptekar, R., et al. 2009, GCN, 9196 [Google Scholar]
  61. Preece, R., Briggs, M. S., Mallozzi, R. S., et al. 2000, ApJ, 126, 19 [Google Scholar]
  62. Qi, S., Wang, F.-Y., & Lu, T. 2008, A&A, 483, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Rau, A., McBreen S., Kruehler T., & Greiner J. 2009, GCN, 9353 [Google Scholar]
  64. Rees, M., & Meszaros, P. 2005, ApJ, 628, 847 [NASA ADS] [CrossRef] [Google Scholar]
  65. Ryde, F., & Pertrosian, V. 2002, ApJ, 578, 290 [NASA ADS] [CrossRef] [Google Scholar]
  66. Ryde, F., Bjornsson, C., Kaneko, Y., et al. 2006, ApJ, 652, 1400 [NASA ADS] [CrossRef] [Google Scholar]
  67. Salvaterra, R., Della Valle, M., Campana, S., et al., Nature, 461, 1258 [Google Scholar]
  68. Shahmoradi, A., & Nemiroff, R. J. 2009, [arXiv:0904.1464] [Google Scholar]
  69. Tajima, H., Bregeon, J., Chiang, J., & Thayer, G. 2008, GCN, 8246 [Google Scholar]
  70. Tanvir, N. R., Fox, D. B., Levan, A. J., et al. 2009, Nature, 461, 1254 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  71. Thompson, C. 2006, ApJ, 651, 333 [NASA ADS] [CrossRef] [Google Scholar]
  72. Thompson, C., Meszaros, P., & Rees M. J. 2007, ApJ, 666, 1012 [NASA ADS] [CrossRef] [Google Scholar]
  73. Toma, K., Yamazaki, R., & Nakamura, T. 2005, ApJ, 635, 481 [Google Scholar]
  74. Xu, D., Dai, Z. G., & Liang, E. W. 2004, ApJ, 633, 603 [Google Scholar]
  75. Yamazaki, R., Ioka, K., & Nakamura, T. 2004, ApJ, 606, L33 [NASA ADS] [CrossRef] [Google Scholar]
  76. Yonetoku, D., Murakami, T., Nakamura, T., et al. 2004, ApJ, 609, 935 [NASA ADS] [CrossRef] [Google Scholar]
  77. Wang, F. Y., & Dai, Z. G. 2006, MNRAS, 368, 371 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1:   Fermi long GRBs with redshift.

Table 2:   The 5 non- Fermi GRBs added in this work to the pre- Fermi list of 90 GRBs from Ghirlanda et al. (2009).

Table 3:   Correlation analysis results.

Table A.1:   Spectral results of the time-resolved analysis.

Table A.2:   Spectral evolution. Continued.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13134fg1.ps}\vspace*{5mm} \end{figure} Figure 1:

The 10 Fermi-GRBs with redshift and $E^{\rm obs}_{\rm peak}$ in the $E_{\rm peak}-E_{\rm iso}$ (top panel) and $E_{\rm peak}-L_{\rm iso}$ (bottom panel) planes. Their position is compared with the correlations defined by the sample of 95 GRBs detected (92 published in Ghirlanda et al. 2009, and updated here) by other instruments (grey filled circles), i.e. pre- Fermi sample. The solid line is the best fit to the pre- Fermi sample, while the dashed lines represent its 3$\sigma $ scatter. The dot-dashed line is the best fit to the 10 Fermi-GRBs. Fermi bursts appear to be fully consistent with both the $E_{\rm peak}-E_{\rm iso}$ and the $E_{\rm peak}-L_{\rm iso}$ correlations.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=18cm,clip]{13134fg2.ps}\vspace*{6mm} \end{figure} Figure 2:

Fermi light curves of the bursts with known redshift detected by the GBM from August 2008 to July 2009. Light curves have a time resolution of 1 s and are not background-subtracted. The vertical dotted lines mark the time intervals selected for the extraction of the time-resolved spectra. The light curve of GRB 081007 is not reported because the data of this burst could not be found.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12.5cm,clip]{13134fg3.ps}\vspace*{5mm} \end{figure} Figure 3:

Time-resolved $E_{\rm peak}-L_{\rm iso}$ correlation of Fermi GRBs with known redshift. Small symbols show the evolution of $E_{\rm peak}$ vs. $L_{\rm iso}$. Large symbols are the location in the $E_{\rm peak}-L_{\rm iso}$ plane of the corresponding bursts when the time-integrated spectra (Table 1) are considered. For GRB 081007 and GRB 090423, only the time-integrated spectrum is available. The solid and dotted lines represent the $E_{\rm peak}-L_{\rm iso}$ correlation and its 3$\sigma $ scatter, respectively, as obtained with the pre- Fermi GRBs. The dot-dashed line represents the fit to the 10 Fermi GRBs (time-integrated) and the triple-dot-dashed line is the fit to the 51 time-resolved spectra. The corresponding parameters (slope and normalisation) are reported in Table 2.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13134fg4.ps}\hspace*{1.5mm} \includegraphics[width=9cm,clip]{13134fg5.ps}\vspace*{5mm} \end{figure} Figure 4:

Left panel: the rest frame energy $E_0=E_{\rm peak}/(2+\alpha )$ as a function of luminosity for the time-resolved spectra and for the corresponding time-integrated spectra (same symbols as in Fig. 3). Right panel: the low-energy spectral index $\alpha $ versus the luminosity $L_{\rm iso}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13134fg6.ps}\hspace*{1.5mm} \includegraphics[width=9cm,clip]{13134fg7.ps}\vspace*{5mm} \end{figure} Figure 5:

High time resolution spectral analysis of GRB 090424 (left) and of GRB 090618 (right). Top: light curve (0.1 s resolution) and time intervals of the extracted spectra (vertical dotted lines). The coloured symbols represent the spectra highlighted in the panels below. Spectral evolution panels (from top to bottom): rest frame peak energy $E_{\rm peak}$, rest frame characteristic energy E0 and photon index $\alpha $ versus isotropic luminosity. The filled circles and the open squares identify the first and the second peak of the light curves. The colour code marks the rise/decay phase within each peak.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.