| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 19 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200912965 | |
| Published online | 10 March 2010 | |
Chemical abundance analysis of the open clusters
Cr 110, NGC 2099 (M 37), NGC 2420, NGC 7789, and M 67 (NGC 2682)![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
E. Pancino1 - R. Carrera1,2 - E. Rossetti1 - C. Gallart2
1 - INAF - Osservatorio Astronomico di Bologna,
via Ranzani 1, 40127 Bologna, Italy
2 -
Instituto de Astrofisica de Canarias,
via Lactea s/n, 38200, La Laguna, Tenerife, Spain
Received 23 July 2009 / Accepted 28 September 2009
Abstract
Context. The present number of Galactic open clusters that
have high resolution abundance determinations, not only of [Fe/H],
but also of other key elements, is largely insufficient to enable a
clear modeling of the Galactic disk chemical evolution.
Aims. To increase the number of Galactic open clusters with high quality measurements.
Methods. We obtained high resolution (
![]() ), high quality (
), high quality (
![]() -100 per
pixel), echelle spectra with the fiber spectrograph FOCES, at Calar
Alto, Spain, for three red clump stars in each of five Open Clusters.
We used the classical equivalent width analysis method to obtain
accurate abundances of sixteen elements: Al, Ba, Ca, Co, Cr, Fe, La,
Mg, Na, Nd, Ni, Sc, Si, Ti, V, and Y. We also derived the oxygen
abundance using spectral synthesis of the 6300 Å forbidden line.
-100 per
pixel), echelle spectra with the fiber spectrograph FOCES, at Calar
Alto, Spain, for three red clump stars in each of five Open Clusters.
We used the classical equivalent width analysis method to obtain
accurate abundances of sixteen elements: Al, Ba, Ca, Co, Cr, Fe, La,
Mg, Na, Nd, Ni, Sc, Si, Ti, V, and Y. We also derived the oxygen
abundance using spectral synthesis of the 6300 Å forbidden line.
Results. Three of the clusters were never studied previously with high resolution spectroscopy: we found
![]() (
(![]() 0.10) dex for Cr 110;
0.10) dex for Cr 110;
![]() (
(![]() 0.10) dex for NGC 2099 (M 37), and
0.10) dex for NGC 2099 (M 37), and
![]() (
(![]() 0.10) dex
for NGC 2420. This last finding is higher than typical literature
estimates by 0.2-0.3 dex approximately and in closer agreement
with Galactic trends. For the remaining clusters, we find that
0.10) dex
for NGC 2420. This last finding is higher than typical literature
estimates by 0.2-0.3 dex approximately and in closer agreement
with Galactic trends. For the remaining clusters, we find that
![]() (
(![]() 0.10) dex for M 67 and
0.10) dex for M 67 and
![]() (
(![]() 0.10) dex for NGC 7789. Accurate (to
0.10) dex for NGC 7789. Accurate (to ![]() 0.5 km s-1)
radial velocities were measured for all targets, and we provide the
first velocity estimate derived from high resolution data for
Cr 110,
0.5 km s-1)
radial velocities were measured for all targets, and we provide the
first velocity estimate derived from high resolution data for
Cr 110,
![]() km s-1.
km s-1.
Conclusions. With our analysis of the new clusters Cr 110,
NGC 2099, and NGC 2420, we increase the sample of clusters
with high-resolution-based abundances by 5%. All our program stars
show abundance patterns which are typical of open clusters, very close
to solar with few exceptions. This is true for all the iron-peak and s-process elements considered, and no significant ![]() -enhancement
is found. No significant (anti-)correlations for Na, Al, Mg, and O
abundances are found. If anticorrelations are present, the involved
spreads must be <0.2 dex. We then compile high resolution data
of 57 OC from the literature and find a gradient of [Fe/H] with
Galactocentric radius of -0.06
-enhancement
is found. No significant (anti-)correlations for Na, Al, Mg, and O
abundances are found. If anticorrelations are present, the involved
spreads must be <0.2 dex. We then compile high resolution data
of 57 OC from the literature and find a gradient of [Fe/H] with
Galactocentric radius of -0.06 ![]() 0.02 dex kpc-1,
in agreement with past work and with results for Cepheids and B stars
in the same range. A change of slope is seen outside
0.02 dex kpc-1,
in agreement with past work and with results for Cepheids and B stars
in the same range. A change of slope is seen outside
![]() kpc and [
kpc and [![]() /Fe] shows a tendency to increase with
/Fe] shows a tendency to increase with
![]() .
We also confirm the absence of a significant age-metallicity relation, finding slopes of -2.6
.
We also confirm the absence of a significant age-metallicity relation, finding slopes of -2.6 ![]() 1.1
1.1 ![]() 10-11 dex Gyr-1 and 1.1
10-11 dex Gyr-1 and 1.1 ![]() 5.0
5.0 ![]() 10-11 dex Gyr-1 for [Fe/H] and [
10-11 dex Gyr-1 for [Fe/H] and [![]() /Fe] respectively.
/Fe] respectively.
Key words: stars: abundances - Galaxy: disk - open clusters and associations: general
1 Introduction
Open clusters (hereafter OC) are ideal test particles in the study of the Galactic disk, providing chemical and kinematical information in different locations for different times. Compared to field stars, they have the obvious advantage of being coeval groups of stars, at the same distance and with a homogeneous composition. Therefore, their properties can be determined with smaller uncertainties. Several attempts have been made to derive two fundamental relations using OC: the metallicity gradient along the disk and the age-metallicity relation (hereafter AMR) of the disk (e.g., Friel et al. 2002; Panagia & Tosi 1980; Janes 1979; Salaris et al. 2004; Twarog et al. 1997; Chen et al. 2003), but they were hampered by the lack of large and homogeneous high quality datasets.
Table 1: Observing logs and program stars data.
In particular, the lack of a metallicity scale extending to solar
metallicity with comparable precision to that of the lower metallicity regime
(i.e., Zinn & West 1984; Carretta & Gratton 1997) represents the main problem from the point of view of
(i) the study of the Galactic disk, (ii) tests of stellar evolution
models for younger and more metal-rich simple stellar populations, and
(iii) the use of those stellar populations as templates for extragalactic studies
of population synthesis. Of the ![]() 1700 known OC (Dias et al. 2002, and updates),
only a subset of
1700 known OC (Dias et al. 2002, and updates),
only a subset of ![]() 140, i.e., 8% of the total, possesses some metallicity
determination. Most of these have been obtained by means of different photometric
studies in the Washington (e.g., Geisler et al. 1991,1992), DDO
(e.g., Clariá et al. 1999), Strömgren (e.g., Twarog et al. 2003; Bruntt et al. 1999), UBV
(e.g., Cameron 1985), and IR (e.g., Tiede et al. 1997) photometric systems and
passbands, often giving rise to considerable differences from those obtained from
spectroscopy (see Gratton 2000, and references therein). In a far smaller
number of clusters, abundances have been derived from low-resolution spectroscopy
(e.g., Warren & Cole 2009; Carrera et al. 2007), and there have been admirable attempts to obtain
large and homogeneous datasets (see Friel et al. 2002; Friel & Janes 1993) in spite of the
non-negligible uncertainties involved in the procedure.
140, i.e., 8% of the total, possesses some metallicity
determination. Most of these have been obtained by means of different photometric
studies in the Washington (e.g., Geisler et al. 1991,1992), DDO
(e.g., Clariá et al. 1999), Strömgren (e.g., Twarog et al. 2003; Bruntt et al. 1999), UBV
(e.g., Cameron 1985), and IR (e.g., Tiede et al. 1997) photometric systems and
passbands, often giving rise to considerable differences from those obtained from
spectroscopy (see Gratton 2000, and references therein). In a far smaller
number of clusters, abundances have been derived from low-resolution spectroscopy
(e.g., Warren & Cole 2009; Carrera et al. 2007), and there have been admirable attempts to obtain
large and homogeneous datasets (see Friel et al. 2002; Friel & Janes 1993) in spite of the
non-negligible uncertainties involved in the procedure.
A few research groups (see Sect. 6 for more details) are presently
obtaining high quality spectra and are deriving more precise abundance
measurements. The study of elements other than the iron-peak ones (such as ![]() ,
s-, and r-process, light elements) allows one to place stronger
constraints on the sites of production of those elements (SNe Ia, SNe II, giants,
supergiants, and Wolf-Rayet stars) and therefore on their production timescales.
These are fundamental ingredients to the chemical evolution modeling of the
Galactic disk (Tosi 1982; Colavitti et al. 2009; Chiappini et al. 2001).
,
s-, and r-process, light elements) allows one to place stronger
constraints on the sites of production of those elements (SNe Ia, SNe II, giants,
supergiants, and Wolf-Rayet stars) and therefore on their production timescales.
These are fundamental ingredients to the chemical evolution modeling of the
Galactic disk (Tosi 1982; Colavitti et al. 2009; Chiappini et al. 2001).
For these reasons, we obtained high resolution spectra for a sample of poorly studied old OC. We present here the detailed abundance analysis of five clusters observed during our first run at Calar Alto. Observations and data reductions are described in Sect. 2; the linelist and equivalent width measurements are described in Sect. 3, while the abundance analysis methods and results are presented in Sect. 4; abundance results are then discussed and compared with literature results in Sects. 5-7; finally, we summarize our results and draw our conclusions in Sect. 8.
2 Observational material
Three red clump stars![]() were
selected in each of the target clusters using the WEBDA
were
selected in each of the target clusters using the WEBDA![]() database (Mermilliod 1995) and the 2MASS
database (Mermilliod 1995) and the 2MASS![]() survey
data for the infrared
survey
data for the infrared ![]() mag (Skrutskie et al. 2006). More details about the
references for star names, coordinates and magnitudes can be found in
Table 1, while the position of our targets in the color magnitude
diagrams (CMDs) obtained from WEBDA are shown in Fig. 1.
mag (Skrutskie et al. 2006). More details about the
references for star names, coordinates and magnitudes can be found in
Table 1, while the position of our targets in the color magnitude
diagrams (CMDs) obtained from WEBDA are shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12965fg1.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg32.png)
|
Figure 1: V, (B-V) Color Magnitude Diagrams of the program clusters (from the WEBDA), with the location of our target stars. |
| Open with DEXTER | |
Observations were performed between the 1st and 10th of January 2004 with the
fiber echelle spectrograph FOCES at the 2.2 m Calar Alto Telescope, in Spain. The
sky was generally clear, although a few nights had thin cirrus and sometimes
clouds, forcing us to increase the exposure times considerably. All stars were
observed in 3-16 exposures lasting 15-90 min each, depending on the magnitude,
until a global S/N ratio between 70 and 100 (per pixel) was reached around
6000 Å (Table 1). Each night, we took a sky exposure with an
exposure time as long as that of the longest scientific exposure. The sky level
was negligible for all exposures with S/N>20, therefore exposures with
S/N<20were neglected and we did not subtract the sky, to avoid adding noise to the
spectra. Sky emission lines, even in the red part of the spectrum, only
occasionally affected the measurements of some absorption lines, which were
discarded. The spectral resolution was
![]() for all spectra.
for all spectra.
2.1 Data reduction
Data reductions were done with IRAF![]() within the imred
and echelle packages. The following steps were performed: bias subtraction,
flatfielding, order tracing with optimal extraction, background subtraction,
wavelength calibration with the help of a Thorium-Argon lamp, and final merging
(and rebinning) of overlapping orders. The one-dimensional spectra obtained from
different exposures (with S/N>20) were median-averaged to produce one single
high S/N spectrum for each star, used for equivalent width measurements
(Sect. 3.3). Finally, the noisy ends of each combined spectrum were cut,
allowing for an effective wavelength coverage from 5000 to 9000 Å.
within the imred
and echelle packages. The following steps were performed: bias subtraction,
flatfielding, order tracing with optimal extraction, background subtraction,
wavelength calibration with the help of a Thorium-Argon lamp, and final merging
(and rebinning) of overlapping orders. The one-dimensional spectra obtained from
different exposures (with S/N>20) were median-averaged to produce one single
high S/N spectrum for each star, used for equivalent width measurements
(Sect. 3.3). Finally, the noisy ends of each combined spectrum were cut,
allowing for an effective wavelength coverage from 5000 to 9000 Å.
Sky absorption lines (telluric bands of O2 and H2O) were removed using the IRAF task telluric with the help of two hot, rapidly rotating stars, HR 3982 and HR 8762, chosen from the Bright Star Catalogue (Hoffleit & Jaschek 1991). HR 3982 and HR 8762 were observed each night at an airmass not too different from the scientific targets. Residuals of the correction in the red part of the spectrum (for example, from the strong O2 band around 7600 Å) prevented us from using most of the corresponding spectral regions in our abundance analysis. Also, after 8400 Å, the echelle orders do not overlap anymore and small gaps appear.
2.2 Radial velocities
Radial velocities were measured with the help of DAOSPEC (Stetson & Pancino 2008, see also
Sect. 3.3). Measurements were based on ![]() 360 absorption
lines of different elements (see Sect. 3) with typical measurement
errors on the mean of about 0.1 km s-1. All measurements were performed
separately on the one-dimensional spectra extracted from the single exposures for
each star, including those with S/N<20, which were not used in the abundance
analysis. In this way, we could check that no significant radial velocity
variations were present.
360 absorption
lines of different elements (see Sect. 3) with typical measurement
errors on the mean of about 0.1 km s-1. All measurements were performed
separately on the one-dimensional spectra extracted from the single exposures for
each star, including those with S/N<20, which were not used in the abundance
analysis. In this way, we could check that no significant radial velocity
variations were present.
Table 2:
Heliocentric radial velocities measurements and their 1![]() errors
(
errors
(
![]() )
)
![]() for each program star.
for each program star.
Table 3: Stellar parameters for the program stars.
Heliocentric corrections were computed with the IRAF task rvcor,
which bears a negligible uncertainty of less than 0.005 km s-1. Since
we did not observe any radial velocity standard and our calibration lamp data
were not acquired simultaneously, we used telluric absorption lines to find
the absolute zeropoint of our radial velocity measurements. In
particular, laboratory wavelengths of the H2O absorption bands around
5800, 6500, 7000, 7200, 8000, and 8900 Å and the O2 absorption
bands around 6300, 6900, and 7600 Å were obtained from the
GEISA![]() database
(Jacquinet-Husson et al. 2005,1999) and we measured
their radial velocity in our program stars. The resulting zeropoint
corrections, based on 200-250 telluric lines, amount to generally no more
than
database
(Jacquinet-Husson et al. 2005,1999) and we measured
their radial velocity in our program stars. The resulting zeropoint
corrections, based on 200-250 telluric lines, amount to generally no more
than ![]() 1 km s-1 with typical errors in the mean of about
0.5 km s-1, approximately five times larger than those in the radial
velocity measurements.
1 km s-1 with typical errors in the mean of about
0.5 km s-1, approximately five times larger than those in the radial
velocity measurements.
After applying the above corrections, and propagating the corresponding
uncertainties, we computed a weighted average of the heliocentric velocities
estimates for each exposure (see Table 2). All the program stars
appear to be radial velocity members of the observed clusters, the possible
exception being star 2108 in Cr 110, which has a slightly higher velocity than
both 2129 and 3144. However, since the value for 2108 is within 3![]() of the
mean value for the cluster, we decided not to reject this star. We can provide the
first radial velocity estimate based on high resolution for Cr 110:
of the
mean value for the cluster, we decided not to reject this star. We can provide the
first radial velocity estimate based on high resolution for Cr 110:
![]() km s-1. Our determinations are generally in good
agreement with literature values within 3
km s-1. Our determinations are generally in good
agreement with literature values within 3![]() ,
except maybe for star 5237 in
NGC 7789, which is marginally dicrepant with the estimate by Gim et al. (1998b).
However, there is perfect agreement between the two studies for the
other two
stars of NGC 7789, and our estimate appears more consistent with
membership of 5237. In conclusion, we considered all the program
stars as likely radial
velocity members of their respective clusters.
,
except maybe for star 5237 in
NGC 7789, which is marginally dicrepant with the estimate by Gim et al. (1998b).
However, there is perfect agreement between the two studies for the
other two
stars of NGC 7789, and our estimate appears more consistent with
membership of 5237. In conclusion, we considered all the program
stars as likely radial
velocity members of their respective clusters.
2.3 Photometric parameters
We first computed the dereddened colors![]() (B-V)0, (
(B-V)0, (
![]() )0
)0![]() , and
(V-KTCS)0
, and
(V-KTCS)0![]() . The adopted E(B-V) values
are indicated in Table 4, where
. The adopted E(B-V) values
are indicated in Table 4, where
![]() )
was obtained with the
reddening laws by Dean et al. (1978), and E(V-KTCS) with Cardelli et al. (1989). We were
then able to obtain
)
was obtained with the
reddening laws by Dean et al. (1978), and E(V-KTCS) with Cardelli et al. (1989). We were
then able to obtain
![]() and the bolometric correction BCV for
each program star, using both the Alonso et al. (1999) and the (theoretical and
empyrical) Montegriffo et al. (1998) color-temperature relations, taking into account the
uncertainties in the magnitudes and reddening estimates. The average difference
between the Alonso et al. (1999) and the Montegriffo et al. (1998) temperatures was
and the bolometric correction BCV for
each program star, using both the Alonso et al. (1999) and the (theoretical and
empyrical) Montegriffo et al. (1998) color-temperature relations, taking into account the
uncertainties in the magnitudes and reddening estimates. The average difference
between the Alonso et al. (1999) and the Montegriffo et al. (1998) temperatures was
![]() K (for the empirical calibration of Montegriffo et al. 1998) and
K (for the empirical calibration of Montegriffo et al. 1998) and
![]() K (for the theoretical calibration
of Montegriffo et al. 1998). We averaged all the above
K (for the theoretical calibration
of Montegriffo et al. 1998). We averaged all the above
![]() estimates to obtain our
photometric reference values and their 1
estimates to obtain our
photometric reference values and their 1![]() uncertainties
(Table 3).
uncertainties
(Table 3).
Gravities were obtained from
![]() and BCV using the fundamental
relations
and BCV using the fundamental
relations
where red clump masses were derived using Table 1 of Girardi & Salaris (2001),
and are also shown in Table 3. We assumed that
![]() ,
,
![]() ,
and
,
and
![]() ,
in conformity
with IAU recommendations (Andersen 1999). The difference between the
Alonso et al. (1999) and the (empirical and theoretical, respectively) Montegriffo et al. (1998)
estimates was
,
in conformity
with IAU recommendations (Andersen 1999). The difference between the
Alonso et al. (1999) and the (empirical and theoretical, respectively) Montegriffo et al. (1998)
estimates was
![]() and
and
![]() .
As above, we averaged all our estimates to obtain photometric
gravities
.
As above, we averaged all our estimates to obtain photometric
gravities
![]() (Table 3) and their 1
(Table 3) and their 1![]() uncertainties.
uncertainties.
Table 4: Input cluster parameters.
Finally, a photometric estimate of the microturbulent velocities vt was
obtained using the prescriptions of both Ramírez & Cohen (2003), i.e.,
![]() ,
and Carretta et al. (2004), i.e.,
,
and Carretta et al. (2004), i.e.,
![]() .
The latter takes into account the systematic effect discussed by Magain (1984)
and is on average lower by
.
The latter takes into account the systematic effect discussed by Magain (1984)
and is on average lower by
![]() km s -1 than the one by
Ramírez & Cohen (2003). However, the correction for the Magain (1984) effect depends
strongly on the data quality (i.e., resolution, S/N ratio, number of lines used,
log gf values etc.). Therefore we chose not to average the two estimates, but to
use them as an indication of the (wide) vt range to explore in our abundance
analysis (see Sect. 4.1).
km s -1 than the one by
Ramírez & Cohen (2003). However, the correction for the Magain (1984) effect depends
strongly on the data quality (i.e., resolution, S/N ratio, number of lines used,
log gf values etc.). Therefore we chose not to average the two estimates, but to
use them as an indication of the (wide) vt range to explore in our abundance
analysis (see Sect. 4.1).
3 Linelist, atomic data and equivalent widths
We created a masterlist of absorption lines by visually comparing our spectra with
the the UVES solar spectrum![]() in
the range 5000-9000 Å, and with the linelists extracted from the
VALD
in
the range 5000-9000 Å, and with the linelists extracted from the
VALD![]() database (Kupka et al. 1999) and
the Moore
database (Kupka et al. 1999) and
the Moore![]() (Moore et al. 1966)
solar atlas. The masterlist was fed to DAOSPEC, and EW were measured for all our
program stars. A first selection was applied to reject all lines measured for 10
stars or less (out of 15) and that had EW systematically larger than 250 mÅ.
Later, after performing a rough abundance analysis (see Sect. 4.1), we
rejected all lines that inferred systematically discrepant abundances, especially
if the formal DAOSPEC relative error (
(Moore et al. 1966)
solar atlas. The masterlist was fed to DAOSPEC, and EW were measured for all our
program stars. A first selection was applied to reject all lines measured for 10
stars or less (out of 15) and that had EW systematically larger than 250 mÅ.
Later, after performing a rough abundance analysis (see Sect. 4.1), we
rejected all lines that inferred systematically discrepant abundances, especially
if the formal DAOSPEC relative error (
![]() ,
Fig. 2) was around 15% or more, and the DAOSPEC quality parameter was above 1.5 (for more details
about the DAOSPEC error and quality parameter, see Sect. 3.3). The final
linelist, including atomic data and EW measurements for all program stars,
contains 358 absorption lines of 17 species, and can be found in the electronic
version of Table 5. Atomic data include laboratory wavelengths,
excitation potentials, and
,
Fig. 2) was around 15% or more, and the DAOSPEC quality parameter was above 1.5 (for more details
about the DAOSPEC error and quality parameter, see Sect. 3.3). The final
linelist, including atomic data and EW measurements for all program stars,
contains 358 absorption lines of 17 species, and can be found in the electronic
version of Table 5. Atomic data include laboratory wavelengths,
excitation potentials, and ![]() values, which are always taken from the VALD
database with the exceptions listed below.
values, which are always taken from the VALD
database with the exceptions listed below.
3.1 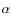 -elements atomic data
-elements atomic data
The only ![]() -element for which we had clear problems with the atomic data was
magnesium. The lines with
-element for which we had clear problems with the atomic data was
magnesium. The lines with
![]() eV (7060 and 7193 Å) gave discrepant
abundances by
eV (7060 and 7193 Å) gave discrepant
abundances by ![]() 1.5 dex with respect to the average of all Mg lines. We
compared our VALD log gf with the NIST
1.5 dex with respect to the average of all Mg lines. We
compared our VALD log gf with the NIST![]() database of atomic data and
noticed a difference of 1.4 dex for the
database of atomic data and
noticed a difference of 1.4 dex for the
![]() eV lines, while all the
other Mg I lines had very similar log gf values in both databases. The NIST
log gf values abundances of the
eV lines, while all the
other Mg I lines had very similar log gf values in both databases. The NIST
log gf values abundances of the
![]() eV lines gave abundances in
much closer agreement with the other Mg I lines and the literature Mg
abundances for OC, therefore we used the NIST values for those lines, instead of
the VALD ones.
eV lines gave abundances in
much closer agreement with the other Mg I lines and the literature Mg
abundances for OC, therefore we used the NIST values for those lines, instead of
the VALD ones.
Another element with uncertain log gf values is calcium.As an example, for the 9
lines that we use, there is an average difference of
log gf
![]() -log gf
-log gf
![]() dex, which is not statistically
significant given the large
dex, which is not statistically
significant given the large ![]() .
The NIST log gf values for those 9 lines
also range from D to E, which means that they are largely uncertain. Finally, our
solar abundance (Sect. 4.6) gives
.
The NIST log gf values for those 9 lines
also range from D to E, which means that they are largely uncertain. Finally, our
solar abundance (Sect. 4.6) gives
![]() (
(![]() 0.03) dex
if we use the VALD log gf and [Ca/H] = +0.08
0.03) dex
if we use the VALD log gf and [Ca/H] = +0.08 ![]() 0.03 (
0.03 (![]() 0.03) dex with the NIST
ones, which is equally compatible with zero within 3
0.03) dex with the NIST
ones, which is equally compatible with zero within 3![]() .
Summarizing, there
is large uncertainty in the calcium log gf determinations, and we should
keep in mind that there is an additional
.
Summarizing, there
is large uncertainty in the calcium log gf determinations, and we should
keep in mind that there is an additional ![]() 0.2 dex uncertainty in all [Ca/Fe]
determinations in the literature.
0.2 dex uncertainty in all [Ca/Fe]
determinations in the literature.
For the synthesis of the [O I]-Ni I blend at 6300 Å, we used the VALD log gfvalue for oxygen, but we chose to use the Johansson et al. (2003) log gf for Ni I at
6300.35 Å, which is lower (-2.11 dex instead of -1.74) and gives oxygen
abundances more in line with the other ![]() -elements.
-elements.
Table 5: Equivalent widths and atomic data of the program stars. The complete version of the table is available at CDS. Here we show a few lines to illustrate its contents.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg2.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg70.png)
|
Figure 2:
The behavior of DAOSPEC relative errors
|
| Open with DEXTER | |
3.2 Heavy element atomic data
For neodymium, we could only find three reliable lines, which apparently did not need any detailed HFS (hyperfine splitting) analysis (Aoki et al. 2001), at 5092, 5249, and 5485 Å. However, the spread in their abundances was quite high (Table 7). The laboratory log gf value published by Den Hartog et al. (2003) are very similar to those from VALD, except for the 5485 Å line, where they differ by 0.14 dex. Therefore, since the log gf values by Den Hartog et al. (2003) slightly reduced the spread in the [Nd/Fe], we used them instead of the VALD ones (see Table 5).
3.3 Equivalent widths with DAOSPEC
The full description of how DAOSPEC works, including comparisons with
the literature and several experiments with artificial and real spectra,
can be found in Stetson & Pancino (2008). The instructions on how to install,
configure and use DAOSPEC can be found in ``Cooking with
DAOSPEC''![]() . In
short, DAOSPEC is a Fortran program that automatically finds absorption
lines in a stellar spectrum, fits the continuum, measures EW, and
identifies lines with a laboratory linelist; it also provides a radial
velocity estimate (Sect. 2.2).
. In
short, DAOSPEC is a Fortran program that automatically finds absorption
lines in a stellar spectrum, fits the continuum, measures EW, and
identifies lines with a laboratory linelist; it also provides a radial
velocity estimate (Sect. 2.2).
As described in Sect. 3, we used the DAOSPEC errors and quality
parameter, Q, to select good absorption lines from our master linelist. Since our
spectra are rebinned linearly in wavelength, we scaled the FWHM with ![]() .
Figure 2 shows their behavior. The formal error in the Gaussian fit that
DAOSPEC outputs is given by
.
Figure 2 shows their behavior. The formal error in the Gaussian fit that
DAOSPEC outputs is given by ![]() ,
and
,
and
![]() can be used to select
good measurements, since smaller lines are noisier and tend to have higher
relative errors. The quality parameter Q, instead, is the result of comparing
local residuals around each line with average residuals for the whole spectrum. As
a result Q tends to be worse for strong lines, because the Gaussian approximation
does not hold so well. Also, Q becomes poorer at the blue side of the spectrum,
where the S/N ratio is lower. In the region around 7700 Å, where the residuals
of the prominent O2 telluric band affect the measurements, Q reaches its
maximum. The measured EW for our program stars are shown in the electronic version
of Table 5 along with the
can be used to select
good measurements, since smaller lines are noisier and tend to have higher
relative errors. The quality parameter Q, instead, is the result of comparing
local residuals around each line with average residuals for the whole spectrum. As
a result Q tends to be worse for strong lines, because the Gaussian approximation
does not hold so well. Also, Q becomes poorer at the blue side of the spectrum,
where the S/N ratio is lower. In the region around 7700 Å, where the residuals
of the prominent O2 telluric band affect the measurements, Q reaches its
maximum. The measured EW for our program stars are shown in the electronic version
of Table 5 along with the ![]() and Q parameter estimated by
DAOSPEC.
and Q parameter estimated by
DAOSPEC.
3.4 EW uncertainties
We used the formal errors in the Gaussian fit computed by DAOSPEC only to reject unreliable measurements from our initial line list. The actual abundance errors due to the EW measurement process itself were instead computed later, as explained in Sect. 4.3.
To compute the EW uncertainty related to the continuum placement, we used Eq. (7)
from Stetson & Pancino (2008) to derive the effective uncertainty in the continuum
placement (![]()
![]() )
which was found to be significantly smaller than 1%. We first lowered the ``best-fit'' continuum level by
)
which was found to be significantly smaller than 1%. We first lowered the ``best-fit'' continuum level by
![]() and
measured the EWs again, obtaining EW(-), then we raised the level by the same
amount and measured EW(+). The differences from the ``correct'' EWmeasurements,
and
measured the EWs again, obtaining EW(-), then we raised the level by the same
amount and measured EW(+). The differences from the ``correct'' EWmeasurements,
![]() and
and
![]() were averaged to estimate
were averaged to estimate
![]() for each line. The typical resultant uncertainty, due only to the
continuum placement, was approximately constant with EW and
for each line. The typical resultant uncertainty, due only to the
continuum placement, was approximately constant with EW and
![]() mÅ approximately (see also Fig. 2 by Stetson & Pancino 2008).
This small uncertainty was neglected because it had a much smaller impact on the
resulting abundances than other sources of uncertainty considered in
Sects. 4.3 and 4.4.
mÅ approximately (see also Fig. 2 by Stetson & Pancino 2008).
This small uncertainty was neglected because it had a much smaller impact on the
resulting abundances than other sources of uncertainty considered in
Sects. 4.3 and 4.4.
3.5 Comparison with literature EW
To our knowledge, only one of our target stars was studied before by
Yong et al. (2005) and Tautvaisiene (2000), with a resolution and S/N similar to ours,
i.e., star 141 in M 67. While Yong et al. (2005) do not publish their EW
measurements, we can compare with those by Tautvaisiene (2000). The authors
provided two sets of EW, the former derived from a spectrum with
![]() 000,
and the latter from a spectrum with
000,
and the latter from a spectrum with
![]() 000. We have 48 lines in common
with the
000. We have 48 lines in common
with the
![]() 000 set and 36 with the
000 set and 36 with the
![]() 000 set.
000 set.
Figure 3 shows good agreement between our EWs and the
![]() 000
set. We only found a systematic offset of
EWT00-EW
000
set. We only found a systematic offset of
EWT00-EW
![]() mÅ, which corresponds to a continuum
placement difference of about 1% (see also Sect. 3.4). A possible
trend with EW was visible when comparing our EWs with the
mÅ, which corresponds to a continuum
placement difference of about 1% (see also Sect. 3.4). A possible
trend with EW was visible when comparing our EWs with the
![]() 000 set,
with no systematic offset (
000 set,
with no systematic offset (
![]() mÅ). On the one hand, this
means that our continuum placement is in far closer agreement with the
mÅ). On the one hand, this
means that our continuum placement is in far closer agreement with the
![]() 000 continuum determined by Tautvaisiene (2000) than with the
000 continuum determined by Tautvaisiene (2000) than with the
![]() 000 one. On the other hand, we note that a possible trend is also
visible when comparing the Tautvaisiene (2000) measurements at
000 one. On the other hand, we note that a possible trend is also
visible when comparing the Tautvaisiene (2000) measurements at
![]() 000 with
those at
000 with
those at
![]() 000. In conclusion, we considered our EW measurements to be
in good agreement with the Tautvaisiene (2000) ones, given the involved uncertainties
(see also Table 6).
000. In conclusion, we considered our EW measurements to be
in good agreement with the Tautvaisiene (2000) ones, given the involved uncertainties
(see also Table 6).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg3.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg80.png)
|
Figure 3:
Comparison of our EW measurements with Tautvaisiene (2000), for star 141 in
M 67. The top panel shows the comparison of DAOSPEC EW with the
|
| Open with DEXTER | |
4 Abundance analysis
4.1 Best model search
A preliminary abundance determination was done using the photometric parameters
(Sect. 4), which allowed us to identify and remove those lines in our
list that gave systematically discrepant abundances. We found largely discrepant
Fe I and Fe II values when using the photometric parameters (by
![]() 0.5-0.9 dex), indicating that something was wrong with the photometric
gravities (Sect. 2.3).
0.5-0.9 dex), indicating that something was wrong with the photometric
gravities (Sect. 2.3).
As a second step, we calculated Fe I and Fe II abundances for a set of
models with parameters extending more than 3![]() around the
photometric estimates of Table 3, i.e., about
around the
photometric estimates of Table 3, i.e., about ![]() 300-500 K in
300-500 K in
![]() ,
,
![]() 0.3-0.6 dex in
0.3-0.6 dex in ![]() and
and ![]() 0.5 km s-1in vt, depending on the star. This large grid of calculated
abundances was used to refine our photometric estimate of the
atmospheric parameters.
0.5 km s-1in vt, depending on the star. This large grid of calculated
abundances was used to refine our photometric estimate of the
atmospheric parameters.
We chose the model that satisfied simultaneously (within the
uncertainties![]() ) the following conditions: (i) the abundance of Fe I lines should not vary with excitation potential
) the following conditions: (i) the abundance of Fe I lines should not vary with excitation potential
![]() ;
(ii) the abundance of Fe I lines should not vary significantly
with EW, i.e., strong and weak lines should infer the same abundance
;
(ii) the abundance of Fe I lines should not vary significantly
with EW, i.e., strong and weak lines should infer the same abundance![]() ;
(iii) the abundance of Fe I lines should not differ sigificantly from the
abundance of Fe II lines; (iv) the abundance of Fe I lines should not vary
significantly with wavelength.
;
(iii) the abundance of Fe I lines should not differ sigificantly from the
abundance of Fe II lines; (iv) the abundance of Fe I lines should not vary
significantly with wavelength.
Table 6: Comparison of our results for star 141 in M 67 with the analysis of Tautvaisiene (2000) and Yong et al. (2005).
Using the spreads in the Fe I and Fe II abundances of various lines, and the
uncertainties in the slopes of the above conditions, we estimated the typical 1![]() uncertainties in the spectroscopic parameters: about
uncertainties in the spectroscopic parameters: about ![]() 100 K for
100 K for
![]() ,
,
![]() 0.2 dex for
0.2 dex for ![]() ,
and
,
and ![]() 0.1 km s-1 for vt.
0.1 km s-1 for vt.
The resulting spectroscopic parameters (Table 3) were always in good agreement with the photometric ones, within the quoted uncertainties, with a tendency for the spectroscopic gravities to be systematically higher by 0.3-0.5 dex (see above). However, these differences are always easily accommodated within the uncertainty ranges (related to photometric errors, uncertainties in distance moduli and reddenings, and bolometric corrections).
4.2 Abundance calculations
Abundance calculations and spectral synthesis (for oxygen) were performed using the latest version of the abundance calculation code originally described by Spite (1967). We used the model atmospheres by Edvardsson et al. (1993). We also made use of ABOMAN, a tool developed by Rossetti at the INAF, Bologna Observatory, Italy, that allows the semi-automatic processing of data for several objects, using the above abundance calculation codes. ABOMAN performs all the steps needed to choose the best model automatically, and provides all the graphical tools to analyze the results.
Table 7: Abundance ratios for sigle cluster stars, with their internal uncertainties (Sect. 4.3). For external uncertainties see Table 9.
When the best model was found for each star, abundances and abundance ratios of
all the species of interest were calculated, by averaging the results for each
line of that element (Table 7). Abundance ratios were always computed
with respect to Fe I. Cluster averages were computed as weighted averages of the
results for each star in the cluster and, if necessary, of different ionization
stages of each element (Table 8). In all tables, [![]() /Fe] is
the weighted average of all
/Fe] is
the weighted average of all ![]() -elements abundances.
-elements abundances.
We can compare our results for star 141 in M 67 (see also Sect. 3.5) with those of Tautvaisiene (2000) and Yong et al. (2005). We find general agreement for both the atmospheric parameters and abundance ratios, with the only significant exception of barium (but see the discussion in Sect. 6.3), calcium (discussed in Sect. 6.2), and titanium. For all the elements discussed, our results, as discussed in Sect. 6, are in broad agreement with the entire collection of high resolution abundances for OC, so we consider our results to be robust.
Table 8: Average cluster abundances, obtained with the weighted average of the single stars abundances.
4.3 Internal abundance uncertainties
Random uncertainties in the EW measurement process and in the loggfdeterminations were taken into account by averaging the abundances determinations
obtained for different lines and using
![]() as the final
internal error. These are reported in Table 7, and they are of
the order of
as the final
internal error. These are reported in Table 7, and they are of
the order of ![]() 0.01 dex for Fe I, which had the highest number of lines, and
could reach up to
0.01 dex for Fe I, which had the highest number of lines, and
could reach up to ![]() 0.2-0.3 dex for elements relying on a handful of lines
such as Nd, for example. Additional systematic (from line to line) and random
(from star to star) uncertainties in EW measurements, related to continuum
placement, had a negligible impact on the final abundances in our specific case
(Sect. 3.4).
0.2-0.3 dex for elements relying on a handful of lines
such as Nd, for example. Additional systematic (from line to line) and random
(from star to star) uncertainties in EW measurements, related to continuum
placement, had a negligible impact on the final abundances in our specific case
(Sect. 3.4).
For the spectral synthesis of oxygen, the uncertainty in the fit was computed by
choosing two spectra, one with abundance higher than the best fitting spectrum,
and another one with lower abundance, each chosen to differ by approximately 1![]() (of the poissonian noise) from the observed spectrum. The abundance
difference of the two ``altered'' spectra with the best-fit spectrum were averaged
together to produce the estimated uncertainty, reported in Table 7 (and
in our solar analysis, Table 10).
(of the poissonian noise) from the observed spectrum. The abundance
difference of the two ``altered'' spectra with the best-fit spectrum were averaged
together to produce the estimated uncertainty, reported in Table 7 (and
in our solar analysis, Table 10).
4.4 Uncertainties due to the choice of stellar parameters
The choice of stellar parameters implies systematic (from line to line) and random
(from star to star) uncertainties in the final abundances. To estimate the impact
of the stellar parameters choice on the derived abundances, each parameter is
usually altered by its estimated uncertainty and the resulting abundance
differences with respect to the best model parameter abundance set are summed in
quadrature to obtain a global uncertainty. We applied this method to our coolest
(508 in NGC 2099) and warmest star (2129 in Cr 110) and obtained various abundance
ratio uncertainties ranging from 0.05 to 0.45 dex, with a typical value around
![]() 0.10 dex.
0.10 dex.
However, as noted by Cayrel et al. (2004), this method produces a very conservative
estimate of the uncertainty, because it neglects the natural correlation between
stellar parameters that occurs when the so-called ``spectroscopic method''
(Sect. 4.1) is adopted. Covariance terms should therefore be included
to properly take into account these dependencies among the parameters
(see McWilliam et al. 1995, for a detailed treatment of the problem). The practical method
proposed by Cayrel et al. (2004) assumes that, among the atmospheric parameters,
![]() has by far the strongest effect on the abundance results and,
therefore,
has by far the strongest effect on the abundance results and,
therefore,
![]() must be varied by its estimated uncertainty
(
must be varied by its estimated uncertainty
(![]() 100 K in our case, Sect. 4.1). A new ``second best'' model
must then be identified with the new value of
100 K in our case, Sect. 4.1). A new ``second best'' model
must then be identified with the new value of
![]() by varying vt and
by varying vt and
![]() accordingly, to minimize as much as possible the slopes of the relations
described in Sect. 4.1. This method naturally and properly takes into
account both the main terms of the error budget and the appropriate
covariance terms.
accordingly, to minimize as much as possible the slopes of the relations
described in Sect. 4.1. This method naturally and properly takes into
account both the main terms of the error budget and the appropriate
covariance terms.
We therefore altered the temperature of our hottest and coolest stars (see above) by both +100 K and -100 K. We reoptimized all the parameters and recalculated all the abundance ratios. The final uncertainties are the average of the uncertainties calculated with the higher and lower temperature and are shown in Table 9. The average between the uncertainties in these two cases is taken as a reliable estimate of the impact of the choice of stellar parameters on our abundance ratios. We added these external uncertainties between parentheses after each abundance ratio and we summed them in quadrature with the internal errors to produce the errorbars in each figure.
Table 9: Uncertanties due to the choice of stellar parameters for the coolest (second column) and the warmest (third column) of our programs stars (see Sect. 4.4).
4.5 Other sources of uncertainty
The following additional sources of systematic uncertainties are not explicitly discussed here, but should be taken into account when comparing our abundance estimates with other works in the literature:
- systematic uncertainties related to the choice of the solar reference abundances, which are not discussed here. Our abundances can be shifted to any solar reference abundance with the information in Table 10;
- uncertainties due to the choice of
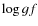 values, which can be estimated
by comparing our
values, which can be estimated
by comparing our 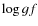 values with other literature values (see
Sect. 3.1);
values with other literature values (see
Sect. 3.1);
- uncertainties in the entire analysis due to more sophisticated effects such as, NLTE, HFS, isotope ratios, which are difficult to evaluate in some cases (these are mentioned whenever known or relevant in Sects. 3 and 6;
- small additional uncertainties related to the particular choices of atmospheric model and abundance calculation code.
Table 10: Solar abundance values.
4.6 The Sun
To test the entire abundance determination procedure, including EW measurement,
the choice of lines and atomic parameters, and the uncertainty determination
criteria, we performed an abundance analysis of the Sun, and checked that we
obtained solar values for all elements, within the uncertainties. We used the solar
spectrum from the ESO spectrograph HARPS, in La Silla, Chile, obtained by
observing
Ganymede![]() .
The spectral resolution,
.
The spectral resolution,
![]() ,
is comparable to ours, while the
,
is comparable to ours, while the
![]() is much higher.
is much higher.
To measure EWs, we used DAOSPEC and the same linelist used for our program stars.
We then compared our solar EWs with two different literature sets, the first by
Moore et al. (1966) and the second by Rutten & van der Zalm (1984). The median difference between our
EW and the ones by Moore is
![]() -
-
![]() mÅ (with an
interquartile range of
mÅ (with an
interquartile range of ![]() 2.7 mÅ), based on 225 lines in common, while the one
with the Rutten & van der Zalm (1984) measurements is
2.7 mÅ), based on 225 lines in common, while the one
with the Rutten & van der Zalm (1984) measurements is
![]() -
-
![]() mÅ
(with an interquartile range of
mÅ
(with an interquartile range of ![]() 2.1 mÅ), based on 112 lines in common. For
completeness, we note that
2.1 mÅ), based on 112 lines in common. For
completeness, we note that
![]() -
-
![]() mÅ (with an
interquartile range of
mÅ (with an
interquartile range of ![]() 2.8 mÅ), based on 390 lines in common. We are
therefore satisfied with our solar EW measurements.
2.8 mÅ), based on 390 lines in common. We are
therefore satisfied with our solar EW measurements.
We then performed our abundance analysis (as in Sect. 4.2) by exploring
the following atmospheric parameter ranges:
![]() -5800,
in steps of 50 K;
-5800,
in steps of 50 K;
![]() -4.5, in steps of 0.1 dex; and
vt=0.5-1.5, in steps of 0.1 km s-1. The resulting best model has
-4.5, in steps of 0.1 dex; and
vt=0.5-1.5, in steps of 0.1 km s-1. The resulting best model has
![]() K,
K,
![]() dex, and
vt=0.8 km s-1, in good agreement with the accepted values (Andersen 1999).
Our adopted reference solar abundances (Grevesse et al. 1996) are shown in Table 10,
along with the abundance ratios derived as described. As can be seen, all the
derived abundance ratios are compatible with zero, within the uncertainties, with
the exception of Al and Ba. For Al, only one (
dex, and
vt=0.8 km s-1, in good agreement with the accepted values (Andersen 1999).
Our adopted reference solar abundances (Grevesse et al. 1996) are shown in Table 10,
along with the abundance ratios derived as described. As can be seen, all the
derived abundance ratios are compatible with zero, within the uncertainties, with
the exception of Al and Ba. For Al, only one (
![]() Å) very weak
(EW=18 mÅ)
line could be measured in the solar spectrum, while we used about
8 lines in the analysis of our red clump giants. The lines
at 6696 and 6698 Å are
known to generally infer lower values than the other Al lines (Gratton et al. 2001; Reddy et al. 2003),
so we do not worry too much about our lone 6698 Å
Å) very weak
(EW=18 mÅ)
line could be measured in the solar spectrum, while we used about
8 lines in the analysis of our red clump giants. The lines
at 6696 and 6698 Å are
known to generally infer lower values than the other Al lines (Gratton et al. 2001; Reddy et al. 2003),
so we do not worry too much about our lone 6698 Å![]() solar line giving a low [Al/Fe] result. We
discuss Ba in Sect. 6.3. For some elements (La, Mg, Nd, Y), no ratio
could be determined either because their lines appear too weak in the sun or
because the solar spectrum range (5000-7000 Å) does not contain the lines that
we used in this paper.
solar line giving a low [Al/Fe] result. We
discuss Ba in Sect. 6.3. For some elements (La, Mg, Nd, Y), no ratio
could be determined either because their lines appear too weak in the sun or
because the solar spectrum range (5000-7000 Å) does not contain the lines that
we used in this paper.
Table 11: Literature abundance determinations for M 67 based on high resolution spectroscopy.
5 Cluster-by-cluster discussion
5.1 Cr 110
Collinder 110 is a poorly studied, intermediate-age OC located at
![]() and
and
![]() :01:00.
We could not find any high resolution spectroscopic study of this cluster in the
literature, but photometric studies were conducted by Tsarevskii & Abakumov (1971),
Dawson & Ianna (1998) and Bragaglia & Tosi (2003). Reddening, distance, and ages determined by
these authors are included in Table 4. Concerning metallicity, while
the first two studies assume solar metallicity, Bragaglia & Tosi (2003) find, as a result
of their synthetic diagram analysis, two equally good solutions, one at solar
metallicity and the other at slightly subsolar metallicity (Z=0.008). A
re-evaluation of the same data by Bragaglia & Tosi (2006) favours the slightly subsolar
value.
:01:00.
We could not find any high resolution spectroscopic study of this cluster in the
literature, but photometric studies were conducted by Tsarevskii & Abakumov (1971),
Dawson & Ianna (1998) and Bragaglia & Tosi (2003). Reddening, distance, and ages determined by
these authors are included in Table 4. Concerning metallicity, while
the first two studies assume solar metallicity, Bragaglia & Tosi (2003) find, as a result
of their synthetic diagram analysis, two equally good solutions, one at solar
metallicity and the other at slightly subsolar metallicity (Z=0.008). A
re-evaluation of the same data by Bragaglia & Tosi (2006) favours the slightly subsolar
value.
Low resolution spectroscopy using the infrared calcium triplet by Carrera et al. (2007)
gave: [Fe/H] = -0.01 ![]() 0.07 dex in the Carretta & Gratton (1997) scale,
[Fe/H] =
0.07 dex in the Carretta & Gratton (1997) scale,
[Fe/H] = ![]() dex in the Zinn & West (1984) scale, and [Fe/H] = -0.19
dex in the Zinn & West (1984) scale, and [Fe/H] = -0.19 ![]() 0.21 dex in the Kraft & Ivans (2003) scale. Our determination of [Fe/H] = +0.03
0.21 dex in the Kraft & Ivans (2003) scale. Our determination of [Fe/H] = +0.03 ![]() 0.02
(
0.02
(![]() 0.10) dex is in good agreement with all these estimates, given the large
uncertainties involved in photometric and low-resolution spectroscopic metallicity
estimates. The other element ratios determined here have no previous literature
values with which to compare, but the comparisons in Sect. 6 show
that they behave as expected for a solar metallicity OC. Our radial velocity
estimate for Cr 110,
0.10) dex is in good agreement with all these estimates, given the large
uncertainties involved in photometric and low-resolution spectroscopic metallicity
estimates. The other element ratios determined here have no previous literature
values with which to compare, but the comparisons in Sect. 6 show
that they behave as expected for a solar metallicity OC. Our radial velocity
estimate for Cr 110,
![]() km s-1 (Sect. 2.2),
is in good agreement with the CaT value determined by Carrera et al. (2007) of
km s-1 (Sect. 2.2),
is in good agreement with the CaT value determined by Carrera et al. (2007) of
![]() km s-1.
km s-1.
5.2 NGC 2099 (M 37)
NGC 2099 (M 37) is located in the Galactic anticenter direction in Auriga
![]() and
and
![]() .
Since it is close-by and appears to be a relatively rich and large cluster, it has
been photometrically studied by several authors to derive accurate magnitudes and
proper motions, and to complete a census of variable stars (for historical
references see Kalirai et al. 2001). All the papers that derived reddening, distance, and
age are also cited in Table 4. Photometric studies generally attribute a
solar metallicity to NGC 2099 (e.g., Mermilliod et al. 1996). Metallicity estimates based
on photometry can only be found in Janes et al. (1988), who infer [Fe/H] = 0.09 dex,
Marshall et al. (2005), who infer [M/H] =
.
Since it is close-by and appears to be a relatively rich and large cluster, it has
been photometrically studied by several authors to derive accurate magnitudes and
proper motions, and to complete a census of variable stars (for historical
references see Kalirai et al. 2001). All the papers that derived reddening, distance, and
age are also cited in Table 4. Photometric studies generally attribute a
solar metallicity to NGC 2099 (e.g., Mermilliod et al. 1996). Metallicity estimates based
on photometry can only be found in Janes et al. (1988), who infer [Fe/H] = 0.09 dex,
Marshall et al. (2005), who infer [M/H] =
![]() ,
and Kalirai & Tosi (2004), who infer
Z<0.02.
,
and Kalirai & Tosi (2004), who infer
Z<0.02.
Surprisingly, when considering the wealth of photometric studies, M 37 lacks any low or high resolution spectroscopic study, designed to determine its chemical composition. Our values therefore fill this gap, and show that in all respects this cluster has a typical solar metallicity, with all element ratios close to zero within the uncertainties. On the other hand, radial velocity determinations for this cluster have been quite numerous (Sect. 2.2) and appear in good agreement with our determination.
5.3 NGC 2420
NGC 2420 (
![]() :38:23 and
:38:23 and
![]() :34:24) has always been considered the definitive
example of the older, moderately metal-deficient OC beyond the solar circle.
Several good quality imaging studies appeared already in the 60 s and 70 s
(Cannon & Lloyd 1970; van Altena & Jones 1970; West 1967b; McClure et al. 1978,1974; Sarma & Walker 1962, to name a few), and more recent
photometries appeared in a variety of photometric systems (the most cited
being Anthony-Twarog et al. 1990). Its intermediate status between the solar-metallicity OC near the
sun and the clearly metal-deficient population of globular clusters indicated it
early on as a potential transition object between the two populations, with
metallicity determinations - both photometric and spectroscopic - placing it
at an [Fe/H] value around the one of 47 Tuc
(e.g., Cohen 1980; Smith & Suntzeff 1987; Pilachowski et al. 1980; Canterna et al. 1986). Photometric studies infer somewhat
higher [Fe/H] values, ranging from -0.5 to -0.3 dex
(e.g., Friel et al. 2002; Twarog et al. 1997; Anthony-Twarog et al. 2006), but still significantly lower than the value
of [Fe/H] = -0.05
:34:24) has always been considered the definitive
example of the older, moderately metal-deficient OC beyond the solar circle.
Several good quality imaging studies appeared already in the 60 s and 70 s
(Cannon & Lloyd 1970; van Altena & Jones 1970; West 1967b; McClure et al. 1978,1974; Sarma & Walker 1962, to name a few), and more recent
photometries appeared in a variety of photometric systems (the most cited
being Anthony-Twarog et al. 1990). Its intermediate status between the solar-metallicity OC near the
sun and the clearly metal-deficient population of globular clusters indicated it
early on as a potential transition object between the two populations, with
metallicity determinations - both photometric and spectroscopic - placing it
at an [Fe/H] value around the one of 47 Tuc
(e.g., Cohen 1980; Smith & Suntzeff 1987; Pilachowski et al. 1980; Canterna et al. 1986). Photometric studies infer somewhat
higher [Fe/H] values, ranging from -0.5 to -0.3 dex
(e.g., Friel et al. 2002; Twarog et al. 1997; Anthony-Twarog et al. 2006), but still significantly lower than the value
of [Fe/H] = -0.05 ![]() 0.03 (
0.03 (![]() 0.10) dex that we found here.
0.10) dex that we found here.
However, both Cohen (1980) and Pilachowski et al. (1980) noted that NGC 2420 should be
significantly more metal-rich than the globular clusters they analyzed, i.e., M 71
(Cohen 1980) and 47 Tuc (Pilachowski et al. 1980), by some ![]() 0.5 dex. Since they placed
M 71 and 47 Tuc around [Fe/H] = -1.3, they consequently placed NGC 2420 at
[Fe/H] = -0.6. The resolution of their spectra (R<10 000) was much lower than
ours, but if we trust their analysis in a relative sense, and consider more recent
metallicity estimates for 47 Tuc and M 71 (-0.76 and -0.73,
respectively, Harris 1996), we would then place NGC 2420 around [Fe/H]
0.5 dex. Since they placed
M 71 and 47 Tuc around [Fe/H] = -1.3, they consequently placed NGC 2420 at
[Fe/H] = -0.6. The resolution of their spectra (R<10 000) was much lower than
ours, but if we trust their analysis in a relative sense, and consider more recent
metallicity estimates for 47 Tuc and M 71 (-0.76 and -0.73,
respectively, Harris 1996), we would then place NGC 2420 around [Fe/H] ![]() -0.1
or -0.2. Having said that, it is surprising that there are no modern high
resolution studies of a cluster that was considered so important in the past. The
highest spectral resolution employed to study NGC 2420 is
-0.1
or -0.2. Having said that, it is surprising that there are no modern high
resolution studies of a cluster that was considered so important in the past. The
highest spectral resolution employed to study NGC 2420 is
![]() (Smith & Suntzeff 1987), with a spectral coverage of only 200 Å, giving [Fe/H] = -0.57. Only
the preliminary work of Freeland et al. (2002) suggested a higher, slightly subsolar [Fe/H]
value for NGC 2420. We also note that our [Fe/H] brings NGC 2420 more in line with
other OC in the Galactic trends discussed in Sect. 7. Also, we
cannot ignore the similarity with the case of NGC 7789 (Sect. 5.5),
where analyses of high resolution spectroscopy by Tautvaisiene et al. (2005) and us provide
much higher abundances than the previous photometric and low/medium-resolution
studies. Clearly, additional high resolution spectroscopy with modern instruments,
possibly with
(Smith & Suntzeff 1987), with a spectral coverage of only 200 Å, giving [Fe/H] = -0.57. Only
the preliminary work of Freeland et al. (2002) suggested a higher, slightly subsolar [Fe/H]
value for NGC 2420. We also note that our [Fe/H] brings NGC 2420 more in line with
other OC in the Galactic trends discussed in Sect. 7. Also, we
cannot ignore the similarity with the case of NGC 7789 (Sect. 5.5),
where analyses of high resolution spectroscopy by Tautvaisiene et al. (2005) and us provide
much higher abundances than the previous photometric and low/medium-resolution
studies. Clearly, additional high resolution spectroscopy with modern instruments,
possibly with
![]() and
and
![]() is needed for this cluster.
is needed for this cluster.
5.4 NGC 2682 (M 67)
Among the old OC, M 67 (
![]() ,
,
![]() )
is quite close to us, with low reddening
(Table 4) and solar metallicity, so it is one of the most well studied
open clusters, and a good target when searching for solar twins and analogs
(Pasquini et al. 2008). Since the first pioneering studies at the beginning of XX century,
a few hundred papershave been published to date (see Burstein et al. 1986; Carraro et al. 1996; Yadav et al. 2008, for more
references). Therefore, we have included M 67 in our sample
because it acts as a fundamental comparison object that enables us to place our
measurements in a more general framework.
)
is quite close to us, with low reddening
(Table 4) and solar metallicity, so it is one of the most well studied
open clusters, and a good target when searching for solar twins and analogs
(Pasquini et al. 2008). Since the first pioneering studies at the beginning of XX century,
a few hundred papershave been published to date (see Burstein et al. 1986; Carraro et al. 1996; Yadav et al. 2008, for more
references). Therefore, we have included M 67 in our sample
because it acts as a fundamental comparison object that enables us to place our
measurements in a more general framework.
Among the vast literature on M 67, there are several determinations of its metallicity, with various methods (e.g., Garcia Lopez et al. 1988; Friel et al. 2002; Foy & Proust 1981; Janes & Smith 1984; Cohen 1980; Janes & Phelps 1994; Balaguer-Núñez et al. 2007; Demarque 1980; Burstein et al. 1986; Friel & Boesgaard 1992; Friel & Janes 1993; Brown 1987; Marshall et al. 2005; Cayrel de Strobel 1990; Hobbs & Thorburn 1991; Burstein et al. 1984, to name a few), all typically converging to a solar value. high resolution abundance determinations have been derived for both giants and dwarfs, with many studies being devoted to light elements such as lithium and beryllium and their implications for mixing theories (Randich et al. 2007; Jones et al. 1999; Pasquini et al. 1997).
Table 11 shows a comparison of our results with some of the most recent
high resolution (![]() 000) determinations
(Santos et al. 2009; Randich et al. 2006; Tautvaisiene 2000; Shetrone & Sandquist 2000; Pace et al. 2008). The overall comparison is extremely
satisfactory for all elements, except maybe for Mg, Na, Ba, and Ca (see also
Sect. 3.1). For Mg, Na, and Ba, the large spread in literature
demonstrates the difficulties in measuring these elements. For Ca, we see that our
value is marginally lower than other literature deterrminations. As explained in
Sect. 3.1, this is most probably due to the large uncertainties on the
calcium log gf values.
000) determinations
(Santos et al. 2009; Randich et al. 2006; Tautvaisiene 2000; Shetrone & Sandquist 2000; Pace et al. 2008). The overall comparison is extremely
satisfactory for all elements, except maybe for Mg, Na, Ba, and Ca (see also
Sect. 3.1). For Mg, Na, and Ba, the large spread in literature
demonstrates the difficulties in measuring these elements. For Ca, we see that our
value is marginally lower than other literature deterrminations. As explained in
Sect. 3.1, this is most probably due to the large uncertainties on the
calcium log gf values.
Table 12: Literature abundance determinations for NGC 7789 based on high resolution spectroscopy.
5.5 NGC 7789
NGC 7789 (
![]() and
and
![]() ,
or l=115.53 and b=-5.39) is a rich
and intermediate-age OC, with a clearly defined giant branch, a well-populated
main-sequence turnoff, and a substantial population of blue stragglers
(Twarog & Tyson 1985; McNamara 1980; Milone & Latham 1994). Several photometric studies have been carried out
(some examples
are Kustner 1923; Jahn et al. 1995; Bramich et al. 2005; Bartasiute & Tautvaisiene 2004; Gim et al. 1998a; Martinez Roger et al. 1994; Vallenari et al. 2000; Janes 1977; Burbidge & Sandage 1958; Reddish 1954) and its
parameters are reasonably well known.
,
or l=115.53 and b=-5.39) is a rich
and intermediate-age OC, with a clearly defined giant branch, a well-populated
main-sequence turnoff, and a substantial population of blue stragglers
(Twarog & Tyson 1985; McNamara 1980; Milone & Latham 1994). Several photometric studies have been carried out
(some examples
are Kustner 1923; Jahn et al. 1995; Bramich et al. 2005; Bartasiute & Tautvaisiene 2004; Gim et al. 1998a; Martinez Roger et al. 1994; Vallenari et al. 2000; Janes 1977; Burbidge & Sandage 1958; Reddish 1954) and its
parameters are reasonably well known.
Table 13:
Literature sources and [Fe/H] values for high resolution (
![]() )
based abundance ratios of old OC.
)
based abundance ratios of old OC.
Abundance determinations obtained from photometry and low/medium-resolution
spectroscopy all give subsolar values around [Fe/H] ![]() -0.2
(Friel et al. 2002; Friel & Janes 1993; Pilachowski 1985; Schönberner et al. 2001), i.e., much lower than our
-0.2
(Friel et al. 2002; Friel & Janes 1993; Pilachowski 1985; Schönberner et al. 2001), i.e., much lower than our
![]() (
(![]() 0.10) dex. However, a more conforting comparison with
Tautvaisiene et al. (2005) is shown in Table 12. Their spectra have a resolution and
S/N that is similar to ours, and most abundance ratios in common show excellent
agreement. Minor discrepancies arise for some elements such as Ca (but see the
discussion in Sects. 3.1 and 5.4), Al (but they used only
one doublet while we used four), Na, and O. Since they do not list their log gfvalues, and other ingredients of the abundance analysis were similar to ours, we
cannot explain the Na-O discrepancies, but we suspect that they must be caused by
log gf differences.
0.10) dex. However, a more conforting comparison with
Tautvaisiene et al. (2005) is shown in Table 12. Their spectra have a resolution and
S/N that is similar to ours, and most abundance ratios in common show excellent
agreement. Minor discrepancies arise for some elements such as Ca (but see the
discussion in Sects. 3.1 and 5.4), Al (but they used only
one doublet while we used four), Na, and O. Since they do not list their log gfvalues, and other ingredients of the abundance analysis were similar to ours, we
cannot explain the Na-O discrepancies, but we suspect that they must be caused by
log gf differences.
6 Discussion of abundance ratios
We compared our abundance ratios with data from the literature, which were assembled as follows. For the Milky Way field stars, we used the thick and thin Galactic disc measurements from Reddy et al. (2003) and Reddy et al. (2006), who performed homeogeneous abundance calculations of a few hundred F/G dwarfs selected from the Hipparcos catalogue. We added abundance ratios, based on high resolution spectroscopy, for 57 old OC from various literature sources (Table 13). When more than one determination was available for one cluster, we simply plotted them all to obtain a realistic idea of the uncertainties involved in the compilation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg4.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg121.png)
|
Figure 4: Comparison between our iron-peak element results (large black dots), the high resolution measurements of other OC listed in Table 13 (large dark grey dots), and field stars belonging to the thin Galactic disc (light grey dots, Reddy et al. 2003) and to the thick Galactic disc (tiny light grey dots, Reddy et al. 2006). Errorbars on our results are the quadratic sum of internal uncertainties and uncertainties due to the choice of stellar parameters (Sect. 4). |
| Open with DEXTER | |
6.1 Iron-peak element ratios
When compared with literature data (Fig. 4), our iron-peak elements appear all solar and in good agreement with the results for the Galactic disc and other OC. In particular, cobalt and chromium are in the closest agreement and have the smallest spreads. Although Sc, V, and Co are known to possess HFS that may lead to an increased scatter and an overestimated ratio, they do not appear to differ significantly from solar for our target stars, so we did not attempt any detailed HFS analysis. Nevertheless, the effect of increased scatter and overestimated abundances are visible, expecially for vanadium, both in our data and in the discs stars, as well as in the other clusters from the literature.
A puzzling effect is seen in Fig. 4 in the [Ni/Fe] ratio. All the data
for disc stars are very close to solar
(
![]() = -0.02
= -0.02 ![]() 0.02), and so are
our determinations (
0.02), and so are
our determinations (
![]() ), but the other OC high resolution
data appear slightly enhanced (
), but the other OC high resolution
data appear slightly enhanced (
![]() ), lying systematically
above the disc ones. Such a
), lying systematically
above the disc ones. Such a ![]() 0.05 dex offset is well within the
uncertainties of abundance determinations in general, but since it appears
systematic in nature, we are still left without a clear explanation. Our [Ni/Fe]
ratios are slightly lower than the other OC determinations, although still
compatible within the uncertainties.
0.05 dex offset is well within the
uncertainties of abundance determinations in general, but since it appears
systematic in nature, we are still left without a clear explanation. Our [Ni/Fe]
ratios are slightly lower than the other OC determinations, although still
compatible within the uncertainties.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{12965fg5.ps}\par
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg125.png)
|
Figure 5:
Comparison between our |
| Open with DEXTER | |
6.2 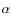 -element ratios
-element ratios
We obtained abundances of Ca, Mg, O, Si, and Ti. As can be seen from Fig. 5, Si and Ti appear practically solar, within their respective uncertainties, and in very good agreement with literature determinations for both the discs stars and those of the other OC. For O, Ca and Mg we instead find marginally discrepant enhancements.
For O, we note that the spread in both our data and that of the literature is
greater that in any other ![]() -element. This is partly due to the well known
problems of determining O from the single 6300 Å line, or the 6363 Å weak
line, or from the IR triplet at 7770 Å(which requires NLTE corrections).
Moreover, some literature works use Solar reference abundances that are as high as
8.93, which may explain some of the lowest [O/Fe] literature estimates. Given the
large spread, the tendency of our [O/Fe] measurements to lie on the upper envelope
of the other OC high resolution data is probably irrelevant. Solar O enhancements
would probably be more in line with those of the other
-element. This is partly due to the well known
problems of determining O from the single 6300 Å line, or the 6363 Å weak
line, or from the IR triplet at 7770 Å(which requires NLTE corrections).
Moreover, some literature works use Solar reference abundances that are as high as
8.93, which may explain some of the lowest [O/Fe] literature estimates. Given the
large spread, the tendency of our [O/Fe] measurements to lie on the upper envelope
of the other OC high resolution data is probably irrelevant. Solar O enhancements
would probably be more in line with those of the other ![]() -elements, while
the subsolar values found generally in the literature suggests Wolf-Rayet as
additional contributors of O, with a stronger metallicity dependence of the
O yields (McWilliam et al. 2008).
-elements, while
the subsolar values found generally in the literature suggests Wolf-Rayet as
additional contributors of O, with a stronger metallicity dependence of the
O yields (McWilliam et al. 2008).
In the case of Ca, our values are marginally inconsistent with the bulk of field
and OC literature determinations. A few literature measurements of OC ratios are
however as low as our values. These inconsistencies could be explained by the
large uncertainties in the literature log gf values for calcium lines
(![]() 0.2 dex, see discussion in Sect. 3.1). Given these large
additional uncertainties, we finally conclude that [Ca/Fe] is basically compatible
with solar values in all the clusters examined.
0.2 dex, see discussion in Sect. 3.1). Given these large
additional uncertainties, we finally conclude that [Ca/Fe] is basically compatible
with solar values in all the clusters examined.
Concerning Mg, we know already that the log gf values of some lines are still
not very well determined (Sect. 3.1). We also know (Gratton et al. 1999) that
some lines require NLTE corrections. We could find no correction factors for the
lines that we were able to measure in our spectra, but we noticed that those lines
examined by Gratton et al. (1999), which have
![]() values similar to our lines,
require NLTE corrections of about +0.1-0.5 dex. This correction would make our
[Mg/Fe] values even higher, reaching an enhancement of 0.2-0.6 dex with respect
to solar. Another possibility is that our lines have a non-negligible HFS, because
they are dominated by odd isotopes, but we could find no further information in
the literature. We only noted that other authors find such relatively high values
of [Mg/Fe] in OC (such as Bragaglia et al. 2008).
values similar to our lines,
require NLTE corrections of about +0.1-0.5 dex. This correction would make our
[Mg/Fe] values even higher, reaching an enhancement of 0.2-0.6 dex with respect
to solar. Another possibility is that our lines have a non-negligible HFS, because
they are dominated by odd isotopes, but we could find no further information in
the literature. We only noted that other authors find such relatively high values
of [Mg/Fe] in OC (such as Bragaglia et al. 2008).
When the average [![]() /Fe] values are calculated, however, all the program
stars and the cluster averages appear perfectly compatible with solar, within the
relatively small uncertainties, as expected (see Tables 7 and 8). The [
/Fe] values are calculated, however, all the program
stars and the cluster averages appear perfectly compatible with solar, within the
relatively small uncertainties, as expected (see Tables 7 and 8). The [![]() /Fe] ratio is discussed also in
Sect. 7.
/Fe] ratio is discussed also in
Sect. 7.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg6.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg126.png)
|
Figure 6: Comparison between our s-process elements ratios and the literature ones. Symbols are the same as in Fig. 4, except for the black star-like symbols in the top [Ba/Fe] panel, which represent the revision of Ba abundances with spectral synthesis performed by D'Orazi et al. (2009). |
| Open with DEXTER | |
6.3 Heavy element ratios
We measured the heavy s-process elements Ba, La, and Nd and the light s-process element Y. Lanthanum does not require any synthesis to take into account HFS, since the three lines that we used are always in the linear part of the curve of growth, and Fig. 6 shows indeed good agreement with the sparse literature values. Yittrium and neodimium are also in agreement with the literature data, although the measurements of Nd in OC are few in number and exhibit significant scatter. Our values of [Nd/Fe] have a tendency to lie towards the upper envelope of the disc stars, but this is not significant if we consider the large uncertainties involved (see also the discussion in Sect. 3.2).
Concerning Ba, we find high values in both our program stars and the Sun itself
(Sect. 4.6). The same result has been found by other authors
(e.g., Bragaglia et al. 2008). While a detailed study of the barium abundance is beyond
the scope of the present paper, we note that recently D'Orazi et al. (2009) used a
detailed HFS analysis of barium in OC to show that the overabundance can thus be
reduced by roughly ![]() 0.2 dex. Looking at Fig. 6, we can see that
our [Ba/Fe] values are in general sligthly higher than the literature OC data,
which in turn have a huge spread. Data from D'Orazi et al. (2009), who revised the Ba
abundances for 20 OC using spectral synthesis to take HFS into account, are
towards the lower envelope of the OC abundances (open stars in
Fig. 6). As can be seen, some [Ba/Fe] enhancement remains in their
high quality data, which is apparently well correlated with the cluster ages (see
their Fig. 1). However, no clear explanation is available yet, since the current
evolution models and yields do not reproduce the data correctly at young ages,
where the enhancement is higher and more uncertain (up to [Ba/Fe]
0.2 dex. Looking at Fig. 6, we can see that
our [Ba/Fe] values are in general sligthly higher than the literature OC data,
which in turn have a huge spread. Data from D'Orazi et al. (2009), who revised the Ba
abundances for 20 OC using spectral synthesis to take HFS into account, are
towards the lower envelope of the OC abundances (open stars in
Fig. 6). As can be seen, some [Ba/Fe] enhancement remains in their
high quality data, which is apparently well correlated with the cluster ages (see
their Fig. 1). However, no clear explanation is available yet, since the current
evolution models and yields do not reproduce the data correctly at young ages,
where the enhancement is higher and more uncertain (up to [Ba/Fe] ![]() 0.6 dex
for ages around 108 yr).
0.6 dex
for ages around 108 yr).
To summarize, most of the [Ba/Fe] enhancement that we see in our measurements should be produced by HFS effects, but some could be real (up to 0.2 dex, see Fig. 2 by D'Orazi et al. 2009). A hint of a negative slope of [Ba/Fe] vs. [Fe/H] in OC appears, that is not appareent among disc stars. Further studies similar to that of D'Orazi et al. (2009) are necessary for large samples of disc and OC stars to place firmer constraints on the chemical evolution of Ba in the Galactic disc.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg7.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg127.png)
|
Figure 7: Comparison between our [Na/Fe] and [Al/Fe] ratios and the literature values. Symbols are the same as in Fig. 4. |
| Open with DEXTER | |
6.4 Ratios of Na and Al and anticorrelations
We also derived Na and Al abundances, since these elements are quite easy to
measure in OC and there is a vast body of literature measurements to compare with.
Figure 7 shows that for Al there is general agreement between our
data, the disc ratios, and the OC ratios, although there is a large scatter in the
literature data. The NLTE corrections for the four Al doublets and the type of
stars studied here could not be found in the literature. Baumüller & Gehren (1997) give
corrections for hotter (
![]() )
and higher gravity (
)
and higher gravity (
![]() )
stars, which suggest that either the corrections are negligible, or they are
slightly negative at lower temperatures and gravities.
)
stars, which suggest that either the corrections are negligible, or they are
slightly negative at lower temperatures and gravities.
In the case of Na, the spread in the literature data is even larger, and there are
data points with both significant Na enhancement and typical solar values. Part
of the scatter depends on the need for NLTE corrections. According to
Gratton et al. (1999), the 5682-5688 Å and the 6154-6160 Å doublets with
![]() mÅ both require corrections of about
mÅ both require corrections of about
![]() 0.05-0.10 dex, for
solar stars such as those considered here. The NLTE-corrected abundances should be
higher than the LTE-uncorrected ones: this should bring our [Na/Fe] LTE
measurements to closer agreement with literature measurements. If the observed
enhancement in [Na/Fe] should prove to be real for OC, this would set OC stars
completely apart form disc stars (De Silva et al. 2009). If the large spread were in
addition intrinsic, this would suggest that light element chemical anomalies are
similar, although much less pronounced, to those found in globular clusters.
0.05-0.10 dex, for
solar stars such as those considered here. The NLTE-corrected abundances should be
higher than the LTE-uncorrected ones: this should bring our [Na/Fe] LTE
measurements to closer agreement with literature measurements. If the observed
enhancement in [Na/Fe] should prove to be real for OC, this would set OC stars
completely apart form disc stars (De Silva et al. 2009). If the large spread were in
addition intrinsic, this would suggest that light element chemical anomalies are
similar, although much less pronounced, to those found in globular clusters.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg8.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg132.png)
|
Figure 8:
A search for (anti)-correlations of Al, Mg, Na and O among our targets
stars. The four panels show different planes of abundance ratios, where stars
belonging to each cluster are marked with different symbols. Dotted lines show
solar values, solid lines show linear regressions and the typical uncertainty
( |
| Open with DEXTER | |
Together with Mg and O (and C and N), Al and Na show puzzling (anti)-correlations in almost all of the studied Galactic globular clusters (Gratton et al. 2004). The most interesting property of the chemical anomalies, is that they have never been found outside globular clusters. They are not present in the field populations of the Milky Way and its surrounding dwarf galaxies, and they have only more recently been found in Fornax and LMC clusters (Letarte et al. 2006; Mucciarelli et al. 2009; Johnson et al. 2006). Dedicated searches for anticorrelations in OC include that of Martell & Smith (2009), on the strength of CH and CN bands in NGC 188, NGC 2158, and NGC 7789, that of Smiljanic et al. (2009), based on high resolution spectroscopy of C, N, O, Na, and 12C/13C and that of De Silva et al. (2009), which compiles and homogenizes literature Na-O high resolution data. No clear-cut sign of any anticorrelation has yet been found.
If we make the usual (anti)-correlation plots for our five OC
(Fig. 8), we find no clear sign of chemical anomalies, and in all
four plots the spread in each ratio is still compatible with the typical
uncertainty in our measurements, which is of the order of 0.1-0.2 dex, depending
on the element. In particular, in the [O/Fe]-[Na/Fe] plane, all 15 stars roughly
occupy the solar region around zero that in Fig. 5 by Carretta et al. (2006) contains only
normal only (see also De Silva et al. 2009). A possible exception to this total absence
of correlations is the [Na/Fe]-[Al/Fe] plane, where a hint of a correlation can
be discerned. Statistically, this is not significant and small variations in
![]() could induce a similarly weak correlation. For this reason,
anticorrelations are usually a more robust sign of chemical anomalies. In light of
the discussion by Smiljanic et al. (2009) about a Na-O anticorrelation, our Na-Al results is
suggestive. If future studies show that some chemical anomalies of these elements
are present in Galactic OC, our analysis (together with that of Smiljanic et al. 2009)
implies that they must be of a much smaller extent than in globular clusters,
i.e., 0.2-0.3 dex at most in [Al/Fe], [Mg/Fe], [Na/Fe], and [O/Fe] for the kind
of clusters studied here. In any case, the lack of relations for OC would point
towards one or more of the following environmental causes for the presence of
anticorrelations in globular clusters: (i) relatively low metallicity (below
solar); (ii) a dense local environment; (iii) total cluster mass of
the order of
could induce a similarly weak correlation. For this reason,
anticorrelations are usually a more robust sign of chemical anomalies. In light of
the discussion by Smiljanic et al. (2009) about a Na-O anticorrelation, our Na-Al results is
suggestive. If future studies show that some chemical anomalies of these elements
are present in Galactic OC, our analysis (together with that of Smiljanic et al. 2009)
implies that they must be of a much smaller extent than in globular clusters,
i.e., 0.2-0.3 dex at most in [Al/Fe], [Mg/Fe], [Na/Fe], and [O/Fe] for the kind
of clusters studied here. In any case, the lack of relations for OC would point
towards one or more of the following environmental causes for the presence of
anticorrelations in globular clusters: (i) relatively low metallicity (below
solar); (ii) a dense local environment; (iii) total cluster mass of
the order of ![]() 104
104 ![]() or more; (iv) an undisturbed position
in the Galaxy (e.g., away from the disc, see also Carretta 2006).
or more; (iv) an undisturbed position
in the Galaxy (e.g., away from the disc, see also Carretta 2006).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg9.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg133.png)
|
Figure 9:
Trends in [Fe/H] ( top panel) and [ |
| Open with DEXTER | |
7 Galactic trends
As said earlier, OC are fundamental test particles in the study of the chemical
evolution of the Galactic disc, and as such, they produce two of the strongest
constraints on chemical models: the Galactic radial trends and the age-metallicity
relation (AMR). Since a careful homogeneization of literature data (including not
only element ratios, but also ages and Galactocentric radii) is beyond the scope
of the present paper, we used the literature data of Table 13,
averaging all estimates for a single cluster together. We complemented our results
with data by Friel et al. (2002) for those OC lacking high resolution measurements.
Using 28 OC in common between the two datasets, we found an average offset of
[Fe/H] = -
![]() dex, in the sense that the measurements by Friel et al. (2002)
are on average lower than those based on high resolution data. We corrected
Friel et al. (2002) data by this amount before plotting them. We extracted OC ages
from the compilation of Dias et al. (2002)
dex, in the sense that the measurements by Friel et al. (2002)
are on average lower than those based on high resolution data. We corrected
Friel et al. (2002) data by this amount before plotting them. We extracted OC ages
from the compilation of Dias et al. (2002)![]() , and for the Galactocentric radii
(
, and for the Galactocentric radii
(
![]() )
data we used primarily Friel et al. (2002), complemented by the WEBDA,
and obtained data points for the few missing clusters from the papers of
Table 13. The resulting radial trends and AMR for [Fe/H] and
[
)
data we used primarily Friel et al. (2002), complemented by the WEBDA,
and obtained data points for the few missing clusters from the papers of
Table 13. The resulting radial trends and AMR for [Fe/H] and
[![]() /Fe] (computed as in Sect. 4.2) are plotted in
Figs. 9 and 10 and discussed below.
/Fe] (computed as in Sect. 4.2) are plotted in
Figs. 9 and 10 and discussed below.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965f10.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg135.png)
|
Figure 10:
Trends in [Fe/H] ( top panel) and [ |
| Open with DEXTER | |
7.1 Trends with Galactocentric radius
The trends in the abundances with Galactocentric radius
![]() provide
strong constraints on the models of Galactic chemical evolution as far as the disc
formation mechanism is concerned
provide
strong constraints on the models of Galactic chemical evolution as far as the disc
formation mechanism is concerned![]() . It is now widely accepted (see for
example Friel et al. 2002; Sestito et al. 2008; Magrini et al. 2009; Twarog et al. 1997; Yong et al. 2005) that there is a clear trend of
decreasing metallicity, measured by [Fe/H], with increasing
. It is now widely accepted (see for
example Friel et al. 2002; Sestito et al. 2008; Magrini et al. 2009; Twarog et al. 1997; Yong et al. 2005) that there is a clear trend of
decreasing metallicity, measured by [Fe/H], with increasing
![]() .
Such a
trend is clearly detected not only in OC, but also in field stars (B-stars and
Cepheids), H II regions, and planetary nebulae
.
Such a
trend is clearly detected not only in OC, but also in field stars (B-stars and
Cepheids), H II regions, and planetary nebulae![]() (see Andrievsky et al. 2004; Lemasle et al. 2008; Chiappini et al. 2001; Yong et al. 2005, for some reviews of literature
data).
(see Andrievsky et al. 2004; Lemasle et al. 2008; Chiappini et al. 2001; Yong et al. 2005, for some reviews of literature
data).
The first large studies of homogeneous OC abundances (summarized in the
review by Friel 1995), found that old OC (older than the Hyades) extend outwards in
the disc, much farther out than young OC, and they found a clerly defined slope
out to
![]() kpc. The spread about this slope was at the time
kpc. The spread about this slope was at the time
![]() 0.2 dex, i.e., generally compatible with (or perhaps slightly larger than)
the measurement uncertainties. This slope follows naturally from most Galactic
chemical evolution models
(Tosi 1996; Andrievsky et al. 2004; Colavitti et al. 2009; Chiappini et al. 2001; Matteucci & Francois 1989; Tosi 1988,1982; Magrini et al. 2009), when different star
formation and infall rates are assumed for the inner and outer disc. To reproduce
most of the observational constraints, a differential disc formation mechanism is
often assumed, in which either the inner disk formed first and then grew in radius
(inside-out formation) or the whole disk evolved simultaneously, but with a far
more intense (and sometimes fast) evolution in its central, denser parts. A
prediction of all models is that the metallicity gradient should change with time
(although different models predict very different time changes; Tosi 1996)
and some predict that it should flatten out at large radii. Indeed, the first
studies of anticenter and distant clusters (Sestito et al. 2008; Carraro et al. 2007; Yong et al. 2005; Carraro et al. 2004)
showed that after
0.2 dex, i.e., generally compatible with (or perhaps slightly larger than)
the measurement uncertainties. This slope follows naturally from most Galactic
chemical evolution models
(Tosi 1996; Andrievsky et al. 2004; Colavitti et al. 2009; Chiappini et al. 2001; Matteucci & Francois 1989; Tosi 1988,1982; Magrini et al. 2009), when different star
formation and infall rates are assumed for the inner and outer disc. To reproduce
most of the observational constraints, a differential disc formation mechanism is
often assumed, in which either the inner disk formed first and then grew in radius
(inside-out formation) or the whole disk evolved simultaneously, but with a far
more intense (and sometimes fast) evolution in its central, denser parts. A
prediction of all models is that the metallicity gradient should change with time
(although different models predict very different time changes; Tosi 1996)
and some predict that it should flatten out at large radii. Indeed, the first
studies of anticenter and distant clusters (Sestito et al. 2008; Carraro et al. 2007; Yong et al. 2005; Carraro et al. 2004)
showed that after
![]() kpc, the relation flattens to around a
value of [Fe/H]
kpc, the relation flattens to around a
value of [Fe/H] ![]() -0.3 dex.
-0.3 dex.
Not much can be said with the present data about the slope variation with time,
but the exact value of the slope has been a matter of some debate. As said,
earlier studies found a value of around -0.09 ![]() 0.01 dex kpc-1, or
-0.07
0.01 dex kpc-1, or
-0.07 ![]() 0.01 dex kpc-1 for the homogenous measurements by Friel et al. (2002).
An alternative interpretation of a different data compilation (Twarog et al. 1997)
describes the trend as two disjoint plateaux, one around solar metallicity
comprising OC within
0.01 dex kpc-1 for the homogenous measurements by Friel et al. (2002).
An alternative interpretation of a different data compilation (Twarog et al. 1997)
describes the trend as two disjoint plateaux, one around solar metallicity
comprising OC within
![]() kpc, and a second one at
[Fe/H]
kpc, and a second one at
[Fe/H] ![]() -0.3 outside the solar circle. More recent work based on high
resolution compilations of OC data (Sestito et al. 2008) find a steeper slope of
-0.17
-0.3 outside the solar circle. More recent work based on high
resolution compilations of OC data (Sestito et al. 2008) find a steeper slope of
-0.17 ![]() 0.01 dex kpc-1 within
0.01 dex kpc-1 within
![]() kpc, which still holds when
considering only the 10 clusters analyzed homogeneously by that group. A sort of
bimodal distribution is observed in their Fig. 9, where between the very steep
slope of the inner clusters and the plateau of the outer ones there is a small gap
that is almost devoid of OC (
kpc, which still holds when
considering only the 10 clusters analyzed homogeneously by that group. A sort of
bimodal distribution is observed in their Fig. 9, where between the very steep
slope of the inner clusters and the plateau of the outer ones there is a small gap
that is almost devoid of OC (
![]() kpc).
kpc).
Our results are plotted in Fig. 9, where we consider the trend in
[Fe/H] and [![]() /Fe] with
/Fe] with
![]() .
We do see a distinct slope in the
inner clusters and a flattening out for the outer ones. However, our sample
contains
.
We do see a distinct slope in the
inner clusters and a flattening out for the outer ones. However, our sample
contains ![]() 15 more OC than that of Sestito et al. (2008), and most of them
(including our five determinations) fall into the gap around
15 more OC than that of Sestito et al. (2008), and most of them
(including our five determinations) fall into the gap around
![]() kpc, discussed above. With the addition of these clusters,
we find a gentler slope of -0.05
kpc, discussed above. With the addition of these clusters,
we find a gentler slope of -0.05 ![]() 0.01 dex kpc-1, in good agreement with
previous work (Friel et al. 2002; Friel 1995) and with the disk Cepheids within
0.01 dex kpc-1, in good agreement with
previous work (Friel et al. 2002; Friel 1995) and with the disk Cepheids within
![]()
![]() 11 kps (Andrievsky et al. 2004; Lemasle et al. 2008). If we exclude the clusters
outside
11 kps (Andrievsky et al. 2004; Lemasle et al. 2008). If we exclude the clusters
outside
![]() kpc and remove the low resolution OC data from
Friel et al. (2002), the slope does not steepen significantly, becoming
-0.06
kpc and remove the low resolution OC data from
Friel et al. (2002), the slope does not steepen significantly, becoming
-0.06 ![]() 0.02 dex kpc-1. The flattening also does not seem so abrupt as in
Fig. 9 by Sestito et al. (2008). The paucity of OC in the flat part of the relation (we
have only Be 20, Be 22, Be 29, and Saurer 1 in our compilation) surely calls for
more high resolution studies, since as the data stand now, they look compatible
with both a plateau and a gradual change in slope. We note that NGC 2420 (already
discussed in Sect. 5.3) was found to have [Fe/H] = -0.57 dex by
Smith & Suntzeff (1987), based on
0.02 dex kpc-1. The flattening also does not seem so abrupt as in
Fig. 9 by Sestito et al. (2008). The paucity of OC in the flat part of the relation (we
have only Be 20, Be 22, Be 29, and Saurer 1 in our compilation) surely calls for
more high resolution studies, since as the data stand now, they look compatible
with both a plateau and a gradual change in slope. We note that NGC 2420 (already
discussed in Sect. 5.3) was found to have [Fe/H] = -0.57 dex by
Smith & Suntzeff (1987), based on ![]() 000 spectra, while we find -0.05 dex, in
much better agreement with the global Galactic trend. This goes in the direction
of filling the gap in the Sestito et al. (2008) compilation, and also in the
Twarog et al. (1997) dataset, pointing more towards a gentle and continuous decrease in [Fe/H].
000 spectra, while we find -0.05 dex, in
much better agreement with the global Galactic trend. This goes in the direction
of filling the gap in the Sestito et al. (2008) compilation, and also in the
Twarog et al. (1997) dataset, pointing more towards a gentle and continuous decrease in [Fe/H].
The trend in ![]() -enhancement with
-enhancement with
![]() is also of some importance,
because it constraints the role of SNe Type Ia and II and their relative
contributions. Yong et al. (2005) found a tendency for the
is also of some importance,
because it constraints the role of SNe Type Ia and II and their relative
contributions. Yong et al. (2005) found a tendency for the ![]() -enhancement to
increase with
-enhancement to
increase with
![]() ,
as did Magrini et al. (2009), who found this tendency to be
in good agreement with their chemical evolution model. Model A by Chiappini et al. (2001)
also predicted an increase in [
,
as did Magrini et al. (2009), who found this tendency to be
in good agreement with their chemical evolution model. Model A by Chiappini et al. (2001)
also predicted an increase in [![]() /Fe] with
/Fe] with
![]() .
In our
compilation, the trend appears as a weak slope that is perfectly compatible with a
flat distribution at the 1
.
In our
compilation, the trend appears as a weak slope that is perfectly compatible with a
flat distribution at the 1![]() level. This, together with the study of slope
changes with time, is one typical case in which a high quality, homogeneous
analysis of
level. This, together with the study of slope
changes with time, is one typical case in which a high quality, homogeneous
analysis of ![]() 100 OC could provide a clear and definitive answer.
100 OC could provide a clear and definitive answer.
7.2 Trends with age
In spite of all models predicting an evolution of disk metallicity with time, albeit maybe only in the first Gyrs, and that this variation is indeed observed in disk stars (Reddy et al. 2003; Bensby et al. 2004), there appears to be no correlation at all between old OC abundances and ages (see the review by Friel 1995). More recent results have not changed this picture substantially. If confirmed, the lack of an AMR in OC would point towards a different source of chemical enrichment for OC stars (Yong et al. 2005) with respect to the disc stars. In essence, the metallicity of OC stars seems to be more dependent on the location in which they formed, than by the time at which they formed.
What we find here is quite encouraging, although still not statistically
significant. We recall that our compilation includes 57 high resolution abundance
determinations, plus a handful of low resolution determinations by
Friel et al. (2002). Although we have made no attempt to homogeneize the data, except
for a -0.16 dex correction to the low resolution abundances, this sample is
![]() 50% larger than any compilation presented before (see
e.g., Sestito et al. 2008; Magrini et al. 2009; De Silva et al. 2009) and shows that the community is proceeding fast in
filling up the gaps in our knowledge of OC. Figure 10 indeed shows a
weak trend of decreasing [Fe/H] and increasing [
50% larger than any compilation presented before (see
e.g., Sestito et al. 2008; Magrini et al. 2009; De Silva et al. 2009) and shows that the community is proceeding fast in
filling up the gaps in our knowledge of OC. Figure 10 indeed shows a
weak trend of decreasing [Fe/H] and increasing [![]() /Fe] with increasing age.
The slopes are very gentle at most and are still compatible with no trends at all.
Nevertheless, if these trends exist, we can place some constraints on them: for
[Fe/H], the gradient should not be significantly greater than
-2.6
/Fe] with increasing age.
The slopes are very gentle at most and are still compatible with no trends at all.
Nevertheless, if these trends exist, we can place some constraints on them: for
[Fe/H], the gradient should not be significantly greater than
-2.6 ![]()
![]() dex Gyr-1 and for [
dex Gyr-1 and for [![]() /Fe] no greater than
/Fe] no greater than
![]() dex Gyr-1.
dex Gyr-1.
8 Summary and conclusions
We have analyzed high resolution spectra of three red clump giants in five OC,
three of them lacking any previous high-resolution-based chemical analysis. Given
the paucity of literature data, such a small sample is enough to increase the
entire body of high resolution data for OC by ![]() 5%. To compare our results
with the literature, we have compiled chemical abundances based on high resolution
data of 57 clusters from the literature. Given the rapid progress in the field,
this sample is
5%. To compare our results
with the literature, we have compiled chemical abundances based on high resolution
data of 57 clusters from the literature. Given the rapid progress in the field,
this sample is ![]() 50% larger than previous literature compilations
(e.g., Friel et al. 2002; Sestito et al. 2008; Magrini et al. 2009). The main results drawn from the analysis
of our five clusters are:
50% larger than previous literature compilations
(e.g., Friel et al. 2002; Sestito et al. 2008; Magrini et al. 2009). The main results drawn from the analysis
of our five clusters are:
- We provide the first high-resolution-data based abundance analysis of Cr 110
([Fe/H] = +0.03
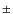 0.02 (
0.02 (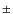 0.10) dex), NGC 2099 ([Fe/H] = +0.01
0.10) dex), NGC 2099 ([Fe/H] = +0.01 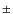 0.05
(
0.05
(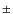 0.10) dex) and NGC 2420 ([Fe/H] = -0.05
0.10) dex) and NGC 2420 ([Fe/H] = -0.05 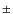 0.03 (
0.03 (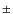 0.10) dex), which
previously had only measurements based on low resolution data, and the
0.10) dex), which
previously had only measurements based on low resolution data, and the
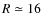 000 analysis by Smith & Suntzeff (1987); our new determination of the
metallicity of NGC 2420 places data for this cluster in far closer agreement with
global Galactic trends.
000 analysis by Smith & Suntzeff (1987); our new determination of the
metallicity of NGC 2420 places data for this cluster in far closer agreement with
global Galactic trends.
- The abundances found for NGC 7789 ([Fe/H] = +0.04
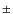 0.07
(
0.07
(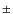 0.10) dex) and M 67 ([Fe/H]= +0.05
0.10) dex) and M 67 ([Fe/H]= +0.05 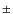 0.02 (
0.02 (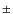 0.10) dex) are in good
agreement with past high resolution studies.
0.10) dex) are in good
agreement with past high resolution studies.
- We provide the first high-resolution-data based radial velocity
determination for Cr 110 (
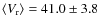 km s-1).
km s-1).
- We found that all our abundance ratios, with few exceptions generally explained by technical details of the analysis procedure, are near-solar, as is typical of OC with similar properties; we also found solar ratios for Na, which is generally found to be overabundant, and for O, which is generally found to be underabundant.
- We detected no significant anticorrelation (or correlation) among Na, Al, Mg, and O, in general agreement with past and recent results, and we can say that if these correlations are indeed present in OC, they must be far less extended than in globular clusters, amounting to no more than 0.2-0.3 dex at most.
We warmly thank A. Bragaglia and A. Mucciarelli for their useful comments and suggestions.We thank M. Tosi and D. Romano for their insights on the chemical evolution modelling of the Milky Way and its Disks. We also warmly thank the Calar Alto Support staff for their hospitality and a good time together. R.C., C.G. and E.P. acknowledge support by the Spanish Ministry of Science and Technology (Plan Nacional de Investigación Científica, Desarrollo, e Investigación Tecnológica, AYA2004-06343). E.P. acknowledges support from the Italian MIUR (Ministero dell'Universitá e della Ricerca) under PRIN 2003029437, ``Continuities and Discontinuites in the Formation of the Galaxy.'' R.C. acknowledges funding by the Spanish Ministry of Science and Innovation under the MICINN/Fullbright post-doctoral fellowship program.
References
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Luck, R. E., Martin, P., & Lépine, J. R. D. 2004, A&A, 413, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andersen, J. 1999, Transactions of the IAU, XXIVA, 36, 24, A36 [Google Scholar]
- Anthony-Twarog, B. J., Kaluzny, J., Shara, M. M., & Twarog, B. A. 1990, AJ, 99, 1504 [NASA ADS] [CrossRef] [Google Scholar]
- Anthony-Twarog, B. J., Tanner, D., Cracraft, M., & Twarog, B. A. 2006, AJ, 131, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Ryan, S. G., Norris, J. E., et al. 2001, ApJ, 561, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Arp, H. 1962, ApJ, 136, 66 [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ASP Conf. Ser., 336, 25 [Google Scholar]
- Balaguer-Núñez, L., Galadí-Enríquez, D., & Jordi, C. 2007, A&A, 470, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbaro, G., & Pigatto, L. 1984, A&A, 136, 355 [NASA ADS] [Google Scholar]
- Bartasiute, S., & Tautvaisiene, G. 2004, Ap&SS, 294, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Baumüller, D., & Gehren, T. 1997, A&A, 325, 1088 [NASA ADS] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2004, A&A, 421, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S. 1979, PASP, 91, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M., Jensen, E. E. C., & Deliyannis, C. P. 2009, AJ, 137, 4949 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., & Tosi, M. 2003, MNRAS, 343, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., & Tosi, M. 2006, AJ, 131, 1544 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Carretta, E., Gratton, R. G., et al. 2001, AJ, 121, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Sestito, P., Villanova, S., et al. 2008, A&A, 480, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bramich, D. M., Horne, K., Bond, I. A., et al. 2005, MNRAS, 359, 1096 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. A. 1987, ApJ, 317, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. A., Wallerstein, G., Geisler, D., & Oke, J. B. 1996, AJ, 112, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H., Frandsen, S., Kjeldsen, H., & Andersen, M. I. 1999, A&AS, 140, 135 [Google Scholar]
- Burbidge, E. M., & Sandage, A. 1958, ApJ, 128, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Burstein, D., Faber, S. M., Gonzalez, J. J., & Spaenhauer, A. 1984, BAAS, 16, 968 [NASA ADS] [Google Scholar]
- Burstein, D., Faber, S. M., & Gonzalez, J. J. 1986, AJ, 91, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, L. M. 1985, A&A, 147, 39 [NASA ADS] [Google Scholar]
- Cannon, R. D., & Lloyd, C. 1970, MNRAS, 150, 279 [NASA ADS] [Google Scholar]
- Canterna, R., Geisler, D., Harris, H. C., Olszewski, E., & Schommer, R. 1986, AJ, 92, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G., & Chiosi, C. 1994, A&A, 287, 761 [NASA ADS] [Google Scholar]
- Carraro, G., Girardi, L., Bressan, A., & Chiosi, C. 1996, A&A, 305, 849 [NASA ADS] [Google Scholar]
- Carraro, G., Bresolin, F., Villanova, S., et al. 2004, AJ, 128, 1676 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G., Villanova, S., Demarque, P., et al. 2006, ApJ, 643, 1151 [Google Scholar]
- Carraro, G., Geisler, D., Villanova, S., Frinchaboy, P. M., & Majewski, S. R. 2007, A&A, 476, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrera, R., Gallart, C., Pancino, E., & Zinn, R. 2007, AJ, 134, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E. 2006, AJ, 131, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., & Gratton, R. G. 1997, A&AS, 121, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Tosi, M. 2004, A&A, 422, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Tosi, M. 2005, A&A, 441, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., & Gratton, R. G. 2007, A&A, 473, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel de Strobel, G. 1990, Mem. Soc. Astron. Ital., 61, 613 [NASA ADS] [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, L., Hou, J. L., & Wang, J. J. 2003, AJ, 125, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Claria, J. J. 1979, Ap&SS, 66, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Clariá, J. J., Mermilliod, J.-C., & Piatti, A. E. 1999, A&AS, 134, 301 [Google Scholar]
- Cohen, J. G. 1980, ApJ, 241, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Colavitti, E., Cescutti, G., Matteucci, F., & Murante, G. 2009, A&A, 496, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, D. W., & Ianna, P. A. 1995, AJ, 115, 1076 [Google Scholar]
- Demarque, P. 1980, Star Formation, 85, 281 [NASA ADS] [Google Scholar]
- Den Hartog, E. A., Lawler, J. E., Sneden, C., & Cowan, J. J. 2003, ApJS, 148, 543 [Google Scholar]
- De Silva, G. M., Sneden, C., Paulson, D. B., et al. 2006, AJ, 131, 455 [NASA ADS] [CrossRef] [Google Scholar]
- De Silva, G. M., Freeman, K. C., Asplund, M., et al. 2007, AJ, 133, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- De Silva, G. M., Gibson, B. K., Lattanzio, J., & Asplund, M. 2009, A&A, 500, L25 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dinescu, D. I., Demarque, P., Guenther, D. B., & Pinsonneault, M. H. 1995, AJ, 109, 2090 [NASA ADS] [CrossRef] [Google Scholar]
- Dean, J. F., Warren, P. R., & Cousins, A. W. J. 1978, MNRAS, 183, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Demarque, P., Guenther, D. B., & Green, E. M. 1992, AJ, 103, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Demarque, P., Sarajedini, A., & Guo, X.-J. 1994, ApJ, 426, 165 [NASA ADS] [CrossRef] [Google Scholar]
- D'Orazi, V., Magrini, L., Randich, S., et al. 2009, ApJ, 693, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Fagerholm, E. 1906, Uppsala dissertation [Google Scholar]
- Fan, X., Burstein, D., Chen, J.-S., et al. 1996, AJ, 112, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, A., Jeffries, R. D., & Smalley, B. 2005, MNRAS, 364, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Foy, R., & Proust, D. 1981, A&A, 99, 221 [NASA ADS] [Google Scholar]
- Freeland, E., Deliyannis, C. P., Steinhauer, A., & Sarajedini, A. 2002, BAAS, 34, 655 [NASA ADS] [Google Scholar]
- Friel, E. D. 1995, ARA&A, 33, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D., & Boesgaard, A. M. 1992, ApJ, 387, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D., & Janes, K. A. 1993, A&A, 267, 75 [NASA ADS] [Google Scholar]
- Friel, E. D., Liu, T., & Janes, K. A. 1989, PASP, 101, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D., Janes, K. A., Tavarez, M., et al. 2002, AJ, 124, 2693 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D., Jacobson, H. R., Barrett, E., et al. 2003, AJ, 126, 2372 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D., Jacobson, H. R., & Pilachowski, C. A. 2005, AJ, 129, 2725 [NASA ADS] [CrossRef] [Google Scholar]
- Frinchaboy, P. M., Marino, A. F., Villanova, S., et al. 2008, MNRAS, 391, 39 [Google Scholar]
- Garcia Lopez, R. J., Rebolo, R., & Beckman, J. E. 1988, PASP, 100, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Gebran, M., & Monier, R. 2008, A&A, 483, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geisler, D., Claria, J. J., & Minniti, D. 1991, AJ, 102, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Geisler, D., Claria, J. J., & Minniti, D. 1992, AJ, 104, 1892 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., & Brown, T. M. 1992, AJ, 103, 1945 [NASA ADS] [CrossRef] [Google Scholar]
- Gim, M., Vandenberg, D. A., Stetson, P. B., Hesser, J. E., & Zurek, D. R. 1998a, PASP, 110, 1318 [NASA ADS] [CrossRef] [Google Scholar]
- Gim, M., Hesser, J. E., McClure, R. D., & Stetson, P. B. 1998b, PASP, 110, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., & Salaris, M. 2001, MNRAS, 323, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G., & Wallerstein, G. 2000, PASP, 112, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., & Contarini, G. 1994, A&A, 283, 911 [NASA ADS] [Google Scholar]
- Gratton, R. G., Carretta, E., Eriksson, K., & Gustafsson, B. 1999, A&A, 350, 955 [NASA ADS] [Google Scholar]
- Gratton, R. 2000, Stellar Clusters and Associations: Convection, Rotation, and Dynamos, ASP Conf. Ser., 198, 225 [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Noels, A., & Sauval, A. J. 1996, Cosmic Abundances, ASP Conf. Ser., 99, 117 [Google Scholar]
- Grocholski, A. J., & Sarajedini, A. 2003, MNRAS, 345, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Hamdani, S., North, P., Mowlavi, N., Raboud, D., & Mermilliod, J.-C. 2000, A&A, 360, 509 [NASA ADS] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Gaudi, B. S., Holman, M. J., et al. 2008, ApJ, 675, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., & Thorburn, J. A. 1991, AJ, 102, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffleit, D., & Jaschek, C. 1991, New Haven (Conn.: Yale University Observatory), 5th rev. edn., ed. D. Hoffleit, & C. Jaschek, |v(coll.) [Google Scholar]
- Houdashelt, M. L., Frogel, J. A., & Cohen, J. G. 1992, AJ, 103, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, H. R., Friel, E. D., & Pilachowski, C. A. 2007, AJ, 134, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, H. R., Friel, E. D., & Pilachowski, C. A. 2008, AJ, 135, 2341 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, H. R., Friel, E. D., & Pilachowski, C. A. 2009, AJ, 137, 4753 [NASA ADS] [CrossRef] [Google Scholar]
- Jacquinet-Husson, N., Arié, E., Ballard, J., et al. 1999, JQSRT, 62, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Jacquinet-Husson, N., Scott, N. A., Garceran, K., Armante, R., & Chédin, A. 2005, JQSRT, 95, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Jahn, K., Kaluzny, J., & Rucinski, S. M. 1995, A&A, 295, 101 [NASA ADS] [Google Scholar]
- Janes, K. A. 1977, AJ, 82, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Janes, K. A. 1979, ApJS, 39, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Janes, K. A., & Smith, G. H. 1984, AJ, 89, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Janes, K. A., Tilley, C., & Lynga, G. 1988, AJ, 95, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Janes, K. A., & Phelps, R. L. 1994, AJ, 108, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Jennens, P. A., & Helfer, H. L. 1975, MNRAS, 172, 681 [NASA ADS] [Google Scholar]
- Johansson, S., Litzén, U., Lundberg, H., & Zhang, Z. 2003, ApJ, 584, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Ivans, I. I., & Stetson, P. B. 2006, ApJ, 640, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, B. F., Fischer, D., & Soderblom, D. R. 1999, AJ, 117, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Kinman, T., & Castelli, F. 2002, A&A, 391, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalirai, J. S., & Tosi, M. 2004, MNRAS, 351, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Kalirai, J. S., Ventura, P., Richer, H. B., et al. 2001, AJ, 122, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Kiss, L. L., Szabo, Gy., Sziladi, K., et al. 2001, A&A, 376, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraft, R. P., & Ivans, I. I. 2003, PASP, 115, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kustner K. 1923, Veroeff. Univ. Sternw., Bonn, 18 [Google Scholar]
- Lasker, B. M., Russel, J. N., Jenkner, H., et al. 1990, AJ, 99, 2019 [NASA ADS] [CrossRef] [Google Scholar]
- Lattanzio, J. C. 1984, MNRAS, 207, 309 [NASA ADS] [Google Scholar]
- Laugalys, V., Kazlauskas, A., Boyle, R. P., et al. 2004, Baltic Astronomy, 13, 1 [Google Scholar]
- Lemasle, B., François, P., Piersimoni, A., et al. 2008, A&A, 490, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Letarte, B., Hill, V., Jablonka, P., et al. 2006, A&A, 453, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, T., & Janes, K. A. 1987, PASP, 99, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Lyngå, G. 1987, European Regional Astronomy Meeting of the IAU, 4, 121 [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Magrini, L., Sestito, P., Randich, S., & Galli, D. 2009, A&A, 494, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marshall, J. L., Burke, C. J., DePoy, D. L., Gould, A., & Kollmeier, J. A. 2005, AJ, 130, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Martell, S. L., & Smith, G. H. 2009, PASP, 121, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez Roger, C., Paez, E., Castellani, V., & Straniero, O. 1994, A&A, 290, 62 [NASA ADS] [Google Scholar]
- Mathieu, R. D., Latham, D. W., Griffin, R. F., & Gunn, J. E. 1986, AJ, 92, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzei, P., & Pigatto, L. 1988, A&A, 193, 148 [NASA ADS] [Google Scholar]
- McClure, R. D., Forrester, W. T., & Gibson, J. 1974, ApJ, 189, 409 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, R. D., Newell, B., & Barnes, J. V. 1978, PASP, 90, 170 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. J. 1980, PASP, 92, 682 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Matteucci, F., Ballero, S., et al. 2008, AJ, 136, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Melo, C. H. F., Pasquini, L., & De Medeiros, J. R. 2001, A&A, 375, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J.-C. 1995, ASSL, Information & On-Line Data in Astronomy, 203, 127 [Google Scholar]
- Mermilliod, J.-C., Huestamendia, G., del Rio, G., & Mayor, M. 1996, A&A, 307, 80 [NASA ADS] [Google Scholar]
- Mermilliod, J. C., Mayor, M., & Udry, S. 2008, A&A, 485, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Mermilliod, J.-C., & Maeder, A. 1993, A&AS, 98, 477 [Google Scholar]
- Milone, A. A. E., & Latham, D. W. 1994, AJ, 108, 1828 [NASA ADS] [CrossRef] [Google Scholar]
- Mochejska, B. J., & Kaluzny, J. 1999, Acta Astron., 49, 351 [NASA ADS] [Google Scholar]
- Montegriffo, P., Ferraro, F. R., Origlia, L., & Fusi Pecci, F. 1998, MNRAS, 297, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Montgomery, K. A., Marschall, L. A., & Janes, K. A. 1993, AJ, 106, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, C. E., Minnaert, M. G. J., & Houtgast, J. 1966, National Bureau of Standards Monograph, Washington: US Government Printing Office (USGPO) [Google Scholar]
- Mucciarelli, A., Origlia, L., Ferraro, F. R., & Pancino, E. 2009, ApJ, 695, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Nilakshi, S. R. 2002, A&A, 381, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., Twarog, B. A., & Crawford, D. L. 1987, AJ, 93, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Valenti, E., Rich, R. M., & Ferraro, F. R. 2006, ApJ, 646, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Pace, G., Pasquini, L., & François, P. 2008, A&A, 489, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panagia, N., & Tosi, M. 1980, A&A, 81, 375 [NASA ADS] [Google Scholar]
- Pasquini, L., Randich, S., & Pallavicini, R. 1997, A&A, 325, 535 [NASA ADS] [Google Scholar]
- Pasquini, L., Randich, S., Zoccali, M., et al. 2004, A&A, 424, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Biazzo, K., Bonifacio, P., Randich, S., & Bedin, L. R. 2008, A&A, 489, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paulson, D. B., Sneden, C., & Cochran, W. D. 2003, AJ, 125, 3185 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, R. C., & Green, E. M. 1998, ApJ, 502, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Pilachowski, A. A. 1985, PASP, 97, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Pilachowski, C. A., Wallerstein, G., & Canterna, R. 1980, ApJ, 235, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Pilachowski, C. 1986, ApJ, 300, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Pilachowski, C. A., Saha, A., & Hobbs, L. M. 1988, PASP, 100, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B., Brett, J. M., & Nordlund, A. 1992, A&A, 256, 551 [NASA ADS] [Google Scholar]
- Pols, O. R., Schroder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., & McWilliam, A. 2000, ApJ, 537, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Racine, R. 1971, ApJ, 168, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, S. V., & Cohen, J. G. 2003, AJ, 125, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Randich, S., Pallavicini, R., Meola, G., Stauffer, J. R., & Balachandran, S. C. 2001, A&A, 372, 862 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randich, S., Sestito, P., & Pallavicini, R. 2003, A&A, 399, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randich, S., Sestito, P., Primas, F., Pallavicini, R., & Pasquini, L. 2006, A&A, 450, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randich, S., Primas, F., Pasquini, L., Sestito, P., & Pallavicini, R. 2007, A&A, 469, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddish, V. C. 1954, MNRAS, 114, 583 [NASA ADS] [Google Scholar]
- Reddy, B. E., Tomkin, J., Lambert, D. L., & Allende Prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allende Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J., & van der Zalm, E. B. J. 1984, A&AS, 55, 171 [Google Scholar]
- Salaris, M., & Cassisi, S. 1998, MNRAS, 298, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Weiss, A., & Percival, S. M. 2004, A&A, 414, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandquist, E. L. 2004, MNRAS, 347, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Lovis, C., Pace, G., Melendez, J., & Naef, D. 2009, A&A, 493, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarajedini, A. 1999, AJ, 118, 2321 [NASA ADS] [CrossRef] [Google Scholar]
- Sarma, M. B. K., & Walker, M. F. 1962, ApJ, 135, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Schönberner, D., Andrievsky, S. M., & Drilling, J. S. 2001, A&A, 366, 490 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuler, S. C., King, J. R., Fischer, D. A., Soderblom, D. R., & Jones, B. F. 2003, AJ, 125, 2085 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, J. E., Friel, E. D., & Janes, K. A. 1995, AJ, 109, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Sestito, P., Randich, S., Mermilliod, J.-C., & Pallavicini, R. 2003, A&A, 407, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sestito, P., Randich, S., & Bragaglia, A. 2007, A&A, 465, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sestito, P., Bragaglia, A., Randich, S., et al. 2008, A&A, 488, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shetrone, M. D., & Sandquist, E. L. 2000, AJ, 120, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R., Gauderon, R., North, P., et al. 2009, A&A, 502, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M. 1967, Annales d'Astrophysique, 30, 211 [Google Scholar]
- Steffen, M. 1985, A&AS, 59, 403 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Smith, V. V., & Suntzeff, N. B. 1987, AJ, 93, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Stanghellini, L., Guerrero, M. A., Cunha, K., Manchado, A., & Villaver, E. 2006, ApJ, 651, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson P. B. 2000, PASP, 112, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Strom, K. M., & Strom, S. E. 1970, ApJ, 162, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Suntzeff, N. B., Schommer, R. A., Olzewski, E. W., & Walker, A. R. 1992, AJ, 104, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Tadross, A. L., Werner, P., Osman, A., & Marie, M. 2002, New Astron., 7, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Tautvaisiene, G., Edvardsson, B., Tuominen, I., & Ilyin, I. 2000, A&A, 360, 499 [NASA ADS] [Google Scholar]
- Tautvaisiene, G., Edvardsson, B., Puzeras, E., & Ilyin, I. 2005, A&A, 431, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiede, G. P., Martini, P., & Frogel, J. A. 1997, AJ, 114, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, M. 1982, ApJ, 254, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, M. 1988, A&A, 197, 47 [NASA ADS] [Google Scholar]
- Tosi, M. 1996, From Stars to Galaxies: the Impact of Stellar Physics on Galaxy Evolution, 98, 299 [Google Scholar]
- Tsarevskii, G. S., & Abakumov, I. E. 1971, Astron. Tsirk., 631, 6 [NASA ADS] [Google Scholar]
- Twarog, B. A., & Tyson, N. 1985, AJ, 90, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Twarog, B. A., Ashman, K. M., & Anthony-Twarog, B. J. 1997, AJ, 114, 2556 [NASA ADS] [CrossRef] [Google Scholar]
- Twarog, B. A., Anthony-Twarog, B. J., & De Lee, N. 2003, AJ, 125, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Vallenari, A., Carraro, G., & Richichi, A. 2000, A&A, 353, 147 [NASA ADS] [Google Scholar]
- van Altena, W. F., & Jones, B. F. 1970, A&A, 8, 112 [NASA ADS] [Google Scholar]
- Vandenberg, D. A. 1985, ApJS, 58, 711 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., & Clem, J. L. 2003, AJ, 126, 778 [NASA ADS] [CrossRef] [Google Scholar]
- van Zeipel, H., & Lindgren, J. 1921, Kungl. Sven. Vet. Handl., 61, 15 [Google Scholar]
- Villanova, S., Carraro, G., Bresolin, F., & Patat, F. 2005, AJ, 130, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Baume, G., & Carraro, G. 2007, MNRAS, 379, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. R., & Cole, A. A. 2009, MNRAS, 393, 272 [NASA ADS] [CrossRef] [Google Scholar]
- West, F. R. 1967, Publications of the Goethe Link Observatory, 75, 359 [NASA ADS] [Google Scholar]
- West, F. R. 1967, ApJS, 14, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K. S., Bedin, L. R., Piotto, G., et al. 2008, A&A, 484, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yong, D., Carney, B. W., & Texeira de Almeida, M. L. 2005, AJ, 130, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, R., & West, M. J. 1984, ApJS, 55, 45 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... 2682)
![[*]](/icons/foot_motif.png)
- Based on data collected with the fiber spectrograph FOCES at the 2.2 m Calar Alto Telescope. Also based on data from the 2MASS survey and the WEBDA, VALD, NIST, and GEISA online databases.
- ...
![[*]](/icons/foot_motif.png)
- Full Table 5 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/511/A56
- ... stars
![[*]](/icons/foot_motif.png)
- Although fainter than the brightest giants, red clump stars have the advantage of a higher gravity and temperature that considerably reduces line crowding. Clump stars are also easy to identify even in the sparsest clusters, maximizing the chance of choosing cluster members.
- ... WEBDA
![[*]](/icons/foot_motif.png)
- http://www.univie.ac.at/webda
- ... 2MASS
![[*]](/icons/foot_motif.png)
- http://www.ipac.caltech.edu/2mass. 2MASS (Two Micron All Sky Survey) is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
- ... IRAF
![[*]](/icons/foot_motif.png)
- Image Reduction and Analysis Facility. IRAF is distributed by the National Optical Astronomy Observatories, which is operated by the association of Universities for Research in Astronomy, Inc., under contract with the National Science Foundation.
- ...
GEISA
![[*]](/icons/foot_motif.png)
- http://ara.lmd.polytechnique.fr/htdOC-public/products/GEISA/HTML-GEISA/
- ... colors
![[*]](/icons/foot_motif.png)
- Since R magnitudes are available for less than half of our sample, we decided to ignore them in the following.
- ...0
![[*]](/icons/foot_motif.png)
- After dereddening, (
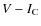 )
was also
converted into (V-IJ) using the prescription by Bessell (1979), to be used with
the color-temperature relations by Alonso et al. (1999).
)
was also
converted into (V-IJ) using the prescription by Bessell (1979), to be used with
the color-temperature relations by Alonso et al. (1999).
- ...V
![[*]](/icons/foot_motif.png)
- We computed the KTCS magnitudes from the 2MASS TCS magnitudes using the prescription by Kinman & Castelli (2002).
- ... spectrum
![[*]](/icons/foot_motif.png)
- http://www.eso.org/observing/dfo/quality/UVES/pipeline/solar_spectrum.html
- ...
VALD
![[*]](/icons/foot_motif.png)
- http://www.astro.uu.se/ vald/
- ... Moore
![[*]](/icons/foot_motif.png)
- ftp://ftp.noao.edu/fts/linelist/Moore
- ... NIST
![[*]](/icons/foot_motif.png)
- http://physics.nist.gov/PhysRefData/ASD/index.html
- ...
DAOSPEC''
![[*]](/icons/foot_motif.png)
- http://www3.cadc-ccda.hia-iha.nrc-cnrc.gc.ca/community/STETSON/daospec/; http://www.bo.astro.it/ pancino/projects/daospec.html
- ...
uncertainties
![[*]](/icons/foot_motif.png)
- We basically considered a slope consistent with zero when
the 3
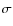 spread around the fit was larger than the maximum [Fe/H] difference
implied by the fitted slope at the extremes of the interval covered by the
abscissae (be it
spread around the fit was larger than the maximum [Fe/H] difference
implied by the fitted slope at the extremes of the interval covered by the
abscissae (be it
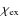 ,
EW or
,
EW or 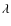 ).
).
- ... abundance
![[*]](/icons/foot_motif.png)
- We
decided not to use the Magain (1984) effect, because we prefer to have internally
consistent abundances from each line, and the difference in the measurements for
the two methods in our case appears small (
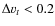 km s-1).
km s-1).
- ...
Ganymede
![[*]](/icons/foot_motif.png)
- http://www.ls.eso.org/lasilla/sciops/3p6/harps/monitoring/sun.html
- ...Å
![[*]](/icons/foot_motif.png)
- Because of the shorter spectral range of the solar spectrum and to spectral defects, we could only measure one Al line in the Sun.
- ...Dias et al. (2002)
![[*]](/icons/foot_motif.png)
- We are aware that at least in the case of NGC 6791, the age given by Dias et al. (2002) is quite different from other literature estimates (citations in Table 13), being lower by at least 2 Gyr. However, building a homogeneous age scale is a non-trivial task, which is beyond the scope of the present paper.
- ... concerned
![[*]](/icons/foot_motif.png)
- A far stronger constraint would be the variation in this trend with age. Such a study is at the moment not possible, given the small number of clusters studied with high resolution in a homogenous way.
- ... nebulae
![[*]](/icons/foot_motif.png)
- However, we know of at
least one dataset in which PNe show flat trends in oxygen and neon abundances with
 (Stanghellini et al. 2006).
(Stanghellini et al. 2006).
All Tables
Table 1: Observing logs and program stars data.
Table 2:
Heliocentric radial velocities measurements and their 1![]() errors
(
errors
(
![]() )
)
![]() for each program star.
for each program star.
Table 3: Stellar parameters for the program stars.
Table 4: Input cluster parameters.
Table 5: Equivalent widths and atomic data of the program stars. The complete version of the table is available at CDS. Here we show a few lines to illustrate its contents.
Table 6: Comparison of our results for star 141 in M 67 with the analysis of Tautvaisiene (2000) and Yong et al. (2005).
Table 7: Abundance ratios for sigle cluster stars, with their internal uncertainties (Sect. 4.3). For external uncertainties see Table 9.
Table 8: Average cluster abundances, obtained with the weighted average of the single stars abundances.
Table 9: Uncertanties due to the choice of stellar parameters for the coolest (second column) and the warmest (third column) of our programs stars (see Sect. 4.4).
Table 10: Solar abundance values.
Table 11: Literature abundance determinations for M 67 based on high resolution spectroscopy.
Table 12: Literature abundance determinations for NGC 7789 based on high resolution spectroscopy.
Table 13:
Literature sources and [Fe/H] values for high resolution (
![]() )
based abundance ratios of old OC.
)
based abundance ratios of old OC.
All Figures
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12965fg1.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg32.png)
|
Figure 1: V, (B-V) Color Magnitude Diagrams of the program clusters (from the WEBDA), with the location of our target stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg2.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg70.png)
|
Figure 2:
The behavior of DAOSPEC relative errors
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg3.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg80.png)
|
Figure 3:
Comparison of our EW measurements with Tautvaisiene (2000), for star 141 in
M 67. The top panel shows the comparison of DAOSPEC EW with the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg4.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg121.png)
|
Figure 4: Comparison between our iron-peak element results (large black dots), the high resolution measurements of other OC listed in Table 13 (large dark grey dots), and field stars belonging to the thin Galactic disc (light grey dots, Reddy et al. 2003) and to the thick Galactic disc (tiny light grey dots, Reddy et al. 2006). Errorbars on our results are the quadratic sum of internal uncertainties and uncertainties due to the choice of stellar parameters (Sect. 4). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{12965fg5.ps}\par
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg125.png)
|
Figure 5:
Comparison between our |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg6.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg126.png)
|
Figure 6: Comparison between our s-process elements ratios and the literature ones. Symbols are the same as in Fig. 4, except for the black star-like symbols in the top [Ba/Fe] panel, which represent the revision of Ba abundances with spectral synthesis performed by D'Orazi et al. (2009). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg7.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg127.png)
|
Figure 7: Comparison between our [Na/Fe] and [Al/Fe] ratios and the literature values. Symbols are the same as in Fig. 4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg8.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg132.png)
|
Figure 8:
A search for (anti)-correlations of Al, Mg, Na and O among our targets
stars. The four panels show different planes of abundance ratios, where stars
belonging to each cluster are marked with different symbols. Dotted lines show
solar values, solid lines show linear regressions and the typical uncertainty
( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965fg9.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg133.png)
|
Figure 9:
Trends in [Fe/H] ( top panel) and [ |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12965f10.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12965-09/Timg135.png)
|
Figure 10:
Trends in [Fe/H] ( top panel) and [ |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


