| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912812 | |
| Published online | 19 February 2010 | |
Nonlinear force-free modelling: influence of inaccuracies in the measured magnetic vector
T. Wiegelmann1 - L. Yelles Chaouche1 - S. K. Solanki1,2 - A. Lagg1
1 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Straße 2, 37191 Katlenburg-Lindau, Germany
2 -
School of Space Research, Kyung Hee University, Yongin, Gyeonggi 446-701, Korea
Received 2 July 2009 / Accepted 2 December 2009
Abstract
Context. Solar magnetic fields are regularly extrapolated
into the corona starting from photospheric magnetic measurements that
can be affected by significant uncertainty.
Aims. We study how inaccuracies introduced into the maps of the
photospheric magnetic vector by the inversion of ideal and noisy Stokes
parameters influence the extrapolation of nonlinear force-free magnetic
fields.
Methods. We compute nonlinear force-free magnetic fields based
on simulated vector magnetograms, by the inversion of Stokes
profiles that were computed by a 3-D radiation
MHD simulation snapshot. These extrapolations are compared with
extrapolations that originate directly in the field in the
MHD simulations, which is our reference. We investigate how
line formation and instrumental effects such as noise, limited spatial
resolution, and the effect of employing a filter instrument influence
the resulting magnetic field structure. The comparison is performed
qualitatively by visually inspecting the magnetic field distribution
and quantitatively by different metrics.
Results. The reconstructed field is most accurate if ideal
Stokes data are inverted and becomes less accurate if instrumental
effects and noise are included. The results demonstrate that the
nonlinear force-free field extrapolation method tested here is
relatively insensitive to the effects of noise in measured polarization
spectra at levels consistent with present-day instruments.
Conclusions. Our results show that we can reconstruct the
coronal magnetic field as a nonlinear force-free field from realistic
photospheric measurements with an accuracy of a few percent,
at least in the absence of sunspots.
Key words: Sun: corona - magnetic fields - Sun: photosphere
1 Introduction
Except for a few individual cases, e.g., in newly developed active regions (Solanki et al. 2003),
we are unable to directly measure the full magnetic vector in the solar
corona at high resolution and we have to rely on extrapolations from
photospheric measurements. Wiegelmann et al. (2005b) compared the direct magnetic field measurements of Solanki et al. (2003)
with extrapolations from the photosphere. This work highlighted the
importance of field-aligned electric currents to an accurate magnetic
field reconstruction and the need to have photospheric vector
magnetograms as boundary data. The photospheric data are affected by a
number of inadequacies, however, whose influence on the quality of the
extrapolations needs to be studied in detail. Firstly, the magnetic
field in the photosphere is far from being force-free, (see, e.g., Metcalf et al. 1995), which
can cause significant errors if used directly for a force-free magnetic field extrapolation (see Metcalf et al. 2008, for details). These errors can, however, be greatly reduced by appropriate preprocessing (Wiegelmann et al. 2006b).
Another well-known problem is that the noise level of the magnetic
field transverse to the line of sight is typically more than one order
of magnitude higher than for the longitudinal component deduced from
the Stokes parameters of Zeeman split spectral lines.
An additional complication is caused by vector magnetic field
measurements
performed far away from the disk centre, where the vertical and
line-of-sight field are far apart (see Gary & Hagyard 1990, for details), for which one has to also use the transverse field to derive the vertical field. Venkatakrishnan & Gary (1989)
showed that the increasing noise caused by using the transverse field
is tolerable for heliocentric distances shorter than ![]() .
For our investigations, we assume that the observations were performed
close to the disk center, where the vertical magnetic field is almost
identical to the line-of-sight field and the horizontal component is
almost identical yo the transverse field. Consequently, our results are
not directly applicable to regions observed at heliocentric distances
greater than about
.
For our investigations, we assume that the observations were performed
close to the disk center, where the vertical magnetic field is almost
identical to the line-of-sight field and the horizontal component is
almost identical yo the transverse field. Consequently, our results are
not directly applicable to regions observed at heliocentric distances
greater than about ![]() ,
where the noise in the transverse field influences significantly the
accuracy of the vertical field. Furthermore, high resolution vector
magnetographs such as Hinode/SOT have a limited field of view, which
often does not allow us to derive the horizontal magnetic field across
an entire active region. The influence of these effects on the accuracy
of nonlinear force-free extrapolations was investigated by DeRosa et al. (2009).
Less often considered effects introduced by extracting the field from
the
Stokes parameters are intrinsically uncertain. For instance, the
measured Stokes profiles that formed in a highly dynamic atmosphere
with a complex thermal and magnetic structure, while inversion methods
that are normally applied impose rather restrictive assumptions (e.g.,
Milne-Eddington atmosphere, Auer et al. 1977).
In addition, because of the spatially fluctuating height of
formation
of the lines, the obtained magnetic vector refers to different heights
in the atmosphere at different locations. In extrapolation
methods, one has to assume the boundary condition to be a single, often
planar, height. Finally, instrumental limitations impose restrictions,
such as limited spatial and spectral resolution, spectral sampling
(in particular for filter instruments), and noise.
,
where the noise in the transverse field influences significantly the
accuracy of the vertical field. Furthermore, high resolution vector
magnetographs such as Hinode/SOT have a limited field of view, which
often does not allow us to derive the horizontal magnetic field across
an entire active region. The influence of these effects on the accuracy
of nonlinear force-free extrapolations was investigated by DeRosa et al. (2009).
Less often considered effects introduced by extracting the field from
the
Stokes parameters are intrinsically uncertain. For instance, the
measured Stokes profiles that formed in a highly dynamic atmosphere
with a complex thermal and magnetic structure, while inversion methods
that are normally applied impose rather restrictive assumptions (e.g.,
Milne-Eddington atmosphere, Auer et al. 1977).
In addition, because of the spatially fluctuating height of
formation
of the lines, the obtained magnetic vector refers to different heights
in the atmosphere at different locations. In extrapolation
methods, one has to assume the boundary condition to be a single, often
planar, height. Finally, instrumental limitations impose restrictions,
such as limited spatial and spectral resolution, spectral sampling
(in particular for filter instruments), and noise.
We investigate how the extrapolated coronal magnetic field is influenced by noise and other instrumental artifacts (spatial resolution, limited spectral sampling), as well as the general limitations of the inversion of the measured Stokes profiles. To do so, we use the results of 3D radiation MHD simulations. We compute synthetic lines from the data cubes of the relevant physical quantities, add noise and apply the influence of typical instrument parameters. Finally we invert these artificial measurements to derive synthetic vector magnetograms, which are then used as boundary conditions for a nonlinear force-free magnetic field extrapolation. We compare the reconstruction from ideal data, taken directly from the MHD simulations, with extrapolations starting from data containing instrumental effects and noise of different levels of severity. Our aim is to investigate how different instrumental effects and noise influence a nonlinear force-free magnetic field extrapolation. Besides generally testing the influence of reduced spatial resolution on the photospheric magnetic field data, we also consider to the extent to which the properties of specific high resolution space instruments affect the quality of the extrapolations. The two instruments we consider are the Spectro-Polarimeter (SP) on the Solar Optical Telescope (SOT) on the Hinode spacecraft (Tsuneta et al. 2008; Shimizu 2004) and the Polarimetric and Helioseismic Imager (PHI) to fly on the Solar Orbiter mission. Instruments with lower spatial resolution, such as the Helioseismic Magnetic Imager (HMI) were not considered, since the number of pixels across the MHD simulation box are then rather small, making a meaningful test more improbable.
2 Method
2.1 Setup of the test case
We start with 3-D radiation MHD simulations resulting from the MURAM code (see Vögler et al. 2005,
for details). The particular snapshot considered here was taken from a
bipolar run and harbours equal amounts of magnetic flux of both
polarities. The configuration has an average field strength of
150 G at the spatially averaged continuum optical depth
![]() at 5000 Å. The horizontal dimensions of the simulation domain are 6
at 5000 Å. The horizontal dimensions of the simulation domain are 6 ![]()
![]() and
and
![]() in the vertical direction. The original resolution is
in the vertical direction. The original resolution is
![]() in the horizontal directions and
in the horizontal directions and
![]() in the vertical direction. Similar snapshots were also used by Khomenko et al. (2005b) for the investigation of magnetoconvection of mixed-polarity quiet-Sun regions and compared with measured Stokes profiles by Khomenko et al. (2005a).
in the vertical direction. Similar snapshots were also used by Khomenko et al. (2005b) for the investigation of magnetoconvection of mixed-polarity quiet-Sun regions and compared with measured Stokes profiles by Khomenko et al. (2005a).
Because of the limited height-range of the MHD simulation, we
first extrapolate the field from the magnetic vector obtained from the
simulations at a fixed geometric height (see Fig. 1). This height,
![]() ,
must be chosen with care since the extrapolation starting from the magnetic field vector at
,
must be chosen with care since the extrapolation starting from the magnetic field vector at
![]() is employed as a reference against which all others are compared.
To avoid introducing a bias it must correspond to a suitably
weighted average height of formation of the spectral line used for
inversion, e.g., Fe I 6173.3 Å. Since different regions
in the MHD-simulation may have different formation height ranges, we
chose a criterion that
selected the reference height obtained by finding the highest
correlation between the magnetic field strength taken directly from the
MHD simulation and from inversion of the Stokes profiles obtained
under ideal conditions (very high spectral and spatial resolutions
and no noise).
is employed as a reference against which all others are compared.
To avoid introducing a bias it must correspond to a suitably
weighted average height of formation of the spectral line used for
inversion, e.g., Fe I 6173.3 Å. Since different regions
in the MHD-simulation may have different formation height ranges, we
chose a criterion that
selected the reference height obtained by finding the highest
correlation between the magnetic field strength taken directly from the
MHD simulation and from inversion of the Stokes profiles obtained
under ideal conditions (very high spectral and spatial resolutions
and no noise).
This extrapolation is used as a reference against which other extrapolations are compared. These later ones use magnetic vector maps that are obtained from the inversion of synthetic Stokes profiles.
Two spectral lines are considered, the very widely used Fe I 6302.5 Å (Landé factor g=2.5) line,
employed by the Advanced Solar Polarimeter and the spectropolarimeter
on the Hinode spacecraft, and Fe I 6173.3 Å (g=2.5),
which was selected for the Helioseismic and Magnetic Imager (HMI) on
the Solar Dynamics Observatory (SDO) and for the Polarimetric and
Helioseismic Imager on the Solar Orbiter mission (SO/PHI). In both
cases
![]() was found to be located approximately at 150 km above
was found to be located approximately at 150 km above
![]() .
.
Using the STOPRO code (Frutiger et al. 2000; Solanki 1987), we then compute the Stokes parameters of these widely used spectral lines. We restrict ourselves to conditions at the solar disk center. These synthetic data are then either directly inverted or inverted after degrading the data by introducing noise and lowering the spatial and/or the spectral resolution. A list of all the considered cases is presented in Table 1 and discussed in Sect. 3. The inversion is carried out for each spectral line individually. The inverted magnetic field vector is then taken as the starting point for a nonlinear force-free extrapolation.
For comparison, we also compute a potential field from the results of the MHD-simulations at
![]() ,
which requires only the vertical component of the photospheric magnetic
field. In addition, we compute nonlinear force-free extrapolations
with a horizontal spatial resolution that is lower by a factor of two
and four, respectively, than the original MHD model.
,
which requires only the vertical component of the photospheric magnetic
field. In addition, we compute nonlinear force-free extrapolations
with a horizontal spatial resolution that is lower by a factor of two
and four, respectively, than the original MHD model.
2.2 Description of the inversion code
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12812f1a.eps}\vspace*{5mm}
...
...c.eps}\vspace*{5mm}
\includegraphics[width=12cm,clip]{12812f1d.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12812-09/Timg13.png)
|
Figure 1:
Bx, By, Bz maps at a fixed reference height
|
| Open with DEXTER | |
The inversion code HeLIx developed by Lagg et al. (2004) is based on fitting the observed Stokes profiles with synthetic ones obtained from an analytic solution of the Unno-Rachkovsky equations (Rachkowsky 1967; Unno 1956) in a Milne-Eddington atmosphere (see e.g., Landi degl'Innocenti 1992). These synthetic profiles are functions of the magnetic field strength |B|, both its inclination and azimuth (with respect to the line of sight), the vertical velocity, the Doppler width, the damping constant, the ratio of the line center to the continuum opacity, and the slope of the source function with respect to optical depth. We assume the filling factor to be unity. Any possible magnetic fine structure within one pixel consisting of a field-free and a magnetic area is smeared out, and the inversion returns the magnetic field vector averaged over the considered pixel. Since the extrapolations are performed on the same pixel scale as the inversions, they must operate with the pixel-averaged magnetic field vector. Setting the filling factor to unity during the inversion process enhances its robustness and reliability. The atmospheric parameters that ensure the minimum of the merit function are obtained using a very reliable genetic algorithm (Charbonneau 1995). The genetic algorithm was extensively tested with synthetic spectra from MHD simulations and the results compared with response-function-averaged physical parameters (e.g., magnetic field strength, inclination, azimuth, line-of-sight velocity). The results of the test indicate that the genetic algorithm retrieves the global minimum of the merit function with high reliability. The parameter sets are chosen to simulate the Hinode/SOT and the future SO/PHI instruments.
Table 1: Influence on the photospheric field for different cases.
2.3 Hinode SOT Spectro-Polarimeter
The Spectro-Polarimeter (SP; Lites et al. 2007)
is part of the focal-plane package of the 50 cm Solar Optical
Telescope (SOT) onboard the Hinode spacecraft. It observes the
line pair Fe I 6302.5 and 6301.5 Å. Here we restrict
ourselves to 6302.5 Å. The spatial resolution at the diffraction
limit of the telescope's primary mirror is about 0.32''
at 6302.5 Å, which corresponds to 230 km on the Sun. The
size of a detector pixel corresponds to approximately 110 km
on the Sun in the spatial direction. The spectral resolution is
30 mÅ and the spectral sampling is 21 mÅ. We used Gaussians
to perform both spectral and spatial smearing. The noise was added to
the Stokes profiles as photon noise F ![]()
![]() ,
where F is white noise with a Gaussian distribution and
,
where F is white noise with a Gaussian distribution and ![]() is the continuum intensity. The chosen standard deviation of F was 10-3,
which corresponds to the typical noise level of modern
spectro-polarimetric observations (e.g. Hinode/SP data).
Noise is included in a similar way when noise is added to the data.
More subtle instrumental effects, such as scattered light or a slight
defocus (e.g., Danilovic et al. 2008), are not considered.
is the continuum intensity. The chosen standard deviation of F was 10-3,
which corresponds to the typical noise level of modern
spectro-polarimetric observations (e.g. Hinode/SP data).
Noise is included in a similar way when noise is added to the data.
More subtle instrumental effects, such as scattered light or a slight
defocus (e.g., Danilovic et al. 2008), are not considered.
2.4 SO/PHI magnetograph
The Solar Orbiter Polarimetric and Helioseismic Imager (SO/PHI),
a vector magnetograph, will be one of the main instruments on the
ESA-NASA Solar Orbiter mission. Of the two mission telescopes, the High
Resolution Telescope (HRT) is of primary importance to the present
investigation (because of the small horizontal extent of the
MHD simulations). The spectral line chosen for SO/PHI,
Fe I 6173.3 Å, combines high Zeeman sensitivity with
spectral purity, needed for simultaneous vector magnetic field and
helioseismology studies. We describe the point spread function (PSF) by
a Gaussian with FWHM =
150 km. The arrays of Stokes parameters obtained are rebinned to a
spatial pixel size of 80 km. We then convolve the Stokes profiles
in the spectral dimension with a Fabry-Pérot type filter of
![]() =
100 mÅ. Since SO/PHI will be a filtergraphic
instrument, we decrease the number of spectral samples per line by
taking 5 positions in the line and one in the continuum at the
positions (from line center at rest): -0.3 Å, -0.15 Å,
-0.075 Å, 0 Å, +0.075 Å, and +0.15 Å.
At that stage, we add noise and perform the inversion of the
Stokes profiles.
=
100 mÅ. Since SO/PHI will be a filtergraphic
instrument, we decrease the number of spectral samples per line by
taking 5 positions in the line and one in the continuum at the
positions (from line center at rest): -0.3 Å, -0.15 Å,
-0.075 Å, 0 Å, +0.075 Å, and +0.15 Å.
At that stage, we add noise and perform the inversion of the
Stokes profiles.
2.5 Extrapolation of the vector magnetogram into the atmosphere
To compute a 3D-nonlinear force-free magnetic field from the result of the HeLIx inversion code, we carry out the following steps:
- If needed, we transform
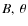 ,
and
,
and 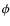 ,
which are outputs of the inversion code to
Bx, By, Bz in the photosphere, which requires a resolution of the
,
which are outputs of the inversion code to
Bx, By, Bz in the photosphere, which requires a resolution of the
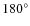 ambiguity in
ambiguity in 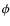 .
(See Sect. 2.5.1.)
.
(See Sect. 2.5.1.)
- We reprocess the vector magnetogram ( Bx, By, Bz), assuming that it refers to the same geometric height at every spatial pixel. (See Sect. 2.6.1.)
- Compute a nonlinear force-free coronal magnetic field from the preprocessed vector magnetogram. (See Sect. 2.6.2.)
- Compare the result with the reference field.
2.5.1 Removal of the 180
 ambiguity
ambiguity
In the present investigation, we chose to remove the
![]() ambiguity
by minimizing the angle to the exact solution. This possibility does
not, of course, exist for real data, and other methods of ambiguity
inversion would need to be tried. The performance of different
ambiguity removal techniques was studied using synthetic data by Metcalf et al. (2006). They found that the most reliable technique managed to recover
ambiguity
by minimizing the angle to the exact solution. This possibility does
not, of course, exist for real data, and other methods of ambiguity
inversion would need to be tried. The performance of different
ambiguity removal techniques was studied using synthetic data by Metcalf et al. (2006). They found that the most reliable technique managed to recover ![]() of the points correctly. The influence of noise and spatial resolution
on the quality of the different ambiguity removal techniques was
investigated by Leka et al. (2009).
We did not consider specific ambiguity removal techniques. An
investigation of their efficiency and influence is beyond the scope of
this paper.
of the points correctly. The influence of noise and spatial resolution
on the quality of the different ambiguity removal techniques was
investigated by Leka et al. (2009).
We did not consider specific ambiguity removal techniques. An
investigation of their efficiency and influence is beyond the scope of
this paper.
2.6 Effects on the photosphere
In Table 1 and Fig. 1
we investigate the effects of different instrument effects and noise on
the vector field in the photosphere. The first line corresponds to the
MHD reference field. The field has an average electric current
density of
![]() and a vertical magnetic field strength of
and a vertical magnetic field strength of
![]() .
Positive and negative values of these quantities are balanced.
In the table, we compute the correlation relative to this
reference case for the horizontal fields
CBx, CBy, the vertical field CBz and the 2D-vector correlation in the photosphere
.
Positive and negative values of these quantities are balanced.
In the table, we compute the correlation relative to this
reference case for the horizontal fields
CBx, CBy, the vertical field CBz and the 2D-vector correlation in the photosphere
![]() and provide the average absolute values
and provide the average absolute values
![]() and
and
![]() .
For all full spatial resolution cases (upper part of the table), the
correlation is 0.97 for the vertical magnetic field strength, and
the average field strength is underestimated by a few percent. Noise
and instrument effects seem to have a relatively small effect on the
vertical field. The effect of a lower resolution (lower part of the
figure, Hinode/SP and SO/PHI cases) on the horizontal photospheric
magnetic fields
Bx, By, and the derived vertical current density Jz is significantly higher. For full profiles, the correlation in the horizontal fields is in the range of
0.85-0.88, but the combined effect of
filter and noise reduces the correlation to only 0.70 and
generates spurious, non-physical electric currents, which causes an
overestimation of Jz by a factor of about 3.
.
For all full spatial resolution cases (upper part of the table), the
correlation is 0.97 for the vertical magnetic field strength, and
the average field strength is underestimated by a few percent. Noise
and instrument effects seem to have a relatively small effect on the
vertical field. The effect of a lower resolution (lower part of the
figure, Hinode/SP and SO/PHI cases) on the horizontal photospheric
magnetic fields
Bx, By, and the derived vertical current density Jz is significantly higher. For full profiles, the correlation in the horizontal fields is in the range of
0.85-0.88, but the combined effect of
filter and noise reduces the correlation to only 0.70 and
generates spurious, non-physical electric currents, which causes an
overestimation of Jz by a factor of about 3.
2.6.1 Preprocessing
The magnetic field in the photosphere is not necessarily force-free (because of the finite ![]() plasma in the photosphere, see Gary 2001) and the horizontal components (Bx and By) of current vector magnetographs have large uncertainties. Aly (1989)
defined a number of integral relations to evaluate whether a measured
photospheric vector magnetogram is consistent with the assumption of a
force-free field. These integral relations (numerator in Eq. (1)) were used to define a dimensionless parameter
plasma in the photosphere, see Gary 2001) and the horizontal components (Bx and By) of current vector magnetographs have large uncertainties. Aly (1989)
defined a number of integral relations to evaluate whether a measured
photospheric vector magnetogram is consistent with the assumption of a
force-free field. These integral relations (numerator in Eq. (1)) were used to define a dimensionless parameter
![]() to be
to be
where force-free extrapolation codes require
For the synthetic magnetograms investigated in Table 1, we find
![]()
![]() 0.19 in the photosphere. Wiegelmann et al. (2006b)
developed a preprocessing procedure to drive the observed non
force-free data towards boundary conditions suitable for a force-free
extrapolation. As a result of the preprocessing, we obtain a
boundary-data set that is consistent with the assumption of a
force-free magnetic field. After applying the preprocessing routine we
archive force-free consistent boundary conditions with
0.19 in the photosphere. Wiegelmann et al. (2006b)
developed a preprocessing procedure to drive the observed non
force-free data towards boundary conditions suitable for a force-free
extrapolation. As a result of the preprocessing, we obtain a
boundary-data set that is consistent with the assumption of a
force-free magnetic field. After applying the preprocessing routine we
archive force-free consistent boundary conditions with
![]()
![]() 10-4. The preprocessing affects mainly the horizontal magnetic field components.
The correlation of original and preprocessed field for the investigated cases is
CBz=0.99
10-4. The preprocessing affects mainly the horizontal magnetic field components.
The correlation of original and preprocessed field for the investigated cases is
CBz=0.99 ![]() 0.006 for the vertical component Bz. For the horizontal components, we find a correlation of
CBx=0.91
0.006 for the vertical component Bz. For the horizontal components, we find a correlation of
CBx=0.91 ![]() 0.05 and
CBy=0.90
0.05 and
CBy=0.90 ![]() 0.05, respectively.
0.05, respectively.
2.6.2 Extrapolation of nonlinear force-free fields
Force-free coronal magnetic fields must obey the equations
We define the functional
where w is a weighting function. It is obvious that (for w>0) the force-free Eqs. (2), (3) are fulfilled when L is equal to zero (Wheatland et al. 2000). We minimize Eq. (4) numerically as explained in detail by Wiegelmann (2004). The program is written in C and was parallelized with OpenMP. Wiegelmann & Neukirch (2003) and Schrijver et al. (2006) tested the program for the conditions of exact nonlinear force-free equilibria developed by Low & Lou (1990), while Wiegelmann et al. (2006a) tested it with another exact equilibrium developed by Titov & Démoulin (1999). The code was applied to vector magnetograph data from the German Vacuum Tower Telescope (VTT) by Wiegelmann et al. (2005b,a) and to data from the Solar Flare Telescope (SFT) by Wiegelmann et al. (2006b). Here we use an updated version of the optimization approach that includes a multi-scale approach described and tested by Metcalf et al. (2008) and applied to Hinode data by (Schrijver et al. 2008).
Table 2: Various figures of merit of the 3D reconstruction for different cases.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12812f2.eps}
\vspace*{1.67mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12812-09/Timg44.png)
|
Figure 2:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12812f3.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12812-09/Timg45.png)
|
Figure 3: Same as Fig. 2, but 400 km above the reference height. |
| Open with DEXTER | |
2.7 Figures of merit
Schrijver et al. (2006) introduced several figures of merit to compare the results of magnetic field extrapolation codes (a 3D-vector field ![]() )
with a reference solution
)
with a reference solution ![]() :
:
- Vector correlation:
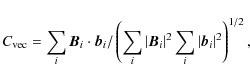
(5)
where i corresponds to all grid points in the entire 3D computational box. - Total magnetic energy of the reconstructed field
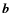 normalized by the energy of the reference field
normalized by the energy of the reference field 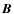 :
:
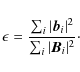
(6)
- We also compute the linear Pearson correlation C of the total magnetic field strength |B| at the heights 100 km, 400 km and 800 km above the reference height,
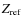 ,
respectively.
Two vector fields agree perfectly if
,
respectively.
Two vector fields agree perfectly if
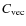 ,
,
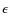 ,
and the Pearson correlation coefficients are all unity.
,
and the Pearson correlation coefficients are all unity.
3 Results
Table 2 contains the
different quantitative measurements that compare the different
reconstructed field from synthetic observations with the reference
field (extrapolations from ideal data). Column 2 contains the
vector correlation
![]() ,
Col. 3 the normalized magnetic energy
,
Col. 3 the normalized magnetic energy ![]() ,
and Cols. 4-6 the linear Pearson correlation C of the total magnetic field strength |B| at the heights 100 km, 400 km, and 800 km above the reference height,
,
and Cols. 4-6 the linear Pearson correlation C of the total magnetic field strength |B| at the heights 100 km, 400 km, and 800 km above the reference height,
![]() ,
respectively.
,
respectively.
Figures 2 and 3 show contourplots of the magnetic field strength
![]() at 100 km and 400 km above
at 100 km and 400 km above
![]() ,
respectively.
,
respectively.
3.1 MHD cases
In the first 4 images of Figs. 2 and 3
we compare the nonlinear force-free 3D magnetic field
reconstructed from ideal data (extracted from the MHD simulations
at
![]() ,
called Reference in Table 2 and in Figs. 2, 3)
with a potential field extrapolation also starting from ideal data
(Potential) and nonlinear force-free computations starting from
magnetic field maps obtained from the inversion of synthetic Stokes
profiles and MHD cases. Potential fields are often calculated in
addition to NLFFF, because they contain the minimum energy for given
vertical boundary conditions and the free energy of a NLFF-field above
that of a potential field has relevance to coronal eruptions.
,
called Reference in Table 2 and in Figs. 2, 3)
with a potential field extrapolation also starting from ideal data
(Potential) and nonlinear force-free computations starting from
magnetic field maps obtained from the inversion of synthetic Stokes
profiles and MHD cases. Potential fields are often calculated in
addition to NLFFF, because they contain the minimum energy for given
vertical boundary conditions and the free energy of a NLFF-field above
that of a potential field has relevance to coronal eruptions.
As seen in Table 2 and Figs. 2 and 3, the computations with reduced spatial resolution of 40 km pixels are in almost perfect agreement, while 80 km pixels provide excellent agreement. The correlation with the reference field is tighter higher in the atmosphere, which is unsurprising since small-scale field structures at the lower boundary do not propagate very high and the larger scales are less affected by the binning to larger horizontal pixels. The magnetic energy is underestimated because small-scale fields and currents at low heights, which contribute significantly to the total magnetic energy, are not resolved here.
3.2 Dependence on the spectral line, noise, and spectral sampling
The remaining images in Figs. 2 and 3 and the remaining entries in Table 2
apply to extrapolations initiating from magnetic maps obtained from
inversions of synthetic spectral lines. The first 3 of these
images (marked 6173 no noise, Filter no noise, and Filter noise in
Figs. 2 and 3) and the entire middle part of Table 2 are test cases for which we move step-by-step away from ideal (i.e., ![]() obtained directly from the MHD simulations) towards more realistic
conditions, i.e., introducing various instrumental effects.
obtained directly from the MHD simulations) towards more realistic
conditions, i.e., introducing various instrumental effects.
The first of these steps is to invert the synthetic line profiles directly, without any further manipulation (ideal Spectro-Polarimeter). This step introduces uncertainties caused by the inversion process per se (e.g., by complex Stokes profiles being fit when assuming purely symmetric or antisymmetric ones), that the line covers a range of heights, and the dependence of the line formation height on the type of solar feature.
The inversion of Stokes spectra expected from an ideal Spectro-Polarimeter leads to agreement with the reference field within a few percent for the vector correlation and we can estimate the magnetic energy with an accuracy of one percent for the 6173.3 Å line. The magnetic energy is an important quantity because it determines the amount of free energy maximally available for eruptive phenomena like flares and coronal mass ejections. The high accuracy achieved in this case is particularly encouraging because it shows that applying a simple Milne-Eddington inversion to the often highly asymmetric profiles (which sometimes exhibit multiple lobes in Stokes V) provides sufficiently accurate results and that the fluctuating height at which the magnetic field is obtained does not significantly influence the extrapolations (although we note that the situation may differ in a sunspot with its rather deep Wilson depression). This result implies that most of the inaccuracies in the extrapolations are caused by limitations to the instrumentation and not because it is in principle impossible to extract the magnetic field vector from the observations.
As Table 2 shows, there is little difference between the two g=2.5 Zeeman triplets
![]() Å line and
Å line and
![]() Å.
The field extrapolated from the magnetic field maps derived from either
of them correlate very well with the reference field. Using the
Å.
The field extrapolated from the magnetic field maps derived from either
of them correlate very well with the reference field. Using the
![]() Å
lines provides a slightly more accurate estimate of the magnetic
energy, but all in all the need to use the Zeeman effect in a
spectral line by itself only leads to errors of a few percent
Å
lines provides a slightly more accurate estimate of the magnetic
energy, but all in all the need to use the Zeeman effect in a
spectral line by itself only leads to errors of a few percent![]() . The addition of noise at a level of 10-3 of the continuum intensity
. The addition of noise at a level of 10-3 of the continuum intensity ![]() ,
which is typical of modern Spectro-Polarimetric observations, has
only a small effect. We note that by adding an equal amount of photon
noise to all Stokes parameters we produce a much lower signal-to-noise
ration (S/N) in the linearly polarized Q and U profiles than in Stokes V because of the lower intensity of the former. The influence of noise of a given amplitude also depends heavily on the
magnetic flux in the area from which we extrapolate. With
,
which is typical of modern Spectro-Polarimetric observations, has
only a small effect. We note that by adding an equal amount of photon
noise to all Stokes parameters we produce a much lower signal-to-noise
ration (S/N) in the linearly polarized Q and U profiles than in Stokes V because of the lower intensity of the former. The influence of noise of a given amplitude also depends heavily on the
magnetic flux in the area from which we extrapolate. With
![]() G,
the chosen snapshot corresponds to an average plage region. We
expect that the same amount of noise will have a considerably stronger
effect on weaker Stokes profiles present in the quiet sun.
G,
the chosen snapshot corresponds to an average plage region. We
expect that the same amount of noise will have a considerably stronger
effect on weaker Stokes profiles present in the quiet sun.
It is important to consider whether measurements for limited wavelength bands and at reduced wavelength resolution, typical of filter polarimeters (filter magnetographs), are acceptable for extrapolations. One advantage of filter polarimeters is that they allow us to perform a time series of a whole region at high cadence. Of particular relevance to magnetic extrapolations is that filter polarimeters record the Stokes vector over the full field of view. This overcomes the main shortcoming of Spectro-Polarimeters, namely that they need to scan a region step by step, so that by the time the second footpoint of a loop is scanned the first may have evolved considerably. These advantages of filter instruments come at the price of a reduced spectral resolution and limited spectral sampling. An extensive series of tests by one of us (L. Yelles) using various MHD simulation snapshots has shown that observations at 5 wavelength points in the line plus one at the continuum should be adequate to obtain the magnetic field vector reliably.
The computations carried out here suggest that this is also
true for the magnetic field extrapolated from vector magnetograms
obtained from filter instruments. According to Table 2 and Figs. 2 and 3,
the application of 100 mÅ broad filters to 5 locations in
the Fe I 6173.3 Å line and additionally to a nearby
continuum position gives an extrapolated nonlinear force-free field
that differs only slightly from the results obtained with the full line
profile. The magnetic energy is overestimated by at most ![]() for a filter width <100 mÅ and at least 5 sampling points in the line and one in the nearby continuum.
for a filter width <100 mÅ and at least 5 sampling points in the line and one in the nearby continuum.
Noise has a greater effect on filter polarimeter measurements than on
spectropolarimetric ones, as can be judged from Table 2.
In particular, the magnetic energy is affected, since it is a
factor of two less accurate than from spectropolarimetric measurements.
If we take the effect of photometric noise of
![]() in all Stokes parameters into account, we overestimate the magnetic energy by
in all Stokes parameters into account, we overestimate the magnetic energy by ![]() .
The higher magnetic energy in these cases is probably the result of
stronger currents in the photosphere, which are inferred from a less
accurate computation of the horizontal photospheric field during the
inversion. The total vertical magnetic field
.
The higher magnetic energy in these cases is probably the result of
stronger currents in the photosphere, which are inferred from a less
accurate computation of the horizontal photospheric field during the
inversion. The total vertical magnetic field
![]() in the photosphere is underestimated by
in the photosphere is underestimated by ![]() after inversion of a set of filter images (irrespective of whether noise is applied or not). The total vertical current
after inversion of a set of filter images (irrespective of whether noise is applied or not). The total vertical current
![]() is overestimated by
is overestimated by ![]() and
and ![]() without
and with noise, respectively. Most of these spurious currents produced
by spectral line inversions fluctuate on very small scales so that they
either truly are or behave like noise. Consequently, they are not
transported into the corona. The preprocessing routine takes care of
this problem and most of the spurious currents vanish. After
preprocessing, the total current is overestimated by
without
and with noise, respectively. Most of these spurious currents produced
by spectral line inversions fluctuate on very small scales so that they
either truly are or behave like noise. Consequently, they are not
transported into the corona. The preprocessing routine takes care of
this problem and most of the spurious currents vanish. After
preprocessing, the total current is overestimated by ![]() and
and ![]() for inversions without and with noise, respectively.
for inversions without and with noise, respectively.
3.3 Hinode-like cases
As discussed in this and the following subsection, we now make the synthetic observations more realistic by employing parameters that are appropriate to high resolution instruments. In this section we consider the important case of the spectropolarimeter on Hinode (see also Sect. 2.3).
After taking the finite spatial resolution (pixel size 110 km) and
spectral smearing into account, we naturally obtain less accurate
results (rows marked Hinode/SP in Table 2).
We find that we cannot reconstruct the magnetic energy accurately in
these cases, because small-scale magnetic fields are not adequately
resolved. We obtain, however, a reasonable estimate of the
correct magnetic field in higher layers of the atmosphere. For the most
involved case (Hinode-like Spectro-Polarimeter with a noise of
![]() and a pixel size of 110 km), we find an error of
and a pixel size of 110 km), we find an error of ![]() ,
,
![]() ,
and
,
and ![]() at the heights 100, 400, and 800 km above
at the heights 100, 400, and 800 km above
![]() ,
respectively. The limited resolution avoids accurate reconstructions of
low-lying small-scale features, but recovers the field at greater
heights approximately correctly. At heights above 400 km,
even the most involved and noisy nonlinear force-free reconstruction
considered here
has an accuracy that is a factor of three times superior to that with a
potential field reconstruction starting from a perfectly known lower
boundary.
,
respectively. The limited resolution avoids accurate reconstructions of
low-lying small-scale features, but recovers the field at greater
heights approximately correctly. At heights above 400 km,
even the most involved and noisy nonlinear force-free reconstruction
considered here
has an accuracy that is a factor of three times superior to that with a
potential field reconstruction starting from a perfectly known lower
boundary.
3.4 SO/PHI-like cases
We also consider instrumental effects appropriate to the
PHI instrument on Solar Orbiter such as the finite spectral
resolution and sampling by a Fabry-Perot interferometer, finite spatial
resolution of approximately 160 km (pixel size 80 km) on the
sun, and photon noise at a level of 10-3 ![]()
![]() .
Details are given in Sect. 2.4. The extrapolated magnetic field displays a very similar spatial distribution as that based on the
inversion of ideal line profiles. On the whole, the influence of degrading the spatial resolution to
a pixel size of 80 km (denoted as Filter+Noise in Figs. 2, 3) introduces a similar level of inaccuracy in the extrapolated field as the uncertainties in Bx, By, and Bz
at the lower boundary introduced by instrumental effects and the
inversion of the line profiles. However, even for these most involved
cases, of comparatively low resolution, instrument effects and noise,
the agreement with the reference is closer than a potential field
computed from ideal data at the lower boundary. The stronger
correlation of
.
Details are given in Sect. 2.4. The extrapolated magnetic field displays a very similar spatial distribution as that based on the
inversion of ideal line profiles. On the whole, the influence of degrading the spatial resolution to
a pixel size of 80 km (denoted as Filter+Noise in Figs. 2, 3) introduces a similar level of inaccuracy in the extrapolated field as the uncertainties in Bx, By, and Bz
at the lower boundary introduced by instrumental effects and the
inversion of the line profiles. However, even for these most involved
cases, of comparatively low resolution, instrument effects and noise,
the agreement with the reference is closer than a potential field
computed from ideal data at the lower boundary. The stronger
correlation of ![]() with the reference value than for Hinode is probably due to the
somewhat higher spatial resolution expected for PHI. This suggests
that for accurate estimates of the magnetic energy it is more important
to achieve high spatial resolution than completely accurate line
profiles. The field at 100 km above
with the reference value than for Hinode is probably due to the
somewhat higher spatial resolution expected for PHI. This suggests
that for accurate estimates of the magnetic energy it is more important
to achieve high spatial resolution than completely accurate line
profiles. The field at 100 km above
![]() and
partly at 400 km is reproduced more accurately for Hinode/SP-like
parameters than for the SO/PHI case. Obviously, studies of low
lying fields would benefit from having the full line profile
(in particular when noise is included).
and
partly at 400 km is reproduced more accurately for Hinode/SP-like
parameters than for the SO/PHI case. Obviously, studies of low
lying fields would benefit from having the full line profile
(in particular when noise is included).
4 Conclusions
We have investigated how strongly inaccuracies in the lower magnetic boundary, introduced by measurement and analysis errors in the Stokes profiles influence the computation of nonlinear force-free coronal magnetic fields.
We have found that instrument effects and noise influence the horizontal component of the photospheric magnetic field vector more strongly than the vertical field. We have found that nonlinear force-free fields extrapolated from both ideal data and the inversion of Stokes profiles deviate significantly more at lower heights. In particular, a limited spatial resolution influences the lowest layers the most. Higher in the atmosphere, we found good agreement (correlation stronger than 0.98) with extrapolations from ideal data. We have found that for an accurate estimation of the magnetic energy, a high spatial resolution is more important than a high spectral resolution.
These basic findings apply to magnetic vector maps obtained from both, spectropolarimetric data, such as those provided by Hinode/SP, and filter magnetographs, such as those to be provided by SO/PHI or SDO/HMI.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12812f4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12812-09/Timg67.png)
|
Figure 4: Scatter plot displaying how errors in the photosphere affect the accuracy of the 3D magnetic field reconstruction. Shown is the 3D vector correlation against the 2D vector correlation in the photosphere. The solid line corresponds to a linear fit and the dotted line corresponds to identical 2D and 3D correlations. |
| Open with DEXTER | |
Finally, we determine how errors in the photosphere influence the quality of the 3D reconstruction. We show a scatter plot in Fig. 4 to compare the 2D-vector correlation in the photosphere (Table 1) with the 3D vector correlation of the reconstructed coronal magnetic field (Table 2). The solid line in Fig. 4 shows a linear fit to the data points and the dotted line corresponds to equal 2D and 3D correlations. As one can see from this figure, the relation between the accuracy of the photospheric and coronal field is linear, but not identical. In particular, the correlation of the full 3D field has a shallower gradient than the photospheric correlation, so that extrapolations based on a filter instrument with noise (which provides the least accurate photospheric field) are more accurate than the vector magnetograms that they are based on.
It would be interesting to repeat this study on larger spatial scales, reaching sizes typical of observed vector magnetograms, as soon as the corresponding radiative MHD-simulations become available (with similar grid size as the simulations employed here). We also need to investigate quiet sun regions, coronal holes, and active regions separately. In particular, our results may not apply when considering extrapolations starting from regions containing sunspots because of their much larger Wilson depression and rather different temperature structure, which influence the line formation height and the line formation in general. We have also not considered subtle but possibly important effects, such as the evolution of the field during the scan of an active region by the slit of a Spectro-Polarimeter or the evolution of a line profile during the spectral scan of a filter instrument.
One might also consider investigating the lower layers of the solar atmosphere, where the plasma is not force-free, in more detail and taking non-magnetic forces into consideration for the magnetic field extrapolation. A first step in this direction was taken by Wiegelmann & Neukirch (2006), who developed a magnetohydrostatic extrapolation code. For an application to data, we require, however, more information about the properties of the non-magnetic forces (e.g., pressure gradients and gravity).
AcknowledgementsWe thank R. Cameron, M. Schüssler and A. Vögler for providing us with the analysed numerical simulation snapshot. The work of T. Wiegelmann was supported by DLR-grant 50 OC 0501. This work was partly supported by WCU grant No. R31-10016 from the Korean Ministry of Education, Science and Technology.
References
- Aly, J. J. 1989, Sol. Phys., 120, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. H., House, L. L., & Heasley, J. N. 1977, Sol. Phys., 55, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 1995, ApJS, 101, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeRosa, M. L., Schrijver, C. J., Barnes, G., et al. 2009, ApJ, 696, 1780 [Google Scholar]
- Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 2000, A&A, 358, 1109 [NASA ADS] [Google Scholar]
- Gary, G. A. 2001, Sol. Phys., 203, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, G. A., & Hagyard, M. J. 1990, Sol. Phys., 126, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E. V., Martínez González, M. J., Collados, M., et al. 2005a, A&A, 436, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khomenko, E. V., Shelyag, S., Solanki, S. K., & Vögler, A. 2005b, A&A, 442, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Woch, J., Krupp, N., & Solanki, S. K. 2004, A&A, 414, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landi degl'Innocenti, E. 1992, Magnetic field measurements, in Solar observations: Techniques and interpretation, ed. F. Sanchez, M. Collados, & M. Vazquez (Cambridge University Press), 71 [Google Scholar]
- Leka, K. D., Barnes, G., Crouch, A. D., et al. 2009, Sol. Phys., 139 [Google Scholar]
- Lites, B. W., Elmore, D. F., Streander, K. V., et al. 2007, in New Solar Physics with Solar-B Mission, ed. K. Shibata, S. Nagata, & T. Sakurai, ASP Conf. Ser., 369, 55 [Google Scholar]
- Low, B. C., & Lou, Y. Q. 1990, ApJ, 352, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, T. R., Jiao, L., McClymont, A. N., Canfield, R. C., & Uitenbroek, H. 1995, ApJ, 439, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, T. R., Leka, K. D., Barnes, G., et al. 2006, Sol. Phys., 237, 267 [Google Scholar]
- Metcalf, T. R., Derosa, M. L., Schrijver, C. J., et al. 2008, Sol. Phys., 247, 269 [Google Scholar]
- Rachkowsky, D. N. 1967, Izv. Krym. Astrofiz. Obs., 37, 56 [Google Scholar]
- Schrijver, C. J., Derosa, M. L., Metcalf, T. R., et al. 2006, Sol. Phys., 235, 161 [Google Scholar]
- Schrijver, C. J., DeRosa, M. L., Metcalf, T., et al. 2008, ApJ, 675, 1637 [Google Scholar]
- Shimizu, T. 2004, in The Solar-B Mission and the Forefront of Solar Physics, ed. T. Sakurai, & T. Sekii, ASP Conf. Ser., 325, 3 [Google Scholar]
- Solanki, S. K. 1987, Ph.D. Thesis, ETH, Zürich, 8309 [Google Scholar]
- Solanki, S. K., Lagg, A., Woch, J., Krupp, N., & Collados, M. 2003, Nature, 425, 692 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Titov, V. S., & Démoulin, P. 1999, A&A, 351, 707 [NASA ADS] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W. 1956, Pub. Astron. Soc. Japan, 8, 108 [Google Scholar]
- Venkatakrishnan, P., & Gary, G. A. 1989, Sol. Phys., 120, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wheatland, M. S., Sturrock, P. A., & Roumeliotis, G. 2000, ApJ, 540, 1150 [Google Scholar]
- Wiegelmann, T. 2004, Sol. Phys., 219, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., & Neukirch, T. 2003, Nonlinear Proc. Geophys., 10, 313 [Google Scholar]
- Wiegelmann, T., & Neukirch, T. 2006, A&A, 457, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T., Inhester, B., Lagg, A., & Solanki, S. K. 2005a, Sol. Phys., 228, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Lagg, A., Solanki, S. K., Inhester, B., & Woch, J. 2005b, A&A, 433, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T., Inhester, B., Kliem, B., Valori, G., & Neukirch, T. 2006a, A&A, 453, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T., Inhester, B., & Sakurai, T. 2006b, Sol. Phys., 233, 215 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... percent
![[*]](/icons/foot_motif.png)
- The
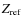 was set to the average formation height for the
was set to the average formation height for the
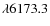 Å line. This might explain the poorer results for the
Å line. This might explain the poorer results for the
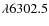 Å line.
Å line.
All Tables
Table 1: Influence on the photospheric field for different cases.
Table 2: Various figures of merit of the 3D reconstruction for different cases.
All Figures
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12812f1a.eps}\vspace*{5mm}
...
...c.eps}\vspace*{5mm}
\includegraphics[width=12cm,clip]{12812f1d.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12812-09/Timg13.png)
|
Figure 1:
Bx, By, Bz maps at a fixed reference height
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12812f2.eps}
\vspace*{1.67mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12812-09/Timg44.png)
|
Figure 2:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12812f3.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12812-09/Timg45.png)
|
Figure 3: Same as Fig. 2, but 400 km above the reference height. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12812f4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12812-09/Timg67.png)
|
Figure 4: Scatter plot displaying how errors in the photosphere affect the accuracy of the 3D magnetic field reconstruction. Shown is the 3D vector correlation against the 2D vector correlation in the photosphere. The solid line corresponds to a linear fit and the dotted line corresponds to identical 2D and 3D correlations. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



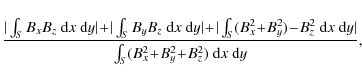
![\begin{displaymath}%
L=\int_{V} \; w \; \left[ \; B^{-2} ~ \vert(\nabla \times {...
...2 +\; \vert\nabla \cdot {\vec B}\vert^2\right] \; {\rm d}^3x
,
\end{displaymath}](/articles/aa/full_html/2010/03/aa12812-09/img38.png)