| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912681 | |
| Published online | 09 March 2010 | |
Radial velocities with CRIRES![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
Pushing precision down to 5-10 m/s
P. Figueira1 - F. Pepe1 - C. H. F. Melo2 - N. C. Santos3 - C. Lovis1 - M. Mayor1 - D. Queloz1 - A. Smette4 - S. Udry1
1 - Geneva Observatory, University of Geneva, 51 Ch. des Maillettes,
1290-Sauverny, Switzerland
2 - European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748
Garching bei Muenchen, Germany
3 - Centro de Astrofísica, Universidade do Porto, Rua das Estrelas,
4150-762 Porto, Portugal
4 - European Southern Observatory, Alonso de Córdova 3107, Vitacura,
Casilla 19001, Santiago 19, Chile
Received 12 June 2009 / Accepted 10 December 2009
Abstract
With the advent of high-resolution infrared spectrographs, radial
relocity (RV) searches enter into a new domain. As of today, the most
important technical question to address is which wavelength reference
is the most suitable for high-precision RV measurements. In this work
we use atmospheric absorption features as wavelength reference on
CRIRES data obtained on two programs and three different targets. We
analyzed the data from the TW Hya campaign again, reaching a
dispersion of about 6 m/s on the RV standard on a time scale
of roughly 1 week. We confirm that there is a low-amplitude RV signal
on TW Hya itself, with an amplitude roughly 3 times
smaller than the one reported at visible wavelengths. We present RV
measurements of Gl 86 as well, showing that our approach is
capable of detecting the signal induced by a planet and correctly
quantifying it. Our data show that CRIRES is capable of reaching an RV
precision of less than 10 m/s on a time scale of one week. The
limitations of this particular approach are discussed, along with the
limiting factors on RV precision in the IR in a general way. The
implications of this work on the design of future dedicated IR
spectrographs are addressed as well.
Key words: stars: planetary systems - infrared: stars - instrumentation: spectrographs - methods: observational - techniques: radial velocities
1 Introduction
The discovery of a hot Jupiter orbiting 51 Peg by Mayor & Queloz (1995) triggered the quest for extrasolar planets. This campaign made use of the radial velocity technique (henceforth RV), by which the presence of a planetary companion is inferred by the wobble it induces on the parent star. Several dedicated surveys have employed this method, concentrating in the beginning on solar-type stars, the most favorable target for high-precision measurements. However, it soon became clear that extrasolar planets were ubiquitous around these hosts. Longing for a better understanding of formation processes, planetary searches started to diversify, targeting young (Setiawan et al. 2007; Sozzetti et al. 2006) and evolved (Lovis & Mayor 2007; Sato et al. 2008), low-mass (Endl et al. 2008; Bonfils et al. 2004) and massive stars (Galland et al. 2005; Hatzes et al. 2005).
Recent technological developments allowed more precise spectrographs to be built, such as HARPS (Mayor et al. 2003), and reduction and analysis methods have been perfected through the years (Lovis & Pepe 2007). As of today, HARPS yields the most accurate RV measurements, with sub-m/s precision, allowing for a succession of ground-breaking detections of the lightest planets known (Lovis et al. 2006; Mayor et al. 2009).
Both the search for more exquisite stellar hosts and the race
for the lightest planets point towards M dwarfs. These stars, which are
the most abundant in the Universe, are also the lightest ones. Since
the RV variation induced by a planet on a star scales with M-2/3,
the amplitude of the effect induced on an M star is significantly
larger. As an example, a planet of an identical mass at the same
distance from the stellar host produces an RV variation with an
amplitude ![]() 3
times larger on an M5 star than on a G2 star. The drawback is that
since they are much colder, M dwarfs are much fainter in optical
wavelengths. The RV survey of light-mass stars points then towards the
exploration of a new wavelength domain, the IR, where the luminosity of
these objects peaks.
3
times larger on an M5 star than on a G2 star. The drawback is that
since they are much colder, M dwarfs are much fainter in optical
wavelengths. The RV survey of light-mass stars points then towards the
exploration of a new wavelength domain, the IR, where the luminosity of
these objects peaks.
As RV searches started to target young and active stars, another advantage of the IR became apparent. RV signals can be created by surface inhomogeneities, such as stellar spots (Queloz et al. 2001). Since the nature of these phenomena can bypass current diagnosis methods like the bisector analysis (see, for instance, Desort et al. 2007), a planetary origin can be assigned to a periodic variation that is, in fact, of stellar origin. By observing in the IR, as opposed to the visible wavelengths, one observes in a domain where the contrast between stellar spots and the stellar disk is reduced. Since the spot/star contrast ratio is at the root of the RV signal detected, the amplitude of the latter is reduced as well (Huélamo et al. 2008; Martín et al. 2006; Prato et al. 2008). By comparing RV drawn from optical and IR spectrographs, one can assign the planetary or stellar nature to an RV signal in an unambiguous way.
However, the exploration of the RV in the IR is in its infancy, and many problems still need to be tackled. In this work we concentrate on describing a precise wavelength calibration technique for the IR domain. In Sect. 2 we discuss the difficulties of wavelength calibration in the IR and present the principles of our technique. In Sect. 3 we describe CRIRES and the observations, and how we applied our approach. Section 4 presents an outline of the data reduction and analysis. Section 5 presents our results. Section 6 discusses these results and their implications for the design of spectrographs dedicated to RV measurements in the IR. We finish by stating our conclusions in Sect. 7.
2 Wavelength references in the IR
To detect small-amplitude RV signals (i.e., of m/s) a simultaneous wavelength reference must be employed. In the visible wavelengths, the Th-Ar emission lamps and the I2 absorption cell have proved to yield a precision of better than 1 m/s (Mayor et al. 2009) and 3 m/s (Howard et al. 2009), respectively. As impressive as they are, the transfer of this knowledge to the IR domain is not straightforward. The density of Th-Ar lines is much lower in the IR than in the visible, making it difficult to use. On top of that a stable spectrograph is required, since the lamp lines do not follow the same instrumental profile (IP) variations as the science targets (they pass through different optical paths). The more frequent gas-cell approach does not provide a better solution, because no known gas creates a dense absorption forest in a wide wavelength range in the IR. Several hybrid alternatives were put forward to attempt to solve this problem, such as gas cell plus emission lamp or coupling of different gas cells. For a detailed description of the problem and proposed solutions the reader is referred to the work of Mahadevan & Ge (2009).
A different approach can be taken by using one of the
peculiarities of the IR: the absorption of light by the Earth's
atmosphere. Our atmosphere is mainly composed of molecular species,
whose rotational and vibrational features correspond to near-IR
wavelengths. Usually seen as a nuisance, they can be used to our
advantage. In some narrow wavelength domains, the presence of
well-defined, sharp, and deep lines can provide for a good local
wavelength solution. While this is only possible locally, it is well
suited for the current high-resolution IR spectrographs, characterized
by a small simultaneous wavelength coverage, typically of ![]() /50-70. As a
free and always present gas cell, using atmospheric features as a
wavelength reference has to be assessed before venturing into other
alternatives.
/50-70. As a
free and always present gas cell, using atmospheric features as a
wavelength reference has to be assessed before venturing into other
alternatives.
However, our ``gas-cell'' suffers from a particular problem: the lines it imprints on the spectra depend on the atmospheric conditions. While some of lines' properties are expected to remain constant, others, such as depth, vary at a level of several %. It is then very hard to apply the typical deconvolution technique (Butler et al. 1996), which assumes a detailed knowledge of the absorbing spectra to calculate the IP and correct for it. While several dedicated models have been developed (Bailey et al. 2007) to address this problem, there is no evaluation of the impact of the remaining residuals on RV, and it is arguably bigger than the m/s level. As a matter of fact, the only campaign that employed the deconvolution approach in the IR in the more standard way, Blake et al. (2007), reported a precision of 300 m/s and stated that a precision down to 100 m/s was within reach. However, this result should be taken with caution, as it was derived for M dwarfs, a demanding stellar host.
We decided to depart from this approach by avoiding the overlapping between target and reference features. While the spectra of the star and of the atmosphere are simultaneous in the sense that they are obtained at the same moment, the lines are separated spectroscopically and can be fitted independently. The center of each line is thus determined in a straightforward way (for instance, the atmospheric lines' depth variation has no impact on the measured RVs). The IP variations that affect stellar lines affect reference lines as well. If the same fitting procedures are employed on both line sets, the effect cancels out.
Several notable experiments on the use of atmospheric absorption features were made in the eighties, of which we highlight the results of Balthasar et al. (1982), Smith (1982), and Caccin et al. (1985). Working with O2 lines, these authors could reach a precision of 5 m/s. The value is made even more relevant by their using different RV determination methods (different instrumentation, different line fitting approaches, etc.), now believed to be obsolete when compared with the cross correlation function (Baranne et al. 1996) or the deconvolution method. Snellen (2004) used the same principle on H2O lines and reached a precision of 5-10 m/s on UVES data. This shows that the accuracy of our wavelength reference is at least of 5 m/s, making it a valuable option for us.
3 Observations
3.1 CRIRES
CRIRES (CRyogenic InfraRed Echelle Spectrograph) is the new ESO IR
spectrograph mounted on the Unit Telescope 1 (UT1, Antu) of the
European Southern Observatory Very Large Telescope (Kaeufl et al. 2004).
The main optical elements consist of a prism acting as a pre-disperser
and a 31.6 lines/mm echelle grating. The instrument provides
for a resolution of up to 100 000 when used with a 0.2'' slit.
It operates in the range 960-5200 nm with an instantaneous
wavelength coverage of ![]()
![]() .
The spectra is imaged on a detector mosaic, composed of four Aladdin
III detectors (
.
The spectra is imaged on a detector mosaic, composed of four Aladdin
III detectors (
![]() pixel) with a gap of
pixel) with a gap of
![]() 250 pix
between the chips. As a consequence, the instantaneous wavelength
coverage is much narrower than for optical cross-dispersed
spectrographs, such as HARPS, HIRES or UCLES. Adaptive Optics (MACAO -
Multi-Applications Curvature Adaptive optics) can be used to optimize
the signal-to-noise ratio and the spatial resolution.
250 pix
between the chips. As a consequence, the instantaneous wavelength
coverage is much narrower than for optical cross-dispersed
spectrographs, such as HARPS, HIRES or UCLES. Adaptive Optics (MACAO -
Multi-Applications Curvature Adaptive optics) can be used to optimize
the signal-to-noise ratio and the spatial resolution.
3.2 The observing set-up
At the time of observations, CRIRES had 200 possible observing set-ups,
most of which overlapped![]() .
To select the most suitable set-up for precise RV, we need to decide
which one carries the higher content of useful spectral information. We
stress here that by ``useful'' we mean domains where both reference -
i.e. atmospheric - and target - i.e. stellar - spectral features are
not superposed.
.
To select the most suitable set-up for precise RV, we need to decide
which one carries the higher content of useful spectral information. We
stress here that by ``useful'' we mean domains where both reference -
i.e. atmospheric - and target - i.e. stellar - spectral features are
not superposed.
We used solar NSO/Kitt Peak FTS data (Wallace et al. 1993; Livingston & Wallace 1991) to simulate CRIRES spectra. To do so, we convolved the spectra with an IP that we assumed as being Gaussian and defined as a function of resolution (fixed at R = 100 000), and re-sampled it on the detector. This procedure was applied for the Sun spectra, atmospheric spectra, and the product of the two. To access the RV uncertainty measured on a sun-like spectrum using the atmosphere as reference, we calculated the final RV uncertainty as the squared sum of the estimated error on the atmospheric lines' RV and on the stellar lines' RV. It is important to stress that the objective was not to obtain an estimation of the value of attainable precision in absolute terms but in a relative way between the different settings.
To estimate the precision on each of the components, two
different methods were employed: 1) a simple rule of thumb that states
that the inverse of RV accuracy ![]() ,
where S/N is the signal-to-noise
ratio of the spectra,
,
where S/N is the signal-to-noise
ratio of the spectra, ![]() the average depth of absorption lines, and
the average depth of absorption lines, and ![]() the number of lines in the spectra; 2) the quality factor described in Bouchy et al. (2001),
which quantifies the spectral information present on each spectra.
the number of lines in the spectra; 2) the quality factor described in Bouchy et al. (2001),
which quantifies the spectral information present on each spectra.
It is clear that the obtained precision depends heavily on the useful spectral domain. In our particular case, the superposition of telluric and stellar spectra can deem several zones as useless for RV calculation. To take this effect into account, we proceeded as follows. We used an automated algorithm to identify stellar lines in the simulated spectra (Sousa et al. 2007). From these we selected only those stellar lines that were not superimposed on atmospheric lines bigger than a fixed threshold, and vice-versa. We added a Doppler shift in the interval [-30, +30] km s-1 in order to reproduce the line shift created by Earth's movement around the Sun (for the case of a star that has an average RV of 0 relative to us). Lines that were found to be superposed after this step were discarded as well. We varied the detection and superposition thresholds at the level of 1-5%, a reasonable value for high S/N spectra. As the superposition of a relatively small line on the measured one can already introduce an RV shift of several hundreds of meters per second, it was mandatory to keep the superposition threshold low.
At the end of this procedure two zones were identified as the most promising:
- the H band, at 1.6
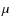 m - the
telluric absorption is dominated by CO2 lines,
while other absorbers have negligible absorption, smaller than
1%. The CO2 spectrum is easily
identified and provides for very regular wavelength anchors, with
around 30 deep lines - from 10 to 60 % - on several detectors. The
stellar spectra provides deep lines, which, while not being very
numerous, allow for an average contrast of around 30%;
m - the
telluric absorption is dominated by CO2 lines,
while other absorbers have negligible absorption, smaller than
1%. The CO2 spectrum is easily
identified and provides for very regular wavelength anchors, with
around 30 deep lines - from 10 to 60 % - on several detectors. The
stellar spectra provides deep lines, which, while not being very
numerous, allow for an average contrast of around 30%;
- the K band, at 2.32
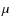 m - the
atmospheric absorption shows features of several molecules, with CH4
being the most prominent. The stellar lines depth is below 10%, but the
high number (around 50) compensates for it. This was the setting chosen
by Blake et al.
(2007).
m - the
atmospheric absorption shows features of several molecules, with CH4
being the most prominent. The stellar lines depth is below 10%, but the
high number (around 50) compensates for it. This was the setting chosen
by Blake et al.
(2007).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12681-fig1.eps}\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg12.png)
|
Figure 1:
Precision as a function of wavelength setting, in arbitrary units, as
described in Sect. 3.2 ( histogram, red in the electronic
version). Over-plotted is the squared root of the average
solar flux, as seen by CRIRES in a given wavelength setting, in
arbitrary units ( thick line, green in the electronic version).
All setting short-wards of 2.4 |
| Open with DEXTER | |
The main qualitative difference between the two domains in what concerns spectral information can be summarized as follows: while in the K band the spectral information is extracted from more numerous and shallower atmospheric lines, in the H band it is extracted from less numerous, deeper lines. The crowding of lines in the K band increases the risk of mutual pollution between the two sets of lines (telluric and stellar), which makes precise measurements more difficult in the K band than in H band.
The final choice was the atmospheric transmission window in the H band, in particular the setting (36/1/i). This setting provides for deep, sharp atmospheric lines of CO2 in detectors 1, 2 and 4. Special attention was given to image the highest number of deep stellar lines in detectors 1 and 2, as the blaze function provides for a much higher transmission in these two. The detector 1 is completely covered by a comb of 22 lines, detector 2 has 14 lines on it, and detector 4 images 20 lines. Deep lines, with relative depths of 10-50%, provide for a homogeneous complete coverage of the first detector; in the second one the depths range from 40 to 10% for the first two thirds of the detector and are smaller than 10% for the last third; finally, lines with a relative depth of 10-55% cover 90% of the fourth detector. It is very important to note that there are no other absorbers than CO2, providing for both an unambiguous identification of spectral features and a well-defined continuum around the sharp reference lines. For illustration purposes, in Fig. 2 we plot the atmospheric transmission measured by observing the telluric standard HD 96146.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12681-fig2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg13.png)
|
Figure 2: Atmospheric transmission at the chosen observing setting, for the detectors 1 (top), 2 (middle), and 4 (bottom). These spectra were obtained by co-adding and then normalizing the telluric standard exposures taken during the first night. |
| Open with DEXTER | |
The simplified study presented here does not intend to be the last word on the choice setting for CRIRES for RV studies. The optimal setting depends not only on the aforementioned superposition parameters chosen but also on the stellar spectra, the mean RV of the target and even the line identification algorithms chosen to pinpoint the lines present in each spectrum. More generally than that, it depends on the RV determination method. Our objective here is to provide for spectrally separated stellar and atmospheric lines, so that the spectral information carried by these well-defined lines can be fully exploited.
To conclude we note that the choice of employing the
atmosphere as a wavelength reference was prompted by very practical
issues. At the time of our observations, there was no CRIRES gas cell
available capable of providing deep absorption lines short-wards of
2.5 ![]() m.
m.
An entrance slit of 0.2'' was chosen, allowing for a
resolution of ![]() 100 000.
To reduce guiding errors (expected to have 1-1 translation on the lines
profile and thus on the measured RV) two cautionary measures were
taken. First of all, no AO was used, to make sure that the star PSF was
spread and larger than the slit width. On top of that, observations
during bad seeing periods were requested. The objective was to provide
enough photons to the slit viewer/guiding camera to ensure a good
centering of the star on the slit and to reduce photo-center effects on
RV. While these effects affect both star and reference in the same way,
minimizing their cause is the best way of ensuring a precise
correspondence between the two.
100 000.
To reduce guiding errors (expected to have 1-1 translation on the lines
profile and thus on the measured RV) two cautionary measures were
taken. First of all, no AO was used, to make sure that the star PSF was
spread and larger than the slit width. On top of that, observations
during bad seeing periods were requested. The objective was to provide
enough photons to the slit viewer/guiding camera to ensure a good
centering of the star on the slit and to reduce photo-center effects on
RV. While these effects affect both star and reference in the same way,
minimizing their cause is the best way of ensuring a precise
correspondence between the two.
3.3 Observations
The TW Hya campaign was performed under Director Discretionary Time (DDT), with program number 280.C-5064(A). The extensively studied TW Hya star was observed five times, from the 22 to 28 February 2008, promptly followed by an RV velocity standard, HD 108309. This star has been observed by HARPS high-precision programs and is known to be stable down to 1.1 m/s. Between the science target and the RV standard the instrumental set-up remained fixed, and no instrumental changes were allowed for. The objective was to track possible zero-point drifts of our wavelength calibration, which could have either an instrumental or atmospheric origin. The observations were made using the wav. setting (36/1/i), characterized by the reference wavelength 1592.7 nm (defined as the wavelength at the center of detector 3).
Originally, a set of 10 RV measurements of TW Hya on preferably consecutive nights was requested. However, due to scheduling difficulties aggravated by multiple instrument interventions, the period ended with only 5 out of the 10 measurements being taken.
The CRIRES calibration plan comprises an RV monitoring of radial velocity standard stars with the objective of studying CRIRES' stability. From this data we recovered the observations on Gl 86. The observations were made on the 5, 9, 17 and 18 January 2008 with a slit of 0.3'' in the setting (36/1/n), and no AO was used.
Table 1 summarizes the properties of the observations.
Table 1: The summary of the observation details on the RV std, TW Hya, and Gl 86, with all NDIT set to 1.
4 Data reduction and analysis
Data were reduced using a custom pipeline written in IRAF's CL![]() (Tody 1993). The
procedures were tailored to CRIRES spectra using first the science
verification data and later the data sets analyzed in this paper. It
provides for automated dark and nonlinearity corrections (using the
nonlinearity coefficients provided by ESO), as well as flagging and
replacement of bad pixels. The images were corrected from sensitivity
variations by dividing by a flat-fielding corrected from the blaze
function effect. The nodding pairs were mutually subtracted and the
orders' tracing was fitted using cubic splines. An optimal extraction
algorithm was employed for extracting the spectra (Horne 1986). The
objective of creating a dedicated pipeline is not only to optimize IRAF
tunable knobs to provide for an optimized reduction but also to ensure
a consistent and homogeneous reduction for all spectra.
(Tody 1993). The
procedures were tailored to CRIRES spectra using first the science
verification data and later the data sets analyzed in this paper. It
provides for automated dark and nonlinearity corrections (using the
nonlinearity coefficients provided by ESO), as well as flagging and
replacement of bad pixels. The images were corrected from sensitivity
variations by dividing by a flat-fielding corrected from the blaze
function effect. The nodding pairs were mutually subtracted and the
orders' tracing was fitted using cubic splines. An optimal extraction
algorithm was employed for extracting the spectra (Horne 1986). The
objective of creating a dedicated pipeline is not only to optimize IRAF
tunable knobs to provide for an optimized reduction but also to ensure
a consistent and homogeneous reduction for all spectra.
The computation of RV from extracted spectra was performed using a Python and FORTRAN pipeline heavily based on HARPS' DRS (Data Reduction Software). The CO2 lines' central wavelength was provided by HITRAN database (Rothman et al. 2005), with an accuracy of 5-50 m/s. The high S/N of the spectra and the wide separation between spectral lines allowed us to fit telluric lines easily and determine their centers. For each frame, the wavelength solution was obtained by fitting a third degree polynomial that matches the fitted centers with the theoretical wavelengths. Earth's RV in its orbit around the Sun was calculated using the ephemerides of Bretagnon & Francou (1988), which also allowed the computation of barycentric julian dates. By using the Earth's RV one can transpose the wavelength solution to the Solar System barycenter. RVs are then calculated by cross-correlating the spectra against a template mask as described in Baranne et al. (1996). In our case we used weighted masks (Pepe et al. 2002) to take the impact of photon noise on lines of different depth into account. We created two sets of masks: one from PHOENIX stellar atmosphere models (Barman et al. 2005) and the other by measuring the position and depth of each stellar line directly on the co-added reduced spectra. The center of the cross-correlation function was determined by fitting a Gaussian function. We note that we used the same line fit for both our reference and our science target lines. IP variations, which affect the two line sets in the same way, were fitted by the same procedure, and its impact on RVs cancels out.
As described in Sect. 2, extreme caution is needed to
reduce mutual pollution between stellar and atmospheric spectra to a
minimum. By knowing Earth's RV and the approximate RV of the target![]() , one can calculate the
approximate position of each telluric and stellar line and discard
those that blend. While this might lead to a significant loss of lines,
it greatly reduces the systematic error introduced by blended lines. As
a result the photon noise calculations on the remaining lines provide
for a realistic assessment of the spectral information carried and
achievable precision.
, one can calculate the
approximate position of each telluric and stellar line and discard
those that blend. While this might lead to a significant loss of lines,
it greatly reduces the systematic error introduced by blended lines. As
a result the photon noise calculations on the remaining lines provide
for a realistic assessment of the spectral information carried and
achievable precision.
Because the RV is computed for each nodding position spectrum and detector, the RV determination is independent for each frame, as the omnipresent reference lines are fitted independently, and their centers are used to construct a dedicated wavelength solution. The dispersion of the RV within the nodding cycle then allows for the direct calculation of the uncertainty on the averaged value for the nodding cycle. The error bar is simply the r.m.s. of the independent nodding measurements divided by the square root of the number of measurements.
Along with each RV calculation, the bisector inverse slope was computed on the stellar cross-correlation function following the procedure described in Queloz et al. (2001).
5 Results
Owing to the very steep blaze function, the low S/N
of TW Hya spectra collected in detector 4 made atmospheric
line fitting impossible. On the other hand, the low number of unblended
stellar lines in detector 2 combined with the lower count number led to
a very high photon noise on the CCF function. For the sake of
consistency and to allow a simple and robust comparison, the standard
RV presented were calculated only using the first detector as well. In
Fig. 3
we plot the spectra of HD 108309, on detector 1, for
illustration purposes. Out of the 22 lines, 14 unblended lines were
used to calculate the wavelength solution; these lines have an average
depth of ![]() % and
% and ![]() pxl.
pxl.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12681-fig3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg17.png)
|
Figure 3: Spectrum of RV standard, HD 108309, as seen on detector 1. These spectra are the result of the stacking and normalization of the 4 nodding spectra obtained during the first night. |
| Open with DEXTER | |
All RV values presented here were obtained with a template mask built
from the reduced CRIRES spectra. Results derived from masks built from
PHOENIX models yielded a lower precision. The dispersion of the RV
standard measurements, the most reliable precision indicator among our
measurements, is of ![]() 25 m/s
for PHOENIX masks. The reason for this difference is not known.
25 m/s
for PHOENIX masks. The reason for this difference is not known.
The RV measurements of TW Hya and the associated
standard star are presented in Table 2 and plotted in
Fig. 4.
The dispersion of the standards' RV measurements is compatible with the
error bars, while that is not the case for TW Hya.
Simultaneous optical RV determinations were performed by CORALIE to
back up CRIRES observations, already described in detail in Huélamo et al. (2008).
TW Hya IR RVs are not compatible with the orbit drawn from
optical RV measurements, with an amplitude of roughly 200 m/s,
defined using CORALIE (Baranne
et al. 1996) data and reproducing Setiawan et al. (2008)
data perfectly. To test the hypothesis of a smaller RV semi-amplitude
in the IR, we left this quantity and the systemic velocity as free
parameters, fixing all others. The fit delivers a semi-amplitude of ![]() m/s
with an rms (O-C) around the fit of 7.93 m/s. The fit is
overplotted on the data.
m/s
with an rms (O-C) around the fit of 7.93 m/s. The fit is
overplotted on the data.
Table 2: The RV calculated per nodding position for the RV standard, HD 108309, and TW Hya, and estimated photon noise of each exposure.
![\begin{figure}
\par\includegraphics[width=16.9cm,clip]{aa12681-fig4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg20.png)
|
Figure 4:
RV variation of the standard star (left) and
TW Hya (right) as a function of time. The
error bars are drawn from the dispersion of the N =
4 nodding positions, divided by 2 |
| Open with DEXTER | |
The RV measurements of Gl 86 are presented in Table 3 and Fig. 5. The orbit presented in Queloz et al. (2000) is superposed on the data. At first, only the systemic velocity and the T0 were allowed to vary. The reason for leaving T0 as a free parameters comes from the error propagation from the 2000 orbit to 2008 leading to a very large error on this parameter. The uncertainty adds up to almost 8 days, which is roughly half of the orbital period. The agreement between the published curve and CRIRES measurements is shown by the small dispersion around it, only 5.4 m/s. Alternatively, one can fix T0 and let P vary: the P remains unchanged within error bars, and the dispersion of the residuals remains roughly the same. We recently obtained several CORALIE measurements on this star that, together with the 2000 data, allowed us to independently determine the T0. This procedure delivered a value compatible, within error bars, with the one provided by CRIRES points alone. There is a measurable drift caused by the presence of an outer companion (Eggenberger et al. 2003) and the determination of the T0 at the moment of CRIRES data (when there are no CORALIE points) is affected by the shape of the unknown orbit. In either case, this T0 value can be used to fit an orbit in the CRIRES data, leaving only the systemic velocity as the free parameter. This delivers a dispersion of 16 m/s, which, while bigger, shows the agreement between the orbit and CRIRES data.
Table 3: The RV per nodding position for Gl 86, and associated photon noise.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12681-fig5.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg21.png)
|
Figure 5:
Phase-folded plot of Gl 86 Rv measurements. The error bars
presented are drawn from the dispersion of the six nodding positions,
divided by |
| Open with DEXTER | |
We can estimate the precision expected on computing the cross-correlation function on each spectrum, drawn from the photon noise alone. To do so we use the method presented in Bouchy et al. (2001). We consider the particular case of a Gaussian absorption line and apply it to the stellar lines present in the correlation mask (the unblended ones actually used in the correlation, so of interest to us). This yields the precision on each individual spectrum, i.e., on each nodding position. To calculate the error on the averaged night value we need to divide it by the square root of the number of independent nodding positions.
We can then compare three different estimators of the reached precision:
- the weighted dispersion of the night-averaged RV points - external dispersion;
- the error on the averaged night value, given by dispersion
on the nodding cycle RV values divided by
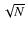 - intra-night dispersion;
- intra-night dispersion;
- the average photon error estimator value (as described
above) divided by
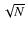 - photon noise.
- photon noise.
Table 4: The different RV precision indicators on the RV std, TW Hya, and Gl 86.
6 Discussion
In our previous work (Huélamo et al. 2008), we reached a precision of 35 m/s over a time span of roughly 1 week. This value was obtained in relative RV: science target - RV standard. This procedure allowed for a correction of the systematics still present in the data after our first reduction. Seifahrt & Käufl (2008), a contemporary study, reached a precision of 20 m/s on one night. A dedicated effort was made to track systematics and understand their possible causes. As a result we could now improve the analysis procedure to extract the RV in an optimized way, leading to a significant increase in precision. We no longer need to calculate relative RV to correct for systematics. The RV standard dispersion is now close to photon noise, showing that there are no systematics present down to 5-10 m/s. The same is valid for TW Hya and Gl 86 (O-C) residuals, which show a similar dispersion.
The RV standard displays a variation of less than 6 m/s (rms)
over 1 week. The probability that a dispersion of 5.77 m/s or
lower is obtained on 5 points belonging to a distribution with ![]() m/s
(the estimated photon noise) is 58.2%. If we consider 5 points drawn
from a distribution characterized by
m/s
(the estimated photon noise) is 58.2%. If we consider 5 points drawn
from a distribution characterized by ![]() m/s
(the measured internal dispersion), the probability then drops to
40.8%, but it is still high. We calculated the probability of drawing a
dispersion of 5.77 m/s from distributions with
m/s
(the measured internal dispersion), the probability then drops to
40.8%, but it is still high. We calculated the probability of drawing a
dispersion of 5.77 m/s from distributions with ![]() from 5 to 10 m/s. The results, presented in Table 5, show that we
cannot exclude that the intrinsic dispersion of our distribution is
slightly larger than the measured one. As a result we consider the
attained precision, in a conservative way, as being 6-8 m/s.
from 5 to 10 m/s. The results, presented in Table 5, show that we
cannot exclude that the intrinsic dispersion of our distribution is
slightly larger than the measured one. As a result we consider the
attained precision, in a conservative way, as being 6-8 m/s.
It is interesting to compare the values of intranight dispersion with photon-noise estimations, for the three targets. When measuring the intranight dispersion, one considers not only the photon noise but also the effect of systematic errors on RV. A straightforward example of such are the errors induced by nodding and locating the target at different positions in the slit, known to have two slit jaws that are not perfectly parallel. While the values are very similar for the RV standard and TW Hya, that is not the case for Gl 86. A possible cause is the use of a larger entrance slit, and the consequent introduction of additional sources of error, such as stellar photocenter variations.
The RV values for the standard and TW Hya are
compatible, within error bars, with the previously published values.
This is mostly caused by the comparatively large dispersion announced
previously (35 m/s) and error bars with even larger amplitude
(30-60 m/s). However, given the higher precision of the
measurements, a low-amplitude signal now emerges now from the noise. As
previously discussed in (Huélamo
et al. 2008), a lower amplitude signal in the IR
than in the optical is expected if a spot is responsible for the RV
variations instead of a planet. The previously presented tests stand as
well. One can calculate the orbit parameters from optical observations.
The probability that the IR RV points are drawn from this orbit by
adding an error comparable to the instrumental precision is below ![]() %, showing
that the spot theory prevails.
%, showing
that the spot theory prevails.
The RV determinations for Gl 86 match the orbit as
established by the announcement paper. It is important to stress that
for this fit the semi-amplitude, P, e,
and ![]() were fixed on the published values in Queloz et al. (2000).
This shows that our method yields the correct value for RV signals,
reproducing the bona-fide planet detected at optical wavelengths.
were fixed on the published values in Queloz et al. (2000).
This shows that our method yields the correct value for RV signals,
reproducing the bona-fide planet detected at optical wavelengths.
Given the very few points for both TW Hya and
Gl 86, the dispersion around the respective orbits should be
taken with caution. At this level the number of free parameters
approaches the number of points and the noise contribution is fitted as
well, leading to a ![]() .
As a representation of this, one can use the TW Hya data in a
slightly different way. One may use the RV values obtained for each
nodding position, with error bars given by the photon-noise estimation.
The fit delivers, within error bars, the same orbit parameters (K
and
.
As a representation of this, one can use the TW Hya data in a
slightly different way. One may use the RV values obtained for each
nodding position, with error bars given by the photon-noise estimation.
The fit delivers, within error bars, the same orbit parameters (K
and ![]() ), a
dispersion of the residuals of 35 m/s and a
), a
dispersion of the residuals of 35 m/s and a ![]() ,
showing that the error bars are underestimated by photon noise alone.
At this point our objective is merely to show that the RV points are
drawn from the orbits. They do not define the orbits and the dispersion
around the same is not representative of the true errors for so few
points.
,
showing that the error bars are underestimated by photon noise alone.
At this point our objective is merely to show that the RV points are
drawn from the orbits. They do not define the orbits and the dispersion
around the same is not representative of the true errors for so few
points.
A question that arises naturally is which factors limit the RV
precision delivered by this method? This is difficult to evaluate
mostly because the data set is small. However, on theoretical ground,
some educated guesses can be made. The precision on each of the
telluric lines central wavelength is not quantified on the HITRAN
database from which the values were drawn. The lines are merely flagged
as having a precision between 5 and 50 m/s. It is thus not surprising
that a precision of 5 m/s can be reached as a whole, but this might
become the limiting factor if one pushes the S/N
to much higher values. The eventual existence of a systematic
wavelength assignment error can also be a trivial source of error. On
the other hand, atmospheric phenomena such as localized jet streams may
imprint an RV on the reference lines themselves. However, its is hard
to evaluate how strong these effects are when we integrate along the
line of sight, up to the outer atmosphere. The conjugation of three
factors point to CO2 features as some of the
most stable in the atmospheric spectrum, though: 1) the abundance of CO2,
2) the constant volume mixing ratio of ![]() 300 ppmv up to 80 km, 3) the
low absorption line intensities. When taken together, these properties
reduce the impact of localized air mass movements on the RV. With the
current set of data, we can only evaluate the short-term stability of
the atmospheric lines. An extended data set with observations under
very different atmospheric conditions is now under evaluation. The
results will be the subject of a forthcoming paper (Figueira
et al., in prep.).
300 ppmv up to 80 km, 3) the
low absorption line intensities. When taken together, these properties
reduce the impact of localized air mass movements on the RV. With the
current set of data, we can only evaluate the short-term stability of
the atmospheric lines. An extended data set with observations under
very different atmospheric conditions is now under evaluation. The
results will be the subject of a forthcoming paper (Figueira
et al., in prep.).
Temperature and pressure changes are known to be one of the
main causes of spectrograph's IP variations. It is important to note
that CRIRES is cryogenic and thus stabilized in temperature. At the
time of writing, the thermal stability of the most important components
of the spectrograph is ![]() 0.05 K
for the prism, 0.2 K for the grating, and 0.3 K for
the Three-Mirror-Astigmat. As a consequence, the IP remains constant
and its impact on RV measurements is reduced. Another possible line
profile variation comes from atmospheric phenomena. The eventual
variations are seen by both our reference and target spectra. The
drawback is that this shows that typical bisector analysis cannot be
used in a straightforward way in stellar spectra, because one must
remove the effect of the variation of atmospheric lines' bisector
beforehand.
It is then not a surprise that the bisector shows no correlation with
the RV. Still, the low number of points and the possibility of
atmospheric profile variations makes this diagnosis very weak. The data
do not provide for a finer analysis, which is not within the scope of
this paper.
0.05 K
for the prism, 0.2 K for the grating, and 0.3 K for
the Three-Mirror-Astigmat. As a consequence, the IP remains constant
and its impact on RV measurements is reduced. Another possible line
profile variation comes from atmospheric phenomena. The eventual
variations are seen by both our reference and target spectra. The
drawback is that this shows that typical bisector analysis cannot be
used in a straightforward way in stellar spectra, because one must
remove the effect of the variation of atmospheric lines' bisector
beforehand.
It is then not a surprise that the bisector shows no correlation with
the RV. Still, the low number of points and the possibility of
atmospheric profile variations makes this diagnosis very weak. The data
do not provide for a finer analysis, which is not within the scope of
this paper.
Table 5: The probability of obtaining a dispersion of 5.77 m/s on a set of 5 points characterized by dispersions in the range 5-10 m/s.
The contribution of photocenter errors was negligible in our error budget, but that might not be the case if the seeing becomes very low, as experienced by Bouchy et al. (2005). However, our situation is fundamentally different, because our reference lines will be affected by these photocenter movements in the same way as the object lines. A simple way to reduce this effect is to use a fiber entrance, providing for an homogeneous illumination over a wide range of seeing conditions.
That PHOENIX-derived masks lead to a lower precision than masks derived from the data themselves is insightful on its own. It states that the line's position precision as calculated by state-of-the art models is lower than the one that can be measured from high S/N spectra. Some RV determination methods are more sensitive to this fact than others. In particular, those that obtain the RV by searching for a match between stellar models and observed spectra struggle against an additional and non-negligible source of noise.
While the application of gas cells on general-purpose slit spectrographs such as CRIRES is very tempting, their yielded precision still needs to be assessed. As already discussed by Mahadevan & Ge (2009), using the gas cell as a simultaneous reference superimposed on the stellar spectrum is limited by the definition of the stellar continuum. In the case of M stars, one of the main drivers for RV in the IR, the continuum is shaped by a dense forest of unresolved spectral lines. These features are convolved with the atmospheric transmission, which is variable through time. These factors together make RV determinations much more demanding, time, and photon-consuming and, in many cases, degenerated. In our particular approach, such a poor continuum definition would introduce systematic errors into the absorption lines wavelength assignment, which would propagate to the final calculated RV.
Several infrared spectrographs dedicated to RV measurements
are being designed, such as NAHUAL (Martín
et al. 2005) and SPIROU![]() .
These spectrographs aim at covering a wide spectral range
simultaneously from around 1 to 2.2
.
These spectrographs aim at covering a wide spectral range
simultaneously from around 1 to 2.2 ![]() m. If a gas cell on the main optical path is
chosen as the calibration procedure, the yielded precision will vary
locally as a function of stellar continuum definition and atmospheric
subtraction quality. On the other hand, using this gas cell on a twin
optical path with an homogeneous continuum source or other methods,
such as a laser coupled to a Fabry-Perot resonant cavity, allows a
simple avoidance of these problems. However, as discussed before, this
approach is only possible in a fiber-fed, stable spectrograph.
m. If a gas cell on the main optical path is
chosen as the calibration procedure, the yielded precision will vary
locally as a function of stellar continuum definition and atmospheric
subtraction quality. On the other hand, using this gas cell on a twin
optical path with an homogeneous continuum source or other methods,
such as a laser coupled to a Fabry-Perot resonant cavity, allows a
simple avoidance of these problems. However, as discussed before, this
approach is only possible in a fiber-fed, stable spectrograph.
7 Conclusions
We proved that RV measurements with a precision of 5-10 m/s are within reach of CRIRES, while using carefully selected atmospheric features as a wavelength reference. This precision was obtained on an RV standard, HD 108309, over a time span of roughly one week. TW Hya RV variation in the IR is not compatible with its optical counterpart, showing that a stellar spot is the best explanation for the observed RV variations. This confirms our previously published results (Huélamo et al. 2008) with better precision and consistency. We also showed that the RV variation of a star harboring a planet, Gl 86, is reproduced well by CRIRES data with a precision that is compatible with photon-noise estimations and at the same noise level.
Using the Earth's atmosphere as a free gas-cell still needs to be fully assessed, and the outcome of these studies will, in all probability, shape the design of future dedicated IR spectrographs. To do so, more lengthy data sets spanning a longer time-span are required. However, while this method seems promising and able to compete with regular gas-cells approaches, it is not yet been proved that higher precision is possible. Strong limitations might arise below 5 m/s steaming from sources such as the knowledge of the precise wavelength of telluric lines or their stability on long time scales.
AcknowledgementsP.F. would like to thank every researcher who contributed to the enthusiastic, fast-paced, and extremely friendly environments of both the Observatoire de Genève and ESO Santiago. This work was shaped by the passionate discussions it triggered. Support from the Fundação para Ciência e a Tecnologia (Portugal) to P.F. in the form of a scholarship (reference SFRH/BD/21502/2005) is gratefully acknowledged. N.C.S. would like to acknowledge the support by the European Research Council/European Community under the FP7 through a Starting Grant, as well as from Fundação para a Ciência e a Tecnologia (FCT), Portugal, through program Ciência 2007, and in the form of grants reference PTDC/CTE-AST/098528/2008 and PTDC/CTE-AST/098604/2008. We thank the ESO Director Office for granting DDT observations. We also thank the anonymous referee for his/her valuable suggestions on how to improve the manuscript.
References
- Bailey, J., Simpson, A., & Crisp, D. 2007, PASP, 119, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Balthasar, H., Thiele, U., & Woehl, H. 1982, A&A, 114, 357 [NASA ADS] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barman, T. S., Hauschildt, P. H., & Allard, F. 2005, ApJ, 632, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C. H., Charbonneau, D., White, R. J., Marley, M. S., & Saumon, D. 2007, ApJ, 666, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2004, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, ed. R. W. Hilditch, H. Hensberge, & K. Pavlovski, ASP Conf. Ser., 318, 286 [Google Scholar]
- Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Pont, F., Melo, C., et al. 2005, A&A, 431, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bretagnon, P., & Francou, G. 1988, A&A, 202, 309 [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Caccin, B., Cavallini, F., Ceppatelli, G., Righini, A., & Sambuco, A. M. 1985, A&A, 149, 357 [NASA ADS] [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, A., Udry, S., & Mayor, M. 2003, in Scientific Frontiers in Research on Extrasolar Planets, ed. D. Deming, & S. Seager, ASP Conf. Ser., 294, 43 [Google Scholar]
- Endl, M., Cochran, W. D., Wittenmyer, R. A., & Boss, A. P. 2008, ApJ, 673, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2005, A&A, 444, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A. P., Guenther, E. W., Endl, M., et al. 2005, A&A, 437, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, A. W., Johnson, J. A., Marcy, G. W., et al. 2009, ApJ, 696, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Huélamo, N., Figueira, P., Bonfils, X., et al. 2008, A&A, 489, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, in SPIE Conf. Ser. 5492, ed. A. F. M. Moorwood, & M. Iye, 1218 [Google Scholar]
- Livingston, W., & Wallace, L., 1991, An atlas of the solar spectrum in the infrared from 1850 to 9000 cm-1 (1.1 to 5.4 micrometer), ed. W. Livingston, & L. Wallace [Google Scholar]
- Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Mayor, M., Pepe, F., et al. 2006, Nature, 441, 305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mahadevan, S., & Ge, J. 2009, ApJ, 692, 1590 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, E. L., Guenther, E., Barrado y Navascués, D., et al. 2005, Astron. Nachr., 326, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, E. L., Guenther, E., Zapatero Osorio, M. R., Bouy, H., & Wainscoat, R. 2006, ApJ, 644, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Udry, S., Lovis, C., et al. 2009, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prato, L., Huerta, M., Johns-Krull, C. M., et al. 2008, ApJ, 687, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Rothman, L. S., Jacquemart, D., Barbe, A., et al. 2005, J. Quant. Spectrosc. Radiat. Transf., 96, 139 [Google Scholar]
- Sato, B., Toyota, E., Omiya, M., et al. 2008, PASJ, 60, 1317 [NASA ADS] [Google Scholar]
- Seifahrt, A., & Käufl, H. U. 2008, A&A, 491, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Setiawan, J., Henning, T., Launhardt, R., et al. 2008, Nature, 451, 38 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Setiawan, J., Weise, P., Henning, T., et al. 2007, ApJ, 660, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. A. 1982, ApJ, 253, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G. 2004, MNRAS, 353, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Udry, S., Zucker, S., et al. 2006, A&A, 449, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [Google Scholar]
- Wallace, L., Hinkle, K., & Livingston, W. C. 1993, An atlas of the photospheric spectrum from 8900 to 13600 cm-1 (7350 to 11230 [angstroms]), ed. L. Wallace, K. Hinkle, & W. C. Livingston [Google Scholar]
Footnotes
- ... CRIRES
![[*]](/icons/foot_motif.png)
- Based on observations taken at the VLT (Paranal), under programs 280.C-5064(A) and 60.A-9051(A), and with the CORALIE spectrograph at the Euler Swiss telescope (La Silla).
- ...
![[*]](/icons/foot_motif.png)
- Tables 2 and 3 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/511/A55
- ... overlapped
![[*]](/icons/foot_motif.png)
- Since May 2009, there are 282 standard wavelength setups available. The standard wavelength setups are designed to provide a complete coverage with no contamination by adjacent orders. In addition, users can select a free wavelength setting.
- ... CL
![[*]](/icons/foot_motif.png)
- IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
- ... target
![[*]](/icons/foot_motif.png)
- Note that the RV variations eventually induced by planets are about 100 m/s and thus much smaller than the line's FWHM. As a consequence, these small amplitude fluctuations can be ignored at this stage.
- ... SPIROU
![[*]](/icons/foot_motif.png)
- http://www.ast.obs-mip.fr/article.php3?id_article=637
All Tables
Table 1: The summary of the observation details on the RV std, TW Hya, and Gl 86, with all NDIT set to 1.
Table 2: The RV calculated per nodding position for the RV standard, HD 108309, and TW Hya, and estimated photon noise of each exposure.
Table 3: The RV per nodding position for Gl 86, and associated photon noise.
Table 4: The different RV precision indicators on the RV std, TW Hya, and Gl 86.
Table 5: The probability of obtaining a dispersion of 5.77 m/s on a set of 5 points characterized by dispersions in the range 5-10 m/s.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12681-fig1.eps}\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg12.png)
|
Figure 1:
Precision as a function of wavelength setting, in arbitrary units, as
described in Sect. 3.2 ( histogram, red in the electronic
version). Over-plotted is the squared root of the average
solar flux, as seen by CRIRES in a given wavelength setting, in
arbitrary units ( thick line, green in the electronic version).
All setting short-wards of 2.4 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12681-fig2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg13.png)
|
Figure 2: Atmospheric transmission at the chosen observing setting, for the detectors 1 (top), 2 (middle), and 4 (bottom). These spectra were obtained by co-adding and then normalizing the telluric standard exposures taken during the first night. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12681-fig3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg17.png)
|
Figure 3: Spectrum of RV standard, HD 108309, as seen on detector 1. These spectra are the result of the stacking and normalization of the 4 nodding spectra obtained during the first night. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.9cm,clip]{aa12681-fig4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg20.png)
|
Figure 4:
RV variation of the standard star (left) and
TW Hya (right) as a function of time. The
error bars are drawn from the dispersion of the N =
4 nodding positions, divided by 2 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa12681-fig5.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12681-09/Timg21.png)
|
Figure 5:
Phase-folded plot of Gl 86 Rv measurements. The error bars
presented are drawn from the dispersion of the six nodding positions,
divided by |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


