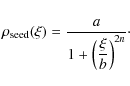| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 19 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200912008 | |
| Published online | 05 February 2010 | |
Non-parametric deprojection of surface brightness profiles of galaxies in generalised geometries
D. Chakrabarty
School of Physics & Astronomy, University of Nottingham, Nottingham NG7 2RD, UK
Received 9 March 2009 / Accepted 12 November 2009
Abstract
Aims. We present a new Bayesian non-parametric deprojection
algorithm DOPING (Deprojection of Observed Photometry using an INverse
Gambit), that is designed to extract 3-D luminosity density
distributions ![]() from observed surface brightness maps I,
in generalised geometries, while taking into account changes in
intrinsic shape with radius, using a penalised likelihood approach and
an Markov Chain Monte Carlo optimiser.
from observed surface brightness maps I,
in generalised geometries, while taking into account changes in
intrinsic shape with radius, using a penalised likelihood approach and
an Markov Chain Monte Carlo optimiser.
Methods. We provide the most likely solution to the integral equation that represents deprojection of the measured I to ![]() .
In order to keep the solution modular, we choose to express
.
In order to keep the solution modular, we choose to express ![]() as a function of the line-of-sight (LOS) coordinate z. We calculate the extent of the system along the z-axis,
for a given point on the image that lies within an identified isophotal
annulus. The extent along the LOS is binned and density is held a
constant over each such z-bin. The code begins with a seed density and at the beginning of an iterative step, the trial
as a function of the line-of-sight (LOS) coordinate z. We calculate the extent of the system along the z-axis,
for a given point on the image that lies within an identified isophotal
annulus. The extent along the LOS is binned and density is held a
constant over each such z-bin. The code begins with a seed density and at the beginning of an iterative step, the trial ![]() is updated. Comparison of the projection of the current choice of
is updated. Comparison of the projection of the current choice of ![]() and the observed I
defines the likelihood function (which is supplemented by Laplacian
regularisation), the maximal region of which is sought by the optimiser
(Metropolis Hastings).
and the observed I
defines the likelihood function (which is supplemented by Laplacian
regularisation), the maximal region of which is sought by the optimiser
(Metropolis Hastings).
Results. The algorithm is successfully tested on a set of test
galaxies, the morphology of which ranges from an elliptical galaxy with
varying eccentricity to an infinitesimally thin disk galaxy marked by
an abruptly varying eccentricity profile. Applications are made to
faint dwarf elliptical galaxy Ic 3019 and another dwarf elliptical
that is characterised by a central spheroidal nuclear component
superimposed upon a more extended flattened component. The result of
deprojection of the X-ray image of cluster A1413 - assumed triaxial -
the axial ratios and inclination of which are taken from the
literature, is also presented.
Key words: methods: statistical - galaxies: fundamental parameters
1 Introduction
An integral step in the construction of dynamical models of galaxies
is the recovery of the intrinsic luminosity density from the surface
brightness that is observed projected on the plane of the sky
(Krajnovic et al. 2004; Magorrian et al. 1998; Kronawitter et al. 2000). Such deprojection is
non-trivial and indeed offers no unique solutions except for very
specific configurations of geometry and inclination. As demonstrated
by Rybicki (1987), the deprojection is degenerate for axisymmetric
systems viewed at inclination angles, i, other than edge-on
(i=90![]() ). This is a consequence of the fact that the observed
surface brightness cannot yield any information on a density term
whose Fourier transform is non-zero only within a cone of half angle
). This is a consequence of the fact that the observed
surface brightness cannot yield any information on a density term
whose Fourier transform is non-zero only within a cone of half angle
![]() (the ``cone of ignorance''). Gerhard & Binney (1996)
report a family of analytical konus densities. Kochanek & Rybicki (1996)
found a family of konus densities that have arbitrary densities in the
equatorial plane. van den Bosch (1997) finds that konus densities
contribute at most a few percent of the total galactic mass to the
centre of elliptical galaxies with nuclear cusps, implying that their
dynamical influence is minimal. Magorrian (1999) suggests that nearly
face-on disk-like konus densities can be recognised via the unique
signature they imprint on the line-of-sight (LOS) velocity profiles.
(the ``cone of ignorance''). Gerhard & Binney (1996)
report a family of analytical konus densities. Kochanek & Rybicki (1996)
found a family of konus densities that have arbitrary densities in the
equatorial plane. van den Bosch (1997) finds that konus densities
contribute at most a few percent of the total galactic mass to the
centre of elliptical galaxies with nuclear cusps, implying that their
dynamical influence is minimal. Magorrian (1999) suggests that nearly
face-on disk-like konus densities can be recognised via the unique
signature they imprint on the line-of-sight (LOS) velocity profiles.
These problems notwithstanding, a great deal of effort has been put into the development of methodologies aimed at deprojecting two-dimensional photometric information. These include parametric formalisms designed by Palmer (1994), Bendinelli (1991) and Cappellari (2002), as well as non-parametric methods, such as the Richardson-Lucy Inversion scheme (Lucy 1974; Richardson 1972) and a method by Romanowsky & Kochanek (1997) (hereafter, RK).
The parametric methods work by making series expansions of the density
(or brightness) and fit the brightness (or density) to the coefficient
of the expansions; convergence is defined at a preset accuracy level.
In Bendinelli (1991), the density is derived via a Gaussian expansion
of the surface brightness profile, an idea further developed by
Cappellari (2002). In Palmer (1994), the density is expanded in terms
of angular polynomials and the projections of these are then fit to
the surface brightness. These methods suffer from the basic drawback
that the answer depends on the choice of the basis functions. Thus,
the solution is forced to conform to a subset of all possible
solutions. Even more worrisome is the fact that the validity of the
goodness of fit measures, or ``![]() quantities'' that are employed
in these schemes to identify acceptable fits, is questionable,
particularly in the presence of inhomogeneous noise
(Bissantz & Munk 2001). On the whole, the fitting of non-linear
functions, to what is usually noise-ridden incomplete data, over large
dynamical ranges, is worrisome.
quantities'' that are employed
in these schemes to identify acceptable fits, is questionable,
particularly in the presence of inhomogeneous noise
(Bissantz & Munk 2001). On the whole, the fitting of non-linear
functions, to what is usually noise-ridden incomplete data, over large
dynamical ranges, is worrisome.
Deprojection of surface brightness profiles has also been attempted with the Abel integral equation, under the assumption of sphericity or axisymmetry with an edge-on inclination (Gebhardt et al. 1996; Merritt & Tremblay 1993; Merritt et al. 1997).
An example of a non-parametric inversion scheme is the Richardson-Lucy algorithm (Lucy 1974; Richardson 1972), which has been widely used in the stellar dynamical context. It is a simple deprojection scheme that works by iterating toward increasingly better approximations to the density that fits the data. However, absolute convergence is not sought in this framework - rather, the iterations are stopped when the density is judged to be a good fit to the observations. In lieu of this imposed clause in the code, progressive iterations would produce increasingly more unphysical densities. This lack of a robust convergence criterion is cause for dissatisfaction with the Richardson Lucy scheme. Moreover, implementations of the same, within Astronomy, have not incorporated either radial variations of intrinsic shape or deviations from sphericity.
The shortcomings of Lucy's algorithm are overcome by the analysis of RK in their incorporation of monotonicity and positivity into the sought solution and by their more satisfying convergence criterion. RK construct their density profile as a series of stacked blocks in the space of one quadrant of the meridional plane of their axisymmetric (by assumption) galaxy. The density values at radially adjacent locations are connected through linear interpolation. The summation of the projections of each of the density blocks along the LOS, give the surface brightness at a given location in the plane of the sky (where a brightness measurement is reported). This estimated brightness is then compared to the observed brightness; the algorithm attempts to minimise this statistic while imposing the smoothing condition through a bias function, thus providing a more satisfying convergence criterion than included in Lucy's algorithm. However, this scheme too fails to allow for deprojection in general triaxial geometries; specifically, it is designed to reproduce axisymmetric systems. Moreover, the validity of interpolation, in systems where local gradients can be steep, is also worrisome.
Magorrian (1999) also advances a scheme similar to RK's expect that he implements a penalty function in his definition of likelihood. The imposed penalty is achieves nearest-neighbour smoothing. The fundamental shortcomings of this scheme are the same as what plagues RK's method. There is no apriori reason to belive that the galaxy under consideration is axisymmetric; triaxiality is a much more general model. Moreover, the requirement in this work, for density to behave like a power-law on local scales, implies that the method will fail in the presence of even moderate gradients in density; in this sense, the recovered answer could be sensitive to the binning details of the 2D grid on which the density structure is placed.
In this paper, we present a new, Bayesian non-parametric algorithm that implements an Markov Chain Monte Carlo (MCMC) optimiser, in order to tackle the deprojection of observed photometry of galaxies. Completely free-form solutions for the 3D density are provided with the constraint of positivity imposed by hand. The scheme is a penalised likelihood procedure. We refer to this algorithm as DOPING - an acronym for Deprojection of Observed Photometry using an INverse Gambit. The algorithm is easy to implement and each run typically takes a few minutes on a state-of-the art personal computer.
The most distinguishing feature of DOPING is that it can tackle
deprojection in virtually any geometry, as long as we can express
the intrinsic shape parameters (such as eccentricities) in analytical
relations with the projected shape parameters. DOPING can be applied to
deproject surface brightness maps of elliptical as well as disk
galaxies. This is possible, while taking intrinsic shape variation
into account![]() .
.
The first major application of this algorithm to galaxies (Chakrabarty & McCall 2009) is the study of the deprojected luminosity profiles of 100 early type galaxies observed as part of the ACS Virgo Cluster Survey (Côté et al. 2004). As these systems do not exhibit significant variations in position angle, the preliminary version of DOPING that is presented here, considers position angle to be a constant. However the code can account for changes in position angle and the skeletal scheme for the inclusion of a radially varying position angle is presented later in Sect. 5.6.
The following section begins with a discussion of the broad framework of our algorithm DOPING, a moves to an exposition of the technical details of the code in Sect. 2. In Sect. 3, we talk about the application of DOPING to a test case and corroborate the robustness of the algorithm. Application to the real ACS photometry of the galaxy vcc9 is also discussed in Sect. 4. Section 3 explores the effects of varying ambient conditions such as inclination and the assumed geometry. Section 5 is devoted to discussions and conclusions that are to be drawn from the work. In the appendix, a discussion of the details of various aspects of DOPING is presented.
2 Overview of the algorithm
DOPING is a code designed to perform 3-D modelling of systems, given their 2-D images, in a variety of spatial geometries. We iterate over trial 3-D luminosity density structures till the best match between the projection of the same and the measured 2-D surface brightness is obtained. Since deprojection is non-unique unless the intrinsic spatial geometry of the system is pinned down, we begin this section with a discussion on the motivation and details of how the detailed description of the geometry is achieved.
In particular, the true shape and inclination of a system can be deciphered, using DOPING, if:
- the system has a regular geometry, (by which we imply that it bears an m-fold symmetry) and;
- the relative extent of the system along any three mutually orthogonal axes are known,
- the system can be viewed at multiple inclinations, i.e. the inclination to the LOS can be varied at will, in which case;
- DOPING can perform in irregular geometries also.
In fact, for galaxy clusters, when SZe measurements are available, it is possible to measure the extent along all three observer coordinate-axes (two axes on the plane of the image and a third along the LOS). Thus, the true intrinsic shape and orientation of galaxy clusters can be predicted by inverting the X-ray surface brightness map at benchmark deprojection geometries (Chakrabarty et al. 2008), under the assumption that one photometric axis is coincident with a principle axis of the system. Thus, the luminosity density of galaxy clusters can be uniquely determined. An example of this is discussed in Sect. 4.2.
However, for triaxial galaxies, the LOS extent is unknown; thus, for galaxies, the true 3-D shape and orientation cannot be deciphered in principle. Therefore, for galaxies, we need to assume values for the polar inclination and the missing axial ratio. The recovery of the 3-D luminosity density is undertaken, given these assumptions. Also, in this work, we hold the azimuthal inclination zero.
It merits mention that our assumptions are not over-indulgent. Any deprojection invokes assumptions about the intrinsic geometry and inclinations of the system. Thus, when axisymmetry is assumed, it implies that one of the intrinsic axial ratios is held as unity, the polar inclination is also assumed and the azimuthal inclination is set to zero. This is similar to DOPING in that the user needs to assume one inclination and one intrinsic axial ratio for galaxies. However, when greater observational information is available, as for galaxy clusters, DOPING does not need to invoke any assumptions, in contrary to axisymmetry-assuming algorithms.
The assumptions are designed to be given as inputs for a given run of DOPING (Sects. 2.1 to 2.10). Given that each run of DOPING takes a few minutes on a 3.2 GHz CPU processor, when started from a judicious initial guess for the density, it is possible to scan over a wide range of inclination and axial ratio values to record a range of corresponding 3-D density distributions. The justification of assumptions is discussed in details in Sects. 5.5 and 5.3.
In order to design a recursive algorithm that can perform deprojection in varied geometries, the trial 3-D density structure should preferably not be treated as function of a coordinate that characterises the geometry at hand. Instead, we need to express the 3-D density as function of generic coordinates. However, a mapping between such generic coordinates and the system geometry is then required. This is what we aim for (Sect. 2.5). In fact, we express this mapping by calculating the extent of the system along the LOS, through any given point on the image. Such a calculation invokes values of all available shape and size related parameters - this is discussed in Sect. 2.5.
Once this is established, we then discuss (Sect. 2.11) details of how to iterate towards the best possible 3-D density structure that projects to the observed surface brightness map.
2.1 Coordinates used
In any kind of deprojection problem, the two coordinate systems that
suggest themselves readily are the body coordinate frame (X,Y,Z)
and the observer's coordinate frame (x,y,z). Here the three
principal axes of the ellipsoidal system are considered to be along
the
![]() vectors. The LOS
coordinate is z while the plane of the image is considered scanned
by the x-y coordinates, i.e the image plane is given by the
equation z = 0. The Z-axis is considered to be at an inclination
angle i relative to the line-of-sight, i.e. the z-axis.
vectors. The LOS
coordinate is z while the plane of the image is considered scanned
by the x-y coordinates, i.e the image plane is given by the
equation z = 0. The Z-axis is considered to be at an inclination
angle i relative to the line-of-sight, i.e. the z-axis.
The X,Y,Z and x,y,z coordinate systems will be related by two
consecutive rotations. For triaxial galaxies, neither of these
rotational angles is an observable in general. Only when the galaxy
is highly flattened, can the inclination of its rotational axis to
the LOS be estimated. The general lack of information about
inclinations in triaxial systems will need to be compensated for by
assumptions - while the assumed value of one inclination angle is
provided as an input to the algorithm, the choice of the other
inclination angle in this unconstrained situation is chosen to be
such that our calculations are rendered easy: we assume that one of
the principle axes lies entirely in the plane of the image. In fact,
we choose this to be the X-axis. Then, the X-axis is also a
photometric axis. We align our observer coordinate system such that
the x-axis lies along the X-axis, i.e.
![]() .
Then,
.
Then,
![]() is along the photometric major axis for an
oblate system but along the photometric minor axis in case of a
prolate system. If the system in hand is triaxial, then there exists
a scope for a degeneracy, depending on whether the x-axis is
considered the major or minor axis. When the input for the assumed
value of one inclination is i, the equations relating the
(X,Y,Z) system of coordinates to the (x,y,z) system are:
is along the photometric major axis for an
oblate system but along the photometric minor axis in case of a
prolate system. If the system in hand is triaxial, then there exists
a scope for a degeneracy, depending on whether the x-axis is
considered the major or minor axis. When the input for the assumed
value of one inclination is i, the equations relating the
(X,Y,Z) system of coordinates to the (x,y,z) system are:
Thus, all 3-D density distributions that are recovered by DOPING are obtained under the assumption that the azimuthal inclination is zero. The algorithm can in principle, also work for a choice of non-zero azimuthal inclinations; a range of 3-D density distributions for a range of choices of this angle is achievable. However, in lieu of measured information, the specification of such a range is impossible. This is discussed in detail in Sect. 5.3.
2.2 Input data
The image or the projection of the galaxy on the plane of the sky is
treated as built of concentric isophotes. Let the image be built of
![]() number of isophotes and the isophotal annulus between the
k-1th and kth isophotes be the kth isophotal annulus.
Here,
number of isophotes and the isophotal annulus between the
k-1th and kth isophotes be the kth isophotal annulus.
Here,
![]() .
.
The observables that DOPING processes are the characteristics of the isophotes, namely, the surface brightness measurement and the shape parameters of a given isophote, along with the value of its extent along the photometric x-axis, i.e. in effect, the surface brightness map of the galaxy. Several routines are available for the production of such a data set; such as the IRAF implementation of the task ELLIPSE (Jedrzejewski et al. 1987).
If the isophotal shape characteristics vary over the extent of the
image, then it is possible to flag their values according to the
isophotal annulus that they are observed in; thus, the projected axial
ratio in the kth isophotal annulus is qpk and the semi-x axis extent of the kth isophote is ak. Thus, the input data
table in our work presents: an index for the isophotal annulus or k,
the semi-x axis ak, projected axial ratio qpk and brightness
values
![]() ,
for each k
i.e. each isophotal annulus that the image is binned into. Now, the
isophotes of elliptical galaxies are
often seen to deviate from pure ellipses (e.g. Bender et al. 1988;
van den Bosch et al. 1994; Ferrarese et al. 2006).
Hence, the boxiness/diskiness parameters can also be included in the
table. To keep the introduction of the algorithm simple, in the
following discussion, we ignore the contribution of these deviations
from the purely elliptical shape, knowing that these effects can be
included easily into the isophotal equation as suggested by
Jedrzejewski (1987). Even more severe deviations from the elliptical
isophotal shape can be accommodated and these cases (that do not bear a
strong
relevance in astrophysics) are discussed later in Sect. 5.1. The
representation of isophotes within DOPING is further discussed in
Appendix A.
,
for each k
i.e. each isophotal annulus that the image is binned into. Now, the
isophotes of elliptical galaxies are
often seen to deviate from pure ellipses (e.g. Bender et al. 1988;
van den Bosch et al. 1994; Ferrarese et al. 2006).
Hence, the boxiness/diskiness parameters can also be included in the
table. To keep the introduction of the algorithm simple, in the
following discussion, we ignore the contribution of these deviations
from the purely elliptical shape, knowing that these effects can be
included easily into the isophotal equation as suggested by
Jedrzejewski (1987). Even more severe deviations from the elliptical
isophotal shape can be accommodated and these cases (that do not bear a
strong
relevance in astrophysics) are discussed later in Sect. 5.1. The
representation of isophotes within DOPING is further discussed in
Appendix A.
In the applications of the code discussed in this paper, the position angle of the isophotal semi-major axis is assumed constant, though scope exists within the algorithm to relax this. The overall scheme for such a relaxation is discussed later in Sect. 5.6 though the incorporation of the same being non-trivial, this will be presented within DOPING in a future contribution.
2.3 Bayesian formulation
We seek the 3D luminosity density ![]() of the system, given the surface
brightness (surface brightness) maps as the input measurements. The probability of spotting the density
of the system, given the surface
brightness (surface brightness) maps as the input measurements. The probability of spotting the density ![]() ,
given the measurements, and all our background knowledge (assumptions) about the system (K) is:
,
given the measurements, and all our background knowledge (assumptions) about the system (K) is:
| (2) |
This is the Bayesian statement of the problem. The first term on the right side of the proportional sign is the likelihood while the second term is the prior.
In general, the prior that we can use is a uniform one:
| |
= | ||
| = | (3) |
by which we imply that the prior probability is unity only if
However, it is possible that for disk galaxies, i can be established
from observations. Thus, if the inclination is given as:
![]() ,
then assuming Gaussian errors, our prior will have
an additional factor that is proportional to
,
then assuming Gaussian errors, our prior will have
an additional factor that is proportional to
![]() .
.
2.4 Methodology
A prescribed system geometry would imply that the coordinates x, y and z are related in terms of the shape parameters, i.e. z can be expressed in terms of x and y. For example, under the assumption of triaxiality, an analytical relation links the x and y to the z as x,y, z is a point on the surface of a homeoid; this relation takes into account the local values of the inclinations and intrinsic axial ratios of the system.
We attempt to express the 3-D density at a point as function of the coordinates on the image plane (i.e. x and y) and the LOS coordinate (z) for that point. However, As x and y are coordinates on the image plane, they can be measured while z can be calculated for a given x-y pair, from the aforementioned relation between x, y and z. Once z is established, a trial 3-D density can be integrated along the LOS, over this established range of z values, and the projection compared to the value of surface brightness observed at the point (x, y, 0). However, for the aforementioned relation to be completely specified, the system geometry needs to be invoked. Here we describe how such a relation is specified in the astrophysical context.
For the deprojection of galactic surface brightness maps, if the galaxy is considered a single-component system, we assume the galaxy to be a triaxial ellipsoid. For multi-component galaxies, such as systems with a central component superimposed on an extended disky component, each component is typically ascribed a triaxial ellipsoidal geometry (Chakrabarty & McCall, in preparation). Isolated off-centred clumps can also be included in the modelling (see Sect. 4.3).
When the galaxy is modelled as triaxial, the details of system
geometry are described in Appendix B. The crux of the matter is that
to compensate for our ignorance about the two inclinations and one of
the two projected axial ratios (qp and
![]() )
of an observed
galaxy, we assume a value for one inclination i, set the other
inclination (angle between X and x-axis) to zero,
assume a value for one intrinsic axial ratio q1 and calculate the
other intrinsic axial ratio q2 from the relation that connects
q2 to q1, qp and i.
The assumptions made to facilitate deprojection under triaxiality are
similar in number with those made when deprojection under axisymmetry
is performed (see Sects. 2 and 5.5), although, for
deprojection of galaxy clusters, DOPING does not need to make such
assumptions (Chakrabarty et al. 2008). Importantly, the
range of 3-D luminosity density distributions recovered for various
assumptions, can be gauged with DOPING.
)
of an observed
galaxy, we assume a value for one inclination i, set the other
inclination (angle between X and x-axis) to zero,
assume a value for one intrinsic axial ratio q1 and calculate the
other intrinsic axial ratio q2 from the relation that connects
q2 to q1, qp and i.
The assumptions made to facilitate deprojection under triaxiality are
similar in number with those made when deprojection under axisymmetry
is performed (see Sects. 2 and 5.5), although, for
deprojection of galaxy clusters, DOPING does not need to make such
assumptions (Chakrabarty et al. 2008). Importantly, the
range of 3-D luminosity density distributions recovered for various
assumptions, can be gauged with DOPING.
The axial ratios mentioned above can all vary with distance away from system centre. Thus, the assumed axial ratio (q1) can be described as any real function of x (as long as the function is non-singular over the range covered in the measurements).
2.5 Mapping the LOS extent to the system geometry
As said before, our aimed deprojection requires evaluation of the characteristic extent along the z-axis of a point on the image plane. To accomplish this, we need to remind ourselves of all the relevant image characteristics of the given point on the image plane; this includes the surface brightness at this point, the local value of projected axial ratio at this point, etc. The determination of the z-height of a point on the image plane is discussed below and graphically represented in Fig.1.
![\begin{figure}
\par\includegraphics[width=8cm, angle=0]{12008fg1.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg38.png)
|
Figure 1:
Geometrical considerations adopted in the
design of the algorithm. The system is represented as the
ellipsoid. The X, Y and Z axes (in thin black lines)
represent the three principle axes of the system while x and y mark the photometric axes and the z-axis is the LOS (in thicker
black lines). A rectangular section of the image plane (i.e. the
z = 0 plane) is represented by the tilted rectangle in the broken
lines; this plane cuts the ellipsoid in an elliptical disk which
is depicted by the translucent gray disk. Generic isophotal
annuli on this disk are depicted in centrally increasing
gray-scale intensity. Two generic points, lying inside the
intermediate isophotal annulus, are shown as the two black
squares. The extent of the system along the positive z-axis, at
these two marked points are represented by the lengths of the
white rectangles that are oriented parallel to the LOS. In the
text, one such point, generically considered to be inside the
kth isophotal annulus, is referred to as
(xjk, yjk, 0),
while the tip of the white rectangle emanating from this point is
ascribed coordinates
|
| Open with DEXTER | |
We put the system on a regular 3-D Cartesian x-y-z grid. We flag
grid points that lie on the image i.e. the z = 0 plane, according to the
isophotal annulus that they lie in. We refer to the jth point inside the
kth isophotal annulus as
(xjk, yjk, 0). Here
![]() ,
where Nk is the number of grid
points with z = 0, inside the kth isophotal annulus.
,
where Nk is the number of grid
points with z = 0, inside the kth isophotal annulus.
Through the point
(xjk, yjk, 0), let the system extend along the
z-axis, (i.e. the LOS), from
![]() to
to
![]() .
To determine
.
To determine
![]() and
and
![]() ,
we pass a thin triaxial ellipsoidal shell through
,
we pass a thin triaxial ellipsoidal shell through
![]() and
and
![]() .
This ellipsoidal shell
.
This ellipsoidal shell
- 1.
- is centred at (0,0,0),
- 2.
- projects at the assumed inclination i, to the kth elliptical annulus on the image, which in turn has an axial ratio of
qpk and semi-axis ak along
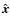 .
.
- 3.
- has intrinsic axial ratios q1k and q2k.
- 4.
- has the points
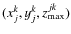 and
and
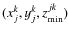 on it, of which the x and y coordinates are
known grid points but
on it, of which the x and y coordinates are
known grid points but
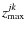 and
and
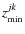 are
undetermined.
are
undetermined.
- its extent along a principal axis - the extent along the x-axis, i.e. X-axis is known (=ak).
- the angle between the Z-axis and the LOS - i is known by assumption.
- its intrinsic axial ratios q1k and q2k. In the
absence of measured
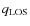 ,
q1k is known by assumption.
q2k is derived as follows.
,
q1k is known by assumption.
q2k is derived as follows.
This relation gives q2k (see Chakrabarty et al. 2008). In this way, we constrain all parameters that define the ellipsoidal shell that passes through the points
Here q1k, q2k, ak and i are all known. xkj and ykj are known since the point xkj, ykj, 0 has been identified to lie inside the kth isophotal annulus. Thus, this quadratic equation is solved for z and its two solutions are
In this way, the extent of the system, along the z-axis, through any point on the 2-D image is determined. A schematic of this procedure is presented in Fig. 1. We now continue with the nomenclature introduced in this section, to describe generic points lying inside generic isophotal annuli.
2.6 z-histograms
In order to keep the formalism flexible, we seek a form of the 3-D density in terms of z.
Thus, we discretise the density structure
![]() where
where
![]() ,
,
![]() .
Actually,
in our work, we bin the range
.
Actually,
in our work, we bin the range
![]() ,
and find the
luminosity density
,
and find the
luminosity density
![]() for only one half of the system (at
positive z only). The density for the other half is given using
the symmetry argument
for only one half of the system (at
positive z only). The density for the other half is given using
the symmetry argument
![]() ,
which is valid
under the assumption of triaxial geometry. In other words, we invert
the projection integral
,
which is valid
under the assumption of triaxial geometry. In other words, we invert
the projection integral
![]() instead of
instead of
![]() .
.
We do this by binning the z-range between
![]() and
and
![]() .
The binning is logarithmic since the
measurements of surface brightness values are typically obtained for
an astronomical system at increasingly wider isophotal
annuli.
.
The binning is logarithmic since the
measurements of surface brightness values are typically obtained for
an astronomical system at increasingly wider isophotal
annuli.
![]() is held a constant over each
z-bin. Thus, the density structure along the z-axis, through the
point
(xjk, yjk, 0) on the image, looks like a 1-D histogram. We refer to this construction as the
is held a constant over each
z-bin. Thus, the density structure along the z-axis, through the
point
(xjk, yjk, 0) on the image, looks like a 1-D histogram. We refer to this construction as the ![]() -histogram, corresponding to the
point
(xjk, yjk, 0). The z-range of a
-histogram, corresponding to the
point
(xjk, yjk, 0). The z-range of a ![]() -histogram spans
the interval:
-histogram spans
the interval:
![]() and
and
![]() .
Thus, this z-range
depends on the point on the image through which the
.
Thus, this z-range
depends on the point on the image through which the ![]() -histogram is
constructed.
-histogram is
constructed.
2.7 Why 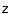 -histograms instead of
-histograms instead of 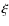 -histograms
-histograms
We choose the basis of ![]() to be z instead of a function of the
system shape such as the ellipsoidal radius
to be z instead of a function of the
system shape such as the ellipsoidal radius ![]() .
Reliance of the
deprojection of the observed surface brightness map on the intrinsic
shape would curb the reach of the algorithm in the following two ways:
.
Reliance of the
deprojection of the observed surface brightness map on the intrinsic
shape would curb the reach of the algorithm in the following two ways:
- systems with different geometries that cannot be ascribed a general triaxial shape cannot then be tracked by the same code. An example of such a system within the astrophysical context could be a galaxy that is better described by a cylindrical intrinsic shape, such as the LMC. surface brightness of such a galaxy can however be deprojected under the flexible DOPING, with minimal changes imposed on the algorithm. In this non-triaxial geometry, the calculation of the intrinsic axial ratios from the measured projected axial ratios (and hence the calculation of the z-height of any point on the image) is different from the triaxial case; these calculations are performed within a modular sub-routine, before the iterations begin. The rest of the algorithm (iterative search for the most likely density structure) is unaffected by the difference in the system geometry. Thus, the same code can be used to undertake deprojection in general geometries.
- luminosity density distributions of systems with imposed substructure or extra galactic components that are imposed on the background galactic structure (such as disk+bulge systems) cannot be obtained in a single-step, integrated fashion if the algorithm is designed exclusively within the geometry of the background structure.
- the determination of the z-height of a given point on the image plane. This value robustly reflects the intrinsic geometry of deprojection.
- penalising all solutions for
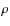 that do not adhere to a form
in which there is maximum variance between densities that are at
different ellipsoidal radii but minimum variance between densities
at the same
that do not adhere to a form
in which there is maximum variance between densities that are at
different ellipsoidal radii but minimum variance between densities
at the same 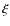 .
This characteristic can be incorporated by
introducing a penalty function that is proportional to the Laplacian
of the current choice of
.
This characteristic can be incorporated by
introducing a penalty function that is proportional to the Laplacian
of the current choice of 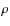 ,
where the Laplacian operator
involves differentiation w.r.t.
,
where the Laplacian operator
involves differentiation w.r.t. 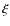 .
This is discussed in detail in
the following subsection.
.
This is discussed in detail in
the following subsection.
2.8 Laplacian regularisation
We understand that the sought solution for
![]() ,
as given
by the assembly of z-histograms, is in need of regularisation. We
choose to introduce this regularisation such that we achieve
low-dimensional representation of higher-dimensional information. In
particular, we are interested to recover density that is a function
of
,
as given
by the assembly of z-histograms, is in need of regularisation. We
choose to introduce this regularisation such that we achieve
low-dimensional representation of higher-dimensional information. In
particular, we are interested to recover density that is a function
of ![]() ,
i.e. we work with a penalty function that reflects the
intrinsic geometric structure of the input space (Wang 2006; Haykin 2008)
,
i.e. we work with a penalty function that reflects the
intrinsic geometric structure of the input space (Wang 2006; Haykin 2008) ![]() .
.
Such sought, similarity based smoothing is ensured by adopting a
penalty function ![]() that is given in terms of the Laplacian
of the object function:
that is given in terms of the Laplacian
of the object function:
Here
2.9 Density structure
DOPING works recursively, via an inverse approach. At every iterative
step, a trial ![]() -histogram is chosen for each grid point on the
image, i.e. for a given j, k. Each such
-histogram is chosen for each grid point on the
image, i.e. for a given j, k. Each such ![]() -histogram is
updated independently during an iterative step, to render the whole
3-D density structure of the galaxy updated. Such updating of the
-histogram is
updated independently during an iterative step, to render the whole
3-D density structure of the galaxy updated. Such updating of the
![]() -histogram is done while maintaining positivity of
-histogram is done while maintaining positivity of ![]() .
.
Once updated, the density structure is projected on the z = 0 plane and this projection is compared to the surface brightness data. This comparison defines the likelihood function which is maximised for the best match. The likelihood is supplemented with a penalty that was discussed in the last paragraph. The global maxima of the likelihood function is sought by our MCMC algorithm to yield the most likely density structure, given the surface brightness data. However, we choose only those solutions which are ``smooth'', as dictated by the used regularisation scheme.
2.10 Likelihood
The probability of the data given the model - i.e. the observed surface brightness map, given a trial 3-D density - is expected to be normal. This is reinforced on the basis of the following.
The likelihood or the probability of a measured surface
brightness map, given a choice of the 3-D density structure, has to
be a function of the distance between the projection of the 3-D
density on the image plane and the measured surface brightness. In
particular,
![]() ,
is such that when the
projection of
,
is such that when the
projection of
![]() on the image plane is concurrent with
the measured surface brightness distribution,
on the image plane is concurrent with
the measured surface brightness distribution,
![]() .
Additionally, the further is
.
Additionally, the further is
![]() from the surface brightness
measurement
from the surface brightness
measurement
![]() in the kth isophotal annulus, the
smaller is the likelihood; in fact, for
in the kth isophotal annulus, the
smaller is the likelihood; in fact, for
![]() ,
,
![]() .
Since the likelihood is a function of the
absolute distance between
.
Since the likelihood is a function of the
absolute distance between
![]() and
and
![]() ,
(for any k), for two different 3-D densities
,
(for any k), for two different 3-D densities
![]() and
and
![]() ,
if
,
if
![]() ,
it implies that
,
it implies that
![]() ,
i.e. the likelihood is symmetric about
,
i.e. the likelihood is symmetric about
![]() .
Also, for two different surface brightness measurements,
.
Also, for two different surface brightness measurements,
![]() and
and
![]() ,
if the likelihood corresponds to the
same value of
,
if the likelihood corresponds to the
same value of
![]() ,
it implies that
,
it implies that
![]() .
Given these to be the only
constraints on our choice of the likelihood
.
Given these to be the only
constraints on our choice of the likelihood ![]() ,
it is
sufficient to consider the distribution
,
it is
sufficient to consider the distribution
![]() to be normal - proportional to a Gaussian of the form
to be normal - proportional to a Gaussian of the form
![]() ,
where the denominator in the exponential is a scale that is invoked to
ensure a dimensionless term; the measurement offers a ready
scale. In, details, the
,
where the denominator in the exponential is a scale that is invoked to
ensure a dimensionless term; the measurement offers a ready
scale. In, details, the ![]() likelihood is
likelihood is
where Nk is the number of
| |
= | 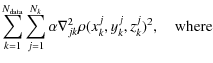
|
|
| (8) |
Here ( xkj, ykj, zkj) is a point at which a value of the density is defined and
2.11 Interval estimation of 3-D density
We choose to implement MCMC optimisation with the
Metropolis-Hastings algorithm (Metropolis et al. 1953; Gelman et al. 1995; Tierney 1994; Hastings 1970; Tanner 1996). The set of models
identified by our optimiser in the maximal region of the
likelihood is really an ensemble of all the ![]() -histograms corresponding to each of the grid points on the
image plane, i.e. the full 3-D density structure. (see Appendix D
for greater details of the optimisation procedure and the choice
of the MCMC parameters). Thus, the dimensionality of the
likelihood function is the product of the number of bins along
each of three spatial axes. When the algorithm identifies the
maximal region of the likelihood function,
-histograms corresponding to each of the grid points on the
image plane, i.e. the full 3-D density structure. (see Appendix D
for greater details of the optimisation procedure and the choice
of the MCMC parameters). Thus, the dimensionality of the
likelihood function is the product of the number of bins along
each of three spatial axes. When the algorithm identifies the
maximal region of the likelihood function, ![]() -histograms
corresponding to this maximal region are recorded. The 3-D density
distributions given by this set of
-histograms
corresponding to this maximal region are recorded. The 3-D density
distributions given by this set of ![]() -histograms are
(identified and for a given (x,y,z), the values of
-histograms are
(identified and for a given (x,y,z), the values of
![]() from these identified density distributions) are sorted. The
from these identified density distributions) are sorted. The
![]() 1-
1-![]() range of values of density, about the medial
density at this point is recorded. Such a range of values of
density, over all x, y and z then defines the most likely
3-D density structure that we identify as corresponding to the
surface brightness data at hand. The implementational details of our interval
estimation of luminosity density at a given point (x,y,z) is
discussed in Appendices D.1-D.3.
range of values of density, about the medial
density at this point is recorded. Such a range of values of
density, over all x, y and z then defines the most likely
3-D density structure that we identify as corresponding to the
surface brightness data at hand. The implementational details of our interval
estimation of luminosity density at a given point (x,y,z) is
discussed in Appendices D.1-D.3.
2.12 Construction of seed or trial luminosity density
In the very first iterative step, the density is ascribed a
arbitrary functional form
![]() - the final answer
should be independent of this choice of the initial guess for the
density or the seed density. We use crude estimates of the
parameters that define
- the final answer
should be independent of this choice of the initial guess for the
density or the seed density. We use crude estimates of the
parameters that define
![]() to begin multiple runs.
to begin multiple runs.
3 Testing and applications
In this section, we present the results of our analysis done with simulated data sets that have been designed to mimic the brightness distributions of disk-like and elliptical galaxies with rapidly varying eccentricity profiles, that achieve very high eccentricities indeed. Our examples include
- Test I: a system that resembles a razor-thin disc with a small
(of scale length of 0
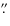 5 as compared to he extent of the system
which is about 100'') round component resembling a tiny bulge
embedded in the centre. The eccentricity evolves from zero at the
centre to about 0.95 by 2
5 as compared to he extent of the system
which is about 100'') round component resembling a tiny bulge
embedded in the centre. The eccentricity evolves from zero at the
centre to about 0.95 by 2
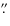 0 and by 3
0 and by 3
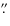 0, is then maintained
at nearly unity. The radial run of the eccentricity of this system
is represented in filled circles in Fig. 2. Thus,
this system, if tested favourably with DOPING, will validate the
following characteristics of the algorithm:
0, is then maintained
at nearly unity. The radial run of the eccentricity of this system
is represented in filled circles in Fig. 2. Thus,
this system, if tested favourably with DOPING, will validate the
following characteristics of the algorithm:
- is able to deal with galaxies of varying morphologies, including disk galaxies.
- is robust even when eccentricity is as high as nearly unity.
- is able to deal with very rapid rise in eccentricity.
- Test II: a system that is rounder in the centre but the eccentricity of which rises to about 0.97, over a length scale of 40''. Thus, this is an elliptical galaxy with widely varying intrinsic shape; the axial ratio changes from nearly 0 at the centre to about 7 at the outer edge of the system. The radial eccentricity profile of this galaxy with widely varying intrinsic shape, is shown in open circles in Fig. 2. This example reinforces DOPING's efficacy in describing systems with different morphologies.
The deprojection in this section is performed under the assumptions of
oblateness and edge-on viewing, i.e.
![]() .
Therefore, for the
test galaxies, q1k=1
.
Therefore, for the
test galaxies, q1k=1
![]() and
qpk =
q2k
and
qpk =
q2k
![]() ,
i.e. the projected and intrinsic eccentricities
concur.
,
i.e. the projected and intrinsic eccentricities
concur.
3.1 Recovery of a known density distribution
The surface brightness![]() and projected eccentricity
profiles which constitute our test data sets are discussed here. The
intrinsic eccentricity is as shown in Fig. 2. The run of
eccentricity with radius
and projected eccentricity
profiles which constitute our test data sets are discussed here. The
intrinsic eccentricity is as shown in Fig. 2. The run of
eccentricity with radius
![]() is given as
follows:
is given as
follows:
where rc is a scale length. The eccentricity is chosen to be function of the spherical radius r, rather than the major axis coordinate, in order to ease the calculation of the projection integral leading to the formulation of the test surface brightness. The analytical luminosity profile, from which the brightness data has been extracted, is
with e(r) given in equation Eq. (9). B is a scale length or core radius and A is the central density scaled by the factor B3.
![\begin{figure}
\par\includegraphics[width=8.3cm]{12008fg2.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg95.png)
|
Figure 2: The chosen eccentricity profile of the test galaxy Test I, shown as a function of r, in filled circles. The same for Test II is shown in open circles. |
| Open with DEXTER | |
We integrate
![]() along z, after plugging in the form of
e(r) from Eq. (9), into Eq. (10).
The result of this integration is the toy surface brightness data that
we want DOPING to invert.
along z, after plugging in the form of
e(r) from Eq. (9), into Eq. (10).
The result of this integration is the toy surface brightness data that
we want DOPING to invert.
In the toy data set Test I, the surface brightness profile is sampled at 64 locations along the galaxy semi-major axis, from 0
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12008fg3.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg98.png)
|
Figure 3:
Performance of DOPING in the simulated
test cases Test I (a disk galaxy with a round ellipsoidal centre that
extends to only about 0
|
| Open with DEXTER | |
The robustness of the comparison between the test 2-D brightness distribution of the test galaxies and the projections of the recovered density distributions is brought out in Figs. 4 and 5.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12008fg4.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg99.png)
|
Figure 4: Left: the 2-D surface brightness (in mag/arcsec2) distribution of our flat test galaxy Test I, as a contour plot on the plane of the sky (x-y plane). The contours in broken lines pertain to the toy brightness data that was fed into DOPING while the solid lines represent the projection of the 3-D luminosity density that DOPING recovers. The gap around y = 0 occurs in the distribution of the projected density since the smallest (logarithmic) spatial bin is about 1pixel, i.e. 0''.05. Right: same as for the left panel, except that in this case, the central rounder part of the test galaxy has been focused upon. |
| Open with DEXTER | |
The recovered density profile as well as its projection appear to tally very favourably with the known distributions.
3.2 Changing inclinations
In this section, we investigate the extent to which the recovered luminosity density is rendered uncertain by our ignorance of the inclination angle i, under a given assumption about the geometry of the system and for a given set of observables.
In order to track this uncertainty, we use the test surface brightness data given in Eq. (11), and constrain the projected eccentricity to be
radially invariant:
ep = ep0. Working with a constant
ep is preferred to a radially dependent projected eccentricity, on
grounds of ease of interpretation of the results. The deprojection of
the test galaxy is performed under the assumption that the galaxy is
oblate in shape. For such a geometry, the inclination cannot be less
than
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg5.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg101.png)
|
Figure 5: 2-D surface brightness (in mag/arcsec2) distribution of the elliptical test galaxy Test II, compared to the plane of the sky projection of the luminosity distribution recovered by DOPING for this system. |
| Open with DEXTER | |
We perform a suite of deprojections of the test surface brightness data with i set to
![]()
![]() ,
where i1 is the minimum
inclination consistent with the observed projected eccentricity of
ep0, i.e.
,
where i1 is the minimum
inclination consistent with the observed projected eccentricity of
ep0, i.e.
![]() .
Here ep0 is chosen to be
one of the following 4 values:
ep0 = 0, 0.71, 0.87, 0.95. These
values of ep0 were chosen to span the range that early type
galaxies are typically observed to bear. Deprojections were
performed for each ep0, at each of the 4 selected i. Thus,
our experiments can track 4 test galaxies which are distinct in
their flattening, each assumed oblate and viewed at a suite of
different inclinations, the smallest of which is set by the
projected eccentricity.
.
Here ep0 is chosen to be
one of the following 4 values:
ep0 = 0, 0.71, 0.87, 0.95. These
values of ep0 were chosen to span the range that early type
galaxies are typically observed to bear. Deprojections were
performed for each ep0, at each of the 4 selected i. Thus,
our experiments can track 4 test galaxies which are distinct in
their flattening, each assumed oblate and viewed at a suite of
different inclinations, the smallest of which is set by the
projected eccentricity.
Figure 6 shows the density profiles recovered by DOPING
by deprojecting the test surface brightness (Eq. (11)), for the choice of
ep0 = 0.71. This corresponds to
![]()
![]() .
For this
configuration, deprojection is performed at four distinct values of
the viewing angle, in the range of [45
.
For this
configuration, deprojection is performed at four distinct values of
the viewing angle, in the range of [45![]() ,
90
,
90![]() ], at
], at
![]() .
It is possible to obtain the given
surface brightness map that manifests a given projected flatness (
ep0 = 0.71) at
these 4 different inclinations, only by projecting the luminosity
densities of 4 distinct oblate galaxies with intrinsic eccentricities
of 0.99, 0.95, 0.87, 0.71.
.
It is possible to obtain the given
surface brightness map that manifests a given projected flatness (
ep0 = 0.71) at
these 4 different inclinations, only by projecting the luminosity
densities of 4 distinct oblate galaxies with intrinsic eccentricities
of 0.99, 0.95, 0.87, 0.71.
Thus, deprojection of the observed brightness map, carried out at
varying inclinations, is characterised by variation in amplitudes as
well as shapes. However, it is only along the major axes (the
semi-axis along
![]() )
that the deprojected profiles will
appear similar in shape but different in amplitude. This owes to our
definition of the toy surface brightness distribution
(Eq. (11)). Along all other directions, the recovered
density distributions will manifest differences in shape as well. It
is for this reason that in Fig. 6 we present the
recovered density profiles along the galaxy minor axes. The variation
in shape across the set of deprojected density profiles is clear from
this figure.
)
that the deprojected profiles will
appear similar in shape but different in amplitude. This owes to our
definition of the toy surface brightness distribution
(Eq. (11)). Along all other directions, the recovered
density distributions will manifest differences in shape as well. It
is for this reason that in Fig. 6 we present the
recovered density profiles along the galaxy minor axes. The variation
in shape across the set of deprojected density profiles is clear from
this figure.
It is to be noted that the projections of the recovered density
profiles coincide with the input surface brightness data in each case. However, once
![]()
![]() (for projected eccentricity = 0.71), the 3-D density
profiles become a sensitive function of i. As expected, the
recovered density is maximum (at every radius) when the intrinsic
eccentricity is highest (i.e., the inclination angle is lowest). When
the galaxy is assigned an even higher projected eccentricity, the
uncertainty in the obtained density shows up at even lower i, i.e. at
inclinations closer to the face-on configuration.
(for projected eccentricity = 0.71), the 3-D density
profiles become a sensitive function of i. As expected, the
recovered density is maximum (at every radius) when the intrinsic
eccentricity is highest (i.e., the inclination angle is lowest). When
the galaxy is assigned an even higher projected eccentricity, the
uncertainty in the obtained density shows up at even lower i, i.e. at
inclinations closer to the face-on configuration.
Figure 7 presents the value of the recovered luminosity
density at the innermost radial bin (about 0
![]() 05), plotted as a
function of the assumed inclination, for varying values of the
intrinsic eccentricity, under the assumption of oblateness. As
expected, the central density values concur (within the error bars),
for the edge-on configuration, while density is highest at the centre
at i=0
05), plotted as a
function of the assumed inclination, for varying values of the
intrinsic eccentricity, under the assumption of oblateness. As
expected, the central density values concur (within the error bars),
for the edge-on configuration, while density is highest at the centre
at i=0![]() , for the intrinsically most eccentric system.
, for the intrinsically most eccentric system.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg6.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg107.png)
|
Figure 6:
Luminosity density distributions recovered
by deprojecting the surface brightness profile given by
Eq. (11), under the assumption of oblateness, given a
projected eccentricity of 0.71, viewed at inclinations of about
46 |
| Open with DEXTER | |
3.3 Changing geometry
In the last section we explored how our unfamiliarity with the
inclination of a galaxy can lead to a non-zero range of possible
density profiles that a single observed brightness profile can
correspond to. This range had been investigated under an assumption for the
geometry of the galaxy, namely oblateness. In this section, we attempt
to gauge the effects of treating an intrinsically oblate system, (our
test system of Eq. (10), conferred a constant ep of 0.99) as triaxial (with the photometric major axis along
![]() and LOS extent set to half the photometric major axis), prolate and spherical, viewed at i = 90
and LOS extent set to half the photometric major axis), prolate and spherical, viewed at i = 90![]() (see
Fig. 8).
(see
Fig. 8).
Assuming this rather flat test system to be oblate implies that q1 is a constant, =1 and
![]() (where we
have used our definition of q1 and qp, as given in
Appendix C). Then from Eq. (4) we get that for
i = 90
(where we
have used our definition of q1 and qp, as given in
Appendix C). Then from Eq. (4) we get that for
i = 90![]() ,
,
![]() .
Similarly, when the system is assumed
prolate, q1 = 1,
.
Similarly, when the system is assumed
prolate, q1 = 1,
![]() and
and
![]() .
When we assume the system to be triaxial as above, then
for i = 90
.
When we assume the system to be triaxial as above, then
for i = 90![]() ,
,
![]() and
and
![]() 7.1,
7.1,
![]() 7.1 and q1 = 2.
7.1 and q1 = 2.
When we input these different values of q2 in Eq. (5), we get values
of
![]() from the oblate case that are different from what we
get for the prolate case. In fact, for edge-on viewing, as in here,
for a given k, the maximum z-height attained by any point in the
kth isophotal annulus is higher for the oblate case than the
prolate case. As a result, the density distribution that is recovered
from the oblate case is lower in amplitude than that from the prolate
case. The triaxial case result falls in between that from the oblate
and prolate cases.
from the oblate case that are different from what we
get for the prolate case. In fact, for edge-on viewing, as in here,
for a given k, the maximum z-height attained by any point in the
kth isophotal annulus is higher for the oblate case than the
prolate case. As a result, the density distribution that is recovered
from the oblate case is lower in amplitude than that from the prolate
case. The triaxial case result falls in between that from the oblate
and prolate cases.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg7.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg116.png)
|
Figure 7: Central luminosity density, plotted as a function of inclination for four different values of the intrinsic eccentricity. When the intrinsic eccentricity is 0.71, the obtained central density points are shown in black. The colour coding for the other values of e is as follows: e = 0.87, 0.95 and 0.99 correspond to red, green and blue, respectively. The case of inclination = 0 obviously indicates the situation when the observed isophotes are circular, i.e. the observed projected eccentricity is zero. |
| Open with DEXTER | |
In the case of galaxy clusters, when
![]() information is available,
DOPING can be called in to perform deprojection in the fully triaxial
geometry without requiring to make any assumption about one of the intrinsic
axial ratios (Chakrabarty et al. 2008).
information is available,
DOPING can be called in to perform deprojection in the fully triaxial
geometry without requiring to make any assumption about one of the intrinsic
axial ratios (Chakrabarty et al. 2008).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg8.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg117.png)
|
Figure 8: Luminosity density of our oblate test galaxy of projected eccentricity 0.99 (shown in red), recovered by DOPING, under the assumptions of prolateness (in blue), oblateness (in black) and triaxiality with ratio between LOS extent and photometric major axis = 0.5 (in green). All the deprojections were carried out for an edge-on viewing. |
| Open with DEXTER | |
3.4 Effect of PSF
We hope to use DOPING to extract luminosity profiles of real galaxies, in particular, the ACS VCS galaxies. It therefore becomes important to gauge the effect of the ACS PSF on the recovered density. This is done by convolving the projection of the density in any iterative step with the ACS PSF and comparing this convolved profile to the observed surface brightness. The result is shown in Fig. 9. As indicated in the figure, the effect of the ACS PSF does not extend beyond the central few arcseconds (in fact, 10'').
4 Applications to real systems
In this section, we demonstrate the application of DOPING to real galaxies. The efficacy of DOPING in dealing with galactic systems that vary over wide ranges of magnitudes and morphology - including a nucleated disky galaxy - is advanced with applications made to the observed galaxies Ic 3019 and Ic 3881. In addition, the recovery of the density for the cluster A1413, without resorting to assumptions about geometry and inclination, is also included.
4.1 Ic 3019 - effect of smoothing
Here we apply DOPING to deproject the measured surface brightness map of the galaxy
Ic 3019 (vcc9) which is observed within the ACS VCS (Ferrarese et al. 2006).
In particular, the effect of the smoothing parameter ![]() is
demonstrated in the context of this example galaxy. Thus, this
section also brings out an application of DOPING to the analysis of
real data. This galaxy is low on brightness and the reason for
choosing it is to adduce evidence for the wide range of systems that
DOPING can tackle.
is
demonstrated in the context of this example galaxy. Thus, this
section also brings out an application of DOPING to the analysis of
real data. This galaxy is low on brightness and the reason for
choosing it is to adduce evidence for the wide range of systems that
DOPING can tackle.
The eccentricity of this galaxy has been measured to vary with radius,
though not radically, under the ACSVCS observational program. In fact,
eccentricity has been reported to be uniform at about 0.85 till about
2.5
![]() ,
from which it drops abruptly to about 0.3 at about 6
,
from which it drops abruptly to about 0.3 at about 6
![]() ,
to
undulate its way up to about 0.7 at about 200
,
to
undulate its way up to about 0.7 at about 200
![]()
The density distribution recovered for Ic 3019 is projected along the
LOS and is plotted as a function of x in Fig. 10 in
black, on top of the observed brightness data for vcc9. The three
panels correspond to runs performed with three increasing values of
the regularisation parameter ![]() ,
namely
,
namely
![]() (i.e. no
smoothing),
(i.e. no
smoothing),
![]() and
and
![]() .
Increasing
.
Increasing ![]() beyond
this value did not make a significant change in the estimated density.
The procedure to choose
beyond
this value did not make a significant change in the estimated density.
The procedure to choose ![]() is discussed in Appendix E.
is discussed in Appendix E.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12008fg10.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg121.png)
|
Figure 9: Left: luminosity density of an oblate test galaxy with uniform eccentricity of 0.99, recovered by comparing the input brightness profile with the PSF convolved projection of the density in any iterative step. The PSF in question is the ACS PSF in the F850W filter. When the convolution with the PSF is ignored, the recovered density is shown in green. Right: difference between the density profiles obtained with and without convolving with the PSF. It is noted that inside the central 10'', this difference is 2 orders of magnitude less than density while outside 10'', the difference tends to zero. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12008fg11.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg122.png)
|
Figure 10:
Effect of increasing the smoothing
parameter |
| Open with DEXTER | |
The projection of the recovered density distribution on the plane of the sky, is compared to the surface brightness map of IC 3019 in Fig. 11.
4.2 Galaxy cluster
In this section we discuss the results of applying DOPING to extract
the X-ray luminosity density of the cluster A1413. The important
feature about recovering the 3-D density of clusters with DOPING is
that the true axial ratios and inclination can be constrained along
the lines advanced by Chakrabarty et al. (2008), as long as
![]() of the
system can be estimated from the available SZe measurements. The
cluster A1413 was reported in Chakrabarty et al. (2008) to be a triaxial
system with the intrinsic axial ratios of 0.96 and 1.64 and
inclination lying between 66
of the
system can be estimated from the available SZe measurements. The
cluster A1413 was reported in Chakrabarty et al. (2008) to be a triaxial
system with the intrinsic axial ratios of 0.96 and 1.64 and
inclination lying between 66![]() and 71
and 71![]() .
.
This configuration was identified upon deprojecting the X-ray surface brightness
at four benchmark deprojection scenarios, namely oblateness and
![]() ,
oblateness and
,
oblateness and
![]() ,
prolateness and
,
prolateness and
![]() ,
prolateness and
,
prolateness and
![]() .
Here
.
Here
![]() is the minimum inclination possible under the assumption
of oblateness, given a projected axial ratio (= 1.473 for A1413).
Inter-comparison of the 3-D density profiles recovered under these
four scenarios leads us to the aforementioned prediction. Since the
relative extent along three mutually orthogonal axes are known in
this case, 3-D modelling is possible, i.e. the true geometry of the
system can be estimated. Thus, we do not need to assume any axial
ratio or inclination value. The density profile recovered under
deprojection in the identified system geometry is presented in
Fig. 12.
is the minimum inclination possible under the assumption
of oblateness, given a projected axial ratio (= 1.473 for A1413).
Inter-comparison of the 3-D density profiles recovered under these
four scenarios leads us to the aforementioned prediction. Since the
relative extent along three mutually orthogonal axes are known in
this case, 3-D modelling is possible, i.e. the true geometry of the
system can be estimated. Thus, we do not need to assume any axial
ratio or inclination value. The density profile recovered under
deprojection in the identified system geometry is presented in
Fig. 12.
4.3 2-component galaxies
It is possible for DOPING to perform the deprojection of a bulge+disk galactic system in an integrated, single step fashion. This is made possible by ascribing two distinct seeds to the two components, namely the central bulge/nucleus and the more extended outer component upon which the central component is superimposed. The deprojection of the nucleated galaxies in the ACS VCS sample has been undertaken in Chakrabarty & McCall (2009, under preparation). An example of the deprojection of the surface brightness profile of such a 2-component, nucleated galaxy is shown in Fig. 13.
5 Discussions and summary
In this paper, we have presented a fast new non-parametric algorithm, DOPING, that works via a penalised likelihood approach. It attempts to deproject the observed surface brightness profiles of galaxies, in general triaxial geometries, while taking into account intrinsic variation in shape.
The algorithm was successfully tested on toy galactic systems of varying morphologies, including an extreme system that was ascribed a small ellipsoidal bulge-like inner component that lay embedded in a highly flattened outer disk. Other experiments were best served by simulated galaxies with constant ellipticities. The code was also applied to a dwarf elliptical galaxy Ic 3019 (vcc9) and another dE, nucleated galaxy Ic 3381 (vcc1087) from the ACS Virgo Cluster Survey (Côté et al. 2004). An application to a real galaxy cluster, A1413, is also included.
5.1 Superior design
The well-defined, inherent convergence criterion of DOPING, buffeted by the sophisticated MCMC optimiser renders it superior to other well used inverse deprojection scheme, namely the Richardson-Lucy algorithm. Besides, the nonparametric inverse design of DOPING helps it avoid risky practises such as parametric fitting, interpolation, etc. Finally, none of these methods can perform deprojection under generalised triaxial geometries, like DOPING can.
Choosing the LOS coordinate or z as the basis for the density helps to keep the code modular. As a result, DOPING can handle deprojections in general geometries. The current version of DOPING relies on the determination of the intrinsic shape parameters (axial ratios) from measurements only of projected shape parameters. Such a relation is possible for unknown inclinations, only if the object shape bears a certain regularity. It is this that causes 3-D modelling with DOPING to be restricted to only objects with m-fold symmetries.
Thus, when the inclination is unknown but the relative extent along
three mutually orthogonal axes are known, DOPING can handle an
assortment of 3-D shapes that resemble m-winged star-fruit-like
shapes, the 2-D projections of which are m-pronged star-fish-like
2-D shapes. Such generalised geometries can be described by the 3-D extension of Gielis's ``superformula'' (Gielis 2003). The
superformula is a 6-parameter generalisation of the superellipse
(which are the Lame' curves with unequal semi-axes). In fact, the
product of two superformulae - one corresponding to a generalised
superellipse in the Z = 0 plane and another in the Y = 0 plane - can
give rise to the m-winged star-fruit-like 3-D shapes![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg9.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg125.png)
|
Figure 11: As in Fig. 5, except that in this case, the plane of the sky brightness distribution of the galaxy IC 3019 is shown. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg13.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg126.png)
|
Figure 12:
X-ray luminosity density profile of cluster A1413,
recovered under the true system geometry (
q1 = 0.96,
q2 = 1.64)
and inclination = 68.5 |
| Open with DEXTER | |
However, a more generalised version of DOPING that allows fast and robust three dimensional modelling in unrestricted geometries is also possible - only in situations in which the system can be viewed at multiple inclinations. Such configurations are not of astronomical context but bear strong application potential; this will be reported in a future contribution.
5.2 DOPING deals with substructure
Continuing on the issue of code generality, we recall that in Sect. 4.2 it was shown that DOPING can deal with galaxies, the light distribution of which betray a bulge+disk structure. In fact, DOPING is capable of deprojecting systems marked with multiple structures that may not necessarily be concentric. As long as the centres of each component are known, the algorithm can be employed for deprojection.
5.3 Why choose
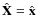
In general, there will be two angles involved in the rotation matrix
that connect the the two Cartesian coordinate frames. However, when
we speak about inclinations of observed astronomical systems, we
typically specify one angle of inclination for a given system. In
other words, it is modelled that one of the two angles of
inclinations is set to zero, while the angle between a principle
axis of the system and the LOS is advanced as the inclination i. Given that the image plane is what is fixed by observations -
and therefore the LOS - one of the system principle axes (one that
we refer to as the Z-axis, say) can be at angle i with the LOS,
i.e.
![]() can lie anywhere on the surface of a cone that
has an axis along the LOS and a semi-angle i. There is no
observational constraint that can restrict our choice of the
location of
can lie anywhere on the surface of a cone that
has an axis along the LOS and a semi-angle i. There is no
observational constraint that can restrict our choice of the
location of
![]() on the surface of this cone. For a given
choice of this location, the X-Y plane is fixed accordingly. The
choice that we make in this work, corresponds to
on the surface of this cone. For a given
choice of this location, the X-Y plane is fixed accordingly. The
choice that we make in this work, corresponds to
![]() .
.
It is true that the recovery of the 3-D density distribution could
be affected by a different choice for the location of
![]() on the surface of the cone. This is so because the system at
hand is triaxial in general, rather than axisymmetric. At the same
time, we need to appreciate that there is no observational
information that would inspire a particular choice. Hence we adopt
the choice that eases calculations, keeping in mind the fact that as
a consequence of this, the recovered 3-D density structure is one
possible answer for a given surface brightness data. Of course, we could undertake
deprojection for other non-zero values of
on the surface of the cone. This is so because the system at
hand is triaxial in general, rather than axisymmetric. At the same
time, we need to appreciate that there is no observational
information that would inspire a particular choice. Hence we adopt
the choice that eases calculations, keeping in mind the fact that as
a consequence of this, the recovered 3-D density structure is one
possible answer for a given surface brightness data. Of course, we could undertake
deprojection for other non-zero values of
![]() .
In fact, a band of uncertainties on the
recovered 3-D density can be derived, corresponding to varying
choices of this angle, though no ``most-likely'' region for the
density can be identified within this band. However, given the state of
equally poor constraint on the density, the solution corresponding
to one given value of the azimuthal inclination is advanced here.
.
In fact, a band of uncertainties on the
recovered 3-D density can be derived, corresponding to varying
choices of this angle, though no ``most-likely'' region for the
density can be identified within this band. However, given the state of
equally poor constraint on the density, the solution corresponding
to one given value of the azimuthal inclination is advanced here.
The other assumptions that we make about geometry and inclination -
provided by the user as inputs into the code - can be varied and the
corresponding range of recovered 3-D density distributions can be
recorded, with
![]() always assumed equal to
always assumed equal to
![]() .
This is particularly easy, given the short run-times of a
typical run of DOPING. It is important to stress here that our
assumptions are not invoked to cover for flaws in algorithm design
but are essential in order to render the deprojection scenario
unique, i.e. to ascertain the deprojection geometry and
inclination. Our assumptions merely compensate for the lack of
(observational) information about such deprojection scenarios.
.
This is particularly easy, given the short run-times of a
typical run of DOPING. It is important to stress here that our
assumptions are not invoked to cover for flaws in algorithm design
but are essential in order to render the deprojection scenario
unique, i.e. to ascertain the deprojection geometry and
inclination. Our assumptions merely compensate for the lack of
(observational) information about such deprojection scenarios.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{12008fg12.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg131.png)
|
Figure 13:
Luminosity density of the two-component galaxy Ic 3881 along the
|
| Open with DEXTER | |
Given the assumptions that we need to make, the question that may be asked is if the proposed ambition of DOPING to deproject in triaxial geometries is inane, in that it is driven by unconstrained assumptions. Such a worry has been addressed in the beginning of Sect. 2 and discussed later in Sect. 5.5. In the following section, we elucidate the follies of assuming axisymmetry, given observations on galactic systems, thus, reinforcing the need for invoking triaxiality.
5.4 The Folly of axisymmetry
A general non-irregular galaxy, whether elliptical or axisymmetric, can be approximated as a triaxial ellipsoid (the third axis is tiny in a disk system, compared to the other two intrinsic axis lengths). The modular structure of DOPING allows for deprojection of galaxies of both elliptical and disky morphologies. As discussed above, other deprojection methods can at most imply axisymmetry.
However, often, the assumption of axisymmetry (Magorrian 1999, RK) is
not just a mild deviation from the truth but is plain wrong - this is
clear in the cases of inclined, disk-like systems. In these systems,
while the extent along the perpendicular to the disk is much smaller
than that along the other two axes in the disk, a non-zero
projected ellipticity (![]() ), measured on the plane of
projection implies that in general, both intrinsic axial ratios -
and particularly the ratio of the principal axes in the disk -
deviate from unity. A few examples of such systems from the ACS Virgo
Cluster Survey (Ferrarese et al. 2006, web site of ACS Virgo Cluster
Survey Databases) include:
), measured on the plane of
projection implies that in general, both intrinsic axial ratios -
and particularly the ratio of the principal axes in the disk -
deviate from unity. A few examples of such systems from the ACS Virgo
Cluster Survey (Ferrarese et al. 2006, web site of ACS Virgo Cluster
Survey Databases) include:
- NGC 4382 (or vcc 798, SA galaxy) in which
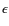 ranges from 0.6 at the centre to 0.2 outside;
ranges from 0.6 at the centre to 0.2 outside;
- NGC 4762 (or vcc 2095, SB) in which
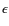 approximately increases to 0.4, starting from about 0;
approximately increases to 0.4, starting from about 0;
- NGC 4442 (or vcc 1062, SB) in which
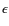 increases outward to 0.6 from about 0.
increases outward to 0.6 from about 0.
5.5 Justification of assumptions
The solution that we will achieve for the most likely 3-D density, given the surface brightness data, will depend on the assumptions that we use for the unconstrained inclination and the axial ratio. Of course, such assumptions will call for physical justification - however, the fundamental issue here is that for galaxies, there is no observational evidence that will constrain such assumptions. For galaxy clusters, the availability of the maximum extent along the LOS, (from SZe measurements), definitely helps to constrict the number of assumptions that we then need to make (see Appendix B). Similarly, for systems which can be viewed at selected inclinations, 3-D modelling is rendered robust and fast. Again, for flattened systems, we can estimate one of the inclinations and therefore deprojection then entails one less assumption. However, the lack of sufficient physically relevant measurements means that assumptions invoked to characterise a general triaxial system cannot be justified to satisfaction. In lieu of this, all that DOPING can offer is a fast estimate of the range of density distributions obtained over the considered range of axial ratios and inclinations. Turning this argument around, we realise that the range of 3-D density distributions that are recovered in Sects. 3.2 and 3.3, for distinct geometry+inclination inputs (assumptions) cannot be narrowed down for general triaxial galactic systems.
The question that then begs addressing is if deprojection in triaxial geometries is any improvement upon the existing deprojection routes that are currently in vogue. That the need for triaxiality over axisymmetry, is physically justified, was delineated in the last sub-section. However, given the dearth of observational information - particularly for galaxies rather than galaxy clusters, as discussed in Sect. 2 and above - assumptions need to be invoked. The superiority of DOPING lies in the fact that when information about intrinsic morphology and inclination are less sparse than for galaxies (as for clusters or deposited nano-particles), identification of the true triaxial geometry is possible (Chakrabarty et al. 2008) and deprojection can then be performed in this geometry, without invoking assumptions about i and q1 (as demonstrated for the Abell cluster A1413 in Sect. 4.2).
5.6 Position angle
Had the two angles of inclination been known to us, we would be in a
position to predict the observed projected position angle as a
function of these inclinations. However, given the projected
position angle, constraining the inclinations requires an inverse
approach, which is possible within DOPING in the triaxial
geometry. We could then relax the assumption of
![]() while continuing to assume the polar
inclination angle. In fact, the coordinate system (and the ensuing
equations) used here is a limiting case of the assumption of a
non-zero, radially varying position angle. In this more generalised
version of DOPING, the angles between
while continuing to assume the polar
inclination angle. In fact, the coordinate system (and the ensuing
equations) used here is a limiting case of the assumption of a
non-zero, radially varying position angle. In this more generalised
version of DOPING, the angles between
![]() and the line of
nodes will be non-zero and varying with radius (Simonneau et al. 1998). This will be dealt with in a future contribution.
and the line of
nodes will be non-zero and varying with radius (Simonneau et al. 1998). This will be dealt with in a future contribution.
When the position angle is included in the calculations the data table
is enhanced by another column yet - ![]() ,
where
,
where ![]() is
the position angle of points in the kth isophotal annulus. Then,
the body coordinate system corresponding to the kth isophotal
annulus is rotated by
is
the position angle of points in the kth isophotal annulus. Then,
the body coordinate system corresponding to the kth isophotal
annulus is rotated by ![]() with respect to the
with respect to the ![]() line,
i.e. the x-axis (by definition), so that the new body coordinate
system governing the triaxial shell - the largest projection (of the
same thickness as itself) of which is the kth isophotal annulus -
is given by X'-Y'-Z', where:
line,
i.e. the x-axis (by definition), so that the new body coordinate
system governing the triaxial shell - the largest projection (of the
same thickness as itself) of which is the kth isophotal annulus -
is given by X'-Y'-Z', where:
| X' | = | (12) | |
| Y' | = | (13) | |
| Z' | = | Z. | (14) |
Having established this, the equivalent of Eq. (5) can be written down. The reformed equation is still a quadratic and is solved for the two solutions of z as before. In the present calculations, we avoided this extra complication in light of the small isophotal twist observed with the ACS VCS galaxies, which are the prime targets of the discussed code.
5.7 Effect of seed selection
Our starting luminosity density is motivated by crude estimates of
the sought function (Gelman et al. 1995); we are guided by the
requirement that the projection of the seed density be close to the
given surface brightness data. The algorithm will indeed fail to
converge for completely irrational choices of the initial parameters
(steepness parameter ![]() 1, scale length different from the
correct choice by more than 4 orders of magnitude). Importantly,
under such circumstances, the projection of the recovered density
will be found to deviate from the brightness data. This brings us to
the important advantage that a deprojection scheme benefits from -
the closeness of the seed to the sought answer can be checked by
comparing the projection of the recovered solution and the
data. Additionally, it may be remarked that it is reasonable to
start with a steepness parameter that is close to unity and a scale
length that is of the order of the core radius that characterises
the surface brightness profile of the system. Given that a typical
run is fast, it is feasible to restart the algorithm for a different
choice of the initial guess, until convergence is reached.
1, scale length different from the
correct choice by more than 4 orders of magnitude). Importantly,
under such circumstances, the projection of the recovered density
will be found to deviate from the brightness data. This brings us to
the important advantage that a deprojection scheme benefits from -
the closeness of the seed to the sought answer can be checked by
comparing the projection of the recovered solution and the
data. Additionally, it may be remarked that it is reasonable to
start with a steepness parameter that is close to unity and a scale
length that is of the order of the core radius that characterises
the surface brightness profile of the system. Given that a typical
run is fast, it is feasible to restart the algorithm for a different
choice of the initial guess, until convergence is reached.
5.8 Effect of data sampling
We also note that the spatial sampling of the data can have some effect on the density distribution recovered by DOPING. For instance, in Fig. F.1, the density profile best reproduces the data at small, rather than large radii. This is a consequence of the fact that, by construction, our simulated data set happens to have substantially more data points in the inner regions of the galaxy than on the outside, with the consequence that the innermost region has larger weight in driving convergence.
6 Conclusion
Thus, DOPING is advanced as a simple but powerful deprojection algorithm, that can be treated as a black-box by the user, is fast and offers 3-D density distributions in general geometries, without resorting to making unconstrained approximations to the form of the density or blindly accepting validity of commonly used goodness of fit measures in light of the inhomogeneous errors of measurement (Bissantz & Munk 2001).
The greatest novelty borne by DOPING is its applicability to general systems. Even though in the above examples, triaxial systems were investigated - ranging from razor thin discs to 2-component or bulge+disk galaxies - even when inclination is unknown DOPING can deal with all systems that offer an analytical relation between the intrinsic and measured projected shape parameters. The class of geometries that bear an m-fold symmetry allows for this. 3-D modelling of images of systems with even more general geometries can also be performed with DOPING, as long as the system can be imaged at various known inclinations. That deprojection into the third dimension is possible in such general geometries, in a non-parametric way, is due to the fact that the representation of the sought density is modular, i.e. not dependent on a characteristic of the system geometry.
The recovery of the 3-D density is performed iteratively, by searching for the most likely 3-D density structure that projects to the observed 2-D image. This search is robustly undertaken by an MCMC optimiser. Since the choice of the 3-D density is constrained via its projection, distinct 3-D density distributions will project to the same 2-D image. To lift this degeneracy, in DOPING, the system geometry and orientation are specified completely. That axisymmetry is an invalid assumption - at least in real disc-like galaxies - was shown above. Consequently, the description of galaxy geometry as triaxial is a suitable alternative. However, triaxiality entails two axial ratios and inclinations, not all of which can be specified, given the constricted level of achievable observed information. When observed information is available, DOPING can perform deprojection under triaxiality without invoking assumptions, while in lieu of the same, assumptions are invoked. The former case is demonstrated above via the example of deprojection of a galaxy cluster. A benefit of the speed of the algorithm is that a suite of 3-D density models, corresponding to a range of assumed values, is achieved quickly.
Thus, the strengths of DOPING include generalised applicability, ability to incorporate substructure and non-parametric density recovery, along with logistical advantages such as high speed of runs and user-friendliness. Such characteristics render DOPING a very useful tool in three dimensional modelling. In particular, the all important estimation of galactic masses will be aided by a tool such as DOPING.
AcknowledgementsThis research was funded by a Royal Society Dorothy Hodgkin Fellowship. The author is delighted to acknowledge the contribution of Laura Ferrarese without whose comments and suggestions, the paper would not have been possible.
Appendix A: Representing isophotes
The shape parameters of the isophotes form the input information, so we can formulate smooth analytical approximations to the isophotes. Of course, it is the fitting of such smooth approximations to the surface brightness data that provides estimates of the isophotal parameters; in other words such approximations are readily available. It is to sort grid points on the image plane, into respective isophotal annuli, that we invoke these approximations. However, real isophotes can be irregular and not altogether smooth. To take this into account, we examine the isophotes first and estimate the typical length scale over which the irregularity in the isophotes occurs. Thus, for example, the isophotal contours of a distant galaxy could be imaged by a given instrument as more jagged than those of a nearby system. We discard grid points on the image plane that lie within this estimated spatial range corresponding to deviations from smoothness.
Appendix B: Specifying the system geometry for triaxial galaxies
The specification of triaxiality of an example galaxy entails knowledge of:
- 2 constant intrinsic axial ratios q1 and q2 for systems with radially independent shape. Alternatively, for systems with radially varying intrinsic eccentricities - 2 intrinsic axial ratios that vary as known functions of distance away from centre of system.
- 2 position angles or inclinations.
- set one inclination angle to 0 by setting one photometric axis
(along the
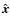 -axis) to be coincident with an
intrinsic principal axis (see Sect. 2.1).
-axis) to be coincident with an
intrinsic principal axis (see Sect. 2.1).
- assume a value for the other inclination i.
- derive the two intrinsic axial ratios from the two projected
axial ratios:
- 1.
- ratio of the photometric semi-axes (qp).
- 2.
- ratio of the semi-axes along the LOS to that along the
photometric major axis (
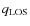 ).
).
- qp=f1(q1, q2, i) and
-
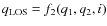 ,
,
Appendix C: Axial ratios
We clarify that the axial ratios
q2k, q1k, qpk are defined
such that the extent along
![]() is in the numerator. Thus,
is in the numerator. Thus,
- qpk is the ratio of the semi-axis along
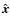 of the kth isophotal annulus, to that along
of the kth isophotal annulus, to that along
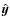 ,
on the image plane,
,
on the image plane,
- q2k is ratio of the semi-axis along
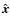 to that along the
to that along the
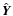 ,
,
- q1k is ratio of the semi-axis along
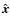 ,
to that along the
,
to that along the
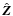 ,
,
In the examples shown later in the paper, we assume the system to be oblate, unless otherwise stated, i.e. then q1k is a constant, (=1) and q2k > 1. If we are considering a prolate system, then q1k is again a constant, (=1) but then q2k < 1.
Appendix D: Optimisation
We seek solutions for ![]() that correspond to the
that correspond to the ![]() 1-
1-![]() neighbourhood of the global maxima of
neighbourhood of the global maxima of ![]() and employ an MCMC
optimiser for this. The particular implementation of this in our
work is the Metropolis Hastings algorithm. Once Metropolis-Hastings
attains the equilibrium stage, it moves around in the maximal region
of
and employ an MCMC
optimiser for this. The particular implementation of this in our
work is the Metropolis Hastings algorithm. Once Metropolis-Hastings
attains the equilibrium stage, it moves around in the maximal region
of ![]() .
During this stage the average of an ensemble of
models should represent the distribution that is to be sampled; this
is reflected in stationarity in the trace of the likelihood. Before
recording the solutions, we typically allow for 5 times the period
of burn-in to lapse, mindful of the fact that burn-in can continue
much longer than suggested by the trace. Details of the optimisation
are presented in Roberts et al. (1997); Roberts & Rosenthal (2001); Roberts & Sahu (1997); Gelman et al. (1996).
.
During this stage the average of an ensemble of
models should represent the distribution that is to be sampled; this
is reflected in stationarity in the trace of the likelihood. Before
recording the solutions, we typically allow for 5 times the period
of burn-in to lapse, mindful of the fact that burn-in can continue
much longer than suggested by the trace. Details of the optimisation
are presented in Roberts et al. (1997); Roberts & Rosenthal (2001); Roberts & Sahu (1997); Gelman et al. (1996).
We use circular iterations, with the 1st to the
![]() th
iterative step repeating in cycles. We define convergence as when
inside the equilibrium stage, the likelihood attained in the ith
step during the Mth cycle, falls below the likelihood attained in
the i+1th step during the M-1th cycle. It is expected
that then the algorithm has indeed passed through the global maxima
in the likelihood. The extent of wandering of Metropolis in this
maximal region is a direct measure of the errors of the analysis.
th
iterative step repeating in cycles. We define convergence as when
inside the equilibrium stage, the likelihood attained in the ith
step during the Mth cycle, falls below the likelihood attained in
the i+1th step during the M-1th cycle. It is expected
that then the algorithm has indeed passed through the global maxima
in the likelihood. The extent of wandering of Metropolis in this
maximal region is a direct measure of the errors of the analysis.
D.1 Uncertainties
In fact, when we say that the errors of our analysis are quantified
by the ![]() 1-
1-![]() spread across the ensemble of identified
density values, we actually imply a as 68% interval. To expound
on the procedure of quantifying the errors: at a point (x,y,z),
the values of the luminosity density corresponding to the maximal
region of the likelihood function are recorded. This vector of
density values is sorted and values at the 16th, 50th and
84th centiles are noted. The interval estimate of the
luminosity density at this given point (x,y,z) is then represented
by the error band bound by values corresponding to the 16th and
84th centiles; the density value at the medial position within
this interval is also shown within this error band.
spread across the ensemble of identified
density values, we actually imply a as 68% interval. To expound
on the procedure of quantifying the errors: at a point (x,y,z),
the values of the luminosity density corresponding to the maximal
region of the likelihood function are recorded. This vector of
density values is sorted and values at the 16th, 50th and
84th centiles are noted. The interval estimate of the
luminosity density at this given point (x,y,z) is then represented
by the error band bound by values corresponding to the 16th and
84th centiles; the density value at the medial position within
this interval is also shown within this error band.
D.2 Updating density
At the beginning of every step, each ![]() -histogram is varied,
independently of each other, while maintaining the realistic
conditions of positivity. In general, the old value of the relevant
variable (X) in step i is related to a new value Y in the next
step: Y = X + Z, where Z is a random variable. A variety of
proposals to move from X to Y are described in the literature
(Mengersen & Tweedie 1996; Gelman et al. 1996). Of these, we choose that the algorithm
proposes to move from X to Y using the random walk jumping
distribution, i.e. Y=X + sU, where U is a Gaussian random
deviate and s is the scale parameter that determines the size of
the jump. If the amount of change is very small, the chain will
require a very large number of steps to become well-mixed and hence
efficiency will be compromised. If the step-size is too large, the
worry is that the resulting configuration will miss the global
maximum and fall into regions of very low likelihoods, wasting a
number of steps in the process (William et al. 2000). Our chosen jump
proposal is adaptive in nature since the updating of
-histogram is varied,
independently of each other, while maintaining the realistic
conditions of positivity. In general, the old value of the relevant
variable (X) in step i is related to a new value Y in the next
step: Y = X + Z, where Z is a random variable. A variety of
proposals to move from X to Y are described in the literature
(Mengersen & Tweedie 1996; Gelman et al. 1996). Of these, we choose that the algorithm
proposes to move from X to Y using the random walk jumping
distribution, i.e. Y=X + sU, where U is a Gaussian random
deviate and s is the scale parameter that determines the size of
the jump. If the amount of change is very small, the chain will
require a very large number of steps to become well-mixed and hence
efficiency will be compromised. If the step-size is too large, the
worry is that the resulting configuration will miss the global
maximum and fall into regions of very low likelihoods, wasting a
number of steps in the process (William et al. 2000). Our chosen jump
proposal is adaptive in nature since the updating of
![]() at a given z, depends on the density at that z.
The details of the density updating is as follows:
at a given z, depends on the density at that z.
The details of the density updating is as follows:
| |
= | ||
| = | (D.1) |
(xkj, ykj, zl) in step n. Also,
We still need to make a change to the overall amplitude of the new
density distribution. This is done by scaling
![]() by another random deviate
by another random deviate
![]() ,
,
![]() ;
here scl2 is another scale that determines the
amount of change of amplitude that is brought about in the density
structure, for a given j, k.
;
here scl2 is another scale that determines the
amount of change of amplitude that is brought about in the density
structure, for a given j, k.
The values of scl1 and scl2 are arrived at experimentally, keeping the effect of large and small scales in mind.
We choose to work with equal binning along all three coordinate axes; this binning is logarithmic in nature. A good choice for the smallest bin size is of the order of the spatial resolution of the data. A typical run takes a few minutes on an Intel Xenon 3.2 GHz CPU processor.
D.3 Temperatures
The probability of accepting the proposed move from likelihood
![]() to
to
![]() is discussed here. Here A generically represents the domain of the likelihood function which is
the set of the
is discussed here. Here A generically represents the domain of the likelihood function which is
the set of the ![]() -histograms and A' is the new set of
-histograms and A' is the new set of
![]() -histograms to which a move has been proposed.
-histograms to which a move has been proposed.
Anxiety over multi-modality of the likelihood function has prompted us
to work both with highly dispersed initial values (or seeds) to
initiate multiple chains (Gelman & Rubin 1992) and also to use simulated
annealing in a single chain. When the latter is implemented, the transmission
probability is
![\begin{displaymath}P(A\rightarrow{A^{'}}) = {\rm min} \displaystyle{\left[ \exp{\frac{\Delta{\cal{L}}}
{T}}, 1 \right]},
\end{displaymath}](/articles/aa/full_html/2010/02/aa12008-09/img156.png)
|
(D.2) |
where
We have implemented both a uniform temperature profile, as well as
played with a cooling schedule that starts with an initial temperature
T0 which is allowed to cool down to a final value of Tf, over a
step number of
![]() .
In practice, we choose Tf/T0 to be 0.1
while
.
In practice, we choose Tf/T0 to be 0.1
while
![]() is typically set to double the number of steps that
correspond to burn-in, as judged from traces of system
characteristics, such as the value of the density that is recovered at
a fiduciary location. We find that the answer depends only very weakly
on the details of the cooling schedule.
is typically set to double the number of steps that
correspond to burn-in, as judged from traces of system
characteristics, such as the value of the density that is recovered at
a fiduciary location. We find that the answer depends only very weakly
on the details of the cooling schedule.
Appendix E: Choice of the regularisation parameter
Thomson et al. (1991) refer to the smoothing parameter as the compromise
between ``fidelity to the data and smoothness''. While different
methods are suggested by Thomson et al. (1991) and
Titterington (1988), to constrain the scalar ![]() ,
we choose
to accept a value that is achieved via an empirical implementation of
the minimisation of the total mean-squared error. We define the total
mean-squared error (TMSE), for a given value of
,
we choose
to accept a value that is achieved via an empirical implementation of
the minimisation of the total mean-squared error. We define the total
mean-squared error (TMSE), for a given value of ![]() as:
as:
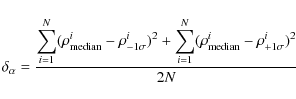
|
(E.1) |
where there are N grid points over which a density profile is recovered and
Appendix F: Choice of seed for density
The robustness of a recursive formalism is reflected in the extent to which the initial guess for the solution is irrelevant to the final result. With this in mind, we undertook extensive experimentation with seed density distributions used by DOPING as starting guesses. For this investigation, we use the same simulated data set of an oblate galaxy, viewed edge-on, as described above: analytical density of Eqs. (10) and a constant eccentricity of 0.99.
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{12008fg14.ps}\\
\includ...
...2008fg15.ps}\\
\includegraphics[width=12.5cm,clip]{12008fg16.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg165.png)
|
Figure F.1:
Top row: robustness of DOPING to changes in the central density of the initial guess for the density
distribution. Density profiles from two runs (in red and green,
superimposed with error-bars), performed with values of the central
density parameter that are apart by eight orders of magnitude, are
shown in the right panel. Superimposed on these is the true density of
the system, shown in black open circles. The initial seeds for the
density distributions in the two runs are shown in dotted lines, in
the corresponding colours. The left panel shows projections of the
recovered density profiles in corresponding colours, with the input
surface brightness data over-plotted as open circles. Middle row: the
scale length parameter of the initial guess is changed. The two runs
correspond to
|
| Open with DEXTER | |
Typically, we use a seed density
![]() ,
where
,
where ![]() denotes the ellipsoidal radius. In fact, we choose a seed density that has a form akin to the Lorentzian distribution:
denotes the ellipsoidal radius. In fact, we choose a seed density that has a form akin to the Lorentzian distribution:
The three parameters in this distribution are:
- the scale length b which determines the width of the profile,
- the central density a and;
- an exponent n that defines the steepness of the fall of the tail of the profile.
The top panels of Fig. F.1 shows the projected surface
brightness and three dimensional luminosity density profiles obtained
from runs done with initial guess characterised by values of central
density (a) that are 8 orders of magnitude different. While one of
the runs (in solid red lines) was started with a central density of
about
![]() /arcsec3, the other (shown in
dotted green lines) corresponds to
/arcsec3, the other (shown in
dotted green lines) corresponds to
![]() /arcsec3. The run shown in Fig. 3 was
carried out with
/arcsec3. The run shown in Fig. 3 was
carried out with
![]() /arcsec3.
/arcsec3.
The panels in the middle row of Fig. F.1 display the
recovered density profiles and their projections when the initial
guess is characterised by scale lengths (the parameter b discussed
above) of 2
![]() 5 and 40''. These values were chosen at two
opposing ends of the value of
b = 10'', which was used in the
run, the results from which are shown in
Fig. 3. It
appears that in spite of the shape of the initial guess being
significantly different from the true profile, the algorithm converges
to the true density profile.
5 and 40''. These values were chosen at two
opposing ends of the value of
b = 10'', which was used in the
run, the results from which are shown in
Fig. 3. It
appears that in spite of the shape of the initial guess being
significantly different from the true profile, the algorithm converges
to the true density profile.
In the lower panel of Fig. F.1, results obtained from runs done with a steepness parameter n=1.8 (in dotted red lines) and n=1.1 (in solid green lines) are shown; the plots in Fig. 3 were retrieved from a run done with n=1.4. The recovered density profiles from these runs are consistent with the true density distribution, within error bars. The implications of these results are discussed in full details in Sect. 5.
References
- Bendinelli, O. 1991, ApJ, 366, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Bissantz, N., & Munk, A. 2001, A&A, 376, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Bosch, F. C. 1997, MNRAS, 287, 543 [NASA ADS] [Google Scholar]
- Cappellari, M. 2002, MNRAS, 333, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarty, D., & Ferrarese, L. 2008, IJMP(D), 17, 195 [NASA ADS] [Google Scholar]
- Chakrabarty, D., de Filippis, E., & Russell, H. 2008, A&A, 487, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Côté, P., Blakeslee, J. P., Ferrarese, L., et al. 2004, ApJS, 153, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D., Rybicki, G., & Gorenstein, P. 1984, ApJ, 286, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., Côté, P., Blakeslee, J. P., et al. 2006, in Black Holes: from Stars to Galaxies - Across the Range of Masses, ed. V. Karas, & G. Matt Proc. IAU Symp., 238 [arXiv:astro-ph/0612139] [Google Scholar]
- Gebhardt, K., Richstone, D., Ajhar, E. A., et al. 1996, AJ, 112, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. B. Statistical Science, 7, 457 [Google Scholar]
- Gelman, A., Carlin, J., Stern, H., et al. 1995, Bayesian Data Analysis (Chapman and Hall) [Google Scholar]
- Gelman, A., Roberts, G. O., et al. 1996, in Bayesian Statistics 5, ed. J. Bernardo et al. (Oxford University Press), 599 [Google Scholar]
- Gerhard, O. E., & Binney, J. J. 1996, MNRAS, 279, 993 [NASA ADS] [Google Scholar]
- Gielis, J. 2003, Am. J. Bot., 90, 333 [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- Haykin, S. S. 2008, Neural Networks and Learning Machines (Prentice Hall) [Google Scholar]
- Jedrzejewski, R. I. 1987, MNRAS, 226, 747 [Google Scholar]
- Jedrzejewski, R. I., Davies, R. L., & Illingworth, G. D. 1987, AJ, 94, 150 [Google Scholar]
- Kochanek, C. S., & Rybicki, G. B. 1996, MNRAS, 280, 1257 [NASA ADS] [Google Scholar]
- Krajnovi, D., Cappellari, M., Emsellem, E., McDermid, R., de Zeeuw, P. T. 2004, MNRAS, 357, 1113 [Google Scholar]
- Kronawitter, A., Saglia, R. P., Gerhard, O., et al. 2000, A&AS, 144, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J. 1999, MNRAS, 302, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Mengersen, K. L., & Tweedie, R. L. 1996, Ann. Statist., 24, 101 [CrossRef] [MathSciNet] [Google Scholar]
- Merritt, D., & Tremblay, B. 1993, AJ, 106, 2229 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., Meylan, G., & Mayor, M. 1997, AJ, 114, 1074 [NASA ADS] [CrossRef] [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., et al. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Palmer, P. L. 1994, MNRAS, 266, 697 [NASA ADS] [Google Scholar]
- Richardson, W. H. 1972, J. Opt. Soc. Am., 62, 55 [Google Scholar]
- Roberts, G., & S. Sahu 1997, J. Roy. Stat. Soc. Ser. B, 59, 291 [CrossRef] [Google Scholar]
- Roberts, G., Gelman, A., & Gilks, W. 1997, The Annals of Applied Probability, 7, 110 [Google Scholar]
- Roberts, G. O., & J. S. Rosenthal 2001, Statistical Science, 16 (4), 351 [Google Scholar]
- Romanowsky, A. J., & Kochanek, C. S. 1997, MNRAS, 287, 35 (RK) [NASA ADS] [Google Scholar]
- Rybicki, G. B. 1987, IAUS, 127, 397 [Google Scholar]
- Sereno, M., De Filippis, E., Longo, G., et al. 2006, ApJ, 645, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Simonneau, E., Varela, A. M., & Munoz-Tunon, C. 1998, Il Nuovo Cimento, 113 B, 927 [Google Scholar]
- Strom, S. E., Strom, K. M., Wells, D. C., et al. 1981, ApJ, 245, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Sha, F., & Saul, L. K. 2005, Proceedings of the Twenty Second International Conference on Machine Learning (ICML-05), Bonn, Germany, 785 [Google Scholar]
- Sun, J., Boyd, S., Xiao, L., et al. 2006, SIAM Rev., 48, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, M. A. 1996, Tools for statistical inference (New York: Springer-Verlag) [Google Scholar]
- Tierney, L. 1994, The Annals of Statistics, 22, 1701 [Google Scholar]
- Titterington, D. M. 1988, IMS Lecture Notes-Monograph Series, ed. A. Possolo, (Hayward, CA: Institute of Mathematical Statistics, 1991), 20, 462 [Google Scholar]
- Thompson, A. M., Brown, J. C., Kay, J. W., et al. 1991, IEEE Transactions to Patten Analysis & Machine Intelligence, 13, 326 [CrossRef] [Google Scholar]
- Weinberger, K. Q., & Saul, L. K. 2006, Proceedings of the Twenty First National Conference on Artificial Intelligence (AAAI-06), Boston, USA [Google Scholar]
- Wang, A., Cherry, C., Lizotte, D., et al. 2006, Proceedings of the 10th Conference on Computational Natural Language Learning (CONLL), NY, USA [Google Scholar]
- William, J. B., Draper, D., Down, D., et al. 2000, Computational Statistics, 15, 391 [CrossRef] [Google Scholar]
- Yong, K., Sahoo, Y., Roy Choudhury, K., et al. 2006, Nano Letters, 6, 709 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Footnotes
- ... account
![[*]](/icons/foot_motif.png)
- Such a broad class of solid shapes are perhaps an overkill for astrophysical applications, but these shapes do indeed show up in nature, for example, the wide range of shapes of images of deposited nanoparticles (taken with Transmission Electron Microscope) indicate that these would require such a description (Yong et al. 2006).
- ... 2008)
![[*]](/icons/foot_motif.png)
- Such motivation is also found in Maximum Variance Unfolding that also implements Laplacian regularisation and has been studied by Sha & Saul (2005); Weinberger & Saul (2006); Sun et al. (2006).
- ... brightness
![[*]](/icons/foot_motif.png)
- Note that although we will use units of magnitude for the surface brightness and density profile, DOPING works in linear units of intensity.
- ... shapes
![[*]](/icons/foot_motif.png)
- Such geometries, though not relevant to astrophysics, occur in nature. For example, 2-D images of grown nanoparticles, taken with a Transmission Electron Microscope, exhibit a wide variety of shapes that can be accommodated by the superformula (Yong et al. 2006).
All Figures
![\begin{figure}
\par\includegraphics[width=8cm, angle=0]{12008fg1.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg38.png)
|
Figure 1:
Geometrical considerations adopted in the
design of the algorithm. The system is represented as the
ellipsoid. The X, Y and Z axes (in thin black lines)
represent the three principle axes of the system while x and y mark the photometric axes and the z-axis is the LOS (in thicker
black lines). A rectangular section of the image plane (i.e. the
z = 0 plane) is represented by the tilted rectangle in the broken
lines; this plane cuts the ellipsoid in an elliptical disk which
is depicted by the translucent gray disk. Generic isophotal
annuli on this disk are depicted in centrally increasing
gray-scale intensity. Two generic points, lying inside the
intermediate isophotal annulus, are shown as the two black
squares. The extent of the system along the positive z-axis, at
these two marked points are represented by the lengths of the
white rectangles that are oriented parallel to the LOS. In the
text, one such point, generically considered to be inside the
kth isophotal annulus, is referred to as
(xjk, yjk, 0),
while the tip of the white rectangle emanating from this point is
ascribed coordinates
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm]{12008fg2.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg95.png)
|
Figure 2: The chosen eccentricity profile of the test galaxy Test I, shown as a function of r, in filled circles. The same for Test II is shown in open circles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12008fg3.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg98.png)
|
Figure 3:
Performance of DOPING in the simulated
test cases Test I (a disk galaxy with a round ellipsoidal centre that
extends to only about 0
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12008fg4.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg99.png)
|
Figure 4: Left: the 2-D surface brightness (in mag/arcsec2) distribution of our flat test galaxy Test I, as a contour plot on the plane of the sky (x-y plane). The contours in broken lines pertain to the toy brightness data that was fed into DOPING while the solid lines represent the projection of the 3-D luminosity density that DOPING recovers. The gap around y = 0 occurs in the distribution of the projected density since the smallest (logarithmic) spatial bin is about 1pixel, i.e. 0''.05. Right: same as for the left panel, except that in this case, the central rounder part of the test galaxy has been focused upon. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg5.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg101.png)
|
Figure 5: 2-D surface brightness (in mag/arcsec2) distribution of the elliptical test galaxy Test II, compared to the plane of the sky projection of the luminosity distribution recovered by DOPING for this system. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg6.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg107.png)
|
Figure 6:
Luminosity density distributions recovered
by deprojecting the surface brightness profile given by
Eq. (11), under the assumption of oblateness, given a
projected eccentricity of 0.71, viewed at inclinations of about
46 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg7.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg116.png)
|
Figure 7: Central luminosity density, plotted as a function of inclination for four different values of the intrinsic eccentricity. When the intrinsic eccentricity is 0.71, the obtained central density points are shown in black. The colour coding for the other values of e is as follows: e = 0.87, 0.95 and 0.99 correspond to red, green and blue, respectively. The case of inclination = 0 obviously indicates the situation when the observed isophotes are circular, i.e. the observed projected eccentricity is zero. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg8.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg117.png)
|
Figure 8: Luminosity density of our oblate test galaxy of projected eccentricity 0.99 (shown in red), recovered by DOPING, under the assumptions of prolateness (in blue), oblateness (in black) and triaxiality with ratio between LOS extent and photometric major axis = 0.5 (in green). All the deprojections were carried out for an edge-on viewing. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12008fg10.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg121.png)
|
Figure 9: Left: luminosity density of an oblate test galaxy with uniform eccentricity of 0.99, recovered by comparing the input brightness profile with the PSF convolved projection of the density in any iterative step. The PSF in question is the ACS PSF in the F850W filter. When the convolution with the PSF is ignored, the recovered density is shown in green. Right: difference between the density profiles obtained with and without convolving with the PSF. It is noted that inside the central 10'', this difference is 2 orders of magnitude less than density while outside 10'', the difference tends to zero. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12008fg11.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg122.png)
|
Figure 10:
Effect of increasing the smoothing
parameter |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg9.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg125.png)
|
Figure 11: As in Fig. 5, except that in this case, the plane of the sky brightness distribution of the galaxy IC 3019 is shown. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12008fg13.ps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg126.png)
|
Figure 12:
X-ray luminosity density profile of cluster A1413,
recovered under the true system geometry (
q1 = 0.96,
q2 = 1.64)
and inclination = 68.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{12008fg12.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg131.png)
|
Figure 13:
Luminosity density of the two-component galaxy Ic 3881 along the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{12008fg14.ps}\\
\includ...
...2008fg15.ps}\\
\includegraphics[width=12.5cm,clip]{12008fg16.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa12008-09/Timg165.png)
|
Figure F.1:
Top row: robustness of DOPING to changes in the central density of the initial guess for the density
distribution. Density profiles from two runs (in red and green,
superimposed with error-bars), performed with values of the central
density parameter that are apart by eight orders of magnitude, are
shown in the right panel. Superimposed on these is the true density of
the system, shown in black open circles. The initial seeds for the
density distributions in the two runs are shown in dotted lines, in
the corresponding colours. The left panel shows projections of the
recovered density profiles in corresponding colours, with the input
surface brightness data over-plotted as open circles. Middle row: the
scale length parameter of the initial guess is changed. The two runs
correspond to
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



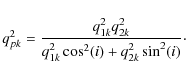
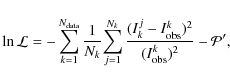
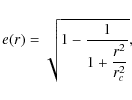
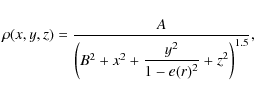
![\begin{displaymath}I (x, y) = 2\displaystyle{\frac{A}{\left[B^2 + (x^2+y^2)
\le...
...ght)\right] \sqrt{1+ \displaystyle{\frac{y^2}{r_c^2}}}}}\cdot
\end{displaymath}](/articles/aa/full_html/2010/02/aa12008-09/img96.png)