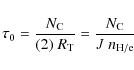| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200911683 | |
| Published online | 04 February 2010 | |
Polycyclic aromatic hydrocarbon processing in a hot gas
E. R. Micelotta1,2 - A. P. Jones2 - A. G. G. M. Tielens1,3
1 - Sterrewacht Leiden, Leiden University, PO Box 9513, 2300 RA Leiden,
The Netherlands
2 - Institut d'Astrophysique Spatiale, Université Paris Sud and CNRS
(UMR 8617), 91405 Orsay, France
3 - NASA Ames Research Center, MS 245-3, Moffett Field, CA 94035, USA
Received 20 January 2009 / Accepted 16 October 2009
Abstract
Context. PAHs are thought to be a ubiquitous and
important dust component of the interstellar medium. However, the
effects of their immersion in a hot (post-shock) gas have never before
been fully investigated.
Aims. We study the effects of energetic ion and
electron collisions on PAHs in the hot post-shock gas behind
interstellar shock waves.
Methods. We calculate the ion-PAH and electron-PAH
nuclear and electronic interactions, above the carbon atom loss
threshold, in H II regions and in
the hot post-shock gas for temperatures ranging from 103-108 K.
Results. PAH destruction is dominated by He
collisions at low temperatures (
![]() K), and by electron
collisions at higher temperatures. Smaller PAHs are destroyed faster
for T < 106 K,
but the destruction rates are roughly the same for all PAHs at higher
temperatures. The PAH lifetime in a tenuous hot gas (
K), and by electron
collisions at higher temperatures. Smaller PAHs are destroyed faster
for T < 106 K,
but the destruction rates are roughly the same for all PAHs at higher
temperatures. The PAH lifetime in a tenuous hot gas (
![]() cm-3,
cm-3,
![]() K), typical of the
coronal gas in galactic outflows, is found to be about thousand years,
orders of magnitude shorter than the typical lifetime of such objects.
K), typical of the
coronal gas in galactic outflows, is found to be about thousand years,
orders of magnitude shorter than the typical lifetime of such objects.
Conclusions. In a hot gas, PAHs are principally
destroyed by electron collisions and not by the absorption of X-ray
photons from the hot gas. The resulting erosion of PAHs occurs via C2
loss from the periphery of the molecule, thus preserving the aromatic
structure. The observation of PAH emission from a million degree, or
more, gas is only possible if the emitting PAHs are ablated from dense,
entrained clumps that have not yet been exposed to the full effect of
the hot gas.
Key words: shock waves - dust, extinction - ISM: jets and outflows
1 Introduction
The mid-infrared spectral energy distribution of the general
interstellar medium of galaxies is dominated by strong and broad
emission features at 3.3, 6.2, 7.7 and 11.3 ![]() m. These
features are now univocally attributed to vibrational fluorescence of
UV pumped, large (
m. These
features are now univocally attributed to vibrational fluorescence of
UV pumped, large (![]() 50 C-atoms)
polycyclic aromatic hydrocarbon (PAHs) molecules. These large molecules
are very abundant (
50 C-atoms)
polycyclic aromatic hydrocarbon (PAHs) molecules. These large molecules
are very abundant (
![]() by number relative
to H-nuclei) and ubiquitous in the ISM (for a recent review see Tielens 2008). Besides large PAH
molecules, the spectra also reveal evidence for clusters of PAHs -
containing some hundreds of carbon atoms - and very small grains (
by number relative
to H-nuclei) and ubiquitous in the ISM (for a recent review see Tielens 2008). Besides large PAH
molecules, the spectra also reveal evidence for clusters of PAHs -
containing some hundreds of carbon atoms - and very small grains (![]() 30 Å).
Indeed, PAHs seem to represent the extension of the interstellar dust
size distribution into the molecular domain (e.g. Draine &
Li 2001; Désert
et al. 1990).
30 Å).
Indeed, PAHs seem to represent the extension of the interstellar dust
size distribution into the molecular domain (e.g. Draine &
Li 2001; Désert
et al. 1990).
PAH molecules are an important component of the ISM, for
example, dominating the photoelectric heating of neutral atomic gas and
the ionization balance of molecular clouds. Small dust grains and PAHs
can also be important agents in cooling a hot gas, at temperatures
above ![]() K (e.g. Dwek 1987), through their
interactions with thermal electrons and ions. The energy transferred in
electron and ion collisions with the dust is radiated as infrared
photons. The evolution of dust in such hot gas (
K (e.g. Dwek 1987), through their
interactions with thermal electrons and ions. The energy transferred in
electron and ion collisions with the dust is radiated as infrared
photons. The evolution of dust in such hot gas (
![]() K), e.g., within
supernova remnants and galactic outflows, is critical in determining
the dust emission from these regions and therefore the cooling of the
hot gas. The destruction of PAHs and small dust grains in a hot gas may
also be an important process in the lifecycle of such species (Jones
et al. 1996; Dwek et al. 1996).
K), e.g., within
supernova remnants and galactic outflows, is critical in determining
the dust emission from these regions and therefore the cooling of the
hot gas. The destruction of PAHs and small dust grains in a hot gas may
also be an important process in the lifecycle of such species (Jones
et al. 1996; Dwek et al. 1996).
Observationally, there is little direct evidence for PAH
emission unequivocally connected to the hot gas in supernova remnants. Reach et al. (2006) have
identified four supernova remnants with IR colors that may indicate PAH
emission. Tappe et al. (2006)
have detected spectral structure in the emission characteristics of the
supernova remnant N132D in the Large Magellanic Cloud that
they attribute to spectral features of PAHs with sizes of ![]() 4000 C-atoms.
Bright 8
4000 C-atoms.
Bright 8 ![]() m
emission has been observed by IRAC/Spitzer associated with the X-ray
emission from the stellar winds of the ionizing stars in the
M 17 H II region (Povich et al. 2007).
Likely, this emission is due to PAHs - probably, in entrained gas
ablated from the molecular clouds to the north and west of the stellar
cluster. Finally, bright PAH emission has been detected associated with
the hot gas of the galactic wind driven by the starburst in the nucleus
of the nearby irregular galaxy, M 82 (Beirão
et al. 2008; Galliano et al. 2008; Engelbracht
et al. 2006).
m
emission has been observed by IRAC/Spitzer associated with the X-ray
emission from the stellar winds of the ionizing stars in the
M 17 H II region (Povich et al. 2007).
Likely, this emission is due to PAHs - probably, in entrained gas
ablated from the molecular clouds to the north and west of the stellar
cluster. Finally, bright PAH emission has been detected associated with
the hot gas of the galactic wind driven by the starburst in the nucleus
of the nearby irregular galaxy, M 82 (Beirão
et al. 2008; Galliano et al. 2008; Engelbracht
et al. 2006).
Electron and ion interactions with dust and the implications of those interactions for the dust evolution and emission have already been discussed in the literature (e.g. Draine & Salpeter 1979; Dwek 1987; Jones et al. 1994,1996; Dwek et al. 1996). In this work we extend this earlier work to the case for PAHs, using our study of PAH evolution due to ion and electron interactions in shock waves in the ISM (Micelotta et al. 2010, hereafter MJT). Here we consider the fate of PAHs in the hot gas behind fast non-radiative shocks and in a hot gas in general.
The aim of this paper is to study the PAH stability against electron and ion collisions (H, He and C) in a thermal gas with temperature T in the range 103-108 K.
The paper is organized as follows: Sects. 2 and 3 describe the treatment of ion and electron interactions with PAHs, Sect. 4 illustrates the application to PAH processing in a hot gas and Sect. 5 presents our results on PAH destruction and lifetime. The astrophysical implications are discussed in Sect. 6 and our conclusions summarized in Sect. 7.
2 Ion interaction with PAHs
2.1 Electronic interaction
The ion - PAH collision can be described in terms of two simultaneous processes which can be treated separately (Lindhard et al. 1963): nuclear stopping or elastic energy loss and electronic stopping or inelastic energy loss.
The nuclear stopping consists of a binary collision between the incoming ion (projectile) and a single atom in the target material. A certain amount of energy will be transferred directly to the target atom, which will be ejected if the energy transferred is sufficient to overcome the threshold for atom removal. The physics of the nuclear interaction for a PAH target was presented in the companion paper (MJT). A summary of the theory is provided in Sect. 2.2 and we here present the results of our calculation.
In this paper we focuse on the electronic stopping, which consists of the interaction between the projectile and the electrons of the target PAH, with a subsequent energy transfer to the whole molecule. The resulting electronic excitation energy will be transferred to the molecular vibrations of the PAH through radiationless processes (e.g., interconversion & intramolecular vibrational redistribution). The vibrationally excited molecule will decay through either (IR) photon emission or through fragmentation (i.e., H-atom or C2Hn loss, where n = 0, 1, 2).
No specific theory describes the energy transfer to a PAH via electronic excitation, so we adopt the same approach developed by e.g. Schlathölter et al. (1999) and Hadjar et al. (2001) who modelled electronic interactions in fullerene, C60. To calculate the energy transferred to a PAH, we treat the large number of delocalized valence electrons in the molecule as an electron gas, where the inelastic energy loss of traveling ions is due to long range coupling to electron-hole pairs (Ferrell 1979).
In the energy range we consider for this study, the energy
transferred scales linearly with the velocity v of
the incident ion and can be described in term of the stopping power S,
which is widely used in the treatment of ion-solid collisions. The
stopping power represents the energy loss per unit length and is
defined as
where dT is the energy loss over the pathlength ds (Sigmund 1981). The total energy loss can then be obtained integrating Eq. (1)
The friction coefficient
where r (in atomic units, a.u.
The similarity in ![]() electronic structure and bonding allows us to apply this jellium model
also to PAHs. However, the spherical geometry
is clearly not appropriate for PAHs, which we model instead as a thick
disk analogously to the distribution from Eq. (3)
electronic structure and bonding allows us to apply this jellium model
also to PAHs. However, the spherical geometry
is clearly not appropriate for PAHs, which we model instead as a thick
disk analogously to the distribution from Eq. (3)
where x is the coordinate along the thickness of the disk. This electron density peaks at the center of the molecule and vanishes outside, leading to a thickness
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{11683fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg32.png)
|
Figure 1:
The coordinate system adopted to calculate the energy transferred to a
PAH via electronic excitation by ion collisions and by impacting
electrons. The molecule is modeled as a disk with radius R
and thickness d. The trajectory of the incoming
particle is identified by the angle |
| Open with DEXTER | |
To calculate the energy transferred from Eq. (2), we adopt
the coordinate system shown in Fig. 1, where the
pathlength through the
PAH s is expressed as a function of the
coordinate x and of the angle ![]() between the axes of the molecule and the direction of the incoming ion.
In this way for each trajectory given by
between the axes of the molecule and the direction of the incoming ion.
In this way for each trajectory given by ![]() the corresponding energy transferred can be computed. We have
the corresponding energy transferred can be computed. We have ![]() and the electron density is then given by
and the electron density is then given by
The density parameter can be rewritten as
where
The energy transferred is then given by the following equation
with
The energy transferred determines the PAH dissociation probability upon electronic excitation, which is required to quantify the destruction induced by inelastic energy loss in the hot gas (see Sect. 4).
2.2 Nuclear interaction above threshold
In the present study we have to consider not only the electronic interaction described above, but the nuclear part of the ionic collision as well. The theory of nuclear interaction above threshold has been described in detail in MJT. We summarize here for clarity the essential concepts and the equations which will be used in the following.
For the nuclear interaction we consider only collisions above
threshold, i.e. collisions able to transfer more than the minimum
energy ![]() required to remove a C-atom from the PAH. To calculate the PAH
destruction due to nuclear
interaction, we use the rate of collisions above threshold between PAHs
and ions in a thermal gas, as given by Eq. (30) in MJT:
required to remove a C-atom from the PAH. To calculate the PAH
destruction due to nuclear
interaction, we use the rate of collisions above threshold between PAHs
and ions in a thermal gas, as given by Eq. (30) in MJT:
where f(v,T) is the Maxwellian velocity distribution function for ion, i, in the gas,
For ![]() we adopt a value of 7.5 eV (see discussion in MJT,
Sect. 2.2.1). The kinetic energy required for the incoming ion
to transfer
we adopt a value of 7.5 eV (see discussion in MJT,
Sect. 2.2.1). The kinetic energy required for the incoming ion
to transfer ![]() is the critical energy E0.
The lower integration limit v0
in Eq. (8)
is the critical velocity corresponding to
is the critical energy E0.
The lower integration limit v0
in Eq. (8)
is the critical velocity corresponding to ![]() ,
which is the minimum kinetic energy for the projectile to have the
nuclear interaction cross section different from zero
(cf. Sect. 2.2 in MJT).
,
which is the minimum kinetic energy for the projectile to have the
nuclear interaction cross section different from zero
(cf. Sect. 2.2 in MJT).
3 Electron collisions with PAHs
Fast electrons are abundant in a hot gas. Because of their low mass,
they can reach very high velocities with respect to the ions, and hence
high
rates of potentially destructive collisions. We consider gas
temperatures
up to 108 K, corresponding to a thermal
electron energy of ![]() 10 keV,
well below the relativistic limit of
10 keV,
well below the relativistic limit of ![]() 500 keV.
Under these low-energy conditions, with respect to the relativistic
regime, elastic collisions between electrons and target nuclei are not
effective. The energy transfer occurs through inelastic interactions
with target electrons (as for electronic excitation by impacting ions),
which lead to a collective excitation of the molecule, followed
eventually by dissociation or relaxation through IR emission.
500 keV.
Under these low-energy conditions, with respect to the relativistic
regime, elastic collisions between electrons and target nuclei are not
effective. The energy transfer occurs through inelastic interactions
with target electrons (as for electronic excitation by impacting ions),
which lead to a collective excitation of the molecule, followed
eventually by dissociation or relaxation through IR emission.
The calculation of the energy transferred by such ``slow'' electrons is in fact a delicate matter. The theory developed under the first Born approximation (Bethe 1930) can be applied only to the most energetic electrons (around few keV) but is unsuitable for the rest of our range. At low energies (<10 keV), where the first Born approximation is no longer valid, the Mott elastic cross section must be used instead of the conventional Rutherford cross section (Mott & Massey 1949; Czyzewski et al. 1990). The Monte Carlo program CASINO (Hovington et al. 1997) computes the Mott cross sections in the simulation of electron interactions with various materials. Unfortunately the stopping power dE/dx is not included in the program output. An empirical expression for dE/dx has been proposed by Joy & Luo (1989), which nevertheless is reliable only down to 50 eV, while we are interested in the region between 10 and 50 eV as well.
We decided thus to derive the electron stopping power from
experimental results.
Measurements of the electron energy loss in PAHs are not available in
our energy
range of interest, so we use the measurement of dE/dx
in solid carbon for electrons
with energy between 10 eV and 2 keV (Joy 1995). The data points are well
fitted (to within few %) by the following function:
where E is the electron energy (in keV). The values of the fitting parameters are reported in Table 1. S(E) has the same functional form as the ZBL reduced stopping cross section for nuclear interaction (cf. Sect. 2.1 in MJT). The datapoints and the fitting function are shown in the top panel of Fig. 2.
Table 1: Analytical fit to the electron stopping power in solid carbon.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11683fg2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg52.png)
|
Figure 2: Top panel - Experimental measurement of dE/dx in solid carbon for electrons with energy between 10 eV and 2 keV, from Joy (1995), overlaid with the fitting function S(E) (solid line). Bottom panel - Integral F calculated numerically as a function of the energy of the incident electron, E. |
| Open with DEXTER | |
The stopping power increases sharply at low electron energies, reaches
its maximum
at ![]() 0.1 keV,
and decreases smoothly afterwards. Between 0.01 and 0.1 keV a
small
variation of the energy of the incident electron will translate into a
large change
in the transferred energy per unit length. The shape of S(E)
implies that
only those electrons with energies that fall in a well defined window
will efficiently
transfer energy, while electrons below
0.1 keV,
and decreases smoothly afterwards. Between 0.01 and 0.1 keV a
small
variation of the energy of the incident electron will translate into a
large change
in the transferred energy per unit length. The shape of S(E)
implies that
only those electrons with energies that fall in a well defined window
will efficiently
transfer energy, while electrons below ![]() 0.02 keV and above
0.02 keV and above ![]() 2 keV
are not
expected to contribute significantly to PAH excitation.
2 keV
are not
expected to contribute significantly to PAH excitation.
Once the stopping power dE/dx
is known, we can calculate the energy
transferred by an electron of given energy when travelling through the
PAH. We adopt
the same configuration used for electronic interaction, shown in
Fig. 1.
The trajectory of the incoming electron is defined by its impact angle ![]() and
by the geometry of the molecule.
and
by the geometry of the molecule.
Because the thickness of the PAH is non-negligible with
respect to its radius,
the stopping power is not constant along the electron path. To
calculate the energy loss we thus follow the procedure described below.
We have ![]() ,
then
,
then
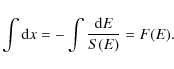
|
(10) |
Thus,
The integral F, calculated numerically as a function of E, is shown in the bottom panel of Fig. 2. We recognize that for low energies, F rises sharply, reflecting the small energy stopping power in this energy range (cf., top panel in Fig. 2). For higher energies, F(E) rises slowly (and linearly) with increasing energy over the relevant energy range. We note that the initial rise depends strongly on the (uncertain) details of the stopping power at low energies. However, it is of no consequence in our determination of the amount of energy deposited since we are only concerned with those collisions for which the energy deposition is in excess of the threshold energy (
4 PAH destruction
4.1 Dissociation probability
Ion or electronic collisions (or UV photon absorption) can leave the
molecule internally (electronically) excited with an energy ![]() .
Internal conversion transfers this energy to vibrational modes, and the
molecule can then relax through dissociation or IR emission. These two
processes are in competition with each other. To quantify the PAH
destruction due to ion and electron collisions we need to determine the
probability of dissociation rather than IR emission.
.
Internal conversion transfers this energy to vibrational modes, and the
molecule can then relax through dissociation or IR emission. These two
processes are in competition with each other. To quantify the PAH
destruction due to ion and electron collisions we need to determine the
probability of dissociation rather than IR emission.
In the microcanonical description of a PAH, the internal
energy, ![]() ,
is (approximately) related to the effective temperature of the system,
,
is (approximately) related to the effective temperature of the system, ![]() ,
by the following equation
,
by the following equation
where
where
Consider the competition between photon emission at a rate ![]() (photons s-1)
and dissociation at a rate of
(photons s-1)
and dissociation at a rate of ![]() (fragments s-1). For simplicity,
we will assume that all photons have the same energy,
(fragments s-1). For simplicity,
we will assume that all photons have the same energy, ![]() .
The
probability that the PAH will fragment between the nth
and (n+1)th photon
emission is given by
.
The
probability that the PAH will fragment between the nth
and (n+1)th photon
emission is given by
The (un-normalized) probability per step pi is given by
If we ignore the dependence of
These equations become very difficult to solve in closed form. However, let us just assume that pi does not vary and is given by
where we adopt
where
If the pi's
were truly constant, then ![]() would be
would be ![]() .
However, they do decrease. So, rather we take it to be when the
probability per step has
dropped by a factor 10. A direct comparison between the full evaluation
and this simple
approximation yields
.
However, they do decrease. So, rather we take it to be when the
probability per step has
dropped by a factor 10. A direct comparison between the full evaluation
and this simple
approximation yields ![]() ,
20 and 40 for
,
20 and 40 for ![]() ,
100 and 200
respectively. The quantity
,
100 and 200
respectively. The quantity ![]() scales with
scales with ![]() because for a constant
temperature (e.g., required to get the dissociation to occur), the
internal energy has to
scale with
because for a constant
temperature (e.g., required to get the dissociation to occur), the
internal energy has to
scale with ![]() .
As a result, the number of photons to be emitted also has to scale
with
.
As a result, the number of photons to be emitted also has to scale
with ![]() .
.
The choice of the values to adopt for ![]() and
and ![]() is a delicate matter. In the laboratory the dissociation of highly
vibrationally excited PAHs is typically measured on timescales of
1-100
is a delicate matter. In the laboratory the dissociation of highly
vibrationally excited PAHs is typically measured on timescales of
1-100 ![]() s
because either the molecules are collisionally de-excited by ambient
gas or the molecules have left the measurement zone of the apparatus.
In contrast, in the ISM, the competing relaxation channel is through IR
emission and occurs typically on a timescale of 1 s. As is always the
case for reactions characterized by an Arrhenius law, a longer
timescale implies that the internal excitation energy can be lower.
This kinetic shift is well established experimentally and can amount to
many eV. Moreover, only small PAHs (up to 24 C-atoms)
have been measured in the laboratory and the derived rates have to be
extrapolated to much larger (
s
because either the molecules are collisionally de-excited by ambient
gas or the molecules have left the measurement zone of the apparatus.
In contrast, in the ISM, the competing relaxation channel is through IR
emission and occurs typically on a timescale of 1 s. As is always the
case for reactions characterized by an Arrhenius law, a longer
timescale implies that the internal excitation energy can be lower.
This kinetic shift is well established experimentally and can amount to
many eV. Moreover, only small PAHs (up to 24 C-atoms)
have been measured in the laboratory and the derived rates have to be
extrapolated to much larger (![]() 50 C-atoms)
PAHs that are astrophysically relevant. In an astrophysical context,
the unimolecular dissociation of highly vibrationally excited PAHs -
pumped by FUV photons - has been studied experimentally by Jochims et al. (1994) and
further analyzed by Le Page
et al. (2001). Here, we will modify the analysis of Tielens (2005) for H-loss by UV
pumped PAHs to determine the parameters for carbon loss. The
dissociation rate - given by Eq. (13) - is governed
by two factors, the pre-exponential factor
50 C-atoms)
PAHs that are astrophysically relevant. In an astrophysical context,
the unimolecular dissociation of highly vibrationally excited PAHs -
pumped by FUV photons - has been studied experimentally by Jochims et al. (1994) and
further analyzed by Le Page
et al. (2001). Here, we will modify the analysis of Tielens (2005) for H-loss by UV
pumped PAHs to determine the parameters for carbon loss. The
dissociation rate - given by Eq. (13) - is governed
by two factors, the pre-exponential factor ![]() and the energy
and the energy ![]() .
The pre-exponential factor is given by
.
The pre-exponential factor is given by
where
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{11683fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg94.png)
|
Figure 3:
The appearance energy as a function of the number of C-atoms in the
PAH. The red line provides a fit to the experimental data using
Eq. (13)
for an assumed pre-exponential factor |
| Open with DEXTER | |
The derived Arrhenius energy of 3.65 eV is small compared to
the binding energy of a C![]() H
H![]() group in a PAH (4.2 eV, Ling
& Lifshitz 1998). This is a well known problem in
statistical unimolecular dissociation theories (cf. Tielens 2008). We emphasize that
these results show that a typical interstellar PAH with a size of 50
C-atoms would have a dissociation probability of
group in a PAH (4.2 eV, Ling
& Lifshitz 1998). This is a well known problem in
statistical unimolecular dissociation theories (cf. Tielens 2008). We emphasize that
these results show that a typical interstellar PAH with a size of 50
C-atoms would have a dissociation probability of ![]() 1/2 after absorption of an FUV
photon of
1/2 after absorption of an FUV
photon of ![]() 12 eV
(cf. Fig. 3).
Hence, PAHs would be rapidly lost in the ISM through photolysis. It
seems that the experiments on small PAHs cannot be readily extrapolated
to larger, astrophysically relevant PAHs. Possibly, this is because
experimentally C2H2 loss
has only been observed for very small catacondensed PAHs with a very
open carbon skeleton (e.g., naphthalene, anthracene, and phenanthrene)
which are likely much more prone to dissociation than the
astrophysically more relevant pericondensed PAHs. Indeed, the small
pericondensed PAHs, pyrene and coronene did not show any dissociation
on the experimental timescales (Ling & Lifshitz 1998; Jochims
et al. 1994).
12 eV
(cf. Fig. 3).
Hence, PAHs would be rapidly lost in the ISM through photolysis. It
seems that the experiments on small PAHs cannot be readily extrapolated
to larger, astrophysically relevant PAHs. Possibly, this is because
experimentally C2H2 loss
has only been observed for very small catacondensed PAHs with a very
open carbon skeleton (e.g., naphthalene, anthracene, and phenanthrene)
which are likely much more prone to dissociation than the
astrophysically more relevant pericondensed PAHs. Indeed, the small
pericondensed PAHs, pyrene and coronene did not show any dissociation
on the experimental timescales (Ling & Lifshitz 1998; Jochims
et al. 1994).
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{11683fg4.eps} \end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg96.png)
|
Figure 4:
The probability for dissociation of a 50 C-atom PAH excited by
10 eV as a function of the Arrhenius energy, |
| Open with DEXTER | |
Turning the problem around, we can determine the Arrhenius energy, ![]() ,
as a function of the dissociation probability by adopting an IR
relaxation rate of 1 s-1 and an internal
excitation energy equal to a typical FUV photon energy
(12 eV). The results for a 50 C-atom PAH are shown in
Fig 4.
If we adopt a lifetime,
,
as a function of the dissociation probability by adopting an IR
relaxation rate of 1 s-1 and an internal
excitation energy equal to a typical FUV photon energy
(12 eV). The results for a 50 C-atom PAH are shown in
Fig 4.
If we adopt a lifetime, ![]() ,
of 100 million years, a PAH in the diffuse ISM will have typically
survived some
,
of 100 million years, a PAH in the diffuse ISM will have typically
survived some ![]() UV photon absorptions (with
UV photon absorptions (with ![]() cm2,
cm2,
![]() photons cm-2 s-1
in a Habing field). Hence, if the lifetime of the smallest PAHs in the
ISM (e.g., with
photons cm-2 s-1
in a Habing field). Hence, if the lifetime of the smallest PAHs in the
ISM (e.g., with ![]() C-atom)
is set by photodissociation of the C-skeleton, the probability for
dissociation has to be
C-atom)
is set by photodissociation of the C-skeleton, the probability for
dissociation has to be ![]() corresponding to an Arrhenius energy of 4.6 eV (Fig. 4). We note that in
a PDR the photon flux is higher (
corresponding to an Arrhenius energy of 4.6 eV (Fig. 4). We note that in
a PDR the photon flux is higher (
![]() )
while the lifetime (of the PDR) is smaller (
)
while the lifetime (of the PDR) is smaller (
![]() yr),
resulting in
yr),
resulting in ![]() UV photons
absorbed over the PDR lifetime. Survival of PAHs in a PDR environment
would therefore require a somewhat larger E0
(or alternatively, only slightly larger PAHs could survive in such an
environment).
UV photons
absorbed over the PDR lifetime. Survival of PAHs in a PDR environment
would therefore require a somewhat larger E0
(or alternatively, only slightly larger PAHs could survive in such an
environment).
We note that the binding energy of a C![]() H
H![]() group to small PAHs is estimated to be 4.2 eV and is probably
somewhat larger for a 50 C-atom condensed PAH. Loss of pure carbon, on
the other hand, requires an energy of 7.5 eV, close to the
binding energy of C to graphite. Loss of C
group to small PAHs is estimated to be 4.2 eV and is probably
somewhat larger for a 50 C-atom condensed PAH. Loss of pure carbon, on
the other hand, requires an energy of 7.5 eV, close to the
binding energy of C to graphite. Loss of C![]() from fullerenes has a measured
from fullerenes has a measured ![]() of
of ![]() eV (Tomita et al. 2001).
These latter two unimolecular dissociation channels are for all
practical purposes closed under interstellar conditions. Finally,
likely, H-loss will be the dominant destruction loss channel for large
PAHs (E0=3.3 eV),
leading to rapid loss of all H's (Le Page et al. 2001; Tielens 2005).
The resulting pure C-skeleton may then isomerize to much more stable
carbon clusters, in particular fullerenes, and this may be the dominant
``loss'' channel for interstellar PAHs (cf. Tielens
2008, and references therein). It is clear that there are
many uncertainties in the chemical destruction routes of interstellar
PAHs and that these can only be addressed by dedicated experimental
studies. For now, in our analysis of the unimolecular dissociation of
PAHs - excited by electron or ion collisions - we will adopt
eV (Tomita et al. 2001).
These latter two unimolecular dissociation channels are for all
practical purposes closed under interstellar conditions. Finally,
likely, H-loss will be the dominant destruction loss channel for large
PAHs (E0=3.3 eV),
leading to rapid loss of all H's (Le Page et al. 2001; Tielens 2005).
The resulting pure C-skeleton may then isomerize to much more stable
carbon clusters, in particular fullerenes, and this may be the dominant
``loss'' channel for interstellar PAHs (cf. Tielens
2008, and references therein). It is clear that there are
many uncertainties in the chemical destruction routes of interstellar
PAHs and that these can only be addressed by dedicated experimental
studies. For now, in our analysis of the unimolecular dissociation of
PAHs - excited by electron or ion collisions - we will adopt ![]() eV
as a standard value. We will however also examine the effects of
adopting
eV
as a standard value. We will however also examine the effects of
adopting ![]() eV
(e.g., p=1/2) and
eV
(e.g., p=1/2) and ![]() eV
(e.g.,
eV
(e.g., ![]() ).
).
4.2 Collision rate
Once the dissociation probability is determined, we can calculate the
destruction rate through electronic excitation following electron or
ion collision. Adopting the configuration shown in Fig. 1, the destruction
rate is given by
with
The term v is the velocity of the incident particle,
which reduces to
We are considering a hot gas and therefore we are interested
in the thermal
collision rate, given by
where
![\begin{figure}
\par\includegraphics[width=13cm,clip]{11683fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg126.png)
|
Figure 5:
Nuclear (dashed lines), electronic (solid lines) and electron
(dashed-dotted lines) rate constant for PAH carbon atom loss due to
collisions with H, He, C and electrons in a thermal gas. The rate
constants are calculated as a function of the gas temperature for three
PAH sizes |
| Open with DEXTER | |
5 Results
5.1 PAH destruction in a hot gas
To describe the destructive effects on PAHs of collisions with ions i (i = H, He, C) and electrons in a thermal gas we have to evaluate the rate constant for carbon atom loss.
For all processes the rate constant J is
defined by
the ratio ![]() ,
where
,
where ![]() is the thermal collision rate appropriate for nuclear and electronic
excitation and electron collisions (cf. Eqs. (8)
and (23)),
and
is the thermal collision rate appropriate for nuclear and electronic
excitation and electron collisions (cf. Eqs. (8)
and (23)),
and ![]() is the density of hydrogen nuclei. For electronic and electron
interactions the rate must be multiplyied by a factor of 2, to take
into account
the fact that each collision leads to the loss of two carbon atoms.
is the density of hydrogen nuclei. For electronic and electron
interactions the rate must be multiplyied by a factor of 2, to take
into account
the fact that each collision leads to the loss of two carbon atoms.
The electron, nuclear and electronic rate constants for three PAH sizes (Nc = 50, 100 and 200 C-atom) are shown in Fig. 5 as a function of the gas temperature. We assume for the nuclear threshold energy T0 the value of 7.5 eV (MJT), and for the electronic dissociation energy the value 4.58 eV (Sect. 4.1).
For the nuclear interaction, the threshold energy ![]() is independent from the PAH size, so the three curves start at the same
temperature (not shown in the plot). The small separation between the
curves is due to the fact that the PAH ``surface area'' - and hence the
rate constant - scales
linearly with
is independent from the PAH size, so the three curves start at the same
temperature (not shown in the plot). The small separation between the
curves is due to the fact that the PAH ``surface area'' - and hence the
rate constant - scales
linearly with ![]() ,
therefore J is higher for bigger PAHs.
,
therefore J is higher for bigger PAHs.
For nuclear (and electronic) interactions, the rate constants
decrease
from hydrogen to carbon because of the lower abundance of the heavier
projectiles with respect to hydrogen (H:He:C = 1:0.1:10-4).
On the other hand, the nuclear curves shift toward lower temperatures
from lighter to heavier projectiles. This is the reflection of the fact
that the critical energy of the particle, required to transfer the
threshold energy T0,
decreases with increasing mass of the projectile itself. Then, a carbon
atom with a temperature of ![]() K
is hot enough to transfer the energy required for atom removal via
nuclear interaction, whereas for hydrogen a temperature of at least 104 K
is necessary. The almost-constant behaviour after the initial rise
reflects the large maximum observed in the nuclear cross section (cf.
Fig. 2 in MJT).
K
is hot enough to transfer the energy required for atom removal via
nuclear interaction, whereas for hydrogen a temperature of at least 104 K
is necessary. The almost-constant behaviour after the initial rise
reflects the large maximum observed in the nuclear cross section (cf.
Fig. 2 in MJT).
The dissociation probability ![]() (Eq. (17))
depends on the binding energy of the fragment E0,
on the PAH size
(Eq. (17))
depends on the binding energy of the fragment E0,
on the PAH size ![]() and on the energy transferred (through
and on the energy transferred (through ![]() ), which in
turns depends on the initial energy (velocity) of the projectile. For a
thermal distribution, this latter will be determined by the gas
temperature T.
), which in
turns depends on the initial energy (velocity) of the projectile. For a
thermal distribution, this latter will be determined by the gas
temperature T.
The electronic rate constant curves for the different PAH
sizes are well separated at the lowest temperatures. This reflects the
fact that, for a fixed value of the transferred energy and of the
electronic dissociation energy E0,
the dissociation probability decreases for increasing ![]() because either more energy is required in the bond that has to be
broken or because the energy is spread over more vibrational modes and
hence the internal excitation temperature is lower. On the other hand,
the more energy that is deposited into the PAH, the higher is the
dissociation probability. The energy transferred via electronic
excitation (and then
because either more energy is required in the bond that has to be
broken or because the energy is spread over more vibrational modes and
hence the internal excitation temperature is lower. On the other hand,
the more energy that is deposited into the PAH, the higher is the
dissociation probability. The energy transferred via electronic
excitation (and then ![]() )
increases with the energy of the projectile up to a maximum value,
corresponding to an incident energy of 100 keV for H
(and higher for more massive particles), and decreases beyond that for
higher energies. The energy content of a thermal gas at T
= 108 K is
)
increases with the energy of the projectile up to a maximum value,
corresponding to an incident energy of 100 keV for H
(and higher for more massive particles), and decreases beyond that for
higher energies. The energy content of a thermal gas at T
= 108 K is ![]() 9 keV, thus, in the
temperature range considered in this study, the energy transferred
increases with temperature (energy) and hence the dissociation
probability increases as well. This is the basis for the monotonic rise
of the electronic rate constant. After the initial separation, the
three curves converge, because the rise in the transferred energy
compensates the effect of increasing
9 keV, thus, in the
temperature range considered in this study, the energy transferred
increases with temperature (energy) and hence the dissociation
probability increases as well. This is the basis for the monotonic rise
of the electronic rate constant. After the initial separation, the
three curves converge, because the rise in the transferred energy
compensates the effect of increasing ![]() .
.
As discussed in Sect. 3, the energy transferred by
impacting electrons rises sharply for energies in excess of
10 eV, peaks at ![]() 100 eV
and decreases more slowly down to 10 keV. This results in a
dissociation probability shaped as a step function: for
100 eV
and decreases more slowly down to 10 keV. This results in a
dissociation probability shaped as a step function: for ![]() keV,
keV,
![]() jumps from values close to zero up to 1. These limiting
energies apply to a 50 C-atom PAH; for
jumps from values close to zero up to 1. These limiting
energies apply to a 50 C-atom PAH; for ![]() the width of the step is smaller (
the width of the step is smaller (
![]() 1 keV), due to the fact that for a bigger PAH more energy has
to be transferred for dissociation. This behaviour is reflected in the
shape of the electron rate constant, where a steep rise is followed by
a maximum, which
is emphasised by the logarithmic scale used for the plot.
As expected, the electron rate constant overcomes the electronic one,
except for the
highest gas temperatures. This results from the fact that, for a given
temperature,
electrons can reach higher velocities with respect to the ions (cf.
Eqs. (21)
and (23)).
1 keV), due to the fact that for a bigger PAH more energy has
to be transferred for dissociation. This behaviour is reflected in the
shape of the electron rate constant, where a steep rise is followed by
a maximum, which
is emphasised by the logarithmic scale used for the plot.
As expected, the electron rate constant overcomes the electronic one,
except for the
highest gas temperatures. This results from the fact that, for a given
temperature,
electrons can reach higher velocities with respect to the ions (cf.
Eqs. (21)
and (23)).
To summarize, from Fig. 5 we can
infer that, according to our model, the destruction process is
dominated by nuclear interaction with helium at low temperatures (below
![]() K),
and by electron
collisions above this value. Small PAHs are easier destroyed than big
ones for temperatures below
K),
and by electron
collisions above this value. Small PAHs are easier destroyed than big
ones for temperatures below ![]() 106 K,
while the difference in the destruction
level reduces significantly for hotter gas.
106 K,
while the difference in the destruction
level reduces significantly for hotter gas.
![\begin{figure}
\par\includegraphics[width=13.22cm,clip]{11683fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg137.png)
|
Figure 6: Analytical fits to the calculated rate constants shown in Fig. 5. The ``Ionic'' curve is the fit to the sum of the nuclear and electronic rate constants, thus represents the total contribution from ion collisions to PAH destruction. |
| Open with DEXTER | |
The calculated rate constants, shown in Fig. 5, are
well fitted by the function ![]() ,
where f(T) is a polynomial of
order 5
,
where f(T) is a polynomial of
order 5
For each PAH size we provide the fit to the electron rate constant; for the ions, the fit is over the sum of the nuclear and electronic rate constants, in order to provide an estimate of the global contribution from ionic collisions. The fits are shown in Fig. 6, and the fitting parameters are reported in Table 2. To provide an example of the accuracy of our fitting procedure, Fig. 7 shows the comparison between the calculated rate constant and the corresponding analytical fit, for electrons and helium impacting on a 50 C-atom PAH. The He fit is over the sum of the nuclear and electronic rate constants. The average fitting discrepancy is
Figure 8
shows the comparison between the carbon loss rate constants for a very
big PAH, ![]() ,
and a 50 C-atom molecule. We
assume
,
and a 50 C-atom molecule. We
assume ![]() eV
and
eV
and ![]() eV.
Because of the decrease of the
dissociation probability when the PAH size increases, as expected, the
electron and electronic rate constants are strongly suppressed, and
both curves shift toward higher temperatures. Indeed, for such a big
PAH, a much higher internal energy is required to reach the internal
temperature where dissociation sets in.
On the other hand, the nuclear rate
constant increases linearly with the PAH size. As a result, for a 1000
carbon atoms PAH, the nuclear interaction is the dominant (and
efficient) destruction mechanism up to
eV.
Because of the decrease of the
dissociation probability when the PAH size increases, as expected, the
electron and electronic rate constants are strongly suppressed, and
both curves shift toward higher temperatures. Indeed, for such a big
PAH, a much higher internal energy is required to reach the internal
temperature where dissociation sets in.
On the other hand, the nuclear rate
constant increases linearly with the PAH size. As a result, for a 1000
carbon atoms PAH, the nuclear interaction is the dominant (and
efficient) destruction mechanism up to
![]() K.
In conclusion, electrons are responsible for the
destruction of small/medium size PAH, while for big molecules this role
is taken by ions.
K.
In conclusion, electrons are responsible for the
destruction of small/medium size PAH, while for big molecules this role
is taken by ions.
![\begin{figure}
\par\includegraphics[width=12.8cm,clip]{11683fg7.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg141.png)
|
Figure 7:
Calculated rate constants for electrons and helium impacting on a 50
C-atom PAH, overlaid are the corresponding analytical fits. The He fit
is for the sum of the nuclear and electronic rate constants. The
average discrepancy is |
| Open with DEXTER | |
As mentioned at the end of Sect. 4.1, we examined the effects of adopting different values for the Arrhenius energy, E0 = 3.65 and 5.6 eV, lower and higher, respectively, than our canonical value 4.6 eV. The results are shown in Fig. 9. The dissociation probability decreases for increasing E0, because more energy is required in the bond that has to be broken. Hence, as expected, both the electron and electronic rate constants decrease in absolute value and shift toward highest temperatures. In particular the electronic thermal shift is very pronounced, indicating how sensitive this process is with respect to the assumed E0. A variation in the adopted electronic excitation energy translates into a significant variation of the rate constant, reemphasizing the importance of experimental studies of this critical energy.
![\begin{figure}
\par\includegraphics[width=12.8cm,clip]{11683fg8.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg142.png)
|
Figure 8:
Carbon atom loss rate constant for electrons and hydrogen impacting
against a 1000 C-atom PAH. The rate constants for |
| Open with DEXTER | |
Table 2: Analytical fit parameters for the PAH carbon atom loss rate constant, calculated for electron and ion collisions.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{11683fg9.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg144.png)
|
Figure 9:
Comparison between carbon atom loss rate constants calculated assuming
three values for the electronic dissociation energy, |
| Open with DEXTER | |
5.2 PAH lifetime
Under the effect of electron and ion collisions in a hot gas, the
number of carbon atoms in a PAH molecule varies with time. After a time
t, this number is
and the number of carbon atoms ejected from this PAH is
The quantity
where
For any given incoming ion and fixed PAH size ![]() ,
,
![]() is
univocally determined by the hydrogen/electron density
is
univocally determined by the hydrogen/electron density ![]() and the gas temperature T. We assume that a PAH is
destroyed after
the ejection of 2/3 of the carbon atoms initially present in the
molecule. This occurs after the time
and the gas temperature T. We assume that a PAH is
destroyed after
the ejection of 2/3 of the carbon atoms initially present in the
molecule. This occurs after the time ![]() (Eq. (27))
which we adopt as the PAH lifetime against electron and ion bombardment
in a gas with given density and temperature.
(Eq. (27))
which we adopt as the PAH lifetime against electron and ion bombardment
in a gas with given density and temperature.
Table 3:
Physical properties and PAH lifetime, ![]() , in objects showing PAH
emission characteristics.
, in objects showing PAH
emission characteristics.
Table 3
summarizes relevant data and PAH lifetime,
![]() ,
for four objects characterized by warm-to-hot gas,
X-ray emission, and (bright) IR emission features. The lifetime has
been calculated for PAHs with
,
for four objects characterized by warm-to-hot gas,
X-ray emission, and (bright) IR emission features. The lifetime has
been calculated for PAHs with ![]() .
.
![]() (ref)
has been evaluated adopting our reference values for the interaction
parameters, E0 =
4.6 eV and T0 =
7.5 eV,
(ref)
has been evaluated adopting our reference values for the interaction
parameters, E0 =
4.6 eV and T0 =
7.5 eV, ![]() (min)
corresponds to the minimum values E0
= 3.65 eV and T0 =
4.6 eV,
and
(min)
corresponds to the minimum values E0
= 3.65 eV and T0 =
4.6 eV,
and ![]() (max)
to the maximum values E0 =
5.6 eV and T0
= 15 eV.
(max)
to the maximum values E0 =
5.6 eV and T0
= 15 eV. ![]() is the lifetime of the object.
is the lifetime of the object.
Clearly, PAHs or related larger species can survive in these
environments. Figure 10 shows
the fractional
C-atom loss, due to electron and ion (H + He + C)
collisions, for two
widely different objects: the Orion Nebula (M 42)
and the M 82
galaxy (cf. Table 3). The famous
Orion Nebula is an
H II region with high density (
![]() cm-3)
and low temperature (T = 7000 K) gas, while
M 82 is a
starburst galaxy, which shows outside the galactic plane, a
spectacular bipolar outflow of hot and tenuous gas (
cm-3)
and low temperature (T = 7000 K) gas, while
M 82 is a
starburst galaxy, which shows outside the galactic plane, a
spectacular bipolar outflow of hot and tenuous gas (
![]() cm-3,
cm-3,
![]() K).
K).
In M 82, PAHs are completely destroyed by electrons,
even for the larger PAH, before electronic and nuclear contributions
start to be relevant. The electron and electronic fractional losses
decrease with PAH size, thus bigger molecules can survive longer, while
the nuclear loss is independent of ![]() .
The destruction timescale is very short: after one thousand years the
PAHs should have completely disappeared.
.
The destruction timescale is very short: after one thousand years the
PAHs should have completely disappeared.
In Orion the situation is reversed. At the temperature considered for this object, electrons and electronic excitation do not contribute to PAH erosion (cf. Fig. 5). The damage is caused by nuclear interaction due to He collisions, with a marginal contribution from carbon because of low abundance, and the timescale is much larger: only after 10 million years the PAH destruction becomes relevant. Of course, we have not evaluated the destruction of PAHs by H-ionizing photons in the Orion H II region, which is expected to be very important.
The young (![]() 2500 yr)
supernova remnant, N132D, in the Large Magellanic Clouds has been
studied in detail at IR, optical, UV, and X-ray wavelengths
(Tappe
et al. 2006; Morse et al. 1995). A
Spitzer/IRS spectrum of the Southern rim shows evidence for the
15-20
2500 yr)
supernova remnant, N132D, in the Large Magellanic Clouds has been
studied in detail at IR, optical, UV, and X-ray wavelengths
(Tappe
et al. 2006; Morse et al. 1995). A
Spitzer/IRS spectrum of the Southern rim shows evidence for the
15-20 ![]() m
plateau - often attributed to large PAHs or PAH clusters (Van Kerckhoven
et al. 2000; Peeters et al. 2004) -
and, tentatively, weak PAH emission features near 6.2, 7.7, and
11.2
m
plateau - often attributed to large PAHs or PAH clusters (Van Kerckhoven
et al. 2000; Peeters et al. 2004) -
and, tentatively, weak PAH emission features near 6.2, 7.7, and
11.2 ![]() m
(Tappe et al. 2006).
Tappe et al. (2006)
attribute these features to emission from large (
m
(Tappe et al. 2006).
Tappe et al. (2006)
attribute these features to emission from large (![]() 4000 C-atom) PAHs
either just swept up by the blast wave and not yet completely destroyed
by the shock or in the radiative precursor of the shock. We calculate a
lifetime of small (50-200 C-atom) PAHs in the relatively
dense, hot gas of this young supernova remnant of
4000 C-atom) PAHs
either just swept up by the blast wave and not yet completely destroyed
by the shock or in the radiative precursor of the shock. We calculate a
lifetime of small (50-200 C-atom) PAHs in the relatively
dense, hot gas of this young supernova remnant of ![]() 4 months
(Table 3).
In contrast, we estimate a lifetime of 150 yr for
4000 C-atom species (cf. Eq. (27) and
Fig. 8).
It is clear that the PAH-grain size distribution will be strongly
affected in this environment. Given advection of fresh material into
the shocked hot gas, the observations are in reasonable agreement with
our model expectations. We note that the observed shift to larger PAH
sizes - so evident in the observations - implies that the emitting
species are not associated with the precursor but are actualy tracing
the postshock gas and are therefore likely heated through collisions
with the hot electrons.
4 months
(Table 3).
In contrast, we estimate a lifetime of 150 yr for
4000 C-atom species (cf. Eq. (27) and
Fig. 8).
It is clear that the PAH-grain size distribution will be strongly
affected in this environment. Given advection of fresh material into
the shocked hot gas, the observations are in reasonable agreement with
our model expectations. We note that the observed shift to larger PAH
sizes - so evident in the observations - implies that the emitting
species are not associated with the precursor but are actualy tracing
the postshock gas and are therefore likely heated through collisions
with the hot electrons.
This discussion clearly shows that in a low density - high temperature gas, small PAHs are rapidly and completely destroyed. Survival of small PAHs in such environnement (and so the possibility to be detected) requires a protective environment and/or an efficient reformation mechanism.
6 Discussion
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11683f10.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg165.png)
|
Figure 10:
Nuclear and electronic fractional C-atom loss as a function of time in
the M 82 galaxy ( top) and in the Orion
Nebula ( bottom), calculated for three PAH sizes |
| Open with DEXTER | |
6.1 X-ray absorption
As our calculations show, PAHs are rapidly destroyed in the hot gas associated with stellar winds and supernova explosions. Any PAHs observed near such regions have to be isolated from this hot gas and are presumably in cold gas entrained in these stellar and galactic winds. However, such PAHs would still be exposed to energetic X-ray photons and these can be very destructive as well (Boechat-Roberty et al. 2008; Voit 1992).
The photon absorption cross section of PAHs shows strong peaks
at about 6 and 17.5 eV associated with transitions involving
the ![]() and
and ![]() electronic manifolds and then another broad peak around 286 eV
due to carbon K-shell transitions (Regier et al. 2007; de Souza
et al. 2002; Keller et al. 1992).
Each of these peaks can show various subpeaks due to electronic and
vibrational structure. Here, we focus on the high energy peak. Because
we are only concerned with the Planck-averaged cross section, all the
fine detail will be washed out and we have elected to evaluate the
X-ray absorption rate adopting the measured absolute cross section of
graphitic carbon taken from the NIST data base (Chantler 2000,1995).
Figure 11
shows the (photon) averaged cross sections as a function of the black
body temperature. As this figure illustrates, even the strong
absorption edge due to the carbon K-shell is washed out by this
averaging process, justifying our neglect of the fine detail in the
absorption cross sections of individual PAHs. Our averaged cross
section is also in good agreement with the recent study of Boechat-Roberty et al. (2008)
for benzene.
electronic manifolds and then another broad peak around 286 eV
due to carbon K-shell transitions (Regier et al. 2007; de Souza
et al. 2002; Keller et al. 1992).
Each of these peaks can show various subpeaks due to electronic and
vibrational structure. Here, we focus on the high energy peak. Because
we are only concerned with the Planck-averaged cross section, all the
fine detail will be washed out and we have elected to evaluate the
X-ray absorption rate adopting the measured absolute cross section of
graphitic carbon taken from the NIST data base (Chantler 2000,1995).
Figure 11
shows the (photon) averaged cross sections as a function of the black
body temperature. As this figure illustrates, even the strong
absorption edge due to the carbon K-shell is washed out by this
averaging process, justifying our neglect of the fine detail in the
absorption cross sections of individual PAHs. Our averaged cross
section is also in good agreement with the recent study of Boechat-Roberty et al. (2008)
for benzene.
The photon absorption rate, ![]() ,
of a PAH exposed to an X-ray photon flux,
,
of a PAH exposed to an X-ray photon flux, ![]() is then given by,
is then given by,
| (28) |
with
Finally, we note that here we have assumed that every X-ray
photon absorption will lead to photodissociation. Actually, H-shell
electron ejection will be rapidly followed by the Auger effect filling
the K-shell again and simultaneously ejecting a second electron. This
process may leave the PAH internally excited with typically
15-35 eV![]() .
This energy is well above the measured appearance energy of PAH
fragmentation for small PAHs under radiative cooling conditions (cf.,
Sect. 4.1) but larger PAHs may survive. Indeed, for an
Arrhenius energy of 4.6 eV, a 50 C-atom PAH requires about
24 eV of internal energy to dissociate with a probability of
1/2 (cf., Sect. 4.1). Hence, not every X-ray photon absorption
will lead to fragmentation, particularly for large PAHs. Further
experiments on larger PAHs are required to settle this issue.
.
This energy is well above the measured appearance energy of PAH
fragmentation for small PAHs under radiative cooling conditions (cf.,
Sect. 4.1) but larger PAHs may survive. Indeed, for an
Arrhenius energy of 4.6 eV, a 50 C-atom PAH requires about
24 eV of internal energy to dissociate with a probability of
1/2 (cf., Sect. 4.1). Hence, not every X-ray photon absorption
will lead to fragmentation, particularly for large PAHs. Further
experiments on larger PAHs are required to settle this issue.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11683f11.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg177.png)
|
Figure 11:
Planck averaged cross section of PAHs as a function of temperature. The
cross section is on a per C-atom basis. The strong
carbon K shell band edge at |
| Open with DEXTER | |
6.2 PAHs as tracers of cold entrained gas
The results in the previous subsection illustrate that PAHs can survive in the surface regions of cold gas clouds embedded in a hot gas for tens to hundreds of million years. The expansion of a stellar or galactic wind in an inhomogeneous environment will in a natural way lead to the entrainment of cold gas clumps (Hartquist & Dyson 1993; Chevalier & Clegg 1985; Smith et al. 1984; Marcolini et al. 2005; Strickland & Stevens 2000; Suchkov et al. 1994). The material in these clumps will only be mildly shocked - and PAH destruction by shocks is not expected as long as the shock velocity is less than about 100 km s-1 (MJT) - and can be transported with the wind while losing its identity only slowly, mainly through evaporation into the hot gas driven by thermal conduction. Multiwavelength observations of such winds support this global view and much of the soft X-ray and O VI absorbing and emitting gas is now thought to originate from the interaction interfaces between the tenuous hot gas and the cold dense clumps (Heckman et al. 2002; Chevalier & Clegg 1985).
A typical 0.5 keV X-ray photon will penetrate a
column of about 1022 H-atoms/cm2
and hence the ``PAH-bright'' surfaces of such PDRs - which are
typically only a column of ![]() H-atoms/cm2
thick - will be slowly depleted of PAHs on the timescale calculated in
Sect. 6.1.
However, at the same time, entrained clumps will slowly evaporate due
to thermal conduction. Considering classical thermal conduction, the
mass loss of a cloud due to evaporation into the hot gas is given by
H-atoms/cm2
thick - will be slowly depleted of PAHs on the timescale calculated in
Sect. 6.1.
However, at the same time, entrained clumps will slowly evaporate due
to thermal conduction. Considering classical thermal conduction, the
mass loss of a cloud due to evaporation into the hot gas is given by
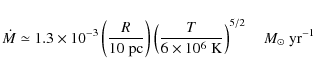
|
(29) |
with T the temperature of the hot gas and R the radius of the clump (cf. Tielens 2005). Consider the galactic wind of M 82 and a typical structure with a size of 10 pc. Assuming thermal pressure equilibrium between the clump and the hot gas (e.g., ignoring ram pressure confinement which may actually be a factor of 10 larger), we estimate a density of
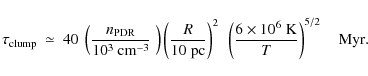
|
(30) |
Hence, ``fresh'' material will continuously be advected to the clump surface where ambient FUV photons can excite it. Thus, we conclude that such clumps can survive for a long time and that, proviso illumination by FUV photons, PAHs will form an excellent ``dye'' for tracing the presence of cold entrained material; or more specifically, for the exposed surfaces of photodissociation regions.
6.3 Comparison with previous studies
Dwek et al. (1996)
determines a sputtering rate for dust in a hot dust gas (![]() K)
that can be used to derive the lifetime,
K)
that can be used to derive the lifetime, ![]() of a grain of a given radius in a hot gas of a given density, i.e.
of a grain of a given radius in a hot gas of a given density, i.e.
where a is the grain size and
The evolution of the dust and PAH thermal emission arising from a hot gas is affected by the changing dust size distribution. As pointed out by Dwek et al. (1996), it is the short wavelength emission, coming from the smallest grains, that is most affected by dust destruction. Our work now indicates that the destruction timescale is much shorter than that predicted by Dwek et al. because the erosion of the smallest grains and PAHs is enhanced by as much as three orders of magnitude compared to the earlier work. Thus, the gas cooling rates derived by Dwek (1987) will need to be reduced if a significant fraction of the dust mass is in the form of small grains and PAHs.
6.4 C2 groups loss
The primary channel for PAH erosion in a hot gas is the progressive loss of C2Hn (n = 0, 1, 2) units following incident electron and ion excitation of the molecule. We note that this can only really occur from the periphery of the PAH (see the lower part of Fig. 11 in MJT for an illustration of this type of erosion). In this case we can see that a coherent aromatic structure will tend to be preserved, which is probably not the case where the inertial sputtering of C atoms is dominant. Thus, we conclude that PAH erosion in a hot gas will tend to preserve the aromatic structure throughout the destruction process.
As emphasized in MJT, PAH destruction may start with complete H-loss followed by isomerization to much more stable pure carbon clusters such as fullerenes (cf. Tielens 2008). While we have not assessed this point, we expect that such species will be more stable than PAHs in a hot gas.
7 Conclusions
We have extensively studied the stability of PAHs against electron and ion collisions (H, He and C) in a hot gas, such as the gas behind fast non-radiative shocks and in galactic outflows. Collisions can lead to carbon atom loss, with a consequent disruption and destruction of the molecule. We consider the case of a thermal gas with temperature T in the range 103 - 108 K.
An ionic collision consists of two simultaneous processes which can be treated separately: a binary collision between the projectile ion and a single atom in the target (nuclear interaction) and energy loss to the electron cloud of the molecule (electronic interaction).
For the nuclear interaction, as described in MJT, we have modified the existing theory in order to treat collisions able to transfer energy above a specific threshold T0. We adopt T0 = 7.5 eV as a reasonable value, but experimental determinations of this quantity are necessary.
The electronic energy transfer has been described in term of the stopping power of an electron gas with appropriate electron density (jellium approximation). For electron collisions, we derived an analytical expression for the measured electron stopping power in graphite and applied this to the case of PAHs.
The dissociation probability for a PAH excited by electronic interactions and electron collisions, has been derived using the theory of unimolecular reactions. The parameter E0, which governs the dissociation probability, is not well constrained. We adopt a value of 4.6 eV consistent with extrapolations to interstellar conditions but better determinations, relevant to the astrophysical situation, are needed.
The PAH destruction process is dominated by electron
collisions for gas temperatures
above ![]() K,
and by nuclear interaction with helium below this value. Small PAHs are
more easily destroyed than larger ones below
K,
and by nuclear interaction with helium below this value. Small PAHs are
more easily destroyed than larger ones below ![]() 106 K,
while the difference reduces significantly for a hotter gas. For a 1000
C-atom PAH, nuclear interactions are the dominant destruction process.
106 K,
while the difference reduces significantly for a hotter gas. For a 1000
C-atom PAH, nuclear interactions are the dominant destruction process.
In a hot and tenuous gas (e.g. M 82 galactic outflows), PAHs with sizes between 50 and 200 C-atom are destroyed by electron collisions in few thousand years. In denser and colder regions (e.g. Orion), PAHs can survive for some 107 yr before being destroyed by nuclear interaction processes.
X-ray photon absorption plays little role in PAH destruction in the hot gas associated with stellar winds and supernova explosions, with respect to electron collisions. The PAH destruction process in a hot gas is therefore dominated by electron collisions. Any PAHs observed near such regions have to be isolated from this hot gas and are presumably in a cooler PDR-type gas entrained in the stellar and galactic winds. In this sense, PAHs represent a good tracer for the presence of entrained denser material.
Our calculated PAH lifetime in a hot tenuous gas (
![]() K,
K, ![]() cm-3),
is much shorter than the lifetime of an
equivalent dust grain of roughly the same size (
cm-3),
is much shorter than the lifetime of an
equivalent dust grain of roughly the same size (
![]() Å). Thus, might then
imply that the destructive effects of ion and electron collisions with
very small grains have previously been underestimated.
The enhanced erosion of the smallest grain and PAHs implies that the
gas cooling rates for a hot gas (T >106 K)
- which depend on the grain/PAH size distribution - may need to be
reduced if a significant fraction of the dust mass is locked in small
grains and PAHs.
Å). Thus, might then
imply that the destructive effects of ion and electron collisions with
very small grains have previously been underestimated.
The enhanced erosion of the smallest grain and PAHs implies that the
gas cooling rates for a hot gas (T >106 K)
- which depend on the grain/PAH size distribution - may need to be
reduced if a significant fraction of the dust mass is locked in small
grains and PAHs.
PAH erosion in a hot gas occurs mainly through the ejection of C2 groups following electron collisions and electronic excitation. The C2 loss occurs at the periphery of the molecule, thus the aromatic structure will tend to be preserved throughout the destruction process.
AcknowledgementsWe are grateful to L. Allamandola and L. Verstraete for useful discussions, and we acknowledge our referee Tom Hartquist for careful reading and helpful comments. E.R.M. thanks G. Lavaux for support and technical assistance and acknowledges financial support by the EARA Training Network (EU grant MEST-CT-2004-504604).
References
- Beirão, P., Brandl, B. R., Appleton, P. N., et al. 2008, ApJ, 676, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Bethe, H. 1930, Ann. Physik, 5, 325 [Google Scholar]
- Boechat-Roberty, H. M., Neves, R., Pilling, S., Lago, A. F., & de Souza, G. G. B. 2008, ArXiv e-prints [Google Scholar]
- Chantler, C. T. 1995, J. Phys. Chem. Ref. Data, 24, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Chantler, C. T. 2000, J. Phys. Chem. Ref. Data, 29(4), 597 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Clegg, A. W. 1985, Nature, 317, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Czyzewski, Z., O'Neill MacCallum, D., Romig, A., & Joy, D. C. 1990, J. Appl. Phys., 68, 3066 [NASA ADS] [CrossRef] [Google Scholar]
- de Souza, G. G. B., Boechat-Roberty, H. M., Rocco, M. L. M., & Lucas, C. A. 2002, J. Electron Spec. Rel. Phen., 123, 315 [CrossRef] [Google Scholar]
- Désert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 438 [Google Scholar]
- Dwek, E. 1987, ApJ, 322, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Foster, S. M., & Vancura, O. 1996, ApJ, 457, 244 [Google Scholar]
- Engelbracht, C. W., Kundurthy, P., Gordon, K. D., et al. 2006, ApJ, 642, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrell, T. 1979, Solid State Commun., 32, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Madden, S. C., Tielens, A. G. G. M., Peeters, E., & Jones, A. P. 2008, ApJ, 679, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Hadjar, O., Hoekstra, R., Morgenstern, R., & Schlathölter, T. 2001, Phys. Rev. A, 63, 033201 [NASA ADS] [CrossRef] [Google Scholar]
- Hartquist, T. W., & Dyson, J. E. 1993, QJRAS, 34, 57 [NASA ADS] [Google Scholar]
- Heckman, T. M., Norman, C. A., Strickland, D. K., & Sembach, K. R. 2002, ApJ, 577, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Hovington, P., Drouin, D., & Gauvin, R. 1997, Scanning, 19, 1 [CrossRef] [Google Scholar]
- Hwang, U., Hughes, J. P., Canizares, C. R., & Markert, T. H. 1993, ApJ, 414, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Jochims, H. W., Ruhl, E., Baumgartel, H., Tobita, S., & Leach, S. 1994, ApJ, 420, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F. 1994, ApJ, 433, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, D. C. 1995, Scanning, 17, 270 [CrossRef] [Google Scholar]
- Joy, D. C., & Luo, S. 1989, Scanning, 11, 176 [Google Scholar]
- Keller, J. W., Coplan, M. A., & Goruganthu, R. 1992, ApJ, 391, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2001, ApJS, 132, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Lindhard, J., Scharff, M., & Schiott, H. E. 1963, Mat. Fys. Medd. Dan. Vid. Selsk., 33, No. 14 [Google Scholar]
- Ling, Y., & Lifshitz, C. 1998, JPC A, 102, 708 [Google Scholar]
- Marcolini, A., Strickland, D. K., D'Ercole, A., Heckman, T. M., & Hoopes, C. G. 2005, MNRAS, 362, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010, A&A, 510, A36 (MJT) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morse, J. A., Winkler, P. F., & Kirshner, R. P. 1995, AJ, 109, 2104 [NASA ADS] [CrossRef] [Google Scholar]
- Mott, N. F., & Massey, H. S. W. 1949, The theory of atomic collisions, ed. N. F. Mott, & H. S. W. Massey (Oxford: Clarendon Press) [Google Scholar]
- Omont, A. 1986, A&A, 164, 159 [NASA ADS] [Google Scholar]
- Peeters, E., Mattioda, A. L., Hudgins, D. M., & Allamandola, L. J. 2004, ApJ, 617, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Povich, M. S., Stone, J. M., Churchwell, E., et al. 2007, ApJ, 660, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Puska, M. J., & Nieminen, R. M. 1983, Phys. Rev. B, 27, 6121 [NASA ADS] [CrossRef] [Google Scholar]
- Puska, M. J., & Nieminen, R. M. 1993, Phys. Rev. A, 47, 1181 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ranalli, P., Comastri, A., Origlia, L., & Maiolino, R. 2008, MNRAS, 386, 1464 [NASA ADS] [CrossRef] [Google Scholar]
- Reach, W. T., Rho, J., Tappe, A., et al. 2006, AJ, 131, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Regier, T. Z., Shi, J., Tersingi, A., et al. 2007, Canadian Light Source, 51 [Google Scholar]
- Schlathölter, T., Hadjar, O., Hoekstra, R., & Morgenstern, R. 1999, Phys. Rev. Lett., 82, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Sigmund, P. 1981, Sputtering by Particle Bombardment Vol. 1, ed. R. Behrisch, in Topics in Applied Physics (Springer-Verlag), 47 [Google Scholar]
- Smith, L. J., Pettini, M., Dyson, J. E., & Hartquist, T. W. 1984, MNRAS, 211, 679 [NASA ADS] [Google Scholar]
- Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Suchkov, A. A., Balsara, D. S., Heckman, T. M., & Leitherer, C. 1994, ApJ, 430, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Tappe, A., Rho, J., & Reach, W. T. 2006, ApJ, 653, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (University of Cambridge Press) [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomita, S., Andersen, J. U., Gottrup, C., Hvelplund, P., & Pedersen, U. V. 2001, Phys. Rev. Lett., 87, 073401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Townsley, L. K., Feigelson, E. D., Montmerle, T., et al. 2003, ApJ, 593, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Van Kerckhoven, C., Hony, S., Peeters, E., et al. 2000, A&A, 357, 1013 [NASA ADS] [Google Scholar]
- Voit, G. M. 1992, MNRAS, 258, 841 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... a.u.
![[*]](/icons/foot_motif.png)
- Length (a.u.) =
a0 = 0.529 Å,
Velocity (a.u.) = 0.2
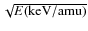 ,
Energy (a.u.) = 27.2116 eV.
,
Energy (a.u.) = 27.2116 eV.
- ... 15-35 eV
![[*]](/icons/foot_motif.png)
- The resulting PAH dication will quickly recombine with electrons and Coulomb explosion is of no consequence for such large PAHs.
All Tables
Table 1: Analytical fit to the electron stopping power in solid carbon.
Table 2: Analytical fit parameters for the PAH carbon atom loss rate constant, calculated for electron and ion collisions.
Table 3:
Physical properties and PAH lifetime, ![]() , in objects showing PAH
emission characteristics.
, in objects showing PAH
emission characteristics.
All Figures
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{11683fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg32.png)
|
Figure 1:
The coordinate system adopted to calculate the energy transferred to a
PAH via electronic excitation by ion collisions and by impacting
electrons. The molecule is modeled as a disk with radius R
and thickness d. The trajectory of the incoming
particle is identified by the angle |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11683fg2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg52.png)
|
Figure 2: Top panel - Experimental measurement of dE/dx in solid carbon for electrons with energy between 10 eV and 2 keV, from Joy (1995), overlaid with the fitting function S(E) (solid line). Bottom panel - Integral F calculated numerically as a function of the energy of the incident electron, E. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{11683fg3.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg94.png)
|
Figure 3:
The appearance energy as a function of the number of C-atoms in the
PAH. The red line provides a fit to the experimental data using
Eq. (13)
for an assumed pre-exponential factor |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{11683fg4.eps} \end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg96.png)
|
Figure 4:
The probability for dissociation of a 50 C-atom PAH excited by
10 eV as a function of the Arrhenius energy, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{11683fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg126.png)
|
Figure 5:
Nuclear (dashed lines), electronic (solid lines) and electron
(dashed-dotted lines) rate constant for PAH carbon atom loss due to
collisions with H, He, C and electrons in a thermal gas. The rate
constants are calculated as a function of the gas temperature for three
PAH sizes |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.22cm,clip]{11683fg6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg137.png)
|
Figure 6: Analytical fits to the calculated rate constants shown in Fig. 5. The ``Ionic'' curve is the fit to the sum of the nuclear and electronic rate constants, thus represents the total contribution from ion collisions to PAH destruction. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.8cm,clip]{11683fg7.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg141.png)
|
Figure 7:
Calculated rate constants for electrons and helium impacting on a 50
C-atom PAH, overlaid are the corresponding analytical fits. The He fit
is for the sum of the nuclear and electronic rate constants. The
average discrepancy is |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.8cm,clip]{11683fg8.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg142.png)
|
Figure 8:
Carbon atom loss rate constant for electrons and hydrogen impacting
against a 1000 C-atom PAH. The rate constants for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{11683fg9.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg144.png)
|
Figure 9:
Comparison between carbon atom loss rate constants calculated assuming
three values for the electronic dissociation energy, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11683f10.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg165.png)
|
Figure 10:
Nuclear and electronic fractional C-atom loss as a function of time in
the M 82 galaxy ( top) and in the Orion
Nebula ( bottom), calculated for three PAH sizes |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11683f11.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa11683-09/Timg177.png)
|
Figure 11:
Planck averaged cross section of PAHs as a function of temperature. The
cross section is on a per C-atom basis. The strong
carbon K shell band edge at |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



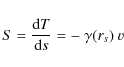
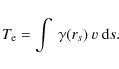
![\begin{displaymath}
n_{0} = 0.15~\exp~[-(r-6.6)^{2}~/~2.7]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11683-09/img24.png)
![\begin{displaymath}
n_{0} = 0.15~\exp~[-(x)^{2}~/~2.7]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11683-09/img27.png)
![\begin{displaymath}
n_{0}(s,\vartheta) = 0.15~\exp~[-(s~\cos~\vartheta)^{2}~/~2.7].
\end{displaymath}](/articles/aa/full_html/2010/02/aa11683-09/img34.png)
![\begin{displaymath}
\gamma(r_{s}) = \Gamma_{0}~\exp~\left[\frac{-(r_{s}(s,\vartheta)-1.5)}{R_{2}}\right]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11683-09/img36.png)
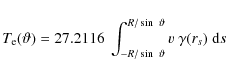
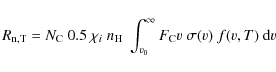
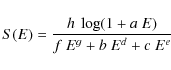
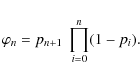
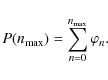
![\begin{displaymath}
\frac{p_{i}}{p_{i-1}} = \exp \left[ \left(\frac{E_{\rm0}}{k...
...ght)~
0.4~\frac{\Delta \varepsilon}{\varepsilon} \right]\cdot
\end{displaymath}](/articles/aa/full_html/2010/02/aa11683-09/img78.png)
![\begin{displaymath}
P(n_{\rm max}) = (n_{\rm max}+1)~p_{\rm av} = \frac{k_{\rm0...
...ft[-E_{\rm0}/k~T_{\rm av} \right]}{k_{\rm IR}/(n_{\rm max}+1)}
\end{displaymath}](/articles/aa/full_html/2010/02/aa11683-09/img80.png)
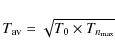
![\begin{displaymath}
k_{\rm0} = \frac{kT_{\rm eff}}{h}~ \exp\left[ 1 + \frac{\Delta S}{R}\right]
\end{displaymath}](/articles/aa/full_html/2010/02/aa11683-09/img90.png)
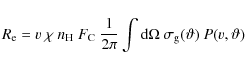
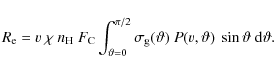
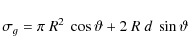
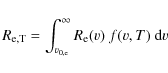
![\begin{displaymath}
F_{\rm L}(t) = \left(1 - \exp \left[ -t~/~\tau_{\rm0} \right] \right).
\end{displaymath}](/articles/aa/full_html/2010/02/aa11683-09/img146.png)