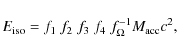| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200811151 | |
| Published online | 18 February 2010 | |
Detection of the high z
GRB 080913 and its implications
on progenitors and energy extraction mechanisms![[*]](/icons/foot_motif.png)
D. Pérez-Ramírez1,2 - A. de Ugarte Postigo3 - J. Gorosabel4 - M. A. Aloy5 - G. Jóhannesson6 - M. A. Guerrero4 - J. P. Osborne2 - K. L. Page2 - R. S. Warwick2 - I. Horváth7 - P. Veres7,8 - M. Jelínek4 - P. Kubánek4,9 - S. Guziy4,10 - M. Bremer11 - J. M. Winters11 - A. Riva12 - A. J. Castro-Tirado4
1 - Departamento de Física, Universidad de Jaén,
Campus Las Lagunillas, 23071 Jaén, Spain
2 - Department of Physics and Astronomy, The University of Leicester,
Leicester, LE1 7RH, UK
3 - European Southern Observatory, Casilla 19001, Santiago 19, Chile
4 - Instituto de Astrofísica de Andalucía (IAA-CSIC), PO Box 3.004, 18.080 Granada, Spain
5 - Departamento de Astronomía y Astrofísica, Universidad de
Valencia, C/ Dr. Moliner s/n,
46100 Burjassot, Valencia, Spain
6 - Department of Physics and SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94305, USA
7 - Dept. of Physics, Bolyai Military University, POB 15, 1581 Budapest, Hungary
8 - Dept. of Physics of Complex Systems, Eötvös University, Pázmány P. s. 1/A, 1117 Budapest, Hungary
9 - Edif. Institutos de Investigación (GACE-ICMOL), Universidad de Valencia, Campus de Paterna, 46980 Paterna, Valencia, Spain
10 - Nikolaev State University, Nikolskaya 24, 54030 Nikolaev, Ukraine
11 - Institute de Radioastronomie Milimétrique (IRAM), 300 rue de la
Piscine, 38406 Saint Martin d'Héres, France
12 - INAF - Osservatorio Astronomico di Brera, Via Emilio Bianchi, 46,
Merate, LC, 23807, Italy
Received 14 October 2008 / Accepted 14 December 2009
Abstract
Aims. We present multiwavelength observations of one of the
most distant gamma-ray bursts detected so far, GRB 080913. Based
on these observations, we consider whether it could be classified as a
short-duration GRB and discuss the implications for the progenitor
nature and energy extraction mechanisms.
Methods. Multiwavelength X-ray, near IR and millimetre observations were made between 20.7 h and ![]() 16.8 days after the event.
16.8 days after the event.
Results. Whereas a very faint afterglow was seen at the 3.5m
CAHA telescope in the nIR, the X-ray afterglow was clearly detected in
both
![]() and XMM-Newton observations. An upper limit is reported in the mm range. We have modeled the data assuming a collimated
and XMM-Newton observations. An upper limit is reported in the mm range. We have modeled the data assuming a collimated ![]()
![]() 3
3![]() blast wave with an energy injection at
blast wave with an energy injection at ![]() days carrying
days carrying
![]() erg or approximately 12 times the initial energy of the blast wave. We
find that GRB 080913 shares many of the gamma-ray diagnostics with
the more recent burst GRB 090423 for being classified as short had they
ocurred at low redshift. If the progenitor were a compact binary
merger, it is likely composed by a NS and BH. The Blandford-Znajek (BZ)
mechanism is the preferred one to extract energy from the central,
maximally-rotating BH. Both the magnetic field close to the event
horizon (B) and the BH mass (
erg or approximately 12 times the initial energy of the blast wave. We
find that GRB 080913 shares many of the gamma-ray diagnostics with
the more recent burst GRB 090423 for being classified as short had they
ocurred at low redshift. If the progenitor were a compact binary
merger, it is likely composed by a NS and BH. The Blandford-Znajek (BZ)
mechanism is the preferred one to extract energy from the central,
maximally-rotating BH. Both the magnetic field close to the event
horizon (B) and the BH mass (
![]() )
are restricted within a relatively narrow range, such that
)
are restricted within a relatively narrow range, such that
![]() .
Similar constraints on the central BH hold for collapsar-like
progenitor systems if the BZ-mechanism works for the system at hand.
.
Similar constraints on the central BH hold for collapsar-like
progenitor systems if the BZ-mechanism works for the system at hand.
Key words: stars: gamma-ray bursts: individual: GRB 080913 - techniques: photometric - Cosmology: observations
1 Introduction
Gamma-ray bursts (GRBs) are generally classified into two main groups (Kouveliotou et al. 1993), those with short duration and hard spectra and those with long duration and soft spectra. This simplistic classification scheme could be more complex, as shown by several studies (Zhang et al. 2009; Horváth et al. 2006, 2008).
For short bursts the general idea is that they originate in the near
Universe, at redshifts significantly lower (
![]() )
than
those of long GRBs (e.g. GRB 060502b at z = 0.287, Bloom
et al. 2007; GRB 051221a at z = 0.5464, Soderberg et al. 2006; GRB
050911 at
z = 0.1646, Berger et al. 2007a; GRB 050724 at z =
0.257, Berger et al. 2005; GRB 050709 at z = 0.160, Fox et al. 2005;
GRB 050509b at z = 0.226; Gehrels et al. 2005). However, de Ugarte
Postigo et al. (2006) observed GRB 060121 (T90=2 s; Arimoto
et al. 2006) and provided a most probable photometric redshift of
z = 4.6. They suggested that this burst could be the first of a class of
short gamma-ray bursts residing at high redshift, which probably
belongs to a different progenitor group. Short high-redshift bursts
were later studied statistically by Berger et al. (2007b), who found
that a significant number of distant short bursts could exist.
)
than
those of long GRBs (e.g. GRB 060502b at z = 0.287, Bloom
et al. 2007; GRB 051221a at z = 0.5464, Soderberg et al. 2006; GRB
050911 at
z = 0.1646, Berger et al. 2007a; GRB 050724 at z =
0.257, Berger et al. 2005; GRB 050709 at z = 0.160, Fox et al. 2005;
GRB 050509b at z = 0.226; Gehrels et al. 2005). However, de Ugarte
Postigo et al. (2006) observed GRB 060121 (T90=2 s; Arimoto
et al. 2006) and provided a most probable photometric redshift of
z = 4.6. They suggested that this burst could be the first of a class of
short gamma-ray bursts residing at high redshift, which probably
belongs to a different progenitor group. Short high-redshift bursts
were later studied statistically by Berger et al. (2007b), who found
that a significant number of distant short bursts could exist.
GRB 080913 was discovered by Swift on 13 Sep. 2008 (Schady et al.
2008). The burst started at 06:46:54 UT and lasted for
![]() s,
placing it, at first sight, in the long-duration class of
GRBs (Stamatikos et al. 2008). It was also observed by
Konus/WIND and had a fluence of
s,
placing it, at first sight, in the long-duration class of
GRBs (Stamatikos et al. 2008). It was also observed by
Konus/WIND and had a fluence of
![]() in the 15-150 keV range, making it an average GRB. In
the combined BAT-WIND spectrum, the observed prompt energy spectrum
could be best-fitted by a power-law with an exponential cutoff model
in the 15-150 keV range, making it an average GRB. In
the combined BAT-WIND spectrum, the observed prompt energy spectrum
could be best-fitted by a power-law with an exponential cutoff model
![]() with
with
![]() and
and
![]() (Pal' shin et al. 2008).
(Pal' shin et al. 2008).
The prompt dissemination (21 s) of the GRB position by Swift
enabled instant responses of robotic telescopes, such as the REM
robotic telescope (D'Avanzo et al. 2008). Rapid observations
obtained by GROND at the 2.2 m telescope in La Silla allowed the identification
of a near-infrared (nIR) counterpart (Rossi et al. 2008)
![]() 3 min after the burst trigger. Shortly after Swift
slewed and started data acquisition, a fading X-ray source was
detected by the Swift/XRT, which was identified as the GRB 080913
afterglow (Beardmore et al. 2008). This triggered a
multiwavelength campaign at different observatories aimed at studying
the afterglow. A photometric redshift in the range 6.1-6.7 was derived
(Greiner et al. 2008), and a spectroscopic z = 6.7 was
later confirmed by a VLT spectrum (Fynbo et al. 2008, Greiner
et al. 2009). This implied rest frame values of
3 min after the burst trigger. Shortly after Swift
slewed and started data acquisition, a fading X-ray source was
detected by the Swift/XRT, which was identified as the GRB 080913
afterglow (Beardmore et al. 2008). This triggered a
multiwavelength campaign at different observatories aimed at studying
the afterglow. A photometric redshift in the range 6.1-6.7 was derived
(Greiner et al. 2008), and a spectroscopic z = 6.7 was
later confirmed by a VLT spectrum (Fynbo et al. 2008, Greiner
et al. 2009). This implied rest frame values of
![]() s and
s and
![]() keV consistent with a
short-duration GRB (Pal'shin et al. 2008). This is
also supported by the negligible spectral time lags found in the BAT
energy range (Xu 2008). For a standard cosmology model with
H0 =71 km s-1Mpc-1,
keV consistent with a
short-duration GRB (Pal'shin et al. 2008). This is
also supported by the negligible spectral time lags found in the BAT
energy range (Xu 2008). For a standard cosmology model with
H0 =71 km s-1Mpc-1,
![]() ,
,
![]() ,
the
isotropic energy release is
,
the
isotropic energy release is
![]() erg
(1 keV-10 MeV, rest frame), with a look-back time of 13.67 Gyr.
erg
(1 keV-10 MeV, rest frame), with a look-back time of 13.67 Gyr.
A more recently detected burst, GRB 090423 (Tanvir et al. 2009,
Salvaterra et al. 2009), is a further extreme redshift (z=8.2) and
potentially short GRB which exhibits similar properties, such as burst
duration (
![]() s, and a rest-frame duration
of
s, and a rest-frame duration
of ![]() s), spectral lag times negligibly small, consistent with
zero, and an intrisincally hard spectrum as GRB 080913.
s), spectral lag times negligibly small, consistent with
zero, and an intrisincally hard spectrum as GRB 080913.
This burst, together with GRB 080913, points to the fact that the current dichotomy is not always consistent. That is, standard indicators of the physical nature of GRBs, such as duration and hardness, may no longer be the only diagnostic used in physically classifying high-redshift GRBs. They reveal a need for a revision of the traditional observational criteria. Zhang et al. (2009) tackled this question proposing new operational procedures in the determination of the physical category of GRBs. According to this work, GRB 080913 and GRB 090423 are considered to belong to the type II category (i.e. massive-star core collapse origin). However, these two high-z bursts may also be compatible with a ``specific type I scenario'' driven by the Blanford-Znajek mechanism in a BH-NS merger.
Here we report multiwavelength observations carried out, from the millimetre to the X-ray band, in order to study the afterglow of GRB 080913. We also discuss the implications of these observations for the nature of short-duration GRBs progenitors. Finally, we include some results extracted from the literature about the implications for the nature of long-duration GRBs progenitors
2 Observations and data reduction
2.1 Near-IR observations
Target of opportunity (ToO) observations in the nIR were triggered starting
20.7 h after the event with the 3.5 m telescope (+OMEGA 2000; Bailer-Jones
et al. 2000) at the German-Spanish Calar Alto Observatory (CAHA). A 5500 s
image was acquired in the J-band filter (see Fig. 1), with a
1.35
![]() average seeing. We followed the standard data reduction
procedures such as dark and sky frame subtraction, plus bad-pixel mask and
master flat-field correction. The photometry for our final image was
performed by means of the PHOT routine under IRAF
average seeing. We followed the standard data reduction
procedures such as dark and sky frame subtraction, plus bad-pixel mask and
master flat-field correction. The photometry for our final image was
performed by means of the PHOT routine under IRAF![]() . A range of apertures were checked, and the one
yielding the minimum photometric error was selected. The candidate initially
reported by Rossi et al. (2008) was barely detected (
. A range of apertures were checked, and the one
yielding the minimum photometric error was selected. The candidate initially
reported by Rossi et al. (2008) was barely detected (
![]() level) in
the J-band image (Fig. 1), with an estimated J-band Vega magnitude of
level) in
the J-band image (Fig. 1), with an estimated J-band Vega magnitude of
![]() ,
including the calibration zero point error (0.15 mag) given by
the 2MASS Catalogue. In order to compare our detection with the lightcurve
for this GRB as presented by Greiner et al. (2009), we have evaluated the
AB-to-Vega system magnitude offset coefficient for the OMEGA 2000 instrument
in the J-band to be 0.97. The converted J-band magnitude in the AB system
for our detection is
,
including the calibration zero point error (0.15 mag) given by
the 2MASS Catalogue. In order to compare our detection with the lightcurve
for this GRB as presented by Greiner et al. (2009), we have evaluated the
AB-to-Vega system magnitude offset coefficient for the OMEGA 2000 instrument
in the J-band to be 0.97. The converted J-band magnitude in the AB system
for our detection is
![]() ,
which at the time of the observation,
agrees with the GROND data (Greiner et al. 2009). Our detection occurred close
to the peak of the re-brightening phase (Fig. 4).
,
which at the time of the observation,
agrees with the GROND data (Greiner et al. 2009). Our detection occurred close
to the peak of the re-brightening phase (Fig. 4).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11151fg1.ps} \vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11151-08/Timg31.png)
|
Figure 1:
The J-band image of the GRB 080913 field
taken at the 3.5 m CAHA telescope on 14 Sep. 2008
(20.7 h after the burst onset). The error circle marks the
XRT position of the counterpart with a radius of
1.9
|
| Open with DEXTER | |
2.2 Millimetre observations
Additional mm observations were obtained at the Plateau de Bure
Interferometer (PdBI) as part of our ToO programme. The PdBI observed
the source on different occasions in the period of time of three days
in compact configuration. We used the carbon star MWC349 as primary
flux calibrator (assuming
![]() )
with the amplitude and phase calibrations relative to the quasar
0454-234. The data reduction was done with the CLIC and MAPPING
software distributed by the Grenoble GILDAS group. We analysed the
data with position-fixed (RA(2000) = 04:22:54.66,
Dec(2000) = -25:07:46.2) fits in the UV plane, which only
yielded upper limits but
allows to constrain the mm-lightcurve. The 3
)
with the amplitude and phase calibrations relative to the quasar
0454-234. The data reduction was done with the CLIC and MAPPING
software distributed by the Grenoble GILDAS group. We analysed the
data with position-fixed (RA(2000) = 04:22:54.66,
Dec(2000) = -25:07:46.2) fits in the UV plane, which only
yielded upper limits but
allows to constrain the mm-lightcurve. The 3![]() -limits are 0.72 mJy
(99 GHz, Sep 16.1 UT), 1.44 Jy (84 GHz, Sep 21.2 UT) and 0.90 mJy
(106 GHz, Sep 30.1 UT).
-limits are 0.72 mJy
(99 GHz, Sep 16.1 UT), 1.44 Jy (84 GHz, Sep 21.2 UT) and 0.90 mJy
(106 GHz, Sep 30.1 UT).
![\begin{figure}
\par\includegraphics[width=6cm,clip]{11151fg2.ps} \vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11151-08/Timg33.png)
|
Figure 2:
The EPIC-pn image of the high redshift GRB 080913
obtained with XMM-Newton |
| Open with DEXTER | |
2.3 X-ray observations
We made use of public Swift/XRT data obtained starting ![]() 94 s
after the BAT trigger time (
94 s
after the BAT trigger time (![]() ). The data were acquired in
the XRT Photon Counting (PC) mode.
). The data were acquired in
the XRT Photon Counting (PC) mode.
The lightcurve in the 0.3-10 keV energy range (Evans et al. 2007) exhibits a
number of flares in the initial orbit, with the peak of the largest flare
observed at
![]() s (in the observer frame). The decay in the time
interval
s (in the observer frame). The decay in the time
interval
![]() s to
s to
![]() s can be fitted by a power-law
with an estimated decay index
s can be fitted by a power-law
with an estimated decay index
![]() (where
(where
![]() ). The spectrum corresponding to the period of flare
activity in the initial orbit, can be fitted by an absorbed power-law with a
photon index of
). The spectrum corresponding to the period of flare
activity in the initial orbit, can be fitted by an absorbed power-law with a
photon index of
![]() ,
assuming that the
Galactic column density value in the direction of the burst is
,
assuming that the
Galactic column density value in the direction of the burst is
![]() (Kalberla et al. 2005).
(Kalberla et al. 2005).
A ToO XMM-Newton observation (Obs. ID. 0560191701) started on Sep 17.61 UT, i.e. 4.3 days after the Swift/BAT trigger. The European Photon Imaging Camera (EPIC) CCD cameras were operated in the Full Frame Mode. The total exposure time for the EPIC-pn camera was 14.0 ks. The Thin1 optical blocking filter was used for the EPIC-pn camera, whereas the medium filter was used for both EPIC-MOS cameras. The XMM-Newton Observation Data Files (ODF) were processed using XMM-Newton Science Analysis Software (SAS version 7.1.0) and the calibration files from the Calibration Access Layer as on 14 Dec. 2007. After excising periods of high-background, the net exposure times of the EPIC-pn, MOS1, and MOS2 observations are reduced to 3.6 ks, 10.8 ks, and 7.9 ks, respectively.
The XMM-Newton EPIC observations of GRB 080913 detected X-ray emission
from its afterglow (see Fig. 2) at EPIC-pn, MOS1, and MOS2 count rates of
![]() ,
,
![]() ,
and
0.0019
,
and
0.0019![]() 0.0008 cnts s-1, respectively. The net count number,
0.0008 cnts s-1, respectively. The net count number, ![]() 90
counts, is not sufficient to carry out a spectral fit. Adopting an absorbed
power-law model of spectral index
90
counts, is not sufficient to carry out a spectral fit. Adopting an absorbed
power-law model of spectral index
![]() and column density
and column density
![]() ,
the EPIC spectral shapes and count
rates imply an absorbed X-ray flux of
,
the EPIC spectral shapes and count
rates imply an absorbed X-ray flux of
![]() and an unabsorbed X-ray flux of
and an unabsorbed X-ray flux of
![]() in the energy band
0.3-10 keV. The X-ray luminosity in this same band at restframe is
in the energy band
0.3-10 keV. The X-ray luminosity in this same band at restframe is
![]() (assuming in XSPEC H0 = 71 km s-1Mpc-1 and
(assuming in XSPEC H0 = 71 km s-1Mpc-1 and
![]() ).
).
3 Results and discussion
Following the discovery of the X-ray afterglow with Swift, we detected a faint nIR afterglow (consistent with the position given by Rossi et al. 2008) and the X-ray afterglow 4.5 days after with XMM-Newton. We discuss in this section the classification and likely progenitor of this burst.
3.1 Spectral Flux Distribution of GRB 080913
Using the model and methods described by Jóhannesson et al. (2006) we fitted the multiband observations of the afterglow to a fireball model with energy injections.
One injection is needed in order to account for the bump seen at
![]() days in the light curves. Since no jet-break is seen in the
light curves up to around 10 days, we can only put a lower limit to
the collimation angle of the jet,
days in the light curves. Since no jet-break is seen in the
light curves up to around 10 days, we can only put a lower limit to
the collimation angle of the jet,
![]() .
This is delayed from the definition of Sari et al. (1999) due to the
energy injection, the sideways expansion of the jet and the detailed
calculation of the equal arrival time surface. Our preferred scenario
(giving the best fit) for a collimation of
.
This is delayed from the definition of Sari et al. (1999) due to the
energy injection, the sideways expansion of the jet and the detailed
calculation of the equal arrival time surface. Our preferred scenario
(giving the best fit) for a collimation of ![]() is an initial
energy release of
is an initial
energy release of
![]() erg into a uniform
medium with density
erg into a uniform
medium with density
![]() .
This fit results in a
.
This fit results in a
![]() d.o.f. = 170/50 where the high value is mainly caused by the
scatter in the X-ray light curve the model is unable to reproduce. In
order to explain the bump at 0.5 days, an energy injection carrying
approximately 12 E0 (
d.o.f. = 170/50 where the high value is mainly caused by the
scatter in the X-ray light curve the model is unable to reproduce. In
order to explain the bump at 0.5 days, an energy injection carrying
approximately 12 E0 (
![]() erg) is needed. Due to
the lack of a turnover in the light curves at early time, we require
the initial Lorentz factor of the blast wave to be
erg) is needed. Due to
the lack of a turnover in the light curves at early time, we require
the initial Lorentz factor of the blast wave to be ![]()
![]() 500. The SFD is best fit with an electron index p = 2.17and micro- physical parameters
500. The SFD is best fit with an electron index p = 2.17and micro- physical parameters
![]() and
and
![]() .
Note that the parametrization of
the electron population has changed from Johannesson et al. (2006) and
we now follow the tradition of Panaitescu & Kumar (2001). The
minimum Lorentz factor of the electron distribution is now defined as
.
Note that the parametrization of
the electron population has changed from Johannesson et al. (2006) and
we now follow the tradition of Panaitescu & Kumar (2001). The
minimum Lorentz factor of the electron distribution is now defined as
![]() .
Figure 3 shows the radio to X-ray SFD predicted by our model
for 3 epochs together with observation data corrected for intrinsic
extinction. The Galaxy extinction is negligible.
.
Figure 3 shows the radio to X-ray SFD predicted by our model
for 3 epochs together with observation data corrected for intrinsic
extinction. The Galaxy extinction is negligible.
Please note the the above values for the best fit parameters are in
many cases highly dependent on the value chosen for ![]() .
The
energy required for the blast wave goes as
.
The
energy required for the blast wave goes as
![]() and lower
values of
and lower
values of ![]() put an upper limit on n0 from the jet break
requirements. Additionally, there is a strong correlation between the
value of n0 and
put an upper limit on n0 from the jet break
requirements. Additionally, there is a strong correlation between the
value of n0 and
![]() because we do not have the required
data to constrain the SFD at lower frequencies. Other parameters are
less sensitive to the value of
because we do not have the required
data to constrain the SFD at lower frequencies. Other parameters are
less sensitive to the value of ![]() ,
especially p that is well
constrained from the nIR SFD.
,
especially p that is well
constrained from the nIR SFD.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11151fg3.eps}\vspace*{-3.5mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11151-08/Timg62.png)
|
Figure 3:
Spectral Flux Distribution of the afterglow from
radio to X-rays 0.01, 0.10, and 3.09 days after the burst in the
observer frame. Filled circles are based on the nIR data from Greiner
et al. (2009) and the X-ray data from Swift/XRT. Triangles
represent upper limit: in the T0+0.01 days plot they correspond
to nIR observation upper limits whereas in the
T0+3.09 days plot
it is the 3- |
| Open with DEXTER | |
3.2 Comparison with high-redshift long GRB 050904 and short GRB 060121
Given their highest redshifts, one could qualitatively compare the
properties of GRB 080913 (z=6.7), GRB 060121 (z=4.6) and GRB
050904 (z=6.295). The reason for choosing the latest cases is that
GRB 060121 is a short duration GRB (
![]() s), very likely at
high-redshift (z=4.6, de Ugarte Postigo et al. 2006),
whereas GRB
050904 is a long GRB (
s), very likely at
high-redshift (z=4.6, de Ugarte Postigo et al. 2006),
whereas GRB
050904 is a long GRB (
![]() s ) at a comparable redshift
(z=6.295; Haislip et al. 2006; Kawai et al. 2006).
We have
constructed the restframe isotropic 0.3-10 keV luminosity lightcurves
of the three GRBs, assuming a power law spectrum with a photon index
s ) at a comparable redshift
(z=6.295; Haislip et al. 2006; Kawai et al. 2006).
We have
constructed the restframe isotropic 0.3-10 keV luminosity lightcurves
of the three GRBs, assuming a power law spectrum with a photon index
![]() .
The time evolution of
.
The time evolution of ![]() was found by using linear
interpolation between the
was found by using linear
interpolation between the ![]() values determined from Swift
/XRT spectra on a logarithmic time scale. This was done to get a
smooth K-correction with time. As seen in Fig. 4 the
0.3-10 keV decay of GRB 080913 is similar in character to those
exhibited by GRB 060121 and GRB 050904. However, its isotropic
luminosity at early stages is lower by a factor
values determined from Swift
/XRT spectra on a logarithmic time scale. This was done to get a
smooth K-correction with time. As seen in Fig. 4 the
0.3-10 keV decay of GRB 080913 is similar in character to those
exhibited by GRB 060121 and GRB 050904. However, its isotropic
luminosity at early stages is lower by a factor ![]() 30. Therefore,
based on the afterglow lightcurve it is not possible to
rule out any of the possible origins for the progenitor.
30. Therefore,
based on the afterglow lightcurve it is not possible to
rule out any of the possible origins for the progenitor.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11151fg4.eps} \vspace*{-3.5mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11151-08/Timg66.png)
|
Figure 4:
The K-corrected (rest frame)
0.3-10 keV isotropic luminosity evolution
of GRB 080913 (red) in comparison to the long-duration GRB 050904
(blue, z=6.3) and the short-duration GRB 060121 (green, z=4.6).
The solid square at
|
| Open with DEXTER | |
3.3 Implications for a short duration progenitor origin
Because of the intrinsically short duration, hard spectrum and the
effectively zero spectral lags of GRB 080913, we consider in the
following the constraints on the typical progenitor systems invoked
for standard short-hard GRBs. We note that a late energy injection,
used to fit the afterglow light curve (Sect. 3.1), does not
necessarily argues against a short GRB progenitor or, equivalently,
imply a long lived central engine, if the ejected material has a
distribution in initial Lorentz factors. Under the assumption that the
initial material powering the afterglow was ejected with a Lorentz
factor of
![]() ,
matter ejected simultaneously with a Lorentz
factor of
,
matter ejected simultaneously with a Lorentz
factor of ![]() would refresh the afterglow at around
0.5 days. The rather large energy injection of 10 times the initial
energy release requires, however, a significant increase in the
efficiency of the central engine that poses constraints on either
short or long lived central engines.
would refresh the afterglow at around
0.5 days. The rather large energy injection of 10 times the initial
energy release requires, however, a significant increase in the
efficiency of the central engine that poses constraints on either
short or long lived central engines.
At a redshift z = 6.7, the burst ocurred when the Universe was only
![]() 0.8 Gyr old. According to Yoshida et al. (2008), the first
stars formed
0.8 Gyr old. According to Yoshida et al. (2008), the first
stars formed
![]() Gyr after the Big Bang. Thus, if GRB 080913
resulted from a merger of compact objects, the whole evolution of the
progenitor stars (
Gyr after the Big Bang. Thus, if GRB 080913
resulted from a merger of compact objects, the whole evolution of the
progenitor stars (
![]() )
and the merger time (
)
and the merger time (
![]() )
happened within
)
happened within
![]() Gyr. Such a small value of
Gyr. Such a small value of ![]() sets a lower limit to
the mass of the progenitor stars. Thus, neither of the two stars
forming the binary system could be less massive than
sets a lower limit to
the mass of the progenitor stars. Thus, neither of the two stars
forming the binary system could be less massive than
![]() .
This only restricts the type of progenitor system if the
burst were a result of the merger of a white dwarf (WD) and a
BH.
.
This only restricts the type of progenitor system if the
burst were a result of the merger of a white dwarf (WD) and a
BH.![]()
As the lower accretion timescales (![]() s) occur for the
higher-mass WD (Popham et al. 1999), the WD should have a
mass close to the Chandrasekar mass (
s) occur for the
higher-mass WD (Popham et al. 1999), the WD should have a
mass close to the Chandrasekar mass (
![]() ). For
NS+NS/BH binaries, the evolution of the progenitor stars is only a
small fraction of
). For
NS+NS/BH binaries, the evolution of the progenitor stars is only a
small fraction of ![]() (
(
![]() Myr;
Belczynski et al. 2006). Thus,
Myr;
Belczynski et al. 2006). Thus, ![]() roughly equals
roughly equals
![]() in this case.
in this case.
Since
![]() Gyr, if the GRB originated from a
double NS (DNS) merger, it could have proceeded through a classical
merger channel, for which
Gyr, if the GRB originated from a
double NS (DNS) merger, it could have proceeded through a classical
merger channel, for which
![]() Gyr
(Belczynski et al. 2006). Considering the large
Gyr
(Belczynski et al. 2006). Considering the large
![]() of
GRB 080913, it is more likely that it was hosted in a NS+BH merger
than in a DNS. The latter type of mergers have typically
of
GRB 080913, it is more likely that it was hosted in a NS+BH merger
than in a DNS. The latter type of mergers have typically
![]() Gyr, but with a non-negligible merger probability
for times
Gyr, but with a non-negligible merger probability
for times
![]() Gyr.
Gyr.
According to Oechslin & Janka (2006) the total equivalent isotropic
energy released in gamma-rays (
![]() )
from a progenitor consisting
of a BH-accretion torus system, which boosts a neutrino driven
ultrarleativistic jet is
)
from a progenitor consisting
of a BH-accretion torus system, which boosts a neutrino driven
ultrarleativistic jet is
where
We note that if
![]() is taken to be the sum of the contributions
due to the initial kinetic energy (E0) and of the late energy
injection (12 E0; Sect. 3.1), then
is taken to be the sum of the contributions
due to the initial kinetic energy (E0) and of the late energy
injection (12 E0; Sect. 3.1), then
![]() ,
implying that all the remaining free efficiency
factors (f1, f2 and f3) have to be, at least, a factor of
5 larger than the largest estimates of them, which suggests that a
neutrino driven outflow cannot account for the observed phenomenolgy.
,
implying that all the remaining free efficiency
factors (f1, f2 and f3) have to be, at least, a factor of
5 larger than the largest estimates of them, which suggests that a
neutrino driven outflow cannot account for the observed phenomenolgy.
We point out that the previous analysis is only sensitive to the value
of ![]() indirectly, if we seek to accommodate with our model the
values of
indirectly, if we seek to accommodate with our model the
values of
![]() .
This is because
.
This is because
![]() ,
but the fitted values of
,
but the fitted values of
![]() depend on
depend on
![]() (Sect. 3.1). Berger (2007) makes the hypothesis that
outflows of short-duration GRBs with the highest energies are strongly
collimated. If the outflow is neutrino-driven, we point out that such
hypothesis seems consistent with the fact that the largest
(Sect. 3.1). Berger (2007) makes the hypothesis that
outflows of short-duration GRBs with the highest energies are strongly
collimated. If the outflow is neutrino-driven, we point out that such
hypothesis seems consistent with the fact that the largest
![]() are linked to BH-torus systems in which either the torus mass is large
or f1 is large. A large torus mass may arise in mergers between
compact objects of different masses (Oechslin & Janka 2006; Shibata
& Taniguchi 2008). The conversion efficiency of the accreted mass
into neutrino emission tends to increase with increasing values of the
torus viscosity (Setiawan et al. 2006). Remarkably, a
large viscosity yields more vertically extended (inflated) accretion
tori, which may help to collimate the ultra-relativistic outflow in
narrow channels.
are linked to BH-torus systems in which either the torus mass is large
or f1 is large. A large torus mass may arise in mergers between
compact objects of different masses (Oechslin & Janka 2006; Shibata
& Taniguchi 2008). The conversion efficiency of the accreted mass
into neutrino emission tends to increase with increasing values of the
torus viscosity (Setiawan et al. 2006). Remarkably, a
large viscosity yields more vertically extended (inflated) accretion
tori, which may help to collimate the ultra-relativistic outflow in
narrow channels.
Given the large efficiencies needed to account for the large
![]() of GRB 080913 if the outflow were neutrino driven, it seems more
natural in this subclass of extremely energetic short GRBs to invoke
an energy extraction mechanism directly linked to the BH spin, e.g.,
the Blandford-Znajek (BZ) process (Blandford & Znajek 1977). In this
case, an estimate of the total power produced by the central engine is
(Lee et al. 2000),
of GRB 080913 if the outflow were neutrino driven, it seems more
natural in this subclass of extremely energetic short GRBs to invoke
an energy extraction mechanism directly linked to the BH spin, e.g.,
the Blandford-Znajek (BZ) process (Blandford & Znajek 1977). In this
case, an estimate of the total power produced by the central engine is
(Lee et al. 2000),
![]() ,
where
,
where
![]() ,
,
![]() ,
and B is the magnetic field strength at the
event horizon of the BH with mass
,
and B is the magnetic field strength at the
event horizon of the BH with mass
![]() .
We obtain the isotropic
equivalent energy released in
.
We obtain the isotropic
equivalent energy released in ![]() -rays due to this process during
the intrinsic event duration (
-rays due to this process during
the intrinsic event duration (
![]() s) as
s) as
![]() .
Note that in the previous estimate,
we use the same efficiency factors
.
Note that in the previous estimate,
we use the same efficiency factors
![]() and f4=0.024 as in
the previous paragraphs to account for the facts that (1) only a
fraction of the released energy will be used to drive a
ultrarelativistic outflow, and that (2) the radiated energy in
and f4=0.024 as in
the previous paragraphs to account for the facts that (1) only a
fraction of the released energy will be used to drive a
ultrarelativistic outflow, and that (2) the radiated energy in
![]() -rays is much smaller than the kinetic energy of the outflow
-rays is much smaller than the kinetic energy of the outflow
![]() .
Hence, the observed energy can be reached if either the
value of the dimensionless angular momentum of the central BH is
.
Hence, the observed energy can be reached if either the
value of the dimensionless angular momentum of the central BH is ![]() ,
the magnetic field surrounding the BH is
,
the magnetic field surrounding the BH is
![]() G or the BH has a mass
G or the BH has a mass
![]() .
We
note that to form a
.
We
note that to form a
![]() BH in a low-metallicity star (which
shall be the case at the redshift of GRB 080913), the initial mass of
such star shall be
BH in a low-metallicity star (which
shall be the case at the redshift of GRB 080913), the initial mass of
such star shall be
![]() (Woosley et al.
2002).
(Woosley et al.
2002).
Since
![]() depends quadratically on both B and
depends quadratically on both B and
![]() ,
we may
estimate which is the range of variation of these two parameters such
that the resulting
,
we may
estimate which is the range of variation of these two parameters such
that the resulting
![]() complies with the energetics observed for
GRB 080913. Lower values of the BH mass,
complies with the energetics observed for
GRB 080913. Lower values of the BH mass,
![]() ,
closer to the typically considered ones in mergers of compact objects,
require extremely large values of the magnetic field strength (
,
closer to the typically considered ones in mergers of compact objects,
require extremely large values of the magnetic field strength (
![]() G). Such magnetic fields would probably
brake excesively the rotation of the stellar progenitor core, likely
inhibiting the formation of a maximally rotating Kerr BH (i.e.,
reducing the value of a sensitively below 1). Hence, in account of
the large estimated mass of the BH, if a merger of compact objects
were the progenitor system of this GRB, a NS+BH merger is favoured,
since the typical mass of the BH resulting from a DNS merger is
G). Such magnetic fields would probably
brake excesively the rotation of the stellar progenitor core, likely
inhibiting the formation of a maximally rotating Kerr BH (i.e.,
reducing the value of a sensitively below 1). Hence, in account of
the large estimated mass of the BH, if a merger of compact objects
were the progenitor system of this GRB, a NS+BH merger is favoured,
since the typical mass of the BH resulting from a DNS merger is
![]() .
On the other hand, if we consider values of the
magnetic field strengh smaller than the reference value of
1016 G, we find that even a factor of three smaller field yields
a BH mass
.
On the other hand, if we consider values of the
magnetic field strengh smaller than the reference value of
1016 G, we find that even a factor of three smaller field yields
a BH mass
![]() .
To form such a massive BH the
progenitor star should have a mass
.
To form such a massive BH the
progenitor star should have a mass
![]() ,
i.e., in the
limit of being stars which are disrupted at the end of their lives by
the pair instability without leaving any remnant BH
(Woosley et al. 2002). Thus, both the magnetic field strength and the BH mass
are restricted within a relatively narrow range,
,
i.e., in the
limit of being stars which are disrupted at the end of their lives by
the pair instability without leaving any remnant BH
(Woosley et al. 2002). Thus, both the magnetic field strength and the BH mass
are restricted within a relatively narrow range,
![]() G, and
G, and
![]() ,
respectively. Within the former range of values for the triad of
parameters a, B and
,
respectively. Within the former range of values for the triad of
parameters a, B and
![]() ,
the most likely ones are those
favouring the largest possible value of a. Because of the fact that
strong magnetic fields tend to slow down the rotation of the stellar
core, and because of the difficulty to build up magnetic fields in
excess of
,
the most likely ones are those
favouring the largest possible value of a. Because of the fact that
strong magnetic fields tend to slow down the rotation of the stellar
core, and because of the difficulty to build up magnetic fields in
excess of
![]() G by the collapse of stellar cores (e.g.,
Obergaulinger et al. 2006a,b), even
considering the action of the magnetorotational instability (Akiyama
et al. 2003; Obergaulinger et al. 2009), values of
G by the collapse of stellar cores (e.g.,
Obergaulinger et al. 2006a,b), even
considering the action of the magnetorotational instability (Akiyama
et al. 2003; Obergaulinger et al. 2009), values of ![]() fit
better with the lowest values of B in the aforementioned
range. Thereby, to reach the appropriate BZ power to fuel GRB 080913,
we favour BH masses in the upper end of the interval stated above.
fit
better with the lowest values of B in the aforementioned
range. Thereby, to reach the appropriate BZ power to fuel GRB 080913,
we favour BH masses in the upper end of the interval stated above.
As noted above, if the total energy of the afterglow is
![]() ,
the reduced value of f4, yields even more stringent
constraints on the central engine, since
,
the reduced value of f4, yields even more stringent
constraints on the central engine, since
![]() has to be 13 times
larger, which needs of
has to be 13 times
larger, which needs of ![]() ,
,
![]() G
and
G
and
![]() .
However, we have to be cautious with
the inferences based on the values of the total kinetic energy in the
afterglow, since differently from
.
However, we have to be cautious with
the inferences based on the values of the total kinetic energy in the
afterglow, since differently from
![]() (directly measured),
(directly measured),
![]() results from a model fit of the afterglow light curve, which
sensitively depends on the value of
results from a model fit of the afterglow light curve, which
sensitively depends on the value of ![]() (Sect. 3.1).
(Sect. 3.1).
Finally, the large redshift of GRB080913 fits in theoretical models where the rate of NS+NS/BH mergers follows either the star formation rate or the star formation rate with delays smaller than 1 Gyr (Janka et al. 2006).
3.4 Implications for a long duration progenitor origin
Recent studies (Zhang et al. 2009; Belczynski et al. 2009) have suggested that GRB 080913 has a long-duration progenitor origin.
Zhang et al. (2009) present a new scheme for classifying bursts based
on criteria more closely related to the progenitor type to
differentiate physical origins, such as SN association, host galaxy
properties and the offset of the GRB location in the host galaxy. They
classify bursts into two main categories: type I (with a compact
star-merger origin) and type II (with a massive-star core collapse
origin). Under such scheme, GRB 080913 and GRB 090423 are identified
as type II candidates based on (i) the geometrically-corrected
gamma-ray (![]() )
and kinetic (
)
and kinetic (![]() )
energies (with large
values); (ii) intrinsic afterglow luminosities (moderately bright);
(iii) the high density of the circumburst medium and, (iv) the
marginal compliance of the
)
energies (with large
values); (ii) intrinsic afterglow luminosities (moderately bright);
(iii) the high density of the circumburst medium and, (iv) the
marginal compliance of the
![]() relation. However,
because these bursts are intrinsically short, but still considered
more likely long, they suggested a possible ``specific type I
scenario'' driven by the Blandford-Znajek mechanism of a BH-NS merger.
relation. However,
because these bursts are intrinsically short, but still considered
more likely long, they suggested a possible ``specific type I
scenario'' driven by the Blandford-Znajek mechanism of a BH-NS merger.
The analysis made in the previous section, regarding the properties of
the central BH in order to be able to deliver the sought
![]() of
GRB 080913, is formally independent of the fact that the progenitor
system is a single massive star or a member of a binary. Thus, we
cannot exclude the possibility that the progenitor system is a massive
low-metallicity star that forms a collapsar-like engine (or a type II
GRB according to the classification of Zhang et al. 2009) whose energy
is extracted by means of a BZ-mechanim. In such a case, the estimated
BH mass and magnetic field are the same as in
Sect. 3.3.
of
GRB 080913, is formally independent of the fact that the progenitor
system is a single massive star or a member of a binary. Thus, we
cannot exclude the possibility that the progenitor system is a massive
low-metallicity star that forms a collapsar-like engine (or a type II
GRB according to the classification of Zhang et al. 2009) whose energy
is extracted by means of a BZ-mechanim. In such a case, the estimated
BH mass and magnetic field are the same as in
Sect. 3.3.
Belczynski et al. (2009) point out that based on the currently used
gamma-ray diagnostics (T90,
![]() ,
hardness ratio) these
bursts would be considered as short had they occured at low
redshift. They argue that based on the average Swift detection
rates (accounting for selection effects), estimated for long GRBs to
exceed 10 times the rates for short GRBs, these bursts might belong to
the long class. At the redshifts of these GRBs, the calculated rates
are 1 yr-1 and
,
hardness ratio) these
bursts would be considered as short had they occured at low
redshift. They argue that based on the average Swift detection
rates (accounting for selection effects), estimated for long GRBs to
exceed 10 times the rates for short GRBs, these bursts might belong to
the long class. At the redshifts of these GRBs, the calculated rates
are 1 yr-1 and
![]() per unit redshift, for long and
short GRBs, respectively.
per unit redshift, for long and
short GRBs, respectively.
4 Conclusions
We report multiwavelength observations of the high z, potentially
short-duration gamma-ray burst GRB 080913 acquired between
20.7 h and 16.8 days after its detection by Swift. Although nIR
and X-ray afterglows were found, no mm afterglow was detected. The
X-ray spectrum is consistent with negligible intrinsic absorption. We
have modeled the data with a collimated (![]()
![]() 3 deg)
blast wave with an energy injection at 0.5 days, requiring a total
energy release of more than
3 deg)
blast wave with an energy injection at 0.5 days, requiring a total
energy release of more than
![]() .
.
At a redshift z = 6.7, the burst ocurred when the Universe was only
![]() 0.8 Gyr old. If GRB 080913 resulted from a merger of compact
objects, the whole evolution of the progenitor stars and the merger
time happened within
0.8 Gyr old. If GRB 080913 resulted from a merger of compact
objects, the whole evolution of the progenitor stars and the merger
time happened within ![]() 0.6 Gyr, following the star formation
rate with delays of
0.6 Gyr, following the star formation
rate with delays of ![]() 1 Gyr (Janka et al. 2006). This
implies that neither of the two stars could be less massive
than
1 Gyr (Janka et al. 2006). This
implies that neither of the two stars could be less massive
than
![]() .
If the system of compact binaries were formed by a WD
and a BH, the short duration of the burst restricts the mass of the WD
to be close to the Chandrasekar mass. If the progenitor system of this
GRB is a merger of compact objects, a NS+BH system is favored over a
DNS mergers, having the BH a rather large mass (
.
If the system of compact binaries were formed by a WD
and a BH, the short duration of the burst restricts the mass of the WD
to be close to the Chandrasekar mass. If the progenitor system of this
GRB is a merger of compact objects, a NS+BH system is favored over a
DNS mergers, having the BH a rather large mass (
![]() )
and being threaded by huge magnetic fields (
)
and being threaded by huge magnetic fields (
![]() G). An electromagnetic energy extraction mechanism directly
linked to the BH spin, like the Blandford-Znajek process, may likely
operate in this subclass of GRBs. We note that only a factor of three
smaller value of B, would request
G). An electromagnetic energy extraction mechanism directly
linked to the BH spin, like the Blandford-Znajek process, may likely
operate in this subclass of GRBs. We note that only a factor of three
smaller value of B, would request
![]() to
explain the observed
to
explain the observed
![]() .
However, to form so massive BHs the
progenitor star shall have a mass
.
However, to form so massive BHs the
progenitor star shall have a mass
![]() ,
i.e., they are
in the limit of being stars whose final fate is to be disrupted by a
single pulse due to the pair instability, without leaving any remnant
BH (Woosley et al. 2002), i.e., without the possibility of
producing a GRB engine. Considering the fact that magnetic fields in
excess of
,
i.e., they are
in the limit of being stars whose final fate is to be disrupted by a
single pulse due to the pair instability, without leaving any remnant
BH (Woosley et al. 2002), i.e., without the possibility of
producing a GRB engine. Considering the fact that magnetic fields in
excess of ![]() 1016 G are difficult to build up by the collapse
of the core of the progenitor star, and that such fields may reduce
the angular momentum of the resulting BH, our preferred choice of
parameters is a combination of magnetic field strenght
1016 G are difficult to build up by the collapse
of the core of the progenitor star, and that such fields may reduce
the angular momentum of the resulting BH, our preferred choice of
parameters is a combination of magnetic field strenght
![]() G and
G and
![]() .
In
regard of these figures, we temptatively suggest that systems with
large BH masses (close to the limit set by the pair instability) and
magnetar-magnetic field strengths may constitute the specific
type I scenario invoking the BZ-mechanism in a NS+BH mergers
ocurring at high-z considered by Zhang et al. (2009). However, we
cannot rule out the possibility that a single massive low-metallicity
star (type II scenario), rather than a NS+BH merger, that yields a BH
with the aforementioned properties, and which fuels an
ultrarelativistic ejecta by means of a BZ-mechanism, constitutes the
central engine of GRB 080913.
.
In
regard of these figures, we temptatively suggest that systems with
large BH masses (close to the limit set by the pair instability) and
magnetar-magnetic field strengths may constitute the specific
type I scenario invoking the BZ-mechanism in a NS+BH mergers
ocurring at high-z considered by Zhang et al. (2009). However, we
cannot rule out the possibility that a single massive low-metallicity
star (type II scenario), rather than a NS+BH merger, that yields a BH
with the aforementioned properties, and which fuels an
ultrarelativistic ejecta by means of a BZ-mechanism, constitutes the
central engine of GRB 080913.
It has been also demonstrated that the synergy between missions like Swift, automated instruments and robotic observatories, facilitate further study of the population of high-z GRBs, and help to assess whether a significant fraction of short-duration GRBs coexist at these high redshifts.
AcknowledgementsWe thank the generous allocation of observing time by different Time Allocation Committees. This work is partially based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC). IRAM is an international institute funded by the Centre National de la Recherche Scientifique (France), the Max Planck Gesellschaft (Germany) and the Instituto Geográfico Nacional (Spain). This work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester and of data products from the Two Micron All Sky Survey (2MASS), 2MASS, which is a joint project of the Univ. of Massachusetts and the IR Processing and Analysis Center/CalTech, funded by NASA and NSF. We thank the assistance of D. Cristóbal Hornillos. DPR acknowledges support from the ``José Castillejo'' program. AdUP acknowledges support from an ESO fellowship. M.A.A. is a Ramón y Cajal Fellow. J.O. and K.P. acknowledge the support of the STFC. I.H. and V.P. acknowledge support from OTKA grants T48870 and K77795. This research has also been partially supported by the Spanish MICINN under the programmes AYA2007-63677, AYA2008-03467/ESP, AYA2007-67626-C03-01 and CSD2007-00050.
References
- Akiyama, S., Wheeler, J. C., Meier, D. L., & Lichtenstadt, I. 2003, ApJ, 584, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Aloy, M. A., Janka, H.-T., Müller, E. 2005, A&A, 436, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arimoto, M., Ricker, G., Atteia, J.-L., Kawai, & N. 2006, GCN Circ., 4550 [Google Scholar]
- Bailer-Jones, C. A. L., Bizenberger, P., & Storz, C. 2000, Proc. SPIE, 4008, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Beardmore, A. P., Evans, P. A., Goad, M. R., & Osborne, J. P. 2008, GCN Circ., 8219 [Google Scholar]
- Belczynski, K., Perna, R., Bulik, T., et al. 2006, ApJ, 648, 1110. [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Holz, D. E., Fryer, C. L., et al. 2010, ApJ, 708, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E. 2007, ApJ, 670, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Price, P. A., Cenko, S. B., et al. 2005, Nature, 438, 988 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Berger, E., Shin, M.-S., Mulchaey, J. S., & Jeltema, T. E. 2007a, ApJ, 660, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Fox, D. B., Price, P. A., et al. 2007b, ApJ, 664, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Birkl, R., Aloy, M. A., Janka, H.-Th., & Müller, E. 2007, A&A, 463, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Perley, D. A., Chen, H.-W., et al. 2007, ApJ, 654, 878 [NASA ADS] [CrossRef] [Google Scholar]
- D'Avanzo, P., Covino, S., Antonelli, L. A. et al. 2008, GCN Circ., 8220 [Google Scholar]
- Evans, P., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fox, D. B., Frail, D. A., Price, P. A., et al. 2005, Nature, 437, 845 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fynbo, J., Greiner, J., Krueler, T., et al. 2008, GCN Circ., 8225 [Google Scholar]
- Gehrels, N., Sarazin, C. L., O'Brien, P. T., et al. 2005, Nature, 437, 851 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Greiner, J., Kruehler, T., & Rossi, A. 2008, GCN Circ., 8223 [Google Scholar]
- Greiner, J., Krühler, T., Fynbo, J. P. U., et al. 2009, ApJ, 693, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Haislip, J. B., Nysenwander, M. C., Reichart, D. E., et al. 2006, Nature, 440, 181 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Horváth, I., Balázs, L. G., Bagoly, Z., et al. 2006, A&A 447, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horváth, I., Balázs, L. G., Bagoly, Z., et al. 2008, A&A 489, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janka, H. -Th., Aloy, M. -A., Mazzali, P. A., & Pian, E. 2006, ApJ, 645, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Jóhannesson, G., Björnsson, G., & Gudmundsson, E. H. 2006, ApJ, 647, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D. et al. 2005, A&A 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawai, N., Kosugi, G., Aoki, K., et al. 2006, Nature 440, 184 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- King, A., Olsson, E., & Davies, M. B. 2007, MNRAS, 374, 34 [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H. K., Wijers, R. A. M. J., & Brown, G. E. 2000, Phys. Rep., 325, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, W.-H., Ramirez-Ruiz, E., & Granot, J. 2005, ApJ, 630, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Mimica, M., & Aloy, M. A. 2010, MNRAS, 401, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Obergaulinger, M., Aloy, M. A., & Müller, E. 2006a, A&A, 450, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Obergaulinger, M., Aloy, M. A., Dimmelmeier, H., & Müller, E. 2006b, A&A, 457, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Obergaulinger, M., Cerdá-Durán, P., Müller, E., & Aloy, M. A. 2009, A&A, 498, 214 [Google Scholar]
- Oechslin, R., & Janka, H.-T. 2006, MNRAS, 368, 1489. [NASA ADS] [CrossRef] [Google Scholar]
- Oechslin, R., Janka, H.-T., & Marek, A. 2007, A&A, 467, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palshin, V., Golenetskii, S., Aptekar, R., et al. 2008, GCN Circ., 8256 [Google Scholar]
- Panaitescu, A., & Kumar, P. 2001, ApJ, 554, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R., Woosley, S. E., & Fryer, C. 1999, ApJ, 518, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, A., Greiner, J., Kruehler, T., et al. 2008, GCN Circ., 8218 [Google Scholar]
- Ruffert M., & Janka, H.-T. 1999, A&A, 344, 573 [NASA ADS] [Google Scholar]
- Salvaterra, N., Della Valle, M., Campana, S., et al. 2009, Nature, 461, 1258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sari, R., Piran, T., & Halpern, J. P. 1999, ApJ, 519, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Setiawan, S., Ruffert, M., & Janka, H.-Th. 2006, A&A, 458, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schady, P., Beardmore, A. P., Cummings, J. R., et al. 2008, GCN Circ., 8217 [Google Scholar]
- Shibata, M., & Taniguchi, K. 2008, PhRvD, 77(8), ID 080415 [Google Scholar]
- Soderberg, A. M., Berger, E., Kasliwal, M., et al. 2006, ApJ, 650, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatikos, M., et al. 2008, GCN Circ., 8222 [Google Scholar]
- Tanvir, N., Fox, D. B., Levan, A. J., et al. 2009, Nature, 461, 1254 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Ugarte Postigo, A., Castro-Tirado, A. J., Guziy, S., et al. 2006, ApJ, 648, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, D. 2008, GCN Circ., 8267 [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, N., Kazuyuki, O., & Hernquist, L. 2008, Science, 321, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zhang, B., Zhang, B.-B., Virgili, F. J. et al. 2009, ApJ, 703, 1696 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... mechanisms
![[*]](/icons/foot_motif.png)
- Based on observations taken with the 3.5m Calar Alto telescope, the Plateau de Bure interferometer and the
 satellite
satellite
- ... IRAF
![[*]](/icons/foot_motif.png)
- IRAF is distributed by the NOAO, which are operated by USRA, under cooperative agreement with the US NSF.
- ...
BH.
![[*]](/icons/foot_motif.png)
- WD+NS mergers possess much longer timescales and are more likely progenitors of long GRBs (e.g., King et al. 2007)
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11151fg1.ps} \vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11151-08/Timg31.png)
|
Figure 1:
The J-band image of the GRB 080913 field
taken at the 3.5 m CAHA telescope on 14 Sep. 2008
(20.7 h after the burst onset). The error circle marks the
XRT position of the counterpart with a radius of
1.9
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{11151fg2.ps} \vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11151-08/Timg33.png)
|
Figure 2:
The EPIC-pn image of the high redshift GRB 080913
obtained with XMM-Newton |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11151fg3.eps}\vspace*{-3.5mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11151-08/Timg62.png)
|
Figure 3:
Spectral Flux Distribution of the afterglow from
radio to X-rays 0.01, 0.10, and 3.09 days after the burst in the
observer frame. Filled circles are based on the nIR data from Greiner
et al. (2009) and the X-ray data from Swift/XRT. Triangles
represent upper limit: in the T0+0.01 days plot they correspond
to nIR observation upper limits whereas in the
T0+3.09 days plot
it is the 3- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11151fg4.eps} \vspace*{-3.5mm}
\end{figure}](/articles/aa/full_html/2010/02/aa11151-08/Timg66.png)
|
Figure 4:
The K-corrected (rest frame)
0.3-10 keV isotropic luminosity evolution
of GRB 080913 (red) in comparison to the long-duration GRB 050904
(blue, z=6.3) and the short-duration GRB 060121 (green, z=4.6).
The solid square at
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.