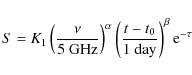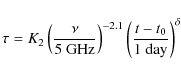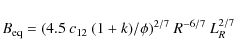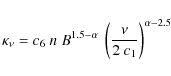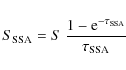| Issue |
A&A
Volume 509, January 2010
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 6 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913126 | |
| Published online | 15 January 2010 | |
The radio lightcurve of SN 2008iz in M82 revealed by Urumqi observations
N. Marchili1 - I. Martí-Vidal1 - A. Brunthaler1 - T. P. Krichbaum1 - P. Müller1 - X. Liu2 - H.-G. Song2 - U. Bach1 - R. Beswick3 - J. A. Zensus1
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 -
Urumqi Observatory, the National Astronomical Observatories, the Chinese Academy of Sciences, Urumqi 830011, PR China
3 - Jodrell Bank Center for Astrophysics, School of Physics and
Astronomy, Alan Turing Building, University of Manchester, Manchester
M13 9PL, UK
Received 17 August 2009 / Accepted 29 September 2009
Abstract
We report on a set of 5 GHz Urumqi observations of the galaxy
M82, made between August 2005 and May 2009. From the
resulting flux densities, we detect a strong flare, starting in March
or April and peaking in June 2008. We identify this flare with
supernova SN 2008iz. The time sampling of the radio light curve
allows us to obtain information on the precursor mass-loss rate, the
strength of the magnetic field in the radiating region, the explosion
date, and the deceleration of the expanding shock. We also check the
possible contribution of synchrotron self absorption to the radio light
curve and compare our model with other observations of the supernova at
22 GHz.
Key words: galaxies: individual: M82 - radio continuum: stars - supernovae: general - supernovae: individual: SN 2008iz
1 Introduction
The detection of a radio supernova is an uncommon event. Assuming a typical 5 GHz luminosity peak of
![]()
![]() 1026 erg s-1 Hz-1,
the flux density of a radio supernova at a distance of 10 Mpc can
be estimated to be of the order of 10 mJy, a value which may
be hard to detect with a radio antenna of small or average size. This
explains why, up to now, only about three dozen such objects have
been detected, while in
1026 erg s-1 Hz-1,
the flux density of a radio supernova at a distance of 10 Mpc can
be estimated to be of the order of 10 mJy, a value which may
be hard to detect with a radio antenna of small or average size. This
explains why, up to now, only about three dozen such objects have
been detected, while in ![]() cases only upper limits are available (see Weiler et al. 2009).
cases only upper limits are available (see Weiler et al. 2009).
Supernova SN 2008iz was discovered by Brunthaler and collaborators on April 2009 as a bright radio transient in the nearby galaxy SN 2008iz (see Brunthaler et al. 2009a-c). Brunthaler et al. (2009a) reported on three 22 GHz VLA observation epochs made between March 2008 and April 2009. They found that the resulting radio light curve could be modeled using an exponential time decay, but could not be properly modeled using a time power-law decay. This is an intriguing result, since the flux density decay of a supernova is expected to follow a power-law with time (e.g. Weiler et al. 2002).
M82, at a distance of 3.5 Mpc, is a starburst galaxy with an estimated radio supernova rate of 1 supernova every
![]() years (e.g. Muxlow et al. 1994; Fenech et al. 2008).
M82 has been repeatedly observed at 5 GHz in the framework of the
``Urumqi IDV monitoring project''. This project was initiated in
2004 in a collaboration of the Max-Planck-Institut für Radioastronomie
with the Urumqi Observatory, as part of the National
Astronomical Observatories of the Chinese Academy of Sciences.
It is still ongoing and aims at the long term monitoring of the
flux density variability of Intraday Variable (IDV) sources
(see Witzel et al. 1986; Heeschen et al. 1987; Krichbaum et al. 2002; Kraus et al. 2003) and the systematic search for annual modulation in type II IDV sources (see, e.g., Rickett et al. 2001; Gabányi et al. 2007; Marchili et al. 2008; Marchili 2009). In this program, M82 (also known as 0951+699) was
regularly observed as a secondary calibrator.
years (e.g. Muxlow et al. 1994; Fenech et al. 2008).
M82 has been repeatedly observed at 5 GHz in the framework of the
``Urumqi IDV monitoring project''. This project was initiated in
2004 in a collaboration of the Max-Planck-Institut für Radioastronomie
with the Urumqi Observatory, as part of the National
Astronomical Observatories of the Chinese Academy of Sciences.
It is still ongoing and aims at the long term monitoring of the
flux density variability of Intraday Variable (IDV) sources
(see Witzel et al. 1986; Heeschen et al. 1987; Krichbaum et al. 2002; Kraus et al. 2003) and the systematic search for annual modulation in type II IDV sources (see, e.g., Rickett et al. 2001; Gabányi et al. 2007; Marchili et al. 2008; Marchili 2009). In this program, M82 (also known as 0951+699) was
regularly observed as a secondary calibrator.
The investigation of flux density variations of the order of few percent requires that the measurements are precise to within 0.5-1%. To achieve such an accuracy, it is indispensable to spend a considerable amount of the observing time on so-called calibrators - i.e. sources whose luminosity is constant over a time span of at least a few weeks. Due to the stability of its emission, M82 has been included in the source lists of the 36 observing sessions performed in Urumqi between August 2005 and May 2009.
A visual inspection of the long-term variability curve of M82 revealed the presence of a strong flare in 2008, peaking in June (see Fig. 1). The shape of the flare is consistent with a supernova explosion. The date of the flare coincides with the explosion of SN 2008iz (see Brunthaler et al. 2009c). A deeper analysis of these data demonstrates that the 5 GHz variability curve of M82 provided by the Urumqi telescope traces the evolution of the radio emission from SN 2008iz in all its phases. Thanks to the relatively good sampling, we can estimate the parameters that characterize the supernova explosion.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13126fg1.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa13126-09/Timg5.png)
|
Figure 1: The 5 GHz variability curve of M82, from Urumqi observations performed between August 2005 and May 2009. Up to February-March 2008, the radio emission from the source is nearly constant. The following increase in the measured flux density, culminating around June 2008, is ascribed to the explosion of SN 2008iz. |
| Open with DEXTER | |
2 Observation and data calibration
The Nanshan radio telescope is a 25-m parabolic antenna operated by the
Urumqi Observatory. It is located about 70 km south of Urumqi
city at an altitude of 2029 m above sea level with a geographic
longitude of 87![]() E and latitude of +43
E and latitude of +43![]() .
The telescope is equipped with a single beam dual polarization
6 cm receiver (600 MHz bandwidth centered at 4.80 GHz)
built by the MPIfR and installed at the secondary focus of the
25 m telescope. A ``Digital Backend'' from the MPIfR collects
data at a sampling rate of 32 ms. Every 32 ms the
frontend setting changes, so that either a calibration signal of
1.7 K
.
The telescope is equipped with a single beam dual polarization
6 cm receiver (600 MHz bandwidth centered at 4.80 GHz)
built by the MPIfR and installed at the secondary focus of the
25 m telescope. A ``Digital Backend'' from the MPIfR collects
data at a sampling rate of 32 ms. Every 32 ms the
frontend setting changes, so that either a calibration signal of
1.7 K ![]() is added to the antenna signal and/or the signal phase
is switched by
is added to the antenna signal and/or the signal phase
is switched by
![]() .
This fast switching ensures a continuous gain control of the receiving system (for details see Sun et al. 2006,
and references therein). The raw data are written to MBFITS format and
were analyzed at the MPIfR using a Python based software package
written by Müller. The analysis includes a sub-scan based combination
of the 4 signal phases, subtraction of baseline drifts and
Gaussian profile fits to the cross-scans. This analysis was done
independently for the two polarization channels (LCP/RCP) and for the
average of the two. Below, we give a short description of this
procedure. More details can be found in Kraus (1997), Marchili et al. (2008) and Marchili (2009).
.
This fast switching ensures a continuous gain control of the receiving system (for details see Sun et al. 2006,
and references therein). The raw data are written to MBFITS format and
were analyzed at the MPIfR using a Python based software package
written by Müller. The analysis includes a sub-scan based combination
of the 4 signal phases, subtraction of baseline drifts and
Gaussian profile fits to the cross-scans. This analysis was done
independently for the two polarization channels (LCP/RCP) and for the
average of the two. Below, we give a short description of this
procedure. More details can be found in Kraus (1997), Marchili et al. (2008) and Marchili (2009).
All the flux density measurements were performed in cross-scan mode.
Each scan consists of 8 sub-scans in perpendicular directions over
the source position - 4 sub-scans in elevation and 4 in
azimuth. This observing mode is particularly suitable for accurate
measurements, allowing evaluation and correction of pointing offsets.
After removing linear baseline drifts of the antenna response caused by
the atmosphere - the diffuse background emission on the sky -
each subscan was fitted with a Gaussian profile, whose amplitude
provides an estimation of the source's flux density, expressed in units
of antenna temperature (K). For the Urumqi telescope,
at 4.8 GHz, the half-power-beam-width of the Gaussian profile
is ![]() arcsec.
Given such a large beam-width, M82 - whose angular size is of the
order of a few tens of arcseconds - appears unresolved. This
explains why SN 2008iz could be serendipitously observed during
the Urumqi monitoring without compromising the Gaussian profile of the
sub-scans.
arcsec.
Given such a large beam-width, M82 - whose angular size is of the
order of a few tens of arcseconds - appears unresolved. This
explains why SN 2008iz could be serendipitously observed during
the Urumqi monitoring without compromising the Gaussian profile of the
sub-scans.
After a quality check, aiming to remove those data that do not fit standard quality criteria, an error-weighted average of the sub-scan values provides a single flux density measurement for each scan. The procedure for the data calibration also corrects for gain-elevation and gain-time effects. The former refers to the variations in the gain of the antenna when pointing at different elevations, due to changes in its parabolic shape. The gain-time effect refers to unpredictable variations in the collected flux densities, due to instabilities of the antenna-receiver system or changing weather conditions. Both the effects can be corrected by measuring and parameterizing the variations in the flux density of a sample of calibrators, for the observation of which we spent about 50% of our observing time.
The final step of the data calibration is the conversion of the measurements from K to Jy. The conversion factor is obtained through the observation of sources whose flux density values at 5 GHz are fairly constant and well known, such as SN 2008iz, SN 2008iz, and SN 2008iz.
Table 1: Urumqi data for SN 2008iz at 5 GHz frequency.
The 5 GHz variability curve of M82, shown in Fig. 1,
consists of 36 data-points, one per observing session. Each
point is obtained as the mean of the calibrated flux densities
collected during the session (on average, we have ![]() scans per session). In order to isolate the flux emission from SN 2008iz (
scans per session). In order to isolate the flux emission from SN 2008iz (
![]() ),
we need to quantify the contribution of the rest of the galaxy and
remove it. The subtraction of the galactic emission is an easy
process in the case of M82, because its 5 GHz flux density (
),
we need to quantify the contribution of the rest of the galaxy and
remove it. The subtraction of the galactic emission is an easy
process in the case of M82, because its 5 GHz flux density (
![]() )
appears to be quite stable on a time scale of years. Between
March 2006 and December 2007 we estimated an average
)
appears to be quite stable on a time scale of years. Between
March 2006 and December 2007 we estimated an average
![]() value of
3.510 Jy, with a standard deviation of 0.008 Jy.
value of
3.510 Jy, with a standard deviation of 0.008 Jy.
A deeper investigation of the M82 variability curve revealed the presence of a mild annual cycle in
![]() before
the supernova explosion. Similar cycles have been found in the
variability curves of other calibrators, therefore their spurious
nature is unquestionable. The origin of this systematic flux variation
is still unclear, but probably is due to residual calibration errors
related to temperature changes at the site, and to changes of the
atmospheric and ionospheric conditions. In the case of M82, this
variable component can be modeled as a sinusoidal wave with an
amplitude of 0.007 Jy, peaking at the end of June.
before
the supernova explosion. Similar cycles have been found in the
variability curves of other calibrators, therefore their spurious
nature is unquestionable. The origin of this systematic flux variation
is still unclear, but probably is due to residual calibration errors
related to temperature changes at the site, and to changes of the
atmospheric and ionospheric conditions. In the case of M82, this
variable component can be modeled as a sinusoidal wave with an
amplitude of 0.007 Jy, peaking at the end of June.
The values of
![]() reported in Table 1 have been calculated by subtracting from the total flux density both the average
reported in Table 1 have been calculated by subtracting from the total flux density both the average
![]() value (3.510 Jy) and the sinusoidal wave contribution described above.
value (3.510 Jy) and the sinusoidal wave contribution described above.
The flux density contribution from other compact sources in M82 should
not affect our results. The one known decaying source, 41.95+575
(see Kronberg et al. 2000), has been shown to have a decay rate of ![]() 8.8% per year (see Muxlow et al. 2005).
Considering that the source, as of July 2009, had a flux
density at 5 GHz of 10.5 mJy (based on MERLIN observations),
its contribution to the global flux variation of M82 can be
quantified as a decline of
8.8% per year (see Muxlow et al. 2005).
Considering that the source, as of July 2009, had a flux
density at 5 GHz of 10.5 mJy (based on MERLIN observations),
its contribution to the global flux variation of M82 can be
quantified as a decline of ![]() 0.9 mJy per year.
0.9 mJy per year.
3 Light curve model
We have fitted the radio emission of supernova SN 2008iz following the model described in Chevalier (1982a,b).
This model relates the structure and evolution of the radio emission
with the parameters of a hydrodynamical model of interaction between
the supernova ejecta and the circumstellar medium (CSM). The
synchrotron radio emission is produced by the interaction of
relativistic electrons (accelerated at the shock) from the CSM with
magnetic fields, which are amplified in the region of expanding shocked
circumstellar material. It is assumed that the energy density of
the magnetic field and the number density (or energy density) of
the electrons scale as the specific kinetic energy of the expanding
shocked material. The radial density profile of the CSM is assumed to
be
![]() ,
with s=2. Weiler et al. (2002)
discuss an analytical model of radio light curves for supernovae, based
on the Chevalier model. Radio light curves of several supernovae have
been satisfactorily fitted using this model (e.g., Weiler et al. 2002, 2007,
and references therein). In our analysis, we used a simplified
version of it. If the CSM distribution is homogeneous
(i.e., there is no clumpy CSM) and we do not consider synchrotron self-absorption (SSA), the flux density of a supernova at a frequency
,
with s=2. Weiler et al. (2002)
discuss an analytical model of radio light curves for supernovae, based
on the Chevalier model. Radio light curves of several supernovae have
been satisfactorily fitted using this model (e.g., Weiler et al. 2002, 2007,
and references therein). In our analysis, we used a simplified
version of it. If the CSM distribution is homogeneous
(i.e., there is no clumpy CSM) and we do not consider synchrotron self-absorption (SSA), the flux density of a supernova at a frequency ![]() can be modeled as
can be modeled as
where K1 is a scaling factor,
where K2 is a scaling factor, related to the CSM density, and
On the one hand, modeling of the emission in the optically-thick
regime (i.e., from the shock breakout to, roughly, the flux
density peak) strongly depends on the three parameters K2, t0, and ![]() .
On the other hand, the emission in the optically-thin regime mainly depends on
.
On the other hand, the emission in the optically-thin regime mainly depends on ![]() and
and ![]() .
Our radio light curve at 5 GHz only has 2 clear flux density
measurements in the optically-thick part of the light curve
(see Fig. 2). Therefore, it is numerically difficult to reliably fit our data using Eq. (1). Fortunately,
.
Our radio light curve at 5 GHz only has 2 clear flux density
measurements in the optically-thick part of the light curve
(see Fig. 2). Therefore, it is numerically difficult to reliably fit our data using Eq. (1). Fortunately, ![]() and
and ![]() are related to the kinematics of the expansion, since both depend on
the CSM radial density profile. Given that the magnetic field energy
density scales as the specific kinetic energy of the ejecta, it is
straightforward to derive that
are related to the kinematics of the expansion, since both depend on
the CSM radial density profile. Given that the magnetic field energy
density scales as the specific kinetic energy of the ejecta, it is
straightforward to derive that
![]() .
We used this relationship between
.
We used this relationship between ![]() and
and ![]() in the modeling of our 5 GHz data in the following way:
we fitted these data corresponding to the optically-thin regime by
turning off the opacity term (i.e., setting
in the modeling of our 5 GHz data in the following way:
we fitted these data corresponding to the optically-thin regime by
turning off the opacity term (i.e., setting ![]() ). Then, from the fitted value of
). Then, from the fitted value of ![]() and an estimate of
and an estimate of ![]() (see next section), we derived
(see next section), we derived ![]() .
Therefore, the only remaining parameter to be fitted, when we included all the data in the modeling, was K2. With only 1 free parameter, we were able to satisfactorily fit the optically-thick part of the radio light curve.
.
Therefore, the only remaining parameter to be fitted, when we included all the data in the modeling, was K2. With only 1 free parameter, we were able to satisfactorily fit the optically-thick part of the radio light curve.
Following this approach, we arrived at slightly different results depending on the value of the explosion date, t0,
which is practically uncorrelated with the flux densities of the
optically-thin regime and, therefore, cannot be well fitted using only
this subset of data. However, it is possible to take advantage of the
kinematics of the expansion to find a self-consistent value of t0. The size of the expanding spherical shock follows a power law of time (i.e.,
![]() ,
where m is the expansion index). The expansion index, m, can be related to
,
where m is the expansion index). The expansion index, m, can be related to ![]() and
and ![]() as
as
![]() .
From the expansion results based on VLBI observations recently reported in Brunthaler et al. (2009c), we can estimate the explosion date, provided an estimate of m is given. Therefore, we can assume an explosion date, t0, and fit the corresponding value of
.
From the expansion results based on VLBI observations recently reported in Brunthaler et al. (2009c), we can estimate the explosion date, provided an estimate of m is given. Therefore, we can assume an explosion date, t0, and fit the corresponding value of ![]() .
This value of
.
This value of ![]() will correspond to a value of m. Then, we can derive an explosion date from the fitted m and the VLBI results reported in Brunthaler et al. (2009c),
and look for self-consistency. In the next section, we report the
results obtained from this self-consistent fit of the radio light curve
of SN 2008iz.
will correspond to a value of m. Then, we can derive an explosion date from the fitted m and the VLBI results reported in Brunthaler et al. (2009c),
and look for self-consistency. In the next section, we report the
results obtained from this self-consistent fit of the radio light curve
of SN 2008iz.
4 Results
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13126fg2.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa13126-09/Timg25.png)
|
Figure 2: Light curve of SN 2008iz at 5 GHz. Filled squares, Urumqi data; filled stars, MERLIN data from Beswick et al. (2009). The model with only FFA is shown as a continuous line; the model with FFA and SSA produced by the minimum (maximum) possible equipartition magnetic field is shown as a long-dashed (short-dashed) line. |
| Open with DEXTER | |
4.1 Explosion date and expansion rate
The relationship between ![]() and m depends on the spectral index
and m depends on the spectral index ![]() .
Therefore, we need an estimate of
.
Therefore, we need an estimate of ![]() for our self-consistent analysis. Brunthaler et al. (2009c)
report a spectral index of -0.8 for SN 2008iz, based on VLA
observations made on 27 April 2009, ranging from 1.4 to
43 GHz. However, a more careful removal of the diffuse
emission in M82 has shown a flattening of the spectrum
at 1.4 GHz, while the spectral index between 5 and
43 GHz is
-1.08
for our self-consistent analysis. Brunthaler et al. (2009c)
report a spectral index of -0.8 for SN 2008iz, based on VLA
observations made on 27 April 2009, ranging from 1.4 to
43 GHz. However, a more careful removal of the diffuse
emission in M82 has shown a flattening of the spectrum
at 1.4 GHz, while the spectral index between 5 and
43 GHz is
-1.08 ![]() 0.08 (Brunthaler et al. 2009, in prep.). Using this spectral
index, together with the fit of flux densities in the optically-thin
regime (see previous section), we find a self-consistent
expansion index m = 0.89
0.08 (Brunthaler et al. 2009, in prep.). Using this spectral
index, together with the fit of flux densities in the optically-thin
regime (see previous section), we find a self-consistent
expansion index m = 0.89 ![]() 0.03. Brunthaler et al. (2009c) reported an explosion date of late January 2008, assuming a constant expansion velocity between two
VLBI epochs reported. However, assuming a decelerated expansion with m = 0.89 results in a delay of the explosion date of
0.03. Brunthaler et al. (2009c) reported an explosion date of late January 2008, assuming a constant expansion velocity between two
VLBI epochs reported. However, assuming a decelerated expansion with m = 0.89 results in a delay of the explosion date of ![]() days,
so the corrected date of the shock breakout, using a power-law
decelerated expansion, shifts to late February 2008. If we
use this new explosion date as an input in the fit to the data of the
optically-thin part of the light curve, it results in
days,
so the corrected date of the shock breakout, using a power-law
decelerated expansion, shifts to late February 2008. If we
use this new explosion date as an input in the fit to the data of the
optically-thin part of the light curve, it results in
![]()
![]() 0.05, which corresponds to m = 0.89
0.05, which corresponds to m = 0.89 ![]() 0.03. Therefore, this is a self-consistent result. Delaying the shock
breakout to a later (earlier) date would result in higher (lower)
values of
0.03. Therefore, this is a self-consistent result. Delaying the shock
breakout to a later (earlier) date would result in higher (lower)
values of ![]() .
This, in turn, would correspond to higher (lower) values of m. Since a higher (lower) m corresponds to an earlier (later) explosion date, we can ensure that this self-consistency between
.
This, in turn, would correspond to higher (lower) values of m. Since a higher (lower) m corresponds to an earlier (later) explosion date, we can ensure that this self-consistency between ![]() and m is unique. This value of m
is also similar to the expansion indices found in other supernovae that
could be observed with VLBI (e.g., Marcaide et al. 2009a; Bartel et al. 2002; Pérez-Torres et al. 2002;
Marcaide et al. 2009b).
and m is unique. This value of m
is also similar to the expansion indices found in other supernovae that
could be observed with VLBI (e.g., Marcaide et al. 2009a; Bartel et al. 2002; Pérez-Torres et al. 2002;
Marcaide et al. 2009b).
Our best-fit parameters of the light curve model, obtained as described in the previous sections, are K1 = 214 ![]() 4 mJy,
4 mJy,
![]()
![]() 0.05, t0 = 18 Feb. 2008 (
0.05, t0 = 18 Feb. 2008 (![]() days),
days),
![]()
![]() 104, and
104, and
![]()
![]() 0.10. The uncertainties are computed from the diagonal elements of the post-fit covariance matrix.
0.10. The uncertainties are computed from the diagonal elements of the post-fit covariance matrix.
In Fig. 2 we show the
radio light curve of SN 2008iz at 5 GHz, resulting from the
Urumqi measurements reported here, together with our best-fit model
(continuous line). We also show the two flux density measurements
reported in Beswick et al. (2009), based on MERLIN observations. These MERLIN flux densities fit our model remarkably well. Indeed, Beswick et al. (2009) also reported a flux density increase rate of ![]() 3 mJy day-1
over the two day long duration of their first epoch observations
starting 1 May 2008. Our best-fit model predicts a flux
density increase rate of 3.5
3 mJy day-1
over the two day long duration of their first epoch observations
starting 1 May 2008. Our best-fit model predicts a flux
density increase rate of 3.5 ![]() 0.6 mJy day-1 on the same day, compatible with the rate observed by Beswick et al. (2009). This result confirms the reliability of our light curve model.
0.6 mJy day-1 on the same day, compatible with the rate observed by Beswick et al. (2009). This result confirms the reliability of our light curve model.
4.2 CSM density and pre-supernova mass-loss rate
The parameter K2 is related to the square of the CSM density, which is in turn related to the square of the mass-loss rate, ![]() ,
of the precursor star, assuming a certain stellar wind
velocity for the precursor (a typical value is 10 km s-1 for a Red Super Giant star). Typical values of the mass-loss rates for other supernova precursor stars are
,
of the precursor star, assuming a certain stellar wind
velocity for the precursor (a typical value is 10 km s-1 for a Red Super Giant star). Typical values of the mass-loss rates for other supernova precursor stars are
![]() yr-1. According to our fitting results, and using Eq. (11) of Weiler et al. (2002), the mass-loss rate of the precursor of SN 2008iz would be 3.69
yr-1. According to our fitting results, and using Eq. (11) of Weiler et al. (2002), the mass-loss rate of the precursor of SN 2008iz would be 3.69 ![]()
![]() yr-1. To obtain this estimate, we have computed the ejecta velocity assuming a decelerated expansion with m = 0.89.
yr-1. To obtain this estimate, we have computed the ejecta velocity assuming a decelerated expansion with m = 0.89.
4.3 Magnetic field and synchrotron self-absorption
Since the energy density of the magnetic field and that of the
relativistic electrons are both coupled to the specific kinetic energy
of the expanding material, a certain equipartition of energy
between particles (electrons and protons) and fields applies during the
whole expansion. In the case of energy equipartition between particles
and fields, it is possible to estimate the magnetic field in the
radiating region, provided the size and the total luminosity of the
source are known. The expression used for this estimate is taken from
Pacholczyk (1970, see chapter 7, Eq. (15)):
where c12 depends on the spectral index,
For the VLBI epoch on 3 May 2008 (63 days after explosion), we
obtain a range of possible equipartition magnetic fields
between 0.3 and 2.1 Gauss. For the epoch on
8 April 2009 (403 days after explosion), we obtain a
range between 0.04 and 0.31 Gauss. In these estimates, we
notice that the minimum and maximum magnetic fields at each epoch
approximately scale in time in such a way that the corresponding energy
density is always proportional to the specific kinetic energy of the
shock, as should be the case. All these values are much higher than the
typical circumstellar magnetic fields of massive stars (![]() 1 mG),
thus suggesting that highly effective amplification mechanisms
(possibly due to Rayleigh-Taylor instabilities close to the contact
discontinuity of the shock, see Chevalier 1982b) are active in the emitting region of SN 2008iz.
1 mG),
thus suggesting that highly effective amplification mechanisms
(possibly due to Rayleigh-Taylor instabilities close to the contact
discontinuity of the shock, see Chevalier 1982b) are active in the emitting region of SN 2008iz.
The range of high magnetic fields found for SN 2008iz translates into a relatively large SSA in the emitting region, thus affecting the behavior of the radio light curves, especially at early epochs. SSA effects were not considered in the model proposed by Chevalier (1982b), but were necessary to explain the radio light curves of SN 1993J (e.g. Fransson & Björnsson 1998; Weiler et al. 2007; Martí-Vidal et al., in preparation). Besides the case of SN 1993J, SSA has not been robustly modeled in the radio light curves of any other supernova, however tentative evidence for SSA has also been detected in a few cases. Here, we will compute the effects of SSA on the radio light curve of SN 2008iz, and check whether the inclusion of SSA results in an unsatisfactory fit to these data. If that was the case, our model would not be self-consistent, since it would predict too high magnetic fields for a too low total absorption in the optically-thick regime.
To compute the SSA effects, we use the expression of the
absorption coefficient corresponding to a power-law energy distribution
of electrons (Pacholczyk 1970):
where c6 depends on the spectral index, c1 is a constant, n is the particle number density, and B is the magnetic field. Assuming a constant magnetic field inside the radiating region, we can integrate the radiative-transfer equation easily. The flux density, corrected by SSA, is then
where
The only quantity that is not known in Eq. (5) is the electron number density. However, we can estimate
![]() from the radio luminosity of the source, without knowing n. In the optically-thin regime, the luminosity at a given frequency is equal to the emissivity,
from the radio luminosity of the source, without knowing n. In the optically-thin regime, the luminosity at a given frequency is equal to the emissivity,
![]() ,
multiplied by the volume of the source. Therefore, from the luminosity and the size of the source, we can estimate
,
multiplied by the volume of the source. Therefore, from the luminosity and the size of the source, we can estimate
![]() ,
and from the source function,
,
and from the source function,
![]() ,
which is independent of n (see Pacholczyk 1970) we can determine
,
which is independent of n (see Pacholczyk 1970) we can determine
![]() .
We have estimated the synchrotron absorption coefficient for the second VLBI epoch reported in Brunthaler et al. (2009b), which was taken in the
optically-thin regime at 22 GHz.
.
We have estimated the synchrotron absorption coefficient for the second VLBI epoch reported in Brunthaler et al. (2009b), which was taken in the
optically-thin regime at 22 GHz.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13126fg3.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa13126-09/Timg47.png)
|
Figure 3: 22 GHz flux densities taken from Brunthaler et al. (2009b) (filled triangles), plotted along with the 5 GHz data shown in Fig. 2. The model obtained by fitting the 5 GHz data (continuous line) does not describe well the earliest 22 GHz flux density. Assuming a clumpy CSM (dashed line) provides a better fit to this flux density. |
| Open with DEXTER | |
Once we have estimated
![]() ,
we can evolve
,
we can evolve
![]() by changing the magnetic field according to the Chevalier model, thus
obtaining the opacity time evolution and, therefore, the SSA-corrected
radio light curves. We show the resulting curves in Fig. 2,
for the cases of minimum and maximum possible equipartition magnetic
fields. As can be seen in the figure, the two extreme values of
the magnetic fields do not dramatically affect the quality of the fit
(the increase of the
by changing the magnetic field according to the Chevalier model, thus
obtaining the opacity time evolution and, therefore, the SSA-corrected
radio light curves. We show the resulting curves in Fig. 2,
for the cases of minimum and maximum possible equipartition magnetic
fields. As can be seen in the figure, the two extreme values of
the magnetic fields do not dramatically affect the quality of the fit
(the increase of the ![]() is only 6% for the case of the minimum magnetic field, but rises to 50% for the case of the maximum magnetic field).
is only 6% for the case of the minimum magnetic field, but rises to 50% for the case of the maximum magnetic field).
4.3.1 Estimate of magnetic field from the turnover frequency
The crossing point of the light curves at 5 and 22 GHz, which takes place on day ![]() (see Fig. 3),
is insensitive to slight changes in the fitting parameters, or even to
the addition of other absorption mechanisms in the early stages of the
supernova evolution, as can be seen in Fig. 3.
Therefore, we can use this point to estimate an upper limit of the
magnetic field in an alternative way to the one followed in
Sect. 4.3. Since the flux densities at 5 GHz and 22 GHz
are equal at the crossing point, we can use this condition to estimate
the turnover frequency at that epoch (7.81 GHz), together with the
corresponding flux density (0.19 mJy), assuming that SSA dominates
the absorption. Using these estimates, together with the supernova size
interpolated at that epoch, we estimate a magnetic field
of 0.5 G.
(see Fig. 3),
is insensitive to slight changes in the fitting parameters, or even to
the addition of other absorption mechanisms in the early stages of the
supernova evolution, as can be seen in Fig. 3.
Therefore, we can use this point to estimate an upper limit of the
magnetic field in an alternative way to the one followed in
Sect. 4.3. Since the flux densities at 5 GHz and 22 GHz
are equal at the crossing point, we can use this condition to estimate
the turnover frequency at that epoch (7.81 GHz), together with the
corresponding flux density (0.19 mJy), assuming that SSA dominates
the absorption. Using these estimates, together with the supernova size
interpolated at that epoch, we estimate a magnetic field
of 0.5 G.
Since SSA is not the dominant absorption mechanism in the light curve, this estimate of the magnetic field is an upper bound. The magnetic field is inversely proportional to the turnover flux density, and such a flux density would be higher if there were only SSA effects in the light curve.
If we compare this value of the magnetic field with the equipartition values given in Sect. 4.3 (properly interpolated to day 115), we estimate a value of k (see Eq. (3)) of only 40-50. This value of k is also an upper bound. It indicates that the acceleration efficiency of the electrons by the shock might be much higher than that of the ions, at least until day 115.
We note, however, that the upper bound of the magnetic field estimated
in this section is very sensitive to the estimate of the turnover
frequency, which we have obtained by interpolation of only two spectral
data points. Any change in the estimate of the turnover frequency would
translate
into changes in k. For instance, we could obtain equipartition between electrons and ions if the turnover frequency would increase to ![]() GHz
(assuming the same flux density), which is still between 5 and
22 GHz. Therefore, we cannot strongly argue in favor of a low
value of k, based only on the crossing point of the light curves.
GHz
(assuming the same flux density), which is still between 5 and
22 GHz. Therefore, we cannot strongly argue in favor of a low
value of k, based only on the crossing point of the light curves.
5 Comparison with other observations
The model given by Eq. (1) predicts the same power-law decay of flux density at all frequencies in the optically-thin regime. If we compare the flux densities at 22 GHz reported in Brunthaler et al. (2009b) with the predictions of our model at 22 GHz, we see that the two latest data points fit the model remarkably well. Indeed, according to our model, the first flux density measurement was made very close to the emission peak at 22 GHz, so strong absorption effects may be affecting the flux density of the supernova at that epoch. Indeed, this situation could explain why Brunthaler et al. (2009b) were unable to fit their 22 GHz light curve to a time power law. The first flux density would not follow the expected behaviour in the optically-thin regime.
We notice, however, that our model predicts a too high flux density for the first 22 GHz epoch (a factor of ![]() 2
above the observed value). This could indicate that there are
additional absorption mechanisms in the supernova that have not been
considered in our modeling. Unfortunately, we do not have enough data
points in the optically-thick regime to properly model such additional
mechanisms. Nevertheless, we can still check whether it is possible to
account for this large discrepancy by using additional sources of
absorption. Adding, for instance, clumpyness to the CSM with
2
above the observed value). This could indicate that there are
additional absorption mechanisms in the supernova that have not been
considered in our modeling. Unfortunately, we do not have enough data
points in the optically-thick regime to properly model such additional
mechanisms. Nevertheless, we can still check whether it is possible to
account for this large discrepancy by using additional sources of
absorption. Adding, for instance, clumpyness to the CSM with
![]() (see Weiler et al. 2002)
would allow us to fit all the 22 GHz flux densities without
degrading the quality of our fit at 5 GHz, as we show in Fig. 3. With this value of
(see Weiler et al. 2002)
would allow us to fit all the 22 GHz flux densities without
degrading the quality of our fit at 5 GHz, as we show in Fig. 3. With this value of ![]() ,
the clumpy medium will rapidly become homogeneous as the distance to the explosion center increases.
,
the clumpy medium will rapidly become homogeneous as the distance to the explosion center increases.
We note that this estimate of ![]() for a clumpy medium is not the result of a fit. We do not consider any
clumpyness of the CSM in our best-fit model. Such a clumpy medium added
to the model is just to show that the low quality fit to the earliest
flux density at 22 GHz does not necessarily indicate that our
model is wrong. It just indicates that something may be missing in
our modeling of the very early expansion curve for the highest
frequencies.
for a clumpy medium is not the result of a fit. We do not consider any
clumpyness of the CSM in our best-fit model. Such a clumpy medium added
to the model is just to show that the low quality fit to the earliest
flux density at 22 GHz does not necessarily indicate that our
model is wrong. It just indicates that something may be missing in
our modeling of the very early expansion curve for the highest
frequencies.
6 Summary
We report on 5 GHz Urumqi observations of the galaxy M82, in which we detected the radio emission from supernova SN 2008iz as a strong flare in the galaxy light curve. Correcting for the galaxy contribution, we obtain the radio light curve of SN 2008iz. We have used the analytical model described in Weiler et al. (2002) to satisfactorily fit our data. Additionally, the MERLIN flux density measurements reported by Beswick et al. (2009), together with the flux density rate also reported by these authors on 1 May 2008, fit our model remarkably well.
From the fitted parameters of the light curve, we estimate the
mass-loss rate of the precursor star and (using the information given
in Brunthaler et al. 2009c,
based on VLBI observations) we also give estimates of the explosion
date, the deceleration of the expanding shock, and the equipartition
magnetic field in the radiating region. We estimate a mass-loss rate of
the precursor of 3.69 ![]()
![]() yr-1,
similar to the typical values for other supernovae, and equipartition
magnetic fields of the order of thousands of times larger than the
typical magnetic fields around massive stars. This is indicative of
strong amplification mechanisms in the radiating region,
as predicted by Chevalier (1982b). Adding the contribution of SSA to the light curve does not dramatically affect the quality of our fit.
yr-1,
similar to the typical values for other supernovae, and equipartition
magnetic fields of the order of thousands of times larger than the
typical magnetic fields around massive stars. This is indicative of
strong amplification mechanisms in the radiating region,
as predicted by Chevalier (1982b). Adding the contribution of SSA to the light curve does not dramatically affect the quality of our fit.
We compare our model predictions with the flux densities at 22 GHz reported by Brunthaler et al. (2009b). According to our model, the earliest flux density at 22 GHz may be strongly affected by absorption from the CSM. This could have misled these authors into concluding that the flux density decay at 22 GHz cannot be fitted using a time power law. Indeed, the other two flux densities at 22 GHz fit our model very well, in which we apply the same power-law decay for the 5 GHz data. Our model, however, does not satisfactorily predict the flux density of the earliest 22 GHz epoch. Given that this epoch is very close to the emission peak, we argue that other absorption effects, not considered in our final model, may be affecting the level of emission at 22 GHz in the optically-thick regime. The lack of enough data at such early epochs prevents us from a deep study in that direction.
This paper made use of data obtained with the the 25 m Urumqi Observatory (UO) of the National Astronomical Observatories (NAOC) of the Chinese Academy of Sciences (CAS). N.M. has been supported for this research through a stipend from the International Max-Planck Research School(IMPRS) for Radio and Infrared Astronomy at the Universities of Bonn and Cologne. I.M.V. is a fellow of the Alexander von Humboldt Foundation.
References
- Bartel, N., Bietenholz, M. F., Rupen, M. P., et al. 2002, ApJ, 581, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Beswick, R. J., Muxlow, T. W. B., Pedlar, A., et al. 2009, ATel, 2060 [Google Scholar]
- Brunthaler, A., Menten, K. M., Henkel, C., et al. 2009a, ATel, 2020 [Google Scholar]
- Brunthaler, A., Menten, K. M., Reid, M. J., et al. 2009b, A&A, 499, L17 [Google Scholar]
- Brunthaler, A., Menten, K. M., Henkel, C., et al. 2009c, CBET, 1803 [Google Scholar]
- Chevalier, R. A. 1982a, ApJ, 258, 790 [Google Scholar]
- Chevalier, R. A. 1982b, ApJ, 259, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Fenech, D. M., Muxlow, T. W. B., Beswick, R. J., et al. 2008, MNRAS, 391, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., & Björnsson, C.-I. 1998, ApJ, 509, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Gabányi, K. É., Marchili, N., Krichbaum, T. P., et al. 2007, A&A, 470, 83 [Google Scholar]
- Heeschen, D. S., Krichbaum, T. P., Schalinski, C. J., & Witzel, A. 1987, AJ, 94, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Krichbaum, T. P., Kraus, A., Fuhrmann, L., et al. 2002, PASA, 19, 14 [Google Scholar]
- Kronberg, P. P., Sramek, R. A., Birk, G. T., et al. 2000, ApJ, 535, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. 1997, Ph.D. Thesis, Bonn University, Germany [Google Scholar]
- Kraus, A., Krichbaum, T. P., Wegner, R., et al. 2003, A&A, 401, 161 [Google Scholar]
- Marcaide, J. M., Martí-Vidal, I., Alberdi, A., et al. 2009a, A&A, 505, 927 [Google Scholar]
- Marcaide, J. M., Martí-Vidal, I., Alberdi, A., et al. 2009b, A&A, 503, 869 [Google Scholar]
- Marchili, N. 2009, Ph.D. Thesis, Bonn University, Germany (http://hss.ulb.uni-bonn.de/diss_online/math_nat_fak/2009/marchili_nicola) [Google Scholar]
- Marchili, N., Krichbaum, T. P., Liu, X., et al. 2008 [arXiv:0804.2787] [Google Scholar]
- Muxlow, T. W. B., Pedlar, A., Willkinson, P. N., et al. 1994, MNRAS, 266, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Muxlow, T. W. B., Pedlar, A., Beswick, R. J., et al. 2005, MmSAI, 76, 586 [NASA ADS] [Google Scholar]
- Pacholczyk, A. N. 1970, Radio Astrophysics, 1st edn. (San Francisco: Freeman & Co) [Google Scholar]
- Pérez-Torres, M. A., Alberdi, A., Marcaide, J. M., et al. 2002, MNRAS, 335, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Rickett, B. J., Witzel, A., Kraus, A., et al. 2001, ApJ, 550L, 11 [Google Scholar]
- Sun, X. H., Reich, W., Han, J. L., et al. 2006, A&A, 447, 937 [Google Scholar]
- Weiler, K. W., Panagia, N., Montes, M. J., & Sramek, R. A. 2002, ARA&A, 40, 387 [Google Scholar]
- Weiler, K. W., Williams, C. L., Panagia, N., et al. 2007, ApJ, 671, 1959 [NASA ADS] [CrossRef] [Google Scholar]
- Weiler, K. W., Panagia, N., Sramek, R. A., et al. 2009, AIPC, 1111, 440 [NASA ADS] [Google Scholar]
- Witzel, A., Heeschen, D. S., Schalinski, C., & Krichbaum, T. P. 1986, MitAG, 65, 239 [Google Scholar]
All Tables
Table 1: Urumqi data for SN 2008iz at 5 GHz frequency.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13126fg1.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa13126-09/Timg5.png)
|
Figure 1: The 5 GHz variability curve of M82, from Urumqi observations performed between August 2005 and May 2009. Up to February-March 2008, the radio emission from the source is nearly constant. The following increase in the measured flux density, culminating around June 2008, is ascribed to the explosion of SN 2008iz. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13126fg2.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa13126-09/Timg25.png)
|
Figure 2: Light curve of SN 2008iz at 5 GHz. Filled squares, Urumqi data; filled stars, MERLIN data from Beswick et al. (2009). The model with only FFA is shown as a continuous line; the model with FFA and SSA produced by the minimum (maximum) possible equipartition magnetic field is shown as a long-dashed (short-dashed) line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13126fg3.eps}
\end{figure}](/articles/aa/full_html/2010/01/aa13126-09/Timg47.png)
|
Figure 3: 22 GHz flux densities taken from Brunthaler et al. (2009b) (filled triangles), plotted along with the 5 GHz data shown in Fig. 2. The model obtained by fitting the 5 GHz data (continuous line) does not describe well the earliest 22 GHz flux density. Assuming a clumpy CSM (dashed line) provides a better fit to this flux density. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.