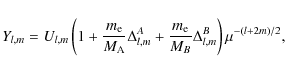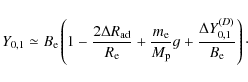| Issue |
A&A
Volume 509, January 2010
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 5 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/200913057 | |
| Published online | 12 January 2010 | |
Rotational spectra of CF+ and  CF+: accurate rest frequencies and spectroscopic parameters
CF+: accurate rest frequencies and spectroscopic parameters
G. Cazzoli1 - L. Cludi1 - C. Puzzarini1 - J. Gauss1,2
1 - Dipartimento di Chimica "G. Ciamician", Università di Bologna, via Selmi 2, 40126 Bologna, Italy
2 -
Institut für Physikalische Chemie, Universität Mainz, 55099 Mainz, Germany
Received 3 August 2009 / Accepted 2 October 2009
Abstract
Context. The astrophysical relevance of the
fluoromethylidynium ion and its importance for the interstellar
chemistry of fluorine motivated the present laboratory spectroscopic
investigation of both 12CF+ and the corresponding 13C-containing isotopologue, 13CF+.
Aims. This investigation has been carried out to provide
accurate rest frequencies for future (radioastronomical) observations,
to improve the accuracy of the values for the spectroscopic parameters
available in the literature for CF+, and to provide them for the first time for 13CF+.
Methods. Rotational spectra of CF+ and 13CF+
were recorded in the millimeter- and submillimeter-wave frequency
ranges. Their investigation was supplemented by high-level
quantum-chemical computations using state-of-the-art coupled-cluster
techniques.
Results. We report the most accurate ground-state rotational parameters available so far for CF+ and 13CF+.
Conclusions. The ground-state rotational parameters as well as the rest frequencies of 13CF+ will be useful for future observational purposes with the aim of improving the knowledge of fluorine interstellar chemistry.
Key words: molecular data - methods: laboratory - methods: data analysis - techniques: spectroscopic - ISM: molecules - radio lines: ISM
1 Introduction
While hydrogen, carbon, nitrogen, oxygen, silicon, and sulfur are
the most abundant elements in the interstellar medium (ISM), about
5% of the ![]() 120 molecules detected in the ISM contains less
abundant atoms, i.e., fluorine, chlorine, phosphorus, etc. Among the
fluorine-containing molecules, only HF and, very recently, also
CF+ have been observed. The recent observation of the J = 1-0, 2-1, and 3-2 rotational transitions of CF+ toward the Orion Bar region (Neufeld et al. 2006) together with the
still very limited knowledge about the interstellar chemistry of
fluorine stimulated the present investigation. As
13C-containing species are of astrophysical relevance, we
decided to further investigate the rotational spectra of
12CF+ and to study that of the 13C-containing species
for the first time.
120 molecules detected in the ISM contains less
abundant atoms, i.e., fluorine, chlorine, phosphorus, etc. Among the
fluorine-containing molecules, only HF and, very recently, also
CF+ have been observed. The recent observation of the J = 1-0, 2-1, and 3-2 rotational transitions of CF+ toward the Orion Bar region (Neufeld et al. 2006) together with the
still very limited knowledge about the interstellar chemistry of
fluorine stimulated the present investigation. As
13C-containing species are of astrophysical relevance, we
decided to further investigate the rotational spectra of
12CF+ and to study that of the 13C-containing species
for the first time.
To the best of our knowledge, the only study concerning the interstellar chemistry of fluorine available in the literature is the one by Neufeld et al. (2005). Their principal conclusion was that hydrogen fluoride is formed rapidly and is the dominant reservoir of fluorine over a wide range of conditions. As a consequence, the reaction of HF with C+ might lead to measurable column densities of CF+, and the fluoromethylidynium ion is predicted to be the second most abundant fluorine-containing molecule in the ISM. This prediction was subsequently confirmed by observations carried out using the IRAM 30 m and APEX 12 m telescopes as reported by Neufeld et al. (2006).
From a spectroscopic point of view, all previous laboratory work was
limited to the main isotopic species. The investigation of the pure
rotational spectrum was reported in the '80s by Plummer et al.
(1986), who recorded the
![]() ,
with J=1-3,
rotational transitions. The ro-vibrational spectra were studied by
Kawaguchi & Hirota (1985), who observed the fundamental band
via diode laser spectroscopy, and Gruebele et al.
(1986), who investigated the lowest six vibrational hot bands
by using velocity-modulation laser spectroscopy.
,
with J=1-3,
rotational transitions. The ro-vibrational spectra were studied by
Kawaguchi & Hirota (1985), who observed the fundamental band
via diode laser spectroscopy, and Gruebele et al.
(1986), who investigated the lowest six vibrational hot bands
by using velocity-modulation laser spectroscopy.
In the present work, the experimental investigation is supported by
high-level quantum-chemical calculations at the coupled-cluster
level (for a recent review, see Bartlett & Musia![]() 2007). The purpose of these calculations is mainly to obtain
reliable predictions for the relevant spectroscopic parameters for
the 13C-containing isotopologue of CF+. In a further step,
the computational results are also used for the determination of the
Born-Oppenheimer breakdown parameters for the rotational constant of
the fluoromethylidynium ion. To achieve sufficient accuracy in the
theoretical treatment, coupled-cluster methods up to pentuple
excitations are used in our calculations together with an adequate
treatment of core correlation, extrapolation to the basis-set limit
and consideration of zero-point vibrational corrections as well as
the electronic contribution to the rotational constants. Previous,
presumably less accurate theoretical studies of CF+ have been
reported by Peterson and coworkers using fourth-order
Møller-Plesset perturbation theory (Peterson et al. 1987)
and multireference configuration-interaction techniques (Peterson et al. 1990).
2007). The purpose of these calculations is mainly to obtain
reliable predictions for the relevant spectroscopic parameters for
the 13C-containing isotopologue of CF+. In a further step,
the computational results are also used for the determination of the
Born-Oppenheimer breakdown parameters for the rotational constant of
the fluoromethylidynium ion. To achieve sufficient accuracy in the
theoretical treatment, coupled-cluster methods up to pentuple
excitations are used in our calculations together with an adequate
treatment of core correlation, extrapolation to the basis-set limit
and consideration of zero-point vibrational corrections as well as
the electronic contribution to the rotational constants. Previous,
presumably less accurate theoretical studies of CF+ have been
reported by Peterson and coworkers using fourth-order
Møller-Plesset perturbation theory (Peterson et al. 1987)
and multireference configuration-interaction techniques (Peterson et al. 1990).
2 Methodology
The fluoromethylidynium ion has been investigated by means of rotational spectroscopy and quantum chemistry with the aim of obtaining accurate spectroscopic parameters. In the following sections the relevant experimental and theoretical details are given.
2.1 Experimental details
A frequency modulated computer-controlled spectrometer, equipped with a liquid helium-cooled InSb detector, was used to record the rotational spectra. The millimeter and submillimeter-wave sources employed are frequency multipliers driven by Gunn diode oscillators. The measurements were carried out in the 190-600 GHz frequency range with the source phase-locked to a rubidium frequency standard, and the frequency modulation obtained by sine-wave modulating the 75 MHz local oscillator of the synchronization loop. The detector output is processed by means of a lock-in amplifier tuned at twice the modulation frequency so that practically the recorded profile is the second derivative of the natural line profile. A detailed description of the spectrometer can be found in Cazzoli & Dore (1990).
Samples of CF+ and 13CF+ were prepared directly inside
the absorption cell starting from a mixture of either H2 and
CF4 or H2 and 13CF4 (99% in 13C), respectively,
approximately in the ratio 1:1 and by applying a DC discharge (2600
V, 15 mA). Measurements were performed in a continuous flow of gas,
maintained by a diffusion pump, in order to constantly provide fresh
precursor gases and to remove the final discharge products. It was
found to be necessary to apply a magnetic field of about 350 G in
order to detect the rotational spectra of the cations under
consideration. By applying discharge and magnetic field, it is
observed that the total pressure decreases from the initial value of
50 mTorr down to ![]() 35 mTorr (effect already observed in Plummer
et al. 1986). The recording of the spectra was performed as
soon as stationarity in the discharge conditions was reached. Since
no rotational parameters were available for the 13C-containing
species, quantum-chemically calculated values of the relevant
spectroscopic parameters were used to predict rotational transition
frequencies. The latter have been further improved by empirically
scaling, thereby using the available literature data for CF+(Plummer et al. 1986).
35 mTorr (effect already observed in Plummer
et al. 1986). The recording of the spectra was performed as
soon as stationarity in the discharge conditions was reached. Since
no rotational parameters were available for the 13C-containing
species, quantum-chemically calculated values of the relevant
spectroscopic parameters were used to predict rotational transition
frequencies. The latter have been further improved by empirically
scaling, thereby using the available literature data for CF+(Plummer et al. 1986).
The
![]() ,
with J=1-4, rotational transitions of
CF+ and the
,
with J=1-4, rotational transitions of
CF+ and the
![]() ,
with J=1, 3-5, rotational
transitions of 13CF+ have been recorded with an accuracy of about
50 kHz.
,
with J=1, 3-5, rotational
transitions of 13CF+ have been recorded with an accuracy of about
50 kHz.
2.2 Dunham fit and Born-Oppenheimer breakdown
In a Dunham-type fit for the analysis of the data (Dunham
1932), a potential function of the form:
is employed, where
with Yl,m as the actual Dunham parameters as well as J and v representing the rotational and vibrational quantum numbers, respectively.
Watson showed that the Dunham parameters Yl,m for different
isotopologues can be expressed to a good approximation in terms of
the isotopically invariant parameters Ul,m,
![]() and
and
![]() (Watson 1973; Watson 1980):
(Watson 1973; Watson 1980):
where MA and MB denote the atomic masses and
In Eq. (4),
| (5) |
needs to be used when applying Eq. (3) for the determination of the parameters Ul,m,
2.3 Quantum-chemical details
Quantum-chemical calculations were performed with the twofold aim of predicting the unknown spectroscopic parameters of 13CF+ and of determining the BO breakdown parameters for the rotational constant of CF+ as discussed above.
Most calculations that are reported here were performed at the
coupled-cluster (CC) level of theory (Bartlett & Musia![]() 2007) employing the CC singles and doubles (CCSD)
approximation (Purvis & Bartlett 1982) augmented by a
perturbative treatment of triple excitations (CCSD(T)) (Raghavachari
et al. 1989). The full CC singles, doubles and triples
(CCSDT) (Noga & Bartlett 1987; Watts & Bartlett
1993), the CC singles, doubles, triples and quadruples
(CCSDTQ), as well as the singles, doubles, triples, quadruples,
pentuples (CCSDTQP) (Kállay & Surján 2001) models were
used in a few additional calculations.
2007) employing the CC singles and doubles (CCSD)
approximation (Purvis & Bartlett 1982) augmented by a
perturbative treatment of triple excitations (CCSD(T)) (Raghavachari
et al. 1989). The full CC singles, doubles and triples
(CCSDT) (Noga & Bartlett 1987; Watts & Bartlett
1993), the CC singles, doubles, triples and quadruples
(CCSDTQ), as well as the singles, doubles, triples, quadruples,
pentuples (CCSDTQP) (Kállay & Surján 2001) models were
used in a few additional calculations.
The calculations were performed using the following
correlation-consistent basis sets: the valence cc-pVnZ (
![]() ,
T)
basis sets (Dunning 1989) and the core-valence cc-pCVnZ
(
,
T)
basis sets (Dunning 1989) and the core-valence cc-pCVnZ
(
![]() -6) basis (Dunning 1989; Woon & Dunning
1995). The frozen-core (fc) approximation, i.e.,
consideration of electron correlation of the valence electrons only,
has been adopted in conjunction with the former basis sets, and, to
account for core-correlation effects, computations correlating all
electrons were carried out with the cc-pCVnZ sets.
-6) basis (Dunning 1989; Woon & Dunning
1995). The frozen-core (fc) approximation, i.e.,
consideration of electron correlation of the valence electrons only,
has been adopted in conjunction with the former basis sets, and, to
account for core-correlation effects, computations correlating all
electrons were carried out with the cc-pCVnZ sets.
All quantum-chemical computations reported here were carried out with the CF OUR program package (2009), except those including higher than triple excitations which were performed with the MRCC package (2001) by Kállay which has been interfaced to CF OUR.
To predict the rotational spectrum of 13CF+, the vibrational
ground-state rotational constant was computed using an approach
similar to the one proposed and thoroughly tested in Puzzarini et al. (2008). This scheme makes use of an additivity scheme for the various electron-correlation
contributions, employs extrapolation techniques to reach the
basis-set limit, and considers additional zero-point vibrational and
electronic contributions. The starting level in this scheme is
CCSD(T) in conjunction with basis sets up to sextuple-zeta quality.
To estimate the CCSD(T) basis-set limit, extrapolation techniques
(Feller 1993; Helgaker et al. 1997) are applied at
the gradient level within the geometry optimization (Heckert et al.
2006). Core-correlation effects are already included at
this level by basing this step on all-electron CCSD(T) calculations
and the core-polarized cc-pCVnZ sets. Higher-order correlation
effects are considered via frozen-core CCSDT/cc-pVTZ,
CCSDTQ/cc-pVDZ, and CCSDTQP/cc-pVDZ calculations with the
corresponding corrections again included at the gradient level. On
the whole, this composite level to obtain the best estimate for the
equilibrium structure and also the equilibrium rotational constant
is best characterized as
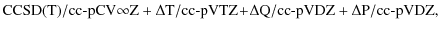
|
where CCSD(T)/cc-pCV
The final prediction of the ground-state rotational constant
B0 necessitates the additional computation of the vibrational and electronic
contributions:
| (6) |
The first of these two contributions requires the evaluation of the harmonic and anharmonic force field to compute the vibration-rotation interaction constant
To complete our prediction, quartic and sextic centrifugal distortion constants were derived from the available harmonic and cubic force fields.
To evaluate the BO breakdown parameters, as explained in Gauss &
Puzzarini (2009), we need theoretical values for ![]() ,
,
![]() ,
g and
,
g and
![]() .
The first of these
quantities,
.
The first of these
quantities, ![]() ,
is defined via the minimum of the BO potential,
while the second is the minimum of the potential in the adiabatic
approximation for which the potential is given by the sum of the BO
potential and the diagonal BO correction (DBOC). The determination
of
,
is defined via the minimum of the BO potential,
while the second is the minimum of the potential in the adiabatic
approximation for which the potential is given by the sum of the BO
potential and the diagonal BO correction (DBOC). The determination
of ![]() was performed as explained above and involves extrapolation
to the complete basis set limit, core-correlation effects, and
higher excitation. In a second step the adiabatic distance
was performed as explained above and involves extrapolation
to the complete basis set limit, core-correlation effects, and
higher excitation. In a second step the adiabatic distance
![]() was obtained by augmenting the previously obtained
was obtained by augmenting the previously obtained ![]() value with
the shift due to the DBOC computed at the CCSD/cc-pVTZ level. The
geometry optimization including DBOC was performed using numerically
evaluated forces. The rotational g factor was computed in the
third step as already discussed. Finally, to evaluate the Dunham
correction, the potential given in Eq. (1) and thus the
corresponding potential constants are required. They are obtained by
calculating a suitable number (in the present case 30) of energy
points around
value with
the shift due to the DBOC computed at the CCSD/cc-pVTZ level. The
geometry optimization including DBOC was performed using numerically
evaluated forces. The rotational g factor was computed in the
third step as already discussed. Finally, to evaluate the Dunham
correction, the potential given in Eq. (1) and thus the
corresponding potential constants are required. They are obtained by
calculating a suitable number (in the present case 30) of energy
points around ![]() .
Those were computed at the CCSD(T)/cc-pCV5Z
level. The Dunham correction is then given by (Watson 1973;
Dunham 1932)
.
Those were computed at the CCSD(T)/cc-pCV5Z
level. The Dunham correction is then given by (Watson 1973;
Dunham 1932)
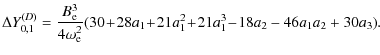
|
(7) |
With the Dunham coefficients Y0,1 computed via Eq. (4) for 12C19F+, 13C19F+, 12C18F+, and 13C18F+, it is then possible via a least-squares fit using Eq. (3) to determine the carbon and fluorine BO breakdown parameters.
3 Results and discussion
The measured frequencies of the
![]() (J=1-4)
rotational transitions of CF+ and the
(J=1-4)
rotational transitions of CF+ and the
![]() (J=1, 3-5) rotational transitions of 13CF+ are given in
Table 1. The values reported were obtained as averages of
several sets of measurements, and for all of them the standard
deviation is well within the given uncertainty of 50 kHz. For
predictive purpose, in Table 1 the calculated frequencies,
together with their estimated accuracy, based on the fit described
below are also reported. Figure 1 shows the J = 4
(J=1, 3-5) rotational transitions of 13CF+ are given in
Table 1. The values reported were obtained as averages of
several sets of measurements, and for all of them the standard
deviation is well within the given uncertainty of 50 kHz. For
predictive purpose, in Table 1 the calculated frequencies,
together with their estimated accuracy, based on the fit described
below are also reported. Figure 1 shows the J = 4
![]() 3 rotational transition for both CF+ and
13CF+ and provides an example of the signal-to-noise (S/N)
ratio obtained in our measurements. The worse S/N ratio observed for
the 13C-containing species is due to the shorter averaging time
employed, a choice made in order to preserve the 13CF4sample as much as possible.
3 rotational transition for both CF+ and
13CF+ and provides an example of the signal-to-noise (S/N)
ratio obtained in our measurements. The worse S/N ratio observed for
the 13C-containing species is due to the shorter averaging time
employed, a choice made in order to preserve the 13CF4sample as much as possible.
Table 1:
![]() (with J''=0-7) rotational
transitions (MHz) and, for measured frequencies, corresponding
observed-calculated (o-c) differences (kHz) for CF+ and
13CF+ together with the determined spectroscopic parameters.
The latter are compared with the theoretical values as well as
previous literature data.
(with J''=0-7) rotational
transitions (MHz) and, for measured frequencies, corresponding
observed-calculated (o-c) differences (kHz) for CF+ and
13CF+ together with the determined spectroscopic parameters.
The latter are compared with the theoretical values as well as
previous literature data.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13057fig.eps} %
\end{figure}](/articles/aa/full_html/2010/01/aa13057-09/Timg34.png)
|
Figure 1:
The
|
| Open with DEXTER | |
To determine the rotational parameters, the transition frequencies were included in a least-squares fit in which each line is weighted proportionally to the inverse square of its experimental uncertainty. This fit was carried out with Pickett's SPCAT/SPFIT program (Pickett 1991). The four transitions observed for each isotopic species allow us to determine the rotational constant B0and the quartic centrifugal distortion constant D0. The results are collected in Table 1, where they are compared to literature and theoretical data. We note that the residuals from the fit, i.e., the differences between observed and calculated values, are small and actually smaller than the ascribed uncertainties in the measured frequencies. In comparison with the results of Plummer et al. (1986), we note that their quartic centrifugal-distortion constant D0 does not agree with our value within the given uncertainties, while the vibrational ground-state rotational constants agree within the given error bars. As we have observed one more transition, higher in frequency, than Plummer et al. (1986) and our fit reproduces observed frequencies well within the stated uncertainty, we consider our results more reliable. Concerning the comparison with the results from the analysis of the rovibrational spectra (Kawaguchi & Hirota 1985; Gruebele et al. 1986), the larger accuracy in determining the vibrational ground-state rotational constant by means of microwave spectroscopy is evident. When comparing to the quantum-chemical results, a good agreement with the experimental data for CF+ is noted. Detailed analysis reveals that core-correlation effects contribute about 250 MHz to the rotational constant of CF+, that corrections due to the full treatment of triples via CCSDT amount to about -20 MHz, and that the corrections due to quadruple and pentuple excitations are of the order of -40 and -15 MHz, respectively. The overall accuracy of our best theoretical estimate for the rotational constant of CF+ can be thus estimated as roughly 20-30 MHz. The computed spectroscopic parameters are therefore clearly able to guide observation of the spectrum of 13CF+. Furthermore, the computations confirm that the sextic centrifugal-distortion constant is very small and therefore barely determinable (i.e., rotational transitions with J > 10-15 are required).
In a second step of the analysis, our frequency values for the main
isotopic species were fitted together with those for the fundamental
band by Kawaguchi & Hirota (1985) and those for the lowest six
vibrational hot bands by Gruebele et al. (1986) to
the Dunham expression given by Eq. (2). The results are
reported in Table 2, where they are compared with the
previously reported parameters by Gruebele et al.
(1986). However, it should be noted here that the fits
performed in the present study and the one reported by Gruebele et al. (1986) are somewhat different. While we fitted the available frequency values directly to Eq. (2),
Gruebele et al. fitted their frequency data to a Dunham expansion
of the vibrorotational energies in terms of the equilibrium rotational
constant ![]() ,
the harmonic frequency
,
the harmonic frequency
![]() and the first six
potential coefficients a1 ... a6 of Eq. (1). They then
used these equilibrium parameters to determine the Dunham
coefficients reported in Table 2 by means of the
expressions given in Dunham (1932). From the comparison it is
apparent that, for the parameters we found determinable in the Dunham
analysis, our results agree well with those by Gruebele et al.
(1986). On the other hand, we found that the parameters
Y3,1, Y2,2, Y0,3, and Y1,3 are not determinable
from the fit. Furthermore, the value reported by Gruebele et al.
(1986) for the latter coefficient seems to be too large, as
Y1,3 is larger than the Y0,3 parameter.
and the first six
potential coefficients a1 ... a6 of Eq. (1). They then
used these equilibrium parameters to determine the Dunham
coefficients reported in Table 2 by means of the
expressions given in Dunham (1932). From the comparison it is
apparent that, for the parameters we found determinable in the Dunham
analysis, our results agree well with those by Gruebele et al.
(1986). On the other hand, we found that the parameters
Y3,1, Y2,2, Y0,3, and Y1,3 are not determinable
from the fit. Furthermore, the value reported by Gruebele et al.
(1986) for the latter coefficient seems to be too large, as
Y1,3 is larger than the Y0,3 parameter.
Table 2: Dunham coefficients for 12CF+.
As mentioned in the computational detail section, the BO breakdown
parameters for the rotational constant were determined based on
quantum-chemical calculations. The results are reported in
Table 3. There, the various individual contributions,
namely
![]() ,
,
![]() and
and
![]() ,
are also collected. With respect to the experiment, unfortunately
the lack of data for 13CF+ in vibrationally excited states
prevented their experimental determination.
,
are also collected. With respect to the experiment, unfortunately
the lack of data for 13CF+ in vibrationally excited states
prevented their experimental determination.
4 Conclusion
Measurements of the rotational spectra of CF+ and 13CF+, carried out in the 190-600 GHz frequency range, allowed us to report improved values for the B0 and D0 parameters of the main isotopic species and to provide for the first time spectroscopic parameters for the 13C-containing isotopologue. Since both isotopic species are of astrophysical relevance, the rest frequencies obtained in the present investigation as well as those predicted from our results will be useful for future observational purposes aiming at an improved understanding of the interstellar chemistry of fluorine.
Table 3:
Summary of the theoretical analysis of the BO breakdown in
CF+. The equilibrium BO rotational constants are reported
together with adiabatic, non-adiabatic, and Dunham corrections for
the four considered isotopologues of CF+ as well as the Dunham
coefficients Y0,1 (all values in MHz), the BO bond distance
![]() (in Å), and the dimensionless BO breakdown parameters. For
computational details, see text.
(in Å), and the dimensionless BO breakdown parameters. For
computational details, see text.
This work has been supported by ``PRIN 2007'' funds (project ``Trasferimenti di energia, carica e molecole in sistemi complessi'') and by University of Bologna (RFO funds) as well as in Mainz by the Deutsche Forschungsgemeinschaft and the Fonds der Chemischen Industrie.
References
- Bartlett, R. J., & Musia▯, M. 2007, Rev. Mod. Phys., 79, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., & Dore, L. 1990, J. Mol. Spectrosc., 141, 49 [NASA ADS] [CrossRef] [Google Scholar]
- CF OUR A quantum chemical program package written by Stanton, J. F., Gauss, J., Harding, et al., For the current version, see http://www.cfour.de [Google Scholar]
- Dunham, J. L. 1932, Phys. Rev., 41, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Dunning, T. H., Jr. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Feller, D. 1993, J. Chem. Phys., 98, 7059 [NASA ADS] [CrossRef] [Google Scholar]
- Gauss, J., & Puzzarini, C. 2009, Mol. Phys., in press,DOI: 10.1080/00268970903433507 [Google Scholar]
- Gauss, J., Ruud, K., & Helgaker, T. 1996, J. Chem. Phys., 105, 2804 [NASA ADS] [CrossRef] [Google Scholar]
- Gauss, J., Ruud, K., & Kállay, M. 2007, J. Chem. Phys., 127, 074101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gruebele, M., Polak, M., & Saykally, R. J. 1986, Chem. Phys. Lett., 125, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Heckert, M., Kállay, M., Tew, D. P., Klopper, W., & Gauss J. 2006, J. Chem. Phys., 125, 044108 [NASA ADS] [CrossRef] [Google Scholar]
- Helgaker, T., Klopper, W., Koch, H., & Noga J. 1997, J. Chem. Phys., 106, 9639 [NASA ADS] [CrossRef] [Google Scholar]
- Kállay, M., & Surján, P. R. 2001, J. Chem. Phys., 115, 2945 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, K., & Hirota, E. 1985, J. Chem. Phys., 83, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Kutzelnigg, W. 2002, in Relativistic Electronic Structure Theory. Part I. Fundamentals, ed. P. Schwerdtfeger (Amsterdam: Elsevier) [Google Scholar]
- Michauk, C., & Gauss, J. 2007, J. Chem. Phys., 127, 044106 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mills, I. A. 1972, in Modern Spectroscopy: Modern Research, ed. K. N. Rao, & C. W. Matthews (New York: Academic) [Google Scholar]
- MRCC, a generalized CC/CI program by Kállay, M., see http://www.mrcc.hu [Google Scholar]
- Neufeld, D. A., Wolfire, M. G., & Schilke, P. 2005, ApJ, 628, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Schilke, P., Menten, K. M., et al. 2006, A&A, 454, L37 [Google Scholar]
- Noga, J., & Bartlett, R. J. 1987, J. Chem. Phys., 86, 7041 [NASA ADS] [CrossRef] [Google Scholar]
- Odashima H. 2006, J. Mol. Spectrosc., 240, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, K. A., & Woods R. C. 1987, J. Chem. Phys., 87, 4409 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, K. A., Woods R. C., Rosmus, P., & Werner H.-J. 1990, J. Chem. Phys., 93, 1889 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H.M. 1991, J. Mol. Spectrosc., 148, 371 [Google Scholar]
- Plummer, G. M., Anderson, T., Herbst, E., & De Lucia F. C. 1986, J. Chem. Phys., 84, 2427 [NASA ADS] [CrossRef] [Google Scholar]
- Purvis, G. D., III, & Bartlett, R. J. 1982, J. Chem. Phys. 76, 1910 [NASA ADS] [CrossRef] [Google Scholar]
- Puzzarini, C., Heckert, M., & Gauss J. 2008, J. Chem. Phys., 128, 194108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Watson J. K. G. 1973, J. Mol. Spectrosc., 45, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Watson J. K. G. 1980, J. Mol. Spectrosc., 80, 411 [Google Scholar]
- Watts, J. D., & Bartlett, R. J. 1993, J. Chem. Phys., 93, 6104 [Google Scholar]
- Woon, D. E., & Dunning, T. H., Jr. 1995, J. Chem. Phys., 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Table 1:
![]() (with J''=0-7) rotational
transitions (MHz) and, for measured frequencies, corresponding
observed-calculated (o-c) differences (kHz) for CF+ and
13CF+ together with the determined spectroscopic parameters.
The latter are compared with the theoretical values as well as
previous literature data.
(with J''=0-7) rotational
transitions (MHz) and, for measured frequencies, corresponding
observed-calculated (o-c) differences (kHz) for CF+ and
13CF+ together with the determined spectroscopic parameters.
The latter are compared with the theoretical values as well as
previous literature data.
Table 2: Dunham coefficients for 12CF+.
Table 3:
Summary of the theoretical analysis of the BO breakdown in
CF+. The equilibrium BO rotational constants are reported
together with adiabatic, non-adiabatic, and Dunham corrections for
the four considered isotopologues of CF+ as well as the Dunham
coefficients Y0,1 (all values in MHz), the BO bond distance
![]() (in Å), and the dimensionless BO breakdown parameters. For
computational details, see text.
(in Å), and the dimensionless BO breakdown parameters. For
computational details, see text.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13057fig.eps} %
\end{figure}](/articles/aa/full_html/2010/01/aa13057-09/Timg34.png)
|
Figure 1:
The
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



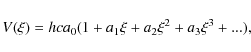
![\begin{displaymath}\nu_{J,v} = \sum_{l,m} Y_{l,m} \left( v + \frac{1}{2} \right) ^l [
J(J+1) ]^m,
\end{displaymath}](/articles/aa/full_html/2010/01/aa13057-09/img10.png)