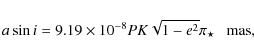EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 509 (January 2010) A&A, 509 (2010) A103 Full HTML
Free Access
Issue
A&A
Volume 509, January 2010
Article Number A103
Number of page(s) 12
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/200912717
Published online 27 January 2010
A&A 509, A103 (2010)

Hipparcos preliminary astrometric masses for the two close-in companions to HD 131664 and HD 131664

A brown dwarf and a low-mass star

A. Sozzetti1 - S. Desidera2

1 - INAF - Osservatorio Astronomico di Torino, via Osservatorio 20, 10025 Pino Torinese, Italy
2 - INAF - Osservatorio Astronomico di Padova, Vicolo dell' Osservatorio 5, 35122 Padova, Italy

Received 18 June 2009 / Accepted 23 September 2009

Abstract
Context. Several mechanisms for forming brown dwarfs have been proposed, which today are not believed to be mutually exclusive. Among the fundamental characteristics of brown dwarfs that are intrinsically tied to their origins, multiplicity is particularly relevant. Any successful determination of the actual mass for such objects in any systems is thus worthwhile, as it allows one to improve on the characterization of the multiplicity properties (e.g., frequency, separation, mass-ratio distribution) of sub-stellar companions.
Aims. We attempt to place better constraints on the masses of two Doppler-detected substellar companions to the nearby G dwarfs HD 131664 and HD 131664.
Methods. We carried out orbital fits to the Hipparcos Intermediate Astrometric Data (IAD) for the two stars, taking advantage of the knowledge of the spectroscopic orbits, and solving for the inclination angle i and the longitude of the ascending node $\Omega $, the two orbital elements that can be determined in principle solely by astrometry, A number of checks were carried out to assess the reliability of the orbital solutions thus obtained.
Results. The best-fit solution for HD 131664 yields $i=55\pm33$ deg and $\Omega=22\pm28$ deg. The resulting inferred true companion mass is then $M_{\rm c} = 23_{-5}^{+26}$$M_{\rm J}$. For HD 131664, we find $i=12\pm7$ deg and $\Omega=288\pm22$ deg, and a corresponding $M_{\rm c} = 120_{-43}^{+167}$$M_{\rm J}$. Based on the statistical evidence from an F-test, the study of the joint confidence intervals of variation in i and $\Omega $ and the comparison of the derived orbital semi-major axes with a distribution of false astrometric orbits obtained for single stars observed by Hipparcos, the astrometric signal of the two companions to HD 131664 and HD 131664 is then considered detected in the Hipparcos IAD, with a level of statistical confidence not exceeding 95%.
Conclusions. We constrain the true mass of HD 131664b to that of a brown dwarf to within a somewhat statistically significant degree of confidence ($\sim$$2-\sigma$). For HD 131664b, a true mass in the brown dwarf regime is ruled out at the $1-\sigma$ confidence level. The results are discussed in the context of the properties of the (few) close substellar and massive planetary companions to nearby solar-type stars and their implications for proposed models of formation and structure of massive planets and brown dwarfs.

Key words: stars: individual: HD 131664, HD 131664 - stars: low-mass - stars: brown dwarfs - planetary systems - astrometry - methods: data analysis

1 Introduction

Similar to the detection of the first Jupiter-mass ($M_{\rm J}$) planet orbiting a star other than the Sun (Mayor & Queloz 1995), the first unambiguous discovery of a brown dwarf[*] dates back $\sim$14 years (e.g., Rebolo et al. 1995; Nakajima et al. 1995). Several mechanisms for forming brown dwarfs have been proposed: turbulent fragmentation of molecular clouds, fragmentation of massive prestellar cores, protoplanetary disk fragmentation, dynamical ejection of protostellar embryos, and photoerosion of protostellar cores (for a review, see Whitworth et al. 2007). Such mechanisms are today believed to not be mutually exclusive, and they all likely operate in nature. Determining their relative contribution to the overall brown dwarf population is a major theoretical challenge. To date, agreement must still be reached on fundamental issues such as what the minimum mass for brown dwarfs is, and how brown dwarfs might be distinguished from planets. For example, if brown dwarfs are identified as objects that form as stars do, on dynamical timescales by gravitational instability, regardless of the formation locus (a molecular cloud or a marginally unstable protoplanetary disk), and if the minimum mass for core collapse is a few $M_{\rm J}$(see Whitworth et al. 2007), then significant overlap between the mass range of brown dwarfs and planets would occur and a simple mass cutoff (such as the one adopted here) may not apply. Given the significant number of open questions in this research field, it is thus essential for theory to accurately reproduce, and for observations to carefully determine, the ensemble properties of brown dwarfs, including the brown dwarfs' initial mass function, the young brown dwarfs' kinematics, distribution, and disk frequency, and the binary statistics of brown dwarfs across a wide range of primary masses and orbital separations (for a review see Luhman et al. 2007; and Burgasser et al. 2007).

Among the fundamental characteristics of brown dwarfs that are intrinsically tied to their origin multiplicity properties (e.g, frequency, separation, mass-ratio distribution) are particularly relevant, because together with the possibility of determining the actual internal composition and atmospheric features of individual objects, they constitute one of the few ways of observationally distinguishing between planets and brown dwarfs in the possible overlap region in mass. For example, the frequency of close (a<5AU) stellar ( $M_{\rm c}>0.08$ $M_{\odot }$) companions to nearby (d<50pc) solar-type stars is $13\pm3$% (Duquennoy & Mayor 1991), while in the same range of separations the frequency of giant planets ( $M_{\rm c} \lesssim 15$$M_{\rm J}$) is today known to be about 7% (Marcy et al. 2008). Brown dwarfs, on the other hand, appear conspicuously absent in the datasets collected by decade-long, high-precision radial-velocity surveys of thousands of bright normal stars, despite how easily their large RV signals would have been spotted. Initial claims that the frequency of close brown dwarf companions seemed to be in fair agreement with a constant distribution of mass ratios (Mayor et al. 1992) were later dismissed by studies, based on a combination of radial velocity measurements and Hipparcos astrometric observations, that showed how most of these putative substellar companions where in fact stars (Halbwachs et al. 2000). Indeed, among close companions, brown dwarfs appear outnumbered by stars and planets by factors of $\sim$100 and $\sim$50, respectively, with typical frequency estimates of $\approx$0.1% (Marcy & Butler 2000). Only about half a dozen close companions with minimum masses in the brown dwarf regime are known today around bright, nearby solar-type stars It is conceivable that observational biases might contribute somewhat to a reduction in the discovery rate of brown dwarfs with respect to planets (because massive companions are typically assigned lower priorities than lower mass planets in Doppler surveys hard-pressed for optimal use of the precious observing time at 10-m class telescopes). However, such biases do not seem capable of explaining two orders of magnitude of difference in the observed frequency of brown dwarf companions with respect to planets and stellar companions.

The dearth of close brown dwarf companions to solar-type stars, commonly referred to as the ``brown dwarf desert'' (e.g, Campbell et al. 1988; Marcy & Butler 2000), is seen to extend at wider separations. Only recently have Patel et al. (2007) reported the first radial velocity detection of a handful of companions with $M_{\rm c}\sin i$firmly established in the brown dwarf mass range at orbital distances of $\sim$4 to 18 AU. These first results do not yet allow an actual number for the brown dwarf frequency to be produced in this separation range. At larger separations ($\sim$50-1000 AU), near-IR direct imaging surveys have confirmed a deficit in substellar companions relative to stellar companions, but not quite as extreme as waht is apparent at orbital radii within a few AUs.  McCarthy & Zuckerman (2004) find $f_{\rm BD} = 1\pm1$%, roughly a factor of ten lower than the stellar companion frequency in the same separation range. More recently  Metchev & Hillenbrand (2009) have derived $f_{\rm BD} = 3.2^{+3.1}_{-2.7}$%, a number formally compatible with that of McCarthy & Zuckerman (2004). In any case, the frequency of wide-separation brown dwarf companions is comparable to that of free-floating brown dwarfs relative to stars. The evidence for a not-so-dry desert at wide separations is usually interpreted as supporting the view that brown dwarfs form by core fragmentation just like stars. However, the finer details of the formation mechanism are not well understood, so a more accurate characterization of the multiplicity of brown dwarfs is needed to shed light on the relative role of the various proposed scenarios.

The dynamical determination of the mass of a few close brown dwarfs companions to low-mass stars and of brown dwarf binaries has been obtained for eclipsing systems for which both spectra can be observed  (e.g., Stassun et al. 2006; Zapatero Osorio et al. 2004) and by a combination of aperture masking interferometry and astrometry (Ireland et al. 2008). As for the sample of companions to nearby dwarfs discovered by Doppler planet surveys with $M_{\rm c}\sin i$values in the range between high-mass planets and brown dwarfs, it is conceivable that some of them are in reality stars seen pole-on. Similar to Halbwachs et al. (2000), several authors have attempted to combine the radial-velocity orbits with Hipparcos astrometry in order to determine the inclination and true mass of the companions (for a review see for example Sozzetti 2009). Recently,  Reffert & Quirrenbach (2006) presented low-significance detections of the astrometric orbits of the two outer companions in the HD 38529 and HD 168443 planetary systems, inferring masses in the brown dwarf regime of 37 $M_{\rm J}$ and 34 $M_{\rm J}$ for HD 38529c and HD 168443c, respectively. High-precision astrometry with HST/FGS allowed Bean et al. (2007) to determine an actual mass of 0.14 $M_{\odot }$ for the companion to HD 33636, originally published with $M_{\rm c}\sin i = 9.3$$M_{\rm J}$. Any successful attempt to resolve the ambiguity in the actual companion mass for such objects is thus worthwhile as it allows improvement of the characterization of the multiplicity of brown dwarfs. This in turn permits better understanding of the global nature of the substellar companions found at larger separations by means of direct imaging surveys.

In this paper we present a new attempt at combining the information from Doppler measurements with Hipparcos astrometry to place better constraints on the mass of two Doppler-detected low-mass companions to HD 131664 (Moutou et al. 2009) and HD 131664 (Minniti et al. 2009), with published minimum masses in the low-mass brown dwarf regime. A summary of the available data in the literature for the two systems is presented in Sect. 2. We derive improved contraints on the actual companion masses in Sect. 3. Finally, in Sect. 4 we a) put the new results in the context of the properties of the (few) close sub-stellar and massive planetary companions to nearby solar-type stars, collected in a catalogue table for ease of consultation and reference in future works and b) discuss some of the implications of the present-day observational evidence for formation and structural models of massive planets and brown dwarfs.

2 Doppler data and Hipparcos astrometry


Table 1:   Stellar characteristics of HD 131664 and HD 131664 and spectroscopic orbital elements for the two Doppler-detected companions.

2.1 HD 131664

Included in the Doppler search for southern extrasolar planets carried out with the HARPS  (Pepe et al. 2003) spectrograph on the ESO 3.6-m telescope at La Silla Observatory, the bright G-type star HD 131664 (HIP 73408) was recently announced by Moutou et al. (2009) to be orbited by a companion with a minimum mass of $M_{\rm c}\sin i = 18$$M_{\rm J}$on an eccentric orbit of period $P\approx5.3$ yr (for convenience, see Table 1 for a summary of the properties of the primary and of the orbital parameters of detected companion). At the distance of HD 131664, the inferred orbital separation ranges between 35 mas and 100 mas (as pointed out by Moutou et al.), making it a potentially interesting target for future direct-imaging observations. The viability of this investigation depends in particular on the true mass of the companion and the actual contrast ratio. In the former case, high-precision astrometry with Gaia in space and VLTI/PRIMA from the ground (e.g., Sozzetti 2009, and references therein) will allow accurate values to be derived of the actual mass of the companion. However, it must be noted that the minimum astrometric signature induced on the primary is just under 1 mas, as opposed to a median single-measurement error $\sigma_{\rm HIP}\approx3$ mas. Hipparcos observations of this star could then help place useful mass constraints on the companion mass. Indeed, the Double and Multiple Star Annex of the Hipparcos Catalogue reports a G flag, indicating that a 7-parameter solution (allowing for acceleration in the proper motion) was found to significantly improve the standard 5-parameter single-star fit. The reported acceleration solution for HD 131664 is based on 96 datapoints, two of which correspond to observations retained only by the NDAC consortium.

2.2 HD 43848

Doppler measurements taken with the MIKE echelle spectrograph (Bernstein et al. 2003) on the 6.5-m Magellan II (Clay) telescope have revealed (Minniti et al. 2009) the nearby solar-type star HD 131664 (HIP 29804) to be orbited by a companion with $M_{\rm c}\sin i = 25$ $M_{\rm J}$on a high-eccentricity orbit with $P\approx6.5$ yr (for completeness, Table 1 also reports the summary of the properties of the primary and of the orbital parameters of detected companion). This system also appears to be of potential interest for future direct-imaging observations, with a separation at apoastron of $\approx$0.2 arcsec. Its minimum astrometric signature, at the distance of HD 43848, is $\approx$2.5 mas, a value comparable to the typical precision of Hipparcos astrometry for this star (median error $\sigma_{\rm HIP}\sim3.3$ mas). An astrometric solution with acceleration terms for this star is also present in the Hipparcos Catalogue, based on a total of 76 measurements[*] (with one abscissa retained only by FAST, one only by NDAC, and another rejected by NDAC in the solution). For both HD 131664 and HD 131664 there appears to be indication of a long-period trend in the Hipparcos data, rendering a further investigation of the available astrometry worthwhile.

3 Combined radial velocity+astrometry solution

When searching for evidence of an orbital signal in the Hipparcos data of a given star due to a spectroscopically discovered low-mass companion, a typical procedure is applied in which information from radial velocities is assumed known, and one resorts to probing the region of the parameter space not covered by spectroscopy. Orbital fits to the Hipparcos IAD are then usually performed (Wittenmyer et al. 2009; Halbwachs et al. 2000; Mazeh et al. 1999; Han et al. 2001; Reffert & Quirrenbach 2006; Zucker & Mazeh 2000) by keeping four orbital elements fixed (P, e, T0, $\omega $) to their spectroscopically determined values and by solving for inclination angle i and position angle of the ascending node $\Omega $, with the additional constraint that the astrometric semi-major axis satisfies the equality (Pourbaix & Jorissen 2000)

\begin{displaymath} a\sin i = 9.19\times 10^{-8}P K\sqrt{1 - e^2}\pi_\star~~~{\rm mas}, \end{displaymath} (1)

where P is in days, the semi-amplitude of the radial velocity curve K is in m s-1, and the orbital parallax $\pi_\star$ is in mas. The resulting fitting procedure then has a total of 7 adjustable parameters, i.e. the five astrometric parameters (two position offsets in right ascension and declination, two differential corrections to the proper motion in right ascension and declination, and the parallax) plus i and $\Omega $.

The experience of various authors indicates that one must be careful not to ask Hipparcos data to tell more than they actually can. Pourbaix (2001), Pourbaix & Arenou (2001), and later Zucker & Mazeh (2001) have for example shown that the Hipparcos IAD, while useful to put upper limits on the size of the astrometric perturbations, must be interpreted with great caution when attempting to derive actual astrometric orbits for substellar companions with semi-major axes close to or even below the typical single-measurement precision of the satellite. While the astrometric orbit does not need to be actually detected in order to derive constraints on the values of i and $M_{\rm c}$, reported detections, when not outright refuted (e.g., Pourbaix & Arenou 2001), usually have relatively low levels of statistical confidence (e.g., Reffert & Quirrenbach 2006). Based on the above considerations, we have adopted a multi-step approach to the treatment of the Hipparcos IAD for HD 131664 and HD 131664 in an attempt to make a statistically solid case for any conclusions.

\begin{figure} \par$\begin{array}{c} \includegraphics[width=8cm]{12717f1a.eps}\\ \includegraphics[width=8cm]{12717f1b.eps}\\ \end{array} $ \end{figure} Figure 1:

Periodograms of HD 131664 ( top) and HD 131664 ( bottom)assuming e and T0 from the known spectroscopic orbit.

Open with DEXTER

As a first step in the process, we decorrelated and weighted all available Hipparcos along-scan measurements for the two stars, following the prescriptions of Pourbaix & Jorissen (2000) and van Leeuwen & Evans (1998). We then asked whether an orbital model could lead to an improved description of the Hipparcos data, and used the Thiele-Innes representation of a photocentric orbit (Heintz 1978) to carry out a linear least squares fit over a large grid of periods bracketing the ones obtained from the radial velocity measurements, while keeping fixed eand T0 to their spectroscopic values. We thus seeked to minimize

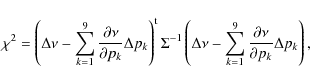
\begin{displaymath}\chi^2 = \left(\Delta\nu-\sum_{k=1}^{9}\frac{\partial\nu}{\pa... ...um_{k=1}^{9}\frac{\partial\nu}{\partial p_k}\Delta p_k\right), \end{displaymath} (2)

where the superscript t indicates transposed, $\Delta\nu$ is the vector of along-scan Hipparcos IAD residuals to a single-star, 5-parameter fit, $\partial\nu/\partial p_k$ is the vector of partial derivatives of the along-scan coordinate with respect to the kth fitted parameter, $\Delta p_k$ the relative correction, and  $\Sigma^{-1}$is the inverse of the covariance matrix of the solution. The fitted model is fully linear in 9 parameters, i.e. the five astrometric ones and the four Thiele-Innes constants A, B, F, and G. The results of this period search are shown for both stars in Fig. 1. A long-period trend in the data appears clear for both HD 131664 and HD 131664, itself in clear accord with the choice of an acceleration solution for both objects at the time of publication of the Hipparcos catalogue.

Table 2:   Orbital fits to the Hipparcos IAD for HD 131664 and HD 131664, assuming knowledge of P, e, T0, and $\omega $ from the spectroscopic orbit.

The orbital period is well-known from spectroscopy in the case of HD 131664 (Moutou et al. (2009) report uncertainties of $\sim$$2\%$), but less so for HD 131664 (uncertainties reported by Minniti et al. (2009) are $\sim$$ 17\%$). Despite this and because Hipparcos only covered a fraction of the orbit path of both objects, it is nonetheless worthwhile investigating whether a full-fledged orbital solution can be extracted from the Hipparcos data, which robustly passes statistical screening. Following a procedure similar to the one adopted by others and outlined above, we then fitted the Hipparcos IAD for the two objects keeping P, e, and T0 fixed at their spectroscopic values, while adjusting the five correction terms to the astrometric parameters[*], i and $\Omega $(with the additional constraint of Eq. (1)). We adopted a dense two-dimensional grid of starting values for both i and $\Omega $ to solve a local non linear minimization problem in which we used a model function expressed in terms of the Campbell orbital elements. To assess the impact of the more or less precise knowledge of the spectroscopic orbit, the procedure was re-run 100 times, each with a different set of (fixed) spectroscopic orbital elements drawn from Gaussian distributions with mean and standard deviation the best-fit value and its formal error, respectively.

The results of the orbital fit to the Hipparcos IAD of both HD 131664 and HD 131664 are summarized in Table 2. The reported uncertainties on i and $\Omega $, as well as the derived mass values for the companions, take the 1-$\sigma$ formal errors on the parameters of the spectroscopic orbits into account. The inferred true masses for HD 131664b and HD 131664b are 23-5+26 $M_{\rm J}$and 120+167-43 $M_{\rm J}$, respectively. Taken at face value, these numbers would imply that the companion to HD 131664 has a mass in the brown dwarf regime at the $2-\sigma$ confidence level, while the unseen object around HD 131664 is likely a low-mass M dwarf (at the $1-\sigma$ confidence level). An attempt at using the FAST and NDAC data separately for both stars resulted in solutions formally compatible with the ones reported here, albeit with larger uncertainties and looser constraints on the derived mass estimates.

To assess the statistical soundness of the derived astrometric orbits, several checks can be performed. First, based on an F-test of the null hypothesis that there is no companion, we find that the addition of two parameters to the model describing the Hipparcos IAD significantly improves the fit in both cases: P(F) = 0.0002 and P(F) = 0.001 for HD 131664 and HD 131664, respectively. Second, similar to Reffert & Quirrenbach (2006), we have further explored the reliability of the orbital solutions by inspecting the joint confidence regions (corresponding to iso-$\chi ^2$ contours) in the $i-\Omega$ plane, for a given statistical level of confidence. As shown in Fig. 2, the 95% (2-$\sigma$) iso-$\chi ^2$ contours cover relatively narrow regions in the $i-\Omega$ plane, ruling out with confidence very small inclinations in the case of HD 131664, and close to edge-on configurations in the case of HD 131664. Ambiguities in the orbit orientation are clearly seen in both cases, highlighted by local minima in the $\chi ^2$ surface corresponding to configurations with the opposite sense of revolution. Nevertheless, one would conclude that Hipparcos astrometry has successfully detected orbital motion induced by the two massive companions to HD 131664 and HD 131664. We consider the 95% confidence level as the appropriate measure of the degree of statistical robustness with which these results can be regarded. Finally, we have applied a standard bootstrap method (Efron 1982), based on 1000 Monte Carlo resamples with replacement, to the available data for both stars in order to derive empirical error estimates on the derived orbital semi-major axes (constrained by Eq. (1) during the fits).

Our procedure closely follows the one adopted by Zucker & Mazeh (2001), who first realized, from the assigned correlation between pairs of Hipparcos measurements for which both FAST and NDAC data are available, the need to preserve the pairing of the measurements while drawing new random datasets, in order to make the bootstrap method applicable in the first place. The two resulting ratios $a/\sigma _a$ have then been compared to the Rayleigh-Rice law distribution of the false $a/\sigma _a$one can expect to obtain in the case of Hipparcos data of single stars (see Halbwachs et al. 2000). As shown in Fig. 3, the nominal values of $a/\sigma _a$ for HD 131664 and HD 131664 fall in the tail of the Rayleigh-Rice distribution: the probability that $a/\sigma _a$exceeds the observed one is found to be 0.03 and $2\times10^{-5}$for HD 131664 and HD 131664, respectively. This can again be interpreted as a detection of a significant Hipparcos astrometric orbit for both stars, at the 97% and 99.99% confidence level, respectively. For the purpose of this study, we adopt the more conservative abovementioned 95% confidence level to gauge the actual degree of statistical confidence with which the orbits of HD 131664b and HD 13664b are considered detected.

\begin{figure} \par\includegraphics[width=8.5cm]{12717f2.eps} \end{figure} Figure 2:

Iso-$\chi ^2$ contours corresponding to confidence intervals in two dimensions containing 68.3% (solid line), 90% (dashed-dotted line), and 95% (dashed line) of the values of i and $\Omega $ as obtained in a 7-parameter fit to the Hipparcos IAD of HD 131664 ( top) and HD 131664 ( bottom), assuming P, e, T0, and $\omega $ from the known spectroscopic orbit. The best-fit (i, $\Omega $) solutions for both stars are indicated with stars.

Open with DEXTER

4 Summary, discussion, and conclusions

We have inspected the Hipparcos IAD for two stars, HD 131664 and HD 131664, with Doppler-detected companions with minimum masses in the brown dwarf regime. We presented a body of supporting evidence that appears to confirm the detection of orbital motion in the Hipparcos IAD of HD 131664 and HD 131664, at a somewhat significant (95%) level of statistical confidence. The inferred actual masses of HD 131664b and HD 131664b are found to be $M_{\rm c} = 120^{+167}_{-43}$$M_{\rm J}$and $M_{\rm c} = 23^{+26}_{-5}$$M_{\rm J}$, respectively. The former thus appears to be a late M dwarf (at the $\sim$$1-\sigma$ confidence level), while the latter appears to be a brown dwarf (at the $\sim$$2-\sigma$ confidence level). Taken at face value, HD 131664 is nominally the lowest mass brown dwarf confirmed with a combination of Hipparcos and precision Doppler measurements (the astrometric orbits of giant planets obtained with HST/FGS + RV data lie in a different ballpark). The larger uncertainties in the spectroscopic orbital elements of HD 131664, combined with the low value of i inferred from the orbital fit, translate into larger uncertainties in the mass estimate, leaving a margin for this unseen object to also be a brown dwarf (as well as a higher mass M dwarf).

\begin{figure} \par\includegraphics[width=8.5cm]{12717f3.eps} \end{figure} Figure 3:

Distribution of the ratio $a/\sigma _a$ of false astrometric orbits for single stars observed by Hipparcos, approximated by a Rayleigh-Rice law following Halbwachs et al. (2000). The two arrows indicate the values of $a/\sigma _a$obtained for HD 131664 and HD 131664 based on a Monte Carlo bootstrap simulation.

Open with DEXTER

Based on the mass-luminosity relations of Delfosse et al. (2000), HD 131664, with its nominal mass of 120 $M_{\rm J}$, is expected to have magnitude differences of about 8.7, 5.7, 5.4, and 5.2 in the V, J, H, and K bands, respectively. With a projected separation of about 0.15 arcsec at apoastron, it should be detectable with current AO instruments at 8 m class telescopes. The magnitude difference between HD 131664 and its parent star depends critically on the age of the system. Moutou et al. (2009) give an age of $2.4\pm1.8$ Gyr for HD 131664 based on isochrone fitting. Additional clues can be derived from stellar activity indicators. Moutou et al. (2009) measure $\log R^{'}_{\rm HK}=-4.82\pm0.07$. This corresponds to an age of 3.5 Gyr using the calibration by Mamajek & Hillenbrand (2008). We also searched for X-ray emission from the system. The ROSAT Faint Source Catalog (Voges et al. 2000) includes a source (HD 131664) at 40 arcsec from HD 131664 (with a quoted positional error of 29 arcsec). The association is then doubtful. Assuming HD 131664 is the X-ray counterpart of HD 131664, we derived (using the flux calibration by Hünsch et al. 1999) $\log L_{\rm X} = 28.5$and an age of 2.1 Gyr (using the calibration by Mamajek & Hillenbrand 2008). Alternatively, a no detection would imply an older age. Stellar activity indicators then exclude the youngest stellar ages compatible with isochrone fitting. A more plausible lower limit to the stellar age is about 1.5 Gyr. Given our best-fit mass value and the age of 2.4 Gyr, HD 131664 is expected to have magnitude differences of about 15.0, 15.2, and 17.2 in J, H, and K bands, respectively, based on the models of Baraffe et al. (2003). The corresponding effective temperature is about 700 K, at the cool end of the currently known T dwarfs. Considering the small projected separation (<0.1 arcsec), such a contrast is not achievable with current instrumentation, and it would also be challenging for the next generation of direct-imaging instruments.

Any successful attempt, such as the one presented here, at deriving true masses of the substellar companion candidates detected from radial velocity surveys is definitely worthwhile, as the results can be seen in the context of the observed paucity of close brown dwarf companions to solar-type stars in the solar neighborhood, the well-known brown dwarf desert, and in particular their binarity properties. For example, taken at face value the rather large eccentricity of HD 131664 (e=0.638) supports the notion that massive planetary companions and brown dwarfs are preferably found on eccentric orbits (Ribas & Miralda-Escudè 2007). On the other hand, the high metallicity of the parent star ([Fe/H = +0.32) does not follow the proposed trend of metallicity vs. mass for substellar companions (Ribas & Miralda-Escudè 2007). While not conclusive, these findings bring new/updated information that can certainly help to deepen our understanding of the formation mechanism of such objects.

Table 3:   Close companions to solar-type stars with (projected) masses between 10 $M_{\rm J}$and 80 $M_{\rm J}$.

4.1 Properties of massive planets and brown dwarf companions to solar-type stars

To put our discussion into a more general context, we summarize in Table 3 the main properties of the companions with projected masses between 10 and 80 $M_{\rm J}$ and a semimajor axis smaller than $\approx$7 AU, orbiting main-sequence stars with masses between 0.7 to 1.5 $M_{\odot }$. This selection matches the sample of most high-precision radial velocity surveys and avoids the additional complications of large variations in the stellar mass and evolutionary status (very small number statistics being one of the most relevant). The literature data collected here are meant to provide ease of consultation and reference for future works on the many outstanding issues we touch upon thereafter. In the table, determinations of or constraints on the inclination and true companion mass derived from astrometry or transit photometry are included when available. For completeness and reference, we also include companions with substellar projected mass and astrometrically derived stellar mass. We have also included HD 131664, whose companion with $M_{\rm c}\sin i$just below the adopted threshold was shown to be a low-mass star (Bean et al. 2007). Orbital elements and projected masses are from listed discovery papers, Butler et al. (2006) or Halbwachs et al. (2000). Stellar masses and metallicities are from Valenti & Fischer (2005), discovery papers, or additional references. Further information, such as additional stellar or planetary companions, the sources for the metallicity values, and the specific treatment of some of the mass and error estimates, can be found in the notes. In the remarks, PL refers to objects with additional companions of planetary mass, MULT to multiple systems (additional stellar companions), HIPG to stars with Hipparcos acceleration solutions.

\begin{figure} \par$\begin{array}{c} \includegraphics[width=8cm]{12717f4a.eps}\\ \includegraphics[width=8cm]{12717f4b.eps}\\ \end{array}$ \end{figure} Figure 4:

Period vs. eccentricity ( top panel) and eccentricity vs. companion mass ( bottom panel). In the lower panel plot, only objects with periods longer than 20 days are shown. Red filled circles: companions with true estimated masses in the range 10-80 $M_{\rm J}$. Blue triangles: companions with projected masses in the range 10-80 $M_{\rm J}$. Green squares: companions with projected masses in the range < $80 ~M_{\rm J}$but true stellar masses > $80 ~M_{\rm J}$. The three objects with larger symbols belong to the multiple systems HD 131664, HD 131664, and HD 131664.

Open with DEXTER

\begin{figure} \par$\begin{array}{c} \includegraphics[width=8cm]{12717f5a.eps}\\... ...ludegraphics[width=8cm]{12717f5c.eps}\\ \end{array}$\vspace*{-3mm} \end{figure} Figure 5:

Orbital period vs. companion mass ( top), metallicity vs. companion mass ( center), stellar mass vs. companion mass ( bottom). Symbols as in the previous figure.

Open with DEXTER

As discussed in the introduction, Halbwachs et al. (2000) have shown how a significant fraction of Doppler-detected candidate substellar companions were in fact low-mass stars viewed at low inclination. Nevertheless, a few candidates have masses firmly in the substellar regime, partially filling the brown dwarf desert. Interestingly, in two cases (HD 131664 and HD 131664), additional companions in the planetary mass regime were found[*] We note that such system configurations are more typical of planetary systems than of multiple stellar systems. In Figs. 4 and 5 we show a set of correlation diagrams among the most relevant quantities of the systems collected in Table 3.

\begin{figure} \par$\begin{array}{c} \includegraphics[width=8.3cm]{12717f6a.eps}\\ \includegraphics[width=8.3cm]{12717f6b.eps}\\ \end{array}$ \end{figure} Figure 6:

Upper panel: cumulative distribution of the eccentricity of objects with periods longer than 20 days orbiting main-sequence stars with mass between 0.7 and 1.5 $M_{\odot }$. Continuous (black) line: planets with $M_{\rm c} \sin i < 4~M_{\rm J}$(from Butler et al. 2006). Dotted (purple) line: planets with $4 < M_{\rm c} \sin i < 10~M_{\rm J}$(from Butler et al. 2006). Dashed (red) line: objects with mass $10 < M_{\rm c} < 80~M_{\rm J}$(this paper), Dashed-dot (blue) line: objects with $10 < M_{\rm c}\sin i < 80~M_{\rm J}$, but excluding objects with astrometric masses in the stellar regime (this paper). Lower panel: cumulative [Fe/H] (with no period cut). Same symbols as in the upper panel.

Open with DEXTER

Ribas & Miralda-Escudè (2007) note a possible trend in the eccentricity-mass distribution of giant planets, with more massive planets ( $M_{\rm c} \sin i > 4~M_{\rm J}$) orbiting on average with higher eccentricities. The recent analysis by Wright et al. (2009), who used 1 $M_{\rm J}$ as the cut-off value, confirm this trend. The Ribas & Miralda-Escudè (2007) analysis also suggests that the metallicity of stars hosting massive planets and brown dwarf candidates is compatible with that of the solar neighborhood ( $\rm [Fe/H]\simeq -0.15$, e.g. Nordström et al. 2004), differing at the 3-$\sigma$ level from the super-solar metallicity distribution of stars hosting lower mass planets ( $\rm [Fe/H]\simeq+0.24$, e.g. Fischer & Valenti 2005). Hints of such a trend had already been seen in a more limited dataset by Rice et al. (2003). We revisit here this statistical analysis, considering all objects included in Table 3, as well as the sample of exoplanets with $M_{\rm c}\sin i < 10$$M_{\rm J}$reported in Butler et al. (2006). For this purpose, we have divided the full sample into three subsets according to minimum mass: $M_{\rm c}\sin i< 4$$M_{\rm J}$, $4 < M_{\rm c}\sin i< 10$$M_{\rm J}$, and $10 < M_{\rm c} \sin i< 80 $ $M_{\rm J}$, plus a fourth subsample formed by those objects in Table 3 with estimated true masses in the range $10 < M_{\rm c}< 80$$M_{\rm J}$. We then performed on these subsets both a Kolmogorov-Smirnov (K-S) test, to measure to what extent their e and [Fe/H] distributions might differ, and a Wilcoxon Rank-Sum (R-S) test, to measure to what degree the mean e and [Fe/H] might be considered different. The resulting values of the probabilities (Pr(D) and Pr(Z), respectively) of the null hypothesis for both tests on the various subsamples are reported in Table 4, while Fig. 6 shows a comparison between the resulting cumulative distributions of e and [Fe/H] for the above-mentioned subsets of systems.

From investigation of Table 4 and Fig. 6, a few conclusions can be drawn. As for the e distribution, the results further corroborate the notion that eccentricities of not-so-massive planets are clearly less pronounced than those of more massive planets and brown dwarf companions[*]. On the other hand, massive planets appear to have an overall e distribution that is indistinguishable from that of brown dwarf candidates. Similarly, the [Fe/H] distribution of the hosts appears significantly different for companions with $M_{\rm c}\sin i< 4$$M_{\rm J}$and for brown dwarf companions, while other trends are marginal, and in particular metallicities of massive planet hosts and of primaries with brown dwarf companions are statistically the same[*].

4.2 Implications for formation and structural models of massive planets and brown dwarfs

The above evidence can be interpreted, keeping in mind the relatively small-number statistics regime we are dealing with here, in the context of the proposed formation scenarios and internal structure models of high-mass planets and brown dwarfs, and as a function of the main properties of the stellar hosts (binarity, mass, metallicity).

Table 4:   Results of the K-S and R-S tests on different subsets of systems.

4.2.1 Formation and orbital evolution of massive planets and brown dwarfs

As already pointed out in the introduction, the lower mass limit for the formation of self-gravitating objects from fragmentation of molecular cloud cores is today thought to be a few $M_{\rm J}$ (e.g., Whitworth et al. 2007; Luhman et al. 2007). Ribas & Miralda-Escudè (2007) and, more recently,  Font-Ribera et al. (2009) have proposed direct cloud fragmentation, followed by inward migration by disk capture, as a formation mechanism for the high-mass tail of the planetary population. The detection of a significant number of free-floating objects down to $\sim$6 $M_{\rm J}$ and the observed continuity of the substellar mass function in young star-forming regions (e.g., Caballero et al. 2007, and references therein; Zuckerman & Song 2009, and references therein) are indications that indeed a star-like formation process may form brown dwarfs, as well as planetary mass objects[*]. Indeed, the process outlined by Font-Ribera et al. (2009) should be effective independently of the metallicity of the parent cloud, and is expected to produce an eccentricity distribution similar to that of binary systems. The results shown in Table 4 and in Fig. 6 can be seen as supporting this scenario. On the other hand, the disk-capture mechanism proposed by Font-Ribera et al. (2009) does not naturally explain the existence of the brown dwarf desert, as increasingly more massive objects should actually be easier to capture in their model. Also, Grether & Lineweaver (2006) have pointed to observable differences in the mass distributions of isolated objects and companions to solar-type stars, the latter exhibiting a minimum (the ``driest part of the brown dwarf desert'') at $\approx$ $30~M_{\rm J}$( $31^{+25}_{-18}~M_{\rm J}$). This evidence does not appear to be readily explained by the mechanism proposed by Font-Ribera et al. (2009).

Massive planets and brown dwarfs can also be formed by gravitational fragmentation of extended disks around solar-type primaries. In the models of e.g. Stamatellos & Whitworth (2009), brown dwarfs form by direct gravitational collapse only in the outer regions of the disks, and tend to be scattered farther out, or even into the field. This mechanism can explain the existence of the brown dwarf desert at small separations. The two other conclusions that can be drawn from these models are that 1) no planets formed by disk instability can really be found as close companions, as they can only form in the outer regions of the disks and are scattered with much higher efficiency than brown dwarfs; and b) as a direct consequence short-period Doppler-detected massive planets and brown dwarfs should primarily be low-mass stars. On the one hand, this mechanism can be seen as supported by the data presented here (the properties of massive planets, brown dwarfs, and low-mass stellar companions being very similar). On the other hand, some of the objects in the sample of Table 3 can hardly be explained by this approach (e.g., the transiting objects HD 131664b and HD 131664).

In the still theoretically debated (e.g., Mayer et al. 2002; Rafikov 2005; Stamatellos & Whitworth 2008; Boss 2009; for a review see Durisen et al. 2007) disk instability model of giant planet formation, massive planets with relatively eccentric orbits and moderate-to-large orbital separations are its more likely product (e.g., Rice et al. 2003;  Boley 2009). No clear prediction of the expected shapes of the orbital elements and mass distributions of planets formed by disk instability is available yet, because of the numerical complexities of the simulations and to some still open theoretical issues on the input physics (see e.g. Boss 2009, and references therein). However, if high-precision measurements of the actual masses of massive planets, as well as of those of the substellar companions listed in Table 3, were to become available, and were they to prove that these objects are not preferentially low-mass stars, this evidence would argue in favor of a common formation mode for massive planets and brown dwarfs.

In the more widely accepted core-accretion mechanism for the formation of giant planets (e.g., Pollack et al. 1996; Alibert et al. 2005; Ida & Lin 2005; for a review see Lissauer & Stevenson 2007) very massive planets and low-mass brown dwarfs on eccentric orbits are not a natural outcome (e.g., Kennedy & Kenyon 2008; Alibert et al. 2005; Ida & Lin 2005; Pollack et al. 1996). However, recent models have shown that this mechanism might also be capable of forming such massive objects. Indeed, in the model of Mordasini et al. (2009), planets with masses as high as $38~M_{\rm J}$are formed in long-lived massive disks around a solar mass star. Given the increasingly lower probability of forming very massive planets or brown dwarfs (``deuterium-burning'' planets in the words of Baraffe et al. 2008), the brown dwarf desert appears compatible with the Mordasini et al. (2009) model (for example, the probability of forming objects with masses exceeding the deuterium-burning threshold is found to be $\sim$$0.4\%$, in accord with the Marcy & Butler (2000) estimate). While the Mordasini et al. (2009) model does not include multi-planet systems and planet-planet interactions, likely to play an important role in shaping the observed mass, period and eccentricity distributions, we note that the expected location of such very massive planets is between 2 to 5 AU, similar to what is observed for HD 131664, HD 131664 and the object studied in this paper, HD 131664. However, no prediction of this model on the eccentricity distribution is available, which would be a critical element for distinguishing between this mechanism and the other aforementioned options. In addition, super-planets and low-mass brown dwarfs also exist at small separation, where they are not expected on the basis of the Mordasini et al. (2009) model. Noticeable examples are the transiting systems HD 131664 (Bakos et al. 2007), HD 131664 (Joshi et al. 2009), HD 131664, and HD 131664, but also other massive objects such as HD 131664 (Udry et al. 2002) and HD 131664 (Zucker et al. 2004).

Finally, of particular interest are the initial claims of a possible correlation between massive planets, eccentric orbits, and high values for the angle between a planetary orbit and the stellar rotation axis, as determined from spectroscopic measurements of the Rossiter-McLaughlin (R-M) effect (McLaughlin 1924; Rossiter 1924) in transiting systems. The HD 131664, HD 131664, and HD 131664 systems all have a close-in, massive planet on a very eccentric orbit and with a significant spin-orbit misalignment (e.g., Johnson et al. 2009, and references therein)[*]. At first glance, this might imply that the orbital migration history of massive, eccentric exoplanets is somehow different for less massive close-in Jupiters, However, the picture is not likely to be so simple, not only because of the evidence of other transiting systems with massive, eccentric planets (HAT-P-2, HD 17156) showing no signs of spin-orbit misalignment (e.g., Winn et al. 2007; Barbieri et al. 2009), but also for the recent measurements of the R-M effect in transiting systems with Jupiter-mass planets on circular orbits, such as CoRot-1, HAT-P-7, and WASP-17 (Pont et al. 2009, and references therein) that point toward high values of the projected spin-orbit angles. Overall, the evidence collected so far is a likely indication of the variety of possible outcomes of the complex process of migration to close-in orbits of companions with a wide range of masses, which include a host of proposed dynamical mechanisms (e.g., interactions between a planet and the gaseous/planetesimal disk, planet-planet resonant interactions, close encounters between planets, and secular interactions with a companion star), as well as different formation scenarios. Statistical studies, such as the one carried out by Fabrycky & Winn (2009), who showed the emergency of a bimodal distribution of spin-orbit angles, on an increasingly larger sample of transiting systems will ultimately be the optimal way to compare an ensemble of measurements of the R-M effect with the predictions of migration theories.

4.2.2 The impact of binarity

Among the distinctive features of exoplanets discovered around members of various types of binary and triple systems (e.g., Eggenberger & Udry 2009, and references therein), one of the most intriguing is the evidence that solar-type stars members of multiple stellar systems appear to be preferential hosts of the most massive planets on short-period orbits (Desidera & Barbieri 2007), and the fact that the planetary companions with the highest eccentricities all have either stellar or brown dwarf companions (Tamuz et al. 2008). These trends seem to indicate that planet formation and/or migration in binaries may proceed differently than around single stars. Indeed, theoretical studies (Fabrycky & Tremaine 2007; Wu & Murray 2003; Kley 2000) within the context of the core accretion model of giant-planet formation suggest that the presence of a fairly close companion significantly enhances the growth rate and makes the migration timescale of the planet shorter. On the other hand, the massive super planets or low-mass brown dwarfs found at separations of about 2-3 AU orbit stars that are single or with very wide companions (HD 131664 has a $0.5~M_{\odot}$common proper motion companion at a projected separation of 12 000 AU), compatible with long-lived, undisturbed disks required to form such objects according to Mordasini et al. (2009). Models of giant planet formation by disk instability, however, come to opposite conclusions, with giant planet formation significantly suppressed in binaries with separations <100 AU (Mayer et al. 2005). From inspection of Table 3, the above-mentioned trends seem to be supported only in part. For example, the short-period objects HD 131664 and HD 131664 orbit one of the components of wide binaries, but this does not appear to be the case for HD 131664. Investigations are encouraged that would aim at verifying the possible existence of binary companions to HD 131664 and HD 131664. Furthermore, the brown-dwarf candidates with the highest eccentricities do not seem to be found primarily in multiple systems.

4.2.3 The role of the primary mass and metallicity

In the core-accretion model of giant-planet formation, the upper limit on the mass of the planetary companion and the final orbital arrangement are expected to depend on stellar mass and metallicity. Based on arguments of protoplanetary disk size and lifetime as a function of $M_\star$, one would expect massive planets to be found with higher probabilities around more massive primaries (Kennedy & Kenyon 2008) and at typically moderate-to-large separations (Burkert & Ida 2007; Currie 2009). Indeed, the observational evidence indicates that, for higher stellar masses, massive companions with $\gtrsim $ $10 M_{\rm J}$are significantly more numerous than around solar type stars (e.g., Johnson 2008; Lovis & Mayor 2007. For a review see Hatzes 2008, and references therein). On the opposite end, M dwarfs are expected to show a paucity of giant planets (Ida & Lin 2005; Laughlin et al. 2004), which is also observed (Endl et al. 2006; Johnson et al. 2007; Bailey et al. 2009). The core-accretion mechanism also naturally predicts that super-massive planets should not be found at all around metal-poor stars, given the lack of material for accumulation (e.g., Ida & Lin 2005). The alternative disk instability mechanism is instead rather insensitive to the values of $M_\star$ and [Fe/H] of the stellar host (e.g., Boss 2002, 2006). As a consequence, a qualitative prediction of this model (e.g., Rice et al. 2003) is that massive planets found on moderate-to-large separations around massive and/or metal-deficient hosts would be likely to have been formed by gravitational instability. In this respect, the data collected here and the results of the statistical analysis, which corroborate the findings of Ribas & Miralda-Escudè (2007), can be read as partly supporting the latter view. Interestingly, the frequency of (massive) planets ($f_{\rm p}$) around intermediate-mass (mostly giant) stars appears to be rather independent of [Fe/H]  (Hatzes 2008). However, the four known planet - brown dwarf systems (HD 131664, HD 131664, HD 131664, HD 131664) all have super-solar mass, very metal-rich (main-sequence) primaries. This last piece of evidence might be seen as supporting the core accretion formation mode, while the former dataset might point to a significant role for the disk instability mechanism. However, the global picture is likely to rather complex. For example, Doppler surveys for giant planets around intermediate-mass stars typically include targets that have evolved to some degree, given that massive main sequence stars are unsuitable for high-precision radial-velocity measurements (too few spectral lines, often broadened by high rotation rates). The very different dependence of $f_{\rm p}$ on [Fe/H] for intermediate-mass stars with respect to their solar-mass counter-parts might then reflect a non-primordial origin to the metallicity enhancement in solar-type planet hosts (Pasquini et al. 2007) rather than point to different formation modes.

As for the possible dependence of brown dwarf frequency on stellar mass and metallicity, this is still a poorly understood issue. A quick look at literature data allows us to speculate on the possibility that the brown dwarf desert may not be very ``dry'' when it comes to close substellar companions to intermediate-mass stars, in light of a handful of systems containing at least one companion with minimum mass in the brown dwarf regime (e.g., Omiya et al. 2009, and references therein). In particular, the recently announced system of brown dwarfs around HD 131664 (Niedzielski et al. 2009) has an architecture very similar to that of HD 131664, with a solar-type primary. It is reminiscent of an origin in a massive circumstellar disk, further suggesting a scenario in which more massive substellar companions are found around more massive stellar hosts (and their frequency also increases with increasing primary mass). Such systems would be more likely to have been formed by local gravitational instabilities in protoplanetary disks (e.g., Rice et al. 2003) rather than protostellar cloud fragmentation, given the difficulties in forming extreme mass-ratio binaries by the latter mechanism (e.g., Bate 2000). However, the combination of small-number statistics, the different priority given to observations of stars with very massive companions in Doppler surveys, the variable detection thresholds as a function of companion mass and separation due to the decreasing radial-velocity precision in increasingly higher mass stars, and the uncertainty on the actual mass values for most of the objects included in Table 3 (as well as those noted above) prevents one, as of today, from drawing any serious conclusions on the possibility that the brown dwarf desert may move in mass and/or separation range depending on $M_\star$ and [Fe/H].

4.2.4 Structural and atmospheric models

Finally, one of the most effective ways of distinguishing between massive planets and brown dwarfs is through a comparison of their internal structure properties and of the composition of their atmospheres (e.g., Chabrier et al. 2009; Burgasser 2009). Studies at this level are still in their infancy, particularly for what concerns the possibility of determining their actual nature based on their condensate cloud formation properties, non-equilibrium chemistry, and atmospheric dynamics (Burgasser 2009).

However, the class of transiting systems is already providing relevant data. For example, Mordasini et al. (2009) have proposed that massive planets might contain a large amount of heavy elements (about $0.8~M_{\rm J}$ for the individual case shown in their Fig. 12). In the case of the transiting massive planet HD 131664 (HAT-P-2b), with a mass of $9.04~M_{\rm J}$(Bakos et al. 2007), just below the threshold of $10~M_{\rm J}$ adopted here for inclusion in Table 3, Baraffe et al. (2008) and Leconte et al. (2009) argue from the measured radius ( $R=0.982~R_{\rm J}$, Bakos et al. 2007) for a total amount of heavy elements of about $1 M_{\rm J}$, excluding a gaseous H/He object with solar composition. This indicates that indeed $10~M_{\rm J}$ planets might be formed by the core accretion mechanism, unless such a high mass is the result of planetary collision, as speculated by Baraffe et al. (2008). In the case of the super-massive transiting planet HD 131664, despite its rather uncertain radius (due to discrepancies in the stellar radius estimates from photometry and spectroscopy), there seems to be no need for a large content of heavy elements in the core (Winn et al. 2008). Similarly, the 22-$M_{\rm J}$ transiting object CoRoT-3b fits the Baraffe et al. (2008) models for solar composition, with no need for large metal enrichment (Leconte et al. 2009). Both HAT-P-2b and CoRoT-3b have surface gravities similar to those of young, very low-mass brown dwarfs such as AB Pic (see Fig. 2 of Burgasser 2009), suggesting an overlap in the parameter space of some physical properties (e.g., gas pressure, temperature). Interestingly, as discussed by Deleuil et al. (2008), all transiting massive planets orbit stars more massive than the Sun, as predicted by the core accretion model of planet formation. On the other hand, their actual existence on such short periods and relatively eccentric orbits (except for CoRoT-3b) and the fact that the metallicities of their parent stars are not skewed towards super-solar values calls for the possibility of differences in their origin.

In conclusion, the present-day evidence on the orbital and structural properties of massive planets and brown dwarfs as close companions to nearby solar-type stars can be interpreted as supporting a picture in which different mechanisms for the formation of such objects are at work. The above discussion also indicates how the lack of a clean, statistically significant sample of high-mass planets and brown dwarf companions to solar-type stars with well-determined mass estimates hampers the possibility of conclusively distinguishing among the various competing modes of formation of such objects. From an observational viewpoint, improvements in determining the multiplicity properties of substellar companions are very much needed, and will be obtained in the near future through the combined contribution of a variety of techniques. For example, some of the massive planets and brown dwarfs objects in Table 3 are within reach of next-generation direct-imaging instruments such as SPHERE (Beuzit et al. 2008) and for many of them true masses will be measured with high precision by ground-based and space-borne astrometric observatories, such as VLTI/PRIMA and Gaia (e.g., Launhardt et al. 2008; Casertano et al. 2008; Sozzetti 2009, and references therein). The possibility that objects with similar masses formed in a different way and exhibit different chemical composition depending on the formation mechanism open exciting perspectives for such instruments. Therefore, they will represent key benchmarks for the calibration of the masses of substellar objects, for furthering our understanding of the dependence of the brown dwarf desert on the properties of the stellar hosts, and even for reaching a final agreement on the actual definition of planets and brown dwarfs themselves that is based not simply on semantics but rather on robust physical grounds.

Acknowledgements

This research has been partially supported by INAF through PRIN 2009 ``Environmental effects in the formation and evolution of extrasolar planetary system''. A.S. gratefully acknowledges support from the Italian Space Agency (Contract ASI-Gaia I/037/08/0). We thank J.-L. Halbwachs for stimulating discussions and the referee for a timely and useful report that helped improve the presentation of the results. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Bibliographic Services.

References

  1. Alibert, Y., Mordasini, C., & Benz, W. 2005, A&A, 434, 343 [Google Scholar]
  2. Bakos, G. A., Kovacs, G., Torres, G., et al. 2007, ApJ, 670, 826 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bakos, G. A., Howard, A. W., Noyes, R. W., et al. 2009, ApJ, 707, 446 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bailey, J., Butler, R. P., Tinney, C. G., et al. 2009, ApJ, 690, 743 [Google Scholar]
  5. Baraffe, I., Chabrier, G., Barman, T., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [Google Scholar]
  6. Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [Google Scholar]
  7. Barbieri, M., Alonso, R., Desidera, S., et al. 2009, A&A, 503, 601 [Google Scholar]
  8. Bate, M. R. 2000, MNRAS, 314, 33 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bate, M. R., Bonnell, I. A., & Bromm, V. 2002, MNRAS, 332, L65 [Google Scholar]
  10. Bean, J. L., McArthur, B. E., Benedict, G. F., et al. 2007, AJ, 134, 749 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [Google Scholar]
  12. Bernstein, R., Shectman, S. A., Gunnels, S. M., Mochnacki, S., & Athey, A. E. 2003, Proc. SPIE, 4841, 1694 [NASA ADS] [CrossRef] [Google Scholar]
  13. Beuzit, J.-L., Segransan, D., Forveille, T., et al. 2004, A&A, 425, 997 [Google Scholar]
  14. Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, Ground-based and Airborne Instrumentation for Astronomy II, ed. I. S. McLean, & M. M. Casali, Proc. SPIE, 7014 [Google Scholar]
  15. Boley, A. C. 2009, ApJ, 695, L53 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bonavita, M., & Desidera, S. 2007, A&A, 468, 721 [Google Scholar]
  17. Boss, A. P. 2000, ApJ, 536, L101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  18. Boss, A. P. 2002, ApJ, 567, L149 [Google Scholar]
  19. Boss, A. P. 2006, ApJ, 643, 501 [NASA ADS] [CrossRef] [Google Scholar]
  20. Boss, A. P. 2009, ApJ, 694, 107 [NASA ADS] [CrossRef] [Google Scholar]
  21. Bouchy, F., Hebrard, G., Udry, S., et al. 2009, A&A, 505, 853 [Google Scholar]
  22. Burgasser, A. J. 2009, in Molecules in the Atmospheres of Extrasolar Planets, ASP Conf. Ser., ed. J.-P. Beaulieu, G. Tinetti & I. Ribas, in press [arXiv:0903.1390] [Google Scholar]
  23. Burgasser, A. J., Reid, I. N., Siegler, N., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 427 [Google Scholar]
  24. Burkert, A., & Ida, S. 2007, ApJ, 660, 845 [NASA ADS] [CrossRef] [Google Scholar]
  25. Butler, R. P., Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505 [NASA ADS] [CrossRef] [Google Scholar]
  26. Caballero, J. A., Béjar, V. J. S., Rebolo, R., et al. 2007, A&A, 470, 903 [Google Scholar]
  27. Campbell, B., Walker, G. A. H., & Yang, S. 1988, ApJ, 331, 902 [NASA ADS] [CrossRef] [Google Scholar]
  28. Casertano, S., Lattanzi, M. G., Sozzetti, A., et al. 2008, A&A, 482, 699 [Google Scholar]
  29. Catalan, S., Ribas, I., Isern, J., & Garcia-Berro, E. 2008, A&A, 477, 901 [Google Scholar]
  30. Chabrier, G., Baraffe, I., Leconte, J., Gallardo, J., & Barman, T. 2009, AIP Conf. Proc., 1094, 102 [NASA ADS] [CrossRef] [Google Scholar]
  31. Correia, A. C. M., Udry, S., Mayor, M., et al. 2005, A&A, 440, 751 [Google Scholar]
  32. Currie, T. 2009, ApJ, 694, L171 [NASA ADS] [CrossRef] [Google Scholar]
  33. Deleuil, M., Deeg, H. J., Alonso, R., et al. 2008, A&A, 491, 889 [Google Scholar]
  34. Durisen, R. H., Boss, A. P., Mayer, L., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 607 [Google Scholar]
  35. Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [Google Scholar]
  36. Delfosse, X., Forveille, T., Segransan, D., et al. 2000, A&A, 364, 217 [Google Scholar]
  37. Desidera, S., & Barbieri, M. 2007, A&A, 462, 345 [Google Scholar]
  38. Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [Google Scholar]
  39. Eggenberger, A., & Udry, S. 2009, EAS Publ. Ser., in press [arXiv:0904.0415] [Google Scholar]
  40. Efron, B. 1982, The Jackknife, the Bootstrap and other resampling plans. Philadelphia: Society for Industrial and Applied Mathematics (SIAM) [Google Scholar]
  41. Endl, M., Hatzes, A. P., Cochran, W. D., et al. 2004, ApJ, 611, 1121 [NASA ADS] [CrossRef] [Google Scholar]
  42. Endl, M., Cochran, W. D., Kürster, M., et al. 2006, ApJ, 649, 436 [NASA ADS] [CrossRef] [Google Scholar]
  43. Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
  44. Fabrycky, D., & Winn, J. N. 2009, ApJ, 696, 1230 [NASA ADS] [CrossRef] [Google Scholar]
  45. Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
  46. Font-Ribera, A., Miralda-Escudè, J., & Ribas, I. 2009, ApJ, 694, 183 [NASA ADS] [CrossRef] [Google Scholar]
  47. Fuhrmann, K. 2008, MNRAS, 384, 173 [NASA ADS] [CrossRef] [Google Scholar]
  48. Glebocki, R., & Stawikowski, A. 1995, Acta Astron., 45, 725 [Google Scholar]
  49. Gray, R. O., Corbally, C. J., Garrison, R. F., McFadden, M. T., & Robinson, P. E. 2003, AJ, 126, 2048 [NASA ADS] [CrossRef] [Google Scholar]
  50. Grether, D., & Lineweaver, C. 2006, ApJ, 640, 1051 [NASA ADS] [CrossRef] [Google Scholar]
  51. Halbwachs, J. L., Arenou, F., Mayor, M., Udry, S., & Queloz, D. 2000, A&A, 355, 581 [Google Scholar]
  52. Han, I., Black, D. C., & Gatewood, G. D. 2001, ApJ, 548, L57 [NASA ADS] [CrossRef] [Google Scholar]
  53. Haywood, M. 2001, MNRAS, 325, 1365 [NASA ADS] [CrossRef] [Google Scholar]
  54. Hatzes, A. P. 2008, Phys. Scr., 130, 014004 [CrossRef] [Google Scholar]
  55. Heintz, W. D. 1978, Double Stars (Dordrecht: D. Reidel Publishing Co.) [Google Scholar]
  56. Heiter, U., & Luck, R. E. 2003, AJ, 126, 2015 [NASA ADS] [CrossRef] [Google Scholar]
  57. Ida, S., & Lin, D. N. C. 2005, ApJ, 626, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  58. Ireland, M. J., Kraus, A., Martinache, F., Lloyd, J. P., & Tuthill, P. G. 2008, ApJ, 678, 463 [NASA ADS] [CrossRef] [Google Scholar]
  59. Jenkins, J. S., Jones, H. R. A., Gozdziewski, K., et al. 2009, MNRAS, 398, 911 [NASA ADS] [CrossRef] [Google Scholar]
  60. Joshi, Y. C., Pollacco, D., Collier Cameron, A., et al. 2009, MNRAS, 392, 1532 [NASA ADS] [CrossRef] [Google Scholar]
  61. Johns-Krull, C. M., McCullough, P. R.. Burke, C. J., et al. 2008, ApJ, 677, 657 [NASA ADS] [CrossRef] [Google Scholar]
  62. Johnson, J. A. 2008, in Extreme Solar Systems, ASP Conf. Ser., 398, 59 [Google Scholar]
  63. Johnson, J. A., Butler, R. P., Marcy, G. W., et al. 2007, ApJ, 670, 833 [NASA ADS] [CrossRef] [Google Scholar]
  64. Johnson, J. A., Winn, J. N., Albrecht, S., et al. 2009, PASP, 121, 1104 [NASA ADS] [CrossRef] [Google Scholar]
  65. Hünsch, M., Schmitt, J. H. M. M., Sterzik, M. F., & Voges, W. 1999, A&AS, 135, 319 [Google Scholar]
  66. Kane, S. R., Mahadevan, S., Cochran, W. D., et al. 2009, ApJ, 692, 290 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
  68. Kley, W. 2000, Proc. IAU Symp., 200, 211 [Google Scholar]
  69. Laughlin, G., Bodenheimer, P., & Adams, F. C. 2004, ApJ, 612, L73 [NASA ADS] [CrossRef] [Google Scholar]
  70. Launhardt, R., Henning, T., Queloz, D., et al. 2008, Proc. IAU Symp., 248, 417 [NASA ADS] [Google Scholar]
  71. Leconte, J., Baraffe, I., Chabrier, G., Barman, T., & Levrard, B. 2009, A&A, 506, 385 [Google Scholar]
  72. van Leeuwen, F., & Evans, D. W. 1998, A&AS, 130, 157 [Google Scholar]
  73. Lissauer, J. J., & Stevenson, D. J. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 591 [Google Scholar]
  74. Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [Google Scholar]
  75. Luhman, K. L., Joergens, V., Lada, C., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 443 [Google Scholar]
  76. Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
  77. Marcy, G. W., & Butler, R. P. 2000, PASP, 112, 137 [NASA ADS] [CrossRef] [Google Scholar]
  78. Marcy, G. W., Butler, R. P., Vogt, S. S., et al. 2001, ApJ, 555, 418 [NASA ADS] [CrossRef] [Google Scholar]
  79. Marcy, G. W., Butler, R. P., Vogt, S. S., et al. 2008, Phys. Scr., 130, 014001 [NASA ADS] [CrossRef] [Google Scholar]
  80. Mayer, L., Quinn, T., Wadsley, J., & Stadel, J. 2002, Science, 298, 1756 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  81. Mayer, L., Quinn, T., Wadsley, J., & Stadel, J. 2005, MNRAS, 363, 641 [NASA ADS] [Google Scholar]
  82. Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
  83. Mayor, M., Duquennoy, A., Halbwachs, J.-L., & Mermilliod, J.-C. 1992, ASP Conf. Ser., 32, 73 [NASA ADS] [Google Scholar]
  84. Mazeh, T., Zucker, S., dalla Torre, A., & van Leeuwen, F. 1999, ApJ, 522, L149 [NASA ADS] [CrossRef] [Google Scholar]
  85. McCarthy, C., & Zuckerman, B. 2004, AJ, 127, 2871 [NASA ADS] [CrossRef] [Google Scholar]
  86. McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
  87. Metchev, S. A., & Hillenbrand, L. A. 2009, ApJS, 181, 62 [NASA ADS] [CrossRef] [Google Scholar]
  88. Minniti, D., Butler, R. P., López-Morales, M., et al. 2009, ApJ, 693, 1424 [NASA ADS] [CrossRef] [Google Scholar]
  89. Mishenina, T. V., Soubiran, C., Kovtyukh, V. V., & Korotin, S. A. 2004, A&A, 418, 551 [Google Scholar]
  90. Mordasini, C., Alibert, Y., & Benz W. 2009, A&A, 501, 1161 [Google Scholar]
  91. Moutou, C., Mayor, M., Lo Curto, G., et al. 2009, A&A, 496, 513 [Google Scholar]
  92. Nakajima, T., Oppenheimer, B. R., Kulkarni, S. R., et al. 1995, Nature, 378, 463 [NASA ADS] [CrossRef] [Google Scholar]
  93. Nidever, D. L., Marcy, G. W., Butler, R. P., Fischer, D. A., & Vogt, S. S. 2002, ApJS, 141, 503 [NASA ADS] [CrossRef] [Google Scholar]
  94. Niedzielski, N. G., Novak, G., Adamów, M., & Wolszczan, A. 2009, ApJ, 707, 768 [NASA ADS] [CrossRef] [Google Scholar]
  95. Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [Google Scholar]
  96. Omiya, M., Izimiura, H., Han, I., et al. 2009, PASJ, 61, 825 [NASA ADS] [Google Scholar]
  97. O'Toole, S. J., Tinney, C. G., Jones, H. R. A., et al. 2009, MNRAS, 392, 641 [NASA ADS] [CrossRef] [Google Scholar]
  98. Pasquini, L., Döllinger, M. P., Weiss, A., et al. 2007, A&A, 473, 979 [Google Scholar]
  99. Patience, J., White, R. J., Ghez, A., et al. 2002, ApJ, 581, 684 [NASA ADS] [Google Scholar]
  100. Patel, S. G., Vogt, S. S., Marcy, G. W., et al. 2007, ApJ, 665, 744 [Google Scholar]
  101. Pepe, F., Rupprecht, G., Avila, G., et al. 2003, Proc. SPIE, 4841, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  102. Perrier, C., Sivan, J.-P., Naef, D., et al. 2003, A&A, 410, 1039 [Google Scholar]
  103. Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
  104. Pont, F., et al. 2009, MNRAS, accepted [arXiv:0908.3032] [Google Scholar]
  105. Pourbaix, D. 2001, A&A, 369, L22 [Google Scholar]
  106. Pourbaix, D., & Arenou, F. 2001, A&A, 372, 935 [Google Scholar]
  107. Pourbaix, D., & Jorissen, A. 2000, A&AS, 145, 161 [Google Scholar]
  108. Rafikov, R. R. 2005, ApJ, 621, L69 [NASA ADS] [CrossRef] [Google Scholar]
  109. Rebolo, R., Zapatero-Osorio, M. R., & Martín, E. L. 1995, Nature, 377, 129 [NASA ADS] [CrossRef] [Google Scholar]
  110. Reffert, S., & Quirrenbach, A. 2006, A&A, 449, 699 [Google Scholar]
  111. Ribas, I., & Miralda-Escudè, J. 2007, A&A, 464, 779 [Google Scholar]
  112. Rice, W. K. M., Armitage, P. J., Bonnell, I. A., et al. 2003, MNRAS, 346, L36 [NASA ADS] [CrossRef] [Google Scholar]
  113. Rossiter, R. A. 1924,ApJ, 60, 15 [Google Scholar]
  114. Sato, B., Fischer, D. A., Ida, S., et al. 2009, ApJ, 703, 671 [NASA ADS] [CrossRef] [Google Scholar]
  115. Shen, Y., & Turner, E. L. 2008, ApJ, 685, 553 [NASA ADS] [CrossRef] [Google Scholar]
  116. Sozzetti, A. 2009, in Extrasolar Planets in Multi-Body Systems: Theory and Observations, EAS Publ. Ser., in press [arXiv:0902.2063] [Google Scholar]
  117. Stamatellos, D., & Whitworth, A. P. 2008, A&A, 480, 879 [Google Scholar]
  118. Stamatellos, D., & Whitworth, A. P. 2009, MNRAS, 392, 413 [Google Scholar]
  119. Stassun, K. G., Mathieu, R. D., & Valenti, J. A. 2006, Nature, 440, 311 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  120. Tamuz, O., Segransan, D., Udry, S., et al. 2008, A&A, 480, L33 [Google Scholar]
  121. Tinney, C. G., Butler, R. P., Marcy, G. W., et al. 2001, ApJ, 551, 507 [NASA ADS] [CrossRef] [Google Scholar]
  122. Triaud, A. H. M. J., Queloz, D., Bouchy, F., et al. 2009, A&A, 506, 377 [Google Scholar]
  123. Udry, S., Mayor, M., Naef, D., et al. 2002, A&A, 390, 267 [Google Scholar]
  124. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  125. Valenti, J. A., Fischer, D. A., Marcy, G. W., et al. 2009, ApJ, 702, 989 [NASA ADS] [CrossRef] [Google Scholar]
  126. Voges, W., Aschenbach, B., Boller, Th., et al. 2000, IAU Circ., 7432, 1 [NASA ADS] [Google Scholar]
  127. Vogt, S. S., Butler, R. P., Marcy, G. W., et al. 2002, ApJ, 568, 352 [NASA ADS] [CrossRef] [Google Scholar]
  128. Whitworth, A., Bate, M. R., Nordlund, Å, Reipurth, B., & Zinnecker, H. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 459 [Google Scholar]
  129. Winn, J. N., Johnson, J. A., Peek, K. M. G., et al. 2007, ApJ, 665, L167 [NASA ADS] [CrossRef] [Google Scholar]
  130. Winn, J. N., Holman, M. J., Torres, G., et al. 2008, ApJ, 683, 1076 [NASA ADS] [CrossRef] [Google Scholar]
  131. Winn, J. N., Johnson, J. A., Fabrycky, D., et al. 2009, ApJ, 700, 302 [NASA ADS] [CrossRef] [Google Scholar]
  132. Wittenmyer, R. A., Endl, M., Cochran, W. D., et al. 2009, AJ, 137, 3529 [Google Scholar]
  133. Wu, Y., & Murray, N. 2003, ApJ, 589, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  134. Zapatero Osorio, M. R., Lane, B. F., Pavlenko, Ya., et al. 2004, ApJ, 615, 958 [NASA ADS] [CrossRef] [Google Scholar]
  135. Zucker, S., & Mazeh, T. 2000, ApJ, 531, L67 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  136. Zucker, S., & Mazeh, T. 2001, ApJ, 562, 549 [NASA ADS] [CrossRef] [Google Scholar]
  137. Zucker, S., Mazeh, T., Santos, N. C., Udry, S., & Mayor, M. 2004, A&A, 426, 695 [Google Scholar]
  138. Zuckerman, B., & Song, I. 2009, A&A, 493, 1149 [Google Scholar]

Footnotes

... dwarf[*]
We operationally adopt the commonly used definition of brown dwarf as a deuterium-burning substellar object with mass in the approximate range 15-80 $M_{\rm J}$.
... 76 measurements[*]
Minniti et al. (2009) looked for, and failed to find, hints of higher dispersion in the Hipparcos measurements for HD 43848 with respect to those of stars of similar magnitude and distance.
... parameters[*]
We used both $\pi_\star$ and its transformed value $\pi_\star^\prime = \log\pi_\star$ in the fitting process, a trick utilized by Pourbaix & Jorissen (2000) to prevent parallaxes from becoming negative, and converting back to $\pi_\star$ at the end of the minimization procedure. No significant differences in the final results were found.
... found[*]
Two additional probable cases of a system with a brown dwarf and a planet in close orbits are those of HD 43848 (Bakos et al. 2009) and HD 43848 (Correia et al. 2005). In the first case, the planetary nature of the inner companion is confirmed by the occurrence of the transit. The true masses of the more massive companions are not available, but there are perspectives for deriving them thanks to the strong dynamical interactions in the case of HD 43848 and the transit timing variations in the case of HD 43848.
... companions[*]
The statistical analysis presented here does not take into account the eccentricity bias in Keplerian fits to Doppler data collected by radial-velocity planet search programs, which a) underestimates the abundance of low-amplitude, low-eccentricity planets, and b) makes low-amplitude, high-eccentricity planets hard to unveil (Shen & Turner 2008; O'Toole et al. 2009; Valenti et al. 2009).
... same[*]
It also appears that the brown dwarfs with the highest actual mass estimates seem to be found more frequently as close companions to stars belonging to the thick disk population of the Milky Way (see Table 3), but this can only be regarded as a tentative speculation, given the very limited statistics, large mass uncertainties, and the heterogeneity of the datasets.
... objects[*]
However, see e.g. Boss (2000) and Bate et al. (2002) for alternative scenarios in which isolated planetary mass objects are the result of ejections through dynamical interactions in protoplanetary disks.
... therein)[*]
While the results are not conclusive due to the presence of systematics in the dataset, it is worth noting that the CoRot-3 system also exhibits a formally non-zero spin-orbit angle (Triaud et al. 2009); however, the large uncertainties reported make the detection of spin-orbit misalignment in the CoRoT-3 system only marginal.
Copyright ESO 2010

All Tables

Table 1:   Stellar characteristics of HD 131664 and HD 131664 and spectroscopic orbital elements for the two Doppler-detected companions.

Table 2:   Orbital fits to the Hipparcos IAD for HD 131664 and HD 131664, assuming knowledge of P, e, T0, and $\omega $ from the spectroscopic orbit.

Table 3:   Close companions to solar-type stars with (projected) masses between 10 $M_{\rm J}$and 80 $M_{\rm J}$.

Table 4:   Results of the K-S and R-S tests on different subsets of systems.

All Figures

  \begin{figure} \par$\begin{array}{c} \includegraphics[width=8cm]{12717f1a.eps}\\ \includegraphics[width=8cm]{12717f1b.eps}\\ \end{array} $ \end{figure} Figure 1:

Periodograms of HD 131664 ( top) and HD 131664 ( bottom)assuming e and T0 from the known spectroscopic orbit.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{12717f2.eps} \end{figure} Figure 2:

Iso-$\chi ^2$ contours corresponding to confidence intervals in two dimensions containing 68.3% (solid line), 90% (dashed-dotted line), and 95% (dashed line) of the values of i and $\Omega $ as obtained in a 7-parameter fit to the Hipparcos IAD of HD 131664 ( top) and HD 131664 ( bottom), assuming P, e, T0, and $\omega $ from the known spectroscopic orbit. The best-fit (i, $\Omega $) solutions for both stars are indicated with stars.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{12717f3.eps} \end{figure} Figure 3:

Distribution of the ratio $a/\sigma _a$ of false astrometric orbits for single stars observed by Hipparcos, approximated by a Rayleigh-Rice law following Halbwachs et al. (2000). The two arrows indicate the values of $a/\sigma _a$obtained for HD 131664 and HD 131664 based on a Monte Carlo bootstrap simulation.

Open with DEXTER
In the text

  \begin{figure} \par$\begin{array}{c} \includegraphics[width=8cm]{12717f4a.eps}\\ \includegraphics[width=8cm]{12717f4b.eps}\\ \end{array}$ \end{figure} Figure 4:

Period vs. eccentricity ( top panel) and eccentricity vs. companion mass ( bottom panel). In the lower panel plot, only objects with periods longer than 20 days are shown. Red filled circles: companions with true estimated masses in the range 10-80 $M_{\rm J}$. Blue triangles: companions with projected masses in the range 10-80 $M_{\rm J}$. Green squares: companions with projected masses in the range < $80 ~M_{\rm J}$but true stellar masses > $80 ~M_{\rm J}$. The three objects with larger symbols belong to the multiple systems HD 131664, HD 131664, and HD 131664.

Open with DEXTER
In the text

  \begin{figure} \par$\begin{array}{c} \includegraphics[width=8cm]{12717f5a.eps}\\... ...ludegraphics[width=8cm]{12717f5c.eps}\\ \end{array}$\vspace*{-3mm} \end{figure} Figure 5:

Orbital period vs. companion mass ( top), metallicity vs. companion mass ( center), stellar mass vs. companion mass ( bottom). Symbols as in the previous figure.

Open with DEXTER
In the text

  \begin{figure} \par$\begin{array}{c} \includegraphics[width=8.3cm]{12717f6a.eps}\\ \includegraphics[width=8.3cm]{12717f6b.eps}\\ \end{array}$ \end{figure} Figure 6:

Upper panel: cumulative distribution of the eccentricity of objects with periods longer than 20 days orbiting main-sequence stars with mass between 0.7 and 1.5 $M_{\odot }$. Continuous (black) line: planets with $M_{\rm c} \sin i < 4~M_{\rm J}$(from Butler et al. 2006). Dotted (purple) line: planets with $4 < M_{\rm c} \sin i < 10~M_{\rm J}$(from Butler et al. 2006). Dashed (red) line: objects with mass $10 < M_{\rm c} < 80~M_{\rm J}$(this paper), Dashed-dot (blue) line: objects with $10 < M_{\rm c}\sin i < 80~M_{\rm J}$, but excluding objects with astrometric masses in the stellar regime (this paper). Lower panel: cumulative [Fe/H] (with no period cut). Same symbols as in the upper panel.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.