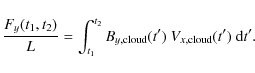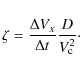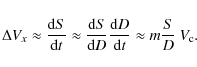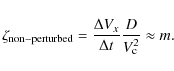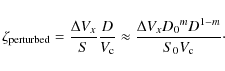| Issue |
A&A
Volume 509, January 2010
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912375 | |
| Published online | 14 January 2010 | |
Global and local expansion of magnetic clouds in the inner heliosphere
A. M. Gulisano1,2 - P. Démoulin3 - S. Dasso1,2 - M. E. Ruiz1,2 - E. Marsch4
1 - Instituto de Astronomía y Física del Espacio, CONICET-UBA,
CC. 67, Suc. 28, 1428 Buenos Aires, Argentina
2 -
Departamento de Física, Facultad de Ciencias Exactas y
Naturales, Universidad de Buenos Aires, 1428 Buenos Aires, Argentina
3 -
Observatoire de Paris, LESIA, UMR 8109 (CNRS),
92195 Meudon Principal Cedex, France
4 -
Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
Received 22 April 2009 / Accepted 22 September 2009
Abstract
Context. Observations of magnetic clouds (MCs) are
consistent with the presence of flux ropes detected in the solar wind
(SW) a few days after their expulsion from the Sun as coronal mass
ejections (CMEs).
Aims. Both the in situ observations of plasma velocity
profiles and the increase of their size with solar distance show that
MCs are typically expanding structures. The aim of this work is to
derive the expansion properties of MCs in the inner heliosphere
from 0.3 to 1 AU.
Methods. We analyze MCs observed by the two Helios spacecraft
using in situ magnetic field and velocity measurements. We split
the sample in two subsets: those MCs with a velocity profile that is
significantly perturbed from the expected linear profile and those that
are not. From the slope of the in situ measured bulk velocity
along the Sun-Earth direction, we compute an expansion speed with
respect to the cloud center for each of the analyzed MCs.
Results. We analyze how the expansion speed depends on the MC
size, the translation velocity, and the heliocentric distance, finding
that all MCs in the subset of non-perturbed MCs expand with almost the
same non-dimensional expansion rate (![]() ). We find departures from this general rule for
). We find departures from this general rule for ![]() only for perturbed MCs, and we interpret the departures as the
consequence of a local and strong SW perturbation by SW fast streams,
affecting the MC even inside its interior, in addition to the direct
interaction region between the SW and the MC. We also compute the
dependence of the mean total SW pressure on the solar distance and we
confirm that the decrease of the total SW pressure with distance is the
main origin of the observed MC expansion rate. We found that
only for perturbed MCs, and we interpret the departures as the
consequence of a local and strong SW perturbation by SW fast streams,
affecting the MC even inside its interior, in addition to the direct
interaction region between the SW and the MC. We also compute the
dependence of the mean total SW pressure on the solar distance and we
confirm that the decrease of the total SW pressure with distance is the
main origin of the observed MC expansion rate. We found that ![]() was
was
![]() for non-perturbed MCs while
for non-perturbed MCs while ![]() was
was
![]() for perturbed MCs, the larger spread in the last ones being due to the
influence of the solar wind local environment conditions on the
expansion.
for perturbed MCs, the larger spread in the last ones being due to the
influence of the solar wind local environment conditions on the
expansion.
Key words: magnetic fields - magnetohydrodynamics (MHD) - Sun: coronal mass ejections (CMEs) - solar wind - interplanetary medium
1 Introduction
Magnetic clouds (MCs) are magnetized plasma structures forming a particular subset of interplanetary coronal mass ejections (ICMEs, e.g., Burlaga 1995). MCs are transient structures in the solar wind (SW) defined by an enhanced magnetic field with respect to that found in the surrounding SW with a coherent rotation of the field of the order of about a day when these structures are observed at 1 AU (Burlaga et al. 1981). A lower proton temperature than the expected one in the SW with the same velocity is another signature of MCs that complement their identification (e.g., Marsch et al. 2009; Richardson & Cane 1995).MCs interact with their environment during their journey in the solar wind (SW) from the Sun to the outer heliosphere and, since the SW pressure (magnetic plus plasma) decreases for increasing heliocentric distance, an expansion of MCs is expected. In a heliospheric frame, the in situ observed bulk plasma velocity typically decreases in magnitude from the front to the back inside MCs, confirming the expectation that MCs are expanding objects in the SW. Furthermore, from observations of large samples of MCs observed at different heliocentric distance, it has been shown that the size of MCs increases for larger heliocentric distances (Leitner et al. 2007, and references therein).
These structures have an initial expansion from their origin in the Sun, as shown from observations of radial expansion at the corona; e.g., an example of the leading edge of a CME traveling faster than its core is shown in Fig. 6 of Tripathi et al. (2006). However their subsequent expansion mainly will be given by the environmental (SW) conditions as a consequence of force balance (Démoulin & Dasso 2009).
Dynamical models have been used to describe clouds in expansion, either considering only a radial expansion (e.g., Osherovich et al. 1993; Farrugia et al. 1997; Nakwacki et al. 2008b; Farrugia et al. 1993), or expansion in both the radial and axial directions (e.g., Shimazu & Vandas 2002; Nakwacki et al. 2008a; Démoulin & Dasso 2009; Berdichevsky et al. 2003; Dasso et al. 2007). The main aim of these models is to take into account the evolution of the magnetic field as the MC crosses the spacecraft. Another goal is to correct the effect of mixing spatial-variation/time-evolution in the one-point observations to obtain a better determination of the MC field configuration. The expansion of several magnetic clouds has been analyzed previously by fitting different velocity models to the data (Shimazu & Vandas 2002; Vandas et al. 2005; Démoulin et al. 2008; Mandrini et al. 2007; Yurchyshyn et al. 2006; Berdichevsky et al. 2003; Dasso et al. 2007; Farrugia et al. 1993).
The expansion of some MCs is not always well marked with in situ velocity measurements. This is in particular the case for
small MCs or those overtaken by fast streams. Slow magnetic clouds,
with velocities lower than or of the order of 400 km s-1, in general
have small sizes, low magnetic field strengths, and only a few of
them present shocks or sheaths (e.g., Tsurutani et al. 2004). Fast
streams overtaking magnetic clouds from behind can compress the
magnetic field in the rear for the overtaken MC, for instance in
some cases forming large structures called merged interaction
regions (e.g., Burlaga et al. 2003). The interaction between a stream
and an MC can affect the internal structure of the cloud
(e.g., as shown from numerical simulations by Xiong et al. 2007).
The difference between the velocities of the front and back
boundaries, called
![]() ,
was frequently used to
qualify how important the expansion of an observed MC is. A larger
,
was frequently used to
qualify how important the expansion of an observed MC is. A larger
![]() is favorable for the presence of shocks
surrounding the MC, especially for the presence of a backward shock
(Gosling et al. 1994). A large
is favorable for the presence of shocks
surrounding the MC, especially for the presence of a backward shock
(Gosling et al. 1994). A large
![]() is less important
for the presence of a frontal shock since a frontal shock is also
created by a large difference between the MC global velocity and the
overtaken SW velocity.
is less important
for the presence of a frontal shock since a frontal shock is also
created by a large difference between the MC global velocity and the
overtaken SW velocity.
![\begin{figure}
\mbox{
\includegraphics[width=7cm, clip=]{figs/12375f1a.eps}\incl...
...5f1b.eps}\includegraphics[width=7cm, clip=]{figs/12375f1d.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg11.png)
|
Figure 1: Examples of two analyzed MCs that are not significantly perturbed by a fast flow. The MC center was observed at 07-Jan.-1975 10:39 and 04-Mar.-1975 21:37 UT, for panels a), c) and b), d), respectively. The vertical dashed lines define the MC boundaries. a), b) Vx is the observed velocity component in the radial direction from the Sun, expressed in km per second. The straight line is the linear least square fit of the velocity in the time interval where an almost linear trend is present (where the observations are presented as a solid line). The linear fitting is extrapolated to the borders of the MC, which are marked with circles. c), d) By is the magnetic field component, in nT, both orthogonal to the MC axis and to the spacecraft trajectory, while the solid line represents Fy, which is the accumulated flux of By (Eq. (7)). The extremum of Fy (proxy of the cloud center) is indicated with diamonds (a color version is available in the electronic version). |
| Open with DEXTER | |
The quantity
![]() is a good proxy of the time
variation of the global size of the MC, however,
is a good proxy of the time
variation of the global size of the MC, however,
![]() does not express how fast the expansion of an element of fluid
is, since
does not express how fast the expansion of an element of fluid
is, since
![]() depends strongly on how big the
studied MC is. For example the MC observed by ACE at 1 AU on 29 October 2004 (Mandrini et al. 2007) is formed by a flux rope with a
large radius,
depends strongly on how big the
studied MC is. For example the MC observed by ACE at 1 AU on 29 October 2004 (Mandrini et al. 2007) is formed by a flux rope with a
large radius,
![]() AU, and it also has a large
AU, and it also has a large
![]() km s-1, and so, at first sight, it can
be qualified as a very rapidly expanding MC. However, let suppose
that the same MC would have most its flux having been reconnected
with the encountered SW during the transit from the Sun, as has been
observed in some cases (e.g., Dasso et al. 2006,2007), so that
only the flux rope core would have been observed as a MC. If the
remaining flux rope would have a radius of only 10-2 AU, it
would have shown
km s-1, and so, at first sight, it can
be qualified as a very rapidly expanding MC. However, let suppose
that the same MC would have most its flux having been reconnected
with the encountered SW during the transit from the Sun, as has been
observed in some cases (e.g., Dasso et al. 2006,2007), so that
only the flux rope core would have been observed as a MC. If the
remaining flux rope would have a radius of only 10-2 AU, it
would have shown
![]() km s-1, so it would have been qualified as a slowly
expanding MC.
km s-1, so it would have been qualified as a slowly
expanding MC.
More generally, small flux ropes are expected to have intrinsically
small
![]() ,
an expectation confirmed by the data
(Figs. 3a,b). MCs have a broad range of sizes,
with flux rope radii of a few 0.1 AU down to a few 10-3 AU
(Lynch et al. 2003; Feng et al. 2007), and it is necessary to quantify their
expansion rate independently of their size. In this study, we
analyze the expansion of MCs in the inner heliosphere, and find a
non-dimensional expansion coefficient (
,
an expectation confirmed by the data
(Figs. 3a,b). MCs have a broad range of sizes,
with flux rope radii of a few 0.1 AU down to a few 10-3 AU
(Lynch et al. 2003; Feng et al. 2007), and it is necessary to quantify their
expansion rate independently of their size. In this study, we
analyze the expansion of MCs in the inner heliosphere, and find a
non-dimensional expansion coefficient (![]() ), which can be
quantified from one-point in situ observations of the bulk
velocity time profile of the cloud. We demonstrate that
), which can be
quantified from one-point in situ observations of the bulk
velocity time profile of the cloud. We demonstrate that ![]() characterizes the expansion rate of the MC, independently of its
size.
characterizes the expansion rate of the MC, independently of its
size.
We first describe the data used, and then the method to define the main properties of the MC (Sect. 2). In Sect. 3, we analyze the properties of the MC expansion, defining a proper expansion coefficient. We derive specific properties of two groups of MCs, defined from their interaction with the SW environment. Then, we relate the MC expansion rate to the decrease of the total SW pressure with solar distance. We summarize our results in Sect. 4 and conclude in Sect. 5.
2 Data and method
2.1 Helios data base
We have studied the MCs reported by different authors from the Helios 1 and 2 missions (Leitner et al. 2007; Bothmer & Schwenn 1998; Liu et al. 2005); from November 1974 to 1985 for Helios 1 and from January 1976 to 1980 for Helios 2. We analyzed observations of plasma properties (Rosenbauer et al. 1977), in particular bulk velocity and density of protons (Marsch et al. 1982), and magnetic field vector (Neubauer et al. 1977), for a time series with a temporal cadence ofThe magnetic and velocity fields observations are in a right-handed
system of coordinates (![]() ,
,
![]() ,
,
![]() ).
). ![]() corresponds to the Sun-Spacecraft direction,
corresponds to the Sun-Spacecraft direction, ![]() is on the
ecliptic plane and points from East to West (in the same direction
as the planetary motion), and
is on the
ecliptic plane and points from East to West (in the same direction
as the planetary motion), and ![]() points to the North
(perpendicular to the ecliptic plane and closing the right-handed
system).
points to the North
(perpendicular to the ecliptic plane and closing the right-handed
system).
2.2 Definition of the MC local frame
To facilitate the understanding of MC properties, we define a system of coordinates linked to the cloud in whichThe observed magnetic field in an MC can be expressed in this local
frame, transforming the observed components (Bx, By,
Bz) with a rotation matrix to (
![]() ,
,
![]() ,
,
![]() ). In particular, for p=0 and an MC
described by a cylindrical magnetic configuration, i.e.
). In particular, for p=0 and an MC
described by a cylindrical magnetic configuration, i.e.
![]() ,
we have
,
we have
![]() and
and
![]() when the
spacecraft leaves the cloud. In this particular case, the magnetic
field data will show:
when the
spacecraft leaves the cloud. In this particular case, the magnetic
field data will show:
![]() ,
a large and coherent
variation of
,
a large and coherent
variation of
![]() (with a change of sign), and an
intermediate and coherent variation of
(with a change of sign), and an
intermediate and coherent variation of
![]() ,
from low
values at one cloud edge, with the largest value at its axis and
returning to low values at the other edge.
,
from low
values at one cloud edge, with the largest value at its axis and
returning to low values at the other edge.
More generally, the local system of coordinates is especially useful
when p is small compared to the MC radius (R) since the
direction of the MC axis can be found using a fitting method or
applying the minimum variance (MV) technique to the normalized time
series of the observed magnetic field (e.g. Dasso et al. 2006, and references
therein). In particular, from the analysis of a set of
cylindrical synthetic MCs, Gulisano et al. (2007) found that the
normalized MV technique provides a deviation of the real orientation
of the main MC axis of less than ![]() even for p as large
as
even for p as large
as ![]() of the MC radius.
of the MC radius.
2.3 Definition of the MC boundaries
As the first step of an iterative process, we choose the MC boundaries reported in the literature, and perform a normalized minimum variance analysis to find the local frame of the MC. We then analyze the magnetic field components in the local frame, and redefine the boundaries of each MC, according to the expected typical behavior of the axial field (![\begin{figure}
\mbox{\includegraphics[width=7cm, clip=]{figs/12375f2a.eps}\incl...
...75f2b.eps}\includegraphics[width=7cm, clip=]{figs/12375f2d.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg35.png)
|
Figure 2: Examples of two analyzed MCs that are perturbed by a fast flow as seen in the upper panels. The MC center was observed at 30-Jan.-1977 03:18 and 23-Jun.-1980 12:25 UT, for panels a), c) and b), d), respectively. The external perturbations enter in a significant part of the MCs. The same quantities, as in Fig. 1, are shown (a color version is available in the electronic version). |
| Open with DEXTER | |
Table 1: List of MC events.
2.4 Characterization of the MC expansion
Most MCs have a higher velocity in their front than in their back, showing that they are expanding magnetic structures in the SW. About half of the studied MCs have well defined linear profile Vx(t)(Figs. 1a,b), while for the other half, Vx(t)is nearly linear only in a part of the MC which includes the MC center (Figs. 2a,b). The distortions of Vx(t) are more frequently due to an overtaking faster SW flow in the back of the MC.We split the data set in two groups:
non-perturbed MCs for cases where the velocity profile presents a
linear trend in more than 75% of the full size of the MC and
perturbed MCs for cases where this is not satisfied. There are
almost as many perturbed as non-perturbed
MCs, considering data from each spacecraft separately and both of them together.
The measured temporal profile Vx(t) is fitted using a least square
fit with a linear function of time,
where
The linear fit is used to define the velocities
![]() and
and
![]() at the MC boundaries
(Sect. 2.3). Then, we define the full expansion
velocity of an MC as:
at the MC boundaries
(Sect. 2.3). Then, we define the full expansion
velocity of an MC as:
For non-perturbed MCs,
![\begin{figure}
\mbox{\includegraphics[width=7.5cm, clip=]{figs/12375f3a.eps}\in...
...5f3c.eps}\includegraphics[width=7.5cm, clip=]{figs/12375f3d.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg46.png)
|
Figure 3:
The panels a)- d) show the correlation analysis between
proxies for MC expansion with different physical quantities. The
MCs are separated in two groups: perturbed (empty square symbol) and
non-perturbed (filled circle symbol). The straight lines are the
result of a least square fit for perturbed (dashed line),
non-perturbed (thin continuous line), and for both set of MCs in the
list of events shown in Table 1 (thick continuous
line).
|
| Open with DEXTER | |
2.5 MC size
From the determination of the boundaries described above, we can estimate the size, S, of the flux rope alongWe perform a linear least square fit in log-log plots of S as a function of the distance to the Sun (D). As expected, the size has a clear dependence with D:
where S and D are in AU. Our results are compatible within the error bars with previous studies:
where d is an estimation of the true diameter of the MC. Our
results are closer to Bothmer & Schwenn (1998) and Liu et al. (2005) who
analyzed MCs and ICMEs, respectively. The larger difference is
between our results and the last two ones while they are based on
the most different sets, as follows. Wang et al. (2005) studied a large
set of ICMEs defined only by a measured temperature lower by a
factor of 2 than expected in the SW with the same speed
(e.g., Richardson & Cane 2004). This set included MCs, but it is
dominated by non-MC ICMEs. Conversely, Leitner et al. (2007) analyzed
only MCs, with a strict classical definition. They fitted the
magnetic field observations with a classical cylindrical linear
force-free field, then they found the impact parameter and the
orientation of the MC axis to estimate the true diameter, d, of
the MCs. So the selected events and the method of
Wang et al. and Leitner et al. are noticeably
different. We also note that Leitner et al. (2007) found a larger
exponent,
![]() ,
when they restrict their data to
,
when they restrict their data to ![]() AU. This indicates that the relation is not strictly a power-law
and this could be the main origin of the different results (which
are so dependent on the distribution of events with solar distance
in the selected sets).
AU. This indicates that the relation is not strictly a power-law
and this could be the main origin of the different results (which
are so dependent on the distribution of events with solar distance
in the selected sets).
![\begin{figure}
\mbox{\includegraphics[width=7cm, clip=]{figs/12375f4a.eps}\inclu...
...75f4c.eps}\includegraphics[width=7cm, clip=]{figs/12375f4d.eps} }
\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg58.png)
|
Figure 4:
Panels a)- d) show the correlation analysis that tests for the dependence of the non-dimensional
expansion factor |
| Open with DEXTER | |
2.6 Magnetic field strength
Another important characteristic of MCs is their magnetic field strength. We define the average fieldwhere the units of
Again the strongest difference exists between our results and the ones of Leitner et al. (2007). The origin of this difference is expected to be the same as for the size. Indeed for
The typical expansion speed in MCs is of the order of half the Alfvén speed (e.g., Klein & Burlaga 1982). In our studied set of MCs, we have also found that the expansion speed was lower than the Alfvén speed [not shown]. This is a necessary condition to expect that the magnetic field evolves globally, adapting its initial magnetic field during its expansion, because the Alfvén speed is the velocity of propagation of information through the magnetic structure.
2.7 MC center and translation velocity
Following Dasso et al. (2006), we define the accumulative flux per unit length L(along the MC axial direction):Here we neglect the evolution of the magnetic field during the spacecraft crossing period (so also the ``aging'' effect, see Dasso et al. 2007). The set of field lines, passing at the position of the spacecraft at t1, with the hyphotesis of symmetry of translation along the main axis, defines a magnetic flux surface, which is wrapped around the flux rope axis. Then, any magnetic flux surface will be crossed at least twice by the spacecraft, once at t1 and once at t2 defined by Fy(t1,t2)=0. Then, this property of Fy(t1,t2) permits us to associate any out-bound position, within the flux rope, to its in-bound position belonging to the same magnetic-flux surface. The global extremum of Fy(t1,t), for t1 having a fixed value, locates the position where the spacecraft trajectory has the closest approach distance to the MC axis (MC center). This position can also be found directly from
The velocity at the MC center (![]() )
is computed from the fitted linear
regression Eq. (1) evaluated at the time when the spacecraft
reaches the MC center.
)
is computed from the fitted linear
regression Eq. (1) evaluated at the time when the spacecraft
reaches the MC center.
3 Expansion rate of MCs
3.1 Correlation involving the expansion velocity
From here on, we classify the MCs belonging to the full set of events, according to the quality of their velocity and magnetic observations. If they were too noisy or with a lot of data gaps, we exclude them from the following study, keeping only those MCs with relatively good quality (listed in Table 1).
![]() ,
as defined by Eq. (2), characterizes
the expansion speed of the crossed MC. However, as outlined in
Sect. 1,
,
as defined by Eq. (2), characterizes
the expansion speed of the crossed MC. However, as outlined in
Sect. 1,
![]() is expected to be strongly
correlated with the MC size, so that it does not express directly
how fast a given parcel of plasma is expanding in the MC. We
therefore define below, after a few steps, a better measure of the
expansion rate.
The size of an MC is proportional to
is expected to be strongly
correlated with the MC size, so that it does not express directly
how fast a given parcel of plasma is expanding in the MC. We
therefore define below, after a few steps, a better measure of the
expansion rate.
The size of an MC is proportional to
![]() and to
and to ![]() .
Figure 3a shows a clear
positive correlation between
.
Figure 3a shows a clear
positive correlation between
![]() and
and ![]() .
Moreover
the least square fit of a straight line for the full set of MCs
gives a fitted curve passing in the vicinity of the origin (within
the uncertainties present on the slope). This affine correlation is
then removed by computing
.
Moreover
the least square fit of a straight line for the full set of MCs
gives a fitted curve passing in the vicinity of the origin (within
the uncertainties present on the slope). This affine correlation is
then removed by computing
![]() .
This quantity
also shows, as expected, a positive correlation with
.
This quantity
also shows, as expected, a positive correlation with ![]() (Fig. 3b), but differently above, the fitted
straight line stays far from the origin, so we cannot simply remove
the correlation by dividing
(Fig. 3b), but differently above, the fitted
straight line stays far from the origin, so we cannot simply remove
the correlation by dividing
![]() by
by ![]() .
However, its dependence on
.
However, its dependence on
![]() brings the fitted straight line
close enough to the origin (within the uncertainties of the fit,
Fig. 3c) so that
brings the fitted straight line
close enough to the origin (within the uncertainties of the fit,
Fig. 3c) so that
![]() is a meaningful quantity. These correlations are present for both
groups of MCs, but they are much stronger for non-perturbed MCs
(Figs. 3b,c).
Other correlations have being attempted with the above methodology.
Either there is no significant correlation, or the fitted curve
passes far from the origin. There is still the exception that
is a meaningful quantity. These correlations are present for both
groups of MCs, but they are much stronger for non-perturbed MCs
(Figs. 3b,c).
Other correlations have being attempted with the above methodology.
Either there is no significant correlation, or the fitted curve
passes far from the origin. There is still the exception that
![]() has an affine correlation with 1/Dfor non-perturbed MCs (Fig. 3d).
has an affine correlation with 1/Dfor non-perturbed MCs (Fig. 3d).
3.2 Non-dimensional expansion rate
The above empirical correlation analysis suggests that we can define the non-dimensional expansion rate as the quantity:The first steps were to remove the MC size dependence, while the last step could be further justified by the need to have a non-dimensional coefficient. Finally, it is remarkable that the correlation analysis of the MC data leads to the definition of the same variable,
We next verify that ![]() is no longer dependent on
is no longer dependent on ![]() ,
,
![]() ,
D or some combination of them.
Figures 4a,b show two examples of this exploration.
Indeed, the non-perturbed MCs show almost no correlation, while
there are still some correlations when the perturbed MCs are
considered. Figure 4b also shows that even for slow MCs
(see Sect. 1), the non-dimensional expansion rate (
,
D or some combination of them.
Figures 4a,b show two examples of this exploration.
Indeed, the non-perturbed MCs show almost no correlation, while
there are still some correlations when the perturbed MCs are
considered. Figure 4b also shows that even for slow MCs
(see Sect. 1), the non-dimensional expansion rate (![]() )
is not correlated with
)
is not correlated with ![]() .
.
Still, does ![]() depend on the properties of the MC considered?
To test this we first need to remove the distance dependence on Sand
depend on the properties of the MC considered?
To test this we first need to remove the distance dependence on Sand
![]() ,
found in Sects. 2.5 and 2.6, by
defining values at a given solar distance (here taken at 1 AU). We
use:
,
found in Sects. 2.5 and 2.6, by
defining values at a given solar distance (here taken at 1 AU). We
use:
We find that there is no significant correlation between
![\begin{figure}
{\includegraphics[width=7.5cm, clip=]{figs/12375f5.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg78.png)
|
Figure 5:
Perturbed and non-perturbed MCs have a remarkably different
behavior of |
| Open with DEXTER | |
3.3 Expansion of non-perturbed MCs
Perturbed and non-perturbed MCs have a remarkable different behavior ofTo explain the different behavior of ![]() let us take into account that
the dependence of the size on the heliocentric distance is of the form
(as observed from several statistical studies,
Eqs. (3)-(4)):
let us take into account that
the dependence of the size on the heliocentric distance is of the form
(as observed from several statistical studies,
Eqs. (3)-(4)):
where S0 is the reference size at the distance D0. Its physical origin is the approximate pressure balance between the MC and the surrounding SW (Démoulin & Dasso 2009, see Sect. 3.5). This physical driving of the expansion is expected to induce a smooth expansion so that the size of an individual MC closely follows Eq. (10). Then, for non-perturbed MCs, we can differentiate Eq. (10) with time to derive the expansion velocity
Then, the non-dimensional expanding rate of Eq. (8) is:
This implies that
3.4 Expansion of perturbed MCs
For perturbed MCs, the estimation ofThe effect of an overtaking stream is simply to compress the MC (at first thought), so MCs perturbed
by this effect are expected to have a lower ![]() than non-perturbed MCs. This is true in average,
but there is a significant fraction (5/16) of perturbed MCs that are in fact expanding faster than
the mean of non-perturbed MCs. The largest
than non-perturbed MCs. This is true in average,
but there is a significant fraction (5/16) of perturbed MCs that are in fact expanding faster than
the mean of non-perturbed MCs. The largest ![]() is also obtained for a perturbed MC.
Moreover,
is also obtained for a perturbed MC.
Moreover, ![]() for perturbed MCs still has a good correlation with
for perturbed MCs still has a good correlation with
![]() ,
opposite to
the result obtained for non-perturbed MCs (Fig. 5). Why do perturbed MCs have these properties?
,
opposite to
the result obtained for non-perturbed MCs (Fig. 5). Why do perturbed MCs have these properties?
When an MC is overtaken by a fast SW stream, it is compressed by the
ram, plasma and magnetic pressure of the overtaking stream, so its
size increases less rapidly with solar distance (than without
interaction). If the interaction is strong enough, this can indeed
stop the natural expansion and create an MC in compression, as in
the 3 cases present in Table 1, where
![]() .
A sketch of such evolution is given in Fig. 6.
However, this interaction will not last for a long period of time
since the overtaking stream can overtake the flux rope from both
sides. As the total pressure in the back of the MC decreases, the
expansion rate of the MC increases. Indeed, its expansion rate
could be faster than the typical one for non-perturbed MCs, as
follows. The compression has provided an internal pressure that is
stronger than the surrounding SW total pressure. Then, when the
extra pressure of the overtaking stream has significantly decreased,
the MC has an over-pressure compared to the surrounding SW, so it
expands faster than usual i. e., an overexpansion, see
Gosling et al. (1995). Indeed, the flux rope is expected to evolve
towards the expected size that it would have achieved without the
overtaken SW flow.
.
A sketch of such evolution is given in Fig. 6.
However, this interaction will not last for a long period of time
since the overtaking stream can overtake the flux rope from both
sides. As the total pressure in the back of the MC decreases, the
expansion rate of the MC increases. Indeed, its expansion rate
could be faster than the typical one for non-perturbed MCs, as
follows. The compression has provided an internal pressure that is
stronger than the surrounding SW total pressure. Then, when the
extra pressure of the overtaking stream has significantly decreased,
the MC has an over-pressure compared to the surrounding SW, so it
expands faster than usual i. e., an overexpansion, see
Gosling et al. (1995). Indeed, the flux rope is expected to evolve
towards the expected size that it would have achieved without the
overtaken SW flow.
![\begin{figure}
{
\includegraphics[width=7.5cm, clip=]{figs/12375f6.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg85.png)
|
Figure 6: Cartoon of a possible evolution of the size of the MC with the helio-distance, showing the expected global expansion (thick solid line), an example of a non-perturbed MC (thin solid) and a perturbed MC (dashed line) (a color version is available in the electronic version). |
| Open with DEXTER | |
So, depending on which time the MC is observed in the interaction
process, a perturbed MC can expand slower or faster than without
interaction (Fig. 6). This explains the dispersion of ![]() found for perturbed MCs, but also the presence of some MCs
with faster expansion than usual.
found for perturbed MCs, but also the presence of some MCs
with faster expansion than usual.
In the case of perturbed MCs, their sizes still follow
Eq. (10) on average (as shown by Eq. (3)), but it
has no meaning to apply this law locally to a given MC. In
particular, we cannot differentiate Eq. (10) with time to
get an estimation of the local expansion velocity of a perturbed MC
(so we cannot write Eq. (11)). Rather we can use
Eq. (10) only to have an approximate size S in the
expression of ![]() :
:
The dependence of
3.5 Physical origin of MC expansion
The main driver of MC expansion is the rapid decrease of the total SW pressure with solar distance (Démoulin & Dasso 2009). Other effects, such as the internal over-pressure, the presence of a shock, as well as the radial distribution and the amount of twist within the flux rope have a much weaker influence on the expansion. This result was obtained by solving the MHD equations for flux ropes having various magnetic field profiles, and with ideal MHD or fully relaxed states (minimizing magnetic energy while preserving magnetic helicity). Within the typical SW conditions, they have shown that any force-free flux rope will have an almost self similar expansion, so a velocity profile almost linear with time as observed by a spacecraft crossing an MC (e.g. Figs. 1, 2). They also relate the normalized expansion rateHere we further test the above theory with the MCs analyzed in this
paper, by comparing the value obtained for ![]() with the value of
with the value of
![]() obtained from previous studies of the SW.
obtained from previous studies of the SW.
According to Mariani & Neubauer (1990), from fitting a power law to observations
of the field strength in the inner heliosphere according to
B = B0 (D/D0)-nB,
a global decay law is obtained with
![]() (
(
![]() nT at D0 = 1 AU) from Helios 1, and
nT at D0 = 1 AU) from Helios 1, and
![]() (
(
![]() nT at D0 = 1 AU) from Helios 2.
nT at D0 = 1 AU) from Helios 2.
For the proton density (
![]() )
we consider
a density of
)
we consider
a density of
![]() cm-3 at 1 AU (averaging slow and fast
SW according to Schwenn 2006) and nN=2 (corresponding to
the 2D expansion for the stationary SW with constant radial
velocity).
cm-3 at 1 AU (averaging slow and fast
SW according to Schwenn 2006) and nN=2 (corresponding to
the 2D expansion for the stationary SW with constant radial
velocity).
According to Schwenn (2006) and Totten et al. (1995), it is possible to
represent a typical dependence of the proton temperature (![]() )
upon D as approximately
)
upon D as approximately
![]() with
with
![]() (
(
![]() K at D0
= 1 AU).
K at D0
= 1 AU).
For electron temperature (
![]() )
we
follow Marsch et al. (1989), in particular their results for the ranges
of velocities (300-500) km s-1 to better represent the typical
conditions of the SW. For the velocity range (300-400) km s-1,
Marsch et al. (1989) found
)
we
follow Marsch et al. (1989), in particular their results for the ranges
of velocities (300-500) km s-1 to better represent the typical
conditions of the SW. For the velocity range (300-400) km s-1,
Marsch et al. (1989) found
![]() K and
K and
![]() ;
for the velocity range (400-500) km s-1,
;
for the velocity range (400-500) km s-1,
![]() K and
K and
![]() .
For
electrons we then consider mean temperature averaged over these two
ranges of SW speeds.
.
For
electrons we then consider mean temperature averaged over these two
ranges of SW speeds.
The partial pressures (magnetic, proton, and electron) are shown in
Fig. 7. Neglecting the small effect of the ![]() particles, the total pressure in the SW (
particles, the total pressure in the SW (
![]() )
is:
)
is:
![]() .
We then propose that the total pressure
also follows a power law (
.
We then propose that the total pressure
also follows a power law (
![]() )
and fit this
power law to
)
and fit this
power law to
![]() .
Then, we fit
.
Then, we fit
![]() with a power law
(
with a power law
(
![]() ). The sum of different power laws is generally not a
power law, however in the present case we still find a total
pressure which is very close to a power law since the magnetic and
plasma pressures have similar exponents. This also implies that the
exponent found,
). The sum of different power laws is generally not a
power law, however in the present case we still find a total
pressure which is very close to a power law since the magnetic and
plasma pressures have similar exponents. This also implies that the
exponent found,
![]() ,
has a low sensitivity to the
plasma
,
has a low sensitivity to the
plasma ![]() and the relative pressure contribution of the
electrons and protons.
and the relative pressure contribution of the
electrons and protons.
Using the result of Démoulin & Dasso (2009) that
![]() for force-free flux rope, we found
for force-free flux rope, we found
![]() ,
in full
agreement, within the error bars, with
,
in full
agreement, within the error bars, with ![]() found from velocity
measurement in non-perturbed MCs (Table 1). This
further demonstrates that MC expansion is mainly driven by the
decrease of the surrounding SW total pressure with solar distance.
The main departure from this global evolution is due to the presence
of overtaking flows.
found from velocity
measurement in non-perturbed MCs (Table 1). This
further demonstrates that MC expansion is mainly driven by the
decrease of the surrounding SW total pressure with solar distance.
The main departure from this global evolution is due to the presence
of overtaking flows.
| Figure 7:
Log-log plots of the SW total pressure and its components
as a function of the solar distance. The solid line shows the least
square straight line fitted to the total pressure as computed from
the points marked with circles. The total pressure in the SW
decreases as
|
|
| Open with DEXTER | |
4 Summary and discussion of main results
MCs have a specific magnetic configuration, forming flux ropes which expand in all directions, unlike the almost 2D expansion of the surrounding SW. But how fast do they expand? Is the expansion rate specific for each MC or is there a common expansion rate? What is the role of the surrounding SW? Finally, what is the main driver of such 3D expansion?
In order to answer these questions we have re-analyzed a significant set of MCs observed by both Helios spacecrafts. In order to better define the MC extension, we first analyzed the magnetic data, finding the direction of the flux rope axis, and then we rotated the magnetic data in the MC local frame. This step is important to separate the axial and ortho-axial field components since they have very different spatial distributions in a flux rope, and since we then can use the magnetic flux conservation of the azimuthal component as a constraint on the boundary positions (e.g., as done in Steed et al. 2008; Dasso et al. 2006). Then, in the local MC frame, we can better define the boundaries of the MC.
The observed velocity profile typically has a linear variation with time, with a larger velocity in front than in the back of the MC. This is a clear signature of expansion. On top of this linear trend, fluctuations of the velocity are relatively weak, with the most noticeable exception occurring when an overtaking fast stream is observed in the back of the MC. Such fast flow can enter the MC, removing the linear temporal trend. We consider these overtaken MCs in a separate group as perturbed MCs (Fig. 2). We exclude from the analysis the MCs where the overtaking flow was extending more than half the MC size and MCs where the data gaps were too large. The remaining MCs are classified as non-perturbed, even if some of them have weak perturbations in their velocity profiles. These perturbations are filtered by considering only the major part of the velocity profile where the profile is almost linear with time (Fig. 1).
The group of non-perturbed MCs has a broad and typical range of
sizes and magnetic field strengths (![]() [0.1,0.75] AU and
[0.1,0.75] AU and
![]() [7,25] nT respectively when rescaled at 1 AU). They also
have a broad range of expansion velocities (
[7,25] nT respectively when rescaled at 1 AU). They also
have a broad range of expansion velocities (![]() [80,500] km s-1). Such a range of expansion velocity cannot be explained by the
range of observing distances, (D in [0.3,1] AU), since the
expansion velocity decreases only weakly within this range of D.
However, we found that the expansion velocity is proportional to the
MC size. By further analyzing the correlation between the observed
expansion velocity and other measured quantities, such as the MC
velocity, we empirically defined a non-dimensional expansion
coefficient
[80,500] km s-1). Such a range of expansion velocity cannot be explained by the
range of observing distances, (D in [0.3,1] AU), since the
expansion velocity decreases only weakly within this range of D.
However, we found that the expansion velocity is proportional to the
MC size. By further analyzing the correlation between the observed
expansion velocity and other measured quantities, such as the MC
velocity, we empirically defined a non-dimensional expansion
coefficient ![]() (Eq. (8)). For the non-perturbed MCs,
(Eq. (8)). For the non-perturbed MCs, ![]() is independent of all the other characteristics of the MCs
(such as size and field strength). Moreover, this empirical
definition of
is independent of all the other characteristics of the MCs
(such as size and field strength). Moreover, this empirical
definition of ![]() ,
obtained by removing the correlation in the
data between the expansion rate and other quantities, finally
defines the same
,
obtained by removing the correlation in the
data between the expansion rate and other quantities, finally
defines the same ![]() quantity as the one defined from
theoretical considerations by Démoulin et al. (2008). We conclude that
quantity as the one defined from
theoretical considerations by Démoulin et al. (2008). We conclude that ![]() characterizes the expansion rate of non-perturbed MCs.
characterizes the expansion rate of non-perturbed MCs.
For the non-perturbed MCs, we found that ![]() is confined to a
narrow interval:
is confined to a
narrow interval:
![]() .
This is consistent with the result
obtained at 1 AU for a set of 26 MCs observed by Wind and ACE
(Démoulin et al. 2008). Indeed, we found that
.
This is consistent with the result
obtained at 1 AU for a set of 26 MCs observed by Wind and ACE
(Démoulin et al. 2008). Indeed, we found that ![]() is independent of
solar distance (within [0.3,1] AU) in the Helios MCs.
is independent of
solar distance (within [0.3,1] AU) in the Helios MCs.
What is the origin of this common expansion rate of MCs?
Démoulin & Dasso (2009) have shown theoretically that the main origin of
MC expansion is the decrease of the total SW pressure with solar
distance D. With a SW pressure decreasing as
![]() ,
they
found that
,
they
found that
![]() independently of the magnetic
structure of the flux rope forming the MC. In the present work, we
re-analyzed the total SW pressure variation with D, revising
previous studies that also analyzed Helios data
(Schwenn 2006; Totten et al. 1995; Marsch et al. 1989; Mariani & Neubauer 1990). We found
independently of the magnetic
structure of the flux rope forming the MC. In the present work, we
re-analyzed the total SW pressure variation with D, revising
previous studies that also analyzed Helios data
(Schwenn 2006; Totten et al. 1995; Marsch et al. 1989; Mariani & Neubauer 1990). We found
![]() ,
which implies
,
which implies
![]() ,
in agreement with
our estimation of
,
in agreement with
our estimation of ![]() from the measured velocity in MCs. We then
confirm that the fast decrease of the total SW pressure with solar
distance is the main cause of the MC expansion rate.
from the measured velocity in MCs. We then
confirm that the fast decrease of the total SW pressure with solar
distance is the main cause of the MC expansion rate.
For MCs overtaken by a fast SW stream (or by another flux rope on
its back, e.g. Dasso et al. 2009), we minimize its importance in the
estimation of the MC expansion rate by considering only the part of
the velocity profile which is nearly linear with time. Still, the
mean computed ![]() for perturbed MCs is significantly lower than
the mean value for non-perturbed MCs, showing that the overtaking
flows have a more global effect on MCs (than the part where the
velocity profiles significantly depart from the linear temporal
behavior). A lower expansion rate is a natural consequence of the
compression induced by the overtaking flow.
for perturbed MCs is significantly lower than
the mean value for non-perturbed MCs, showing that the overtaking
flows have a more global effect on MCs (than the part where the
velocity profiles significantly depart from the linear temporal
behavior). A lower expansion rate is a natural consequence of the
compression induced by the overtaking flow.
More surprising, some perturbed MCs are found to expand faster
(larger ![]() )
than non-perturbed MCs. We conclude that such MC
are probably observed after the main interaction phase with the
overtaking flow, so that they expand faster than usual in order to
sustain an approximate pressure balance with the surrounding SW
(Fig. 6). More precisely, as the overtaking flow
disappears from the back of the MC, the MC is expected to tend
towards the size that it would have reached without the interaction
with the fast stream. Since it was compressed, it is expanding
faster than usual to return to its expected size in a normal SW.
)
than non-perturbed MCs. We conclude that such MC
are probably observed after the main interaction phase with the
overtaking flow, so that they expand faster than usual in order to
sustain an approximate pressure balance with the surrounding SW
(Fig. 6). More precisely, as the overtaking flow
disappears from the back of the MC, the MC is expected to tend
towards the size that it would have reached without the interaction
with the fast stream. Since it was compressed, it is expanding
faster than usual to return to its expected size in a normal SW.
5 Conclusions
Our present results confirm and extend our previous work on the expansion of MCs. The non-dimensional expansion factorHowever, for perturbed MCs, ![]() has a much broader range, a
result linked to its proportionality to the local expansion
velocity. So for perturbed MCs,
has a much broader range, a
result linked to its proportionality to the local expansion
velocity. So for perturbed MCs, ![]() is a measure of the local
expansion rate and of the importance of the overtaking stream (i.e.,
a quantification of the influence of the MC/stream interaction on
the expansion of the MC).
is a measure of the local
expansion rate and of the importance of the overtaking stream (i.e.,
a quantification of the influence of the MC/stream interaction on
the expansion of the MC).
Finally for non-perturbed MCs, ![]() is independent of the solar
distance in the inner heliosphere. Presently we do not know how far
this result extends to larger distances, even if it is an expected
result as long as the flux ropes still exist. This will be the subject of a future study.
is independent of the solar
distance in the inner heliosphere. Presently we do not know how far
this result extends to larger distances, even if it is an expected
result as long as the flux ropes still exist. This will be the subject of a future study.
We thank the referee for reading carefully, and improving the manuscript. The authors acknowledge financial support from ECOS-Sud through their cooperative science program (No. A08U01). This work was partially supported by the Argentinean grants: UBACyT X425 and PICTs 2005-33370 and 2007-00856 (ANPCyT). S.D. is member of the Carrera del Investigador Científico, CONICET. A.M.G. is a fellow of Universidad de Buenos Aires. M.E.R is a fellow of CONICET.
References
- Berdichevsky, D. B., Lepping, R. P., & Farrugia, C. J. 2003, Phys. Rev. E, 67, 036405 [NASA ADS] [CrossRef] [Google Scholar]
- Bothmer, V., & Schwenn, R. 1998, Annales Geophys., 16, 1 [Google Scholar]
- Burlaga, L., Berdichevsky, D., Gopalswamy, N., Lepping, R., & Zurbuchen, T. 2003, J. Geophys. Res., 108, A01425 [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
- Burlaga, L. F. 1995, Interplanetary magnetohydrodynamics (New York: Oxford University Press) [Google Scholar]
- Dasso, S., Mandrini, C. H., Démoulin, P., & Luoni, M. L. 2006, A&A, 455, 349 [Google Scholar]
- Dasso, S., Mandrini, C. H., Schmieder, B., et al. 2009, J. Geophys. Res., 114, A02109 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Nakwacki, M. S., Démoulin, P., & Mandrini, C. H. 2007, Sol. Phys., 244, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P., & Dasso, S. 2009, A&A, 498, 551 [Google Scholar]
- Démoulin, P., Nakwacki, M. S., Dasso, S., & Mandrini, C. H. 2008, Sol. Phys., 250, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Farrugia, C. J., Burlaga, L. F., Osherovich, V. A., et al. 1993, J. Geophys. Res., 98, 7621 [NASA ADS] [CrossRef] [Google Scholar]
- Farrugia, C. J., Osherovich, V. A., & Burlaga, L. F. 1997, Annales Geophysicae, 15, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, H. Q., Wu, D. J., & Chao, J. K. 2007, J. Geophys. Res., 112, A02102 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., Bame, S. J., McComas, D. J., et al. 1994, Geophys. Res. Lett., 21, 237 [Google Scholar]
- Gosling, J. T., Bame, S. J., McComas, D. J., et al. 1995, Space Sci. Rev., 72, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Gulisano, A. M., Dasso, S., Mandrini, C. H., & Démoulin, P. 2007, Adv. Spa. Res., 40, 1881 [CrossRef] [Google Scholar]
- Klein, L. W., & Burlaga, L. F. 1982, J. Geophys. Res., 87, 613 [Google Scholar]
- Leitner, M., Farrugia, C. J., Möstl, C., et al. 2007, J. Geophys. Res., 112, A06113 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Richardson, J. D., & Belcher, J. W. 2005, Planet. Space Sci., 53, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, B. J., Zurbuchen, T. H., Fisk, L. A., & Antiochos, S. K. 2003, J. Geophys. Res., 108, A01239 [NASA ADS] [CrossRef] [Google Scholar]
- Mandrini, C. H., Nakwacki, M., Attrill, G., et al. 2007, Sol. Phys., 244, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Mariani, F., & Neubauer, F. M. 1990, The Interplanetary Magnetic Field (Physics of the Inner Heliosphere I), 183 [Google Scholar]
- Marsch, E., Yao, S., & Tu, C.-Y. 2009, Annales Geophys., 27, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Schwenn, R., Rosenbauer, H., et al. 1982, J. Geophys. Res., 87, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Thieme, K. M., Rosenbauer, H., & Pilipp, W. G. 1989, J. Geophys. Res., 94, 6893 [Google Scholar]
- Nakwacki, M., Dasso, S., Démoulin, P., & Mandrini, C. H. 2008a, Geof. Int., 47, 295 [Google Scholar]
- Nakwacki, M., Dasso, S., Mandrini, C., & Demoulin, P. 2008b, J. Atmos. Sol. Terr. Phys., 70, 1318 [Google Scholar]
- Neubauer, F. M., Beinroth, H. J., Barnstorf, H., & Dehmel, G. 1977, J. Geophys., 42, 599 [Google Scholar]
- Osherovich, V. A., Farrugia, C. J., & Burlaga, L. F. 1993, J. Geophys. Res., 98, 13225 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I. G., & Cane, H. V. 1995, J. Geophys. Res., 100, 23397 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I. G., & Cane, H. V. 2004, J. Geophys. Res., 109, A09104 [Google Scholar]
- Rosenbauer, H., Schwenn, R., Marsch, E., et al. 1977, J. Geophys., 42, 561 [Google Scholar]
- Schwenn, R. 2006, Living Rev. Sol. Phys., 3, 2 [NASA ADS] [Google Scholar]
- Shimazu, H., & Vandas, M. 2002, Earth, Planets, and Space, 54, 783 [Google Scholar]
- Steed, K., Owen, C. J., Harra, L. K., et al. 2008, Annales Geophys., 26, 3159 [NASA ADS] [CrossRef] [Google Scholar]
- Totten, T. L., Freeman, J. W., & Arya, S. 1995, J. Geophys. Res., 100, 13 [Google Scholar]
- Tripathi, D., Solanki, S. K., Schwenn, R., et al. 2006, A&A, 449, 369 [Google Scholar]
- Tsurutani, B. T., Gonzalez, W. D., Zhou, X.-Y., Lepping, R. P., & Bothmer, V. 2004, J. Atmos. Sol. Terr. Phys., 66, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Vandas, M., Romashets, E. P., & Watari, S. 2005, in ed. B. Fleck, T. H. Zurbuchen, & H. Lacoste, Solar Wind 11/SOHO 16, Connecting Sun and Heliosphere, ESA SP-592, 159.1 (on CDROM) [Google Scholar]
- Wang, C., Du, D., & Richardson, J. D. 2005, J. Geophys. Res., 110, A10107 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, M., Zheng, H., Wu, S. T., Wang, Y., & Wang, S. 2007, J. Geophys. Res., 112, A011103 [Google Scholar]
- Yurchyshyn, V., Liu, C., Abramenko, V., & Krall, J. 2006, Sol. Phys., 239, 317 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Table 1: List of MC events.
All Figures
![\begin{figure}
\mbox{
\includegraphics[width=7cm, clip=]{figs/12375f1a.eps}\incl...
...5f1b.eps}\includegraphics[width=7cm, clip=]{figs/12375f1d.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg11.png)
|
Figure 1: Examples of two analyzed MCs that are not significantly perturbed by a fast flow. The MC center was observed at 07-Jan.-1975 10:39 and 04-Mar.-1975 21:37 UT, for panels a), c) and b), d), respectively. The vertical dashed lines define the MC boundaries. a), b) Vx is the observed velocity component in the radial direction from the Sun, expressed in km per second. The straight line is the linear least square fit of the velocity in the time interval where an almost linear trend is present (where the observations are presented as a solid line). The linear fitting is extrapolated to the borders of the MC, which are marked with circles. c), d) By is the magnetic field component, in nT, both orthogonal to the MC axis and to the spacecraft trajectory, while the solid line represents Fy, which is the accumulated flux of By (Eq. (7)). The extremum of Fy (proxy of the cloud center) is indicated with diamonds (a color version is available in the electronic version). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\mbox{\includegraphics[width=7cm, clip=]{figs/12375f2a.eps}\incl...
...75f2b.eps}\includegraphics[width=7cm, clip=]{figs/12375f2d.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg35.png)
|
Figure 2: Examples of two analyzed MCs that are perturbed by a fast flow as seen in the upper panels. The MC center was observed at 30-Jan.-1977 03:18 and 23-Jun.-1980 12:25 UT, for panels a), c) and b), d), respectively. The external perturbations enter in a significant part of the MCs. The same quantities, as in Fig. 1, are shown (a color version is available in the electronic version). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\mbox{\includegraphics[width=7.5cm, clip=]{figs/12375f3a.eps}\in...
...5f3c.eps}\includegraphics[width=7.5cm, clip=]{figs/12375f3d.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg46.png)
|
Figure 3:
The panels a)- d) show the correlation analysis between
proxies for MC expansion with different physical quantities. The
MCs are separated in two groups: perturbed (empty square symbol) and
non-perturbed (filled circle symbol). The straight lines are the
result of a least square fit for perturbed (dashed line),
non-perturbed (thin continuous line), and for both set of MCs in the
list of events shown in Table 1 (thick continuous
line).
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\mbox{\includegraphics[width=7cm, clip=]{figs/12375f4a.eps}\inclu...
...75f4c.eps}\includegraphics[width=7cm, clip=]{figs/12375f4d.eps} }
\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg58.png)
|
Figure 4:
Panels a)- d) show the correlation analysis that tests for the dependence of the non-dimensional
expansion factor |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
{\includegraphics[width=7.5cm, clip=]{figs/12375f5.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg78.png)
|
Figure 5:
Perturbed and non-perturbed MCs have a remarkably different
behavior of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
{
\includegraphics[width=7.5cm, clip=]{figs/12375f6.eps} }\end{figure}](/articles/aa/full_html/2010/01/aa12375-09/Timg85.png)
|
Figure 6: Cartoon of a possible evolution of the size of the MC with the helio-distance, showing the expected global expansion (thick solid line), an example of a non-perturbed MC (thin solid) and a perturbed MC (dashed line) (a color version is available in the electronic version). |
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
Log-log plots of the SW total pressure and its components
as a function of the solar distance. The solid line shows the least
square straight line fitted to the total pressure as computed from
the points marked with circles. The total pressure in the SW
decreases as
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.