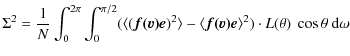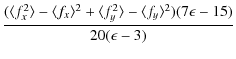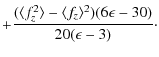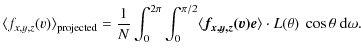| Issue |
A&A
Volume 508, Number 3, December IV 2009
|
|
|---|---|---|
| Page(s) | 1429 - 1442 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200913149 | |
| Published online | 04 November 2009 | |
A&A 508, 1429-1442 (2009)
3D simulations of M star atmosphere velocities and their influence on molecular FeH lines
S. Wende1 - A. Reiners1 - H.-G. Ludwig2
1 - Institut für Astrophysik, Georg-August-Universität
Göttingen, Friedrich-Hund Platz 1, 37077 Göttingen, Germany
2 -
GEPI, CIFIST, Observatoire de Paris-Meudon, 5 place Jules Janssen,
92195 Meudon Cedex, France
Received 19 August 2009 / Accepted 13 October 2009
Abstract
Context. The measurement of line broadening in cool stars is
in general a difficult task. In order to detect slow rotation or weak
magnetic fields, an accuracy of 1 km s-1 is
needed. In this regime the broadening from convective motion becomes
important. We present an investigation of the velocity fields in early
to late M-type star hydrodynamic models, and we simulate their
influence on FeH molecular line shapes. The M star model parameters
range between ![]() of 3.0-5.0 and effective temperatures from 2500 K to 4000 K.
of 3.0-5.0 and effective temperatures from 2500 K to 4000 K.
Aims. Our aim is to characterize the
![]() - and
- and ![]() -dependence
of the velocity fields and express them in terms of micro- and
macro-turbulent velocities in the one dimensional sense. We present a
direct comparison between 3D hydrodynamical velocity fields and 1D
turbulent velocities. The velocity fields strongly affect the line
shapes of FeH, and it is our goal to give a rough estimate of the
-dependence
of the velocity fields and express them in terms of micro- and
macro-turbulent velocities in the one dimensional sense. We present a
direct comparison between 3D hydrodynamical velocity fields and 1D
turbulent velocities. The velocity fields strongly affect the line
shapes of FeH, and it is our goal to give a rough estimate of the ![]() and
and
![]() parameter range in which 3D spectral synthesis is necessary and
where 1D synthesis suffices. We want to distinguish between the
velocity-broadening from convective motion and the rotational- or
Zeeman-broadening in M-type stars we are planning to measure. For the
latter, FeH lines are an important indicator.
parameter range in which 3D spectral synthesis is necessary and
where 1D synthesis suffices. We want to distinguish between the
velocity-broadening from convective motion and the rotational- or
Zeeman-broadening in M-type stars we are planning to measure. For the
latter, FeH lines are an important indicator.
Methods. In order to calculate M-star structure models, we employ the 3D radiative-hydrodynamics (RHD) code CO5BOLD. The spectral synthesis in these models is performed with the line synthesis code LINFOR3D.
We describe the 3D velocity fields in terms of a Gaussian standard
deviations and project them onto the line of sight to include
geometrical and limb-darkening effects. The micro- and macro-turbulent
velocities are determined with the ``curve of growth'' method and
convolution with a Gaussian velocity profile, respectively. To
characterize the ![]() and
and
![]() dependence of FeH lines, the equivalent width, line width, and line depth are examined.
dependence of FeH lines, the equivalent width, line width, and line depth are examined.
Results. The velocity fields in M-stars strongly depend on ![]() and
and
![]() .
They become stronger with decreasing
.
They become stronger with decreasing ![]() and increasing
and increasing
![]() .
The projected velocities from the 3D models agree within
.
The projected velocities from the 3D models agree within ![]() 100 m s-1 with the 1D micro- and macro-turbulent velocities. The FeH line quantities systematically depend on
100 m s-1 with the 1D micro- and macro-turbulent velocities. The FeH line quantities systematically depend on ![]() and
and
![]() .
.
Conclusions. The influence of hydrodynamic velocity fields on
line shapes of M-type stars can well be reproduced with 1D broadening
methods. FeH lines turn out to provide a means to measure ![]() and
and
![]() in M-type stars. Since different FeH lines all behave in a similar
manner, they provide an ideal measure for rotational and magnetic
broadening.
in M-type stars. Since different FeH lines all behave in a similar
manner, they provide an ideal measure for rotational and magnetic
broadening.
Key words: hydrodynamics: stars: low-mass, brown dwarfs - line: profiles - turbulence - stars: late-type
1 Introduction
Most of our knowledge about stars comes from spectroscopic investigation of atomic or molecular lines. In sun-like and hotter stars, the strength and shape of atomic spectral lines provides information on atmospheric structure, velocity fields, rotation, magnetic fields, etc. Measuring the effects of velocity fields on the shape of spectral lines requires a spectral resolving power betweenIn slowly rotating sun-like stars, usually a large number of relatively isolated spectral lines are available for the investigation of Doppler broadened spectral lines. These lines are embedded in a clearly visible continuum allowing a detailed analysis of individual lines at high precision. At cooler temperature, the number of atomic lines increases so that more and more lines become blended, rendering the investigation of individual lines more difficult. At temperatures around 4000 K, molecular lines, predominantly VO and TiO, start to become important. At optical wavelengths, molecular bands in general consist of many lines that are blended so that the absorption mainly appears as an absorption band; individual molecular lines are difficult to identify. At temperatures in the M type star regime (4000 K and less), atomic lines start to vanish because atoms are mainly neutral and higher ionization levels are weakly populated. Only alkali lines appear that are strongly affected by pressure broadening. Thus, the detailed spectroscopic investigation of velocity fields in M dwarfs is very difficult at optical wavelengths.
Table 1:
Overview of different model quantities for models at constant
![]() and different
and different ![]() (upper part) and at constant
(upper part) and at constant
![]() and different
and different
![]() (lower part).
(lower part).
Examples of analyses using FeH lines are the investigation of the rotation activity connection in field M-dwarfs, which requires the measurement of rotational line broadening with an accuracy of 1 km s-1(Reiners 2007). Another example is the measurement of magnetic fields comparing Zeeman broadening in magnetically sensitive and insensitive absorption lines (see e.g. Reiners & Basri 2006). A precise analysis of FeH lines, however, is only possible if the underlying velocity fields of the M dwarf atmospheres are thoroughly understood. In this paper, we model the surface velocity fields of M type stars and their influence on the narrow spectral lines of FeH.
We calculate 3D-CO5BOLD structure models
(Ludwig et al. 2002) which serve as an input for the line
formation program LINFOR3D (based on Baschek et al. 1966).
Turbulence is included in a natural way using hydrodynamics, so
that we are able to investigate the modeled spectral lines for effects
from micro- and macro-turbulent velocities in the classical sense and
their influence on the line shapes. The comparison with 1D-models
gives a rough estimate of the necessity of using 3D-models in the
spectral domain of cool stars. In the first part of this paper, we
investigate the velocity fields in the models and their dependence on
![]() and
and
![]() .
In the second part, we investigate the
influence of velocity fields,
.
In the second part, we investigate the
influence of velocity fields, ![]() ,
and
,
and
![]() on the
FeH molecular lines.
on the
FeH molecular lines.
2 3D model atmospheres
The three-dimensional time-dependent model atmospheres (hereafter ``3D models'') are calculated with the radiation-hydrodynamics code CO5BOLD (abbreviation for ``COnservative COde for the COmputation of COmpressible COnvection in a BOx of L Dimensions with L=2, 3''). It is designed to model solar and stellar surface convection. For sun-like stars like the M-type objects considered here, CO5BOLD employs a local set-up in which the governing equations are solved in a small (relative to the stellar radius) Cartesian domain located at the stellar surface (``box in a star set-up''). The optically thin stellar photosphere and the upper-most part of the underlying convective envelope are embedded in the computational domain. CO5BOLD solves the coupled non-linear equations of compressible hydrodynamics in an external gravitational field in three spatial dimensions (Freytag et al. 2002; Wedemeyer et al. 2004), together with non-local frequency-dependent radiative transfer. In these 3D models, convection is treated without any assumptions as in 1D mixing-length theory. The velocity fields and their related transport properties are a direct result of the solution of the hydrodynamic equations. Due to this, CO5BOLD is a well-suited tool to investigate the influence of velocity fields on spectral line shapes. A CO5BOLD model consists of a sequence of 3D flow fields (``snapshots'') representing the temporal evolution and spatial structure of the flow. To perform spectral synthesis calculations based on the 3D CO5BOLD-models, we use the 3D line formation code Linfor3D. It takes into account the full 3D thermal structure and velocity field in the calculation of the line profiles. It assumes strict Local Thermodynamic Equilibrium (LTE). In this paper, we will call the spectral lines computed from three-dimensional atmosphere models ``3D-lines''.
In order to analyze the influence of velocity fields in M-stars on
FeH lines, we construct a set of CO5BOLD-models with
![]() K-4000 K and
K-4000 K and
![]() [cgs]. Table 1
gives the model parameters. In the
[cgs]. Table 1
gives the model parameters. In the
![]() -sequence, we simulated
main sequence stars and varied the surface gravity slightly with increasing
effective temperature. For the
-sequence, we simulated
main sequence stars and varied the surface gravity slightly with increasing
effective temperature. For the ![]() -sequence, we computed models with
different
-sequence, we computed models with
different ![]() values aiming at the same effective temperature of
3300 K but the models settle to slightly higher or lower
values aiming at the same effective temperature of
3300 K but the models settle to slightly higher or lower
![]() values. We
decided not to adjust these resulting effective temperatures, because slight
differences in
values. We
decided not to adjust these resulting effective temperatures, because slight
differences in
![]() do not change the line profiles significantly. We
accepted the
do not change the line profiles significantly. We
accepted the
![]() deviations to
avoid the large computational effort which would be necessary to adjust the
models to a common effective temperature. However,
we apply corrections to the line shape related quantities such as equivalent width
(see Sect. 4.3).
deviations to
avoid the large computational effort which would be necessary to adjust the
models to a common effective temperature. However,
we apply corrections to the line shape related quantities such as equivalent width
(see Sect. 4.3).
The opacities used in the CO5BOLD model calculations originate
from the PHOENIX stellar atmosphere package
(Hauschildt & Baron 1999) assuming a solar chemical composition according to
Asplund et al. (2005). The opacity tables were computed after
Ferguson et al. (2005) and Freytag et al. (2009). These opacities are particularly
well-suited for our investigation since they are adapted to very cool stellar
atmospheres. The raw data consist of opacities sampled at 62 890 wavelength
points for a grid of temperatures and gas pressures. to represent the
wavelength dependence of the radiation field in the CO5BOLD models,
the opacities are re-sampled into six wavelength groups using the opacity
binning method
(Nordlund 1982; Ludwig et al. 1994; Ludwig 1992).
In this approach, the frequencies that reach monochromatic optical
depth unity within a certain depth range of the model atmosphere will
be grouped into one frequency bin on the basis of their opacities.
For each investigated atmospheric parameter combination, the sorting of the
wavelengths into groups is performed according the run of monochromatic
optical depth in a corresponding PHOENIX 1D model atmosphere. The
thresholds for the sorting are chosen in logarithmic Rosseland optical depth
as
![]() .
In each group a
switching is done from a Rosseland average in the optically thick regime to a
Planck average in the optically thin regime, except for the group representing
the highest opacities, where the Rosseland average is used throughout. In this
last bin, which describes the optically thick regions, only the Rosseland average is
used because the radiative transfer
is local and can be described as a diffusive process (Vögler et al. 2004).
.
In each group a
switching is done from a Rosseland average in the optically thick regime to a
Planck average in the optically thin regime, except for the group representing
the highest opacities, where the Rosseland average is used throughout. In this
last bin, which describes the optically thick regions, only the Rosseland average is
used because the radiative transfer
is local and can be described as a diffusive process (Vögler et al. 2004).
The horizontal size of the models provide, sufficient space to allow the
development of a small number (10-20) of convective cells. Their number has
to be large enough to avoid box-size dependent effects, but also small
enough that there is a sufficient number of grid points available to resolve
each individual cell. The size of the convective cells scales roughly
inversely proportional to the surface gravity. Accordingly, the horizontal size
of the computational box is set to larger sizes towards lower ![]() values.
The horizontal size of the model with
values.
The horizontal size of the model with
![]() K is just large enough to
fulfill the criteria of the minimal number of 10 convective cells (see
Fig. 5), and we saw in
test simulations that the results will not change with a larger model (in
horizontal size). Therefore we will use this well evolved model as well.
The vertical dimension is set to embed the optically thin photosphere, and a
number of pressure scale heights of the sub-photospheric layers below. We
deliberately
keep the depth of our models rather small to avoid problems due to
numerical instabilities analogous to the ones encountered and discussed in our
previous works on the hydrodynamics of M-type stellar atmospheres
(Ludwig et al. 2006,2002).
K is just large enough to
fulfill the criteria of the minimal number of 10 convective cells (see
Fig. 5), and we saw in
test simulations that the results will not change with a larger model (in
horizontal size). Therefore we will use this well evolved model as well.
The vertical dimension is set to embed the optically thin photosphere, and a
number of pressure scale heights of the sub-photospheric layers below. We
deliberately
keep the depth of our models rather small to avoid problems due to
numerical instabilities analogous to the ones encountered and discussed in our
previous works on the hydrodynamics of M-type stellar atmospheres
(Ludwig et al. 2006,2002).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f01.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg53.png)
|
Figure 1:
From top to bottom, the temperature, entropy, vertical, and horizontal velocity
are plotted as a function of optical depth. The column on the left side shows models with
different
|
| Open with DEXTER | |
For the comparison with 1D models, we spatially average the 3D-model over
surfaces of equal Rosseland optical depth at selected instants in time. We
call the obtained sequence of 1D structures the
![]() -model. We follow the procedure
of Steffen et al. (1995) and average the fourth moment of the temperature
and first moment of the gas pressure to preserve the radiative properties of
the 3D-model as far as possible. The 3D velocity information is ignored in the
-model. We follow the procedure
of Steffen et al. (1995) and average the fourth moment of the temperature
and first moment of the gas pressure to preserve the radiative properties of
the 3D-model as far as possible. The 3D velocity information is ignored in the
![]() -model and replaced by a micro- and macro-turbulent velocity. By
construction, the
-model and replaced by a micro- and macro-turbulent velocity. By
construction, the
![]() -model has the same thermal profile as the 3D-model, but
evidently without the horizontal inhomogeneities related to the convective
granulation pattern. We will call the spectral lines synthesized from
-model has the same thermal profile as the 3D-model, but
evidently without the horizontal inhomogeneities related to the convective
granulation pattern. We will call the spectral lines synthesized from
![]() -models ``
-models ``
![]() -lines''.
-lines''.
2.1 Atmosphere structures
The temperature stratification shown in Fig. 1 (top left) of the models with changingThe entropy stratification for models with varying
![]() (mid left in
Fig. 1) shows a similar behavior for all models. It is adiabatic
(d
(mid left in
Fig. 1) shows a similar behavior for all models. It is adiabatic
(d
![]() )
in layers below
)
in layers below
![]() and has a superadiabatic
region (d
and has a superadiabatic
region (d
![]() )
between
)
between
![]() and
and
![]() that moves
slightly towards smaller optical depth for hotter models. In these regions, with
d
that moves
slightly towards smaller optical depth for hotter models. In these regions, with
d
![]() ,
the models are convectively unstable and become
convectively stable in the outer parts of the atmosphere where d
,
the models are convectively unstable and become
convectively stable in the outer parts of the atmosphere where d
![]() .
In the models with changing
.
In the models with changing ![]() (mid right in Fig. 1),
we can see that the entropy behaves almost as in the
(mid right in Fig. 1),
we can see that the entropy behaves almost as in the
![]() case. At lower
surface gravities, the superadiabatic region is more significant. In higher
layers, the models become convectively stable except for the model with
case. At lower
surface gravities, the superadiabatic region is more significant. In higher
layers, the models become convectively stable except for the model with
![]() [cgs] which shows a second decrease of entropy in the outer
layers. To understand this behavior, we have to investigate the
adiabatic gradient of this region which is very small and changes very little
along the upper atmosphere. This is due to the equation of state used in the
models and can be seen in Fig. 16 of
Ludwig et al. (2006) (model H4 in this figure equates to our
[cgs] which shows a second decrease of entropy in the outer
layers. To understand this behavior, we have to investigate the
adiabatic gradient of this region which is very small and changes very little
along the upper atmosphere. This is due to the equation of state used in the
models and can be seen in Fig. 16 of
Ludwig et al. (2006) (model H4 in this figure equates to our
![]() model). This figure shows that the upper atmosphere lies in a plane of
small and constant adiabatic gradient. Due to this, the model becomes
convectively unstable again in the upper layers. This is probably the reason
for the, higher velocities in this model, in comparison to other models.
model). This figure shows that the upper atmosphere lies in a plane of
small and constant adiabatic gradient. Due to this, the model becomes
convectively unstable again in the upper layers. This is probably the reason
for the, higher velocities in this model, in comparison to other models.
In the left bottom panel of Fig. 1, the
horizontal and vertical rms-velocities are plotted for models with different
![]() .
Both velocity components increase with increasing
.
Both velocity components increase with increasing
![]() .
The maxima
of the vertical velocity moves to slightly deeper layers with higher
temperatures and the maxima of the horizontal velocity stays almost at the
same optical depth. We can see a qualitatively similar dependence in the
.
The maxima
of the vertical velocity moves to slightly deeper layers with higher
temperatures and the maxima of the horizontal velocity stays almost at the
same optical depth. We can see a qualitatively similar dependence in the
![]() model sequence in the right bottom plot in Fig. 1. Only
the model with
model sequence in the right bottom plot in Fig. 1. Only
the model with
![]() [cgs] shows peculiar behavior in the upper
atmospheric layers, which is probably related to the entropy stratification in
this model. We will describe the velocity fields in the models in more detail
and with a slightly different method in the next section.
[cgs] shows peculiar behavior in the upper
atmospheric layers, which is probably related to the entropy stratification in
this model. We will describe the velocity fields in the models in more detail
and with a slightly different method in the next section.
3 Velocity fields in the CO5BOLD-models
Before we investigate the effect of velocity fields on spectral lines, we
analyze the velocity fields in the models themselves and we will do this
relative to the broadening of spectral lines. Spectral lines are broadened by velocity fields
where the wavelength of absorption or emission of a particle is shifted due to
its motion in the gas. Here we are mostly concerned with the macroscopic,
hydrodynamic motion but have in mind that thermal motion also
constitutes a significant contribution. If we consider each voxel in the RHD
model cube to form its own spectral line, the whole line consists of a
(weighted) sum of single lines. The velocity distribution might be
represented by a histogram of the velocities of the voxels which gives us the
velocity dispersion. We try to describe the velocity fields in that sense
instead of using the rms-velocities shown in Fig. 1. In the
CO5BOLD-models, a velocity vector is assigned to each voxel and
consists of the velocities in the x-, y-, and z-direction. We will investigate the
vertical and horizontal component of the velocity dispersion in the models and
the total velocity dispersion
![]() .
In order to describe the height-dependent velocity dispersion, we applied a binning method,
i.e. we plot all velocity components of a certain horizontal plane of equal
optical depth
.
In order to describe the height-dependent velocity dispersion, we applied a binning method,
i.e. we plot all velocity components of a certain horizontal plane of equal
optical depth ![]() in the CO5BOLD cube in a histogram with a bin
size of 25 m s-1.
in the CO5BOLD cube in a histogram with a bin
size of 25 m s-1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{pictures/13149f02.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg67.png)
|
Figure 2:
Histogram of the
velocity distribution in the vertical direction. The normalized number of points
is plotted against the vertical velocity in m/s (solid line).
The Gaussian (dashed line) fits the velocity distribution and
determined an FWHM value (dashed-dotted line), which is related to |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{pictures/13149f03.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg71.png)
|
Figure 3:
Upper panel: radial ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{pictures/13149f04.ps}\par
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg74.png)
|
Figure 4:
Upper panel: radial ( |
| Open with DEXTER | |
In Fig.4 we can see at lower
surface gravities that the maxima of the horizontal velocity dispersion are not centered
around a specified optical depth any longer; it spreads out in the vertical direction
and spans the widest range at
![]() [cgs]. The pressure stratification
changes, and the convective turn-over point moves to lower gas-pressure (not
shown here) but stays at almost constant optical depth between
[cgs]. The pressure stratification
changes, and the convective turn-over point moves to lower gas-pressure (not
shown here) but stays at almost constant optical depth between
![]() and
and
![]() .
With varying
temperature, the position of the convective
turn-over point stays at almost constant optical depth.
.
With varying
temperature, the position of the convective
turn-over point stays at almost constant optical depth.
3.1 Reduction of the 3D velocity fields
Commonly, micro- and macro-turbulence derived from spectroscopy
are interpreted as being associated with actual velocity fields present in the
stellar atmosphere. In our simulations, no oscillations are induced
externally but small oscillations are generated in the simulations itself. The
velocity amplitudes of these oscillations reach a maximum of ![]() of the
convective velocities and have no significant influence on the
macro-turbulent velocity. We would also not expect global oscillations for
these objects, except for young stars with solar masses lower than 0.1
of the
convective velocities and have no significant influence on the
macro-turbulent velocity. We would also not expect global oscillations for
these objects, except for young stars with solar masses lower than 0.1 ![]() induced by D-burning (Palla & Baraffe 2005). In the following, we try to make the connection
between micro- and macro-turbulence and actual hydrodynamical velocity fields
by considering the velocity dispersion determined directly from the
hydrodynamical model data, and comparing it with the micro- and macro-turbulence
derived from synthesized spectral lines (see Sect. 3.2). This connection is
algebraically not simple, and we only apply a simple model to translate
the hydrodynamical velocities into turbulent velocities relevant to
spectroscopy (see Appendix). When interpreting the comparisons shown below,
the very approximate nature of our model should be kept in mind. In
this model, we include the geometric projection of the components of
induced by D-burning (Palla & Baraffe 2005). In the following, we try to make the connection
between micro- and macro-turbulence and actual hydrodynamical velocity fields
by considering the velocity dispersion determined directly from the
hydrodynamical model data, and comparing it with the micro- and macro-turbulence
derived from synthesized spectral lines (see Sect. 3.2). This connection is
algebraically not simple, and we only apply a simple model to translate
the hydrodynamical velocities into turbulent velocities relevant to
spectroscopy (see Appendix). When interpreting the comparisons shown below,
the very approximate nature of our model should be kept in mind. In
this model, we include the geometric projection of the components of
![]() to the line of sight of the observer. We also have to
consider the effect of limb-darkening of the stellar disk. For
each velocity dispersion component, we calculate a projection factor which includes both
geometrical projection and limb-darkening effects (more described in the
Appendix). We take a limb-darkening coefficient of 0.4 which
follows from the continuum from the angle dependent line synthesis performed in
LINFOR3D. These simulations suggest that a linear limb-darkening law
with a limb-darkening coefficient of 0.4 is suited to describe the
brightness variation. The projected velocity dispersions are also plotted in
Figs. 3 and 4 (red solid and dotted lines). The
reducing effect of this projection factor is stronger in the horizontal
components than in the vertical because the projected area at the limb of the
stellar disk, where
to the line of sight of the observer. We also have to
consider the effect of limb-darkening of the stellar disk. For
each velocity dispersion component, we calculate a projection factor which includes both
geometrical projection and limb-darkening effects (more described in the
Appendix). We take a limb-darkening coefficient of 0.4 which
follows from the continuum from the angle dependent line synthesis performed in
LINFOR3D. These simulations suggest that a linear limb-darkening law
with a limb-darkening coefficient of 0.4 is suited to describe the
brightness variation. The projected velocity dispersions are also plotted in
Figs. 3 and 4 (red solid and dotted lines). The
reducing effect of this projection factor is stronger in the horizontal
components than in the vertical because the projected area at the limb of the
stellar disk, where
![]() reaches its maximum value, is much smaller
than in the center where
reaches its maximum value, is much smaller
than in the center where ![]() has its maximum value. The influence of
limb-darkening is not strong and the dependence of the projection
factor from the limb-darkening coefficient is only small (described in more
detail in the Appendix).
has its maximum value. The influence of
limb-darkening is not strong and the dependence of the projection
factor from the limb-darkening coefficient is only small (described in more
detail in the Appendix).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f05.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg91.png)
|
Figure 5:
Horizontal cross-section around
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f06.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg93.png)
|
Figure 6:
2D cross-section in x-z direction of the x-z velocity
in a model with
|
| Open with DEXTER | |
3.1.1 Weighted velocities
To investigate the influence
of broadening from the projected and unprojected velocity dispersion on spectral
lines, we use contribution functions for the equivalent width
![]() and the depression at the line center of an
FeH line at
and the depression at the line center of an
FeH line at
![]() (Magain 1986). The line gains its
(Magain 1986). The line gains its
![]() and
depression in the region between
and
depression in the region between
![]() and
and
![]() ,
i.e. that is the region of main continuum absorption caused by FeH molecules.
The maximum is roughly centered around
,
i.e. that is the region of main continuum absorption caused by FeH molecules.
The maximum is roughly centered around
![]() and moves
to slightly lower optical depth with lower temperatures (at
the lowest
and moves
to slightly lower optical depth with lower temperatures (at
the lowest
![]() of 2575 K, the maximum is centered around
of 2575 K, the maximum is centered around
![]() )
or
higher surface gravities.
The contribution function of
)
or
higher surface gravities.
The contribution function of
![]() ranges over the region of the convection zone and reflects its
influence on the line shape. Due to the latter fact, FeH lines
are a good means to explore the convective regions in M-dwarfs. In order to
measure the velocities in the region where the lines originate, we compute the
mean of the (projected) velocities weighted by the contribution function of
ranges over the region of the convection zone and reflects its
influence on the line shape. Due to the latter fact, FeH lines
are a good means to explore the convective regions in M-dwarfs. In order to
measure the velocities in the region where the lines originate, we compute the
mean of the (projected) velocities weighted by the contribution function of
![]() .
.
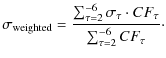
|
(1) |
The horizontal and vertical components of these weighted velocity dispersions are plotted in Figs. 7 and 8. We can see an increase of
The strong increase of the velocity dispersions in the atmospheres to higher layers
(Figs. 3 and 4) which some
models show is related to convective overshoot into formally stable
layers. These velocities are generated by waves excited by
stochastic fluid motion and by advective motion
(Ludwig et al. 2002, and references therein).
However, it will not affect the spectral lines, because
the lines are generated in the region between an optical depth of
![]() and
and
![]() .
The lines in the model with
.
The lines in the model with
![]() K are an
exception, they are formed in the outermost layers of the model and it is not
possible to compute the full range of formation of these lines, because the
atmosphere is not extended enough. One has to keep this in mind when regarding
the line dependent results of this model later in this chapter.
K are an
exception, they are formed in the outermost layers of the model and it is not
possible to compute the full range of formation of these lines, because the
atmosphere is not extended enough. One has to keep this in mind when regarding
the line dependent results of this model later in this chapter.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f07.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg103.png)
|
Figure 7:
The weighted projected and unprojected velocity dispersions
of the horizontal and vertical component for models with different
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f08.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg106.png)
|
Figure 8:
The weighted projected and unprojected velocity dispersions
of the horizontal and vertical component for
models with different |
| Open with DEXTER | |
Table 2:
Displacement
![]() and
and
![]() in m/s of the position of an FeH line from the rest wavelength
in models with different
in m/s of the position of an FeH line from the rest wavelength
in models with different
![]() (left side) and different
(left side) and different ![]() (right side).
(right side).
3.2 Radial velocity shifts
Due to the fact that in convective motion the up-flowing area is larger, because it is hotter and less dense than the down-flowing one, one expects a net shift of the velocity distribution to positive velocities. That means the net amount of up-flowing area with hotter temperature, i.e. more flux in comparison to the down-flowing area, results in a blue shift in the rest wavelength position of a spectral line (see e.g. Dravins 1982).
To see how the area of up-flowing material affects the rest
wavelength position of a spectral line, we computed ten FeH
spectral lines (described in Sect. 4) in 3D models to measure the
displacement of the line positions. In order to determine the center of the
line, we used the weighted mean
![]() which accounts for the asymmetric line shape.
(To use the weighted mean is appropriate here since we have no
noise in the computed data.) The line shifts of the flux and the
intensity are given in Table 2. A negative value stands for a
blue shift, and a positive for a red shift.
The values for each model are the mean of five temporal snapshots.
The absolute displacement of the flux and intensity in the
which accounts for the asymmetric line shape.
(To use the weighted mean is appropriate here since we have no
noise in the computed data.) The line shifts of the flux and the
intensity are given in Table 2. A negative value stands for a
blue shift, and a positive for a red shift.
The values for each model are the mean of five temporal snapshots.
The absolute displacement of the flux and intensity in the ![]() series reflects the
dependence of the velocity fields on surface gravity, but for the
series reflects the
dependence of the velocity fields on surface gravity, but for the
![]() series a connection is barely visible (see Figs. 7
and 8). This could be due to the small geometrical size of
the atmospheres in the
series a connection is barely visible (see Figs. 7
and 8). This could be due to the small geometrical size of
the atmospheres in the
![]() series (see Table 1). Only the the one with
series (see Table 1). Only the the one with
![]() K
shows a significant line shift and in this model the atmosphere is 1150 km
high due to the slightly smaller
K
shows a significant line shift and in this model the atmosphere is 1150 km
high due to the slightly smaller ![]() value of 4.5 [cgs]. At this point
we will not continue with a deeper analysis of this topic.
value of 4.5 [cgs]. At this point
we will not continue with a deeper analysis of this topic.
Since we only use
five snapshots, we are dealing with statistics of small numbers and hence a
large scatter in the results. This scatter
![]() is in general one order
lower than the shift of the line and the integrated jitter of the line, which is
important for radial-velocity measurements, scales as
is in general one order
lower than the shift of the line and the integrated jitter of the line, which is
important for radial-velocity measurements, scales as
![]() ,
where N is the number of snapshots. Since in a
star N is of
the order of 106, the jitter will be of the order of mm s-1.
,
where N is the number of snapshots. Since in a
star N is of
the order of 106, the jitter will be of the order of mm s-1.
We did not further investigate the effect of granulation patterns on the line profiles but, as we will see below, the lines are almost Gaussian and show no direct evidence for significant granulation effects.
3.3 Micro- and macro-turbulent velocities
Due to the large amount of CPU time required to compute 3D RHD models and spectral lines in these models, we study the necessity of 3D models in the range of M-stars. Our goal is to compare the broadening effects of the 3D velocity fields on the shape of spectral lines with the broadening in terms of the classical micro- and macro-turbulence profiles (see e.g. Gray 2008,1977). The latter description is commonly used in 1D atmosphere models like ATLAS9 (Kurucz 1970) or PHOENIX and related line formation codes. If the difference between 1D and 3D velocity broadening is small, the usage of fast 1D atmosphere codes to simulate M-stars for comparison with observations, e.g. to determine rotational- or Zeeman-broadening, would be an advantage.
If the size of a turbulent element is small compared to unit optical depth,
we are in the regime of micro-turbulence. The micro-turbulent velocities
might differ strongly from one position to another and have a
statistical nature. The broadening effect on spectral lines can be described
with a Gaussian which enters the line absorption coefficient
(Gray 2008).
It can be treated similarly to the thermal
Doppler broadening. The effect on the shapes of saturated lines is an enhancement of line wings
due to the fact that at higher velocities the absorption cross section increases and as a consequence
the equivalent width (
![]() )
of the line is increased.
)
of the line is increased.
If the size of a turbulent element is large compared to unit optical depth (or of the same size), we are in the regime of macro-turbulence. This can be treated similarly to rotational broadening as a global broadening of spectral lines. The effect is an increase of the line width but the equivalent width remains constant.
As we saw before, the velocity fields in M-stars are not very strong in comparison to the sound speed (see Table 2) and one could expect that their influence on line shapes does not deviate strongly from Gaussian broadening.
We compared line broadening with the radial-tangential profile from
Gray (1975) and a simple Gaussian profile and found that the
latter is a good approximation with an accuracy high enough for
determination of rotational- or Zeeman-broadening. Hence, in this
investigation we will assume Gaussian broadening profiles. That means, that we
can assume a height-independent isotropic velocity distribution for micro-
and macro-turbulent velocities. This is a
very convenient way to simulate the velocity fields. One would expect that
the anisotropic nature and the height dependence of the hydrodynamical
velocity fields have a significant influence on line shapes, so it is remarkable that
their influence on spectral lines can be described with high
accuracy in this way (at least in the investigated M-type stars). In
Fig. 9, a few examples of
![]() - FeH spectral lines
are plotted, which were computed with a given micro-turbulent velocity
(determined below) and then convolved with a Gaussian broadening profile with a given
macro-turbulent velocity. The broadened
- FeH spectral lines
are plotted, which were computed with a given micro-turbulent velocity
(determined below) and then convolved with a Gaussian broadening profile with a given
macro-turbulent velocity. The broadened
![]() - FeH lines fit the
3D- FeH lines very well. The difference in the 1D and 3D centroid
(
- FeH lines fit the
3D- FeH lines very well. The difference in the 1D and 3D centroid
(
![]() )
is of the order of m/s for small
velocity fields up to 30-40 m s-1 for strong velocity fields in hot M star models
or with low
)
is of the order of m/s for small
velocity fields up to 30-40 m s-1 for strong velocity fields in hot M star models
or with low ![]() .
The error in flux is less than
.
The error in flux is less than ![]() (see
Fig. 9); this corresponds to an uncertainty in velocity, for example rotational
velocity, of less than 150 m s-1 depending on the position on the line.
It is also visible in Fig. 9 that at low
effective temperature, effects from velocity broadening are not visible in
comparison with an unbroadened
(see
Fig. 9); this corresponds to an uncertainty in velocity, for example rotational
velocity, of less than 150 m s-1 depending on the position on the line.
It is also visible in Fig. 9 that at low
effective temperature, effects from velocity broadening are not visible in
comparison with an unbroadened
![]() -line in which the van de Waals broadening is
dominant. At higher effective temperatures, the difference between broadened
and unbroadened
-line in which the van de Waals broadening is
dominant. At higher effective temperatures, the difference between broadened
and unbroadened
![]() -lines is clearly visible. We found that in the range of
M-type stars, 1D spectral synthesis of
FeH-lines using
micro- and macro-turbulent velocities in the classical description is
sufficient to include the effects of the velocity fields.
In the following we will determine the velocities needed.
-lines is clearly visible. We found that in the range of
M-type stars, 1D spectral synthesis of
FeH-lines using
micro- and macro-turbulent velocities in the classical description is
sufficient to include the effects of the velocity fields.
In the following we will determine the velocities needed.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f9a.ps} \includegraphics[width=9cm,clip]{pictures/13149f9b.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg113.png)
|
Figure 9:
FeH lines for models with
|
| Open with DEXTER | |
3.3.1 Determination of micro- and macro-turbulent velocities
Investigation of the micro-turbulent velocities was done with the
curve of growth (CoG) method (e.g., Gray 2008). We
artificially increase the line strength of an absorption-line (increase the
![]() value), which in turn increases the saturation of the line and its
influence on the micro-turbulent velocity, which results in an enhancement of
value), which in turn increases the saturation of the line and its
influence on the micro-turbulent velocity, which results in an enhancement of
![]() .
In order to determine micro-turbulent-velocities, we use
Fe I- and FeH-lines produced in
.
In order to determine micro-turbulent-velocities, we use
Fe I- and FeH-lines produced in
![]() -models with different
micro-turbulent velocities (there are no differences in micro-turbulent
velocities between either type of line), i.e. for each
-models with different
micro-turbulent velocities (there are no differences in micro-turbulent
velocities between either type of line), i.e. for each ![]() -value we
compute a
-value we
compute a
![]() -line with micro-turbulent velocities between 0 km s-1and 1 km s-1 in 0.125 km s-1 steps. In this way we obtained
CoGs for 9 different micro-turbulent velocities. We compare the equivalent
widths in the CoGs with the ones computed in the 3D-models and
selected the velocity of the CoG which fits the 3D CoG best in the sense of
-line with micro-turbulent velocities between 0 km s-1and 1 km s-1 in 0.125 km s-1 steps. In this way we obtained
CoGs for 9 different micro-turbulent velocities. We compare the equivalent
widths in the CoGs with the ones computed in the 3D-models and
selected the velocity of the CoG which fits the 3D CoG best in the sense of
![]() -residuals.
-residuals.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f10.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg117.png)
|
Figure 10:
Macro- (solid) and micro- (dotted) turbulent velocities and the sum
of both (long dashed line) as a function of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f11.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg118.png)
|
Figure 11:
Macro- (solid) and micro- (dotted) turbulent velocities and the sum
of both (long dashed line) as a function of |
| Open with DEXTER | |
The dependence of the micro- (![]() )
and macro- (
)
and macro- (![]() )
turbulent velocities on surface gravity and
effective temperature is plotted in Figs. 10 and 11. The macro-turbulent velocities in both cases show a quadratic
dependence, and we can fit them with a second order polynomial. The
micro-turbulent velocities could be fitted by a linear function or a second
order polynomial. We decided to
use the second order polynomial, too.
)
turbulent velocities on surface gravity and
effective temperature is plotted in Figs. 10 and 11. The macro-turbulent velocities in both cases show a quadratic
dependence, and we can fit them with a second order polynomial. The
micro-turbulent velocities could be fitted by a linear function or a second
order polynomial. We decided to
use the second order polynomial, too.
Micro- and
macro-turbulence velocities both show a similar dependence on surface gravity and
effective temperature, which implies that there is a direct connection between both.
A comparison of the macro (![]() )- and micro (
)- and micro (![]() )-turbulent velocities
with the sum of both (
)-turbulent velocities
with the sum of both (
![]() )
and the total projected weighted velocity dispersion
)
and the total projected weighted velocity dispersion
![]() (see Sec. 3) is also shown in
Figs. 10 and 11.
The total projected weighted velocity dispersion (see Sect. 3) is very similar
to the macro-turbulent velocities
and in most cases smaller than the sum of micro- and macro-turbulent
velocity. It is possible, with this simple description of the total projected weighted velocity,
to describe the broadening influence of the hydrodynamical velocity fields on spectral lines
in comparison with the classical micro- and macro-turbulent description.
(see Sec. 3) is also shown in
Figs. 10 and 11.
The total projected weighted velocity dispersion (see Sect. 3) is very similar
to the macro-turbulent velocities
and in most cases smaller than the sum of micro- and macro-turbulent
velocity. It is possible, with this simple description of the total projected weighted velocity,
to describe the broadening influence of the hydrodynamical velocity fields on spectral lines
in comparison with the classical micro- and macro-turbulent description.
In order to obtain a good estimate of the line profile in 1D spectral line synthesis, knowledge of the micro- and macro-turbulent velocities is very important. Otherwise one could underestimate the equivalent width or the line width and hence obtain a wrong line depth.
We compare our micro- and macro-turbulent velocities to observational results
from
(Bean et al. 2006b,a) and (Bean 2007).
Our value of the macro-turbulent velocities are roughly of the same order. The
higher macro-turbulent velocities from Bean et al. possibly contain rotational
broadening, but the Bean et al. micro-turbulent velocities are roughly a
factor of two or three higher than ours. These velocities were obtained from
observed spectra by the authors of the afore mentioned papers using spectral
fitting procedures. They used PHOENIX atmosphere models
and the stellar analysis code MOOG (Sneden 1973). One
has to keep in mind that the empirical determination of micro-turbulence may
also suffer from systematic errors. For most of the lines
that Bean and collaborators employ (line data from Barklem et al. 2000),
the van de Waals damping constant is available. However, if not, then
Unsöld's hydrogenic approximation is applied to calculate the value,
and different authors use significantly different enhancement factors, changing
its value. This illustrates the level of uncertainty inherent to this
approach. For instance, Schweitzer et al. (1996) used an enhance factor of 5.3 (for the resulting ![]() values) for their Fe I lines, while
Bean et al. prefer 2.5 for Ti I lines (Bean 2007).
To investigate the detailed influence of
van de Waals broadening on determination of micro-turbulence velocities is very
interesting, but is beyond the scope of this paper. Uncertainties in the
damping constant may introduce
significant systematic biases in the resulting value of spectroscopically
micro- and macro-turbulence which could easily be overestimated.
values) for their Fe I lines, while
Bean et al. prefer 2.5 for Ti I lines (Bean 2007).
To investigate the detailed influence of
van de Waals broadening on determination of micro-turbulence velocities is very
interesting, but is beyond the scope of this paper. Uncertainties in the
damping constant may introduce
significant systematic biases in the resulting value of spectroscopically
micro- and macro-turbulence which could easily be overestimated.
As mentioned above and illustrated Fig. 10, our prediction of the micro-turbulence grossly underestimates the micro-turbulence values measured by Bean et al. This might hint at deficits in the hydrodynamical modeling and we cannot exclude the possibility that a process is missing in our 3D models leading to a substantially higher micro-turbulence. But due to the argumentation above and a comparison with the solar micro- and macro-turbulence, we argue that the Bean et al. values for the micro-turbulence are too high. However, before being able to draw definite conclusions, the observational basis has to be enlarged.
4
 - and log g-dependence of FeH molecular lines
- and log g-dependence of FeH molecular lines
In this section we study the dependence of FeH molecular
lines on
![]() and
and ![]() in our 3D- and
in our 3D- and
![]() -models. Again, the intention
is to identify multi-D effects which might hamper the use of the
FeH line diagnostics in standard 1D analyses. For this purpose,
we compute the
-models. Again, the intention
is to identify multi-D effects which might hamper the use of the
FeH line diagnostics in standard 1D analyses. For this purpose,
we compute the
![]() -lines with no micro- and macro-turbulence velocity. With
this method we can study the FeH lines without any velocity
effects and can, through direct comparison between 3D- and
-lines with no micro- and macro-turbulence velocity. With
this method we can study the FeH lines without any velocity
effects and can, through direct comparison between 3D- and
![]() -lines, clearly
identify velocity-induced effects.
-lines, clearly
identify velocity-induced effects.
4.1 FeH line data
Wing & Ford (1969) were the first to detect a broad molecular
absorption band around 991 nm in late M dwarfs. This band was later found in
S stars (Wing 1972) and in sun spots.
Nordh et al. (1977) identified the Wing-Ford band as the 0-0 band of
a
![]() electronic transition. The
electronic transition. The
![]() molecule
is well suited for the measurements mentioned in the introduction because of
its intrinsically narrow and well isolated spectral lines. These lines are
also an ideal tracer of line broadening in M-stars due to convection or very
slow rotation (Reiners 2007). Since FeH lines were
not very commonly used for the interpretation of stellar spectra in the past,
only little data is available in the literature. With the work of
Dulick et al. (2003), it is possible to determine the
molecule
is well suited for the measurements mentioned in the introduction because of
its intrinsically narrow and well isolated spectral lines. These lines are
also an ideal tracer of line broadening in M-stars due to convection or very
slow rotation (Reiners 2007). Since FeH lines were
not very commonly used for the interpretation of stellar spectra in the past,
only little data is available in the literature. With the work of
Dulick et al. (2003), it is possible to determine the ![]() value
and the transition energies. For the partition function, a combination of the
tabulated function in Dulick et al. (2003) and an analytically
determined one from Eq. (1) in Sauval & Tatum (1984) is used.
value
and the transition energies. For the partition function, a combination of the
tabulated function in Dulick et al. (2003) and an analytically
determined one from Eq. (1) in Sauval & Tatum (1984) is used.
Due to the high atmospheric pressures, van de Waals broadening is often significant in cool M-type dwarfs. No detailed calculations exist for the van de Waals broadening of FeH molecular lines. Lacking a more accurate treatment, we follow the approximate approach of Schweitzer et al. (1996) and apply Unsöld's hydrogenic approximation, although - different from Schweitzer and co-workers - we do not apply an enhancement factor to the calculated broadening constant C6.
The ionization energy of the FeH molecule enters the calculation
of C6 which, unfortunately, is not known. Only the dissociation energy of
![]() eV at 0 K is published (e.g. Dulick et al. 2003).
To derive an estimate of the ionization energy, we heuristically compare the
ionization and dissociation energies of a large number of hydrides taking data
from Wilkinson (1963). We find an approximately linear
relationship between the ionization and the dissociation energies of hydrides.
For FeH we obtain an ionization energy of 6 eV for the known
dissociation energy from a linear fit. Computation of this value from the
ionization potential of Fe and the dissociation energies of FeH
and FeH+ yields 7.3 eV (Bernath 2008, private
communication), which is compatible with our value considering our rather
crude procedure. The difference in FWHM of synthesized
FeH-lines in the range between 6 and 7.3 eV amounts to
eV at 0 K is published (e.g. Dulick et al. 2003).
To derive an estimate of the ionization energy, we heuristically compare the
ionization and dissociation energies of a large number of hydrides taking data
from Wilkinson (1963). We find an approximately linear
relationship between the ionization and the dissociation energies of hydrides.
For FeH we obtain an ionization energy of 6 eV for the known
dissociation energy from a linear fit. Computation of this value from the
ionization potential of Fe and the dissociation energies of FeH
and FeH+ yields 7.3 eV (Bernath 2008, private
communication), which is compatible with our value considering our rather
crude procedure. The difference in FWHM of synthesized
FeH-lines in the range between 6 and 7.3 eV amounts to
![]() 25 m/s. This uncertainty is acceptable in comparison to the
total broadening of typically several 100 m s-1 in this investigation.
25 m/s. This uncertainty is acceptable in comparison to the
total broadening of typically several 100 m s-1 in this investigation.
4.2 An ensemble of 3D- and  3D
3D -FeH lines
-FeH lines
We investigate ten FeH lines between 9950 Å and
9990 Å chosen from Reiners & Basri (2006) (see Table 3). We
choose lines from different branches (Br), orbital angular momentum ![]() ,
and rotational
quantum number J. The wavelengths in Table 3 are given in vacuum
and El is the lower transition energy. While not directly relevant in the present context,
because we do not study the effects of magnetic fields, we note that five lines
are magnetically sensitive and five insensitive. We performed the line
synthesis for fixed abundances with the CO5BOLD atmosphere models listed in
Table 1. The spectral resolution is
,
and rotational
quantum number J. The wavelengths in Table 3 are given in vacuum
and El is the lower transition energy. While not directly relevant in the present context,
because we do not study the effects of magnetic fields, we note that five lines
are magnetically sensitive and five insensitive. We performed the line
synthesis for fixed abundances with the CO5BOLD atmosphere models listed in
Table 1. The spectral resolution is
![]() (
(![]()
![]() Å) corresponding to a Doppler
velocity of
Å) corresponding to a Doppler
velocity of
![]() m s-1 at the wavelength of the considered lines
(
m s-1 at the wavelength of the considered lines
(![]()
![]() ).
Figures 12 and 13 illustrate the strong influence of surface gravity and effective
temperature on the line shape for the 3D-models. In Fig. 12, one
can see that for both
).
Figures 12 and 13 illustrate the strong influence of surface gravity and effective
temperature on the line shape for the 3D-models. In Fig. 12, one
can see that for both
![]() - and 3D-lines, the line depth, line width
and equivalent width
- and 3D-lines, the line depth, line width
and equivalent width
![]() decrease strongly with increasing effective
temperature. The decrease of
decrease strongly with increasing effective
temperature. The decrease of
![]() is due to
stronger dissociation of the FeH molecules at higher
temperatures, i.e the number of FeH molecule absorbers
decreases. Differences in the line shape between 3D- and
is due to
stronger dissociation of the FeH molecules at higher
temperatures, i.e the number of FeH molecule absorbers
decreases. Differences in the line shape between 3D- and
![]() -lines with
changing temperature are barely visible. At higher
-lines with
changing temperature are barely visible. At higher
![]() values, the
influence of broadening on the 3D lines due to velocity fields is slightly
visible and not covered by thermal and van de Waals broadening any longer. At cooler
temperatures, the velocity fields decrease and the differences between the
values, the
influence of broadening on the 3D lines due to velocity fields is slightly
visible and not covered by thermal and van de Waals broadening any longer. At cooler
temperatures, the velocity fields decrease and the differences between the
![]() - and 3D-line shapes vanish. The van de Waals broadening is larger
then the thermal broadening or that from the small velocity fields in the RHD models. In the
model with
- and 3D-line shapes vanish. The van de Waals broadening is larger
then the thermal broadening or that from the small velocity fields in the RHD models. In the
model with
![]() K, the lines start to become saturated. The
FeH lines in the z-band at effective temperatures below
K, the lines start to become saturated. The
FeH lines in the z-band at effective temperatures below
![]() 2600 K become
too saturated and too broad for investigations of quantities like magnetic
field strength or rotational broadening below 10 km s-1.
2600 K become
too saturated and too broad for investigations of quantities like magnetic
field strength or rotational broadening below 10 km s-1.
The differences between 3D- and
![]() -line shapes of the
-line shapes of the ![]() -series in
Fig. 13 is more obvious than in the
-series in
Fig. 13 is more obvious than in the
![]() case. The differences
in line depth and line width become significant
with decreasing
case. The differences
in line depth and line width become significant
with decreasing ![]() .
The lines in the 3D-models are significantly
broadened due to the velocity fields in the RHD models, hence the line width is
larger and the line depth lower. As we saw in Chapter 3, these velocity fields
increase with decreasing
.
The lines in the 3D-models are significantly
broadened due to the velocity fields in the RHD models, hence the line width is
larger and the line depth lower. As we saw in Chapter 3, these velocity fields
increase with decreasing ![]() and could be described in the 1D case in
terms of macro- and micro-turbulent velocities.
and could be described in the 1D case in
terms of macro- and micro-turbulent velocities.
Table 3: Several quantities of the investigated FeH lines (Reiners & Basri 2006).
The
![]() -lines become slightly shallower and narrower towards smaller
-lines become slightly shallower and narrower towards smaller ![]() .
The equivalent width of the lines decreases with decreasing
.
The equivalent width of the lines decreases with decreasing ![]() due to
decreasing pressure and hence decreasing concentration of of FeH molecules.
Also the van de Waals broadening loses its influence at lower pressures and the
line width decreases.
We use in all models the same chemical
compositions, hence the concentration of Fe and H
stays the same. The creation of FeH also depends on the number
of H2-molecules, which becomes larger towards lower temperatures and
will be important in cool models.
due to
decreasing pressure and hence decreasing concentration of of FeH molecules.
Also the van de Waals broadening loses its influence at lower pressures and the
line width decreases.
We use in all models the same chemical
compositions, hence the concentration of Fe and H
stays the same. The creation of FeH also depends on the number
of H2-molecules, which becomes larger towards lower temperatures and
will be important in cool models.
The slightly different effective
temperatures in the models with different ![]() (see Table 1)
affect the line depths as well. If the effective temperatures were the
same in the
(see Table 1)
affect the line depths as well. If the effective temperatures were the
same in the ![]() -models, one would expect a monotonic behavior with
decreasing line strength for decreasing surface gravity in the
-models, one would expect a monotonic behavior with
decreasing line strength for decreasing surface gravity in the
![]() -lines. However, because the model with
-lines. However, because the model with
![]() is
cooler, the line depth is deeper than that of the one with
is
cooler, the line depth is deeper than that of the one with
![]() .
In the following analysis, we will correct the
FWHM,
.
In the following analysis, we will correct the
FWHM,
![]() ,
and the line depth of the lines in models with different
,
and the line depth of the lines in models with different
![]() for their slightly different effective temperatures.
for their slightly different effective temperatures.
The ten FeH lines all behave in the same way as the presented ones. We
do not see any effect of different excitation potentials or ![]() values
on the line shapes that cannot be explained by their different height of formation. Thus,
we expect that we can exclude an extraordinary interaction between these quantities and
effective temperature or surface gravity. We will quantify this preliminary
result in the next section.
values
on the line shapes that cannot be explained by their different height of formation. Thus,
we expect that we can exclude an extraordinary interaction between these quantities and
effective temperature or surface gravity. We will quantify this preliminary
result in the next section.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f12.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg139.png)
|
Figure 12:
FeH lines with constant |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f13.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg141.png)
|
Figure 13:
FeH lines wit constant
|
| Open with DEXTER | |
4.3 FeH Line shapes
To quantify the visual results of Figs. 12 and 13, we measured
![]() ,
the FWHM, and
the line depth of the ten investigated FeH-lines (see
Table 3). We compare 3D- and
,
the FWHM, and
the line depth of the ten investigated FeH-lines (see
Table 3). We compare 3D- and
![]() -lines with each other to study
the effects of the velocity fields in the 3D models and to explore the
behavior of the FeH without broadening effects from the
hydrodynamical motion. These quantities are plotted in
Figs. 14 and 15.
-lines with each other to study
the effects of the velocity fields in the 3D models and to explore the
behavior of the FeH without broadening effects from the
hydrodynamical motion. These quantities are plotted in
Figs. 14 and 15.
As we mentioned above, we have to correct the line
quantities in models with changing ![]() for their slightly different
for their slightly different
![]() .
In Figs. 12 and 14 one can see how the
investigated quantities depend on
.
In Figs. 12 and 14 one can see how the
investigated quantities depend on
![]() .
We determined spline fits
.
We determined spline fits ![]() for
the three quantities of each line. For these fitting functions
for
the three quantities of each line. For these fitting functions ![]() we took into
account all five
different effective temperatures. In order to correct
the line quantities to a reference temperature of
we took into
account all five
different effective temperatures. In order to correct
the line quantities to a reference temperature of
![]() K, we
use a correction factor
K, we
use a correction factor
![]() and multiply
the quantity for the
and multiply
the quantity for the ![]() -model by
-model by ![]() .
This gives us the value of
the quantity for a
.
This gives us the value of
the quantity for a ![]() -model which would have
-model which would have
![]() K.
K.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f14.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg146.png)
|
Figure 14:
|
| Open with DEXTER | |
4.3.1 Equivalent width W
In the
![]() -series,
-series,
![]() (see Fig. 14
upper panel) decreases with increasing
(see Fig. 14
upper panel) decreases with increasing
![]() .
At higher
.
At higher
![]() the number
of FeH molecules decreases due to dissociation and
hence
the number
of FeH molecules decreases due to dissociation and
hence
![]() .
This can be seen in the 3D lines as well as in the
.
This can be seen in the 3D lines as well as in the
![]() -lines.
At
-lines.
At
![]() K, the influence of van de Waals broadening in the 3D- and
K, the influence of van de Waals broadening in the 3D- and
![]() -lines becomes clearly visible in the line profile due to saturation of the FeH
lines.
The ten different FeH lines all behave in a similar
manner. The only difference is the absolute value of
-lines becomes clearly visible in the line profile due to saturation of the FeH
lines.
The ten different FeH lines all behave in a similar
manner. The only difference is the absolute value of
![]() ,
which depends
on the
,
which depends
on the ![]() -value and the excitation potential El of each line.
-value and the excitation potential El of each line.
In the ![]() -series, the
-series, the
![]() (see Fig. 15
upper panel) increases with increasing
(see Fig. 15
upper panel) increases with increasing ![]() .
The change in concentration
of FeH with lower
.
The change in concentration
of FeH with lower ![]() ,
which results in smaller
,
which results in smaller
![]() ,
depends on the changing pressure and density stratification. The difference
between 3D- and
,
depends on the changing pressure and density stratification. The difference
between 3D- and
![]() -lines at small
-lines at small ![]() -values stems from the
broadening by micro-turbulent velocities and vanishes at higher
-values stems from the
broadening by micro-turbulent velocities and vanishes at higher ![]() values. This
time the FeH lines are only mildly saturated, but the velocity
fields in the RHD models (see Sect. 3) are strong enough to affect
the
values. This
time the FeH lines are only mildly saturated, but the velocity
fields in the RHD models (see Sect. 3) are strong enough to affect
the
![]() as well.
As in the
as well.
As in the
![]() -series, the ten different lines show
no significant variations in their behavior. They only vary in the amount of
-series, the ten different lines show
no significant variations in their behavior. They only vary in the amount of
![]() due to different
due to different ![]() -values.
-values.
Since the differences in
![]() are very small, one can expect that the
3D correction to the FeH abundance is very small too. We derive
abundance corrections from a comparison between 3D and
are very small, one can expect that the
3D correction to the FeH abundance is very small too. We derive
abundance corrections from a comparison between 3D and
![]() curve of growths for
each set of lines on the different model atmospheres. The results are plotted
in Fig. 16. In this case the correction to the different
curve of growths for
each set of lines on the different model atmospheres. The results are plotted
in Fig. 16. In this case the correction to the different
![]() of
the
of
the ![]() models is not applied. The 3D-
models is not applied. The 3D-
![]() abundance correction is
between -0.001 dex for the coolest high
abundance correction is
between -0.001 dex for the coolest high ![]() model and -0.07 dex for
the
model and -0.07 dex for
the
![]() model. In all cases the abundance correction is negative
which mean that the 3D lines appear stronger due to the enhanced opacity which
becomes larger due to the micro-turbulent velocity.
model. In all cases the abundance correction is negative
which mean that the 3D lines appear stronger due to the enhanced opacity which
becomes larger due to the micro-turbulent velocity.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f15.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg147.png)
|
Figure 15:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f16.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg149.png)
|
Figure 16:
3D -
|
| Open with DEXTER | |
4.3.2 FWHM
The dependence of the line width (measured as the width of the line
at their half maximum (FWHM)) on
![]() is shown in the middle
panel of Fig. 14. At low
is shown in the middle
panel of Fig. 14. At low
![]() ,
one can see that the FWHM of the
3D- and
,
one can see that the FWHM of the
3D- and
![]() - FeH lines decreases with increasing
- FeH lines decreases with increasing
![]() .
The van de Waals broadening loses influence and also the dissociation of
FeH molecules leads to smaller and
narrower lines. After
.
The van de Waals broadening loses influence and also the dissociation of
FeH molecules leads to smaller and
narrower lines. After
![]() around 3380 K, the FWHM of the 3D lines reaches a
flat minimum and starts to become larger again at higher
around 3380 K, the FWHM of the 3D lines reaches a
flat minimum and starts to become larger again at higher
![]() .
This rise in the line
width is probably related to the rising velocity fields in the RHD models, since
thermal broadening takes place in both 3D- and
.
This rise in the line
width is probably related to the rising velocity fields in the RHD models, since
thermal broadening takes place in both 3D- and
![]() -lines and the
latter still decrease. The rise of the velocity in the models with
a
-lines and the
latter still decrease. The rise of the velocity in the models with
a
![]() of 3380 K and 4000 K could also be due to the slightly lower
surface gravity in these models, but we think that the main influence stems
from the higher temperatures. The
of 3380 K and 4000 K could also be due to the slightly lower
surface gravity in these models, but we think that the main influence stems
from the higher temperatures. The
![]() -lines decrease monotonically
with increasing
-lines decrease monotonically
with increasing
![]() and reflects, the behavior of
and reflects, the behavior of
![]() .
The
difference in FWHM between 3D- and
.
The
difference in FWHM between 3D- and
![]() -lines is very small at
-lines is very small at
![]() K and increases with increasing
K and increases with increasing
![]() to
to ![]() 0.8 km s-1 at the
highest
0.8 km s-1 at the
highest
![]() .
We have seen in Sect. 3.2 that this can be explained with the micro-
and macro-turbulence description. The offset between the FWHM of the ten lines
is due to their different
.
We have seen in Sect. 3.2 that this can be explained with the micro-
and macro-turbulence description. The offset between the FWHM of the ten lines
is due to their different ![]() -values i.e. large
-values i.e. large ![]() -values
results in large FWHM. But since we are interested in broadening by the
velocity fields, we have to take into account that lines with small
-values
results in large FWHM. But since we are interested in broadening by the
velocity fields, we have to take into account that lines with small ![]() -values,
i.e. weak lines, formed deeper in the atmosphere where the convective motions
are stronger. These lines are more broadened by the hydrodynamical velocity
fields and hence more widened. We can see in
Fig. 14 that the difference in FWHM between the ten 3D lines becomes
smaller to high
-values,
i.e. weak lines, formed deeper in the atmosphere where the convective motions
are stronger. These lines are more broadened by the hydrodynamical velocity
fields and hence more widened. We can see in
Fig. 14 that the difference in FWHM between the ten 3D lines becomes
smaller to high
![]() .
This is also valid for the lines in the
.
This is also valid for the lines in the
![]() -series where the difference in FWHM between the ten 3D lines
becomes smaller at small
-series where the difference in FWHM between the ten 3D lines
becomes smaller at small ![]() -values.
-values.
In the ![]() -series, the dependence of FWHM (Fig. 15 middle
panel) is very different for 3D- and
-series, the dependence of FWHM (Fig. 15 middle
panel) is very different for 3D- and
![]() -lines. In the 3D case, the FWHM
stays almost constant with decreasing surface gravity between
-lines. In the 3D case, the FWHM
stays almost constant with decreasing surface gravity between ![]() of 5.0and 4.0 for most lines. This is due to the
smaller amount
of van de Waals broadening, which loses its influence due to lower pressure
in models with smaller surface gravity. This is compared with the broadening
due to the rising velocity fields. With
of 5.0and 4.0 for most lines. This is due to the
smaller amount
of van de Waals broadening, which loses its influence due to lower pressure
in models with smaller surface gravity. This is compared with the broadening
due to the rising velocity fields. With ![]() smaller than 4.0, the width starts to increase for all lines. This increase of line width in the
3D case is a consequence of the hydrodynamic velocity fields which increase
strongly with decreasing
smaller than 4.0, the width starts to increase for all lines. This increase of line width in the
3D case is a consequence of the hydrodynamic velocity fields which increase
strongly with decreasing ![]() .
In the
.
In the
![]() case, without the velocity fields, the FWHM decreases with
decreasing surface gravity and reflects the behavior of the
case, without the velocity fields, the FWHM decreases with
decreasing surface gravity and reflects the behavior of the
![]() .
The
difference between 3D- and
.
The
difference between 3D- and
![]() -lines reaches its maximal value at
-lines reaches its maximal value at
![]() [cgs] and is around 1.3 km s-1. This is of the order of
the velocity fields in the RHD models (see Fig. 8). One could
fit 1D spectral synthesis FeH lines to observed ones (with known
[cgs] and is around 1.3 km s-1. This is of the order of
the velocity fields in the RHD models (see Fig. 8). One could
fit 1D spectral synthesis FeH lines to observed ones (with known
![]() )
with the micro- and macro-turbulence description (see Sect. 3.2) and it
will be possible with the obtained velocities to determine a surface gravity
with the help of Fig. 11.
)
with the micro- and macro-turbulence description (see Sect. 3.2) and it
will be possible with the obtained velocities to determine a surface gravity
with the help of Fig. 11.
We did not see any significantly different behavior between
the ten FeH lines in the
![]() -series or in the
-series or in the
![]() -series.
-series.
4.3.3 Line depth
In the bottom panel of Fig. 14 one can see the dependence of the line depth onThe line depth of the ![]() -series is shown in the bottom panel of
Fig. 15. At low
-series is shown in the bottom panel of
Fig. 15. At low ![]() ,
the line depths of the 3D and
,
the line depths of the 3D and
![]() -lines increase
almost linearly with increasing
-lines increase
almost linearly with increasing ![]() .
The 3D lines increase with a strong
slope and the
.
The 3D lines increase with a strong
slope and the
![]() -lines with a weaker slope. The difference in line
depth between 3D- and
-lines with a weaker slope. The difference in line
depth between 3D- and
![]() -models is maximal at
-models is maximal at
![]() [cgs] and
vanishes almost at
[cgs] and
vanishes almost at
![]() [cgs]. It is consistent with the velocity
fields present in the atmospheres of the RHD models broadening the lines
and lower the line strength of the 3D lines. The
[cgs]. It is consistent with the velocity
fields present in the atmospheres of the RHD models broadening the lines
and lower the line strength of the 3D lines. The
![]() -lines reflect the
decreasing number of FeH molecules with decreasing
-lines reflect the
decreasing number of FeH molecules with decreasing ![]() due
to the lower pressures.
due
to the lower pressures.
5 Summary and conclusion
We investigated a set of M-star models withA line shift due to the larger up-flowing area in the convection zone was investigated. It is of the order of a few m/s up to 50 m s-1 for a very low gravity model. The time dependent jitter in line positions is only about m/s and would be reduced to mm s-1 in a real star, due to the high number of contributing elements.
In order to use
FeH molecular lines for investigations of spectroscopic/physical
properties in cool
stars (e.g. Zeeman- or rotational broadening), we explored the behavior in a
set of lines of
![]() and
and
![]() .
We investigated ten FeH lines between
9950 Å and 9990 Å on our models with the
spectral synthesis code LINFOR3D. FeH
lines react to different effective temperatures as expected due to
the change in chemical composition and pressure. The lines also showed a weak
dependence on surface gravity due to changing densities and pressure. The
broadening from velocity fields in the 3D models of the
.
We investigated ten FeH lines between
9950 Å and 9990 Å on our models with the
spectral synthesis code LINFOR3D. FeH
lines react to different effective temperatures as expected due to
the change in chemical composition and pressure. The lines also showed a weak
dependence on surface gravity due to changing densities and pressure. The
broadening from velocity fields in the 3D models of the ![]() series is
very strong, but for the
series is
very strong, but for the
![]() series the broadening from velocity fields is
almost covered by van de Waals broadening. The difference in line width for hot
models is up to 0.5 km s-1 and for low gravity models around
1 km s-1. This
means for the 1D spectral synthesis, one has to include correct micro-
and macro-turbulent velocities for small surface gravities or hot
series the broadening from velocity fields is
almost covered by van de Waals broadening. The difference in line width for hot
models is up to 0.5 km s-1 and for low gravity models around
1 km s-1. This
means for the 1D spectral synthesis, one has to include correct micro-
and macro-turbulent velocities for small surface gravities or hot
![]() .
Due
to the fact that the FWHM
.
Due
to the fact that the FWHM ![]() dependence of FeH lines goes
in the opposite direction as the
dependence of FeH lines goes
in the opposite direction as the ![]() dependence of the velocity fields,
the FeH lines become a good way to measure surface gravities
in cool stars because the velocity fields scale with
dependence of the velocity fields,
the FeH lines become a good way to measure surface gravities
in cool stars because the velocity fields scale with ![]() and it should
be easily possible to detect them.
and it should
be easily possible to detect them.
FeH lines with different quantum numbers do not
show significant differences for both ![]() - and
- and
![]() -series. This
means the broadening of the lines does not depend on J,
-series. This
means the broadening of the lines does not depend on J, ![]() ,
or the
branch. Furthermore, lines with weak magnetic sensitivity behave just like
lines with strong magnetic sensitivity. All lines are broadened in the same way
by thermal and hydrodynamical motion. Only the transition probability
expressed in the
,
or the
branch. Furthermore, lines with weak magnetic sensitivity behave just like
lines with strong magnetic sensitivity. All lines are broadened in the same way
by thermal and hydrodynamical motion. Only the transition probability
expressed in the ![]() value influences the behavior of the
lines. The line with the lowest gf-values did not saturate at low
value influences the behavior of the
lines. The line with the lowest gf-values did not saturate at low
![]() ,
but in general they are similar to the other FeH lines.
,
but in general they are similar to the other FeH lines.
It is possible to treat the FeH molecular lines with different quantum numbers as homogenous in the absence of magnetic fields. This allows one to use FeH lines to measure magnetic fields (Reiners & Basri 2007,2006). Hence we conclude that these lines also are an appropriate means to measure magnetic field strength in M-type stars.
AcknowledgementsSW would like to acknowledge the support from the DFG Research Training Group GrK - 1351 ``Extrasolar Planets and their host stars''. A.R. acknowledges research funding from the DFG under an Emmy Noether Fellowship (RE 1664/4- 1). H.G.L. acknowledges financial support from EU contract MEXT-CT-2004-014265 (CIFIST). We thank Derek Homeier for providing us with the opacity tables.
Appendix
![\begin{figure}\par\includegraphics[width=9cm,clip]{pictures/13149f17.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg150.png)
|
Figure 17:
Projection factors (vertical solid line and horizontal dotted line)
as a function of the limb darkening coefficient |
| Open with DEXTER | |
| (2) |
where V(v) is a line profile function,
| (3) |
with d
| (4) |
with
With Eq. (5) we are left with a flux-like expression for the velocity function. The dispersion of the velocity function is given by
| (6) |
and we can write for the projected velocity dispersion
where
 is the velocity vector containing all velocities in a
model cube,
is the velocity vector containing all velocities in a
model cube,
 is the basis
vector in spherical coordinates, and
is the basis
vector in spherical coordinates, and
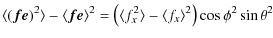
|
|||
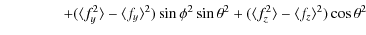
|
|||
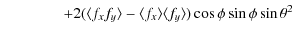
|
|||
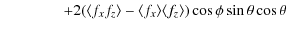
|
|||
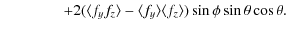
|
(8) |
If we want to compute the average of this quantity, we need the mean and the
squared mean of the quantities, but not the combinations of the velocity components,
because these products vanish in the integration over the half sphere due to
their angle-dependent coefficients. After the integration of Eq. (7),
![]() becomes
becomes
We can see, that for an isotropic velocity field fx(v)=fy(v)=fz(v)=f(v)follows that
The projection factors for the vertical
![]() and horizontal
and horizontal
![]() component are plotted as a
function of the limb-darkening coefficient
component are plotted as a
function of the limb-darkening coefficient ![]() in
Fig. 17. They vary only about
in
Fig. 17. They vary only about ![]() from no darkening to a full
darkened disk. The reduction for the vertical velocity is about
from no darkening to a full
darkened disk. The reduction for the vertical velocity is about ![]() and for
the horizontal components
and for
the horizontal components ![]() .
.
For completeness, we obtain in a similar
way the mean velocities in three spatial directions
![]() which are given by
which are given by
The horizontal velocities vanish due to projection but there is still a vertical component which is reduced to geometrical and limb-darkening effects.
| (11) |
References
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25
- Barklem, P. S., Piskunov, N., & O'Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [EDP Sciences] [CrossRef]
- Baschek, B., Holweger, H., & Traving, G. 1966, Astronomische Abhandlung der Hamburger Sternwarte, 8, 26 [NASA ADS]
- Bean, J. L., Benedict, G. F., & Endl, M. 2006a, ApJ, 653, L65 [NASA ADS] [CrossRef]
- Bean, J. L., Sneden, C., Hauschildt, P. H., Johns-Krull, C. M., & Benedict, G. F. 2006b, ApJ, 652, 1604 [NASA ADS] [CrossRef]
- Bean, J. L. 2007, Ph.D. Thesis, The University of Texas at Austin
- Dravins, D. 1982, ARA&A, 20, 61 [NASA ADS] [CrossRef]
- Dulick, M., Bauschlicher, Jr., C. W., Burrows, A., et al. 2003, APJ, 594, 651 [NASA ADS] [CrossRef]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, APJ, 623, 585 [NASA ADS] [CrossRef]
- Freytag, B., Allard, F., Ludwig, H., Homeier, D., & Steffen, M. 2009, A&A, submitted
- Freytag, B., Steffen, M., & Dorch, B. 2002, Astron. Nachr., 323, 213 [NASA ADS] [CrossRef]
- Gray, D. F. 1975, ApJ, 202, 148 [NASA ADS] [CrossRef]
- Gray, D. F. 1977, ApJ, 218, 530 [NASA ADS] [CrossRef]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres, ed. D. F. Gray (Cambridge: Cambridge University Press)
- Hauschildt, P. H., & Baron, E. 1999, J. Comp. Appl. Math., 109, 41 [NASA ADS] [CrossRef]
- Kurucz, R. L. 1970, SAO Special Report, 309
- Ludwig, H. G. 1992, Ph.D. Thesis, University of Kiel
- Ludwig, H.-G., Jordan, S., & Steffen, M. 1994, A&A, 284, 105 [NASA ADS]
- Ludwig, H.-G., Allard, F., & Hauschildt, P. H. 2002, A&A, 395, 99 [NASA ADS] [EDP Sciences] [CrossRef]
- Ludwig, H.-G., Allard, F., & Hauschildt, P. H. 2006, A&A, 459, 599 [NASA ADS] [EDP Sciences] [CrossRef]
- Magain, P. 1986, A&A, 163, 135 [NASA ADS]
- Nordh, H. L., Lindgren, B., & Wing, R. F. 1977, A&A, 56, 1 [NASA ADS]
- Nordlund, A. 1982, A&A, 107, 1 [NASA ADS]
- Palla, F., & Baraffe, I. 2005, A&A, 432, L57 [NASA ADS] [EDP Sciences] [CrossRef]
- Reiners, A. 2007, A&A, 467, 259 [NASA ADS] [EDP Sciences] [CrossRef]
- Reiners, A., & Basri, G. 2006, ApJ, 644, 497 [NASA ADS] [CrossRef]
- Reiners, A., & Basri, G. 2007, ApJ, 656, 1121 [NASA ADS] [CrossRef]
- Sauval, A. J., & Tatum, J. B. 1984, ApJS, 56, 193 [NASA ADS] [CrossRef]
- Schweitzer, A., Hauschildt, P. H., Allard, F., & Basri, G. 1996, MNRAS, 283, 821 [NASA ADS]
- Sneden, C. A. 1973, Ph.D. Thesis, AA, The University of Texas at Austin
- Steffen, M., Ludwig, H.-G., & Freytag, B. 1995, A&A, 300, 473 [NASA ADS]
- Vögler, A., Bruls, J. H. M. J., & Schüssler, M. 2004, A&A, 421, 741 [NASA ADS] [EDP Sciences] [CrossRef]
- Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., & Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [EDP Sciences] [CrossRef]
- Wilkinson, P. G. 1963, ApJ, 138, 778 [NASA ADS] [CrossRef]
- Wing, R. F. 1972, in Les Spectres des Astres dans l'Infrarouge et les Microondes, 123
- Wing, R. F., & Ford, W. K. J. 1969, PASP, 81, 527 [NASA ADS] [CrossRef]
All Tables
Table 1:
Overview of different model quantities for models at constant
![]() and different
and different ![]() (upper part) and at constant
(upper part) and at constant
![]() and different
and different
![]() (lower part).
(lower part).
Table 2:
Displacement
![]() and
and
![]() in m/s of the position of an FeH line from the rest wavelength
in models with different
in m/s of the position of an FeH line from the rest wavelength
in models with different
![]() (left side) and different
(left side) and different ![]() (right side).
(right side).
Table 3: Several quantities of the investigated FeH lines (Reiners & Basri 2006).
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f01.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg53.png)
|
Figure 1:
From top to bottom, the temperature, entropy, vertical, and horizontal velocity
are plotted as a function of optical depth. The column on the left side shows models with
different
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{pictures/13149f02.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg67.png)
|
Figure 2:
Histogram of the
velocity distribution in the vertical direction. The normalized number of points
is plotted against the vertical velocity in m/s (solid line).
The Gaussian (dashed line) fits the velocity distribution and
determined an FWHM value (dashed-dotted line), which is related to |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{pictures/13149f03.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg71.png)
|
Figure 3:
Upper panel: radial ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{pictures/13149f04.ps}\par
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg74.png)
|
Figure 4:
Upper panel: radial ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f05.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg91.png)
|
Figure 5:
Horizontal cross-section around
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f06.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg93.png)
|
Figure 6:
2D cross-section in x-z direction of the x-z velocity
in a model with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f07.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg103.png)
|
Figure 7:
The weighted projected and unprojected velocity dispersions
of the horizontal and vertical component for models with different
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f08.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg106.png)
|
Figure 8:
The weighted projected and unprojected velocity dispersions
of the horizontal and vertical component for
models with different |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f9a.ps} \includegraphics[width=9cm,clip]{pictures/13149f9b.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg113.png)
|
Figure 9:
FeH lines for models with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pictures/13149f10.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg117.png)
|
Figure 10:
Macro- (solid) and micro- (dotted) turbulent velocities and the sum
of both (long dashed line) as a function of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f11.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg118.png)
|
Figure 11:
Macro- (solid) and micro- (dotted) turbulent velocities and the sum
of both (long dashed line) as a function of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f12.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg139.png)
|
Figure 12:
FeH lines with constant |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f13.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg141.png)
|
Figure 13:
FeH lines wit constant
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f14.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg146.png)
|
Figure 14:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f15.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg147.png)
|
Figure 15:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{pictures/13149f16.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg149.png)
|
Figure 16:
3D -
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=9cm,clip]{pictures/13149f17.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13149-09/Timg150.png)
|
Figure 17:
Projection factors (vertical solid line and horizontal dotted line)
as a function of the limb darkening coefficient |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.