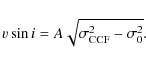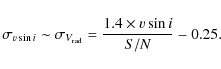| Issue |
A&A
Volume 508, Number 3, December IV 2009
|
|
|---|---|---|
| Page(s) | 1301 - 1312 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200913125 | |
| Published online | 27 October 2009 | |
A&A 508, 1301-1312 (2009)
Evidence of early disk-locking among low-mass members of the Orion Nebula Cluster![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
K. Biazzo1,2,3 - C. H. F. Melo2 - L. Pasquini2 - S. Randich1 - J. Bouvier4 - X. Delfosse4
1 - INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
2 - ESO - European Southern Observatory, Karl-Schwarzschild-Str. 3, 85748 Garching bei München, Germany
3 - INAF - Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
4 - Laboratoire d'Astrophysique, Observatoire de Grenoble, BP 53, 38041 Grenoble Cedex 9, France
Received 16 August 2009 / Accepted 24 September 2009
Abstract
Context. We present new high-resolution spectroscopic
observations for 91 pre-main sequence stars in the Orion Nebular
Cluster (ONC) with masses in the range
![]() carried out with the multi-fiber spectrograph FLAMES attached to the UT2 at the Paranal Observatory.
carried out with the multi-fiber spectrograph FLAMES attached to the UT2 at the Paranal Observatory.
Aims. Our aim is to better understand the disk-locking scenario in very low-mass stars.
Methods. We have derived radial velocities, projected rotational velocities, and full width at 10% of the H![]() emission peak. Using published measurements of infrared excess (
emission peak. Using published measurements of infrared excess (
![]() ), as disk tracer and equivalent width of the nead-infrared Ca
), as disk tracer and equivalent width of the nead-infrared Ca
Results. ii Line ![]() 8542, mid-infrared difference [3.6]-[8.0]
8542, mid-infrared difference [3.6]-[8.0] ![]() m derived by Spitzer data, and 10% H
m derived by Spitzer data, and 10% H![]() width as diagnostic of the level of accretion, we looked for any
correlation between projected angular rotational velocity divided by
the radius (
width as diagnostic of the level of accretion, we looked for any
correlation between projected angular rotational velocity divided by
the radius (![]() )
and presence of disk and accretion.
)
and presence of disk and accretion.
Conclusions. For 4 low-mass stars, the cross-correlation
function is clearly double-lined, indicating that the stars are SB2
systems. The distribution of rotation periods derived from our ![]() measurements is unimodal with a peak of a few days, in agreement with previous results for
measurements is unimodal with a peak of a few days, in agreement with previous results for
![]() .
The photometric periods were combined with our
.
The photometric periods were combined with our ![]() to derive the equatorial velocity and the distribution of rotational axes. Our
to derive the equatorial velocity and the distribution of rotational axes. Our
![]() is lower than the one expected for a random distribution, as previously
found. We find no evidence of a population of fast rotators close to
the break-up velocity. A clear correlation between
is lower than the one expected for a random distribution, as previously
found. We find no evidence of a population of fast rotators close to
the break-up velocity. A clear correlation between ![]() and
and
![]() has been found. While a spread in the rotation rates is seen for stars with no circumstellar disk (
has been found. While a spread in the rotation rates is seen for stars with no circumstellar disk (
![]() ), stars with a circumstellar disk (
), stars with a circumstellar disk (
![]() )
show an abrupt drop in their rotation rates by a factor of
)
show an abrupt drop in their rotation rates by a factor of ![]() 5. On the other hand, only a partial correlation between
5. On the other hand, only a partial correlation between ![]() and accretion is observed when other indicators are used. The X-ray coronal activity level (
and accretion is observed when other indicators are used. The X-ray coronal activity level (
![]() )
shows no dependence on
)
shows no dependence on ![]() ,
suggesting that all stars are in a saturated regime limit. The critical velocity is probably below our
,
suggesting that all stars are in a saturated regime limit. The critical velocity is probably below our ![]() detection limit of 9 km s-1.
detection limit of 9 km s-1.
Arg5. The ONC low-mass stars in our sample, close to the
hydrogen burning limit, at present do not seem to be locked, but the
clear correlation we find between rotation and infrared color excess
suggests that they were locked once. In addition, the percentage of
accretors seems to scale inversely to the stellar mass.
Key words: open clusters and associations: individual: Orion Nebula Cluster - stars: low-mass, brown dwarfs - stars: pre-main sequence - stars: late-type - accretion, accretion disks - techniques: spectroscopic
1 Introduction
Surface rotation is a key observational parameter for stellar evolution because it is linked to the internal angular momentum transport and to the mechanisms responsible for stellar angular momentum loss. Its initial conditions are set during the star formation process.There are four main ingredients describing the angular momentum (AM) evolution of
![]() star: i) Solid
body rotation. Stars begin their lives as fully convective objects. Since the timescale for convective transport is
much shorter than for angular momentum loss, the stars probably rotate as solid bodies
(Stassun & Tendrup 2003, and references therein). ii) Disk-locking. The idea of magnetic disk-locking
originated with the theory developed by Ghosh & Lamb (1979) for neutron stars, but in the context of pre-main sequence
(PMS) stars was proposed for the first time by Camenzind (1990) and König (1991). The stellar magnetic field
threads the slowly rotating circumstellar disk of the young star, truncating it at several stellar radii
(Bouvier et al. 2007). Due to the difference in angular velocity, magnetic torques will transfer angular
momentum from the star to the disk causing them to corotate, i.e. the spin-up torque on the star is exactly balanced
by a spin-down torque transmitted by the field lines threading the disk beyond the corotation radius. In
the end, the stellar rotational angular velocity equals the Keplerian angular velocity of the
inner disk (Shu et al. 1994). iii) Stellar winds. Angular momentum loss continues via a magnetized wind
during the evolution to and on the main-sequence. The rate of angular momentum loss depends on whether the angular
rotation rate is above the saturation limit (Barnes & Sofia 1996). iv) Core-envelope decoupling. Surface
rotation is eventually replenished by AM brought from the rapid rotating core in a characteristic time
star: i) Solid
body rotation. Stars begin their lives as fully convective objects. Since the timescale for convective transport is
much shorter than for angular momentum loss, the stars probably rotate as solid bodies
(Stassun & Tendrup 2003, and references therein). ii) Disk-locking. The idea of magnetic disk-locking
originated with the theory developed by Ghosh & Lamb (1979) for neutron stars, but in the context of pre-main sequence
(PMS) stars was proposed for the first time by Camenzind (1990) and König (1991). The stellar magnetic field
threads the slowly rotating circumstellar disk of the young star, truncating it at several stellar radii
(Bouvier et al. 2007). Due to the difference in angular velocity, magnetic torques will transfer angular
momentum from the star to the disk causing them to corotate, i.e. the spin-up torque on the star is exactly balanced
by a spin-down torque transmitted by the field lines threading the disk beyond the corotation radius. In
the end, the stellar rotational angular velocity equals the Keplerian angular velocity of the
inner disk (Shu et al. 1994). iii) Stellar winds. Angular momentum loss continues via a magnetized wind
during the evolution to and on the main-sequence. The rate of angular momentum loss depends on whether the angular
rotation rate is above the saturation limit (Barnes & Sofia 1996). iv) Core-envelope decoupling. Surface
rotation is eventually replenished by AM brought from the rapid rotating core in a characteristic time
![]() .
How the decoupling characteristic depends on mass (and on other stellar parameters) is still unsettled.
.
How the decoupling characteristic depends on mass (and on other stellar parameters) is still unsettled.
Although many details remain to be understood, these four ingredients seem to regulate the broad aspects of
the AM evolution from PMS to solar age for
![]() stars. Among these four ingredients, the disk-locking
hypothesis is believed to play a fundamental role in the early AM evolution during the T-Tauri phase, when young stars
are expected to have circumstellar disks. This scenario has been supported through the years by different observational
photometric studies which show that T-Tauri stars with disks (CTTS) have significantly longer periods than
their disk-less counterparts (WTTS), i.e. they rotate at a small fraction (10-20%) of the break-up velocity
(Bouvier et al. 1993; Attridge & Herbst 1992; Marilli et al. 2007; Edwards et al. 1993; Choi & Herbst 1996). This indicates an efficient
method for shedding AM, which is contrary to the expectation that these stars should spin close to break-up
speed, having recently contracted from their natal clouds (Stassun et al. 1999).
stars. Among these four ingredients, the disk-locking
hypothesis is believed to play a fundamental role in the early AM evolution during the T-Tauri phase, when young stars
are expected to have circumstellar disks. This scenario has been supported through the years by different observational
photometric studies which show that T-Tauri stars with disks (CTTS) have significantly longer periods than
their disk-less counterparts (WTTS), i.e. they rotate at a small fraction (10-20%) of the break-up velocity
(Bouvier et al. 1993; Attridge & Herbst 1992; Marilli et al. 2007; Edwards et al. 1993; Choi & Herbst 1996). This indicates an efficient
method for shedding AM, which is contrary to the expectation that these stars should spin close to break-up
speed, having recently contracted from their natal clouds (Stassun et al. 1999).
In contrast to the
![]() mass regime, the AM evolution for lower mass stars is far from being
understood. In particular, there are contrasting opinions regarding the distribution of rotational period
(
mass regime, the AM evolution for lower mass stars is far from being
understood. In particular, there are contrasting opinions regarding the distribution of rotational period
(
![]() )
for very low-mass stars (
)
for very low-mass stars (
![]() ). From an observative point of view, Stassun et al. (1999)
have challenged the disk-locking scenario in 254 stars of the young Orion OBIc/d association by showing that there
is no evidence of the bimodal period distribution originally attributed to disk braking. In addition, no correlation
between observed
). From an observative point of view, Stassun et al. (1999)
have challenged the disk-locking scenario in 254 stars of the young Orion OBIc/d association by showing that there
is no evidence of the bimodal period distribution originally attributed to disk braking. In addition, no correlation
between observed
![]() and accretion diagnostics and no differences between
and accretion diagnostics and no differences between
![]() distributions of
WTTS and CTTS were found, calling the standard disk-locking scenario into question.
Herbst et al. (2000,2001,2002) obtain a bimodal period distribution
for the Orion Nebula Cluster (ONC) confirming the findings of Choi & Herbst (1996) and point out the
dependence of the rotation on mass. They find a bimodal distribution of rotation periods for higher masses
(
distributions of
WTTS and CTTS were found, calling the standard disk-locking scenario into question.
Herbst et al. (2000,2001,2002) obtain a bimodal period distribution
for the Orion Nebula Cluster (ONC) confirming the findings of Choi & Herbst (1996) and point out the
dependence of the rotation on mass. They find a bimodal distribution of rotation periods for higher masses
(
![]() )
with a gap near 4 days, while lower masses (
)
with a gap near 4 days, while lower masses (
![]() )
have a unimodal distribution
and generally spin faster. They show a statistically significant anti-correlation between IR excess emission
and rotation: slower rotators are more likely to show evidence of circumstellar disks. Rebull (2001)
looked for the mass dependence in ONC flaking fields, but found only weak evidence of a
change in rotational period distribution for low-mass stars. Later, Rebull et al. (2002) have shown that in stars
of the ONC and NGC2264 AM is depleted very early during the T-Tauri phase and have concluded that disk-locking is
indeed the most likely mechanism to be acting. Hartmann (2002), adopting accretion rates of
)
have a unimodal distribution
and generally spin faster. They show a statistically significant anti-correlation between IR excess emission
and rotation: slower rotators are more likely to show evidence of circumstellar disks. Rebull (2001)
looked for the mass dependence in ONC flaking fields, but found only weak evidence of a
change in rotational period distribution for low-mass stars. Later, Rebull et al. (2002) have shown that in stars
of the ONC and NGC2264 AM is depleted very early during the T-Tauri phase and have concluded that disk-locking is
indeed the most likely mechanism to be acting. Hartmann (2002), adopting accretion rates of
![]() yr-1 taken from Rebull et al. (2000) for the ONC flaking fields for
yr-1 taken from Rebull et al. (2000) for the ONC flaking fields for
![]() and an initial rotation rate at 10% of the break-up velocity, concluded that the time-scale
needed to remove stellar angular momentum by disk-locking is close to the ONC age (
and an initial rotation rate at 10% of the break-up velocity, concluded that the time-scale
needed to remove stellar angular momentum by disk-locking is close to the ONC age (![]() 1-3 Myr). In addition,
he suggested that if these properties change with mass in a way to enhance the braking for higher masses, this could explain
the bimodal distribution found in some studies. Then, Makidon et al. (2004) report for stars of NGC 2264 (
1-3 Myr). In addition,
he suggested that if these properties change with mass in a way to enhance the braking for higher masses, this could explain
the bimodal distribution found in some studies. Then, Makidon et al. (2004) report for stars of NGC 2264 (![]() 2-4 Myr)
no conclusive evidence that more slowly rotating stars show disk indicators or that faster rotating stars are less likely
to show disk indicators. Later, Littlefair et al. (2005) find in IC 348 (
2-4 Myr)
no conclusive evidence that more slowly rotating stars show disk indicators or that faster rotating stars are less likely
to show disk indicators. Later, Littlefair et al. (2005) find in IC 348 (![]() 2-4 Myr)
2-4 Myr)
![]() bimodality at
bimodality at
![]() and unimodality at
and unimodality at
![]() and claim a strong mass effect as explanation. The same year,
Lamm et al. (2005) find evidence of disk-locking for stars of the same OB association, less pronounced for low
masses (
and claim a strong mass effect as explanation. The same year,
Lamm et al. (2005) find evidence of disk-locking for stars of the same OB association, less pronounced for low
masses (
![]() ). For this mass regime they speak about ``moderate angular momentum loss''. More recently,
Rebull et al. (2006) and Cieza & Baliber (2007) find that in Orion and NGC 2264 stars with long
periods are more likely than those with short periods to have IR excesses suggestive of disks. Very recently,
Nguyen et al. (2009) find in Taurus-Auriga and Chamaeleon I (
). For this mass regime they speak about ``moderate angular momentum loss''. More recently,
Rebull et al. (2006) and Cieza & Baliber (2007) find that in Orion and NGC 2264 stars with long
periods are more likely than those with short periods to have IR excesses suggestive of disks. Very recently,
Nguyen et al. (2009) find in Taurus-Auriga and Chamaeleon I (![]() 2 Myr) that both accretors and non-accretors
have similar distributions of
2 Myr) that both accretors and non-accretors
have similar distributions of ![]() ,
while Rodriguez-Ledesma et al. (2009) confirm the result found by
Herbst et al. (2000,2001,2002) in ONC.
,
while Rodriguez-Ledesma et al. (2009) confirm the result found by
Herbst et al. (2000,2001,2002) in ONC.
From a theoretical point of view, Matt & Pudritz (2004) critically examined the disk-locking theory and showed that in stars, such as CTTSs, where the magnetic field is strong, it is also highly twisted and disordered. The differential rotation between the star and disk naturally leads to an opening (i.e. disconnecting) of the magnetic field between the two. Consequently, the resulting spin-down torque on the star by the disk is significantly reduced, and the disk-locking model cannot account for accreting stars that spin slowly (e.g., about 10% of the break-up velocity). Hence, the disk-locking scenario does not explain the angular momentum loss of the slow rotators. They conclude that, in order for accreting protostars to spin as slowly as 10% of the break-up speed, there must be spin-down torques acting on the star other than those carried by magnetic field lines connecting the star to the disk. The presence of open stellar field lines leads them to the possibility that excess angular momentum is carried by a stellar wind along those open lines (Matt & Pudritz 2004).
Therefore, it is clear that the angular momentum evolution for very low-mass stars is still not well understood. For a review concerning the rotation and angular momentum evolution of young and very low-mass stars from observative and theoretical points of view, see Herbst & Mundt (2005), Herbst et al. (2007), and Irwin & Bouvier (2009).
In this work we measure H![]() excesses, projected rotational velocities (
excesses, projected rotational velocities (![]() ), and radial velocities (
), and radial velocities (
![]() )
of stars in the ONC with masses between 0.10 and 0.25
)
of stars in the ONC with masses between 0.10 and 0.25 ![]() .
The ONC is the nearest large region of on-going star formation. Our
study of this star-forming region is aimed at investigating whether
there is any observational evidence supporting disk-locking in this
still poorly studied mass range. More specifically, in order to shed
more light on the disk-locking scenario for very low-mass stars, we
look for any relation between rotation and accretion, and rotation and
disk presence. We also look for the fast rotators population first
reported by Stassun et al. (1999)
and compare our rotational velocity distribution to the one derived by Herbst et al. (2000,2001,2002).
.
The ONC is the nearest large region of on-going star formation. Our
study of this star-forming region is aimed at investigating whether
there is any observational evidence supporting disk-locking in this
still poorly studied mass range. More specifically, in order to shed
more light on the disk-locking scenario for very low-mass stars, we
look for any relation between rotation and accretion, and rotation and
disk presence. We also look for the fast rotators population first
reported by Stassun et al. (1999)
and compare our rotational velocity distribution to the one derived by Herbst et al. (2000,2001,2002).
2 Observations, data reduction, and analysis
2.1 Sample selection and observations
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{13125fg1.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg40.png)
|
Figure 1:
H-band 2MASS image showing the spatial distribution of our sample. The field is centered on Trapezium cluster and
covers an area of about 0.5 |
| Open with DEXTER | |
This project has been executed as part of the Science Verification of the Fiber Large Array Multi-Element Spectrograph
( FLAMES; Pasquini et al. 2002) attached to the Kueyen Telescope (UT2) at the Paranal Observatory (ESO). Additional
observations were obtained with FLAMES GTO observations in Period 76A. Both observing runs were performed
with the multi-object GIRAFFE spectrograph in MEDUSA mode![]() . We selected from Hillenbrand (1997) 96 stars with a membership probability
given by Jones & Walker (1988) higher than 95%. Their spatial location is shown in Fig. 1, while their position
in the HR diagram is shown in Fig. 2. Five stars in our sample, namely, JW50, JW99, JW239, JW669, and JW961 following
the Jones & Walker (1988) number, have a mass higher than
. We selected from Hillenbrand (1997) 96 stars with a membership probability
given by Jones & Walker (1988) higher than 95%. Their spatial location is shown in Fig. 1, while their position
in the HR diagram is shown in Fig. 2. Five stars in our sample, namely, JW50, JW99, JW239, JW669, and JW961 following
the Jones & Walker (1988) number, have a mass higher than
![]() and
and
![]() K. In the end, 91 targets were selected covering a mass range of
K. In the end, 91 targets were selected covering a mass range of
![]() according to Siess et al. (2000), i.e. 35% of the
Hillenbrand (1997) sample with
according to Siess et al. (2000), i.e. 35% of the
Hillenbrand (1997) sample with
![]() (cf. Sect. 3.4.2).
(cf. Sect. 3.4.2).
Observations were carried out in 2003 from January 25th to February 3rd
(5 h in 5 nights) and in 2005-2006 from October 15th to
January 20th (8.4 h in 11 nights). Two different GIRAFFE
setups were chosen. The first setup, HR14 (resolution R=28 300)
covers the range 638.3-662.6 nm containing the H![]() line. The second one, HR15 (R=19 300), covers the range 659.9-695.5 nm
containing the Li I line at 6708 Å. A log of the observations is given in Table 1. In particular, 5 stars (namely JW50, JW99, JW239, JW669, and JW961) were observed only with the lithium set-up.
line. The second one, HR15 (R=19 300), covers the range 659.9-695.5 nm
containing the Li I line at 6708 Å. A log of the observations is given in Table 1. In particular, 5 stars (namely JW50, JW99, JW239, JW669, and JW961) were observed only with the lithium set-up.
The GIRAFFE Base-Line Data Reduction Software (girBLDRS![]() ; Blecha et al. 2000)
was used to reduce the data. Sky subtraction is described in Sect. 2.5.2.
; Blecha et al. 2000)
was used to reduce the data. Sky subtraction is described in Sect. 2.5.2.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13125fg2.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg45.png)
|
Figure 2: Positions on the HR diagram of the stars included in our sample. Luminosities and effective temperatures (and their mean errors) are taken from Hillenbrand (1997). The Siess et al. (2000) pre-main sequence evolutionary tracks at X=0.703, Y=0.277, and Z=0.020 are also displayed with the labels representing their masses. The Palla & Stahler (1999) birth-line and isochrones (from 1 to 100 Myr) are showed with dash-dotted and dotted lines, respectively. |
| Open with DEXTER | |
Table 1: Log of the observations.
2.2 Rotational and radial velocity analysis
Radial velocities (
![]() )
and projected rotational velocities (
)
and projected rotational velocities (![]() )
were derived using a cross-correlation
of the object spectrum from 660.6 to 696.5 nm against a CORAVEL-type numerical mask (Benz & Mayor 1984; Baranne et al. 1979)
based on a M4 stellar spectrum (Delfosse et al. 1998). Regions containing telluric lines and strong photospheric lines
(such as the hydrogen lines) were removed from the mask. The cross-correlation function (CCF) can be fairly well fitted
by a Gaussian function where the abscissa of its minimum gives the radial velocity and its width,
)
were derived using a cross-correlation
of the object spectrum from 660.6 to 696.5 nm against a CORAVEL-type numerical mask (Benz & Mayor 1984; Baranne et al. 1979)
based on a M4 stellar spectrum (Delfosse et al. 1998). Regions containing telluric lines and strong photospheric lines
(such as the hydrogen lines) were removed from the mask. The cross-correlation function (CCF) can be fairly well fitted
by a Gaussian function where the abscissa of its minimum gives the radial velocity and its width,
![]() ,
is related to the broadening mechanisms intrinsic to the stars
affecting the photospheric lines convolved by the instrumental profile.
,
is related to the broadening mechanisms intrinsic to the stars
affecting the photospheric lines convolved by the instrumental profile.
In order to compute ![]() using
using
![]() ,
the constants A, and
,
the constants A, and ![]() need to be determined in
the expression below:
need to be determined in
the expression below:
The constant A coupling the differential broadening of the CCF to the
As an example, the CCF for the FLAMES solar spectrum acquired with the same set-up and fiber mode as the stars studied
here was computed![]() . Assuming a
. Assuming a ![]() km s-1 for the Sun,
we found a
km s-1 for the Sun,
we found a
![]() km s-1. Such a difference in the
km s-1. Such a difference in the ![]() would translate to a difference of
1.2 km s-1 in
would translate to a difference of
1.2 km s-1 in
![]() (i.e. the minimum
(i.e. the minimum ![]() we can measure with this GIRAFFE set-up; see cf.
Sect. 2.4). Therefore, we adopt A=1.9 and
we can measure with this GIRAFFE set-up; see cf.
Sect. 2.4). Therefore, we adopt A=1.9 and
![]() km s-1 as the constants in Eq. (1).
km s-1 as the constants in Eq. (1).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13125fg3.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg56.png)
|
Figure 3:
CCF of the Th-Ar emission-line spectrum against a Th-Ar template. The fit gives a
|
| Open with DEXTER | |
2.3 v sin i and
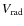 errors
errors
Photon noise errors were estimated as in Melo et al. (2001a). The procedure is summarized as follows. A grid of artificially
rotated spectra from 5 to 20 km s-1 was created based on the GIRAFFE solar spectrum. Gaussian noise was added to
simulate a S/N varying from 5 to 40. For each point on the grid, 96 spectra were generated. The error of
![]() is
similar to the error of
is
similar to the error of ![]() ,
which is given by:
,
which is given by:
For almost all targets several measurements are available. In such cases, the errors quoted in Table 2 are simply based on the scatter of the individual measurements. For four stars (namely, JW99, JW689, JW964, and JW1032) we obtained only one good measurement. In such cases, the errors quoted in Table 2 were computed from the Eq. (2).
2.4 v sin i detection limit
The smallest ![]() that can be measured was estimated using Eq. (4) of Melo et al. (2001a). Visual inspection of
different lines of Th-Ar shows that the typical
that can be measured was estimated using Eq. (4) of Melo et al. (2001a). Visual inspection of
different lines of Th-Ar shows that the typical
![]() is close to 1 km s-1. To
this value, one has to add the typical (external) error (
is close to 1 km s-1. To
this value, one has to add the typical (external) error (
![]() )
of the measurement of
)
of the measurement of
![]() itself. For stars in our sample with multiple observations the mean rms of
itself. For stars in our sample with multiple observations the mean rms of
![]() is about 0.7 km s-1.
is about 0.7 km s-1.
Plugging these values into Eq. (4) of Melo et al. (2001a), we find:
![]() km s-1,
where A=1.9,
km s-1,
where A=1.9,
![]() km s-1, and
km s-1, and
![]() km s-1.
km s-1.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13125fg4.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg62.png)
|
Figure 4:
H |
| Open with DEXTER | |
2.5 Disk and accretion diagnostics
2.5.1  (I
(I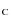 - K) excess
- K) excess
The ![]() -band fluxes are least affected by circumstellar activity and typically dominated by photospheric emission,
while emission arising from accretion disks is maximized at K-band. Hillenbrand et al. (1998) defined a quantity that they used
to measure the magnitude of the near-infrared excess:
-band fluxes are least affected by circumstellar activity and typically dominated by photospheric emission,
while emission arising from accretion disks is maximized at K-band. Hillenbrand et al. (1998) defined a quantity that they used
to measure the magnitude of the near-infrared excess:
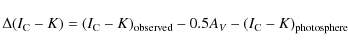
|
(3) |
which represent the difference between the observed
2.5.2 H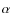 line
line
The width of H![]() profiles is commonly used as an indicator of accretion in T-Tauri stars. Accreting T-Tauri stars (CTTS)
show strong, broad H
profiles is commonly used as an indicator of accretion in T-Tauri stars. Accreting T-Tauri stars (CTTS)
show strong, broad H![]() profiles whose origin is related to infall of high-velocity material forming their circumstellar
disk onto the photosphere (e.g., Hartmann et al. 1994), while weak-line T-Tauri stars (WTTS) show a much narrower H
profiles whose origin is related to infall of high-velocity material forming their circumstellar
disk onto the photosphere (e.g., Hartmann et al. 1994), while weak-line T-Tauri stars (WTTS) show a much narrower H![]() profile,
mostly produced by strong chromospheric activity. Due to differences in the continuum level in the region close to the H
profile,
mostly produced by strong chromospheric activity. Due to differences in the continuum level in the region close to the H![]() line
for different temperatures, no unique value of its equivalent width can be used to distinguish between CTTS and WTTS (Martin 1998).
Hence, the threshold for classifying an object as an accretor depends on the spectral type. White & Basri (2003)
proposed a full width of H
line
for different temperatures, no unique value of its equivalent width can be used to distinguish between CTTS and WTTS (Martin 1998).
Hence, the threshold for classifying an object as an accretor depends on the spectral type. White & Basri (2003)
proposed a full width of H![]() at 10% of the line's peak intensity (what they called the 10% width) as
a more robust and unified criterion to diagnose stellar accretion
regardless the spectral type. Using the presence of veiling as an
accretion criterion, they proposed that a 10% width larger than
270 km s-1 indicates the
star is accreting, and therefore can be classified as a CTTS. Using physical reasons and empirical findings,
Jayawardhana et al. (2003) adopted 200 km s-1 as the accretion cutoff for the very low-mass regime
(down to the limit of hydrogen burning). This value corresponds to a mass accretion rate of about
at 10% of the line's peak intensity (what they called the 10% width) as
a more robust and unified criterion to diagnose stellar accretion
regardless the spectral type. Using the presence of veiling as an
accretion criterion, they proposed that a 10% width larger than
270 km s-1 indicates the
star is accreting, and therefore can be classified as a CTTS. Using physical reasons and empirical findings,
Jayawardhana et al. (2003) adopted 200 km s-1 as the accretion cutoff for the very low-mass regime
(down to the limit of hydrogen burning). This value corresponds to a mass accretion rate of about
![]() yr-1.
Measurements of 10% widths are advantageous over optical veiling and H
yr-1.
Measurements of 10% widths are advantageous over optical veiling and H![]() equivalent width measurements because
they can be extracted over a short wavelength range, do not depend on the underlying stellar luminosity, and do not depend
on the availability of a comparison template (White & Basri 2003).
equivalent width measurements because
they can be extracted over a short wavelength range, do not depend on the underlying stellar luminosity, and do not depend
on the availability of a comparison template (White & Basri 2003).
In order to be able to compute the 10% widths for all fibers (i.e., stellar and sky spectra), we first fitted and then subtracted the continuum around 654 nm up to 660 nm. The continuum subtracted spectra were then normalized by their highest intensity. Some examples of the final spectra used to computed the 10% widths are shown in Fig. 4.
The H![]() profiles in the ONC are known to be strongly contaminated by the nebular emission. However, at our spectral resolution,
the sky emission lines are much narrower than the profile expected for an accreting star (Stassun et al. 1999).
As an additional check of the level of contamination, we compared the
10% widths measured for the object fibers and those allocated to sky
positions. As we can see in Fig. 5, sky fibers show a rather narrow distribution of 10% widths in the range of
50-70 km s-1. In contrast, stars have values from 50 to 250 km s-1. It is worth noticing that, according to
White & Basri (2003) criterion, none of the ONC stars studied here is accreting. This will be better discussed in Sect. 4.
profiles in the ONC are known to be strongly contaminated by the nebular emission. However, at our spectral resolution,
the sky emission lines are much narrower than the profile expected for an accreting star (Stassun et al. 1999).
As an additional check of the level of contamination, we compared the
10% widths measured for the object fibers and those allocated to sky
positions. As we can see in Fig. 5, sky fibers show a rather narrow distribution of 10% widths in the range of
50-70 km s-1. In contrast, stars have values from 50 to 250 km s-1. It is worth noticing that, according to
White & Basri (2003) criterion, none of the ONC stars studied here is accreting. This will be better discussed in Sect. 4.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13125fg5.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg68.png)
|
Figure 5:
Distribution of 10% widths. Sky emission distribution is shown with the filled grey histogram whereas the objects are
displayed in continuous black line. Stars showing 10% widths below |
| Open with DEXTER | |
2.5.3 [3.6]-[8.0] 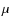 m flux
m flux
The Orion Molecular Cloud was surveyed with the Spitzer Space Telescope as part of GTO program (Megeath et al. 2008).
The IRAC@Spitzer mid-infrered bands can be used as circumstellar disk diagnostics (Rebull et al. 2006). In particular,
the color index based on the two most widely separated bands, namely 3.6 ![]() m and 8
m and 8 ![]() m,
is a very useful method for distinguishing disk and non-disk
candidates, with [3.6]-[8.0] = 1 the boundary between disk
and non-disk candidates (Rebull et al. 2006).
m,
is a very useful method for distinguishing disk and non-disk
candidates, with [3.6]-[8.0] = 1 the boundary between disk
and non-disk candidates (Rebull et al. 2006).
2.5.4 Ca II infrared triplet
As pointed out by Hillenbrand et al. (1998), the Ca II infrared triplet (3 Results and discussion
3.1 Radial velocities and spectroscopic binaries
A histogram of radial velocity measurements for the sample of low-mass stars is shown in Fig. 6. The Gaussian fit of the distribution yields a mean![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg6.ps} \end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg72.png)
|
Figure 6:
Radial velocity distribution for our sample of stars with
|
| Open with DEXTER | |
Among the 96 stars observed, 6 (JW50, JW54, JW239, JW276, JW500, and JW840) show a double-lined CCF (Fig. 7).
Three of these, JW50, JW239, and JW840, were already classified as binaries by Jones & Walker (1988) and Tobin et al. (2009),
and two of them (namely JW50 and JW239) have
![]() (Fig. 2). For our most probable low-mass binaries we show in
Fig. 6 an average of the radial velocities of the two components. The
(Fig. 2). For our most probable low-mass binaries we show in
Fig. 6 an average of the radial velocities of the two components. The
![]() values for both the components
and their mean values are also listed in Table 2 for all the sample.
values for both the components
and their mean values are also listed in Table 2 for all the sample.
Future radial velocity follow-up of such targets would help to solve their orbits and to determine the circularization period in this mass range which can bring interesting information about the frequency of spectroscopic binaries and internal dissipation mechanisms of angular momentum related to the convective motion within the stars (e.g., Melo et al. 2001b).
![\begin{figure}
\par\includegraphics[height=5cm,width=5cm,clip]{13125fg7.eps}\hsp...
...*{5mm}
\includegraphics[height=5cm,width=5cm,clip]{13125fg12.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg74.png)
|
Figure 7: Double-lined CCF profiles for our most probable binary stars. |
| Open with DEXTER | |
3.2 Rotation period and radius from v sin i
We considered the low-mass stars having both ![]() (Fig. 8) above our detection limit of 9 km s-1 as well
as radii determined by Hillenbrand (1997). For these 57 objects we computed
(Fig. 8) above our detection limit of 9 km s-1 as well
as radii determined by Hillenbrand (1997). For these 57 objects we computed
![]() .
For the binary stars,
we considered
.
For the binary stars,
we considered ![]() values of the first component listed in Table 2. These periods distribute according to
a unimodal distribution peaked around
values of the first component listed in Table 2. These periods distribute according to
a unimodal distribution peaked around
![]() day/rad (Fig. 9). Considering a statistical
correction of
day/rad (Fig. 9). Considering a statistical
correction of
![]() (cf. Sect. 3.3), our period distribution seems to have a peak at
(cf. Sect. 3.3), our period distribution seems to have a peak at ![]() 2.4-3.9 days,
while with our
2.4-3.9 days,
while with our
![]() (cf. Sect. 3.3) the peak is around 1.8-3.1 days. This result is in agreement with previous
ones present in the literature for stars with
(cf. Sect. 3.3) the peak is around 1.8-3.1 days. This result is in agreement with previous
ones present in the literature for stars with
![]() (see, e.g., Herbst et al. 2007, and references therein). Namely,
whereas stars with
(see, e.g., Herbst et al. 2007, and references therein). Namely,
whereas stars with
![]() present a bimodal rotational period distribution with two peaks near 2 and 8 days, low-mass stars
(
present a bimodal rotational period distribution with two peaks near 2 and 8 days, low-mass stars
(
![]() )
show a unimodal distribution peaked near 2 days.
)
show a unimodal distribution peaked near 2 days.
Combining our ![]() km s-1 values with the rotation period measured by Herbst et al. (2002) we can constrain the minimum stellar
radii for 23 low-mass stars. Taking into account the relationship
km s-1 values with the rotation period measured by Herbst et al. (2002) we can constrain the minimum stellar
radii for 23 low-mass stars. Taking into account the relationship
![]() ,
we find our
,
we find our ![]() ranges from
0.7 to 1.2
ranges from
0.7 to 1.2
![]() ,
with a distribution peaked to around
,
with a distribution peaked to around
![]() if we consider
if we consider
![]() ,
and
,
and
![]() for our
for our
![]() (cf. Sect. 3.3). The Hillenbrand (1997)'s radii for the same stars
show a peak around
(cf. Sect. 3.3). The Hillenbrand (1997)'s radii for the same stars
show a peak around
![]() .
.
3.3 v sin i and
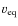
We compared ![]() with equatorial velocities
with equatorial velocities
![]() calculated adopting the radii and rotational
periods by Hillenbrand (1997) and Herbst et al. (2002), respectively (Fig. 10).
calculated adopting the radii and rotational
periods by Hillenbrand (1997) and Herbst et al. (2002), respectively (Fig. 10).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg13.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg87.png)
|
Figure 8:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg14.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg97.png)
|
Figure 9:
Rotational period distribution obtained with our |
| Open with DEXTER | |
Moreover, Fig. 10 shows there is a correlation between ![]() and
and
![]() ,
demostrating, as pointed
out by Rhode et al. (2001), that the periodicity of our T Tauri stars is caused by the rotation of stars with spotted photospheres.
,
demostrating, as pointed
out by Rhode et al. (2001), that the periodicity of our T Tauri stars is caused by the rotation of stars with spotted photospheres.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg15.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg98.png)
|
Figure 10:
|
| Open with DEXTER | |
3.4 Correlations with v sin i
Our ![]() results are given in Table 2. Of the 91 stars observed with
results are given in Table 2. Of the 91 stars observed with
![]() ,
4 stars are bona-fide spectroscopic binaries. The binary stars
will be marked with different symbols in the following plots since
tidal effect may be influencing their surface rotations. Since the
,
4 stars are bona-fide spectroscopic binaries. The binary stars
will be marked with different symbols in the following plots since
tidal effect may be influencing their surface rotations. Since the ![]() values of the binary system components are very similar to each
other, we decided to plot only the first component listed in Table 2. Finally, 34 stars have
values of the binary system components are very similar to each
other, we decided to plot only the first component listed in Table 2. Finally, 34 stars have ![]() less
than or equal to our limit of 9 km s-1.
less
than or equal to our limit of 9 km s-1.
3.4.1 Are stars rotating close to break-up velocity?
In Fig. 11 we show the cumulative distribution normalized to the break-up velocity
![]() (where G is the gravitational constant) for our low-mass stars. The break-up velocities from our stars were computed using
the radii R and masses M taken from Hillenbrand (1997). We compare our results with the
(where G is the gravitational constant) for our low-mass stars. The break-up velocities from our stars were computed using
the radii R and masses M taken from Hillenbrand (1997). We compare our results with the
![]() values derived
by Stassun et al. (1999) for
values derived
by Stassun et al. (1999) for
![]() and with the values obtained considering the
and with the values obtained considering the
![]() derived by Herbst et al. (2002)
and mass and radii taken from Hillenbrand (1997) in the same low-mass regime.
derived by Herbst et al. (2002)
and mass and radii taken from Hillenbrand (1997) in the same low-mass regime.
We show with different lines our results obtained considering ![]() (without the
(without the ![]() correction) and the values
we obtain for our
correction) and the values
we obtain for our ![]() mean value of 0.61 and the statistical value of about 0.785 expected for a random oriented
distribution of stellar rotation axes. A visual inspection suggests that our distributions are very different from the
Stassun et al. (1999) findings. While 23% of the 56 Stassun et al. (1999)'s low-mass stars are rotating faster than
mean value of 0.61 and the statistical value of about 0.785 expected for a random oriented
distribution of stellar rotation axes. A visual inspection suggests that our distributions are very different from the
Stassun et al. (1999) findings. While 23% of the 56 Stassun et al. (1999)'s low-mass stars are rotating faster than
![]() ,
only four stars (namely JW122, JW168, JW530, and JW964) in our sample of 91 stars seems to exceed
the
,
only four stars (namely JW122, JW168, JW530, and JW964) in our sample of 91 stars seems to exceed
the
![]() limit when we consider
limit when we consider
![]() .
This number obviously increases to 8 if we consider our
.
This number obviously increases to 8 if we consider our
![]() .
Similar results are found for the 183 low-mass stars of the Herbst et al. (2002)'s sample, where the percentage of stars
with
.
Similar results are found for the 183 low-mass stars of the Herbst et al. (2002)'s sample, where the percentage of stars
with
![]() is about 10%. Thus, we can definitely assert that in our sample, no
star is rotating close to the break-up velocity estimated for its mass and radius. Excluding effects due to mass selection
effects of the samples, an effect linked to the spatial segregation cannot be excluded, because the stellar population observed
by Stassun et al. (1999) spans a big area of
is about 10%. Thus, we can definitely assert that in our sample, no
star is rotating close to the break-up velocity estimated for its mass and radius. Excluding effects due to mass selection
effects of the samples, an effect linked to the spatial segregation cannot be excluded, because the stellar population observed
by Stassun et al. (1999) spans a big area of
![]() centered on the Trapezium in ONC, while our stars are localized in an
smaller area of
centered on the Trapezium in ONC, while our stars are localized in an
smaller area of
![]() .
Also the stars of Herbst et al. (2002) are localized in a smaller area (
.
Also the stars of Herbst et al. (2002) are localized in a smaller area (
![]() ).
In particular, as shown in Fig. 1, about 62% of our sample is almost inside the circle with radius equal to
the so-called cluster radius (
).
In particular, as shown in Fig. 1, about 62% of our sample is almost inside the circle with radius equal to
the so-called cluster radius (
![]() ;
Hillenbrand 1997) where Rodriguez-Ledesma et al. (2009) find an indication of higher
;
Hillenbrand 1997) where Rodriguez-Ledesma et al. (2009) find an indication of higher
![]() compared to the stars outside
compared to the stars outside
![]() .
This could indicate objects closer to the Trapezium center tend
to rotate on average slower than the outer ones. An inspection of the Stassun et al. (1999)'s
.
This could indicate objects closer to the Trapezium center tend
to rotate on average slower than the outer ones. An inspection of the Stassun et al. (1999)'s
![]() data seems to indicate
an almost flat distribution for radii smaller than
data seems to indicate
an almost flat distribution for radii smaller than
![]() and the hint of a peak at low
and the hint of a peak at low
![]() for radii bigger
than
for radii bigger
than
![]() .
With our smaller sample, we are not able to reach any successful conclusion. We would need more stars and/or
.
With our smaller sample, we are not able to reach any successful conclusion. We would need more stars and/or
![]() measurements for all their stars. As a consequence, we caution the reader about this issue.
measurements for all their stars. As a consequence, we caution the reader about this issue.
We also computed the Kolmogorov-Smirnov (KS) probability (Press et al. 1992) that the our arrays of data obtained with
![]() and the Stassun et al. (1999)'s values for low-mass stars are drawn from the same distribution. We find that the
KS probability that these data were drawn from the same distribution is only of 0.04%. A value of 0.5% is obtained
considering the stars of Stassun et al. (1999) with
and the Stassun et al. (1999)'s values for low-mass stars are drawn from the same distribution. We find that the
KS probability that these data were drawn from the same distribution is only of 0.04%. A value of 0.5% is obtained
considering the stars of Stassun et al. (1999) with
![]() locatized in the same spatial region of our sample. This
comparison shows that, at least as far as our data is concerned, there is not a fast rotator population in the mass
regime covered by our data.
locatized in the same spatial region of our sample. This
comparison shows that, at least as far as our data is concerned, there is not a fast rotator population in the mass
regime covered by our data.
3.4.2 Is there any evidence supporting disk-locking?
One of the well known implications of the disk-locking scenario is that slowly rotating stars should have accreting disks around them while rapidly rotating stars should not. In fact, this picture has been supported over the years in many different papers (e.g., Bouvier et al. 1993; Rebull et al. 2002; Herbst et al. 2001; Choi & Herbst 1996; Edwards et al. 1993).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg16.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg108.png)
|
Figure 11: Cumulative distribution of equatorial velocities normalized to break-up velocity. Our sample (dashed, continuous, and dotted lines) is compared to the Stassun et al. (1999) low-mass sample (dash-dotted line) and to the Herbst et al. (2002)'s low-mass sample (dot-dot-dot-dashed line). |
| Open with DEXTER | |
In particular, if the diagnostics we use here (
![]() excess, 10% H
excess, 10% H![]() width, [3.8]-[8.0],
and Ca II infrared triplet) and rotation are correlated, in the sense that slow rotators are more likely to show excess and
variability, this is evidence in support of the disk-locking paradigm. As pointed out recently by Irwin & Bouvier (2009),
this means that the population of slowly-rotating stars should show the
presence of a disk (e.g., mid-IR excess) or of active accretion (i.e.
be CTTS), whereas the rapidly-rotating stars should not have disk, or
have recently-dissipated disks, and not be active accretors (i.e.
WTTS). Rebull et al. (2006), analyzing Spitzer mid-IR data for about 900 stars in Orion in the
mass range
width, [3.8]-[8.0],
and Ca II infrared triplet) and rotation are correlated, in the sense that slow rotators are more likely to show excess and
variability, this is evidence in support of the disk-locking paradigm. As pointed out recently by Irwin & Bouvier (2009),
this means that the population of slowly-rotating stars should show the
presence of a disk (e.g., mid-IR excess) or of active accretion (i.e.
be CTTS), whereas the rapidly-rotating stars should not have disk, or
have recently-dissipated disks, and not be active accretors (i.e.
WTTS). Rebull et al. (2006), analyzing Spitzer mid-IR data for about 900 stars in Orion in the
mass range
![]() find that slowly-rotating stars are indeed more likely to posses disks
than rapidly-rotating stars. However, they also find a puzzling
population of slow-rotating stars without disks. This result has been
also confirmed subsequently (e.g., Cieza & Baliber 2007).
find that slowly-rotating stars are indeed more likely to posses disks
than rapidly-rotating stars. However, they also find a puzzling
population of slow-rotating stars without disks. This result has been
also confirmed subsequently (e.g., Cieza & Baliber 2007).
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{13125fg17.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg110.png)
|
Figure 12:
Rotation against disk tracers. Rotational velocity as a function of the near infrared excess. A
drop in the rotation rate is clearly seen for stars with a circumstellar disk (i.e.,
|
| Open with DEXTER | |
Concerning Orion, Stassun et al. (1999) have challenged the disk-locking scenario claiming no correlation
between rotation and infrared properties related to circumstellar disks. The issue was re-examined by Herbst et al. (2002)
using the
![]() color excess derived by Hillenbrand et al. (1998) as a disk tracer and their own rotation measurements. They
found that the mean value of
color excess derived by Hillenbrand et al. (1998) as a disk tracer and their own rotation measurements. They
found that the mean value of
![]() for the rapidly rotating sample (i.e., rotation period shorter than
3.14 days) is of 0.17 mag, whereas for the slowly rotating
sample (i.e., rotation period longer than 6.28 days) this value
rises to 0.55 mag well above the limit of
for the rapidly rotating sample (i.e., rotation period shorter than
3.14 days) is of 0.17 mag, whereas for the slowly rotating
sample (i.e., rotation period longer than 6.28 days) this value
rises to 0.55 mag well above the limit of
![]() .
The trend observed in Fig. 12 is in agreement with the
results reported by Herbst et al. (2001,2002).
.
The trend observed in Fig. 12 is in agreement with the
results reported by Herbst et al. (2001,2002).
According to the disk-locking theory, a star is thought to be anchored
or locked to its disk via its magnetic field that threads the
circumstellar disk. Accretion of disk material occurs along the
magnetic field lines. Thus, correlations between accretion indicators
such as H![]() equivalent width or veiling index and rotation are expected (e.g., Hillenbrand et al. 1998; Hartigan et al. 1995).
Sicilia-Aguilar et al. (2005) carried out a careful analyses of the H
equivalent width or veiling index and rotation are expected (e.g., Hillenbrand et al. 1998; Hartigan et al. 1995).
Sicilia-Aguilar et al. (2005) carried out a careful analyses of the H![]() profiles for a sample of 237 members of the ONC. They show that although
the distribution of
profiles for a sample of 237 members of the ONC. They show that although
the distribution of
![]() -excess for CTTS and WTTS overlap, a
-excess for CTTS and WTTS overlap, a
![]() -excess of 0.5 can be taken as a
trustful criteria to distinguish between CTTS and WTTS. As in Herbst et al. (2002), Sicilia-Aguilar et al. (2005) also found evidence of a
different behavior in rotation between the CTTS and WTTS in line with that predicted by the disk-locking scenario.
-excess of 0.5 can be taken as a
trustful criteria to distinguish between CTTS and WTTS. As in Herbst et al. (2002), Sicilia-Aguilar et al. (2005) also found evidence of a
different behavior in rotation between the CTTS and WTTS in line with that predicted by the disk-locking scenario.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg18.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg114.png)
|
Figure 13:
Rotation against accretion tracers. Rotational velocity as a function of the full width of
the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.2cm,clip]{13125fg19.eps}\hspace*{7mm...
...eps}\hspace*{7mm}
\includegraphics[width=5.2cm,clip]{13125fg21.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg115.png)
|
Figure 14: Schematic view of the diagram angular rotational velocity versus color excess for three different evolutive times. |
| Open with DEXTER | |
As already pointed out in Sect. 2.5.2, if the 10% width criterion suggested by White & Basri (2003) is used to trace
accretors, none of the stars in our sample is actually accreting. In Fig. 13 we
plot again the projected angular velocity as a function of the measured 10% widths. The vertical line marks the
maximum value of 10% width measured in our sky spectra (at ![]() 76 km s-1). Therefore, stars with a 10%-width
less than this value are likely to be dominated by the sky emission. We promptly see that only 8 stars appear clearly to the
right side of the vertical line. Two of them (JW937 and JW1036) show color excess
76 km s-1). Therefore, stars with a 10%-width
less than this value are likely to be dominated by the sky emission. We promptly see that only 8 stars appear clearly to the
right side of the vertical line. Two of them (JW937 and JW1036) show color excess
![]() .
The other 4 slowly-rotating stars (JW52, JW296, JW559, and JW574) are sligthly on the right side of the vertical line,
and with their values of
.
The other 4 slowly-rotating stars (JW52, JW296, JW559, and JW574) are sligthly on the right side of the vertical line,
and with their values of ![]() 77-79 km s-1 seem to be not highly influenced by the sky fibers (Fig. 5).
Thus, even if all these objects are taken as bona-fide accretors, we can safely state that
essentially only a fraction of about 14% are accretors in our sample of
77-79 km s-1 seem to be not highly influenced by the sky fibers (Fig. 5).
Thus, even if all these objects are taken as bona-fide accretors, we can safely state that
essentially only a fraction of about 14% are accretors in our sample of
![]() ,
which is lower than the
range 61-88% obtained by Hillenbrand et al. (1998) and 40-80% obtained by Sicilia-Aguilar et al. (2005). We do not
believe this is due to an effect of sample selection, because our targets represent about 35% of the Hillenbrand et al. (1998)
sample with
,
which is lower than the
range 61-88% obtained by Hillenbrand et al. (1998) and 40-80% obtained by Sicilia-Aguilar et al. (2005). We do not
believe this is due to an effect of sample selection, because our targets represent about 35% of the Hillenbrand et al. (1998)
sample with
![]() ,
available
,
available
![]() ,
and membership probability higher than 95%. Moreover,
our sample is well sampled in
,
and membership probability higher than 95%. Moreover,
our sample is well sampled in
![]() .
In particular, considering the range
.
In particular, considering the range
![]() suitable
as disk diagnostics, our sample represents about 25% of the Hillenbrand et al. (1998) targets. Thus, in order to
better understand our results, we considered the Sicilia-Aguilar et al. (2005) sample in the low-mass range
suitable
as disk diagnostics, our sample represents about 25% of the Hillenbrand et al. (1998) targets. Thus, in order to
better understand our results, we considered the Sicilia-Aguilar et al. (2005) sample in the low-mass range
![]() ,
and we found a percentage of accretors of 13-26%, which is more consistent with our findings. Thus, our results
seem to be explained by assuming that low-mass stars are by percentage less active accretors than higher-mass
stars. Relationships between accretion rates and mass of the central object have been investigated by several authors
(see, e.g., the case of
,
and we found a percentage of accretors of 13-26%, which is more consistent with our findings. Thus, our results
seem to be explained by assuming that low-mass stars are by percentage less active accretors than higher-mass
stars. Relationships between accretion rates and mass of the central object have been investigated by several authors
(see, e.g., the case of ![]() Ophiucus, where Natta et al. (2006) find
Ophiucus, where Natta et al. (2006) find
![]() in
in
![]() stars).
stars).
Contrary to the case of more massive stars where disk-locking is supported by rotation-color excess and rotation-accretion
correlations (Sicilia-Aguilar et al. 2005; Herbst et al. 2002), the lack of strong concordance between Fig. 12
and Fig. 13 is intriguing. Dividing the data in Fig. 13 in four boxes by
![]() rad/day and
rad/day and
![]() km s-1, the one-sided
km s-1, the one-sided ![]() Fisher's exact test leads to a p-value
of 0.936, implying a probability of correlation of only 6.4%.
Fisher's exact test leads to a p-value
of 0.936, implying a probability of correlation of only 6.4%.
Herbst et al. (2002) showed evidence in the ONC for a
clear difference in the rotation behavior for stars below 0.25![]() and those more massive than 0.25
and those more massive than 0.25![]() and this was also observed by Lamm et al. (2005) for the older cluster NGC 2264. When the angular velocities of both
groups are compared (Fig. 19 of Herbst et al. 2002), the distribution of angular velocity for the more massive stars is highly
concentrated in one bin only at
and this was also observed by Lamm et al. (2005) for the older cluster NGC 2264. When the angular velocities of both
groups are compared (Fig. 19 of Herbst et al. 2002), the distribution of angular velocity for the more massive stars is highly
concentrated in one bin only at
![]() rad day-1. This is in contrast to the angular velocity distribution for
stars
rad day-1. This is in contrast to the angular velocity distribution for
stars
![]() ,
which spread out essentially between
,
which spread out essentially between
![]() rad day-1. A possible interpretation given by
Herbst et al. (2002) for this difference is that low-mass stars remained locked to their disks for a shorter period of
time as compared to the more massive group. Thus, the distribution seen in ONC for the low-mass stars is already the result of
the spin-up of a group of unlocked stars. Similar findings are reported by Lamm et al. (2005) for NGC 2264.
rad day-1. A possible interpretation given by
Herbst et al. (2002) for this difference is that low-mass stars remained locked to their disks for a shorter period of
time as compared to the more massive group. Thus, the distribution seen in ONC for the low-mass stars is already the result of
the spin-up of a group of unlocked stars. Similar findings are reported by Lamm et al. (2005) for NGC 2264.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg22.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg125.png)
|
Figure 15:
Ca II |
| Open with DEXTER | |
Figure 13 suggests that indeed almost none of the stars observed here are locked to their disks. Are
Fig. 12 and Fig. 13 in contradiction? In other words, can unlocked stars (i.e.,
non accreting stars) still hold a rotation-color-excess relation? In Fig. 14 we schematically describe
the evolution of a rotation (![]() )
and color-excess (disk) diagram. Disk-locking operates for a fixed duration of
time long enough to establish a rotation-color-excess relation. At a time t0 all stars are unlocked
(Fig. 14a). As the contractions proceed all stars (slow and fast rotators) spin-up by a factor proportional
to the value
(Rt0/Rt1)2. Although color-excess diminishes due to disk dissipation, a rotation-color-excess
relation is even stronger since the spin-up depends on
)
and color-excess (disk) diagram. Disk-locking operates for a fixed duration of
time long enough to establish a rotation-color-excess relation. At a time t0 all stars are unlocked
(Fig. 14a). As the contractions proceed all stars (slow and fast rotators) spin-up by a factor proportional
to the value
(Rt0/Rt1)2. Although color-excess diminishes due to disk dissipation, a rotation-color-excess
relation is even stronger since the spin-up depends on ![]() .
Eventually disks disappear completely and we end up
with a large spread in rotation as observed in the ZAMS clusters. Therefore, our Figs. 12 and 13 indicate that: i) the low-mass stars in the ONC are not currently locked, but
ii) the rotation-color-excess relation suggests that these stars were locked once.
.
Eventually disks disappear completely and we end up
with a large spread in rotation as observed in the ZAMS clusters. Therefore, our Figs. 12 and 13 indicate that: i) the low-mass stars in the ONC are not currently locked, but
ii) the rotation-color-excess relation suggests that these stars were locked once.
From Fig. 15, the EW of ![]() 8542 Ca II seems to have values indicating the presence
of broad (also close to one hundred km s-1) Ca II line emission or a partially filled-in line,
phenomena associated with an accreting disk, for low
8542 Ca II seems to have values indicating the presence
of broad (also close to one hundred km s-1) Ca II line emission or a partially filled-in line,
phenomena associated with an accreting disk, for low ![]() ,
while for higher rotational velocities there is
almost no evidence of line emission or filling-in. Hillenbrand et al. (1998) conclude that stars with higher accretion rates should
exhibit detectable Ca II emission above continuum levels, while stars that lack accretion disks should show net Ca II
absorption with absorption equivalent widths
,
while for higher rotational velocities there is
almost no evidence of line emission or filling-in. Hillenbrand et al. (1998) conclude that stars with higher accretion rates should
exhibit detectable Ca II emission above continuum levels, while stars that lack accretion disks should show net Ca II
absorption with absorption equivalent widths
![]() .
Possible explanations of the observed descrepancy
between Figs. 12 and 15 could include the difficulty of measuring
.
Possible explanations of the observed descrepancy
between Figs. 12 and 15 could include the difficulty of measuring
![]() for very late-type stars due to a low spectral resolution and to contrast effects. Moreover, as shown by
Batalha et al. (1984), one expects a strong correlation between optical veiling (i.e., accretion) and the broad component
of the Ca II line. In addition, at the spectral resolution used by Hillenbrand et al. (1998),
the broad component and the narrow component of this line always appear
blended. Finally, small emission-line equivalent widths are more
difficult to detect for low-mass stars because of the photospheric
calcium line and the strong TiO bands. Thus, we think this diagnostic
at present is not reliable and should be revisited using higher
spectral resolution. Nevertheless, the fact that indeed most of the
stars with broader Ca II line are those with
for very late-type stars due to a low spectral resolution and to contrast effects. Moreover, as shown by
Batalha et al. (1984), one expects a strong correlation between optical veiling (i.e., accretion) and the broad component
of the Ca II line. In addition, at the spectral resolution used by Hillenbrand et al. (1998),
the broad component and the narrow component of this line always appear
blended. Finally, small emission-line equivalent widths are more
difficult to detect for low-mass stars because of the photospheric
calcium line and the strong TiO bands. Thus, we think this diagnostic
at present is not reliable and should be revisited using higher
spectral resolution. Nevertheless, the fact that indeed most of the
stars with broader Ca II line are those with
![]() km s-1 (our detection limit) prevent us in connecting
this diagnostic to the disk-locking scenario.
km s-1 (our detection limit) prevent us in connecting
this diagnostic to the disk-locking scenario.
Figure 16 shows the [3.8]-[8.0] color versus ![]() for the stars in common with Rebull et al. (2006). The number
of stars is very limited (13), so it would seem conclusions could not be drown. We notice, however, that all the stars
with strong color excess (i.e. above [3.8]-[8.0] = 1) are slow rotators, and 7/10 have only detection limit
for the stars in common with Rebull et al. (2006). The number
of stars is very limited (13), so it would seem conclusions could not be drown. We notice, however, that all the stars
with strong color excess (i.e. above [3.8]-[8.0] = 1) are slow rotators, and 7/10 have only detection limit ![]() measurements.
Applying the one-sided Fisher's exact test, after the division of the plot at
measurements.
Applying the one-sided Fisher's exact test, after the division of the plot at
![]() km s-1 and
[3.8]-[8.0] = 1, we find a p-value of 0.038, which supports an association between the data at the
km s-1 and
[3.8]-[8.0] = 1, we find a p-value of 0.038, which supports an association between the data at the ![]() 96% confidence level
(i.e. more than 2 sigma) even though the numbers of measurements is small. Edwards et al. (1993) and
Rebull et al. (2006) found similar results and speculated that the long-period diskless objects have recently released
their disks (within a few hundred thousand years).
96% confidence level
(i.e. more than 2 sigma) even though the numbers of measurements is small. Edwards et al. (1993) and
Rebull et al. (2006) found similar results and speculated that the long-period diskless objects have recently released
their disks (within a few hundred thousand years).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg23.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg129.png)
|
Figure 16:
Rotation against disk tracers. [3.8]-[8.0] as a function of |
| Open with DEXTER | |
3.4.3 Rotation and X-ray activity
Based on X-ray measurements carried out by Chandra in the ONC, Feigelson et al. (2003) have shown that the ONC
stars have stronger X-ray emission than main-sequence stars with similar rotation periods and that the strong
anti-correlation between X-rays and period observed for main-sequence stars is not seen for the ONC population. Instead,
they claim that a marginal correlation (i.e., X-rays increasing with the rotation period) is seen in the data. In
Fig. 17 we show the logarithm of the ratio
![]() of total band X-ray to bolometric
luminosity as a function our
of total band X-ray to bolometric
luminosity as a function our ![]() divided by the theoretical radii for the stars in our sample in common to
Feigelson et al. (2003). In spite of the scatter seen in the X-rays levels, the X-rays-rotation relation seems to be flat,
suggesting that all stars in the sample are close to a ``saturated regime'' down to our detection limit in
divided by the theoretical radii for the stars in our sample in common to
Feigelson et al. (2003). In spite of the scatter seen in the X-rays levels, the X-rays-rotation relation seems to be flat,
suggesting that all stars in the sample are close to a ``saturated regime'' down to our detection limit in ![]() .
Recently,
Mohanty & Basri (2003) find that the chromospheric H
.
Recently,
Mohanty & Basri (2003) find that the chromospheric H![]() activity saturates at
activity saturates at ![]() 3 km s-1 and at
3 km s-1 and at ![]() 10 km s-1
for M4-M5- and for M5.5-M8.5-field dwarfs, respectively, while the X-ray activity saturates at
10 km s-1
for M4-M5- and for M5.5-M8.5-field dwarfs, respectively, while the X-ray activity saturates at ![]() 3 km s-1 for early M stars. Considering their results and our
3 km s-1 for early M stars. Considering their results and our ![]() detection limit, the unsaturated part of the possible activity-rotation
relation is clearly beyond our sensitivity.
detection limit, the unsaturated part of the possible activity-rotation
relation is clearly beyond our sensitivity.
For very low-mass stars (late M and L spectral types), the rotation-activity relationship is not really known, because their low rotation velocity is often below the detection limits (e.g., Stauffer et al. 1997; Mohanty & Basri 2003; Messina 2007).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg24.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg131.png)
|
Figure 17:
Rotation versus activity for our stars. In spite of the scatter seen in the X-rays levels,
the data suggest that all stars in the sample are close to a saturated regime down to our detection limit in |
| Open with DEXTER | |
4 Summary and conclusion
We have presented the results of a search for evidence of the
disk-locking scenario as a mechanism for angular momentum depletion in
a region centered on the Trapezium and extending beyond the ONC. We use
our spectroscopic observations to derive radial velocities, and
rotation rates, and to identify possible stars undergoing active disk
accretion. In addition, we use IR photometric data from the
literature to identify those stars possessing circumstellar disks. The
results for our most probable single low-mass (
![]() )
stars can be summarized as follows.
)
stars can be summarized as follows.
- -
- We find a correlation between
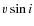 and
and
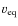 confirming that the observed modulation is due to migrating
inhomogeneities (Rhode et al. 2001).
confirming that the observed modulation is due to migrating
inhomogeneities (Rhode et al. 2001).
- -
- We measure an average
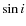 lower than the mean value expected for a random distribution of stellar rotation axes, as already
found by other authors (see, e.g., Rhode et al. 2001).
lower than the mean value expected for a random distribution of stellar rotation axes, as already
found by other authors (see, e.g., Rhode et al. 2001).
- -
- We do not find evidence of a population of fast rotators close to the break-up velocity. This supports the suggestions by Hartmann (2002) that the timescale for angular momentum loss is comparable to the age of the ONC stars, so that disk braking may not be completely effective, at least among the lowest mass stars.
- -
- From the
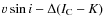 relation we find: 1) slow-rotators with disks, where the low
relation we find: 1) slow-rotators with disks, where the low 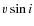 is due
to the coupling between star and disk; 2) slow-rotators without disks, as found by Rebull et al. (2006) and corresponding
to stars that are losing their disks, and hence continuing to rotate slowly for some time, but gradually spinning-up as they
contract towards the ZAMS; 3) fast rotators without disks, where stars get free from their disks becoming fast rotators;
4) almost no fast rotators with disks (with the exception of a single star).
is due
to the coupling between star and disk; 2) slow-rotators without disks, as found by Rebull et al. (2006) and corresponding
to stars that are losing their disks, and hence continuing to rotate slowly for some time, but gradually spinning-up as they
contract towards the ZAMS; 3) fast rotators without disks, where stars get free from their disks becoming fast rotators;
4) almost no fast rotators with disks (with the exception of a single star).
- -
- From the
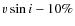 -width relation, we do not find stars are actually accreting, but we argue that all non-accretors
are either low or fast rotators, as found by Jayawardhana et al. (2006) in
-width relation, we do not find stars are actually accreting, but we argue that all non-accretors
are either low or fast rotators, as found by Jayawardhana et al. (2006) in 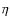 Cha and TW Hydrae (
Cha and TW Hydrae (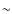 6-8 Myr).
6-8 Myr).
- -
- The Ca II line indicates possible phenomena associated with an accreting disk in stars around our
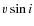 limit, but we are very cautious about this diagnostic at present. A revision at higher resolution to arrive
at a firmer conclusion.
limit, but we are very cautious about this diagnostic at present. A revision at higher resolution to arrive
at a firmer conclusion.
- -
- The few [3.8]-[8.0] colors available for our sample show that all stars with color excess are slow rotators.
- -
- There is no clear relation between rotation and X-ray activity essentially due to the fact that all of our stars occupy ``saturated regime''.
- -
- very low-mass stars in our sample are not locked now, but they were locked in the past;
- -
- the percentage of accretors seems to scale inversely to the mass of the stars.
The authors are very grateful to the referee William Herbst for a careful reading of the paper and constructive suggestions. KB has been supported by the ESO DGDF 2008, and by the Italian Ministero dell'Istruzione, Università e Ricerca (MIUR). CHFM is very obliged to the FLAMES Science Verification team. This research has made use of the SIMBAD database, operated at CDS (Strasbourg, France), and the WEBDA database, operated at the Institute for Astronomy of the University of Vienna. This research made use of Montage, funded by the National Aeronautics and Space Administration's Earth Science Technology Office, Computational Technnologies Project, under Cooperative Agreement Number NCC5-626 between NASA and the California Institute of Technology. The code is maintained by the NASA/IPAC Infrared Science Archive.
References
- Agresti, A. 1992, Statistical Science, 7, 131 [CrossRef]
- Alcalà, J. M., Covino, E., Torres, G., et al. 2000, A&A, 353, 186 [NASA ADS]
- Attridge, J. M., & Herbst, W. 1992, ApJ, 398, L61 [NASA ADS] [CrossRef]
- Barnes, S., & Sofia, S. 1996, ApJ, 462, 746 [NASA ADS] [CrossRef]
- Baranne, A., Mayor, M., & Poncet, J. 1979, Vistas Astron., 23, 279 [NASA ADS] [CrossRef]
- Batalha, C., Stout-Batalha, N. M., Basri, G., & Terra, M. A. O. 1996, ApJS, 103, 211 [NASA ADS] [CrossRef]
- Benz, W., & Mayor, M. 1984, A&A, 138, 183 [NASA ADS]
- Blecha, A., Cayatte, V., North, P., et al. 2000, ed. M. Iye, & A. F. Moorwood, SPIE Conf., 4008, 367
- Bouvier, J., Cabrit, S., Fernandez, M., Martin, E., & Matthews, J. 1993, A&A, 101, 495 [NASA ADS]
- Bouvier, J., Alencar, S. H. P., Harries, T. J., Johns-Krull, C. M., & Romanova, M. M. 2007, Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 479
- Camenzind, M. 1990, Rev. Mex. Astron. Astrofis., 3, 234
- Chandrasekhar, S., & Munch, G. 1950, ApJ, 111, 142 [NASA ADS] [CrossRef]
- Choi, P. I., & Herbst, W. 1996, AJ, 111, 283 [NASA ADS] [CrossRef]
- Cieza, L., & Baliber, N. 2007, ApJ, 671, 605 [NASA ADS] [CrossRef]
- Cohen, M., & Kuhi, L. V. 1979, ApJS, 41, 743 [NASA ADS] [CrossRef]
- Covino, E., Melo, C., Alcalà, J. M., et al. 2001, A&A, 375, 130 [NASA ADS] [EDP Sciences] [CrossRef]
- Delfosse, X., Forveille, T., Perrier, C., & Mayor, M. 1998, A&A, 331, 581 [NASA ADS]
- Edwards, S., Strom, S. E., Hartigan, P., et al. 1993, AJ, 106, 372 [NASA ADS] [CrossRef]
- Feigelson, E. D., Gaffney, J. A., III, Garmire, G., Hillenbrand, L., & Townsley, L. 2003, ApJ, 584, 911 [NASA ADS] [CrossRef]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef]
- Hartigan, P., Edwards, S., & Ghandour, L. 1995, ApJ, 452, 736 [NASA ADS] [CrossRef]
- Hartmann, L. 2002, ApJ, 566, L29 [NASA ADS] [CrossRef]
- Hartmann, L., Hewett, R., & Calvet, N. 1994, ApJ, 426, 669 [NASA ADS] [CrossRef]
- Herbst, W., & Mundt, R. 2005, ApJ, 633, 967 [NASA ADS] [CrossRef]
- Herbst, W., Rhode, K. L., Hillenbrand, L. A., & Curran, G. 2000, AJ, 119, 261 [NASA ADS] [CrossRef]
- Herbst, W., Bailer-Jones, C. A. L., & Mundt, R. 2001, ApJ, 554, L197 [NASA ADS] [CrossRef]
- Herbst, W., Bailer-Jones, C. A. L., Mundt, R., Mesenheimer, K., & Wackermann, R. 2002, A&A, 396, 513 [NASA ADS] [EDP Sciences] [CrossRef]
- Herbst, W., Eislöffel, J., Mundt, R., & Scholz, A. 2007, Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 297
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef]
- Hillenbrand, L. A., Strom, S. E., Calvet, N., et al. 1998, AJ, 116, 1816 [NASA ADS] [CrossRef]
- Jayawardhana, R., Mohanty, S., & Basri, G. 2003, ApJ, 592, 282 [NASA ADS] [CrossRef]
- Jayawardhana, R., Coffey, J., Scholz, A., Brandeker, A., & van Kerkwijk, M. H. 2006, ApJ, 648, 126 [CrossRef]
- Jones, B. F., & Walker, M. F. 1988, AJ, 95, 1755 [NASA ADS] [CrossRef]
- König, K. 1991, ApJ, 370, L37 [NASA ADS]
- Irwin, J., & Bouvier, J. 2009, IAUS, 258, 363 [NASA ADS]
- Lamm, M. H., Mundt, R., Bailer-Jones, C. A. L., & Herbst, W. 2005, A&A, 430, 1005 [NASA ADS] [EDP Sciences] [CrossRef]
- Langsrud, Ø., Jørgensen, K., Ofstad, R., & Næs, T. 2007, J. Appl. Stat., 34, 1275 [CrossRef]
- Littlefair, S. P., Naylor, T., Burningham, B., et al. 2005, MNRAS, 358, 341 [NASA ADS] [CrossRef]
- Makidon, R. B., Rebull, L. M., Strom, S. E., et al. 2004, AJ, 127, 2228 [NASA ADS] [CrossRef]
- Marilli, E., Frasca, A., Covino, E., et al. 2007, A&A, 463, 1081 [NASA ADS] [EDP Sciences] [CrossRef]
- Martín, E. L. 1998, AJ, 115, 351 [NASA ADS] [CrossRef]
- Matt, S., & Pudritz, R. E. 2004, Rev. Mex. Astron. Astrofis., 22, 69
- Megeath, S. T., Allen, L., Calvet, N., et al. 2008, 2008sptz.prop50374M
- Melo, C., Pasquini, L., & De Medeiros, J. R. 2001a, A&A, 375, 851 [NASA ADS] [EDP Sciences] [CrossRef]
- Melo, C., Covino, E., Alcalá, J. M., & Torres, G. 2001b, A&A, 378, 898 [NASA ADS] [EDP Sciences] [CrossRef]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [EDP Sciences] [CrossRef]
- Messina, S. 2007, Mem. Soc. Astron. Ital., 78, 628 [NASA ADS]
- Mohanty, S., & Basri, G. 2003, ApJ, 583, 451 [NASA ADS] [CrossRef]
- Natta, A., Testi, L., & Randich, S. 2006, A&A, 452, 295 [NASA ADS] [EDP Sciences] [CrossRef]
- Nguyen, D. C., Jayawardhana, R., van Kerkwijk, M. H., et al. 2009, ApJ, 694, L153 [NASA ADS] [CrossRef]
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef]
- Parenago, P. P. 1954, Trudy Gosud. Astron. Sternberga, 25, 1 [NASA ADS]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C: The Art of Scientific Computing (New York: Cambridge University Press), 2nd edition
- Prosser, C. F. 1994, ApJ, 421, 517 [NASA ADS] [CrossRef]
- Rebull, L. M. 2001, AJ, 121, 1676 [NASA ADS] [CrossRef]
- Rebull, L. M., Hillenbrand, L. A., Strom S. E., et al. 2000, AJ, 119, 3026 [NASA ADS] [CrossRef]
- Rebull, L. M., Wolff, S. C., Strom S. E., & Makidon, R. B. 2002, AJ, 124, 546 [NASA ADS] [CrossRef]
- Rebull, L. M., Stauffer, J. R., Megeath, S. T., Hora, J. L., & Hartmann, L. 2006, ApJ, 646, 297 [NASA ADS] [CrossRef]
- Rhode, K., Herbst, W., & Mathieu, R. D. 2001, AJ, 122, 3258 [NASA ADS] [CrossRef]
- Rodriguez-Ledesma, M., Mundt, R., & Eislöffel, J. 2009, A&A, 502, 883 [NASA ADS] [EDP Sciences] [CrossRef]
- Shu, F., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [NASA ADS] [CrossRef]
- Sicilia-Aguilar, A., Hartmann, L. W., Szentgyorgyi, A. H., et al. 2005, AJ, 129, 363 [NASA ADS] [CrossRef]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS]
- Stassun, K. G., & Tendrup, D. 2003, PASP, 115, 505 [NASA ADS] [CrossRef]
- Stassun, K. G., Mathieu, R. D., Mazeh, T., & Vrba, F. J. 1999, AJ, 117, 2941 [NASA ADS] [CrossRef]
- Stauffer, J. R., Hartmann, L. W., Prosser, C. F., et al. 1997, ApJ, 479, 776 [NASA ADS] [CrossRef]
- Tobin, J. J., Hartmann, L., Furesz, G., et al. 2009, ApJ, 697, 1103 [NASA ADS] [CrossRef]
- White, R. J., & Basri, G. 2003, ApJ, 582, 1109 [NASA ADS] [CrossRef]
Online Material
Table 2: Our sample.
Footnotes
- ... Cluster
![[*]](/icons/foot_motif.png)
- Based on the FLAMES Science Verification proposal 60.A-9145(A) and the FLAMES proposal 76.C-0524(A).
- ...
![[*]](/icons/foot_motif.png)
- Table 2 is only available in electronic form at http://www.aanda.org
- ... mode
![[*]](/icons/foot_motif.png)
- This is the observing mode in FLAMES
in which 132 fibres with a projected diameter on the sky of 1
 2
feed the GIRAFFE spectrograph. Some fibres are set on the target stars
and others on the sky background.
2
feed the GIRAFFE spectrograph. Some fibres are set on the target stars
and others on the sky background.
- ... (girBLDRS
![[*]](/icons/foot_motif.png)
- http://girbldrs.sourceforge.net/
- ... computed
![[*]](/icons/foot_motif.png)
- Solar spectra for all the GIRAFFE fiber modes and set-ups are available at the web site http://www.eso.org/observing/dfo/quality/GIRAFFE/pipeline/solar.html.
- ... test
![[*]](/icons/foot_motif.png)
- We used the following web calculator (Langsrud et al. 2007): http://www.langsrud.com/fisher.htm
All Tables
Table 1: Log of the observations.
Table 2: Our sample.
All Figures
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{13125fg1.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg40.png)
|
Figure 1:
H-band 2MASS image showing the spatial distribution of our sample. The field is centered on Trapezium cluster and
covers an area of about 0.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13125fg2.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg45.png)
|
Figure 2: Positions on the HR diagram of the stars included in our sample. Luminosities and effective temperatures (and their mean errors) are taken from Hillenbrand (1997). The Siess et al. (2000) pre-main sequence evolutionary tracks at X=0.703, Y=0.277, and Z=0.020 are also displayed with the labels representing their masses. The Palla & Stahler (1999) birth-line and isochrones (from 1 to 100 Myr) are showed with dash-dotted and dotted lines, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13125fg3.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg56.png)
|
Figure 3:
CCF of the Th-Ar emission-line spectrum against a Th-Ar template. The fit gives a
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13125fg4.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg62.png)
|
Figure 4:
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13125fg5.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg68.png)
|
Figure 5:
Distribution of 10% widths. Sky emission distribution is shown with the filled grey histogram whereas the objects are
displayed in continuous black line. Stars showing 10% widths below |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg6.ps} \end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg72.png)
|
Figure 6:
Radial velocity distribution for our sample of stars with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=5cm,width=5cm,clip]{13125fg7.eps}\hsp...
...*{5mm}
\includegraphics[height=5cm,width=5cm,clip]{13125fg12.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg74.png)
|
Figure 7: Double-lined CCF profiles for our most probable binary stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg13.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg87.png)
|
Figure 8:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg14.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg97.png)
|
Figure 9:
Rotational period distribution obtained with our |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg15.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg98.png)
|
Figure 10:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg16.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg108.png)
|
Figure 11: Cumulative distribution of equatorial velocities normalized to break-up velocity. Our sample (dashed, continuous, and dotted lines) is compared to the Stassun et al. (1999) low-mass sample (dash-dotted line) and to the Herbst et al. (2002)'s low-mass sample (dot-dot-dot-dashed line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{13125fg17.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg110.png)
|
Figure 12:
Rotation against disk tracers. Rotational velocity as a function of the near infrared excess. A
drop in the rotation rate is clearly seen for stars with a circumstellar disk (i.e.,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg18.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg114.png)
|
Figure 13:
Rotation against accretion tracers. Rotational velocity as a function of the full width of
the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.2cm,clip]{13125fg19.eps}\hspace*{7mm...
...eps}\hspace*{7mm}
\includegraphics[width=5.2cm,clip]{13125fg21.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg115.png)
|
Figure 14: Schematic view of the diagram angular rotational velocity versus color excess for three different evolutive times. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg22.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg125.png)
|
Figure 15:
Ca II |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg23.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg129.png)
|
Figure 16:
Rotation against disk tracers. [3.8]-[8.0] as a function of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13125fg24.ps}
\end{figure}](/articles/aa/full_html/2009/48/aa13125-09/Timg131.png)
|
Figure 17:
Rotation versus activity for our stars. In spite of the scatter seen in the X-rays levels,
the data suggest that all stars in the sample are close to a saturated regime down to our detection limit in |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.