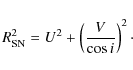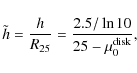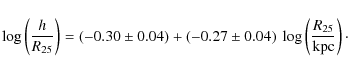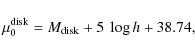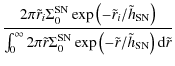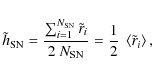The radial distribution of core-collapse supernovae in spiral host galaxies

A. A. Hakobyan; G. A. Mamon; A. R. Petrosian; D. Kunth; M. Turatto

doi:10.1051/0004-6361/200912795

Home

All issues

Volume 508 / No 3 (December IV 2009)

A&A, 508 3 (2009) 1259-1268

Full HTML

Free Access

Issue		A&A Volume 508, Number 3, December IV 2009


Page(s)		1259 - 1268
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/200912795
Published online		27 October 2009

A&A 508, 1259-1268 (2009)

The radial distribution of core-collapse supernovae in spiral host galaxies

A. A. Hakobyan¹ - G. A. Mamon^2,3 - A. R. Petrosian¹ - D. Kunth² - M. Turatto⁴

1 - Byurakan Astrophysical Observatory (BAO) and Isaac Newton Institute (INI) of Chile, Armenian Branch, Byurakan 0213, Aragatzotn province, Armenia
2 - Institut d'Astrophysique de Paris (UMR 7095: CNRS & Université Pierre et Marie Curie), 98bis Bd Arago, 75014 Paris, France
3 - Astrophysics & BIPAC, University of Oxford, Keble Road, Oxford OX1 3RH, UK
4 - INAF, Osservatorio Astrofisico di Catania, via Santa Sofia 78, 95123 Catania, Italy

Received 30 June 2009 / Accepted 7 October 2009

Abstract
Aims. With the goal of providing constraints on the nature of the progenitors of core-collapse (CC) supernovae (SNe), we compare their radial distribution within their spiral host galaxies with the distributions of stars and ionized gas in spiral disks.
Methods. SNe positions are taken from the Asiago catalog for a well-defined sample of 224 SNe within 204 host galaxies. The SN radial distances are estimated from the deprojected separations from the host galaxy nuclei, and normalized both to the 25th ${\rm mag~arcsec}^{-2}$ blue-band isophotal radius and (for the first time) to the statistically-estimated disk scale length.
Results. The normalized radial distribution of all CCSNe is consistent with an exponential law, as previously found, with a possible depletion of CCSNe within one-fifth of the isophotal radius (less significant with scale-length normalization). There are no signs of truncation of the exponential distribution of CCSNe out to 7 disk scale lengths. The scale length of the distribution of type II SNe appears to be significantly larger than that of the stellar disks of their host galaxies, but consistent with the scale lengths of Freeman disks. SNe Ib/c have a significantly smaller scale length than SNe II, with little difference between types Ib and Ic. The radial distribution of type Ib/c SNe is more centrally concentrated than that of the stars in a Freeman disk, but is similar to the stellar disk distribution that we infer for the host galaxies. All CCSN subsamples are consistent with the still uncertain distribution of H II regions. The scale length of the CCSN radial distribution shows no significant correlation with the host galaxy morphological type, or the presence of bars. However, low luminosity as well as inclined hosts have a less concentrated distribution (with the scale-length normalized radial distances) of CCSNe, which are probably a consequence of metallicity and selection effects, respectively.
Conclusions. The exponential distribution of CCSNe shows a scale length consistent with that of the ionized gas confirming the generally accepted hypothesis that the progenitors of these SNe are young massive stars. Given the lack of correlation of the normalized radial distances of CCSNe with the morphological type of the host galaxy, we conclude that the more concentrated distribution of SNe Ib/c relative to SNe II must arise from the higher metallicity of their progenitors or possibly from a shallower initial mass function in the inner regions of spirals.

Key words: supernovae: general - galaxies: spiral - galaxies: stellar content

1 Introduction

Most SNe can be assigned to two main physical classes (e.g., Turatto et al. 2007; Turatto 2003): the gravitational collapse of young massive stellar cores (Types Ib, Ic and II SNe) and the thermonuclear explosions of a white dwarf in close binary systems (Type Ia SNe). While SNe with no or weak hydrogen lines were classified into type I, it is now understood that there are actually three spectroscopically and photometrically distinct subclasses of SNe I. Type Ia SNe are characterized by spectra with no hydrogen lines and strong Si II lines (e.g., Livio 2001; Leibundgut 2000). These SNe appear in galaxies of all morphological types (e.g., van den Bergh et al. 2005; Barbon et al. 1999). Type Ib SNe are characterized by spectra with no evident hydrogen lines, weak or absent Si II and strong He I lines. The third subclass, type Ic SNe, discovered later, shows weak or absent hydrogen, helium lines, and Si II. Type II SNe are characterized by the obvious presence of hydrogen lines. This SN type displays a wide variety of properties: type II Plateau SNe (SNe IIP) with flat light curves in the first few months; type II Linear SNe (SNe IIL) with a rapid, steady decline in the same period; the narrow-lined SNe (SNe IIn), dominated by emission lines with narrow components, a sign of energetic interaction between the SN ejecta and the circumstellar material; and type IIb SNe (SNe IIb), a transitional type, which have early time spectra similar to SNe II and late time spectra similar to SNe Ib/c (e.g., Filippenko et al. 1994,1990).

With the exception of SNe Ia, all types of SNe are rare in early-type galaxies (e.g., van den Bergh et al. 2005). Surprisingly, among morphologically classified hosts of SNe Ib/c and SNe II Hakobyan et al. (2008) found 22 cases where the host has been classified as an Elliptical or S0 galaxy. However, all the early-type hosts of SNe Ib/c and SNe II display independent indicators of recent star formation due to merging or gravitational interactions.

According to theoretical models, the progenitors of SNe Ib/c are massive O type stars that have lost most or all of their hydrogen (and their helium in the case of SN Ic progenitors) envelopes, either by strong winds as in Wolf-Rayet stars (e.g., Eldridge & Tout 2004), or through the transfer of material to a binary companion via Roche lobe overflow (e.g., Heger et al. 2003). Progenitors of SNe II are massive stars that retain their hydrogen envelopes (e.g., Hamuy 2003; Woosley & Weaver 1986).

Many observational studies confirm these theoretical interpretations of these classes of core-collapse SNe (CCSNe). The rates of all CCSN types depend on the morphology of the host galaxies. The rates of SNe Ib/c and II per unit stellar mass increase by factors of 3 and 5 respectively from early- to late-type spiral host galaxies (e.g., Mannucci et al. 2005). Given the short lifetime of their massive progenitors, the rate of CCSNe in host galaxies directly traces the current star formation rate (e.g., Malek et al. 2003). Conversely, when the star formation rate is known, it can be used to verify the consistency of the progenitor scenario (e.g., Hopkins & Beacom 2006).

The observation of progenitor stars of CCSNe in archival pre-explosion images provides a direct test of the theoretical predictions. Since massive evolved stars are the most luminous objects in a galaxy, the progenitors of CCSNe should be directly detectable on pre-explosion images of nearby host galaxies. The advent of data archives of large telescopes with high image quality, most importantly that of the Hubble Space Telescope, has allowed to extend the progenitor detection to distances larger than 20 Mpc (e.g., Maund & Smartt 2005; Van Dyk et al. 2003). These observations have generally confirmed the theoretical predictions mentioned above (e.g., Smartt et al. 2009; Crockett et al. 2007; Pastorello et al. 2007).

The spatial distribution of SNe in host galaxies provides another strong constraint on the nature of SN progenitors. Various studies show that CCSNe are tightly connected to the disk (e.g., Johnson & MacLeod 1963) and to the spiral arm structure (Johnson & MacLeod; Maza & van den Bergh 1976; Van Dyk et al. 1996; Bartunov et al. 1994), which dramatically differs from the SN Ia distribution (e.g., Förster & Schawinski 2008). In addition, CCSNe are well associated with star-forming sites: OB-associations, and H II regions (Tsvetkov et al. 2001; Van Dyk et al. 1996; Bartunov et al. 1994). SNe Ib/c show a higher degree of association with H II regions than do type II SNe, suggesting that the former arise from a higher mass progenitor population than the SNe II (Anderson & James 2008). Most recently, Anderson & James (2009) found that the radial positions of a sample of 177 CCSNe closely follow the radial distribution of H $\alpha$ emission, implying that these SNe are excellent tracers of star formation within galaxies.

One can better constrain the nature of the progenitors of CCSNe by considering quantitative measures of their radial distribution within their host galaxies, after correcting for the inclination of the disk. In their pioneering study, Johnson & MacLeod found a rapidly decreasing surface density distribution of SNe, except for an important lack of SNe in the central regions of spiral galaxies. The surface density of SNe is known to be exponential (Barbon et al. 1975; Vettolani & Zamorani 1977), although two studies (Iye & Kodaira 1975; Guseinov et al. 1980) suggested a ring like distribution. Barbon et al. quantified the exponential to have a slope that amounts to a scale length of $0.46\pm0.03$ times the optical radius, while Vettolani & Zamorani found a scale length of $0.12\pm0.01$ times the optical radius. The difference in scale length arises from the different definitions of optical radius. All SN types, even the SNe Ia, were included in these early studies. Using a large sample of CCSNe (of known types), i.e. 74 SNe Ib/c and SNe II, van den Bergh (1997) found a scale length of 0.22 R₂₅(with no error bar given), where R₂₅ is the isophotal radius for the blue-band surface brightness of $\mu_{\rm B}=25~\rm mag~arcsec^{-2}$ . Also, Bartunov et al. (1992) found that their 99 SNe II have an exponential distribution with scale length that amounts to $(0.27\pm0.08)~R_{25}$ , extending far beyond the optical radius of galaxies. Moreover, Bartunov et al. noticed a sharp decrease in slope of both SNe II and SNe Ib at 1.4 R₂₅.

It has rapidly become apparent that SNe Ib/c are more centrally concentrated within galaxy disks than are SNe II. Bartunov et al. noticed that their 22 SNe Ib show a non-exponential distribution that increases slope with radius so that the scale length varies from $(0.15\pm0.02)~R_{25}$ inside 0.5 R₂₅ to $(0.10\pm0.02)~R_{25}$ between 0.5 and 1.0 R₂₅. The more centrally concentrated distribution of SNe Ib/c in comparison to that of SNe II was also noticed by van den Bergh (1997) and Wang et al. (1997), but, in contrast to the study of Bartunov et al., the difference with the distribution of SNe II was not statistically significant.

Finally, Tsvetkov et al. (2004) found that, while in the central regions, SNe Ib/c are more concentrated than are the SNe II, in the outer regions the two distributions are similar. This result is at odds with the results of Bartunov et al. (1992), who found increasingly dissimilar slopes for the surface densities of SNe II and of SNe Ib/c in the outer regions of spirals.

Additional insight is obtained by comparing the radial distribution of CCSNe in galaxies of different activity or environment. Petrosian & Turatto (1990) found that their sample of 8 SNe II and SNe Ib within galaxies hosting AGN were significantly more radially concentrated in their galaxy hosts than analogous CCSNe in galaxies without active nuclei. Petrosian et al. (2005) studying a sample of 12 SNe II and SNe Ib/c in galaxies hosting AGN, confirmed this result and found that SNe Ib/c in active/star-forming galaxies are more centrally concentrated than are the SNe II, but given the small sample, this difference was not statistically significant. These results were confirmed with larger samples of CCSNe by Hakobyan (2008), who used both one-dimensional and multivariate statistics.

The locations of SN explosions in multiple systems have also been studied. In interacting galaxies, CCSNe are not preferentially located towards the companion galaxy (Navasardyan et al. 2001; Petrosian & Turatto 1995). Similarly, the azimuthal distributions inside the host members of galaxy groups are consistent with being isotropic (Navasardyan et al. 2001).

In this paper, we make use of a considerably larger sample of CCSNe to reanalyze the distribution of deprojected SN radii normalized both to R₂₅ and, for the first time, to indirect estimates of individual stellar disk scale lengths. We make statistical comparisons between the radial distributions of CCSNe and the distribution of blue light and H II regions in the disks of spiral galaxies.

The plan of the paper is as follows. The samples of CCSNe and host galaxies are presented in Sect. 2. We discuss the normalizations in Sect. 3. The results, given in Sect. 4, are discussed and summarized in Sect. 5. Throughout this article we have assumed a value of $H_0=75 ~\rm km ~s^{-1} ~Mpc^{-1}$ for the Hubble constant.

2 The CCSN and host galaxy sample

The present investigation is based upon the Asiago Supernova Catalogue (ASC) (Barbon et al. 1999), updated on 30 September 2008. This version contains 4730 SNe (86 SNe I, 2196 SNe Ia, 304 SNe Ib/c, 1141 SNe II and 1003 unclassified SNe) and data for their host galaxies. Note that for SNe II it includes also subtypes IIP, IIL, IIn, IIb. SNe classified as type I or type Ia, or for which the classification was uncertain (marked as : and ?) or SNe classified from the light curve only (labelled as *) were excluded from the present study. The last SN included in the present investigation is SN 2008fq, discovered on 15 September 2008.

The analysis of the radial distribution of SNe in host galaxies requires a well-defined sample. We have selected all CCSNe and their hosts with the following criteria:

1.: existing SN spectroscopic classification;
2.: host galaxy with morphological type between Sa and Sd, excluding peculiar morphologies;
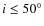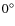3.: host galaxy inclination $i \leq 50^\circ$ to minimize absorption and projection effects ( $0^\circ$ means face-on);
4.: known position angle of the major axis of the host galaxy;
5.: known host galaxy heliocentric radial velocity;
6.: known integrated B magnitude of the host galaxy;
7.: known position of the SN with respect to the galaxy center.

These criteria led to the selection of 239 CCSNe within 216 host galaxies, of which 61 are of type Ib/c (in 61 hosts) and 178 are of type II (in 162 hosts). Our sample includes galaxies with multiple SNe, in particular 19 galaxies with 2 SNe and 1 with 5 SNe. In order to use homogeneous, updated information for all these galaxies, we re-extracted all the main galaxy data from HyperLeda (Paturel et al. 2003) such as absolute magnitudes and isophotal diameters, both corrected for Galactic and host galaxy internal extinction (Schlegel et al. 1998; Bottinelli et al. 1995, respectively) and the former corrected for Virgocentric infall (Terry et al. 2002).

The distribution of morphological types of the 216 host galaxies is peaked around Sbc and Sc. 130 host galaxies are not barred with 38 SNe of type Ib/c and 105 SNe of type II. 86 hosts are barred and have 23 SNe of type Ib/c and 73 SNe of type II.

Because of projection effects, some of the SNe showing small distances to the center may lie quite far away from the center. With the assumption that the CCSNe have young progenitors that are located in the disks of the galaxies, a more realistic separation may be derived, using the inclinations of the host galaxies.

$\begin{figure} \par\includegraphics[width=8.3cm,clip]{aa12795-fig1.eps} \end{figure}$

Figure 1:

Location of the SN within its host galaxy. The center of the galaxy is at the origin of coordinate systems and the star symbol is the projected location of the SN. $\Delta \alpha$ and $\Delta \delta$ are offsets of the SN in equatorial coordinate system, U and V are the coordinates of the SN in the host galaxy coordinate system along the major (U) and minor (V) axes, respectively. The inset in the upper-left corner illustrates the inclination of the polar axis of the galaxy with respect to the line of sight.

Open with DEXTER

Figure 1 illustrates the geometrical location of a SN in the plane of the host galaxy. The coordinates of the SN in its host galaxy coordinate system are

U	=	$\displaystyle \Delta \alpha ~\sin {\rm PA} + \Delta \delta ~\cos {\rm PA} ,$
V	=	$\displaystyle \Delta \alpha ~\cos {\rm PA} - \Delta \delta ~\sin {\rm PA} ,$	(1)

and the true radial distance of the SN to the galactic center satisfies

$\begin{displaymath}R_{\rm SN}^2 = U^2+\left({V\over \cos i} \right)^2 \cdot \end{displaymath}$

(2)

3 Radius normalization

Following Petrosian & Turatto (1990), Bartunov et al. (1992) and van den Bergh (1997), we first normalize the SN radius to the 25th magnitude isophotal radius, R₂₅ (corrected for dust extinction).

The radial surface brightness distribution of spiral disks are well described by an exponential law (e.g., Freeman 1970) $\Sigma^d(R)=\Sigma_0^d \exp(-R/h)$ , where R is radius measured along the disk from the center, h is the scale length of the exponential disk, and $\Sigma_0^d$ is the central surface brightness. In terms of r=R/R₂₅, the surface brightness distribution of disks is $\Sigma^d(r)=\Sigma_0^d \exp(-r/\tilde{h})$ , where the scale length follows the relation

$\begin{displaymath}\tilde{h} = {h\over R_{25}} = {2.5/\ln 10\over 25-\mu_0^{\rm disk}} , \\ \end{displaymath}$

(3)

where $\mu_0^{\rm disk}$ is the disk central B-band surface brightness.

Freeman (1970) asserted that the extrapolated disk central surface blue brightness, corrected for inclination and Galactic absorption, is almost constant and equal to $\mu_0^{\rm Freeman}=21.65\pm0.30$ ${\rm mag~arcsec}^{-2}$ . Inserting $\mu_0^{\rm Freeman}$ into Eq. (3), we obtain the stellar disk scale length of $\tilde{h}_{\rm Freeman}=0.32\pm0.03$ . Hereafter, we denote this stellar distribution as the Freeman disk.

However, the Freeman disk is an oversimplified model: the central disk surface brightness is fainter for late-type spirals, and also decreases with increasing scale length h, as found by Graham & de Blok (2001) in the B and Rbands, as well as Graham (2001) in the K band.

Therefore, rather than assuming that the surface density profile of SNe has a characteristic scale that is proportional to the isophotal radius of their host galaxy, as above, we can alternatively assume that this SN scale is proportional to the stellar disk scale length of their host galaxy, and thus normalize the SN galactocentric radii to the scale lengths of the disks of their host galaxies.

Ideally, we could perform a bulge/disk decomposition for each of our galaxies to obtain the individual disk scale length. However, this is beyond the scope of the present paper, and we have chosen instead to adopt a statistical approach, by relying on the fits of $\log h$ as a function of disk absolute magnitude $M_{\rm disk}$ by Graham & Worley (2008). Noting that the slope in the $\log h$ vs. $M_{\rm disk}$ relation of types Sc and earlier depends little on the waveband (Table 9 of Graham & Worley), we assume that the same holds for later morphological types, and thus take the slopes in the B band from those established by Graham & Worley (their Table 10) in the K band for each morphological type. We also assume that the difference in $\log h$ normalizations between the B and K bands is independent of morphological type. This finally gives us

$\begin{displaymath}\log h = a - 0.4~ b \left (M_{\rm disk}+20\right) , \end{displaymath}$

(4)

where h is in kpc and $M_{\rm disk}$ is the disk absolute blue magnitude. The values for the normalization a and slope b are given in Table 1. Note that Graham & Worley obtained their parameters after correcting for extinction.

$\begin{figure} \par\includegraphics[width=9cm,clip]{aa12795-fig2.eps} \end{figure}$	Figure 2: Comparison of h / R₂₅ and R₂₅, where the scale length h is computed according to Eq. (4) and Table 1. Red filled circles and blue crosses respectively show the early-type (Sa-Sbc) and late-type (Sc-Sd) galaxies. The solid line is a best fit to the full sample of CCSNe.
Open with DEXTER

Table 1: Parameters of the scale length vs. luminosity relation (Eq. (4)).

We estimate the disk magnitudes by adopting the median B band bulge-to-disk ratios $\log({\rm B/D})$ from Fig. 7 of Graham & Worley (2008), i.e. $M_{\rm disk} = M +2.5~\log \left (1+ {\rm B/D} \right )$ .

Figure 2 illustrates the comparison of the two normalized radius indicators. Also shown is the best fit line

$\begin{displaymath}\log \left ({h \over R_{\rm 25}}\right ) = (-0.30\pm0.04) + (-0.27\pm0.04) ~ \log \left ({R_{25}\over {\rm kpc}}\right) \cdot \end{displaymath}$

(5)

The galaxies with large isophotal radii have a smaller ratio of disk scale length to isophotal radius, suggesting (Eq. (3)) that large spiral galaxies have higher central disk surface brightness, as found by Driver et al. (2006). Moreover, since the central disk surface brightness can be written

$\begin{displaymath}\mu_0^{\rm disk} = M_{\rm disk} + 5~\log h + 38.74 , \end{displaymath}$

(6)

where h is in kpc, and combining Eqs. (4) and (6), one finds that $\mu_0^{\rm disk} = 2.5~b/(2~b-1)~\log h + {\rm const.}$ , i.e. higher central surface brightness for larger scale length when b<1/2, which, according to Graham & Worley, occurs for late-type spirals (see Table 1 above).

On average, we find $\langle h /R_{25} \rangle = 0.26\pm0.02$ (where the errors here and below are on the mean). Using Eq. (3), one deduces $\mu_0^{\rm disk} = 20.82~\pm~0.30$ , i.e. about 0.8 mag brighter than the Freeman disk.

From a statistical point of view the central disk surface brightness for the galaxies of our sample can be obtained in either two ways:

1.: given the galaxy isophotal radius R₂₅ and Graham & Worley's statistical estimate of h, using Eq. (3);
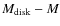2.: given the galaxy absolute magnitude M and Graham & Worley's statistical estimates of $M_{\rm disk}-M$ (given the galaxy type) and h(given the galaxy type and disk luminosity), using Eq. (6).

The first method yields $\mu_0^{\rm disk}=20.91^{+1.36}_{-1.00}$ , 3/4 of a magnitude brighter than the Freeman disk, with some scatter, while the second method yields $\mu_0^{\rm disk}=20.79^{+0.15}_{-0.26}$ , which is even brighter, but with very little scatter. The distribution of the central disk surface brightness is given in Fig. 3.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{aa12795-fig3.eps} \end{figure}$	Figure 3: Distribution of central disk surface brightness obtained from Eqs. (3) ( open bars) and (6) ( filled bars), using our statistical measurement of disk scale length.
Open with DEXTER

Which measure of $\mu_0^{\rm disk}$ is more accurate? The uncertainty on the first measure of $\mu_0^{\rm disk}$ (Eq. (3)) is

$\begin{displaymath}\sigma_{\mu_0^{\rm disk}}^2 = \left ({2.5\over \ln 10}~{R_{25... ...left ({\sigma_{R_{25}}\over R_{25}} \right )^2 \right ] \cdot \end{displaymath}$

Using Eq. (6), the uncertainty on the second measure of $\mu_0^{\rm disk}$ is

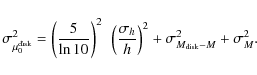
$\begin{displaymath}\sigma_{\mu_0^{\rm disk}}^2 = \left ({5\over \ln 10}\right )^... ...\over h}\right )^2 + \sigma_{M_{\rm disk}-M}^2 + \sigma_M^2 . \end{displaymath}$

Hence the difference in the square uncertainties on the first (Eq. (3)) and second (Eq. (6)) measures of $\mu_0^{\rm disk}$ is equal to

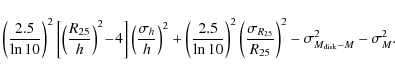
$\begin{displaymath}\left ({2.5\over \ln 10}\right)^2 \left[\left ({R_{25}\over h... ...r R_{25}} \right )^2 - \sigma_{M_{\rm disk}-M}^2 - \sigma_M^2. \end{displaymath}$

Given that, on average, $R_{25}/h \simeq 3.6$ , i.e. (R₂₅/h)² = 12.8, and given typical uncertainties $\sigma_h/h \approx 0.25$ (from Fig. 10a of Graham & Worley), $\sigma_{M_{\rm disk}-M} = 2.5 ({\rm B/D})/(1+{\rm B/D})~ \sigma \log ({\rm B/D}) \la 0.25$ (from Fig. 6 of Graham & Worley), then, even with negligible errors on R₂₅, the uncertainty on the first measure of $\mu_0^{\rm disk}$ (Eq. (3)) is considerably greater than that of the second measure of $\mu_0^{\rm disk}$ (Eq. (6)). We therefore adopt Eq. (6) to estimate $\mu_0^{\rm disk}$ .

In comparison, repeating the same analysis for the 1500 galaxies in a reference sample found in HyperLeda with the same selection as in points 2 to 6 of Sect. 2 (plus a limit on redshift), we find (with Eq. (6)) a mean central disk surface brightness of $\left\langle \mu_0^{\rm disk} \right\rangle = 20.78$ , very similar to the central surface brightness inferred from Eq. (6), indicating that SN hosts do not have centrally brighter disks than other galaxies selected in the same way.

4 Data analysis and results

4.1 Isophotal radius normalization

Figure 4 presents the histograms of the relative radial distributions of types Ib/c and II SNe in the sample of spiral host galaxies. 45 out of 61 SNe Ib/c (74%) are found to be located within relative distance $R_{\rm SN}/R_{25}=0.5$ from the nuclei of their host galaxies, compared to 79 out of 178 (44%) of all SNe II. The average relative radial distances for types SNe Ib/c, SNe II, and all CCSNe are $0.45\pm0.04$ ( $N_{\rm SN}=61$ ), $0.62\pm0.03$ ( $N_{\rm SN}=178$ ) and $0.58\pm0.03$ ( $N_{\rm SN}=239$ ), respectively.

$\begin{figure} \par\includegraphics[width=9cm,clip]{aa12795-fig4.eps} \end{figure}$	Figure 4: Distribution of deprojected isophotal-normalized radial distances for SNe of types Ib/c ( open bars) and II ( filled bars).
Open with DEXTER

The observational deficit of SNe in the central regions of remote galaxies relative to nearer galaxies, the Shaw (1979) effect, is found to be more important for deep photographic SN searches and negligible for visual and CCD searches in nearby galaxies (e.g., Cappellaro et al. 1997). The relative lack of CCSNe at the largest relative galactocentric distances for nearby galaxies might be caused by the limited fields of view of various SN search programs.

Figure 5, similar to Fig. 1 of Wang et al. (1997), illustrates the relative distance of CCSNe from the centers of their hosts vs. the radial velocity of the host galaxy. Spearman rank correlation tests indicate that SNe II show no trend for $R_{\rm SN}/R_{25}$ vs. host galaxy radial velocity (rank correlation coefficient $r_{\rm S} = -0.002$ ). However, these tests indicate strong positive trends between galaxy radial velocity and $R_{\rm SN}/h$ ( $r_{\rm S} = 0.13$ with probability P=0.04 of a stronger trend occurring by chance) for SNe II on one hand, and both $R_{\rm SN}/R_{25}$ ( $r_{\rm S}=0.19, P=0.06$ ) and $R_{\rm SN}/h$ ( $r_{\rm S}=0.20, P=0.05$ ) for SNe Ib/c on the other hand. However, if one removes the nearest galaxies ( $V_{\rm r} < 1000 ~ \rm km ~ s^{-1}$ ), the trends become weaker and no longer statistically significant: $r_{\rm S}=0.10$ , P=0.10 for SNe II with scale length normalization, and $r_{\rm S}=0.08, P=0.27$ for SNe Ib/c with either normalization.

$\begin{figure} \par\includegraphics[width=9cm,clip]{aa12795-fig5.eps}\vspace*{1.5mm} \end{figure}$	Figure 5: Deprojected isophotal-normalized SN-to-host distances vs. radial velocity of host galaxy (as a proxy for distance). SNe Ib/c and SNe II are shown as green filled circles and red plus signs, respectively.
Open with DEXTER

We therefore limit our CCSN sample to distances $V_{\rm r} > 1000~ \rm km ~ s^{-1}$ , thus retaining 224 SNe of the original 239, living in 204 host galaxies. Table 2 displays the matrix of SNe type versus host galaxy morphological type in this reduced sample. The SNe Ib/c are equally split into 25 early-type spiral hosts (Sa to Sbc) and 30 late-type (Sc to Sd), while among the SNe II, 102 are in early-type spirals and only 67 in late-types. But this preference of SNe Ib/c for late-type spirals is not statistically significant (from binomial statistics).

Table 2: Distribution of SN types and host galaxy morphological types.

The distribution of radial distances can be better understood by considering the normalized surface density profile of SNe within their host galaxies. We have determined the surface density of CCSNe, $\Sigma_{j}^{\rm SN} = n_{j} / \pi (r_{j+1}^2 - r_{j}^2)$ where r_jis the relative inner radius of the circular annuli of width r_j+1 - r_j (jth bin), and n_j indicates the number of CCSNe in the jth bin. The top left panel of Fig. 6 shows that the stacked surface density distribution of all 224 CCSNe appears consistent with an exponential law, except for a lack of SNe in the central regions ( $R_{\rm SN} < 0.2~R_{25}$ ).

$\begin{figure} \par\includegraphics[width=17cm,clip]{aa12795-fig6.eps} \end{figure}$

Figure 6:

Top: surface density profiles (with arbitrary normalization) of all CCSNe, with host galaxy isophotal radius normalization ( left), and with disk scale length normalization ( right). The thick solid line shows the maximum likelihood exponential surface density profile of CCSNe. The thin solid line represents the stellar exponential disk of the host galaxies. Bottom: same as top panels, for SNe Ib/c ( green open circles) and SNe II ( red filled circles). The thick lines indicate the maximum likelihood exponential surface density profiles for the SNe Ib/c ( green dashed) and SNe II ( red solid). The error bars assume a Poisson distribution (with $\pm$ 1 object if none is found).

Open with DEXTER

If the surface density of CCSNe is an exponential function of $\tilde{r}=R_{\rm SN}/R_{25}$ (i.e. $\Sigma^{\rm SN}(\tilde{r})=\Sigma_0^{\rm SN} \exp(-\tilde{r}/\tilde{h}_{\rm SN})$ , where $\tilde{h}_{\rm SN}$ is the scale length for the distribution on disk, and $\Sigma_0^{\rm SN}$ is the central surface density of CCSNe), then the probability that a SN is observed at normalized radius $\tilde{r}_i=R_{\rm SN}^i/R_{25}^i$ is

$\displaystyle p\left(\tilde{r}_i \vert \tilde{h}_{\rm SN}\right)$	=	$\displaystyle {2\pi \tilde{r}_i\Sigma_0^{\rm SN}\exp\left(-\tilde{r}_i/\tilde{h... ...gma_0^{\rm SN}\exp\left(-\tilde{r} /\tilde{h}_{\rm SN}\right) {\rm d}\tilde{r}}$
	=	$\displaystyle {\tilde{r}_i\over \tilde{h}_{\rm SN}^2}~ \exp\left(-\tilde{r}_i/\tilde{h}_{\rm SN}\right) .$	(7)

Equation (7) assumes no truncation in the normalized SN radii, and indeed we consider all SN, whatever their distance to the center of their host galaxy. The likelihood of the set of $\{\tilde{r}_i\}$ is

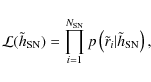
$\begin{displaymath}{\cal L}(\tilde{h}_{\rm SN})=\prod_{i=1}^{N_{\rm SN}} p\left(\tilde{r}_i \vert \tilde{h}_{\rm SN}\right) , \end{displaymath}$

(8)

and maximizing $\ln {\cal L}$ amounts to maximizing

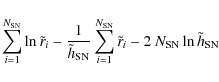
$\begin{displaymath}{\sum_{i=1}^{N_{\rm SN}} \ln \tilde{r}_i} - {1\over{\tilde{h}... ...N_{\rm SN}} \tilde{r}_i - 2 ~N_{\rm SN} \ln \tilde{h}_{\rm SN} \end{displaymath}$

for $\tilde{h}_{\rm SN}$ (where we made use of Eq. (7)). This yields

$\begin{displaymath}\tilde{h}_{\rm SN} = {{\sum_{i=1}^{N_{\rm SN}} \tilde{r}_i}\o... ...rm SN}}} = {1\over2}~\left\langle \tilde{r}_i\right \rangle , \end{displaymath}$

(9)

i.e., the maximum likelihood exponential scale length is half the arithmetic mean of the radial distances. The integral of the denominator of Eq. (7) yields the normalization

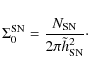
$\begin{displaymath}\Sigma_0^{\rm SN} = {{N_{\rm SN}}\over {2 \pi \tilde{h}_{\rm SN}^2}} {\cdot} \end{displaymath}$

(10)

We check the goodness of fit using the Kolmogorov-Smirnov (KS) test on the normalized cumulative distributions of all SN types, where the exponential model has a cumulative normalized distribution $E(\tilde{r}) = 1 - (1 + {\tilde{r}/\tilde{h}_{\rm SN}}) \exp (- {\tilde{r}/ \tilde{h}_{\rm SN}})$ .

Table 3: Maximum likelihood fits of an exponential surface density profile to the radial distribution of CCSNe.

Table 3 presents the maximum likelihood fits of the exponential surface density profiles. One sees that all SN samples show stacked surface number density distributions that are consistent with an exponential model, with the exception of non-barred early-type spiral hosts (among which are the three galaxies of our 224 SN host galaxy sample with CCSNe beyond 2 R₂₅).

However, Table 3 indicates that the distribution of SNe Ib/c is significantly more centrally concentrated than the distribution of stars in a Freeman disk. More precisely, SNe Ib/c appear 30% more centrally concentrated than SNe II. The scale length of SNe Ib/c is consistent with the scale length of stars in the host galaxies, while the SNe II appear 20% less concentrated than the stars in the host galaxies, but as concentrated as the stars in Freeman disks. The host galaxy morphological type appears to play no role in the distribution of SNe. However, the SNe in nearly face-on host galaxies appear more centrally concentrated than the SNe in more inclined host galaxies. This indicates that observational selection effects (dust extinction and confusion) prevent the observation of SNe near the centers of inclined disks.

The bottom left panel of Fig. 6 highlights the differences in the radial distributions of SNe Ib/c and SNe II. While SNe II have a 30% larger scale length, both classes of SN types show an important (statistically significant for the SNe II) drop in the center ( $R_{\rm SN} < 0.2~R_{25}$ ).

The surface density distributions of H II regions in spiral galaxy disks can also be represented reasonably well by an exponential function (e.g., Hodge & Kennicutt 1983; Athanassoula et al. 1993; García-Gómez et al. 2002), the exceptions being mainly due to unsatisfactory fits of the maxima near the center. Athanassoula et al. found that the H II regions are marginally more concentrated to the centers of spiral galaxies than are the disk stars, with a ratio of scale lengths of $h^{\rm H {\sc ii}} / h$ is $0.8\pm0.4$ . In units of R₂₅, the ionized gas scale length is then $\tilde{h}_{\rm Freeman}^{\rm H {\sc ii}} = 0.26\pm0.13$ if we use the Freeman disk normalization, i.e. Freeman disk scale length of $\tilde{h}_{\rm Freeman}=0.32\pm0.03$ . If we use the CCSN host disk normalization, i.e. CCSN host disk average scale length of $\tilde{h}_{\rm hosts} = \left\langle h/R_{25}\right\rangle = 0.26~\pm~0.02$ , then $\tilde{h}_{\rm hosts}^{\rm H {\sc ii}} = 0.21\pm0.11$ . Given the large uncertainty on the ratio of gas to stellar disk scale length, the SN distribution is not inconsistent with that of the ionized gas.

In reality, the surface brightness profile of massive young stars in galaxies is more complex than a simple exponential disk model: indeed, the surface density of the star formation rate (SFR) has a hole in the center of our galaxy (Rana & Wilkinson 1986), and in other galaxies the SFR follows the surface density of the total (atomic and molecular) gas (Kennicutt 1998a; Buat et al. 1989), which is known to present a hole in the central regions (e.g., Kennicutt 1998b).

Table 4: Kolmogorov-Smirnov tests of the consistency of different CCSN distributions with two exponential disk models.

Table 4 presents, for the full 224 CCSN sample and different subsamples, the KS test probabilities that the isophotal-radius-normalized distributions are consistent with those of the stars in a Freeman disk ( $\tilde{P}_{\rm KS}^{\rm Freeman}$ ), and of the CCSN host disks ( $\tilde{P}_{\rm KS}^{\rm hosts}$ ). While there are several departures from the Freeman exponential disk, most subsamples are consistent with the exponential disk that we infer for the galaxy hosts. This is most significant for the full CCSN sample compared to the Freeman disk, because of the central drop and of the few SNe lying very far out.

Table 5: Kolmogorov-Smirnov tests of the consistency of the radial distributions of CCSNe among different pairs of subsamples.

KS tests comparing different subsamples of CCSNe are given in Table 5. These tests confirm our conclusions based upon the maximum likelihood scale lengths: 1) the radial distribution of SNe Ib/c is highly inconsistent with that of SNe II, because the former are more centrally concentrated (Table 3); 2) the radial distribution of CCSNe is not significantly affected by the morphological type of the host galaxy, the presence of bars, the luminosity of the host galaxy or its disk inclination.

4.2 Scale length normalization

When we normalize the deprojected radial distances of CCSNe to the indirectly determined scale lengths of the disks of their host galaxies, we find that their distribution is even better described by an exponential law. With the exponential model of $\Sigma^{\rm SN}(\hat{r})=\Sigma_0^{\rm SN} \exp(-\hat{r}/\hat{h}_{\rm SN})$ , where $\hat{r}=R_{\rm SN}/h$ , the maximum likelihood estimate of $\hat{h}_{\rm SN} = h_{\rm SN}/h$ will satisfy $\hat{h}_{\rm SN} = {1\over 2}~\left \langle \hat{r}_i \right \rangle$ , as can be found in the same way as Eq. (9). The top right panel of Fig. 6 shows that the stacked surface density profile of all 224 CCSNe appears consistent with an exponential law, with only a very small drop in the central regions ( $R_{\rm SN} < 0.5~h$ ).

Table 3 indicates that all subsamples have surface density profiles that are consistent with the exponential model. The Table also confirms that the mean scale length of SNe II is 35% greater than that of SNe Ib/c, with the scale length of stars in between.

The bottom right panel of Fig. 6 illustrates the different radial distributions of the SNe Ib/c and SNe II. For both SN types, the drop in the center is much less pronounced than with the isophotal radius normalization, and not statistically significant.

Table 4 indicates that nearly all subsamples have surface densities distributions that are consistent with the exponential disks of their host galaxies. The exceptions are early-type, barred, and low luminosity and highly inclined galaxies, as well as SNe II (there are 1 SNe Ic and 4 SNe II lying beyond 7 scale lengths).

Table 5 shows that the distributions of subsamples are consistent when coupled in pairs, except that also with scale-length normalization, SNe Ib/c are significantly more centrally concentrated than are SNe II and that CCSNe are more concentrated in high luminosity host galaxies.

We also find marginal trends for the CCSNe to be more centrally concentrated in face-on host galaxies, and no significant difference between the radial distributions of SNe Ib and SNe Ic.

In addition, we performed KS tests for dividing our subsamples of both types of CCSNe into different distance bins, of the half most nearby and half most distant host galaxies. These tests confirm that the distribution of CCSNe in our sample (both isophotal and scale-length normalizations) is not significantly affected by the distance of the host galaxy (see Table 5).

5 Discussion and conclusions

Our results reported in Sect. 4 (the top panels of Fig. 6, and Table 3) indicate that the global surface density of CCSNe within their host galaxies is exponential with a scale length of $h_{\rm SN} = 0.29\pm0.01~R_{25}$ , which is 30% larger than the scale length found by van den Bergh (1997) with a 5 times smaller sample.

There are several reasons why the observed radial distribution of CCSNe might not be a perfect exponential:

1.: the total radial distribution may be the combination of several components with different distributions;
2.: the inner disk may be destroyed or perturbed by an important bulge;
3.: the inner CCSNe may be confused with the light of the bulge;
4.: dust extinction may prevent the observation of CCSNe in the more opaque inner regions of edge-on spiral galaxies;
5.: the progenitors of CCSNe may follow a truncated exponential disk.

Indeed, the exponential surface density profile is the combination of a dominant exponential surface density profile of SNe II and a secondary steeper exponential surface density profile of SNe Ib/c (see bottom panels of Fig. 6), so it is more prudent to consider the SN types separately. For the SNe II alone, we find a scale length of $0.31\pm0.02~R_{25}$ which is consistent with the result of $0.27\pm0.08~R_{25}$ found by Bartunov et al. (1992) with a sample half the size of ours. But contrary to Bartunov et al., we see no signs of the break in the exponential slope for SNe Ib/c at 0.5 R₂₅ with a sample nearly three times as large (bottom left panel of Fig. 6). An exponential model also fits well the surface density of both types of CCSNe with radii normalized to the (statistically-determined) disk scale lengths (bottom right panel of Fig. 6).

There is a small loss of CCSNe in the central regions of host galaxies (bottom panels of Fig. 6). This is not unexpected since the observed radial distribution of CCSNe can be affected by the internal dust extinction of their hosts as well as the confusion with the high surface brightness of their bulges. In our Galaxy, the star formation rate as a function of galactocentric radius does not follow a pure exponential disk, but is vigorous near the center and is strongly peaked around $R \sim 5 ~\rm kpc$ (e.g., Kennicutt 1989). Since the mean normalized distances of CCSNe in inclined galaxies turn out to be larger than those in face-on ones (Tables 3 and 5), dust extinction plays a quantitative role, and should also explain the central dip in the CCSN surface density profile, mainly seen with the isophotal normalization (bottom left panel of Fig. 6). This dip cannot be explained by confusion with the light from the galaxy bulge, since CCSNe appear more centrally concentrated in the more luminous galaxies.

The dip in the inner distribution of SNe II has also been recently reported by Anderson & James (2009). These authors found that this central deficit of SNe II is offset by a central excess of SNe Ib/c. Instead, our analysis (Fig. 6) shows no central excess for SNe Ib/c. In fact with the isophotal normalization one sees fairly significant central dips in the distributions of both SNe II and SNe Ib/c, while with the scale length normalization there is a small dip for the SNe Ib/c, and only a weak dip at best for the SNe II (neither being statistically significant).

Whereas several authors have suggested that stellar disks are sharply truncated at several scale lengths (e.g., Ruphy et al. 1996, found that the Milky Way is truncated at 6.5 scale lengths), there are no signs of such a truncation in the distribution of CCSNe out to 7 scale lengths (right panels of Fig. 6) and SNe are observed out to nearly 11 scale lengths. In fact, with our fairly large sample, we find weak signs of a shallower slope at large radii, which does not occur at 1.4 R₂₅ as reported by Bartunov et al., but at $R \simeq 2.0~R_{25}$ for SNe II, as we have two SNe II near 2.4 R₂₅(see bottom left panel of Fig. 6).

Since CCSNe are believed to originate from massive stars, one expects that the radial distribution of CCSNe should resemble that of tracers of recent star formation such as ionized gas or perhaps even of future star formation such as molecular gas. The values of scale length $\tilde{h}_{\rm SN}$ for CCSNe in spiral host galaxies (see Col. 3 of Table 3) are in good agreement with the data reported by Athanassoula et al. (1993) on scale lengths of H II regions on exponential disks in spiral galaxies of different types. But the huge uncertainty on the scale length of the ionized gas prevents us from making a firm conclusion here.

We thus focused our analysis of the surface density profiles of CCSNe by comparing them to the surface density profile of stars in spiral disks, which admittedly is a poorer proxy for CCSNe progenitors than are the H II regions. With the isophotal radius normalization, the stacked surface density profile of SNe II is similar to that of the Freeman stellar disk, while the surface density profile of the SNe Ib/c has a smaller scale length than that of the Freeman disk. Given the uncertainties on the relevance of the Freeman disk for spiral galaxies, we also scaled the SN galactocentric distances to our statistical estimate of the scale length of each galaxy. Then, we find that the disk scale length is in between the small scale length of the SNe Ib/c and the larger scale length of the SNe II.

As mentioned above, we also find that SNe Ib/c are significantly more concentrated towards the centers of their host galaxies than are the SNe II, for the isophotal radius normalization (bottom left panel of Fig. 6, as well as Table 5). This result has been known for some time (e.g., Wang et al. 1997; Hakobyan 2008; van den Bergh 1997; Petrosian et al. 2005) for the distribution of radii normalized to R₂₅, but we confirm the more centrally concentrated distribution of SNe Ib/c with our normalization to the disk scale lengths (Fig. 6 and Table 5). For both normalizations, the scale length of the SN Ib/c distribution is roughly 30% smaller than that of the SN II distribution.

We find no statistically significant difference in the radial distributions of SNe Ib and SNe Ic, regardless of the normalization used. This result may appear in conflict with Anderson & James (2009), who found that SNe Ic are more centrally concentrated than SNe Ib, while our measures of the concentration are consistent (see values of $\tilde{h}_{\rm SN}$ and $\hat{h}_{\rm SN}$ in Table 3). However Anderson & James admit that their result is not statistically significant. Moreover, the mean distance of SNe Ic in our sample is pushed up by one SN Ic that lies very far from its host galaxy ( 1.8 R₂₅ and over 10 scale lengths). Still, even if this apparent outlier is omitted from our sample, the normalized radial distributions of SNe Ib and SNe Ic are similar enough that the KS test fails to distinguish them with statistical significance. Admittedly, the analysis of Anderson & James had the advantage of a much more precise measurement of the normalization, as they actually went through the trouble of measuring the light distribution around each host galaxy.

It is a well established fact that the metallicity in spiral disks decreases with increasing galactocentric distance (e.g., Henry & Worthey 1999). The obvious physical explanation for the more peaked radial distribution of SNe Ib/c with respect to SNe II is the effect of metallicity of SN progenitor environment. The local metallicity of the SN progenitor environment (Boissier & Prantzos 2009) as well as the global metallicity of the host galaxy (e.g., Meynet & Maeder 2005; Prantzos & Boissier 2003; Prieto et al. 2008) are approximately correlated with the SN progenitor metallicity: the ratio of the number of SNe Ib/c to SNe II increases with increasing local metallicity in CCSN hosts. In this respect, Eggenberger et al. (2002) found that the number ratio of the blue to red supergiants and the local metallicity in the Milky Way decreases with increasing galactocentric radius. Anderson & James (2009) also concluded that the more concentrated distribution of SNe Ib/c must be related to a strong metallicity dependence on the relative production of these CCSNe, with SNe Ib/c arising from higher metallicity progenitors than SNe II. Note that, since higher luminosity spirals have higher metallicity at the effective radius (Garnett 2002), the more concentrated distribution (with scale-length normalization) of CCSNe in high luminosity galaxies may also be a sign of the higher metallicity of these hosts.

In summary, our reanalysis of a considerably large sample of CCSNe has allowed us to derive precise surface density profiles for different subsamples of CCSNe. These in turn led us to the following statistically based conclusions:

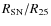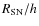1.: The surface density of CCSNe in all studied subsamples (different CCSN type or galaxy host type or luminosity or inclination) falls exponentially with relative radius $R_{\rm SN}/R_{25}$ and $R_{\rm SN}/h$ , with no signs of truncation out to 7 disk scale lengths.
2.: The radial distribution of CCSNe is not significantly affected by the host galaxy type, or by the presence of a bar in the host.
3.: The radial distribution of CCSNe, measured with scale-length normalization, is more concentrated in high luminosity host galaxies.
4.: The radial distribution of SNe Ib/c is significantly more concentrated than the Freeman disk distribution and consistent with the radial distribution of H II regions.
5.: The radial distribution of SNe II is consistent with both the Freeman disk and the H II regions distributions, but significantly less concentrated than the host disks.
6.: There is a small lack of CCSNe within one-fifth of the isophotal radius ( 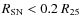$R_{\rm SN} < 0.2~R_{25}$ ), not well visible with scale-length normalization.
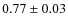7.: The radial distribution of type Ib/c SNe in their host galaxies is more centrally concentrated than that of type II SNe, the ratio of scale lengths is $0.77\pm0.03$ , probably because of a metallicity effect.

It would be worthwhile to extend these analyses, by comparing the radial distribution of CCSNe with recent accurate measures of the radial distribution of molecular gas (i.e. CO), as well as ionized gas (see compilation by Boissier et al. 2003) and even neutral gas, and by extending the analysis to two dimensions (extending previous analyses such as those by Johnson & MacLeod 1963; Bartunov et al. 1994; Van Dyk et al. 1996; and Tsvetkov et al. 2001, making use of the much larger CCSN sample used here).

Acknowledgements

We thank F. Matteucci, N. Prantzos, and J. Silk for useful discussions. This research was supported in part by a grant from the PICS France-Arménie and a scholarship to A.A.H. from the French Government. A.R.P. wishes to thank the Institut d'Astrophysique de Paris (France) for the hospitality and support (via the EARA network) during the beginning stage of this work and the Osservatorio Astrofisico di Catania (Italy) for hospitality during the last stage of this work. This research has made use of the Asiago Supernova Catalogue, which is available at http://web.oapd.inaf.it/supern/cat and the HyperLeda database, available at http://leda.univ-lyon1.fr/. Finally, we are especially grateful to our referee for his/her constructive comments.

References

Anderson, J. P., & James, P. A. 2008, MNRAS, 390, 1527 [NASA ADS]
Anderson, J. P., & James, P. A. 2009, MNRAS, 399, 559 [CrossRef]
Athanassoula, E., García-Gómez, C., & Bosma, A. 1993, A&AS, 102, 229 [NASA ADS]
Barbon, R., Capaccioli, M., & Ciatti, F. 1975, A&A, 44, 267 [NASA ADS]
Barbon, R., Buondí, V., Cappellaro, E., & Turatto, M. 1999, A&AS, 139, 531 [NASA ADS] [EDP Sciences] [CrossRef]
Bartunov, O. S., Makarova, I. N., & Tsvetkov, D. I. 1992, A&A, 264, 428 [NASA ADS]
Bartunov, O. S., Tsvetkov, D. Y., & Filimonova, I. V. 1994, PASP, 106, 1276 [NASA ADS] [CrossRef]
Boissier, S., & Prantzos, N. 2009, A&A, 503, 137 [NASA ADS] [EDP Sciences] [CrossRef]
Boissier, S., Prantzos, N., Boselli, A., & Gavazzi, G. 2003, MNRAS, 346, 1215 [NASA ADS] [CrossRef]
Bottinelli, L., Gouguenheim, L., Paturel, G., & Teerikorpi, P. 1995, A&A, 296, 64 [NASA ADS]
Buat, V., Deharveng, J. M., & Donas, J. 1989, A&A, 223, 42 [NASA ADS]
Cappellaro, E., Turatto, M., Tsvetkov, D. Y., et al. 1997, A&A, 322, 431 [NASA ADS]
Crockett, R. M., Smartt, S. J., Eldridge, J. J., et al. 2007, MNRAS, 381, 835 [NASA ADS] [CrossRef]
Driver, S. P., Allen, P. D., Graham, A. W., et al. 2006, MNRAS, 368, 414 [NASA ADS]
Eggenberger, P., Meynet, G., & Maeder, A. 2002, A&A, 386, 576 [NASA ADS] [EDP Sciences] [CrossRef]
Eldridge, J. J., & Tout, C. A. 2004, MNRAS, 353, 87 [NASA ADS] [CrossRef]
Filippenko, A. V., Porter, A. C., & Sargent, W. L. W. 1990, AJ, 100, 1575 [NASA ADS] [CrossRef]
Filippenko, A. V., Matheson, T., & Barth, A. J. 1994, AJ, 108, 2220 [NASA ADS] [CrossRef]
Förster, F., & Schawinski, K. 2008, MNRAS, 388, L74 [NASA ADS]
Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef]
García-Gómez, C., Athanassoula, E., & Barberà, C. 2002, A&A, 389, 68 [NASA ADS] [EDP Sciences] [CrossRef]
Garnett, D. R. 2002, ApJ, 581, 1019 [NASA ADS] [CrossRef]
Graham, A. W. 2001, MNRAS, 326, 543 [NASA ADS] [CrossRef]
Graham, A. W., & de Blok, W. J. G. 2001, ApJ, 556, 177 [NASA ADS] [CrossRef]
Graham, A. W., & Worley, C. C. 2008, MNRAS, 388, 1708 [NASA ADS] [CrossRef]
Guseinov, O. H., Kasumov, F. K., & Kalinin, E. V. 1980, Ap&SS, 68, 385 [NASA ADS] [CrossRef]
Hakobyan, A. A. 2008, Astrophysics, 51, 69 [NASA ADS] [CrossRef]
Hakobyan, A. A., Petrosian, A. R., McLean, B., et al. 2008, A&A, 488, 523 [NASA ADS] [EDP Sciences] [CrossRef]
Hamuy, M. 2003, in Core Collapse of Massive Stars, ed. C. L. Fryer (Dordrecht: Kluwer) [arXiv:astro-ph/0301006]
Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef]
Henry, R. B. C., & Worthey, G. 1999, PASP, 111, 919 [NASA ADS] [CrossRef]
Hodge, P. W., & Kennicutt, Jr., R. C. 1983, ApJ, 267, 563 [NASA ADS] [CrossRef]
Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef]
Iye, M., & Kodaira, K. 1975, PASJ, 27, 411 [NASA ADS]
Johnson, H. M., & MacLeod, J. M. 1963, PASP, 75, 123 [NASA ADS] [CrossRef]
Kennicutt, Jr., R. C. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef]
Kennicutt, Jr., R. C. 1998a, ApJ, 498, 541 [NASA ADS] [CrossRef]
Kennicutt, Jr., R. C. 1998b, ARA&A, 36, 189 [NASA ADS] [CrossRef]
Leibundgut, B. 2000, A&ARv, 10, 179 [NASA ADS]
Livio, M. 2001, in Supernovae and Gamma-Ray Bursts: the Greatest Explosions since the Big Bang, ed. M. Livio, N. Panagia, & K. Sahu, 334
Malek, M., Morii, M., Fukuda, S., et al. 2003, Phys. Rev. Lett., 90, 061101 [NASA ADS] [CrossRef]
Mannucci, F., Della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [NASA ADS] [EDP Sciences] [CrossRef]
Maund, J. R., & Smartt, S. J. 2005, MNRAS, 360, 288 [NASA ADS] [CrossRef]
Maza, J., & van den Bergh, S. 1976, ApJ, 204, 519 [NASA ADS] [CrossRef]
Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [NASA ADS] [EDP Sciences] [CrossRef]
Navasardyan, H., Petrosian, A. R., Turatto, M., Cappellaro, E., & Boulesteix, J. 2001, MNRAS, 328, 1181 [NASA ADS] [CrossRef]
Pastorello, A., Smartt, S. J., Mattila, S., et al. 2007, Nature, 447, 829 [NASA ADS] [CrossRef]
Paturel, G., Petit, C., Prugniel, P., et al. 2003, A&A, 412, 45 [NASA ADS] [EDP Sciences] [CrossRef]
Petrosian, A. R., & Turatto, M. 1990, A&A, 239, 63 [NASA ADS]
Petrosian, A. R., & Turatto, M. 1995, A&A, 297, 49 [NASA ADS]
Petrosian, A., Navasardyan, H., Cappellaro, E., et al. 2005, AJ, 129, 1369 [NASA ADS] [CrossRef]
Prantzos, N., & Boissier, S. 2003, A&A, 406, 259 [NASA ADS] [EDP Sciences] [CrossRef]
Prieto, J. L., Stanek, K. Z., & Beacom, J. F. 2008, ApJ, 673, 999 [NASA ADS] [CrossRef]
Rana, N. C., & Wilkinson, D. A. 1986, MNRAS, 218, 497 [NASA ADS]
Ruphy, S., Robin, A. C., Epchtein, N., et al. 1996, A&A, 313, L21 [NASA ADS]
Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef]
Shaw, R. L. 1979, A&A, 76, 188 [NASA ADS]
Smartt, S. J., Eldridge, J. J., Crockett, R. M., & Maund, J. R. 2009, MNRAS, 395, 1409 [NASA ADS] [CrossRef]
Terry, J. N., Paturel, G., & Ekholm, T. 2002, A&A, 393, 57 [NASA ADS] [EDP Sciences] [CrossRef]
Tsvetkov, D. Y., Blinnikov, S. I., & Pavlyuk, N. N. 2001, Astron. Lett., 27, 411 [NASA ADS] [CrossRef]
Tsvetkov, D. Y., Pavlyuk, N. N., & Bartunov, O. S. 2004, Astron. Lett., 30, 729 [NASA ADS] [CrossRef]
Turatto, M. 2003, in Supernovae and Gamma-Ray Bursters, ed. K. Weiler, Lecture Notes in Physics (Berlin: Springer Verlag), 598, 21
Turatto, M., Benetti, S., & Pastorello, A. 2007, in Supernova 1987A: 20 Years After: Supernovae and Gamma-Ray Bursters, ed. S. Immler, K. Weiler, & R. McCray, AIP Conf. Ser., 937, 187
van den Bergh, S. 1997, AJ, 113, 197 [NASA ADS] [CrossRef]
van den Bergh, S., Li, W., & Filippenko, A. V. 2005, PASP, 117, 773 [NASA ADS] [CrossRef]
Van Dyk, S. D., Hamuy, M., & Filippenko, A. V. 1996, AJ, 111, 2017 [NASA ADS] [CrossRef]
Van Dyk, S. D., Li, W., & Filippenko, A. V. 2003, PASP, 115, 1 [NASA ADS] [CrossRef]
Vettolani, G., & Zamorani, G. 1977, MNRAS, 178, 693 [NASA ADS]
Wang, L., Hoeflich, P., & Wheeler, J. C. 1997, ApJ, 483, L29 [NASA ADS] [CrossRef]
Woosley, S. E., & Weaver, T. A. 1986, ARA&A, 24, 205 [NASA ADS] [CrossRef]

Footnotes

...(Barbon et al. 1999): http://web.oapd.inaf.it/supern/cat
... HyperLeda: http://leda.univ-lyon1.fr

All Tables

Table 1: Parameters of the scale length vs. luminosity relation (Eq. (4)).

Table 2: Distribution of SN types and host galaxy morphological types.

Table 3: Maximum likelihood fits of an exponential surface density profile to the radial distribution of CCSNe.

Table 4: Kolmogorov-Smirnov tests of the consistency of different CCSN distributions with two exponential disk models.

Table 5: Kolmogorov-Smirnov tests of the consistency of the radial distributions of CCSNe among different pairs of subsamples.

All Figures

$\begin{figure} \par\includegraphics[width=8.3cm,clip]{aa12795-fig1.eps} \end{figure}$	Figure 1: Location of the SN within its host galaxy. The center of the galaxy is at the origin of coordinate systems and the star symbol is the projected location of the SN. $\Delta \alpha$ and $\Delta \delta$ are offsets of the SN in equatorial coordinate system, U and V are the coordinates of the SN in the host galaxy coordinate system along the major (U) and minor (V) axes, respectively. The inset in the upper-left corner illustrates the inclination of the polar axis of the galaxy with respect to the line of sight.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{aa12795-fig2.eps} \end{figure}$	Figure 2: Comparison of h / R₂₅ and R₂₅, where the scale length h is computed according to Eq. (4) and Table 1. Red filled circles and blue crosses respectively show the early-type (Sa-Sbc) and late-type (Sc-Sd) galaxies. The solid line is a best fit to the full sample of CCSNe.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{aa12795-fig3.eps} \end{figure}$	Figure 3: Distribution of central disk surface brightness obtained from Eqs. (3) ( open bars) and (6) ( filled bars), using our statistical measurement of disk scale length.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{aa12795-fig4.eps} \end{figure}$	Figure 4: Distribution of deprojected isophotal-normalized radial distances for SNe of types Ib/c ( open bars) and II ( filled bars).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{aa12795-fig5.eps}\vspace*{1.5mm} \end{figure}$	Figure 5: Deprojected isophotal-normalized SN-to-host distances vs. radial velocity of host galaxy (as a proxy for distance). SNe Ib/c and SNe II are shown as green filled circles and red plus signs, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm,clip]{aa12795-fig6.eps} \end{figure}$	Figure 6: Top: surface density profiles (with arbitrary normalization) of all CCSNe, with host galaxy isophotal radius normalization ( left), and with disk scale length normalization ( right). The thick solid line shows the maximum likelihood exponential surface density profile of CCSNe. The thin solid line represents the stellar exponential disk of the host galaxies. Bottom: same as top panels, for SNe Ib/c ( green open circles) and SNe II ( red filled circles). The thick lines indicate the maximum likelihood exponential surface density profiles for the SNe Ib/c ( green dashed) and SNe II ( red solid). The error bars assume a Poisson distribution (with $\pm$ 1 object if none is found).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.