Companion stars of type Ia supernovae and hypervelocity stars

B. Wang; Z. Han

doi:10.1051/0004-6361/200913326

Free Access

Issue		A&A Volume 508, Number 2, December III 2009


Page(s)		L27 - L30
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200913326
Published online		19 November 2009

A&A 508, L27-L30 (2009)

LETTER TO THE EDITOR

Companion stars of type Ia supernovae and hypervelocity stars

B. Wang^1,2 - Z. Han¹

1 - National Astronomical Observatories/Yunnan Observatory, the Chinese Academy of Sciences, Kunming 650011, PR China
2 - Graduate University of the Chinese Academy of Sciences, Beijing 100049, PR China

Received 21 September 2009 / Accepted 17 November 2009

Abstract
Context. Recent investigations of the white dwarf (WD) + He star channel of Type Ia supernovae (SNe Ia) imply that this channel can produce SNe Ia with short delay times. The companion stars in this channel would survive and potentially be identifiable.
Aims. In this Letter, we study the properties of the companion stars of this channel at the moment of SN explosion, which can be verified by future observations.
Methods. According to SN Ia production regions of the WD + He star channel and three formation channels of WD + He star systems, we performed a detailed binary population synthesis study to obtain the properties of the surviving companions.
Results. We obtained the distributions of many properties of the companion stars of this channel at the moment of SN explosion. We find that the surviving companion stars have a high spatial velocity (>400 km s^-1) after SN explosion, which could be an alternative origin for hypervelocity stars (HVSs), especially for HVSs such as US 708.

Key words: binaries: general - supernovae: general - stars: evolution - white dwards

1 Introduction

Type Ia supernovae (SNe Ia) play an important role in the study of cosmic evolution, especially in cosmology. They have been applied successfully in determining cosmological parameters (e.g., $\Omega$ and $\Lambda$ ; Riess et al. 1998; Perlmutter et al. 1999). It is generally believed that SNe Ia are thermonuclear explosions of carbon-oxygen white dwarfs (CO WDs) in binaries (for the review see Nomoto et al. 1997). However, there is still no agreement on the nature of their progenitors (Hillebrandt & Niemeyer 2000; Podsiadlowski et al. 2008; Wang et al. 2008), and no SN Ia progenitor system has been conclusively identified from before the explosion.

Over the past few decades, two families of SN Ia progenitor models have been proposed, i.e., the double-degenerate (DD) and single-degenerate (SD) models. Of these two models, the SD model is widely accepted at present (Nomoto et al. 1984). It is suggested that the DD model, which involves the merger of two CO WDs (Iben & Tutukov 1984; Webbink 1984; Han 1998), likely leads to an accretion-induced collapse rather than to an SN Ia (Nomoto & Iben 1985). For the SD model, the companion is probably a main-sequence (MS) star, a slightly evolved subgiant star (WD + MS channel), or a red-giant star (WD + RG channel) (e.g., Hachisu et al. 1996, 1999a,b; Li $\&$ van den Heuvel 1997; Langer et al. 2000; Han $\&$ Podsiadlowski 2004, 2006; Chen $\&$ Li 2007, 2009; Meng et al. 2009; Lü et al. 2009; Wang et al. 2009c). An explosion following the merger of two WDs would leave no remnant, while the companion star in the SD model would survive and be potentially identifiable (Podsiadlowski 2003). There has been no conclusive proof yet that any individual object is the surviving companion star of an SN Ia. It will be a promising method to test SN Ia progenitor models by identifying their surviving companions.

Yoon $\&$ Langer (2003) followed the evolution of a CO WD + He star system with a $1.0~M_{\odot}$ CO WD and a $1.6~M_{\odot}$ He star in a 0.124 d orbit. In this binary, the WD accretes He from the He star and grows in mass to the Chandrasekhar (Ch) mass. SNe Ia from this binary channel can neatly avoid H lines. Recently, Wang et al. (2009a) systematically studied the WD + He star channel of SNe Ia. In the study, they carried out binary evolution calculations of this channel for about 2600 close WD binaries, in which a CO WD accretes material from an He MS star or an He subgiant to increase its mass to the Ch mass. The study shows the parameter spaces for the progenitors of SNe Ia. By using a detailed binary population synthesis (BPS) approach, Wang et al. (2009b) find that the Galactic SN Ia birthrate from this channel is $\sim$ $0.3\times 10^{-3}~ {\rm yr}^{-1}$ and that this channel can produce SNe Ia with short delay times ( $\sim$ 45-140 Myr). The companion star in this channel would survive and show distinguishing properties.

In recent years hypervelocity stars (HVSs) have been observed in the halo of the Galaxy. HVSs are stars with a velocity so great that they are able to escape the gravitational pull of the Galaxy. However, the formation of HVSs is still unclear (for a recent review see Tutukov & Fedorova 2009). It has been suggested that such HVSs can be formed by the tidal disruption of a binary through interaction with the super-massive black hole (SMBH) at the Galactic center (GC) (Hills 1988; Yu & Tremaine 2003). The first three HVSs have only recently been discovered serendipitously (e.g., Brown et al. 2005; Hirsch et al. 2005; Edelmann et al. 2005). Up to now, about 17 HVSs have been discovered in the Galaxy (Brown et al. 2009; Tillich et al. 2009), most of which are B-type stars, probably with masses ranging from 3 to 5 $M_\odot$ (Brown et al. 2005, 2009; Edelmann et al. 2005). One HVS, HE 0437-5439, is known to be an apparently normal early B-type star. Edelmann et al. (2005) suggests that the star could have originated in the Large Magellanic Cloud, because it is much closer to this galaxy (18 kpc) than to the GC (see also Przybilla et al. 2008).

At present, only one HVS, US 708, is a subdwarf O (sdO) star, and Hirsch et al. (2005) speculatS that US 708 is formed by the merger of two He WDs in a close binary induced by the interaction with the SMBH in the GC and then escaped. Recently, Perets (2009) has suggested that US 708 may have been ejected as a binary from a triple disruption by the SMBH, which later on evolved and merged to form an sdO star. Because of the existence of the short orbital periods ( $\sim$ 1 h) for the WD + He star systems, Justham et al. (2009) argues that the WD + He star channel of SNe Ia may provide a natural explanation for stars like US 708.

Han (2008a) obtained the distributions of many properties of the surviving companions from the WD + MS channel of SNe Ia. The properties can be verified by future observations. The purpose of this Letter is to investigate the properties of the surviving companions of the WD + He star channel and to explore whether HVSs such as US 708 could have been released from the binaries that produced SNe Ia. In Sect. 2, we describe the BPS approach and the simulation results for the properties of the surviving companions. Finally, a discussion is given in Sect. 3.

2 The distributions of properties of the companion stars

In the WD + He star channel, the progenitor of an SN Ia is a close WD binary system, which has most likely emerged from the CE evolution (Paczynski 1976) of a giant binary system. The CE ejection is still an open problem. Here, we use the standard energy equations (Webbink 1984) to calculate the output of the CE phase. The CE is ejected if

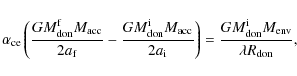
$\begin{displaymath}\alpha_{\rm ce} \left( {G M_{\rm don}^{\rm f} M_{\rm acc} \ov... ...{G M_{\rm don}^{\rm i} M_{\rm env} \over \lambda R_{\rm don}}, \end{displaymath}$

(1)

where $\lambda$ is a structure parameter that depends on the evolutionary stage of the donor, $M_{\rm don}$ is the mass of the donor, $M_{\rm acc}$ the mass of the accretor, a the orbital separation, $M_{\rm env}$ the mass of the donor's envelope, $R_{\rm don}$ the radius of the donor, and the indices ${\rm i}$ and ${\rm f}$ denote the initial and final values, respectively. The right side of the equation represents the binding energy of the CE, the left side shows the difference between the final and initial orbital energy, and $\alpha_{\rm ce}$ is the CE ejection efficiency, i.e., the fraction of the released orbital energy used to eject the CE. For this prescription of the CE ejection, there are two highly uncertain parameters (i.e., $\lambda$ and $\alpha_{\rm ce}$ ). As in previous studies, we combine $\alpha_{\rm ce}$ and $\lambda$ into one free parameter $\alpha_{\rm ce}\lambda$ , and set it to be 0.5 (e.g., Wang et al. 2009b).

To obtain the distributions of properties of the surviving companions, we performed a Monte Carlo simulation in the BPS study. In the simulation, by using the Hurley's rapid binary evolution code (Hurley et al. 2000, 2002), we followed the evolution of $4\times10^{\rm 7}$ sample binaries from the star formation to the formation of the WD + He star systems according to three evolutionary channels (i.e., the He star channel, the EAGB channel, and the TPAGB channel; for details see Wang et al. 2009b). If a binary system evolves to a WD + He star system, and if the system, at the beginning of the Roche lobe overflow (RLOF) phase, is located in the SN Ia production regions in the plane of ( $\log P^{\rm i}$ , $M_2^{\rm i}$ ) for its $M_{\rm WD}^{\rm i}$ , where $P^{\rm i}$ , $M_2^{\rm i}$ and $M_{\rm WD}^{\rm i}$ are, respectively, the orbital period, the secondary's mass, and the WD's mass of the WD + He star system at the beginning of the RLOF (see Fig. 8 of Wang et al. 2009a), we assume that an SN Ia is produced, and the properties of the WD binary at the moment of SN explosion are obtained by interpolation in the three-dimensional grid ( $M_{\rm WD}^{\rm i}$ , $M_2^{\rm i}$ , $\log P^{\rm i}$ ) of the $\sim$ 2600 close WD binaries calculated in Wang et al. (2009a).

In the BPS study, the primordial binary samples are generated in the Monte Carlo way. We adopted the following input for the simulation (e.g., Han et al. 1995a, 2002, 2003, 2007; Han 2008b; Wang et al. 2009b). (1) The star-formation rate (SFR) is taken to be constant over the past 15 Gyr. For the constant SFR, we assume that a binary with its primary more massive than $0.8~M_{\odot}$ is formed annually (e.g., Han et al. 1995b); (2) The initial mass function (IMF) of Miller & Scalo (1979) is adopted; (3) The mass-ratio distribution is taken to be constant; (4) The distribution of separations is taken to be constant in $\log a$ for wide binaries, where a is the orbital separation; (5) The orbits are assumed to be circular.

The simulation gives current-epoch distributions of many properties of companions at the moment of SN explosion, e.g., the masses, the orbital periods, the orbital separations, the orbital velocities, the effective temperatures, the luminosities, the surface gravities, the surface abundances, the mass-transfer rates, the mass-loss rates of the optically thick stellar winds, etc. The simulation also shows the initial parameters of the primordial binaries and the WD binaries that lead to SNe Ia. Figures 1-5 are selected distributions that may be helpful for identifying the surviving companion stars.

3 Discussion

$\begin{figure} \par\includegraphics[width=5.6cm,angle=270]{13326fg1.ps} \end{figure}$	Figure 1: The distribution of properties of companion stars in the plane of ( $V_{\rm orb}$ , $M_2^{\rm SN}$ ) at the current epoch, where $V_{\rm orb}$ is the orbital velocity and $M_2^{\rm SN}$ the mass at the moment of SN explosion.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=5.6cm,angle=270]{13326fg2.ps} \end{figure}$

Figure 2:

Similar to Fig. 1, but in the plane of ( $\log T_{\rm eff}$ , $\log g$ ), where $T_{\rm eff}$ is the effective temperature of companion stars at the moment of SN explosion and $\log g$ the surface gravity. The companion stars are out of thermal equilibrium, e.g., a 1.243 $~M_\odot$ He star with 0.274 $~R_\odot$ and ( $\log T_{\rm eff}$ , $\log g$ ) = (4.70, 5.65) will be a 0.267 $~R_\odot$ He star and with ( $\log T_{\rm eff}$ , $\log g$ ) = (4.75, 5.67) after the He star back to the thermal equilibrium.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.6cm,angle=0]{13326fg3.ps} \end{figure}$	Figure 3: The distribution of spatial velocity for surviving companion stars of SNe Ia. The dotted line denotes the results of ejecta velocity 11 000 km s^-1, while the solid line shows ejecta velocity 13 500 km s^-1.
Open with DEXTER

Figures 1 and 2 show the distributions of the masses, the orbital velocities, the effective temperatures, and the surface gravities of companion stars at the moment of SN explosion. In Fig. 1, the companion star has an orbital velocity of $\sim$ 300-500 ${\rm km~s^{-1}}$ for a corresponding mass of $\sim$ 0.6-1.7 $M_\odot$ at the moment of SN explosion. In the three formation channels of the WD + He star systems, SNe Ia mainly come from the He star channel. For this formation channel, the recorded properties at each step show that a primordial binary system with a primary mass $M_{\rm 1i}\sim 5.0{-}8.0~M_\odot$ , a secondary mass $M_{\rm 2i} \sim 2.0{-}6.5~M_\odot$ , and an orbital period $P_{\rm i} \sim 10{-}40~{\rm d}$ would evolve to a close WD + He star system with a WD mass $M^{\rm i}_{\rm WD} \sim 0.87{-}1.2~M_\odot$ , a He star mass $M^{\rm i}_{\rm 2} \sim 1.0{-}2.6~M_\odot$ , and an orbital period $P^{\rm i} \sim 0.04{-}0.2~{\rm d}$ . Finally, the WD + He star system results in an SN Ia explosion and survives a companion star.

However, Figs. 1 and 2 are for the moment of SN explosion, which could be modified by the explosion. The SN ejecta will interact with its companion. The companion stars will be stripped of some mass and receive a kick velocity that is perpendicular to the orbital velocity. Adopting a similar method to Meng et al. (2007), we estimated the stripped mass for the companion stars of the WD + He star channel and find that the stripped mass is very low, e.g., a 1.243 $~M_\odot$ companion star with 0.274 $~R_\odot$ only loses a mass of 0.015 $~M_\odot$ in our simulation. We also roughly obtain the kick velocity based on the momentum conservation equation. The kick velocity mainly depends on the ratio of separation to the radius of companions at the moment of SN explosion, $A/R_{\rm 2}^{\rm SN}$ , and the leading head velocity of SN ejecta, which is assumed to be in the range of 11 000 to 13 500 km s^-1. The velocity of 11 000 km s^-1 is from the SN ejecta kinetic energy $1.0\times10^{51}$ erg corresponding to the lower limit of normal SN Ia kinetic energy, while the velocity of 13 500 km s^-1 is from the SN ejecta kinetic energy $1.5\times10^{51}$ erg corresponding to the upper limit of the kinetic energy (Gamezo et al. 2003). We can obtain the spatial velocity by the formula $V_{\rm 2}^{\rm SN}=\sqrt{V_{\rm kick}^{2}+V_{\rm orb}^{2}}$ , where $V_{\rm kick}$ and $V_{\rm orb}$ are the kick velocity and the orbital velocity of the companion star at the moment of SN explosion, respectively. In Fig. 3, we show the distribution of the spatial velocity for the surviving companion stars of the WD + He star channel. We see that the surviving companion stars have high spatial velocities (>400 km s^-1) that almost entirely exceed the gravitational pull of the Galaxy nearby the sun. Thus, the surviving companion stars from the WD + He star channel could be an alternative origin for HVSs.

$\begin{figure} \par\includegraphics[width=5.6cm,angle=270]{13326fg4.ps} \end{figure}$	Figure 4: Similar to Fig. 1, but in the plane of ( $\log P^{\rm SN}$ , $M_2^{\rm SN}$ ), where $P^{\rm SN}$ is the orbital period at the moment of SN explosion.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=5.6cm,angle=270]{13326fg5.ps} \end{figure}$	Figure 5: Similar to Fig. 1, but in the plane of ( $V_{\rm rot}$ , $M_2^{\rm SN}$ ), where $V_{\rm rot}$ is the equatorial rotational velocity of companion stars at the moment of SN explosion.
Open with DEXTER

US 708 is an extremely He-rich sdO star in the Galaxy halo, with a heliocentric radial velocity of + $708\pm15$ ${\rm km~s^{-1}}$ (Hirsch et al. 2005). We note that the local velocity relative to the Galatic center may lead to a higher observation velocity for the surviving companion stars, but this may also lead to a lower observation velocity. Considering the local velocity near the sun ( $\sim$ 220 km s^-1), we find that $\sim$ 30% of the surviving companion stars may be observed to have velocity $V>700~{\rm km~s^{-1}}$ for a given SN ejecta velocity 13 500 km s^-1. In addition, the asymmetric explosion of SNe Ia may also enhance the velocity of the surviving companions. Thus, a surviving companion star in the WD + He star channel may have a high velocity like US 708 (see also Justham et al. 2008).

The companion stars are out of thermal equilibrium at the moment of SN explosion. For He stars, the equilibrium radii are lower than at the moment of SN explosion. Thus, the surface gravity at equilibrium should be greater than the one in Fig. 2; e.g., a 1.243 $~M_\odot$ He star with 0.274 $~R_\odot$ and ( $\log T_{\rm eff}$ , $\log g$ ) = (4.70, 5.65) will be a 0.267 $~R_\odot$ He star and with ( $\log T_{\rm eff}$ , $\log g$ ) = (4.75, 5.67) after the He star is back to the thermal equilibrium. It is well known that a shock will develop after impact by the ejecta. A large part of the material in the companion's envelope is heated by the shock, and some of the material is vaporized from the surface of the companion stars. Following a similar method to Chen & Li (2007), we also estimated the vaporized mass, and find that the mass loss from the companion stars is not significant (<5%). Such a surviving companion star may be significantly overluminous or underluminous depending on the amount of heating (e.g., Podsiadlowski 2003). Figure 2 could be a starting point for further studies of this kind.

Figure 4 shows the distributions of orbital periods and secondary masses of the WD + He star systems at the moment of SN explosion. The orbital periods and secondary masses of the WD + He star systems at this moment are basic input parameters when one simulates the interaction between SN ejecta and its companion. It is suggested that, for hot stars with radiative envelopes (such as He stars), tidal forces may be inefficient for synchronization (e.g., Zahn 1977). However, the recent study by Charpinet et al. (2008) supports efficient tidal synchronization for hot subdwarf stars. The work by Toledano et al. (2007) also indicates, on the other hand, that even stars with radiative envelopes may have efficient tidal interaction on a time scale comparable to convective envelopes. Thus, we make an assumption that the companion stars co-rotate with their orbits. In Fig. 5, we show the distributions of equatorial rotational velocities of the companions stars. We see that the surviving companion stars are fast rotators, so their spectral lines should be broadened noticeably.

The simulation in this Letter was made with $\alpha_{\rm ce}\lambda =0.5$ . If we adopt a higher value for $\alpha_{\rm ce}\lambda$ , e.g., 1.5, the birthrate of SNe Ia would be a little bit higher and the delay time from the star formation to SN explosion longer. This is because binaries emerging from CE ejections tend to have longer orbital periods for a large $\alpha_{\rm ce}\lambda$ and are more likely to be located in the SN Ia production region (Fig. 8 of Wang et al. 2009a). Due to the lack of WD binaries with short orbital periods ( $\log P^{\rm i} < -1.2$ ) for a large $\alpha_{\rm ce}\lambda$ , the companions with orbital velocity $V_{\rm orb}>430~{\rm km~s^{-1}}$ would be noticeably absent in Fig. 1.

The distributions are results of the current epoch for a constant SFR. For a single starburst, most of the SN explosions occur between $\sim$ 45 Myr and $\sim$ 140 Myr after the starburst; i.e., SNe Ia from the WD + He star channel will be absent in old galaxies. The Galactic SN Ia birthrate from this channel is $\sim$ $0.3\times 10^{-3}\ {\rm yr}^{-1}$ (Wang et al. 2009b). By multiplying the birthrate with a typical MS lifetime of He stars, $\sim$ 10⁷ yr, we estimated the current number of this type of HVSs in the Galaxy to be $\sim$ 10³. In future investigations, we will employ the Large sky Area Multi-Object fiber Spectral Telescope (LAMOST) to search the HVSs originating from the surviving companion stars of SNe Ia.

Acknowledgements

We thank an anonymous referee for his/her valuable comments that helped us to improve the paper. B.W. thanks Drs S. Justham, X.-C. Meng and W.-C. Chen for their helpful discussions. This work is supported bythe National Natural Science Foundation of China (Grant No. 10821061), the National Basic Research Program of China (Grant No. 2007CB815406), and the Yunnan Natural Science Foundation (Grant No. 08YJ041001).

References

Brown, W. R., Geller, M. J., Kenyon, S. J., & Kurtz, M. J. 2005, ApJ, 622, L33 [NASA ADS] [CrossRef]
Brown, W. R., Geller, M. J., & Kenyon, S. J. 2009, ApJ, 690, 1639 [NASA ADS] [CrossRef]
Charpinet, S., van Grootel, V., Reese, D., et al. 2008, A&A, 489, 377 [NASA ADS] [EDP Sciences] [CrossRef]
Chen, W.-C., & Li, X.-D. 2007, ApJ, 658, L51 [NASA ADS] [CrossRef]
Chen, W.-C., & Li, X.-D. 2009, ApJ, 702, 686 [NASA ADS] [CrossRef]
Edelmann, H., Napiwotzki, R., Heber, U., Christlieb, N., & Reimers, D. 2005, ApJ, 634, L181 [NASA ADS] [CrossRef]
Gamezo, V. N., Khokhlov, A. M., Oran, E. S., Chtchelkanova, A. Y., & Rosenberg, R. O. 2003, Sci, 299, 77 [NASA ADS] [CrossRef]
Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef]
Hachisu, I., Kato, M., Nomoto, K., & Umeda, H. 1999a, ApJ, 519, 314 [NASA ADS] [CrossRef]
Hachisu, I., Kato, M., & Nomoto, K. 1999b, ApJ, 522, 487 [NASA ADS] [CrossRef]
Han, Z. 1998, MNRAS, 296, 1019 [NASA ADS] [CrossRef]
Han, Z. 2008a, ApJ, 677, L109 [NASA ADS] [CrossRef]
Han, Z. 2008b, A&A, 484, L31 [NASA ADS] [EDP Sciences] [CrossRef]
Han, Z., & Podsiadlowski, Ph. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef]
Han, Z., & Podsiadlowski, Ph. 2006, MNRAS, 368, 1095 [NASA ADS] [CrossRef]
Han, Z., Eggleton, P. P., Podsiadlowski, Ph., & Tout, C. A. 1995a, MNRAS, 277, 1443 [NASA ADS]
Han, Z., Podsiadlowski, Ph., & Eggleton, P. P. 1995b, MNRAS, 272, 800 [NASA ADS]
Han, Z., Podsiadlowski, Ph., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef]
Han, Z., Podsiadlowski, Ph., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef]
Han, Z., Podsiadlowski, Ph., & Lynas-Gray, A. E. 2007, MNRAS, 380, 1098 [NASA ADS] [CrossRef]
Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef]
Hills, J. G. 1988, Nature, 331, 687 [NASA ADS] [CrossRef]
Hirsch, H. A., Heber, U., O'Toole, S. J., & Bresolin, F. 2005, A&A, 444, L61 [NASA ADS] [EDP Sciences] [CrossRef]
Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef]
Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef]
Iben, I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef]
Justham, S., Wolf, C., Podsiadlowski, Ph., & Han, Z. 2009, A&A, 493, 1081 [NASA ADS] [EDP Sciences] [CrossRef]
Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS]
Li, X.-D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS]
Lü, G., Zhu, C., Wang, Z., & Wang, N. 2009, MNRAS, 396, 1086 [NASA ADS] [CrossRef]
Meng, X., Chen, X., & Han, Z. 2007, PASJ, 59, 835 [NASA ADS]
Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 2103 [NASA ADS] [CrossRef]
Miller, G. E., & Scalo, J. M. 1979, ApJS, 41, 513 [NASA ADS] [CrossRef]
Nomoto, K., & Iben, I. 1985, ApJ, 297, 531 [NASA ADS] [CrossRef]
Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [NASA ADS] [CrossRef]
Nomoto, K., Iwamoto, K., & Kishimoto, N. 1997, Science, 276, 1378 [NASA ADS] [CrossRef]
Paczynski, B. 1976, Structure and Evolution of Close Binaries, ed. P. P. Eggleton, S. Mitton, & J. Whelan (Dordrecht: Kluwer), 75
Perets, H. B. 2009, ApJ, 698, 1330 [NASA ADS] [CrossRef]
Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef]
Podsiadlowski, Ph. 2003 [arXiv:astro-ph/0303660], unpublished
Podsiadlowski, Ph., Mazzali, P., Lesaffre, P., Han, Z., & Förster, F. 2008, New Astron. Rev., 52, 381 [NASA ADS] [CrossRef]
Przybilla, N., Nieva, M. F., Heber, U., et al. 2008, A&A, 480, L37 [NASA ADS] [EDP Sciences] [CrossRef]
Riess, A., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef]
Tillich, A., Przybilla, N., Scholz, R.-D., & Heber, U. 2009, A&A, 507, L37 [EDP Sciences] [CrossRef]
Toledano, O., Moreno, E., Koenigsberger, G., Detmers, R., & Langer, N. 2007, A&A, 461, 1057 [NASA ADS] [EDP Sciences] [CrossRef]
Tutukov, A. V., & Fedorova, A. V. 2009, Astron. Rep., 53, 839 [CrossRef]
Yoon, S.-C., & Langer, N. 2003, A&A, 412, L53 [NASA ADS] [EDP Sciences] [CrossRef]
Yu, Q., & Tremaine, S. 2003, ApJ, 599, 1129 [NASA ADS] [CrossRef]
Wang, B., Meng, X., Wang, X.-F., & Han, Z. 2008, Chin. J. Astron. Astrophys., 8, 71 [NASA ADS] [CrossRef]
Wang, B., Meng, X., Chen, X., & Han, Z. 2009a, MNRAS, 395, 847 [NASA ADS] [CrossRef]
Wang, B., Chen, X., Meng, X., & Han, Z. 2009b, ApJ, 701, 1540 [NASA ADS] [CrossRef]
Wang, B., Li, X.-D., & Han, Z. 2009c, MNRAS, in press [arXiv:0910.2138], DOI:10.1111/j.1365-2966.2009.15857.x
Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef]
Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS]

Footnotes

... equation: However, in reality, the collision between the SN ejecta and its companion cannot be elastic. If we adopt the inelastic collision in our calculations, the kick velocity will only decrease by 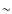$\sim$ 3%-5%. Thus, the inelastic collision is no significant influence on the kick velocity.

All Figures

$\begin{figure} \par\includegraphics[width=5.6cm,angle=270]{13326fg1.ps} \end{figure}$	Figure 1: The distribution of properties of companion stars in the plane of ( $V_{\rm orb}$ , $M_2^{\rm SN}$ ) at the current epoch, where $V_{\rm orb}$ is the orbital velocity and $M_2^{\rm SN}$ the mass at the moment of SN explosion.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5.6cm,angle=270]{13326fg2.ps} \end{figure}$	Figure 2: Similar to Fig. 1, but in the plane of ( $\log T_{\rm eff}$ , $\log g$ ), where $T_{\rm eff}$ is the effective temperature of companion stars at the moment of SN explosion and $\log g$ the surface gravity. The companion stars are out of thermal equilibrium, e.g., a 1.243 $~M_\odot$ He star with 0.274 $~R_\odot$ and ( $\log T_{\rm eff}$ , $\log g$ ) = (4.70, 5.65) will be a 0.267 $~R_\odot$ He star and with ( $\log T_{\rm eff}$ , $\log g$ ) = (4.75, 5.67) after the He star back to the thermal equilibrium.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.6cm,angle=0]{13326fg3.ps} \end{figure}$	Figure 3: The distribution of spatial velocity for surviving companion stars of SNe Ia. The dotted line denotes the results of ejecta velocity 11 000 km s^-1, while the solid line shows ejecta velocity 13 500 km s^-1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5.6cm,angle=270]{13326fg4.ps} \end{figure}$	Figure 4: Similar to Fig. 1, but in the plane of ( $\log P^{\rm SN}$ , $M_2^{\rm SN}$ ), where $P^{\rm SN}$ is the orbital period at the moment of SN explosion.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5.6cm,angle=270]{13326fg5.ps} \end{figure}$	Figure 5: Similar to Fig. 1, but in the plane of ( $V_{\rm rot}$ , $M_2^{\rm SN}$ ), where $V_{\rm rot}$ is the equatorial rotational velocity of companion stars at the moment of SN explosion.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.