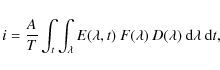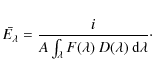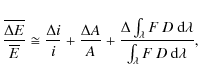| Issue |
A&A
Volume 508, Number 2, December III 2009
|
|
|---|---|---|
| Page(s) | 1085 - 1094 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200913089 | |
| Published online | 04 November 2009 | |
A&A 508, 1085-1094 (2009)
Pre-flight calibration of LYRA, the solar VUV radiometer on board PROBA2
A. BenMoussa1,9 - I. E. Dammasch1 - J.-F. Hochedez1 - U. Schühle2 - S. Koller3 - Y. Stockman4 - F. Scholze5 - M. Richter5 - U. Kroth5 - C. Laubis5 - M. Dominique1 - M. Kretzschmar6 - S. Mekaoui7 - S. Gissot1 - A. Theissen2 - B. Giordanengo1 - D. Bolsee8 - C. Hermans 8 - D. Gillotay8 - J.-M. Defise4 - W. Schmutz.3
1 - Royal Observatory of Belgium, SIDC, Circular Avenue 3, 1180 Brussels, Belgium
2 -
Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
3 -
Physikalisch-Meteorologisches Observatorium Davos - World Radiation Center, 7260 Davos Dorf, Switzerland
4 -
Centre Spatial de Liège, Av. Pré Aily 4031 Angleur, Belgium
5 -
Physikalisch-Technische Bundesanstalt (PTB), Abbestr. 2-12, 10587 Berlin, Germany
6 -
LPCE, UMR 6115 CNRS-Université d'Orléans, 3A Av. de la Recherche Scientifique, 45071 Orléans Cedex 2, France
7 -
Royal Meteorological Institute of Belgium, Circular Avenue 3, 1180 Brussels, Belgium
8 -
Belgian Institute for Space Aeronomy, Circular Avenue 3, 1180 Brussels, Belgium
9 -
Solar Terrestrial Center of Excellence (STCE), Circular Avenue 3, 1180 Brussels, Belgium
Received 7 August 2009 / Accepted 25 October 2009
Abstract
Aims. LYRA, the Large Yield Radiometer, is a vacuum
ultraviolet (VUV) solar radiometer, planned to be launched in November
2009 on the European Space Agency PROBA2, the Project for On-Board
Autonomy spacecraft.
Methods. The instrument was radiometrically calibrated in the
radiometry laboratory of the Physikalisch-Technische Bundesanstalt
(PTB) at the Berlin Electron Storage ring for SYnchroton radiation
(BESSY II). The calibration was done using monochromatized synchrotron
radiation at PTB's VUV and soft X-ray radiometry beamlines using
reference detectors calibrated with the help of an electrical
substitution radiometer as the primary detector standard.
Results. A total relative uncertainty of the radiometric
calibration of the LYRA instrument between 1% and 11% was achieved.
LYRA will provide irradiance data of the Sun in four UV passbands and
with high temporal resolution down to 10 ms. The present state of the
LYRA pre-flight calibration is presented as well as the expected
instrument performance.
Key words: instrumentation: detectors - instrumentation: photometers - Sun: UV radiation
1 Introduction
LYRA, the Large Yield RAdiometer (Hochedez et al. 2006), is a solar vacuum ultraviolet (VUV) radiometer onboard PROBA2 (PRoject for On-Board Autonomy), a technologically oriented European Space Agency (ESA) micro-mission conceived for the purpose of demonstrating new technologies with prototype payloads. LYRA is designed and manufactured by a Belgian-Swiss-German consortium with additional international contributions from Japan, USA and Russia (see http://lyra.oma.be). LYRA will monitor the solar irradiance in four selected UV passbands simultaneously. These passbands have been chosen for their relevance to aeronomy, space weather and solar physics. Its four channels are labeled (1) the H I 121.6 nm Lyman-alpha line, (2) the 200-220 nm Herzberg continuum range, (3) the 17-80 nm aluminium filter range including the He II 30.4 nm line, and (4) the 6-20 nm zirconium filter range, where solar variability is highest. LYRA will be unique in adding the capability of fast measurements aiming at a highest possible cadence of 100 Hz, i.e., providing a set of measurements every 10 ms. LYRA measurements will provide the Aeronomy community with relevant solar irradiance observations and will reveal the sub-second structure of the solar flux for the first time. A main driver of the mission is the first-time use of novel diamond photodetectors in space. LYRA will be the first space assessment of a pioneering UV diamond detector program (see http://bold.oma.be). LYRA will be operated together with the extreme-ultraviolet telescope using new active pixel sensor (APS) technology - the Sun Watcher using APS and image Processing (SWAP) experiment (Berghmans et al. 2006). SWAP will provide images of the solar corona at a temperature of above one million degrees (Fe IX/X 17.4 nm emission line) at an improved image cadence typically one image every minute.

|
Figure 1:
Photograph of LYRA and an exploded view of one of the 3 redundant LYRA units. The total dimensions of LYRA are 315 mm |
| Open with DEXTER | |
2 LYRA overview
2.1 Design
The dimensions of LYRA are 315 mm ![]() 92.5 mm
92.5 mm ![]() 222 mm, and its weight is 3.533 kg. The detectors are grouped into three units (see Fig. 1),
each containing four individual detection channels for each of the
spectral bands mentioned above. Each detection channel consists of a
cover mechanism, a collimator, a precision aperture, a spectral filter,
a detector and two LED light sources. These LEDs, emitting at 375 and
470 nm wavelengths at room temperature, will help disentangle
aging of the detectors from the filters (see Fig. 12).
The three units are operated as redundant radiometers to maximize the
accuracy and the reliability of the measurements. The two redundant
groups of multiplexers/voltage-to-frequency converters (VFC) can be
used to read one unit simultaneously to achieve a test of the VFC or
two units (eight spectral channels) can be acquired in parallel to
inter-calibrate the spectral channels. The selected filter-detector
combinations representing the four UV passbands on the three redundant
units will subsequently be called channels 1-1 to 3-4 (see Table 1).
222 mm, and its weight is 3.533 kg. The detectors are grouped into three units (see Fig. 1),
each containing four individual detection channels for each of the
spectral bands mentioned above. Each detection channel consists of a
cover mechanism, a collimator, a precision aperture, a spectral filter,
a detector and two LED light sources. These LEDs, emitting at 375 and
470 nm wavelengths at room temperature, will help disentangle
aging of the detectors from the filters (see Fig. 12).
The three units are operated as redundant radiometers to maximize the
accuracy and the reliability of the measurements. The two redundant
groups of multiplexers/voltage-to-frequency converters (VFC) can be
used to read one unit simultaneously to achieve a test of the VFC or
two units (eight spectral channels) can be acquired in parallel to
inter-calibrate the spectral channels. The selected filter-detector
combinations representing the four UV passbands on the three redundant
units will subsequently be called channels 1-1 to 3-4 (see Table 1).
Figure 2 shows the
optical path of a LYRA channel. Given the geometry of the collimator,
view-limiting apertures of 8 mm diameter, precision apertures of
3 mm diameter and detector sensitive area of 4.0 mm diameter,
the field of view (FOV) is ![]()
![]() reduced by mounting tolerances to
reduced by mounting tolerances to ![]()
![]() .
Provisions have been taken for mounting tolerances, spacecraft
off-points, and possible jitter. Note that there are no baffles between
the view-limiting and the precision aperture. But after the precision
aperture the four channels are totally separated and different tests in
the optics laboratory showed that there is no need for stray light
correction.
.
Provisions have been taken for mounting tolerances, spacecraft
off-points, and possible jitter. Note that there are no baffles between
the view-limiting and the precision aperture. But after the precision
aperture the four channels are totally separated and different tests in
the optics laboratory showed that there is no need for stray light
correction.
| Figure 2: Schematic representation of the optical path of a LYRA channel (not to scale) which consists of a view-limiting aperture (1), a precision aperture (2), an optical filter (3) and the detector (4). |
|
| Open with DEXTER | |
2.2 Cover mechanism
Each of the LYRA units is equipped with an individual cover mechanism,
which provides a reduction of contamination during ground activities
and a shutter mechanism for the filter radiometer. The design of the
LYRA cover mechanism is shown in Fig. 3.
The mechanism consists of a stepper motor procured from CDA Intercorp,
a rotating cover, two position sensors and a launch lock device from
Starsys Research. The stepper motor rotates the cover by
![]() to open and close the optical path of LYRA instrument. Two hall sensors
allow detection of fully open and closed position. A cover movement
requires approximately 400 ms. The cover is manufactured of aluminum
alloy 6082 and its Sun exposed surface is coated with a Back Surface
Mirror (BSM) in order to reduce energy absorption during closed phases.
An actuator locks the cover in closed position during launch. The
implemented paraffin actuator allows a linear movement of the locking
pin by approximately 10 mm. A heating element melts the paraffin,
it expands during melting and thus the pin moves out. The needed power
to be applied is in the order of 4.7 W for a period of 180 s. This is
transformed into a gentle high force shaft extension of the piston. An
internal spring returns the mechanism to its initial position when the
current is turned off.
to open and close the optical path of LYRA instrument. Two hall sensors
allow detection of fully open and closed position. A cover movement
requires approximately 400 ms. The cover is manufactured of aluminum
alloy 6082 and its Sun exposed surface is coated with a Back Surface
Mirror (BSM) in order to reduce energy absorption during closed phases.
An actuator locks the cover in closed position during launch. The
implemented paraffin actuator allows a linear movement of the locking
pin by approximately 10 mm. A heating element melts the paraffin,
it expands during melting and thus the pin moves out. The needed power
to be applied is in the order of 4.7 W for a period of 180 s. This is
transformed into a gentle high force shaft extension of the piston. An
internal spring returns the mechanism to its initial position when the
current is turned off.
| Figure 3: Design and picture of the LYRA cover mechanism. |
|
| Open with DEXTER | |
2.3 Contamination plan
At EUV wavelengths, molecular contamination on optical surfaces is
an absorbing layer. Consequently to prevent contamination of optical
surfaces, it is required that LYRA be continuously purged with nitrogen
prior to launch and the cover always closed. The cover actually reduces
the cleanliness requirements during the spacecraft tests activities, so
that the contamination levels are acceptable. When during the tests the
cover must be open, the environmental conditions are such that the
cleanliness level can be met. This requires in general a controlled
clean room area of class 10 000 if the instrument must stay open
for more than one hour.
It should be added that LYRA has the possibility to switch periodically
heaters located close to the detectors and filters, in order to achieve
a few degrees over temperature against the surrounding parts. Note that
the photodetectors are operating close to the room temperature (between
20-30 ![]() C)
to avoid cold trapping. Once in flight, the LYRA instrument will open
the entrance covers for a period venting of the optical compartment
without UV light entering into the optical path. During orbital
manoeuvres, the LYRA covers will be closed, in order to prevent
contamination of the filters. The degradation of LYRA will be
quantitatively accessible through the redundancy concept and the
onboard LEDs.
C)
to avoid cold trapping. Once in flight, the LYRA instrument will open
the entrance covers for a period venting of the optical compartment
without UV light entering into the optical path. During orbital
manoeuvres, the LYRA covers will be closed, in order to prevent
contamination of the filters. The degradation of LYRA will be
quantitatively accessible through the redundancy concept and the
onboard LEDs.
3 LYRA calibrations
One scientific goal of LYRA is to improve the absolute accuracy of solar irradiance measurements, hence the need for sub-systems and system calibration, on ground and in flight. The radiometric responsivity of each LYRA channel has to be determined over a wavelength range that is very large: from the soft X-ray (1 nm) to the near infrared (NIR) regime. First, subsystems (filters and detectors) were characterized for their UV responsivity, visible light blocking, background noise, dark current, linearity, and temporal stability within different wavelength ranges. Second, the LYRA instrument was calibrated, channel per channel.
3.1 Calibration setup and measurements
The measurements were carried out by several teams at radiometric
calibration facilities. PTB with its radiometry laboratory at the
electron storage ring BESSY II provided the traceability to a primary
detector standard. Calibration campaigns were conducted in 2005, 2006,
and 2007. The synchrotron radiation calibration campaigns were carried
out at the soft X-ray grazing incidence (GI) radiometry beamline
(wavelength range 1 to 30 nm) and at the VUV normal incidence
beamline (NI, 40 to 240 nm). Details of the description of the
measuring stations can be found in Scholze et al. (2000) and Richter et al. (2003).
The radiometric beamlines of PTB were operated with settings optimized
for highest spectral purity of the monochromatized radiation. The
relative contribution of all wavelengths to the detector wavelength
range, the spectral impurities was kept below 1%. The relative standard
uncertainty of the measurements was estimated to be better than a few
percent. Individual measurements were repeated to check stability and
reproducibility. For the longer wavelength range, monochromatic light
was generated with a UV-enhanced 100 W deuterium lamp (
![]() nm), a double monochromator, and appropriate filters. For the low energy region (
nm), a double monochromator, and appropriate filters. For the low energy region (
![]() nm),
the lamp was replaced by a tungsten halogen lamp or by different lasers
with a beam homogeneity improved by an arrangement of pinhole and
lenses. The intensity of the light could also be modulated by means of
a mechanical chopper placed in front of the entrance slit. A schematic
representation of the setup can be found in BenMoussa et al. (2004).
Corrections for offset were applied. The estimated uncertainties are
around 10% in the visible (VIS) and NIR region and roughly correspond
to the size of the symbols used to plot data points.
nm),
the lamp was replaced by a tungsten halogen lamp or by different lasers
with a beam homogeneity improved by an arrangement of pinhole and
lenses. The intensity of the light could also be modulated by means of
a mechanical chopper placed in front of the entrance slit. A schematic
representation of the setup can be found in BenMoussa et al. (2004).
Corrections for offset were applied. The estimated uncertainties are
around 10% in the visible (VIS) and NIR region and roughly correspond
to the size of the symbols used to plot data points.
3.2 Aperture area
The precision aperture (3.0 mm) of LYRA is not critical but its size must be carefully calibrated. After manufacturing, the apertures were sent to the Swiss Federal Office of Metrology and Accreditation (METAS) for calibration. The manufacturing tolerance of the precision apertures is H7 or +10/-03.3 Filter transmittance
The optical filters were manufactured by Acton Research Corporation (ARC) for channels 1 and 2, i.e. Lyman-Table 1: Selected configuration of LYRA channels.
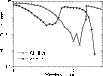
Figures 4 and 5 show the results of the spectral transmittance measurements carried out at different facilities, e.g., PTB/BESSY II, lasers and monochromatic light between 200-1100 nm, and Fourier Transform IR Spectrometer (FTIR) for wavelengths up to 2600 nm. It should be noted that within the uncertainties, the LYRA filters of the different units show the same transmittance curves, respectively.

|
Figure 4:
Measured spectral transmittance of the Acton Research corp. filters: Lyman- |
| Open with DEXTER | |
|
Figure 5: Measured spectral transmittance of the Al (157.9 nm thick) and the Zr (141.3 nm thick) filters from Luxel corp. between 1 and 30 nm. |
| Open with DEXTER | |
3.4 Diamond photodetectors
For the LYRA project, two types of diamond detectors were developed: metal-semiconductor-metal (MSM) photoconductor and PIN photodiode detectors. Diamond detector structures were developed in a joint collaboration between IMO-IMOMEC in Belgium, NIMS in Japan, and Garching Analytics GmbH in Germany. Photographs of the diamond MSM and PIN detectors mounted inside their rectangular ceramic package are shown in Fig. 6. Device operation and fabrication procedure details are given elsewhere (BenMoussa et al. 2006a,b). Their particular advantage compared to Si detectors (AXUV from IRD) lies in their solar-blindness with an UV/VIS rejection ratio of at least four orders of magnitude. Indeed diamond is a wide bandgap semiconductor, which makes the sensors ``solar-blind'', i.e. insensitive to the solar spectrum below the Earth's atmosphere, at sea level, with a good UV/VIS rejection ratio. By using diamond detectors, the number of filters, blocking the unwanted visible radiation, can be reduced and the serious attenuation of the desired UV radiation can be minimized. Diamond exhibits several other superior properties compared to silicon. It has high charge carrier mobility at room temperature and a higher breakdown electric field, a low dielectric constant (thus low capacitance). The low intrinsic carrier density (smaller by seven orders of magnitude than silicon) makes cooling for noise reduction unnecessary. Its dense tetrahedral structure and stable covalent sp3 bonding are the reasons for the expected radiation hardness of diamond detectors.
| Figure 6: Photograph of the diamond photodetectors a) MSM and detail of the Ti/Pt/Au contact structures; b) the PIN photodiode. |
|
| Open with DEXTER | |
3.4.1 Dark current
The variation of the dark current with temperature was investigated in pre-flight tests. Thermal cycles were performed between
![]() C and
C and
![]() C. As an example, the signal of the MSM photodetector shows a sub-pA variation following the temperature evolution (
C. As an example, the signal of the MSM photodetector shows a sub-pA variation following the temperature evolution (
![]() C
steps) with a small hysteresis when repeated. The performance of the
detector does not change after the thermal cycling. Indeed, the
performance of the MSM photodetectors depends significantly on the
surface properties of the active layer (diamond), on the applied
voltage, and on the geometrical design, especially the distance between
electrodes. The MSM detector channels show negligibly small (few pA)
dark current over the area of the entire detector at room temperature.
The PIN detector channels (channel *-2) are faster devices due to their
low capacitance. Diamond PIN photodiodes typically have no dark
currents (background detrapping 10-14 A). Note that the
PIN photodiodes (both diamond and Si-AXUV) are operated in a
photovoltaic mode (unbiased) while the diamond MSM operational voltage
is 5 V bias.
C
steps) with a small hysteresis when repeated. The performance of the
detector does not change after the thermal cycling. Indeed, the
performance of the MSM photodetectors depends significantly on the
surface properties of the active layer (diamond), on the applied
voltage, and on the geometrical design, especially the distance between
electrodes. The MSM detector channels show negligibly small (few pA)
dark current over the area of the entire detector at room temperature.
The PIN detector channels (channel *-2) are faster devices due to their
low capacitance. Diamond PIN photodiodes typically have no dark
currents (background detrapping 10-14 A). Note that the
PIN photodiodes (both diamond and Si-AXUV) are operated in a
photovoltaic mode (unbiased) while the diamond MSM operational voltage
is 5 V bias.
3.4.2 Photodetectors spectral responsivity
The typical absolute spectral responsivity of the LYRA photodetectors is shown in Fig. 7. The data from 210 nm to 1000 nm (measured on a relative scale) were matched to the absolute data from PTB/BESSY II (1 nm to 240 nm). The responsivities of the diamond photodetectors (MSM and PIN) show the diamond band edge to be around 225 nm and display a UV/VIS rejection ratio (200 nm /500 nm) of more than 4 orders of magnitude. The responsivity of the diamond PIN photodiode (used only for the Herzberg channels) decreases dramatically below 180 nm due to the absorption of the 300 nm thick n-type layer associated with the abrupt drop of the diamond penetration depth which is about 20 nm at 170 nm wavelength. Thus, electron-hole pairs are created very close to the surface and recombine before reaching the depletion region. The MSM diamond detector sensitivity covers the spectral range going from 1 nm up to 220 nm and the Si AXUV detectors from 1 nm to 1100 nm.
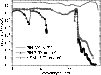
|
Figure 7: Spectral response of a typical Si AXUV n-on-p photodiode (unbiased), diamond PIN photodiode (unbiased) and diamond MSM (under 5 V bias) between 1 nm and 1000 nm. |
| Open with DEXTER | |
3.5 LYRA calibration results
3.5.1 Absolute spectral responsivity
We report on the calibration results needed for future scientific analysis. This includes in-depth characterization and understanding of the global LYRA instrument response. Figures 8 show the spectral responsivity values (in A/W) for the LYRA selected filter-detector combinations of its four channels. For clarity we did not plot the corresponding error bars. A compilation of their contributions to the measurement uncertainties in the spectral responsivity is given in Scholze et al. (2003) and Richter et al. (2003). The observed differences in the absolute combined responsivity in Figs. 8 (see top panels) are mainly due to the discrepancies between the various prototype diamond flight sensors. These diamond photodetectors prove their general suitability for space solar observations, nevertheless diamond must still be acknowledged as relying on new/emerging technology. Further improvements of their performance characteristics are still needed.

|
Figure 8:
Top left: absolute responsivity of the Lyman- |
| Open with DEXTER | |
3.5.2 Uniformity of the photoresponse (flat-field)
The spatial homogeneity varies from detector to detector and
necessitates the need for calibrating each channel's detector over a
wide wavelength range. The detector calibration chambers at the
beamlines of PTB at BESSY II allow the sample to be moved along three
axes relative to the beam axis in ultrahigh vacuum. This makes it
possible to raster scan the sample area with the incoming beam.
Toggling between test and reference detectors is possible as well. The
spot size of the raster beam is approximately 0.3 mm ![]() 0.3 mm (FWHM) in the GI beamline, and 0.6 mm
0.3 mm (FWHM) in the GI beamline, and 0.6 mm ![]() 0.6 mm (FWHM)
in the NI beamline, depending slightly on the chosen wavelength.
Individual measurements were repeated to check stability and
reproducibility. The beamline power was readjusted between scans to
better conform to detector sensitivities. The relative responsivity
maps were built by normalizing the current to its maximum value to help
comparison. Figure 9 shows
a 3-dimensional representation of the LYRA channel raster scans at
10 nm. The flat field quality is wavelength dependent. As we can
see, the homogeneity of the MSM diamond photodetector (left panel)
seems to be moderate. The sharp dip in responsivity (40 to 50%
deviation) observed at the centre of the MSM channels is related to the
geometrical arrangement of the contact electrodes (cf. Fig. 6a)
and the width of the raster beam (convolution). The shadowing of the
active area by the interdigitated contacts is the main drawback of
those particular MSM detectors and results in a significant efficiency
reduction. New device architectures are under development to maximize
the fill factor and increase the homogeneity of the MSM photodetectors (BenMoussa et al. 2008) but they will not fly on LYRA.
0.6 mm (FWHM)
in the NI beamline, depending slightly on the chosen wavelength.
Individual measurements were repeated to check stability and
reproducibility. The beamline power was readjusted between scans to
better conform to detector sensitivities. The relative responsivity
maps were built by normalizing the current to its maximum value to help
comparison. Figure 9 shows
a 3-dimensional representation of the LYRA channel raster scans at
10 nm. The flat field quality is wavelength dependent. As we can
see, the homogeneity of the MSM diamond photodetector (left panel)
seems to be moderate. The sharp dip in responsivity (40 to 50%
deviation) observed at the centre of the MSM channels is related to the
geometrical arrangement of the contact electrodes (cf. Fig. 6a)
and the width of the raster beam (convolution). The shadowing of the
active area by the interdigitated contacts is the main drawback of
those particular MSM detectors and results in a significant efficiency
reduction. New device architectures are under development to maximize
the fill factor and increase the homogeneity of the MSM photodetectors (BenMoussa et al. 2008) but they will not fly on LYRA.
| Figure 9: Homogeneity of the responsivity (3-D representation) of channel 2-4 (MSM diamond photodetector, left panel) and channel 1-4 (Si-AXUV, right panel) at 10 nm wavelength. |
|
| Open with DEXTER | |
Note that the knowledge of the flat field is used to correct the
measured responsivity of each LYRA channel. Taking into account that
the beam at the PTB/BESSYII covered only a sub-area in the centre of
the detector, the expected effect was simulated and responsivity values
were accordingly modified, between 0% and -28% (Dammasch 2008).
Knowledge of the flat field will also be necessary to correct for
off-pointing effects when the circular image of the Sun through the
3 mm precision aperture will move outward from the center of the
detector. Pre-flight simulations will be tested and updated, in order
to construct a table that delivers correction factors. Simulations show
that
![]() off-pointing leads to approximately 20-25% reduction from the nominal response (see Dammasch 2006). Off-pointing on the order of the nominal jitter of PROBA2 (5 arcmin) leads to fluctuations of approximately
off-pointing leads to approximately 20-25% reduction from the nominal response (see Dammasch 2006). Off-pointing on the order of the nominal jitter of PROBA2 (5 arcmin) leads to fluctuations of approximately ![]() around the nominal response. Note that off-pointing on the order of the
offset between SWAP and LYRA will therefore not be detectable.
around the nominal response. Note that off-pointing on the order of the
offset between SWAP and LYRA will therefore not be detectable.
3.5.3 Linearity vs. photon flux
The linearity of the different LYRA channels has been investigated over 3 orders of magnitude (from 1 nW to 1 ![]() W)
at PTB/BESSY II, using different aperture stops to reduce the radiant
power to lowest measurable values (minimum 1% of the full beam power),
or by varying the exit slit of the monochromator. The absolute input
radiant power was determined for each aperture by direct comparison
with a calibrated Si reference photodiode.
A power law:
W)
at PTB/BESSY II, using different aperture stops to reduce the radiant
power to lowest measurable values (minimum 1% of the full beam power),
or by varying the exit slit of the monochromator. The absolute input
radiant power was determined for each aperture by direct comparison
with a calibrated Si reference photodiode.
A power law:
was used to fit the data where I is the signal current and P the incident beam power. As shown in Fig. 10, the fitted parameters for channel 1-1 are a = (
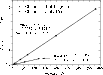
|
Figure 10: Flux linearity of LYRA channels 1-1 and 1-2 (photocurrent versus incident power) at 121.6 nm and 210 nm respectively, with the fitted function (see Eq. (1)). |
| Open with DEXTER | |
Table 2: Linearity fit parameters and their quality (b>1 denotes super-linear and b<1 sub-linear behavior).
3.5.4 Signal stability
The stability of the output signal under irradiation over prolonged periods is an important mission goal for a radiometer. The redundancy concept (although the units are not strictly identical) completes the strategy to stability monitoring. One unit will be used continuously, another one on a weekly basis, while the last one will remain closed most of the time and will only be used a few times during the mission. In this way, the radiometric evolution of the sensors and filters will be assessed. Furthermore, the responsivity of the detectors, i.e. the sub-gap photoresponse for diamond, will be monitored by on-board light sources (LEDs) in order to distinguish a detector's drift from degradations of the filters. The LEDs (VIS LEDs emitting at 470 nm and NUV LEDs emitting at 375 nm) are situated between the filter and detector, but outside the optical path from the sun viewed by the detector through a precision hole (see in Fig. 12). Thus the LEDs will monitor only the degradation of the detector (not the optical filters).Note that reliability measurements on the LEDs have been carried out.
In particular the 12 NUV and 12 VIS LEDs selected for LYRA have been
measured between -40 and +
![]() C.
At each measurement point, a diode emission spectra has been taken.
From the measured spectra it is clear that the emission intensity is
strongly temperature dependent. Also the LED emission maximum is
shifted with the temperature. The temperature changes from -40 to +
C.
At each measurement point, a diode emission spectra has been taken.
From the measured spectra it is clear that the emission intensity is
strongly temperature dependent. Also the LED emission maximum is
shifted with the temperature. The temperature changes from -40 to +
![]() C
cause a shift of typically 5 nm, for both NUV and VIS LEDs. This
shift is from 373 to 378 nm for NUV diodes and from 468 to
473 nm for the VIS diodes. The LED calibration has been carried
out in the LYRA head with mounted detectors. There were several hours
of LED tests performed with the PTB-BESSY II beamlines. For the
resulting data, see Dammasch (2007). Note also that the LEDs can be operated in pulse mode (10 Hz max.) to avoid an increase of its junction temperature.
C
cause a shift of typically 5 nm, for both NUV and VIS LEDs. This
shift is from 373 to 378 nm for NUV diodes and from 468 to
473 nm for the VIS diodes. The LED calibration has been carried
out in the LYRA head with mounted detectors. There were several hours
of LED tests performed with the PTB-BESSY II beamlines. For the
resulting data, see Dammasch (2007). Note also that the LEDs can be operated in pulse mode (10 Hz max.) to avoid an increase of its junction temperature.
Similarly as for the linearity, the signal stability at room
temperature was measured at five wavelengths: 121.6 nm for the
Lyman-![]() channels, 210 nm for the Herzberg channels, 50 nm and
18 nm for the Al channels, and 10 nm for the Zr channels. In
order to characterize the temporal response of the detectors, the
beamline shutter was opened and closed approximately every 600 s.
The data are corrected for the small decline (1%) of the current of the
synchrotron storage ring during the time period of each measurement.
Figure 11
shows the total signal as a function of time, for different LYRA
channels using diamond MSM, PIN and Si AXUV detectors on the same time
scale, in order to demonstrate the differences in temporal behavior.
For additional information see BenMoussa et al. (2006b) and BenMoussa (2006a,b).
channels, 210 nm for the Herzberg channels, 50 nm and
18 nm for the Al channels, and 10 nm for the Zr channels. In
order to characterize the temporal response of the detectors, the
beamline shutter was opened and closed approximately every 600 s.
The data are corrected for the small decline (1%) of the current of the
synchrotron storage ring during the time period of each measurement.
Figure 11
shows the total signal as a function of time, for different LYRA
channels using diamond MSM, PIN and Si AXUV detectors on the same time
scale, in order to demonstrate the differences in temporal behavior.
For additional information see BenMoussa et al. (2006b) and BenMoussa (2006a,b).

|
Figure 11: Signal current (log scale) as a function of time for LYRA detectors at different wavelengths. |
| Open with DEXTER | |
All LYRA channels show a good stability on a wide temporal range with a
small room-temperature dark current. At 121.6 nm (Lyman-![]() line), the MSM detectors appear to be less stable. Indeed the
penetration depth has extremely small values, of the order of a few
nanometers. The photons are, thus, being absorbed in the first atomic
layers, leading to carrier recombination in the surface and
consequently to a reduction of the stability. The time to reach a
stable signal varied depending on the irradiation power. During the
first minutes approximately, the signal increases progressively and
then tends to be stable with a signal drift of less than 1%. One
possible explanation for the initial increase of the signal is
attributed to the filling of localized empty states (due to surface
defects) until no more electron-hole pairs can be trapped. When the
traps are filled, the signal remains stable. During prolonged duration
without irradiation, the progressive return to an equilibrium condition
with the release of trapped charge (detrapping) of different defect
levels in the bandgap results in the slow decrease of the dark current.
line), the MSM detectors appear to be less stable. Indeed the
penetration depth has extremely small values, of the order of a few
nanometers. The photons are, thus, being absorbed in the first atomic
layers, leading to carrier recombination in the surface and
consequently to a reduction of the stability. The time to reach a
stable signal varied depending on the irradiation power. During the
first minutes approximately, the signal increases progressively and
then tends to be stable with a signal drift of less than 1%. One
possible explanation for the initial increase of the signal is
attributed to the filling of localized empty states (due to surface
defects) until no more electron-hole pairs can be trapped. When the
traps are filled, the signal remains stable. During prolonged duration
without irradiation, the progressive return to an equilibrium condition
with the release of trapped charge (detrapping) of different defect
levels in the bandgap results in the slow decrease of the dark current.
4 Radiometric model
A radiometric model based on the solar spectral irradiance, transmittance of the filters, and detectors' responsivity is used to determine the anticipated photocurrents and their spectral purity (see http://lyra.oma.be). Based on these simulations, twelve channel configurations for the three LYRA units were selected and equipped as summarized in Table 1.
4.1 Principle
Photons from the sun with the spectral irradiance
![]() enter the LYRA instrument through a circular aperture A of 3 mm in diameter, pass one set of filters of a certain (dimensionless) transmittance
enter the LYRA instrument through a circular aperture A of 3 mm in diameter, pass one set of filters of a certain (dimensionless) transmittance
![]() ,
and are converted to an electric current by a detector with a certain spectral responsivity
,
and are converted to an electric current by a detector with a certain spectral responsivity
![]() ,
measured in A/W. The aperture A determines the amount of optical power incident upon the detector from the sun (see Fig. 12).
Here, the diffraction effect can be ignored, since the aperture is
large compared to the wavelength of light being used, and the detector
has a diameter sufficient to intercept all the radiation exiting
through the aperture. With the integration time T, the expected photocurrent is then,
,
measured in A/W. The aperture A determines the amount of optical power incident upon the detector from the sun (see Fig. 12).
Here, the diffraction effect can be ignored, since the aperture is
large compared to the wavelength of light being used, and the detector
has a diameter sufficient to intercept all the radiation exiting
through the aperture. With the integration time T, the expected photocurrent is then,
where
| Figure 12: Schematic representation of a LYRA unit (head) with its detectors, filters, LEDs and its two apertures (not to scale). |
|
| Open with DEXTER | |

|
Figure 13: Combined simulated spectral responsivity [detector + filter] for LYRA unit 1 between 1 and 1100 nm. |
| Open with DEXTER | |
4.2 Simulations
Some approximations such as extrapolations towards the EUV and the NIR of the Al and Zr filters transmittance were carried out where the rejection of light was too high to be adequately measured. In the EUV, the filter transmittance was modelled and matched to the absolute data from PTB/BESSY II using the data of the Center for X-Ray Optics (CXRO) at the Lawrence Berkeley National Laboratory (LBNL), available at http://www-cxro.lbl.gov/. A Jobin-Yvon software was used to determine the transmittance of the Al and Zr filters in the NUV and VIS range. The oxide thicknesses of the metallic filters were taken into account by fitting the absolute transmittance between 1 nm and 30 nm. The 70-lines-per-inch nickel mesh used to support the Al and Zr filters transmits about 82%. Theoretical calculations of long-wavelength extensions were corrected by on-ground measurements performed at PMOD/WRC in Davos. As a result, Fig. 13 shows the combined spectral responsivity of the four LYRA channels of unit 1 between 1 and 1100 nm.

|
Figure 14: Examples for LYRA radiometric model simulations. From top to bottom: channel 1-3's responsivity curve (MSM detector + Al filter), the solar spectrum (maximum and minimum solar spectrum from 2003 and 2008, respectively), and the product of both; the integral of the last curve estimates the total output signal of the LYRA channel, when multiplied with the area of the precision aperture A. |
| Open with DEXTER | |

|
Figure 15: Examples of LYRA radiometric model simulations for channels 1-1, 1-2 and 1-4. |
| Open with DEXTER | |
To determine the anticipated photocurrents, the spectral responsivities were multiplied with solar sample spectra originating from instruments already in space, namely TIMED/SEE (http://www.timed.jhuapl.edu/WWW/index.php) for sho- rter wavelengths, suitable for LYRA channels 3 and 4, and SORCE (http://lasp.colorado.edu/sorce/index.htm) for longer wavelengths, suitable for LYRA channels 1 and 2. By now, these instruments have covered several years of the solar cycle, thus spectra could be selected representing solar minimum and maximum conditions, as well as situations of various solar activities such as pre-flare and post-flare conditions. Seven sample spectra were tested against twelve responsivity curves (see Dammasch 2009a). Figure 14 shows an example for the LYRA radiometric model simulations.
As can be seen from Figs. 14 and 15, LYRA channels are not merely responding in their nominal spectral intervals, but also receive contaminations from other ranges. The purity of a channel is defined as the ratio of the flux in the nominal wavelength range (LYRA bandwidth channels) to the total output signal. Table 3 shows the total signals and purities as expected according to the radiometric model described in the section above. Listed are the total values estimated for the minimal and maximal solar spectra as observed by the TIMED/SEE and SORCE instruments, namely, a minimum solar spectrum of 29 June 2008, and a maximum (flare) spectrum of 28 October 2003.
As a result, Lyra will measure an estimated signal between 0.01
to 17 nA. The high sensitivity of the MSM detectors at around
200-220 nm results in a portion of the solar continuum to the
Lyman-![]() channel signal and thus in a lower signal purity, around 25% compared
to the 32% when using Si-AXUV photodetector (see channel 3-1). Note
that the purity of the Lyman-
channel signal and thus in a lower signal purity, around 25% compared
to the 32% when using Si-AXUV photodetector (see channel 3-1). Note
that the purity of the Lyman-![]() channels increases slightly at solar maximum. Indeed the 200-220 nm contribution is quite stable while the Lyman-
channels increases slightly at solar maximum. Indeed the 200-220 nm contribution is quite stable while the Lyman-![]() line shows a higher variability between the solar minimum and maximum.
For the Herzberg channels, the expected signal and purities are high
and stable. The Herzberg channel is well defined by its bandwidth with
a low contamination from the other wavelengths. It shows a purity of
about 84% under all solar spectrum conditions. Note that channels 1 and
2 display smaller solar signal variability as compared to the channels
3 and 4. The advantage of the first two channels is that their purity
appears to be rather stable. On the contrary, the solar EUV radiation
is highly variable (Woods & Chamberlin 2009; Woods et al. 2005a,b).
Al and Zr channels display extreme variability with the solar
conditions, as purity abruptly decreases when strong contamination from
the soft X-ray range begins to dominate the signal in the case of high
flux. One of the advantages of these two channels is that, although
their purity is highly dependent on the incoming signal, additional
information may be gained by a clever signal separation (Dammasch 2009b). As soon as the pure
signal of the channels is determined, the relationship to the
respective solar irradiance appears quite straightforward according to
the radiometric model simulations. Another advantage of the latter two
LYRA channels (*-3 and *-4) is the fact that they have a small overlap
in responsivity around 17 nm, which is also the interval in which
SWAP will observe the Sun.
line shows a higher variability between the solar minimum and maximum.
For the Herzberg channels, the expected signal and purities are high
and stable. The Herzberg channel is well defined by its bandwidth with
a low contamination from the other wavelengths. It shows a purity of
about 84% under all solar spectrum conditions. Note that channels 1 and
2 display smaller solar signal variability as compared to the channels
3 and 4. The advantage of the first two channels is that their purity
appears to be rather stable. On the contrary, the solar EUV radiation
is highly variable (Woods & Chamberlin 2009; Woods et al. 2005a,b).
Al and Zr channels display extreme variability with the solar
conditions, as purity abruptly decreases when strong contamination from
the soft X-ray range begins to dominate the signal in the case of high
flux. One of the advantages of these two channels is that, although
their purity is highly dependent on the incoming signal, additional
information may be gained by a clever signal separation (Dammasch 2009b). As soon as the pure
signal of the channels is determined, the relationship to the
respective solar irradiance appears quite straightforward according to
the radiometric model simulations. Another advantage of the latter two
LYRA channels (*-3 and *-4) is the fact that they have a small overlap
in responsivity around 17 nm, which is also the interval in which
SWAP will observe the Sun.
Table 3: Example of the expected LYRA total output signals (nA) and purities (%) between brackets. Since not the entire IR spectrum is taken into account, these values rather represent a lower limit.
Table 4:
Example of the LYRA total uncertainty budget with 1s integration time (
![]() )
at solar minimum (spectrum of 29 June 2008).
)
at solar minimum (spectrum of 29 June 2008).
![]() is the relative uncertainty of the LYRA instrument.
is the relative uncertainty of the LYRA instrument.
4.3 LYRA uncertainty budget
The uncertainties for each LYRA channel are estimated taking into
consideration possible uncertainties from responsivity measurements,
extrapolations, and small fluctuations of the room temperature.
According to Eq. (2), the mean spectral irradiance
![]() at the respective channel wavelength may be approximated by:
at the respective channel wavelength may be approximated by:
All the relative uncertainties (uncorrelated) are evaluated for producing the LYRA standard uncertainty, as follows:
with
Note that the dark current (![]() )
is measured with the cover closed before and after the signal
acquisition with the same integration time. It is then substracted from
the integrated signal to calculate
)
is measured with the cover closed before and after the signal
acquisition with the same integration time. It is then substracted from
the integrated signal to calculate ![]() .
The uncertainty on the integrated signal (i)
is evaluated using three levels of a reference calibration voltage.
Indeed the voltage-to-frequency converters (VFC) are not perfectly
linear. To correct the measured values, three calibration voltages
(0 V, 2.5 V, 5 V) are used. After the measurements, a
polynomial fit (second order) can be applied to correct the measured
values, if necessary. Note that a small offset is integrated, in order
that 0 V input does not correspond to 0 Hz output. The VFC's
are set to 5.635 V full-scale input, which equals to 1.2288 MHz.
To convert the voltage to current, an uncertainty on the measuring gain
resistor R and on the VFC offset are taken into account.
.
The uncertainty on the integrated signal (i)
is evaluated using three levels of a reference calibration voltage.
Indeed the voltage-to-frequency converters (VFC) are not perfectly
linear. To correct the measured values, three calibration voltages
(0 V, 2.5 V, 5 V) are used. After the measurements, a
polynomial fit (second order) can be applied to correct the measured
values, if necessary. Note that a small offset is integrated, in order
that 0 V input does not correspond to 0 Hz output. The VFC's
are set to 5.635 V full-scale input, which equals to 1.2288 MHz.
To convert the voltage to current, an uncertainty on the measuring gain
resistor R and on the VFC offset are taken into account.
The LYRA integration time is generated with a 4.9152 MHz quartz crystal with a temporal resolution of 0.2 ![]() s. The relative uncertainty of the quartz is
s. The relative uncertainty of the quartz is ![]() (50
+ 25) ppm for stability and tolerance of the frequency, which
corresponds to a maximal uncertainty between two integration times of
1.5 ms (worst case) at 10 s and below 1.5
(50
+ 25) ppm for stability and tolerance of the frequency, which
corresponds to a maximal uncertainty between two integration times of
1.5 ms (worst case) at 10 s and below 1.5 ![]() s for the 10 ms integration time.
The contributions to the measurement uncertainties of the filter-detector responsivities are given in Scholze et al. (2000); Richter et al. (2003).
In addition, a relative uncertainty of 5% was applied to the detector
photoresponse measured between 200 nm and 1100 nm, and 10% on
the filter transmittance when extrapolated or measured above
240 nm. As an example, the relative uncertainty for each channel
is reported in Table 4 with the expected output signals at solar minimum (spectrum of 29 June 2008).
s for the 10 ms integration time.
The contributions to the measurement uncertainties of the filter-detector responsivities are given in Scholze et al. (2000); Richter et al. (2003).
In addition, a relative uncertainty of 5% was applied to the detector
photoresponse measured between 200 nm and 1100 nm, and 10% on
the filter transmittance when extrapolated or measured above
240 nm. As an example, the relative uncertainty for each channel
is reported in Table 4 with the expected output signals at solar minimum (spectrum of 29 June 2008).
5 Conclusions
LYRA is exceptional in several respects. It is the first time UV diamond detectors are going to be used in space, and particularly for solar physics. They offer new potential to the future solar observation missions. The high cadence rate and low measurement uncertainty attainable by LYRA stems from them, and they promise radiation hardness. Additionally, LYRA profits from a redundancy design for tracking instrument degradation, LED light sources for in-flight monitoring, calibrations traceable to synchrotron source standards, and scientific synergies with SWAP, the sister solar instrument on board the PROBA2 satellite. For the calibration of LYRA, the responsivity, linearity, stability and homogeneity have been measured before final integration on the PROBA2 platform. The responsivity has been calibrated thoroughly in the wavelength range from 1 nm to 240 nm. LYRA channels show a high response for short wavelengths and a good NUV/VIS/IR rejection due to the combination of diamond photodetectors and optical filters. In the wavelength range of interest, LYRA channels are reasonably homogenous, linear, and stable under irradiation with a negligible dark current drift. A calibration software based on a radiometric model is used to determine spectral purity of the individual observation channels in dependence of the solar activity. These calibration functions will be tested in the commissioning phase and will be permanently updated to account for observed degradation and incorporate the results of cross-calibration among LYRA units and with other instruments.
AcknowledgementsThe authors acknowledge the support from the Belgian Federal Science Policy Office through the ESA-PRODEX programme, the Max-Planck-Institut für Sonnensystemforschung and ISSI, Bern, funding of SCSL.
References
- BenMoussa, A. 2006a, Pre-Analysis Report - Final calibration GI beamline (1-30 nm) - PROBA2/LYRA, Tech. Rep., Royal Observatory of Belgium
- BenMoussa, A. 2006b, Pre-Analysis Report - Final calibration NI beamline (40-240 nm) - PROBA2/LYRA, Tech. Rep., Royal Observatory of Belgium
- BenMoussa, A., Schühle, U., Haenen, K., et al. 2004, Physica Status Solidi Applied Research, 201, 2536 [NASA ADS] [CrossRef]
- BenMoussa, A., Schühle, U., Scholze, F., et al. 2006a, Measurement Science and Technology, 17, 913 [NASA ADS] [CrossRef]
- BenMoussa, A., Theissen, A., Scholze, F., et al. 2006b, Nucl. Instr. Meth. Phys. Res. A, 568, 398 [NASA ADS] [CrossRef]
- BenMoussa, A., Soltani, A., Haenen, K., et al. 2008, Semiconductor Science Technology, 23, 035026 [NASA ADS] [CrossRef]
- Berghmans, D., Hochedez, J. F., Defise, J. M., et al. 2006, Adv. Space Res., 38, 1807 [NASA ADS] [CrossRef]
- Dammasch, I. 2006, LYRA Flatfield Software: Relative Output as Function of Pointing, Tech. Rep., Royal Observatory of Belgium
- Dammasch, I. 2007, LYRA Dark Current and LED Measurements, Tech. Rep., Royal Observatory of Belgium
- Dammasch, I. 2008, LYRA Responsivity: Update, Tech. Rep., Royal Observatory of Belgium
- Dammasch, I. 2009a, LYRA Calibration Methods: New channels, Tech. Rep., Royal Observatory of Belgium
- Dammasch, I. 2009b, LYRA Output: Expected Variations, Tech. Rep., Royal Observatory of Belgium
- Hochedez, J.-F., Schmutz, W., Stockman, Y., et al. 2006, Adv. Space Res., 37, 303 [NASA ADS] [CrossRef]
- Richter, M., Hollandt, J., Kroth, U., et al. 2003, Metrologia, 40, 107 [NASA ADS] [CrossRef]
- Scholze, F., Beckhoff, B., Brandt, G., et al. 2000, in SPIE Conf. Ser. 4146, ed. W. M. Kaiser & R. H. Stulen, 72
- Scholze, F., Tummler, J., & Ulm, G. 2003, Metrologia, 40, S224 [NASA ADS] [CrossRef]
- Woods, T. N., & Chamberlin, P. C. 2009, Adv. Space Res., 43, 349 [NASA ADS] [CrossRef]
- Woods, T. N., Eparvier, F. G., Bailey, S. M., et al. 2005a, J. Geophys. Res. (Space Phys.), 110, 1312 [CrossRef]
- Woods, T. N., Rottman, G., & Vest, R. 2005b, Sol. Phys., 230, 345 [NASA ADS] [CrossRef]
All Tables
Table 1: Selected configuration of LYRA channels.
Table 2: Linearity fit parameters and their quality (b>1 denotes super-linear and b<1 sub-linear behavior).
Table 3: Example of the expected LYRA total output signals (nA) and purities (%) between brackets. Since not the entire IR spectrum is taken into account, these values rather represent a lower limit.
Table 4:
Example of the LYRA total uncertainty budget with 1s integration time (
![]() )
at solar minimum (spectrum of 29 June 2008).
)
at solar minimum (spectrum of 29 June 2008).
![]() is the relative uncertainty of the LYRA instrument.
is the relative uncertainty of the LYRA instrument.
All Figures

|
Figure 1:
Photograph of LYRA and an exploded view of one of the 3 redundant LYRA units. The total dimensions of LYRA are 315 mm |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: Schematic representation of the optical path of a LYRA channel (not to scale) which consists of a view-limiting aperture (1), a precision aperture (2), an optical filter (3) and the detector (4). |
| Open with DEXTER | |
| In the text | |
| |
Figure 3: Design and picture of the LYRA cover mechanism. |
| Open with DEXTER | |
| In the text | |

|
Figure 4:
Measured spectral transmittance of the Acton Research corp. filters: Lyman- |
| Open with DEXTER | |
| In the text | |

|
Figure 5: Measured spectral transmittance of the Al (157.9 nm thick) and the Zr (141.3 nm thick) filters from Luxel corp. between 1 and 30 nm. |
| Open with DEXTER | |
| In the text | |
| |
Figure 6: Photograph of the diamond photodetectors a) MSM and detail of the Ti/Pt/Au contact structures; b) the PIN photodiode. |
| Open with DEXTER | |
| In the text | |

|
Figure 7: Spectral response of a typical Si AXUV n-on-p photodiode (unbiased), diamond PIN photodiode (unbiased) and diamond MSM (under 5 V bias) between 1 nm and 1000 nm. |
| Open with DEXTER | |
| In the text | |

|
Figure 8:
Top left: absolute responsivity of the Lyman- |
| Open with DEXTER | |
| In the text | |
| |
Figure 9: Homogeneity of the responsivity (3-D representation) of channel 2-4 (MSM diamond photodetector, left panel) and channel 1-4 (Si-AXUV, right panel) at 10 nm wavelength. |
| Open with DEXTER | |
| In the text | |

|
Figure 10: Flux linearity of LYRA channels 1-1 and 1-2 (photocurrent versus incident power) at 121.6 nm and 210 nm respectively, with the fitted function (see Eq. (1)). |
| Open with DEXTER | |
| In the text | |

|
Figure 11: Signal current (log scale) as a function of time for LYRA detectors at different wavelengths. |
| Open with DEXTER | |
| In the text | |
| |
Figure 12: Schematic representation of a LYRA unit (head) with its detectors, filters, LEDs and its two apertures (not to scale). |
| Open with DEXTER | |
| In the text | |

|
Figure 13: Combined simulated spectral responsivity [detector + filter] for LYRA unit 1 between 1 and 1100 nm. |
| Open with DEXTER | |
| In the text | |

|
Figure 14: Examples for LYRA radiometric model simulations. From top to bottom: channel 1-3's responsivity curve (MSM detector + Al filter), the solar spectrum (maximum and minimum solar spectrum from 2003 and 2008, respectively), and the product of both; the integral of the last curve estimates the total output signal of the LYRA channel, when multiplied with the area of the precision aperture A. |
| Open with DEXTER | |
| In the text | |

|
Figure 15: Examples of LYRA radiometric model simulations for channels 1-1, 1-2 and 1-4. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.