A&A 508, 173-180 (2009)

Extremely energetic Fermi gamma-ray bursts obey spectral energy correlations

L. Amati¹ - F. Frontera^1,2 - C. Guidorzi²

1 - INAF - IASF Bologna, via P. Gobetti 101, 40129 Bologna, Italy
2 - University of Ferrara, Department of Physics, via Saragat 1, 44100 Ferrara (FE), Italy

Received 29 June 2009 / Accepted 10 September 2009

Abstract
The origin, reliability, and dispersion of the  -  and other spectral energy correlations is a highly debated topic in GRB astrophysics. GRB 080916C, with its enormous radiated energy (   10⁵⁵ erg in the 1 keV-10 GeV cosmological rest-frame energy band) and its intense GeV emission measured by Fermi, provides a unique opportunity to investigate this issue. In our analysis, we also study another extremely energetic event, GRB 090323, more recently detected and localized by Fermi/LAT, whose radiated energy is comparable to that of GRB 080916C in the 1 keV-10 MeV energy range. Based on Konus/WIND and Fermi spectral measurements, we find that both events are fully consistent with the  -   correlation (updated to include 95 GRBs with the data available as of April 2009), thus further confirming and extending it, and providing evidence against a possible flattening or increased dispersion at very high energies. This also suggests that the physics behind the emission of peculiarly bright and hard GRBs is the same as for medium-bright and soft-weak long events (XRFs), which all follow the correlation. In addition, we find that the normalization of the correlation obtained by considering these two GRBs and the other long ones for which was measured to high accuracy by the Fermi/GBM are fully consistent with those obtained by other instruments (e.g., BeppoSAX, Swift, Konus/WIND), thus indicating that the correlation is not affected significantly by ``data truncation'' because of detector thresholds and limited energy bands. A Fermi/GBM accurate estimate of the peak energy of a very bright and hard short GRB with a measured redshift, GRB 090510, provides robust evidence that short GRBs do not follow the  -   correlation and that the  -   plane can be used to discriminate between, and understand, the two classes of events. Prompted by the extension of the spectrum of GRB 080916C to several GeV (in the cosmological rest-frame) without any excess or cut-off, we also investigated whether the evaluation of in the commonly adopted 1 keV-10 MeV energy band may bias the  -   correlation and/or contribute to its scatter. By computing from 1 keV to 10 GeV, the slope of the correlation becomes slightly flatter, while its dispersion does not change significantly. Finally, we find that GRB 080916C is also consistent with most of the other spectral energy correlations derived from it, with the possible exception of the  -   -  correlation.

Key words: gamma rays: bursts - gamma rays: observations

1 Introduction

Despite the enormous amount of observational and theoretical advances, several open issues cloud our understanding of the GRB phenomenon. Among these, the correlation between the photon energy at which the  spectrum (in the cosmological rest-frame) of the prompt emission reaches its peak, , and the total radiated energy computed by assuming isotropic emission, , in long GRBs remains one of the most debated and intriguing. Discovered in 2002 based on a sample of BeppoSAX GRBs with known redshift (Amati et al. 2002), the  -  correlation was then confirmed and shown to hold for all GRBs, soft or bright, with known z and constrained values of and fluence, with the only exception of the peculiar sub-energetic GRB 980425 (Amati et al. 2007; Amati 2006a). This correlation was also proposed by Lloyd et al. (2000) based on the analysis of a sample of bright BATSE GRBs without measured redshift. The implications of this observational evidence involve the physics and geometry of the prompt emission, the identification and understanding of different subclasses of GRBs (e.g., short, sub-energetic), and the use of GRBs to estimate cosmological parameters (Amati et al. 2008; Ghirlanda et al. 2006; Amati 2006a; Amati et al. 2007).

Thus, testing the  -  correlation and the other ``spectral energy'' correlations derived from it, understanding their origin, and investigating their dispersion and the existence of possible outliers are relevant issues for GRB physics and cosmology. These issues can be approached in three ways: a) by adding new data for GRBs with known redshift detected by different instruments, each one having its own sensitivity and spectral response and thus covering different regions of the  - fluence plane (Ghirlanda et al. 2008; Amati 2006a,b); b) by verifying its validity with large samples of GRBs with no measured redshift (Ghirlanda et al. 2005a,2008); and c) by studying the behaviour in the  -   plane of peculiar GRBs (Amati et al. 2007). Selection effects on this correlation have also been investigated with contrasting results (Ghirlanda et al. 2005a; Shahmoradi & Nemiroff 2009; Butler et al. 2009; Ghirlanda et al. 2008; Band & Preece 2005; Butler et al. 2007).

In this article, the  -  correlation and its related spectral energy correlations are studied for the most energetic GRBs yet detected, GRB 080916C (Abdo et al. 2009; Greiner et al. 2009) and GRB 090323 (van der Horst 2009; Golenetskii et al. 2009b). In particular, GRB 080916C, with its enormous energy release, the extended spectrum of its prompt emission up to tens of GeV without any excess or cut-off, and the accurate measurements of its spectral parameters provided by Fermi/GBM and Konus/WIND, provide a unique opportunity to test the robustness and extension of these correlations and investigate their properties. We also revise the  -   correlation by including the newly detected GRBs with known redshift and  , and compare the estimate of its normalization obtained by using only GRBs detected by Fermi/GBM with those estimated by other instruments. Our study is based on published spectral results by Konus/WIND, Fermi/GBM, Swift, and on specific data analyses of publicly available data.

	Figure 1: Light curve of the prompt emission of GRB 080916C as measured by the Fermi/GBM - n3 detector (8-1000 keV). The horizontal dotted line is the best-fit function of the background level measured before and after the GRB. Also shown (vertical dashed lines) are the time intervals for which time-resolved spectra from 8 keV to 10 GeV were reported by Abdo et al. (2009).
Open with DEXTER

2 Observations and data analysis

GRB 080916C was detected by the Fermi/GBM on 16 September 2008 at 00:12:45 UT as a long, multi-peak structured GRB of duration T₉₀  66 s in 50-300 keV (Goldstein & van der Horst 2008). The light curve of the prompt emission measured by one of the Fermi/GBM NaI detectors that triggered the event is shown in Fig. 1. The burst was also observed by AGILE (MCAL, SuperAGILE, and ACS), RHESSI, INTEGRAL (SPI-ACS), Konus/Wind, and MESSENGER (Hurley et al. 2008). Remarkably, very high energy photons from GRB 080916C were detected by Fermi/LAT up to 10 GeV, more than 145 photons having energies of above 100 MeV and 14 photons above 1 GeV (Tajima et al. 2008; Abdo et al. 2009).

Because of the prompt dissemination of the Fermi/LAT and IPN positions, GRB 080916C was followed-up by Swift and other ground telescopes, leading to the detection of both the X-ray and optical fading counterparts. Of particular interest are the afterglow measurements by Swift/XRT and GROND. The X-ray afterglow light curve (Fig. 2) shows the canonical shape: a steep decay followed by a flat decay and than a steeper power-law decay of index 1.4 and no break-up until 1.3 Ms from the GRB onset (Stratta et al. 2008). The optical afterglow light curve shows a different behaviour, with strong evidence of a simple power-law decay (Greiner et al. 2009).

A photometric redshift of 4.35  0.15 was later reported by the GROND team (Greiner et al. 2009). By combining this value with the fluence and spectral parameters of the prompt emission provided by Fermi/GBM and Konus/WIND, 080916C was found to be the most energetic GRB ever, with an of 4  10⁵⁴ erg in the standard 1-10 000 keV cosmological rest-frame energy band. Moreover, the joint spectral analysis of Fermi/GBM and LAT data published by the Fermi team (Abdo et al. 2009) showed that the spectrum extends up to 1-10 GeV without any excess or cut-off, and that the computed by integrating up to 10 GeV is as high as 10⁵⁵ erg.

	Figure 2: X-ray afterglow light curve of GRB 080916C measured by the Swift/XRT in 0.3-10 keV. The continuous line shows the best-fit double broken power-law; the dashed line shows the triple broken power-law obtained by fixing the last slope to 2.4 and corresponding to the 90% c.l. lower limit to (see text).
Open with DEXTER

More recently, another very bright event, GRB 090323, has been detected and localized by the Fermi/LAT (Ohno et al. 2009). Follow-up observations were performed by Swift and other ground-based facilities, leading to the discovery of X-ray, optical, and radio counterparts (Harrison et al. 2009; Updike et al. 2009; Kennea et al. 2009). A spectroscopic redshift of 3.57 was measured by Gemini south (Chornock et al. 2009). Spectral parameters and fluence for GRB 090323 were provided by both the Fermi/GBM (van der Horst 2009) and Konus/WIND (Golenetskii et al. 2009b). Based on the spectrum and fluence measured by Konus/WIND and the redshift of 3.57 measured by Gemini south, the  value of this event in the 1-10 000 keV cosmological rest-frame energy band can be inferred to be 4  10⁵⁴ erg, thus comparable to that of GRB 080916C. No refined analysis of the VHE emission measured by the LAT from this event has been published.

Figure 3: Location in the  - fluence ( left) and  -  ( right) planes of the 95 GRBs with firm redshift and estimates as of April 2009 (see text). In both panels, the points corresponding to the extremely energetic GRBs 080916C and 090323 are highlighted. In addition, in the left panel we mark with red dots those GRBs with spectral parameters and fluence provided by the Fermi/GBM, and in the right panel we also show the GRB 080916C point obtained with computed in the 1 keV-10 GeV cosmological rest-frame energy band and the point corresponding to the short GRB 090510. The continuous lines in the right panel correspond to the best-fit power-law and the 2 dispersion region of the  -   correlation derived by Amati et al. (2008).

Open with DEXTER

In our analysis, we used results published in the above references and specific data analysis of the public Fermi/GBM and Swift/XRT data. In particular, for GRB 080916C we extracted the light curve of each Fermi/GBM detection unit that triggered the event (n3, n4 and b0) by using the gtbin tool included in the data reduction and analysis tools. The Swift/XRT data of this burst were processed using the heasoft package (v.6.4). We ran the task xrtpipeline (v.0.11.6) by applying calibration and standard filtering and screening criteria.

Radiated energies and luminosities are computed by assuming a standard CDM cosmology with H₀= 70 km s^-1 Mpc^-1,  = 0.27, and  = 0.73. The quoted uncertainties are at 68% c.l., unless stated otherwise.

Table 1:   The 25 GRBs with known redshift and measured added to the sample of Amati et al. (2008) in our analysis of the  -   correlation, providing a total of 95 GRBs.

3 The 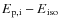correlation: update and comparison among different instruments

In Fig. 3 (right panel), we show the  -  correlation for long GRBs (short GRBs and the peculiar sub-energetic GRB 980425 are not included) obtained by adding to the sample of 70 events of Amati et al. (2008) 25 more GRBs for which measurements of the redshift and/or of the spectral parameters have in the meantime become available (as of April 2009). As in previous evaluations,  was derived in the 1-10 000 keV energy band. The and of these events, together with their redshift and relevant references, are reported in Table 1. These values and their uncertainties were computed based on published spectral parameters and fluences, and following the methods and criteria reported, e.g., in Amati (2006a) and Amati et al. (2008). As can be seen, this updated sample of 95 GRBs is fully consistent with the  -   correlation and its dispersion as derived by Amati et al. (2008). This is quantitatively confirmed by the fit with both the classical  method and the adopted maximum likelihood method by Amati (2006a) and Amati et al. (2008), which allows us to quantify the extrinsic scatter in the correlation ( ). We obtain a slope of m = 0.57  0.01 and a  of 594, by means of a linear fit to the log( ) versus log( ) data points with the  method, and m = 0.54  0.03 and  = 0.18  0.02 (68% c.l.) with the maximum likelihood method. These values are fully consistent with those obtained by Amati et al. (2008).

In their study of the selection effects, Butler et al. (2009) claim that the dispersion and significance of the  -   correlation in the intrinsic plane is comparable to that of the  - fluence in the observer plane, and that the normalization of the  -   correlation depends on the instrument used to detect GRBs. In Fig. 3 (left panel), we show the distribution of these 95 GRBs in the  - fluence observer plane. To allow a reliable comparison, the X and Y scales of this plot cover the same orders of magnitude as the  -   plane shown in Fig. 3 (right panel). As can be seen, when we move from the observer to the intrinsic plane the dispersion the correlation between spectral peak photon energy and fluence (radiated energy) decreases significantly (  from 0.31 to 0.18, and from 3110 to 594), its extension covers more orders of magnitudes, and its significance increases (Spearman's correlation coefficient  from 0.75 to 0.88). In Fig. 4, we compare the normalization of the  -   correlation obtained with all the most relevant instruments with that derived by Amati et al. (2008). As can be seen, no significant (i.e. above 1) change is evident. In particular, the  -   correlation derived using the Swift GRB data for which, unlike those considered by Butler et al. (2009),  is really measured with BAT (from the official Swift team catalog by Sakamoto et al. (2008), and/or GCNs) or with broad-band instruments (mainly Konus/WIND), is fully consistent with that determined with other instruments. The  -   correlation derived from GRBs detected with Fermi/GBM is fully consistent with the correlation determined by other instruments with narrower energy ranges. Given the unprecedented broad energy coverage of the GBM (from 8 keV up to more than 30 MeV), the derived  -   correlation is certainly not affected by biases in the estimate of the spectral parameters (the so-called ``data truncation'' effect, see e.g., Lloyd et al. 2000).

We also tested the effect of redshift on the  versus fluence dependence. Starting from  versus fluence data, we derived 10 000   -  simulated correlations by randomly exchanging the z values among the 95 GRBs, and we computed for each sample the Spearman's correlation coefficient  between the and  values so obtained. We found a  distribution that is fully consistent with a Gaussian of centroid 0.75, which is exactly the value obtained for the  versus fluence correlation in the observer plane, and of dispersion   0.035, extending up to 0.85. For comparison, the  value of the true  -   correlation, as we have seen, is 0.88 which is 3.8 away from that obtained from the simulation and corresponds to a chance probability of less than 1 over 1000, that the true  -   correlation is randomly extracted from the simulated ones.

An exhaustive paper devoted to the discussion of the selection effects affecting the  -   correlation is in preparation.

4 Fermi highly energetic GRBs in th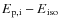e plane

Based on Fermi/GBM observations, the fluence of GRB 080916C in 8 keV-30 MeV was measured to be 1.9  10^-4 erg cm^-2 and its time-averaged spectrum in the same energy band can be fit by a Band function (Band et al. 1993) with  = -0.91  0.02,  = -2.08  0.06, and  = 424  24 keV (van der Horst & Goldstein 2008). For the 20 keV-10 MeV energy band, the Konus/WIND team reported a fluence of (1.24  0.17)  10^-4 erg cm^-2, a 256-ms peak flux of (1.19  0.30)  10^-5 erg cm^-2 s^-1 and a time-averaged spectrum with  = -1.04  0.06,  = -2.26  0.3, and  = 505  75 keV (Golenetskii et al. 2008f).

By taking into account these fluences and spectral parameters, with their uncertainties, the redshift, with its uncertainty, provided by GROND, and by integrating the cosmological rest-frame spectrum in the commonly adopted 1 keV-10 MeV energy band (Amati 2006a; Amati et al. 2002), we derive  = (3.8  0.8)  10⁵⁴ erg, and  = 2646  566 keV. As can be seen in Fig. 3, these parameters imply that the location of GRB 080916C in the  -   plane is very close to the best-fit power-law obtained for a sample of 70 long GRBs considered by Amati et al. (2008). This confirms that GRB 080916C follows the  -   correlation and extends its range of validity along by a factor of 2. If GRB 080916C is excluded from the fit to the correlation, the values of the parameters and their uncertainties do not change significantly with respect to those reported in the previous section, which is however the case when the softest/weakest events are excluded. This confirms that both the significance and the characterization of the  -   correlation do not depend on events at the most extreme ranges of the ranges of and  values.

The spectral analysis performed by Abdo et al. (2009) indicates that the time-resolved spectra of this event can be fit with the simple Band function from 8 keV up to more than 1 GeV. This implies that the above 10 MeV should not be negligible. Indeed, by extending the integration up to 10 GeV (cosmological rest-frame) and using the  value provided by Fermi/GBM (which, given the extension of the energy band of this instrument, is expected to be more accurate than that provided by Konus/WIND), we obtain a value of of (1.1  0.2)  10⁵⁵ erg, which is higher than the value obtained by integrating up to 10 MeV by a factor of 2.5. As can be seen in Fig. 3, for this (enormous) value of  , GRB 080916C remains still consistent with the  -   correlation to within 2 and extends its dynamic range along by about half an order of magnitude.

Figure 4: Location in the  -   plane of those GRBs with localization and provided by different instruments. The top panels show those GRBs whose detection, localization, and spectrum were provided by BeppoSAX ( left) and HETE-2 ( right). The bottom-left panel shows those GRBs detected and localized by Swift/BAT for which has been provided by either BAT itself or by other instruments (excluding the Fermi/GBM). The bottom-right panel shows those GRBs for which the localization has been provided by either Swift or Fermi/LAT, and has been measured by Fermi/GBM ( right panel). In all panels, the continuous lines correspond to the best-fit power-law and the 2 dispersion region of the correlation as computed by including all 95 GRBs with known z and and the dashed line is the best-fit power-law obtained by considering the plotted points only.

Open with DEXTER

In Fig. 3, we also show the location in the  -   plane of data for the other ultra-energetic GRB detected by Fermi, GRB 090323. For this event, no refined analysis of the VHE emission measured by the LAT has been published, thus no reliable extrapolation and integration of the spectrum up to the GeV range can be made. Hence, we restrict the analysis to the standard 1 keV-10 MeV energy band. In addition, the published GBM spectral analysis concerns only the first 70 s of the event (which shows a total duration of 120 s), and thus these data do not provide a reliable estimate of and . By using the spectral parameters  = -0.96 _-0.09^+0.12,  = -2.09 _-0.22^+0.16, and  = 416 _-73⁺⁷⁶ keV, the fluence of (2.0  0.3)  10^-4 erg cm^-2 (20 keV-10 MeV) provided by Konus/WIND (Golenetskii et al. 2009b), and the redshift of 3.57 measured by Gemini south, we find that  = (4.1  0.5)  10⁵⁴ erg and  = 1901  343 keV. These values are very close to those of GRB 080916C and also make this event fully consistent with the  -   correlation. This provides additional evidence that the newly discovered class of extremely energetic GRBs follows the correlation. The detection of more GRBs with photons at GeV energies (e.g., from Fermi/LAT) will strengthen this result.

The extension of the spectrum of GRB 080916C supports the possibility that, at least for a fraction of long GRBs, the commonly adopted 1 keV-10 MeV cosmological rest-frame energy band for the computation of may underestimate this quantity and be a source of systematic errors and extra-scatter in the  -   correlation. To test this, we again considered the sample of Amati et al. (2008) in addition to the 25 GRBs reported in Table 1. For each event, we re-computed the  value by extending the integration up to 10 GeV using the and  values reported in the literature. For those events without a reported value of , e.g., in the case of a fit with a cut-off power-law, we adopted a Band function with . The fit with the  method provides m = 0.55  0.01 with a best-fit of 619, while the maximum likelihood method provides m = 0.51  0.03 and  = 0.18  0.02 (68% c.l.). We conclude that extending the computation of up to 10 GeV slightly flattens the slope of the  -   correlation but does not significantly change its scatter.

Finally, the Fermi/LAT detected and localized GeV emission from the bright short (0.5 s) GRB 090510 Ohno & Pelassa (2009). This event was also detected by AGILE at energies above 100 MeV (Longo et al. 2009). By combining the VLT redshift estimate of z = 0.903 Rau et al. (2009) and the spectral parameters and fluence obtained with the Fermi/GBM Guiriec et al. (2009), the parameters and of this event are found to be (4  1)  10⁵² erg and 8370  760 keV, respectively. With these values, GRB 090510 is located in the  -   plane significantly above the region populated by long GRBs (Fig. 3, right panel), helping to confirm that short GRBs do not follow the  -   correlation.

Figure 5: a) Correlation between and . The red triangle corresponds to GRB 080916C and the red continuous lines correspond to the best-fit and 2 range determined by Yonetoku et al. (2004). The blue square is the of GRB 080916C multiplied by T0.450.43 and the blue dotted lines correspond to the best-fit and 2 range of the  -   - T0.45 correlation as determined by Rossi et al. (2008). b) Correlation between and within the GRB (red triangles) based on the time-resolved spectral analysis reported by Abdo et al. (2009). The letters indicate the corresponding time interval (see Fig. 1). The blue square corresponds to the luminosity of the whole GRB as determined from the time-averaged spectrum. The red continuous lines show the best-fit power-law and the 2 region of the (t) -  (t) correlation (from Ghirlanda et al. 2007); the blue dotted line is the best-fit power-law to the 6 points of GRB 080916C. c) Correlation between and the collimation-corrected radiated energy  . The red continuous lines and triangles refer to the homogeneous circumburst medium case, while the blue dotted lines and squares refer to the wind case. The lines indicate the best-fit power-laws and 2 regions reported by Ghirlanda et al. (2007). For both cases, we report the lower limits to corresponding to  > 1 Ms and  > 0.5 Ms (see text). d) Correlation between , and . The lines correspond to the best-fit power-laws and 2 region reported by Ghirlanda et al. (2007). The two lower limits correspond to  > 1 Ms and  > 0.5 Ms (see text).

Open with DEXTER

5 GRB 080916C and other spectral energy correlations

After the discovery and first studies of the  -   correlation, it was pointed out that also correlates with other GRB intensity indicators, such as the peak luminosity, , (Ghirlanda et al. 2005b; Yonetoku et al. 2004) or the average luminosity, , (Ghirlanda et al. 2009; Lamb et al. 2004). In addition, it was found that by including the break time of the afterglow light curve, , either directly (Ghirlanda et al. 2007; Liang & Zhang 2005; Nava et al. 2006) or by using it to derive the jet opening angle and thus compute the collimation-corrected radiated energy (Ghirlanda et al. 2004; Nava et al. 2006), the extrinsic scatter decreases significantly. As discussed, e.g., by Amati (2008), given the strong correlation between , , and , the two-parameter spectral energy correlations are equivalent. In addition, in the light of the Swift results on X-ray afterglow light curves, the measurement of and its use to derive the jet opening angle are questionable (Ghirlanda et al. 2007; Campana et al. 2007). It was also proposed that the inclusion of the ``high signal timescale'', T_0.45, introduced and used for variability studies, reduces the dispersion in the  -   correlation (Firmani et al. 2006), but this property was not confirmed by later studies (Collazzi & Schaefer 2008; Rossi et al. 2008). Finally, there is evidence that, at least for a significant fraction of GRBs, the correlation between and luminosity also holds for the time-resolved spectra of individual events (Liang et al. 2004; Firmani et al. 2008; Frontera et al., in prep.). Given its extreme energetics and the good sampling of its optical and X-ray afterglow light curve, GRB 080916C can also be used to test these correlations.

For the  -  correlation, the 256 ms peak flux measured by Konus, by assuming the best-fit model of the time-averaged spectrum, allows us to infer that  = (1.9  0.6)  10⁵⁴ erg s^-1. This value, combined with the  value of 2646  566 keV derived above, gives a data point fully consistent with this correlation (Fig. 5a).

For the - - T_0.45 correlation, the background subtracted 8-1000 keV light curves obtained with the two (n3 and n4) Fermi/GBM NaI detectors (see Fig. 1) allow us to estimate T_0.45 (19.5  0.6 s for n3 and 19.2  0.5 s for n4) following the same approach as Rossi et al. (2008). The result is that GRB 080916C is also consistent with this correlation (Fig. 5a).

From the time-resolved spectral analysis reported by Abdo et al. (2009), an accurate estimate of was obtained. By using these results, we computed the for each of the corresponding time intervals and reconstructed the track of GRB 080916C in the  -   plane (Fig. 5b). As can be seen, the spectral and luminosity evolution of this GRB is fully consistent with the  -   correlation, as typically observed for bright events (Liang et al. 2004; Firmani et al. 2008; Frontera et al., in prep.). The slope of the power-law that best fits the 6 GRB 080916C data points is 0.4, slightly flatter than the commonly found value of 0.5. This is mostly due to the data point corresponding to the first time interval (A) (Fig. 1), which deviates slightly from the  -   correlation.

For the  -  correlation, no evidence of a jet break  is found either in the X-ray light curve (see Fig. 2) until the end of the XRT observations (1.3 Ms from the trigger) or in the optical light curve up to the end of the GROND (Greiner et al. 2009) observations (0.5 Ms from the trigger). A 90% lower limit to the jet break time of about 0.5 Ms is inferred from the X-ray light curve when assuming a typical post-break slope of 2.4 (see Fig. 2). By adopting a lower limit to of 0.5 Ms, standard assumptions about the conversion efficiency of the fireball kinetic energy into radiated energy, on the ISM density and profile, and on the ratio of mass loss rate to wind velocity (Ghirlanda et al. 2007; Nava et al. 2006), we obtain  > 8.8  10⁵¹ erg in the case of a homogeneous circumburst medium, and  > 1.6  10⁵¹ erg in the case of a wind medium. If  > 1 Ms, these values become  > 1.5  10⁵² erg (homogeneous circumburst medium),  > 2.4  10⁵¹ erg (wind medium). These lower limits take into account the uncertainty both in and the GRB redshift. As can be seen in Fig. 5c, the lower limits to obtained with   1 Ms are around 1.5-2 from the best-fit function reported by Ghirlanda et al. (2007), while for   0.5 Ms they are fully consistent with the fit.

Intriguingly, we find that GRB 080916C is a possible outlier of the  -   -  correlation (Fig. 5d). Indeed, its deviation from the best-fit power-law (determined by Ghirlanda et al. 2007) is >3.5, for  > 1 Ms, and more than 2.2, for  > 0.5 Ms.

6 Discussion

Prompt emission GRB models are challenged by both the extreme energetics of GRB 080916C and its spectrum following the simple Band function without any break or excess up to several tens of GeVs (in the cosmological rest-frame). For instance, Abdo et al. (2009) and Wang et al. (2009) suggest that the most probable emission mechanism is the standard non-thermal synchrotron radiation from shock-accelerated electrons within a fireball of bulk Lorentz factor  > 600-1000 (Abdo et al. 2009; Li 2009; Greiner et al. 2009). Nevertheless, the lack of a synchrotron self-Compton component cannot be explained by this scenario, and inverse Compton process in residual collisions may be needed to explain the time-delayed GeV photons (Li 2009). That GRB 080916C is fully consistent with the  -   correlation (Sect. 4 and Fig. 3) and most of its related correlations (Fig. 5), provides additional support to the hypothesis that, despite its huge isotropic-equivalent radiated energy and the extension to its emission up to VHE, the physics behind the emission of this event is not unusual compared to that governing less energetic long GRBs and XRFs. We note that the  -  correlation itself can be explained by the non-thermal synchrotron radiation scenario, e.g., by assuming that the minimum Lorentz factor, , and the normalization of the power-law distribution of the radiating electrons do not vary significantly from burst to burst or when imposing limits on the slope of the correlation between the fireball bulk Lorentz factor, , and the burst luminosity (Zhang & Mészáros 2002; Lloyd et al. 2000). The consistency of time-resolved spectra of GRB 080916C with the -luminosity correlation (Fig. 5) confirms that the prompt emission is dominated by a single emission mechanism. However, the slight deviation from this correlation of the peak energy and luminosity measured during the first time interval (Fig. 5b) may suggest that during the rise phase of the GRB, the main emission mechanism is still not fully operating and other mechanisms may play a relevant role.

In turn, the results for GRB 080916C confirm the robustness of the  -   correlation at least in the range of intrinsically medium-bright GRBs and, when integrating the spectrum up to 10 GeV, extend its range in by half an order of magnitude (Fig. 3). The flattening of the slope predicted in some scenarios, e.g., the multiple sub-jet model by Toma et al. (2005) or an increase in the dispersion at very high energies is not observed.

The above considerations are also supported by another extremely energetic GRB 090323 detected by the Fermi/LAT, which shows and  values similar to those of GRB 080916C and is thus also consistent with the  -   correlation (Fig. 3). The measurement by Fermi of the and GeV emission of the short bright GRB 090510, combined with a redshift measurement by VLT, provides additional strong evidence that short GRBs do not follow the correlations that hold for long GRBs, and that the  -   plane is a powerful tool for discriminating between the two classes and understanding their different emission mechanisms and origins.

As a part of our study, we have shown (Sect. 3) that: i) the distribution of the updated sample of 95 long GRBs with firm estimates of and z in the  -   plane is fully consistent with the slope, normalization, and dispersion determined for previous samples (Fig. 3); ii) moving from the observer frame ( - fluence) to the intrinsic plane (  -  ), the dispersion in the correlation decreases and its significance significantly increases (Fig. 3); iii) if we randomly redistribute the redshift values among the 95 GRBs of the sample, the  versus  distribution is similar to that of  versus fluence; iv) not only all Fermi/GBM GRBs but also all other long GRBs of known redshift (except GRB 980425) detected with BeppoSAX, HETE-2, and Swift, follow  -   correlations that are fully consistent with both each other and the  -   correlation derived by Amati et al. (2008) (Fig. 4).

All this evidence conflicts with the conclusions of Butler et al. (2009)) that the  -   correlation is strongly affected by instrumental effects. In addition, since GRBs detected and localized in different energy bands and by different instruments all follow the  -   correlation, the spectral energy correlations do not appear to be strongly affected by selection effects introduced in the observational process that lead to the redshift estimate. An exhaustive analysis of instrumental and selection effects on the  -   correlation is underway and will be reported elsewhere.

Following the Band function without any cut-off up to a few tens of GeVs (in the cosmological rest-frame), the spectrum of GRB 080916C may suggest that the commonly adopted 1 keV-10 MeV energy band is too narrow for a correct computation of , thus biasing the  -   correlation. However, our analysis reported in Sect. 4 shows that the extension of the energy band up to 10 GeV at which is computed has a marginal impact on the slope and the dispersion of the correlation, providing support for its robustness.

Finally, the testing of the consistency between data of very high energy GRBs and both the  -  and other spectral energy correlations (Sect. 5) is important for their potential use in cosmology (Amati et al. 2008; Ghirlanda et al. 2006). Because of detector sensitivity thresholds and possible evolutionary effects, more luminous GRBs are those more easily detectable at high redshifts (e.g., Amati 2006a). Besides the  -   correlation, which is fully satisfied by both GRB 080916C and GRB 090323, the lack of accurate enough long-term monitoring of the optical afterglow of these events (Kann et al. 2009; Greiner et al. 2009) prevents a stringent test of correlations involving the break-time . However, we find that GRB 080916C deviates by more than 2.5 from the best-fit function of the  -   -  correlation (Fig. 5), suggesting that the dispersion in this correlation either is higher than understood previously or is not satisfied at very high energies. This is an important issue, given that, with respect to the  -   correlation, the  -   -  has the advantage, as for the simple  -   correlation, of being model independent.

Due to Fermi and AGILE, we expect that the number of these extremely bright GRBs selected on the basis of their GeV emission will increase in the near future, giving us the possibility of improving our understanding of the physics of the prompt emission of GRBs and deriving important clues about the reliability and origin of spectral energy correlations.

We thank Guido Barbiellini and Francesco Longo at (Trieste, Italy) for discussions that prompted this work and Sara Cutini (at ASI/ASDC, Roma, Italy) for useful hints on the reduction of Fermi/GBM data.

References

• Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Science, 323, 1688 [NASA ADS] [CrossRef]
• Amati, L. 2006a, MNRAS, 372, 233 [NASA ADS] [CrossRef]
• Amati, L. 2006b, N.Cim.B., 121, 1081 [NASA ADS]
• Amati, L. 2008, AIPC, 966, 3 [NASA ADS]
• Amati, L., Frontera, F., Tavani, M., et al. 2002, A&A, 390, 81 [NASA ADS] [CrossRef] [EDP Sciences]
• Amati, L., Della Valle, M., Frontera F., et al. 2007, A&A, 463, 913 [NASA ADS] [CrossRef] [EDP Sciences]
• Amati, L., Guidorzi, C., Frontera, F., et al. 2008, MNRAS, 391, 577 [NASA ADS] [CrossRef]
• Band, D., & Preece, R. D. 2005, ApJ, 627, 319 [NASA ADS] [CrossRef]
• Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef]
• Barthelmy, S. D., Baumgartner, W., Cummings, J., et al. 2008a, GCN Circ., 7606
• Barthelmy, S. D., Baumgartner, W., Cummings, J., et al. 2008b, GCN Circ., 8428
• Baumgartner, W., Barthelmy, S. D., Cummings, J., et al. 2008, GCN Circ., 8243
• Bhat, P. N., Preece, R. D., & van der Horst, A. J. 2008, GCN Circ., 8526
• Bissaldi, E., & McBreen, S. 2008, GCN Circ., 8715
• Bissaldi, E., McBreen, S., Wilson-Hodge, C. A., & von Kienlin, A. 2008a, GCN Circ., 8263
• Bissaldi, E., McBreen, S., & Connaughton, V. 2008b, GCN Circ., 8369
• Butler, N. R., Kocevski, D., Bloom, J. S., & Curtis, J. L. 2007, ApJ, 671, 656 [NASA ADS] [CrossRef]
• Butler, N. R., Kocevski, D., & Bloom, J. S. 2009, ApJ, 694, 76 [NASA ADS] [CrossRef]
• Campana, S., Guidorzi, C., Tagliaferri, G., et al. 2007, A&A, 472, 395 [NASA ADS] [CrossRef] [EDP Sciences]
• Chornock, R., Perley, D. A., Cenko, S. B., & Bloom, J. S. 2009, GCN Circ., 9028
• Collazzi, A. C., & Schaefer, B. E. 2008, ApJ, 688, 456 [NASA ADS] [CrossRef]
• Connaughton, V. 2009, GCN Circ., 9230
• Firmani, C., Ghisellini, G., Avila-Rees, V., & Ghirlanda, G. 2006, MNRAS, 370, 185 [NASA ADS]
• Firmani, C., Cabrera, J. I., Avila-Rees, V., et al. 2008, MNRAS, 393, 1209 [NASA ADS] [CrossRef]
• Ghirlanda, G., Ghisellini, G., & Lazzati, D. 2004, ApJ, 616, 331 [NASA ADS] [CrossRef]
• Ghirlanda, G., Ghisellini, G., & Firmani, C. 2005a, MNRAS, 361, L10 [NASA ADS]
• Ghirlanda, G., Ghisellini, G., Firmani, C., Celotti, A., & Bosnjak, Z. 2005b, MNRAS, 360, L45 [NASA ADS]
• Ghirlanda, G., Ghisellini, G., & Firmani, C. 2006, New J. Phys., 8, 123 [CrossRef]
• Ghirlanda, G., Nava, L., Ghisellini, G., & Firmani, C. 2007, A&A, 466, 127 [NASA ADS] [CrossRef] [EDP Sciences]
• Ghirlanda, G., Nava, L., Ghisellini, G., Firmani, C., & Cabrera, J. I. 2008, MNRAS, 387, 319 [NASA ADS] [CrossRef]
• Ghirlanda, G., Nava, L., Ghisellini, G., Celotti, A., & Firmani, C. 2009, A&A, 496, 585 [NASA ADS] [CrossRef] [EDP Sciences]
• Goldstein, A., & van der Horst, A. 2008, GCN Circ., 8245
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2007, GCN Circ., 6849
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2008a, GCN Circ., 7751
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2008b, GCN Circ., 7812
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2008c, GCN Circ., 7854
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2008d, GCN Circ., 7862
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2008e, GCN Circ., 7995
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2008f, GCN Circ., 8258
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2008g, GCN Circ., 8548
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2009a, GCN Circ., 8776
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2009b, GCN Circ., 9030
• Golenetskii, H., Aptekar, R., Mazets, E., et al. 2009c, GCN Circ., 9050
• Greiner, J., Clemens, C., Kruehler, T., et al. 2009, A&A, 498, 89 [NASA ADS] [CrossRef] [EDP Sciences]
• Guiriec, S., Connaughton, V., & Briggs, M. 2009, GCN Circ., 9336
• van der Horst, A. 2009, GCN Circ., 9035
• van der Horst, A., & Goldstein, A. 2008, GCN Circ., 8278
• Harrison, F., Cenko, B., Frail, D. A., Chandra, P., & Kulkarni, S. 2009, GCN Circ., 9043
• Hurley, K., Goldsten, J., Golenetskii, S., et al. 2008, GCN Circ., 8251
• Kann, D. A., Laux, U., Ludwig, F., & Stecklum, S. 2009, GCN Circ., 9063
• Kennea, J., Evans, P., & Goad, M. 2009, GCN Circ., 9024
• von Kienlin, A. 2009, GCN Circ., 9229
• Lamb, D. Q., Ricker, G. R., Atteia, J.-L., et al. 2004, NewAR, 48, 423 [NASA ADS] [CrossRef]
• Liang, E., Dai, Z. G., & Wu, X. F. 2004, ApJ, 606, L29 [NASA ADS] [CrossRef]
• Liang, E., & Zhang, B. 2005, ApJ, 633, 311 [NASA ADS] [CrossRef]
• Li, Z. 2009, ApJ, submitted [arXiv:0810.2932]
• Lloyd, N. M., Petrosian, V., & Mallozzi, R. S. 2000, ApJ, 534, 227 [NASA ADS] [CrossRef]
• Longo, F., Moretti, E., Barbiellini, G., et al. 2009, GCN Circ., 9343
• Meegan, C. A., Greiner, J., Bhat, N. P., et al. 2008, GCN Circ., 8100
• Nava, L., Ghisellini, G., Ghirlanda, G., Tavecchio, F., & Firmani, C. 2006, A&A, 450, 471 [NASA ADS] [CrossRef] [EDP Sciences]
• Ohno, M., & Pelassa, V. 2009, GCN Circ., 9334
• Ohno, M., Kokubun, M., Suzuki, M., et al. 2008, GCN Circ., 7630
• Ohno, M., Cutini, S., McEnery, J., et al. 2009, GCN Circ., 9021
• Palmer, D. M., Barthelmy, S. D., Baumgartner, W., et al. 2008a, GCN Circ., 8351
• Palmer, D. M., Barthelmy, S. D., Baumgartner, W., et al. 2008b, GCN Circ., 8526
• Pal'shin, V., Golenetskii, S., Aptekar, R., et al. 2008, GCN Circ., 8256
• Pal'shin, V., Golenetskii, S., Aptekar, R., et al. 2009, GCN Circ., 9196
• Rau, A., McBreen, S., Kruehler, T., & Greiner, J. 2009, GCN Circ., 9353
• Rossi, F., Guidorzi, C., Amati, L., et al. 2008, MNRAS, 388, 1284 [NASA ADS]
• Sakamoto, T., Lamb, D. Q., Kawai, N., et al. 2005, ApJ, 629, 311 [NASA ADS] [CrossRef]
• Sakamoto, T., Barthelmy, S. D., Barbier, L., et al. 2008, ApJS, 175, 179 [NASA ADS] [CrossRef]
• Shahmoradi, A., & Nemiroff, R. J. 2009, MNRAS, submitted [arXiv:0904.1464]
• Stratta, G., Perri, M., Preger, B., et al. 2008, GCN Rep., 166, 1 [NASA ADS]
• Tajima, H., Bregeon, J., Chiang, J., et al. 2008, GCN Circ., 8246
• Toma, K., Yamazaki, R., & Nakamura, T. 2004, ApJ, 635, 481 [NASA ADS] [CrossRef]
• Updike, A. C., Filgas, R., Kruehler, T., Greiner, J., & McBreen, S. 2009, GCN Circ., 9026
• Wang, X. Y., Li, Z., Dai, Z. G., & Mészáros, P. 2009, ApJ, 698, L98 [NASA ADS] [CrossRef]
• Yonetoku, D., Murakami, T., Nakamura, T., et al. 2004, ApJ, 609, 935 [NASA ADS] [CrossRef]
• Zhang, B., & Mészáros, P. 2002, ApJ, 581, 1236 [NASA ADS] [CrossRef]

Footnotes

... data

The Fermi/GBM data and analysis tools are available at ftp://legacy.gsfc.nasa.gov/fermi/; the Swift/XRT data are available at
http://swift.gsfc.nasa.gov/docs/swift/archive/

... tools

Available at http://fermi.gsfc.nasa.gov/ssc/data/analysis/

... criteria

See http://swift.gsfc.nasa.gov/docs/swift/analysis/

All Tables

Table 1:   The 25 GRBs with known redshift and measured added to the sample of Amati et al. (2008) in our analysis of the  -   correlation, providing a total of 95 GRBs.

All Figures

	Figure 1: Light curve of the prompt emission of GRB 080916C as measured by the Fermi/GBM - n3 detector (8-1000 keV). The horizontal dotted line is the best-fit function of the background level measured before and after the GRB. Also shown (vertical dashed lines) are the time intervals for which time-resolved spectra from 8 keV to 10 GeV were reported by Abdo et al. (2009).
Open with DEXTER
In the text

	Figure 2: X-ray afterglow light curve of GRB 080916C measured by the Swift/XRT in 0.3-10 keV. The continuous line shows the best-fit double broken power-law; the dashed line shows the triple broken power-law obtained by fixing the last slope to 2.4 and corresponding to the 90% c.l. lower limit to (see text).
Open with DEXTER
In the text

	Figure 3: Location in the  - fluence ( left) and  -  ( right) planes of the 95 GRBs with firm redshift and estimates as of April 2009 (see text). In both panels, the points corresponding to the extremely energetic GRBs 080916C and 090323 are highlighted. In addition, in the left panel we mark with red dots those GRBs with spectral parameters and fluence provided by the Fermi/GBM, and in the right panel we also show the GRB 080916C point obtained with computed in the 1 keV-10 GeV cosmological rest-frame energy band and the point corresponding to the short GRB 090510. The continuous lines in the right panel correspond to the best-fit power-law and the 2 dispersion region of the  -   correlation derived by Amati et al. (2008).
Open with DEXTER
In the text

	Figure 4: Location in the  -   plane of those GRBs with localization and provided by different instruments. The top panels show those GRBs whose detection, localization, and spectrum were provided by BeppoSAX ( left) and HETE-2 ( right). The bottom-left panel shows those GRBs detected and localized by Swift/BAT for which has been provided by either BAT itself or by other instruments (excluding the Fermi/GBM). The bottom-right panel shows those GRBs for which the localization has been provided by either Swift or Fermi/LAT, and has been measured by Fermi/GBM ( right panel). In all panels, the continuous lines correspond to the best-fit power-law and the 2 dispersion region of the correlation as computed by including all 95 GRBs with known z and and the dashed line is the best-fit power-law obtained by considering the plotted points only.
Open with DEXTER
In the text

	Figure 5: a) Correlation between and . The red triangle corresponds to GRB 080916C and the red continuous lines correspond to the best-fit and 2 range determined by Yonetoku et al. (2004). The blue square is the of GRB 080916C multiplied by T0.450.43 and the blue dotted lines correspond to the best-fit and 2 range of the  -   - T0.45 correlation as determined by Rossi et al. (2008). b) Correlation between and within the GRB (red triangles) based on the time-resolved spectral analysis reported by Abdo et al. (2009). The letters indicate the corresponding time interval (see Fig. 1). The blue square corresponds to the luminosity of the whole GRB as determined from the time-averaged spectrum. The red continuous lines show the best-fit power-law and the 2 region of the (t) -  (t) correlation (from Ghirlanda et al. 2007); the blue dotted line is the best-fit power-law to the 6 points of GRB 080916C. c) Correlation between and the collimation-corrected radiated energy  . The red continuous lines and triangles refer to the homogeneous circumburst medium case, while the blue dotted lines and squares refer to the wind case. The lines indicate the best-fit power-laws and 2 regions reported by Ghirlanda et al. (2007). For both cases, we report the lower limits to corresponding to  > 1 Ms and  > 0.5 Ms (see text). d) Correlation between , and . The lines correspond to the best-fit power-laws and 2 region reported by Ghirlanda et al. (2007). The two lower limits correspond to  > 1 Ms and  > 0.5 Ms (see text).
Open with DEXTER
In the text