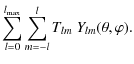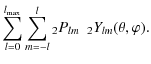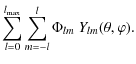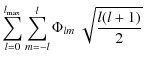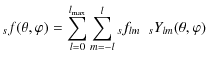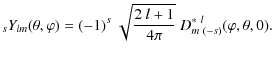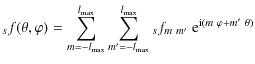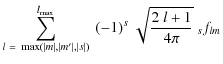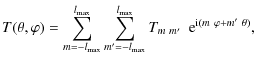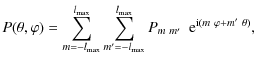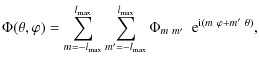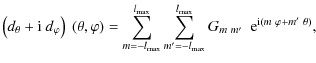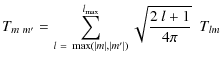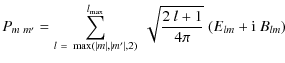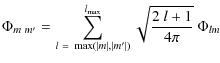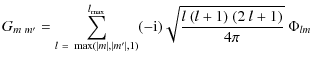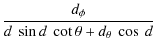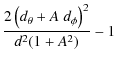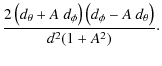| Issue |
A&A
Volume 508, Number 1, December II 2009
|
|
|---|---|---|
| Page(s) | 53 - 62 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912679 | |
| Published online | 15 October 2009 | |
A&A 508, 53-62 (2009)
Simulating weak lensing of CMB maps
S. Basak - S. Prunet - K. Benabed
Institut d'Astrophysique de Paris, CNRS, UMR 7095, 98 bis Boulevard Arago, 75014 Paris, France
Received 11 June 2009 / Accepted 7 September 2009
Abstract
Aims. Accurate predictions of cosmic microwave background
(CMB) anisotropies and polarization are required for analyzing future
CMB data sets, which ultimately require accurately simulated lensed
maps.
Methods. We present a fast, arbitrarily accurate method to
simulate the effect of gravitational lensing of the CMB anisotropies
and polarization fields by large-scale structures on arbitrarily spaced
grid points over a unit sphere using a non-equispaced fast Fourier
transform (NFFT).
Results. The angular power spectrum of the simulated lensed CMB
map, particularly the B-mode of polarization, agrees extremely well
with analytical predictions. The analytical derivation of CMB-lensed
spectra is based on non-trivial, partially resummed perturbative
expansions of the correlation functions, for which our simulations
therefore provide an accurate numerical validation. We demonstrate the
efficiency and accuracy of the method and exhibit their dependence on
the algorithm parameters. Lensed CMB maps simulated in this method are
a useful tool for the analysis and interpretation of upcoming CMB
experiments, such as PLANCK and ACT. Our code is available on request.
Key words: cosmic microwave background
1 Introduction
Weak lensing effects on the cosmic microwave background (CMB)
temperature and polarization anisotropies has been proposed as a probe
of the total matter distribution in large-scale structures (LSS) between
us and the surface of last scattering
(Hu 2000; Seljak 1996; Benabed et al. 2001; Hu 1999; Hirata & Seljak 2003a; Kesden et al. 2002; Guzik et al. 2000; Lewis 2005; Hirata et al. 2004; Smith et al. 2007; Lewis & Challinor 2006; Van Waerbeke et al. 2000; Hu & Tegmark 1999; Zaldarriaga & Seljak 1999; Kesden et al. 2003; Challinor & Lewis 2005; Hirata & Seljak 2003b; Zaldarriaga & Seljak 1998; Blanchard & Schneider 1987).
Although sensitive to the cumulative distribution of matter, it is quite
complementary to other probes of the matter distribution of the
LSS. It does not suffer from bias effects (such as e.g. galaxy
redshift surveys, Lyman-![]() forest), or incorrect
determination of the redshift sources (e.g., as cosmic shear measurements on
galaxies). In addition, because of the high redshift of the source (last
scattering surface) and the lensing efficiency function, weak lensing of
CMB anisotropies is mostly sensitive to large-scale structures that remain
(mainly) in the linear regime, which makes it a very useful tool
for cosmology, in particular for constraining the properties of neutrinos
(Perotto et al. 2006; Lesgourgues et al. 2006).
forest), or incorrect
determination of the redshift sources (e.g., as cosmic shear measurements on
galaxies). In addition, because of the high redshift of the source (last
scattering surface) and the lensing efficiency function, weak lensing of
CMB anisotropies is mostly sensitive to large-scale structures that remain
(mainly) in the linear regime, which makes it a very useful tool
for cosmology, in particular for constraining the properties of neutrinos
(Perotto et al. 2006; Lesgourgues et al. 2006).
Unlike shear measurements of galaxies, where the (reduced) shear field is directly sampled by measurement of galaxy ellipticities, measuring weak lensing effects on the CMB is complicated by the intrinsic stochasticity of the source. However, theoretical arguments lead us to think that CMB anisotropies are highly Gaussian (Linde 1982; Guth 1981; Albrecht & Steinhardt 1982), which has been confirmed on the data, at large scales, using different non-Gaussianity estimators (probability distribution function, bispectrum, wavelet skewness and kurtosis, Minkowski functionals). These properties of the CMB anisotropies can be used to help disentangle the stochastic properties of the (unlensed) CMB anisotropies from the stochastic properties of the lens (i.e., the LSS) since the lensing effect induces small specific non-Gaussian features in the CMB maps. In particular, it correlates the anisotropies locally with their gradient (Cooray & Hu 2002,2001a,b; Seljak 1996; Cooray et al. 2000), which led to the development of specific estimators of the lensing potential field and its power spectrum (Hu & Okamoto 2002; Hirata & Seljak 2003b,a; Okamoto & Hu 2003).
Weak lensing of the CMB anisotropies by LSS was measured in WMAP data (Smith et al. 2007) by its cross-correlation with a high-redshift radio galaxy catalog. Although only marginally detectable in WMAP data because of its noise level, CMB lensing should be measured with a high signal-to-noise ratio by Planck with temperature anisotropies alone (Cooray & Hu 2002; Hu & Okamoto 2004) without needing to rely on any external data set. However, to carry out this measurement on realistic CMB data, the impact of instrumental (anisotropic beams, missing data, correlated noise) and astrophysical (e.g., Galaxy contamination, point sources, etc.) systematic effects on the CMB lensing estimators must be studied with great care.
The power spectra (temperature and polarization) can be computed, using a simple Taylor expansion at large scales (Hu 2000), or a more clever resummation scheme at smaller scales where the displacement field amplitude is comparable to the wavelength of the anisotropies (Challinor & Lewis 2005). For smaller scales, or to investigate the different systematics described above, the development of fast, accurate methods for simulating the lensed CMB maps are needed.
This simulation comes in two distinct parts. On the one hand, an accurate
simulation of the
large-scale structure induced lensing deflection field is needed. On the
other hand, one needs a method to apply this deflection field to an
unlensed, simulated CMB. We do not consider the first part of this
program, because approximating the lensing effect with a single lens
plane in the so-called Born approximation (Hu 2000)
has been shown to provide an excellent approximation, both for temperature
and polarization anisotropies. In this case, the simulation of lensed
CMB maps reduces to an accurate resampling of the unlensed anisotropies
at displaced positions. To solve this last problem, several technical
solutions were implemented. In the publicly distributed Lenspix
code![]() , different possibilities
are available, namely
, different possibilities
are available, namely
- brute-force resampling by direct resummation of spherical harmonics at displaced positions (being slow, but very accurate, this option should be considered as the ``benchmark'' for all other resampling methods);
- resampling on locally Cartesian grids with subsequent polynomial interpolation.
In this paper, we investigate a development of Hirata's idea
(Das & Bode 2008; Hirata et al. 2004), where the oversampling
plus polynomial interpolation is replaced by an approximate (but
arbitrarily accurate) FFT resampling at
irregularly spaced grid points![]() .
.
The remainder of this paper is organized as follows. In Sect. 2 we briefly describe the resampling technique (hereafter NFFT), and the weak lensing of primary CMB fields in Sect. 3. We also demonstrate how the remapping of CMB fields onto the surface of the unit sphere is equivalent to the remapping of the same field on the surface of a 2-d torus. Section 4 describes the simulation procedure for lensed CMB fields, which applies NFFT to the surface of a 2-d torus. Finally, we summarize our results in Sect. 5.
2 Non-equispaced fast Fourier transform (NFFT)
The fast Fourier transform for non-equispaced grid points (NFFT) is a generalization of FFT (Kunis & Potts 2008; Fourmont 2003). The essential idea is that the reproducing kernel of the standard FFTHere the window function
3 Weak lensing of CMB
The CMB radiation field is characterized completely
by its temperature anisotropy,
![]() ,
and polarization,
,
and polarization,
![]() ,
in every direction of the sky. Since temperature
anisotropy is a spin-0 field on the sphere, it can be
conveniently expanded in terms of spin-0 spherical harmonics,
,
in every direction of the sky. Since temperature
anisotropy is a spin-0 field on the sphere, it can be
conveniently expanded in terms of spin-0 spherical harmonics,
The polarization field can be described by the Stokes parameters,
In the above equation,
Weak lensing induces a deflection field
![]() ,
i.e., a mapping between the direction of a given light ray on the last
scattering surface and the direction in which we observe it. Since the
deflection field is a vector field on the sphere, it can be decomposed
into gradient-free and curl-free components in the most general
form as
,
i.e., a mapping between the direction of a given light ray on the last
scattering surface and the direction in which we observe it. Since the
deflection field is a vector field on the sphere, it can be decomposed
into gradient-free and curl-free components in the most general
form as
| (4) |
where
| (5) |
| (6) |
| (7) |
The gradient-free component can be ignored because it is negligible in most cases (Cooray & Hu 2002) and is exactly zero for the Born approximation that adopt here, as this term is generated only by the lens-lens couplings. In the Born approximation, the lensing deflection is calculated along the unlensed line of sight, so the lensed map is a local function of the deflection vector
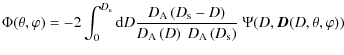
|
(8) |
where D is the comoving coordinate distance along the line of sight,
As for the CMB temperature anisotropy, the lensing potential transforms like
a spin-zero field on the sphere. Hence, it may also be
expanded in terms of spin-0 spherical harmonics as
Since the deflection field
NFFT in 2 dimensions can be applied on the 2-d torus, and we have thus rewritten Eqs. (2)-(10) into a form suitable for simulating unlensed CMB maps at irregularly spaced grid points using NFFT (see Appendix B). This is possible because a band-limited function on a unit sphere can be rewritten as a band-limited function on a 2-d torus. To achieve this, we exploited the relation of spin-weighted spherical harmonics to Wigner rotation matrices (A.3) and the factorization of Wigner rotation matrices into two separate rotations (A.5).
To compute lensed CMB fields at a particular position on the sphere, it
is enough to compute the unlensed CMB at some other position on the
sphere determined by the identities of the spherical triangle (see
Appendix C). The most popular pixelization scheme
used in CMB analysis is the
HEALPix![]() pixelization
(Górski et al. 2005), which is an irregular grid on the surface of
the unit sphere in
pixelization
(Górski et al. 2005), which is an irregular grid on the surface of
the unit sphere in
![]() coordinates. Since gravitational
lensing remaps the CMB signal, the modified angular coordinates due to
lensing will not, in general, correspond to any other pixel center of
the HEALPix grid, even if the unlensed CMB is defined over HEALPix grid
points. Hence, to compute the lensed CMB field on
HEALPix grid points, we should be able to resample the unlensed CMB at
arbitrary positions on the sphere. Since remapping on a sphere can be
recast into remapping on a 2-d torus (see
Appendix A), we have used NFFT to compute lensed CMB
anisotropies at HEALPix grid points.
coordinates. Since gravitational
lensing remaps the CMB signal, the modified angular coordinates due to
lensing will not, in general, correspond to any other pixel center of
the HEALPix grid, even if the unlensed CMB is defined over HEALPix grid
points. Hence, to compute the lensed CMB field on
HEALPix grid points, we should be able to resample the unlensed CMB at
arbitrary positions on the sphere. Since remapping on a sphere can be
recast into remapping on a 2-d torus (see
Appendix A), we have used NFFT to compute lensed CMB
anisotropies at HEALPix grid points.
4 Simulation of lensed CMB map
4.1 How to simulate a lensed map
We have seen in the last section that, for the Born approximation, gravitational lensing of the CMB anisotropies results in a simple resampling of the unlensed anisotropies (with an extra rotation in the case of polarization lensing, see Appendix C). We summarize here the main steps of the simulation procedure of lensed CMB maps, which are to
- generate a realization of the (unlensed) CMB harmonic coefficients (both temperature and polarization) from their (unlensed) power spectra;
- generate in the same way the harmonic coefficients of the lensing potential, or alternatively extract them from an N-body simulation (Carbone et al. 2009,2008);
- transform the harmonic coefficients of the unlensed CMB fields into their 2-d torus Fourier counterparts using Eqs. (B.5), (B.6), and derive the Fourier coefficients of the displacement field from the harmonic coefficients of the lensing potential using Eq. (B.8);
- sample the displacement field at HEALPix centers (using Eq. (B.4) and NFFT), apply this displacement field to HEALPix pixel centers to obtain displaced positions on the sphere (using Eqs. (C.3) and (C.4)), and compute the additional rotation needed for the polarized fields (using Eqs. (C.5)-(C.7));
- resample the temperature and polarization fields at the displaced positions using Eqs. (B.1), (B.2) and NFFT, and apply the extra rotation to the polarized fields, to provide us with the simulated lensed CMB fields, sampled at HEALPix pixel centers.
4.2 Validation of the method on a known case: unlensed maps
To test the part of the algorithm that computes temperature or
polarization fields at arbitrary real-space sampled positions from
their harmonic coefficients, by means of 2-d torus Fourier modes and
NFFT transforms,
we test the method on unlensed temperature or polarization fields,
sampled at HEALPix centers. This is a valid test of the method
because HEALPix pixel centers are irregularly distributed in
![]() coordinates. In addition, we can directly compare the output of the
method with a direct resummation of the spherical harmonics decomposition
of the fields at HEALPix centers by using the fast spherical harmonics
transforms of the HEALPix package, which serve as a reference.
coordinates. In addition, we can directly compare the output of the
method with a direct resummation of the spherical harmonics decomposition
of the fields at HEALPix centers by using the fast spherical harmonics
transforms of the HEALPix package, which serve as a reference.
![\begin{figure}
\par\includegraphics[angle=90,width=6.1cm,clip]{12679_1a.ps}\par\vspace*{6mm}
\includegraphics[angle=90,width=6.1cm,clip]{12679_1b.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg57.png)
|
Figure 1:
Top: a realization of unlensed CMB temperature
anisotropies map (nside = 1024) that we have obtained using NFFT
(oversampling factor |
| Open with DEXTER | |
In Fig. 1, we show an (unlensed)
realization of the CMB temperature anisotropies obtained using our
method, as well as a map of the difference between our method and
the HEALPix reference map. Note the difference in the color scales.
To quantify more precisely the accuracy of our method, we
computed two kinds of error statistics
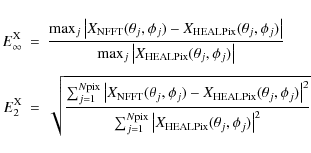
where X represents T, Q, U,
For field X
![]() is the maximum (relative) error, while
is the maximum (relative) error, while
![]() is the relative root mean square
error. Tables 1 and 2 provide
the value of these statistics for unlensed CMB temperature only. Values
of these error norms for the displacement field and the unlensed CMB
polarization fields are of the same order of magnitude.
is the relative root mean square
error. Tables 1 and 2 provide
the value of these statistics for unlensed CMB temperature only. Values
of these error norms for the displacement field and the unlensed CMB
polarization fields are of the same order of magnitude.
Table 1: Variation in the typical orders of magnitude of error norms with the convolution length K for an unlensed CMB map simulated using NFFT.
![\begin{figure}
\par\includegraphics[angle=90,width=6.1cm,clip]{12679_2a.ps}\par\...
...ace*{6mm}
\includegraphics[angle=90,width=6.1cm,clip]{12679_2c.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg73.png)
|
Figure 2:
Top: a realization of lensed CMB map
(
|
| Open with DEXTER | |
Table 2:
Variation in the typical orders of magnitude of error norms
with the oversampling factor ![]() for an unlensed CMB map simulated
using NFFT.
for an unlensed CMB map simulated
using NFFT.
To achieve this accuracy, we used the Kaiser-Bessel window (Kunis & Potts 2008; Fourmont 2003) as the NFFT interpolating function. Since the full precomputation of the window function at each node in spatial and frequency domains requires a large amount of memory space, we used a tensor product form for the multivariate window function, which requires only unidimensional precomputations. This method uses less memory at the price of some extra multiplications (Kunis & Potts 2008; Fourmont 2003). The accuracy (Kunis & Potts 2008; Fourmont 2003) of our simulation can be improved by increasing both the oversampling factor and the convolution length, at the price of extra memory consumption and CPU time (see Tables 1 and 2).
4.3 Simulation of lensed maps
We applied our simulation algorithm of lensed CMB maps (both temperature
and polarization), described in Sect. 4.1, to
1000 independent realizations with HEALPix resolution
![]() ,
and a maximum multipole
,
and a maximum multipole
![]() .
In
Fig. 2, we show one such
realization of a lensed CMB temperature field, as well as the difference
between the lensed and unlensed fields.
.
In
Fig. 2, we show one such
realization of a lensed CMB temperature field, as well as the difference
between the lensed and unlensed fields.
![\begin{figure}
\par\includegraphics[angle=90,width=3.6cm,clip]{12679_3a.ps}\hspa...
...pace*{3mm}
\includegraphics[angle=90,width=3.6cm,clip]{12679_3d.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg76.png)
|
Figure 3:
Top left: a small portion of a simulated unlensed CMB
temperature anisotropy map. Top right: a small portion of the
corresponding lensed CMB temperature anisotropy map. Bottom left:
a small portion of the amplitude of the simulated deflection field
map. Bottom right: a small portion of the difference of simulated
lensed and unlensed CMB maps. These maps are obtained using NFFT for the
oversampling factor |
| Open with DEXTER | |
Since weak lensing of CMB is a tiny effect on small angular scales, we show a realization of a small portion of the unlensed CMB temperature anisotropies, lensed CMB temperature anisotropies, amplitude of deflection field and, the difference of lensed and unlensed CMB temperature anisotropies in Fig. 3 to illustrate the lensing effect more clearly. Although unlensed and lensed CMB temperature anisotropies are indistinguishable to the naked eye, the correlation between the deflection field and the difference between the lensed and unlensed CMB temperature anisotropies is clearly visible.
Table 3 shows the typical CPU time and memory required to simulate a single realization of unlensed and lensed CMB temperature and polarization, at different resolutions. These timings correspond to an AMD880 CPU running at 2.4 GHz. Storage of the window function at the grid points in both the spatial and frequency domain before computing the Fourier transform consumes a fair amount of memory, which ultimately increases the overall memory requirement for the simulation of lensed CMB maps (Kunis & Potts 2008; Fourmont 2003).
Table 3:
Variation in CPU time and memory requirements with resolution
to simulate CMB maps (unlensed and lensed, oversampling
factor ![]() ,
convolution length K=4) using NFFT.
,
convolution length K=4) using NFFT.
Table 4:
Variation in the CPU time and memory requirements with the
convolution length K to simulate a CMB map (both unlensed and lensed,
with nside = 1024,
![]() )
using NFFT.
)
using NFFT.
Table 5:
Variation in CPU time and memory requirements with the
oversampling factor ![]() for simulating a realization CMB
map (both unlensed and lensed, nside = 1024,
for simulating a realization CMB
map (both unlensed and lensed, nside = 1024,
![]() )
using NFFT.
)
using NFFT.
On the same plots, Fig. 4 shows the theoretical power spectra ClXY, where XY represents TT,EE,TE and BB respectively, for the lensed and unlensed cases, as predicted by CAMB (Challinor & Lewis 2005). In the cosmological model, we decided to include no primordial tensors, hence ClBB is entirely due to lensing.
![\begin{figure}
\mbox{\includegraphics[width=6cm,clip]{12679_4a.ps}\hspace*{2mm}
...
...c.ps}\hspace*{2mm}
\includegraphics[width=6cm,clip]{12679_4d.ps} }\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg77.png)
|
Figure 4: Red solid line is the theoretical angular power spectrum of unlensed CMB fields, Green dashed line is the theoretical angular power spectrum of lensed CMB fields, for the same underlying cosmological model with no tensors. |
| Open with DEXTER | |
An accurate recovery of this power spectrum from lensed polarization
maps is therefore a powerful test of our simulation method. In
Fig. 5, we show, on top of the lensed theoretical
spectra (lines), the average empirical power spectra computed from
1000 simulations (circles). We can see that the agreement is
excellent, which is remarkable for
ClBB as explained above. We
have ignored the lensed angular power spectrum beyond the multipole
l=1700 in the comparison, because the accurate computation of the
average empirical power spectra for the multipoles l > 1700 requires
lensed CMB maps simulated from the power spectra of unlensed CMB and a
lensing potential beyond the multipole
![]() ,
which is the
maximum multipole we used in the simulations. It is worth noting here
that theoretical predictions for the B-mode power spectra induced from
lensing, as computed in CAMB, are based on non-trivial, partially
resummed expansions of correlation functions
(Challinor & Lewis 2005). Figure 5 clearly shows
very good agreement between the power spectra predicted from CAMB and
measured from our simulations, therefore validating a posteriori
the theoretical predictions.
,
which is the
maximum multipole we used in the simulations. It is worth noting here
that theoretical predictions for the B-mode power spectra induced from
lensing, as computed in CAMB, are based on non-trivial, partially
resummed expansions of correlation functions
(Challinor & Lewis 2005). Figure 5 clearly shows
very good agreement between the power spectra predicted from CAMB and
measured from our simulations, therefore validating a posteriori
the theoretical predictions.
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip]{12679_5a.ps}\hspace*{2...
...c.ps}\hspace*{2mm}
\includegraphics[width=6cm,clip]{12679_5d.ps} }\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg78.png)
|
Figure 5:
Green solid line is the theoretical angular
power spectrum
|
| Open with DEXTER | |
![\begin{figure}
\mbox{\includegraphics[width=6cm,clip]{12679_6a.ps}\hspace*{2mm}
...
...c.ps}\hspace*{2mm}
\includegraphics[width=6cm,clip]{12679_6d.ps} }\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg79.png)
|
Figure 6:
Fractional difference of average angular power spectrum
recovered from 1000 realizations of CMB maps (nside = 1024 and
|
| Open with DEXTER | |
To obtain a more quantitative view of the accuracy of the method, we show
in Fig. 6
the relative difference
between the average empirical power spectra computed on the
1000 simulations and the theoretical spectra from CAMB, both for
the unlensed
(red solid) and lensed (green dashed) cases. In each plot, we also show
the theoretical root-mean-square deviation of the averaged empirical
spectra,
computed by neglecting the small lensing-induced non-Gaussianity in the
lensed cases. Note that this corresponds to a very small
underestimation
of the scatter (Smith et al. 2006; Rocher et al. 2007). Taking
into account that the averaged power spectra are nearly
Gaussian distributed (due to the central limit theorem), we can assess
the presence of possible biases in the recovered spectra by computing
the reduced ![]() statistics:
statistics:
![$\displaystyle Z^{2}_{XY}=\frac{N_{rlz}}{(l_{\max}-1)}\sum^{l_{\max}}_{l=2}\frac...
...\left[(C^{XY}_{l,{\rm th}})^{2}+C^{XX}_{l,{\rm th}}C^{YY}_{l,{\rm th}}\right]},$](/articles/aa/full_html/2009/46/aa12679-09/img80.png)
|
(11) |
here Nrlz is the number of independent realizations of angular power spectra under consideration.
Table 6:
Reduced ![]() statistics of the recovered unlensed angular
power spectrum.
statistics of the recovered unlensed angular
power spectrum.
Table 7:
Reduced ![]() statistics for the recovered lensed angular
power spectrum.
statistics for the recovered lensed angular
power spectrum.
5 Summary
Accurate predictions of the expected CMB anisotropies are required when analyzing future CMB data sets, which ultimately require accurately simulated lensed maps. The most popular pixelization used to analyze full-sky CMB maps is the HEALPix pixelization. To simulate lensed CMB anisotropies at HEALPix grid points, we must compute unlensed CMB anisotropies at irregularly spaced grid points over the sphere, determined by the deflection field and remapping equations. Since remapping on a sphere can be recast into remapping on a 2-d torus, we have used the NFFT library to compute lensed CMB anisotropies at HEALPix grid points and experimented with different settings of the accuracy parameters. We have found that for a nside = 1024 map a 10-8 accuracy is easily reached when setting theThese simulations will be a useful tool for the analysis and interpretation of upcoming CMB experiments such as Planck and ACT. However, they are not the only possible use of this technique. The simulation of the lensing deflection field can be improved by replacing the simple Born approximation with ray-tracing in dark matter N-nody simulations (Carbone et al. 2009,2008). Ray-tracing is affected by similar problems as the simulation of the lens effect on CMB maps, i.e., difficulties in accurately resampling a vector field on the sphere. Current state-of-the-art ray-tracing algorithms, such as (Teyssier et al. 2009), could be made more accurate by using the technique described here.
Appendix A: Spin s functions on a sphere and 2-d torus
Spin s square-integrable functions
![]() on a unit sphere are conveniently expanded in spin-weighted spherical
harmonics
on a unit sphere are conveniently expanded in spin-weighted spherical
harmonics
![]() of same spin
(Goldberg et al. 1967; Newman & Penrose 1966; Zaldarriaga & Seljak 1997)
of same spin
(Goldberg et al. 1967; Newman & Penrose 1966; Zaldarriaga & Seljak 1997)
with the inverse transform,
These harmonics, with
With our assumed conventions for the Euler angles (Varshalovich et al. 1988; Edmonds 1957), we have,
These rotation matrices (A.4) basically characterize the rotation of spin-weighted spherical harmonics. The decomposition shown in Eq. (A.4) is exploited by factoring the rotation matrices into two separate rotation matrices as (McEwen et al. 2007; Wiaux et al. 2006),
Expressing the Wigner rotation matrices in Eq. (A.4) in the above manner of Eq. (A.5), Eq. (A.1) can be rewritten as
where
The advantage of writing the rotation matrices in this manner is that now the Euler angles only occur in complex exponentials and we only need to evaluate
Computation of
![]() using
Eq. (A.6) may not be the most efficient way, but the
presence of exponentials may be exploited such that techniques of fast
Fourier transform either on irregular or regular grid may be used for
rapid computation of double summations simultaneously. In both cases,
the domain of spin s function
using
Eq. (A.6) may not be the most efficient way, but the
presence of exponentials may be exploited such that techniques of fast
Fourier transform either on irregular or regular grid may be used for
rapid computation of double summations simultaneously. In both cases,
the domain of spin s function
![]() must be
extended from the sphere,
must be
extended from the sphere,
![]() to
the 2-dimensional torus,
to
the 2-dimensional torus,
![]() using the symmetry
using the symmetry
![]() of spin-weighted spherical harmonics, so that
Eq. (A.6) becomes a complex-to-complex Fourier
transform over a 2-dimensional torus. The computation of
sfm
m' for
of spin-weighted spherical harmonics, so that
Eq. (A.6) becomes a complex-to-complex Fourier
transform over a 2-dimensional torus. The computation of
sfm
m' for
![]() ,
involves performing a
1-dimensional summation over a 2-dimensional grid, hence it is of order
,
involves performing a
1-dimensional summation over a 2-dimensional grid, hence it is of order
![]() .
.
Appendix B: Unlensed CMB fields on 2-d torus
Factoring the rotation matrices in two separate rotation matrices (A.4) and extending the domain of CMB, lensing potential and defection fields from sphere to 2-d torus, Eqs. (2), (3), (9), (10) can be rewritten asand the corresponding Fourier modes are given by,
The extra factor of
Appendix C: Lensed CMB fields on 2-d torus
Using the identities of the spherical triangle, lensed temperature anisotropies and polarization in a particular directionThe angular coordinates corresponding to the modified direction of the photon path
The extra factor
The Euler angles
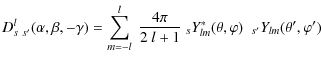
|
(C.8) |
Appendix D: Parallelization of the algorithm
Significant speed improvements should be achieved by parallelizing the code. We review here the main parts of the code, and indicate possible ways of parallelizing them. We recall that the code is divided into two distinct parts. The first part computes the 2-d Fourier modes, starting from the spherical harmonic coefficients. This involves computing the Wigner coefficientsThe second is the FFT on irregular grid points, where we used the external library NFFT. Here the computation is divided into three parts: (i) precomputation of the window function around each real space node; (ii) diagonal correction of the Fourier modes and regular FFT; and (iii) discrete convolution for each node. Part (i) can be trivially parallelized since calculations are independent for each node. Part (ii) can also be easily parallelized using independent 1-d FFT calculation first along each line, and then along each column of the mode matrix (this scheme was already implemented into the FFTW library). Finally, part (iii) can also be parallelized by spatial domain decomposition of the nodes, with minor overlapping copies accounting for the support (K) of the truncated window. We note that in principle two different domain decompositions occur for the parallelization of the regular FFT and the parallelization of the operations on nodes (i.e., window function precomputation, discrete convolution). This could lead to important communication overheads and/or strong load imbalance in the case of very clustered nodes; in the case of weak lensing applications however, because of the small amplitude of the displacement field and the regularity of the HEALPix pixels, we do not expect this to be a major issue.
AcknowledgementsWe acknowledge the use of the HEALPix package for our map pixelization. We also acknowledge the use of the NFFT package for our work. We thank Eric Hivon for helpful discussions and suggestions. One (SB) of the author's research at the Institut d'Astrophysique de Paris was supported by the Indo-French centre for promotion of advanced scientific research (CEFIPRA) through grant 3504-3. S.B. thanks Francois R. Bouchet and Tarun Souradeep for their constant encouragement and support throughout.
References
- Albrecht, A., & Steinhardt, P. J. 1982, Phys. Rev. Lett., 48, 1220 [NASA ADS] [CrossRef]
- Benabed, K., Bernardeau, F., & van Waerbeke, L. 2001, Phys. Rev. D, 63, 043501 [NASA ADS] [CrossRef]
- Blanchard, A., & Schneider, J. 1987, A&A, 184, 1 [NASA ADS]
- Carbone, C., Springel, V., Baccigalupi, C., Bartelmann, M., & Matarrese, S. 2008, MNRAS, 388, 1618 [NASA ADS] [CrossRef]
- Carbone, C., Baccigalupi, C., Bartelmann, M., Matarrese, S., & Springel, V. 2009, MNRAS, 576
- Challinor, A., Fosalba, P., Mortlock, D., et al. 2000, Phys. Rev. D, 62, 123002 [NASA ADS] [CrossRef]
- Challinor, A., & Lewis, A. 2005, Phys. Rev. D, 71, 103010 [NASA ADS] [CrossRef]
- Cooray, A., & Hu, W. 2001a, ApJ, 554, 56 [NASA ADS] [CrossRef]
- Cooray, A., & Hu, W. 2001b, ApJ, 548, 7 [NASA ADS] [CrossRef]
- Cooray, A., & Hu, W. 2002, ApJ, 574, 19 [NASA ADS] [CrossRef]
- Cooray, A., Hu, W., & Miralda-Escudé, J. 2000, ApJ, 535, L9 [NASA ADS] [CrossRef]
- Das, S., & Bode, P. 2008, ApJ, 682, 1 [NASA ADS] [CrossRef]
- Edmonds, A. R. 1957, Angular Momentum in Quantum Mechanics (Princeton, N.J.: Princeton University Press)
- Fourmont, K. 2003, Journal of Fourier Analysis and Applications, 9, 431 [CrossRef]
- Goldberg, J. N., Macfarlane, A. J., Newman, E. T., Rohrlich, F., & Sudarshan, E. C. G. 1967, Journal of Mathematical Physics, 8, 2155 [NASA ADS] [CrossRef]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef]
- Guth, A. H. 1981, Phys. Rev. D, 23, 347 [NASA ADS] [CrossRef]
- Guzik, J., Seljak, U., & Zaldarriaga, M. 2000, Phys. Rev. D, 62, 043517 [NASA ADS] [CrossRef]
- Hirata, C. M., Padmanabhan, N., Seljak, U., Schlegel, D., & Brinkmann, J. 2004, Phys. Rev. D, 70, 103501 [NASA ADS] [CrossRef]
- Hirata, C. M., & Seljak, U. 2003a, Phys. Rev. D, 67, 043001 [NASA ADS] [CrossRef]
- Hirata, C. M., & Seljak, U. 2003b, Phys. Rev. D, 68, 083002 [NASA ADS] [CrossRef]
- Hu, W. 1999, ApJ, 522, L21 [NASA ADS] [CrossRef]
- Hu, W. 2000, Phys. Rev. D, 62, 043007 [NASA ADS] [CrossRef]
- Hu, W., & Tegmark, M. 1999, ApJ, 514, L65 [NASA ADS] [CrossRef]
- Hu, W., & Okamoto, T. 2002, ApJ, 574, 566 [NASA ADS] [CrossRef]
- Hu, W., & Okamoto, T. 2004, Phys. Rev. D, 69, 043004 [NASA ADS] [CrossRef]
- Kesden, M., Cooray, A., & Kamionkowski, M. 2002, Phys. Rev. D, 66, 083007 [NASA ADS] [CrossRef]
- Kesden, M., Cooray, A., & Kamionkowski, M. 2003, Phys. Rev. D, 67, 123507 [NASA ADS] [CrossRef]
- Kunis, S., & Potts, D. 2008, Sampling Theory in Signal and Image Processing, 7, 77
- Lesgourgues, J., Perotto, L., Pastor, S., & Piat, M. 2006, Phys. Rev. D, 73, 045021 [NASA ADS] [CrossRef]
- Lewis, A. 2005, Phys. Rev. D, 71, 083008 [NASA ADS] [CrossRef]
- Lewis, A., & Challinor, A. 2006, Phys. Rep., 429, 1 [NASA ADS] [CrossRef]
- Linde, A. D. 1982, Phys. Lett. B, 108, 389 [NASA ADS] [CrossRef]
- McEwen, J. D., Hobson, M. P., Mortlock, D. J., & Lasenby, A. N. 2007, IEEE Transactions on Signal Processing, 55, 520 [NASA ADS] [CrossRef]
- Newman, E. T., & Penrose, R. 1966, J. Math. Phys., 7, 863 [NASA ADS] [CrossRef]
- Okamoto, T., & Hu, W. 2003, Phys. Rev. D, 67, 083002 [NASA ADS] [CrossRef]
- Perotto, L., Lesgourgues, J., Hannestad, S., Tu, H., & Wong, Y. Y. 2006, J. Cosmol. Astro-Part. Phys., 10, 13 [NASA ADS] [CrossRef]
- Risbo, T. 1996, Journal of Geodesy, 70, 383 [NASA ADS]
- Rocher, J., Benabed, K., & Bouchet, F. R. 2007, J. Cosmol. Astro-Part. Phys., 5, 13 [NASA ADS] [CrossRef]
- Seljak, U. 1996, ApJ, 463, 1 [NASA ADS] [CrossRef]
- Smith, K. M., Hu, W., & Kaplinghat, M. 2006, Phys. Rev. D, 74, 123002 [NASA ADS] [CrossRef]
- Smith, K. M., Zahn, O., & Doré, O. 2007, Phys. Rev. D, 76, 043510 [NASA ADS] [CrossRef]
- Teyssier, R., Pires, S., Prunet, S., et al. 2009, A&A, 497, 335 [NASA ADS] [CrossRef] [EDP Sciences]
- Thorne, K. S. 1980, Rev. Mod. Phys., 52, 299 [NASA ADS] [CrossRef]
- Trapani, S., & Navaza, J. 2006, Acta Crystallographica A, 62, 262 [CrossRef]
- Van Waerbeke, L., Bernardeau, F., & Benabed, K. 2000, ApJ, 540, 14 [NASA ADS] [CrossRef]
- Varshalovich, D. A., Moskalev, A. N., & Khersonskii, V. K. 1988, Quantum Theory of Angular Momentum (Singapore: World Scientific Publishing Co.)
- Wandelt, B. D., & Górski, K. M. 2001, Phys. Rev. D, 63, 123002 [NASA ADS] [CrossRef]
- Wiaux, Y., Jacques, L., Vielva, P., & Vandergheynst, P. 2006, ApJ, 652, 820 [NASA ADS] [CrossRef]
- Zaldarriaga, M., & Seljak, U. 1997, Phys. Rev. D, 55, 1830 [NASA ADS] [CrossRef]
- Zaldarriaga, M., & Seljak, U. 1998, Phys. Rev. D, 58, 023003 [NASA ADS] [CrossRef]
- Zaldarriaga, M., & Seljak, U. 1999, Phys. Rev. D, 59, 123507 [NASA ADS] [CrossRef]
Footnotes
- ...
code
![[*]](/icons/foot_motif.png)
- http://cosmologist.info/lenspix
- ... points
![[*]](/icons/foot_motif.png)
- http://www-user.tu-chemnitz.de/ potts/nfft
- ... FFT
![[*]](/icons/foot_motif.png)
- http://www.fftw.org
- ...
HEALPix
![[*]](/icons/foot_motif.png)
- http://healpix.jpl.nasa.gov
- ... CAMB
![[*]](/icons/foot_motif.png)
- http://camb.info
All Tables
Table 1: Variation in the typical orders of magnitude of error norms with the convolution length K for an unlensed CMB map simulated using NFFT.
Table 2:
Variation in the typical orders of magnitude of error norms
with the oversampling factor ![]() for an unlensed CMB map simulated
using NFFT.
for an unlensed CMB map simulated
using NFFT.
Table 3:
Variation in CPU time and memory requirements with resolution
to simulate CMB maps (unlensed and lensed, oversampling
factor ![]() ,
convolution length K=4) using NFFT.
,
convolution length K=4) using NFFT.
Table 4:
Variation in the CPU time and memory requirements with the
convolution length K to simulate a CMB map (both unlensed and lensed,
with nside = 1024,
![]() )
using NFFT.
)
using NFFT.
Table 5:
Variation in CPU time and memory requirements with the
oversampling factor ![]() for simulating a realization CMB
map (both unlensed and lensed, nside = 1024,
for simulating a realization CMB
map (both unlensed and lensed, nside = 1024,
![]() )
using NFFT.
)
using NFFT.
Table 6:
Reduced ![]() statistics of the recovered unlensed angular
power spectrum.
statistics of the recovered unlensed angular
power spectrum.
Table 7:
Reduced ![]() statistics for the recovered lensed angular
power spectrum.
statistics for the recovered lensed angular
power spectrum.
All Figures
![\begin{figure}
\par\includegraphics[angle=90,width=6.1cm,clip]{12679_1a.ps}\par\vspace*{6mm}
\includegraphics[angle=90,width=6.1cm,clip]{12679_1b.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg57.png)
|
Figure 1:
Top: a realization of unlensed CMB temperature
anisotropies map (nside = 1024) that we have obtained using NFFT
(oversampling factor |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=6.1cm,clip]{12679_2a.ps}\par\...
...ace*{6mm}
\includegraphics[angle=90,width=6.1cm,clip]{12679_2c.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg73.png)
|
Figure 2:
Top: a realization of lensed CMB map
(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=3.6cm,clip]{12679_3a.ps}\hspa...
...pace*{3mm}
\includegraphics[angle=90,width=3.6cm,clip]{12679_3d.ps}
\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg76.png)
|
Figure 3:
Top left: a small portion of a simulated unlensed CMB
temperature anisotropy map. Top right: a small portion of the
corresponding lensed CMB temperature anisotropy map. Bottom left:
a small portion of the amplitude of the simulated deflection field
map. Bottom right: a small portion of the difference of simulated
lensed and unlensed CMB maps. These maps are obtained using NFFT for the
oversampling factor |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\mbox{\includegraphics[width=6cm,clip]{12679_4a.ps}\hspace*{2mm}
...
...c.ps}\hspace*{2mm}
\includegraphics[width=6cm,clip]{12679_4d.ps} }\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg77.png)
|
Figure 4: Red solid line is the theoretical angular power spectrum of unlensed CMB fields, Green dashed line is the theoretical angular power spectrum of lensed CMB fields, for the same underlying cosmological model with no tensors. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip]{12679_5a.ps}\hspace*{2...
...c.ps}\hspace*{2mm}
\includegraphics[width=6cm,clip]{12679_5d.ps} }\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg78.png)
|
Figure 5:
Green solid line is the theoretical angular
power spectrum
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\mbox{\includegraphics[width=6cm,clip]{12679_6a.ps}\hspace*{2mm}
...
...c.ps}\hspace*{2mm}
\includegraphics[width=6cm,clip]{12679_6d.ps} }\end{figure}](/articles/aa/full_html/2009/46/aa12679-09/Timg79.png)
|
Figure 6:
Fractional difference of average angular power spectrum
recovered from 1000 realizations of CMB maps (nside = 1024 and
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle \times\sum^{N/2-1}_{k=-N/2}\exp\left[-\frac{2\pi {\rm i}m~k}{\sigma~N}\right]
\frac{f_{k}}{\phi(2\pi~k/\sigma~N)}$](/articles/aa/full_html/2009/46/aa12679-09/img12.png)