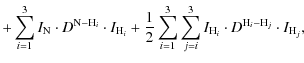The hyperfine structure of the inversion-rotation transition JK = of NH3 investigated by Lamb-dip spectroscopy

G. Cazzoli; L. Dore; C. Puzzarini

doi:10.1051/0004-6361/200912950

Free Access

Issue		A&A Volume 507, Number 3, December I 2009


Page(s)		1707 - 1710
Section		Atomic, molecular, and nuclear data
DOI		https://doi.org/10.1051/0004-6361/200912950
Published online		08 October 2009

A&A 507, 1707-1710 (2009)

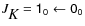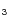The hyperfine structure of the inversion-rotation transition ${\sf\textit{J}}_{\sf\textit{\large K}} = {\sf 1}_{\sf0}\leftarrow {\sf0}_{\sf0}$ of NH $_{\sf 3}$ investigated by Lamb-dip spectroscopy

G. Cazzoli - L. Dore - C. Puzzarini

Dipartimento di Chimica ``G. Ciamician'', via F. Selmi 2, 40126 Bologna, Italy

Received 21 July 2009 / Accepted 10 September 2009

Abstract
The ground-state inversion-rotation transition of ammonia at 572.498 GHz has been investigated in the laboratory using a source-modulation microwave spectrometer equipped with a double-pass cell. The experiment has been carried out at a pressure lower than 0.5 mTorr, thus enabling to record a Lamb-dip spectrum showing a partial resolution of the magnetic hyperfine structure due to the three proton spins. The achieved high resolution proved to be comparable to that of molecular beam experiments. This measurement provides very precise rest frequencies of the $J_K = 1_0 \leftarrow 0_0$ transition and of its hyperfine components, which fall in a spectral region covered by the HIFI instrument on board the Herschel satellite.

Key words: molecular data - methods: laboratory - techniques: spectroscopic - radio lines: ISM

1 Introduction

Ammonia is one of the first molecules that was found in the interstellar medium (Cheung et al. 1969), detected by observing one of its several inversion transitions falling near 1.3 cm. The rotational energy levels (for a diagram see Ho & Townes 1983) of this oblate symmetric top molecule are denoted by the quantum numbers J and K corresponding, respectively, to the total angular momentum and its projection along the ternary symmetry axis. Considering the C_3v point group, the ground-state rotational states can have A₁+A₂ symmetry (K=3n, n integer) or E symmetry ( $K\neq 3n$ ): since the total wavefunction has to be antisymmetric (A₂ symmetry) upon exchange of two fermions, only H-spin functions of species A₁ are allowed for the K=3n states, and of species E for $K\neq 3n$ . The former are called ortho states, with all H spins parallel, and the latter are para states. In addition, because of the inversion motion of the N atom through the plane of the H atoms, each rotational energy level but the K=0 levels is split into an inversion doublet; in the K=0 case one level of the inversion pair has null statistical weight.

Transitions within this complex energy scheme must obey the dipole selection rules $\Delta K=0$ and $\Delta J=0,\pm1$ , thus there are nonmetastable states (J>K), which can be relaxed through $\Delta J=-1$ transitions, and metastable states (J=K), which can be relaxed only through slow collisions connecting K-ladders with K differing by 3. Therefore, the $\Delta J=0$ , $\Delta K=0$ inversion transitions across the doublets with J=K have been extensively used to observe molecular clouds from ground; with Einstein A coefficients of the order of 10^-7 s^-1 (Ho & Townes 1983), they have critical densities of about 10³ cm^-3.

On the other hand, inversion-rotation transitions have Einstein A coefficients larger by about four orders of magnitude and higher critical densities (>10⁷ cm^-3) (Liseau et al. 2003), but fall in the submillimeter-wave and far-infrared regions, therefore they cannot be observed from ground because of the opacity of the terrestrial atmosphere.

The ground-state rotation-inversion transition of ammonia, the subject of the present study, occurs at 572.5 GHz, and it connects the J_K=0₀ level, with - parity upon inversion, to the J_K=1₀ level, with + parity; it was detected for the first time by Keene et al. (1983) in OMC-1 by NASA's Kuiper Airborne Observatory; more recently, it has been detected with the spaceborne submillimeter telescope Odin (Persson et al. 2009; Liseau et al. 2003; Larsson et al. 2003).

In the laboratory, after the first studies of Gordy and coworkers (Helminger et al. 1971, and references therein), it was recorded by Winnewisser et al. (1996) with sub-Doppler resolution, allowing them to resolve three hyperfine components. The inversion-rotation levels with $J\neq 0$ are split by hyperfine interactions, specifically they are split into three hyperfine states by the electric quadrupole coupling of the N nucleus, resulting in three components of the $J_K = 1_0 \leftarrow 0_0$ line. However, weaker magnetic interactions due to the three protons induce further splittings, which could be resolved in inversion transitions detected in quiescent dark clouds (see Ho & Townes 1983) and, in the laboratory, by the molecular beam technique (Ruben & Kukolich 1974, and references therein).

To measure a very accurate rest frequency of the J_K=1₀-0₀ transition of ammonia, which may also be affected by pressure shift, we carried out saturation measurements at very low pressure; in this regime we could record a very high-resolution Lamb-dip spectrum with the magnetic hyperfine structure partially resolved. After a brief discussion about the hyperfine Hamiltonian, an analysis of the experimental spectrum and the resulting accurate rest frequency is presented in the following.

2 Hyperfine Hamiltonian

The complex hyperfine structure (hfs) of the inversion-rotation transitions of ammonia is due to the interactions of the electric and magnetic multipole moments of the nuclei with their molecular environment. For NH₃ there are five physical interactions, namely: N quadrupole coupling, N spin-rotation coupling, H spin-rotation coupling, N-H spin-spin interaction, and H-H spin-spin interaction.

The hfs Hamiltonian, in Cartesian form, including these interactions can be written as:

$\displaystyle H_{\rm hfs}$	=	$\displaystyle \frac{1}{6}V^{\rm N} \cdot Q^{\rm N} - I_{\rm N}\cdot M^{\rm N} \cdot J$
		$\displaystyle -\sum_{i=1}^3 I_{{\rm H}_i} \cdot M^{{\rm H}_i} \cdot J$
		$\displaystyle + \sum_{i=1}^3 I_{\rm N}\cdot D^{{\rm N-H}_i} \cdot I_{{\rm H}_i}... ...3 \sum_{j=i}^3 I_{{\rm H}_i} \cdot D^{{\rm H}_i-{\rm H}_j} \cdot I_{{\rm H}_j},$	(1)

where J, $I_{\rm N}$ , and $I_{{\rm H}_i}$ represent, respectively, the total rotational angular momentum of the molecule, the spin of the nitrogen nucleus, and the spin of the ith proton; $Q^{\rm N}$ is the nuclear quadrupole moment tensor, and the $V^{\rm N}$ is the electric field gradient tensor for the N nucleus: the coupling tensor corresponding to the quadrupole Hamiltonian is indicated as $(eQq_{ij})_{\rm N}$ ; $M^{\rm N/H}$ is the spin-rotation coupling tensor for the N or the H nucleus, and $D^{\rm N-H}$ and $D^{\rm H-H}$ are, respectively, spin-spin coupling tensors for the N-H and H-H pairs.

The matrix elements of these Hamiltonian terms may be conveniently evaluated in the coupling scheme:

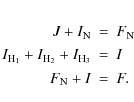
$\begin{eqnarray*}J+I_{\rm N}&=& F_{\rm N}\\ I_{{\rm H}_1}+I_{{\rm H}_2}+I_{{\rm H}_3} &=& I \\ F_{\rm N}+ I &=& F. \end{eqnarray*}$

Cook & De Lucia (1971) used the theory of irreducible tensor operators to evaluate such elements, which are now implemented in Pickett's SPCAT/SPFIT program suite (Pickett 1991) for accurate prediction and analysis of hfs in spectra.

In the case of the J_K=1₀-0₀ transition, only the upper state is affected by hyperfine interactions. Because of the N quadrupole coupling ( $I_{\rm N}=1$ ), there is a larger splitting into three states ( $F_{\rm N}=1,2,0$ ), and each of them is further split by magnetic interactions. Because J_K=1₀ is an ortho state, the total spin of the protons is $I=\frac{3}{2}$ , therefore $F_{\rm N}=1,2$ , and 0 states are split into 3, 4, and 1 levels, respectively. This hyperfine structure was studied by Marshall & Muenter (1981) by means of Stark-hyperfine measurements using molecular beam electric resonance (MBER) spectroscopy: their hyperfine constants have been used to analyze our spectrum.

3 Experimental details and spectra analysis

The spectrum was observed with a frequency-modulated millimeter-wave spectrometer (Cazzoli & Dore 1990a) equipped with a double-pass absorption cell (Dore et al. 1999) made of a Pyrex tube 3.25 m long and 5 cm in diameter. The radiation source was a frequency sextupler (Radiometer Physics) driven by a Gunn oscillator working in the region 77-116 GHz (Carlstrom Co). Two phase-lock loops allow the stabilisation of the Gunn oscillator with respect to a frequency synthesizer, which is driven by a 5-MHz rubidium frequency standard. The frequency modulation of the radiation is obtained by the sine-wave at 1.666 or 0.666 kHz modulating the reference signal of the wide-band Gunn-synchronizer (total harmonic distortion less than $0.01\%$ ); the signal, detected by a liquid-helium-cooled InSb hot electron bolometer (QMC Instr. Ltd. type QFI/2), was demodulated at 2-f by a lock-in amplifier.

A commercial sample of NH₃, without any further purification, was employed to fill the cell at a pressure of a few mTorrs, later the gas was pumped out, and, maintaining a slow-flow pumping, the very tiny degassing from the cell walls provided a sample pressure of a few tenth of mTorr, which proved to be appropriate for saturation spectroscopy. This very low pressure regime, the double-pass arrangement, and proper source power allowed the detection of a Lamb-dip spectrum (Costain 1969; Winton & Gordy 1970), whose high resolution is shown in the magnified windows of Fig. 1, where splittings of $\sim$ 30 kHz are well resolved.

Another advantage of working at low pressure is to minimize the frequency shift due to intermolecular collisions: its value for the transition under study was determined to be +6.10(7) MHz/Torr (Belov et al. 1984), which is in good agreement with the theoretical value of +5.2 MHz/Torr (Buffa & Tarrini 1983) estimated to be equal for all hyperfine components (2009, private comm.), Therefore, the measured hyperfine frequencies are all affected by a small systematic error, which can be estimated to be about +2 kHz.

Lamb-dip spectroscopy suffers from an apparent drawback, the occurrence of crossover resonances (Winton 1972; Letokhov & Chebotayev 1977). These are dips due to the saturation of overlapping Gaussian profiles of two transitions with a common energy level and which occur midway between the two transition frequencies; there is a sample of velocity-selected molecules with equal but opposite Doppler shifts from each of the central frequencies, if the radiation travels forward or backward. These additional spectral features add complexity to the possibly crowded spectrum, but on the other hand they provide additional, and not always redundant, data relative to the transition frequencies.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12950fg1.eps} \end{figure}$

Figure 1:

Lamb-dip spectrum of the NH₃ transition showing ¹⁴N hfs and H hfs. The numbers below each of the three nitrogen quadrupole components refer to $F_{\rm N}' \leftarrow F_{\rm N}$ quantum numbers, crossover resonances are indicated by an arrow. The magnified windows show the splittings due to the proton spin interactions, and the spectral features are labelled by the final value of the total angular momentum quantum number.

Open with DEXTER

Table 1: Observed hyperfine frequencies and residuals of the $J_K = 1_0 \leftarrow 0_0$ transition of NH₃.

Table 2: Hyperfine constants and central frequency of the $J_K = 1_0 \leftarrow 0_0$ transition of NH₃.

In the spectrum shown in Fig. 1, the nitrogen hfs appears as a well resolved triplet. The hydrogen hfs should appear as a quartet in the $F_{\rm N}=2 \leftarrow 1$ component, and as a triplet in the $F_{\rm N}=1 \leftarrow 1$ component; in fact, the quartet and the triplet are both partially blended into a doublet, and in the former a crossover resonance appears in the middle. The full profiles of such multiplets have been analyzed (Cazzoli & Dore 1990b; Dore 2003) to derive the frequencies of the hyperfine components and of the crossover resonances: they are listed in Table 1.

Contributions to the hfs come from the nitrogen quadrupole coupling and perpendicular spin-rotation constants ( $(eQq_{zz})_{\rm N}$ and $C_{\rm N}$ ), the average of two diagonal components of the hydrogen spin-rotation coupling tensor $\frac{1}{2} (M_{xx}^{\rm H}+M_{yy}^{\rm H})$ , and, in addition, there is the slight contribution due to the zcomponents of the N-H spin-spin and H spin-spin coupling tensors $(D_1=-\frac{1}{2}D_{zz}^{\rm N-H},\;D_3=D_{zz}^{\rm H-H})$ . The derived frequencies reported in Table 1 were fitted by means of Pickett's SPFIT fitting program (Pickett 1991), dealing with the hyperfine constants in two ways: i) fixed at the values determined by Marshall & Muenter (1981), and ii) as fit parameters. The rms error of residuals is lower than 1 kHz for both fits (see Table 1), and the results, reported in Table 2 as Fit I and Fit II, show an agreement between the two sets of hf-constants within 3 $\sigma$ . Therefore, we may conclude that present Lamb-dip data carry information with frequency resolution comparable to molecular beam data.

4 Conclusion

The Lamb-dip spectrum of the ground-state transition $J_K = 1_0 \leftarrow 0_0$ of ammonia recorded at very high resolution allowed us to resolve not only the hyperfine structure due to N electric quadrupole coupling, but also, partially, the structure due to the magnetic coupling of N and H spins. This resolution has been achieved for the first time using conventional absorption spectroscopy and the hyperfine results obtained are comparable to the molecular beam data. MBER spectroscopy has been used to measure radiofrequency transitions within the inversion-rotation level J_K=1₀ (Marshall & Muenter 1981) to obtain its hyperfine properties with the high accuracy allowed by this technique, where line broadening is drastically reduced. However, the present sub-Doppler measurements, carried out in the submillimeter-wavelength region, allowed us to directly detect the hyperfine components of the $J_K = 1_0 \leftarrow 0_0$ inversion-rotation transition.

Because of the low-pressure regime of the experiment, the collisional frequency shift occurring in laboratory measurements has been minimized, therefore the consequent systematic error affecting the transition frequency is reduced. The pressure shift for the present measurements can be estimated to be about +2 kHz, a value that can be used to correct the hyperfine frequencies: they are listed in Table 3 as predicted from the central frequency and the hf-constants reported in column Fit I of Table 2.

The hyperfine structure is useful primarily in determining the optical depth of a transition. Any spectrum observed in optically-thin conditions should show an intensity ratio between its hf components corresponding to the ratio of their line strengths, while if the spectrum is optically thick, the hf transitions will be observed with the same intensity: therefore, the observed hyperfine line intensity ratio gives information on the optical depth of the spectrum. Thus, the present results may help in analyzing future detections at high resolution of the inversion-rotation transition $J_K = 1_0 \leftarrow 0_0$ of NH₃ by the HIFI instrument on board the Herschel satellite.

Table 3: Predicted hyperfine frequencies of the $J_K = 1_0 \leftarrow 0_0$ transition of NH₃.

Acknowledgements

This work was supported by MIUR (PRIN 2007 funds, project ``Trasferimenti di energia, carica e molecole in sistemi complessi'') and by University of Bologna (RFO funds).

References

Belov, S. P., Krupnov, A. F., Markov, V. N., et al. 1984, Opt. Spectrosc., 56, 506 [NASA ADS]
Buffa, G., & Tarrini, O. 1983, J. Mol. Spectrosc., 101, 271 [NASA ADS] [CrossRef]
Cazzoli, G., & Dore, L. 1990a, J. Mol. Spectrosc., 141, 49 [NASA ADS] [CrossRef]
Cazzoli, G., & Dore, L. 1990b, J. Mol. Spectrosc., 143, 231 [NASA ADS] [CrossRef]
Cheung, A. C., Rank, D. M., Townes, C. H., Knowles, S. H., & Sullivan, W. T. 1969, ApJ, 157, L13 [NASA ADS] [CrossRef]
Cook, R. L., & De Lucia, F. C. 1971, Am. J. Phys., 39, 1433 [NASA ADS] [CrossRef]
Costain, C. C. 1969, Can. J. Phys., 47, 2431 [NASA ADS]
Dore, L. 2003, J. Mol. Spectrosc., 221, 93 [NASA ADS] [CrossRef]
Dore, L., Degli Esposti, C., Mazzavillani, A., et al. 1999, Chem. Phys. Lett., 300, 489 [NASA ADS] [CrossRef]
Helminger, P., De Lucia, F. C., & Gordy, W. 1971, J. Mol. Spectrosc., 39, 94 [NASA ADS] [CrossRef]
Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef]
Keene, J., Blake, G. A., & Phillips, T. G. 1983, ApJ, 271, L27 [NASA ADS] [CrossRef]
Larsson, B., Liseau, R., Bergman, P., et al. 2003, A&A, 402, L69 [NASA ADS] [CrossRef] [EDP Sciences]
Letokhov, V. S., & Chebotayev, V. P. 1977, Nonlinear Laser Spectroscopy (Berlin/Heidelberg/New York: Springer-Verlag), 238, and references therein
Liseau, R., Larsson, B., Brandeker, A., et al. 2003, A&A, 402, L73 [NASA ADS] [CrossRef] [EDP Sciences]
Marshall, M. D., & Muenter, J. S. 1981, J. Mol. Spectrosc., 85, 322 [NASA ADS] [CrossRef]
Persson, C. M., Olberg, M., Hjalmarson, A., et al. 2009, A&A, 494, 637 [NASA ADS] [CrossRef] [EDP Sciences]ï¿½
Pickett, H. M. 1991, J. Mol. Spectrosc., 148, 371 [NASA ADS] [CrossRef]
Ruben, D. J., & Kukolich, S. G. 1974, J. Chem. Phys., 61, 3780 [NASA ADS] [CrossRef]
Winnewisser, G., Belov, S. P., Klaus, T., et al. 1996, Z. Naturforsch., 51a, 200
Winton, R. S., & Gordy, W. 1970, Phys. Lett. A, 32, 219 [NASA ADS] [CrossRef]
Winton, R. S. 1972, Ph.D. Thesis, Duke University, Durham, NC

Footnotes

... integer: For nondegenerate K = 0 states, A₁ and A₂ species alternate with J, thus A₁ states should have null statistical weight. In fact, because of the inversion, all Js are present in the K=0 ladder, but with alternating inversion symmetry.
... middle: The higher-frequency component of this doublet is a blend of two dips 10 kHz far apart, as apparent from its width. The two dip frequencies have been determined by a full-profile analysis.
... strengths: The line strength S_ij is the square of the ij component of the electric dipole transition moment computed with 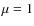$\mu=1$ : values of S_ij for the present hfs are reported in Table 3.

All Tables