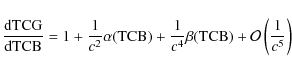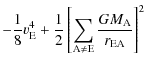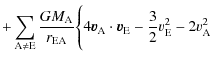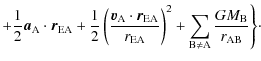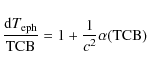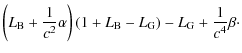| Issue |
A&A
Volume 507, Number 3, December I 2009
|
|
|---|---|---|
| Page(s) | 1675 - 1686 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/200911755 | |
| Published online | 17 September 2009 | |
A&A 507, 1675-1686 (2009)
INPOP08, a 4-D planetary ephemeris: from asteroid and time-scale computations to ESA Mars Express and Venus Express contributions
A. Fienga1,2 - J. Laskar1 - T. Morley3 - H. Manche1 - P. Kuchynka1 - C. Le Poncin-Lafitte4 - F. Budnik3 - M. Gastineau1 - L. Somenzi1,2
1 - Astronomie et Systèmes Dynamiques,
IMCCE-CNRS UMR8028,
77 Av. Denfert-Rochereau, 75014 Paris, France
2 -
Observatoire de Besançon, CNRS UMR6213,
41bis Av. de l'Observatoire, 25000 Besançon, France
3 -
ESOC, Robert-Bosch-Str. 5, Darmstadt 64293, Germany
4 -
SYRTE, CNRS UMR8630,
Observatoire de Paris,
77 Av. Denfert-Rochereau, 75014 Paris, France
Received 31 January 2009 / Accepted 24 August 2009
Abstract
The latest version of the planetary ephemerides developed at the
Paris Observatory and at the Besançon Observatory is presented.
INPOP08 is a 4-dimension ephemeris since it provides positions and
velocities of planets and the relation between Terrestrial Time and
Barycentric Dynamical Time.
Investigations to improve the modeling of asteroids are described as
well as the new sets of observations used for the fit of INPOP08.
New observations provided by the European Space Agency deduced from the
tracking of the Mars Express and Venus Express missions are presented
as well as the normal point deduced from the Cassini mission. We show
importance of these observations in the fit of INPOP08, especially in
terms of Venus, Saturn and Earth-Moon barycenter orbits.
Key words: ephemerides - astrometry - time - minor planets, asteroids - solar system: general - space vehicules
1 Introduction
Since the first release, INPOP06, of the planetary ephemerides developed at Paris and Besançon Observatories (Fienga et al. 2008, www.imcce.fr/inpop), several improvements have been made to the dynamical modeling of the INPOP ephemeris. The observation dataset has also been substantially increased, especially with the addition of ranging data from the ESA space missions Mars Express and Venus Express. The resulting new version of INPOP planetary ephemerides, INPOP08, is presented here with the description of its new features. The INPOP08 ephemeris has also been fitted to all available Lunar Laser Ranging data (Manche et al. 2007).
One of the novelties present in INPOP08 is the addition, in the distribution of the ephemeris, of a time scale transformation (TT-TDB) that is coherent with the ephemeris. The idea is to provide positions and velocities of Solar System celestial objects, and also time ephemerides relating the Terrestrial time-scale (TT) and the time argument of INPOP, the so-called barycentric dynamical time (TDB) based on the definition adopted by the International Astronomical Union in 2006. Such a release of planet and time ephemerides enables us to move towards four-dimensional planetary ephemerides. Section 2 describes the INPOP procedure for the computation of the TT-TDB relation.
Section 3 is devoted to a brief account of the new constraints and modeling implemented in INPOP for the asteroid perturbations. As in INPOP06, 300 asteroids are included in the dynamical equations of INPOP08, and the remaining ones are modeled as a ring. With respect to INPOP06, the ring model and the asteroid selection have been improved, and the precise description of these advances is given in Kuchynka et al. (2009).
An important part of the new observations used for the INPOP08 fit is the tracking data provided by the ESA space missions Mars Express and Venus Express (Morley 2006a, 2007a,b). These datasets are the first radio ranging data provided by ESA, and their acquisition and reduction process is described in Sect. 4. VEX observations provide important information on the Venus orbit. It is especially of interest since this orbit is much less perturbed by asteroids than Mars and therefore has greater potential for precise ephemeris motion, fundamental physics testing and reference frame establishment.
Section 5 deals with the INPOP fit obtained by comparison between the dynamical modeling and observations. In this process, 34 asteroid masses were fitted against only 5 in INPOP06. Comparisons are made between obtained asteroid masses and other published masses. Values for the fitted Earth-Moon barycenter and Sun oblateness J2 are also given. We have also fitted the AU and comparisons are provided with the latest determinations of DE414 (Standish 2006; Konopliv et al. 2006) and DE421 (Folkner 2008).
In addition, we performed a second fit, where the AU is given the IERS Conventions 2003 value (IERS03), and the Solar GM is deduced where G is the newtonian gravitational constant and M is the mass of the Sun.
On several occasions, for planned high precision observations, users ask us about the accuracy of the position or velocities given by the planetary ephemerides. This is difficult to evaluate, but in Sect. 6 we provide some estimates of these uncertainties, by comparison with INPOP06 and DE421. The last section is devoted to the conclusions and perspectives.
2 INPOP as a 4-D planetary ephemeris
With INPOP08, we aim to produce planetary ephemerides as fully compatible as possible with the relativistic background recently adopted by the astronomical community and summarized by the IAU2000 and IAU2006 conventions (Soffel et al. 2003). This leads to the production of an ephemeris in TDB, and to the construction of a TT-TDB transformation. The following subsections describe the various steps involved in this process and its impact for ephemeris users.
2.1 The TCB-TCG transformation
Two reference systems are defined: a global one, the barycentric celestial reference system (BCRS), covering the whole Solar System and a local one, the geocentric celestial reference system (GCRS), which is physically suitable for the modeling of processes in the vicinity of the Earth. BCRS is particularly useful when one wants to model the light propagation or motion of celestial objects in the Solar System. We can then, in the mass-monopole approximation, write the equation of motion of bodies as well as the conservation laws satisfied by the Solar System barycenter (see Damour & Vokrouhlický 1995); all these features are already implemented in INPOP06. Damour & Vokrouhlický (1995) give the complete conservation equations based on Damour et al. (1991) formalism including spin/spin, mass/mass and mass/spin couplings. However, each fundamental reference system has its own time-scale: TCB for the BCRS and TCG for the GCRS. The relation between TCB and TCG can be derived, but time transformations are only determined for specified space-time events (one coordinate time and three spatial positions) so, at the geocenter, the transformation reads (Damour et al. 1991; Soffel et al. 2003):c being the speed of light in a vacuum and where
Subscripts A and B are massive bodies, E corresponds to the Earth,
Equations (1)-(3) show that the time transformation between TCB and TCG is explicitly related to the positions and velocities of Solar System bodies, so to the planetary ephemeris itself. As stressed by Klioner (2008), if we are distributing a time transformation together with positions and velocities, we are building a four-dimensional planetary ephemeris. In the following, this time transformation will be called time ephemeris to be close to the terminology of Irwin & Fukushima (1999).
An issue remains. The use of TCB in planetary ephemerides should induce important changes in numerical values of planet masses, initial conditions and astronomical unit commonly adopted by users.
Therefore, even if a TCB-based ephemeris and a TDB-based ephemeris are related linearly, caution has to be taken when one wants to shift from one ephemeris to an other as it will induce large changes for all users. For a more complete discussion, see for instance (Klioner 2008).
2.2 The TT-TCG transformation
The IAU time is the International Atomic Time (TAI) with a service running since 1958. TAI attempts to match the rate of proper time on the geoid by using atomic clocks spread over the Earth surface and on low Earth orbits. TAI is conventionally related to the Terrestrial Time (TT) and the Universal Coordinate Time (UTC) by the two following relations:and
leap seconds being added by the International Earth Rotation Service at irregular intervals to compensate for the Earth's rotation irregularities. Leap seconds mainly are used to allow UTC to closely track UT1, which effectively represents the Earth rotation.
It is thus more convenient to consider a regular time-scale like
TT. Due to its IAU1991 definition, TT is related to TCG by a fixed
linear function as follows:
where
2.3 The TDB-TCB transformation
The TDB was introduced by IAU1976 in order to remain close to TT up to periodic variations.
However, such a definition was flawed because in that case TDB cannot be a linear function of TCB.
Consequently, the relativistic equations
derived in TCB cannot be simply adapted to TDB.
In practice, Caltech/JPL, Harvard/CfA, and RAS/IAA ephemeris programs have used a relativistic coordinate time whose
mean rate is automatically adjusted to the mean rate of TT by the ephemeris fits. Those times, often referred to as
![]() ,
can be related to TCB by the following equation with the notation of Eq. (1):
,
can be related to TCB by the following equation with the notation of Eq. (1):
and then from (Irwin & Fukushima 1999),
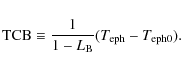
|
(8) |
Differences between
This situation changed with the recommendation B3 of IAU2006 which made TDB a fixed linear function of TCB as follows:
where T0 = 2 443 144.5003725,
2.4 Implementation in INPOP08
From Eqs. (1), (6) and (9), we have (Klioner 2007, private comm.):The values of
The central part of our implementation into INPOP is to numerically integrate Eq. (10) together with the equations of motion of all bodies.
Because the right side of (10) does not depend on
![]() ,
the Eq. (10) is not strictly an ordinary differential equation.
In the computation of
,
the Eq. (10) is not strictly an ordinary differential equation.
In the computation of ![]() ,
A enumerates all massive bodies of the Solar System, that is, the
Sun, the planets, Pluto, the Moon and the 303 asteroids.
In
,
A enumerates all massive bodies of the Solar System, that is, the
Sun, the planets, Pluto, the Moon and the 303 asteroids.
In ![]() (which is divided by c4, and so is less important than
(which is divided by c4, and so is less important than ![]() ), A and B enumerate all bodies except the 298 ``small'' asteroids.
For the acceleration term
), A and B enumerate all bodies except the 298 ``small'' asteroids.
For the acceleration term
![]() ,
all the interactions are taken into account, including Newtonian
interactions, relativistic corrections, figure and tide effects. It was
already needed for the equation of motion of the corresponding body,
and no additional work is therefore necessary to compute it.
,
all the interactions are taken into account, including Newtonian
interactions, relativistic corrections, figure and tide effects. It was
already needed for the equation of motion of the corresponding body,
and no additional work is therefore necessary to compute it.
Because the
![]() value
is unknown at J2000 (it depends on the ephemeris), the initial
condition is set to zero. The quantity integrated in the state vector
(including positions and velocities vectors of bodies) is then
value
is unknown at J2000 (it depends on the ephemeris), the initial
condition is set to zero. The quantity integrated in the state vector
(including positions and velocities vectors of bodies) is then
![]() where k
is an offset determined later, just before building the Chebychev
polynomials, by using the following condition: for the event
1977 January 1st 00h 00m 00s TAI at the geocenter, the TDB
Julian day is
where k
is an offset determined later, just before building the Chebychev
polynomials, by using the following condition: for the event
1977 January 1st 00h 00m 00s TAI at the geocenter, the TDB
Julian day is
![]() and
and
![]() .
.
At this point, the difference
![]() can be computed from any value of TDB. But in the reduction process of
observations and because they are dated on the UTC time scale, the
transformation
can be computed from any value of TDB. But in the reduction process of
observations and because they are dated on the UTC time scale, the
transformation
![]() as a function of TT (denoted
as a function of TT (denoted
![]() )
is needed.
)
is needed.
A similar differential equation as Eq. (10) can be found for
![]() (Klioner 2007), but it is not necessary to integrate it.
From the relation
(Klioner 2007), but it is not necessary to integrate it.
From the relation
![]() computed with INPOP, one can notice that
computed with INPOP, one can notice that
![]() .
.
![]() is then the solution of an implicit equation, which can be solved by
iterations. In fact, only one is necessary, the discrepancies between
TT and TDB being smaller than 2 ms.
is then the solution of an implicit equation, which can be solved by
iterations. In fact, only one is necessary, the discrepancies between
TT and TDB being smaller than 2 ms.
The formal differences between the present procedure and TE405 (Irwin & Fukushima 1999) are small, as illustrated in Fig. 1. The linear drift is measured as 6.74 ns per century (
![]() ).
This value is consistent with the IAU 2006 resolution B3 (less
than 1 ns per year between TT and TDB). These small discrepancies
could be surprising because TE405 does not take into account the terms
in 1/c4. Neglecting them in Eq. (10) induces an important drift of
).
This value is consistent with the IAU 2006 resolution B3 (less
than 1 ns per year between TT and TDB). These small discrepancies
could be surprising because TE405 does not take into account the terms
in 1/c4. Neglecting them in Eq. (10) induces an important drift of
![]() ,
close to the value
,
close to the value
![]() from Irwin & Fukushima (1999). But this drift can be compensated for by a change of the constant
from Irwin & Fukushima (1999). But this drift can be compensated for by a change of the constant ![]() or
or ![]() .
Now that TDB is defined as a conventional and fixed linear function of TCB (see Eq. (9)) and
.
Now that TDB is defined as a conventional and fixed linear function of TCB (see Eq. (9)) and ![]() is fixed to the value given by the IAU 2006 resolution B3, terms in 1/c4 are thus essential.
is fixed to the value given by the IAU 2006 resolution B3, terms in 1/c4 are thus essential.
Because the discrepancies are small, no impact is noticeable in the
differences between observed planet positions and positions computed
with TE405, the relation of Fairhead & Bretagnon (1990), or with the Chebychev polynomials representing the INPOP TT
![]() TDB.
No additional iteration is then necessary, even if at each step of the
adjustment of INPOP to observations, the computation of TT
TDB.
No additional iteration is then necessary, even if at each step of the
adjustment of INPOP to observations, the computation of TT
![]() TDB coefficients is automatically iterated.
TDB coefficients is automatically iterated.
| Figure 1:
Differences (in nanoseconds) between TE405 (corrected for the
|
|
| Open with DEXTER | |
3 New constraint on asteroid modeling
3.1 Supplementary selection of asteroids
For INPOP08, we also slightly revised the INPOP06 selection of asteroids perturbing Mars and the inner planets.
This was done with the same method as the estimation of the mass of the ring described in Sect. 3.2:
24 635 selected asteroids are assigned a reasonable
distribution of masses according to available data and the Statistical
Asteroid Model (Tedesco et al. 2003). A Monte Carlo study allows
us to assign to each asteroid the probability of being among the 300
most perturbing asteroids in terms of amplitude of the perturbation of
the Earth-Mars distance between 1969 and 2010: for each of
the 24 635 asteroids, two integrations have been done between
1969 and 2010: one with and one without the asteroid i, i
varying from 1 to 24 635. The differences between the
two integrations give the impact induced by the asteroid i.
To built our list of asteroids, we have studied the impact not only on
the Earth-Mars distances, but also the Earth-Venus and Earth-Mercury
distances.
We are thus able to compile the most probable list of the 300 most
perturbing asteroids and compare it to the INPOP06 selection used in
INPOP06![]() .
Three asteroids have predicted perturbation amplitudes well over
30 m and are absent from the INPOP06 selection: 60 Echo (amplitude
reaches 170 m), 585 Bilkis and 516 Amherstia.
We added these to the 300 already integrated in INPOP06 and thus there
are in total 303 asteroids integrated individually in INPOP08. More
details on the methodology used to obtain the most probable list of the
top 300 perturbing asteroids can be found in Kuchynka et al. (2009).
.
Three asteroids have predicted perturbation amplitudes well over
30 m and are absent from the INPOP06 selection: 60 Echo (amplitude
reaches 170 m), 585 Bilkis and 516 Amherstia.
We added these to the 300 already integrated in INPOP06 and thus there
are in total 303 asteroids integrated individually in INPOP08. More
details on the methodology used to obtain the most probable list of the
top 300 perturbing asteroids can be found in Kuchynka et al. (2009).
3.2 The ring
In the former version of INPOP (Fienga et al. 2008), perturbations of asteroids on planets were modeled with 300 individual asteroids and a static circular ring at 2.8 AU. Five asteroid masses, 3 taxonomic densities (attributed to the remaining 295 asteroids) and the mass of the ring were fitted to observations.
After the integration of such a model on a 100-year time interval, it appeared that the asteroid ring induced a drift of several meters in the position of the Solar System barycenter (Fig. 2). The static ring was then replaced by a more realistic implementation that now conserves the total linear and angular momenta of the system: the ring interacts fully with the planets and is no longer assumed to act only in their ecliptic planes. Its center is attached to the Sun and its orientation is an integrated parameter which evolves with time. The ring's interaction with other objects is identical to the interactions of an asteroid on a circular orbit averaged over the asteroid's mean orbital motion. Besides eliminating the barycenter drift, the advantage of the new implementation is that the ring is taken into account in a more realistic way and its presence in the model is more meaningful. The ring's radius was chosen as 3.14 AU.
Another novelty is that the mass of the ring is not fitted to
observations but estimated independently. This estimation is made by
calculating the amplitude of the perturbation on the Earth-Mars
distance exerted by all main-belt asteroids but the 303 most perturbing
ones determined previously. 24 635 asteroids are considered
as a model of the main belt and a simple scheme based on the
Statistical Asteroid Model (Tedesco et al. 2005)
is used to assign each asteroid with a reasonable distribution of
masses. A Monte Carlo experiment where asteroids are assigned random
(but reasonable) masses allows us to calculate the corresponding
perturbation from all the asteroids but the 303 most perturbing ones.
For each random set of masses, a ring's mass is determined so as to fit
the perturbation of the ring to the global effect. This leads to the
estimation of the ring's mass as
![]() for a ring at 3.14 AU (Kuchynka et al. 2009).
for a ring at 3.14 AU (Kuchynka et al. 2009).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11755fg2}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg50.png)
|
Figure 2: Impact of the asteroid ring on the position of the SSB over100-year integration. |
| Open with DEXTER | |
4 Presentation of MEX and VEX observations
The tracking of Mars Express (MEX) and Venus Express (VEX), while orbiting their planetary namesakes, comprises two-way coherent Doppler and range measurements. The Doppler data are converted to range-rate: the component of the spacecraft's velocity relative to the ground station along the direction from the station to the spacecraft. The determination of the spacecraft orbits uses only the range-rate data since, under normal circumstances, the additional inclusion of the range data leads to only insignificant improvement in the accuracy of the orbit solutions.
Within the orbit determination, the computed values of the observables rely on high fidelity modeling of the dynamics and the signal path (Budnik et al. 2004; Moyer 2000). As part of this modeling, the orbital states of Mars and Venus are taken from the JPL DE405 planetary ephemerides (Standish 1998b). Over time the range residuals exhibit a signature whose predominant contribution is the error in the distance from the Earth to the planet as given by the planetary ephemerides. The range residuals are therefore derived data that are very useful to improve the accuracy of planetary ephemerides. The accuracy of the range residuals depends on a number of factors, which are described in the following subsections.
4.1 Accuracy of the MEX orbit determinations
MEX, the first European mission to Mars, was launched on 2nd June 2003 and inserted into Mars orbit on 25 December 2003 and was extended until May 2009.
MEX is tracked with both ESA 35 m deep space antennas and those of the NASA Deep Space Network (DSN) (mainly at the Goldstone complex), in almost equal proportions in terms of tracking duration. Most of the ESA tracking is from New Norcia (NNO), in Western Australia, the rest from Cebreros, near Madrid in Spain.
The quantity of DSN range data and hence range residuals is far higher than the quantity of ESA range residuals due to the extraction of one ESA raw data point every 20 min whereas DSN range measurements of MEX are made at intervals of 3 min 27 s. The standard deviation of range residuals for individual passes gives a good indication of the random noise on the measurements. For ESA data, the average standard deviation of the (two-way) residuals is less than 1 m. For NASA/DSN data it is below 0.5 m.
In terms of orbit geometry, the operational orbit is near polar and elliptic with an apoapsis altitude of a little over 10 000 km and a periapsis altitude that has varied between 250 km and 340 km. The orbital period averaged 6.72 h until late in 2007 when a series of five manoeuvres at periapsis increased the period to 6.84 h. MEX is equipped with a fixed high-gain antenna (HGA) that must be pointed towards the Earth during tracking passes and tracking is done in X-band up- and downlink. The primary science data collection is around periapsis passage when the spacecraft HGA is not Earth-pointing. For orbit determination purposes, the information content within the Doppler data is highest around periapsis, so the orbit solution accuracy is adversely affected by the lack of such data. The orbit determination accuracy is also limited by other factors; most notably the imperfect calibration of perturbing velocity increments caused by thrusting, to off-load the accumulated angular momentum of the reaction wheels, and also the problems in accurately modeling small forces due to solar radiation pressure and the tiny but highly variable atmospheric drag at each periapsis passage.
For much of the MEX operational mission, routine orbit determinations were made twice per week based on tracking data arcs of 5-7 days duration, corresponding to approximately 18-25 orbital revolutions, with a typical overlap of 2 days between successive arcs. Nowadays, orbit determination is made weekly using an arc of about 10 days duration and therefore with similar overlaps. The differences between the values of common range residuals computed from successive orbit determinations provide an indication of the effect of orbit determination errors on the accuracy of the residuals. Outside of periods of superior solar conjunction, these differences are almost always below 3 m. The range residuals that are retained are taken from the earlier of each overlapping solution.
4.2 Accuracy of the VEX orbit determinations
VEX, the first European mission to Venus, was launched on 9th November 2005 and inserted into Venus orbit on 11th April 2006. Its mission is presently extended until May 2009.
The primary ground station supporting VEX is Cebreros, which tracks the spacecraft almost every day. Between 27th April 2006 and 13th March 2008, there were 663 Cebreros passes whose accumulated duration accounts for 97.7% of the total tracking duration. New Norcia has provided two-way coherent radiometric data during 12 passes and NASA DSN stations during 26 passes, of which 16 were made with DSS 43 at Canberra, mainly during the superior solar conjunction in autumn 2006. The sampling rates of the range data and the random noise on the measurements are the same as for MEX.
The operational orbit is polar and highly elliptic. There is hardly any precession of
the line of apsides, so the periapsis, whose argument is currently at 95![]() ,
remains close to the planet north pole. The apoapsis altitude is about
66 500 km and the periapsis altitude has been controlled to
stay within the range of 185 km to 390 km. The orbital period
is nominally 24 h and the maximum excursion has never been
more than 6 min. Every orbital revolution, in the vicinity of
apoapsis but not within ground station visibility, the momentum of the
reaction wheels is off-loaded by thrusting. The perturbing
,
remains close to the planet north pole. The apoapsis altitude is about
66 500 km and the periapsis altitude has been controlled to
stay within the range of 185 km to 390 km. The orbital period
is nominally 24 h and the maximum excursion has never been
more than 6 min. Every orbital revolution, in the vicinity of
apoapsis but not within ground station visibility, the momentum of the
reaction wheels is off-loaded by thrusting. The perturbing ![]() into the orbit is typically in the range 15-25 mm/s which is substantially higher than for
the MEX wheel off-loadings. The spacecraft attitude and the direction of the thrust are
chosen so that the manoeuvres help to control the orbit phasing. The control is such that
the signal elevation from the daily Cebreros passes rises to 10
into the orbit is typically in the range 15-25 mm/s which is substantially higher than for
the MEX wheel off-loadings. The spacecraft attitude and the direction of the thrust are
chosen so that the manoeuvres help to control the orbit phasing. The control is such that
the signal elevation from the daily Cebreros passes rises to 10![]() (when telecommanding
may start) always close to 2 h after periapsis passage. The pass ends either 10 h
later, close to apoapsis, or at 10
(when telecommanding
may start) always close to 2 h after periapsis passage. The pass ends either 10 h
later, close to apoapsis, or at 10![]() descending elevation, whichever is earlier. Tracking
data obtained in X-band
up and downlink are thus almost never acquired during the descending
leg of the orbit, nor around periapsis. The combination of the
unfavourable pattern of tracking data arcs, imperfect calibration of
the wheel off-loadings and deficiencies in modeling forces due to solar
radiation pressure, together with other factors depending on the nature
of the orbit cause the accuracy of the orbit determination to be worse
than that for MEX. Typical values of the differences between range
residuals derived from successive orbit solutions are a few metres but,
occasionally, even away from solar conjunction periods, the differences
can reach as high as 10 m.
descending elevation, whichever is earlier. Tracking
data obtained in X-band
up and downlink are thus almost never acquired during the descending
leg of the orbit, nor around periapsis. The combination of the
unfavourable pattern of tracking data arcs, imperfect calibration of
the wheel off-loadings and deficiencies in modeling forces due to solar
radiation pressure, together with other factors depending on the nature
of the orbit cause the accuracy of the orbit determination to be worse
than that for MEX. Typical values of the differences between range
residuals derived from successive orbit solutions are a few metres but,
occasionally, even away from solar conjunction periods, the differences
can reach as high as 10 m.
4.3 Spacecraft transponder group delay
Subtracted from each range measurement is the nominal value of the group delay of the on-board transponder. For MEX, the value corresponding to the normally used X-band up- and downlink signals is 2076 ns (about 622 m). For VEX, that has a virtually identical transponder, the value is 2085 ns (about 625 m). The nominal value is the average value measured at different occasions on ground before launch. From the variations in measured values, ostensibly made under identical conditions, it is thought that the systematic error of the nominal value should not be larger than 30 ns (about 10 m). In addition, it is known that the group delay is not perfectly stable and can fluctuate by a few ns, depending upon variations in a number of parameters such as temperature and signal strength. For MEX, these error estimates appear reasonable, and perhaps a little conservative, based upon the consistency with results determined from the NASA MGS and MO spacecraft range data during the spring of 2005. For VEX, there is no independent means to verify the error estimates.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{11755fg3}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg53.png)
|
Figure 3: VEX 1-way residuals with the new INPOP08 fitted to VEX and MEX data (dark curve) and INPOP06 not fitted to VEX observations (light curve). The solar conjonction is clearly identified with the peak of residuals in October 2006. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{11755fg4}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg54.png)
|
Figure 4: MEX and MGS/MO 1-way residuals with the new INPOP08 fitted to VEX, MEX and MGS/MO data ( right-hand side plots) and INPOP06 fitted to all MGS/MO and a part of MEX data ( left-hand side plots). The improvement of INPOP08 is mainly induced by changes in the asteroid mass determinations and the addition of MEX data (see Sect. 3 in the text). The y-axis unit is meters. |
| Open with DEXTER | |
4.4 Superior solar conjunction
During the time that MEX and VEX range residuals have been generated and archived,
both missions have experienced a superior solar conjunction. The MEX Sun-Earth-probe
(SEP) angle remained below 10![]() for two months centred on 23rd October 2006, when the
minimum SEP angle was 0.39
for two months centred on 23rd October 2006, when the
minimum SEP angle was 0.39![]() (1.6 solar radii). The VEX SEP angle was continuously
less than 8
(1.6 solar radii). The VEX SEP angle was continuously
less than 8![]() over two months centred on 27th October 2006, when the minimum SEP
angle was 0.95
over two months centred on 27th October 2006, when the minimum SEP
angle was 0.95![]() (3.8 solar radii).
The effects on spacecraft radiometric data at these conjunctions have been described by
Morley & Budnik (2007). The signals to and from the spacecraft pass through the solar
corona. The free electrons in the plasma cause a group delay on ranging measurements.
Since the electron density increases with decreasing distance from the
Sun, following, at least approximately, an inverse square law, the delay increases as the
SEP angle diminishes.
No solar corona model was applied when computing the range residuals, so the increased
delay is the cause of the peak in Fig. 3 and gaps in Fig. 4.
The existing solar corona models that could be used to correct the range residuals are not
very accurate. They cannot take into account the quite large day-to-day variations in the
signal delay caused by short-term fluctuations in solar activity like sunspot formation,
flares and coronal mass ejections, all of which can influence the surrounding electron density.
A secondary cause of increased errors in range residuals at solar conjunction is due to the
main effect on Doppler measurements of a substantial increase in noise. When the SEP
angle falls to about 1
(3.8 solar radii).
The effects on spacecraft radiometric data at these conjunctions have been described by
Morley & Budnik (2007). The signals to and from the spacecraft pass through the solar
corona. The free electrons in the plasma cause a group delay on ranging measurements.
Since the electron density increases with decreasing distance from the
Sun, following, at least approximately, an inverse square law, the delay increases as the
SEP angle diminishes.
No solar corona model was applied when computing the range residuals, so the increased
delay is the cause of the peak in Fig. 3 and gaps in Fig. 4.
The existing solar corona models that could be used to correct the range residuals are not
very accurate. They cannot take into account the quite large day-to-day variations in the
signal delay caused by short-term fluctuations in solar activity like sunspot formation,
flares and coronal mass ejections, all of which can influence the surrounding electron density.
A secondary cause of increased errors in range residuals at solar conjunction is due to the
main effect on Doppler measurements of a substantial increase in noise. When the SEP
angle falls to about 1![]() ,
the measurement noise typically increases up to two orders of
magnitude higher than is usual at large SEP angles. The accuracy of range residuals is
then indirectly and adversely affected by a degradation in the accuracy of the orbit determination solutions.
This is why the decision was taken to omit 30 days before and after the solar conjunction in range residuals.
To illustrate the impact of solar conjunction, the peak in residuals is plotted in the case of VEX data in Fig. 3. In Fig. 4,
the gap in MEX data around October 2006 is induced by the solar
conjunction. Such solar conjunctions also occured during the MGS and MO
missions and caused observation gaps such as those seen around
January 2000 and mid-2002.
,
the measurement noise typically increases up to two orders of
magnitude higher than is usual at large SEP angles. The accuracy of range residuals is
then indirectly and adversely affected by a degradation in the accuracy of the orbit determination solutions.
This is why the decision was taken to omit 30 days before and after the solar conjunction in range residuals.
To illustrate the impact of solar conjunction, the peak in residuals is plotted in the case of VEX data in Fig. 3. In Fig. 4,
the gap in MEX data around October 2006 is induced by the solar
conjunction. Such solar conjunctions also occured during the MGS and MO
missions and caused observation gaps such as those seen around
January 2000 and mid-2002.
5 INPOP08 Fit
For the fit of INPOP08, MEX and VEX observations provided by ESA and described previously were added to the INPOP06 data sets used for its adjustment (see Fienga et al. 2008, for a more detailed description of this data set). Observations deduced from the tracking of the Cassini spacecraft processed and provided by JPL (Folkner et al. 2008) were also added to the set of observations.
Global adjustments of planet initial conditions, Earth-Moon mass ratios, Astronomical Unit, Sun oblateness J2 as well as 34 asteroid masses were fitted to obtain INPOP08. The obtained values are presented in Tables 2 and 3 including comparable values found in the literature. The fit procedures are discussed in the following sections.
Table 1: Residuals obtained from INPOP06 and INPOP08.
5.1 Global results
5.1.1 Contribution of VEX data
The impact of VEX observations on the INPOP08 adjustment is great. As one can see in Fig. 3 and Table 1, INPOP08 provides a much more accurate Venus orbit thanks to the VEX input data. This improvement is mainly induced by the fit of planet initial conditions and also by the improvement of the modeling of the asteroid perturbations on the inner planets. A mean dispersion of 4 m (1-sigma formal dispersion) with a bias of 1.5 m is obtained after the fit, which corresponds to the level of accuracy of the VEX observations. This is an improvement in the estimation of the Earth-Venus distance of about a factor 42 compared to the previous ephemeris, INPOP06, which was not fitted to VEX data. The large effect that one can see in Fig. 3 is actually induced by the propagation of the previous planetary ephemerides uncertainties on Earth and Venus orbits. Such ephemerides as INPOP06, but also DE405, were only fitted to direct radar observations of the Venus surface (see Standish 1998b; Fienga et al. 2008) and to the VLBI data deduced from the tracking of the Venus mission Magellan in 1994. The Venus data sets suffer from a lack of observations since 1994 and from the low accuracy of the direct radar observations. The combination of both explains the spectacular improvement observed in Fig. 3. One can also notice in Table 1 that even if the new Venus INPOP08 orbit induces significant changes in the values of VEX residuals compared to INPOP06 ones, the residuals obtained by comparison between this new orbit and the observations used previously for the INPOP06 fit are quite similar to those obtained with INPOP06. This means that the VEX data are consistent with the old ones and their addition in the fit does not degrade the ephemerides over a large time interval.
5.1.2 Mars observations and asteroids
Using MEX tracking data and the INPOP06 Mars data set, we fitted the
new asteroid ring model as well as the selection of asteroids described
in Sect. 3.
Compared to INPOP06, the ring model was modified to a non-static ring,
3 more asteroids were included in the list of main perturbers and more
asteroids have their masses fitted individually in using a priori
sigmas (Moyer 1971) of about 30![]() constraints to their initial values. The choice of the fitted asteroid
masses was done so as to have only positive masses even without the
constraints.
In INPOP08, 34 asteroids have their masses fitted individually against
5 in INPOP06.
constraints to their initial values. The choice of the fitted asteroid
masses was done so as to have only positive masses even without the
constraints.
In INPOP08, 34 asteroids have their masses fitted individually against
5 in INPOP06.
As one can see in Table 1 and Fig. 4, this new approach and the input of information brought by the MEX data improve the ephemerides by significantly reducing the residuals. This improvement can be noticed with the new MEX data set which was not included in the previous solution, but also with the MGS/MO data set included both in INPOP08 and INPOP06 adjustments. For the MGS/MO residuals we have an improvement of the results of a factor 4.
Table 2: Physical parameters fitted in INPOP08.
Furthermore, as one can see in Fig. 4, during the overlap period of the mission (from 2005.5 to 2006), the link between MGS/MO and MEX data is done properly by INPOP08 with a offset of about 3.5 m between MGS/MO and MEX. This offset is in the error estimations presented in Sect. 4 and the calibration done by ESA before the MEX launch. Even if a large improvement can be noticed in Fig. 4, signals still remain in INPOP08 residuals due to incomplete asteroid mass determinations but also to systematics induced by solar conjunction gaps in the data sets.
In Tables 2 and 3,
asteroid masses fitted in INPOP08 are compared to other published
masses as well as values for taxonomic densities and physical
characteristics of the asteroid ring. In the case of INPOP08, the ring
mass and distance were not fitted during the global adjustment but
rather during the construction of the ring (see Sect. 3).
Due to the direct correlation between the mass of the ring and its
distance to the Sun, we decided to arbitrarily fix the distance at 3.14
AU. If this distance is chosen at 2.8 AU, the mass of the
ring is estimated to be
![]() which is comparable to the GM estimated by DE414 and very close to the one given by INPOP06.
In Table 2,
the taxonomic densities estimated by INPOP08 stay of the same order as
those estimated by DE414 or DE421 and the values of masses estimated
for the 5 biggest asteroids are also in good agreement with those
published previously. Figure 5 shows the same conclusion.
The values estimated since 1991 (Baer & Chesley 2008)
of GMs of Ceres, Pallas and Vesta are plotted as well as the values
provided by INPOP06, DE414, DE421 and INPOP08 which correspond to the
four last points in 2008 and 2009. On this graph, we show
(using darked circles) asteroid masses estimated by close encounters
(see for instance Baer & Chesley 2008; Hilton 1999), asteroid masses obtained after radar imaging (Michalak 2000)
and masses fitted during the global adjustments of planetary
ephemerides marked as black crosses. The close encounter method was
used a lot in the 90 s but due to the difficulty of the method
(accurate observations of the perturbed objects to obtain very accurate
estimation of their orbit and to survey the orbit during the close
encounters), the effort was not maintained during the last decade. On
the other hand, the evolution of planetary ephemerides gives very
stable estimations for the largest asteroids with uncertainties smaller
than the close encounters determinations. In 2008, Baer & Chesley
published values established on the basis of several encounters and
obtained values of masses for Ceres, Pallas and Vesta very close to the
ones obtained by the planetary ephemerides. For Ceres and Vesta, the
uncertainties of the close encounters determinations are at the same
level of accuracy as planetary ephemerides. INPOP08 gives original
values offset from the previous estimations but at the limit of the
error bars.
which is comparable to the GM estimated by DE414 and very close to the one given by INPOP06.
In Table 2,
the taxonomic densities estimated by INPOP08 stay of the same order as
those estimated by DE414 or DE421 and the values of masses estimated
for the 5 biggest asteroids are also in good agreement with those
published previously. Figure 5 shows the same conclusion.
The values estimated since 1991 (Baer & Chesley 2008)
of GMs of Ceres, Pallas and Vesta are plotted as well as the values
provided by INPOP06, DE414, DE421 and INPOP08 which correspond to the
four last points in 2008 and 2009. On this graph, we show
(using darked circles) asteroid masses estimated by close encounters
(see for instance Baer & Chesley 2008; Hilton 1999), asteroid masses obtained after radar imaging (Michalak 2000)
and masses fitted during the global adjustments of planetary
ephemerides marked as black crosses. The close encounter method was
used a lot in the 90 s but due to the difficulty of the method
(accurate observations of the perturbed objects to obtain very accurate
estimation of their orbit and to survey the orbit during the close
encounters), the effort was not maintained during the last decade. On
the other hand, the evolution of planetary ephemerides gives very
stable estimations for the largest asteroids with uncertainties smaller
than the close encounters determinations. In 2008, Baer & Chesley
published values established on the basis of several encounters and
obtained values of masses for Ceres, Pallas and Vesta very close to the
ones obtained by the planetary ephemerides. For Ceres and Vesta, the
uncertainties of the close encounters determinations are at the same
level of accuracy as planetary ephemerides. INPOP08 gives original
values offset from the previous estimations but at the limit of the
error bars.
In Table 3, we show the masses of the 28 asteroids, other than the 5 Bigs given in Table 2, fitted individually in INPOP08. The estimated mass values are put in the table as their mean impact on the Earth-Mars distance (estimated over 20 years) decreases. For some of them, the INPOP08 masses agree in the limit of 30% with values estimated previously either by close encounters methods (for (16) Psyche, (52) Europa, (88) Thisbe, (8) Flora, (15) Eunomia, (18) Melpomene (19) Fortuna, and (21) Lutecia) or by adjustment of planetary ephemerides (for (41) Daphne, (29) Amphitrite, (409) Aspasia, (704) Interamnia, or (532) Herculina). However, for some others, the differences from previous estimations can reach 500 % as for the case of (9) Metis or even worse (as for (6) Hebe). We estimate that 50% of estimations are close to previously published masses (differences below 50%), 21% first estimations and 4 very insufficent estimations (differences greater than 500%).
Such differences can be explained by the differences in the modeling used to fit the data. For instance, by the differences in the data reduction, the weight used in the fit as well as by individually fitting a different number of asteroids and by diminushing the effect of all the other minor bodies by the fit of the taxonomic classes and the addition of a ring, one removes in the fit of individual masses dynamical effects which are not really caused by one particular asteroid but by a group of asteroids inducing effects very similar in amplitude and period. The fitted mass for this particular asteroid then represents not only its gravitational potential but also the one induced by other asteroids. This remark can be illustrated by the unrealistic values of some densities deduced from masses and presented in Table 3 as well as the almost zero mass of the asteroid (747) Winchester, the perturbations induced by (747) that are negligible or not clearly separated from another asteroid perturbations like in the case of (6) Hebe. In order to better estimate the real mass value of one particular asteroid, one could isolate the arc of the Mars orbit where and when this asteroid has the biggest impact and try to estimate its mass only on that arc. Such an investigation is presented in Somenzi et al. (2009).
5.1.3 Cassini normal points
Cassini normal points for Saturn were provided by JPL and are described in detail by Folkner et al. (2008). The impact of these data is not negligeable. They give very important information about the Saturn orbit by providing very accurate estimations of the Earth-Saturn distance and geocentric angular position of Saturn. Thanks to these, our knowledge of its distance from the Earth reduces from about 27 km to 22 m at the epoch of Cassini normal points.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11755fg5}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg62.png)
|
Figure 5: Estimations of Ceres, Pallas and Vesta masses found in the literature. The GMs (in units of 10-10 solar mass y-axis) are plotted by year of publication (x-axis). The dark red circles represent the GMs estimated in using close encounters as described by Baer & Chesley (2008). The crosses represent GMs fitted with the planetary ephemerides. The upper triangles represent masses deduced from radar observations as described by Michalak (2000). The last crosses corresponding to 2009 give values obtained by INPOP08. |
| Open with DEXTER | |
Table 3: Asteroid GMs fitted in INPOP08.
5.2 AU fixed and rescaled GM of the sun version
As a first step towards a new generation of planetary ephemerides
fitting the GM of the sun and using a fixed value of AU, an
alternative version of INPOP08 was built. This version is based on the
INPOP08 ephemeris presented in the previous section. However, instead
of providing a value of AU fitted to observations, the AU is fixed to
the IERS 2003 value and the change is included by the multiplication of
all the initial conditions of planets and asteroids as well as all the
masses including the GM of the sun by a factor equivalent to
![]() over
over
![]() .
A new value for the GM of the Sun is then deduced and presented in Table 4.
This version of INPOP08 is equivalent to the previous one but allows
the next versions of planetary ephemerides to fit directly the GM of
the sun instead of the AU.
.
A new value for the GM of the Sun is then deduced and presented in Table 4.
This version of INPOP08 is equivalent to the previous one but allows
the next versions of planetary ephemerides to fit directly the GM of
the sun instead of the AU.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{11755fg6}\hspace*{4mm}\includegraphics[width=7.3cm,clip]{11755fg7}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg66.png)
|
Figure 6: Residuals obtained by comparison between INPOP08 and MEX tracking data ( left) and VEX ( right) observations. The small dark points represent residuals of observations which were used in the fit of INPOP08 and the large dark points represent residuals of observations not used in the fit. The large slope of MEX residuals may be improved in the future with better determination of asteroid masses. |
| Open with DEXTER | |
6 Estimation of uncertainties
Often, users need to know the accuracy of planet ephemerides. There are two methods to determine it. The first one is to compare the ephemerides to observed positions not used in the fit, and preferably to observations situated out of the time interval of observations used for the adjustment. Such results give information to the users who directly deal with observations of planets or satellites: with what accuracy in millarcseconds can we predict the position of such a planet in right ascension and declination, what accuracy in meters is obtained for the estimation of Earth-Mars distances etc. In Sect. 6.1, we present such an extrapolation of INPOP08 compared to observations not used in the fit and usually outside the fit interval.However, for all the other users, the comparison with observations is interesting only if these observations correspond to the user's specific use. In general, users prefer to have a more theoretical estimation such as the uncertainties in the barycentric positions and velocities of the Earth. To evaluate these values, we use comparisons between different ephemerides to estimate the level of variations induced by an improvement of modeling or adjustment (Sect. 6.2).
6.1 Extrapolation tests
Table 4: AU and GM of the sun values used for the construction of INPOP08 and INPOP08b.
Two sets of observations of MEX and VEX were kept out of the fit procedure as a test sample of INPOP08. These sets were obtained from April 2008 to September 2008. Differences in meters obtained between the observed and INPOP08 distances can be found in Fig. 6. For Mars, the linear drift observed is of the order of the error expected (about 20 m over half a year) and is mainly due to asteroid modeling and adjustment.
For Venus, the distribution is noisier, but in good continuity with the postfit residuals obtained after the INPOP08 fit and presented in Fig. 6. The biggest noticeable effect on these residuals is induced by the VEX solar conjunction that occured on June 9th 2008. This solar conjunction introduced unmodeled noise into the doppler and ranging data of VEX during a period of few days (06 to 11 June inclusive) during which time the spacecraft tracking was stopped. The peak in Fig. 6 is mainly induced by this conjunction.
Table 5: Maximum differences between INPOP06 and INPOP08 estimated in interval A from 1990 to 2010 and in interval B from 1900 to 2050.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11755fg8}\hspace*{4mm}\includegraphics[width=8cm,clip]{11755fg9}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg68.png)
|
Figure 7: Differences between INPOP08 and INPOP06 ( left-hand side) and between INPOP08 and DE421 ( right-hand side). For each planet, comparisons are made between heliocentric longitudes (barycentric for the Sun) in the ecliptic frame. Units are milliarcseconds for Y-axis and years around J2000 for X-axis. |
| Open with DEXTER | |
6.2 Uncertainties by comparison with other ephemerides
Table 6: Maximum differences between DE421 and INPOP08 estimated in interval A from 1990 to 2010 and in interval B from 1900 to 2050.
Another way to estimate the uncertainties of a planet orbit is to compare several ephemerides. By such comparisons, one estimates first the impact of the differences in dynamical modeling of each ephemeris and adjusted to observations: the ephemerides could have been fitted over different sets of observations with different sets of weight and with different sets of parameters. Table 5 presents the maximum differences in barycentric positions and velocities between INPOP08 and INPOP06. Table 6 presents the corresponding maximum differences between INPOP08 and DE421. Two intervals of time are considered to estimate these differences: interval A from 1990 to 2010 and interval B from 1900 to 2050. Plots of heliocentric differences in ecliptic longitudes obtained by comparison between the same ephemerides are presented in Fig. 7. The use of Cassini normal points in DE421 and INPOP08 make the differences between the two ephemerides decrease significantly for the longitude of Saturn, as well as for the other outer planets.If one consider that these differences give a good estimation of their actual accuracies, then using the Cassini data, we can see an improvement of the orbit at the epoch of these observations.
Limited improvements of the outer planet orbits will be possible by the addition of more accurate data in the fit, mainly tracking data of spacecraft orbiting or passing through one of these systems, such as the New Millenium mission. Important improvements will be obtained after having a significant portion of the orbit covered by accurate observations which will require at least five years of continuous observations for Jupiter's orbit.
For Mars and the EMB, one can see in Fig. 7 that the differences are also reduced between DE421 and INPOP08 compared to the differences between INPOP06 and INPOP08. As well for the EMB in Table 5, if one uses the differences between ephemerides as a tool to estimate the ephemerides accuracy, the uncertainties on its barycentric positions are about 900 m over 10 years and 4 km over 100 years, and about 10 m per day to 50 m per day for its barycentric velocities.
7 Perspectives and conclusions
In this article, INPOP08 was fully described as a new 4-D planetary ephemeris.
New modeling of asteroid perturbations were introduced and as described by Kuchynka et al. (2009), improvements in the methods of asteroid mass determinations are possible. Introduction of these new methods will be done in the next INPOP version, leading to an improvement of the extrapolation capabilities of the ephemerides as well as more realistic determination of asteroid masses.
New sets of observations were used for the construction of INPOP08: the Mars Express and Venus Express tracking data processed by ESA and normal points deduced from the Cassini mission. Thanks to these data, large improvements were made in the determination of the orbits of Venus and Saturn. They open doors to new tests of gravity which were hitherto limited to only accurate Earth-Mars distance observations. These tests and their results will be presented in a dedicated paper.
However, as was already stressed in Sect. 5.1.1, VEX tracking data and Saturn Cassini normal points have a crucial role to play in such investigations.
The LLR data have been used for the adjustment of the lunar orbit and libration in INPOP08 (Manche et al. 2007). The fit to these data as well as the complete lunar model will be described in a forthcoming paper.
The INPOP08 planetary ephemeris is available for users on the INPOP website (www.imcce.fr/inpop) as Chebychev polynomial coefficients interpolated via provided routines in C and Fortran. Positions and velocities of the nine planets, the Sun, the moon libration and the 3 Euler angles of the Earth rotation can be extracted as well as the TT-TDB relation at any time. An alternative version with rescaled GM of the sun and fixed AU can also be provided on request.
In the next version, we plan to directly adjust the GM of the sun instead of the AU. Simulations of Mercury mission data and use of fly-by data will be introduce in order to evaluate the improvements in terms of accuracy limits in the determination of PPN parameters and J2.
AcknowledgementsWe thank S. Klioner for multiple dicussions during this work and M. Standish for constructive comments. This work was supported by CNES under contract 05/CNES//00-DCT 094, by the CS of Paris Observatory, and by PNP-CNRS.
References
- Baer, J., & Chesley, S. R. 2008, Celest. Mechan. Dynam. Astron., 100, 27 [NASA ADS] [CrossRef]
- Baer, J., Milani, A., Chesley, S., & Matson, R. D. 2008, AAS/Division for Planetary Sciences Meeting Abstracts, 09-28, 40
- Budnik, F., Morley, T. A., & Mackenzie, R. A. 2004, ESA SP, 548, 387 [NASA ADS]
- Damour, T., & Vokrouhlický, D. 1995, Phys. Rev. D, 52, 4455 [NASA ADS] [CrossRef]
- Damour, T., Soffel, M., & Xu, C. 1991, Phys. Rev. D, 43, 3273 [NASA ADS] [CrossRef]
- Fairhead, L., & Bretagnon, P. 1990, A&A, 229, 240 [NASA ADS]
- Fienga, A., Manche, H., Laskar, J., & Gastineau, M. 2008, A&A, 477, 315 [NASA ADS] [CrossRef] [EDP Sciences]
- Folkner, W. M. 2008, JPL Interoffice Memorandum, 343R, 08
- Irwin, A. W., & Fukushima, T. 1999, A&A, 348, 642 [NASA ADS]
- Hilton, J. L. 1999, AJ, 117, 1077 [NASA ADS] [CrossRef]
- IERS Conventions 2003, 2004, IERS Technical Note, 32, Frankfurt am Main: Verlag des Bundesamts fur Kartographie und Geodesie
- Klioner, S. A. 2008, IAU Symp., 248, 356 [NASA ADS]
- Konopliv, A. S., Yoder, C. F., Standish, E. M., Yuan, D.-N., & Sjogren, W. L. 2006, Icarus, 182, 23 [NASA ADS] [CrossRef]
- Kuchynka, P., Laskar, J., Fienga, A., Manche, H., & Somenzi, L. 2009, JOURNEES-2008, Astrometry, Geodynamics and Astronomical Reference Systems, ed. M. Soffel, & N. Capitaine (Dresden)
- Manche, H., Bouquillon, S., Fienga, A., Laskar, J., & Francou, G. 2007, JOURNEES-2007, The Celestial Reference Frame for the Future, ed. N. Capitaine (Paris)
- Michalak, G. 2000, A&A, 360, 363 [NASA ADS]
- Moyer, T. 1971, Technical report 32-1527, JPL, May 15
- Moyer, T. 2000, Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation, ed. J. H. Yuen (John Wiley & Sons)
- Morley, T. 2006a, MEX data release
- Morley, T. 2007a, MEX data release
- Morley, T. 2007b, MEX data release
- Morley, T., & Budnik, F. 2007, Proc. 20th Inter. Symp. on Space Flight Dynamics, Annapolis, MD
- Pitjeva, E. V. 2008, JOURNEES-2008, Astrometry, Geodynamics and Astronomical Reference Systems, ed. M. Soffel, & N. Capitaine (Dresden)
- Soffel, M., Klioner, S. A., Petit, G., et al. 2003, AJ, 126, 2687 [NASA ADS] [CrossRef]
- Somenzi, L., Fienga, A., & Laskar, J. 2009, A&A, submitted
- Standish, E. M. 1998a, A&A, 336, 381 [NASA ADS]
- Standish, E. M. 1998b, JPL Interoffice Memorandum, 312.F, 98
- Standish, E. M. 2006, JPL Interoffice Memorandum, 343R-06-002, 1
- Standish, E. M., & Williams, J. G. 2001, ftp://ssd.jpl.nasa.gov/pub/eph/planets/ioms/ExplSupplChap8.pdf
- Tedesco, E. F., Cellino, A., & Zappalá, V. 2005, AJ, 129, 2869 [NASA ADS] [CrossRef]
Footnotes
- ... INPOP06
![[*]](/icons/foot_motif.png)
- The list of asteroids integrated individually in INPOP06 or DE405 is given in (Standish & Williams 2001).
All Tables
Table 1: Residuals obtained from INPOP06 and INPOP08.
Table 2: Physical parameters fitted in INPOP08.
Table 3: Asteroid GMs fitted in INPOP08.
Table 4: AU and GM of the sun values used for the construction of INPOP08 and INPOP08b.
Table 5: Maximum differences between INPOP06 and INPOP08 estimated in interval A from 1990 to 2010 and in interval B from 1900 to 2050.
Table 6: Maximum differences between DE421 and INPOP08 estimated in interval A from 1990 to 2010 and in interval B from 1900 to 2050.
All Figures
| |
Figure 1:
Differences (in nanoseconds) between TE405 (corrected for the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11755fg2}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg50.png)
|
Figure 2: Impact of the asteroid ring on the position of the SSB over100-year integration. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{11755fg3}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg53.png)
|
Figure 3: VEX 1-way residuals with the new INPOP08 fitted to VEX and MEX data (dark curve) and INPOP06 not fitted to VEX observations (light curve). The solar conjonction is clearly identified with the peak of residuals in October 2006. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{11755fg4}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg54.png)
|
Figure 4: MEX and MGS/MO 1-way residuals with the new INPOP08 fitted to VEX, MEX and MGS/MO data ( right-hand side plots) and INPOP06 fitted to all MGS/MO and a part of MEX data ( left-hand side plots). The improvement of INPOP08 is mainly induced by changes in the asteroid mass determinations and the addition of MEX data (see Sect. 3 in the text). The y-axis unit is meters. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11755fg5}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg62.png)
|
Figure 5: Estimations of Ceres, Pallas and Vesta masses found in the literature. The GMs (in units of 10-10 solar mass y-axis) are plotted by year of publication (x-axis). The dark red circles represent the GMs estimated in using close encounters as described by Baer & Chesley (2008). The crosses represent GMs fitted with the planetary ephemerides. The upper triangles represent masses deduced from radar observations as described by Michalak (2000). The last crosses corresponding to 2009 give values obtained by INPOP08. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{11755fg6}\hspace*{4mm}\includegraphics[width=7.3cm,clip]{11755fg7}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg66.png)
|
Figure 6: Residuals obtained by comparison between INPOP08 and MEX tracking data ( left) and VEX ( right) observations. The small dark points represent residuals of observations which were used in the fit of INPOP08 and the large dark points represent residuals of observations not used in the fit. The large slope of MEX residuals may be improved in the future with better determination of asteroid masses. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11755fg8}\hspace*{4mm}\includegraphics[width=8cm,clip]{11755fg9}
\end{figure}](/articles/aa/full_html/2009/45/aa11755-09/Timg68.png)
|
Figure 7: Differences between INPOP08 and INPOP06 ( left-hand side) and between INPOP08 and DE421 ( right-hand side). For each planet, comparisons are made between heliocentric longitudes (barycentric for the Sun) in the ecliptic frame. Units are milliarcseconds for Y-axis and years around J2000 for X-axis. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.