| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 251 - 259 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200912596 | |
| Published online | 08 September 2009 | |
A&A 507, 251-259 (2009)
Reaching the boundary between stellar kinematic groups and very wide binaries
The Washington double stars with the
widest angular separations![[*]](/icons/foot_motif.png)
J. A. Caballero
Departamento de Astrofísica y Ciencias de
la Atmósfera, Facultad de
Física, Universidad Complutense de Madrid, 28040 Madrid, Spain
Received 29 May 2009 / Accepted 12 August
2009
Abstract
Aims. I look for and characterise very wide
binaries and multiple systems with projected physical separations
larger than s = 0.1 pc, which is generally
believed to be a sharp upper limit to the distribution of wide binary
semimajor axes.
Methods. I investigated in detail 30
Washington double stars with angular separations of  arcsec.
I discarded 23 of them as probably unbound systems based on
discordant astrometry, photometry, spectral types, and radial
velocities. The remaining seven systems were subject to a comprehensive
data compilation and derivation (multi-wavelength photometry,
heliocentric distance, multiplicity, age, mass, metallicity, membership
in a young kinematic group).
arcsec.
I discarded 23 of them as probably unbound systems based on
discordant astrometry, photometry, spectral types, and radial
velocities. The remaining seven systems were subject to a comprehensive
data compilation and derivation (multi-wavelength photometry,
heliocentric distance, multiplicity, age, mass, metallicity, membership
in a young kinematic group).
Results. Of the seven very wide systems, six have
projected physical separations greater than the hypothetical cutoff at s
= 0.1 pc and four have separations s
> 0.2 pc. Although there are two systems in young
kinematic
groups (namely HD 136654 and BD+32 2572 in the Hyades
Supercluster, and AU Mic and AT Mic AB in
the  Pictoris
moving group), there is no clear prevalence of young systems (
Pictoris
moving group), there is no clear prevalence of young systems ( Ga)
among these very wide binaries. Finally, I compare the binding
energies of the seven systems with those of other weakly bound systems
in the field.
Ga)
among these very wide binaries. Finally, I compare the binding
energies of the seven systems with those of other weakly bound systems
in the field.
Key words: astronomical data bases: miscellaneous -
binaries: general - binaries: visual - stars: kinematics
1 Introduction
Aims. I look for and characterise very wide binaries and multiple systems with projected physical separations larger than s = 0.1 pc, which is generally believed to be a sharp upper limit to the distribution of wide binary semimajor axes.
Methods. I investigated in detail 30 Washington double stars with angular separations of
Results. Of the seven very wide systems, six have projected physical separations greater than the hypothetical cutoff at s = 0.1 pc and four have separations s > 0.2 pc. Although there are two systems in young kinematic groups (namely HD 136654 and BD+32 2572 in the Hyades Supercluster, and AU Mic and AT Mic AB in the
Binaries can be classified by physical separation into close
and wide
binaries.
Close binaries include spectroscopic, astrometric, interferometric,
eclipsing, cataclysmic, and semi-detached binaries, which have quite
differentiated astrophysical properties.
However there is subjectiveness in the determination of the boundary
between
close and wide binaries. While for some authors a wide binary is a
detached pair with a physical separation of a few tens solar radii,
enough to avoid Roche lobe filling and mass transfer after the main
sequence, for others the stars in a wide binary must be separated by at
least 103-104 AU
(0.005-0.05 pc)![]() ,
depending on the total mass of the system.
,
depending on the total mass of the system.
It remains an open question whether the definition of wide binaries
must be
``stretched a little'' to include common proper motion pairs (pairs of
stars
traveling together through space without any discernible relative
orbital
motion; Batten 1973). For
example, just in the very closest solar neighbourhood, the
gravitational binding between Proxima Centauri (M5.5Ve) and ![]() Cen A
and B (G2V+K2IV), a celebrated common proper motion ``pair''
(Innes 1915) with a
physical separation
Cen A
and B (G2V+K2IV), a celebrated common proper motion ``pair''
(Innes 1915) with a
physical separation ![]() AU
(
AU
(
![]() pc) and a
long-expected orbital period (
pc) and a
long-expected orbital period (
![]() Ma), has been
repeatedly questioned (Voûte 1917; Wertheimer
& Laughlin 2006, and
references therein).
Ma), has been
repeatedly questioned (Voûte 1917; Wertheimer
& Laughlin 2006, and
references therein).
Some authors have proposed that ![]() Cen A
and B are the brightest members
in a stellar kinematic group that includes Proxima Centauri (e.g.
Anosova &
Orlov 1991). Stars in
a stellar kinematic group share a common origin and Galactic spatial
velocities (UVW) and are typically young, with
Hyades-like or younger ages
(
Cen A
and B are the brightest members
in a stellar kinematic group that includes Proxima Centauri (e.g.
Anosova &
Orlov 1991). Stars in
a stellar kinematic group share a common origin and Galactic spatial
velocities (UVW) and are typically young, with
Hyades-like or younger ages
(
![]() Ma - Soderblom
& Mayor 1993; Montes
et al. 2001; Zuckerman
& Song 2004). Youth may
partly explain the existence of some very wide
binaries (or very wide common proper motion
pairs), with physical separations of more than 0.1 pc.
The younger a wide (or very wide) binary in the Galactic disc, the less
time
it has had to encounter individual stars and giant molecular clouds,
whose
gravity will eventually tear them apart (e.g. Bahcall & Soneira
1981; Retterer
& King 1982; Weinberg
et al. 1987; Saarinen
& Gilmore 1989; Poveda
& Allen 2004).
For instance, the common proper motion ``pair'' AU Mic and
AT Mic A and B has one of the widest
projected physical
separations ever measured,
Ma - Soderblom
& Mayor 1993; Montes
et al. 2001; Zuckerman
& Song 2004). Youth may
partly explain the existence of some very wide
binaries (or very wide common proper motion
pairs), with physical separations of more than 0.1 pc.
The younger a wide (or very wide) binary in the Galactic disc, the less
time
it has had to encounter individual stars and giant molecular clouds,
whose
gravity will eventually tear them apart (e.g. Bahcall & Soneira
1981; Retterer
& King 1982; Weinberg
et al. 1987; Saarinen
& Gilmore 1989; Poveda
& Allen 2004).
For instance, the common proper motion ``pair'' AU Mic and
AT Mic A and B has one of the widest
projected physical
separations ever measured, ![]() pc,
and belongs to one of the youngest stellar kinematic groups, the
pc,
and belongs to one of the youngest stellar kinematic groups, the ![]() Pictoris
moving group (
Pictoris
moving group (
![]() Ma - Zuckerman
et al. 2001; Ortega
et al. 2004).
Ma - Zuckerman
et al. 2001; Ortega
et al. 2004).
Another way for a very wide binary to avoid encounters in the Galactic
disc
is to belong to the Galactic halo stellar population. Because of the
large inclination of their orbits, halo stars spend most of their
lives far from the Galactic plane, where the probability of
encountering
stars and molecular clouds is at a minimum. As another example, the
system HD 149414 AB and BD-03 3968B
was the widest metal-poor ``binary'' in the imaging search by Zapatero
Osorio & Martín (2004). The
projected physical separation between both components is ![]() pc.
Low metallicities, such as measured in the primary of the system (the
F8
subdwarf HD 149414 AB has [Fe/H]
pc.
Low metallicities, such as measured in the primary of the system (the
F8
subdwarf HD 149414 AB has [Fe/H] ![]() -1.4), are typical of halo
population II stars. The three systems (
-1.4), are typical of halo
population II stars. The three systems (![]() Cen,
AU Mic, and HD 149414 AB) are discussed
next.
Cen,
AU Mic, and HD 149414 AB) are discussed
next.
There is a sharp cutoff in the number of very wide binaries with
physical
separations greater than 0.1 pc, possibly dictated by
dynamical evolution, as
stated in classical (Tolbert 1964; Kraicheva
et al. 1985; Abt 1988; Weinberg
&
Wasserman 1988; Weis 1988; Close
et al. 1990; Latham
et al. 1991; Wasserman
&
Weinberg 1991 and
references above) and modern works (Allen et al. 2000; Palasi 2000; Chanamé
& Gould 2004; Lépine
& Bongiorno 2007; Makarov
et al. 2008).
My aim is to characterise and look for very wide binaries and multiple
systems with projected physical separations larger than s
= 0.1 pc (
![]() AU).
Some of these systems will be among the least bound ones and might help
trace the boundaries between very wide binaries, common proper motion
pairs, and stellar kinematic groups on the point of being disrupted.
AU).
Some of these systems will be among the least bound ones and might help
trace the boundaries between very wide binaries, common proper motion
pairs, and stellar kinematic groups on the point of being disrupted.
In this paper, I start a programme of identifying and investigating the widest common proper motion pairs with a detailed analysis of the binary and multiple system candidates with angular separations over 1000 arcsec in the Washington Double Star Catalog (WDS; Mason et al. 2001). It is expected that these large angular separations translate into large physical separations, of the order of a tenth of a parsec. However, the membership in a proper motion pair of many doubles has not been confirmed since their discovery dates (as early as the 19th century in some cases) and most of them were last characterised in the pre-Hipparcos era (i.e. no accurate projected physical separations could be measured).
2 Analysis and results
2.1 Data retrieval
First, I compiled the angular separations, ![]() ,
position angles,
,
position angles, ![]() ,
coordinates, visual magnitudes, and identifiers of 104 312 WDS
pairs (as
in 2009 May). As can be seen in Fig. 1, the
cumulative number of pairs approximately increases with a power law in
the interval
,
coordinates, visual magnitudes, and identifiers of 104 312 WDS
pairs (as
in 2009 May). As can be seen in Fig. 1, the
cumulative number of pairs approximately increases with a power law in
the interval ![]() to
20 arcsec. The distribution of angular separations is the Öpik
law
(which formally applies to the distribution of physical separations -
Öpik 1924; Poveda
& Allen 2004)
folded with the distribution of observed systems with heliocentric
distance. The number of pairs increases at a more moderate rate from
to
20 arcsec. The distribution of angular separations is the Öpik
law
(which formally applies to the distribution of physical separations -
Öpik 1924; Poveda
& Allen 2004)
folded with the distribution of observed systems with heliocentric
distance. The number of pairs increases at a more moderate rate from
![]() to 200 arcsec and practically becomes constant at larger
separations. Only 1% [0.1%] of the WDS pairs have angular separations
to 200 arcsec and practically becomes constant at larger
separations. Only 1% [0.1%] of the WDS pairs have angular separations
![]() arcsec
[500 arcsec]. There are 36 WDS pairs with tabulated
separations
arcsec
[500 arcsec]. There are 36 WDS pairs with tabulated
separations ![]() arcsec
(actually, the WDS catalogue lists them as
arcsec
(actually, the WDS catalogue lists them as ![]() arcsec).
I have carefully investigated all 36 of them, mainly
using the Aladin sky atlas (Bonnarel et al. 2000).
arcsec).
I have carefully investigated all 36 of them, mainly
using the Aladin sky atlas (Bonnarel et al. 2000).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12596fig1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12596-09/Timg23.png)
|
Figure 1:
Cumulative number of WDS pairs as a function of the angular separation,
|
| Open with DEXTER | |
Of the 36 WDS binaries, I was not able to identify five binary candidates:
- WDS 05463+5627 (LDS 3673; W. J. Luyten, proper motion catalogues).
- WDS 04022+2808 (STF 481AD; F. G. W. Struve). The primary in the system in the G8II triple star system HD 25296 ABC.
- WDS 09510+0105 (GRV 1149; J. Greaves, private communication). The system might consist of the faint white dwarfs WD 0948+013 and 2QZ J095234.0+011046, but I could not confirm it.
- WDS 18382+2543 (BUP 185AC; S. W. Burnham, proper motion stars). Coordinates have large uncertainties.
- WDS 21435+2721 (A 299DE; R. G. Aitken). Bright star BD+26 4249 is likely the primary in the system.
The stars in the system WDS 03330+0306 (G 80-8 and
NLTT 11184) are actually separated by less
than 1000 arcsec (
![]() arcsec), so
I did not keep it in the next analysis.
arcsec), so
I did not keep it in the next analysis.
2.2 Rejected binary candidates
Table 1: Rejected wide binary candidatesa.
I classified the 30 WDS identified binaries with true angular
separations ![]() arcsec
into confirmed and unconfirmed physical
systems based on their basic properties in Table A.1.
First, I made a preliminary filtering by rejecting 12
binary candidates
whose membership in a physically bound system is impractical because of
their
different proper motions (
arcsec
into confirmed and unconfirmed physical
systems based on their basic properties in Table A.1.
First, I made a preliminary filtering by rejecting 12
binary candidates
whose membership in a physically bound system is impractical because of
their
different proper motions (![]() ), heliocentric distances (photometric
), heliocentric distances (photometric ![]() ,
spectroscopic
,
spectroscopic ![]() ,
or parallactic
,
or parallactic ![]() ),
and/or radial
velocities (
),
and/or radial
velocities (![]() ),
as summarised in Table 1.
),
as summarised in Table 1.
WDS 03442-6448.
The binary candidate formed byWDS 00435+3351, WDS 00520+2035, WDS 07590-6338, WDS 11125+3549, WDS 13599+2520, WDS 20302+2651, and WDS 23228+2208.
The components in the seven binary candidates have different proper motions. These differences range betweenWDS 00152+2454, WDS 00400-1533, WDS 01163-3217, and WDS 13410+6808.
The secondaries of the four binary candidates are fainter and bluer than their corresponding primaries. For example, secondary G 57-17 in Giclas' WDS 11452+1821 is2.3 Dedicated astro-photometric follow-up
Next, I performed an astro-photometric follow-up and investigated the possible physical bounding of the remaining 18 binary candidates. Of them, five have hypothetical primaries and secondaries with reliable published common proper motions and parallaxes from the Hipparcos catalogue. The hypothetical secondary in a sixth system, WDS 13090+3353, in contrast to the primary, does not have a Hipparcos measurement, but its proper motion is tabulated in the accurate Tycho-2 catalogue. In all six cases, the similarity between proper motions (and parallaxes) of primaries and secondaries indicate that they are probably bound wide systems (Sect. 2.4).
The other 12 binary candidates were the subject of a detailed
proper
motion
study. For each of them, I collected precise coordinates of
secondaries (and primaries, if not too bright) at different astrometric
epochs from SuperCOSMOS (Hambly et al. 2001)
digitisations of the Palomar Observatory Sky Survey (POSS-I Red,
POSS-II Red, POSS-II Blue, POSS-II Infrared) and the 2MASS and CMC14
(Carlsberg Meridian Catalogue; Evans et al. 2002)
catalogues. In a couple of cases, I was also able to use SDSS and Guide
Star Catalog data. With at least six astrometric epochs covering more
than 45 a, I could measure new proper motions
of 16
stars (12 secondaries, three primaries, one tertiary) with
unprecendented accuracy (
![]() %).
%).
I display the proper motions of the components in the 12
followed-up systems in Table 2.
Primaries and secondaries in nine of them have very different measured
proper motions (
![]() -90 mas a-1),
and are likely not to
form physically bound systems. There is accurate SDSS photometry for at
least one of them (WDS 11452+1821) that supports this
assumption
(the
-90 mas a-1),
and are likely not to
form physically bound systems. There is accurate SDSS photometry for at
least one of them (WDS 11452+1821) that supports this
assumption
(the ![]() magnitudes and
magnitudes and ![]() colours of the hypothetical primary and secondary are
colours of the hypothetical primary and secondary are ![]() and
and ![]() ,
and
,
and ![]() mag
and
mag
and ![]() mag,
respectively). There are only three discarded candidate systems,
WDS 10197+1928, WDS 11455+4740, and
WDS 18111+3241, with
the (incorrect) WDS note about binarity ``V''
(``proper motion or other technique indicates that this pair is
physical'').
mag,
respectively). There are only three discarded candidate systems,
WDS 10197+1928, WDS 11455+4740, and
WDS 18111+3241, with
the (incorrect) WDS note about binarity ``V''
(``proper motion or other technique indicates that this pair is
physical'').
The proper motions of the faint white dwarfs WD 0223-092 and
WD 0221-095 in
the WDS 02255-0904 system differ by about
14 mas a-1,
which translates
into a relative difference of about 17%. Given the relatively
low
absolute value of the proper motions (the same order of magnitude as
those of typical background thick disc and halo stars and white
dwarfs), the very large expected projected physical separation (
![]() pc
for a minimum heliocentric distance of d =
100 pc), and the low mass of the
objects (
pc
for a minimum heliocentric distance of d =
100 pc), and the low mass of the
objects (
![]() ),
asserting that the system may be gravitationally bound is rather
speculative.
),
asserting that the system may be gravitationally bound is rather
speculative.
Table 2: New proper motions of components in wide binary candidates.
Of the other two systems, the identical parallactic distances and
similar
proper motions and isochronal ages of binary star
HD 6101 AB and white dwarf
G 1-45 AB in system WDS 01024+0504 support a
true physical connection
(see below). However, HD 101 and LP 404-21 in system
WDS 00059+1805, although having similar proper motions, are not
physically connected.
WDS 00059+1805 is a hierarchical triple system at ![]() pc.
The non-tabulated system members are
HD 113 A and B (HIP 495),
which is
a K0+K0 binary (
pc.
The non-tabulated system members are
HD 113 A and B (HIP 495),
which is
a K0+K0 binary (![]() =
= ![]() arcsec,
arcsec, ![]() mag)
at about 9.4 arcmin to the south of the F8 primary
HD 101. The hypothetical fourth component, LP 404-21,
is 7.7 mag fainter in the Jband than the
primary. This magnitude difference would imply that LP 404-21
is an M5-6 dwarf with a colour
mag)
at about 9.4 arcmin to the south of the F8 primary
HD 101. The hypothetical fourth component, LP 404-21,
is 7.7 mag fainter in the Jband than the
primary. This magnitude difference would imply that LP 404-21
is an M5-6 dwarf with a colour ![]() mag
if it were located at the same heliocentric distance to HD 101
(assuming a typical age of 0.5-5 Ga). However, its actual V-J
colour is only about 2.5 mag and LP 404-21 is thus
a late-K- or early-M-type dwarf or subdwarf at a larger heliocentric
distance.
Lépine & Bongiorno (2007)
also suggest its subdwarf nature.
mag
if it were located at the same heliocentric distance to HD 101
(assuming a typical age of 0.5-5 Ga). However, its actual V-J
colour is only about 2.5 mag and LP 404-21 is thus
a late-K- or early-M-type dwarf or subdwarf at a larger heliocentric
distance.
Lépine & Bongiorno (2007)
also suggest its subdwarf nature.
2.4 Probable bound systems
From previous section, only seven systems remain (six with reliable common proper motions from Hipparcos or Tycho-2 catalogues, plus the HD 6101 AB + G 1-45 AB system) with a high probability of being physically connected, as discussed in detail just below.
2.4.1 WDS 01024+0504 (HD 6101 AB and G 1-45 AB)
This is a hierarchical quadruple system. HD 6101 AB
is a relatively bright (V = 8.16 mag) close
binary star of
combined spectral type K3V and low activity (
![]() ;
Gray
et al. 2003). It was
first resolved by the Hipparcos mission (
;
Gray
et al. 2003). It was
first resolved by the Hipparcos mission (
![]() arcsec,
arcsec,
![]() mag).
Afterwards, it has been astrometrically followed up by several authors
(Mason
et al. 1999; Balega
et al. 2002, 2004, 2007; Richichi
et al. 2007). Using
mostly speckle interferometric observations, Balega et al. (2006)
present new orbital parameters for HD 6101 AB, from
where they derive a
period
mag).
Afterwards, it has been astrometrically followed up by several authors
(Mason
et al. 1999; Balega
et al. 2002, 2004, 2007; Richichi
et al. 2007). Using
mostly speckle interferometric observations, Balega et al. (2006)
present new orbital parameters for HD 6101 AB, from
where they derive a
period ![]() a,
a semi-major axis
a,
a semi-major axis ![]() AU,
and a
total mass
AU,
and a
total mass ![]() .
Accounting for the magnitude difference in the optical (
.
Accounting for the magnitude difference in the optical (
![]() 1.7 mag), the Siess
et al. (2000) grid of tracks for low- and intermediate-mass
stars of 1-5 Ga and the Balega et al. (2006) total
mass, one may derive that the secondary must have a spectral type
between K7V and M2V.
1.7 mag), the Siess
et al. (2000) grid of tracks for low- and intermediate-mass
stars of 1-5 Ga and the Balega et al. (2006) total
mass, one may derive that the secondary must have a spectral type
between K7V and M2V.
At 1276 arcsec to the east of HD 6101 AB, it
is located the binary white dwarf
G 1-45 AB (WD 0101+048). It was discovered
in the Lowell proper motion survey of Giclas et al. (1959), who
assigned it a DAs spectral type (currently, it is determined at DA5).
Because of its relative brightness (V =
14.10 mag), G 1-45 AB has been
investigated and catalogued on numerous occasions (Shipman 1979; Green
et al. 1986; Liebert
et al. 1988; McCook
& Sion 1999; Bergeron
et al. 2001; Zuckerman
et al. 2003; Farihi
et al. 2005;
Mullally et al. 2007).
The white dwarf is a double degenerate, as it shows radial velocity
variations
with an uncertain period of 0.7-6.5 d (Saffer et al. 1998; Maxted
et al. 2000). The
spectroscopic (total) mass of 0.77 ![]() provided by Lajoie & Bergeron
(2007) is
consistent with the parallactic distance of G 1-45 AB
measured by van Altena et al. (1995) and of
HD 6101 AB measured by Hipparcos
(however, many papers list photometric distances at about
13.5 pc, which do not fit white dwarf
theoretical models).
provided by Lajoie & Bergeron
(2007) is
consistent with the parallactic distance of G 1-45 AB
measured by van Altena et al. (1995) and of
HD 6101 AB measured by Hipparcos
(however, many papers list photometric distances at about
13.5 pc, which do not fit white dwarf
theoretical models).
Proper motions of both binary objects differ by only ![]() mas a-1(Sect. 2.3).
Because of the similarity in parallactic distance and proper motion,
the WDS note ``V'' about the wide binarity of
HD 6101 AB and
G 1-45 AB (``[...] this pair is physical'') may be
correct.
mas a-1(Sect. 2.3).
Because of the similarity in parallactic distance and proper motion,
the WDS note ``V'' about the wide binarity of
HD 6101 AB and
G 1-45 AB (``[...] this pair is physical'') may be
correct.
2.4.2 WDS 13090+3353 (LP 268-35 and LP 268-33)
The system LEP 62AC is proposed by Lépine & Bongiorno (2007).
It is, therefore, one of the very wide binary candidates in this work
that have
been identified more recently. It is also the faintest system in this
section (only the primary is listed in
the Hipparcos catalogue).
As a result, both stars have been poorly investigated. The most
remarkable fact in the literature is that Ryan (1992) classified
the
primary, LP 268-35, as a normal dwarf based on UBVRI
photometry (i.e., it is
not a subdwarf of the Galactic halo). Previously, it had been proposed
in one of the Luyten proper motion catalogues
that the primary forms a closer pair with a star located at about
3 arcmin to
the southwest (LP 268-34).
The USNO-B1 proper motion of this hypothetical companion,
``WDS 13090+3353 B'',
is (
![]() ,
,
![]() )
)
![]() (-218,
-38) mas a-1, consistent with
an accurate measurement by Lépine &
Shara (2005),
but different from those of LP 268-35 and LP 268-33
by more than 70 mas a-1 (i.e.,
LP 268-34 is not part of the proper motion
system).
(-218,
-38) mas a-1, consistent with
an accurate measurement by Lépine &
Shara (2005),
but different from those of LP 268-35 and LP 268-33
by more than 70 mas a-1 (i.e.,
LP 268-34 is not part of the proper motion
system).
In Table 3,
I compile SDSS and 2MASS photometry of both
LP 268-35 and LP 268-33. There is good agreement
between the observed magnitudes and those expected for
K7-M1V and M4-5V stars at the Hipparcos distance
of the primary, ![]() pc.
For the comparison, I used the colours and absolute magnitudes
as functions
of late spectral type as tabulated by Bochanski et al. (2007), West
et al. (2008), and
Caballero et al. (2008).
While the fit of the colours from
pc.
For the comparison, I used the colours and absolute magnitudes
as functions
of late spectral type as tabulated by Bochanski et al. (2007), West
et al. (2008), and
Caballero et al. (2008).
While the fit of the colours from ![]() -band
magnitudes of LP 268-33 to an M4.5
-band
magnitudes of LP 268-33 to an M4.5 ![]() 0.5V
template is excellent, the dwarf displays an obvious blueing in the u
and g bands. This is not unforeseen, since
roughly 50% of M4-5V stars display activity,
which is associated to an excess of flux in the blue optical (West
et al. 2008).
Activity lifetimes of M4-5V stars vary between 4.0 and 7.5 Ga,
which may be understood as an upper (conservative) limit for the age of
LP 268-33.
0.5V
template is excellent, the dwarf displays an obvious blueing in the u
and g bands. This is not unforeseen, since
roughly 50% of M4-5V stars display activity,
which is associated to an excess of flux in the blue optical (West
et al. 2008).
Activity lifetimes of M4-5V stars vary between 4.0 and 7.5 Ga,
which may be understood as an upper (conservative) limit for the age of
LP 268-33.
The difference in proper motion between LP 268-35 and
LP 268-33, (
![]() ,
,
![]() )
=
)
= ![]() ,
,
![]() ) mas/a,
is null within 1-2
) mas/a,
is null within 1-2![]() .
Given the resemblance between proper motions and parallactic and
photometric
distances of the two of them, I will assume that they travel
togetherthrough
the Galaxy. No radial velocity measurements exist for the two dwarfs,
from where one could confirm the common space velocity or identify
membership in a young moving group.
.
Given the resemblance between proper motions and parallactic and
photometric
distances of the two of them, I will assume that they travel
togetherthrough
the Galaxy. No radial velocity measurements exist for the two dwarfs,
from where one could confirm the common space velocity or identify
membership in a young moving group.
Using the 2MASS J-band magnitudes in Table 3, the
hypothetical common distance ![]() pc,
a solar age, and the
theoretical models of Baraffe et al. (1998),
I derive masses
pc,
a solar age, and the
theoretical models of Baraffe et al. (1998),
I derive masses ![]() and
and ![]() for LP 268-35 and LP 268-33 (at late spectral types,
the near-infrared J band works better for
comparison with the Lyon theoretical models than optical ones -
e.g. V).
for LP 268-35 and LP 268-33 (at late spectral types,
the near-infrared J band works better for
comparison with the Lyon theoretical models than optical ones -
e.g. V).
Table 3: Photometry of system WDS 13090+3353.
2.4.3
WDS 14396-6050 ( Cen AB
and Proxima)
Cen AB
and Proxima)
The ![]() Cen
system has been the subject of intensive and extensive studies
in the literature (Gasteyer 1966; Kamper
& Wesselink 1978; Matthews
& Gilmore 1993; Wertheimer
& Laughlin 2006).
As already mentioned in Sect. 1,
Anosova & Orlov (1991)
proposed that
Cen
system has been the subject of intensive and extensive studies
in the literature (Gasteyer 1966; Kamper
& Wesselink 1978; Matthews
& Gilmore 1993; Wertheimer
& Laughlin 2006).
As already mentioned in Sect. 1,
Anosova & Orlov (1991)
proposed that ![]() Cen AB
and Proxima are stars in the ``moving group
of
Cen AB
and Proxima are stars in the ``moving group
of ![]() Cen''.
The other stars in the moving group would be the binary
HD 21209 AB
(K3.5V + K8Vk:) and the triple system V1089 Her and
V1090 Her AB (K5.0V + [K5.0V + M1.0V]; Reid
et al. 2004). Anosova
et al. (1994) went on
the discussion
Cen''.
The other stars in the moving group would be the binary
HD 21209 AB
(K3.5V + K8Vk:) and the triple system V1089 Her and
V1090 Her AB (K5.0V + [K5.0V + M1.0V]; Reid
et al. 2004). Anosova
et al. (1994) went on
the discussion![]() ,
and enlarged the list of ``satellites of
,
and enlarged the list of ``satellites of ![]() Cen''.
However, in spite of the chromospheric activity of Proxima (with flares
and
strong Mg II h+k
Cen''.
However, in spite of the chromospheric activity of Proxima (with flares
and
strong Mg II h+k ![]() 280 nm
in emission), the
280 nm
in emission), the ![]() Cen
triple
system is accepted to be relatively old, with an age at about
5-6 Ga. Since I do not present new data that help
answering the original question in
Voûte (1917),
that if ``they [
Cen
triple
system is accepted to be relatively old, with an age at about
5-6 Ga. Since I do not present new data that help
answering the original question in
Voûte (1917),
that if ``they [![]() Cen AB
and Proxima] are physically
connected or members of the same drift'', I follow Ludwig
Wittgenstein's
proposition of ``passing over in silence'' and will follow the general
agreement that they are gravitationally bound.
Cen AB
and Proxima] are physically
connected or members of the same drift'', I follow Ludwig
Wittgenstein's
proposition of ``passing over in silence'' and will follow the general
agreement that they are gravitationally bound.
The masses compiled by Wertheimer & Laughlin (2006) for ![]() Cen AB
and Proxima were
Cen AB
and Proxima were ![]() (combined) and
(combined) and ![]() ,
respectively.
,
respectively.
2.4.4 WDS 15208+3129 (HD 136654 and BD+32 2572)
This system, formed by an F5V and a K0V star, was also proposed by
Lépine &
Bongiorno (2007).
However, in contrast to system WDS 13090+3353, there exist Hipparcos
parallax measurements for both HD 136654 and
BD+32 2572.
From the new data reduction by van Leeuween (2007), the
differences between proper motions and parallactic distances are (
![]() ,
,
![]() ,
,
![]() ) mas/a and
) mas/a and ![]() pc.
The difference between radial velocities is also very small and
probably not significant:
pc.
The difference between radial velocities is also very small and
probably not significant: ![]() km s-1
(Montes et al. 2001;
Nordström et al. 2004).
As a result, they seem to form a real common proper
motion pair.
km s-1
(Montes et al. 2001;
Nordström et al. 2004).
As a result, they seem to form a real common proper
motion pair.
The primary in the system, HD 136654, is a single (Mason
et al. 2001),
non-variable (McMillan et al. 1976), high
metallicity (Fischer & Valenti 2005; Robinson
et al. 2006) star. The
secondary, BD+32 2572, has not been investigated so well:
Strassmeier et al. (2000)
found Ca II H+K in emission
and Violat-Bordonau & Violat-Martín (2006) measured a
low amplitude of photometric variability (
![]() mag)
with a period near 9.24 d. However, the most important fact is
that BD+32 2572 is a probable member in the Hyades
Supercluster (``Kapteyn's stream I''; Montes
et al. 2001),
which
automatically puts HD 136654 in as well. Indeed, the
HD 136654 high metallicity and space velocities from Nordström
et al. (2004)
and Karatas et al. (2004) agree
well with such a membership
and, thus, an Hyades-like age.
At
mag)
with a period near 9.24 d. However, the most important fact is
that BD+32 2572 is a probable member in the Hyades
Supercluster (``Kapteyn's stream I''; Montes
et al. 2001),
which
automatically puts HD 136654 in as well. Indeed, the
HD 136654 high metallicity and space velocities from Nordström
et al. (2004)
and Karatas et al. (2004) agree
well with such a membership
and, thus, an Hyades-like age.
At ![]() Ma, theoretical
masses of HD 136654 and BD+32 2572 are
Ma, theoretical
masses of HD 136654 and BD+32 2572 are
![]() -1.3
-1.3 ![]() and
and ![]() -1.0
-1.0 ![]() (Baraffe et al. 1998;
Siess et al. 2000).
(Baraffe et al. 1998;
Siess et al. 2000).
2.4.5 WDS
20124-1237 (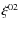 Cap
and LP 754-50)
Cap
and LP 754-50)
The primary star, ![]() Cap,
is a single (McAlister et al. 1987;
Lagrange et al. 2009), F7V-type
star that has been subject of numerous analyses.
Some basic stellar parameters are
Cap,
is a single (McAlister et al. 1987;
Lagrange et al. 2009), F7V-type
star that has been subject of numerous analyses.
Some basic stellar parameters are ![]() K,
[Fe/H]
K,
[Fe/H] ![]() -0.27,
-0.27, ![]() 1.10
1.10 ![]() ,
,
![]() ,
,
![]() Ga (Chen
et al. 2001; Lambert
& Reddy 2004). Its solar
age is consistent with a relatively large modulus of vertical
heliocentric space velocity component, W =
-42 km s-1 (Nordström
et al. 2004).
Ga (Chen
et al. 2001; Lambert
& Reddy 2004). Its solar
age is consistent with a relatively large modulus of vertical
heliocentric space velocity component, W =
-42 km s-1 (Nordström
et al. 2004).
Table 4: Probable bound wide systems.
The secondary star, LP 754-50, has been referred to a few
times in the
literature. It is a Luyten star whose astrometry was improved by Salim
& Gould (2003)
and
whose spectral type was determined at M0Vk by Gray et al. (2006).
The latter authors also measured ![]() ,
which is at the
active-inactive boundary (but with redder B-V
colour).
The star was tabulated in the Hipparcos
catalogue.
Its parallactic distance in the new reduction by van Leeuwen (2007),
,
which is at the
active-inactive boundary (but with redder B-V
colour).
The star was tabulated in the Hipparcos
catalogue.
Its parallactic distance in the new reduction by van Leeuwen (2007), ![]() pc,
differs from the one in the original catalogue by Perryman
et al. (1997),
pc,
differs from the one in the original catalogue by Perryman
et al. (1997),
![]() pc, and from those
of
pc, and from those
of ![]() Cap
(
Cap
(
![]() and
and ![]() pc, respectively).
In general, the new reduction by van Leeuwen (2007) provided
better accuracy,
by up to a factor four, than in the original Hipparcos
catalogue.
However, it was not infallible. For example, Caballero & Dinis (2008) show some
stars whose astrometric
solution got worse with the new reduction.
If LP 754-50 were located at the distance to
pc, respectively).
In general, the new reduction by van Leeuwen (2007) provided
better accuracy,
by up to a factor four, than in the original Hipparcos
catalogue.
However, it was not infallible. For example, Caballero & Dinis (2008) show some
stars whose astrometric
solution got worse with the new reduction.
If LP 754-50 were located at the distance to ![]() Cap,
it would have an
absolute J-band magnitude
Cap,
it would have an
absolute J-band magnitude ![]() mag,
which translates into a theoretical mass
mag,
which translates into a theoretical mass ![]() and an effective
temperature typical of an early M dwarf of solar age (Baraffe
et al. 1998).
Using the original Hipparcos astrometry
(parallaxes, proper motions),
there are grounds for considering WDS 20124-1237 a physical
pair.
and an effective
temperature typical of an early M dwarf of solar age (Baraffe
et al. 1998).
Using the original Hipparcos astrometry
(parallaxes, proper motions),
there are grounds for considering WDS 20124-1237 a physical
pair.
2.4.6 WDS 20452-3120 (AU Mic and AT Mic AB)
It is a late-type, hierarchical triple system in the very young ![]() Pictoris
moving group (
Pictoris
moving group (
![]() Ma).
The secondary, AT Mic AB, is a binary resolved by Hipparcos
(
Ma).
The secondary, AT Mic AB, is a binary resolved by Hipparcos
(
![]() arcsec,
arcsec,
![]() mag).
Numerous investigations and reviews have targeted the three
stars, which
are among the youngest pre-main sequence stars in the solar
neighbourhood.
They display X-ray emission, flaring activity, flux excess in the
infrared
due to a circumstellar disc (AU Mic), photometric variability
(of BY Dra type),
active coronae, Ca II H+K in
emission, and other properties typical of
young stars (Linsky et al. 1982; Kundu
et al. 1987;
Pallavicini et al. 1990; Batalha
et al.
1996; Barrado y
Navascués et al. 1999; Katsova
et al. 1999; Zuckerman
et al. 2001;
Kalas et al. 2004).
There is a difference between Hipparcos
heliocentric distances of
mag).
Numerous investigations and reviews have targeted the three
stars, which
are among the youngest pre-main sequence stars in the solar
neighbourhood.
They display X-ray emission, flaring activity, flux excess in the
infrared
due to a circumstellar disc (AU Mic), photometric variability
(of BY Dra type),
active coronae, Ca II H+K in
emission, and other properties typical of
young stars (Linsky et al. 1982; Kundu
et al. 1987;
Pallavicini et al. 1990; Batalha
et al.
1996; Barrado y
Navascués et al. 1999; Katsova
et al. 1999; Zuckerman
et al. 2001;
Kalas et al. 2004).
There is a difference between Hipparcos
heliocentric distances of
![]() pc, which could be
real (as in the case of
pc, which could be
real (as in the case of ![]() Cen AB
and
Proxima) or stem from a poor accuracy in the parallax measurement (e.g.
as in
the case of WDS 13090+3353 and WDS 20124-1237).
Cen AB
and
Proxima) or stem from a poor accuracy in the parallax measurement (e.g.
as in
the case of WDS 13090+3353 and WDS 20124-1237).
Using the parallactic distances by van Leeuwen (2007), the 2MASS
![]() -band
magnitudes, an estimated age
-band
magnitudes, an estimated age ![]() Ma,
and the
NextGen models from Baraffe et al. (1998), and
assuming that the difference of
magnitudes in the near infrared between AT Mic A and
AT Mic B are
Ma,
and the
NextGen models from Baraffe et al. (1998), and
assuming that the difference of
magnitudes in the near infrared between AT Mic A and
AT Mic B are ![]() ,
I derive masses of
,
I derive masses of ![]() ,
0.27
+0.04-0.09,
and 0.25
,
0.27
+0.04-0.09,
and 0.25
![]() for AU Mic (M1Ve),
AT Mic A (M4.5Ve), and AT Mic B
(M5:).
for AU Mic (M1Ve),
AT Mic A (M4.5Ve), and AT Mic B
(M5:).
Although the stars in the ![]() Pictoris
moving group are spread over a
space region with a size of only about 74 pc (Ortega
et al. 2002), the
short separation between AU Mic and
AT Mic AB (projected physical separation
Pictoris
moving group are spread over a
space region with a size of only about 74 pc (Ortega
et al. 2002), the
short separation between AU Mic and
AT Mic AB (projected physical separation ![]() pc)
is remarkable and may indicate a common origin within the
birthplace.
pc)
is remarkable and may indicate a common origin within the
birthplace.
2.4.7 WDS 20599+4016 (HD 200077 AE-D and G 210-44 AB)
It is a hierarchical quintuple system of complicated
nomenclature
and structure. On the one hand, HD 200077 is a triple star of
combined F8V spectral type. In the year 1908, Burnham proposed
that two stars of ![]() mag
at
mag
at ![]() -3 arcmin to the
southeast and southwest of HD 200077, labelled ``B'' and
``C'', were common proper motion companions.
They are, however, background stars of lower proper motion.
Almost a century later, the Hipparcos mission
resolved HD 200077 into a
close binary with
-3 arcmin to the
southeast and southwest of HD 200077, labelled ``B'' and
``C'', were common proper motion companions.
They are, however, background stars of lower proper motion.
Almost a century later, the Hipparcos mission
resolved HD 200077 into a
close binary with ![]() arcsec,
arcsec,
![]() mag;
the faintest component receives the label ``D''.
The brightest one is, in its turn, a double-lined spectroscopic binary
discovered by Latham et al. (1988) and
confirmed by Goldberg et al. (2002); the
low-mass spectroscopic companion is labelled ``E''.
Mazeh et al. (2003) tabulated
mag;
the faintest component receives the label ``D''.
The brightest one is, in its turn, a double-lined spectroscopic binary
discovered by Latham et al. (1988) and
confirmed by Goldberg et al. (2002); the
low-mass spectroscopic companion is labelled ``E''.
Mazeh et al. (2003) tabulated
![]() d,
d,
![]() ,
and [Fe/H]
,
and [Fe/H]
![]() .
These authors used the estimated mass
.
These authors used the estimated mass ![]() 0.84
0.84 ![]() for
the primary from Carney et al. (1994), which is inconsistent
with the F8V
spectral type and several effective temperature determinations of
components A
and E (e.g. Goldberg et al. 2002). These
determinations favour masses
for
the primary from Carney et al. (1994), which is inconsistent
with the F8V
spectral type and several effective temperature determinations of
components A
and E (e.g. Goldberg et al. 2002). These
determinations favour masses ![]() and
and ![]() 0.9-1.0
0.9-1.0 ![]() (and spectral types G1V and G6-9V, respectively). The component D,
given its magnitude difference with respect to AE, may be
a late K-type dwarf with a mass
(and spectral types G1V and G6-9V, respectively). The component D,
given its magnitude difference with respect to AE, may be
a late K-type dwarf with a mass ![]() .
The triple system as a whole does not display X-ray activity (Ottmann
et al. 1997).
.
The triple system as a whole does not display X-ray activity (Ottmann
et al. 1997).
On the other hand, G 210-44 AB, of combined spectral
type M1V, is another close
binary first resolved by Hipparcos (
![]() arcsec,
arcsec,
![]() mag
- see also Balega et al. 2004, 2007). Using
the theoretical models of Baraffe et al. (1998),
G 210-44 AB matches the
scenario of an 0.65
mag
- see also Balega et al. 2004, 2007). Using
the theoretical models of Baraffe et al. (1998),
G 210-44 AB matches the
scenario of an 0.65 ![]() - and an 0.55
- and an 0.55 ![]() -mass pair
at
-mass pair
at ![]() pc
moving in the same direction as HD 200077 AE-D.
pc
moving in the same direction as HD 200077 AE-D.
3 Discussion
3.1 The 0.1 pc ``cutoff'', young moving groups, orbital periods, and missing binaries
Parallax, proper motion, and photometry measurements are all consistent
with
the seven systems being physical pairs. Six of them have projected
physical separations s > 0.1 pc
(
![]() AU; fourth column in
Table 4).
The exception is the
AU; fourth column in
Table 4).
The exception is the ![]() Cen
system.
Even accounting for the different heliocentric distances, the true
physical
separation between
Cen
system.
Even accounting for the different heliocentric distances, the true
physical
separation between ![]() Cen AB
and Proxima,
Cen AB
and Proxima, ![]() pc
(r >
s), is shorter than the tenth of a parsec. However,
the existence of six systems with s
> 0.1 pc, if really bound, shows
that there are deviations to the hypothetical cutoff in binary
frequency at this value, as proposed originally by Bahcall &
Soneira (1981)
and Retterer & King (1982).
pc
(r >
s), is shorter than the tenth of a parsec. However,
the existence of six systems with s
> 0.1 pc, if really bound, shows
that there are deviations to the hypothetical cutoff in binary
frequency at this value, as proposed originally by Bahcall &
Soneira (1981)
and Retterer & King (1982).
The widest systems are WDS 13090+3353 (LP 268-35; ![]() pc)
and
WDS 15208+3129 (HD 136654;
pc)
and
WDS 15208+3129 (HD 136654; ![]() pc),
which is a probable
member in the Hyades Supercluster (
pc),
which is a probable
member in the Hyades Supercluster (
![]() Ma).
Systems WDS 20599+4016 (HD 200077) and
AU Mic in the
Ma).
Systems WDS 20599+4016 (HD 200077) and
AU Mic in the ![]() Pictoris
group
(
Pictoris
group
(
![]() Ma) also have
projected physical separations larger than
0.2 pc. Three of the latter four systems were first proposed
by Lépine & Bongiorno (2007)
as faint companions of Hipparcos stars.
This is an indication of how much we still must learn of wide binarity
in the
solar neighbourhood.
Ma) also have
projected physical separations larger than
0.2 pc. Three of the latter four systems were first proposed
by Lépine & Bongiorno (2007)
as faint companions of Hipparcos stars.
This is an indication of how much we still must learn of wide binarity
in the
solar neighbourhood.
Remarkably, two of the seven systems belong to young kinematic groups
(HD 136654 and AU Mic). This agrees with the simple
idea that young wide binary systems have
had less time to be perturbed and disrupted by Galactic material of all
types.
However, a few of the remaining systems have relatively well-determined
ages at
about the Solar value, such as WDS 01024+0504
(HD 6101, which has a relatively
cool binary white dwarf companion that had to leave the main sequence
several
108 a ago), ![]() Cen, and WDS
20124-1237 (
Cen, and WDS
20124-1237 (![]() Cap).
The absence of X-ray emission from HD 200077 probably
indicates that its system is older than 1 Ga as well.
It only leaves the LP 268-35 system (the widest one) as a
suitable target for
investigating its membership in a young kinematic group.
Cap).
The absence of X-ray emission from HD 200077 probably
indicates that its system is older than 1 Ga as well.
It only leaves the LP 268-35 system (the widest one) as a
suitable target for
investigating its membership in a young kinematic group.
The minimum orbital periods P*
(Table 4)
range
between less than 1 Ma for ![]() Cen and
24 Ma for LP 268-35.
I computed P* using
the Kepler's Third Law and the projected physical
separation between components in system, s,
assuming that they are located at
the distance of the primary (i.e. s instead of r
or a). With an age not older than
Cen and
24 Ma for LP 268-35.
I computed P* using
the Kepler's Third Law and the projected physical
separation between components in system, s,
assuming that they are located at
the distance of the primary (i.e. s instead of r
or a). With an age not older than ![]() Ma,
the AU Mic system in the
Ma,
the AU Mic system in the
![]() Pictoris
moving group has only completed at most two orbital periods
since its formation. However, although it is also young and has a long
orbital period of about 12 Ma, the HD 136654 system
in the
Hyades Supercluster (
Pictoris
moving group has only completed at most two orbital periods
since its formation. However, although it is also young and has a long
orbital period of about 12 Ma, the HD 136654 system
in the
Hyades Supercluster (
![]() Ma)
has revolved roughly 50 times about a common centre of mass.
The
rest of the wide systems have had enough time to complete several
hundred orbits.
Ma)
has revolved roughly 50 times about a common centre of mass.
The
rest of the wide systems have had enough time to complete several
hundred orbits.
There can be missing binaries in the WDS catalogue with angular
separations ![]() arcsec
but projected physical separations s >
105 AU
(i.e. at larger heliocentric distances than the systems studied here
and, therefore, more difficult to follow up in general) or even not
listed in
the WDS catalogue. For example, the system Fomalhaut +
TW PsA in the young Castor moving group was proposed
by
Gliese (1969) and does
not appear in the catalogue
as a possible wide binary (
arcsec
but projected physical separations s >
105 AU
(i.e. at larger heliocentric distances than the systems studied here
and, therefore, more difficult to follow up in general) or even not
listed in
the WDS catalogue. For example, the system Fomalhaut +
TW PsA in the young Castor moving group was proposed
by
Gliese (1969) and does
not appear in the catalogue
as a possible wide binary (
![]() arcsec,
arcsec, ![]() pc,
pc,
![]() mas a-1).
The halo system HD 149414 (Sect. 1) is
neither in the WDS.
The search for such missing wide binaries will be carried out in
another work.
mas a-1).
The halo system HD 149414 (Sect. 1) is
neither in the WDS.
The search for such missing wide binaries will be carried out in
another work.
3.2 A comparison of binding energies
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12596fig2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12596-09/Timg218.png)
|
Figure 2:
Binding energy-total mass diagram.
Open (blue) circles with error bars are for the seven systems in
Sect. 2.4
and (red) crosses are for the ensemble of
systems with very low-mass components presented in the text.
The dotted line indicates a boundary for the selection of multiple
systems
in the solar neighbourhood with at least one low-mass component (
|
| Open with DEXTER | |
Table
5:
Multiple systems in the solar neighbourhood with at least one low-mass
component (
![]() )
and the lowest binding energies for their total masses.
)
and the lowest binding energies for their total masses.
Wide binarity is synonymous with multiplicity of systems with very low
(absolute values of) gravitational potential energies, Ug
= -G M1 M2
/ r. In the last column of Table 4,
I show the gravitational potential (binding) energy, Ug*,
using ![]() (except for
(except for ![]() Cen),
and the corresponding combined masses (e.g. at a large
separation, Proxima feels the gravitational attraction of
Cen),
and the corresponding combined masses (e.g. at a large
separation, Proxima feels the gravitational attraction of ![]() Cen AB
as if it were a single, more massive star). The asterisk in Ug*
indicates that the absolute values of the ``true'' potential energies Ug
using the physical separation r must be
lower than in
Table 4.
Cen AB
as if it were a single, more massive star). The asterisk in Ug*
indicates that the absolute values of the ``true'' potential energies Ug
using the physical separation r must be
lower than in
Table 4.
In Fig. 2, I show a -Ug* vs. M1 + M2 diagram for the seven systems in Sect. 2.4 (circles) and a collection of 399 multiple systems including mostly:
- the Sun and the four giant planets in the Solar System (Jupiter, Saturn, Uranus, and Neptune);
- transit and radial-velocity exoplanets and candidates from the Extrasolar Planet Encyclopaedia;
- ``classic'' late-M-type binaries of the Solar neighbourhood with mass ratios q > 0.5, such us EZ Aqr AB, EI Cnc AB, QY Aur AB, and GJ 1005 AB;
- field late-M-, L-, and T-type binaries in systems with q > 0.5 (e.g. Lane et al. 2001; Bouy et al. 2003; Siegler et al. 2005; Forveille et al. 2005; Burgasser & McElwain 2006; Caballero 2007a - see also Bouy et al. 2005 and Burgasser et al. 2007 for compilations);
- ``classic'' systems in the Solar neighbourhood with late-M-type companions and q < 0.5, such us V1054 Oph + GJ 643 + vB 8, GX And + GQ And, EQ Peg AB, V1428 Aql + vB 10, and o2 Eri AC;
- field stellar systems with late-M-, L-, and T-type companions and q < 0.5 (e.g. Rebolo et al. 1998; Goldman et al. 1999; Burgasser et al. 2000; Kirkpatrick et al. 2001; Gizis et al. 2001; Scholz et al. 2003; Seifahrt et al. 2005).
The seven systems in Sect. 2.4
are among the
multiple systems in the solar neighbourhood with the lowest binding
energies for their total masses. Of the collection of
399 multiple
systems, only eight (not counting ![]() Cen) have comparably
low values of |Ug*|(Table 5; they
are the systems below the dotted line in Fig. 2). Two
of them are not resolved multiple stellar systems, but planetary
systems: the Sun and Uranus, and the Sun and Neptune.
Cen) have comparably
low values of |Ug*|(Table 5; they
are the systems below the dotted line in Fig. 2). Two
of them are not resolved multiple stellar systems, but planetary
systems: the Sun and Uranus, and the Sun and Neptune.
The brown dwarf-exoplanet pair 2M1207-39 AB (Chauvin
et al. 2004,
2005), because
of its high mass ratio (
![]() )
and young age (
)
and young age (
![]() Ma; it is a member
of the TW Hydrae Association) if compared to
those of the rest of exoplanetary systems, resembles a recently-born,
low-mass, substellar binary more than an exo-planetary system (Chauvin,
priv. comm.). Other similar systems, some of them with wider
projected physical separations
but without common proper-motion confirmation, have also been
discovered in the
Orion OB1 association (Caballero et al. 2006; Barrado y
Navascués et al. 2007),
Upper Scorpius (Kraus & Hillenbrand 2007; Béjar
et al. 2008), and
highly extinguished star-forming regions in the Southern Hemisphere,
such as Chamaeleon and Lupus (López Martí et al. 2004, 2005; Luhman 2004).
Ma; it is a member
of the TW Hydrae Association) if compared to
those of the rest of exoplanetary systems, resembles a recently-born,
low-mass, substellar binary more than an exo-planetary system (Chauvin,
priv. comm.). Other similar systems, some of them with wider
projected physical separations
but without common proper-motion confirmation, have also been
discovered in the
Orion OB1 association (Caballero et al. 2006; Barrado y
Navascués et al. 2007),
Upper Scorpius (Kraus & Hillenbrand 2007; Béjar
et al. 2008), and
highly extinguished star-forming regions in the Southern Hemisphere,
such as Chamaeleon and Lupus (López Martí et al. 2004, 2005; Luhman 2004).
Five proper-motion-confirmed, low binding-energy systems remain, of
which three
have total masses ![]() .
They are the only representatives of the rare class of very wide
(s > 1000 AU), very low-mass (
.
They are the only representatives of the rare class of very wide
(s > 1000 AU), very low-mass (
![]() ),
equal-mass (
),
equal-mass (![]() )
binaries: Koenigstuhl 1, 2M0126-50, and 2M1258+40. The other
two systems with total masses
)
binaries: Koenigstuhl 1, 2M0126-50, and 2M1258+40. The other
two systems with total masses ![]() have
L-type companions at 3600 (
have
L-type companions at 3600 (![]() CrB) and 11 900 AU
(Koenigstuhl 3) to bright stars.
CrB) and 11 900 AU
(Koenigstuhl 3) to bright stars.
Because of the relatively high value of |Ug*|,
typical of binaries in
the solar neighbourhood, the quintuple system HD 200077 in
Table 4
is likely bound. The same can be applied to HD 6101, ![]() Cen,
HD 136654, and
Cen,
HD 136654, and ![]() Cap,
with values
Cap,
with values ![]() J.
However, both LP 268-35 and AU Mic systems have very
low absolute values
of potential energy, similar to those of the most weakly bound known
binaries, which are the Chauvin et al. (2004)
substellar pair and the three binaries of very low-mass stars or brown
dwarfs separated by more than
1000 AU. LP 268-35 and AU Mic, with
projected physical
separations between two and three orders of magnitude larger, must be
very fragile and will be soon
torn apart by third bodies, if they are not already in the process of
disruption.
J.
However, both LP 268-35 and AU Mic systems have very
low absolute values
of potential energy, similar to those of the most weakly bound known
binaries, which are the Chauvin et al. (2004)
substellar pair and the three binaries of very low-mass stars or brown
dwarfs separated by more than
1000 AU. LP 268-35 and AU Mic, with
projected physical
separations between two and three orders of magnitude larger, must be
very fragile and will be soon
torn apart by third bodies, if they are not already in the process of
disruption.
4 Summary
Of the 104 312 pairs in the Washington Double Star Catalog (as
in
2009 May), I selected for follow-up the 36 pairs with
tabulated angular
separations ![]() arcsec.
Of them, I was not able to identify five, and a sixth pair had
an
actual angular separation under 1000 arcsec.
I rejected 12 of the remaining 30 pairs as binary
candidates
based on discordant published proper motions, heliocentric distances,
and radial velocities. After a careful astro-photometric examination,
with several astrometric epochs covering at least 45 a and
proper-motion accuracies of 0.4-1.9 mas a-1,
only seven of the other 18 systems remained as probable bound
systems. They were:
arcsec.
Of them, I was not able to identify five, and a sixth pair had
an
actual angular separation under 1000 arcsec.
I rejected 12 of the remaining 30 pairs as binary
candidates
based on discordant published proper motions, heliocentric distances,
and radial velocities. After a careful astro-photometric examination,
with several astrometric epochs covering at least 45 a and
proper-motion accuracies of 0.4-1.9 mas a-1,
only seven of the other 18 systems remained as probable bound
systems. They were:
- WDS 01024+0504: a quadruple system containing HD 6101 AB, a K3V close binary, and G 1-45 AB, a spectroscopic white dwarf binary.
- WDS 13090+3353: LP 268-35 and LP 268-33, two poorly-know, late-type dwarfs separated by about 84 000 AU. It is the widest (and most fragile) system in my sample. The hypothetical secondary displays flux excess in the blue optical (SDSS u and g) that can be ascribed to activity.
- WDS 14396-6050: the celebrated system
 Cen AB
and Proxima.
Cen AB
and Proxima. - WDS 15208+3129: a pair of F5V and K0V stars in the Hyades Supercluster. I first assign membership of the primary, HD 136654, in this moving group.
- WDS 20124-1237: the bright star
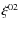 Cap
and the M0Vk high-proper
motion star LP 754-50.
Cap
and the M0Vk high-proper
motion star LP 754-50. - WDS 20452-3120: the very young stars
AU Mic and AT Mic AB in the
 Pictoris
moving group.
They have completed two orbital periods at most since their birth.
Pictoris
moving group.
They have completed two orbital periods at most since their birth. - WDS 20599+4016: a hierarchical quintuple system
around an F8V star.
With a total mass of about 4.1
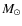 ,
it is the most massive system in my
sample.
,
it is the most massive system in my
sample.
Only two wide systems belong to young moving groups (Hyades
Supercluster and
![]() Pictoris),
which indicates that the origin of such wide separations
resides not only in the binary formation process, but also in the
subsequent
dynamical evolution (e.g. by interaction with another stars in the
Galactic disc or with the interstellar medium).
Pictoris),
which indicates that the origin of such wide separations
resides not only in the binary formation process, but also in the
subsequent
dynamical evolution (e.g. by interaction with another stars in the
Galactic disc or with the interstellar medium).
All the systems except AU Mic + AT Mic AB
and LP 268-35 + LP 268-33
are consistent with being physical doubles.
To ascertain that, I computed the minimum absolute values of
binding energies,
|Ug*(s)|
of the seven systems, and compared them with those of a large
ensemble of systems containing at least one component less massive than
0.15 ![]() .
.
Bound systems that are wider than 105 AU
may exist if they have enough
gravitational energy (i.e. total mass ![]() ),
but
they are likely to be young systems on the point of disruption by
dynamical
encounters in the Galactic disc.
),
but
they are likely to be young systems on the point of disruption by
dynamical
encounters in the Galactic disc.
I thank the anonymous referee for his/her helpful report and careful reading of the manuscript. I am an investigador Juan de la Cierva at the Universidad Complutense de Madrid. This research has made use of the Washington Double Star Catalog maintained at the United States Naval Observatory, the SIMBAD, operated at Centre de Données astronomiques de Strasbourg, France, and NASA's Astrophysics Data System. Financial support was provided by the Universidad Complutense de Madrid, the Comunidad Autónoma de Madrid, the Spanish Ministerio Educación y Ciencia, and the European Social Fund under grants: AyA2005-02750, AyA2005-04286, AyA2005-24102-E, AyA2008-06423-C03-03, AyA2008-00695, PRICIT S-0505/ESP-0237, and CSD2006-0070.
References
- Abt, H. A. 1988, ApJ, 331, 922 [CrossRef] [NASA ADS]
- Adelman-McCarthy, J., Agüeros, M. A., & Allam, S. S. 2008, ApJS, 175, 297 [CrossRef] [NASA ADS]
- Allen, C., Poveda, A., & Herrera, M. A. 2000, A&A, 356, 529 [NASA ADS]
- Anosova, J. P., & Orlov, V. V. 1991, A&A, 252, 123 [NASA ADS]
- Anosova, J. P., Orlov, V. V., & Pavlova, N. A. 1994, A&A, 292, 115 [NASA ADS]
- Artigau, É., Lafrenière, D., Doyon, R., et al. 2007, ApJ, 659, L49 [CrossRef] [NASA ADS]
- Artigau, É., Lafrenière, D., Albert, L., et al. 2009, ApJ, 692, 149 [CrossRef] [NASA ADS]
- Bahcall, J. N., & Soneira, R. M. 1981, ApJ, 246, 122 [CrossRef] [NASA ADS]
- Bakos, G. Á., Sahu, K. C., & Németh, P. 2002, ApJS, 141, 187 [CrossRef] [NASA ADS]
- Balega, I. I., Balega, Y. Y., Hofmann, K.-H., et al. 2002, A&A, 385, 87 [EDP Sciences] [CrossRef] [NASA ADS]
- Balega, I. I., Balega, Y. Y., Maksimov, A. F., et al. 2004, A&A, 422, 627 [EDP Sciences] [CrossRef] [NASA ADS]
- Balega, I. I., Balega, Y. Y., Hofmann, K.-H., et al. 2006, A&A, 448, 703 [EDP Sciences] [CrossRef] [NASA ADS]
- Balega, I. I., Balega, Y. Y., Maksimov, A. F., et al. 2007, AstBu, 62, 339 [NASA ADS]
- Baraffe, I., Chabrier, G., Allard, F., et al. 1998, A&A, 337, 403 [NASA ADS]
- Barrado y Navascués, D., Stauffer, J. R., Song, I., et al. 1999, ApJ, 520, L123 [CrossRef] [NASA ADS]
- Barrado y Navascués, D., Bayo, A., Morales-Calderón, M., et al. 2007, A&A, 468, L5 [EDP Sciences] [CrossRef] [NASA ADS]
- Batalha, C. C., Stout-Batalha, N. M., Basri, G., et al. 1996, ApJS, 103, 211 [CrossRef] [NASA ADS]
- Batten, A. H. 1973, Binary and multiple systems of stars, Oxford (New York: Pergamon Press, International series of monographs in natural philosophy, 51)
- Béjar, V. J. S., Zapatero Osorio, M. R., Pérez-Garrido, A., et al. 2008, ApJ, 673, L185 [CrossRef] [NASA ADS]
- Bergeron, P., Leggett, S. K., & Ruiz, M. T. 2001, ApJS, 133, 413 [CrossRef] [NASA ADS]
- Bessel, F. W. 1833, AN, 10, 389 [NASA ADS]
- Bochanski, J. J., West, A. A., Hawley, S. L., et al. 2007, AJ, 133, 531 [CrossRef] [NASA ADS]
- Bonnarel, F., Fernique, P., Bienaymé, O., et al. 2000, A&AS, 143, 3 [CrossRef] [NASA ADS]
- Bouy, H., Brandner, W., Martín, E. L., et al. 2003, AJ, 126, 1526 [CrossRef] [NASA ADS]
- Bouy, H., Martín, E. L., Brandner, W., et al. 2005, AN, 326, 969 [NASA ADS]
- Burgasser, A. J., & McElwain, M. W. 2006, AJ, 131, 1007 [CrossRef] [NASA ADS]
- Burgasser, A. J., Kirkpatrick, J. D., Cutri, R. M., et al. 2000, ApJ, 531, L57 [CrossRef] [NASA ADS]
- Burgasser, A. J., Reid, I. N., Siegler, N., et al. 2007, Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 427
- Burnham, S. W. 1906, A general catalogue of double stars within 121 deg of the North Pole, Carnegie Institution of Washington (University of Chicago press)
- Caballero, J. A. 2007a, A&A, 462, L61 [EDP Sciences] [CrossRef] [NASA ADS]
- Caballero, J. A. 2007b, ApJ, 667, 520 [CrossRef] [NASA ADS]
- Caballero, J. A., & Dinis, L. 2008, AN, 329, 801 [NASA ADS]
- Caballero, J. A., Martín, E. L., Dobbie, P. D., et al. 2006, A&A, 460, 635 [EDP Sciences] [CrossRef] [NASA ADS]
- Caballero, J. A., Burgasser, A. J., & Klement, R. 2008, A&A, 488, 181 [EDP Sciences] [CrossRef] [NASA ADS]
- Carney, B. W., Latham, D. W., Laird, J. B., et al. 1994, AJ, 107, 2240 [CrossRef] [NASA ADS]
- Chanamé, J., & Gould, A. 2004, ApJ, 601, 289 [CrossRef] [NASA ADS]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L29 [EDP Sciences] [CrossRef] [NASA ADS]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2005, A&A, 438, L25 [EDP Sciences] [CrossRef] [NASA ADS]
- Chen, Y. Q., Nissen, P. E., Benoni, T., et al. 2001, A&A, 371, 943 [EDP Sciences] [CrossRef] [NASA ADS]
- Close, L. M., Richer, H. B., & Crabtree, D. R. 1990, AJ, 100, 1968 [CrossRef] [NASA ADS]
- Eisenstein, D. J., Liebert, J., Harris, H. C., et al. 2006, ApJS, 167, 40 [CrossRef] [NASA ADS]
- Evans, D. S. 1967, Determination of Radial Velocities and their Applications. Proc. IAU Symp. No. 30. University of Toronto, 20-24 June 1966, ed. A. H. Batten, & J. F. Heard. (London: Academic Press), 57
- Evans, D. W., Irwin, M. J., & Helmer, L. 2002, A&A, 395, 347 [EDP Sciences] [CrossRef] [NASA ADS]
- Farihi, J., Becklin, E. E., & Zuckerman, B. 2005, ApJS, 161, 394 [CrossRef] [NASA ADS]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [CrossRef] [NASA ADS]
- Forveille, T., Beuzit, J.-L., Delorme, P., et al. 2005, A&A, 435, L5 [EDP Sciences] [CrossRef] [NASA ADS]
- Gasteyer, C. 1966, AJ, 71, 1017 [CrossRef] [NASA ADS]
- Giclas, H. L., Slaughter, C. D., & Burnham, R. 1959, LowOB, 4, 136 [NASA ADS]
- Giclas, H. L., Burnham, R., & Thomas, N. R. 1961, LowOB, 5, 61 [NASA ADS]
- Gizis, J. E., Monet, D. G., & Reid, I. N., et al. 2000, AJ, 120, 1085 [CrossRef] [NASA ADS]
- Gizis, J. E., Kirkpatrick, J. D., & Burgasser, A., et al. 2001, ApJ, 551, L163 [CrossRef] [NASA ADS]
- Gizis, J. E., Reid, I. N., Knapp, G. R., et al. 2003, AJ, 125, 3302 [CrossRef] [NASA ADS]
- Gliese, W. 1969, Veröffentlichungen des Astronomischen Rechen-Instituts Heidelberg, No. 22, ed. G. Braun, Karlsruhe
- Gliese, W., & Jahreiss, H. 1988, Ap&SS, 142, 49 [CrossRef] [NASA ADS]
- Goldberg, D., Mazeh, T., Latham, D. W., et al. 2002, AJ, 124, 1132 [CrossRef] [NASA ADS]
- Goldman, B., Delfosse, X., Forveille, T., et al. 1999, A&A, 351, L5 [NASA ADS]
- Gray, R. O., Corbally, C. J., Garrison, R. F. et al. 2003, AJ, 126, 2048 [CrossRef] [NASA ADS]
- Gray, R. O., Corbally, C. J., Garrison, R. F. et al. 2006, AJ, 132, 161 [CrossRef] [NASA ADS]
- Green, R. F., Schmidt, M., & Liebert, J. 1986, ApJS, 61, 305 [CrossRef] [NASA ADS]
- Hambly, N. C., MacGillivray, H. T., Read, M. A., et al. 2001, MNRAS, 326, 1279 [CrossRef] [NASA ADS]
- Harrington, R. S., & Dahn, C. C. 1980, AJ, 85, 454 [CrossRef] [NASA ADS]
- Herschel, W. 1783, RSPT, 73, 4 [CrossRef]
- Herschel, J. F. W. 1833, RSPT, 123, 359 [CrossRef] [NASA ADS]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS]
- Innes, R. T. A. 1915, Union Obs, Circ., 30
- Joy, A. H., & Abt H. A. 1974, ApJS, 28, 1 [CrossRef] [NASA ADS]
- Kalas, P., Liu, M. C., & Matthews, B. C. 2004, Science, 303, 1990 [CrossRef] [NASA ADS]
- Kamper, K. W., & Wesselink, A. J. 1978, AJ, 83, 1653 [CrossRef] [NASA ADS]
- Karatas, Y., Bilir, S., Eker, Z., et al. 2004, MNRAS, 349, 1069 [CrossRef] [NASA ADS]
- Katsova, M. M., Drake, J. J., & Livshits, M. A. 1999, ApJ, 510, 986 [CrossRef] [NASA ADS]
- Kirkpatrick, J. D., Dahn, C. C., Monet, D. G., et al. 2001, AJ, 121, 3235 [CrossRef] [NASA ADS]
- Kraicheva, Z. T., Popova, E. I., Tutukov, A. V., et al. 1985, Afz, 22, 105 [NASA ADS]
- Kraus, A. L., & Hillenbrand, L. A. 2007, ApJ, 662, 413 [CrossRef] [NASA ADS]
- Kundu, M. R., Jackson, P. D., White, S. M., et al. 1987, ApJ, 312, 822 [CrossRef] [NASA ADS]
- Lagrange, A.-M., Desort, M., Galland, F., Udry, S., & Mayor, M. 2009, A&A, 495, 335 [EDP Sciences] [CrossRef] [NASA ADS]
- Lajoie, C.-P., & Bergeron, P. 2007, ApJ, 667, 1126 [CrossRef] [NASA ADS]
- Lambert, D. L., & Reddy, B. E. 2004, MNRAS, 349, 757 [CrossRef] [NASA ADS]
- Lane, B. F., Zapatero Osorio, M. R., Britton, M. C., et al. 2001, ApJ, 560, 390 [CrossRef] [NASA ADS]
- Latham, D. W., Mazeh, T., Carney, B. W., et al. 1988, AJ, 96, 567 [CrossRef] [NASA ADS]
- Latham, D. W., Davis, R. J., Stefanik, R. P., et al. 1991, AJ, 101, 625 [CrossRef] [NASA ADS]
- Latham, D. W., Stefanik, R. P., Torres, G., et al. 2002, AJ, 124, 1144 [CrossRef] [NASA ADS]
- Lépine, S., & Shara, M. M. 2005, AJ, 129, 1483 [CrossRef] [NASA ADS]
- Lépine, S., & Bongiorno, B. 2007, AJ, 133, 889 [CrossRef] [NASA ADS]
- Le Verrier, U. J. 1847, AN, 25, 85 [NASA ADS]
- Liebert, J., Dahn, C. C., & Monet, D. G. 1988, ApJ, 332, 891 [CrossRef] [NASA ADS]
- Linsky, J. L., Bornmann, P. L., Carpenter, K. G. et al. 1982, ApJ, 260, 670 [CrossRef] [NASA ADS]
- López Martí, B., Eislöffel, J., Scholz, A., et al. 2004, A&A, 416, 555 [EDP Sciences] [CrossRef] [NASA ADS]
- López Martí, B., Eislöffel, J., & Mundt, R. 2005, A&A, 440, 139 [EDP Sciences] [CrossRef] [NASA ADS]
- Luhman, K. L. 2004, ApJ, 614, 318 [CrossRef] [NASA ADS]
- Luyten, W. J. 1941, Bruce proper motion survey, Minneapolis
- Makarov, V. V., Zacharias, N., & Hennessy, G. S. 2008, ApJ, 687, 566 [CrossRef] [NASA ADS]
- Mason, B. D., Martin, C., Hartkopf, W. I., et al. 1999, AJ, 117, 1890 [CrossRef] [NASA ADS]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., et al. 2001, AJ, 122, 3466 [CrossRef] [NASA ADS]
- Matthews, R., & Gilmore, G. 1993, MNRAS, 261, L5 [NASA ADS]
- Maxted, P. F. L., Marsh, T. R., & Moran, C. K. J. 2000, MNRAS, 319, 305 [CrossRef] [NASA ADS]
- Mazeh, T., Simon, M., Prato, L., et al. 2003, ApJ, 599, 1344 [CrossRef] [NASA ADS]
- McAlister, H. A., Hartkopf, W. I., Hutter, D. J., et al. 1987, AJ, 93, 183 [CrossRef] [NASA ADS]
- McCook, G. P., & Sion, E. M. 1999, ApJS, 121, 1 [CrossRef] [NASA ADS]
- McMillan, R. S., Breger, M., Ferland, G. J., et al. 1976, PASP, 88, 495 [CrossRef] [NASA ADS]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [CrossRef] [NASA ADS]
- Montes, D., López-Santiago, J., Gálvez, M. C., et al. 2001, MNRAS, 328, 45 [CrossRef] [NASA ADS]
- Mullally, F., Kilic, M., Reach, W. T., et al. 2007, ApJS, 171, 206 [CrossRef] [NASA ADS]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [EDP Sciences] [CrossRef] [NASA ADS]
- Öpik, E. 1924, Tartu Obs. Publ. 25, No. 6
- Ortega, V. G., de la Reza, R., Jilinski, E., et al. 2004, ApJ, 575, L75 [CrossRef] [NASA ADS]
- Ortega, V. G., de la Reza, R., Jilinski, E., et al. 2004, ApJ, 609, 243 [CrossRef] [NASA ADS]
- Ottmann, R., Fleming, T. A., & Pasquini, L. 1997, A&A, 322, 785 [NASA ADS]
- Palasi, J. 2000, Birth and Evolution of Binary Stars, Poster Proc. IAU Symp. 200 on The Formation of Binary Stars, held 10-15 April, in Potsdam, Germany, ed. B. Reipurth, & H. Zinnecker, 145
- Pallavicini, R., Tagliaferri, G., & Stella, L. 1990, A&A, 228, 403 [NASA ADS]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS]
- Poveda, A., & Allen, C. 2004, RMxAC, 21, 49 [NASA ADS]
- Radigan, J., Lafrenière, D., Jayawardhana, R., et al. 2009, ApJ, 698, 405 [CrossRef] [NASA ADS]
- Rebolo, R., Zapatero Osorio, M. R., Madruga, S., et al. 1998, Science, 282, 1309 [CrossRef] [NASA ADS]
- Reid, I. N., Cruz, K. L., Allen, P., et al. 2004, AJ, 128, 463 [CrossRef] [NASA ADS]
- Retterer, J. M., & King, I. R. 1982, ApJ, 254, 214 [CrossRef] [NASA ADS]
- Richichi, A., Fors, O., Merino, M., et al. 2006, A&A, 445, 1081 [EDP Sciences] [CrossRef] [NASA ADS]
- Robinson, S. E., Strader, J., Ammons, S. M., et al. 2006, ApJ, 637, 1102 [CrossRef] [NASA ADS]
- Röser, S., Schilbach, E., Schwan, H., et al. 2008, A&A, 488, 401 [EDP Sciences] [CrossRef] [NASA ADS]
- Ryan, S. G. 1992, AJ, 104, 1144 [CrossRef] [NASA ADS]
- Saarinen, S., & Gilmore, G. 1989, MNRAS, 237, 311 [NASA ADS]
- Saffer, R. A., Livio, M., & Yungelson, L. R. 1998, ApJ, 502, 394 [CrossRef] [NASA ADS]
- Salim, S., & Gould, A. 2003, ApJ, 582, 1011 [CrossRef] [NASA ADS]
- Scholz, R.-D., McCaughrean, M. J., Lodieu, N., et al. 2003, A&A, 398, L2 [CrossRef]
- Seifahrt, A., Guenther, E., & Neuhäuser, R. 2005, A&A, 440, 967 [EDP Sciences] [CrossRef] [NASA ADS]
- Shipman, H. L. 1979, ApJ, 228, 240 [CrossRef] [NASA ADS]
- Siegler, N., Close, L. M., Cruz, K. L., et al. 2005, ApJ, 621, 1023 [CrossRef] [NASA ADS]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [CrossRef] [NASA ADS]
- Strassmeier, K., Washuettl, A., Granzer, T., et al. 2000, A&AS, 142, 275 [EDP Sciences] [CrossRef] [NASA ADS]
- Soderblom, D. R., & Mayor, M. 1993, AJ, 105, 226 [CrossRef] [NASA ADS]
- Tolbert, C. R. 1964, ApJ, 139, 1105 [CrossRef] [NASA ADS]
- Torres, C. A. O., Quast, G. R., da Silva, L., et al. 2006, A&A, 460, 695 [EDP Sciences] [CrossRef] [NASA ADS]
- van Altena, W. F., Lee, J. T., & Hoffleit, E. D. 1995, The general catalogue of trigonometric [stellar] parallaxes, New Haven, CT: Yale University Observatory, 4th ed.
- van Leeuwen, F. 2007, A&A, 474, 653 [EDP Sciences] [CrossRef] [NASA ADS]
- Violat-Bordonau, F., & Violat-Martín, D. 2006, Open European Journal on Variable Stars, 53, 1 [NASA ADS]
- Voûte, J. 1917, MNRAS, 77, 650 [NASA ADS]
- Wasserman, I., & Weinberg, M. D. 1991, ApJ, 382, 149 [CrossRef] [NASA ADS]
- Weinberg, M. D., & Wasserman, I. 1988, ApJ, 329, 253 [CrossRef] [NASA ADS]
- Weinberg, M. D., Shapiro, S. L., & Wasserman, I. 1987, ApJ, 312, 367 [CrossRef] [NASA ADS]
- Weis, E. W. 1984, ApJS, 55, 289 [CrossRef] [NASA ADS]
- Weis, E. W. 1984, AJ, 96, 1710 [CrossRef] [NASA ADS]
- West, A. A., Hawley, S. L., & Bochanski, J. J., et al. 2008, AJ, 135, 785 [CrossRef] [NASA ADS]
- Wertheimer, J. G., & Laughlin, G. 2006, AJ, 132, 1995 [CrossRef] [NASA ADS]
- Zapatero Osorio, M. R., & Martín, E. L. 2004, A&A, 419, 167 [EDP Sciences] [CrossRef] [NASA ADS]
- Zuckerman, B., & Song, I. 2004, ARA&A, 42, 685 [CrossRef] [NASA ADS]
- Zuckerman, B., Song, I., Bessell, M. S. et al. 2001, ApJ, 562, L87 [CrossRef] [NASA ADS]
- Zuckerman, B., Koester, D., Reid, I. N., et al. 2003, ApJ, 596, 477 [CrossRef] [NASA ADS]
Online Material
Appendix
A: Washington double stars with  arcsec
arcsec
Table
A.1:
Basic data from the literature of Washington double stars with
tabulated angular separations ![]() arcsec.
arcsec.
Footnotes
- ... separations
![[*]](/icons/foot_motif.png)
- Appendix A is only available in electronic form at http://www.aanda.org
- ...0.005-0.05 pc)
![[*]](/icons/foot_motif.png)
- 1 pc
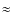 206 264.806 AU.
206 264.806 AU.
- ...1995)
![[*]](/icons/foot_motif.png)
- The value of
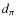 of
G 1-45 AB tabulated in the fourth edition of the
general catalogue of
trigonometric parallaxes of van Altena et al. (1995) has a
lower uncertainty than the one in Harrington & Dahn (1980),
which is
of
G 1-45 AB tabulated in the fourth edition of the
general catalogue of
trigonometric parallaxes of van Altena et al. (1995) has a
lower uncertainty than the one in Harrington & Dahn (1980),
which is 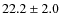 pc.
pc.
- ... discussion
![[*]](/icons/foot_motif.png)
- A critical reading is needed: Anosova et al. (1994) assumed a
mass of 0.020
 for Proxima,
close to the brown dwarf-planet boundary, which is about five times
lower than
currently assumed.
for Proxima,
close to the brown dwarf-planet boundary, which is about five times
lower than
currently assumed.
All Tables
Table 1: Rejected wide binary candidatesa.
Table 2: New proper motions of components in wide binary candidates.
Table 3: Photometry of system WDS 13090+3353.
Table 4: Probable bound wide systems.
Table
5: Multiple systems in the solar neighbourhood with at least
one low-mass component (
![]() )
and the lowest binding energies for their total masses.
)
and the lowest binding energies for their total masses.
Table
A.1: Basic data from the literature of Washington double
stars with tabulated angular separations ![]() arcsec.
arcsec.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


