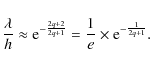| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 573 - 579 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/200912348 | |
| Published online | 03 September 2009 | |
A&A 507, 573-579 (2009)
A local prescription for the softening length in self-gravitating gaseous discs
J.-M. Huré1,2 - A. Pierens3
1 - Université de Bordeaux, OASU, France
2 - CNRS/INSU-UMR 5804/LAB; BP 89, 33271 Floirac Cedex, France
3 - LAL-IMCCE/USTL, 1 Impasse de l'Observatoire, 59000 Lille, France
Received 17 April 2009 / Accepted 2 July 2009
Abstract
In 2D-simulations of self-gravitating gaseous discs, the potential is
often computed in the framework of ``softened gravity'' initially
designed for N-body codes. In this special context,
the role of the softening length ![]() is twofold: i) to avoid numerical singularities in the integral
representation of the potential (i.e., arising when the separation
is twofold: i) to avoid numerical singularities in the integral
representation of the potential (i.e., arising when the separation
![]() );
and ii) to account for stratification of matter in the direction
perpendicular to the disc mid-plane. So far, most studies have
considered
);
and ii) to account for stratification of matter in the direction
perpendicular to the disc mid-plane. So far, most studies have
considered ![]() as a free parameter and various values or formulae have been proposed
without much mathematical justification. In this paper, we demonstrate
by means of a rigorous calculus that it is possible to define
as a free parameter and various values or formulae have been proposed
without much mathematical justification. In this paper, we demonstrate
by means of a rigorous calculus that it is possible to define ![]() such that the gravitational potential of a flat disc coincides at order
zero with that of a geometrically thin disc of the same surface
density. Our prescription for
such that the gravitational potential of a flat disc coincides at order
zero with that of a geometrically thin disc of the same surface
density. Our prescription for ![]() ,
valid in the local, axisymmetric limit, has the required properties i)
and ii). It is mainly an analytical function of the radius and disc
thickness, and is sensitive to the vertical stratification. For mass
density profiles considered (namely, profiles expandable over even
powers of the altitude), we find that
,
valid in the local, axisymmetric limit, has the required properties i)
and ii). It is mainly an analytical function of the radius and disc
thickness, and is sensitive to the vertical stratification. For mass
density profiles considered (namely, profiles expandable over even
powers of the altitude), we find that ![]() :
i) is independant of the numerical mesh, ii) is always a fraction of
the local thickness H; iii) goes through a
minimum at the singularity (i.e., at null separation); and iv)
is such that
:
i) is independant of the numerical mesh, ii) is always a fraction of
the local thickness H; iii) goes through a
minimum at the singularity (i.e., at null separation); and iv)
is such that ![]() typically (depending on the separation and on density profile). These
results should help us to improve the quality of 2D- and
3D-simulations of gaseous discs in several respects (physical realism,
accuracy, and computing time).
typically (depending on the separation and on density profile). These
results should help us to improve the quality of 2D- and
3D-simulations of gaseous discs in several respects (physical realism,
accuracy, and computing time).
Key words: accretion, accretion discs - gravitation - methods: numerical
1 Introduction
The computation of gravitational potentials and forces is a
critical
step in many astrophysical problems where gravity plays an important
role. Because Newton's law of gravitation diverges as the relative
separation ![]() between particles vanishes, one classically adds a positive constant
between particles vanishes, one classically adds a positive constant ![]() referred as the ``softening length''. This technique of singularity
avoidance, initially developped to prevent binary collisions and
particle evaporation in N-body simulations, has led
to the concept of ``softened gravity'' (Sommer-Larsen
et al. 1998; Nelson
2006; Hockney
& Eastwood 1988; Anthony
& Carlberg 1988).
Soon, people realized that the use of a softening length introduces a
noticeable bias in models, especially for the stability properties of
stellar systems, and there have been several attempts to search for the
most appropriate
referred as the ``softening length''. This technique of singularity
avoidance, initially developped to prevent binary collisions and
particle evaporation in N-body simulations, has led
to the concept of ``softened gravity'' (Sommer-Larsen
et al. 1998; Nelson
2006; Hockney
& Eastwood 1988; Anthony
& Carlberg 1988).
Soon, people realized that the use of a softening length introduces a
noticeable bias in models, especially for the stability properties of
stellar systems, and there have been several attempts to search for the
most appropriate ![]() -value
(e.g., Sommer-Larsen
et al. 1998; Dehnen
2001; Romeo
1994,1997).
-value
(e.g., Sommer-Larsen
et al. 1998; Dehnen
2001; Romeo
1994,1997).
Softened gravity has also been employed in the computation of the
gravitational potential of gaseous discs (e.g., Sterzik
et al. 1995; Adams
et al. 1989; Laughlin
et al. 1997; Morishima
& Saio 1994; Li
et al. 2009; Laughlin
et al. 1998; Shu
et al. 1990; Tremaine
2001; Papaloizou
& Lin 1989; Baruteau
& Masset 2008; Caunt
& Tagger 2001; Saio
& Yoshii 1990)
with the additional justification that the softening length takes into
account the vertical stratification of matter. Various prescriptions,
generally in the form of a function of the cylindrical radius and/or of
the disc parameters, have been adopted (see references above) without
convergence towards a ``universal formula''. As for systems of
particles, it is recognized that the softening length can dramatically
affect the stability of gaseous discs (again, see references
hereabove). It is therefore fundamental to ask i) whether or not
softened gravity can definitively help to determine or mimic the Newtonian
potential of a gaseous disc
with a certain level of accuracy; and ii) eventually which formula - if
one exists - is the most appropriate. This is the aim of this paper. By
equating the softened potential of a flat disc to that of a
geometrically thin disc, we find that we can define a softening
length ![]() which has the required properties. We therefore report the first
reliable formula for the softening length on the basis of approximate
but rigorous calculus. In the axisymmetric limit,
which has the required properties. We therefore report the first
reliable formula for the softening length on the basis of approximate
but rigorous calculus. In the axisymmetric limit, ![]() is found to be a sharp function of the relative separation
is found to be a sharp function of the relative separation ![]() ;
it is a fraction (of the order of
;
it is a fraction (of the order of ![]() at the singularity) of the disc local thickness (see also Baruteau
& Masset 2008; Huré
& Pierens 2006), and it does not depend on the
numerical resolution (see Li
et al. 2009).
The formula, easy to implement into hydrodynamical codes of
self-gravitating 2D- and 3D-discs, will enable to increase the
degree of reaslim of simulations, both by preserving the
Newtonian character of the potential and force field, and by accounting
for the vertical structure.
at the singularity) of the disc local thickness (see also Baruteau
& Masset 2008; Huré
& Pierens 2006), and it does not depend on the
numerical resolution (see Li
et al. 2009).
The formula, easy to implement into hydrodynamical codes of
self-gravitating 2D- and 3D-discs, will enable to increase the
degree of reaslim of simulations, both by preserving the
Newtonian character of the potential and force field, and by accounting
for the vertical structure.
The paper is organized as follows. In Sect. 2,
we recall the expression for the midplane gravitational potential of a
geometrically thin disc as well as that of a flat (i.e., zero
thickness) disc. Because of the hypothesis of axial symmetry, the
integral kernel contains a complete elliptic integral of the first kind
that can be appropriately expanded at the singularity
![]() and its neighborhood. In Sect. 3, we
estimate the effect of vertical stratification by performing the
analytical integration along the z-direction.
Various mass density profiles corresponding to finite size discs are
considered, namely the homogeneous case and mixtures of even powers of
the altitude. In Sect. 4, we show
that this calculus naturally leads to a local prescription for the
softening length
and its neighborhood. In Sect. 3, we
estimate the effect of vertical stratification by performing the
analytical integration along the z-direction.
Various mass density profiles corresponding to finite size discs are
considered, namely the homogeneous case and mixtures of even powers of
the altitude. In Sect. 4, we show
that this calculus naturally leads to a local prescription for the
softening length ![]() .
We present a table showing the great diversity (and incoherence) of
prescriptions used so far and derive the general relation for
.
We present a table showing the great diversity (and incoherence) of
prescriptions used so far and derive the general relation for ![]() .
We discuss the sensitivity of the softening length to the separation
and disc aspect ratio. In Sect. 5, we
summarize the results and suggest a few possible extensions and
generalizations of this work.
.
We discuss the sensitivity of the softening length to the separation
and disc aspect ratio. In Sect. 5, we
summarize the results and suggest a few possible extensions and
generalizations of this work.
2 Mid-plane gravitational potential in both flat discs and geometrically thin discs: local treatment
2.1 Notation and background
We consider two axially symmetric discs (see Fig. 1):
i) a flat (i.e., zero thickness) disc with inner edge ![]() ,
outer edge
,
outer edge
![]() ,
and total surface density
,
and total surface density
![]() ;
and ii) a geometrically thin disc with the same edges and same total
surface density, but local thickness H = 2h>0.
For the geometrically thin disc, the condition
;
and ii) a geometrically thin disc with the same edges and same total
surface density, but local thickness H = 2h>0.
For the geometrically thin disc, the condition
is assumed at any radius
where
| Figure 1:
A flat disc and a geometrically thin disc, axially symmetric and
symmetric with respect to the mid-plane. The disc edges are |
|
| Open with DEXTER | |
For the thin disc, the mid-plane gravitational potential at radius R
is given by the double integral (e.g. Durand 1953)
where
is the modulus and
where
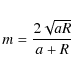
|
(6) |
is the associated modulus (note that k=m for z=0). Both Eqs. (3) and (5) involve a logarithmic singularity when the modulus of the elliptic integral approaches unity. In spite of this divergence, the potential is generally finite at any radius. It is interesting to see that Eq. (3) can also be written as
where
Clearly,
2.2 Expansion around the singularity
The presence of the function ![]() does not allow us to derive
does not allow us to derive ![]() analytically for any mass density distribution. The expansion of
analytically for any mass density distribution. The expansion of ![]() appropriate for treating the logarithmic singularity is (e.g. Gradshteyn &
Ryzhik 1965)
appropriate for treating the logarithmic singularity is (e.g. Gradshteyn &
Ryzhik 1965)
where
By construction, this expansion is efficient when
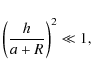
|
(11) |
and
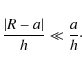
|
(12) |
The first inequality is automatically fulfilled within the geometrically thin disc approximation (see Eq. (1)). The second inequality means that the present calculus is valid only at the singularity R=a and for a few disc thicknesses in radius. This is precisely the radial domain where the numerical determination of
To the lowest order, ![]() and
and ![]() ,
and Eq. (8)
becomes:
,
and Eq. (8)
becomes:
with an error of
3 Effect of vertical stratification: an estimate of the 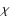 -function
-function
3.1 Vertically homogeneous discs
We can estimate ![]() from Eq. (13)
in a few particular cases, for instance when the disc is vertically
homogeneous (
from Eq. (13)
in a few particular cases, for instance when the disc is vertically
homogeneous (![]() is denoted
is denoted ![]() in this case). If
in this case). If ![]() does not depend on z, then
does not depend on z, then ![]() and we find that
and we find that
where
This is a complicated function of R/a, where the local aspect ratio 2h/a is the unique parameter. If we define the variable
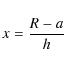
|
(16) |
which measures the radial separation from the singularity R=a in units of the disc semi-thickness h, and
| (17) |
which is the quarter of the aspect ratio, we find that
The function
We see that
![\begin{figure}
\par\includegraphics[width=8.9cm, bb=44 51 706 529, clip=]{12348fig2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12348-09/Timg61.png)
|
Figure 2:
Variation of |
| Open with DEXTER | |
3.2 Effect of vertical stratification
We can probe the sensitivity of ![]() to vertical stratification by considering the following profiles:
to vertical stratification by considering the following profiles:
where
We can calculate ![]() again from Eq. (13),
but using Eq. (20).
From Eq. (2),
we get
again from Eq. (13),
but using Eq. (20).
From Eq. (2),
we get ![]() ,
and then
,
and then
where we have defined
We can perform the integration using the expansion of
where
This expression can be rewritten in a different form since each sum represent the first q+1 terms of the expansion of the
|
|
= | 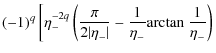
|
|
![$\displaystyle \left. -\sum_{k=0}^q{\frac{(-1)^k}{2k+1} \eta_-^{2(k-q)}} \right] + \eta_+^2\sum_{k=0}^\infty{\frac{(-1)^k \eta_+^{2k}}{2(k+q)+3} }\cdot$](/articles/aa/full_html/2009/43/aa12348-09/img74.png)
|
(25) |
We see that
The function
and we note that
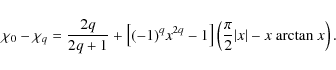
|
(28) |
The maximum of
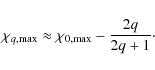
|
(29) |
Again, we note that the difference
Finally, for the vertical profile defined by Eqs. (20), ![]() follows from Eqs. (18),
(21),
and (26).
We see that
follows from Eqs. (18),
(21),
and (26).
We see that ![]() reaches a maximum at R=a, and
reaches a maximum at R=a, and
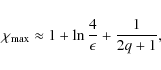
|
(30) |
for
![\begin{figure}
\par\includegraphics[width=8.9cm, bb=44 51 706 529, clip=]{12348fig3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12348-09/Timg87.png)
|
Figure 3:
Variation of |
| Open with DEXTER | |
3.3 Full generalization
The generalization of the above result is relatively straightforward
for profiles of the form
where cn are real coefficients. In this case, we find that
where
| (33) |
where
We see that
![\begin{figure}
\par\includegraphics[width=8.9cm, bb=14 51 706 529, clip=]{12348fig4.eps}\end{figure}](/articles/aa/full_html/2009/43/aa12348-09/Timg96.png)
|
Figure 4:
|
| Open with DEXTER | |
4 Application to softened gravity: a prescription for the softening length
4.1 The avoidance of point mass singularities
As mentioned, the complete elliptic integral ![]() exhibits a logarithmic divergence as its modulus
exhibits a logarithmic divergence as its modulus
![]() .
This is the direct consequence of the point mass singularity (i.e.,
.
This is the direct consequence of the point mass singularity (i.e., ![]() ). The
determination of accurate potentials from Eqs. (3)
and (5)
is therefore not straightforward and requires a careful treatment of
improper integrals (e.g., Stemwedel et al.
1990; Huré
2005; Huré
& Pierens 2005). This technical difficulty is usually
circumvented by changing the relative separation according to
). The
determination of accurate potentials from Eqs. (3)
and (5)
is therefore not straightforward and requires a careful treatment of
improper integrals (e.g., Stemwedel et al.
1990; Huré
2005; Huré
& Pierens 2005). This technical difficulty is usually
circumvented by changing the relative separation according to
where
In the case of gaseous discs of interest here, the
modification of the relative distances according to Eq. (36) changes the
expressions for
![]() and
and
![]() .
It is however easy to show that the associated ``softened'' potentials
denoted
.
It is however easy to show that the associated ``softened'' potentials
denoted
![]() and
and ![]() ,
respectively, can still be written in terms of Eqs. (3)
and (5),
respectively, provided that the modulus k
is replaced by
,
respectively, can still be written in terms of Eqs. (3)
and (5),
respectively, provided that the modulus k
is replaced by
and m is replaced by
In disc models and simulations, one never (or rarely) computes
where
Table 1: Various prescriptions for the softening length adopted in some simulations of self-gravitating gaseous discs (see also Fig. 1).
4.2 A prescription for the softening length 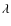
Many prescriptions for ![]() have been proposed. In general, this is not a constant but a certain
function of the radius and/or disc parameters. Table 1
gathers a few formulae for
have been proposed. In general, this is not a constant but a certain
function of the radius and/or disc parameters. Table 1
gathers a few formulae for ![]() used
by different authors over twenty years. Although not exhaustive, this
list clearly shows that there is no trend in magnitude and variation in
space (and possible dependency on the disc parameters). The results
obtained in Sect. 3
can help substantially to define the appropriate prescription
for
used
by different authors over twenty years. Although not exhaustive, this
list clearly shows that there is no trend in magnitude and variation in
space (and possible dependency on the disc parameters). The results
obtained in Sect. 3
can help substantially to define the appropriate prescription
for ![]() .
We can see from Eqs. (5)
and (7)
that the gravitational potential in the mid-plane of a thin
disc is equivalent to the softened potential caused by a flat disc
provided that
.
We can see from Eqs. (5)
and (7)
that the gravitational potential in the mid-plane of a thin
disc is equivalent to the softened potential caused by a flat disc
provided that ![]() is the root of the equation
is the root of the equation
for all R. Only a numerical approach can yield the exact value of
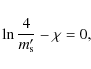
|
(41) |
where
We therefore conclude that the appropriate prescription for
![\begin{figure}
\par\includegraphics[width=8.9cm, bb=32 51 706 522, clip=]{12348fig5.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12348-09/Timg125.png)
|
Figure 5: Softening length normalized to the local semi-thickness h versus x as computed from Eq. (39) for h/a=0.1 in the homogeneous case. |
| Open with DEXTER | |
4.3 Results for various stratifications
It follows that ![]() is proportional to h, and depends both on x
and
is proportional to h, and depends both on x
and ![]() .
It is also sensitive to the vertical stratification through the
function
.
It is also sensitive to the vertical stratification through the
function ![]() .
Figure 5
displays
.
Figure 5
displays ![]() versus x for h/a=0.1
in the homogenous case (i.e., for
versus x for h/a=0.1
in the homogenous case (i.e., for ![]() ,
or
,
or ![]() ). We see
that, in the range of validity,
). We see
that, in the range of validity, ![]() goes through a minimum for x=0. There, we have
goes through a minimum for x=0. There, we have ![]() and
and ![]() and then the minimum is
and then the minimum is
This value is almost insensitive to the disc aspect ratio, provided that the disc is geometrically thin. This is shown in Fig. 6, where we plot
Figure 7
displays ![]() for the mass density profile given by Eq. (20)
and for
for the mass density profile given by Eq. (20)
and for ![]() .
At x=0, we have the general formula
.
At x=0, we have the general formula
Since
![\begin{figure}
\par\includegraphics[width=8.9cm, bb=-2 44 706 532, clip=]{12348fig6.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12348-09/Timg135.png)
|
Figure 6: The softening length at the minimum x=0 for the vertically homogeneous profile. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.9cm, bb=0 51 706 522, clip=]{12348fig7.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12348-09/Timg136.png)
|
Figure 7:
Softening length normalized to the local semi-thickness h
versus x as computed from Eq. (39) for h/a=0.1.
The density profile is according to Eq. (20)
with |
| Open with DEXTER | |
4.4 An example of vertical mass density profile expandable in infinite series
To illustrate the generality and power of the result, we consider a
cosine profile of the form ![]() which
is a typical example where matter distribution is expandable in
infinite series of the altitude. Actually, this profile can also be
expanded by means of Eq. (31)
with the following coefficients:
which
is a typical example where matter distribution is expandable in
infinite series of the altitude. Actually, this profile can also be
expanded by means of Eq. (31)
with the following coefficients:
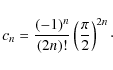
|
(46) |
The corresponding function
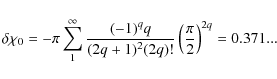
|
(47) |
which results in
5 Concluding remarks
In this paper, we have reported the first reliable prescription for the
softening length ![]() to
be used in the numerical determination of the gravitational potential
of geometrically thin discs within the framework of softened gravity.
This expression has been found by rigorously comparing the Newtonian
potential of a geometrically thin disc (of finite thickness) with the
softened potential of a flat disc. This is a function of the radius and
disc local aspect ratio, and also depends on vertical stratification.
It is accurate at the singularity and around (typically a few disc
thicknesses in radius). Although this formula is valid only locally,
and obtained in the axisymmetric limit, it should help to improve the
quality (realism, accuracy, and computing time) of 2D- and
3D-simulations
to
be used in the numerical determination of the gravitational potential
of geometrically thin discs within the framework of softened gravity.
This expression has been found by rigorously comparing the Newtonian
potential of a geometrically thin disc (of finite thickness) with the
softened potential of a flat disc. This is a function of the radius and
disc local aspect ratio, and also depends on vertical stratification.
It is accurate at the singularity and around (typically a few disc
thicknesses in radius). Although this formula is valid only locally,
and obtained in the axisymmetric limit, it should help to improve the
quality (realism, accuracy, and computing time) of 2D- and
3D-simulations![]() .
If necessary, the accuracy of the prescription can be improved by
considering higher order terms in the expanded complete elliptic
integrals of the first kind.
.
If necessary, the accuracy of the prescription can be improved by
considering higher order terms in the expanded complete elliptic
integrals of the first kind.
Finally, it would then be interesting to generalize our results i) to mass density profiles that extend to infinity, such as the Gaussian profile (which corresponds to vertically isothermal discs); and ii) to the entire disc since this prescription is expected to be inaccurate far from the singularity.
AcknowledgementsIt is a pleasure to thank C. Baruteau, D. Bernard, A. Collioud, F. Hersant and A. Romeo for valuable comments.
References
- Adams, F. C., Ruden, S. P., & Shu, F. H. 1989, ApJ, 347, 959 [CrossRef] [NASA ADS]
- Anthony, D. M., & Carlberg, R. G. 1988, ApJ, 332, 637 [CrossRef] [NASA ADS]
- Baruteau, C., & Masset, F. 2008, ApJ, 678, 483 [CrossRef] [NASA ADS]
- Caunt, S. E., & Tagger, M. 2001, A&A, 367, 1095 [EDP Sciences] [CrossRef] [NASA ADS]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [CrossRef] [NASA ADS]
- Dehnen, W. 2001, MNRAS, 324, 273 [CrossRef] [NASA ADS]
- Durand, E. 1953, Electrostatique, Vol. I. Les distributions (Masson)
- Edgar, R. G., & Quillen, A. C. 2008, MNRAS, 387, 387 [CrossRef] [NASA ADS]
- Gradshteyn, I. S., & Ryzhik, I. M. 1965, Table of integrals, series and products (New York: Academic Press), 4th edn., ed. Yu.V. Geronimus, & M. Yu. Tseytlin
- Hirose, S., Krolik, J. H., & Stone, J. M. 2006, ApJ, 640, 901 [CrossRef] [NASA ADS]
- Hockney, R. W., & Eastwood, J. W. 1988, Computer simulation using particles, ed. R. W. Hockney, & J. W. Eastwood
- Huré, J.-M. 2005, A&A, 434, 1 [EDP Sciences] [CrossRef] [NASA ADS]
- Huré, J.-M., & Pierens, A. 2005, ApJ, 624, 289 [CrossRef] [NASA ADS]
- Huré, J.-M., & Pierens, A. 2006, in SF2A-2006: Semaine de l'Astrophysique Francaise, ed. D. Barret, F. Casoli, G. Lagache, A. Lecavelier, & L. Pagani, 105
- Laughlin, G., Korchagin, V., & Adams, F. C. 1997, ApJ, 477, 410 [CrossRef] [NASA ADS]
- Laughlin, G., Korchagin, V., & Adams, F. C. 1998, ApJ, 504, 945 [CrossRef] [NASA ADS]
- Li, S., Buoni, M. J., & Li, H. 2009, ApJS, 181, 244 [CrossRef] [NASA ADS]
- Morishima, T., & Saio, H. 1994, MNRAS, 267, 766 [NASA ADS]
- Nelson, A. F. 2006, MNRAS, 373, 1039 [CrossRef] [NASA ADS]
- Papaloizou, J. C. B., & Lin, D. N. C. 1989, ApJ, 344, 645 [CrossRef] [NASA ADS]
- Pringle, J. E. 1981, ARA&A, 19, 137 [CrossRef] [NASA ADS]
- Romeo, A. B. 1994, A&A, 286, 799 [NASA ADS]
- Romeo, A. B. 1997, A&A, 324, 523 [NASA ADS]
- Saio, H., & Yoshii, Y. 1990, ApJ, 363, 40 [CrossRef] [NASA ADS]
- Shu, F. H., Tremaine, S., Adams, F. C., & Ruden, S. P. 1990, ApJ, 358, 495 [CrossRef] [NASA ADS]
- Sommer-Larsen, J., Vedel, H., & Hellsten, U. 1998, MNRAS, 294, 485 [CrossRef] [NASA ADS]
- Stemwedel, S. W., Yuan, C., & Cassen, P. 1990, ApJ, 351, 206 [CrossRef] [NASA ADS]
- Sterzik, M. F., Herold, H., Ruder, H., & Willerding, E. 1995, Planet. Space Sci., 43, 259 [CrossRef] [NASA ADS]
- Tremaine, S. 2001, AJ, 121, 1776 [CrossRef] [NASA ADS]
Footnotes
- ...3D-simulations
![[*]](/icons/foot_motif.png)
- A Fortran 90 package called SingLe is available at: http://www.obs.u-bordeaux1.fr/radio/JMHure/intro2single.php
All Tables
Table 1: Various prescriptions for the softening length adopted in some simulations of self-gravitating gaseous discs (see also Fig. 1).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



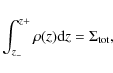
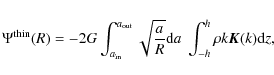
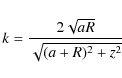
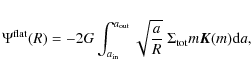
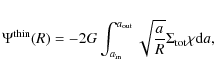
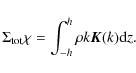
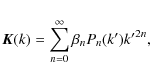
![\begin{displaymath}\left\{
\begin{array}{l}
P_0= \ln \frac{4}{k'},\\
P_{n+1}(k'...
...}\right]^2, \qquad{\rm for }\qquad n \ge 0.
\end{array}\right.
\end{displaymath}](/articles/aa/full_html/2009/43/aa12348-09/img38.png)
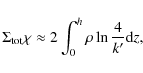
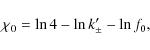
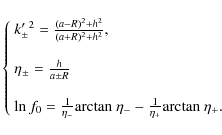
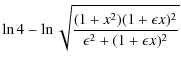
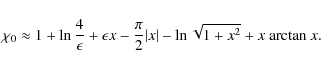
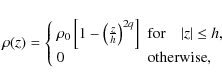
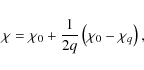
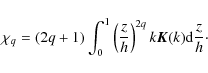
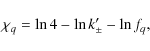
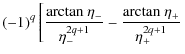
![$\displaystyle \left. -\sum_{k=0}^q{(-1)^k \frac{\eta_-^{2(k-q)}-\eta_+^{2(k-q)}}{2k+1}} \right]\cdot$](/articles/aa/full_html/2009/43/aa12348-09/img71.png)
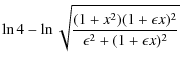
![$\displaystyle - (-1)^q \left[ x^{2q} \left( \frac{\pi}{2}\vert x\vert - x ~ {\r...
...ctan ~}x \right) -\sum_{k=0}^q{\frac{(-1)^k}{2k+1} x^{2(q-k)}} \right]\nonumber$](/articles/aa/full_html/2009/43/aa12348-09/img78.png)
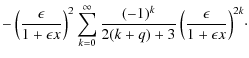
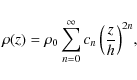
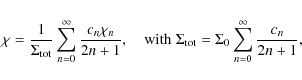
![$\displaystyle \delta \chi_0 = - \frac{\Sigma_0}{\Sigma_{\rm tot}} \sum_{n=0}^\i...
... \right] \left( \frac{\pi}{2}\vert x\vert - x~{\rm arctan ~}x \right) \right\}.$](/articles/aa/full_html/2009/43/aa12348-09/img94.png)
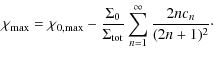
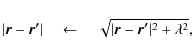
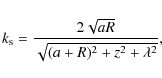
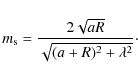
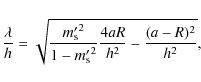
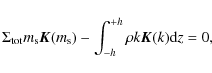
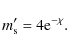
![\begin{displaymath}\frac{\lambda}{h} \approx \frac{1}{e} \times \frac{1}{\sqrt{1...
...ft[ 1 + \left(\frac{\epsilon}{\sqrt{2}e}\right)^2 \right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/43/aa12348-09/img131.png)
![\begin{displaymath}\frac{\lambda}{h} \approx \frac{{\rm e}^{-(1 + \delta \chi_0)...
...ft[\frac{h}{2 a}
{\rm e}^{- (1+\delta \chi_0)}\right]^2}}\cdot
\end{displaymath}](/articles/aa/full_html/2009/43/aa12348-09/img132.png)