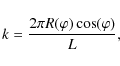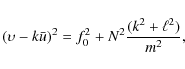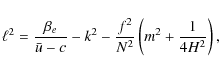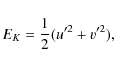Evolution of the cloud field and wind structure of Jupiter's highest speed jet during a huge disturbance

N. Barrado-Izagirre; S. Pérez-Hoyos; E. García-Melendo; A. Sánchez-Lavega

doi:10.1051/0004-6361/200912282

Free Access

Issue		A&A Volume 507, Number 1, November III 2009


Page(s)		513 - 522
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/200912282
Published online		03 September 2009

A&A 507, 513-522 (2009)

Evolution of the cloud field and wind structure of Jupiter's highest speed jet during a huge disturbance

N. Barrado-Izagirre¹ - S. Pérez-Hoyos¹ - E. García-Melendo² - A. Sánchez-Lavega¹

1 - Grupo de Ciencias Planetarias, Dpto. Física Aplicada I, Escuela Técnica Superior de Ingenieros, EHU-UPV, Alda. Urquijo s/n, 48013 Bilbao, Spain
2 - Esteve Duran Observatory Foundation, c/Montseny 46, 08553 Seva, Spain

Received 6 April 2009 / Accepted 31 July 2009

Abstract
Aims. Despite the banded visual aspect of cloud patterns in Jupiter, high resolution images indicate that these regions are markedly turbulent. One region of particular interest is the north temperate belt (NTB) at 21 $^\circ$ N planetocentric latitude, where the most intense Jovian jet resides with eastward peak speeds of 160-180 m s^-1. Almost every 15 years, the NTB is known to experience an eruption or disturbance that dramatically changes its appearance, a phenomenon known as NTB disturbance (NTBD). In this work, we characterize the morphology of the disturbed cloud field in the wake of the plumes that caused the perturbation, and check for changes in the velocity or shape of the jet.
Methods. The 2007 disturbance was witnessed with unprecedented resolution by the Hubble Space Telescope and by a long-term survey based on the ``International Outer Planet Watch'' (IOPW) network. Our analysis is based on the brightness spectral distribution to characterize both the typical spatial frequency of the perturbation and its turbulent and wavy nature. We also compare our characterization with non-linear dynamical simulations of the disturbance using the EPIC dynamical model. Finally, we obtain a renewed wind profile for the region of interest by cloud tracking.
Results. We detect a change in the power spectral slope of the cloud brightness following the disturbance that is related to a change in the typical size of the observed structures. We model the initial disturbance as a Rossby wave. A comparison of the jet profile in the NTB just after the disturbance ended (June 2007) with one observed a year later (July 2008), illustrates a net change occurred in the westward jet at 16 $^\circ$ N with a speed change of 25 m s^-1. As implied by the power spectra analysis, the disturbance and its related Rossby wave dissipate. We propose that this dissipation produced a momentum transfer to the anticyclonic side of the NTB jet increasing the speed of the westward jet at 16 $^\circ$ N as also supported by numerical simulations.

Key words: planets and satellites: general - planets and satellites: individual: Jupiter - turbulence

1 Introduction

Jupiter's wind system, formed by zonal jets (along parallel circles) alternating in direction with latitude, is known to be constant in time at cloud level (Vasavada & Showman 2005; Porco et al. 2003; García-Melendo & Sánchez-Lavega 2001). The most intense jet in Jupiter's atmosphere is located at 21 $^\circ$ planetocentric latitude in the North Temperate Belt, where the winds reach velocities of between 140 m s^-1 and 180 m s^-1 (Ingersoll et al. 2004). The region is historically well known for the development of intense disturbances (Rogers 1995). The last one occurred on 25 March 2007 when a vigorous eruption of two convective spots occurred at the NTB, in the peak of the jet, that were fortuitously captured in its growing stage by Hubble Space Telescope (HST) observations (Sánchez-Lavega et al. 2008). Its subsequent evolution into a planetary scale disturbance was covered mostly by ground-based telescopes, including the International Outer Planets Watch (IOPW) network, and later by additional HST observations. The first eruption on 25 March gave rise to a plume (called B), while the second one (A) appeared on 27 March, both being named after their discovery order. Plume A (moving at 169 m s^-1) produced a turbulent planetary-scale disturbance in its wake, whose pattern, moving slowly at $\sim$ 100 m s^-1, destroyed plume B as they met each other. This type of phenomenon, called the North Temperate Belt Disturbance (NTBD), is known to occur every now and then in Jupiter (Rogers 1995; Peek 1958; Sánchez-Lavega & Quesada 1988; Sánchez-Lavega et al. 1991), the last three occurring in intervals of approximately 15 years (in 1975, 1990 and 2007). The observations, altitude, and temperature retrievals, and dynamical modeling of the 2007 events were described by Sánchez-Lavega et al. (2008). They reported that the plumes moved with a uniform zonal velocity faster than any other feature of the planet (169 m s^-1) at visual levels and reached a height of 30 km above the surrounding clouds. The origin of the plumes was probably convective and the conditions for their development were also constrained using previously developed models of convective storms (Hueso et al. 2002). They found no overall change in the jet wind profile when comparing it before, during, and after the disturbance development over a four month period (March-June 2007). From non-linear dynamical models of the phenomena, they concluded that the NTB jet must extend with no significant vertical shear much deeper than the solar radiation deposition level, down to at least the 7 bar pressure level, a layer (between $\sim$ 0.1 bar-7 bar), which is usually referred as the ``weather layer''. This conclusion was previously proposed following similar simulations, although they provided weaker constraints of the previous 1990-event (García-Melendo 2005).

In this work, we focus on the cloud brightness distribution during the NTB disturbance to analyze and characterize the pattern of turbulence caused by the plumes in their wake, and their influence on the jet structure using further observations obtained one year later by the HST (May-July 2008). Therefore, as a continuation of the work by Sánchez-Lavega et al. (2008), we first present a detailed analysis of the NTBD cloud morphology and related brightness spatial frequencies at very different stages, applying a technique similar to that in Barrado-Izagirre et al. (2009). The image properties selected in this work, together with the method employed in their analysis, are described in Sect. 2. Section 3 contains the study of the NTBD brightness spectral distribution analysis. In Sect. 4, we compare our spectral analysis results with the predictions of the disturbance pattern produced by numerical simulations using the EPIC dynamical model. In Sect. 5, we present new measurements of the NTB jet wind velocity profile, one year after the disturbance ended. Finally, Sect. 6 summarizes the main conclusions of our work.

2 Observations and method

For this work, we used images from two different sources: the HST and IOPW archives (see Table 1). All HST images were taken with the Wide Field Planetary Camera 2 (WFPC2), three image sets in 2007 and another one in 2008. Each of the three 2007 sets observe a different NTB dynamical stage (Sánchez-Lavega et al. 2008): (1) a quiescent phase (pre-disturbance) on 25 March; (2) an active NTB disturbance phase from 1 to 11 May; and (3) the post-disturbance phase on 5 June, when both plumes disappear and a uniform low albedo NTB band forms. The only 2008 set that is utilized here shows the situation one year after the perturbation. The filters used in this work are shown in Table 1 (see e.g., Baggett et al. 2002; Sánchez-Lavega et al. 2006, for details). All of these images have a spatial resolution of around 150 km pix^-1. To complete the temporal coverage during the most disturbed period (March-June 2007), we used images obtained with ground-based telescopes contributing to the IOPW survey effort. These images are of lower resolution (about 1000 km pix^-1) but are good enough to study the temporal evolution of the cloud morphology and complete a periodogram analysis of the disturbance features. All of these images are summarized in Table 1. For ``image navigation'', i.e., transformation of pixel position (x, y) on the image into longitude-latitude planetary coordinates, we used the LAIA software (Cano 1998; García-Melendo & Sánchez-Lavega 2001, for details). The images were corrected for limb darkening by applying Minnaert's law (Minnaert 1941) and added to obtain smooth albedo maps (cylindrical projections, see Fig. 1) using the same technique as in Barrado-Izagirre et al. (2009). From these maps, we extract longitudinal scans in a latitude band from 15 $^\circ$ N to 27 $^\circ$ N (planetocentric), every 0.1 $^\circ$ . The scans are transformed to the frequency domain using the Fast Fourier Transform.

Table 1: Summary of the observations.

2.1 Spectral analysis method

The FFT has a two-fold use in this work. First, it is used to determine the characteristic frequency of periodic structures formed after the plume eruption (turbulent patterns in the plumes' wakes). Secondly, to investigate the contribution of each wavenumber to the observed reflectivity field. This helps to compare the spectral slope for the different active or quiescent periods of the NTB. A similar analysis for the entire planet was performed in a previous work Barrado-Izagirre et al. (2009). We use here a non-dimensional wavenumber k

$\begin{displaymath}% k = \frac{{2\pi R(\varphi )\cos (\varphi )}}{L}, \end{displaymath}$

(1)

where $R(\varphi)$ is the planetary radius, $\varphi$ is the planetocentric latitude and L is the spatial wavelength. Therefore, k represents the number of waves that fits into entire longitude circle. Nevertheless, only one of the constituent maps has a complete longitudinal coverage (March 2007) and not all of them cover the same longitude ranges. The different zonal extent between maps requires special care to be taken in the periodogram analysis. To do so, we rescale the transform such that retrieved wavenumbers in a partial map are converted into planetary wavenumbers. We tested this technique using the complete March 2007 map, comparing the analysis of the map (full longitude coverage) with some arbitrarily selected partial scans. We obtained very similar results (see Table 2), which are thoroughly explained later.

Table 2: Power spectrum slopes of the cloud brightness evolution.

Periodogram analysis:

we use the term periodogram here to describe a smooth Fast Fourier Transform with a Lomb-Scargle spectral analysis method (Scargle 1982; Lomb 1976). The periodograms are used to find the characteristic frequency or wavenumber of a periodic signal, evenly or un-evenly spaced. In our case, the periodic signal comes from the reflectivity scans with dark and bright patches that appeared during the disturbance of the NTB after the eruption.

Power spectra analysis:

in this analysis, we analyze how each wavenumber both contributes to the observed intensity and provides information about how this brightness or energy for the numerical simulations is distributed among all spatial scales. This is approximated by a power law function

P(k) = P₀ k^{- n}

(2)

of power spectrum slope n. There are some limitations and drawbacks of this method as explained in Barrado-Izagirre et al. (2009), the most important being the spatial resolution in the images. For this reason, the spectral slope analysis was restricted to higher-resolution HST images. The minimum wavenumber (i.e., the maximum spatial scale) attainable with this method is strongly influenced by the longitudinal coverage of the maps. So we assume a minimum value of k = 10. On the other hand, the resolution and digitalization effects restrict the maximum available wavenumbers, so above k = 90, the power spectra results are unreliable for some images. For all of this, we restricted the power spectra analysis to 10 < k < 90. See Peralta et al. (2007) and Barrado-Izagirre et al. (2009) for further details of the brightness power spectral analysis.

$\begin{figure} \par\includegraphics[width=17cm,clip]{12282fg1.eps} \end{figure}$

Figure 1:

Albedo maps used in the analysis. (A) Complete map of 25 March 2007 from 60 $^\circ$ N to 60 $^\circ$ S, the longitude is represented in System III. Between the two white lines the region of interest is located: the NTB. A steady image is shown of the band, the day that the first eruption appeared in the F410M filter (Sánchez-Lavega et al. 2008). (B) A sequence of planispheres of the NTB from the 12 April to the 11 May, where the evolution in the disturbance can be seen. The first 5 maps consist of images from the IOPW, while the last one consist of two sets of images from HST. The longitudes are represented in a system that rotates with the plume, which is always centered on 20 $^\circ$ . (C) Partial June map with the new quiescent NTB. The IOPW images' authors are Mike Salway, Fabio Carvalho, Christopher Go, and Anthony Wesley.

Open with DEXTER

2.2 Wind measurements

To compare the NTB jet profile with the cloud brightness distribution and search for its temporal variability (Sánchez-Lavega et al. 2008), we measured the motions of atmospheric features by cloud tracking, visually identifying common tracers in image pairs (see Table 1) separated approximately by one planetary rotation ( $\sim 10$ hours). Images were processed using the LAIA software (Cano 1998). The features selected for tracking were usually small enough to ensure a passive behavior of the flow but large enough to survive one Jupiter rotation. Large features, such as vortices, were not used as wind tracers because of their possible own peculiar dynamics. Because of feature pointing and navigation errors, typical velocity errors are formally of the order of the pixel scale to time interval ratio, i.e., about 5 m s^-1. A binning procedure was applied to the resulting profiles in boxes of 1 $^\circ$ latitude. The standard deviation inside these boxes was commonly found to be of the order or lower than the formal velocity error, except in regions of greater meridional shear and a lower number of tracers.

3 Brightness spectral distribution in the jet's clouds

3.1 Morphology

As happened with previous events, the NTB was in a quiescent state when the two plumes erupted, producing a turbulent field in their wake (Sánchez-Lavega et al. 2008). This turbulent field therefore moved slower than the plumes covering an increasing region of the latitude band. This led to a great change in the general morphology of the belt, called the NTBD. Our goal in this section is to characterize the morphology of the region during the evolution of the disturbance.

The plumes (A and B) moved at 169 m s^-1, so they were faster than any other feature in the planet. The cloud-tops of the plumes reached an altitude of $\sim$ 30 km above the surrounding clouds. As a consequence, they were one of the brightest observed features of the planet even being observed in the 2.3 $\mu$ m absorption band. In the 12 April images, when plumes expanded to their largest recorded size, their brightest part covered an area of 20 $\pm$ 1 $\times$ 10⁶ km², and had a zonal extension of 7600 $\pm$ 150 km. Afterwards, the plume started to become progressively dimmer and smaller, and about two weeks later, in the 30 April image set, it appeared with a horizontal area of 6 $\pm$ 0.5 $\times$ 10⁶ km² and a total zonal extension of 3400 $\pm$ 150 km. Other images before and after these two dates are not good enough to determine the size properly. The remaining physical properties of the plumes, including dynamical modeling, are discussed in detail elsewhere (Sánchez-Lavega et al. 2008), so we focus now on the turbulent region formed in the wake of the plumes, especially in the dark patches (Fig. 1).

As can be seen in Fig. 2a, the plumes' wakes consisted of a series of ``dark patches'' that were in general ground-based telescopes to have an elongated shape in the zonal direction. We measured the size (length and area) and shape (aspect ratio) of many of these patches in the maps consisting of IOPW and HST images (from 12 April to 11 May). The patches' areas ranged from 45 $\pm$ 5 $\times$ 10⁶ km² to 1.2 $\pm$ 0.25 $\times$ 10⁶ km². All measured areas are summarized in Fig. 2B (left part) in a histogram that shows the amount of patches in each area range. We note that about 40% of the patches had areas of between 1.3 $\times$ 10⁶ km² and 1.7 $\times$ 10⁶ km². On the other hand, we show in Fig. 2B (right part) a histogram that represents the patches' aspect ratio (zonal elongation divided by meridional elongation), 1-3 being the most common range, indicating the elongated shape.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12282fg2.eps} \end{figure}$	Figure 2: Comparison of local IOPW and HST maps showing the typical morphology of turbulent patches. The bottom panels show the relative frequency histograms of area ( left) and aspect ratio ( right).
Open with DEXTER

In Fig. 3, we can appreciate the apparent morphological differences of the cloud field in each of the maps when observing at different wavelengths: F336W, F410M, F502N, F673N, and F953N. In the ultraviolet (F336W), we observe the higher hazes in the troposphere, while as the wavelength increases to the red, the sounded level becomes deeper in the troposphere until we reach the near infrared (F953N), where we detect the deepest clouds. In general, the cloud morphology in the wake of the plumes, as shown in these high resolution images for the period of activity in May 2007, is consistent with the structure of the meridional jet profile. The clouds acquired a filamentary shape in a tilted linear pattern, longitudinally periodic, associated with the meridional windshear between the adjacent opposing currents at both sides of the jet at 21 $^\circ$ N planetographic latitude. The chevron-like or V-shaped stripes (visible at shorter wavelengths) have their apex in the peak of the eastward jet. The structures oriented according to the ambient shear are more homogeneous and linear at short wavelengths but become turbulent and complex at longer red wavelengths. This is a clear indication of the lower altitude location of the turbulent cloud pattern relative to that of the top of the plumes.

3.2 Spectral analysis

All the maps (HST and IOPW, Fig. 1) were analyzed with the periodogram technique. Since the IOPW images are more sensitive to the red part of the spectra, we focus on the study of the regularly spaced dark patches formed by the disturbance. We used a photometric scan in the latitude region where these structures and the plumes are placed (21 $^\circ$ N planetocentric latitude). Since we wanted to retrieve the periodicity of the dark patch distribution we did not consider the pixels eastward and westward of the perturbed area. As shown in Fig. 4, a strong peak with wavenumber around 20 is retrieved, which is common to all the maps from 12 April to 11 May (NTB disturbed phase). This wavenumber corresponds to a wavelength of $\sim$ 22 000 km and seems to be the dominant spatial frequency of this almost regularly spaced perturbation.

To obtain the brightness power spectra, we applied the second technique. To reduce the noise that accompanies each individual FFT, we performed meridional averages according to the jet profile. Some examples of power spectra are shown in Fig. 5. We defined three latitude domains: the anticyclonic band that extends from 15 $^\circ$ to 21 $^\circ$ planetocentric latitude, the cyclonic band from 21 $^\circ$ to 27 $^\circ$ , and the flanks and peak of the jet from 18 $^\circ$ to 24 $^\circ$ , a region that overlaps with the previous ones. By calculating these averages and a least squares linear fit to the power spectra, we obtain the values of the slopes that are summarized in Table 2. We divided the study into the three dates in 2007 that correspond to three different phases: 25 March (quiescent stage), 1 and 11 May (disturbance), and both 5 June (post-disturbance) and 8 July 2008 (a year later).

$\begin{figure} \par\includegraphics[width=17cm,clip]{12282fg3.eps} \end{figure}$	Figure 3: HST maps of the disturbed NTB in 1 and 11 May 2007 as a function of wavelength from ultraviolet to near-infrared. The horizontal white arrow marks the position of the eastward 21 $^\circ$ N jet peak.
Open with DEXTER

It is obvious that there is a change in the retrieved slope during the development of the disturbance. In the anticyclonic region, the slope value is -1.1 in March. In contrast, we have slopes of around -1.6 for 11 May and in June when the band was completely disturbed. What happens in the jet domain is very similar but the change is steeper, from -0.8 to -1.5. On the other hand, the change in the cyclonic area is milder and in the opposite sense, i.e., the slope decreases in absolute value. The 1 May slopes deviate from this trend but this result is probably incorrect because we have very little longitudinal coverage. This longitude sector appears not to be fully disturbed and lacking in characteristic dark patches (see Sánchez-Lavega et al. 2008, and Fig. 1). The situation in 2008 is somewhat different, with more pronounced slopes, as high as a -1.8 value. Although this is inside the error bars of post-NTBD results, this also indicates the increase in amplitude of large-scale features, as discussed below. In summary, comparison of the power spectral slopes of the pre-disturbed NTB (March 25, 2007) with those of the post-disturbed quiescent NTB (one year later on July 8, 2008) shows a drastic change from -1.0 to -1.8.

4 Wave interpretation of the initial stage

During the NTBD development, the dominant wavenumber (20) suggests that a wave phenomenon may be involved. We know from Sánchez-Lavega et al. (2008) that dark patches move slower than the remaining features of the surroundings at a velocity of about 100 m s^-1. It is tempting to interpret this phenomenon as a wave and in this case we would measure the phase speed c. The mean zonal wind would be that of the jet $\bar u \sim 160$ m s^-1, and therefore $\bar u-c=-60$ m s^-1. The typical wavenumber 20 is transformed to the dimensional wavenumber k=2.8 $\times$ 10^-7 m^-1. Since the wave moves apparently westward relative to the mean flow, it could be a Rossby wave or an inertio-gravity wave. We can check both dispersion relationships from a simple linear perturbation model (Holton 2004). For the inertio-gravity wave

$\begin{displaymath}% (\upsilon - k \bar u)^2 = f_0 ^2 + N^2 \frac{{(k^2 + \ell ^2 )}}{{m^2 }}, \end{displaymath}$

(3)

where k, $\ell$ , and m are the zonal, meridional, and vertical wavenumbers, respectively, $\upsilon$ is the frequency, f₀ is the Coriolis parameter, and N is the Brunt-V $\ddot{\rm a}$ is $\ddot{\rm a}$ l $\ddot{\rm a}$ frequency. We find that $(\upsilon-ku)^2=2.8$ $\times$ 10^-10 s^-2 from our data and that f₀²=1.6 $\times$ 10^-8 s^-2 at 21 $^\circ$ N, so the last term of the equation is always positive, and the dispersion relationship cannot hold. The three dimensional Rossby wave, instead, satisfies

$\begin{displaymath}% \ell ^2 = \frac{{\beta _e }} {{\bar u - c}} - k^2 - \frac{{f^2 }} {{N^2 }}\left( {m^2 + \frac{1} {{4H^2 }}} \right), \end{displaymath}$

(4)

following Salby (1996), Li et al. (2006), and Barrado-Izagirre et al. (2008). The meridional gradient of the zonal mean vorticity $\beta_e$ can be estimated as described in Barrado-Izagirre et al. (2008), so we obtain $\beta_e=15$ $\times$ 10^-12 m^-1 s^-1 (as in Li et al. 2006), $N^{2}\sim 5$ $\times$ 10^-4 s^-2 is the Brunt-V $\ddot{\rm a}$ is $\ddot{\rm a}$ l $\ddot{\rm a}$ frequency, and H = 20 km is the height scale. Therefore, if we use these figures with the dispersion relationship, we obtain

$\begin{displaymath}% \ell ^2 = 1.5 \times 10^{ - 13} - 3.8 \times 10^{ - 5}~{m}^2. \end{displaymath}$

(5)

For no meridional oscillation, i.e., $\ell=0$ , we obtain the maximun value for m, and therefore 0<m<6.3 $\times$ 10^-5 m^-1. This value of m corresponds to a vertical wavelength $L_z=100~{\rm km} = 5H$ , implying wave penetration into the stratosphere. Meanwhile, when there is no vertical oscillation, and m=0, we find that $0<\ell<3.9$ $\times$ 10^-7 m^-1, which corresponds to a minimum value of the meridional wavelength of 16 000 km and is about the width of the jet. This provides an idea of the confinement of the energy if this wave mechanism underlies the observed distribution of dark patches.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12282fg4.eps} \end{figure}$	Figure 4: Photometric scans overhead a map projection ( top) and its corresponding periodogram ( bottom) for three different dates: (A) 12 April 2007, (B) 16 April 2007 and (C) 11 May 2007.
Open with DEXTER

5 Jet speed measurements in 2008

In Fig. 9, we summarize the NTB jet wind profile retrieved from the study of the motions of individual cloud features in the images corresponding to the list of dates in Table 1. The plots for year 2007 come from Sánchez-Lavega et al. (2008). The new result here is the July 2008 profile, obtained one year after the end of the disturbance. This profile was measured by two independent researchers and yielded a total of 76 points from 11 $^\circ$ N to 34 $^\circ$ N. The profile is almost identical to that obtained on 2007 June 5 (Sánchez-Lavega et al. 2008) in both the jet peak value and its shape. However, the most striking variation is found for the westward jet located closer to the equator (18 $^\circ$ N planetographic latitude). This jet changes its peak velocity at cloud level from about -25 m s^-1 in 2007 to almost -50 m s^-1 in 2008, one year after the NTB disturbance. As discussed in Sect. 2.2, this is about five times the maximum expected measurement error and therefore statistically significant. The morphology of this anticyclonic region of the NTB jet and its nearby westward jet is dominated by some large-scale structures and vortices that formed months after the disturbance ended (Fig. 6), wich are not very diferent from those reported after the previous 1990 event (García-Melendo et al. 2000).

6 Numerical simulations of the NTBD

García-Melendo (2005) and Sánchez-Lavega et al. (2008) reported numerical simulations of the NTB disturbance based on the ``explicit planetary isentropic-coordinate'' atmospheric model EPIC (Dowling et al. 1998), a code that numerically solves in terms of spherical geometry, the primitive equations of meteorology. The EPIC calculations allow us to simulate in three dimensions the potential vorticity and energy field of the NTB jet when subjected to a localized small-scale disturbance (in our case, a pulse of heat representing the convective eruption of the plume). The potential vorticity (q) serves as a flow tracer because it is a conserved variable that follows the motion and is defined as (Salby 1996)

$\begin{displaymath}% q = \frac{{\xi + f}} {{ - \frac{1} {g}\left( {\frac{{\partial p}} {{\partial \theta }}} \right)}}, \end{displaymath}$

(6)

where $\xi = \partial v/\partial x - \partial u/\partial y$ is the vertical component of the relative vorticity, (u, v) are the horizontal components of the velocity field, p is pressure, $\theta$ is the potential temperature, g is the acceleration of gravity, and $f = 2\Omega \sin\varphi$ is the Coriolis parameter ( $\Omega$ is Jupiter's angular frequency, and $\varphi$ the latitude). Our simulations were restricted to a narrow channel ranging from latitudes 16 $^\circ$ to 31 $^\circ$ and only 120 $^\circ$ in longitude that covers the NTB jet region, which had a temporal span of 50 days (the duration of the NTBD phenomenon) and a resolution of 0.23 $^\circ$ /pixel. The wind speed was assumed to increase with depth to a certain level and the free parameters were basically, the location of that turning point and the slope of the wind speed versus pressure below it. The dynamical implications of these simulations have been presented elsewhere (see supplementary information in Sánchez-Lavega et al. 2008).

In Fig. 7, we show a frame of this simulation (vorticity and the turbulent kinetic energy, hereafter TKE) corresponding to day 26 when the disturbance was well developed. TKE is defined here to be the kinetic energy per unit mass associated with the turbulent component of the zonal and meridional velocities (u', v')

$\begin{displaymath}% E_K = \frac{1}{2}(u'^2 + v'^2 ), \end{displaymath}$

(7)

where u' and v' are the local deviations from the spatially averaged zonal and meridional velocities

$\begin{displaymath}% u' = \bar u - u; \qquad v' = \bar v - v. \end{displaymath}$

(8)

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12282fg5.eps} \end{figure}$	Figure 5: Three sample brightness power spectra of the planispheres on 25 March's ( left), 11 May's ( middle) and 5 June's ( right) anticyclonic region.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=15.6cm,clip]{12282fg6.eps} \end{figure}$

Figure 6:

Morphology of the NTB region before (25 March 2007), during (11 May 2007), inmediately after (5 June 2007) and one year after the disturbance (8 July 2008). In March 2007, we see a steady NTB, in May 2007, dark patches appear in the wake of the plume, and in June some vortex-like structures being to form. A year later, some ovals emerge at 17 $^\circ$ latitude, equatorward of the jet where the wind speed changes are found. Longitude values are arbitrary. Wind profiles corresponding to each epoch have been superimposed.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=17cm,clip]{12282fg7.eps} %\end{figure}$	Figure 7: EPIC simulations of the disturbance. In the top panels, the potential vorticity and the corresponding periodogram analysis are shown. The bottom panels correspond to the turbulent kinetic energy and its power spectrum.
Open with DEXTER

We assume that the cloud elements act as passive tracers of the flow. The potential vorticity field that traces the flow is then assumed to be directly related to the cloud field structure. This field was analyzed by applying the same procedures used for the reflectivity maps (Fig. 7, upper part). In the periodogram analysis of the potential vorticity field, we obtain results similar to those shown in Fig. 4 with a peak around a planetary wavenumber k = 20 (this peak was obtained by rescaling the wavenumber obtained for a 120 $^\circ$ domain to the complete 360 $^\circ$ domain). The potential vorticity field resembles the NTBD (Fig. 7) reasonably well with this peak disappearing as expected when the head of the disturbance reached the tail of the wake that forms on its western side. However, the power spectrum of the potential vorticity field (same domains as for the reflectivity) is not so satisfactory. The EPIC vorticity field exhibits a very steep slope compared to that produced by the true albedo field. The simulation may have insufficient resolution in potential vorticity values to capture the higher wavenumber features (i.e., smaller spatial scales) present in the images and as a result it may derive slopes that are too steep.

Additionally, we completed a power spectrum analysis of the TKE field (Fig. 7, lower part). The results obtained for the part of the simulation that represents the situation of the disturbed NTB give a slope of around -3 for wavenumbers of between 10 and 100 (Fig. 7). This value varies slightly during the simulated evolution of the disturbance but it is always a little steeper in the cyclonic region than in the anticyclonic one. Across the planetary scale range from 2 to 10, we retrieve a smoother slope of -1.8, close to -5/3. The power spectral slopes from the potential vorticity and TKE simulations differ from those obtained from our cloud brightness distribution analysis.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{12282fg8.eps} \end{figure}$	Figure 8: Evolution of the mean turbulent kinetic energy as a function of the latitude for several simulation days. Shaded areas represent the cyclonic (dark grey) and anticyclonic (light grey) sides of the NTB jet. The dark filled circle sets the latitude where the disturbance emerged.
Open with DEXTER

In Fig. 8, we show the latitudinal profile of the TKE as a function of time during the first 40 days. This graph was obtained by averaging TKE values in narrow channels in EPIC simulations between contiguous latitudes. These results suggest a transfer of turbulent kinetic energy from the latitude circle where the eruption started (the source of the disturbance in our simulations), i.e., the peak of the jet, toward the anticyclonic side of the jet.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12282fg9.eps} \end{figure}$	Figure 9: Zonal wind profile of the NTB jet for 2007 (March 25 and June 6) and 2008 (July 8) observations. The 2007 profiles are taken from (Sánchez-Lavega et al. 2008). The 2008 profile (binned in 1 $^\circ$ boxes) is from this work.
Open with DEXTER

7 Discussion and conclusions

We have used a comprehensive set of images at different wavelengths in the visible range (from ultraviolet to near-infrared) to study the spatial spectral characteristics of the cloud brightness distribution, before, during, and after a large disturbance occurred in the most intense jet of Jupiter. The resulting data were compared with those obtained using numerical simulations of the disturbance that employed the EPIC code. In addition, we have studied the jet stability one year after the disturbance dissipated, when, the NTB jet had the same peak velocities and only a more symmetric configuration, relative to the latitude of the peak velocity, but where we find a substantial change in the westward jet located equatorwards of the NTB. The EPIC non-linear dynamical simulations that most closely represented the evolution of the early perturbation stages inferred an expansion of TKE to the anticyclonic side of the jet. Our conclusion is that the disturbance produced a redistribution of the spatial structure of the cloud brightness within the anticyclonic flank of the eastward jet. At the same time, a change occurred in the contiguous westward jet of this anticyclonic band. We propose that a momentum transfer occurred from the disturbance structures, to the westward zonal jet. The band changed from being chaotic and dominated by small-scale structure before and during the disturbance, to a more organized configuration dominated by large-scale vortices. This is in good agreement with the increase in the slope of the brightness power spectra reported above. We have also verified that the disturbed cloud field (dark patches) could be consistent with the Rossby wave dispersion relationship. The dissipation of this wave could have injected westward momentum into the 16 $^\circ$ jet, in the anticyclonic region of the high speed jet, increasing its speed as observed. Salyk et al. (2006) reported a momentum injection from eddies to some zonal jets. This agrees with our simulation results reported in the previous section, where the change in the westward jet velocity and morphology could be the result of momentum injection from the disturbance into the jet. So, in short, what we are witnessing here is a change in the brightness distribution and a simultaneous change in the dynamics. A correct understanding of how these two problems are linked, or even if they are linked at all, could be essential to understanding how energy is transferred in the Jovian atmosphere.

Acknowledgements

This work has been funded by Spanish MEC AYA2006-07735 with FEDER support and Grupos UPV 15946/2004 and Grupos GV IT464-07. N. Barrado-Izagirre acknowledges a fellowship from UPV/EHU. We acknowledge the IOPW (International Outer PlanetWatch) team for their dedication in observing Jupiter and, specially, the observers who mainly contributed to this research, specially: F. Carvalho, C. Go, M. Salway and A. Wesley. Based on observations made with the NASA/ESA Hubble Space Telescope, obtained from the data archive at the Space Telescope Institute. STScI is operated by the association of Universities for Research in Astronomy, Inc. under the NASA contract NAS 5-26555. We made use of the computer facilities at CESCA in Barcelona with the help of the Ministerio de Educación y Ciencia.

References

Baggett, S., McMaster, M., Biretta, J., et al. 2002, HST WFPC2 Data Handbook, B. Mobasher, Baltimore, STScI
Barrado-Izagirre, N., Sánchez-Lavega, A., Pérez-Hoyos, S., & Hueso, R. 2008, Icarus, 194, 173 [CrossRef] [NASA ADS]
Barrado-Izagirre, N., Sánchez-Lavega, A., & Pérez-Hoyos, S. 2009, Icarus, 202, 181 [CrossRef] [NASA ADS]
Cano, J. 1998, in Grup d'Estudis Astronómics, Barcelona
Dowling, T. E., Fischer, A. S., Gierasch, P. J., et al. 1998, Icarus, 132, 221 [CrossRef] [NASA ADS]
García-Melendo, E. 2005, Ph.D. Thesis, Universidad Politécnica de Cataluña, Barcelona
García-Melendo, E., & Sánchez-Lavega, A. 2001, Icarus, 152, 316 [CrossRef] [NASA ADS]
García-Melendo, E., Sánchez-Lavega, A., Gómez, J. M., et al. 2000, Icarus, 146, 514 [CrossRef] [NASA ADS]
Holton, J. R. 2004, An introduction to dynamic meteorology, International Geophys. Ser. (San Diego, New York: Academic Press), 4rd edn.
Hueso, R., Sánchez-Lavega, A., & Guillot, T. 2002, J. Geophys. Research (Planets), 107, 5075 [CrossRef] [NASA ADS]
Ingersoll, A. P., Dowling, T. E., Gierasch, P. J., et al. 2004, Dynamics of Jupiter's atmosphere, Jupiter. The Planet, Satellites and Magnetosphere, 105
Li, L., Ingersoll, A. P., Vasavada, A. R., et al. 2006, Icarus, 185, 416 [CrossRef] [NASA ADS]
Lomb, N. R. 1976, Ap&SS, 39, 447 [CrossRef] [NASA ADS]
Minnaert, M. 1941, ApJ, 93, 403 [CrossRef] [NASA ADS]
Peek, P. M. 1958, The planet Jupiter (London: Faber and Faber)
Peralta, J., Hueso, R., & Sánchez-Lavega, A. 2007, Icarus, 188, 305 [CrossRef] [NASA ADS]
Porco, C. C., West, R. A., McEwen, A., et al. 2003, Science, 299, 1541 [CrossRef] [NASA ADS]
Rogers, J. H. 1995, The giant planet Jupiter (Cambridge, New York, NY, USA: Cambridge University Press)
Salby, M. L. 1996, Fundamentals of Atmospheric Physics (San Diego, USA: Academic Press), International Geophys. Ser., 61
Salyk, C., Ingersoll, A. P., Lorre, J., Vasavada, A., & Del Genio, A. D. 2006, Icarus, 185, 430 [CrossRef] [NASA ADS]
Sánchez-Lavega, A., & Quesada, J. A. 1988, Icarus, 76, 533 [CrossRef] [NASA ADS]
Sánchez-Lavega, A., Miyazaki, I., Parker, D., Laques, P., & Lecacheux, J. 1991, Icarus, 94, 92 [CrossRef] [NASA ADS]
Sánchez-Lavega, A., Hueso, R., Pérez-Hoyos, S., & Rojas, J. 2006, Icarus, 184, 524 [CrossRef] [NASA ADS]
Sánchez-Lavega, A., Orton, G. S., Hueso, R., et al. 2008, Nature, 451, 437 [CrossRef] [NASA ADS]
Scargle, J. D. 1982, ApJ, 263, 835 [CrossRef] [NASA ADS]
Vasavada, A. R., & Showman, A. P. 2005, Reports on Progress in Phys., 68, 1935 [CrossRef] [NASA ADS]

All Tables

Table 1: Summary of the observations.

Table 2: Power spectrum slopes of the cloud brightness evolution.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.