| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 85 - 103 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912246 | |
| Published online | 27 August 2009 | |
A&A 507, 85-103 (2009)
The ESO/VLT 3rd year Type Ia supernova
data set
from the supernova legacy survey![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
C. Balland1,2 - S. Baumont1 - S. Basa3 - M. Mouchet4,5 - D. A. Howell6,7 - P. Astier1 - R. G. Carlberg8 - A. Conley8 - D. Fouchez9 - J. Guy1 - D. Hardin1 - I. M. Hook10 - R. Pain1 - K. Perrett8 - C. J. Pritchet11 - N. Regnault1 - J. Rich12 - M. Sullivan10 - P. Antilogus1 - V. Arsenijevic13,14 - J. Le Du9 - S. Fabbro13 - C. Lidman15 - A. Mourão13 - N. Palanque-Delabrouille12 - E. Pécontal16,17 - V. Ruhlmann-Kleider12
1 - LPNHE, CNRS-IN2P3 and Universities of Paris 6 & 7, 75252
Paris Cedex 05, France
2 - University Paris 11, 91405 Orsay, France
3 - LAM, CNRS, BP8, Pôle de l'étoile, Site de Château-Gombert,
38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
4 - APC, UMR 7164 CNRS, 10 rue Alice Domon et Léonie Duquet, 75205
Paris Cedex 13, France
5 - LUTH, UMR 8102 CNRS, Observatoire de Paris, Section de Meudon,
92195 Meudon Cedex, France
6 - Las Cumbres Observatory Global Telescope Network, 6740 Cortona Dr.,
Suite 102, Goleta, CA 93117, USA
7 - Department of Physics, University of California, Santa Barbara,
Broida Hall, Mail Code 9530, Santa Barbara, CA 93106-9530, USA
8 - Department of Astronomy and Astrophysics, 50 St. George Street,
Toronto, ON M5S 3H4, Canada
9 - CPPM, CNRS-Luminy, Case 907, 13288 Marseille Cedex 9, France
10 - University of Oxford, Astrophysics, Denys Wilkinson Building,
Keble Road, Oxford OX1 3RH, UK
11 - Department of Physics and Astronomy, University of Victoria, PO
Box 3055, Victoria, BC V8W 3P6, Canada
12 - CEA/Saclay, DSM/Irfu/Spp, 91191 Gif-sur-Yvette Cedex, France
13 - CENTRA-Centro M. de Astrofisica and Department of Physics, IST,
Lisbon, Portugal
14 - SIM/IDL, Faculdade de Ciências da Universidade de Lisboa, Campo
Grande, C8, 1749-016 Lisbon, Portugal
15 - Oskar Klein Center, Roslagstullsbacken 21, 106 91 Stockholm,
Sweden
16 - CRAL, Observatoire de Lyon; CNRS, UMR 5574; ENS de Lyon, France
17 - Université de Lyon, 69622, Lyon, France; Université Lyon 1, France
Received 1 April 2009 / Accepted 20 August 2009
Abstract
Aims. We present 139 spectra of 124 Type Ia
supernovae (SNe Ia) that were observed at the ESO/VLT during
the first three years of the Canada-France-Hawaï Telescope (CFHT)
supernova legacy survey (SNLS). This homogeneous data set is used to
test for redshift evolution of SN Ia spectra, and will be used
in the SNLS 3rd year cosmological analyses.
Methods. Spectra have been reduced and extracted
with a dedicated pipeline that uses photometric information from deep
CFHT legacy survey (CFHT-LS) reference images to trace, at sub-pixel
accuracy, the position of the supernova on the spectrogram as a
function of wavelength. It also separates the supernova and its host
light in ![]() 60%
of cases. The identification of the supernova candidates is performed
using a spectrophotometric SN Ia model.
60%
of cases. The identification of the supernova candidates is performed
using a spectrophotometric SN Ia model.
Results. A total of 124 SNe Ia, roughly 50%
of the overall SNLS spectroscopic sample, have been identified using
the ESO/VLT during the first three years of the survey. Their redshifts
range from z=0.149 to z=1.031.
The average redshift of the sample is
![]() .
This constitutes the largest SN Ia spectral set to date in
this redshift range. The spectra are presented along with their
best-fit spectral SN Ia model and a host model where relevant.
In the latter case, a host subtracted spectrum is also presented. We
produce average spectra for pre-maximum, maximum and post-maximum
epochs for both z<0.5 and
.
This constitutes the largest SN Ia spectral set to date in
this redshift range. The spectra are presented along with their
best-fit spectral SN Ia model and a host model where relevant.
In the latter case, a host subtracted spectrum is also presented. We
produce average spectra for pre-maximum, maximum and post-maximum
epochs for both z<0.5 and ![]() SNe Ia. We find that z<0.5 spectra
have deeper intermediate mass element absorptions than
SNe Ia. We find that z<0.5 spectra
have deeper intermediate mass element absorptions than ![]() spectra. The differences with redshift are consistent with the
selection of brighter and bluer supernovae at higher redshift.
spectra. The differences with redshift are consistent with the
selection of brighter and bluer supernovae at higher redshift.
Key words: cosmology: observations - supernovae: general - methods: data analysis - techniques: spectroscopic
1 Introduction
Since the direct detection of the accelerated expansion of the universe 10 years ago (Riess et al. 1998; Perlmutter et al. 1999), constraining the equation of state of the dark energy component responsible for this acceleration has been a major goal of observational cosmology. Type Ia supernovae (SNe Ia hereafter) samples have been gathered at low and high redshift and extensively used for this purpose. When combined with other probes, the picture of a universe dominated by dark energy emerges (Astier et al. 2006; Wood-Vasey et al. 2007; Kowalski et al. 2008; Riess et al. 2007; Tonry et al. 2003).
Over the past five years![]() ,
the
supernova legacy survey (SNLS) has gathered more than 1000 light
curves of SN Ia candidates on the Canada-France-Hawaï
telescope
(CFHT) using MEGACAM (Boulade
et al. 2003),
thanks to a rolling
search technique for discovery and photometric follow up of
SNe Ia in
four 1 square degree fields (Astier
et al. 2006). Spectra of a subset
(about half) of these SNe Ia candidates have been observed on
various 8
to 10-m class telescopes (VLT, Gemini N and S, Keck I and II). About
50% of spectroscopically observed SN candidates were observed at the
VLT.
,
the
supernova legacy survey (SNLS) has gathered more than 1000 light
curves of SN Ia candidates on the Canada-France-Hawaï
telescope
(CFHT) using MEGACAM (Boulade
et al. 2003),
thanks to a rolling
search technique for discovery and photometric follow up of
SNe Ia in
four 1 square degree fields (Astier
et al. 2006). Spectra of a subset
(about half) of these SNe Ia candidates have been observed on
various 8
to 10-m class telescopes (VLT, Gemini N and S, Keck I and II). About
50% of spectroscopically observed SN candidates were observed at the
VLT.
In this paper, we present the VLT SN Ia spectral set
for the first
three years of operation of the SNLS. The non SN Ia spectral
set,
together with a description of the ``real-time'' operations and
procedures will be presented elsewhere (Basa
et al. 2009). The spectra
shown here were obtained in the period running from June 1st, 2003 up
to July 31st, 2006, as part of two large VLT programs![]() . The spectra
have been analysed using novel techniques for extraction and
identification which have been described in detail elsewhere
(Baumont
2007; Baumont
et al. 2008). For each spectrum we provide a
redshift
estimate. The identification of SNe Ia relies in part on human
judgement, using the SALT2 spectral template of Guy
et al. (2007) as a
guide (see Baumont
et al.
2008).
. The spectra
have been analysed using novel techniques for extraction and
identification which have been described in detail elsewhere
(Baumont
2007; Baumont
et al. 2008). For each spectrum we provide a
redshift
estimate. The identification of SNe Ia relies in part on human
judgement, using the SALT2 spectral template of Guy
et al. (2007) as a
guide (see Baumont
et al.
2008).
The SN spectra presented here will be used, along with
SN Ia spectra
obtained at Gemini and Keck telescopes, to build the 3rd year
SNLS
Hubble diagram. Our primary goal is that the type and redshift of the
SNe Ia used for cosmological analysis are secure. In this
paper, we
consider two classes of events: secure SNe Ia
(``SN Ia'') and probable
SNe Ia (``SN Ia![]() ''). Studying the statistical
properties of these
two classes, in order to assess the validity of using SN Ia
''). Studying the statistical
properties of these
two classes, in order to assess the validity of using SN Ia![]() events
together with SN Ia events, is therefore a goal of this paper.
events
together with SN Ia events, is therefore a goal of this paper.
SN Ia spectra are a rich source of physical
information about their
progenitor history and environment. The possibility of evolution
among SN Ia populations at low and high redshifts has been the
subject
of considerable attention in recent years, as more and more
SN Ia spectral sets become available
(Ellis
et al. 2008; Foley
et al. 2008a; Blondin
et al. 2006; Garavini
et al. 2007; Bronder
et al. 2008). Recently,
evidence has even been found for a demographic evolution among
SN Ia
populations, resulting in higher stretch, more luminous SNe Ia
at
higher redshift (Sullivan
et al. 2009; Howell
et al. 2007).
Using SN Ia spectra to
compare their physical properties at low- and high-redshift is
therefore a useful cross-check when using SN Ia to constrain
the
expansion history of the universe. In this paper, we take advantage of
the large number of high quality spectra obtained at the VLT to build
average composite spectra at various phases with respect to maximum
light for z<0.5 and ![]() .
We also compare our average spectra
to composite spectra obtained in a similar way with different data
sets (Ellis
et al. 2008; Foley et al.
2008a) and
discuss the significance of the
differences found in terms of possible evolution or selection effects.
.
We also compare our average spectra
to composite spectra obtained in a similar way with different data
sets (Ellis
et al. 2008; Foley et al.
2008a) and
discuss the significance of the
differences found in terms of possible evolution or selection effects.
A plan of the paper follows. In Sect. 2, we briefly
describe
the SNLS photometric survey and the VLT spectral observation programs.
In Sect. 3,
we summarise the main steps of the data
reduction and spectrum extraction. We detail our identification
procedure and classification scheme in Sect. 4. In
Sect. 5,
the spectra are
individually presented. Composite
spectra at z<0.5 and ![]() are built in Sect. 6.
In Sect. 7,
we discuss our sample in the light of
other existing SN Ia spectroscopic data. Concluding remarks
are made in
Sect. 8.
are built in Sect. 6.
In Sect. 7,
we discuss our sample in the light of
other existing SN Ia spectroscopic data. Concluding remarks
are made in
Sect. 8.
2 SNLS observations
2.1 The SNLS imaging survey
The SNLS is composed of an imaging survey devoted to the detection and
the photometric follow up of SN candidates, and a spectroscopic survey
of a sample of the detected candidates, prioritised for spectroscopy
on various telescopes. The imaging survey ran from June 2003,
after a
period of pre-survey, until June 2008. It was based on the Deep survey
of the Canada-France-Hawaii Telescope legacy survey (CFHT-LS)
(amounting to half of the 474 nights allocated to the CFHT-LS). Full
details of the survey can be found elsewhere (Astier
et al. 2006). In
brief, SNLS observed 4 fields (D1-4) every 3-5 nights during
dark/grey time in the griz filters, each field
followed for 5-6 lunations per year. Around 1000 well
sampled multi-colour light
curves of SN Ia candidates have been obtained up to ![]() .
.
2.2 Spectroscopic follow-up
Spectroscopy of SNLS SN candidates was performed on several 8 to 10-m class telescopes in both hemispheres, namely the VLT, Gemini-N and S, Keck I and II. Almost 50% of SNLS candidates identified as certain or probable SN Ia were spectroscopically observed at the VLT. Howell et al. (2005) and Bronder et al. (2008) describe the SNLS first three years of Gemini spectral data (up to May 2006), while Ellis et al. (2008) present 36 high signal-to-noise ratio (S/N) SN Ia spectra obtained at Keck. In this paper, we focus on spectra taken at the VLT on Cerro Paranal.
Candidate selection for spectroscopic follow-up was based on the multi-band photometry procedure of Sullivan et al. (2006). This selection was performed on the rising part of the light curves, routinely available thanks to the rolling search strategy (see e.g., Perrett et al. 2009). Candidates were generally sent for spectroscopy at, or slightly after, maximum light, which optimised the time budget allocated for spectroscopy. We triggered a target on VLT every three to four days during dark and grey time.
During the first large program (2003-2005), we performed long
slit
spectroscopy (LSS) of SN candidates on FORS1 for a total
of 60 h
of dark/grey time per semester. During the second large program
(2005-2007), we observed using both FORS1 and FORS2 with the standard
collimator in LSS and multi object spectroscopy (MOS)
mode![]() . Most observations were
carried out with the 300V grism,
along with the GG435 order-sorting filter. Grism 300V was chosen to
optimise spectral resolution, spectral coverage and high enough S/Nfor
an unambiguous identification, even for the faintest candidates of
our survey (
. Most observations were
carried out with the 300V grism,
along with the GG435 order-sorting filter. Grism 300V was chosen to
optimise spectral resolution, spectral coverage and high enough S/Nfor
an unambiguous identification, even for the faintest candidates of
our survey (
![]() ). Moreover, using the 300V
grism for
high redshift SNe allows us to study the interesting rest frame UV
region of the spectra. The pixel scale is 0.2'' along the spatial
axis and 2.65
). Moreover, using the 300V
grism for
high redshift SNe allows us to study the interesting rest frame UV
region of the spectra. The pixel scale is 0.2'' along the spatial
axis and 2.65 ![]() along the dispersion axis. At 5000
along the dispersion axis. At 5000 ![]() ,
the
resolution limit with this setup is
,
the
resolution limit with this setup is ![]() 11
11 ![]() .
The
efficiency of the 300V grism peaks around 4700
.
The
efficiency of the 300V grism peaks around 4700 ![]() at a level of
at a level of
![]()
![]() .
The 300I grism along with the OG590 order-sorting
filter was sometimes used for the faintest (z>
0.8)
SNe. Being
typically more distant, and due to strong sky emission and fringing
beyond 6000
.
The 300I grism along with the OG590 order-sorting
filter was sometimes used for the faintest (z>
0.8)
SNe. Being
typically more distant, and due to strong sky emission and fringing
beyond 6000 ![]() ,
spectra obtained in this way have a much lower S/Nthan
those acquired with the 300V grism.
,
spectra obtained in this way have a much lower S/Nthan
those acquired with the 300V grism.
The slit width was chosen according to the following rule of
thumb:
``slit width ![]() seeing + 0.2'''', as a compromise between
observing most of the flux from the targeted candidate and limiting
the sky background flux. An air mass
seeing + 0.2'''', as a compromise between
observing most of the flux from the targeted candidate and limiting
the sky background flux. An air mass ![]() was required for each
spectroscopic observation. A ``blind offset'' technique was used to
target the candidate, using a bright star located
within <1' of the
target and then offsetting the telescope to position the slit onto the
candidate. When possible, the slit position was chosen to observe both
the SN and its host. Differential slit losses were corrected by a
Longitudinal Atmospheric Dispersion Corrector (LADC). Residual losses
are taken into account with the recalibration procedure described in
Sect. 4.2.
was required for each
spectroscopic observation. A ``blind offset'' technique was used to
target the candidate, using a bright star located
within <1' of the
target and then offsetting the telescope to position the slit onto the
candidate. When possible, the slit position was chosen to observe both
the SN and its host. Differential slit losses were corrected by a
Longitudinal Atmospheric Dispersion Corrector (LADC). Residual losses
are taken into account with the recalibration procedure described in
Sect. 4.2.
All spectra were acquired in Service Observing mode. With a
limiting
magnitude of ![]() ,
3-4 exposures of 750 or 900 s were taken
for each candidate, with small offsets along the spatial axis (Y;
the dispersion axis X is horizontal with our
setup). Thanks to the
regular time sampling of the rolling search, it was possible to
acquire most of candidates around or slightly past maximum light.
,
3-4 exposures of 750 or 900 s were taken
for each candidate, with small offsets along the spatial axis (Y;
the dispersion axis X is horizontal with our
setup). Thanks to the
regular time sampling of the rolling search, it was possible to
acquire most of candidates around or slightly past maximum light.
3 Data processing
Data reduction and spectral extraction were performed in two separate ways. A quick, ``real-time'' analysis (within a day of acquisition) was used to assess the type and redshift of the candidate (Basa et al. 2009), an essential task for efficiently allocating other candidates to the various telescopes. In parallel, we developed tools ``off-line'' to cleanly extract the SN from its host. A dedicated pipeline, PHASE (PHotometry Assisted Spectral Extraction), was used for the final reduction and extraction (Baumont 2007; Baumont et al. 2008). Full details can be found in these papers; we give only a brief description here. All extractions presented in this paper used the PHASE technique.
The PHASE reduction technique improves over the real-time reductions in refinements of the master flat-fields, the dispersion relation, and in the sky estimation. As an example, the 2D dispersion relation is modeled by a fourth order polynomial in Xi (and of 2nd order in Yi and XYi) to further reduce the residuals. For flux calibration, we build a single average response curve (one for UT1 and one for UT2 as FORS1 moved from UT1 to UT2 in June 2005) from previous individual standard star observations. We prefer using a well controlled average response for the whole set, rather than using a response built from standard star observations of a different night. This is at the expense of absolute flux calibration, as we average out sky transmission variations from night to night, but permits a more robust estimation of the sensitivity function near the blue edge of the order sorting filter.
PHASE extraction uses photometric
information on the SN location
and host brightness from the deep reference images (
![]() )
used for building the SN light curves
)
used for building the SN light curves![]() .
This allows us to accurately trace the SN
position along the dispersion axis on the two-dimensional spectrogram.
Moreover, we build a multi-component model of the galaxies present in
the slit (including the host, if resolved) by measuring the spatial
photometric profiles of these galaxies on the deep stacked reference
images projected along the slit direction. We then add a SN component,
modeled as a Gaussian of width equal to the seeing of the
spectroscopic observation. The location of the SN is accurately known
from the light curves. The flux of each component (SN + host and
potentially other galaxies in the slit) is a free parameter, the sum
of the profile fluxes being normalised to unity. Such a model is built
for each column (the dispersion direction is horizontal with our
setup) and fluxes assigned to each component in each column i
are
estimated by a
.
This allows us to accurately trace the SN
position along the dispersion axis on the two-dimensional spectrogram.
Moreover, we build a multi-component model of the galaxies present in
the slit (including the host, if resolved) by measuring the spatial
photometric profiles of these galaxies on the deep stacked reference
images projected along the slit direction. We then add a SN component,
modeled as a Gaussian of width equal to the seeing of the
spectroscopic observation. The location of the SN is accurately known
from the light curves. The flux of each component (SN + host and
potentially other galaxies in the slit) is a free parameter, the sum
of the profile fluxes being normalised to unity. Such a model is built
for each column (the dispersion direction is horizontal with our
setup) and fluxes assigned to each component in each column i
are
estimated by a ![]() minimisation where:
minimisation where:
Here,
- PSF: unresolved, point-like galaxies;
- EXT: extended, but regularly shaped profiles, e.g. ellipticals;
- Mix: extended, but irregularly shaped profiles, e.g. galaxies with spiral arms.
In the first case, the galactic component of the model is a
Gaussian
of width equal to the seeing of the deep reference observation. The
seeing variation with wavelength is estimated from standard star
spectra as a power law of index ![]() -0.3, in good agreement with
Blondin
et al. (2005)
measurements on FORS1 spectra. In the second case,
the model is the ``bolometric'' spatial profile (the sum of the
galactic profile in all observed filters) as measured on the MEGACAM
combined deep reference images. For the third case, we use
a mixture of a Gaussian with width equal to the spectroscopic seeing
to model the core and the photometric spatial profile to model the
extended arms. From a pure algorithmic point of view, this latter case
is equivalent to have two distinct galaxies, a point-like source and
an extended one.
-0.3, in good agreement with
Blondin
et al. (2005)
measurements on FORS1 spectra. In the second case,
the model is the ``bolometric'' spatial profile (the sum of the
galactic profile in all observed filters) as measured on the MEGACAM
combined deep reference images. For the third case, we use
a mixture of a Gaussian with width equal to the spectroscopic seeing
to model the core and the photometric spatial profile to model the
extended arms. From a pure algorithmic point of view, this latter case
is equivalent to have two distinct galaxies, a point-like source and
an extended one.
Host models used to extract our VLT spectra are about equally
divided
into EXT and PSF models (![]() 30% each),
with only a few percent of
cases being Mix models. In the remaining
30% each),
with only a few percent of
cases being Mix models. In the remaining ![]()
![]() of cases, no
separate extraction of the SN and the host was possible.
of cases, no
separate extraction of the SN and the host was possible.
PHASE uses a set of default parameters to select the correct host model and make the extraction as automatic as possible. These parameters include cuts on flux, galactic compactness, extension minimum level, colour variation between the centre and the extended part of the host (identifying ``Mix'' host types), and a minimum value of the SN to host centre distance to perform a separate extraction (usually 0.15'', a bit less than one pixel). These default parameters allow an automatic extraction of most spectra, though the parameters can be adjusted for specific cases. PHASE performance and limitations have been discussed in Baumont et al. (2008) and we refer the reader to that paper.
The main hypotheses in using PHASE are that 1) the PSF is a
Gaussian
of width equal to the seeing; 2) the coordinates of the SN are
accurate; 3) CFHT-LS reference images and VLT spectrograms have
comparable seeings; 4) no flux of the SN is present in the reference
image. Any deviation from these assumptions result in weak flux
losses, increased noise, and contamination of a SN spectrum by its
host. PHASE performs well for most spectra encountered. In particular,
it succeeds at recovering the SN from the host, even in the case of a
SN located close to the host centre (typically ![]() 1 pixel):
strong correlations between the host and the SN are often unavoidable
in standard extractions. Even for ``non favourable'' cases, such as
sub-pixel SN/host separations, both component spectra are recovered
and are essentially non correlated. This is a remarkable feature of
our pipeline, as most SN spectral extractions are hampered by host
contamination in these cases. Nevertheless, if the SN is too close to
the host centre (separation less than one fifth of the seeing), no
separate extraction is possible. In that case, a host spectral
template is used at the stage of identification to estimate the host
contamination (see Sect. 4.3).
1 pixel):
strong correlations between the host and the SN are often unavoidable
in standard extractions. Even for ``non favourable'' cases, such as
sub-pixel SN/host separations, both component spectra are recovered
and are essentially non correlated. This is a remarkable feature of
our pipeline, as most SN spectral extractions are hampered by host
contamination in these cases. Nevertheless, if the SN is too close to
the host centre (separation less than one fifth of the seeing), no
separate extraction is possible. In that case, a host spectral
template is used at the stage of identification to estimate the host
contamination (see Sect. 4.3).
A comparison between PHASE and standard extractions has been
done and
illustrated on a few examples in Baumont
et al. (2008). A major
difference is that, in PHASE, we do not re-sample the data until the
final step of flux calibration. This avoids introducing correlations
across pixels and allows us to trace the statistical noise along the
reduction and extraction procedure. For the same reason, we also avoid
rebinning the data at a constant wavelength step, as is done in most
standard spectroscopic reduction pipelines. As a consequence, the
final PHASE calibrated spectrum has unequal steps. We have checked
that the statistical noise is properly propagated with PHASE by
computing ![]() ,
the S/N per pixel averaged over
the whole spectral
range, and
,
the S/N per pixel averaged over
the whole spectral
range, and ![]() ,
the signal-to-rms ratio. Here,
,
the signal-to-rms ratio. Here, ![]() is
the standard deviation of a group of measurements around a low-order
polynomial fit. We find relatively good agreement between these two
quantities for PHASE extracted spectra.
is
the standard deviation of a group of measurements around a low-order
polynomial fit. We find relatively good agreement between these two
quantities for PHASE extracted spectra.
4 Spectral analysis
4.1 Redshift determination
Where possible, a redshift is obtained from the host galaxy spectrum
using characteristic emission or absorption lines, yielding a typical
uncertainty of 0.001 on the redshift (Baumont
et al. 2008). When no lines
are detected, the redshift is determined from the fit of a model to
the SN spectrum (see Sect. 4.2). The
typical redshift
uncertainty is then ![]() ,
due to the diversity of
ejecta velocities among SNe Ia, (e.g., Hachinger
et al. 2006).
In
about 80% of cases, the redshift is obtained from host emission
and/or absorption lines. The redshifts (as well as identifications,
see below) have been carefully cross-checked using the two-dimensional
data to match host lines. Checking the corresponding noise map,
``bright'' spots visible on the 2D frames are easily identified as
true emission lines or cosmic/sky subtraction residuals.
,
due to the diversity of
ejecta velocities among SNe Ia, (e.g., Hachinger
et al. 2006).
In
about 80% of cases, the redshift is obtained from host emission
and/or absorption lines. The redshifts (as well as identifications,
see below) have been carefully cross-checked using the two-dimensional
data to match host lines. Checking the corresponding noise map,
``bright'' spots visible on the 2D frames are easily identified as
true emission lines or cosmic/sky subtraction residuals.
4.2 Identifying SNe Ia
To identify SNe Ia, we use a minimisation procedure using the
SALT2
spectral template of Guy
et al.
(2007) with a combined fit of the light
curves and the spectrum consistently performed (Baumont
et al. 2008). As
the training sample of the SALT2 model only contains SN Ia
spectra and
light-curves, it does not allow a direct identification of
non-SN Ia
objects. However, the best-fitting parameter values obtained when
fitting a non-SN Ia with SALT2 are in themselves an indirect
indication of the SN type (see Sect. 5.4). In
addition,
a ![]() template-fitting code (Howell
et al. 2005) has been used for
cross-check. Both techniques use varying levels of human judgement.
template-fitting code (Howell
et al. 2005) has been used for
cross-check. Both techniques use varying levels of human judgement.
The main output parameters of the SALT2 fit
are 1) the light curve fit
parameters x0 (overall
normalisation), x1 (light
curve shape),
and colour c;
and 2) spectroscopic fit parameters: the host
fraction
![]() in the model when relevant,
and recalibration parameters.
The latter enter a recalibration function applied to the photometric
model in order to fit the spectrum and account for possible errors in
flux calibration (Guy
et al. 2007).
This function is a polynomial of
order n, with coefficients
in the model when relevant,
and recalibration parameters.
The latter enter a recalibration function applied to the photometric
model in order to fit the spectrum and account for possible errors in
flux calibration (Guy
et al. 2007).
This function is a polynomial of
order n, with coefficients ![]() inside an exponential (to
ensure positivity). We usually only use two recalibration parameters:
an overall normalisation
inside an exponential (to
ensure positivity). We usually only use two recalibration parameters:
an overall normalisation ![]() and a first order coefficient
and a first order coefficient
![]() (tilt
applied at rest frame 4400
(tilt
applied at rest frame 4400 ![]() ), adding higher
order corrections for a few objects. The x1
parameter is a light
curve shape parameter that can be converted into a stretch factor sor
), adding higher
order corrections for a few objects. The x1
parameter is a light
curve shape parameter that can be converted into a stretch factor sor
![]() parameter of Phillips (1993);
see Guy
et al. (2007).
The colour c parameter is defined as the difference
between
parameter of Phillips (1993);
see Guy
et al. (2007).
The colour c parameter is defined as the difference
between
![]() and the average
and the average
![]() value at maximum light for the
whole training sample of SALT2.
value at maximum light for the
whole training sample of SALT2.
There are some advantages in using SALT2 as a tool for
identification.
First, the fit of the light curve yields the date of maximum light.
The phase ![]() of the spectrum (the number of rest frame days
between the date of B-band maximum and the date of
acquisition of
the spectrum) is accurately known, usually within a fraction of day.
This alleviates possible degeneracies between SN types, such as
between pre-maximum Type Ic supernovae (SNe Ic) and
post-maximum
SNe Ia, whose spectra show similarities. Second, the training
set of
the SALT2 model is built from a large collection of spectra and light
curves from local and distant SNe Ia. These latter include
SNLS SNe
themselves, added to the training sample once identified. Third,
using a model instead of a set of spectrum templates (as is typical of
standard identification techniques) alleviates the problems due to
unavoidable incompleteness in phase and wavelength coverage of the
template libraries: all SNe are treated on an equal footing. Note also
that only SNe typed as SN Ia (as opposed to SNIa
of the spectrum (the number of rest frame days
between the date of B-band maximum and the date of
acquisition of
the spectrum) is accurately known, usually within a fraction of day.
This alleviates possible degeneracies between SN types, such as
between pre-maximum Type Ic supernovae (SNe Ic) and
post-maximum
SNe Ia, whose spectra show similarities. Second, the training
set of
the SALT2 model is built from a large collection of spectra and light
curves from local and distant SNe Ia. These latter include
SNLS SNe
themselves, added to the training sample once identified. Third,
using a model instead of a set of spectrum templates (as is typical of
standard identification techniques) alleviates the problems due to
unavoidable incompleteness in phase and wavelength coverage of the
template libraries: all SNe are treated on an equal footing. Note also
that only SNe typed as SN Ia (as opposed to SNIa![]() )
are included
in the training set of SALT2. As an erroneous typing of a
SN Ic as a
SN Ia is very unlikely, this limits the chance of polluting
the
training sample. Even in such unlikely case, SALT2 being a model, it
is robust against the inclusion of a non-SN Ia object.
)
are included
in the training set of SALT2. As an erroneous typing of a
SN Ic as a
SN Ia is very unlikely, this limits the chance of polluting
the
training sample. Even in such unlikely case, SALT2 being a model, it
is robust against the inclusion of a non-SN Ia object.
Once the SALT2 fit is performed, the identification is guided by the best-fitting spectral parameter values. As the phase is fixed by the light curve fit, the spectral fit implicitly uses the photometry. However, we will not classify a SN candidate as a certain SN Ia if we do not get an adequate fit of the spectrum, even if the light curve fit is good. On the contrary, a convincing spectral fit is sufficient for an SN Ia identification, even if the light curve fit is poor. Our goal is to obtain a clean, spectroscopically confirmed, SN Ia sample.
4.3 Host galaxy subtraction
Spectroscopic identification of distant SNe is challenging. One of the
key issues discussed in the literature is host contamination. Low S/Nspectra
are common, either due to high redshift or because sometimes
candidates are observed at a late phase (up to a few weeks past
maximum) due to telescope scheduling. Several techniques have been
developed to improve host-SN separation. Standard techniques involve
template ![]() fitting (e.g., Lidman
et al. 2005; Howell et al.
2005)
once the
spectrum has been extracted, and/or cross-correlation methods, such as
the SuperNova IDentification (SNID) algorithm (Blondin
& Tonry 2007), used
for the first two years of the ESSENCE project
(Matheson
et al. 2005; Foley
et al. 2008b). Blondin
et al. (2005)
proposed a PSF
deconvolution technique that separates the two components, provided
that the spatial extension of the Gaussian profile is very different
for the SN and for its host. Zheng
et al. (2008) use a principal
component analysis decomposition, combined with template fitting to
assess the level of host contamination.
fitting (e.g., Lidman
et al. 2005; Howell et al.
2005)
once the
spectrum has been extracted, and/or cross-correlation methods, such as
the SuperNova IDentification (SNID) algorithm (Blondin
& Tonry 2007), used
for the first two years of the ESSENCE project
(Matheson
et al. 2005; Foley
et al. 2008b). Blondin
et al. (2005)
proposed a PSF
deconvolution technique that separates the two components, provided
that the spatial extension of the Gaussian profile is very different
for the SN and for its host. Zheng
et al. (2008) use a principal
component analysis decomposition, combined with template fitting to
assess the level of host contamination.
SNLS has a key advantage in that deep photometric ugriz data are available for the host galaxy that can assist with SN-host separation. Bronder et al. (2008) used deep iM-band photometry to estimate host contamination. More recently, Ellis et al. (2008) used the multi-colour SNLS photometry to do a more sophisticated estimate of host contamination in extracting Keck SNe Ia spectra. This approach is very efficient at removing the host contribution. Though a wide range of host templates are used and are colour-matched to the host galaxy photometric data, it nevertheless has the drawback of using synthetic templates. By contrast, PHASE, while relying on photometric priors, does not use fixed host templates (Baumont et al. 2008).
PHASE measures the photometric profile of the host and, once
combined
with a PSF model for the SN placed at the SN position, estimates the
flux of each component in each pixel along the SN trace on the
spectrogram using a ![]() minimisation procedure. Inspection of
the residual image after extraction shows that this technique is
efficient provided the centre of the two components is separated by
more than
minimisation procedure. Inspection of
the residual image after extraction shows that this technique is
efficient provided the centre of the two components is separated by
more than ![]() 0.15
'' and the seeings of the reference and
spectroscopic images are similar. Baumont
et al. (2008) have shown that
fitting a SN spectrum extracted separately from its host, with a
SN+host SALT2 model, yields a small amount of residual galactic
contribution, i.e. less than 10% on average. This is a good hint
that our component separation performs well. Note that our technique
is designed within the framework of a rolling search (very deep
reference images are required) and may not be well suited for other
search techniques.
0.15
'' and the seeings of the reference and
spectroscopic images are similar. Baumont
et al. (2008) have shown that
fitting a SN spectrum extracted separately from its host, with a
SN+host SALT2 model, yields a small amount of residual galactic
contribution, i.e. less than 10% on average. This is a good hint
that our component separation performs well. Note that our technique
is designed within the framework of a rolling search (very deep
reference images are required) and may not be well suited for other
search techniques.
When it is not possible to extract the two components
separately, a
![]() fit of the
full (SN+host) spectrum using SALT2 is done. SALT2
has been adapted to fit a galaxy template in addition to the SN model
whenever a separate extraction of the SN from its host was not
possible with PHASE (Baumont
et al. 2008). These galaxy templates include
Kinney et al.
(1996)
types, as well as a series of template spectra
synthesised using PEGASE2 (Fioc
& Rocca-Volmerange 1999,1997)
ranging from
ellipticals to late-type spirals. Templates are ordered in a regular
sequence from red to blue spectra and the best-fit model is
interpolated between two contiguous templates in the sequence. We do
not add emission lines to the PEGASE templates: whenever PEGASE
templates are used to model the host contribution, residual emission
lines might be found in the host subtracted spectrum. This technique
is then essentially comparable to the PCA+
fit of the
full (SN+host) spectrum using SALT2 is done. SALT2
has been adapted to fit a galaxy template in addition to the SN model
whenever a separate extraction of the SN from its host was not
possible with PHASE (Baumont
et al. 2008). These galaxy templates include
Kinney et al.
(1996)
types, as well as a series of template spectra
synthesised using PEGASE2 (Fioc
& Rocca-Volmerange 1999,1997)
ranging from
ellipticals to late-type spirals. Templates are ordered in a regular
sequence from red to blue spectra and the best-fit model is
interpolated between two contiguous templates in the sequence. We do
not add emission lines to the PEGASE templates: whenever PEGASE
templates are used to model the host contribution, residual emission
lines might be found in the host subtracted spectrum. This technique
is then essentially comparable to the PCA+![]() fitting technique
used by Zheng
et al. (2008)
to evaluate the host contamination in the
first season of the SDSS-II survey.
fitting technique
used by Zheng
et al. (2008)
to evaluate the host contamination in the
first season of the SDSS-II survey.
At high redshift and/or for SNe close to their host centre,
host
subtraction remains a difficulty. We find a higher average host
fraction for probable SNe Ia (SN Ia![]() type) than for certain
SNe Ia (SN Ia type) spectra (see Sect. 5.4), which
shows
that, as expected, significant host contamination can alter the
quality of the identification. A major improvement would be to have a
spectrum of the host. We are currently in the process of obtaining
``SN free'' spectra for those cases in which the subtraction of the
host failed. We plan to use those to improve the efficiency of the
host subtraction in the final 5-year SNLS sample.
type) than for certain
SNe Ia (SN Ia type) spectra (see Sect. 5.4), which
shows
that, as expected, significant host contamination can alter the
quality of the identification. A major improvement would be to have a
spectrum of the host. We are currently in the process of obtaining
``SN free'' spectra for those cases in which the subtraction of the
host failed. We plan to use those to improve the efficiency of the
host subtraction in the final 5-year SNLS sample.
4.4 SN Classification
We classify candidate spectra into six categories adapted from the
classification of Lidman
et al. (2005). We define SN Ia (certain
SNe Ia),
SN Ia![]() (probable SNe Ia but other types, in particular
SNe Ic,
can not be excluded given the S/N
or the phase of the spectrum),
SN Ia_pec (peculiar SNe Ia), SN? (possible SN of
unclear type), SN Ib/c
and SN II. In this paper, we only present SNe from the first
3 categories:
(probable SNe Ia but other types, in particular
SNe Ic,
can not be excluded given the S/N
or the phase of the spectrum),
SN Ia_pec (peculiar SNe Ia), SN? (possible SN of
unclear type), SN Ib/c
and SN II. In this paper, we only present SNe from the first
3 categories:
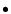
- A SN Ia classification requires the presence of at
least one
of the following features: Si II
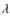 4000 or
Si II
4000 or
Si II 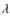 6150, or the S II
W-shaped
feature around 5600
6150, or the S II
W-shaped
feature around 5600  .
Where these features are not clearly
visible, a SN Ia classification is still possible provided
that the
following criteria are met:
.
Where these features are not clearly
visible, a SN Ia classification is still possible provided
that the
following criteria are met:
- 1.
- the overall fit is visually good over the entire spectral range;
- 2.
- the spectral phase is earlier than about +5 days. At about one week past maximum, it has been noted that SNe Ia and SNe Ic show strong similarities and confusion between types is possible (e.g., Howell et al. 2005; Hook et al. 2005);
- 3.
- no strong recalibration is necessary to obtain a good fit (typical flux correction less than 20%). A large recalibration usually indicates that the candidate is not a SN Ia, a fact that would also be reflected in unusual photometric parameters (very red or blue colour, i.e. positive or negative c respectively, very high or low x1 value).
- Classifying a candidate spectrum as a SN Ia
 implies
that no typical SN Ia absorption (Si or S) can be found but
that the
overall fit is acceptable over a large spectral range and broad
features are well reproduced. Spectra of low S/N,
or spectra one week
(or more) past maximum fall into the SN Ia
implies
that no typical SN Ia absorption (Si or S) can be found but
that the
overall fit is acceptable over a large spectral range and broad
features are well reproduced. Spectra of low S/N,
or spectra one week
(or more) past maximum fall into the SN Ia category unless
Si II is clearly seen.
category unless
Si II is clearly seen.
- A spectrum is classified as a SN Ia_pec when spectral features characteristic of under- or over-luminous objects (e.g., Li et al. 2001) are present.
All types presented in this paper have been
cross-checked independently using two techniques: PHASE/SALT2, and the
code developed by Howell
et al. (2005). Difficult spectra were discussed,
on a case-by-case basis, until agreement was reached. In case of
disagreement, the most conservative typing was chosen. This procedure
makes the identification of the SNe Ia presented in this paper
homogeneous to the identification of Gemini spectra of
Howell
et al.
(2005) and Bronder
et al. (2008). Note however that we do not
use here the confidence index (CI) classification of Howell et al.
(2005).
As a guide, the SNe Ia of the present paper correspond to ![]() and 5
while our SNe Ia
and 5
while our SNe Ia![]() correspond to
correspond to ![]() .
.
5 Results
5.1 Individual spectra
In this section, we present the spectra of the 124 identified
SNe Ia of
the SNLS 3rd year VLT spectroscopic survey, along with their
identification as SN Ia, SN Ia![]() or SN Ia_pec. Only two objects
have been identified as SN Ia_pec (SNLS-03D4ag and
SNLS-05D1hk).
Their properties are described individually in Sect. 5.3. In
the
following, we include them into the SN Ia
subsample.
or SN Ia_pec. Only two objects
have been identified as SN Ia_pec (SNLS-03D4ag and
SNLS-05D1hk).
Their properties are described individually in Sect. 5.3. In
the
following, we include them into the SN Ia
subsample.
Table 1
lists the SN Ia and SN Ia![]() spectra and
their observing conditions. In some cases, several spectra of the same
candidate were taken due to poor conditions at the telescope, or an
insufficient S/N for a secure
identification. The asterisk in the
column
spectra and
their observing conditions. In some cases, several spectra of the same
candidate were taken due to poor conditions at the telescope, or an
insufficient S/N for a secure
identification. The asterisk in the
column ![]() denotes cases for which a separate extraction of the
SN from the host component was not possible (including, for some
candidates, the absence of a detectable host).
denotes cases for which a separate extraction of the
SN from the host component was not possible (including, for some
candidates, the absence of a detectable host).
Table 2
summarises the results of our identification for
each of the 139 spectra corresponding to the whole set of 124
SNe Ia.
Name, type, redshift, redshift source, i.e. host (H) or SN (S), phase,
host type, fraction of host used in the best-fitting model, and
average S/N per 5 ![]() bin are given. This latter quantity is
computed on the host subtracted spectrum (when relevant) for each SN.
PEGASE best-fitting host model is given as a letter for the morphology
(E, S0, Sa, Sb, Sc, Sd) followed by a figure between parentheses
indicating the age (in Gyrs). When the best-fit is obtained for a
Kinney
et al. (1996)
template, we indicate the two contiguous Hubble types
between which the best-fitting galaxy model is interpolated. Note that
a host component is always allowed (this includes a null template),
even when the SN spectrum has been extracted separately from its host.
Where the best-fit is obtained for a model with no host contribution,
the label ``NoGalaxy'' is given.
bin are given. This latter quantity is
computed on the host subtracted spectrum (when relevant) for each SN.
PEGASE best-fitting host model is given as a letter for the morphology
(E, S0, Sa, Sb, Sc, Sd) followed by a figure between parentheses
indicating the age (in Gyrs). When the best-fit is obtained for a
Kinney
et al. (1996)
template, we indicate the two contiguous Hubble types
between which the best-fitting galaxy model is interpolated. Note that
a host component is always allowed (this includes a null template),
even when the SN spectrum has been extracted separately from its host.
Where the best-fit is obtained for a model with no host contribution,
the label ``NoGalaxy'' is given.
Table 3
gives the number of SNe for each class
(SN Ia and SN Ia![]() )
per field and in total. Figures A.1
to A.139
show the full (host+SN)
PHASE extracted spectrum (left panel). For each spectrum, the name of
the SN is followed by the date of spectroscopy, in terms of the number
of days elapsed since January 1st, 2003. The red dashed line is the
SALT2 model obtained with no recalibration, the red solid line being
the same model after recalibration. Whenever fitting with a host
galaxy template is necessary, we show the best-fitting host spectrum
model (blue solid line). In these cases, we present in the right panel
the host subtracted SN spectrum obtained by subtracting the host model
(blue solid line in left panel) from the PHASE extracted spectrum. The
best-fit, recalibrated, SN Ia model (solid red line) is
overplotted on
the host-subtracted SN spectrum.
)
per field and in total. Figures A.1
to A.139
show the full (host+SN)
PHASE extracted spectrum (left panel). For each spectrum, the name of
the SN is followed by the date of spectroscopy, in terms of the number
of days elapsed since January 1st, 2003. The red dashed line is the
SALT2 model obtained with no recalibration, the red solid line being
the same model after recalibration. Whenever fitting with a host
galaxy template is necessary, we show the best-fitting host spectrum
model (blue solid line). In these cases, we present in the right panel
the host subtracted SN spectrum obtained by subtracting the host model
(blue solid line in left panel) from the PHASE extracted spectrum. The
best-fit, recalibrated, SN Ia model (solid red line) is
overplotted on
the host-subtracted SN spectrum.
As discussed above, host subtraction is a key issue and techniques are not perfect. In particular, the PEGASE templates we use have no emission lines. As a consequence a number of our spectra show residual host lines, e.g., SNLS-04D1sa (Fig. A.40) with residual [O II] emission and Ca II H&K absorption. In some cases, the fit is poor in some portion of the wavelength range. There can be different explanations for this. In the case of SNLS-04D1hx (Fig. A.27), there are two galaxies along the line of sight. The PHASE host model used for the extraction is not accurate, and the extracted spectrum shows strong host residuals. In the case of SNLS-03D4gf, SNLS-03D4gg and SNLS-04D2cw (Figs. A.19, A.20 and A.52), the SALT2 model is unable to reproduce the UV wavelength region due to the lack of UV coverage in the SALT2 training sample used. More specific comments on individual SNe Ia are given in the corresponding caption.
5.2 Average properties of the SN Ia and SN Ia samples
samples
The main parameters characterising the SN Ia and SN Ia![]() subsamples
are given in Table 4
and are discussed
below. Figures 1
and 2
show the
redshift and phase distributions of both SN Ia and
SN Ia
subsamples
are given in Table 4
and are discussed
below. Figures 1
and 2
show the
redshift and phase distributions of both SN Ia and
SN Ia![]() samples.
Redshifts range from 0.149 to 1.031. As expected, the
SN Ia
samples.
Redshifts range from 0.149 to 1.031. As expected, the
SN Ia![]() subsample has a higher average redshift
(
subsample has a higher average redshift
(
![]() )
than the SN Ia subsample (
)
than the SN Ia subsample (
![]() ).
The average redshift of the whole sample is
).
The average redshift of the whole sample is
![]() and
the median redshift is 0.62. Below
and
the median redshift is 0.62. Below
![]() ,
all
SNe Ia are identified as certain SN Ia.
,
all
SNe Ia are identified as certain SN Ia.
The average phase of the SN Ia![]() subsample is significantly
higher (
subsample is significantly
higher (
![]() days)
than for the SN Ia
(
days)
than for the SN Ia
(
![]() days).
This is generally caused by
similarities between SN Ia spectra one week past maximum and
SN Ic
spectra. These cases are labeled SN Ia
days).
This is generally caused by
similarities between SN Ia spectra one week past maximum and
SN Ic
spectra. These cases are labeled SN Ia![]() unless Si II
is clearly seen. Figure 2 shows
that
most spectra at
phases later than 10 days are classified as SN Ia
unless Si II
is clearly seen. Figure 2 shows
that
most spectra at
phases later than 10 days are classified as SN Ia![]() .
This also
reflects the lower-S/N in these
(fainter) spectra. The average S/Nper
5
.
This also
reflects the lower-S/N in these
(fainter) spectra. The average S/Nper
5 ![]() bin is
bin is ![]() for SN Ia,
for SN Ia, ![]() 2
for SN Ia
2
for SN Ia![]() .
.
We now compare the rest frame B-band
magnitudes, at maximum light,
for the two samples. For each SN, mB*,
the apparent rest frame
B-band magnitude, is determined as part of the light
curve fit with
SALT2. In order to assess the significance of any discrepancy between
the SN Ia and SN Ia![]() samples in terms of physical properties of
the SNe, we compute, for each SN, the ``distance corrected''
magnitude
samples in terms of physical properties of
the SNe, we compute, for each SN, the ``distance corrected''
magnitude![]()
![]() ,
where
,
where ![]() is the luminosity distance, c is here the
speed of light and
is the luminosity distance, c is here the
speed of light and
![]() the
set of cosmological parameters of the underlying cosmology. Here, we
adopt the values
the
set of cosmological parameters of the underlying cosmology. Here, we
adopt the values
![]()
![]() (Astier
et al. 2006). We find
(Astier
et al. 2006). We find
![]() and
and
![]() .
As expected, the SNe we
classify as SN Ia
.
As expected, the SNe we
classify as SN Ia![]() are fainter, on average, than the ones we
classify as SN Ia (by
are fainter, on average, than the ones we
classify as SN Ia (by
![]() mag).
This
reflects the fact that low S/N
spectra at a given phase fall
preferentially into the SN Ia
mag).
This
reflects the fact that low S/N
spectra at a given phase fall
preferentially into the SN Ia![]() category, as they are more
difficult to identify.
category, as they are more
difficult to identify.
It is of interest to account for the difference found in the
![]() values.
One obvious explanation is that it is related to
the well-known ``brighter-slower'' (Phillips
1993) and
``brighter-bluer'' (Tripp &
Branch 1999) relationships observed in SNe Ia
populations. Figures 3
and 4
show the
SALT2 colour c and x1
parameter distributions for the two
subsamples. The SN Ia
values.
One obvious explanation is that it is related to
the well-known ``brighter-slower'' (Phillips
1993) and
``brighter-bluer'' (Tripp &
Branch 1999) relationships observed in SNe Ia
populations. Figures 3
and 4
show the
SALT2 colour c and x1
parameter distributions for the two
subsamples. The SN Ia![]() appear to be slightly redder, as their
average colour
appear to be slightly redder, as their
average colour
![]() is higher than for
SN Ia:
is higher than for
SN Ia:
![]() .
Regarding x1, we find
.
Regarding x1, we find
![]() and
and
![]() ,
which are consistent within
,
which are consistent within ![]() errors (the SN Ia sample having
faster, narrower light curves than the SN Ia
errors (the SN Ia sample having
faster, narrower light curves than the SN Ia![]() sample, on
average). The ``brighter-slower'' and ``brighter-bluer'' relationships
translate into a magnitude difference between the two samples of
sample, on
average). The ``brighter-slower'' and ``brighter-bluer'' relationships
translate into a magnitude difference between the two samples of
![]() .
Using
.
Using
![]() and
and
![]() (Guy et al.
2007), we
find
(Guy et al.
2007), we
find
![]() .
The ``observed''
.
The ``observed'' ![]() difference
between the two samples is therefore consistent with the
``brighter-slower'' and ``brighter-bluer'' relationships. This gives
us confidence that our SN Ia
difference
between the two samples is therefore consistent with the
``brighter-slower'' and ``brighter-bluer'' relationships. This gives
us confidence that our SN Ia![]() sample is not significantly
polluted by the inclusion of red, non-SN Ia objects, such as
SNe Ic.
We can estimate the contamination of the SN Ia
sample is not significantly
polluted by the inclusion of red, non-SN Ia objects, such as
SNe Ic.
We can estimate the contamination of the SN Ia![]() sample by
core-collapse SNe by comparing the number of certain SN Ib/c
we have
typed to the number of certain SNe Ia. In the whole SNLS data,
sample by
core-collapse SNe by comparing the number of certain SN Ib/c
we have
typed to the number of certain SNe Ia. In the whole SNLS data, ![]() 3% of
securely identified SNe are of the SN Ib/c type. Applying this
ratio to the 38 SN Ia
3% of
securely identified SNe are of the SN Ib/c type. Applying this
ratio to the 38 SN Ia![]() of the VLT sample shows that we should
expect at most 1 contaminant. Note however that the detection
efficiency of the SNLS does not allow us to detect SN Ib/c SNe
beyond
z<0.4 (Bazin
et al. 2009). As we only have 3 SN Ia
of the VLT sample shows that we should
expect at most 1 contaminant. Note however that the detection
efficiency of the SNLS does not allow us to detect SN Ib/c SNe
beyond
z<0.4 (Bazin
et al. 2009). As we only have 3 SN Ia![]() with z<0.4,
this leads to a more realistic estimate of 0.1 SN Ia
with z<0.4,
this leads to a more realistic estimate of 0.1 SN Ia![]() that might
be contaminant.
that might
be contaminant.
Table
1:
List of SNLS 3rd year ESO-VLT SN Ia and SN Ia![]() spectraa.
spectraa.
Table
2:
Results of identifications of the SNLS 3rd year ESO-VLT SN Ia
and SN Ia![]() spectra.
spectra.
5.3 Peculiar SN Ia
We have identified two SN Ia in our sample showing strong
similarities
with the spectra of SN 1999aa (Garavini
et al. 2004) (see Fig. 5). These
are
03D4ag and 05D1hk (this latter SN was
already noted as a peculiar SN Ia by Ellis
et al. 2008).
Table 5
summarises the properties of these two SNe as
well as the parameters obtained when fitting their spectra with SALT2.
Both SNe are at relatively low redshift (z=0.285 and
0.263 for
03D4ag and 05D1hk respectively) and at early phase (![]() -9
and
-9
and ![]() -5 days).
05D1hk has a large x1 value,
which translates into
a
-5 days).
05D1hk has a large x1 value,
which translates into
a ![]() parameter (Phillips
1993)
of 0.89 using the
formula given in Guy
et al.
(2007). By comparison, SN 1999aa has
parameter (Phillips
1993)
of 0.89 using the
formula given in Guy
et al.
(2007). By comparison, SN 1999aa has
![]() (Jha et al. 2006).
For
03D4ag, we find
(Jha et al. 2006).
For
03D4ag, we find ![]() .
Visual inspection of the spectra shows that 03D4ag and 05D1hk have
properties typical of high stretch SN Ia: shallow silicon
absorption and
a blue spectrum, even for the early phases under consideration.
.
Visual inspection of the spectra shows that 03D4ag and 05D1hk have
properties typical of high stretch SN Ia: shallow silicon
absorption and
a blue spectrum, even for the early phases under consideration.
The possibility of SNLS-03D1co being a 1991bg-like event has
been
discussed in Bronder
et al.
(2008), as there is also a Gemini spectrum of
this event. Bronder
et al.
(2008) found that 03D1co had a large
Mg II ![]() 4300 equivalent width (EW),
consistent with
the excess absorption measured in under-luminous, low-z
SNe spectra.
However, the presence of Si II
4300 equivalent width (EW),
consistent with
the excess absorption measured in under-luminous, low-z
SNe spectra.
However, the presence of Si II ![]() 4000 in the
Gemini
spectrum contradicts this hypothesis, as this feature is not seen in
under-luminous SNe because of extra absorption due to Ti II
and Fe II in the same wavelength range.
Based on this
observation, Bronder
et al.
(2008) concluded that 03D1co was likely to be a
``normal'' SN Ia, in agreement with its normal light curves
(Astier
et al. 2006).
The SALT2 fit of the VLT spectrum of 03D1co confirms
this conclusion (see Fig. A.5).
4000 in the
Gemini
spectrum contradicts this hypothesis, as this feature is not seen in
under-luminous SNe because of extra absorption due to Ti II
and Fe II in the same wavelength range.
Based on this
observation, Bronder
et al.
(2008) concluded that 03D1co was likely to be a
``normal'' SN Ia, in agreement with its normal light curves
(Astier
et al. 2006).
The SALT2 fit of the VLT spectrum of 03D1co confirms
this conclusion (see Fig. A.5).
5.4 Contamination by non-SN Ia
An obvious challenge in the identification of distant SNe Ia is to avoid confusion with other types, such as SNe Ic, especially one week after maximum light and beyond. Template cross-correlation techniques such as SNID can help (Matheson et al. 2005), but still rely on (unavoidably) incomplete template libraries. Our SALT2 identification procedure provides some additional information on non SN Ia types (or peculiar SNe Ia) through the fitted parameter values, which can differ from those of a typical SN Ia, e.g., an unusually red colour, and/or a high x1 parameter, and/or a high recalibration parameter. This is not equivalent to a direct identification of non SN Ia objects, but does allow a mechanism by which peculiar events can be identified. We explore these parameters in this section.
We start with the SALT2 ``recalibration parameters'' used to
adjust
the SALT2 photometric model to the observed data. We focus on the
first order recalibration parameter ![]() (Sect. 4.2).
This parameter can be interpreted as the ``tilt''
required to adjust the observed spectrum to the SALT2 colour model. A
large recalibration is a sign that the SALT2 model is not able to
properly model the data, as would be the case if we were trying to fit
a non-SN Ia spectrum, but could also occur for a SN Ia
spectrum whose
properties were very different from those of the training sample.
Large tilts can also be needed when the host subtraction has failed
due to inadequate host modelling or too strong a contamination,
although no strong correlation exists between
(Sect. 4.2).
This parameter can be interpreted as the ``tilt''
required to adjust the observed spectrum to the SALT2 colour model. A
large recalibration is a sign that the SALT2 model is not able to
properly model the data, as would be the case if we were trying to fit
a non-SN Ia spectrum, but could also occur for a SN Ia
spectrum whose
properties were very different from those of the training sample.
Large tilts can also be needed when the host subtraction has failed
due to inadequate host modelling or too strong a contamination,
although no strong correlation exists between ![]() and the host
fraction.
and the host
fraction.
The average ![]() value for the SN Ia
value for the SN Ia![]() is
is
![]() ,
with
,
with ![]() for the
SN Ia: the required tilts needed to recalibrate the
photometric model
are only moderate. The dispersions in the
for the
SN Ia: the required tilts needed to recalibrate the
photometric model
are only moderate. The dispersions in the ![]() values are quite
large for both samples, with a larger variation for the SN Ia
values are quite
large for both samples, with a larger variation for the SN Ia![]() :
:
![]() and
and
![]() .
This can be explained by the
inclusion in the SN Ia
.
This can be explained by the
inclusion in the SN Ia![]() sample of more host-contaminated
spectra. If we select only SNe for which a separate extraction from
their host was not possible, the mean host fractions fg
(i.e. the
contribution of the host model to the full spectrum averaged over the
whole spectral range) are
sample of more host-contaminated
spectra. If we select only SNe for which a separate extraction from
their host was not possible, the mean host fractions fg
(i.e. the
contribution of the host model to the full spectrum averaged over the
whole spectral range) are
![]() and
and ![]() for the SN Ia and SN Ia
for the SN Ia and SN Ia![]() subsamples, respectively (see
Table 4).
Clearly, spectra identified as
SN Ia
subsamples, respectively (see
Table 4).
Clearly, spectra identified as
SN Ia![]() are more host contaminated than SN Ia spectra.
are more host contaminated than SN Ia spectra.
We do not find any systematic trend with redshift or phase in
the
``tilt'' values needed to accomodate the SALT2 model with the spectra.
In Fig. 6,
we show the magnitude ![]() of the
recalibration of the photometric model as a function of wavelength,
for a subset of our spectra chosen between z=0.4
and z=0.6(
of the
recalibration of the photometric model as a function of wavelength,
for a subset of our spectra chosen between z=0.4
and z=0.6(
![]() and
and
![]() for this subset).
The light blue area is for SNe Ia
for this subset).
The light blue area is for SNe Ia![]() ,
the dark blue one SNe Ia. At
this redshift, we find that a
,
the dark blue one SNe Ia. At
this redshift, we find that a ![]() 15% recalibration is needed
at both ends of the effective spectral range, for both the
SN Ia and
SN Ia
15% recalibration is needed
at both ends of the effective spectral range, for both the
SN Ia and
SN Ia![]() categories.
categories.
A potentially more quantitative criterion is the (reduced)
![]() of the SALT2 spectral fits. We
show in Fig. 7
the
reduced
of the SALT2 spectral fits. We
show in Fig. 7
the
reduced ![]() histogram of all SALT2
fits (both for the SNe Ia and SNe Ia
histogram of all SALT2
fits (both for the SNe Ia and SNe Ia![]() samples). The bulk of the
samples). The bulk of the
![]() values are around 1 (or
slightly higher), but with a tail
of 11 objects with
values are around 1 (or
slightly higher), but with a tail
of 11 objects with ![]() (Fig. 7;
the two
highest
(Fig. 7;
the two
highest ![]() objects are not shown). With these objects, we
find
objects are not shown). With these objects, we
find ![]() ,
while excluding them yields
,
while excluding them yields
![]() .
Among the 11 high
.
Among the 11 high ![]() objects, one
finds 03D4ag and 05D1hk, the over-luminous events identified in
Sect. 5.3.
Their best-fit
objects, one
finds 03D4ag and 05D1hk, the over-luminous events identified in
Sect. 5.3.
Their best-fit ![]() values are 2.48
and 3.12 respectively. The other objects are (ordered by increasing
values are 2.48
and 3.12 respectively. The other objects are (ordered by increasing
![]() ): SNLS-03D1fc(2.01),
SNLS-04D4ht(2.03),
SNLS-05D2ct(2.04), SNLS-05D4cw(2.18), SNLS-04D2bt(2.23),
SNLS-04D2fs(2.42), SNLS-04D1dc(3.24), SNLS-03D4au(4.63) and
SNLS-05D4ff(16.33).
): SNLS-03D1fc(2.01),
SNLS-04D4ht(2.03),
SNLS-05D2ct(2.04), SNLS-05D4cw(2.18), SNLS-04D2bt(2.23),
SNLS-04D2fs(2.42), SNLS-04D1dc(3.24), SNLS-03D4au(4.63) and
SNLS-05D4ff(16.33).
03D1fc (Fig. A.7;
SN Ia at z=0.332) has a separate
extraction from its host. The spectrum has a high S/N
and the SALT2
fit parameters are typical of a normal SN Ia. Si II ![]() 6150 is
visible but shallow. The spectrum is not as blue as
the one of 05D1hk (which is at about the same phase, i.e.
-5 days),
but the photometric model requires three recalibration parameters to
consistently fit the spectrum. Although the stretch is normal
(s=1.006), this SN might be slightly peculiar.
6150 is
visible but shallow. The spectrum is not as blue as
the one of 05D1hk (which is at about the same phase, i.e.
-5 days),
but the photometric model requires three recalibration parameters to
consistently fit the spectrum. Although the stretch is normal
(s=1.006), this SN might be slightly peculiar.
04D4ht (Fig. A.71;
SN Ia at z=0.217) is heavily host
contaminated (>![]() of host in the best-fitting model). It has an
high colour value (c=0.5). 04D4ht is very red but
with strong
Si II in its spectrum and is identified as
a SN Ia.
However, it is located very near the core of its host (a late type
spiral) and potentially heavily extinguished.
of host in the best-fitting model). It has an
high colour value (c=0.5). 04D4ht is very red but
with strong
Si II in its spectrum and is identified as
a SN Ia.
However, it is located very near the core of its host (a late type
spiral) and potentially heavily extinguished.
05D2ct (Fig. A.95;
SN Ia![]() at z=0.734) is
another example of a SN close to its host centre (more than half of
the extracted signal is modeled by a Sd galaxy), slightly red
(c=0.14) but with a normal stretch (s=0.994).
It is likely to be
extinguished. Due to its fairly high redshift and host contamination,
no Si II is visible either at 6150 or at
4000
at z=0.734) is
another example of a SN close to its host centre (more than half of
the extracted signal is modeled by a Sd galaxy), slightly red
(c=0.14) but with a normal stretch (s=0.994).
It is likely to be
extinguished. Due to its fairly high redshift and host contamination,
no Si II is visible either at 6150 or at
4000 ![]() and it
is identified as a SN Ia
and it
is identified as a SN Ia![]() .
.
Table 3: Distribution of types per SNLS Deep field and in total.
05D4cw (Fig. A.116; SN Ia at z=0.375) is a blue (c=-0.15) SN. It is heavily host-contaminated, probably an early type galaxy. As it is close to its host centre, a separate extraction was not possible. However, Si II04D2bt (Fig. A.46; SN Ia at z=0.220) is located in the bulge of its early type host. It is red (c=0.18), likely due to host extinction. Si II and S II are clearly visible, the classification is SN Ia.
04D2fs (Fig. A.54;
SN Ia at z=0.357) has a large S/Nwith
Si II and S II
clearly visible. The high
![]() value can be explained by the
high S/N
(low noise) of the
spectrum.
value can be explained by the
high S/N
(low noise) of the
spectrum.
Table
4:
Average properties of the SN Ia and SN Ia![]() subsamples.
subsamples.
03D4au (Fig. A.12;
SN Ia![]() at z=0.468) is red
(c=0.18) and host contaminated, a week past maximum
light. It is
located right at the centre of its late-type host, probably
extinguished, and with strong emission lines that are difficult to
subtract, explaining the high
at z=0.468) is red
(c=0.18) and host contaminated, a week past maximum
light. It is
located right at the centre of its late-type host, probably
extinguished, and with strong emission lines that are difficult to
subtract, explaining the high ![]() value.
value.
05D4ff (Fig. A.123;
SN Ia![]() at z=0.402) is
heavily buried in its late-type host. The presence of strong
[O II], [O III]
and H
at z=0.402) is
heavily buried in its late-type host. The presence of strong
[O II], [O III]
and H![]() emission lines, not
present in the host PEGASE template, explains the poor
emission lines, not
present in the host PEGASE template, explains the poor
![]() .
.
In conclusion, a cut in
![]() can help with the identification
of peculiar (and possibly non-SN Ia) events, but it is not a
straightforward identification. Several effects can conspire to give a
high
can help with the identification
of peculiar (and possibly non-SN Ia) events, but it is not a
straightforward identification. Several effects can conspire to give a
high ![]() value, even in the case of obvious SNe Ia. The
results of this section suggest that our two subsamples are unlikely
to be significantly contaminated by non-SNe Ia.
value, even in the case of obvious SNe Ia. The
results of this section suggest that our two subsamples are unlikely
to be significantly contaminated by non-SNe Ia.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12246_fig1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg242.png)
|
Figure 1:
Redshift distribution of SNLS candidates identified as SN Ia
or
SN Ia |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12246_fig2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg243.png)
|
Figure 2:
Phase distribution of SNLS candidates identified as SN Ia or
SN Ia |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12246_fig3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg246.png)
|
Figure 3:
Colour distribution of SNLS candidates identified as SN Ia or
SN Ia |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12246_fig4.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg249.png)
|
Figure 4:
SALT2 x1 distribution of
SNLS candidates identified as SN Ia or
SN Ia |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12246_fig5a.eps}\par\includegraphics[width=8cm,clip]{12246_fig5b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg250.png)
|
Figure 5:
SNLS-03D4ag ( top) and SNLS-05D1hk ( bottom)
rest frame spectra compared to SN 1999aa templates
at -8 and -5 days
respectively (from Matheson
et al. 2008). SN 1999aa spectra are not
de-redshifted. None of the spectra are corrected for peculiar
velocities, which explains the shifts observed in the positions of
absorption features. In both cases, note the very blue spectrum and
shallow Si II |
| Open with DEXTER | |
6 Composite spectra of the SN Ia sample
In this section, we build average VLT spectra in six regions of phase-redshift space to compare the evolution of their properties with redshift.
6.1 Methodology
We select spectra with phase ![]() days (pre-maximum spectra);
days (pre-maximum spectra);
![]() days
(maximum spectra);
days
(maximum spectra); ![]() days (post-maximum
spectra) for SNe at redshift z<0.5 and
days (post-maximum
spectra) for SNe at redshift z<0.5 and ![]() ,
respectively. We
only use SN Ia spectra, as the SN Ia
,
respectively. We
only use SN Ia spectra, as the SN Ia![]() spectra number in each of
the six regions is small and even zero for z<0.5
around maximum
(since the spectra in this phase-space region are of sufficient S/Nand
quality to be identified as SN Ia). The number of spectra in
each
phase bin for both z<0.5 and
spectra number in each of
the six regions is small and even zero for z<0.5
around maximum
(since the spectra in this phase-space region are of sufficient S/Nand
quality to be identified as SN Ia). The number of spectra in
each
phase bin for both z<0.5 and
![]() is summarised in Table 6.
For the
SN Ia spectra, we have 12 pre-maximum
spectra (of which 7 are at z<0.5),
57 spectra at maximum light (of
which 12 are at z<0.5) and 24 post-maximum
spectra (of which 6 are
at z<0.5). The average redshift is
is summarised in Table 6.
For the
SN Ia spectra, we have 12 pre-maximum
spectra (of which 7 are at z<0.5),
57 spectra at maximum light (of
which 12 are at z<0.5) and 24 post-maximum
spectra (of which 6 are
at z<0.5). The average redshift is
![]() for the
z<0.5 sample and
for the
z<0.5 sample and
![]() for
the z>0.5 sample. We have
more spectra in the
for
the z>0.5 sample. We have
more spectra in the ![]() bins (68 spectra) than in the z<0.5bins
(25), as the median redshift of our sample is 0.62. The spectra
of 03D4ag and 05D1hk are excluded from the z<0.5
pre-maximum light
region, as they have been identified as peculiar SNe Ia (see
Sect. 5.3).
bins (68 spectra) than in the z<0.5bins
(25), as the median redshift of our sample is 0.62. The spectra
of 03D4ag and 05D1hk are excluded from the z<0.5
pre-maximum light
region, as they have been identified as peculiar SNe Ia (see
Sect. 5.3).
To construct the average spectrum in each region, all
individual
spectra (shown in the right panels of Figs. A.1
to A.139
whenever a host model has been subtracted) are
brought into the rest frame and rebinned to 5 ![]() .
All spectra are
colour-corrected using an up-to-date version of the SALT2 colour law
and the colour value c obtained from the SALT2 fit
for each SN.
Using a Cardelli
et al.
(1989) extinction law with RV=3.1
and E(B-V)values
obtained for each SN from their light curve fit, yields very
similar results in the wavelength range under consideration. We adopt
the SALT2 colour correction in the following. Fluxes are normalised to
the same integral in the range 4450-4550
.
All spectra are
colour-corrected using an up-to-date version of the SALT2 colour law
and the colour value c obtained from the SALT2 fit
for each SN.
Using a Cardelli
et al.
(1989) extinction law with RV=3.1
and E(B-V)values
obtained for each SN from their light curve fit, yields very
similar results in the wavelength range under consideration. We adopt
the SALT2 colour correction in the following. Fluxes are normalised to
the same integral in the range 4450-4550 ![]() .
For each wavelength
bin, an average weighted flux and its corresponding uncertainty are
computed from all spectra included in this bin. Because of the
variety of the redshifts involved, the number of spectra entering the
average varies from one bin to the other, as does the average phase in
a given bin. In practice, the number of spectra in each bin decreases
at both ends of the wavelength scale but is approximately constant in
the range 4000-7000
.
For each wavelength
bin, an average weighted flux and its corresponding uncertainty are
computed from all spectra included in this bin. Because of the
variety of the redshifts involved, the number of spectra entering the
average varies from one bin to the other, as does the average phase in
a given bin. In practice, the number of spectra in each bin decreases
at both ends of the wavelength scale but is approximately constant in
the range 4000-7000 ![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12246_fig6.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg258.png)
|
Figure 6:
Illustration of the magnitude |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12246_fig7.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg259.png)
|
Figure 7:
Distribution of SALT2 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12246_fig8.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg261.png)
|
Figure 8:
In grey/blue: average spectrum built from all VLT SN Ia
spectra of this study for z<0.5 (
left column) and |
| Open with DEXTER | |
As a consequence of this averaging procedure, the mean phase of the
average spectra varies from one wavelength bin to the other. In
practice, this variation distorts only very moderately the spectra as
the mean phase is roughly the same from one end to the other of the
wavelength scale. However, for a given phase range (pre-maximum,
maximum or post-maximum), the mean phases of the average spectrum at
z<0.5 can significantly differ from the
corresponding one at ![]() ,
which should be borne in mind when comparing the average
spectrum at z<0.5 with that at
,
which should be borne in mind when comparing the average
spectrum at z<0.5 with that at ![]() .
In practice, due to a
similar phase sampling of our spectra with redshift, this difference
is marginal. We find the following average phases (in days):
.
In practice, due to a
similar phase sampling of our spectra with redshift, this difference
is marginal. We find the following average phases (in days):
![]() and
and
![]() for pre-maximum spectra,
for pre-maximum spectra,
![]() and
and
![]() for spectra at maximum, and
for spectra at maximum, and
![]() and
and
![]() for post-maximum spectra.
for post-maximum spectra.
Table 5: Properties of SNLS-03D4ag and SNLS-05D1hk VLT spectra.
Table 6: Number of SN Ia spectra in each phase bin (in days) used to create VLT composite spectra.
6.2 Comparison to Hsiao et al. template spectra
Figure 8
shows the result of averaging the SN Ia
spectra (in blue). The left column is for z<0.5
spectra, the right
for ![]() spectra. From top to bottom, pre-maximum, maximum and
post-maximum spectra are shown. Average spectra built from the
Hsiao
et al. (2007)
template series (red curve) are overlaid on top of the
VLT average spectra. Note that about two-thirds of the spectra used in
constructing the Hsiao
et al.
(2007) template are at low redshift
(z<0.1) and lack UV coverage, so the UV
section of the red curves
come from the remaining high-redshift spectra used in building the
Hsiao
et al. (2007)
template. In each region of
Fig. 8,
phases in each wavelength bin are the
same for the template and the VLT composite spectrum, weighted in
exactly the same way.
spectra. From top to bottom, pre-maximum, maximum and
post-maximum spectra are shown. Average spectra built from the
Hsiao
et al. (2007)
template series (red curve) are overlaid on top of the
VLT average spectra. Note that about two-thirds of the spectra used in
constructing the Hsiao
et al.
(2007) template are at low redshift
(z<0.1) and lack UV coverage, so the UV
section of the red curves
come from the remaining high-redshift spectra used in building the
Hsiao
et al. (2007)
template. In each region of
Fig. 8,
phases in each wavelength bin are the
same for the template and the VLT composite spectrum, weighted in
exactly the same way.
The overall agreement between the VLT average spectra and the
Hsiao
et al. (2007)
template is good in all regions. Note that no colour
correction has been applied to the Hsiao
et al. (2007) templates. As this
template is designed for use in light curve fitters that implement
``warping'' techniques (e.g., SiFTO, Conley
et al. 2008), there is no a priori reason
that the continuum should agree with our
composite spectra. However, we find that the agreement is almost
perfect in the optical region of the spectra except around the
Ca II ![]() 3700, Si II
3700, Si II ![]() 4000 and
Si II
4000 and
Si II ![]() 6150 features, for the maximum
average
spectrum at z<0.5. In the UV region, one
notices more discrepancies
in the fluxes (a low number of spectra are used in this region). Part
of this effect might be due to the fact that we normalise the spectra
in the optical region. This spectral region is also the most sensitive
to differential slit losses. We find a satisfying match of the
positions of the UV
6150 features, for the maximum
average
spectrum at z<0.5. In the UV region, one
notices more discrepancies
in the fluxes (a low number of spectra are used in this region). Part
of this effect might be due to the fact that we normalise the spectra
in the optical region. This spectral region is also the most sensitive
to differential slit losses. We find a satisfying match of the
positions of the UV ![]() 3000-3400
features. Note that the peak
around 3200
3000-3400
features. Note that the peak
around 3200 ![]() decreases from pre- to post-maximum phases in a
proportion that is well reproduced by the Hsiao
et al. (2007) model, both
at z<0.5 and
decreases from pre- to post-maximum phases in a
proportion that is well reproduced by the Hsiao
et al. (2007) model, both
at z<0.5 and ![]() .
.
6.3
Comparison
of z < 0.5 and z 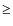 0.5
spectra
0.5
spectra
We now compare the average spectra at z<0.5
and ![]() for
pre-maximum phases (upper panels of Fig. 9),
maximum-light (middle panels) and post-maximum (lower panels). The
comparison is done in the region of intersection, from the UV up to
the mid-optical wavelengths. For each panel, the blue curve is the
for
pre-maximum phases (upper panels of Fig. 9),
maximum-light (middle panels) and post-maximum (lower panels). The
comparison is done in the region of intersection, from the UV up to
the mid-optical wavelengths. For each panel, the blue curve is the
![]() average
spectrum, and the black curve is the corresponding
z<0.5 spectrum. At the bottom of each panel,
we plot the residual
average
spectrum, and the black curve is the corresponding
z<0.5 spectrum. At the bottom of each panel,
we plot the residual
![]() (solid
black line) with
(solid
black line) with ![]()
![]() errors.
errors.
The mean spectra can be different for two reasons: they might
be
intrinsically different (i.e. evolution in spectral properties), or
the phase distribution of the samples can differ. We therefore compute
the residual ![]() (solid thick red curve) for the
Hsiao
et al. (2007)
templates shown in Fig. 8.
As
the underlying assumption in building such spectral templates is that
there is no evolution between low and high redshift,
(solid thick red curve) for the
Hsiao
et al. (2007)
templates shown in Fig. 8.
As
the underlying assumption in building such spectral templates is that
there is no evolution between low and high redshift,
![]() should
in principle be zero over the whole
spectral range. Any deviation from zero, in a given wavelength range,
can be attributed to a difference in the average phase of the z<0.5and
should
in principle be zero over the whole
spectral range. Any deviation from zero, in a given wavelength range,
can be attributed to a difference in the average phase of the z<0.5and
![]() composite
spectra in this range. When inspecting
differences in the VLT composite spectra at z<0.5
and
composite
spectra in this range. When inspecting
differences in the VLT composite spectra at z<0.5
and ![]() ,
it is important to refer to
,
it is important to refer to
![]() :
if
:
if
![]() follows
follows
![]() ,
deviations
can be traced back to differing phase distributions of the z<0.5
and
,
deviations
can be traced back to differing phase distributions of the z<0.5
and
![]() composite
spectra. In the opposite case (
composite
spectra. In the opposite case (
![]() is
not zero while
is
not zero while
![]() is zero), any differences
should be real.
is zero), any differences
should be real.
To quantitatively assess the significance of the differences,
we
define a reduced ![]() measure of the agreement of the
measure of the agreement of the ![]() VLT composite spectrum and the z<0.5
composite spectrum. The
variance entering the definition of
VLT composite spectrum and the z<0.5
composite spectrum. The
variance entering the definition of
![]() is the sum of the
variances of the two composite spectra. A value
is the sum of the
variances of the two composite spectra. A value
![]() indicates
that the two spectra are consistent with one another. We now
examine each phase bin in turn.
indicates
that the two spectra are consistent with one another. We now
examine each phase bin in turn.
6.3.1 Pre-maximum spectra
For pre-maximum spectra (
![]() ), the composite spectra are
typically consistent (
), the composite spectra are
typically consistent (
![]() for
588 degrees of
freedom - d.o.f.). The spectra are most discrepant in the UV region
(3300 to 4000
for
588 degrees of
freedom - d.o.f.). The spectra are most discrepant in the UV region
(3300 to 4000 ![]() ). A possible explanation is that, as the bands
bluer than the rest frame B-band are given a lower
weight in the
SALT2 light curve fit, the colour correction applied to the spectra
that uses the colour parameter c derived from the
light curve fit,
is more efficient in the red than in the blue. Alternatively, this
might reflect a greater variability in this spectral region
(e.g., Ellis
et al. 2008).
More variability is expected here due to
variations in metallicities of the progenitors, particularly at
pre-maximum phases (Hoeflich
et al. 1998; Lentz
et al. 2000). The
residuals in Fig.
9
show
the UV region of the pre- and maximum spectra
shows more discrepancy than at post-maximum.
). A possible explanation is that, as the bands
bluer than the rest frame B-band are given a lower
weight in the
SALT2 light curve fit, the colour correction applied to the spectra
that uses the colour parameter c derived from the
light curve fit,
is more efficient in the red than in the blue. Alternatively, this
might reflect a greater variability in this spectral region
(e.g., Ellis
et al. 2008).
More variability is expected here due to
variations in metallicities of the progenitors, particularly at
pre-maximum phases (Hoeflich
et al. 1998; Lentz
et al. 2000). The
residuals in Fig.
9
show
the UV region of the pre- and maximum spectra
shows more discrepancy than at post-maximum.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{12246_fig9.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg277.png)
|
Figure 9:
Comparison of z<0.5 (in black) and |
| Open with DEXTER | |
6.3.2 Maximum-light spectra
The largest discrepancy between z<0.5 and ![]() is found at
maximum light (
is found at
maximum light (![]() ).
This is the phase where we have the
highest number of spectra (12 at z<0.5, 45
at
).
This is the phase where we have the
highest number of spectra (12 at z<0.5, 45
at ![]() ), and the
statistical errors are the smallest. We find
), and the
statistical errors are the smallest. We find
![]() for
601 d.o.f. - the two average spectra are formally not consistent.
The largest differences are seen around Ca II
for
601 d.o.f. - the two average spectra are formally not consistent.
The largest differences are seen around Ca II ![]() 3700, Si II
3700, Si II ![]() 4000, Mg II
4000, Mg II ![]() 4300
and Fe II
4300
and Fe II ![]() 4800. Overall, the z<0.5
maximum
spectrum has deeper absorptions than its
4800. Overall, the z<0.5
maximum
spectrum has deeper absorptions than its ![]() counterpart.
counterpart.
In the UV up to 3500 ![]() ,
the residuals
,
the residuals ![]() correlate
with the template residuals
correlate
with the template residuals
![]() ,
and
the discrepancies between z<0.5 and
,
and
the discrepancies between z<0.5 and ![]() may be due to
differences in mean phases between z<0.5 and
may be due to
differences in mean phases between z<0.5 and
![]() spectra
(recall that due to our averaging procedure, the mean phase varies
with
spectra
(recall that due to our averaging procedure, the mean phase varies
with ![]() and depends on the phase of the spectra used to build
the average spectrum in a given wavelength bin). Around Ca II
and depends on the phase of the spectra used to build
the average spectrum in a given wavelength bin). Around Ca II ![]() 3700 and
beyond, the discrepancies are seen in the
spectra, not in the template, and could be real.
3700 and
beyond, the discrepancies are seen in the
spectra, not in the template, and could be real.
Bronder
et al.
(2008) indicate a possible difference in the EW
of
Mg II ![]() 4300 between low and high
redshift, but
they conclude that it is likely due to differences in the epoch
sampling and number of objects at low- and high-redshift. This
difference is not found by Foley
et al. (2008a) when comparing their
composite ESSENCE spectrum with a Lick low-z
composite (note that
they use a simpler method for host subtraction, which may alter the
significance of their comparison). More recently, Sullivan
et al. (2009)
studied the possible evolution in the EW of
intermediate mass elements
(IMEs) in the 0<z<1.3 redshift range.
They do not have a
Mg II measurement in their highest-redshift
bin, but the
predicted variation of Mg II EW
is consistent with zero
over their redshift range.
4300 between low and high
redshift, but
they conclude that it is likely due to differences in the epoch
sampling and number of objects at low- and high-redshift. This
difference is not found by Foley
et al. (2008a) when comparing their
composite ESSENCE spectrum with a Lick low-z
composite (note that
they use a simpler method for host subtraction, which may alter the
significance of their comparison). More recently, Sullivan
et al. (2009)
studied the possible evolution in the EW of
intermediate mass elements
(IMEs) in the 0<z<1.3 redshift range.
They do not have a
Mg II measurement in their highest-redshift
bin, but the
predicted variation of Mg II EW
is consistent with zero
over their redshift range.
The Si II-Fe II-Fe
III ![]() 4800
blend feature is shallower in our
4800
blend feature is shallower in our ![]() spectrum than at
z<0.5, in qualitative agreement with Foley et al.
(2008a), who
find that
this feature is much weaker in their ESSENCE spectrum. They interpret
this difference as due to a weaker Fe III
spectrum than at
z<0.5, in qualitative agreement with Foley et al.
(2008a), who
find that
this feature is much weaker in their ESSENCE spectrum. They interpret
this difference as due to a weaker Fe III ![]() 5129
line in the high-z spectrum.
5129
line in the high-z spectrum.
The Si II ![]() 4000 feature
is shallower at high
redshift, in agreement with the findings of Sullivan
et al. (2009).
Bronder
et al. (2008)
do not mention such a difference, but
Foley
et al. (2008a)
find the same kind of trend for Si II
4000 feature
is shallower at high
redshift, in agreement with the findings of Sullivan
et al. (2009).
Bronder
et al. (2008)
do not mention such a difference, but
Foley
et al. (2008a)
find the same kind of trend for Si II
![]() 6150 (this
feature being shallower in their high-redshift
ESSENCE spectrum than in the low-redshift Lick spectrum), although
they do not mention this for Si II
6150 (this
feature being shallower in their high-redshift
ESSENCE spectrum than in the low-redshift Lick spectrum), although
they do not mention this for Si II ![]() 4000. We do
not find this difference in our pre-maximum spectra, though it may be
present at post-maximum.
4000. We do
not find this difference in our pre-maximum spectra, though it may be
present at post-maximum.
6.3.3 Post-maximum spectra
At post-maximum (![]() ),
we find a good agreement between the
),
we find a good agreement between the
![]() average
spectrum and its lower z counterpart:
average
spectrum and its lower z counterpart:
![]() (547 d.o.f.).
Variations in the spectral
residuals closely match those in the template residual and reflect
mean phase variations between the z<0.5 and
(547 d.o.f.).
Variations in the spectral
residuals closely match those in the template residual and reflect
mean phase variations between the z<0.5 and ![]() average
spectra. Once again, the level of discrepancy, though small, is
highest in the UV and in the Si II
average
spectra. Once again, the level of discrepancy, though small, is
highest in the UV and in the Si II ![]() 4000 region.
It is interesting to note that, as for the maximum light spectra, the
flux at the position of this line (which has almost disappeared a week
past maximum) is shallower for
4000 region.
It is interesting to note that, as for the maximum light spectra, the
flux at the position of this line (which has almost disappeared a week
past maximum) is shallower for ![]() than for the z<0.5spectrum. For Mg II
than for the z<0.5spectrum. For Mg II ![]() 4300 and Fe II
4300 and Fe II
![]() 4800, no
difference is found with redshift.
4800, no
difference is found with redshift.
Inspection of the spectra shows the presence of a residual
[O II] host line in the ![]() spectrum, for which a
separate extraction of the SN and the host is often difficult.
Moreover, our PEGASE host templates do not have emission lines. Other
residual absorption (e.g., Ca II H and K
and Balmer lines)
is also found in individual spectra.
spectrum, for which a
separate extraction of the SN and the host is often difficult.
Moreover, our PEGASE host templates do not have emission lines. Other
residual absorption (e.g., Ca II H and K
and Balmer lines)
is also found in individual spectra.
Our main conclusion of this redshift comparison is that
despite the
overall agreement between low (z<0.5) and
high (![]() )
spectral data, some discrepancies are found in characteristic
absorption features. This may indicate evolution with redshift, or a
signature of some selection effect. We discuss this in the next
section.
)
spectral data, some discrepancies are found in characteristic
absorption features. This may indicate evolution with redshift, or a
signature of some selection effect. We discuss this in the next
section.
7 Discussion
In recent years, various large-scale SN programs have published sets of SN Ia spectra at intermediate (Balland et al. 2006,2007; Zheng et al. 2008; Foley et al. 2008b) and distant (Lidman et al. 2005; Ellis et al. 2008; Foley et al. 2008a; Howell et al. 2005; Matheson et al. 2008; Bronder et al. 2008) redshifts. The SNLS VLT SN Ia spectral data set presented in this paper supplements these existing sets with 124 new SNe Ia, or probable SNe Ia. This constitutes the largest high-redshift SNe Ia spectroscopic sample published so far.
Comparing our data to this literature, we have the highest
SN Ia![]() /SN Ia
ratio. Howell
et al. (2005) publish the 1st year of
SNLS spectroscopy at Gemini. The redshift range targeted is
0.155 < z
< 1.01, the median redshift being 0.81, higher than our
median
redshift 0.62. Attributing an index of spectral quality to the Gemini
spectra, they identify 34 SN Ia and
7 SN Ia
/SN Ia
ratio. Howell
et al. (2005) publish the 1st year of
SNLS spectroscopy at Gemini. The redshift range targeted is
0.155 < z
< 1.01, the median redshift being 0.81, higher than our
median
redshift 0.62. Attributing an index of spectral quality to the Gemini
spectra, they identify 34 SN Ia and
7 SN Ia![]() among 64 SN candidates (recall that Howell et al.
(2005)
index
among 64 SN candidates (recall that Howell et al.
(2005)
index ![]() and 5 to SN Ia and
index
and 5 to SN Ia and
index ![]() to SN Ia
to SN Ia![]() ).
Lidman
et al. (2005)
find 15 SN Ia and 5
SN Ia
).
Lidman
et al. (2005)
find 15 SN Ia and 5
SN Ia![]() in the range 0.212<z<1.181
(
in the range 0.212<z<1.181
(
![]() ).
In both
cases, SN Ia
).
In both
cases, SN Ia![]() amount to
amount to ![]() 20%
of their total SN Ia sample.
We find 86 SN Ia (of which two are SN Ia_pec) and 38
SN Ia
20%
of their total SN Ia sample.
We find 86 SN Ia (of which two are SN Ia_pec) and 38
SN Ia![]() in
our VLT sample, that is
in
our VLT sample, that is ![]() 30%
of SN Ia
30%
of SN Ia![]() .
Other surveys
such as SDSS-II (Zheng
et al.
2008) and ESSENCE (Matheson
et al. 2005) both
find about 10% of probable SN Ia (equivalent to our
SN Ia
.
Other surveys
such as SDSS-II (Zheng
et al.
2008) and ESSENCE (Matheson
et al. 2005) both
find about 10% of probable SN Ia (equivalent to our
SN Ia![]() ).
The
SDSS-II survey targets low to intermediate redshifts (
0.05<z<0.4,
).
The
SDSS-II survey targets low to intermediate redshifts (
0.05<z<0.4,
![]() ),
which probably makes identification easier. The
average redshift of the ESSENCE SNe Ia is
),
which probably makes identification easier. The
average redshift of the ESSENCE SNe Ia is
![]() (Foley et al.
2008b),
significantly lower than ours.
(Foley et al.
2008b),
significantly lower than ours.
We identify fewer SN Ia![]() towards the end of the SNLS 3rd year
period. The average spectroscopic MJD of SN Ia classified
spectra is
53393 whereas it is 53272 for SN Ia
towards the end of the SNLS 3rd year
period. The average spectroscopic MJD of SN Ia classified
spectra is
53393 whereas it is 53272 for SN Ia![]() spectra. As all spectra are
treated on an equal footing from the point of view of extraction and
identification, this can not be due to improvement in data processing
or refinements in classification, but more likely indicates an
improved target selection efficiency and optimisation of spectroscopic
time during the course of the survey.
spectra. As all spectra are
treated on an equal footing from the point of view of extraction and
identification, this can not be due to improvement in data processing
or refinements in classification, but more likely indicates an
improved target selection efficiency and optimisation of spectroscopic
time during the course of the survey.
A key result of this work is the construction of average
spectra for
various phases and redshift bins from the homogeneous sample of VLT
SNe Ia. We have used these high quality average spectra to
compare
spectral properties at z<0.5 and ![]() .
We find differences
in the depth of some optical absorption features (Si II
and
Ca II) around maximum light. We find that
the absorptions
due to these elements in the z<0.5 spectrum
have weakened in the
corresponding
.
We find differences
in the depth of some optical absorption features (Si II
and
Ca II) around maximum light. We find that
the absorptions
due to these elements in the z<0.5 spectrum
have weakened in the
corresponding ![]() spectrum. Recently, Sullivan
et al. (2009) have
shown evidence for a similar weakening of singly ionized IME EWs
at
higher redshift. Using data from various searches, Howell et al.
(2007)
find an
spectrum. Recently, Sullivan
et al. (2009) have
shown evidence for a similar weakening of singly ionized IME EWs
at
higher redshift. Using data from various searches, Howell et al.
(2007)
find an ![]() 8%
increase in average light curve width for
non-subluminous SNe Ia in the
0.03<z<1.12 redshift range and
interpret it as a demographic evolution. High-z
SNe Ia have an
average stretch higher than at low redshift, thus are more luminous
and hotter, and should ionize more IMEs, depleting singly ionized
absorptions in high redshift spectra (e.g., Ellis
et al. 2008).
8%
increase in average light curve width for
non-subluminous SNe Ia in the
0.03<z<1.12 redshift range and
interpret it as a demographic evolution. High-z
SNe Ia have an
average stretch higher than at low redshift, thus are more luminous
and hotter, and should ionize more IMEs, depleting singly ionized
absorptions in high redshift spectra (e.g., Ellis
et al. 2008).
The average stretches of our two redshift subsamples are
![]() and
and
![]() respectively.
These two values are similar given the uncertainties.
This is not inconsistent with the results of
Howell
et al. (2005); Sullivan
et al. (2009),
as the predicted change in the spectra
over our redshift range due to a demographic shift is likely to be
very small. The average colours
respectively.
These two values are similar given the uncertainties.
This is not inconsistent with the results of
Howell
et al. (2005); Sullivan
et al. (2009),
as the predicted change in the spectra
over our redshift range due to a demographic shift is likely to be
very small. The average colours![]() are
are ![]() and
and
![]() .
The average rest frame distance
corrected magnitudes (using
.
The average rest frame distance
corrected magnitudes (using
![]() Astier et al.
2006) are
Astier et al.
2006) are
![]() (
(
![]() )
and
)
and
![]() (
(
![]() ),
the
),
the ![]() subsample having brighter supernovae,
on average, in qualitative agreement with what is expected from
Malmquist bias, as brighter supernovae, preferentially selected at
higher redshift, tend to be bluer. In order to assess the
significance of the apparent spectral differences in our maximum light
spectra, we have built two new subsamples (one for each redshift bin)
by selecting spectra with phase in the range
subsample having brighter supernovae,
on average, in qualitative agreement with what is expected from
Malmquist bias, as brighter supernovae, preferentially selected at
higher redshift, tend to be bluer. In order to assess the
significance of the apparent spectral differences in our maximum light
spectra, we have built two new subsamples (one for each redshift bin)
by selecting spectra with phase in the range
![]() and
bluer than average (i.e. spectra of SN Ia with colour c<0).
Using
these cuts, we end up with only 6 spectra for the z<0.5
bin, and 26
spectra for the
and
bluer than average (i.e. spectra of SN Ia with colour c<0).
Using
these cuts, we end up with only 6 spectra for the z<0.5
bin, and 26
spectra for the ![]() bin. As we expect to observe bluer objects
at higher redshift due to Malquist bias and to the ``brighter-bluer''
correlation, this should select two subsamples with roughly comparable
photometric properties. The average distance corrected magnitudes and
dispersions of these new subsamples are
bin. As we expect to observe bluer objects
at higher redshift due to Malquist bias and to the ``brighter-bluer''
correlation, this should select two subsamples with roughly comparable
photometric properties. The average distance corrected magnitudes and
dispersions of these new subsamples are
![]() (
(
![]() )
and
)
and
![]() (
(
![]() ).
The two first moments of the mB*cdistributions
are thus similar. We build new average spectra at
maximum light in the same way as in Sect. 6. The
results are shown in Fig. 10 and
must
be compared
to the middle panel of Fig. 9. Most
of the
differences have diseappeared, except around 3700
).
The two first moments of the mB*cdistributions
are thus similar. We build new average spectra at
maximum light in the same way as in Sect. 6. The
results are shown in Fig. 10 and
must
be compared
to the middle panel of Fig. 9. Most
of the
differences have diseappeared, except around 3700 ![]() and 3900
and 3900 ![]() .
We find
.
We find ![]() (544 d.o.f.). The difference at 3700
(544 d.o.f.). The difference at 3700 ![]() is due to a residual [O II] line in the
is due to a residual [O II] line in the ![]() spectrum. If the differences seen in Fig. 9 were
due to
imperfect calibration, slit losses or imperfect host subtraction, we
would expect to see comparable differences when selecting the two
``blue'' populations shown in Fig. 10.
The fact
that
the composite spectra nicely overlap for these two populations is in
itself an indication that the differences with redshift in our maximum
light spectra are real. We have checked that the differences remain
when selecting a subset of spectra with a host galaxy fraction below
20%. They also remain when we select a subset of spectra with little
recalibration (
spectrum. If the differences seen in Fig. 9 were
due to
imperfect calibration, slit losses or imperfect host subtraction, we
would expect to see comparable differences when selecting the two
``blue'' populations shown in Fig. 10.
The fact
that
the composite spectra nicely overlap for these two populations is in
itself an indication that the differences with redshift in our maximum
light spectra are real. We have checked that the differences remain
when selecting a subset of spectra with a host galaxy fraction below
20%. They also remain when we select a subset of spectra with little
recalibration (
![]() ). Thus it is unlikely that
the
differences are due to slit losses or a poorer host subtraction at
higher redshift. These differences more likely result from the
selection of brighter and bluer supernovae at higher redshift.
). Thus it is unlikely that
the
differences are due to slit losses or a poorer host subtraction at
higher redshift. These differences more likely result from the
selection of brighter and bluer supernovae at higher redshift.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12246_fig10.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg300.png)
|
Figure 10:
Comparison of z<0.5 (in black) and |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12246_fig11.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg301.png)
|
Figure 11:
Comparison of the VLT average spectra obtained from a subset of 51
spectra in the range z=0.35-0.7
(black), with the Keck average spectra from Ellis
et al. (2008) (in grey/red), for pre-maximum phases (
top), and at maximum phases ( bottom). VLT
spectra have been individually colour corrected using the SALT2 colour
law and recalibrated at the first order using the |
| Open with DEXTER | |
The two sets of pre-maximum spectra are consistent:
![]() (500 d.o.f.). For around maximum spectra, we find
(500 d.o.f.). For around maximum spectra, we find
![]() (500 d.o.f.).
The VLT average spectra are on
the lower limit of the Keck spectra in the UV region for both phase
ranges. In the optical region, the average spectra are in remarkable
agreement for pre-maximum spectra. For maximum-light spectra, the
agreement is fair in the optical, with some structure seen in the
residuals. It is in the UV region that differences are most
noticeable. There could be several explainations: this region is more
sensitive to differential slit losses, and we have normalised the
spectra at 3900
(500 d.o.f.).
The VLT average spectra are on
the lower limit of the Keck spectra in the UV region for both phase
ranges. In the optical region, the average spectra are in remarkable
agreement for pre-maximum spectra. For maximum-light spectra, the
agreement is fair in the optical, with some structure seen in the
residuals. It is in the UV region that differences are most
noticeable. There could be several explainations: this region is more
sensitive to differential slit losses, and we have normalised the
spectra at 3900 ![]() (had we chosen a shorter wavelength, the UV
discrepancies would have been less apparent, but the optical
differences greater). Also, the SALT2 colour law has been used to
build the average VLT spectra, whereas Ellis
et al. (2008) use the SALT1
colour law, though this has a negligible effect on the average
spectra. We find that the Ca II
(had we chosen a shorter wavelength, the UV
discrepancies would have been less apparent, but the optical
differences greater). Also, the SALT2 colour law has been used to
build the average VLT spectra, whereas Ellis
et al. (2008) use the SALT1
colour law, though this has a negligible effect on the average
spectra. We find that the Ca II ![]() 3700 and the
Si II
3700 and the
Si II ![]() 4000 absorptions are
consistent, both in
pre-maximum and at maximum spectra.
4000 absorptions are
consistent, both in
pre-maximum and at maximum spectra.
Recently, Foley
et al. (2008a) have published composite spectra from
ESSENCE data and they compare them in various bins of redshift and
phase, to the Lick z<0.1 counterpart
composite spectrum. Comparing
the ESSENCE and VLT spectra in a similar fashion to our comparison
with the Ellis spectra, we find substantial differences at all phases.
This may be due to the fact that Foley
et al. (2008a) subtract a single
average host spectrum, derived from a PCA analysis, from all of their
SNe. Regarding specific spectral features, they find that the most
important differences at maximum light between low- and high-redshift
are 1) Fe II ![]() 5129, that
yields a smaller EW of
the {Fe II
5129, that
yields a smaller EW of
the {Fe II ![]() 4800} blend in the ESSENCE
spectra
than in the Lick composite; and 2) the lack of
absorption at 3000
4800} blend in the ESSENCE
spectra
than in the Lick composite; and 2) the lack of
absorption at 3000 ![]() in the highest redshift bins of their ESSENCE composite spectra.
We qualitatively agree with their analysis of Fe II
in the highest redshift bins of their ESSENCE composite spectra.
We qualitatively agree with their analysis of Fe II
![]() 4800. We
however find the presence of absorption at 3000
4800. We
however find the presence of absorption at 3000 ![]() in our average spectra, for all phases at
in our average spectra, for all phases at ![]() ,
as seen
in Fig. 8.
For z<0.5, the absorption is at the
limit of our effective spectral range (see Fig. 8),
but
the absorption seems present, at least
for pre-maximum and at maximum spectra (it is very noisy for
post-maximum spectra). Following Foley
et al. (2008a), this difference
could arise from a selection bias in the ESSENCE sample that is not
present in the VLT sample.
,
as seen
in Fig. 8.
For z<0.5, the absorption is at the
limit of our effective spectral range (see Fig. 8),
but
the absorption seems present, at least
for pre-maximum and at maximum spectra (it is very noisy for
post-maximum spectra). Following Foley
et al. (2008a), this difference
could arise from a selection bias in the ESSENCE sample that is not
present in the VLT sample.
8 Conclusion
We have presented 139 spectra of 124 SNe Ia (SN Ia
type) or probable SNe Ia (SN Ia![]() type) at 0.149<z<1.031
observed mostly with the FORS1
instrument at the VLT during the first three years of the SNLS survey.
This is the largest SN Ia spectral dataset in this redshift range. We
have developed a dedicated pipeline, PHASE, for extracting clean SN
spectra free from host contamination. Our approach takes advantage of
the rolling search mode of the SNLS by using deep stacked reference
images to estimate the host spatial profile, used during the SN
extraction. We have also developed an identification technique based
on the simultaneous fit of light curve and spectral data with SALT2.
We have obtained two sets of certain and probable SNe Ia (the
SN Ia
and SN Ia
type) at 0.149<z<1.031
observed mostly with the FORS1
instrument at the VLT during the first three years of the SNLS survey.
This is the largest SN Ia spectral dataset in this redshift range. We
have developed a dedicated pipeline, PHASE, for extracting clean SN
spectra free from host contamination. Our approach takes advantage of
the rolling search mode of the SNLS by using deep stacked reference
images to estimate the host spatial profile, used during the SN
extraction. We have also developed an identification technique based
on the simultaneous fit of light curve and spectral data with SALT2.
We have obtained two sets of certain and probable SNe Ia (the
SN Ia
and SN Ia![]() categories), whose statistical properties have been
studied in detail. We find that:
categories), whose statistical properties have been
studied in detail. We find that:
- The statistical properties of our SN Ia and
SN Ia
 samples are similar. The SALT2 colour c and x1
parameters are consistent for both subsamples, as is the ``tilt''
parameter,
samples are similar. The SALT2 colour c and x1
parameters are consistent for both subsamples, as is the ``tilt''
parameter, 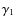 .
These are indications that our samples are not strongly contaminated by
non SNe Ia, validating the inclusion of SN Ia
.
These are indications that our samples are not strongly contaminated by
non SNe Ia, validating the inclusion of SN Ia in the Hubble diagram.
in the Hubble diagram. - The average redshift and phase for SN Ia
 are higher than for SN Ia. In particular, the average phase of
SN Ia
are higher than for SN Ia. In particular, the average phase of
SN Ia is 5.8 days, a phase at which the spectral S/N
has decreased with respect to maximum and SNe Ia spectra
closely resemble SNe Ic.
is 5.8 days, a phase at which the spectral S/N
has decreased with respect to maximum and SNe Ia spectra
closely resemble SNe Ic. - The uncorrected peak SN Ia
 magnitudes appear fainter than the SN Ia, consistent with the
SN Ia ``brighter-bluer'' relationship.
magnitudes appear fainter than the SN Ia, consistent with the
SN Ia ``brighter-bluer'' relationship. - On average, spectra of SNe identified as SN Ia
 have a higher host contamination than SN Ia spectra.
have a higher host contamination than SN Ia spectra. - We find two peculiar SNe whose spectra and properties resemble those of the over-luminous SN 1999aa supernova.
We have also internally compared the average SN Ia
spectra for z<0.5and ![]() .
We find evidence for differences in the intermediate
mass element absorptions in the average optical spectrum of
SNe Ia
between
.
We find evidence for differences in the intermediate
mass element absorptions in the average optical spectrum of
SNe Ia
between ![]() and
and ![]() (the average redshifts of the
z<0.5 and
(the average redshifts of the
z<0.5 and ![]() bins). The brighter SNe spectra have weaker
absorptions of singly ionized IMEs. Some discrepancy arises in the UV
region of the spectra. As far as our spectroscopic sample is
concerned, we have shown that these spectral differences can be
essentially accounted for by the Malmquist bias. The use of
SNe Ia as
``calibrated candles'' for cosmological purposes is thus fully
justified.
bins). The brighter SNe spectra have weaker
absorptions of singly ionized IMEs. Some discrepancy arises in the UV
region of the spectra. As far as our spectroscopic sample is
concerned, we have shown that these spectral differences can be
essentially accounted for by the Malmquist bias. The use of
SNe Ia as
``calibrated candles'' for cosmological purposes is thus fully
justified.
Finally, we have compared our VLT composite spectra with the Ellis et al. (2008) ones, both for pre- and at maximum phases.We find a good agreement between the two sets of spectra, which, given their fully independent processing, gives us confidence in the quality of both spectral sets.
The VLT spectra presented in this paper for which sufficient photometric information exists, once merged with the Gemini and Keck SNLS spectra (Ellis et al. 2008; Howell et al. 2005; Bronder et al. 2008), will constitute the spectroscopic sample for the SNLS 3rd year cosmological analyses.
AcknowledgementsWe gratefully acknowledge the assistance of the VLT Queue Scheduling Observing Team. We thank the anonymous referee for helpful comments on the manuscript. French authors acknowledge support from CNRS/IN2P3, CNRS/INSU and PNC. CENTRA members were supported by Fundação para a Ciência e Tecnologia (FCT), Portugal under POCTI/CTE-AST/57664/2004. V.A. acknowledges support from FCT under grant no SFRH/BD/11119/2002 and SF grant no SFRH/BPD/31817/2006. M.S. acknowledges support from the Royal Society.
References
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [EDP Sciences] [CrossRef] [NASA ADS]
- Balland, C., Mouchet, M., Pain, R., et al. 2006, A&A, 445, 387 [EDP Sciences] [CrossRef] [NASA ADS]
- Balland, C., Mouchet, M., Amanullah, R., et al. 2007, A&A, 464, 827 [EDP Sciences] [CrossRef] [NASA ADS]
- Basa, S., et al. 2009, A&A, in prep.
- Baumont, S. 2007, Ph.D. Thesis, Univ. D. Diderot, Paris 7, supernovae.in2p3.fr/ baumont/outreach/baumont_these.pdf
- Baumont, S., Balland, C., Astier, P., et al. 2008, A&A, 491, 567 [EDP Sciences] [CrossRef] [NASA ADS]
- Bazin, G., Palanque-Delabrouille, N., Rich, J., et al. 2009, A&A, 499, 653 [EDP Sciences] [CrossRef] [NASA ADS]
- Blondin, S., & Tonry, J. L. 2007, ApJ, 666, 1024 [CrossRef] [NASA ADS]
- Blondin, S., Walsh, J. R., Leibundgut, B., & Sainton, G. 2005, A&A, 431, 757 [EDP Sciences] [CrossRef] [NASA ADS]
- Blondin, S., Dessart, L., Leibundgut, B., et al. 2006, AJ, 131, 1648 [CrossRef] [NASA ADS]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, ed. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 72
- Bronder, T. J., Hook, I. M., Astier, P., et al. 2008, A&A, 477, 717 [EDP Sciences] [CrossRef] [NASA ADS]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, APJ, 345, 245 [CrossRef] [NASA ADS]
- Conley, A., Sullivan, M., Hsiao, E. Y., et al. 2008, ApJ, 681, 482 [CrossRef] [NASA ADS]
- Ellis, R. S., Sullivan, M., Nugent, P. E., et al. 2008, ApJ, 674, 51 [CrossRef] [NASA ADS]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS]
- Fioc, M., & Rocca-Volmerange, B. 1999, [arXiv:astro-ph/9912179]
- Foley, R. J., Filippenko, A. V., Aguilera, C., et al. 2008a, ApJ, 684, 68 [CrossRef] [NASA ADS]
- Foley, R. J., Matheson, T., Blondin, S., et al. 2008b, AJ, 137, 3731 [CrossRef] [NASA ADS]
- Garavini, G., Folatelli, G., Goobar, A., et al. 2004, AJ, 128, 387 [CrossRef] [NASA ADS]
- Garavini, G., Folatelli, G., Nobili, S., et al. 2007, A&A, 470, 411 [EDP Sciences] [CrossRef] [NASA ADS]
- Guy, J., Astier, P., Baumont, S., et al. 2007, A&A, 466, 11 [EDP Sciences] [CrossRef] [NASA ADS]
- Hachinger, S., Mazzali, P. A., & Benetti, S. 2006, MNRAS, 370, 299 [NASA ADS]
- Hoeflich, P., Wheeler, J. C., & Thielemann, F. K. 1998, ApJ, 495, 617 [CrossRef] [NASA ADS]
- Hook, I. M., Howell, D. A., Aldering, G., et al. 2005, AJ, 130, 2788 [CrossRef] [NASA ADS]
- Howell, D. A., Sullivan, M., Perrett, K., et al. 2005, ApJ, 634, 1190 [CrossRef] [NASA ADS]
- Howell, D. A., Sullivan, M., Conley, A., & Carlberg, R. 2007, ApJ, 667, L37 [CrossRef] [NASA ADS]
- Hsiao, E. Y., Conley, A., Howell, D. A., et al. 2007, ApJ, 663, 1187 [CrossRef] [NASA ADS]
- Jha, S., Kirshner, R. P., Challis, P., et al. 2006, AJ, 131, 527 [CrossRef] [NASA ADS]
- Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [CrossRef] [NASA ADS]
- Kowalski, M., Rubin, D., Aldering, G., et al. 2008, ApJ, 686, 749 [CrossRef] [NASA ADS]
- Lentz, E. J., Baron, E., Branch, D., Hauschildt, P. H., & Nugent, P. E. 2000, ApJ, 530, 966 [CrossRef] [NASA ADS]
- Li, W., Filippenko, A. V., Treffers, R. R., et al. 2001, ApJ, 546, 734 [CrossRef] [NASA ADS]
- Lidman, C., Howell, D. A., Folatelli, G., et al. 2005, A&A, 430, 843 [EDP Sciences] [CrossRef] [NASA ADS]
- Matheson, T., Blondin, S., Foley, R. J., et al. 2005, AJ, 129, 2352 [CrossRef] [NASA ADS]
- Matheson, T., Kirshner, R. P., Challis, P., et al. 2008, ArXiv e-prints, 803
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [CrossRef] [NASA ADS]
- Perrett, K. et. al. 2009, PASP, in prep.
- Phillips, M. M. 1993, ApJL, 413, 105 [CrossRef] [NASA ADS]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [CrossRef] [NASA ADS]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [CrossRef] [NASA ADS]
- Sullivan, M., Howell, D. A., Perrett, K., et al. 2006, AJ, 131, 960 [CrossRef] [NASA ADS]
- Sullivan, M., Ellis, R. S., Howell, D. A., et al. 2009, ApJ, 693, L76 [CrossRef] [NASA ADS]
- Tonry, J. L., Schmidt, B. P., Barris, B., et al. 2003, ApJ, 594, 1 [CrossRef] [NASA ADS]
- Tripp, R., & Branch, D. 1999, ApJ, 525, 209 [CrossRef] [NASA ADS]
- Wood-Vasey, W. M., Miknaitis, G., Stubbs, C. W., et al. 2007, ApJ, 666, 694 [CrossRef] [NASA ADS]
- Zheng, C., Romani, R. W., Sako, M., et al. 2008, AJ, 135, 1766 [CrossRef] [NASA ADS]
Online Material
Appendix A: Spectra
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a1.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a2.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg307.png)
|
Figure A.1:
SNLS- 03D1ar270: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a3.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a4.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg308.png)
|
Figure A.2:
SNLS- 03D1bf269: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a5.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a6.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg309.png)
|
Figure A.3:
SNLS- 03D1bm272: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a7.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a8.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg310.png)
|
Figure A.4:
SNLS- 03D1bp270: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a9.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a10.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg311.png)
|
Figure A.5: SNLS- 03D1co307: a SN Ia supernova at z=0.679. The spectrum phase is -4.1. A E(8) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a11.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a12.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg312.png)
|
Figure A.6: SNLS- 03D1dt333: a SN Ia supernova at z=0.612. The spectrum phase is 5.1. A Sc(4) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a13.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a14.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg313.png)
|
Figure A.7: SNLS- 03D1fc358: a SN Ia supernova at z=0.332. The spectrum phase is -4.4. A E(3) host model has been subtracted. Three re-calibration parameters have been used to fit this spectrum. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a15.eps}
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg314.png)
|
Figure A.8: SNLS- 03D1fl355: a SN Ia supernova at z=0.687. The spectrum phase is 0.5. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a16.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a17.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg315.png)
|
Figure A.9: SNLS- 03D1gt385: a SN Ia supernova at z=0.560. The spectrum phase is 7.0. A E(4) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a18.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a19.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg316.png)
|
Figure A.10:
SNLS- 03D4ag180: a SN Ia_pec supernova at z=0.285.
The spectrum phase is -8.6. A E(2) host model has been
subtracted. Note the poor fit below rest-frame 4000 |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a20.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a21.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg317.png)
|
Figure A.11: SNLS- 03D4at186: a SN Ia supernova at z=0.634. The spectrum phase is 5.5. A Sb-Sc host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a22.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a23.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg318.png)
|
Figure A.12:
SNLS- 03D4au186: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a24.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg319.png)
|
Figure A.13: SNLS- 03D4cx245: a SN Ia supernova at z=0.949. The spectrum phase is 1.2. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a25.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a26.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg320.png)
|
Figure A.14: SNLS- 03D4cx248: a SN Ia supernova at z=0.949. Spectrum obtained with the 300I Grism. The spectrum phase is 2.7. A S0(4) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a27.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a28.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg321.png)
|
Figure A.15: SNLS- 03D4cy269: a SN Ia supernova at z=0.927. The spectrum phase is 4.6. A Sb-Sc host model has been subtracted. The identification of this supernova as a SN Ia is based on a Gemini spectrum of this same SN (Howell et al. 2005). |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a29.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a30.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg322.png)
|
Figure A.16:
SNLS- 03D4di245: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a31.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg323.png)
|
Figure A.17:
SNLS- 03D4di249: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a32.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg324.png)
|
Figure A.18: SNLS- 03D4dy272: a SN Ia supernova at z=0.61. The spectrum phase is 4.8. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a33.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a34.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg325.png)
|
Figure A.19:
SNLS- 03D4gf329: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a35.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a36.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg326.png)
|
Figure A.20:
SNLS- 03D4gg330: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a37.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a38.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg327.png)
|
Figure A.21: SNLS- 04D1ag383: a SN Ia supernova at z=0.557. The spectrum phase is 4.3. A E(12) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a39.eps}
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg328.png)
|
Figure A.22:
SNLS- 04D1aj381: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a40.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg329.png)
|
Figure A.23:
SNLS- 04D1aj384: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a41.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg330.png)
|
Figure A.24:
SNLS- 04D1ak388: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a42.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg331.png)
|
Figure A.25: SNLS- 04D1dc589: a SN Ia supernova at z=0.211. The spectrum phase is -0.4. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a43.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a44.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg332.png)
|
Figure A.26: SNLS- 04D1ff619: a SN Ia supernova at z=0.86. The spectrum phase is 4.6. A Sc(2) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a45.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg333.png)
|
Figure A.27:
SNLS- 04D1hx628: a SN Ia supernova at z=0.560.
The spectrum phase is 5.9. Best-fit obtained for a model with no host
galaxy component. Note the model is unable to reproduce the large
feature at rest-frame 4500 |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a46.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg334.png)
|
Figure A.28: SNLS- 04D1iv630: a SN Ia supernova at z=0.998. The spectrum phase is 3.0. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a47.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a48.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg335.png)
|
Figure A.29:
SNLS- 04D1jd630: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a49.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg336.png)
|
Figure A.30: SNLS- 04D1kj650: a SN Ia supernova at z=0.585. The spectrum phase is -3.7. Best-fit obtained for a model with no host galaxy component |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a50.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg337.png)
|
Figure A.31: SNLS- 04D1ks649: a SN Ia supernova at z=0.798. The spectrum phase is -1.0. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a51.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg338.png)
|
Figure A.32: SNLS- 04D1ow683: a SN Ia supernova at z=0.915. The spectrum phase is 6.4. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a52.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a53.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg339.png)
|
Figure A.33: SNLS- 04D1pc684: a SN Ia supernova at z=0.770. The spectrum phase is 0.1. A E(3) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a54.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a55.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg340.png)
|
Figure A.34: SNLS- 04D1pd682: a SN Ia supernova at z=0.95. The spectrum phase is 2.5. A E(1) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a56.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a57.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg341.png)
|
Figure A.35: SNLS- 04D1pg684: a SN Ia supernova at z=0.515. The spectrum phase is -1.3. A Sa-Sb host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a58.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg342.png)
|
Figure A.36: SNLS- 04D1pp683: a SN Ia supernova at z=0.735. The spectrum phase is 2.2. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a59.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a60.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg343.png)
|
Figure A.37:
SNLS- 04D1qd688: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a61.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg344.png)
|
Figure A.38: SNLS- 04D1rh710: a SN Ia supernova at z=0.436. The spectrum phase is 0.0. Best-fit obtained for a model with no host galaxy. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a62.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg345.png)
|
Figure A.39:
SNLS- 04D1rx713: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a63.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a64.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg346.png)
|
Figure A.40: SNLS- 04D1sa716: a SN Ia supernova at z=0.585. The spectrum phase is -2.6. A E(1) host model has been subtracted. Note the bad fit in the UV region due to subtracting too blue a host model. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a65.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a66.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg347.png)
|
Figure A.41: SNLS- 04D1si716: a SN Ia supernova at z=0.702. The spectrum phase is -1.7. A Sa(9) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a67.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a68.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg348.png)
|
Figure A.42: SNLS- 04D2ac395: a SN Ia supernova at z=0.348. The spectrum phase is 1.3. A Sa-Sb host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a69.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a70.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg349.png)
|
Figure A.43: SNLS- 04D2al390: a SN Ia supernova at z=0.836. The spectrum phase is -2.5. A E(2) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a71.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg350.png)
|
Figure A.44:
SNLS- 04D2an386: a SN Ia supernova at z=0.62.
The spectrum phase is -3.4. Best-fit obtained for a model with no host
galaxy component. Note that the Ca II
feature at rest-frame 3700 |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a72.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a73.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg351.png)
|
Figure A.45: SNLS- 04D2an392: a SN Ia supernova at z=0.62. The spectrum phase is 0.3. A Sc(9) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a74.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a75.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg352.png)
|
Figure A.46: SNLS- 04D2bt444: a SN Ia supernova at z=0.220. The spectrum phase is 6.6. A E(6) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a76.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg353.png)
|
Figure A.47:
SNLS- 04D2ca445: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a77.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg354.png)
|
Figure A.48:
SNLS- 04D2ca447: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a78.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a79.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg355.png)
|
Figure A.49:
SNLS- 04D2cc446: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a80.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a81.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg356.png)
|
Figure A.50:
SNLS- 04D2cc448: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a82.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg357.png)
|
Figure A.51:
SNLS- 04D2cf447: a SN Ia supernova at z=0.369.
The spectrum phase is 8.5. Best-fit obtained for a model with no host
galaxy component. Note that the model is unable to reproduce the
feature at rest-frame 4900 |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a83.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a84.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg358.png)
|
Figure A.52:
SNLS- 04D2cw445: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a85.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg359.png)
|
Figure A.53: SNLS- 04D2fp470: a SN Ia supernova at z=0.415. The spectrum phase is 1.8. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a86.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg360.png)
|
Figure A.54: SNLS- 04D2fs470: a SN Ia supernova at z=0.357. The spectrum phase is 1.7. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a87.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a88.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg361.png)
|
Figure A.55: SNLS- 04D2gc471: a SN Ia supernova at z=0.521. The spectrum phase is -4.9. A E(1) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a89.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg362.png)
|
Figure A.56: SNLS- 04D2gp475: a SN Ia supernova at z=0.732. The spectrum phase is 2.7. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a90.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg363.png)
|
Figure A.57:
SNLS- 04D2iu497: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a91.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a92.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg364.png)
|
Figure A.58:
SNLS- 04D2iu498: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a93.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a94.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg365.png)
|
Figure A.59:
SNLS- 04D2ja499: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a95.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a96.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg366.png)
|
Figure A.60:
SNLS- 04D2ja500: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a97.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a98.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg367.png)
|
Figure A.61: SNLS- 04D2mc736: a SN Ia supernova at z=0.348. The spectrum phase is 6.5. A Sa-Sb host model has been subtracted. Three re-calibration parameters have been used to fit this spectrum. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a99.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg368.png)
|
Figure A.62: SNLS- 04D4an558: a SN Ia supernova at z=0.613. The spectrum phase is 8.1. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a100.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a101.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg369.png)
|
Figure A.63:
SNLS- 04D4bk558: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a102.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg370.png)
|
Figure A.64: SNLS- 04D4bq558: a SN Ia supernova at z=0.55. The spectrum phase is 2.6. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a103.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg371.png)
|
Figure A.65: SNLS- 04D4bq562: a SN Ia supernova at z=0.55. The spectrum phase is 5.1. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a104.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a105.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg372.png)
|
Figure A.66:
SNLS- 04D4dw566: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a106.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg373.png)
|
Figure A.67: SNLS- 04D4fx589: a SN Ia supernova at z=0.629. The spectrum phase is -8.4. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a107.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a108.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg374.png)
|
Figure A.68:
SNLS- 04D4gz598: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a109.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg375.png)
|
Figure A.69:
SNLS- 04D4gz620: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a110.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg376.png)
|
Figure A.70:
SNLS- 04D4hf598: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a111.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a112.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg377.png)
|
Figure A.71: SNLS- 04D4ht628: a SN Ia supernova at z=0.217. The spectrum phase is 6.6. A Sa-Sb host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a113.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a114.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg378.png)
|
Figure A.72: SNLS- 04D4ib629: a SN Ia supernova at z=0.699. The spectrum phase is 0.7. A S0-Sa host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a115.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg379.png)
|
Figure A.73: SNLS- 04D4id628: a SN Ia supernova at z=0.769. The spectrum phase is 3.0. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a116.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg380.png)
|
Figure A.74: SNLS- 04D4jr650: a SN Ia supernova at z=0.47. The spectrum phase is -5.9. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a117.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a118.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg381.png)
|
Figure A.75: SNLS- 04D4ju650: a SN Ia supernova at z=0.472. The spectrum phase is -2.2. A S0(1) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a119.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a120.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg382.png)
|
Figure A.76:
SNLS- 04D4jw651: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a121.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a122.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg383.png)
|
Figure A.77: SNLS- 05D1cb984: a SN Ia supernova at z=0.632. The spectrum phase is 4.3. A Sb-Sc host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a123.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a124.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg384.png)
|
Figure A.78: SNLS- 05D1ck983: a SN Ia supernova at z=0.617. The spectrum phase is -2.7. A Sb-Sc host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a125.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a126.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg385.png)
|
Figure A.79:
SNLS- 05D1cl999: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a127.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg386.png)
|
Figure A.80: SNLS- 05D1dn1002: a SN Ia supernova at z=0.566. The spectrum phase is -4.7. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a128.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a129.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg387.png)
|
Figure A.81: SNLS- 05D1hk1072: a SN Ia_pec supernova at z=0.263. The spectrum phase is -5.0. A Sc(5) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a130.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg388.png)
|
Figure A.82: SNLS- 05D1hn1073: a SN Ia supernova at z=0.149. The spectrum phase is -1.0. Best-fit obtained for a model with no host galaxy component. This is a very reddened SN Ia due to host interstellar absorption. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a131.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a132.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg389.png)
|
Figure A.83:
SNLS- 05D1iz1069: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a133.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg390.png)
|
Figure A.84: SNLS- 05D1ke1094: a SN Ia supernova at z=0.69. The spectrum phase is 2.2. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a134.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg391.png)
|
Figure A.85: SNLS- 05D2ac738: a SN Ia supernova at z=0.479. The spectrum phase is 2.0. Best-fit obtained for a model with no host galaxy component. Note that the model overestimates the flux in the UV region of the spectrum. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a135.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a136.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg392.png)
|
Figure A.86:
SNLS- 05D2ay746: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a137.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg393.png)
|
Figure A.87: SNLS- 05D2bt764: a SN Ia supernova at z=0.68. The spectrum phase is 1.4. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a138.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a139.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg394.png)
|
Figure A.88:
SNLS- 05D2bv764: a SN Ia supernova at z=0.474.
The spectrum phase is -0.1. A Sb-Sc host model has been subtracted.
Note that the Ca II feature at rest-frame
3700 |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a140.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a141.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg395.png)
|
Figure A.89: SNLS- 05D2bw764: a SN Ia supernova at z=0.92. The spectrum phase is 1.9. A Sb-Sc host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a142.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a143.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg396.png)
|
Figure A.90:
SNLS- 05D2by775: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a144.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a145.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg397.png)
|
Figure A.91:
SNLS- 05D2cb775: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a146.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg398.png)
|
Figure A.92: SNLS- 05D2ci795: a SN Ia supernova at z=0.630. The spectrum phase is 3.6. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a147.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg399.png)
|
Figure A.93: SNLS- 05D2ci796: a SN Ia supernova at z=0.630. The spectrum phase is 4.9. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a148.eps}
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg400.png)
|
Figure A.94: SNLS- 05D2ci799: a SN Ia supernova at z=0.630. The spectrum phase is 6.7. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a149.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a150.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg401.png)
|
Figure A.95:
SNLS- 05D2ct799: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a151.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a152.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg402.png)
|
Figure A.96: SNLS- 05D2dt807: a SN Ia supernova at z=0.574. The spectrum phase is -1.7. A E(3) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a153.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a154.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg403.png)
|
Figure A.97:
SNLS- 05D2dw807: a SN Ia supernova at z=0.417.
The spectrum phase is -5.3. A S0(1) host model has been subtracted.
Note that the model is unable to reproduce the deep Ca II
feature at rest-frame 3700 |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a155.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a156.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg404.png)
|
Figure A.98:
SNLS- 05D2dy805: a SN Ia supernova at z=0.51.
The spectrum phase is 1.1. A Sb-Sc host model has been subtracted. Note
that the Ca II feature at rest-frame
3700 |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a157.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a158.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg405.png)
|
Figure A.99:
SNLS- 05D2eb805: a SN Ia supernova at z=0.534. The spectrum
phase is -4.7. A S0(1) host model has been subtracted. Note
that the model is unable to reproduce the deep Ca II
feature at rest-frame 3700 |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a159.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg406.png)
|
Figure A.100: SNLS- 05D2ec805: a SN Ia supernova at z=0.640. The spectrum phase is 2.7. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a160.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a161.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg407.png)
|
Figure A.101:
SNLS- 05D2ei833: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a162.eps}
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg408.png)
|
Figure A.102: SNLS- 05D2fq827: a SN Ia supernova at z=0.733. The spectrum phase is 2.1. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a163.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a164.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg409.png)
|
Figure A.103: SNLS- 05D2he833: a SN Ia supernova at z=0.608. The spectrum phase is 3.0. A E(1) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a165.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a166.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg410.png)
|
Figure A.104: SNLS- 05D2ie829: a SN Ia supernova at z=0.348. The spectrum phase is -8.9. A Sc(4) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a167.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a168.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg411.png)
|
Figure A.105: SNLS- 05D2nn1071: a SN Ia supernova at z=0.87. The spectrum phase is -1.3. A Sa(8) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a169.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg412.png)
|
Figure A.106: SNLS- 05D4af914: a SN Ia supernova at z=0.499. The spectrum phase is 11.3. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a170.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a171.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg413.png)
|
Figure A.107:
SNLS- 05D4ag922: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a172.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a173.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg414.png)
|
Figure A.108:
SNLS- 05D4ay914: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a174.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a175.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg415.png)
|
Figure A.109:
SNLS- 05D4ay916: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a176.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a177.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg416.png)
|
Figure A.110: SNLS- 05D4be918: a SN Ia supernova at z=0.537. The spectrum phase is 3.9. A E(1) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a178.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a179.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg417.png)
|
Figure A.111: SNLS- 05D4bi918: a SN Ia supernova at z=0.775. The spectrum phase is -1.5. A Sc(1) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a180.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a181.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg418.png)
|
Figure A.112: SNLS- 05D4bj921: a SN Ia supernova at z=0.701. The spectrum phase is -2.0. A Sc(9) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a182.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a183.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg419.png)
|
Figure A.113: SNLS- 05D4cn952: a SN Ia supernova at z=0.763. The spectrum phase is 4.7. A S0(1) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a184.eps}
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg420.png)
|
Figure A.114: SNLS- 05D4cq946: a SN Ia supernova at z=0.701. The spectrum phase is -0.1. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a185.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a186.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg421.png)
|
Figure A.115: SNLS- 05D4cs946: a SN Ia supernova at z=0.79. The spectrum phase is -1.7. A Sc(12) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a187.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a188.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg422.png)
|
Figure A.116: SNLS- 05D4cw950: a SN Ia supernova at z=0.375. The spectrum phase is 7.0. A S0(6) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a189.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a190.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg423.png)
|
Figure A.117: SNLS- 05D4dw983: a SN Ia supernova at z=0.855. The spectrum phase is 4.7. A Sc(12) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a191.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a192.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg424.png)
|
Figure A.118:
SNLS- 05D4ef997: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a193.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg425.png)
|
Figure A.119: SNLS- 05D4ej1000: a SN Ia supernova at z=0.585. The spectrum phase is 7.6. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a194.eps}
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg426.png)
|
Figure A.120: SNLS- 05D4ek999: a SN Ia supernova at z=0.536. The spectrum phase is 2.1. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a195.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg427.png)
|
Figure A.121: SNLS- 05D4ev985: a SN Ia supernova at z=0.722. The spectrum phase is -3.6. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a196.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a197.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg428.png)
|
Figure A.122:
SNLS- 05D4fe1000: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a198.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a199.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg429.png)
|
Figure A.123:
SNLS- 05D4ff1003: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a200.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a201.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg430.png)
|
Figure A.124: SNLS- 05D4fg1002: a SN Ia supernova at z=0.839. The spectrum phase is -0.3. A S0(5) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a202.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a203.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg431.png)
|
Figure A.125:
SNLS- 06D1ab1100: a SN Ia supernova at z=0.182.
The spectrum phase is -4.4. A E(7) host model has been subtracted. Note
that the model is unable to reproduce the large feature at
rest-frame 4500 |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a204.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a205.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg432.png)
|
Figure A.126: SNLS- 06D2bk1135: a SN Ia supernova at z=0.499. The spectrum phase is 0.9. A Sb-Sc host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a206.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a207.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg433.png)
|
Figure A.127: SNLS- 06D2ca1153: a SN Ia supernova at z=0.531. The spectrum phase is 0.0. A Sd(5) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a208.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a209.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg434.png)
|
Figure A.128: SNLS- 06D2ca1154: a SN Ia supernova at z=0.531. The spectrum phase is 0.7. A Sd(3) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a210.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg435.png)
|
Figure A.129:
SNLS- 06D2cb1155: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a211.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg436.png)
|
Figure A.130: SNLS- 06D2cc1153: a SN Ia supernova at z=0.532. The spectrum phase is 3.3. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a212.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg437.png)
|
Figure A.131: SNLS- 06D2cd1157: a SN Ia supernova at z=0.930. Spectrum obtained with the 300I Grism on FORS2. The spectrum phase is 4.2. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a213.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg438.png)
|
Figure A.132: SNLS- 06D2ce1156: a SN Ia supernova at z=0.82. Spectrum obtained with the 300I Grism on FORS2. The spectrum phase is 0.0. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a214.eps} \hspace*{4mm} \includegraphics[width=8.8cm]{12246a215.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg439.png)
|
Figure A.133:
SNLS- 06D2ck1162: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\mbox{ \includegraphics[width=8.8cm]{12246a216.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a217.eps} }
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg440.png)
|
Figure A.134:
SNLS- 06D2ga1241: a SN Ia |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a218.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg441.png)
|
Figure A.135: SNLS- 06D4ce1295: a SN Ia supernova at z=0.85. The spectrum phase is 2.7. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a219.eps}\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg442.png)
|
Figure A.136: SNLS- 06D4ce1296: a SN Ia supernova at z=0.85. The spectrum phase is 3.3. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a220.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a221.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg443.png)
|
Figure A.137: SNLS- 06D4cl1297: a SN Ia supernova at z=1.00. The spectrum phase is -2.5. A E(1) host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\mbox{\includegraphics[width=8.8cm]{12246a222.eps} \hspace*{4mm}
\includegraphics[width=8.8cm]{12246a223.eps} }
\par
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg444.png)
|
Figure A.138: SNLS- 06D4co1306: a SN Ia supernova at z=0.437. The spectrum phase is 3.5. A E-S0 host model has been subtracted. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=8.8cm]{12246a224.eps}
\par\end{figure}](/articles/aa/full_html/2009/43/aa12246-09/Timg445.png)
|
Figure A.139: SNLS- 06D4cq1306: a SN Ia supernova at z=0.411. The spectrum phase is -1.4. Best-fit obtained for a model with no host galaxy component. |
| Open with DEXTER | |
Footnotes
- ...
from the supernova legacy survey
![[*]](/icons/foot_motif.png)
- Based on observations obtained with FORS1 and FORS2 at the Very Large Telescope on Cerro Paranal, operated by the European Southern Observatory, Chile (ESO Large Programs 171.A-0486 and 176.A-0589).
- ...
![[*]](/icons/foot_motif.png)
- Appendix is only available in electronic form at http://www.aanda.org
- ... years
![[*]](/icons/foot_motif.png)
- The SNLS started in June 2003.
- ... programs
![[*]](/icons/foot_motif.png)
- These dates correspond to the first three years of the SNLS.
- ...
mode
![[*]](/icons/foot_motif.png)
- Only eight candidates from SNLS3 were observed in MOS mode and have been identified as SN Ia in real-time. As the MOS mode is currently not supported by our new extraction pipeline (see Baumont et al. 2008), we do not include them in here. Note also that only 3 SNe Ia were observed on FORS2 in the period covered in this study.
- ... curves
![[*]](/icons/foot_motif.png)
- We use gM, rM and iM for spectra obtained with grism 300V (Baumont et al. 2008).
- ...
magnitude
![[*]](/icons/foot_motif.png)
- Note that mB*c is not the quantity used to constrain the cosmological parameters, as it is not corrected for x1 and c.
- ...
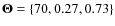
![[*]](/icons/foot_motif.png)
- H0 is in units of km s-1 Mpc-1.
- ... colours
![[*]](/icons/foot_motif.png)
- We limit our set to SNe Ia with
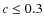 to reject red, heavily extinguished objects. This cuts three
SNe Ia out of the sample.
to reject red, heavily extinguished objects. This cuts three
SNe Ia out of the sample.
All Tables
Table
1: List of SNLS 3rd year ESO-VLT SN Ia and
SN Ia![]() spectraa.
spectraa.
Table
2: Results of identifications of the SNLS 3rd year ESO-VLT
SN Ia
and SN Ia![]() spectra.
spectra.
Table 3: Distribution of types per SNLS Deep field and in total.
Table
4: Average properties of the SN Ia and SN Ia![]() subsamples.
subsamples.
Table 5: Properties of SNLS-03D4ag and SNLS-05D1hk VLT spectra.
Table 6: Number of SN Ia spectra in each phase bin (in days) used to create VLT composite spectra.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.