| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 377 - 384 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200911900 | |
| Published online | 03 September 2009 | |
A&A 507, 377-384 (2009)
Using binaries containing giants to constrain theories of stellar and tidal evolution
A. Claret
Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
Received 20 February 2009 / Accepted 4 August 2009
Abstract
Aims. Investigations of stellar and tidal evolution
of binary
stars with giant components are rare. In this paper, we will
investigate such features in three binary systems for which at least
one component is a giant star. As some of these giants seem to be in
the blue loop, it is an excellent opportunity to investigate the
sensitivity of core overshooting on their location in the HR Diagram.
We expect that these characteristics shall serve as an incentive to
observers to investigate such kinds of binaries, increasing the
accuracy of measurements and the number of systems to test the
evolutionary models.
Methods. Prior to performing the study of the
circularization
and synchronization levels, an analysis of the capability of our
stellar evolutionary models to reproduce the observed masses, radii and
effective temperatures is carried out. Next, the differential equations
of tidal evolution are integrated and the corresponding critical times
are compared with the inferred age of the system and with the observed
eccentricity and rotational velocities (when available).
Results. We have found good agreement between our
stellar models and the astrophysical properties of ![]() And, V2291 Oph and SZ Cen by adopting a moderate core overshooting
amount (
And, V2291 Oph and SZ Cen by adopting a moderate core overshooting
amount (
![]() ).
Three mechanisms were used to try to explain the observed levels of
circularization and synchronization: the hydrodynamical mechanism,
turbulent dissipation and radiative damping. In the cases of
).
Three mechanisms were used to try to explain the observed levels of
circularization and synchronization: the hydrodynamical mechanism,
turbulent dissipation and radiative damping. In the cases of ![]() And and SZ Cen, for which the rotational velocities are available, by
assuming solid body rotation for both stars of each system we have
found that the theoretical ratio between the rotational velocities
And and SZ Cen, for which the rotational velocities are available, by
assuming solid body rotation for both stars of each system we have
found that the theoretical ratio between the rotational velocities
![]() at the inferred ages are in good agreement with the observational
ratios.
at the inferred ages are in good agreement with the observational
ratios.
Key words: stars: binaries: general - stars: evolution - stars: rotation
1 Introduction
Tidal interactions in a binary system may lead to a final coalescence
of both stars or, less drastically, to an equilibrium state,
characterized by a circular coplanar orbit and with the rotational
velocities synchronized with the orbital period. The evolutionary
models, on the other hand, can provide in many cases a good
approximation to the age of the system. By comparing this age with the
critical times of circularization and synchronization computed by using
current tidal theories, we can extract some information from the
observed rotational velocities and eccentricity. As the time scales are
strongly dependent on the absolute dimensions (mainly the radius), the
best candidates for such a study are the double-lined eclipsing
binaries with good determination of absolute dimensions. This kind of
systematic investigation was already carried out by Claret &
Cunha (1997), for
example. However, the sample adopted in that paper and others was
constituted basically of Main-Sequence stars and the behaviour of more
evolved components, concerning tidal interactions, was studied only in
a few systems: ![]() And, AY Cet and TZ For (Habets & Zwaan 1989;
Claret & Giménez 1995).
Only in the case of TZ For was it possible to determine the masses,
radii and effective temperature with good accuracy.
And, AY Cet and TZ For (Habets & Zwaan 1989;
Claret & Giménez 1995).
Only in the case of TZ For was it possible to determine the masses,
radii and effective temperature with good accuracy.
Tidal evolution also can be investigated in binaries located in clusters since they can give information on the level of circularization of these coeval samples. One of the most important observations concerning binaries in clusters is the cut-off period (Mayor & Mermilliod 1984), that is the period characterizing a transition between circular and eccentric orbits. This concept was recently revised (see for example Claret 2005; Meibom & Mathieu 2005). Comparison between the cut-off periods (or their recently introduced equivalents) with those inferred from the different mechanisms of circularization is also a good tool to test current tidal theories.
In the present work we investigate the stellar and tidal evolution of
three binary systems for which at least one component is a giant star.
There are some advantages to the use of such rare systems: a) although
the precision is not as high as in the case of the double-lined
eclipsing binaries, the masses and radii of giants are determined with
an acceptable accuracy; b) from the stellar evolution point of view,
there is an extra advantage since the components are well separated and
the models for single stars can be applied; c) as pointed out by
Schröder, Pols & Eggleton (1997),
some of the ![]() Aur
giants are in the blue loop phase, which makes them an excellent test
of the amount of core overshooting. The uncertainties involved in the
analysis of our sample stars are admitedly quite large, if compared
with those derived from double-lined eclipsing binaries. Therefore, the
conclusions should be taken with caution. In order to illustrate the
potential of the method in more accurate systems, we also introduce a
double-lined eclipsing binary (SZ Cen) which presents moderately
evolved stars with good determinations of the absolute dimensions.
Aur
giants are in the blue loop phase, which makes them an excellent test
of the amount of core overshooting. The uncertainties involved in the
analysis of our sample stars are admitedly quite large, if compared
with those derived from double-lined eclipsing binaries. Therefore, the
conclusions should be taken with caution. In order to illustrate the
potential of the method in more accurate systems, we also introduce a
double-lined eclipsing binary (SZ Cen) which presents moderately
evolved stars with good determinations of the absolute dimensions.
The paper is organized as follows: first we introduce the main astrophysical parameters of our sample and the evolutionary stellar models which fit such properties. Next, the differential equations of tidal evolution are presented and some discussion on its derivation is also introduced, as well as the numerical method used to integrate them. Finally, once the stellar models are able to reproduce the observations, we use them to compute the critical times of circularization and synchronization and compare them to the observed rotational velocities (if available) and orbital eccentricities.
2 Stellar
models for 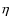 And ,V2291 Oph and SZ Cen
And ,V2291 Oph and SZ Cen
![]() And (this
star is also designed as HR 271, HD 5516 and HIP 4463) was discovered
to be a spectroscopic binary by Campbell & Wright (1900).
Gordon (1946)
obtained several spectrograms and determined its spectroscopic orbit.
More recently Hummel et al. (1993)
determined the orbit of the system by using optical interferometry. The
masses of the primary and secondary inferred from these observations
and from the spectroscopic studies by Gordon are
And (this
star is also designed as HR 271, HD 5516 and HIP 4463) was discovered
to be a spectroscopic binary by Campbell & Wright (1900).
Gordon (1946)
obtained several spectrograms and determined its spectroscopic orbit.
More recently Hummel et al. (1993)
determined the orbit of the system by using optical interferometry. The
masses of the primary and secondary inferred from these observations
and from the spectroscopic studies by Gordon are ![]() and
and ![]() .
.
The astrophysical parameters of ![]() And have been used to test the capability of evolutionary stellar
models (Schröder et al. 1997;
Iwamoto & Saio 1999). In
both works the primary seems to be in the core helium burning phase
while the secondary is in the ascending giant branch. However, no
studies on tidal effects were carried out in these papers. The masses
used in such papers are somewhat different from those derived by Hummel
et al. (1993).
Here we adopted the masses from a recent spectroscopic orbital solution
(Griffin, private communication). We will use the following values:
And have been used to test the capability of evolutionary stellar
models (Schröder et al. 1997;
Iwamoto & Saio 1999). In
both works the primary seems to be in the core helium burning phase
while the secondary is in the ascending giant branch. However, no
studies on tidal effects were carried out in these papers. The masses
used in such papers are somewhat different from those derived by Hummel
et al. (1993).
Here we adopted the masses from a recent spectroscopic orbital solution
(Griffin, private communication). We will use the following values: ![]() and
and ![]() ,
where M1 and M2
are the masses of the primary and secondary, respectively (see
Table 1).
On the other hand, Massarotti et al. (2008)
presented rotational and radial velocities for 761 Hipparcos giants,
including
,
where M1 and M2
are the masses of the primary and secondary, respectively (see
Table 1).
On the other hand, Massarotti et al. (2008)
presented rotational and radial velocities for 761 Hipparcos giants,
including ![]() And.
Considering the observational values of the eccentricity and the
rotational velocities, it is possible to carry out an investigation of
the tidal braking of this system, in addition to the traditional
comparison between the observed astrophysical parameters (masses,
radii, effective temperatures) and the theoretical predictions provided
by the evolutionary models.
And.
Considering the observational values of the eccentricity and the
rotational velocities, it is possible to carry out an investigation of
the tidal braking of this system, in addition to the traditional
comparison between the observed astrophysical parameters (masses,
radii, effective temperatures) and the theoretical predictions provided
by the evolutionary models.
Table
1:
Astrophysical parameters for ![]() And, V2291 Oph, SZ Cen (solar, K units, km s-1,
days).
And, V2291 Oph, SZ Cen (solar, K units, km s-1,
days).
Prior to comparing the observed and theoretical levels of
circularization and synchronization of ![]() And, V2291 Oph and SZ Cen, we need to check the capability of our
stellar models to fit their observed properties. The basic properties
of the code we use to generate the stellar models can be found in
Claret (2004) and references given therein. For completeness, we
enumerate below its main characteristics:
And, V2291 Oph and SZ Cen, we need to check the capability of our
stellar models to fit their observed properties. The basic properties
of the code we use to generate the stellar models can be found in
Claret (2004) and references given therein. For completeness, we
enumerate below its main characteristics:
-
- 1.
- The convective core overshooting can be introduced by means
of an excess distance beyond the formal convective border (as
determined by the Schwarzchild criterion). This distance is defined as
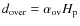 ,
where
,
where 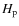 is the pressure scale height taken at the edge of the convective core
as given by Schwarzschild's criterion and
is the pressure scale height taken at the edge of the convective core
as given by Schwarzschild's criterion and  is a free parameter (see Claret 2007, for
a semi-empirical determination of
is a free parameter (see Claret 2007, for
a semi-empirical determination of  using double-lined eclipsing binaries). The overshooting is applied
only at the core boundary.
using double-lined eclipsing binaries). The overshooting is applied
only at the core boundary.
- 2.
- Opacities. The code uses the tables of opacities provided
by Iglesias & Rogers (1996),
completed by the calculations by Alexander & Ferguson (1994)
for lower temperatures.
- 3.
- Convection. We adopted the mixing-length theory to describe
the envelopes of colder models. Mixing-length is also adopted in the
convective cores and can be either adiabatic or superadiabatic.
- 4.
- The nuclear network is essentially the same as that
described in Claret (2004). The
only novelty is the incorporation of measurements of the nuclear
reaction 14N(p,
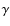 )15O
(Runkle 2003;
Formicola et al. 2004).
)15O
(Runkle 2003;
Formicola et al. 2004).
- 5.
- Numerical details. In the integration of the outer layers,
in order to save computational time, we do not assume a fixed
luminosity and effective temperature but rather we allow the model to
lie within a given area in the HR diagram. In practice, three envelope
computations are performed corresponding to a triangle in the HR
diagram. To guarantee more accurate computations we decreased the
triangle size used in defining an envelope in the HR diagram to
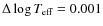 and
and 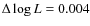 or smaller. This is particularly important to define the depth of the
convective envelope, needed to compute
or smaller. This is particularly important to define the depth of the
convective envelope, needed to compute 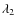 (see next section).
(see next section).
The first panel of Fig. 1 shows the best
fit we found for ![]() And. The inferred hydrogen content X was 0.724. We have adopted
moderate core overshooting, characterized by
And. The inferred hydrogen content X was 0.724. We have adopted
moderate core overshooting, characterized by ![]() that is in good agreement with the determination by Schröder
et al. (1997),
though those authors used a different chemical composition. The adopted
mixing-length parameter
that is in good agreement with the determination by Schröder
et al. (1997),
though those authors used a different chemical composition. The adopted
mixing-length parameter ![]() was
1.68, the same value as we use to calibrate our solar model. We also
confirm that the more massive component is the blue loop phase while
the secondary is found to be on the giant branch. The derived age is
was
1.68, the same value as we use to calibrate our solar model. We also
confirm that the more massive component is the blue loop phase while
the secondary is found to be on the giant branch. The derived age is
![]() .
The isochrone that fits the observational data for
.
The isochrone that fits the observational data for ![]() And is shown more clearly in Fig. 3.
And is shown more clearly in Fig. 3.
![\begin{figure}
\par\includegraphics[height=21.cm,width=9.cm]{fig1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11900-09/Timg29.png)
|
Figure 1:
Theoretical HR diagram and observational parameters for |
| Open with DEXTER | |
The other two combinations of Z also give
acceptable fits, as we can see in the second (Z=0.018)
and third (Z=0.006) panel of Fig. 1.
In the case of the subsolar metallicity, we have to change the
mixing-length ad hoc to 1.45 because the measured effective temperature
of the giant star is too low when we use the solar mixing-length
parameter with a sub-solar composition. The inferred age is
![]() which means that it is not as well determined as the previous case.
This should be compared with the models computed by Iwamoto &
Saio (1999):
these authors found that core overshooting is not necessary to explain
the astrophysical parameters of
which means that it is not as well determined as the previous case.
This should be compared with the models computed by Iwamoto &
Saio (1999):
these authors found that core overshooting is not necessary to explain
the astrophysical parameters of ![]() And if models with subsolar metallicity are adopted; their mixing
length parameter is very similar to ours (1.40). The approximately
solar composition also requires some changes in the input physics. The
mixing-length parameter was increased to 1.85 and the final solution is
better than that by adopting the models with subsolar metallicity since
the inferred age is
And if models with subsolar metallicity are adopted; their mixing
length parameter is very similar to ours (1.40). The approximately
solar composition also requires some changes in the input physics. The
mixing-length parameter was increased to 1.85 and the final solution is
better than that by adopting the models with subsolar metallicity since
the inferred age is ![]() .
Comparing our models with Z=0.018 with those by
Iwamoto & Saio (1999)
(both adopting core overshooting), the mixing-length parameter is
similar, as the core overshooting parameter (
.
Comparing our models with Z=0.018 with those by
Iwamoto & Saio (1999)
(both adopting core overshooting), the mixing-length parameter is
similar, as the core overshooting parameter (
![]() and 0.15, respectively).
and 0.15, respectively).
Core overshooting is frequently invoked to explain some properties of
double-lined eclipsing binaries and colour-magnitude diagrams of
clusters. Such an expression is often related to an extra mixing beyond
the classical Schwarzchild criterion. Extra mixing produces stellar
models with prolonged Main-Sequence times because more fuel is
available in the core. In addition, extra mixing also produces effects
on later stages of the stellar evolution. A good summary of the global
effects of the extra mixing can be found in Schröder et al. (1997).
However, other mechanisms may also be acting to increase the core size,
for example internal gravity waves or rotation. Talon et al. (1997)
investigate the properties of a 9 ![]() rotating model, and conclude that the resulting extra mixing is similar
to that obtained by adopting moderate core overshooting. We have
investigated the dependence of
rotating model, and conclude that the resulting extra mixing is similar
to that obtained by adopting moderate core overshooting. We have
investigated the dependence of
![]() on stellar mass, i.e. we attributed the extra mixing only to core
overshooting, (Claret 2007).
One of the conclusions of the study is that core overshooting (or
equivalently other mechanisms such as induced mixing by rotation) seems
to be necessary to match the absolute dimensions of key double-lined
eclipsing binaries as well as the colour-magnitude diagrams of
clusters. Keeping this in mind and given the mass range of the systems
we are investigating here, we decided to adopt only models with
moderate core overshooting. On the other hand, due to the uncertainty
in the chemical composition determination of
on stellar mass, i.e. we attributed the extra mixing only to core
overshooting, (Claret 2007).
One of the conclusions of the study is that core overshooting (or
equivalently other mechanisms such as induced mixing by rotation) seems
to be necessary to match the absolute dimensions of key double-lined
eclipsing binaries as well as the colour-magnitude diagrams of
clusters. Keeping this in mind and given the mass range of the systems
we are investigating here, we decided to adopt only models with
moderate core overshooting. On the other hand, due to the uncertainty
in the chemical composition determination of ![]() And, we will center our attention on models with an intermediate Z,
although the conclusions concerning tidal evolution are unaltered.
And, we will center our attention on models with an intermediate Z,
although the conclusions concerning tidal evolution are unaltered.
V2291 Oph is a rare ![]() Aur-type system. The absolute dimensions are given by Griffin et al. (1995) and
by Schröder et al. (1996).
More or less at the same epoch, Marshal (1996)
determined the chemical composition of V2291 Oph. The resulting [Fe/H]
is
Aur-type system. The absolute dimensions are given by Griffin et al. (1995) and
by Schröder et al. (1996).
More or less at the same epoch, Marshal (1996)
determined the chemical composition of V2291 Oph. The resulting [Fe/H]
is ![]() and we adopt Z=0.03 to characterize the system.
Schröder, Pols & Eggleton (1997)
analysed V2291 Oph and found an acceptable fit by adopting Z=0.02
and a moderate amount of core overshooting
and we adopt Z=0.03 to characterize the system.
Schröder, Pols & Eggleton (1997)
analysed V2291 Oph and found an acceptable fit by adopting Z=0.02
and a moderate amount of core overshooting ![]() .
Iwamoto & Saio (1999),
on the other hand, using the same astrophysical parameters but adopting
a different chemical composition (Z=0.03 according
to Marshal 1996),
also found a good match. In both cases, a larger value of the
mixing-length parameter was adopted (2.0 and 2.3, respectively). We
have adopted
( X, Z) = (0.64, 0.03),
.
Iwamoto & Saio (1999),
on the other hand, using the same astrophysical parameters but adopting
a different chemical composition (Z=0.03 according
to Marshal 1996),
also found a good match. In both cases, a larger value of the
mixing-length parameter was adopted (2.0 and 2.3, respectively). We
have adopted
( X, Z) = (0.64, 0.03), ![]() and
and ![]() .
The comparison is shown in the first panel of Fig. 2. The position
of the secondary (less massive component) is more difficult to fit and
defines the age error bars. The inferred age is
.
The comparison is shown in the first panel of Fig. 2. The position
of the secondary (less massive component) is more difficult to fit and
defines the age error bars. The inferred age is ![]() .
.
![\begin{figure}
\par\includegraphics[height=11.cm,width=9.cm]{fig2.eps} .
\end{figure}](/articles/aa/full_html/2009/43/aa11900-09/Timg37.png)
|
Figure 2: Theoretical HR diagram and observational parameters for V2291 Oph ( first panel), and SZ Cen ( second panel). Same symbols as in Fig. 1. |
| Open with DEXTER | |
SZ Cen is a double-lined eclipsing binary whose primary has
evolved
beyond the TAMS while the secondary is still in the Main-Sequence
(Andersen 1975, 1991)
As far as we know, there are no chemical observations for SZ Cen. The
models which fit its absolute dimensions better are those with moderate
core overshooting and
( X, Z) = (0.70, 0.02), (see
second panel of Fig. 2).
The derived age is ![]() .
.
3 Equations of tidal evolution
In binary systems, the viscous dissipation of time-dependent
tides
acts to synchronize the stellar rotation and circularize the orbit. As
a consequence of tidal interactions we expect either a coalescence due
to the spiralling of both stars or an equilibrium situation
characterized by a coplanar circular orbit and with both rotational
angular velocities synchronized with the orbital period P.
The explicit equations of tidal evolution are complicated and they are
coupled. The derivative de/dt
depends on the internal structure of the stars, on the eccentricity as
well as on the ratio ![]() where
where ![]() is the angular velocity of the star i and
is the angular velocity of the star i and ![]() is the mean orbital angular velocity. On the other hand, the derivative
d
is the mean orbital angular velocity. On the other hand, the derivative
d![]() /dt
also depends on the same parameters. Such differential equations can be
integrated if we know the initial conditions. Unfortunately this is not
the case. In order to obtain some information on the tidal evolution of
binary stars, some simplifications are assumed in the mentioned
equations: small eccentricities and small departure of synchronism
which lead to the time scales of circularization/synchronization
(Eqs. (1)-(9)). In this way, only relative values of the
eccentricity and rotational angular velocity can be obtained. The
integrations are carried out until the relative variations of
eccentricity and angular velocities become 0.5 per cent of the original
values (for more details, see Zahn 1977, 1989). The
evolutionary ages at which this occurs are the critical time
/dt
also depends on the same parameters. Such differential equations can be
integrated if we know the initial conditions. Unfortunately this is not
the case. In order to obtain some information on the tidal evolution of
binary stars, some simplifications are assumed in the mentioned
equations: small eccentricities and small departure of synchronism
which lead to the time scales of circularization/synchronization
(Eqs. (1)-(9)). In this way, only relative values of the
eccentricity and rotational angular velocity can be obtained. The
integrations are carried out until the relative variations of
eccentricity and angular velocities become 0.5 per cent of the original
values (for more details, see Zahn 1977, 1989). The
evolutionary ages at which this occurs are the critical time ![]() and
and ![]() ,
respectively. The mentioned simplifications limit our conclusions
concerning tidal evolution, specially for those systems showing high
values of eccentricities and/or high levels of asynchronism. As
mentioned above, a better approach to the tidal evolution problem
consist of integrating the complete set of coupled differential
equations simultaneously with the stellar evolution equations, as done
for example by Eggleton & Kiseleva-Eggleton (2002)
for cool Algols systems, or more recently by Stancliffe &
Eldridge (2009)
for the evolution of the progenitor of Supernova 1993J. However, the
combination of initial trial parameters (period, rotational velocities
and eccentricity) is large and a more detailed treatment is needed. At
present we are involved in a new code version which takes into account
such combinations, as well as a Monte Carlo error analysis to estimate
the uncertainties in the circularization/synchronization levels (Torres
et al. 2009).
However,
such calculations are beyond the scope of the present paper. We hope to
present the results in the near future by using double-lined eclipsing
binaries with more accurate absolute dimensions that are suitable to
test the current tidal evolution theories.
,
respectively. The mentioned simplifications limit our conclusions
concerning tidal evolution, specially for those systems showing high
values of eccentricities and/or high levels of asynchronism. As
mentioned above, a better approach to the tidal evolution problem
consist of integrating the complete set of coupled differential
equations simultaneously with the stellar evolution equations, as done
for example by Eggleton & Kiseleva-Eggleton (2002)
for cool Algols systems, or more recently by Stancliffe &
Eldridge (2009)
for the evolution of the progenitor of Supernova 1993J. However, the
combination of initial trial parameters (period, rotational velocities
and eccentricity) is large and a more detailed treatment is needed. At
present we are involved in a new code version which takes into account
such combinations, as well as a Monte Carlo error analysis to estimate
the uncertainties in the circularization/synchronization levels (Torres
et al. 2009).
However,
such calculations are beyond the scope of the present paper. We hope to
present the results in the near future by using double-lined eclipsing
binaries with more accurate absolute dimensions that are suitable to
test the current tidal evolution theories.
The simplified differential equations that describe the variations of
the eccentricity and the angular rotational velocities in a binary
system are

|
(1) |
where ![]() and
and ![]() were already defined, k=1, 2 refer to the primary
and secondary component, respectively and
were already defined, k=1, 2 refer to the primary
and secondary component, respectively and ![]() is the time scale of synchronization and
is the time scale of synchronization and
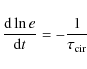
|
(2) |
where e is the eccentricity and ![]() is time scale of circularization. To integrate the above differential
equation we have to consider the contribution of both components
is time scale of circularization. To integrate the above differential
equation we have to consider the contribution of both components

|
(3) |
where subscripts 1 and 2 refer to the primary and the secondary component.
There are three mechanisms which have been invoked to explain the orbital evolution of binary systems. The first braking mechanism is due to Tassoul (1987, 1988). Following this description, the stars in a binary system tend to synchronize and circularize the orbit due to the tidal distortions which cause large scale hydrodynamical currents. Following Tassoul: ``The hydrodynamical mechanism involves a large scale meriodional flow, superposed on the motion around the rotation axis of the tidally distorted component. These transients (due to the lack of axial symmetry), mechanically driven currents - which are much faster than the steady, termally driven Eddington-Vogt currents - cease to exist as soon as synchronization has been achieved in the star''. On the other hand, in a binary system, a star is subject to the gravitational field of its companion and from this interaction a tidal bulge appears. If we assume that both stars are synchronized, this bulge is aligned but if there is departure from synchronism a delay gives rise to a torque. This torque tends to bring the star back into the synchronism. Zahn (1975, 1989) indentified two mechanisms: turbulent dissipation and radiative damping. Both mechanisms are responsible for the tidal friction on late-type and early-type stars, respectively. For a more extensive discussion on the three mechanisms see Claret & Cunha (1997).
For the hydrodynamical mechanism we compute the time scales for
circularization and synchronization following Tassoul (1988):
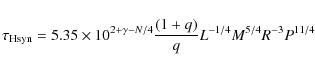
|
(4) |
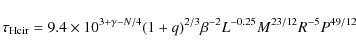
|
(5) |
where q is the mass ratio, ![]() the radius of gyration, P the orbital period in
days, and M, L and R
are the stellar mass, luminosity and radius in solar units. The
parameter N is related to the different ways to
transport energy into the outer layers of the stars in such way that
the radius of gyration, P the orbital period in
days, and M, L and R
are the stellar mass, luminosity and radius in solar units. The
parameter N is related to the different ways to
transport energy into the outer layers of the stars in such way that ![]() ,
where
,
where ![]() and
and ![]() are the eddy and radiative viscosities, respectively. For stars with
envelopes in
convective equilibrium, it is often assumed that N
= 10, while N = 0 is assumed for stars whose
envelopes are in radiative equilibrium. The adjustable parameter
are the eddy and radiative viscosities, respectively. For stars with
envelopes in
convective equilibrium, it is often assumed that N
= 10, while N = 0 is assumed for stars whose
envelopes are in radiative equilibrium. The adjustable parameter ![]() was introduced by Tassoul in order to take into account some
limitations inherent to the time scale derivation, for example, that
the spin-down times is only a lower limit. It was calibrated by Claret
et al. (1995) who
obtained
was introduced by Tassoul in order to take into account some
limitations inherent to the time scale derivation, for example, that
the spin-down times is only a lower limit. It was calibrated by Claret
et al. (1995) who
obtained ![]() by using double-lined eclipsing binaries.
by using double-lined eclipsing binaries.
For the case of turbulent dissipation (convective envelopes):
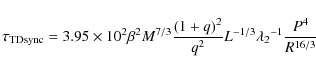
|
(6) |
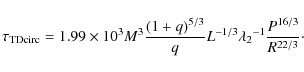
|
(7) |
For stars with convective cores and radiative envelopes (radiative damping) the time scales are:
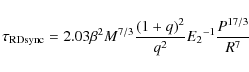
|
(8) |

|
(9) |
In these equations M, R and L are in solar units while P is given in days and the time scales are given in years. The torque constant E2 is related to the dynamic tidal contribution to the total perturbed potential and it is similar to k2 (the apsidal motion constant) but it is much more dependent on the stellar structure than the mentioned constant. Concerning the calculation of
4 The
tidal evolution of  And, V2291 Oph and SZ Cen; final remarks
And, V2291 Oph and SZ Cen; final remarks
4.1  And
And
The orbital elements of ![]() And present some ambiguities, for example, the derived eccentricity.
Hummel et al. (1993)
give the value
And present some ambiguities, for example, the derived eccentricity.
Hummel et al. (1993)
give the value ![]() while Pourbaix et al. (2004)
found e =
0.0081 and Massarotti et al. (2008)
derived the value
while Pourbaix et al. (2004)
found e =
0.0081 and Massarotti et al. (2008)
derived the value ![]() .
The most recent determination of e was provided by
Griffin (private communication,
.
The most recent determination of e was provided by
Griffin (private communication, ![]() ). Given
that value and the error bars, we can conclude that the orbit is
practically circular and this imposes a constraint on the calculations
of the critical times of circularization through Eqs. (2),
(3), (5), (7) and (9).
). Given
that value and the error bars, we can conclude that the orbit is
practically circular and this imposes a constraint on the calculations
of the critical times of circularization through Eqs. (2),
(3), (5), (7) and (9).
Massarotti et al. (2008)
obtained the projected rotational velocities for both components of ![]() And:
And: ![]() km s-1
and
km s-1
and ![]() km s-1.
Hummel et al. (1993)
derived the inclination of the orbit,
km s-1.
Hummel et al. (1993)
derived the inclination of the orbit, ![]() ,
which gives for both components
,
which gives for both components ![]() 9 km s-1.
The theoretical values are, respectively,
9 km s-1.
The theoretical values are, respectively, ![]() km s-1
and
km s-1
and ![]() km s-1.
Within the uncertainties, we can consider that both components are not
synchronized with the orbital period.
km s-1.
Within the uncertainties, we can consider that both components are not
synchronized with the orbital period.
Considering such data and integrating the above differential equations,
we are finally able to analyse the tidal evolution of ![]() And. Note that during the integration we assume that the orbital period
is constant since the rotational angular momentum of both stars is much
smaller than the orbital one. While on the main sequence,
And. Note that during the integration we assume that the orbital period
is constant since the rotational angular momentum of both stars is much
smaller than the orbital one. While on the main sequence, ![]() And and V2291 Oph have convective cores and radiative envelopes.
However, as they evolve to giants, core convection shuts down and a
convective envelope develops. This has the effect of changing which
tidal mechanism is important: for the hydrodynamical mechanism, we will
have a transition in N
which is related to the different mechanisms of transport of energy in
the outer layers. Equally, we have a transition between the radiative
damping and turbulent dissipation for the same reasons explained above.
For practical purpose, we prefer to use the effective temperature as a
criterion, instead of masses, to select the best value of N.
And and V2291 Oph have convective cores and radiative envelopes.
However, as they evolve to giants, core convection shuts down and a
convective envelope develops. This has the effect of changing which
tidal mechanism is important: for the hydrodynamical mechanism, we will
have a transition in N
which is related to the different mechanisms of transport of energy in
the outer layers. Equally, we have a transition between the radiative
damping and turbulent dissipation for the same reasons explained above.
For practical purpose, we prefer to use the effective temperature as a
criterion, instead of masses, to select the best value of N.
We select the model with (X,
Z) = (0.724, 0.012) and ![]() to investigate the tidal evolution of
to investigate the tidal evolution of ![]() And. The hydrodynamical mechanism predicts that the orbit of
And. The hydrodynamical mechanism predicts that the orbit of ![]() And should be circular (Fig. 3, first panel)
since its critical time for circularization is log
And should be circular (Fig. 3, first panel)
since its critical time for circularization is log ![]() ,
which is smaller than the inferred age of the system considering its
error bars; therefore it is compatible with the observed eccentricity.
Theoretical calculations predict that the primary component should be
synchronized (
,
which is smaller than the inferred age of the system considering its
error bars; therefore it is compatible with the observed eccentricity.
Theoretical calculations predict that the primary component should be
synchronized (
![]() )
which is in contradiction to observations. On the other hand, the
prediction for the secondary is
)
which is in contradiction to observations. On the other hand, the
prediction for the secondary is ![]() ,
which is shorter than the inferred age, and this is also in
disagreement with observations.
,
which is shorter than the inferred age, and this is also in
disagreement with observations.
The radiative damping and turbulent dissipation are analysed using the
same stellar models and the main results are shown in Fig. 3 (second
panel). Following these mechanisms, the orbit should be circular; the
critical time for circularization is ![]() which is shorter than the inferred age. This is in agreement with the
observed level of circularization. The situation of synchronization is
similar to that predicted by the hydrodynamical mechanism: the primary
achieves synchronization near the tip of the red giant branch (
which is shorter than the inferred age. This is in agreement with the
observed level of circularization. The situation of synchronization is
similar to that predicted by the hydrodynamical mechanism: the primary
achieves synchronization near the tip of the red giant branch (
![]() )
while the secondary achieves the equilibrium state at the same phase at
)
while the secondary achieves the equilibrium state at the same phase at
![]() .
As previously commented, both components of
.
As previously commented, both components of ![]() And are still not synchronized and the theoretical predictions are in
clear disagreement with these data. Concerning synchronization, some
words of caution should be given. Unlike the case of circularization,
where the eccentricity is more clearly established, the analysis of the
rotational velocities is not so straightforward. As is known, the
observed rotational velocities correspond to the upper layers of the
stars. However, there is a possibility that these are decoupled from
the rotational velocities in the core.
And are still not synchronized and the theoretical predictions are in
clear disagreement with these data. Concerning synchronization, some
words of caution should be given. Unlike the case of circularization,
where the eccentricity is more clearly established, the analysis of the
rotational velocities is not so straightforward. As is known, the
observed rotational velocities correspond to the upper layers of the
stars. However, there is a possibility that these are decoupled from
the rotational velocities in the core.
As we have previously seen, the critical time of synchronization for the primary indicates that this would be synchronized near the tip of the giant branch. However, from Fig. 3, we note that it immediately contracts. Assuming that it rotates as a rigid body (see Fig. 4) we can estimate the spin-up due to contraction: around 4 times faster than it achieves the tip of the giant branch. This might be a possible explanation for the disagreement between the observed rotational velocity and the critical time of synchronization.
![\begin{figure}
\par\includegraphics[height=11.cm,width=9.cm]{fig3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11900-09/Timg75.png)
|
Figure 3:
Radius evolution of |
| Open with DEXTER | |
Although there are uncertainties in the rotational velocities of the
components of ![]() And, they can be used to infer, in a first approximation, the angular
momentum distribution within the stars. If we assume that both stars
rotate as rigid bodies, we can predict the rotation evolution with
respect to the ZAMS velocities. In spite of the uncertainty in
And, they can be used to infer, in a first approximation, the angular
momentum distribution within the stars. If we assume that both stars
rotate as rigid bodies, we can predict the rotation evolution with
respect to the ZAMS velocities. In spite of the uncertainty in ![]() or in the intrinsic values of the rotational velocities, the observed
ratio
or in the intrinsic values of the rotational velocities, the observed
ratio ![]() is unaltered by these sources of error and can be followed as a
function of time. We show such an evolution in Fig. 4. The observed
ratio
is unaltered by these sources of error and can be followed as a
function of time. We show such an evolution in Fig. 4. The observed
ratio ![]() 1.0
and the theoretical
1.0
and the theoretical ![]() we derive at the inferred age of the system in Fig. 4 is 1.09. This
should be compared with the value obtained for TZ For (Claret &
Giménez 1995)
for which an observed ratio of 10 was measured, also in good agreement
with the theoretical value.
we derive at the inferred age of the system in Fig. 4 is 1.09. This
should be compared with the value obtained for TZ For (Claret &
Giménez 1995)
for which an observed ratio of 10 was measured, also in good agreement
with the theoretical value.
![\begin{figure}
\par\includegraphics[angle=270,width=9.cm]{fig4.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11900-09/Timg77.png)
|
Figure 4:
The rotational evolution of |
| Open with DEXTER | |
4.2 V2291 Oph
One of the most serious limitations of V2291 Oph concerning its tidal
evolution is the evolutionary time scales of both components. The mass
of the primary is about 30![]() higher
that the secondary and the time scales are so different that a direct
integration of the differential equations is not possible, mainly in
the case of the turbulent dissipation/radiative damping mechanisms.
This is because of the condition assuring that the system is
synchronized (or circularized) - relative variations of eccentricity
and
angular velocities became 0.5 per cent of the original values - cannot
be
fulfilled for both time scales of V2291 Oph simultaneously (even if we
allow a less restrictive condition). As is well known, the
hydrodynamical
mechanism is more efficient than turbulent dissipation and radiative
damping. Therefore, we present here only the calculations made by
adopting the hydrodynamical mechanism. On the other hand, no
information is available on the rotational velocities. Of course, no
substantial amount of information can be extracted from the study of
this system. However, even without the observed rotational velocities,
we can predict the synchronization time for both components to be
compared with future observations.
higher
that the secondary and the time scales are so different that a direct
integration of the differential equations is not possible, mainly in
the case of the turbulent dissipation/radiative damping mechanisms.
This is because of the condition assuring that the system is
synchronized (or circularized) - relative variations of eccentricity
and
angular velocities became 0.5 per cent of the original values - cannot
be
fulfilled for both time scales of V2291 Oph simultaneously (even if we
allow a less restrictive condition). As is well known, the
hydrodynamical
mechanism is more efficient than turbulent dissipation and radiative
damping. Therefore, we present here only the calculations made by
adopting the hydrodynamical mechanism. On the other hand, no
information is available on the rotational velocities. Of course, no
substantial amount of information can be extracted from the study of
this system. However, even without the observed rotational velocities,
we can predict the synchronization time for both components to be
compared with future observations.
The results by adopting the hydrodynamical mechanism are shown in
Fig. 5.
The critical times of synchronization of both components is predicted
to be near the tip of the giant branch. On the other hand, the orbit of
V2291 Oph is highly eccentric (
![]() )
and the critical time for circularization (
)
and the critical time for circularization (
![]() )
is slightly longer than the inferred age (
)
is slightly longer than the inferred age (
![]() )
but well within the error bars for the age. Although this critical time
is compatible with the observed eccentricity, due to the high value of e
and due to the small difference between the critical time for
circularization and age one would expect that this difference is not
enough to circularize the orbit. The high eccentricity of V2291 Oph
leads to an interesting question: did this system originally begin with
a very high initial eccentricity (say, 0.8) that has been reduced to
0.3? Or maybe that the eccentricity was initially near 0.30 and has not
undergone strong tidal forces? As the system shows a long orbital
period, the corresponding tidal forces are relatively weak and the
latter option seems to be the most probable. However, the above
analysis should be taken with caution. As mentioned in the beginning of
Sect. 3, the high value of the present eccentricity is clearly
not
consistent with the adopted assumption used to derive the time scale of
circularization. More complete and accurate data may shed some light on
this ambiguous situation although they will be not enough to remove the
mentioned inconsistency. We encourage observers to improve and complete
the astrophysical data for V2291 Oph and other similar systems. The
benefits are worth the effort since we have good information of only
one system showing very evolved components (TZ For).
)
but well within the error bars for the age. Although this critical time
is compatible with the observed eccentricity, due to the high value of e
and due to the small difference between the critical time for
circularization and age one would expect that this difference is not
enough to circularize the orbit. The high eccentricity of V2291 Oph
leads to an interesting question: did this system originally begin with
a very high initial eccentricity (say, 0.8) that has been reduced to
0.3? Or maybe that the eccentricity was initially near 0.30 and has not
undergone strong tidal forces? As the system shows a long orbital
period, the corresponding tidal forces are relatively weak and the
latter option seems to be the most probable. However, the above
analysis should be taken with caution. As mentioned in the beginning of
Sect. 3, the high value of the present eccentricity is clearly
not
consistent with the adopted assumption used to derive the time scale of
circularization. More complete and accurate data may shed some light on
this ambiguous situation although they will be not enough to remove the
mentioned inconsistency. We encourage observers to improve and complete
the astrophysical data for V2291 Oph and other similar systems. The
benefits are worth the effort since we have good information of only
one system showing very evolved components (TZ For).
![\begin{figure}
\par\includegraphics[angle=270,width=9.cm]{fig5.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11900-09/Timg82.png)
|
Figure 5: The same as in Fig. 3 but for V2291 Oph. Hydrodynamical mechanism. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=11.cm,width=9.cm]{fig6.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11900-09/Timg83.png)
|
Figure 6: The same as in Fig. 3 but for SZ Cen. Hydrodynamical mechanism and turbulent dissipation/radiative damping. The critical times for synchronization for the hydrodynamical mechanism are not shown due to the difference in time scale. Because the critical times of circularization and synchronization are very similar, only one arrow is show for the radiative damping mechanism. |
| Open with DEXTER | |
4.3 SZ Cen
SZ Cen presents a circular orbit and the observed values of the
rotation velocities are ![]() and
and ![]() km s-1
for the primary and secondary, respectively. The theoretical rotational
velocities at the periastron are 56 and 45 km s-1
and we can consider both components as synchronized. The calculations
made by adopting the hydrodynamical mechanism reveal that the critical
time for circularization is
km s-1
for the primary and secondary, respectively. The theoretical rotational
velocities at the periastron are 56 and 45 km s-1
and we can consider both components as synchronized. The calculations
made by adopting the hydrodynamical mechanism reveal that the critical
time for circularization is
![]() ,
that is smaller than the inferred age (
,
that is smaller than the inferred age (
![]() ).
Such a result is compatible with the circular orbit of SZ Cen.
Concerning the levels of synchronization, the hydrodynamical mechanism
seems to be able to explain the rotational velocities since the
critical times are about 2 order of magnitude shorter than the inferred
age (
).
Such a result is compatible with the circular orbit of SZ Cen.
Concerning the levels of synchronization, the hydrodynamical mechanism
seems to be able to explain the rotational velocities since the
critical times are about 2 order of magnitude shorter than the inferred
age (
![]() ).
).
On the other hand, the radiative damping mechanism predicts a
critical time for circularization longer that the age of the system (
![]() )
and therefore it is not compatible with the circular orbit of SZ Cen.
Following this mechanism, the primary should be synchronized at
)
and therefore it is not compatible with the circular orbit of SZ Cen.
Following this mechanism, the primary should be synchronized at
![]() ,
more or less at the same time as the system circularizes. The secondary
will synchronize the orbit a little later, at
,
more or less at the same time as the system circularizes. The secondary
will synchronize the orbit a little later, at ![]() .
This seems to be in disagreement with the observed rotational
velocities since they indicate that both components are synchronized.
However, given the small differences between the critical times for
synchronization, and the inferred age, the associated stellar models,
the tidal theories and the observational data may be not accurate
enough to elucidate the question. On the other hand, by applying the
same simple method to follow the rotational evolution as described in
the case of
.
This seems to be in disagreement with the observed rotational
velocities since they indicate that both components are synchronized.
However, given the small differences between the critical times for
synchronization, and the inferred age, the associated stellar models,
the tidal theories and the observational data may be not accurate
enough to elucidate the question. On the other hand, by applying the
same simple method to follow the rotational evolution as described in
the case of ![]() And, we have found that the predicted
And, we have found that the predicted ![]() is around 1.2 while the observed value is 1.3.
is around 1.2 while the observed value is 1.3.
Although the actual theories of tidal braking are able to
explain
some tidal characteristics of our three systems, some predictions are
in disagreement with the observed eccentricities and rotational
velocities. In addition, we should remember that there are also
problems of modelling double-lined binary systems with very evolved
components, such as the unique case of TZ For. Only for a high value of
![]() was it possible to place both components in the same isochrone (Claret 2007).
This may be an evidence that there are problems with the late stellar
evolutionary stages. It is clear that we need to obtain more accurate
data for binaries with very evolved components to elucidate such
discrepancies and ambiguities.
was it possible to place both components in the same isochrone (Claret 2007).
This may be an evidence that there are problems with the late stellar
evolutionary stages. It is clear that we need to obtain more accurate
data for binaries with very evolved components to elucidate such
discrepancies and ambiguities.
I thank R. Griffin for providing up-to-date data ofAnd. The Spanish MEC (AYA2006-06375) is gratefully acknowledged for its support during the development of this work.
References
- Andersen, J. 1975, A&A, 45, 203 [NASA ADS]
- Andersen, J. 1991, A&AR, 3, 91 [NASA ADS]
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [CrossRef] [NASA ADS]
- Campbell, W. W.,& Wright, W. H. 1900, ApJ, 12, 256 [NASA ADS]
- Claret, A. 2004, A&A, 424, 919 [EDP Sciences] [CrossRef] [NASA ADS]
- Claret, A. 2005, in Tidal Evolution and Oscillations in Binary Stars, ed. A. Claret, A. Giménez, & J.-P. Zahn, ASP Conf. Ser., 333, 122
- Claret, A. 2007, A&A, 475, 1019 [EDP Sciences] [CrossRef] [NASA ADS]
- Claret, A., & Cunha, N. C. S. 1997, A&A, 318, 187 [NASA ADS]
- Claret, A., & Giménez, A. 1995, A&A, 296, 180 [NASA ADS]
- Claret, A., Giménez, A., & Cunha, N. C. S. 1995, A&A, 299, 724 [NASA ADS]
- Eggleton, P. P., & Kiseleva-Eggleton, L. 2002, ApJ, 575, 461 [CrossRef] [NASA ADS]
- Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Physics Letters B, 591, 61 [CrossRef] [NASA ADS]
- Gordon, K. C. 1946, ApJ, 103, 13 [CrossRef] [NASA ADS]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [CrossRef] [NASA ADS]
- Griffin, R. E. M., Marshall, K. P., Griffin, R. F., & Schroder, K.-.P. 1995, A&A, 301, 217 [NASA ADS]
- Hummel, C. A., Armstrong, J. T., Quirrenbach, et al. 1993, AJ, 106, 2486 [CrossRef] [NASA ADS]
- Habets, G. M. H. J., & Zwaan, C. 1989, A&A, 211, 56 [NASA ADS]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [CrossRef] [NASA ADS]
- Iwamoto, N., & Saio, H. 1999, ApJ, 521, 297 [CrossRef] [NASA ADS]
- Marshall, K. P. 1996, MNRAS, 280, 977 [NASA ADS]
- Massarotti, A., Latham, D. W., Stefanik, R. P., & Fogel, J. 2008, AJ, 135, 209 [CrossRef] [NASA ADS]
- Mayor, M., & Mermilliod, J. C. 1984, in Observational tests of the stellar evolution theory, ed. A. Maeder, & A. Renzini, (Dordretch: D. Reidel Publ. Co.), 411
- McWilliam, A. 1990, ApJS, 74, 1075 [CrossRef] [NASA ADS]
- Meibom, S., & Mathieu, R. 2005, in Tidal Evolution and Oscillations in Binary Stars, ed. A. Claret, A. Giménez, & J.-P. Zahn, ASP Conf. Ser., 333, 95
- Pourbaix, D., Tokovinin, A. A., Batter, A. H., et al. 2004, A&A, 424, 727 [EDP Sciences] [CrossRef] [NASA ADS]
- Runkle, R. C. 2003, Ph.D. Thesis, University of North Carolina, unpublished
- Schröder, K.-P., Marshall, K. P., & Griffin, R. E. M. 1996, A&A, 311, 631 [NASA ADS]
- Schröder, K.-P., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 285, 696 [NASA ADS]
- Stancliffe, R. J., & Eldridge, J. J. 2009, MNRAS, 396, 1699 [CrossRef] [NASA ADS]
- Talon, S., Zahn, J.P., Maeder, A., & Meynet, G. 1997, A&A, 322, 209 [NASA ADS]
- Taylor, B. J. 1991, ApJS, 76, 715 [CrossRef] [NASA ADS]
- Tassoul, J. L. 1987, ApJ, 322, 856 [CrossRef] [NASA ADS]
- Tassoul, J. L. 1988, ApJ, 324, L71 [CrossRef] [NASA ADS]
- Torres, G., Lacy, C. H. S., & Claret, A. 2009, AJ, in press
- Zahn, J. P. 1975, A&A, 41, 329 [NASA ADS]
- Zahn, J. P. 1977, A&A, 57, 383 [NASA ADS]
- Zahn, J. P. 1989, A&A, 220, 112 [NASA ADS]
All Tables
Table
1: Astrophysical parameters for ![]() And, V2291 Oph, SZ Cen (solar, K units, km s-1,
days).
And, V2291 Oph, SZ Cen (solar, K units, km s-1,
days).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


