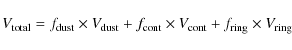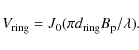| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 301 - 316 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200911723 | |
| Published online | 03 September 2009 | |
A&A 507, 301-316 (2009)
Resolving the asymmetric inner wind
region of the yellow hypergiant IRC +10420 with
VLTI/AMBER in low and high spectral resolution mode![[*]](/icons/foot_motif.png)
T. Driebe1 - J. H. Groh1 - K.-H. Hofmann1 - K. Ohnaka1 - S. Kraus1 - F. Millour1 - K. Murakawa1 - D. Schertl1 - G. Weigelt1 - R. Petrov2 - M. Wittkowski3 - C. A. Hummel3 - J. B. Le Bouquin4 - A. Merand4 - M. Schöller3 - F. Massi5 - P. Stee6 - E. Tatulli7
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121
Bonn, Germany
2 - Laboratoire Universitaire d'Astrophysique de Nice, UMR 6525,
Université de Nice/CNRS, 06108 Nice Cedex 2, France
3 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching bei München, Germany
4 - European Southern Observatory, Alonso de Cordova 3107, Vitacura,
Casilla 19001, Santiago 19, Chile
5 - INAF - Osservatorio Astrofisico di Arcetri, Istituto Nazionale di
Astrofisica, Largo E. Fermi 5, 50125 Firenze, Italy
6 - Observatoire de la Côte d'Azur/CNRS, UMR 6525 H. Fizeau, Univ. Nice
Sophia Antipolis, Avenue Copernic, 06130 Grasse, France
7 - Laboratoire d'Astrophysique de Grenoble, UMR 5571, Université
Joseph Fourier/CNRS, 38041 Grenoble Cedex 9, France
Received 26 January 2009 / Accepted 1 August 2009
Abstract
Context. IRC +10420 is a massive
evolved star belonging to the group of yellow hypergiants. Currently,
this star is rapidly evolving through the Hertzprung-Russell diagram,
crossing the so-called yellow void. IRC +10420 is
suffering from intensive mass loss which led to the formation of an
extended dust shell. Moreover, the dense stellar wind of
IRC +10420 is subject to strong line emission.
Aims. Our goal was to probe the photosphere and the
innermost circumstellar environment of IRC +10420,
to measure the size of its continuum- as well as the Br![]() line-emitting
region on milliarcsecond scales, and to search for evidence of an
asymmetric distribution of IRC +10420's dense,
circumstellar gas.
line-emitting
region on milliarcsecond scales, and to search for evidence of an
asymmetric distribution of IRC +10420's dense,
circumstellar gas.
Methods. We obtained near-infrared long-baseline
interferometry of IRC +10420 with the AMBER
instrument of ESO's Very Large Telescope Interferometer (VLTI). The
measurements were carried out in May/June 2007 and May 2008 in
low-spectral resolution mode in the JHK bands using
three auxillary telescopes (ATs) at projected baselines ranging from 30
to 96 m, and in October 2008 in high-spectral resolution mode
in the K band around the Br![]() emission line using three unit
telescopes (UTs) with projected baselines between 54 and
129 m. The high-spectral resolution mode observations were
analyzed by means of radiative transfer modeling using CMFGEN and the
2D Busche & Hillier codes.
emission line using three unit
telescopes (UTs) with projected baselines between 54 and
129 m. The high-spectral resolution mode observations were
analyzed by means of radiative transfer modeling using CMFGEN and the
2D Busche & Hillier codes.
Results. For the first time, we have been able to
absolutely calibrate the H- and K-band
data and, thus, to determine the angular size of IRC+10420's continuum-
and Br![]() line-emitting regions. We found that both the low resolution
differential and closure phases are zero within the uncertainty limits
across all three bands. In the high-spectral resolution observations,
the visibilities show a noticeable drop across the Br
line-emitting regions. We found that both the low resolution
differential and closure phases are zero within the uncertainty limits
across all three bands. In the high-spectral resolution observations,
the visibilities show a noticeable drop across the Br![]() line on all three baselines. We found differential phases up to -25
line on all three baselines. We found differential phases up to -25![]() in
the redshifted part of the Br
in
the redshifted part of the Br![]() line and a non-zero closure phase close to the line center. The
calibrated visibilities were corrected for AMBER's limited
field-of-view to appropriately account for the flux contribution of
IRC +10420's extended dust shell. From our
low-spectral resolution AMBER data we derived FWHM
Gaussian sizes of
line and a non-zero closure phase close to the line center. The
calibrated visibilities were corrected for AMBER's limited
field-of-view to appropriately account for the flux contribution of
IRC +10420's extended dust shell. From our
low-spectral resolution AMBER data we derived FWHM
Gaussian sizes of ![]() and
and ![]() mas for
IRC +10420's continuum-emitting region in the H
and K bands, respectively. From the high-spectral
resolution data, we obtained a FWHM Gaussian size
of
mas for
IRC +10420's continuum-emitting region in the H
and K bands, respectively. From the high-spectral
resolution data, we obtained a FWHM Gaussian size
of ![]() mas in the K-band
continuum. The Br
mas in the K-band
continuum. The Br![]() -emitting
region can be fitted with a geometric ring model with a diameter of
4.18+0.19-0.09 mas,
which is approximately 4 times the stellar size. The geometric model
also provides some evidence that the Br
-emitting
region can be fitted with a geometric ring model with a diameter of
4.18+0.19-0.09 mas,
which is approximately 4 times the stellar size. The geometric model
also provides some evidence that the Br![]() line-emitting region is
elongated towards a position angle of 36
line-emitting region is
elongated towards a position angle of 36![]() ,
well aligned with the symmetry axis of the outer reflection nebula.
Assuming an unclumped wind and a luminosity of
,
well aligned with the symmetry axis of the outer reflection nebula.
Assuming an unclumped wind and a luminosity of
![]() ,
the spherical radiative transfer modeling with CMGFEN yields a current
mass-loss rate of 1.5-
,
the spherical radiative transfer modeling with CMGFEN yields a current
mass-loss rate of 1.5-
![]() based
on the Br
based
on the Br![]() equivalent
width. However, the spherical CMFGEN model poorly reproduces the
observed line shape, blueshift, and extension, definitively showing
that the IRC +10420 outflow is asymmetric. Our 2D
radiative transfer modeling shows that the blueshifted Br
equivalent
width. However, the spherical CMFGEN model poorly reproduces the
observed line shape, blueshift, and extension, definitively showing
that the IRC +10420 outflow is asymmetric. Our 2D
radiative transfer modeling shows that the blueshifted Br![]() emission and
the shape of the visibility across the emission line can be explained
with an asymmetric bipolar outflow with a high density contrast from
pole to equator (8-16), where the redshifted light is substantially
diminished.
emission and
the shape of the visibility across the emission line can be explained
with an asymmetric bipolar outflow with a high density contrast from
pole to equator (8-16), where the redshifted light is substantially
diminished.
Key words: instrumentation: high angular resolution - instrumentation: interferometers - stars: circumstellar matter - stars: individual: IRC +10 420 - stars: mass-loss - stars: supergiants
1 Introduction
Due to its distance (d = 4-6 kpc; Jones et al.
1993), the
relatively high wind velocity (40
![]() ), and the remarkable
photometric history, IRC +10 420
(=V 1302 Aql =
IRAS 19244+1115) is most likely not a post-AGB star
evolving through the proto-planetary nebula stage as suggested earlier
(e.g. Fix
& Cobb 1987; Hrivnak
et al. 1989; Trammell
et al. 1994; Bowers
& Knapp 1989),
but a yellow hypergiant (
), and the remarkable
photometric history, IRC +10 420
(=V 1302 Aql =
IRAS 19244+1115) is most likely not a post-AGB star
evolving through the proto-planetary nebula stage as suggested earlier
(e.g. Fix
& Cobb 1987; Hrivnak
et al. 1989; Trammell
et al. 1994; Bowers
& Knapp 1989),
but a yellow hypergiant (
![]() ,
see Jones
et al. 1993; Oudmaijer
et al. 1996).
Such extremly luminous stars are extremely rare, and only a dozen are
known in the Galaxy (Clark
et al. 2005). Yellow hypergiants (YHG) have high
mass-loss rates (
,
see Jones
et al. 1993; Oudmaijer
et al. 1996).
Such extremly luminous stars are extremely rare, and only a dozen are
known in the Galaxy (Clark
et al. 2005). Yellow hypergiants (YHG) have high
mass-loss rates (
![]() )
and are in a short, transitional evolutionary stage, thereby rapidly
crossing the so-called ``yellow void'' in the Hertzsprung-Russell
diagram (Humphreys
et al.
2002). Their link to other advanced evolutionary phases of
massive stars such as Luminous Blue Variables and Wolf-Rayet stars is
still an open issue in stellar evolution theory.
)
and are in a short, transitional evolutionary stage, thereby rapidly
crossing the so-called ``yellow void'' in the Hertzsprung-Russell
diagram (Humphreys
et al.
2002). Their link to other advanced evolutionary phases of
massive stars such as Luminous Blue Variables and Wolf-Rayet stars is
still an open issue in stellar evolution theory.
Because of its large number of remarkable observational features, IRC +10420 has been subject to extensive studies over the last 30 years. The spectral type of IRC +10420 has changed from F8 Ia+ in 1973 (Humphreys et al. 1973) through A5Ia in the mid 90s (Klochkova et al. 1997; Oudmaijer et al. 1996) to A2 in 2000 (Klochkova et al. 2002). Correspondingly, the effective temperature has changed by more than 3000 K in the last two and a half decades. This makes IRC +10420 a unique object for the study of stellar evolution since it is one of the very rare stars believed to be in the rapid transition from the Red-Supergiant stage to the Wolf-Rayet phase.
HST/WFPC2 images of IRC +10420's
surrounding nebula (Humphreys
et al. 1997) revealed a variety of structures
including condensations or knots, ray-like features, and several arcs
or loops within 2'' from the star, plus one or more distant reflection
shells. All these features suggest frequent episodes of high mass loss
during the past centuries. Castro-Carrizo
et al. (2001) found thermal SiO emission in a huge
hollow shell around IRC +10420, with a typical
radius of ![]() 1017 cm
(=6680 AU = 1
1017 cm
(=6680 AU = 1
![]() 34
at a distance of 5 kpc), a shell width smaller than half of
the radius, and an expansion velocity of 35
34
at a distance of 5 kpc), a shell width smaller than half of
the radius, and an expansion velocity of 35
![]() .
Castro-Carrizo
et al. (2007)
mapped IRC +10420 's nebula in the
.
Castro-Carrizo
et al. (2007)
mapped IRC +10420 's nebula in the
![]() J = 2-1 and 1-0 transitions and found that
the nebula shows an approximately spherical, extended halo surrounding
a bright inner region, with both components clearly presenting smaller
aspherical features. The CO nebula expands isotropically with an
expansion rate similar to the SiO shell.
J = 2-1 and 1-0 transitions and found that
the nebula shows an approximately spherical, extended halo surrounding
a bright inner region, with both components clearly presenting smaller
aspherical features. The CO nebula expands isotropically with an
expansion rate similar to the SiO shell.
The chemical composition of IRC +10420's
nebula is dominated by O-rich chemistry as suggested by several
observations (e.g. the OH maser emission by Reid
et al. 1979), and is similar to O-rich AGB stars as
recently found by Quintana-Lacaci
et al. (2007). IRC +10420 is also
among the brightest IRAS objects and one of the warmest stellar OH
maser sources known
(Nedoluha
& Bowers 1992; Diamond
et al. 1983; Mutel
et al. 1979; Bowers
1984; Giguere
et al. 1976). Ammonia emission has been reported by McLaren & Betz
(1980) and Menten & Alcolea
(1995).
From CO observations, high mass-loss rates of the order of several 10-4
![]() (Knapp &
Morris 1985; Oudmaijer
et al. 1996;
Castro-Carrizo
et al. 2007) have been derived.
(Knapp &
Morris 1985; Oudmaijer
et al. 1996;
Castro-Carrizo
et al. 2007) have been derived.
As inferred by many studies, the structure of the inner circumstellar envelope (CSE; spatial scale of milliarcseconds) of IRC +10420 appears to be as complex as that of the outer nebula, and numerous scenarios have been proposed to explain its observed features. These models include a rotating equatorial disk (Jones et al. 1993), bipolar outflows (Oudmaijer et al. 1994), infall of circumstellar material (Oudmaijer 1998), wind blowing in a preferential direction (Humphreys et al. 2002), and even the simultaneous presence of inflowing and outflowing matter (Humphreys et al. 2002).
Despite very intensive observing campaigns, the overall
geometry of IRC +10420's CSE is still a matter of
debate. Humphreys
et al.
(2002) obtained HST/STIS spatially resolved spectroscopy of
IRC +10420 and its reflection nebula. They suggested
that given the stellar
temperature and the high mass-loss rate, the strong stellar wind of
IRC +10420 must be optically thick and, thus,
the observed variations in the apparent spectral type and temperature
are due to changes in the wind
and do not reflect an interior evolution on short timescales. The
detection of a nearly spherical CSE by Humphreys
et al. (2002) is in marked contrast to other
observations that
reveal a rather axis-symmetric wind geometry in
IRC +10420, such as the earlier HST images (Humphreys
et al. 1997),
integral-field spectroscopy (Davies
et al. 2007), or recent spectropolarimetry (Patel et al.
2008). These
latter observations suggest a symmetry axis at a position angle of
![]() .
.
Infrared interferometric and coronographic observations of
IRC +10420 were reported by, e.g., Dyck et al.
(1984), Ridgway
et al. (1986), Cobb & Fix (1987),
Christou
et al. (1990),
Kastner &
Weintraub (1995),
Blöcker
et al. (1999),
Sudol et al.
(1999),
Lipman et al.
(2000),
and Monnier et al.
(2004).
Blöcker
et al. (1999)
presented
diffraction-limited 73 mas K-band
bispectrum speckle-interferometry observations of
IRC +10420's dust shell. They found that the K-band
visibility steeply drops to a plateau-like value of ![]() 0.6 at
6 m baseline and, thus, concluded that 40% of the total K-band
flux comes
from the extended dust shell. The best radiative transfer model found
by Blöcker
et al. (1999)
to simultaneously explain the spectral energy distribution (SED) and K-band
visibility contains a two-component shell composed of silicate dust
with an inner rim at 69 stellar radii where the dust temperature is
1000 K.
Moreover, Blöcker
et al.
(1999) found that a phase of heavy mass loss with mass-loss
rates approximately 40 times higher than the current
0.6 at
6 m baseline and, thus, concluded that 40% of the total K-band
flux comes
from the extended dust shell. The best radiative transfer model found
by Blöcker
et al. (1999)
to simultaneously explain the spectral energy distribution (SED) and K-band
visibility contains a two-component shell composed of silicate dust
with an inner rim at 69 stellar radii where the dust temperature is
1000 K.
Moreover, Blöcker
et al.
(1999) found that a phase of heavy mass loss with mass-loss
rates approximately 40 times higher than the current
![]() must have ceased roughly 60 to 90 yrs ago.
must have ceased roughly 60 to 90 yrs ago.
Monnier
et al. (2004)
obtained both K-band aperture-masking observations
of IRC +10420 using the Keck I telescope
and long-baseline interferometric observations with the beam-combiner
instrument FLUOR at the IOTA interferometer (e.g. Traub
1998). While the aperture masking observations basically
confirmed
the results of the speckle observations of Blöcker
et al. (1999), i.e. a sharp visibility drop for
baselines
shorter than 2 m and a plateau-like visibility of ![]() 0.6 up to a
8 m baseline, from the IOTA measurements Monnier
et al. (2004) found a K-band
visibility of
0.6 up to a
8 m baseline, from the IOTA measurements Monnier
et al. (2004) found a K-band
visibility of ![]() 0.7,
from which they concluded that the compact stellar
component is not resolved at baselines as long as
0.7,
from which they concluded that the compact stellar
component is not resolved at baselines as long as ![]() 35 m.
35 m.
Recently, de Wit
et al. (2008) presented the first near-infrared
long-baseline interferometric observations of
IRC +10420 obtained with the AMBER instrument at
ESO's Very Large Telescope Interferometer (VLTI).
The observations presented by de Wit
et al. (2008) were carried out in medium spectral
resolution mode (
![]() )
around the Br
)
around the Br![]() emission
line. de Wit
et al. (2008)
resolved the Br
emission
line. de Wit
et al. (2008)
resolved the Br![]() line-emitting
region and derived a Gaussian FWHM size of
3.3 milliarcseconds (mas), but due to calibration problems,
the size of the continuum-emitting region could not be constrained.
line-emitting
region and derived a Gaussian FWHM size of
3.3 milliarcseconds (mas), but due to calibration problems,
the size of the continuum-emitting region could not be constrained.
In this paper, we present the first VLTI/AMBER observations of
IRC +10420 in the H and
K bands in low-spectral resolution mode and the
first AMBER measurements of its Br![]() -emitting region
with a spectral resolution of
-emitting region
with a spectral resolution of
![]() (high-spectral resolution mode of AMBER)
and baselines up to 128 m. From these new AMBER observations,
the size of the continuum-emitting region in several spectral channels
across the H and K bands could
be derived and, by comparison of the high-spectral resolution AMBER
data with 2D gas radiative transfer models, details on the size and
geometry of the Br
(high-spectral resolution mode of AMBER)
and baselines up to 128 m. From these new AMBER observations,
the size of the continuum-emitting region in several spectral channels
across the H and K bands could
be derived and, by comparison of the high-spectral resolution AMBER
data with 2D gas radiative transfer models, details on the size and
geometry of the Br![]() line-emitting
region could be obtained.
line-emitting
region could be obtained.
The observations presented here are the first step of an observing campaign to better constrain the geometry of the inner wind region of IRC +10420 at a scale of a few stellar radii.
The paper is structured as follows. In Sects. 2 we will present the AMBER observations of IRC +10420 and discuss the data reduction. In Sect. 3.1 we discuss the implications of AMBER's limited field-of-view for the observations of the very extended object IRC +10420. In Sects. 3.2 and 3.3, the absolute calibration, radiative transfer modeling, and interpretation of the AMBER data will be discussed. The paper closes with a summary and conclusions in Sect. 4.
2 Observations and data reduction
2.1 General remarks on the data reduction process
In the following two subsections we describe our VLTI/AMBER
observations of IRC +10420 in low (LR) and high
spectral resolution (HR) mode. AMBER is the near-infrared closure-phase
beam combiner of ESO's VLTI, simultaneously
operating in the J, H, and K
bands. This instrument is capable of interfering the light of either
three 1.8 m auxiliary telescopes (ATs) or three of the
8.2 m unit telescopes (UTs) located on Paranal. A detailed
description of the AMBER instrument and its optical design is given in Petrov et al.
(2007) and
Robbe-Dubois
et al. (2007).
The AMBER data presented here were reduced using version 2.2 of the
data reduction package amdlib![]() .
The reduction software is based on the so-called
Pixel-to-Visibility-Matrix (P2VM) algorithm, which is described in Tatulli
et al. (2007).
.
The reduction software is based on the so-called
Pixel-to-Visibility-Matrix (P2VM) algorithm, which is described in Tatulli
et al. (2007).
Following previous experiences with the reduction
of low and high-spectral resolution AMBER data (e.g. Weigelt
et al. 2007; Wittkowski
et al. 2008),
the data selection was carried as follows: As primary selection
criteria we used the signal-to-noise ratio (SNR) of the fringe signal.
For the LR data, we kept 20% of the data with the highest fringe SNR,
while for the HR data taken with the
fringe tracker FINITO (e.g. Gai
et al. 2003; Le
Bouquin
et al. 2008)
we kept 80% of the data with the highest fringe SNR. In both cases, the
optimal fringe SNR selection value was found by increasing the fraction
of discarded data frames from 0 to 80%. A stronger selection than given
above only led to an increase of the noise; i.e., finally there was
only a decrease of the data quality rather than a significant
improvement. In addition to the fringe SNR selection, to ensure a
proper deselection of all frames which are far from zero optical path
difference, we also discarded in the low- as well as high-spectral
resolution data all frames with a piston of more than ![]() m. For the
high-spectral resolution
data, this seems to be a too strong selection, since in this case the
coherence length is of the order of
m. For the
high-spectral resolution
data, this seems to be a too strong selection, since in this case the
coherence length is of the order of
![]() cm,
but due to the use of FINITO the piston variation is typically much
small than 100 micron in the HR data. Since it turned out that
the HR results do not show a strong variation with piston selection, we
finally decided to use the same piston selection criteria for both the
HR and LR data.
cm,
but due to the use of FINITO the piston variation is typically much
small than 100 micron in the HR data. Since it turned out that
the HR results do not show a strong variation with piston selection, we
finally decided to use the same piston selection criteria for both the
HR and LR data.
Concerning the error estimates of our AMBER measurements, we were facing the problem that for each observation only one suitable calibrator measurement was available. Thus, in addition to the statistical error of the observables calculated from the average over all frames of a given data set, it was problematic to address also any systematic error sources. Therefore, to account for systematic uncertainties of the absolute calibration process, we looked up previous AMBER measurements taken under similar weather conditions. From these comparisons, we concluded to add an absolute error of 0.03 to all visibility data and 3 degrees to all phases to account for the systematic uncertainties.
Table 1: Summary of the AMBER low-spectral resolution observations of IRC+10420 and the calibrator star HD 190327.
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{11723F1.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg65.png)
|
Figure 1: (u,v) coverage of the VLTI/AMBER observations of IRC +10420 in low (LR) and high (HR) spectral resolution mode presented in this paper. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0,width=18cm]{11723F2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg66.png)
|
Figure 2: VLTI/AMBER observations of IRC +10420 in low-spectral resolution mode. The panels in the left and middle columns show the calibrated K-band visibility as a function of wavelength for the observations listed in Table 1. The top right panel shows the calibrated H-band visibility of IRC +10420 as a function of wavelength from the May 2008 observations. As will be outlined in 3.1 in more detail, all visibilities suffer from a strong field-of-view effect. Finally, the bottom right panel presents the differential phase in the H and K bands (left y-axis scale) and the closure phase (right y-axis scale) in the J, H, and K bands as a function of wavelength for the observations carried out in May 2008. |
| Open with DEXTER | |
2.2 The low-spectral resolution data
The low-spectral resolution (hereafter LR) AMBER observations of
IRC +10420 were obtained with the Auxiliary
Telescopes (ATs) in May/June 2007 and May 2008 using the linear
baseline configurations E0-G0-H0 and A0-D0-H0.
A summary of the LR observations is given in Table 1.
As this table as well as the (u,v)
coverage in Fig. 1
shows, the total baseline and position angle ranges covered by the LR
observations of IRC +10420
are 15 to 94 m and 69 to 75![]() ,
respectively, i.e. the observations
were essentially carried out in the same direction on the sky. All
measurements were made under sub-average to
average seeing conditions (see Tables 1 and
2).
For the
calibration of all LR AMBER data on IRC +10420 we
used the calibrator HD 190327. A record of the calibrator
observations is also provided
in Table 1.
,
respectively, i.e. the observations
were essentially carried out in the same direction on the sky. All
measurements were made under sub-average to
average seeing conditions (see Tables 1 and
2).
For the
calibration of all LR AMBER data on IRC +10420 we
used the calibrator HD 190327. A record of the calibrator
observations is also provided
in Table 1.
Unfortunately, due to technical problems during the observations, from the measurements carried out in June 2007 reliable data could only be retrieved from one of the three baselines. Thus, in this case only one visibility instead of a triplet was obtained. Due to unfavorable weather conditions and limitations of the technical performance, reliable differential and closure phases from the LR observations could not be derived for any of the 2007 observations, but only for those from May 2008.
The results of the AMBER LR observations of IRC +10420 are shown in Fig. 2. The panels in the left and middle column show the AMBER K-band visibilities as a function of wavelength for the three epochs covered by our study, the top right panel shows the the AMBER H-band visibilities as a function of wavelength, and the bottom right panel illustrates the differential and closure phases in the J,H, and K bands obtained from the May 2008 observations of IRC +10420.
Two main results can be seen in Fig. 2. First, both the H- and K-band visibilities show only a weak wavelength dependence, and the visibility change with baseline for a given wavelength is only moderate. This corresponds to the fact that even with the shortest baselines of our AMBER observations, the extended dust shell of IRC +10420 is already fully resolved, and thus, AMBER probes the compact stellar component, i.e. the continuum emission from the central star and the dense circumstellar wind. The second result from the calibrated LR observables shown in Fig. 2 is that both the differential and closure phases show zero phase signals across all three near-infrared bands within the uncertaintly limits. Thus, in the LR AMBER data which mainly probe the continuum emission IRC +10420 does not show detectable deviations from point symmetry.
2.3 The high-spectral resolution data
In addition to the low-spectral resolution H- and K-band
AMBER observations of IRC +10420 presented in the
previous section, we also obtained the first AMBER measurement of
IRC +10420 in high-spectral resolution mode
(spectral resolution
![]() ).
The observations
were carried out in October 2008 under average seeing conditions as
part of an AMBER science verification run in order to test the
performance of
AMBER using the UTs and the fringe tracker FINITO. In the context of
this science verification run, a single measurement of
IRC +10420 and the calibrator star
HD 232078 was carried out in the K band,
centered
around the Br
).
The observations
were carried out in October 2008 under average seeing conditions as
part of an AMBER science verification run in order to test the
performance of
AMBER using the UTs and the fringe tracker FINITO. In the context of
this science verification run, a single measurement of
IRC +10420 and the calibrator star
HD 232078 was carried out in the K band,
centered
around the Br![]() emission
line (
emission
line (
![]() m),
with an exposure time of 3 s. Due to this
long exposure time, a window covering 512 pixels, i.e. all spectral
channels of the AMBER detector, could be read out, corresponding to a
wavelength coverage between
m),
with an exposure time of 3 s. Due to this
long exposure time, a window covering 512 pixels, i.e. all spectral
channels of the AMBER detector, could be read out, corresponding to a
wavelength coverage between ![]() 2.145
and
2.145
and ![]()
![]() m.
m.
Table 2: Summary of the AMBER observations of IRC+10420 and the calibrator star HD 232078 in high-spectral resolution mode from Oct 14, 2008 using the UT telescope configuration UT1-UT2-UT4.
It should be noted that a second measurement of
IRC +10420 with an exposure time of 1 s was
discarded for
two reasons. First of all, the data quality of this second measurement
is lower than that with the longer
detector integration time (DIT), simply because the SNR is lower.
Second, there is no corresponding calibrator
measurement with the same DIT close in time to the science target
measurement. From the ESO data archive,
we found two other calibrator measurements with
DIT = 1 s from different science programs in
the same night,
but these measurements of the calibrators HD 902 and
HD 13692 were taken 1 and 2 h after the observations
of IRC +10420. Since current high-spectral
resolution AMBER data suffer from a time-variable
high-frequency beating introduced by the VLTI Infrared Image Sensor
IRIS (Gitton et al. 2004),
we decided to discard these additional measurements because a proper
calibration of the science target data turned out to be impossible.
This seems to be a general problem for observations in high-spectral
resolution mode if the time span between the science target and
calibrator measurement becomes longer than approximately
30-45 min.
For the same reason, we also discarded two other calibrator data sets
with the same exposure time (DIT = 3 s)
as the measurement of IRC +10420 presented here
since these calibrator observations were carried out ![]() 5.5 and
8 h after the IRC +10420 observations. To
further reduce the effect of the IRIS fringes in our
data, we spectrally binned our final visibilities and phases with a bin
size of 7 and a step size of 1. To avoid
a loss of spectral resolution across the Br
5.5 and
8 h after the IRC +10420 observations. To
further reduce the effect of the IRIS fringes in our
data, we spectrally binned our final visibilities and phases with a bin
size of 7 and a step size of 1. To avoid
a loss of spectral resolution across the Br![]() line, this binning was only
performed in the continuum region, i.e. for wavelength channels with
line, this binning was only
performed in the continuum region, i.e. for wavelength channels with
![]() m
or
m
or ![]() m.
A summary of the HR observations discussed in this paper is given in
Table 2.
m.
A summary of the HR observations discussed in this paper is given in
Table 2.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11723F3A.eps}\\ \vspace*{1mm}
\includegraphics[width=14cm,clip]{11723F3B.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg76.png)
|
Figure 3:
VLTI/AMBER observations of IRC +10420 in
high-spectral resolution mode around the Br |
| Open with DEXTER | |
The calibrated observables of the AMBER high-spectral resolution
measurements are presented in Fig. 3.
The panels in the three left columns show (from left to right) the
visibilities, differential phases, closure phases (top), and the
spectrum (bottom) for the full wavelength range covered by the
observations. All panels in the three columns on the right-hand side of
Fig. 3
show the same quantities as the corresponding panels in the three left
columns, but only for a small wavelength range close to the Br![]() emission
line.
For the sake of clarity, in each panel, only a single averaged error
bar is shown on the right-hand side.
emission
line.
For the sake of clarity, in each panel, only a single averaged error
bar is shown on the right-hand side.
The wavelength
calibration of the HR data was performed by comparison of the AMBER raw
spectra of both IRC +10420 and the calibrator
HD 232078 with high-spectral resolution (
![]() )
telluric spectra kindly provided by
the Kitt Peak Observatory
)
telluric spectra kindly provided by
the Kitt Peak Observatory![]() .
The vertical dashed line shown in all panels on the right-hand side of
Fig. 3
marks the zero velocity with respect to earth, assuming a radial system
velocity of 73
.
The vertical dashed line shown in all panels on the right-hand side of
Fig. 3
marks the zero velocity with respect to earth, assuming a radial system
velocity of 73
![]() as given by Humphreys
et al. (2002), and a heliocentric correction of
as given by Humphreys
et al. (2002), and a heliocentric correction of
![]() for the time of the observations. The spectrum shown in Fig. 3 is the
average over the photometric beams
from the three single telescopes and the interferometric signal.
for the time of the observations. The spectrum shown in Fig. 3 is the
average over the photometric beams
from the three single telescopes and the interferometric signal.
![\begin{figure}
\par\includegraphics[angle=0,width=18cm]{11723F4.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg82.png)
|
Figure 4:
Top row: a) Azimuthally
averaged K-band visibility (
|
| Open with DEXTER | |
In the case of the HR measurements of IRC +10420
presented in this paper, the calibration relies on only a single
calibrator measurement of HD 23078 which is approximately
0.5 mag fainter in the K band than
IRC +10420
(
![]() ).
From the weather data
).
From the weather data![]() ,
we can see that at the time of the calibrator and science target
measurements the seeing was varying between
0
,
we can see that at the time of the calibrator and science target
measurements the seeing was varying between
0
![]() 85
and 1
85
and 1
![]() 15,
and the wind speed on the ground was steadily declining from 9 to
7.5
15,
and the wind speed on the ground was steadily declining from 9 to
7.5
![]() .
Thus, there is a noticeable, but not dramatic change in the weather
conditions between the calibrator and IRC +10420
observation. Together with the 0.5 mag brightness difference,
this might explain why, for instance, the calibrated visibility at the
shortest baseline (see Fig. 3) is
slightly
larger than unity. In fact, when using data from other calibrators of
the same night (HD 25680; HD 33833) which were taken
several hours later and with a seeing of 1
.
Thus, there is a noticeable, but not dramatic change in the weather
conditions between the calibrator and IRC +10420
observation. Together with the 0.5 mag brightness difference,
this might explain why, for instance, the calibrated visibility at the
shortest baseline (see Fig. 3) is
slightly
larger than unity. In fact, when using data from other calibrators of
the same night (HD 25680; HD 33833) which were taken
several hours later and with a seeing of 1
![]() 4,
the calibrated visibility of IRC +10420 reaches
values >1.2.
4,
the calibrated visibility of IRC +10420 reaches
values >1.2.
While the weaker emission peaks seen in the full AMBER
spectrum of IRC +10420 in Fig. 3 are
telluric
artifacts of the calibration process and therefore do not indicate real
emission features, the spectrum clearly
shows a strong Br![]() emission
line arising from IRC +10420 which contributes
approximately 50% to the total flux at
emission
line arising from IRC +10420 which contributes
approximately 50% to the total flux at
![]() m.
The Br
m.
The Br![]() line
is
clearly blueshifted with
line
is
clearly blueshifted with
![]() with respect to the systemic velocity, in agreement with previous
findings by, e.g., Oudmaijer
et al. (1994) (
with respect to the systemic velocity, in agreement with previous
findings by, e.g., Oudmaijer
et al. (1994) (
![]() )
and Humphreys
et al.
(2002) (
)
and Humphreys
et al.
(2002) (
![]() ).
From the
).
From the ![]() -calibration
process of our data, we estimate that the uncertainty of the
wavelength calibration is of the order of
-calibration
process of our data, we estimate that the uncertainty of the
wavelength calibration is of the order of
![]() .
The equivalent width of the Br
.
The equivalent width of the Br![]() line in the AMBER spectrum is
line in the AMBER spectrum is ![]() ,
in good agreement with the value found by de
Wit et al. (2008) from medium-spectral resolution
AMBER observations in June 2006.
The Br
,
in good agreement with the value found by de
Wit et al. (2008) from medium-spectral resolution
AMBER observations in June 2006.
The Br![]() line
is slightly asymmetric in the sense that the redshifted tail of the
line is more pronounced
with velocities up to
line
is slightly asymmetric in the sense that the redshifted tail of the
line is more pronounced
with velocities up to ![]()
![]() compared to
compared to ![]()
![]() on the blueshifted side.
on the blueshifted side.
At the wavelengths of the Br![]() emission, the visibilities on
all three baselines show a strong decrease, indicating
that the line-emitting zone is clearly resolved by our AMBER
observations and more extended than the continuum-emitting region. At
the longest baseline, the visibility in the center of the Br
emission, the visibilities on
all three baselines show a strong decrease, indicating
that the line-emitting zone is clearly resolved by our AMBER
observations and more extended than the continuum-emitting region. At
the longest baseline, the visibility in the center of the Br![]() line is as
low as 0.14. It should be noted here that similar to the LR data
presented in Sect. 2.2
the HR data also suffer from a strong field-of-view (FOV) effect as
will be discussed in more detail in the next section.
line is as
low as 0.14. It should be noted here that similar to the LR data
presented in Sect. 2.2
the HR data also suffer from a strong field-of-view (FOV) effect as
will be discussed in more detail in the next section.
The differential phases in the region of the Br![]() -emission
line show a clear non-zero signal within the uncertainty limits. On all
three baselines, we obtained the strongest phase signal in the
redshifted wing
of the Br
-emission
line show a clear non-zero signal within the uncertainty limits. On all
three baselines, we obtained the strongest phase signal in the
redshifted wing
of the Br![]() -emission
line, with phases up to
-emission
line, with phases up to
![]() on the two shorter baselines and
on the two shorter baselines and
![]() on the longest baseline. The closure phase
on the longest baseline. The closure phase ![]() ,
on the other hand, is in good agreement with the differential closure
phase
,
on the other hand, is in good agreement with the differential closure
phase
![]() .
.
![]() also shows a strong signal in the redshifted
wing of the Br
also shows a strong signal in the redshifted
wing of the Br![]() -emission
line (
-emission
line (![]()
![]() )
and the strongest non-zero signal (
)
and the strongest non-zero signal (![]()
![]() )
at the line center.
)
at the line center.
3 Results and discussion
3.1 The field-of-view effect
Since VLTI/AMBER is a single-mode fiber instrument, the field-of-view
(FOV) is limited to the Airy disk of the telescope aperture. Therefore,
for AMBER observations with the 1.8 m ATs of the VLTI,
the FOV is 250 mas in the K band, while
for AMBER observations with the 8.2 m UTs, the FOV is only ![]() 60 mas.
Thus, when observing an object as extended as IRC +10420
with AMBER, it is of great importance
to take AMBER's limited FOV into account, since a non-negligible
fraction of the total flux will be located
well outside the FOV of the observations.
60 mas.
Thus, when observing an object as extended as IRC +10420
with AMBER, it is of great importance
to take AMBER's limited FOV into account, since a non-negligible
fraction of the total flux will be located
well outside the FOV of the observations.
To account for the FOV effect in the AMBER data of IRC +10420, we used the dust radiative transfer model of Blöcker et al. (1999). This radiative transfer model was developed with the code DUSTY (Ivezic & Elitzur 1997; Nenkova et al. 1999,2000) to simultaneously explain the spectral energy distribution (SED) and K-band speckle-interferometric observations obtained with the SAO 6 m telescope.
The azimuthally averaged K-band
visibility of Blöcker
et al. (1999) is shown in the top-left panel of
Fig. 4
as a function of
baseline length. As one can see, the steep visibility drop ends in a
plateau at a visibility level of ![]() 60%.
The plateau itself is associated with the unresolved stellar component
plus the dense stellar wind of IRC +10420, which can
be probed by interferometry with baselines longward of approximately
10 m. On the other hand, the extended dust shell is fully
resolved already with a few meter baseline.
According to the best-fitting model of Blöcker et al., as a
result of its heavy mass loss IRC +10420 is
surrounded by an optically thick dust shell composed of silicate dust,
which contributes approximately 40% to the total K-band
flux of IRC +10420.
The inner boundary of the dust shell which marks the dust sublimation
radius is located at
60%.
The plateau itself is associated with the unresolved stellar component
plus the dense stellar wind of IRC +10420, which can
be probed by interferometry with baselines longward of approximately
10 m. On the other hand, the extended dust shell is fully
resolved already with a few meter baseline.
According to the best-fitting model of Blöcker et al., as a
result of its heavy mass loss IRC +10420 is
surrounded by an optically thick dust shell composed of silicate dust,
which contributes approximately 40% to the total K-band
flux of IRC +10420.
The inner boundary of the dust shell which marks the dust sublimation
radius is located at
![]() mas
and exhibits a dust temperature of 1000 K. Moreover, Blöcker
et al. found that in addition to the steady stellar wind a
phase of enhanced mass loss (superwind) that ceased roughly 60 to 90
yrs ago is required to explain both the K-band
visibility and the SED.
In the intensity profiles shown in Fig. 4b,
this
temporal superwind phase results in the
bump seen at an angular displacement of
mas
and exhibits a dust temperature of 1000 K. Moreover, Blöcker
et al. found that in addition to the steady stellar wind a
phase of enhanced mass loss (superwind) that ceased roughly 60 to 90
yrs ago is required to explain both the K-band
visibility and the SED.
In the intensity profiles shown in Fig. 4b,
this
temporal superwind phase results in the
bump seen at an angular displacement of ![]() 170 mas. Thus,
according to Blöcker et al. IRC +10420 's
dust shell comprises two components: An outer
shell resulting from the previous superwind phase and, directly
adjacent to this outer shell, an inner shell resulting from the
present-day mass loss which followed the superwind phase.
During the superwind phase, the mass-loss rate was approximately 40
times higher than the current mass-loss rate of
170 mas. Thus,
according to Blöcker et al. IRC +10420 's
dust shell comprises two components: An outer
shell resulting from the previous superwind phase and, directly
adjacent to this outer shell, an inner shell resulting from the
present-day mass loss which followed the superwind phase.
During the superwind phase, the mass-loss rate was approximately 40
times higher than the current mass-loss rate of
![]() .
.
![\begin{figure}
\par\includegraphics[angle=0,width=16cm]{11723F5.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg102.png)
|
Figure 5:
VLTI/AMBER observations of IRC +10420 corrected for
the field-of-view effect. Top: the two panels show
the K-band AMBER visibilities as a function of
wavelength for two of our LR measurements in May 2007 and May 2008,
corrected for the limited FOV, as discussed in Sect. 3.1.
Bottom left: AMBER H-band visibilities as
a function of wavelength from our LR observations in May 2008,
corrected for the limited FOV. Bottom right: AMBER
K-band visibilities at
|
| Open with DEXTER | |
Since the speckle data of Blöcker et al. were taken with a
comparably large FOV (![]() 14
14
![]() ),
the infinite FOV of the DUSTY model was well suited for the speckle
data analysis. In the context of our AMBER observations, we re-examined
the final radiative transfer model of Blöcker et al. as
follows. We used the radial H- and K-band
intensity profiles of their final model (see the top-right panel in
Fig. 4)
and calculated the visibilities from the intensity
profiles, which were truncated to match a given FOV. We note that it
would have been more precise to convolve
the intensity profiles with the corresponding telescope aperture before
the truncation, but the effect of the
convolution on the final result is only weak and, therefore, has been
omitted here. The H- and K-band
visibilities resulting from our FOV correction are shown in the middle
panels of Fig. 4
for the FOVs given by the plot labels. As expected,
the smaller the FOV, the higher the plateau value of the visibility,
since an increasing fraction of the
extended dust shell lies outside the FOV and will, therefore, no longer
contribute to the flux and visibility,
respectively.
),
the infinite FOV of the DUSTY model was well suited for the speckle
data analysis. In the context of our AMBER observations, we re-examined
the final radiative transfer model of Blöcker et al. as
follows. We used the radial H- and K-band
intensity profiles of their final model (see the top-right panel in
Fig. 4)
and calculated the visibilities from the intensity
profiles, which were truncated to match a given FOV. We note that it
would have been more precise to convolve
the intensity profiles with the corresponding telescope aperture before
the truncation, but the effect of the
convolution on the final result is only weak and, therefore, has been
omitted here. The H- and K-band
visibilities resulting from our FOV correction are shown in the middle
panels of Fig. 4
for the FOVs given by the plot labels. As expected,
the smaller the FOV, the higher the plateau value of the visibility,
since an increasing fraction of the
extended dust shell lies outside the FOV and will, therefore, no longer
contribute to the flux and visibility,
respectively.
In the bottom right panel of Fig. 4, the
AMBER
visibility correction for IRC +10420 is shown as a
function of wavelength across the H and K
bands. This wavelength-dependent correction has to be
subtracted from the measured visibility in order to correct AMBER's
finite FOV when observing with
the ATs. The figure reveals that the visibility correction decreases
with increasing wavelength from approximately 0.42 at ![]() m to 0.1 at
m to 0.1 at ![]() m.
This decrease reflects the decreasing flux contribution of the dust
shell (scattering + thermal emission) with increasing wavelength (see
upper right panel in Fig. 4).
For
instance, at
m.
This decrease reflects the decreasing flux contribution of the dust
shell (scattering + thermal emission) with increasing wavelength (see
upper right panel in Fig. 4).
For
instance, at ![]() m
the contribution of the attenuated stellar flux to the stellar flux is
only 35%, while it is almost
60% at
m
the contribution of the attenuated stellar flux to the stellar flux is
only 35%, while it is almost
60% at ![]() m.
Correspondingly, the FOV correction is stronger in the H
band than in the K band.
At the center of the H and K
bands the visibilities of the unresolved stellar component in the model
with a 250 mas FOV are approximately higher by 0.18 and 0.35
compared to the DUSTY model with an infinite FOV. For a 60 mas
FOV, the effect is even more dramatic. Here, almost the complete dust
shell is truncated due to the small FOV, and the visibility approaches
unity, since mainly the compact stellar component contributes to the
total flux. According to Fig. 4, we
can
expect that only
m.
Correspondingly, the FOV correction is stronger in the H
band than in the K band.
At the center of the H and K
bands the visibilities of the unresolved stellar component in the model
with a 250 mas FOV are approximately higher by 0.18 and 0.35
compared to the DUSTY model with an infinite FOV. For a 60 mas
FOV, the effect is even more dramatic. Here, almost the complete dust
shell is truncated due to the small FOV, and the visibility approaches
unity, since mainly the compact stellar component contributes to the
total flux. According to Fig. 4, we
can
expect that only ![]() 6%
instead of the originally 40% of flux from the extended dust shell
remains, if the FOV is as small as 60 mas.
6%
instead of the originally 40% of flux from the extended dust shell
remains, if the FOV is as small as 60 mas.
3.2 The low-spectral resolution data
As discussed in the previous section, the AMBER visibilities of IRC +10420 obtained with both ATs and UTs are highly affected by the limited FOV of the observations. From the radiative transfer model of Blöcker et al. (1999), we estimated the effect of AMBER's limited FOV on the H- and K-band visibilities for baselines which start to resolve the stellar component and its dense wind. We lowered all LR H- and K-band visibilities shown in Fig. 2 according to the wavelength-dependent visibility correction shown in the bottom panel of Fig. 4. Figure 5 shows the rescaled K-band AMBER visibilities from May 2007 and May 2008 (top panels) and the rescaled H-band AMBER visibilities from May 2008 (bottom left panel) which would be obtained in the case of an infinite AMBER FOV.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm]{11723F6A.ps}\\
\includegraphics[angle=-90,width=7.5cm]{11723F6B.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg107.png)
|
Figure 6:
Stellar diameter |
| Open with DEXTER | |
As the bottom-right panel in Fig. 5
illustrates,
the rescaled AMBER K-band data at
![]() m
(red
bullets with error bars) are in good agreement with the visibilities
from the speckle-interferometric observations by Blöcker
et al. (1999)
(blue bullets) within the uncertainties of both measurements. The solid
green curve in
Fig. 5
shows a Gaussian fit of the compact stellar component, assuming a fully
resolved dust
shell with an a priori unknown flux contribution. As indicated in the
plot, a two-parameter fit with stellar diameter
m
(red
bullets with error bars) are in good agreement with the visibilities
from the speckle-interferometric observations by Blöcker
et al. (1999)
(blue bullets) within the uncertainties of both measurements. The solid
green curve in
Fig. 5
shows a Gaussian fit of the compact stellar component, assuming a fully
resolved dust
shell with an a priori unknown flux contribution. As indicated in the
plot, a two-parameter fit with stellar diameter
![]() and the
fractional flux contribution of the dust shell as
and the
fractional flux contribution of the dust shell as
![]() free parameters gives a Gaussian FWHM diameter of
free parameters gives a Gaussian FWHM diameter of
![]() mas
and a dust shell flux contribution of
mas
and a dust shell flux contribution of
![]() .
The fitted diameter is in agreement with the stellar diameter d=1.01 mas
derived for a bolometric flux of
.
The fitted diameter is in agreement with the stellar diameter d=1.01 mas
derived for a bolometric flux of
![]() ,
a distance of 5 kpc, and a central star effective temperature
of 7000 K (see, e.g., Blöcker
et al. 1999).
,
a distance of 5 kpc, and a central star effective temperature
of 7000 K (see, e.g., Blöcker
et al. 1999).
After rescaling all AMBER H- and K-band
visibilities, we fitted all visibility points for a given wavelength
with the simple two-component model described above (Gaussian stellar
component + infinitely extended dust shell).
The result of the fit procedure is shown in Fig. 6,
where
the fit parameters are displayed as a function of wavelength for the H-
(bottom panel) and K-band data (top panel). As the
figure reveals, within the error bars we essentially obtained both a
wavelength-independent continuum diameter and a wavelength-independent
flux contribution from the extended dust shell across the K
band. On the other hand, a slight decrease of the dust shell's flux
contribution is seen across the H band from
![]() at the lower band edge to
at the lower band edge to
![]() at the upper band edge. A comparison with the lower left panel in
Fig. 4
shows that the wavelength dependence
and the absolute level of the stellar flux contribution derived from
the AMBER data is in basic agreement with the predictions
from the DUSTY model of Blöcker
et al. (1999). In this model, the attenuated stellar
flux amount to approximately 0.58 in the
K band with only a moderate wavelength dependence,
while the stellar flux contribution rises from approximately
0.32 to 0.5 across the H band.
at the upper band edge. A comparison with the lower left panel in
Fig. 4
shows that the wavelength dependence
and the absolute level of the stellar flux contribution derived from
the AMBER data is in basic agreement with the predictions
from the DUSTY model of Blöcker
et al. (1999). In this model, the attenuated stellar
flux amount to approximately 0.58 in the
K band with only a moderate wavelength dependence,
while the stellar flux contribution rises from approximately
0.32 to 0.5 across the H band.
Averaged over all K-band data, for
IRC +10420 we derived a stellar continuum diameter
of
![]() mas
(
mas
(
![]() mas
assuming a uniform disk) and a fractional flux
contribution of
mas
assuming a uniform disk) and a fractional flux
contribution of
![]() from the dust shell. From the H-band AMBER data, we
found
from the dust shell. From the H-band AMBER data, we
found ![]() mas
(
mas
(
![]() mas)
and
mas)
and ![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{11723F7A.ps}\\
\inclu...
...includegraphics[angle=-90,width=6cm]{11723F7C.ps}\hspace*{5mm}}
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg119.png)
|
Figure 7:
Top: HR AMBER visibilities of
IRC +10420 around the Br |
| Open with DEXTER | |
3.3 The high-spectral resolution data
3.3.1 FOV effect correction
To account for the larger uncertainties in the absolutely calibrated
data, we used a slightly different strategy
to correct the HR AMBER data for the FOV effect described in
Sect. 3.1.
Looking at Fig. 4e
we see that for AMBER+UT observations with a FOV of ![]() 60 mas,
the fractional flux
contribution of the dust shell in the K band is
only of the order of 6%. On the other hand, from the fit
of our LR AMBER data, we found that IRC +10420's K-band
continuum diameter is 0.98 mas. Therefore, we corrected
our HR AMBER visibilities in the following way:
for a given baseline, we first rescaled the visibility as a function of
wavelength to match the value expected
for a single, compact component with 0.98 mas diameter. Then,
we globally lowered the rescaled visibilities by 6% to account for the
diffuse, extended flux contribution of the dust shell.
60 mas,
the fractional flux
contribution of the dust shell in the K band is
only of the order of 6%. On the other hand, from the fit
of our LR AMBER data, we found that IRC +10420's K-band
continuum diameter is 0.98 mas. Therefore, we corrected
our HR AMBER visibilities in the following way:
for a given baseline, we first rescaled the visibility as a function of
wavelength to match the value expected
for a single, compact component with 0.98 mas diameter. Then,
we globally lowered the rescaled visibilities by 6% to account for the
diffuse, extended flux contribution of the dust shell.
The final result of this rescaling process in order to take
the FOV effect into account is shown in the upper panel of
Fig. 7.
Here, we show for a small wavelength range around the Br![]() line the K-band
visibilities one would retrieve for IRC +10420 in
the case of an infinite AMBER FOV. As the figure reveals,
the continuum visibilities are now
line the K-band
visibilities one would retrieve for IRC +10420 in
the case of an infinite AMBER FOV. As the figure reveals,
the continuum visibilities are now ![]() 0.9 for the shortest baseline,
0.83 for the intermediate baseline, and
0.68 for the longest baseline.
0.9 for the shortest baseline,
0.83 for the intermediate baseline, and
0.68 for the longest baseline.
3.3.2 Simple geometrical model
Attempting to get a first idea of the size of the Br![]() line-emitting region and
disregarding a possible deviation from spherical symmetry, we fitted a
spherical Gaussian to all continuum data for a given wavelength with
line-emitting region and
disregarding a possible deviation from spherical symmetry, we fitted a
spherical Gaussian to all continuum data for a given wavelength with
![]() m
and
m
and ![]() m,
taking into account the 6% flux contribution from the extended dust
shell. Averaged over all spectral channels (approximately
490 channels), we obtained a FWHM Gaussian
size of
m,
taking into account the 6% flux contribution from the extended dust
shell. Averaged over all spectral channels (approximately
490 channels), we obtained a FWHM Gaussian
size of ![]() mas
for the continuum-emitting region. We note that the error given here
includes not only
the the pure fitting error, which is only of the order of
0.001 mas, but also reflects the uncertainties of
the overall calibration process, including the FOV-related rescaling of
the data.
mas
for the continuum-emitting region. We note that the error given here
includes not only
the the pure fitting error, which is only of the order of
0.001 mas, but also reflects the uncertainties of
the overall calibration process, including the FOV-related rescaling of
the data.
To derive the size of the Br![]() line-emitting zone, we fitted
the visibilities in the spectral channels
with noticeable Br
line-emitting zone, we fitted
the visibilities in the spectral channels
with noticeable Br![]() line-emission
in the spectrum, i.e. for
line-emission
in the spectrum, i.e. for
![]() m,
with a three-component model. For the sake of simplicity, in this
simple model, we neglect likely deviations from a spherical or even
point-symmetric distribution of the Br
m,
with a three-component model. For the sake of simplicity, in this
simple model, we neglect likely deviations from a spherical or even
point-symmetric distribution of the Br![]() line-emitting region. de Wit et al.
(2008)
convincingly argued that the Br
line-emitting region. de Wit et al.
(2008)
convincingly argued that the Br![]() line-emitting region cannot
have a spherical shape, but is most likely elongated towards a position
angle of 20
line-emitting region cannot
have a spherical shape, but is most likely elongated towards a position
angle of 20![]() .
Unfortunately, as in the case of the study
of de Wit
et al. (2008),
also our single measurement with a position angle coverage of
.
Unfortunately, as in the case of the study
of de Wit
et al. (2008),
also our single measurement with a position angle coverage of ![]() 40
40![]() is
only of limited use to put reliable constraints on the shape of the
emission zone. Nevertheless, we studied
the emission region also in the context of a 2D radiative transfer
model as will be shown in more detail in the next section. However,
independent from a more sophisticated modeling,
qualitatively we can conclude that the clear non-zero detection in the
differential and closure phases across the Br
is
only of limited use to put reliable constraints on the shape of the
emission zone. Nevertheless, we studied
the emission region also in the context of a 2D radiative transfer
model as will be shown in more detail in the next section. However,
independent from a more sophisticated modeling,
qualitatively we can conclude that the clear non-zero detection in the
differential and closure phases across the Br![]() line in our AMBER HR
measurement shows that the geometry of the line-emitting region
deviates
from a point-symmtric configuration. On the other hand, in the center
of the Br
line in our AMBER HR
measurement shows that the geometry of the line-emitting region
deviates
from a point-symmtric configuration. On the other hand, in the center
of the Br![]() line
the differential and closure phases are of the order of
line
the differential and closure phases are of the order of ![]() 10
10![]() .
Thus, in order to determine the typical size of the Br
.
Thus, in order to determine the typical size of the Br![]() -emitting
zone
with the simple model approach discussed here we decided to neglect the
non-zero phases.
-emitting
zone
with the simple model approach discussed here we decided to neglect the
non-zero phases.
Our simple three-component model consists of the following
components:
(a) a fully resolved, infinitely large dust shell with a fixed
fractional flux contribution of 6%; (b) the stellar continuum,
approximated by a Gaussian with a fixed size of 0.98 mas
according to our continuum fit; and (c) the Br![]() line-emitting region, which is
represented in our simple model by a ring with infinitely thin
thickness (
line-emitting region, which is
represented in our simple model by a ring with infinitely thin
thickness (
![]() ). The total visibility can
then be written as
). The total visibility can
then be written as
with
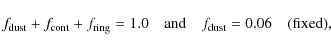
|
(2) |
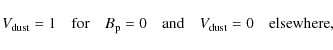
|
(3) |
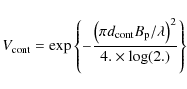
|
(4) |
with
Our best-fit result for the central wavelength channel in the
Br![]() line is
shown in the middle panel of Fig. 7.
Here,
the visibility according to Eqs. (1)-(5) is plotted as
a
function of baseline for
line is
shown in the middle panel of Fig. 7.
Here,
the visibility according to Eqs. (1)-(5) is plotted as
a
function of baseline for
![]() m.
The blue bullets with error bars are
the three AMBER data points, and the three curves visualize the best
fit model and its tolerance. We found
that our AMBER data in the center of the Br
m.
The blue bullets with error bars are
the three AMBER data points, and the three curves visualize the best
fit model and its tolerance. We found
that our AMBER data in the center of the Br![]() emission line can be well
fitted with a ring with a diameter of
emission line can be well
fitted with a ring with a diameter of
![]() ,
whose fractional flux contribution is
,
whose fractional flux contribution is
![]() .
We note that the size of the Br
.
We note that the size of the Br![]() line-emitting region obtained
from our fit is in general agreement, although slightly larger than the
3.3 mas found by de
Wit
et al. (2008) from a single-component Gaussian fit
of the line data.
From
line-emitting region obtained
from our fit is in general agreement, although slightly larger than the
3.3 mas found by de
Wit
et al. (2008) from a single-component Gaussian fit
of the line data.
From ![]() ,
we directly obtain
,
we directly obtain
![]() ;
i.e., from our best fit, we indeed find a photosperic absorption in the
Br
;
i.e., from our best fit, we indeed find a photosperic absorption in the
Br![]() line of the
order of
line of the
order of
![]() .
.
Despite the limited amount of data and the limited position
angle coverage, we also briefly addressed the
question of an aspherical shape of the Br![]() line-emitting region in the
context of our simple model fits. For this study, we used the
three-component model described above and fixed
line-emitting region in the
context of our simple model fits. For this study, we used the
three-component model described above and fixed
![]() to the value found from the 1D fit (
to the value found from the 1D fit (
![]() )
of the
)
of the ![]() m
data. Then, we first fitted all three data points with the
three-component model
with only
m
data. Then, we first fitted all three data points with the
three-component model
with only ![]() as free parameter, and finally, we fitted an ellipse to the three ring
diameters as
a function of position angle. The result is shown in the bottom panel
of Fig. 7,
where
the fitted ring diameters and the ellipse are displayed in a polar
diagram. As the figure shows, the position-angle
dependence of the ring diameter can be fitted with an ellipse with
major and minor axes of
as free parameter, and finally, we fitted an ellipse to the three ring
diameters as
a function of position angle. The result is shown in the bottom panel
of Fig. 7,
where
the fitted ring diameters and the ellipse are displayed in a polar
diagram. As the figure shows, the position-angle
dependence of the ring diameter can be fitted with an ellipse with
major and minor axes of ![]() mas
and
mas
and ![]() mas, respectively,
and a position angle of the major axis of
mas, respectively,
and a position angle of the major axis of
![]()
![]() .
Interestingly,
the major axis is nearly aligned with the elongation of the outer
reflection nebula of IRC +10420 seen
in the HST images of Humphreys
et al. (1997, PA = 33
.
Interestingly,
the major axis is nearly aligned with the elongation of the outer
reflection nebula of IRC +10420 seen
in the HST images of Humphreys
et al. (1997, PA = 33![]() ) and the
symmetry axis of the H
) and the
symmetry axis of the H![]() emission as inferred by Davies
et al. (2007).
emission as inferred by Davies
et al. (2007).
Table 3: Physical parameters of the CMFGEN models for IRC +10420 .
3.3.3 Radiative transfer modeling of the Br
 line emission
line emission
A simple geometrical model as presented in the previous section cannot
explain the AMBER observations in detail.
Thus, a more physical model is required to interpret, for instance, the
blueshift of the Br![]() emission,
the visibility across the emission line, and the non-zero phases.
Therefore, in a second step of our analysis
we interpreted the AMBER data of IRC +10420 using
the iterative, spherical symmetric, full line-blanketed, non-LTE
radiative transfer code CMFGEN (Hillier
& Miller 1998).
emission,
the visibility across the emission line, and the non-zero phases.
Therefore, in a second step of our analysis
we interpreted the AMBER data of IRC +10420 using
the iterative, spherical symmetric, full line-blanketed, non-LTE
radiative transfer code CMFGEN (Hillier
& Miller 1998).
The radiative transfer code
In CMFGEN, a spherically-symmetric outflow in steady-state is assumed, and line and continuum formation are calculated in a non-LTE regime. Each model is specified by its effective temperatureWhile CMFGEN can handle the effects of clumping via a volume filling
factor f, we decided to assume a unclumped wind
(i.e. f=1) since no strong electron scattering
wings are present around the Br![]() line. The strength of such
electron scattering wings is sensitive to the amount of wind clumping (Hillier 1991),
and even assuming
an unclumped wind model (which produces the maximum strength possible
in the electron scattering wings), no detectable electron scattering
wings are seen in Br
line. The strength of such
electron scattering wings is sensitive to the amount of wind clumping (Hillier 1991),
and even assuming
an unclumped wind model (which produces the maximum strength possible
in the electron scattering wings), no detectable electron scattering
wings are seen in Br![]() .
.
Line blanketing affects the ionization structure of the wind and, consequently, the spectrum. CMFGEN employs the concept of super-levels to include thousands of spectral lines in non-LTE, making it feasible to solve the equations of statistical equilibrium and radiative transfer simultaneously. The atomic model used for IRC +10420 included lines of H, He, C, N, O, and Fe.
Although CMFGEN handles only spherical-symmetric outflows, the wind asymmetry was also analyzed using a recently developed modification in CMFGEN to compute the emerging spectrum in two-dimensional geometry (Busche & Hillier 2005). We refer the reader to Busche & Hillier (2005) for further details about the code, and to that paper and Groh et al. (2006,2008) for additional details about applications of the BH05 code. In the following, we briefly describe the main aspects of the code.
As input the BH05 code requires several quantities
(energy-level populations, ionization structure, temperature structure,
emissivities, opacities, and specific intensity J)
calculated by the original, spherically-symmetric CMFGEN model in the
co-moving frame. Latitude-dependencies of the wind density and wind
terminal velocity can then be taken into account using any arbitrary
latitude-dependent density/wind terminal velocity variation. Due to our
very limited amount of data, we restricted the analysis to changes only
in the wind density, using oblate and prolate density parameterizations
as follows,
![\begin{displaymath}{\rm oblate\!\!:} ~~~ \rho_{2D} \propto \rho_{1D} \{1+ [a (1-{\rm cos}^2 \theta)^b]\}~~
\end{displaymath}](/articles/aa/full_html/2009/43/aa11723-09/img162.png)
|
(6) |
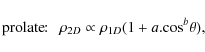
|
(7) |
where
The scaling laws given above are applied only for distances greater than that where the wind velocity is equal to the sonic velocity. For smaller distances, no scaling was applied. The 2D source function, emissivities, and opacities are then calculated, assuming that these quantities depend only on the new values of the scaled density. Appropriate scaling laws are used for different physical processes (e.g. density-squared scaling for free-free and bound-free transitions, and linear-density scaling for electron scattering). Finally, for a direct comparison with the AMBER observables the spectrum in the observer's frame and intensity maps for all wavelengths of interest are computed. In our analysis, we first considered a spherically symmetric model and then a model with a prolate/oblate wind structure.
Spherical model
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=4.2cm]{11723F8A.eps} \in...
...23F8G.eps} \includegraphics[angle=0,width=4.2cm]{11723F8H.eps} }
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg169.png)
|
Figure 8:
Upper row: monochromatic images of
IRC +10420 predicted by the spherical CMFGEN model
with the physical parameters given in Table 3. The
panels
show ( from left to right) model images in the K
band continuum (at a velocity
|
| Open with DEXTER | |
The stellar and wind parameters of our best-fitting spherically
symmetric CMFGEN model are presented in Table 3. Our
CMFGEN
model has a luminosity of
![]() ,
in good
agreement with previous determinations (e.g.,
,
in good
agreement with previous determinations (e.g.,
![]() ,
Jones
et al. 1993)
Together with an assumed mass of
,
Jones
et al. 1993)
Together with an assumed mass of
![]() ,
we find
,
we find
![]() .
Since IRC +10420 has already lost about half of its
initial mass (Humphreys
et al. 1997), it is likely that the He content is
enhanced on the surface compared to the solar value. Thus, apart from
solar metallicity our model assumes a He abundance of
He/H = 0.4 (by number). Finally, we assumed a
distance of 3.5 kpc.
.
Since IRC +10420 has already lost about half of its
initial mass (Humphreys
et al. 1997), it is likely that the He content is
enhanced on the surface compared to the solar value. Thus, apart from
solar metallicity our model assumes a He abundance of
He/H = 0.4 (by number). Finally, we assumed a
distance of 3.5 kpc.
The AMBER high-resolution K-band spectrum
covers only a short wavelength region around Br![]() ,
and does not provide enough diagnostic lines to derive a precise value
for the effective temperature of IRC +10420.
However, the absence of He I
,
and does not provide enough diagnostic lines to derive a precise value
for the effective temperature of IRC +10420.
However, the absence of He I
![]() m and He I
m and He I
![]() m
lines imply an upper limit for
m
lines imply an upper limit for
![]() of about 10 500 K. Since Klochkova
et al. (2002) obtained
of about 10 500 K. Since Klochkova
et al. (2002) obtained
![]() for the observations of IRC +10420 in 2000 and an
annual increase in
for the observations of IRC +10420 in 2000 and an
annual increase in
![]() of
of ![]() 120 K,
we assume in our models
120 K,
we assume in our models
![]() .
We note that conclusions of the present paper such as the evidence for
wind asymmetry in IRC +10420, are only weakly
affected by reasonable changes in
.
We note that conclusions of the present paper such as the evidence for
wind asymmetry in IRC +10420, are only weakly
affected by reasonable changes in
![]() .
.
Our model requires a mass-loss rate of
![]() in order to reproduce the equivalent width of the observed Br
in order to reproduce the equivalent width of the observed Br![]() line in IRC +10420 (
line in IRC +10420 (
![]() ,
Fig. 8).
A wind terminal velocity of
,
Fig. 8).
A wind terminal velocity of
![]() and
and ![]() were used in order to roughly reproduce the Br
were used in order to roughly reproduce the Br![]() line width. However, the Br
line width. However, the Br![]() -emitting region of such a
model is rather compact, not reproducing the spatial extension of the Br
-emitting region of such a
model is rather compact, not reproducing the spatial extension of the Br![]() emitting
region as measured by AMBER. As a consequence, this
model fails to reproduce the observed visibilities (see red curves in
the lower panels of Fig. 8).
Moreover,
while the observed spectrum is blueshifted relative to the systemic
velocity, the CMFGEN model spectrum is slightly redshifted (
emitting
region as measured by AMBER. As a consequence, this
model fails to reproduce the observed visibilities (see red curves in
the lower panels of Fig. 8).
Moreover,
while the observed spectrum is blueshifted relative to the systemic
velocity, the CMFGEN model spectrum is slightly redshifted (![]()
![]() ).
The redshift in the model is caused by the turbulent velocity field of
the wind (Catala
et al. 1984; Hillier
1989,1987),
which was parameterized using a microturbulent velocity of
).
The redshift in the model is caused by the turbulent velocity field of
the wind (Catala
et al. 1984; Hillier
1989,1987),
which was parameterized using a microturbulent velocity of
![]() .
.
An additional model with the same parameters as the model
described above, but with
![]() ,
was calculated in order to analyze the effects of a larger
,
was calculated in order to analyze the effects of a larger
![]() on the fit of the AMBER observables. As expected, the increase in
on the fit of the AMBER observables. As expected, the increase in
![]() results in a larger Br
results in a larger Br![]() -emitting
region, but while such a model with an increased mass-loss rate is now
able to reasonably reproduce the observed visibilities (see blue curves
in the lower panels of Fig. 8), it
also
predicts a much higher amount of Br
-emitting
region, but while such a model with an increased mass-loss rate is now
able to reasonably reproduce the observed visibilities (see blue curves
in the lower panels of Fig. 8), it
also
predicts a much higher amount of Br![]() line emission compared to the
observations (lower left panel in Fig. 8). On
the
other hand, lower turbulent velocities provide slightly lower Br
line emission compared to the
observations (lower left panel in Fig. 8). On
the
other hand, lower turbulent velocities provide slightly lower Br![]() redshifts.
However, as a general result we conclude that spherically symmetric
wind models are intrinsically unable to reproduce the observed blueshifted
Br
redshifts.
However, as a general result we conclude that spherically symmetric
wind models are intrinsically unable to reproduce the observed blueshifted
Br![]() line.
Moreover, a reasonable simultaneous fit of both the
observed Br
line.
Moreover, a reasonable simultaneous fit of both the
observed Br![]() spectrum
and the corresponding visibilities with a spherical model could not be
obtained.
spectrum
and the corresponding visibilities with a spherical model could not be
obtained.
2D
modeling of the AMBER data around the Br
 line - evidence for wind
asymmetry
line - evidence for wind
asymmetry
In the previous paragraph we showed that spherical models are
unable to simultaneously reproduce the observed AMBER visibilities and
the Br![]() spectrum of IRC +10420 and, in particular, the
blueshift of the Br
spectrum of IRC +10420 and, in particular, the
blueshift of the Br![]() emission. Thus,
one can conclude that a non-spherical outflow must be present. This is
supported by the fact that non-zero differential
and closure phases have been measured with AMBER. Thus, in order to
obtain insights on the wind asymmetry of IRC +10420,
we calculated 2D axisymmetric radiative transfer models using the Busche & Hillier
(2005) code
described above.
emission. Thus,
one can conclude that a non-spherical outflow must be present. This is
supported by the fact that non-zero differential
and closure phases have been measured with AMBER. Thus, in order to
obtain insights on the wind asymmetry of IRC +10420,
we calculated 2D axisymmetric radiative transfer models using the Busche & Hillier
(2005) code
described above.
Due to the limited amount of spatial frequencies and position
angles sampled by our data, in our analysis we gave highest priority to
the simultaneous reproduction of the observed amount of Br![]() line emission compared to the continuum, the blueshift of this
emission, and the wavelength dependence of the visibility. Given the
limitations of our 2D model and the likely three-dimensional nature of
IRC +10420 's outflow, a full analysis of the
wavelength dependencies of the
differential and closure phases are deferred to a future paper.
Nevertheless, we believe that the modeling results presented in the
following are crucial for constraining the parameter space in future
studies using more sophisticated 2D radiative transfer models such as
ASTAROTH (Zsargó et al.
2008).
line emission compared to the continuum, the blueshift of this
emission, and the wavelength dependence of the visibility. Given the
limitations of our 2D model and the likely three-dimensional nature of
IRC +10420 's outflow, a full analysis of the
wavelength dependencies of the
differential and closure phases are deferred to a future paper.
Nevertheless, we believe that the modeling results presented in the
following are crucial for constraining the parameter space in future
studies using more sophisticated 2D radiative transfer models such as
ASTAROTH (Zsargó et al.
2008).
We analyzed both prolate and oblate density enhancements and
found that, in general, both geometries require a remarkably large
density contrast (![]() -16)
in order to reproduce the low visibility detected within the Br
-16)
in order to reproduce the low visibility detected within the Br![]() line. Interestingly, the observed blueshift of the Br
line. Interestingly, the observed blueshift of the Br![]() emission
could only be reproduced by models in which the receding part of the
wind, which is responsible for the major fraction of the redshifted Br
emission
could only be reproduced by models in which the receding part of the
wind, which is responsible for the major fraction of the redshifted Br![]() emission, is blocked. For a given density contrast, oblate models
provided less projected separation on the sky between the redshifted
and blueshifted hemispheres than prolate models, making it challenging
for oblate models to produce a blueshifted Br
emission, is blocked. For a given density contrast, oblate models
provided less projected separation on the sky between the redshifted
and blueshifted hemispheres than prolate models, making it challenging
for oblate models to produce a blueshifted Br![]() line with a similar strength and spatial extension as the observations.
Therefore, the preferred geometry to fit the observations is prolate
and the blocking of the redshifted hemisphere could possibly be caused
either by an optically-thick disk, a putative binary companion, or by
the wind being ejected by specific parts of the stellar surface.
line with a similar strength and spatial extension as the observations.
Therefore, the preferred geometry to fit the observations is prolate
and the blocking of the redshifted hemisphere could possibly be caused
either by an optically-thick disk, a putative binary companion, or by
the wind being ejected by specific parts of the stellar surface.
The best fit to simultaneously reproduce the observed amount
of Br![]() line emission with respect to the continuum, the line blueshift, and
the wavelength dependence of the visibility was obtained by using a
prolate model with a density contrast of
line emission with respect to the continuum, the line blueshift, and
the wavelength dependence of the visibility was obtained by using a
prolate model with a density contrast of ![]() 16 from pole to equator (see
Fig. 9)
oriented at
16 from pole to equator (see
Fig. 9)
oriented at ![]() .
The optimal fit to the line's blueshift was obtained by starting the
blocking of the redshifted emission at a projected offset distance from
the center of the star of
.
The optimal fit to the line's blueshift was obtained by starting the
blocking of the redshifted emission at a projected offset distance from
the center of the star of ![]() RA = -0.3 mas
and
RA = -0.3 mas
and ![]() Dec = -0.3 mas
(Fig. 9).
As Fig. 9
reveals, while the 2D models can basically resemble the AMBER spectrum
and visibilities across
the Br
Dec = -0.3 mas
(Fig. 9).
As Fig. 9
reveals, while the 2D models can basically resemble the AMBER spectrum
and visibilities across
the Br![]() line
and, in the the case of the blocked model, also the observed blueshift
of the emission, neither the unblocked nor the blocked model is able to
reproduce the observed wavelength dependence of the differential and
closure phases.
Both models predict much stronger phase signals across the line,
especially in the blueshifted wing of the emission line.
As noted above, a consistent fit of all AMBER observables including the
phases is beyond the scope of this paper and will
be subject to a more detailed analysis which also includes follow-up
AMBER oberservations of IRC +10420 which will help
to
better constrain the 2D model.
line
and, in the the case of the blocked model, also the observed blueshift
of the emission, neither the unblocked nor the blocked model is able to
reproduce the observed wavelength dependence of the differential and
closure phases.
Both models predict much stronger phase signals across the line,
especially in the blueshifted wing of the emission line.
As noted above, a consistent fit of all AMBER observables including the
phases is beyond the scope of this paper and will
be subject to a more detailed analysis which also includes follow-up
AMBER oberservations of IRC +10420 which will help
to
better constrain the 2D model.
Compared to our spherical model presented before, the
mass-loss rate of the 2D model had to be increased to
![]() ,
since a fraction of the Br
,
since a fraction of the Br![]() emission
is blocked. Lower polar density enhancements did not provide enough
extension of the Br
emission
is blocked. Lower polar density enhancements did not provide enough
extension of the Br![]() line-emitting
region, while higher mass-loss rates provided a stronger Br
line-emitting
region, while higher mass-loss rates provided a stronger Br![]() emission
line than observed with AMBER. The value of
emission
line than observed with AMBER. The value of
![]() is admittedly biased by the visibility measurement of the longest
baseline, which had an orientation on the sky of
is admittedly biased by the visibility measurement of the longest
baseline, which had an orientation on the sky of
![]() .
Different PAs provide a worse fit to the Br
.
Different PAs provide a worse fit to the Br![]() visibilities and the
differential and closure phases have less amplitude than the model with
visibilities and the
differential and closure phases have less amplitude than the model with
![]() .
Interferometric measurements using baselines oriented at different PAs
on the sky are urgently needed to better constrain the position angle
of IRC +10420 's prolate wind.
.
Interferometric measurements using baselines oriented at different PAs
on the sky are urgently needed to better constrain the position angle
of IRC +10420 's prolate wind.
An intermediate inclination angle of
![]() is required in order to provide enough separation between the projected
redshifted and blueshifted lobes and the star. In this case, the
redshifted part of the line emission can be efficiently blocked and,
thus, the observed blueshifted Br
is required in order to provide enough separation between the projected
redshifted and blueshifted lobes and the star. In this case, the
redshifted part of the line emission can be efficiently blocked and,
thus, the observed blueshifted Br![]() emission can be reproduced and
yet produce sufficient spatial extension on the sky to also fit the
AMBER visibilities. Models with
emission can be reproduced and
yet produce sufficient spatial extension on the sky to also fit the
AMBER visibilities. Models with
![]() provide too much redshifted emission even if one of the hemispheres is
completely blocked, while even for a polar density enhancement of 16
models with i <
provide too much redshifted emission even if one of the hemispheres is
completely blocked, while even for a polar density enhancement of 16
models with i <
![]() do not provide enough spatial
extension of the Br
do not provide enough spatial
extension of the Br![]() emission
region on the sky due
to projection effects. If the inclination angle of the line-of-sight to
IRC +10420 is less than
emission
region on the sky due
to projection effects. If the inclination angle of the line-of-sight to
IRC +10420 is less than
![]() ,
we estimate that a very large density contrast between pole and equator
of >30 is required, which seems unlikely.
,
we estimate that a very large density contrast between pole and equator
of >30 is required, which seems unlikely.
To summarize, from the 2D modeling of our AMBER data we
conclude that the wind of IRC +10420 has a
significantly non-spherical geometry, and the viewing angle and the
physical conditions must be such that a large fraction of the
redshifted Br![]() emission is blocked from our view.
emission is blocked from our view.
4 Summary and conclusions
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=4.2cm]{11723F9A.eps} \in...
...9O.eps} \includegraphics[angle=0,width=4.2cm]{11723F9P.eps} }\\
\end{figure}](/articles/aa/full_html/2009/43/aa11723-09/Timg190.png)
|
Figure 9:
First row: monochromatic images of
IRC +10420 predicted by the unblocked prolate CMFGEN
model with the physical parameters given in Table 3.
From left to right, the panels show images in the K-band
continuum (at a velocity
|
| Open with DEXTER | |
We presented the first VLTI/AMBER observations of the yellow
hypergiant IRC +10420 in low-spectral
resolution (LR) mode covering the J, H,
and K bands and the first AMBER
observation of IRC +10420 around the Br![]() emission
line in high-spectral resolution (HR) mode with
a spectral resolution of 12 000 and projected baselines
between 54 and 129 m.
emission
line in high-spectral resolution (HR) mode with
a spectral resolution of 12 000 and projected baselines
between 54 and 129 m.
From the low-spectral resolution observations carried out with
two linear AT arrays
(baselines ranging from 15 to 96 m), we were able to extract H-
and K-band visibilities at spatial scales which
probe the stellar continuum emission. Differential and closure phases
could be derived from the LR data for two near-infrared bands
(differential phases) and all three near-infrared bands (closure
phases) covered by AMBER. Within the error bars, all LR phases turn out
to be zero. We corrected all visibilities for AMBER's limited
field-of-view (FOV = 250 mas for AT
observations) to account for the truncation of
IRC +10420's extended dust shell. From the
visibilities we derived FWHM Gaussian diameters of
IRC +10420's stellar component of
![]() mas
and
mas
and ![]() ,
averaged over all spectral channels in the H- and K-bands,
respectively. The stellar flux contribution in the case of an infinite
FOV was found to be
,
averaged over all spectral channels in the H- and K-bands,
respectively. The stellar flux contribution in the case of an infinite
FOV was found to be ![]() in the H band and
in the H band and
![]() in the K band.
in the K band.
On the other hand, we carried out high-spectral resolution
AMBER observations of IRC +10420 centered
around the Br![]() emission
line and combining three UTs. We found that the Br
emission
line and combining three UTs. We found that the Br![]() emission is
blueshifted with
emission is
blueshifted with ![]() with respect to the systemic velocity and that the Br
with respect to the systemic velocity and that the Br![]() emitting-region
of IRC +10420's dense stellar wind contributes
roughly 50% to the total flux at the peak wavelength of the nearly
symmetric emission line. The equivalent width of the Br
emitting-region
of IRC +10420's dense stellar wind contributes
roughly 50% to the total flux at the peak wavelength of the nearly
symmetric emission line. The equivalent width of the Br![]() line is
line is ![]() ,
in agreement with recent findings (e.g. de
Wit et al. 2008).
The HR visibilities of IRC +10420 show a strong
decrease at the wavelength of the Br
,
in agreement with recent findings (e.g. de
Wit et al. 2008).
The HR visibilities of IRC +10420 show a strong
decrease at the wavelength of the Br![]() -line emission, indicating
that the region in the wind of IRC +10420 where the
Br
-line emission, indicating
that the region in the wind of IRC +10420 where the
Br![]() emission
arises is fully resolved by our observations
and considerably more extended than the continuum-emitting region. In
addition,
the HR AMBER observation of IRC +10420 revealed
non-zero differential and closure phases with absolute values up to
emission
arises is fully resolved by our observations
and considerably more extended than the continuum-emitting region. In
addition,
the HR AMBER observation of IRC +10420 revealed
non-zero differential and closure phases with absolute values up to ![]()
![]() for several spectral channels covering the central and redshifted wing
of the Br
for several spectral channels covering the central and redshifted wing
of the Br![]() -emission
line. This finding indicates that the shape of the Br
-emission
line. This finding indicates that the shape of the Br![]() line-emitting
region is not point-symmetric.
line-emitting
region is not point-symmetric.
The HR data of IRC +10420 around the Br![]() emission
line have been analyzed by simple geometrical models as well
as 1D and 2D gas radiative transfer models using the code CMFGEN. From
simple geometrical models,
we found a size of the stellar continuum-emitting region comparable to
our LR observations (
emission
line have been analyzed by simple geometrical models as well
as 1D and 2D gas radiative transfer models using the code CMFGEN. From
simple geometrical models,
we found a size of the stellar continuum-emitting region comparable to
our LR observations (
![]() mas).
Approximating the line-emitting region with an infinitely thin ring,
we found
mas).
Approximating the line-emitting region with an infinitely thin ring,
we found
![]() mas,
i.e.
mas,
i.e. ![]() .
The size of the line-emitting region is in basic agreement, although
slightly larger than the value
3.3 mas found by de
Wit
et al. (2008) from AMBER observations in
medium-spectral resolution mode
(
.
The size of the line-emitting region is in basic agreement, although
slightly larger than the value
3.3 mas found by de
Wit
et al. (2008) from AMBER observations in
medium-spectral resolution mode
(
![]() ).
The difference between the two results can
be explained by the differences in the details of the two modeling
approaches and the different spectral
resolution of the data, but probably mainly reflects the overall
calibration uncertainties.
).
The difference between the two results can
be explained by the differences in the details of the two modeling
approaches and the different spectral
resolution of the data, but probably mainly reflects the overall
calibration uncertainties.
To get a first idea of the deviation from sphericity, we
fitted an elliptical Gaussian
ring to the 3 AMBER visibility data points at the central wavelength of
the Br![]() emission.
From this fit, we
find that the Br
emission.
From this fit, we
find that the Br![]() line-emitting
region is elongated, with major and minor FWHM ring
diameters of
line-emitting
region is elongated, with major and minor FWHM ring
diameters of ![]() and
and
![]() mas,
and an elongation towards a position angle of
mas,
and an elongation towards a position angle of ![]()
![]() ,
perfectly
aligned with the elongation axis of the outer reflection seen from HST
images. Follow-up observations
with higher redundancy, a more robust calibration, and a better
position angle coverage are indispensable to confirm this result.
,
perfectly
aligned with the elongation axis of the outer reflection seen from HST
images. Follow-up observations
with higher redundancy, a more robust calibration, and a better
position angle coverage are indispensable to confirm this result.
Apart from simple geometrical models, we also analyzed the
AMBER HR data of IRC +10420 around the Br![]() emission
line
by comparison with 1D and 2D gas radiative transfer models obtained
with the code CMFGEN. We found that spherical models definitely fail to
reproduce the observed blueshift of the Br
emission
line
by comparison with 1D and 2D gas radiative transfer models obtained
with the code CMFGEN. We found that spherical models definitely fail to
reproduce the observed blueshift of the Br![]() emission
while they can well reproduce the amount of line emission. Spherical
wind models also fail to reproduce, at the same time, the amount of
line emission and the wavelength dependence of the visibility across
the emission line and, hence, the extension of the Br
emission
while they can well reproduce the amount of line emission. Spherical
wind models also fail to reproduce, at the same time, the amount of
line emission and the wavelength dependence of the visibility across
the emission line and, hence, the extension of the Br![]() line-emitting
region.
On the other hand, we found that 2D models with a prolate wind
structure can simultaneously reproduce the amount of Br
line-emitting
region.
On the other hand, we found that 2D models with a prolate wind
structure can simultaneously reproduce the amount of Br![]() emission,
the wavelength dependence of the visibility across the line and, in
addition, the observed blueshift of the Br
emission,
the wavelength dependence of the visibility across the line and, in
addition, the observed blueshift of the Br![]() emission, but only if a
substantial fraction of the redshifted Br
emission, but only if a
substantial fraction of the redshifted Br![]() emission is blocked. A model
without any diminishing of the redshifted emission cannot explain the
blueshift of the emission while simultaneously
reproducing the amount of line emission and the spatial extension of
the line-emitting region. In our best-fitting model, the outflow
exhibits a strong density enhancement towards the poles with a
pole-to-equator density ratio of 16, and the outflow is oriented
towards a PA of 60
emission is blocked. A model
without any diminishing of the redshifted emission cannot explain the
blueshift of the emission while simultaneously
reproducing the amount of line emission and the spatial extension of
the line-emitting region. In our best-fitting model, the outflow
exhibits a strong density enhancement towards the poles with a
pole-to-equator density ratio of 16, and the outflow is oriented
towards a PA of 60![]() and inclined by 45
and inclined by 45![]() .
Since the uncertainty of the position angle of the best-fitting model
is approximately 20
.
Since the uncertainty of the position angle of the best-fitting model
is approximately 20![]() ,
we find that the
orientation of the symmetry axis of our radiative transfer model is in
rough agreement with the orientation
of the elongation derived from our simple elliptical ring model (
,
we find that the
orientation of the symmetry axis of our radiative transfer model is in
rough agreement with the orientation
of the elongation derived from our simple elliptical ring model (
![]() ,
see Sect. 3.3.2).
Nevertheless, it should be noted that both results might be biased
towards the derived values due to the sparse position angle coverage of
our measurements.
,
see Sect. 3.3.2).
Nevertheless, it should be noted that both results might be biased
towards the derived values due to the sparse position angle coverage of
our measurements.
Interestingly, our best-fitting model gives a temperature of
1500 K at a radial distance of 100 mas from the
central star, assuming a distance of 5 kpc for direct
comparison with the Blöcker
et al. (1999) results. In their best model, based on
speckle-interferometric observations from 1998,
the inner dust shell boundary with a dust temperature of
1000 K is located at a radial distance of ![]() 70 mas.
Thus, our gas-radiative transfer model nicely fits the previously
developed dust-shell model, especially if
we believe that we indeed see an outward shift of the inner dust shell
boundary which is driven by the noticeable
increase of the stellar effective temperature within the last decades.
70 mas.
Thus, our gas-radiative transfer model nicely fits the previously
developed dust-shell model, especially if
we believe that we indeed see an outward shift of the inner dust shell
boundary which is driven by the noticeable
increase of the stellar effective temperature within the last decades.
The signature of the differential- and closure-phase signal of
IRC +10420 detected with AMBER is totally different
from what would be expected, for instance, for a rotating circumstellar
disk (e.g. Meilland
et al.
2007). On the other hand, we find that the wavelength
dependence of both differential and closure phases shows some
qualitative similarities to measurements obtained for the Luminous Blue
Variable ![]() Carinae
(Weigelt
et al. 2007).
In the interpretation of
the
Carinae
(Weigelt
et al. 2007).
In the interpretation of
the ![]() Car
AMBER data, the phase signature was associated with enhanced mass loss
of the rapidly
rotating, massive primary star in polar direction, and the observer is
basically looking towards the blueshifted part of the outflow. The
qualitative similiarty of the phase signals between
IRC +10420 and Br
Car
AMBER data, the phase signature was associated with enhanced mass loss
of the rapidly
rotating, massive primary star in polar direction, and the observer is
basically looking towards the blueshifted part of the outflow. The
qualitative similiarty of the phase signals between
IRC +10420 and Br![]() motivates the assumption that
also in the case of IRC +10420 rapid rotation drives
a non-spherical and polar enhanced mass loss as inferred from
theoretical considerations (e.g. Owocki
et al. 1998). This would be in line with the fact
that IRC +10420 is a massive star in a highly
evolved evolutionary stage and would also qualitatively fit to the
observed blueshift of the Br
motivates the assumption that
also in the case of IRC +10420 rapid rotation drives
a non-spherical and polar enhanced mass loss as inferred from
theoretical considerations (e.g. Owocki
et al. 1998). This would be in line with the fact
that IRC +10420 is a massive star in a highly
evolved evolutionary stage and would also qualitatively fit to the
observed blueshift of the Br![]() line.
However, the major difference between the differential and closure
phases of
line.
However, the major difference between the differential and closure
phases of ![]() Car
and IRC +10420 is that
in IRC +10420 the phase signal in stronger in the
redshifted wing of the Br
Car
and IRC +10420 is that
in IRC +10420 the phase signal in stronger in the
redshifted wing of the Br![]() emission
and not in the blueshifted wing as
in the case of
emission
and not in the blueshifted wing as
in the case of ![]() Car.
This makes the modeling of the IRC +10420 data more
puzzling and probably indicates that the
complexity of the overall structure of the innermost wind region
IRC +10420 goes well beyond the capabilities
of a 2D modeling as carried out in this paper.
Car.
This makes the modeling of the IRC +10420 data more
puzzling and probably indicates that the
complexity of the overall structure of the innermost wind region
IRC +10420 goes well beyond the capabilities
of a 2D modeling as carried out in this paper.
Nevertheless, our modeling indicates that a substantial fraction of the redshifted line emission does not reach the observer. Since our modeling is restricted to an axisymmetric outflow geometry, the fact that we were not able to reproduce all AMBER observables simultaneously (in particular the phases) might indicate the following:
- The mass outflow from IRC +10420 is
indeed intrinsically highly asymmetric. In this case, one of the
hemispheres (which is pointing towards us and, thus, emitting
blueshifted Br
 )
has a much higher mass-loss rate than the other hemisphere (responsible
for the redshifted light). We can only speculate on the reason for such
a strong asymmetry in the outflow but, in principle, such asymmetries
could be connected to large-scale asymmetries in the surface structure
of the central star (e.g., hot spots) which lead to preferred
directions of mass ejection (Humphreys
et al. 2002). In this context, it is interesting to
note that recent CO measurements (Dinh-V.-Trung
et al. 2009; Castro-Carrizo
et al. 2007)
detected a flux deficit in the CO shells in the south-western
direction. Thus, IRC +10420 seems to exhibit an
asymmetry in the same direction as found in our study also on much
larger spatial scales, indicating that this asymmetry
might be of a long-term nature.
)
has a much higher mass-loss rate than the other hemisphere (responsible
for the redshifted light). We can only speculate on the reason for such
a strong asymmetry in the outflow but, in principle, such asymmetries
could be connected to large-scale asymmetries in the surface structure
of the central star (e.g., hot spots) which lead to preferred
directions of mass ejection (Humphreys
et al. 2002). In this context, it is interesting to
note that recent CO measurements (Dinh-V.-Trung
et al. 2009; Castro-Carrizo
et al. 2007)
detected a flux deficit in the CO shells in the south-western
direction. Thus, IRC +10420 seems to exhibit an
asymmetry in the same direction as found in our study also on much
larger spatial scales, indicating that this asymmetry
might be of a long-term nature. 
- The wind of IRC +10420 is axisymmetric,
but the redshifted light is blocked by an optically-thick disk which
would also explain the strong phase signal in the redshifted part of
the Br
 emission.
Interestingly, such a disk has to be located very close to the star (
emission.
Interestingly, such a disk has to be located very close to the star ( 5 mas)
in order to block the Br
5 mas)
in order to block the Br emission,
and would have to be formed of mainly neutral+molecular gas in order to
effectively absorb the redshifted light, since the presumed dust
sublimation radius is located much farther out, at scales of
emission,
and would have to be formed of mainly neutral+molecular gas in order to
effectively absorb the redshifted light, since the presumed dust
sublimation radius is located much farther out, at scales of  100 mas.
An yet undetected binary companion could also cause the presence of an
equatorial disk.
100 mas.
An yet undetected binary companion could also cause the presence of an
equatorial disk. 
- IRC +10420 exhibits an inflow rather than an outflow, or maybe matter infall and outflow are present at the same time (Humphreys et al. 2002), for example in terms of an equatorial infall and a polar outflow. Such an equatorial infall could lead to the formation of an optically thick disk.
The study presented here has illustrated AMBER's great potential to probe the innermost circumstellar gas environment of evolved stars with spectral resolutions up to 12 000. New observations of IRC +10420 covering more baselines and position angles, which are foreseen for forthcoming observing periods, will undoubtably provide a much clearer picture of the geometry of IRC +10420's inner wind zone. For instance, new observations will help to support or disprove the model according to which IRC +10420 is exhibiting a prolate wind structure with a substantial shielding of the redshifted emission. Thus, further AMBER observations probing the inner wind zone of IRC +10420 will help to answer long-standing questions on the physical conditions and the mass-loss processes of this outstanding, rapidly evolving object and shed more light on the question of the mass-loss conditions in highly evolved massive stars.
AcknowledgementsWe thank the ESO VLTI team on Paranal and in Garching for carrying out the AMBER observations presented in this paper. The data presented here were reduced using the publicly available data reduction software package amdlib kindly provided by the Jean-Marie Mariotti Center (http://www.jmmc.fr/data_processing_amber.htm). We warmly thank John Hillier and Joe Busche for making CMFGEN and the Busche & Hillier (2005) codes available, and for continuous support with the codes. The high spectral resolution telluric spectra used in this work for spectral calibration of the AMBER data were created from data that was kindly made available by the NSO/Kitt Peak Observatory. Finally, we thank the anonymous referee for valuable comments which helped to considerably improve the manuscript.
References
- Blöcker, T., Balega, Y., Hofmann, K.-H., et al. 1999, A&A, 348, 805 [NASA ADS]
- Bowers, P. F. 1984, ApJ, 279, 350 [CrossRef] [NASA ADS]
- Bowers, P. F., & Knapp, G. R. 1989, ApJ, 347, 325 [CrossRef] [NASA ADS]
- Busche, J. R., & Hillier, D. J. 2005, AJ, 129, 454 [CrossRef] [NASA ADS]
- Castro-Carrizo, A., Lucas, R., Bujarrabal, V., Colomer, F., & Alcolea, J. 2001, A&A, 368, L34 [EDP Sciences] [CrossRef] [NASA ADS]
- Castro-Carrizo, A., Quintana-Lacaci, G., Bujarrabal, V., Neri, R., & Alcolea, J. 2007, A&A, 465, 457 [EDP Sciences] [CrossRef] [NASA ADS]
- Catala, C., Kunasz, P. B., & Praderie, F. 1984, A&A, 134, 402 [NASA ADS]
- Christou, J. C., Ridgway, S. T., Buscher, D. F., Haniff, C. A., & McCarthy, Jr., D. W. 1990, in Astrophysics with Infrared Arrays, ed. R. Elston, ASP Conf. Ser., 14, 133
- Clark, J. S., Larionov, V. M., & Arkharov, A. 2005, A&A, 435, 239 [EDP Sciences] [CrossRef] [NASA ADS]
- Cobb, M. L. & Fix, J. D. 1987, ApJ, 315, 325 [CrossRef] [NASA ADS]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources. (The IRSA 2MASS All-Sky Point Source Catalog, NASA/IPAC Infrared Science Archive. http://irsa.ipac.caltech.edu/applications/Gator/)
- Davies, B., Oudmaijer, R. D., & Sahu, K. C. 2007, ApJ, 671, 2059 [CrossRef] [NASA ADS]
- de Wit, W. J., Oudmaijer, R. D., Groenewegen, M. A. T., Hoare, M. G., & Malbet, F. 2008, A&A, 480, 149 [EDP Sciences] [CrossRef] [NASA ADS]
- Diamond, P. J., Norris, R. P., & Booth, R. S. 1983, A&A, 124, L4 [NASA ADS]
- Dinh-V.-Trung, Muller, S., Lim, J., Kwok, S., & Muthu, C. 2009, ApJ, 697, 409 [CrossRef] [NASA ADS]
- Dyck, H. M., Zuckerman, B., Leinert, C., & Beckwith, S. 1984, ApJ, 287, 801 [CrossRef] [NASA ADS]
- Fix, J. D. & Cobb, M. L. 1987, ApJ, 312, 290 [CrossRef] [NASA ADS]
- Gai, M., Corcione, L., Lattanzi, M. G., et al. 2003, Mem. Soc. Astron. It., 74, 472 [NASA ADS]
- Giguere, P. T., Woolf, N. J., & Webber, J. C. 1976, ApJ, 207, L195 [CrossRef] [NASA ADS]
- Gitton, P. B., Leveque, S. A., Avila, G., & Phan Duc, T. 2004, in SPIE Conf. Ser. 5491, ed. W. A. Traub, 944
- Groh, J. H., Hillier, D. J., & Damineli, A. 2006, ApJ, 638, L33 [CrossRef] [NASA ADS]
- Groh, J. H., Oliveira, A. S., & Steiner, J. E. 2008, A&A, 485, 245 [EDP Sciences] [CrossRef] [NASA ADS]
- Hillier, D. J. 1987, ApJS, 63, 947 [CrossRef] [NASA ADS]
- Hillier, D. J. 1989, ApJ, 347, 392 [CrossRef] [NASA ADS]
- Hillier, D. J. 1991, A&A, 247, 455 [NASA ADS]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [CrossRef] [NASA ADS]
- Hrivnak, B. J., Kwok, S., & Volk, K. M. 1989, ApJ, 346, 265 [CrossRef] [NASA ADS]
- Humphreys, R. M., Strecker, D. W., Murdock, T. L., & Low, F. J. 1973, ApJ, 179, L49 [CrossRef] [NASA ADS]
- Humphreys, R. M., Smith, N., Davidson, K., et al. 1997, AJ, 114, 2778 [CrossRef] [NASA ADS]
- Humphreys, R. M., Davidson, K., & Smith, N. 2002, AJ, 124, 1026 [CrossRef] [NASA ADS]
- Ivezic, Z., & Elitzur, M. 1997, MNRAS, 287, 799 [NASA ADS]
- Jones, T. J., Humphreys, R. M., Gehrz, R. D., et al. 1993, ApJ, 411, 323 [CrossRef] [NASA ADS]
- Kastner, J. H., & Weintraub, D. A. 1995, ApJ, 452, 833 [CrossRef] [NASA ADS]
- Klochkova, V. G., Chentsov, E. L., & Panchuk, V. E. 1997, MNRAS, 292, 19 [NASA ADS]
- Klochkova, V. G., Yushkin, M. V., Chentsov, E. L., & Panchuk, V. E. 2002, Astronomy Reports, 46, 139 [CrossRef] [NASA ADS]
- Knapp, G. R., & Morris, M. 1985, ApJ, 292, 640 [CrossRef] [NASA ADS]
- Le Bouquin, J.-B., Bauvir, B., Haguenauer, P., et al. 2008, A&A, 481, 553 [EDP Sciences] [CrossRef] [NASA ADS]
- Lipman, E. A., Hale, D. D. S., Monnier, J. D., et al. 2000, ApJ, 532, 467 [CrossRef] [NASA ADS]
- McLaren, R. A., & Betz, A. L. 1980, ApJ, 240, L159 [CrossRef] [NASA ADS]
- Meilland, A., Millour, F., Stee, P., et al. 2007, A&A, 464, 73 [EDP Sciences] [CrossRef] [NASA ADS]
- Menten, K. M., & Alcolea, J. 1995, ApJ, 448, 416 [CrossRef] [NASA ADS]
- Monnier, J. D., Millan-Gabet, R., Tuthill, P. G., et al. 2004, ApJ, 605, 436 [CrossRef] [NASA ADS]
- Mutel, R. L., Fix, J. D., Benson, J. M., & Webber, J. C. 1979, ApJ, 228, 771 [CrossRef] [NASA ADS]
- Nedoluha, G. E., & Bowers, P. F. 1992, ApJ, 392, 249 [CrossRef] [NASA ADS]
- Nenkova, M., Ivezic, Z., & Elitzur, M. 1999, LPI Contributions, 969, 20 [NASA ADS]
- Nenkova, M., Ivezic, Z., & Elitzur, M. 2000, Thermal Emission Spectroscopy and Analysis of Dust, Disks, and Regoliths, 196, 77
- Oudmaijer, R. D. 1998, A&AS, 129, 541 [EDP Sciences] [CrossRef] [NASA ADS]
- Oudmaijer, R. D., Geballe, T. R., Waters, L. B. F. M., & Sahu, K. C. 1994, A&A, 281, L33 [NASA ADS]
- Oudmaijer, R. D., Groenewegen, M. A. T., Matthews, H. E., Blommaert, J. A. D. L., & Sahu, K. C. 1996, MNRAS, 280, 1062 [NASA ADS]
- Owocki, S. P., Cranmer, S. R., & Gayley, K. G. 1998, Ap&SS, 260, 149 [CrossRef] [NASA ADS]
- Patel, M., Oudmaijer, R. D., Vink, J. S., et al. 2008, MNRAS, 385, 967 [CrossRef] [NASA ADS]
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [EDP Sciences] [CrossRef] [NASA ADS]
- Quintana-Lacaci, G., Bujarrabal, V., Castro-Carrizo, A., & Alcolea, J. 2007, A&A, 471, 551 [EDP Sciences] [CrossRef] [NASA ADS]
- Reid, M. J., Moran, J. M., Leach, R. W., et al. 1979, ApJ, 227, L89 [CrossRef] [NASA ADS]
- Richichi, A., Percheron, I., & Khristoforova, M. 2005, A&A, 431, 773 [EDP Sciences] [CrossRef] [NASA ADS]
- Ridgway, S. T., Joyce, R. R., Connors, D., Pipher, J. L., & Dainty, C. 1986, ApJ, 302, 662 [CrossRef] [NASA ADS]
- Robbe-Dubois, S., Lagarde, S., Petrov, R. G., et al. 2007, A&A, 464, 13 [EDP Sciences] [CrossRef] [NASA ADS]
- Sudol, J. J., Dyck, H. M., Stencel, R. E., Klebe, D. I., & Creech-Eakman, M. J. 1999, AJ, 117, 1609 [CrossRef] [NASA ADS]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [EDP Sciences] [CrossRef] [NASA ADS]
- Trammell, S. R., Dinerstein, H. L., & Goodrich, R. W. 1994, AJ, 108, 984 [CrossRef] [NASA ADS]
- Traub, W. A. 1998, in SPIE Conf. Ser. 3350, ed. R. D. Reasenberg, 848
- Weigelt, G., Kraus, S., Driebe, T., et al. 2007, A&A, 464, 87 [EDP Sciences] [CrossRef] [NASA ADS]
- Wittkowski, M., Boboltz, D. A., Driebe, T., et al. 2008, A&A, 479, L21 [EDP Sciences] [CrossRef] [NASA ADS]
- Zsargó, J., Hillier, D. J., & Georgiev, L. N. 2008, A&A, 478, 543 [EDP Sciences] [CrossRef] [NASA ADS]
Footnotes
- ... mode
![[*]](/icons/foot_motif.png)
- The low-spectral resolution data have been obtained as part of the Guaranteed Time Programme for VLTI/AMBER (program ID: 079.D-0356(B)), while the high-spectral resolution data were obtained in the context of science verification observations (program ID: 60.A-9053(D)).
- ... amdlib
![[*]](/icons/foot_motif.png)
- This software package is kindly provided by the Jean-Marie Mariotti Center and publicly available from http://www.jmmc.fr/data_processing_amber.htm
- ... Observatory
![[*]](/icons/foot_motif.png)
- The spectra are retrievable from http://www.eso.org/sci/facilities/paranal/instruments/isaac/tools/spectroscopic_standards.html#Telluric
- ...
data
![[*]](/icons/foot_motif.png)
- Apart from the information provided by ESO with the raw data itself, the ambient weather conditions during an observation can be looked up at http://archive.eso.org/asm/ambient-server
All Tables
Table 1: Summary of the AMBER low-spectral resolution observations of IRC+10420 and the calibrator star HD 190327.
Table 2: Summary of the AMBER observations of IRC+10420 and the calibrator star HD 232078 in high-spectral resolution mode from Oct 14, 2008 using the UT telescope configuration UT1-UT2-UT4.
Table 3: Physical parameters of the CMFGEN models for IRC +10420 .
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.