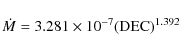| Issue |
A&A
Volume 506, Number 3, November II 2009
|
|
|---|---|---|
| Page(s) | 1277 - 1296 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912678 | |
| Published online | 27 August 2009 | |
A&A 506, 1277-1296 (2009)
Luminosities and mass-loss rates of SMC
and LMC AGB stars and red supergiants![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
M. A. T. Groenewegen1 - G. C. Sloan2 - I. Soszynski3 - E. A. Petersen4,5
1 - Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussels,
Belgium
2 - Cornell University, Astronomy Department, Ithaca, NY 14853-6801,
USA
3 - Warsaw University Observatory, Al. Ujazdowskie 4, 00-478 Warszawa,
Poland
4 - University of Nebraska, Department of Physics and Astronomy,
Lincoln, NE 68588,
USA
5 - NSF REU Research Assistant, Cornell University, Astronomy
Department, Ithaca, NY 14853-6801, USA
Received 11 June 2009 / Accepted 20 August 2009
Abstract
Context. Mass loss is one of the fundamental
properties of Asymptotic Giant Branch (AGB) stars, and through the
enrichment of the interstellar medium, AGB stars are key players in the
life cycle of dust and gas in the universe. However, a quantitative
understanding of the mass-loss process is still largely lacking,
particularly its dependence on metallicity.
Aims. To investigate the relation between mass loss,
luminosity and pulsation period for a large sample of evolved stars in
the Small and Large Magellanic Cloud.
Methods. Dust radiative transfer models are
presented for 101 carbon stars and 86 oxygen-rich evolved
stars in the Magellanic Clouds for which 5-35 ![]() m Spitzer
IRS spectra are available. The spectra are complemented with available
optical and infrared photometry to construct the spectral energy
distribution. A minimisation procedure is used to fit luminosity,
mass-loss rate and dust temperature at the inner radius. Different
effective temperatures and dust content are also considered. Periods
from the literature and from new OGLE-III data are compiled and
derived.
m Spitzer
IRS spectra are available. The spectra are complemented with available
optical and infrared photometry to construct the spectral energy
distribution. A minimisation procedure is used to fit luminosity,
mass-loss rate and dust temperature at the inner radius. Different
effective temperatures and dust content are also considered. Periods
from the literature and from new OGLE-III data are compiled and
derived.
Results. We derive (dust) mass-loss rates and
luminosities for the entire sample. Based on luminosities, periods and
amplitudes and colours, the O-rich stars are classified as foreground
objects, AGB stars and Red Super Giants. For the O-rich stars silicates
based on laboratory optical constants are compared to ``astronomical
silicates''. Overall, the grain type by Volk & Kwok
(1988, ApJ, 331, 435) fits the data best. However, the fit
based on laboratory optical constants for the grains can be improved by
abandoning the small-particle limit. The influence of grain size,
core-mantle grains and porosity are explored. A computationally
convenient method that seems to describe the observed properties in the
10 ![]() m
window are a distribution of hollow spheres with a large vacuum
fraction (typically 70%), and grain size of about 1
m
window are a distribution of hollow spheres with a large vacuum
fraction (typically 70%), and grain size of about 1 ![]() m.
m.
Relations between mass-loss rates and luminosity and pulsation period are presented and compared to the predictions of evolutionary models, those by Vassiliadis & Wood (1993, ApJ, 413, 641) and their adopted mass-loss recipe, and those based on a Reimers mass-loss law with a scaling of a factor of five. The Vassiliadis & Wood models describe the data better, although there are also some deficiencies, in particular to the maximum adopted mass-loss rate. The derived mass-loss rates are compared to predictions by dynamical wind models and appear consistent with them at a level of a factor 2-4. A better understanding requires the determination of the expansion velocity from future observations from ALMA.
The OGLE-III data reveal an O-rich star in the SMC with a
period of 1749 days. Its absolute magnitude of
![]() makes it a good candidate for a super-AGB star.
makes it a good candidate for a super-AGB star.
Key words: stars: AGB and post-AGB - stars: mass loss - Magellanic Clouds
1 Introduction
Almost all stars with initial masses in the range ![]() 0.9-8
0.9-8 ![]() will pass through the asymptotic giant branch (AGB) phase, which is
the last stage of active nuclear burning before they become post-AGB
stars, planetary nebulae and finally white dwarfs. Slightly more
massive stars will pass through the red supergiant (RSG) phase before
they may end as supernovae.
In both cases, mass-loss dominates the final evolutionary stages of the
star.
will pass through the asymptotic giant branch (AGB) phase, which is
the last stage of active nuclear burning before they become post-AGB
stars, planetary nebulae and finally white dwarfs. Slightly more
massive stars will pass through the red supergiant (RSG) phase before
they may end as supernovae.
In both cases, mass-loss dominates the final evolutionary stages of the
star.
Although this is well-known and studied in detail in galactic sources with the advent of the Infrared Astronomical Satellite (IRAS) and the Infrared Space Observatory (ISO), uncertainties in distances lead to uncertainties in luminosities and mass-loss rates. Sources at known distances, as in Large and Small Magellanic Clouds (LMC and SMC), reduce this problem, and also allow one to study the effect of metallicity on the mass-loss rate.
In a previous paper, Groenewegen et al. (2007) modelled the spectral energy distribution (SED) and spectra taken with the Infrared Spectrograph (IRS; Houck et al. 2004) onboard the Spitzer Space Telescope (Werner et al. 2004) for a sample of 60 carbon (C) stars. They concluded that, assuming similar expansion velocities and dust-to-gas ratios as in Galactic stars, mass-loss rates versus luminosity or pulsation period scatter around the galactic relation for sources in both the LMC and SMC sources. In other words, there is no evidence that the mass-loss rate of C stars depends on metallicity. Recent theoretical work also suggests that lower metallicity does not necessarily imply smaller mass-loss rates for carbon stars (Mattsson et al. 2008; Wachter et al. 2008). The detection of dust forming around a C star in the Sculptor Dwarf Spheroidal galaxy (Sloan et al. 2009), with a metallicity of [Z/H] = -1.3, supports the theory observationally.
Sloan et al. (2008) compared Spitzer spectroscopy of C stars and oxygen-rich AGB stars and RSGs (hereafter referred to as M stars). They found that while the carbon stars showed little dependence of mass loss on metallicity, the amount of dust produced by M stars declined in more metal-poor environments. The aim of the present paper is to extend the analysis by considering nearly 90 M stars and enlarging the sample of C stars to over 100.
Section 2 describes the sample of AGB stars and RSG with IRS spectra, the photometry to be fitted, and the derivation of pulsation periods. Section 3 describes the radiative transfer model and the properties of the dust species considered. Section 4 presents the results in the form of tables with the fitted parameters and figures comparing the models to the SEDs and IRS spectra. Section 5 discusses the results. In particular, we attempt to separate the O-rich stars into foreground, AGB stars and RSG. We discuss the influence of different assumptions on the shape and size of the grain on the fit to the IRS spectra. We also examine how the mass-loss rate depends on luminosity and period and compare our results to evolutionary models. Section 6 summarises the findings.
Table 1: The C-star sample: identifiers and pulsation periods for the first few entries.
Table 2: The M-star sample: identifiers and pulsation periods for the first few entries.
2 The sample
Several groups have obtained Spitzer IRS
data of evolved stars in the LMC and SMC.
In this paper we consider the currently publically available data from
the following programmes: 200 (P.I. J. Houck), 3277 (P.I.
M. Egan), 3426 (P.I. J. Kastner), 3505 (P.I.
P. Wood), and 3591 (P.I. F. Kemper).
The data in these programs are described by Sloan et al. (2008, program
200), Sloan et al. (2006,
program 3277), Buchanan et al. (2006, program
3426), Zijlstra et al. (2006) and
Lagadec et al. (2007)
for program 3505, and Leisenring et al. (2008,
program 3591).
We have retrieved the spectra from these programs from the public
archive and reduced them in a uniform manner, as described by Sloan
et al. (2006,
2008). The
reader should refer to these works for
more details. Here, we outline how spectra are produced from the
IRS data. All of the spectra were taken
using the low-resolution modules on the IRS, Short-Low (SL) covering
5.2-14.3 ![]() m,
and Long-Low (LL) covering 14.2-37.0
m,
and Long-Low (LL) covering 14.2-37.0 ![]() m. The
standard low-resolution observation placed the source in two nod
positions in each spectral aperture. The spectral images were
differenced to remove background emission and cleaned to correct bad
pixels. Spectra were extracted from the images using the tools
available in SPICE, which is distributed by the Spitzer
Science Center. Spectra from the separate nods were combined
using a spike-rejection algorithm to remove features in one nod
spectrum but not the other. Spectra from the separate apertures
and modules were then combined, using multiplicative shifts to
remove discontinuities between them and finally removing extraneous
data from the ends of each spectral segment.
m. The
standard low-resolution observation placed the source in two nod
positions in each spectral aperture. The spectral images were
differenced to remove background emission and cleaned to correct bad
pixels. Spectra were extracted from the images using the tools
available in SPICE, which is distributed by the Spitzer
Science Center. Spectra from the separate nods were combined
using a spike-rejection algorithm to remove features in one nod
spectrum but not the other. Spectra from the separate apertures
and modules were then combined, using multiplicative shifts to
remove discontinuities between them and finally removing extraneous
data from the ends of each spectral segment.
The five programs considered here did not exclusively observe
AGB
stars and RSGs.
Targets were selected from these programs by examining the IRS spectra,
collecting additional photometry (see below), consulting SIMBAD and the
papers describing these programs, and considering our radiative
transfer models (see Sect. 3). Excluded
sources include those with very poor S/N IRS data,
sources where the SED and spectrum did not match at all (indicating
that
the IRS peak-up was on a source other than the intended target),
sources with a likely disk geometry (invalidating the spherically
symmetric radiative transfer model used here),
a post-AGB star (MSX SMC 029; Kraemer et al. 2006), two RCrB
stars (MSX SMC 014, MSX SMC 155; Kraemer et al. 2005),
O/Be-stars, and
objects showing PAH emission![]() .
The remaining sample includes the very interesting object WOH G 64,
even though Ohnaka et al. (2008) have
recently demonstrated with
interferometric observations that the mid-IR visibility curves and the
SED can be better modelled with a torus.
.
The remaining sample includes the very interesting object WOH G 64,
even though Ohnaka et al. (2008) have
recently demonstrated with
interferometric observations that the mid-IR visibility curves and the
SED can be better modelled with a torus.
The sample under consideration consists of 101 C-stars and 86 M-stars. Tables 1 and 2 list basic information: some common names (as listed by SIMBAD), an OGLE- III identifier when this lightcurve is analysed and shown in Fig. 3, R.A. and declination in decimal degrees, the identifier used in figures and tables below, the adopted pulsation period, the (semi-)amplitude of the adopted pulsation period in the filter where the lightcurve was obtained, i.e. OGLE I, MACHO B,R, ASAS V,I, or in the K-band (Only the first entries are shown for guidance; both tables are available in their complete form at the CDS). The stars are listed in order of their luminosity, from brightest to faintest as determined below (and assuming these sources are in the LMC and SMC).
Many of the periods quoted in Tables 1 and 2 come from the
published literature, but in some cases publically
available data were re-analysed if the quoted period did not seem to
match the lightcurve or if published periods did not agree with each
other.
Figures 1
and 2
show our fits to publically availably
ASAS![]() (Pojmanski 2002) and
MACHO data
(Pojmanski 2002) and
MACHO data![]() .
In addition, we used unpublished data from the OGLE- III
survey
(Udalski et al. 2008),
and when available, combined this with OGLE- II
data. In these cases, Fig. 3
shows the observed data and the fitted lightcurve.
Tables 1
and 2
list the adopted
pulsation period, but many of the stars for which we (re-)analysed the
light curve show additional periods. These are listed in
Appendix A.
.
In addition, we used unpublished data from the OGLE- III
survey
(Udalski et al. 2008),
and when available, combined this with OGLE- II
data. In these cases, Fig. 3
shows the observed data and the fitted lightcurve.
Tables 1
and 2
list the adopted
pulsation period, but many of the stars for which we (re-)analysed the
light curve show additional periods. These are listed in
Appendix A.
For all stars additional broad-band photometry ranging from
the
optical to the mid-IR was collected from the literature,
primarily using
VizieR![]() and the
NASA/IPAC Infrared Science
Archive
and the
NASA/IPAC Infrared Science
Archive![]() , using the coordinates
listed in Tables 1
and 2.
In particular, we considered
, using the coordinates
listed in Tables 1
and 2.
In particular, we considered
- In the optical: UBVI data from Zaritsky et al. (2002, 2004) for the Magellanic Clouds (MCs). UBVR data from Massey (2002) for the MCs, BVRI data from Oestreicher et al. (1997) for RSG in the LMC, OGLE BVI data from Udalski et al. (1998), VRI data from Wood et al. (1983, hereafter WBF).
- In the near-infrared: DENIS IJK data from Cioni et al. (2000) and the third data release (The DENIS consortium 2005), the all-sky JHK release of 2MASS (Skrutskie et al. 2006), and the extended mission 6x long-exposure release, JHK data from the IRSF survey (Kato et al. 2007), SAAO JHKL data from Whitelock et al. (1989, 2003), and CASPIR JHKL data specifically taken for the IRS observations (Sloan et al. 2006, 2008; Groenewegen et al. 2007), and from Wood et al. (1992), Wood (1998).
- In the mid-IR:
IRAS data from the Point Source Catalog, and the
Faint Source Catalog (Moshir et al. 1989),
IRAC 3.6,4.5,5.8,8.0 and MIPS 24
 m data from the SAGE catalog
(Meixner et al. 2006,
first epoch data) and S3MC catalog (Bolatto
et al. 2007).
m data from the SAGE catalog
(Meixner et al. 2006,
first epoch data) and S3MC catalog (Bolatto
et al. 2007).
The literature considered is not exhaustive but does include all recent survey data available in the near- and mid-IR, where these stars emit most of their energy.
| Figure 1: Sample lightcurves and fits to ASAS data. The identifier used in the present paper and the ASAS identifier are listed on top of the plot. The complete figure is available in the electronic edition. Julian Date plotted is JD-2 450 000. |
|
| Open with DEXTER | |
| Figure 2: Sample lightcurves and fits to MACHO data. MACHO identifiers are listed on top of the plot, and are cross-referenced in Tables 1 and 2. The complete figure is available in the electronic edition. Julian Date plotted is JD-2 400 000. |
|
| Open with DEXTER | |
| Figure 3: Sample lightcurves and fits to OGLE- III data (and OGLE- II data when available). OGLE- III identifiers are listed on top of the plot, and are cross-referenced in Tables 1 and 2. The complete figure is available in the electronic edition. Julian Date plotted is JD-2 450 000. |
|
| Open with DEXTER | |
3 The model
The models are based on the dust radiative transfer (RT) algorithm of Groenewegen (1993; also see Groenewegen 1995), which was developed to handle non-r-2 density distributions in spherically symmetric dust shells. The algorithm simultaneously solves the radiative transfer equation and the thermal balance equation for the dust.
The models for C stars begin with the stellar atmosphere
models by Loidl et al. (2001;
available for ![]() ,
2800, 3000, 3200, 3600 K), while for M stars the M0-M10 model
atmospheres of Fluks et al. (1994)
are used. These range from 3850 to 2500 K. Strictly speaking,
the models are valid for giants at solar metallicities, but we have
applied them to Magellanic supergiants and AGB stars.
MARCS models
,
2800, 3000, 3200, 3600 K), while for M stars the M0-M10 model
atmospheres of Fluks et al. (1994)
are used. These range from 3850 to 2500 K. Strictly speaking,
the models are valid for giants at solar metallicities, but we have
applied them to Magellanic supergiants and AGB stars.
MARCS models![]() are not yet available for
abundances typical of AGB stars (i.e. with non-solar C/O ratios).
are not yet available for
abundances typical of AGB stars (i.e. with non-solar C/O ratios).
Our models assume that the dust around C stars is a
combination of
amorphous carbon (AMC) and silicon carbide (SiC), with optical
constants from, respectively, Rouleau & Martin (1991; the AC1
species), ![]() -SiC
from Pégourié (1988), and
-SiC
from Pégourié (1988), and ![]() -SiC
from Borghesi
et al. (1985),
taking into account the matrix correction factors (see footnote in
Groenewegen 1995).
These choices are based on the practical fact that these two types of
dust fit actual observations. We are aware of the discussion by, e.g.,
Pitman et al. (2008)
about inadequacies in the derivation of optical constants in the
literature, and that
-SiC
from Borghesi
et al. (1985),
taking into account the matrix correction factors (see footnote in
Groenewegen 1995).
These choices are based on the practical fact that these two types of
dust fit actual observations. We are aware of the discussion by, e.g.,
Pitman et al. (2008)
about inadequacies in the derivation of optical constants in the
literature, and that ![]() -SiC
is probably the primary carrier of the 11.3
-SiC
is probably the primary carrier of the 11.3 ![]() m feature in
C stars, rather than
m feature in
C stars, rather than ![]() -SiC,
in agreement with meteoritic data (see the discussion by Speck
et al. 2009).
However, SiC features are known that clearly peak shortward of
11.3
-SiC,
in agreement with meteoritic data (see the discussion by Speck
et al. 2009).
However, SiC features are known that clearly peak shortward of
11.3 ![]() m,
and these are better
fitted with the constants of Borghesi et al. Section 5.4.1 discusses this
point further.
m,
and these are better
fitted with the constants of Borghesi et al. Section 5.4.1 discusses this
point further.
Speck et al. also proposed that graphite rather then
amorphous carbon dominates the dust, at least in the C-stars with
extreme mass-loss rates they considered. Only one set of optical
constants seems to have been published for graphite, those by Draine
& Lee (1984),
as used by e.g. Volk et al. (1992), and Speck
et al. Calculating the absorption coefficients for spherical
grains using these optical constants results in a broad shoulder ![]() 40
40 ![]() m, as is
evident already in Fig. 4b
in Draine & Lee. This is not observed in C-stars, and is the
reason why e.g. Martin & Rogers (1987) already
dismissed graphite in favour of AMC. Independently, graphite is
expected to form at temperatures as high as 1800 K. As we will show
below, when the condensation temperature is left as a free parameter it
will typically be of order 1000 K, which is consistent with the
condensation temperature of AMC.
m, as is
evident already in Fig. 4b
in Draine & Lee. This is not observed in C-stars, and is the
reason why e.g. Martin & Rogers (1987) already
dismissed graphite in favour of AMC. Independently, graphite is
expected to form at temperatures as high as 1800 K. As we will show
below, when the condensation temperature is left as a free parameter it
will typically be of order 1000 K, which is consistent with the
condensation temperature of AMC.
Many C stars show a broad feature around 30 ![]() m which is
believed
to arise from MgS dust (Goebel & Moseley 1985). Hony
et al. (2002)
showed that the absorption coefficients depend strongly on the shape of
the grains and that if MgS is the carrier, a continuous distribution
of ellipsoids (CDE) is required.
In addition they find that the temperature of the MgS grains is very
low, 100-400 K typically, and is thus unrelated to the warm dust
close to the star which is primarily responsible for the infrared
excess that we are modelling. Consequently, we exclude this wavelength
region and MgS from our initial models. IRS observations confirm that
MgS is associated with cool dust
temperatures, leading Zijlstra et al. (2006) to argue
that the MgS
condenses onto existing grain surfaces. Leisenring et al. (2008)
noted that the apparent SiC strength decreases as MgS increases, and
they suggested that the MgS coating hides the SiC emission feature.
In this scenario, our models would give only a lower limit to the
fraction of the SiC in the dust. While we do not model the MgS, the
reader should keep in mind that its presence may mask spectral
features at shorter wavelengths. Section 5.4.2 discusses the
30
m which is
believed
to arise from MgS dust (Goebel & Moseley 1985). Hony
et al. (2002)
showed that the absorption coefficients depend strongly on the shape of
the grains and that if MgS is the carrier, a continuous distribution
of ellipsoids (CDE) is required.
In addition they find that the temperature of the MgS grains is very
low, 100-400 K typically, and is thus unrelated to the warm dust
close to the star which is primarily responsible for the infrared
excess that we are modelling. Consequently, we exclude this wavelength
region and MgS from our initial models. IRS observations confirm that
MgS is associated with cool dust
temperatures, leading Zijlstra et al. (2006) to argue
that the MgS
condenses onto existing grain surfaces. Leisenring et al. (2008)
noted that the apparent SiC strength decreases as MgS increases, and
they suggested that the MgS coating hides the SiC emission feature.
In this scenario, our models would give only a lower limit to the
fraction of the SiC in the dust. While we do not model the MgS, the
reader should keep in mind that its presence may mask spectral
features at shorter wavelengths. Section 5.4.2 discusses the
30 ![]() m
feature further.
m
feature further.
For the M stars, several types of ``astronomical silicates'' are available, as well as combinations of optical constants taken from laboratory data. For ``astronomical silicates'' we used the absorption coefficients of Volk & Kwok (1988, hereafter VK, scaled down by a factor of 5 to agree with most other silicates), Draine & Lee (1984, hereafter DL), ``warm'' silicates from Suh (1999), Ossenkopf et al. (1992, hereafter OHM), David & Pegourie (1995, hereafter DP), and combinations of DP with aluminium oxide (AlOx; amorphous porous Al2O3), with optical constants from Begemann et al. (1997), as used to model the SEDs of M stars in the Galactic Bulge (Blommaert et al. 2006).
We constructed ``laboratory silicates'' using mixtures of olivine (Mg0.8Fe1.2 SiO4, from Dorschner et al. 1995) and AlOx and metallic iron (Ordal et al. 1988). Harwit et al. (2001) and Kemper et al. (2002) have advocated the use of metallic iron to increase the opacity in the near-IR region, and the present models confirm this need. We used discrete combinations with 3, 4 or 5% Fe, and 0, 10, 20, 30 or 40% AlOx, with olivine accounting for the remainder.
Other dust components have been identified in the spectra of M-stars, e.g. spinel or corundum (Posch et al. 1999; Sloan et al. 1996), but these are only minor components and remain controversial (e.g., Sloan et al. 2003; Heras & Hony 2005; Depew et al. 2006). The aim of the present paper is to globally fit the SED as opposed to fitting the details of the IRS spectra of the stars.
For the dust mixtures in both C and M stars, the extinction
coefficients have been calculated in the small-particle limit, and
(
![]() )
is calculated from adding in proportion the
extinction coefficients of the individual species. In other words, the
grains are treated separately, but all have the same temperature. The
standard model does not consider core-mantle grains, and the
composition of the grains is independent of distance to the star. See
Sect. 5.3
for further discussion.
)
is calculated from adding in proportion the
extinction coefficients of the individual species. In other words, the
grains are treated separately, but all have the same temperature. The
standard model does not consider core-mantle grains, and the
composition of the grains is independent of distance to the star. See
Sect. 5.3
for further discussion.
Distances of 50 kpc to the LMC and 61 kpc to the SMC
are adopted.
The models have been corrected for a typical
![]() for all stars. The exact value is of little importance as this
corresponds to
for all stars. The exact value is of little importance as this
corresponds to ![]() 0.02
mag of reddening in the near-IR.
For all stars an expansion velocity,
0.02
mag of reddening in the near-IR.
For all stars an expansion velocity,
![]() ,
of 10 km s-1 and a dust-to-gas ratio of
0.005 have been adopted.
,
of 10 km s-1 and a dust-to-gas ratio of
0.005 have been adopted.
We fitted the models to the SEDs in the following manner.
The RT model was included as a subroutine in a
minimisation code using the the MRQMIN
routine (using the
Levenberg-Marquardt method from Press et al. 1992). Parameters
that
were fitted in the minimisation process include the mass-loss rate (![]() ),
luminosity, and the dust temperature at the inner radius (
),
luminosity, and the dust temperature at the inner radius (![]() ), although
we sometimes fixed
), although
we sometimes fixed ![]() and/or
and/or ![]() .
The output of a model is an SED, and this is folded with the relevant
filter response curves to produce magnitudes to compare to the
observations (see Groenewegen 2006).
.
The output of a model is an SED, and this is folded with the relevant
filter response curves to produce magnitudes to compare to the
observations (see Groenewegen 2006).

|
Figure 4: Dust temperature at the inner radius versus mass-loss rate for C stars. Plus-signs indicate stars excluded from the fit (the solid line, Eq. (1)). |
| Open with DEXTER | |
Typically, for a fixed effective temperature the model was
minimised
for the different grain types, for both fitted and fixed ![]() .
For the grain type with the lowest
.
For the grain type with the lowest ![]() error, the model was run for different model atmospheres. This is
reasonable because the IRS spectrum largely determines the best-fitting
model atmosphere, while the
effective temperature is largely determined from the optical and
near-IR
broad-band photometry. When fixed,
error, the model was run for different model atmospheres. This is
reasonable because the IRS spectrum largely determines the best-fitting
model atmosphere, while the
effective temperature is largely determined from the optical and
near-IR
broad-band photometry. When fixed, ![]() was set at temperatures
typically expected, i.e. 900, 1000, 1100, 1200 K. For C stars
it has
been suggested (e.g. Groenewegen 1995) that
was set at temperatures
typically expected, i.e. 900, 1000, 1100, 1200 K. For C stars
it has
been suggested (e.g. Groenewegen 1995) that ![]() decreases with optical depth. This effect has been investigated by
first allowing
decreases with optical depth. This effect has been investigated by
first allowing ![]() to vary. Excluding mass-loss rates below
to vary. Excluding mass-loss rates below
![]()
![]() yr-1
where
yr-1
where ![]() and
and ![]() are not simultaneously fitted well, and stars where the fit converged
to temperatures above 1400 K or below 800 K, a linear relation
gives
are not simultaneously fitted well, and stars where the fit converged
to temperatures above 1400 K or below 800 K, a linear relation
gives
based on 82 stars, with a mean of 1030 K, see Fig. 4. In subsequent model runs,
For some C-stars it also turned out that lowering the outer
radius of
the dust shell markedly improved the fit. Groenewegen et al. (2007)
discussed two cases previously, and Sloan et al. (2009) found this
necessary for a C star in the Sculptor Dwarf. The default outer radius
(as a multiple of the inner radius) is typically of order
10 000 and is
determined by considering a dust temperature at the outer radius of 20
K. For stars where a smaller outer radius seemed necessary, new models
were run decreasing the outer radius by a factor of 3 each time until
the value of ![]() rose again. For none of the M stars a smaller
outer radius was necessary, but for a non-negligible fraction of the
C stars (20%), it was. Although not explicitly tested, the same net
effect (less flux at longer wavelengths) can be achieved by a steeper
density law than the r-2
assumed in the RT model.
rose again. For none of the M stars a smaller
outer radius was necessary, but for a non-negligible fraction of the
C stars (20%), it was. Although not explicitly tested, the same net
effect (less flux at longer wavelengths) can be achieved by a steeper
density law than the r-2
assumed in the RT model.
Table 3: Fit results of the C-star sample for the first few entries.
Table 4: Fit results of the M-star sample for the first few entries.
The quality of the fit is based on a ![]() analysis
analysis
with m the observed or predicted magnitude (for the broadband photometry) or flux (for the spectrum) with error bar
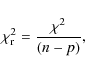
|
(3) |
with p the number of free parameters, and the quantity
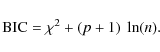
|
(4) |
This is based on the Bayesian information criterion (Schwarz 1978) and measures whether an increase in the number of free parameters and the resulting lower
In Eq. (2)
broadband data and spectral data are included in
one formalism. However it is not evident how to weigh the typically
10-40 available photometric data points with the ![]() 350 spectral data points.
For a few stars, where the fit to the SED alone already provided a
good match to the IRS spectrum both in absolute flux and spectral
shape the following experiment was done. The IRS spectrum covers the 5
to 38
350 spectral data points.
For a few stars, where the fit to the SED alone already provided a
good match to the IRS spectrum both in absolute flux and spectral
shape the following experiment was done. The IRS spectrum covers the 5
to 38 ![]() m
region, and broad-band photometry available in this region
(IRAC 5.8 and 8.0
m
region, and broad-band photometry available in this region
(IRAC 5.8 and 8.0 ![]() m,
MSX A, MIPS 24
m,
MSX A, MIPS 24 ![]() m,
and IRAS 12 and 25
m,
and IRAS 12 and 25 ![]() m
bands) has a typical resolution of order 4-6. At such a resolution,
10-13 such filters fit within the 5-37
m
bands) has a typical resolution of order 4-6. At such a resolution,
10-13 such filters fit within the 5-37 ![]() m region covered by the IRS.
In the experiment we added, effectively duplicated, 10-13 of the
available IRAC, MSX, MIPS, and IRAS, data points and calculated the
resulting reduced
m region covered by the IRS.
In the experiment we added, effectively duplicated, 10-13 of the
available IRAC, MSX, MIPS, and IRAS, data points and calculated the
resulting reduced ![]() .
Then the original photometric dataset was fitted including the IRS
spectrum, and the uncertainties of the spectral data were scaled so as
to produce the same reduced
.
Then the original photometric dataset was fitted including the IRS
spectrum, and the uncertainties of the spectral data were scaled so as
to produce the same reduced ![]() .
We
examined four stars in this manner, found the scaling factors to be
in the range 3-8, and concluded that the uncertainties of the IRS
spectral data should be scaled by a factor of 5.
.
We
examined four stars in this manner, found the scaling factors to be
in the range 3-8, and concluded that the uncertainties of the IRS
spectral data should be scaled by a factor of 5.
We masked those portions of the IRS spectra with poor S/N or
those
affected by background subtraction problems and did not include them
in the minimisation procedure. In addition, regions where strong
molecular features dominate that are not included in the simple C-star
model atmospheres are also excluded for the C stars, i.e. the regions
4.3-6.2 ![]() m
(CO + C3, see e.g. Jørgensen et al. 2000),
6.6-8.5
m
(CO + C3, see e.g. Jørgensen et al. 2000),
6.6-8.5 ![]() m
and 13.5-13.9
m
and 13.5-13.9 ![]() m
(C2H2 + HCN band, see
e.g. Matsuura et al. 2006),
and
22.0-38.0
m
(C2H2 + HCN band, see
e.g. Matsuura et al. 2006),
and
22.0-38.0 ![]() m
(the region of the MgS dust feature, which is not considered).
m
(the region of the MgS dust feature, which is not considered).
4 Results
Tables 3
and 4 lists
the parameters of the models which best fit the observed data. (Only
the first entries are
shown for guidance. Both tables are fully available at the CDS). For
the
M stars, the first line lists the best overall fit, while the second
lists the best fit with an ``astronomical silicate'' if the overall
best fit is for a ``laboratory silicate'', and vice versa.
Listed are the identifier, effective temperature or spectral type,
dust type, luminosity, mass-loss rate, whether ![]() was fitted (1)
or fixed (0),
was fitted (1)
or fixed (0), ![]() ,
whether
,
whether ![]() was fitted or fixed, outer radius (in units of inner radius), dust
optical depth in the V-band,
optical depth at 11.3
was fitted or fixed, outer radius (in units of inner radius), dust
optical depth in the V-band,
optical depth at 11.3 ![]() m
(C-stars), or the peak of the silicate
feature. (This depends on the type of silicate used, but is near 10
m
(C-stars), or the peak of the silicate
feature. (This depends on the type of silicate used, but is near 10 ![]() m)
m)
Figures 5-7 in the
electronic edition show the best fits, for the M stars again for both
``astronomical silicates'' and ``laboratory silicates''.
The top panel shows the observed SED and IRS spectrum and the fitted
model on an absolute scale, while the bottom panel shows the IRS
spectrum, scaled to a quasi-continuum point based on the average flux
in the 6.4-6.5 ![]() m
region.
m
region.
The fitting routine also provides uncertainties for the
mass-loss rate, dust temperature at the inner radius, and luminosity.
These are typically small, of order 1%. The true errors are larger, and
can be estimated from a comparison of model runs with different
parameters. They are typically 10% in luminosity, 25% in mass-loss rate
and 50 K in ![]() .
.
![\begin{figure}
\par\mbox{\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{rt_ira...
...box{8.8cm}{!}{\includegraphics[angle=-90]{rt_iras04557.ps}} }
\par
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg37.png)
|
Figure 5: Fits to the SEDs and IRS spectra of C-stars. The complete figure is available in the electronic edition. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{rt_msx...
...box{8.8cm}{!}{\includegraphics[angle=-90]{rt_w60d22Lab.ps}} }
\par
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg38.png)
|
Figure 6: Fits to the SEDs and IRS spectra of M-stars using ``laboratory silicates''. The complete figure is available in the electronic edition. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{rt_msx...
...sizebox{8.8cm}{!}{\includegraphics[angle=-90]{rt_w60d22Ast.ps}} }
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg39.png)
|
Figure 7: Fits to the SEDs and IRS spectra of M-stars using ``astronomical silicates''. The complete figure is available in the electronic edition. |
| Open with DEXTER | |
5 Discussion
5.1 Foreground objects and the division between AGB stars and supergiants
The brightest M stars in the sample have luminosities in excess of one
million solar luminosities if they are indeed in the MCs. The present
section tries to identify likely foreground (FG) objects. In addition
the separation between RSGs and (oxygen-rich) AGB stars is of interest.
WBF separated RSGs and AGB Stars based on (1) the location of a source
in a diagram plotting ![]() versus period, and (2) the
amplitude of pulsation, with AGB stars showing larger amplitudes.
Smith et al. (1995)
used a similar diagram, and they also considering
the presence or absence in the atmosphere of lithium, which indicates
that the star has experienced hot bottom burning (HBB) and is thus at
the upper end of the mass range for stars on the AGB.
versus period, and (2) the
amplitude of pulsation, with AGB stars showing larger amplitudes.
Smith et al. (1995)
used a similar diagram, and they also considering
the presence or absence in the atmosphere of lithium, which indicates
that the star has experienced hot bottom burning (HBB) and is thus at
the upper end of the mass range for stars on the AGB.
Figure 8 shows this diagram, using different symbols for different I-band amplitudes (see caption). Stars without (known) period are plotted as crosses at negative period. Amplitudes in B,V,R, and K have been multiplied by, respectively, 0.14, 0.18, 0.66, and 2.3 to estimate the amplitude in I. These ratios are based on values actually determined for the stars in our sample. Colour is another useful criterion, as it indicates the presence of circumstellar material. In the electronic edition, [3.6]-[8.0] colours are coded by different colours (see caption).
A check of the literature indicates two obvious FG objects. RS Men has a radial velocity of 140 km s-1, far lower then the 250-300 km s-1 typical of LMC objects. HD 269788 is listed as having a significant proper motion, and has a spectral type of K4 III. None of the other stars have spectral types, radial velocities, parallaxes or proper motion that would suggest a foreground nature.
HD 271832 is another likely FG object. The object is plotted at its period (514 days) which shows the largest amplitude (0.16 in V). This may not be its pulsation period but possibly related to the LSP (long secondary period) phenomenon observed in AGB stars (see e.g. Soszynski 2007, and references therein). The object also shows a period of 52.7 days with an amplitude of 0.06 mag. This period and amplitude suggest that the object is a probable early-type giant in the FG.
Early-type FG stars are expected to have essentially no
mass-loss rate
(hereafter MLR) and higher temperatures than AGB stars. HD 269788 and
HD 271832 have a fitted optical depth at 10 ![]() m of
m of ![]() 0.001, and
a [3.6]-[8.0] colour
0.001, and
a [3.6]-[8.0] colour ![]() 0.09.
Three other stars fulfill both
criteria, and are also classified as FG: W60 D29, MSX LMC 1212 and HV
11366. The last object has a period of 183 days (derived from MACHO
data), but a small amplitude. WBF reported a spectral type of MS and
a period of 366 days for HV 11366, and based on this period Sloan
et al. (2008)
assumed it was a member of the SMC. The period quoted by
WBF comes from Payne-Gaposhkin (1971).
Either the shorter period was
missed, or the star has switched from fundamental to overtone mode.
0.09.
Three other stars fulfill both
criteria, and are also classified as FG: W60 D29, MSX LMC 1212 and HV
11366. The last object has a period of 183 days (derived from MACHO
data), but a small amplitude. WBF reported a spectral type of MS and
a period of 366 days for HV 11366, and based on this period Sloan
et al. (2008)
assumed it was a member of the SMC. The period quoted by
WBF comes from Payne-Gaposhkin (1971).
Either the shorter period was
missed, or the star has switched from fundamental to overtone mode.
Buchanan et al. (2006)
identified RS Men as a FG object because
it is a Mira variable and its luminosity is not consistent with the
Mira period-luminosity relation (Feast et al. 1989) if
it were at the distance of the LMC, corroborating the FG nature
suggested by its radial velocity. Buchanan et al. also used
the PL relation to identify MSX LMC 1677 and MSX
LMC 1686 as FG Mira variables. If MSX LMC 1686 were in the LMC, its
luminosity would exceed that of a very bright RSG (![]() 1.2 million
1.2 million
![]() ).
Similarly, WOH G 17 would have have a luminosity of
600 000
).
Similarly, WOH G 17 would have have a luminosity of
600 000 ![]() ,
and thus we suspect that it is also FG.
The circumstellar reddening and the [3.6]-[8.0] colours of
MSX LMC 1686 and WOH G 17 are consistent with this suspicion.
,
and thus we suspect that it is also FG.
The circumstellar reddening and the [3.6]-[8.0] colours of
MSX LMC 1686 and WOH G 17 are consistent with this suspicion.
MSX LMC 946 is a SR with a period of 112 days. If it were in
the LMC, it would also be too bright (with ![]() 300 000
300 000 ![]() ).
We believe it also is a FG star.
).
We believe it also is a FG star.
Both WBF and Smith et al. (1995) consider
the maximum luminosity of
an AGB star to be ![]() .
This limit is based on the
maximum possible core mass of 1.4
.
This limit is based on the
maximum possible core mass of 1.4 ![]() before core He ignition and
the core-mass luminosity relation of Paczynski (1970) or Wood
&
Zarro (1981).
Other limits have also been suggested. Wagenhuber &
Groenewegen (1998)
give a limit of L
= 16 400, 31 800 and 119 000
before core He ignition and
the core-mass luminosity relation of Paczynski (1970) or Wood
&
Zarro (1981).
Other limits have also been suggested. Wagenhuber &
Groenewegen (1998)
give a limit of L
= 16 400, 31 800 and 119 000
![]() for
for
![]() ,
1.0 and 1.4
,
1.0 and 1.4 ![]() or
or ![]() ,
respectively (although none of the full evolutionary
calculations on which all of these core-mass luminosity relations are
based have actually evolved a star to the Chandrasekhar limit).
Poelarends et al. (2008)
in their recent study of super-AGB stars
examined a 9
,
respectively (although none of the full evolutionary
calculations on which all of these core-mass luminosity relations are
based have actually evolved a star to the Chandrasekhar limit).
Poelarends et al. (2008)
in their recent study of super-AGB stars
examined a 9 ![]() star. Their model had a core mass of 1.17
star. Their model had a core mass of 1.17 ![]() after the second dredge-up at the start of the first thermal
pulse, and it reached
after the second dredge-up at the start of the first thermal
pulse, and it reached ![]() (
L=
118 000
(
L=
118 000 ![]() ,
,
![]() )
at the twelfth pulse shortly after.
These limits are consistent with the bolometric magnitude of the
longest-period variable in the sample, MSX SMC 055, which
has a period of 1749 days and an I-band amplitude
of 0.81.
Among the stars in the sample, this object is the most likely candidate
for a super-AGB star.
)
at the twelfth pulse shortly after.
These limits are consistent with the bolometric magnitude of the
longest-period variable in the sample, MSX SMC 055, which
has a period of 1749 days and an I-band amplitude
of 0.81.
Among the stars in the sample, this object is the most likely candidate
for a super-AGB star.
Stars (with or without period) brighter than
![]() are
classified as RSG. All of these turn out to have amplitudes lower than
that expected for Mira variability. Therefore all stars with
amplitudes smaller than 0.45 and in between the solid and dashed line
in Fig. 8
are classified as RSG, and all remaining stars
with amplitudes larger than 0.45 are classified as AGB stars.
are
classified as RSG. All of these turn out to have amplitudes lower than
that expected for Mira variability. Therefore all stars with
amplitudes smaller than 0.45 and in between the solid and dashed line
in Fig. 8
are classified as RSG, and all remaining stars
with amplitudes larger than 0.45 are classified as AGB stars.
Four stars with a known period have uncertain classifications. MSX LMC 1318 and HV 11223 are slightly fainter than the lower limit used by WBF, but have blue colours and small amplitudes and are tentatively classified as RSGs. MSX SMC 134 has a small amplitude but reasonable red colours and is suspected to be an AGB star. Similarly, WBP 77 has an amplitude close to that of a Mira variable and is treated as an AGB star.
Of the remaining stars without period, MSX LMC 807 is fainter
than
![]() ,
has a red colour, [3.6]-[8.0] >4, and is
classified as an AGB star. The remainder are brighter than
,
has a red colour, [3.6]-[8.0] >4, and is
classified as an AGB star. The remainder are brighter than
![]() ,
have blue colours, [3.6]-[8.0] <0.1, and are
classified as RSG.
,
have blue colours, [3.6]-[8.0] <0.1, and are
classified as RSG.
We have separated RSGs and AGB stars primarily to study the mass-loss process in these two classes of objects (see Sect. 5.5). However, the conclusions drawn there are not sensitive to the uncertainties in classification described here.
The brightest C star in the sample has a luminosity of
35 000 ![]() ,
or
,
or ![]() .
The faintest has 4100
.
The faintest has 4100 ![]() ,
or
,
or ![]() .
The brightest C star in the SMC is the third
brightest overall.
The largest MLR is
.
The brightest C star in the SMC is the third
brightest overall.
The largest MLR is ![]()
![]() yr-1,
for the seventh most luminous C star.
Although generally speaking, a lower luminosity implies a smaller MLR,
there are some exceptions. The fourth smallest MLR in the sample,
yr-1,
for the seventh most luminous C star.
Although generally speaking, a lower luminosity implies a smaller MLR,
there are some exceptions. The fourth smallest MLR in the sample,
![]()
![]() yr-1,
is for CV 78, with the thirteenth highest luminosity of
16 000
yr-1,
is for CV 78, with the thirteenth highest luminosity of
16 000 ![]() .
.
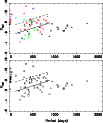
|
Figure 8: Top panel. Bolometric magnitude versus pulsation period for the M stars. Stars without period are plotted as plus signs at negative periods. The full line indicates the lower luminosity limit for RSGs by WBF, and the dashed line is 1.8 mag brighter. Top panel. I-band semi-amplitudes larger than 0.45 mag are denoted by triangles. Amplitudes between 0.2 and 0.45 by filled squares. Amplitudes smaller then 0.2 by circles. In the electronic edition, [3.6]-[8.0] colours redder than 1.2 are shown in black, between 0.5 and 1.2 in red, between 0.15 and 0.5 in green, and less than 0.15 in blue. Bottom panel. As top panel, but the objects are identified as foreground objects (open circles), RSG (filled triangles), and AGB stars (open squares) based on the discussion in Sect. 5.1. |
| Open with DEXTER | |
Figure 9
shows the Hertzsprung-Russell diagram with
evolutionary tracks of Bertelli et al. (2008),
extended to unpublished
tracks of more massive stars (Girardi, priv. comm.) for Z=
0.008. For the intermediate-mass stars the evolution is stopped at the
beginning of the AGB, which is why the tracks do not pass through the
cloud of points marking the O- and C-rich AGB stars. Most of the RSGs
are consistent with the 10-20 ![]() tracks (cf. the discussion on
the revised spectral type effective temperature calibration in
Levesque et al. 2005,
2006).
The coolest RSG is MSX LMC 891 for which we assign a spectral type of
M7 (3129 K).
tracks (cf. the discussion on
the revised spectral type effective temperature calibration in
Levesque et al. 2005,
2006).
The coolest RSG is MSX LMC 891 for which we assign a spectral type of
M7 (3129 K).
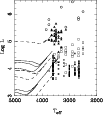
|
Figure 9:
The Hertzsprung-Russell diagram.
C-stars are plotted as filled squares, M-type AGB stars as open
squares, RSGs as filled triangles, and foreground objects as open
circles.
Lines indicate evolutionary tracks by Bertelli et al. (2008) for 20,
10, 8, 5, and 3 |
| Open with DEXTER | |
5.2 Colour-magnitude and colour-colour diagrams
Figure 10 shows two colour-magnitude diagrams based on IRAC and NIR colours. The background of stars plotted as dots are taken from a random subset of S3MC and SAGE data (and having errors in the magnitudes of less than 0.1 mag). The photometry plotted for the sample is the synthetic photometry calculated for the best fit model, and not the observed magnitudes.
Matsuura et al. (2009), Vijh et al. (2009), and others have recently published colour-magnitude diagrams with IRAC and/or NIR colours showing regions where particular types of objects can be found or overplotting stars with known spectral types. Our results agree with these previous works.

|
Figure 10: Colour-magnitude diagrams from two combinations of colours for the SMC ( left-hand panel) and LMC ( right-hand panel). Dots are stars picked randomly from the S3MC and SAGE surveys. M stars are plotted as squares (foreground objects), triangles (supergiants), and circles (AGB stars). C stars are plotted as filled circles. |
| Open with DEXTER | |
Figure 11 shows two colour-colour diagrams, in particular those that Kastner et al. (2008) indicate are effective in distinguishing M from C stars. We confirm this, in particular for the [5.8]-[8.0] vs. [8]-[24] diagram.
| Figure 11: Colour-colour diagrams for two combinations of colours for the SMC ( left-hand panel) and LMC ( right-hand panel). Dots are from the S3MC and SAGE survey. M stars are plotted as squares (foreground objects), triangles (supergiants), and circles (AGB stars). C stars are plotted as filled circles. |
|
| Open with DEXTER | |
Figure 12
shows the bolometric correction (BC) at 3.6
![]() m versus
[3.6]-[8.0] colour, and at K versus J-K
colour for
the synthetic colours (also see WBF and Whitelock et al. 2003, for BCs
involving K and other colours).
Relations like those presented here make it is possible to estimate
bolometric magnitudes with an estimated uncertainty of about 0.2 mag,
which might be sufficient for many applications. Such an estimate
could even serve as a starting point for more detailed modelling.
m versus
[3.6]-[8.0] colour, and at K versus J-K
colour for
the synthetic colours (also see WBF and Whitelock et al. 2003, for BCs
involving K and other colours).
Relations like those presented here make it is possible to estimate
bolometric magnitudes with an estimated uncertainty of about 0.2 mag,
which might be sufficient for many applications. Such an estimate
could even serve as a starting point for more detailed modelling.
5.3 Dust in the M-stars
The primary aim of the present paper is to derive luminosities and MLRs by fitting models to the broad-band data, as opposed to fitting the IRS spectra in detail. Nonetheless, some interesting remarks can and should be made.
We have considered two families of oxygen-rich dust. The first is the ``astronomical silicates''. These are derived empirically from observed spectroscopic data, generally galactic AGB stars. The second family is based on the optical constants measured in the laboratory, denoted here as ``laboratory silicates''. Figures 6 and 7 show the best fitting models determined independently for the two families.
Of the 86 M stars, the MLR is fitted in 75 objects, and in 57
of
those cases, an astronomical silicate provides the best overall fit. In
most of those cases (70%), the best fit comes from the
``astronomical silicate'' produced by Volk & Kwok (1988), which is
based on data from the Low-Resolution Spectrograph and photometry at
12, 25, 60, and 100 ![]() m
from IRAS of oxygen-rich AGB stars.
m
from IRAS of oxygen-rich AGB stars.
An inspection of Figs. 6 and 7 illustrates,
however, that the best fitting models often give a
far from perfect match to the data.
In the astronomical silicates the 18 ![]() m feature is often too weak w.r.t. the
10
m feature is often too weak w.r.t. the
10 ![]() m
feature, and broader than observed, Additionally, the 10
m
feature, and broader than observed, Additionally, the 10 ![]() m peak is
often too strong.
The laboratory silicates produce the opposite problem: the 18
m peak is
often too strong.
The laboratory silicates produce the opposite problem: the 18 ![]() m feature is
often too strong compared to the 10
m feature is
often too strong compared to the 10 ![]() m feature and peaks at too short of a wavelength.
The 10
m feature and peaks at too short of a wavelength.
The 10 ![]() m
feature peaks at slightly too short of a wavelength as well.
In the 19 cases where the laboratory silicate provided the best fit,
the model with the maximum considered value of 5% metallic iron worked
best in 17 cases. Kemper et al. (2002) used 4% in
their study of a Galactic OH/IR star. The use of metallic iron is
linked to the fact that laboratory silicates like olivine provide too
little opacity in the near-IR, a notion that goes back to the
introduction of the term ``dirty silicates'' by Jones & Merrill
(1976).
m
feature peaks at slightly too short of a wavelength as well.
In the 19 cases where the laboratory silicate provided the best fit,
the model with the maximum considered value of 5% metallic iron worked
best in 17 cases. Kemper et al. (2002) used 4% in
their study of a Galactic OH/IR star. The use of metallic iron is
linked to the fact that laboratory silicates like olivine provide too
little opacity in the near-IR, a notion that goes back to the
introduction of the term ``dirty silicates'' by Jones & Merrill
(1976).
The opacity of the laboratory silicates has been calculated for small particles and for olivine and aluminium oxide for single-sized spherical grains. (For iron we followed the procedure of Kemper et al. to use a CDE.) The opacity of the mixture was calculated by adding the absorption coefficients of the components in proportion. The true composition and shape of the dust particles is immensely more complex than adopted here. One could consider the effects of ellipsoidal grains, CDE distributions, core-mantle grains, multi-layered grains, or even fluffy aggregates. It is likely that shape and size distribution and composition will all vary with distance from the central star, and may even vary with the phase of the pulsation cycle. We will briefly address some of these effects below, by comparing different models to observations of HV 12793. This source has an SED which is very well fitted, an optically thin shell, and is best fit with a mixture of laboratory silicates with 5% iron and 95% olivine. This mixture is typical for our best-fitting laboratory silicate models.
Figure 13
shows the effect of different shapes, calculated for small particles,
that have analytical solutions for the absorption properties (see Min
et al. 2003):
CDE, continuous distribution of spheroids (CDS), and a distribution of
hollow spheres (DHS). In the last case, the optical properties are
averaged over a uniform distribution in volume fraction between 0 and
![]() of a vacuum core, where the material volume is kept constant. While CDE
and CDS models probe the effect of deviations from homogeneous
spherical grains, DHS models probe the effect of porosity. As Min
et al. showed, the simple core-mantle approach in DHS is
essentially equivalent to the general case of random vacuum inclusions
according to effective medium theory (EMT). In the models,
of a vacuum core, where the material volume is kept constant. While CDE
and CDS models probe the effect of deviations from homogeneous
spherical grains, DHS models probe the effect of porosity. As Min
et al. showed, the simple core-mantle approach in DHS is
essentially equivalent to the general case of random vacuum inclusions
according to effective medium theory (EMT). In the models, ![]() was fixed and luminosity and MLR
were fitted for grains with 3, 4 and 5% iron.
It turns out that CDE, CDS and DHS models show very similar results
(with CDS models producing the best fits, formally).
In all cases the best-fitting models have 5% iron.
Figure 13
shows the best fit with small spherical grains and with a CDS (both
with 5% iron). Using a CDS (or CDE
or DHS) improves the fit to the features at 10 and 18
was fixed and luminosity and MLR
were fitted for grains with 3, 4 and 5% iron.
It turns out that CDE, CDS and DHS models show very similar results
(with CDS models producing the best fits, formally).
In all cases the best-fitting models have 5% iron.
Figure 13
shows the best fit with small spherical grains and with a CDS (both
with 5% iron). Using a CDS (or CDE
or DHS) improves the fit to the features at 10 and 18 ![]() m.
m.
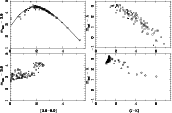
|
Figure 12:
The bolometric correction at 3.6 |
| Open with DEXTER | |
Figure 14
shows the effect of different grain size, for a DHS with
![]() = 0
(homogeneous spheres). It shows that grain size also has an effect on
the fit to the 10-18
= 0
(homogeneous spheres). It shows that grain size also has an effect on
the fit to the 10-18 ![]() m
region and that grains with a size around 1
m
region and that grains with a size around 1 ![]() m fit
reasonably well.
m fit
reasonably well.
Figure 15
shows the effect of porosity, with
![]() ,
0.7 and 0.9 for a grain size of 1.2
,
0.7 and 0.9 for a grain size of 1.2 ![]() m. Min et al. (2005, 2007) show that a
DHS with
m. Min et al. (2005, 2007) show that a
DHS with ![]() provides
a good fit to the shape of the interstellar silicate feature at
10
provides
a good fit to the shape of the interstellar silicate feature at
10 ![]() m,
while with a value of 0.4 they can reproduce the polarisation
properties of quartz measured in laboratory data. The effect of
increasing the porosity on the spectra does not appear
to be very large, mostly increasing the opacity at long wavelengths, so
the value of
m,
while with a value of 0.4 they can reproduce the polarisation
properties of quartz measured in laboratory data. The effect of
increasing the porosity on the spectra does not appear
to be very large, mostly increasing the opacity at long wavelengths, so
the value of ![]() is not well constrained from the present data.
Luminosity and MLR were minimised in all of these calculations, and
the best-fitting values do change: from
L=
118 000
is not well constrained from the present data.
Luminosity and MLR were minimised in all of these calculations, and
the best-fitting values do change: from
L=
118 000 ![]() and
and ![]()
![]()
![]() yr-1
for
yr-1
for ![]() to L=
136 000
to L=
136 000 ![]() and
and ![]()
![]()
![]() yr-1
for
yr-1
for ![]() .
.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{hv12793_org_cds_models_016_217.ps}}\par
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg62.png)
|
Figure 13: The effect of grain shape, showing the original best-fitting model with small spherical olivine grains (red dashed line) and with a CDS (green dot-dashed line), both with 5% iron. Models assuming a CDE or DHS give results nearly identical to the CDS model. |
| Open with DEXTER | |
We conclude that, compared to the small-particle limit, a
distribution of shapes shifts the peak of the 9.8 and 18 ![]() m feature to
slightly longer wavelengths, in better agreement with
observations. Assuming porous grains achieves the same effect.
When considering grains of finite size and a DHS we find for HV 12793
that a grain size of around 1
m feature to
slightly longer wavelengths, in better agreement with
observations. Assuming porous grains achieves the same effect.
When considering grains of finite size and a DHS we find for HV 12793
that a grain size of around 1 ![]() m fits the observations. This
result is typical of many of the M giants in the sample, although the
porosity is not well constrained.
m fits the observations. This
result is typical of many of the M giants in the sample, although the
porosity is not well constrained.
Höfner (2008) recently studied the winds of M giants
using a dynamical atmosphere and wind models and concluded that
radiation pressure is sufficient to drive the outflow if the
restriction of small particles is relaxed. She also showed that grain
growth naturally halts at particle sizes of about 1 ![]() m. The
present study provides observational
support to these theoretical conclusions.
m. The
present study provides observational
support to these theoretical conclusions.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{hv12793_dhs0_06_12_15_models32_29_26.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg63.png)
|
Figure 14:
The effect of grain size for homogeneous spheres (95% olivine and 5%
iron). Grain sizes are 1.5 (red dashed line), 1.2 (green dot-dashed
line) and 0.6 |
| Open with DEXTER | |
5.4 Dust in the C-stars
5.4.1 Silicon carbide
While amorphous carbon dominates the dust produced by carbon
stars (e.g. Martin & Rogers 1987), silicon
carbide (SiC) produces the most recognisable dust emission feature at ![]() 11.3
11.3 ![]() m (Treffers
& Cohen 1974,
and references
therein). The models here utilise the SiC optical constants
of Borghesi et al. (1985)
and Pégourié (1988). In reality, more complex situations
may occur than assumed in the standard model, namely the coexistence of
two grains (SiC and AMC) at the same temperature (adding the absorption
coefficients in proportion) in the small particle limit.
m (Treffers
& Cohen 1974,
and references
therein). The models here utilise the SiC optical constants
of Borghesi et al. (1985)
and Pégourié (1988). In reality, more complex situations
may occur than assumed in the standard model, namely the coexistence of
two grains (SiC and AMC) at the same temperature (adding the absorption
coefficients in proportion) in the small particle limit.
Some of the possible effects are illustrated here, using IRAS
05360-6648 as the test case.
Figure 16
compares the best fit using 8% ![]() -SiC from Borghesi
et al. (1985),
8%
-SiC from Borghesi
et al. (1985),
8% ![]() -SiC from
Pégourié (1988), and 2%
-SiC from
Pégourié (1988), and 2% ![]() -SiC
from Pitman
et al. (2008),
assuming small spherical particles. The constants from Borghesi
et al. fit the data best; the
other two are too sharply peaked compared to the observations.
-SiC
from Pitman
et al. (2008),
assuming small spherical particles. The constants from Borghesi
et al. fit the data best; the
other two are too sharply peaked compared to the observations.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{hv12793_dhs479_12_models38_50_62.ps}}\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg64.png)
|
Figure 15:
The effect of porosity using a DHS with
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_3sics.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg65.png)
|
Figure 16:
A comparison of different types of SiC assuming small spherical
particles: 8% |
| Open with DEXTER | |
Figure 17 shows the effects of the CDE and CDS approximations. Since the SiC from Pégourié (1988) peaks to the right of that of Pitman et al. (2008) this effect is enhanced when using a distribution of shapes, and the latter clearly provides the better fit. On the other hand, the shape of the feature becomes ``boxy'' which is not observed.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_models7_15_18.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg66.png)
|
Figure 17:
The effect of shape distribution: CDE with 6% |
| Open with DEXTER | |
Figure 18
shows the effect of using DHS with different values of
![]() in the case of
in the case of ![]() -SiC
from Pitman et al. (2008).
The model with
-SiC
from Pitman et al. (2008).
The model with ![]() = 0.8 fits the data reasonably well and slightly better than the CDE
and CDS approximation, but still there is a lack of emission on the
blue side of the feature.
= 0.8 fits the data reasonably well and slightly better than the CDE
and CDS approximation, but still there is a lack of emission on the
blue side of the feature.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_models20_26_22.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg67.png)
|
Figure 18:
The effect of using a DHS with
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_models32_33_37.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg68.png)
|
Figure 19:
The effect of using spherical core-mantle grains, with a SiC core of
0.01 |
| Open with DEXTER | |
Kozasa et al. (1996),
and more recently Papoular (2008),
considered grains with a core of SiC and a mantle of AMC, as an
explanation for the observed variations in the strength
of the SiC feature. Figure 19
shows the best-fitting models for grains with a 0.01 ![]() m SiC core,
and a total radius of 0.03, 0.04, 0.08
m SiC core,
and a total radius of 0.03, 0.04, 0.08 ![]() m. The figure shows that changing the volume
fraction of the SiC core from about 4 to 2 to 0.2% changes the strength
of the SiC feature from stronger than in any spectrum in the present
sample to effectively zero. In the test calculation by Papoular, the
grain reached its final size about one year after its initial
condensation, with a core volume of 12%, which would produce
a SiC feature stronger than any in the sample considered here.
Assuming an expansion velocity of 10 km s-1,
a dust particle would travel about 1 stellar radius per year in the
case of IRAS 05360-6648. The formation of the coating must therefore
proceed much more efficiently than in the test calculation of Papoular
for core-mantle grains to be a viable option for explaining the maximum
observed strength of the SiC feature. Speck et al. (2009) note only
one case where presolar SiC grains are found in the cores of carbon
grains in meteoritic samples, adding further doubt about the importance
of grains with SiC cores and AMC mantles.
m. The figure shows that changing the volume
fraction of the SiC core from about 4 to 2 to 0.2% changes the strength
of the SiC feature from stronger than in any spectrum in the present
sample to effectively zero. In the test calculation by Papoular, the
grain reached its final size about one year after its initial
condensation, with a core volume of 12%, which would produce
a SiC feature stronger than any in the sample considered here.
Assuming an expansion velocity of 10 km s-1,
a dust particle would travel about 1 stellar radius per year in the
case of IRAS 05360-6648. The formation of the coating must therefore
proceed much more efficiently than in the test calculation of Papoular
for core-mantle grains to be a viable option for explaining the maximum
observed strength of the SiC feature. Speck et al. (2009) note only
one case where presolar SiC grains are found in the cores of carbon
grains in meteoritic samples, adding further doubt about the importance
of grains with SiC cores and AMC mantles.
Lagadec et al. (2007) argue for
a SiC ![]() C condensation
sequence in Galactic C-stars and Leisenring et al. (2008, their
Fig. 13)
discuss three condensation sequences, two of which start
with SiC cores. The absence of a very strong SiC feature in any
Galactic and MC C-star predicted for a core-mantle grains with even
moderate SiC volume fraction appears to rule out condensation
sequences II and III
in Leisenring et al. (2008).
Leisenring et al. also argue that SiC and C condense
near-simultaneously. In that case a mix of condensation
sequences I (SiC on top of C) and
II could take place.
C condensation
sequence in Galactic C-stars and Leisenring et al. (2008, their
Fig. 13)
discuss three condensation sequences, two of which start
with SiC cores. The absence of a very strong SiC feature in any
Galactic and MC C-star predicted for a core-mantle grains with even
moderate SiC volume fraction appears to rule out condensation
sequences II and III
in Leisenring et al. (2008).
Leisenring et al. also argue that SiC and C condense
near-simultaneously. In that case a mix of condensation
sequences I (SiC on top of C) and
II could take place.
5.4.2 Magnesium sulfide
In their sample Leisenring et al. (2008) found 6 out of 29 (21%) C-stars in the SMC to show MgS, and 27/44 = 61% stars in the LMC (and 14/34 = 41% for Galactic sources). In our larger sample the ratio for the SMC now becomes 8/33 = 24%, and 48/68 = 71% for the LMC.
Only one of the 22 stars with
![]() show MgS. (The exception is MSX LMC 1213 with
show MgS. (The exception is MSX LMC 1213 with
![]() .)
The dust temperature at the outer radius ranges from 175 to 400 K in
these stars, suggesting that MgS forms at temperatures below 400 K,
consistent with the MgS temperatures derived by Hony et al. (2002).
.)
The dust temperature at the outer radius ranges from 175 to 400 K in
these stars, suggesting that MgS forms at temperatures below 400 K,
consistent with the MgS temperatures derived by Hony et al. (2002).
Recently, Zhukovska & Gail (2008) studied
the condensation of MgS in the outflows of C-stars using
thermo-chemical models including grain growth. They preferred a
scenario where MgS mantles grew on SiC cores.
Unfortunately, they did not consider the case of SiC+AMC+MgS.
However,
as MgS forms at the lowest temperatures, one could expect to have
grains consisting of a SiC core, an inner mantle of AMC (in spite of
the remarks in the previous section) and an outer mantle of MgS.
Alternatively, a model with pure AMC grains on the one hand and
grains with a MgS mantle on a core of SiC on the other hand are
considered below.
Some test calculations are done for such grains![]() .
Our model does not permit a gradient in grain properties within the
circumstellar dust shell; thus we cannot account for the possibility
that grains might have an outer layer of
MgS only in the outerparts of the shell.
We remind the reader that the presence of MgS may mask the SiC
strength, making our estimates of the SiC mass fraction a lower
limit in spectra showing MgS emission.
.
Our model does not permit a gradient in grain properties within the
circumstellar dust shell; thus we cannot account for the possibility
that grains might have an outer layer of
MgS only in the outerparts of the shell.
We remind the reader that the presence of MgS may mask the SiC
strength, making our estimates of the SiC mass fraction a lower
limit in spectra showing MgS emission.
Hony et al. (2002)
showed the importance of grain shape in fitting MgS to the observed
30 ![]() m
feature. They found that a CDE provided a good fit. Here we also
consider CDE, and in this respect one would not favour core-mantle
grains with MgS+SiC+AMC (see Fig. 20). The Mie-code
employed also provides the optical constant of the aggregate following
EMT, and we used this to calculate the absorption coefficients in a
CDE. As MgS is a minor species, the effect of broadening the MgS
feature as seen in the models of Hony et al. does not occur.
In this respect, AMC as one grain, with a separate core-mantle grain of
SiC+MgS fits the data better. The volume fraction of MgS in such a
grain is substantial, and using the optical constants of the aggregate
in the CDE approximation does broaden
the feature sufficiently.
m
feature. They found that a CDE provided a good fit. Here we also
consider CDE, and in this respect one would not favour core-mantle
grains with MgS+SiC+AMC (see Fig. 20). The Mie-code
employed also provides the optical constant of the aggregate following
EMT, and we used this to calculate the absorption coefficients in a
CDE. As MgS is a minor species, the effect of broadening the MgS
feature as seen in the models of Hony et al. does not occur.
In this respect, AMC as one grain, with a separate core-mantle grain of
SiC+MgS fits the data better. The volume fraction of MgS in such a
grain is substantial, and using the optical constants of the aggregate
in the CDE approximation does broaden
the feature sufficiently.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_models47_57_66.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg72.png)
|
Figure 20: Some models that include MgS. (1) Core with 2% SiC, inner mantle with 91% AMC, outer mantle with 7% MgS. CDE using the optical constants calculated using EMT (red dashed line), (2) two grain model, 90% AMC and 10% of a core-mantle grain with 45% SiC core and 55% MgS mantle (green dot-dashed line), and (3) two grain model, 94% AMC and 6% of a core-mantle grain with 3% SiC core and 97% MgS mantle, assuming CDE using the optical constants calculated using EMT (blue dotted line). |
| Open with DEXTER | |
5.5 Mass-loss and stellar evolution
This section compares the derived MLRs and other quantities by
comparing the observations with the AGB models of Vassiliadis &
Wood
(1993,
hereafter VW) and synthetic models based on recipes developed
by Wagenhuber & Groenewegen (1998,
hereafter WG), tuned to reproduce
the VW models, as explained in Appendix C of Groenewegen &
Blommaert (2005).
This last option allows us to investigate initial masses and MLRs
different from those available from the VW models alone (with a
maximum initial mass of 5 ![]() ).
From VW we take the models with Z=0.008 as
representative of the LMC, since they show qualitatively similar
behaviour. Using the WG implementation of the VW models, we have
calculated a model for 7.9
).
From VW we take the models with Z=0.008 as
representative of the LMC, since they show qualitatively similar
behaviour. Using the WG implementation of the VW models, we have
calculated a model for 7.9 ![]() ,
which is the largest mass for which the WG models converge.
In addition we have used the WG recipes to calculate models using the
Reimers law with a scaling factor of 5 (hereafter the Reimers models),
which Groenewegen & de Jong (1993)
advocated to fit many of the observables of C stars in the LMC.
The major divergence is the recipe to determine the MLR on the AGB. In
the case of the Reimers law this is
,
which is the largest mass for which the WG models converge.
In addition we have used the WG recipes to calculate models using the
Reimers law with a scaling factor of 5 (hereafter the Reimers models),
which Groenewegen & de Jong (1993)
advocated to fit many of the observables of C stars in the LMC.
The major divergence is the recipe to determine the MLR on the AGB. In
the case of the Reimers law this is ![]()
![]() ,
while in the case of VW it is basically the minimum of the single
scattering limit
,
while in the case of VW it is basically the minimum of the single
scattering limit ![]()
![]() ,
and an empirical relation between
,
and an empirical relation between
![]() and P.
The (fundamental mode) period, P, is calculated
from a period-mass-radius relation (see VW for details).
and P.
The (fundamental mode) period, P, is calculated
from a period-mass-radius relation (see VW for details).
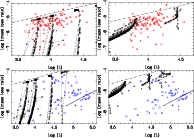
|
Figure 21:
Mass-loss rate versus luminosity for C stars ( top panel,
red colours),
M stars ( bottom panel, blue colours), VW models (
left), and Reimers models ( right).
AGB stars in the SMC are plotted as squares, in the LMC as triangles.
Objects with Mira like pulsation amplitudes are plotted with open
symbols, objects with smaller amplitudes as filled symbols.
RSG are plotted as plus-signs independent of host galaxy and pulsation
amplitude.
The VW and Reimers models are plotted as crosses connected by the
dotted line for initial masses of 1.5, 2.5, 5.0 and 7.9 |
| Open with DEXTER | |
Figure 21
shows the relation between MLR and
luminosity, with the VW and Reimers model tracks overplotted (the
crosses connected with the dotted lines). From the individual
evolutionary tracks, a model is plotted every 5000 years. The
density of points is therefore representative for the time spent at the
certain position in the diagram. It also explains the ``excursions''
which are due to the finite probability of catching a star during a
thermal pulse or during the ``luminosity dip'' that follows. Models are
plotted for initial masses of 1.5, 2.5, 5.0 and 7.9 ![]() ,
which evolve at increasing luminosity. The Reimers 1.5
,
which evolve at increasing luminosity. The Reimers 1.5 ![]() model is only identified by the few points near
model is only identified by the few points near
![]()
![]() and MLRs below 10-7
and MLRs below 10-7 ![]() yr-1.
yr-1.
Several conclusions can be drawn. From the observational point of view, the MLRs of the C stars in the sample are located in a strip with a width of about 1 dex, slightly lower than the single-scattering limit. At the lowest MLRs, the majority of stars have smaller amplitudes (filled symbols). The dot-dashed line indicates that the single-scattering limit for a velocity of 10 km s-1 which is the same velocity as adopted in the RT models. However there is an additional systematic uncertainty in the y-scale because of the adopted dust-to-gas ratio in the RT modelling.
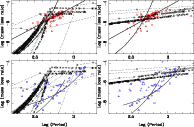
|
Figure 22: Mass-loss rate versus period for C stars ( top panel, red colours), M stars ( bottom panel, blue colours), VW models ( left), and Reimers models ( right). Symbols are as in Fig. 21. In the upper panels, the curved solid line indicates the MLR-period relation from VW, the straight solid line the relation derived for Galactic C-rich Miras by Groenewegen et al. (1998). In the bottom panel, the two lines indicate a fit to most of the M stars, and the VW relation for a period 0.6 times the pulsation period. |
| Open with DEXTER | |
The MLR distribution for the O-rich AGB stars is less clear.
One could describe two sequences, one of low MLRs
(10-7-10-6 ![]() yr-1)
for
yr-1)
for ![]() -4.7 and one
of large MLRs (
-4.7 and one
of large MLRs (
![]() -
-
![]()
![]() yr-1for
yr-1for
![]() -4.8), which is roughly
consistent with the VW models, as discussed below.
-4.8), which is roughly
consistent with the VW models, as discussed below.
The MLRs of the RSG scatter around the relation of Galactic RSG recently derived by Verhoelst et al. (2009).
The comparison to the evolutionary models is interesting, and
favours overall the mass-loss recipe adopted in VW. Taking M and C
stars together it is clear from Fig. 21 that there is
a large scatter in MLR for a given luminosity. This is clearly not
predicted by the Reimers models, where the luminosity fixes the MLR.
The VW models do predict a large variation of MLR at a
given luminosity, as observed, and consistent with other evolutionary
considerations. The majority of C stars are bound between the 1.5- and
5.0-![]() models, which indeed is the range where one believes that C-stars form
in the LMC (Groenewegen & de Jong 1993). The
lowest luminosity C-stars in the sample are located in the SMC (the
open squares) where the initial mass to become a C star is slightly
lower then in the LMC (Groenewegen 1993). The
VW models also explain that, in the 1.5-5-
models, which indeed is the range where one believes that C-stars form
in the LMC (Groenewegen & de Jong 1993). The
lowest luminosity C-stars in the sample are located in the SMC (the
open squares) where the initial mass to become a C star is slightly
lower then in the LMC (Groenewegen 1993). The
VW models also explain that, in the 1.5-5-![]() mass range, the M stars have lower MLRs than the C stars at earlier
times in their evolution.
mass range, the M stars have lower MLRs than the C stars at earlier
times in their evolution.
There are essentially no C stars brighter than
![]() ,
but
many M stars are brighter than that, and they span a large range in
MLRs. The separation near 5
,
but
many M stars are brighter than that, and they span a large range in
MLRs. The separation near 5 ![]() is thought to be due to HBB (Smith
et al. 1995).
The 7.9
is thought to be due to HBB (Smith
et al. 1995).
The 7.9 ![]() model based on the VW mass-loss recipe
nicely passes through the data.
model based on the VW mass-loss recipe
nicely passes through the data.
Although the VW models generally provide a qualitatively correct picture of mass-loss evolution along the AGB for both M and C stars, they fail on one point. If the sample under study were complete, then the distribution of observed data should match the distribution of the crosses, but this is clearly not the case. While the observations give a fairly uniform distribution of MLRs at a given luminosity for the C-stars, the VW models predict that most of the MLRs are in fact limited by the single-scattering limit. As in VW the expansion velocity is assumed to be a function of period. With a maximum of 15 km s-1, the maximum MLR in the VW is slightly lower than the dot-dashed line which represents the single-scattering limit for 10 km s-1.
One could argue that this a a selection effect and that the
present
sample is incomplete for the low MLRs and lowest luminosities, which
would predominantly be O-rich stars.
It was verified however, by comparing the cumulative absolute
magnitude distribution function of the C-stars in this sample to the
sample of about 1800 C-stars selected on colour from the entire SAGE
survey by Matsuura et al. (2009), and
using the relation in
Fig. 12
to transform colours to bolometric magnitudes, that
the present C-star sample is unbiased in absolute magnitude down to
![]() (
(
![]() ).
).

|
Figure 23: Mass-loss rate versus (estimated or measured) I-band pulsation amplitude for C stars ( top panel) and M stars ( bottom panel). C stars in the LMC are plotted as open squares, in the SMC as filled squares. O-rich AGB stars in the LMC are plotted as open circles, and in the SMC as filled circles. RSG are plotted as plus signs. |
| Open with DEXTER | |
Figure 22
shows the derived MLR plotted against pulsation period, for the C stars
and M stars, with the VW
and Reimers models overplotted. Overall, the VW models cover the area
occupied by the C stars, except in the early phases of evolution when
the stars are not yet carbon-rich.
The Reimers models do not cover the range in mass-loss of the C stars.
It is surprising that the M stars do not follow the VW relation, even
though it was derived for a sample that included O-rich Mira variables.
A relation similar to Eq. (2) of VW that fits most of the
O-rich data is
![]() .
An alternative interpretation is that the largest MLRs of the M stars
are consistent with the VW model, namely that they are on the
horizontal part of the most massive evolutionary tracks, and that the
lower MLRs are roughly consistent with a track parallel to
the VW relation for a period roughly 0.6 times the pulsation period. A
connection with overtone pulsation comes to mind although the
amplitudes of these M stars indicate Mira-like (fundamental-mode)
pulsations.
.
An alternative interpretation is that the largest MLRs of the M stars
are consistent with the VW model, namely that they are on the
horizontal part of the most massive evolutionary tracks, and that the
lower MLRs are roughly consistent with a track parallel to
the VW relation for a period roughly 0.6 times the pulsation period. A
connection with overtone pulsation comes to mind although the
amplitudes of these M stars indicate Mira-like (fundamental-mode)
pulsations.
Figure 23 plots the MLR versus the observed or estimated pulsation amplitude in the I-band. Whitelock et al. (2003) showed a similar diagram with MLR vs. the K-band. For the larger amplitudes there is a reasonably well defined and almost flat relation. Outside the regime of Mira-like pulsation there is much more scatter. For the M stars there may be a trend of larger MLRs with larger amplitudes that is steeper than for the C stars but there is even more scatter.
Figure 24 plots the MLR as a function of [3.6]-[8.0] colour. Whitelock et al. (2003) presented a similar diagram with MLR vs. [K]-[12]. Generally, redder colours are associated with larger MLR, as expected. For C stars the relation is tight, with no dependence on metallicity apparent (assuming that the expansion velocity and dust-to-gas ratio are on average the same in the LMC and SMC).
For the M stars there appear to be two relations, with both RSGs and AGB stars following the same relation up to a certain colour, with a discontinuity for stars that are associated with the final stages of evolution of the most massive intermediate stars according to the VW models (see Fig. 21). Together with the relations in Fig. 12, the [3.6]-[8.0] colour can be used to estimate luminosity and MLR.

|
Figure 24: Mass-loss rate versus colour for C-stars ( top panel), and M-stars ( bottom panel). Symbols as in Fig. 23. |
| Open with DEXTER | |

|
Figure 25: Mass-loss rate as a function of [7]-[15] color ( top panel) and DEC (dust emission contrast; bottom panel). In both panels, the solid line plots the functions given in Eqs. (5) and (6), and the dotted lines show the average uncertainty, which is formally the standard deviation of the difference between the actual data and the fitted function. The dashed line in the bottom panel separates the data excluded from the fit. Also excluded were the four points with negative DECs. Neither panel includes foreground objects. |
| Open with DEXTER | |
Sloan et al. (2008)
presented two tools to measure the amount
of dust in their sample of evolved oxygen-rich Magellanic
stars. The first, dust emission contrast (DEC) was originally
introduced by Sloan & Price (1995), and is the
ratio of the
dust emission to stellar emission from 7.67 to 14.03 ![]() m,
based on a stellar photosphere fitted to the spectrum over
the range 6.8-7.4
m,
based on a stellar photosphere fitted to the spectrum over
the range 6.8-7.4 ![]() m
m![]() . The second was the
[7]-[15] color,
integrated at 6.8-7.4 and 14.4-15.0
. The second was the
[7]-[15] color,
integrated at 6.8-7.4 and 14.4-15.0 ![]() m, wavelength ranges
chosen to avoid molecular absorption from H2O at
6.6
m, wavelength ranges
chosen to avoid molecular absorption from H2O at
6.6 ![]() m
and SiO, starting at 7.5
m
and SiO, starting at 7.5 ![]() m, and dust emission features from
silicates and alumina. Figure 25 plots the
mass-loss rates derived here with these quantities obtained
from the IRS data. The mass-loss rates follow the [7]-[15]
color closely:
m, and dust emission features from
silicates and alumina. Figure 25 plots the
mass-loss rates derived here with these quantities obtained
from the IRS data. The mass-loss rates follow the [7]-[15]
color closely:
with an average uncertainty of 0.43 dex, or 27% of the mass-loss rate. Thus, the [7]-[15] color provides an excellent means of estimating mass-loss rates from infrared spectra, provided the dust is configured in an outflowing shell as opposed to a disc.
Figure 25
also plots the mass-loss rate as a
function of DEC, and the relation is more complex than with
[7]-[15] color. The DEC was originally defined for
optically thin dust shells, and it breaks down as a useful
measure when the dust grows optically thick. Once mass-loss
rates exceed ![]() 10-5.5
10-5.5 ![]() yr-1,
the 10
yr-1,
the 10 ![]() m
silicate
emission feature will begin to self-absorb, and the DEC will
begin to decrease, even as the mass-loss rate grows. The
[7]-[15] color is thus a more robust measure. There is
still a relation between mass-loss rate and DEC, provided
certain caveats are kept in mind. Fitting the data where
the DEC is positive and the mass-loss rate is less than
10-5.5
m
silicate
emission feature will begin to self-absorb, and the DEC will
begin to decrease, even as the mass-loss rate grows. The
[7]-[15] color is thus a more robust measure. There is
still a relation between mass-loss rate and DEC, provided
certain caveats are kept in mind. Fitting the data where
the DEC is positive and the mass-loss rate is less than
10-5.5 ![]() yr-1
gives the relation
yr-1
gives the relation
with an average uncertainty of 0.45 dex, or 28% of the mass-loss rate. As Fig. 25 shows, though, the data do not fit this relation well when the DEC exceeds
One must keep in mind that these mass-loss rates assume a gas-to-dust ratio of 200, since that is the value assumed in the radiative transfer modelling. The spectroscopy really measures the dust, so it would be appropriate to scale these relations accordingly for different gas-to-dust ratios.
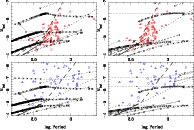
|
Figure 26:
Bolometric magnitude versus pulsation period for C-stars ( top
panel, red colours), and M-stars ( bottom panel,
blue colours), and for VW models ( left) and Reimers
models ( right).
AGB stars in the SMC are plotted as squares, in the LMC as triangles.
Objects with Mira like pulsation amplitudes are plotted with open
symbols, and filled symbols otherwise.
RSG are plotted as plus-signs independent of host galaxy and pulsation
amplitude.
For the C-star panels, the solid line indicates the PL-relation
from
Groenewegen & Whitelock (1996) and
the dotted line the extrapolation beyond
|
| Open with DEXTER | |
Figure 26 shows the bolometric PL-relation with the VW and Reimers models overplotted, together with various (extrapolated) PL-relations for C- and O-stars (Feast et al. 1989; Hughes & Wood 1990; Groenewegen & Whitelock 1996).
Most of the VW points are to the left of the data points, which can be interpreted as meaning that pulsation in the fundamental period is only reached towards the end of AGB evolution, which is consistent with the findings of Lebzelter & Wood (2005, 2007) for the clusters 47 Tuc and NGC 1846.
Figure 27
shows the data in a different light, only
plotting the large amplitude (Mira) variables, and highlighting the
knowledge regarding the presence of Lithium, an indicator of HBB (data
from Smith & Lambert 1989,
1990; Smith
et al. 1995).
It shows the
well known result that the known Li-rich stars are O-rich stars
located in the interval
![]() (see the
discussion and Fig. 6
in Smith et al. 1995).
The C-star marked as
undergoing HBB is IRAS 04496-6958 which was suggested to be in that
state by Trams et al. (1999).
At that time ISO spectra suggested a
silicate dust shell, although the central star is C-rich. They
suggested that the star had just become a C-star, after HBB had
ceased. The fact that it had the largest deviation from the
PL-relation in the sample studied by Whitelock
et al. (2003)
seemed
to support this hypothesis as this is also observed in O-rich stars.
The much higher quality IRS spectrum shows no evidence for the
presence of a silicate feature, as was originally discussed by Speck
et al. (2006),
who suggested that this apparent silicate emission is an artifact of
the underestimation of the level of the continuum emission in the ISO
spectrum. In fact, there is no evidence that this star is currently
undergoing HBB.
(see the
discussion and Fig. 6
in Smith et al. 1995).
The C-star marked as
undergoing HBB is IRAS 04496-6958 which was suggested to be in that
state by Trams et al. (1999).
At that time ISO spectra suggested a
silicate dust shell, although the central star is C-rich. They
suggested that the star had just become a C-star, after HBB had
ceased. The fact that it had the largest deviation from the
PL-relation in the sample studied by Whitelock
et al. (2003)
seemed
to support this hypothesis as this is also observed in O-rich stars.
The much higher quality IRS spectrum shows no evidence for the
presence of a silicate feature, as was originally discussed by Speck
et al. (2006),
who suggested that this apparent silicate emission is an artifact of
the underestimation of the level of the continuum emission in the ISO
spectrum. In fact, there is no evidence that this star is currently
undergoing HBB.

|
Figure 27: As Fig. 26 but without the model tracks, without supergiants, and only variables with large amplitudes are plotted. Open squares indicate stars without information on the presence of HBB, plus-signs are stars without HBB (no Lithium detected), filled squares stars which undergo HBB (or supposed to, like the C-star IRAS 04496-6958, but which probably is not, see text). |
| Open with DEXTER | |
In the Whitelock et al. sample it was the only C-star that lay significantly above the PL-relation, but one of the strengths of the present study is that it enlarges significantly the number of heavy mass-losing stars with a pulsation period. Figure 27 shows that IRAS 04496 still is the C-star that has the largest overluminosity w.r.t. classical PL-relations derived for shorter period miras, but no longer the only one. The relation proposed by Hughes & Wood (1990) seems to delineate the upper boundary of luminosities that can be reached. For periods longer than P= 450 days, where Hughes & Wood proposed a break in the PL-relation, there is enormous scatter, which is not present in the PL-relation at shorter periods (the scatter found by Groenewegen & Whitelock is 0.26 mag). This may be in part due to the fact that the luminosities in the present study are not from single-epoch photometry.
One peculiar object is MSX LMC 775, which is plotted at the
period
with the largest amplitude, 2063 days as derived from OGLE data, 2210
days as derived from MACHO red data. This is very unusual as the
periods of C-stars are confined to
![]() 1000
days (see Fig. 27;
Whitelock et al. 2003;
Kerschbaum et al. 2006;
for Galactic C-stars),
and this is consistent with the picture that HBB prevents the
formation of C-stars for large initial masses. This star could truly
be an object that has turned into a C-star after
HBB ceased. On
the other hand this star also shows a significant period of 269 days
with an amplitude of 0.46 in the I-band, also
suggestive of mira
pulsation. This would place the star in the upper left part in
Fig. 27,
also in a location not occupied by other C-stars. From the MACHO data a
third period of 549 days can be derived, which
would place it among other C-stars, but the amplitude is smaller and
unlike the pulsation of a Mira.
1000
days (see Fig. 27;
Whitelock et al. 2003;
Kerschbaum et al. 2006;
for Galactic C-stars),
and this is consistent with the picture that HBB prevents the
formation of C-stars for large initial masses. This star could truly
be an object that has turned into a C-star after
HBB ceased. On
the other hand this star also shows a significant period of 269 days
with an amplitude of 0.46 in the I-band, also
suggestive of mira
pulsation. This would place the star in the upper left part in
Fig. 27,
also in a location not occupied by other C-stars. From the MACHO data a
third period of 549 days can be derived, which
would place it among other C-stars, but the amplitude is smaller and
unlike the pulsation of a Mira.
Regarding the O-rich Miras there are a few that follow the extrapolation of the classical PL-relation derived for short-period miras, but most are overluminous. Some are known to be rich in Lithium (the filled symbols) and it would be interesting to investigate this for all objects in Fig. 27 brighter than -6.0 in bolometric magnitude (although for some this will be difficult as they are very red).
6 Summary and conclusions
Mass-loss rates for the sample are derived under the assumption of a constant expansion velocity and dust-to-gas ratio with values similar to galactic AGB stars.
Wachter et al. (2008) compute
dynamical wind models for subsolar
metallicities for carbon stars. They find that the outflow
velocities of the solar metallicity models are higher by about a
factor of 2.2 ![]() 0.2 than those of the LMC, and 4
0.2 than those of the LMC, and 4 ![]() 1
than those of the SMC. The dust-to-gas ratios are larger by factors
1
than those of the SMC. The dust-to-gas ratios are larger by factors
![]() and
and
![]() ,
respectively. For the modelling in
this paper this means that the assumption of typical velocities and
dust-to-gas ratios of galactic stars may lead to an overestimate of
the mass-loss rates by a factor of
,
respectively. For the modelling in
this paper this means that the assumption of typical velocities and
dust-to-gas ratios of galactic stars may lead to an overestimate of
the mass-loss rates by a factor of
![]() for the LMC,
and 1.7
for the LMC,
and 1.7 ![]() 0.5 for the SMC targets, respectively (since the dust
optical depth
0.5 for the SMC targets, respectively (since the dust
optical depth ![]()
![]()
![]() is fitted). From their
Eqs. (1)-(3) for default parameter
values (M= 1
is fitted). From their
Eqs. (1)-(3) for default parameter
values (M= 1 ![]() ,
,
![]() K, L=
104
K, L=
104 ![]() ), the ratio of mass-loss
rates is GAL : LMC : SMC = 1: 0.84 : 0.52.
), the ratio of mass-loss
rates is GAL : LMC : SMC = 1: 0.84 : 0.52.
Mattsson et al. (2009) computed
a grid of 900 dynamical model
atmospheres for carbon stars for solar metallicities spanning a range
in luminosity, pulsation velocity amplitude, effective temperature,
(C-O) excess and stellar mass. The online material includes output
(mass-loss rates, expansion velocities and dust-to-gas ratios) for
about 325 models. Taking only models with expansion velocities in the
range 2-45 km s-1 only 253
``plausible'' models remain. The 98%
percentile on ![]() = (
= (![]()
![]() .
Given the scaling parameters as derived by Wachter et al. one
would
expect maximum values for
.
Given the scaling parameters as derived by Wachter et al. one
would
expect maximum values for ![]() a factor of 2.6 lower in the LMC and
7.7 lower in the SMC, respectively, than in our galaxy, or about 1.1
and 0.39. From Table 3 the 98%
percentile on
a factor of 2.6 lower in the LMC and
7.7 lower in the SMC, respectively, than in our galaxy, or about 1.1
and 0.39. From Table 3 the 98%
percentile on ![]() ,
while the
largest value for an SMC C-star is 0.52. These values are consistent
with predictions.
The range in dust-to-gas ratio in the 253 models by Mattsson
et al. is (3-80)
,
while the
largest value for an SMC C-star is 0.52. These values are consistent
with predictions.
The range in dust-to-gas ratio in the 253 models by Mattsson
et al. is (3-80)
![]() ,
which encompasses the adopted value of 0.005.
,
which encompasses the adopted value of 0.005.
At the level of a factor 2-4, the predicted and observed mass-loss rates agree and confirm that there is no strong dependence of mass-loss rate on metallicity. To have a better understanding of the mass-loss process it is crucial to measure the expansion velocity and determine the gas-to-dust ratio by observing the CO thermal emission lines in the (sub-)mm. In addition it would be valuable if the C/O ratio could be determined for some stars in the sample, as the wind properties are predicted to depend on the excess of carbon over oxygen atoms.
In this last paragraph of the paper we want again to draw the
attention to
the pulsation properties of two remarkable objects (see
Sect. 5.5). The C-star MSX LMX 775, which we classified as
having a pulsation period of over 2000 days.
This is much longer than the maximum period of all known Galactic and
MC C-stars which is near 900 days. This period is located however on an
extension
of the C-star PL-relation derived for unobscured
stars. If true,
MSX LMC 775 could be a very massive star that has become a C-star after
HBB ceased.
The other remarkable object is the O-rich star MSX SMC 055 with a
period of 1749 days and at
![]() .
Its pulsation
amplitude and colour are consistent with that of a (mass-losing) Mira,
and not an RSG star. Its luminosity is consistent with that predicted
for super-AGB stars, and therefore we propose this object as the most
likely super-AGB star candidate from an observational point of view.
.
Its pulsation
amplitude and colour are consistent with that of a (mass-losing) Mira,
and not an RSG star. Its luminosity is consistent with that predicted
for super-AGB stars, and therefore we propose this object as the most
likely super-AGB star candidate from an observational point of view.
This publication is partly based on the OGLE observations obtained with the Warsaw Telescope at the Las Campanas Observatory, Chile, operated by the Carnegie Institution of Washington.
This paper utilizes public domain data originally obtained by the MACHO Project, whose work was performed under the joint auspices of the US Department of Energy, National Nuclear Security Administration by the University of California, Lawrence Livermore National Laboratory under contract No. W-7405-Eng-48, the National Science Foundation through the Center for Particle Astrophysics of the University of California under cooperative agreement AST-8809616, and the Mount Stromlo and Siding Spring Observatory, part of the Australian National University.
This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
The authors would like to thank Dr. Mikako Matsuura for making the lists of O- and C-stars discussed in Matsuura et al. (2009) available.
M.G. would like to thanks Ariane Lançon and Eric Josselin for organising the ``Intermediate Mass StarsMassive Stars, A workshop around causes and consequences of differing evolutionary paths'' meeting in Strasbourg, which was inspiring and resulted in some ideas being explored in this paper.
Appendix A: Multi-periodic AGB stars
Some of the stars for which we (re-)analysed ASAS, MACHO and OGLE data show multiple periods. Tables 1 and 2 list the (adopted) pulsation period. In the table below all derived periods are given The first period is the adopted pulsation period, then the other periods are listed. Typically only one additional period is fitted, because of the irregular behaviour. Only in exceptional cases a third period is fitted. Formal errors in the periods are also given. In the case of MACHO data, the blue channel was analysed only if the red channel data was corrupt.
There are 41 unique stars listed in the table. The second period fitted is in the range 0.4-0.6 times the primary period in 10 cases. The amplitude of the second period is in the range 0.1-1.0 times the amplitude of the primary period. These cases probably represent the situation where a pulsation mode and the next higher overtone mode are detected. When there is an LSP, it is mostly in the range 3-10 times the primary period.
Table A.1: Multi-period information.
References
- Begemann, B., Dorschner, J., Henning, Th., et al. 1997, ApJ, 476, 199 [NASA ADS] [CrossRef]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences]
- Blommaert, J. A. D. L., Groenewegen, M. A. T., Okumura, K., et al. 2006, A&A, 460, 555 [NASA ADS] [CrossRef] [EDP Sciences]
- Bolatto, A. D., Simon, J. D., Stanimirovic, S., et al. 2007, ApJ, 655, 212 [NASA ADS] [CrossRef]
- Borghesi, A., Bussoletti, E., Colangeli, L., & de Blasi, C. 1985, A&A, 153, 1 [NASA ADS]
- Buchanan, C. L., Kastner, J. H., Forrest, W. J., et al. 2006, AJ, 132, 1890 [NASA ADS] [CrossRef]
- Cioni M.-R., Loup C., Habing H. J., et al. 2000, A&AS, 144, 235 [NASA ADS] [CrossRef] [EDP Sciences]
- Cioni, M.-R. L., Blommaert, J. A. D. L., Groenewegen, M. A. T., et al. 2003, A&A, 406, 51 [NASA ADS] [CrossRef] [EDP Sciences]
- David, P., & Pégourié, B. 1995, A&A, 293, 833 [NASA ADS]
- DENIS Consortium 2005, available via ViZier
- DePew, K., Speck, A., & Dijkstra, C. 2006, ApJ, 640, 971 [NASA ADS] [CrossRef]
- Dodion, J. 2003, M.Sc. Thesis, University of Leuven
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [NASA ADS] [CrossRef]
- Feast, M. W., Glass, I. S., Whitelock, P. A., & Catchpole, R. M. 1989, MNRAS, 241, 375 [NASA ADS]
- Fluks, M. A., Plez, B., Thé, P. S., et al. 1994, A&AS, 105, 311 [NASA ADS]
- Fraser, O., Hawley, S. L, & Cook, K. 2008, AJ, 136, 1242 [NASA ADS] [CrossRef]
- Goebel, J. H., & Moseley, S. H. 1985, ApJ, 290, L35 [NASA ADS] [CrossRef]
- Groenewegen, M. A. T. 1993, Ph.D. Thesis, Chapter 5, University of Amsterdam
- Groenewegen, M. A. T. 1995, A&A, 293, 463 [NASA ADS]
- Groenewegen, M. A. T. 2004, A&A, 425, 595 [NASA ADS] [CrossRef] [EDP Sciences]
- Groenewegen, M. A. T. 2006, A&A, 448, 181 [NASA ADS] [CrossRef] [EDP Sciences]
- Groenewegen, M. A. T., & Blommaert, J. A. D. L. 2005, A&A, 443, 143 [NASA ADS] [CrossRef] [EDP Sciences]
- Groenewegen, M. A. T., & de Jong, T. 1993, A&A, 267, 410 [NASA ADS]
- Groenewegen, M. A. T., & Whitelock, P. A., 1996, MNRAS, 281, 1347 [NASA ADS]
- Groenewegen, M. A. T., Whitelock, P. A., Smith, C. H., & Kerschbaum F. 1998, MNRAS, 293, 18 [NASA ADS] [CrossRef]
- Groenewegen, M. A. T., Wood, P. R., Sloan, G. C., et al. 2007, MNRAS, 367, 313 [NASA ADS] [CrossRef]
- Harwit, M., Malfait, K., Decin, L., et al. 2001, ApJ, 557, 844 [NASA ADS] [CrossRef]
- Heras, A. M., & Hony, S. 2005, A&A, 439, 171 [NASA ADS] [CrossRef] [EDP Sciences]
- Höfner, S. 2008, A&A, 491, L1 [NASA ADS] [CrossRef] [EDP Sciences]
- Hony, S., Waters, L. B. F. M., & Tielens, A. G. G. M. 2002, A&A, 390, 533 [NASA ADS] [CrossRef] [EDP Sciences]
- Houck J. R., Roelling T. L., van Cleve J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef]
- Hughes, S. M. G. 1989, AJ, 97, 1634 [NASA ADS] [CrossRef]
- Hughes, S. M. G., & Wood, P. R. 1990, AJ,99, 784
- Izzard, R. G., Tout, C. A., Karakas, A. I., & Pols, O. R. 2004, MNRAS, 350, 407 [NASA ADS] [CrossRef]
- Jones, T. W., & Merrill, K. M. 1976, ApJ, 209, 509 [NASA ADS] [CrossRef]
- Jørgensen, U. G., Hron, J., & Loidl, R. 2000, A&A, 356, 253 [NASA ADS]
- Kastner, J. H., Thorndike, S. L., Romanczyk, P. A., et al. 2008, AJ 136, 1221
- Kato, D., Nagashima, C., Nagayama, T., et al. 2007, PASJ, 59, 615 [NASA ADS]
- Kemper, F., de Koter, A., Waters, L. B. F. M., Bouwman, J., & Tielens, A. G. G. M. 2002, A&A, 384, 585 [NASA ADS] [CrossRef] [EDP Sciences]
- Kerschbaum, F., Groenewegen, M. A. T., & Lazaro, C. 2006, A&A, 460, 539 [NASA ADS] [CrossRef] [EDP Sciences]
- Kozasa, T., Dorschner, J., Henning, T., & Stognienko, R. 1996, A&A, 307, 551 [NASA ADS]
- Kraemer, K. E., Sloan, G. C., Wood, P. R., Price, S. D. & Egan, M. P. 2005, ApJ, 631, L147 [NASA ADS] [CrossRef]
- Kraemer, K. E., Sloan, G. C., Bernard-Salas, J., et al. 2006, ApJ, 652, L25 [NASA ADS] [CrossRef]
- Lagadec, E., Zijlstra, A. A., Sloan, G. C., et al., 2007, MNRAS, 376, 1270 [NASA ADS] [CrossRef]
- Lebzelter, T., & Wood, P. R. 2005, A&A, 441, 1117 [NASA ADS] [CrossRef] [EDP Sciences]
- Lebzelter, T., & Wood, P. R. 2007, A&A, 475, 643 [NASA ADS] [CrossRef] [EDP Sciences]
- Leisenring, J. M., Kemper, F., & Sloan, G. C. 2008, ApJ, 681, 1557 [NASA ADS] [CrossRef]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, AJ, 628, 973 [NASA ADS] [CrossRef]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2006, AJ, 645, 1102 [NASA ADS] [CrossRef]
- Loidl R., Lançon A., & Jrgensen U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences]
- Lloyd Evans, T. 1985, MNRAS, 212, 955 [NASA ADS]
- Martin, P. G., & Rogers, C. 1987, ApJ, 322, 374 [NASA ADS] [CrossRef]
- Massey, P. 2002, ApJS, 141, 81 [NASA ADS] [CrossRef]
- Matsuura, M., Wood, P. R., Sloan G. C., et al., 2006, MNRAS, 371, 415 [NASA ADS] [CrossRef]
- Matsuura, M., Barlow, M. J., Zijlstra, A. A., et al. 2009, MNRAS, accepted
- Mattsson, L., Wahlin, R., Höfner, S., & Eriksson, K. 2008, A&A, 484, L5 [NASA ADS] [CrossRef] [EDP Sciences]
- Mattsson, L., Wahlin, R., & Höfner, S. 2009, A&A, submitted
- Meixner, M., Gordon, K. D., Indebetouw, R., et al. 2006, AJ, 132, 2268 [NASA ADS] [CrossRef]
- Min, M., Hovenier, J. W., & de Koter, A. 2003, A&A, 404, 35 [NASA ADS] [CrossRef] [EDP Sciences]
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [NASA ADS] [CrossRef] [EDP Sciences]
- Min, M., Waters, L. B. F. M., de Koter, A., et al. 2007, A&A, 462, 667 [NASA ADS] [CrossRef] [EDP Sciences]
- Moshir, M., Copan, G., Conrow, T., et al. 1989, The IRAS Faint Source Catalog, version 2
- Nishida, S., Tanabé, T., Nakada, Y., et al. 2000, MNRAS, 313, 136 [NASA ADS] [CrossRef]
- Oestreicher M. O., Schmidt-Kaler T., & Wargau W. 1997, MNRAS, 289, 729 [NASA ADS]
- Ohnaka, K., Driebe, T., Hofmann, K.-H., Weigelt, G., & Wittkowski, M. 2008, A&A, 484, 371 [NASA ADS] [CrossRef] [EDP Sciences]
- Ordal, M. A., Bell, R. J., Alexander, R. W., Jr., Newquist, L. A., & Querry, M. R. 1988, ApOpt, 27, 1203 [NASA ADS]
- Ossenkopf, V., Henning, Th., & Mathis, J. S. 1992, A&A, 261, 567 [NASA ADS]
- Paczynski B. 1970, AcA, 20, 47 [NASA ADS]
- Papoular, R. 2008, MNRAS, 388, 457 [NASA ADS] [CrossRef]
- Payne-Gaposchkin, C. H. 1971, Smithsonian Contr. Ap., 13, 1
- Pégourié B. 1988, A&A, 194, 335 [NASA ADS]
- Pitman, K. M., Hofmeister, A. M., Corman, A. B., & Speck, A. K. 2008, A&A, 483, 661 [NASA ADS] [CrossRef] [EDP Sciences]
- Poelarends, A. J. T., Herwig, F., Langer, N., & Heger, A. 2008, ApJ, 675, 614 [NASA ADS] [CrossRef]
- Pojmanski, G. 2002, AcA, 52,397
- Posch, T., Kerschbaum, F., Mutschke, H., et al. 1999, A&A, 352, 609 [NASA ADS]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, in Numerical Recipes in Fortran (Cambridge U. P.), 77
- Raimondo, G., Cioni, M.-R. L., Rejkuba, M., & Silva, D. R. 2005, A&A, 438, 521 [NASA ADS] [CrossRef] [EDP Sciences]
- Reid, N., Glass, I. S., & Catchpole, R. M. 1988, MNRAS, 232, 53 [NASA ADS]
- Rouleau, F., & Martin, P. G., 1991, ApJ, 377, 526 [NASA ADS] [CrossRef]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [CrossRef]
- Skrutskie M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef]
- Sloan, G. C., & Price, S. D. 1995, ApJ, 451, 758 [NASA ADS] [CrossRef]
- Sloan, G. C., LeVan, P. D., & Little-Marenin, I. R. 1996, ApJ, 463, 310 [NASA ADS] [CrossRef]
- Sloan, G. C., Kraemer, K. E., Goebel, J. H., & Price, S. D. 2003, ApJ, 594, 483 [NASA ADS] [CrossRef]
- Sloan, G. C., Kraemer, K. E., Matsuura, M. 2006, ApJ, 645, 1118 [NASA ADS] [CrossRef]
- Sloan, G. C., Kraemer, K. E., Wood, P. R., et al. 2008, ApJ, 686, 1056 [NASA ADS] [CrossRef]
- Sloan, G. C., Matsuura, M., Zijlstra, A. A., et al. 2009, Science 323, 353
- Smith, V. V., & Lambert, D. L. 1989, ApJ, 345, L75 [NASA ADS] [CrossRef]
- Smith, V. V., & Lambert, D. L. 1990, ApJ, 361, L69 [NASA ADS] [CrossRef]
- Smith, V. V., Plez, B., Lambert, D. L., & Lubowich, D. A. 1995, ApJ, 441, 735 [NASA ADS] [CrossRef]
- Soszynski, I. 2007, ApJ, 660, 1486 [NASA ADS] [CrossRef]
- Speck, A. K., Cami, J, Marwick-Kemper, C., et al. 2006, ApJ, 650, 892 [NASA ADS] [CrossRef]
- Speck, A. K., Corman, A. B., Wakeman K., Wheeler, C. H., & Thompson, G. 2009, ApJ, 691, 1202 [NASA ADS] [CrossRef]
- Suh, K.-W. 1999, MNRAS, 304, 389 [NASA ADS] [CrossRef]
- Treffers, R., & Cohen, M. 1974, ApJ, 188, 545 [NASA ADS] [CrossRef]
- Trams, N. R., van Loon, J.Th., Zijlstra, A. A., et al. 1999, A&A, 344, L17 [NASA ADS]
- Udalski, A., Szymanski, M., & Kubiak, M. 1998, AcA, 48, 147 [NASA ADS]
- Udalski, A., Szymanski, M. K., Soszynski, I., & Poleski, R. 2008, AcA 58, 69
- Vassiliadis, E, & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef]
- Verhoelst, T., Van der Zypen, N., Hony, S., et al. 2009, A&A, 498, 127 [NASA ADS] [CrossRef] [EDP Sciences]
- Vijh, U. P., Meixner, M., Babler, B., et al. 2009, AJ, 137, 3139 [NASA ADS] [CrossRef]
- Volk, K., & Kwok, S. 1988, ApJ, 331, 435 [NASA ADS] [CrossRef]
- Volk, K., Kwok, S., & Langill, P. P. 1992, ApJ, 391, 285 [NASA ADS] [CrossRef]
- Wachter, A., Winters, J. M., Schröder, K.-P., & Sedlmayr, E. 2008, A&A, 486, 497 [NASA ADS] [CrossRef] [EDP Sciences]
- Wagenhuber, J., & Groenewegen, M. A. T. 1998, A&A, 340, 183 [NASA ADS]
- Werner M. W., Roellig T. L., Low F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef]
- Whitelock, P., Menzies, J., Feast, M., et al. 1994, MNRAS, 267, 711 [NASA ADS]
- Whitelock P. A., Feast M. W., Menzies J. W., & Catchpole R. M., 1989, MNRAS, 238, 769 [NASA ADS]
- Whitelock, P. A., Feast, M. W., van Loon, J.Th., & Zijlstra, A. A. 2003, MNRAS, 342, 86 [NASA ADS] [CrossRef]
- Wood, P. R. 1998, A&A, 338, 592 [NASA ADS]
- Wood, P. R., & Zarro, D. M. 1981, ApJ, 247, 247 [NASA ADS] [CrossRef]
- Wood, P. R., Bessell, M. S., & Fox, M. W. 1983, ApJ, 272 99 (WBF)
- Wood, P. R., Whiteoak, J. B., Hughes, S. M. G., et al. 1992, ApJ, 397, 552 [NASA ADS] [CrossRef]
- Zaritsky D., Harris J., Thompson I. B., Grebel E. K., & Massey P. 2002, AJ, 123, 855 [NASA ADS] [CrossRef]
- Zaritsky D., Harris J., Thompson I. B., & Grebel E. K. 2004, AJ, 128, 1606 [NASA ADS] [CrossRef]
- Zijlstra, A. A., Matsuura, M., Wood, P. R., et al., 2006, MNRAS, 370, 1961 [NASA ADS]
- Zhukovska, S., & Gail, H.-P. 2008, A&A, 486, 229 [NASA ADS] [CrossRef] [EDP Sciences]
Online Material
![\begin{figure}
\par\includegraphics[width=16cm,clip]{Fig1_ASAS_corrected-NEW.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg110.png)
|
Figure 1: Sample lightcurves and fits to ASAS data. The identifier used in the present paper and the ASAS identifier are listed on top of the plot. Julian Date plotted is JD-2 450 000. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{Fig2_MACHO_corrected-NEW.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg111.png)
|
Figure 2: Sample lightcurves and fits to MACHO data. MACHO identifiers are listed on top of the plot, and are cross-referenced in Tables 1 and 2. Julian Date plotted is JD-2 400 000. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{Fig3_OGLE.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg112.png)
|
Figure 3: Sample lightcurves and fits to OGLE- III data (and OGLE- II data when available). OGLE- III identifiers are listed on top of the plot, and are cross-referenced in Tables 1 and 2. Julian Date plotted is JD-2 450 000. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.3cm,clip]{Fig5_Cstars.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg113.png)
|
Figure 5: Fits to the SEDs and IRS spectra of C-stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{Fig6_Ostar_LabSil.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg114.png)
|
Figure 6: Fits to the SEDs and IRS spectra of M-stars using ``laboratory silicates''. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{Fig7_Ostar_AstrSil.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg115.png)
|
Figure 7: Fits to the SEDs and IRS spectra of M-stars using ``astronomical silicates''. |
| Open with DEXTER | |
Footnotes
- ... supergiants
![[*]](/icons/foot_motif.png)
- Complete Figs. 1-3 and 5-7 are only available in electronic form at http://www.aanda.org
- ...
![[*]](/icons/foot_motif.png)
- Complete Tables 1-4 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/506/1277
- ... emission
![[*]](/icons/foot_motif.png)
- In detail, the following sources from these programs are not considered. From program 200: WBP 219, WBP 29, WBP51, NGC 371 LE8, NGC 381 LE31, NGC 371 LE28, WBP 104, WBP 116, HV 5810, HV 5680, IRAS 04530-6916; from program 3277: MSX SMC 014, 029, 079, 125, 155, 180; from program 3426: MSX LMC 559, 1306, 1794, 217, 222, 22, 764, 836, 889, 894, 934, 773, 769, 890; from program 3505: NGC 419 LE 35, GM 106, RAW 1559, ISO-MCMS J005149.4-731315 (iso00518), IRAS 05328-6827; from program 3591: MSX LMC 616, LHA 120-N 89, LHA 120-N 77d, BSDL 2894, BSDL 126, [O96] D010b-262, HD 38489, NGC 1978 WBT2665, NGC 1948 WBT2215, HD 269924, MSX LMC 795, MSX LMC 1786, [L63] 31, MSX LMC 906, [SL63] 482, IRAS 04514-6913, MSX LMC 610.
- ...
ASAS
![[*]](/icons/foot_motif.png)
- http://www.astrouw.edu.pl/asas/
- ... data
![[*]](/icons/foot_motif.png)
- See http://wwwmacho.anu.edu.au/
- ...
VizieR
![[*]](/icons/foot_motif.png)
- http://vizier.u-strasbg.fr/viz-bin/VizieR
- ...
Archive
![[*]](/icons/foot_motif.png)
- http://irsa.ipac.caltech.edu/
- ... models
![[*]](/icons/foot_motif.png)
- http://marcs.astro.uu.se/
- ... grains
![[*]](/icons/foot_motif.png)
- Adapting the code for n-layered spherical grains available at http://www.astro.spbu.ru/JPDOC/CODES/NMIE/n-miev3a.for
- ...
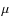 m
m![[*]](/icons/foot_motif.png)
- Sloan et al. (2008) shifted this range for the IRS data from the range originally defined for the LRS data.
All Tables
Table 1: The C-star sample: identifiers and pulsation periods for the first few entries.
Table 2: The M-star sample: identifiers and pulsation periods for the first few entries.
Table 3: Fit results of the C-star sample for the first few entries.
Table 4: Fit results of the M-star sample for the first few entries.
Table A.1: Multi-period information.
All Figures
| |
Figure 1: Sample lightcurves and fits to ASAS data. The identifier used in the present paper and the ASAS identifier are listed on top of the plot. The complete figure is available in the electronic edition. Julian Date plotted is JD-2 450 000. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: Sample lightcurves and fits to MACHO data. MACHO identifiers are listed on top of the plot, and are cross-referenced in Tables 1 and 2. The complete figure is available in the electronic edition. Julian Date plotted is JD-2 400 000. |
| Open with DEXTER | |
| In the text | |
| |
Figure 3: Sample lightcurves and fits to OGLE- III data (and OGLE- II data when available). OGLE- III identifiers are listed on top of the plot, and are cross-referenced in Tables 1 and 2. The complete figure is available in the electronic edition. Julian Date plotted is JD-2 450 000. |
| Open with DEXTER | |
| In the text | |

|
Figure 4: Dust temperature at the inner radius versus mass-loss rate for C stars. Plus-signs indicate stars excluded from the fit (the solid line, Eq. (1)). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{rt_ira...
...box{8.8cm}{!}{\includegraphics[angle=-90]{rt_iras04557.ps}} }
\par
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg37.png)
|
Figure 5: Fits to the SEDs and IRS spectra of C-stars. The complete figure is available in the electronic edition. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{rt_msx...
...box{8.8cm}{!}{\includegraphics[angle=-90]{rt_w60d22Lab.ps}} }
\par
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg38.png)
|
Figure 6: Fits to the SEDs and IRS spectra of M-stars using ``laboratory silicates''. The complete figure is available in the electronic edition. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{rt_msx...
...sizebox{8.8cm}{!}{\includegraphics[angle=-90]{rt_w60d22Ast.ps}} }
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg39.png)
|
Figure 7: Fits to the SEDs and IRS spectra of M-stars using ``astronomical silicates''. The complete figure is available in the electronic edition. |
| Open with DEXTER | |
| In the text | |

|
Figure 8: Top panel. Bolometric magnitude versus pulsation period for the M stars. Stars without period are plotted as plus signs at negative periods. The full line indicates the lower luminosity limit for RSGs by WBF, and the dashed line is 1.8 mag brighter. Top panel. I-band semi-amplitudes larger than 0.45 mag are denoted by triangles. Amplitudes between 0.2 and 0.45 by filled squares. Amplitudes smaller then 0.2 by circles. In the electronic edition, [3.6]-[8.0] colours redder than 1.2 are shown in black, between 0.5 and 1.2 in red, between 0.15 and 0.5 in green, and less than 0.15 in blue. Bottom panel. As top panel, but the objects are identified as foreground objects (open circles), RSG (filled triangles), and AGB stars (open squares) based on the discussion in Sect. 5.1. |
| Open with DEXTER | |
| In the text | |

|
Figure 9:
The Hertzsprung-Russell diagram.
C-stars are plotted as filled squares, M-type AGB stars as open
squares, RSGs as filled triangles, and foreground objects as open
circles.
Lines indicate evolutionary tracks by Bertelli et al. (2008) for 20,
10, 8, 5, and 3 |
| Open with DEXTER | |
| In the text | |

|
Figure 10: Colour-magnitude diagrams from two combinations of colours for the SMC ( left-hand panel) and LMC ( right-hand panel). Dots are stars picked randomly from the S3MC and SAGE surveys. M stars are plotted as squares (foreground objects), triangles (supergiants), and circles (AGB stars). C stars are plotted as filled circles. |
| Open with DEXTER | |
| In the text | |
| |
Figure 11: Colour-colour diagrams for two combinations of colours for the SMC ( left-hand panel) and LMC ( right-hand panel). Dots are from the S3MC and SAGE survey. M stars are plotted as squares (foreground objects), triangles (supergiants), and circles (AGB stars). C stars are plotted as filled circles. |
| Open with DEXTER | |
| In the text | |

|
Figure 12:
The bolometric correction at 3.6 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{hv12793_org_cds_models_016_217.ps}}\par
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg62.png)
|
Figure 13: The effect of grain shape, showing the original best-fitting model with small spherical olivine grains (red dashed line) and with a CDS (green dot-dashed line), both with 5% iron. Models assuming a CDE or DHS give results nearly identical to the CDS model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{hv12793_dhs0_06_12_15_models32_29_26.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg63.png)
|
Figure 14:
The effect of grain size for homogeneous spheres (95% olivine and 5%
iron). Grain sizes are 1.5 (red dashed line), 1.2 (green dot-dashed
line) and 0.6 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{hv12793_dhs479_12_models38_50_62.ps}}\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg64.png)
|
Figure 15:
The effect of porosity using a DHS with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_3sics.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg65.png)
|
Figure 16:
A comparison of different types of SiC assuming small spherical
particles: 8% |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_models7_15_18.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg66.png)
|
Figure 17:
The effect of shape distribution: CDE with 6% |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_models20_26_22.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg67.png)
|
Figure 18:
The effect of using a DHS with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_models32_33_37.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg68.png)
|
Figure 19:
The effect of using spherical core-mantle grains, with a SiC core of
0.01 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=-90]{iras05360_models47_57_66.ps}}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg72.png)
|
Figure 20: Some models that include MgS. (1) Core with 2% SiC, inner mantle with 91% AMC, outer mantle with 7% MgS. CDE using the optical constants calculated using EMT (red dashed line), (2) two grain model, 90% AMC and 10% of a core-mantle grain with 45% SiC core and 55% MgS mantle (green dot-dashed line), and (3) two grain model, 94% AMC and 6% of a core-mantle grain with 3% SiC core and 97% MgS mantle, assuming CDE using the optical constants calculated using EMT (blue dotted line). |
| Open with DEXTER | |
| In the text | |

|
Figure 21:
Mass-loss rate versus luminosity for C stars ( top panel,
red colours),
M stars ( bottom panel, blue colours), VW models (
left), and Reimers models ( right).
AGB stars in the SMC are plotted as squares, in the LMC as triangles.
Objects with Mira like pulsation amplitudes are plotted with open
symbols, objects with smaller amplitudes as filled symbols.
RSG are plotted as plus-signs independent of host galaxy and pulsation
amplitude.
The VW and Reimers models are plotted as crosses connected by the
dotted line for initial masses of 1.5, 2.5, 5.0 and 7.9 |
| Open with DEXTER | |
| In the text | |

|
Figure 22: Mass-loss rate versus period for C stars ( top panel, red colours), M stars ( bottom panel, blue colours), VW models ( left), and Reimers models ( right). Symbols are as in Fig. 21. In the upper panels, the curved solid line indicates the MLR-period relation from VW, the straight solid line the relation derived for Galactic C-rich Miras by Groenewegen et al. (1998). In the bottom panel, the two lines indicate a fit to most of the M stars, and the VW relation for a period 0.6 times the pulsation period. |
| Open with DEXTER | |
| In the text | |

|
Figure 23: Mass-loss rate versus (estimated or measured) I-band pulsation amplitude for C stars ( top panel) and M stars ( bottom panel). C stars in the LMC are plotted as open squares, in the SMC as filled squares. O-rich AGB stars in the LMC are plotted as open circles, and in the SMC as filled circles. RSG are plotted as plus signs. |
| Open with DEXTER | |
| In the text | |

|
Figure 24: Mass-loss rate versus colour for C-stars ( top panel), and M-stars ( bottom panel). Symbols as in Fig. 23. |
| Open with DEXTER | |
| In the text | |

|
Figure 25: Mass-loss rate as a function of [7]-[15] color ( top panel) and DEC (dust emission contrast; bottom panel). In both panels, the solid line plots the functions given in Eqs. (5) and (6), and the dotted lines show the average uncertainty, which is formally the standard deviation of the difference between the actual data and the fitted function. The dashed line in the bottom panel separates the data excluded from the fit. Also excluded were the four points with negative DECs. Neither panel includes foreground objects. |
| Open with DEXTER | |
| In the text | |

|
Figure 26:
Bolometric magnitude versus pulsation period for C-stars ( top
panel, red colours), and M-stars ( bottom panel,
blue colours), and for VW models ( left) and Reimers
models ( right).
AGB stars in the SMC are plotted as squares, in the LMC as triangles.
Objects with Mira like pulsation amplitudes are plotted with open
symbols, and filled symbols otherwise.
RSG are plotted as plus-signs independent of host galaxy and pulsation
amplitude.
For the C-star panels, the solid line indicates the PL-relation
from
Groenewegen & Whitelock (1996) and
the dotted line the extrapolation beyond
|
| Open with DEXTER | |
| In the text | |

|
Figure 27: As Fig. 26 but without the model tracks, without supergiants, and only variables with large amplitudes are plotted. Open squares indicate stars without information on the presence of HBB, plus-signs are stars without HBB (no Lithium detected), filled squares stars which undergo HBB (or supposed to, like the C-star IRAS 04496-6958, but which probably is not, see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{Fig1_ASAS_corrected-NEW.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg110.png)
|
Figure 1: Sample lightcurves and fits to ASAS data. The identifier used in the present paper and the ASAS identifier are listed on top of the plot. Julian Date plotted is JD-2 450 000. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{Fig2_MACHO_corrected-NEW.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg111.png)
|
Figure 2: Sample lightcurves and fits to MACHO data. MACHO identifiers are listed on top of the plot, and are cross-referenced in Tables 1 and 2. Julian Date plotted is JD-2 400 000. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{Fig3_OGLE.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg112.png)
|
Figure 3: Sample lightcurves and fits to OGLE- III data (and OGLE- II data when available). OGLE- III identifiers are listed on top of the plot, and are cross-referenced in Tables 1 and 2. Julian Date plotted is JD-2 450 000. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.3cm,clip]{Fig5_Cstars.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg113.png)
|
Figure 5: Fits to the SEDs and IRS spectra of C-stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{Fig6_Ostar_LabSil.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg114.png)
|
Figure 6: Fits to the SEDs and IRS spectra of M-stars using ``laboratory silicates''. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{Fig7_Ostar_AstrSil.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12678-09/Timg115.png)
|
Figure 7: Fits to the SEDs and IRS spectra of M-stars using ``astronomical silicates''. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



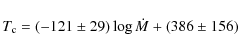
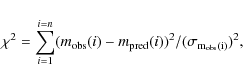
![\begin{displaymath}\log \dot{M} = 1.759 \; ([7]-[15]) - 8.664,
\end{displaymath}](/articles/aa/full_html/2009/42/aa12678-09/img90.png)