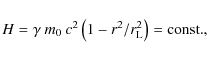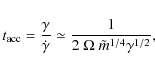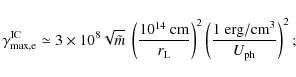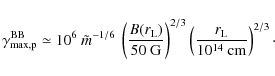| Issue |
A&A
Volume 506, Number 3, November II 2009
|
|
|---|---|---|
| Page(s) | L41 - L44 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200912562 | |
| Published online | 01 October 2009 | |
A&A 506, L41-L44 (2009)
LETTER TO THE EDITOR
Centaurus A as TeV 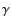 -ray and possible UHE cosmic-ray source
-ray and possible UHE cosmic-ray source
F. M. Rieger1,2 - F. A. Aharonian1,3
1 - Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
2 - European Associated Laboratory for Gamma-Ray Astronomy, jointly supported by CNRS and MPG, Europe
3 - Dublin Institute for Advanced Studies, 31 Fitzwilliam Place, Dublin 2, Ireland
Received 25 May 2009 / Accepted 18 September 2009
Abstract
Context. The most nearby active galaxy Cen A has attracted
considerable attention as a detected TeV gamma-ray and possible
ultra-high energy (UHE) cosmic-ray emitter.
Aims. We investigate the efficiency of particle acceleration
close to the supermassive black hole (BH) horizon assuming that
accretion in the innermost part of the disk occurs in an
advection-dominated (ADAF) mode.
Methods. We analyze the constraints on the achievable particle
energies imposed by radiative losses and corotation for conditions
inferred from observations.
Results. We show that for an underluminous source such as
Cen A, centrifugally accelerated electrons may reach Lorentz
factors of up to
![]() ,
allowing inverse Compton (Thomson) upscattering of ADAF sub-mm disk
photons into the TeV regime with an associated maximum (isotropic)
luminosity of the order of a few times 1039 erg/s. Upscattering of Comptonized disk photons is expected to lead to a TeV spectrum
,
allowing inverse Compton (Thomson) upscattering of ADAF sub-mm disk
photons into the TeV regime with an associated maximum (isotropic)
luminosity of the order of a few times 1039 erg/s. Upscattering of Comptonized disk photons is expected to lead to a TeV spectrum
![]() with a spectral index
with a spectral index
![]() ,
consistent with HESS results. The corresponding minimum variability timescale could be as low as
,
consistent with HESS results. The corresponding minimum variability timescale could be as low as
![]() h for a typical light cylinder radius of
h for a typical light cylinder radius of
![]() .
While efficient electron acceleration appears to be well possible,
protons are unlikely to be accelerated into the extreme UHECR regime
close to the central black hole. We argue that if Cen A is indeed
an extreme UHECR emitting source, then shear acceleration along the
kpc-scale jet could represent one of the most promising mechanisms
capable of pushing protons up to energies beyond 50 EeV.
.
While efficient electron acceleration appears to be well possible,
protons are unlikely to be accelerated into the extreme UHECR regime
close to the central black hole. We argue that if Cen A is indeed
an extreme UHECR emitting source, then shear acceleration along the
kpc-scale jet could represent one of the most promising mechanisms
capable of pushing protons up to energies beyond 50 EeV.
Key words: acceleration of particles - black hole physics - radiation mechanisms: non-thermal - galaxies: active - galaxies: jets
1 Introduction
Centaurus A (NGC 5128, Cen A) is the closest (distanceCen A is the only AGN of the non-blazar type detected at MeV (COMPTEL: Steinle et al. 1998) and GeV energies (EGRET: Sreekumar
et al. 1999). The nuclear spectral energy distribution (SED) of Cen A, as inferred from non-simultaneous data, appears to consist
of two peaks, one reaching its maximum at several times 1013 Hz and one peaking around 0.1 MeV (Chiaberge et al. 2001;
Meisenheimer et al. 2007). The SED below 1 GeV has been successfully modeled within a simple jet synchrotron self-Compton (SSC)
framework, assuming Cen A to be a misaligned BL Lac object (Chiaberge et al. 2001). In the early days of gamma-ray astronomy, a
tentative detection (>![]() )
of Cen A at very high energies >0.3 TeV was reported during a phase of high X-ray activity in
1972-1974 (Grindlay 1975). HESS results (Aharonian et al. 2009a) have established Cen A as a TeV emitting source (the
second radio galaxy after M 87) with integral VHE flux of
)
of Cen A at very high energies >0.3 TeV was reported during a phase of high X-ray activity in
1972-1974 (Grindlay 1975). HESS results (Aharonian et al. 2009a) have established Cen A as a TeV emitting source (the
second radio galaxy after M 87) with integral VHE flux of ![]()
![]() of the Crab Nebula.
of the Crab Nebula.
Chandra and XMM-Newton observations between 2 and 7 keV indicate
that the nuclear X-ray continuum spectrum in Cen A may consist of
both a disk and a jet component, the disk contribution being consistent
with a hybrid disk configuration where a standard disk is truncated at ![]() and replaced by an ADAF in the inner regions close to the central black hole (Evans et al. 2004; cf. also Pellegrini et al. 2005, and Meisenheimer et al. 2007). A transition to an inner ADAF disk could also explain the lack of a big blue bump UV feature
expected in the standard disk scenario (Marconi et al. 2001). The accretion rate for Cen A seems uncertain by about an order of
magnitude, with model-dependent estimates ranging from several 10-4 to some
and replaced by an ADAF in the inner regions close to the central black hole (Evans et al. 2004; cf. also Pellegrini et al. 2005, and Meisenheimer et al. 2007). A transition to an inner ADAF disk could also explain the lack of a big blue bump UV feature
expected in the standard disk scenario (Marconi et al. 2001). The accretion rate for Cen A seems uncertain by about an order of
magnitude, with model-dependent estimates ranging from several 10-4 to some
![]() .
Taking the measured
nuclear X-ray luminosity of
.
Taking the measured
nuclear X-ray luminosity of
![]() erg/s (Evans et al. 2004) as a robust upper limit to a possible ADAF disk
contribution gives
erg/s (Evans et al. 2004) as a robust upper limit to a possible ADAF disk
contribution gives
![]() ,
which for the canonical viscosity parameter
,
which for the canonical viscosity parameter
![]() is still below
the critical mass accretion rate
is still below
the critical mass accretion rate
![]() required for a two-temperature ADAF to occur
(Narayan et al. 1998; Yi 1999).
required for a two-temperature ADAF to occur
(Narayan et al. 1998; Yi 1999).
If the first SED peak below 1014 Hz is indeed caused by synchrotron emission from the jet (Chiaberge et al. 2001; Meisenheimer et al. 2007), inverse Compton upscattering in a conventional homogeneous SSC framework is unable to account for VHE ![]() -rays
in the TeV regime. On the other hand, it could be that the situation
for Cen A is similar to that for M 87, where efficient
particle acceleration close to the BH horizon seems to be responsible
for the production of the observed TeV
-rays
in the TeV regime. On the other hand, it could be that the situation
for Cen A is similar to that for M 87, where efficient
particle acceleration close to the BH horizon seems to be responsible
for the production of the observed TeV ![]() -rays (Aharonian et al. 2009b; Rieger
& Aharonian 2008a,
henceforth: RA08a). Here we analyze possible VHE characteristics
associated with this scenario. We show that for parameters inferred
from observations, inverse Compton upscattering of ADAF disk photons by
centrifugally accelerated electrons could result in variable (
-rays (Aharonian et al. 2009b; Rieger
& Aharonian 2008a,
henceforth: RA08a). Here we analyze possible VHE characteristics
associated with this scenario. We show that for parameters inferred
from observations, inverse Compton upscattering of ADAF disk photons by
centrifugally accelerated electrons could result in variable (![]() 1 h) VHE
1 h) VHE ![]() -rays
with a relatively hard TeV spectrum. We show that the mechanism
considered is unable to accelerate protons to ultra high energy
cosmic-ray (UHECR) energies, although shear acceleration along the jet
could potentially provide a means.
-rays
with a relatively hard TeV spectrum. We show that the mechanism
considered is unable to accelerate protons to ultra high energy
cosmic-ray (UHECR) energies, although shear acceleration along the jet
could potentially provide a means.
2 Cen A as a TeV 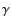 -ray source
-ray source
2.1 Particle acceleration close to the BH horizon
Magnetic fields are widely considered to play a key role in the
formation of collimated relativistic outflows from compact objects.
According to, e.g., MHD scenarios, magnetic flux dragged in by the
accretion flow and suitably amplified by dynamo actions in the inner
accretion disk can build up a rigidly rotating (quasi-dipolar) disk
magnetosphere. Depending on the field-line rotation and the current
distribution, the bulk of the plasma may then be centrifugally
accelerated along open flux surfaces to relativistic speeds (
![]() )
and become collimated outside the light cylinder
)
and become collimated outside the light cylinder
![]() (e.g., Camenzind
1995; Fendt 1997). In what follows, we explore an approach where efficient particle acceleration is supposed to occur
close to the light cylinder (e.g., Machabeli & Rogava 1994;
Gangadhara & Lesch 1997;
Rieger & Mannheim 2000; Osmanov et al. 2007). Within the MHD framework this could occur if, e.g., the longitudinal current becomes smaller than a critical value
(Beskin & Rafikov 2000). Let us suppose, thus, that a significant fraction of the electromagnetic energy may be transformed into
the kinetic energy of particles by means of magneto-centrifugal effects close to
(e.g., Camenzind
1995; Fendt 1997). In what follows, we explore an approach where efficient particle acceleration is supposed to occur
close to the light cylinder (e.g., Machabeli & Rogava 1994;
Gangadhara & Lesch 1997;
Rieger & Mannheim 2000; Osmanov et al. 2007). Within the MHD framework this could occur if, e.g., the longitudinal current becomes smaller than a critical value
(Beskin & Rafikov 2000). Let us suppose, thus, that a significant fraction of the electromagnetic energy may be transformed into
the kinetic energy of particles by means of magneto-centrifugal effects close to ![]() .
Consider for illustration a charged test
particle, corotating with the magnetic field and gaining energy while moving outwards (Machabeli & Rogava 1994).
The motion of this particle may be analyzed conveniently in the
framework of Hamiltonian dynamics: for length scales much smaller than
the curvature radius of the field, the field topology is monopole-like
and the associated Hamiltonian H for a particle of rest
mass m0 moving along a relativistically, rigidly rotating field-line (angular velocity
.
Consider for illustration a charged test
particle, corotating with the magnetic field and gaining energy while moving outwards (Machabeli & Rogava 1994).
The motion of this particle may be analyzed conveniently in the
framework of Hamiltonian dynamics: for length scales much smaller than
the curvature radius of the field, the field topology is monopole-like
and the associated Hamiltonian H for a particle of rest
mass m0 moving along a relativistically, rigidly rotating field-line (angular velocity
![]() )
becomes
a constant of motion
)
becomes
a constant of motion
where
valid for
2.2 Constraints on achievable Lorentz factors
Under realistic astrophysical conditions, the acceleration
efficiency is constrained by radiation reaction (e.g., inverse Compton
in the ambient photon field), the breakdown of the bead-on-the-wire
(BW) approximation for a single particle or the bending of the field
line with increasing inertia. For a mass accretion rate in the
concordant range
![]() (e.g., Marconi et al. 2001; Evans et al. 2004; Pellegrini 2005; Meisenheimer et al. 2007), the ADAF equipartition magnetic field
(e.g., Marconi et al. 2001; Evans et al. 2004; Pellegrini 2005; Meisenheimer et al. 2007), the ADAF equipartition magnetic field
![]() (Yi 1999) becomes
(Yi 1999) becomes
![]() G, suggesting (radial) jet magnetic field
strengths near the light cylinder of
G, suggesting (radial) jet magnetic field
strengths near the light cylinder of
![]() G. In the case of BL Lac objects, transition radii from tens to several hundred
G. In the case of BL Lac objects, transition radii from tens to several hundred
![]() have been inferred from observations (e.g., Cao 2003;
Wu & Cao 2005). Similarly, the apparent lack of a standard disk feature
in the observed SED of Cen A seems to indicate as well that
have been inferred from observations (e.g., Cao 2003;
Wu & Cao 2005). Similarly, the apparent lack of a standard disk feature
in the observed SED of Cen A seems to indicate as well that
![]() .
By assuming that all of the measured X-ray luminosity in
Cen A of
.
By assuming that all of the measured X-ray luminosity in
Cen A of
![]() erg/s is produced by an inner ADAF, the implied energy densities is
erg/s is produced by an inner ADAF, the implied energy densities is
![]() erg/cm3 for
erg/cm3 for
![]() .
A similar constraint might be obtained based on the ADAF synchrotron peak luminosity
.
A similar constraint might be obtained based on the ADAF synchrotron peak luminosity
![]() (Yi 1999) close to
(Yi 1999) close to ![]() ,
where
,
where
![]() Hz, which give
Hz, which give
![]() erg/s, using the fiducial parameters
erg/s, using the fiducial parameters
![]() ,
,
![]() ,
and
,
and
![]() (giving
(giving
![]() G), implying a photon
energy density
G), implying a photon
energy density
![]() erg/cm3:
erg/cm3:
- (i)
- inverse Compton losses (Thomson regime) for electrons, occurring on timescales of
![$t_{\rm cool} \simeq 3 \times 10^7/[\gamma~
U_{\rm ph}]$](/articles/aa/full_html/2009/42/aa12562-09/img45.png) s, then imply (see Eq. (2)) that achievable electron Lorentz factors are limited to
s, then imply (see Eq. (2)) that achievable electron Lorentz factors are limited to
- (ii)
- for motion along the field synchrotron losses are negligible, while curvature losses, occurring on characteristic timescales of
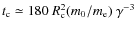 ,
do not impose stronger constraints (compared to Eq. (3)) for curvature
radii
,
do not impose stronger constraints (compared to Eq. (3)) for curvature
radii
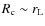 ;
;
- (iii)
- the validity of the BW approximation for protons, on the other
hand, requires that their characteristic acceleration timescale is
always longer than the inverse of the relativistic gyro-frequency (cf.
Rieger & Aharonian 2008b), which constrains the achievable proton Lorentz
factors to be
2.3 Expected TeV characteristics
The above considerations suggest that electron acceleration close to the central BH in Cen A may produce Lorentz factors
![]() .
This would allow Thomson inverse Compton upscattering of ambient disk photons to TeV energies of
.
This would allow Thomson inverse Compton upscattering of ambient disk photons to TeV energies of
![]() TeV. The resultant TeV spectral index at the high energy end then traces, over a decade or so,
the underlying disk seed photon spectrum (Rieger & Aharonian 2008b). In the ADAF case, comptonization of thermal synchrotron soft
photons is expected to lead to a power-law-like tail in the disk spectrum above
TeV. The resultant TeV spectral index at the high energy end then traces, over a decade or so,
the underlying disk seed photon spectrum (Rieger & Aharonian 2008b). In the ADAF case, comptonization of thermal synchrotron soft
photons is expected to lead to a power-law-like tail in the disk spectrum above
![]() ,
i.e.,
,
i.e.,
![]() ,
where
,
where
![]() depends on the accretion rate (Mahadevan 1997; Yi 1999). For the inferred mass accretion
rate of Cen A,
depends on the accretion rate (Mahadevan 1997; Yi 1999). For the inferred mass accretion
rate of Cen A,
![]() ,
the spectral index becomes
,
the spectral index becomes
![]() assuming a standard ADAF viscosity coefficient
assuming a standard ADAF viscosity coefficient
![]() .
This suggests that the upscattered TeV spectrum in
Cen A might in fact be softer than that observed in M 87 (see Aharonian et al. 2006). A spectral fit to the VHE (>300 GeV) data
obtained by HESS indeed suggests a power-law spectral index in the range
.
This suggests that the upscattered TeV spectrum in
Cen A might in fact be softer than that observed in M 87 (see Aharonian et al. 2006). A spectral fit to the VHE (>300 GeV) data
obtained by HESS indeed suggests a power-law spectral index in the range
![]() (Aharonian et al. 2009a). A soft spectrum
with, e.g.,
(Aharonian et al. 2009a). A soft spectrum
with, e.g.,
![]() ,
may then indicate that accretion occurs at the lower end of the concordant interval noted above.
Since particle acceleration occurs close to the light surface, the expected minimum TeV variability timescale is
,
may then indicate that accretion occurs at the lower end of the concordant interval noted above.
Since particle acceleration occurs close to the light surface, the expected minimum TeV variability timescale is ![]()
![]() h.
h.
Is it possible that TeV photons, produced by inverse Compton
upscattering, can escape from the vicinity of the central black hole in
Cen A? In principle, photons of energy E [TeV] will interact most
efficiently with target photons in the infrared regime, i.e., of energy
![]() (1 TeV/E) eV. For the radio luminosity
(1 TeV/E) eV. For the radio luminosity ![]() estimated above, the implied infrared (1 eV) ADAF disk
luminosity is on the order of
estimated above, the implied infrared (1 eV) ADAF disk
luminosity is on the order of
![]() erg/s. The optical depth for
erg/s. The optical depth for
![]() -absorption
-absorption
![]() thus becomes
thus becomes
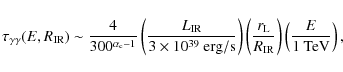
|
(5) |
indicating that TeV photons may well escape from the vicinity of the black hole provided the spectrum is sufficiently soft (i.e., for
One can estimate the maximum possible TeV luminosity output
![]() based on the Alfvén corotation
condition
based on the Alfvén corotation
condition
![]() ,
which provides an upper limit for the accelerated particle number density close to
,
which provides an upper limit for the accelerated particle number density close to ![]() .
By noting that for the relevant volume one has
.
By noting that for the relevant volume one has
![]() ,
that
,
that ![]() can be
approximated by the single particle Thomson power, and that particles are accumulated for
can be
approximated by the single particle Thomson power, and that particles are accumulated for
![]() (correcting a typo in RA08a, Eq. (12)), the maximum possible inverse Compton TeV luminosity is of order
(correcting a typo in RA08a, Eq. (12)), the maximum possible inverse Compton TeV luminosity is of order
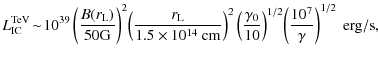
|
(6) |
which is consistent with the HESS results of Aharonian et al. (2009a). Since
3 On Cen A as a possible UHECR proton source
According to the Pierre Auger results, 4 out of 27 events detected
above 57 EeV may be associated with the location of Cen A (Abraham
et al. 2007, 2008).
If some of these cosmic ray events were indeed associated with
Cen A, it seems unlikely that their energization could occur close
to the central BH. Neither a Blandford-Znajek-type nor a
centrifugal disk wind scenario seems to allow for that: for example, if
the black hole in Cen A rotates and is embedded in a magnetic field of
equipartition strength
![]() G, it could act as a unipolar inductor (membrane
paradigm) and induce a voltage difference of the order of
G, it could act as a unipolar inductor (membrane
paradigm) and induce a voltage difference of the order of
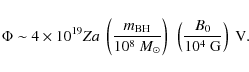
|
(7) |
However in reality, it seems unlikely that protons might be able to fully tap this potential. Even if the ordered magnetic field component could be as high as B0, screening of the electric field in the plasma-rich AGN environment and curvature losses, for example, are readily expected to reduce achievable proton energies to below
Furthermore, if radio observations are a reliable tracer of the true
fluid speeds in the jet of Cen A, internal shocks are also
probably not able to account for UHECRs beyond 50 EeV. On both
VLBA subparsec-scales and VLA scales of hundreds of parsecs, the jet
bulk speed seems to be at most mildly relativistic, not exceeding 0.5c by much (Tingay et al. 2001; Hardcastle et al. 2003). If the shocks are
internal with characteristic speeds comparable to the relative velocity between layers, shock speeds
![]() well below 0.5c are
expected. Balancing the minimum timescale for non-relativistic shock acceleration (Bohm limit, e.g. see Rieger et al. 2007) with the
timescale for cross-field diffusion then implies, that possible cosmic ray energies are limited to
well below 0.5c are
expected. Balancing the minimum timescale for non-relativistic shock acceleration (Bohm limit, e.g. see Rieger et al. 2007) with the
timescale for cross-field diffusion then implies, that possible cosmic ray energies are limited to
![]() ,
where
,
where ![]() is the (transverse) source size and B the local magnetic field strength. Even if one would allow for some local magnetic field
amplification by a factor
is the (transverse) source size and B the local magnetic field strength. Even if one would allow for some local magnetic field
amplification by a factor ![]() (e.g., due to shock compression or shear-driven instabilities) and assume that radiative losses could be
neglected, possible proton energies are unlikely to exceed
(e.g., due to shock compression or shear-driven instabilities) and assume that radiative losses could be
neglected, possible proton energies are unlikely to exceed
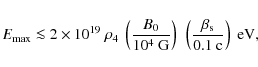
|
(8) |
where the strength of the local field at
Hardcastle et al. (2009) recently proposed that efficient stochastic particle acceleration could occur in the giant radio lobes of Cen A on
scales of
![]() kpc. In the Bohm limit, the characteristic acceleration timescale for stochastic second order Fermi acceleration is of
order
kpc. In the Bohm limit, the characteristic acceleration timescale for stochastic second order Fermi acceleration is of
order
![]() (e.g., Rieger et al. 2007). Comparing this timescale with that for cross-field diffusion,
i.e.,
(e.g., Rieger et al. 2007). Comparing this timescale with that for cross-field diffusion,
i.e.,
![]() ,
suggests that proton energies are limited to
,
suggests that proton energies are limited to
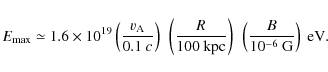
|
(9) |
Hence, if relativistic turbulent wave speeds can be achieved (of order
Based on the above considerations, it seems questionable whether protons could indeed be accelerated to energies beyond 1019 eV
in Cen A. However, one possible mechanism that may help particles
to reach beyond this limit could be shear acceleration along the
large-scale jet (Rieger & Duffy 2004).
Strong internal jet stratification (e.g., a fast spine surrounded by
slower moving layers) is naturally expected for jets interacting with
their environments or launched by different processes (e.g., disk and
black-hole driven wind), and indeed seen in hydrodynamical simulations
(e.g., Meliani & Keppens 2007;
Aloy & Mimica 2008).
In the case of Cen A, there are some observational hints, e.g.,
limb-brightening in the X-ray jet, the higher energy emission being
more confined to the jet axis, longitudinal magnetic field polarization
in the large-scale jet (Kataoka et al. 2006;
Kraft et al. 2002; Hardcastle et al. 2003)
that might be indicative of internal jet stratification. Energetic
particles scattered across such a shear flow can sample the kinetic
difference in the flow and be accelerated to higher energies. The
timescale for particle acceleration in a continuous shear flow is
inversely proportional to the particle mean free path
![]() (Rieger & Duffy 2004). In order to compete with radiative losses, and in the case of Cen A with advection
along the jet, high energy seed particles are thus needed to ensure efficient particle acceleration.
Assuming a gyro-dependent particle mean free path
(Rieger & Duffy 2004). In order to compete with radiative losses, and in the case of Cen A with advection
along the jet, high energy seed particles are thus needed to ensure efficient particle acceleration.
Assuming a gyro-dependent particle mean free path
![]() ,
the minimum acceleration time scale in a linearly decreasing
velocity shear profile is on the order of
,
the minimum acceleration time scale in a linearly decreasing
velocity shear profile is on the order of
![]() assuming
assuming
![]() (see Rieger & Duffy 2004). Advection along the jet occurs on a characteristic timescale
(see Rieger & Duffy 2004). Advection along the jet occurs on a characteristic timescale
![]() s, where
s, where
![]() kpc is the (projected) X-ray jet length (Hardcastle et al. 2007). The observed kpc radio jet slightly expands and has
a transverse width of
kpc is the (projected) X-ray jet length (Hardcastle et al. 2007). The observed kpc radio jet slightly expands and has
a transverse width of ![]() 1 kpc close to its end (Kraft et al. 2002). Protons injected at the crossover to the kpc-scales, for example, would
thus need seed energies of
1 kpc close to its end (Kraft et al. 2002). Protons injected at the crossover to the kpc-scales, for example, would
thus need seed energies of
![]() eV to ensure that shear acceleration can operate efficiently (using, e.g.,
eV to ensure that shear acceleration can operate efficiently (using, e.g.,
![]() kpc,
kpc,
![]() G).
Such energetic seed particles may well be provided by e.g. shock
acceleration. In this case, protons escaping from the inner shock
region and diffusing into the outer shear layers will naturally
experience an additional increase in energy. In 3d-hydrodynamical
simulations (Aloy et al. 1999), the shear layer is found to broaden with distance along the jet, eventually becoming comparable to the beam width.
If one thus takes
G).
Such energetic seed particles may well be provided by e.g. shock
acceleration. In this case, protons escaping from the inner shock
region and diffusing into the outer shear layers will naturally
experience an additional increase in energy. In 3d-hydrodynamical
simulations (Aloy et al. 1999), the shear layer is found to broaden with distance along the jet, eventually becoming comparable to the beam width.
If one thus takes
![]() kpc near to the jet end (we note that the full width of the turbulent shear layer may be even larger than that seen
in the radio), the classical Hillas confinement condition would constrain maximum protons energies to be
kpc near to the jet end (we note that the full width of the turbulent shear layer may be even larger than that seen
in the radio), the classical Hillas confinement condition would constrain maximum protons energies to be
![]() eV. This value might be somewhat higher, if the magnetic field is amplified in the shear (e.g., due to
Kelvin-Helmholtz-driven shear instabilities, see
Zhang et al. 2009). On the other hand, for smaller transverse shear widths, non-gradual shear acceleration (Ostrowski 1998; Rieger & Duffy 2004)
is expected to take over earlier, leading to similar maximum energy
considerations but different spectral characteristics.
eV. This value might be somewhat higher, if the magnetic field is amplified in the shear (e.g., due to
Kelvin-Helmholtz-driven shear instabilities, see
Zhang et al. 2009). On the other hand, for smaller transverse shear widths, non-gradual shear acceleration (Ostrowski 1998; Rieger & Duffy 2004)
is expected to take over earlier, leading to similar maximum energy
considerations but different spectral characteristics.
4 Conclusions
If Cen A hosts a radiatively inefficient inner accretion disk, efficient electron acceleration in its BH-jet magnetosphere and inverse Compton upscattering of ambient disk photons to the TeV regime appears to be possible. After M 87, Cen A could thus be another primary candidate source in which VHE processes close to the black hole may allow a fundamental diagnosis of its immediate environment, offering important insights into the central engine in AGNs.
Whether Cen A indeed proves to be an UHECR emitting source may require confirmation by additional observations. From a theoretical point of view and based on conventional acceleration concepts, it seems challenging to account for a possible production of UHECR protons beyond 1019 eV. On the other hand, as shown above, shear acceleration along the large-scale jet in Cen A may help to overcome this problem by increasing the energy of shock-accelerated seed particles by a factor of some tens. If this would be the case, spectral changes in the cosmic ray spectrum might be partly due to the operation of a new acceleration mechanism and not simply propagation effects.
AcknowledgementsDiscussions with B. Reville, A. Taylor, C. Fendt and V. Beskin, and useful comments by the referee are gratefully acknowledged.
References
- Abraham, J., Abreu, P., Aglietta, M., et al. (Pierre Auger Coll.) 2007, Science, 318, 938
- Abraham, J., Abreu, P., Aglietta, M., et al. (Pierre Auger Coll.) 2008, APh, 29, 188
- Aharonian, F. A., et al. 2002, Phys. Rev. D, 66, 023005 [NASA ADS] [CrossRef]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Coll.) 2006, Science, 314, 1424
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. (HESS Coll.) 2009a, ApJ, 695, L40
- Aharonian, F., Aliu, E., Arlen, T., et al. (HESS Coll.) 2009b, Science, 325, 444
- Aloy, M. A., & Mimica, P. 2008, ApJ, 681, 84 [NASA ADS] [CrossRef]
- Aloy, M. A., Ibáñez, J. M. Â., Martí, J. M. Â., et al. 1999, ApJ, 523, L125 [NASA ADS] [CrossRef]
- Beskin, V. S., & Rafikov, R. R. 2000, MNRAS, 313, 433 [NASA ADS] [CrossRef]
- Chiaberge, M., Capetti, A., & Celotti, A. 2001, MNRAS, 324, L33 [NASA ADS] [CrossRef]
- Camenzind, M. 1995, RvMA, 8, 201 [NASA ADS]
- Cao, X. 2003, ApJ 599, 147
- Daly, R. A. 2009, ApJ 691, L72
- Dermer, C. D., et al. 2009, NJP, 11, 065016 [NASA ADS] [CrossRef]
- Di Matteo, T., Tiziana, A., Steven, W., et al. 2003, ApJ, 582, 133 [NASA ADS] [CrossRef]
- Evans, D. A., Kraft, R. P., Worrall, D. M., et al. 2004, ApJ, 612, 786 [NASA ADS] [CrossRef]
- Fendt, C. 1997, A&A, 319, 1025 [NASA ADS]
- Gangadhara, R. T., & Lesch, H. 1997, A&A, 323, L45 [NASA ADS]
- Grindlay, J. E., Helmken, H. F., Brown, R. H., Davis, J., & Allen, L. R. 1975, ApJ, 197, L9 [NASA ADS] [CrossRef]
- Häring-Neumayer, A., Cappellari, M., Rix, H.-W., et al. 2006, ApJ, 643, 226 [NASA ADS] [CrossRef]
- Hardcastle, M. J., Worrall, D. M., Kraft, R. P., et al. 2003, ApJ, 593, 169 [NASA ADS] [CrossRef]
- Hardcastle, M. J., Kraft, R. P., Sivakoff, G. R., et al. 2007, ApJ, 670, L81 [NASA ADS] [CrossRef]
- Hardcastle, M. J., Cheung, C. C., Feain, I. J., et al. 2009, MNRAS, 393, 1041 [NASA ADS] [CrossRef]
- Israel, W. 1998, A&A Rev., 8, 237 [NASA ADS]
- Kataoka J., Stawarz, ., Aharonian, F., et al. 2006, ApJ, 641, 158 [NASA ADS] [CrossRef]
- Kraft, R. P., Forman, W. R., Jones, C., et al. 2002, ApJ, 569, 54 [NASA ADS] [CrossRef]
- Levinson, A. 2000, Phys. Rev. Lett., 85, 912 [NASA ADS] [CrossRef]
- Machabeli, G. Z., & Rogava, A. D. 1994, Phys. Rev. A, 50, 98 [NASA ADS] [CrossRef]
- Mahadevan, R. 1997, ApJ, 477, 585 [NASA ADS] [CrossRef]
- Marconi, A., Capetti, A., Axon, D. J., et al. 2001, ApJ, 549, 915 [NASA ADS] [CrossRef]
- Marconi, A., Pastorini, G., Pacini, F., et al. 2006, A&A, 448, 921 [NASA ADS] [CrossRef] [EDP Sciences]
- Meisenheimer, K., Tristram, K. R. W., Jaffe, W., et al. 2007, A&A, 471, 453 [NASA ADS] [CrossRef] [EDP Sciences]
- Meliani, Z., & Keppens, R. 2007, A&A, 475, 785 [NASA ADS] [CrossRef] [EDP Sciences]
- Narayan, R., Mahadevan R., & Quataert, E. 1998, in Theory of Black Hole Accretion Disks, ed. M. A. Abramowicz, et al. (Cambridge), 148
- Osmanov, Z., Rogava, A., & Bodo, G. 2007, A&A, 470, 395 [NASA ADS] [CrossRef] [EDP Sciences]
- Ostrowski, M. 1998, A&A, 335, 134 [NASA ADS]
- O'Sullivan, S., Reville, B., & Taylor, A. 2009, MNRAS, in press [arXiv:0903.1259]
- Pellegrini, S. 2005, ApJ 624, 155
- Radomski, J. T., Packham, C., Levenson, N. A., et al. 2008, ApJ, 681, 141 [NASA ADS] [CrossRef]
- Rieger, F. M., & Mannheim, K. 2000, A&A, 353, 473 [NASA ADS] (RM00)
- Rieger, F. M., & Duffy, P. 2004, ApJ, 617, 155 [NASA ADS] [CrossRef]
- Rieger, F. M., Bosch-Ramon, V., & Duffy, P. 2007, Ap&SS, 309, 119 [NASA ADS] [CrossRef]
- Rieger, F. M., & Aharonian, F. A. 2008a, A&A, 479, L5 [NASA ADS] [CrossRef] [EDP Sciences] (RA08a)
- Rieger, F. M., & Aharonian, F. A. 2008b, IJMPD, 17, 1569 [NASA ADS] [CrossRef]
- Sreekumar, P., Bertsch, D. L., Hartman, R. C., Nolan, P. L., & Thompson, D. J. 1999, APh, 11, 221 [NASA ADS]
- Steinle, H., Bennett, K., Bloemen, H., et al. 1998, A&A, 330, 97 [NASA ADS]
- Tingay, S. J., Jauncey, D. L., Reynolds, J. E., et al. 1998, AJ, 115, 960 [NASA ADS] [CrossRef]
- Tingay, S. J., Preston, R. A., & Jauncey, D. L. 2001, AJ, 122, 1697 [NASA ADS] [CrossRef]
- Wu, Q., & Cao, X. 2005, ApJ, 621, 130 [NASA ADS] [CrossRef]
- Yi, I. 1999, in Astrophysical Disks, ed. J. A. Sellwood, & J. Goodman, ASP Conf. Ser., 160, 279
- Zhang, W., MacFadyen, A., & Wang, P. 2009, ApJ, 692, L40 [NASA ADS] [CrossRef]
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.