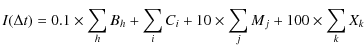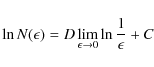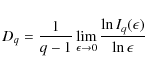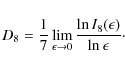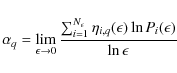| Issue |
A&A
Volume 506, Number 3, November II 2009
|
|
|---|---|---|
| Page(s) | 1429 - 1436 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912044 | |
| Published online | 27 August 2009 | |
A&A 506, 1429-1436 (2009)
Magnetic evolution of superactive regions
Complexity and potentially unstable magnetic discontinuities![[*]](/icons/foot_motif.png)
S. Criscuoli1 - P. Romano2 - F. Giorgi1 - F. Zuccarello3
1 - INAF - Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monte Porzio Catone, Italy
2 -
INAF - Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
3 -
Dipartimento di Fisica e Astronomia - Sezione Astrofisica, Universitá di Catania, via S. Sofia 78, 95123 Catania, Italy
Received 12 March 2009 / Accepted 23 July 2009
Abstract
Context. It is widely accepted that solar flares are
manifestations of magnetic reconnection events taking place in the
solar atmosphere. Several aspects of these events remain unclear,
although many efforts have been devoted to the investigation of
magnetic field configurations at flare occurrence sites.
Aims. In this work, we have studied the temporal evolution of
some properties of a sample of superactive regions with the aim to
single out the most significant for flare activity forecasting.
Methods. We have investigated properties of 14 superactive
regions, observed between January 1st 2000 and
December 31st 2006 with MDI/SOHO instrument and characterized
by a particularly intense flare activity during their passage on the
solar disk. We have analyzed the temporal evolution of fractal and
multifractal properties of photospheric magnetic fields, namely the
generalized fractal dimension and the contribution and dimensional
diversities, which describe geometrical properties of the magnetic
field, as well as the potential unstable volumes of magnetic
discontinuities above the studied ARs, which may provide information
about the magnetic field configuration in upper layers of the
atmosphere. Correlations of these quantities with the flare index,
which provides information about the flare activity of a region, have
also been estimated.
Results. We found that in 50% of our sample the generalized
fractal dimension is correlated with the flare index computed over
windows of 50 h, while the contribution diversity and the
dimensional diversity are anticorrelated with the same index.
A clear increase of the potential unstable volume of magnetic
discontinuities in the corona is observed before the phases
characterized by more frequent and intense flares. We also found that
the free energy distribution functions of unstable volumes of the
analyzed superactive regions can be fitted with straight lines whose
slope is larger than the values found in previous works for less active
magnetic regions.
Conclusions. The generalized fractal dimension and the potential
unstable volume of magnetic discontinuities are the most suitable for
statistical investigations of relations with flare activity over longer
(50 h) and shorter (few hours) time intervals, respectively.
Key words: Sun: activity - Sun: magnetic fields - Sun: flares
1 Introduction
It is largely accepted that solar flares are magnetic reconnection phenomena that can occur at different scales of time and energy (Aschwanden et al. 2000). Although the flare intensity and frequency are proportional to the magnetic field strength involved in these events, it is still unclear what the magnetic configurations are that drive these energy releases. In the past decade the theory and the numerical simulations of magnetic reconnection have shown that the dissipation of magnetic energy, responsible for the flare activity, occurs along unstable magnetic discontinuities (Parker 1988). The formation and disappearance of these discontinuities, also named current sheets, is a continuous process which occurs in all magnetic concentrations as in the solar active regions. Due to the thickness of these discontinuities, below current telescope resolution, many authors have tried to deduce their presence and location from the global topology of active regions.
Many statistical studies have been devoted to the investigation of physical properties and topology of the magnetic field in the photosphere, compatible with the events (see Schrijver 2007,2009, and references therein), but the results are controversial (Georgoulis 2007). Romano & Zuccarello (2007) (Paper I, hereafter) investigated the correlation of flare productivity and some properties of 26 superactive regions. They found that the deviations from magnetic polarity balance and the length of the inversion lines characterized by a horizontal magnetic gradient greater than 0.3 G km-1 seem to have a major role in producing a magnetic field topology able to trigger flares. This result has been confirmed by Song et al. (2009), who analyzed 174 active regions and employed a ordinal logistic regression model to predict solar flares. Different conclusions were drawn by Leka & Barnes (2007), who applied discriminant analyses to almost thirty properties of the photospheric magnetic field estimated for 496 active regions. Their results indicate that available data do not provide a basis for reliable flare prediction. However, these authors also suggest that different results might be found by including descriptors of the self-similar properties of the photospheric magnetic field in the analyses.
Self-similar properties of the solar magnetic field are a signature of the turbulent physical processes which determine the generation, evolution and dissipation of magnetic structures (see for instance Stein & Nordlund 2006; Cattaneo et al. 2003; Abramenko & Longcope 2005, and references therein) and have been investigated in several studies (see for instance Georgoulis 2005, for a review). In this context, investigation of fractal and multifractal properties of photospheric magnetic features provide important information about the physical properties of convective plasma (Balke et al. 1993; Tao et al. 1995; Nesme-Ribes et al. 1996), of the magnetic field (Pietarila Graham et al. 2009; Stenflo & Holzreuter 2002) and about the physical processes that govern their interaction (Bushby & Houghton 2005; Crouch et al. 2007; Lawrence et al. 1995,1999). Studies carried out on short temporal ranges (hours-days), have showed that fractal and multifractal properties vary with the evolution of the photospheric magnetic field of the regions analyzed (e.g. Georgoulis 2005; Conlon et al. 2008; Abramenko 2005a; Hewett et al. 2008). Several authors have also investigated the self-similar properties of ARs in connection with their flare productivity. For instance Abramenko (2005b) found that the magnetic power spectrum of 16 investigated ARs becomes steeper with the increase of the flare productivity. Abramenko (2005a) also compared the multifractal properties of two regions characterized by different flare activity levels and found that the more flare productive region showed a higher level of multifractality. A similar investigation was carried out by Georgoulis (2005), who also presented the multifractal analyses as more suitable than the fractal one for flare forecasting. Statistical analysis of large samples of data have shown that variations of fractal properties of ARs in photosphere (Meunier 2004) and low chromosphere (Criscuoli et al. 2007) do not present clear trends with the activity cycle. On the contrary, McAteer et al. (2005) reported a correlation between variations of photospheric fractal properties of ARs with flare productivity.
Precursors to flares have also been looked for in the solar corona, where the sites of magnetic reconnection are usually located. Variations of magnetic field characteristics and topology in connection with occurrence of eruptive phenomena have been investigated (e.g. Ugarte-Urra et al. 2007; Schrijver 2009). Among the most recent studies, Barnes & Leka (2006) applied discriminant analyses to several properties of coronal fields above three active regions and concluded that coronal field descriptors are more efficient than photospheric ones to distinguish between flaring and non-flaring regions. Self-similarity is also a characteristic of coronal magnetic fields (e.g. Georgoulis 2005; Bélanger et al. 2007, and references therein). Aschwanden & Aschwanden (2008a,b) measured the fractal dimension of flare arcades and found it to be linearly correlated with the flare flux in EUV. Abramenko et al. (2008) estimated the intermittency of the magnetic field of an AR and found a time delay of about one day between the evolution of intermittency in photosphere and in corona. Vlahos & Georgoulis (2004) investigated properties of the magnetic discontinuities of the solar corona, i.e. regions characterized by magnetic field variations occurring on short scale lengths and where the nonpotential magnetic energy is accumulated. While most of these discontinuities remain relatively stable, a fraction of them may become unstable, thus causing rapid magnetic reconnection that releases the free magnetic energy and provides the energy content for flaring events. Vlahos & Georgoulis (2004) studied an active region characterized by no flare or subflare occurrence and an active region showing a number of subflares but no major flares over the course of several hours. They used linear force-free field extrapolations to calculate the 3D magnetic configuration and various selection criteria to identify these discontinuities. They found that the free magnetic energies and volumes contained in these discontinuities obey power-law distribution functions, with power-law indices for the free energies in the range [-1.6, -1.35].
In this paper, we extend the work presented in Paper I by investigating other properties of photospheric and coronal magnetic fields of the same sample of superactive regions. We consider the temporal evolution of some fractal and multifractal properties of the photospheric field, namely the generalized dimension and the contribution and dimensional diversities (Conlon et al. 2008) (see Sect. 3.1 for the definition of these parameters), estimated by the analyses of MDI magnetograms. We also investigate the evolution of the free energy distribution and the potentially unstable volume of the magnetic discontinuities (Vlahos & Georgoulis 2004) of the coronal field (see Sect. 3.2) as derived by force-free field extrapolation. We investigate the temporal correlation with the flare activity in order to single out the indicators that best describe the flare productivity potential of a region. We choose these indicators because they describe the topological complexity of the magnetic field in different layers of the solar atmosphere.
This paper is organized as follows. The data-set analyzed and the indicators employed for this study are described in Sects. 2 and 3, respectively. In Sect. 4 we present the results we obtained and in Sect. 5 we discuss them and draw our conclusions.
2 Data
According to criteria explained in Paper I, we selected
26 superactive regions (ARs) which appeared on the solar disk
during the middle of the 23th solar cycle, between
January 1st 2000 and December 31st 2006 and
characterized by a flare index (Li et al. 2004)
greater than 500, computed over time intervals of 50 h.
The X-ray flare index I computed over the time interval ![]() is defined as:
is defined as:
where Bh, Ci, Mj and Xk refer to the soft X-ray classification based on the flux in the 1-8
For each region we used MDI/SOHO line-of-sight full-disk
magnetograms taken during the time interval between the first and the
last flare, with a time resolution of 96 min and a plate scale of
1.98 arcsec/pixel. We considered only those magnetograms where the
longitudinal angular distance of the active region from disk center was
less than 41 degrees. Among these 26 ARs we neglected those for
which MDI showed a saturation effect in sunspot umbra (Liu et al. 2007),
thus reducing the analysis to 14 ARs. For each region we
considered a sub-field centered on the baricenter of the AR such that
the maximum magnetic flux imbalance was less than 20![]() .
Sub fields of size smaller than 100
.
Sub fields of size smaller than 100 ![]() 100 pixels were discarded. The number of magnetograms for each AR
selected according to these criteria is given in Table 1. Geometrical projection was compensated for by the ideproject Solar Soft routine (Freeland et al. 1998).
100 pixels were discarded. The number of magnetograms for each AR
selected according to these criteria is given in Table 1. Geometrical projection was compensated for by the ideproject Solar Soft routine (Freeland et al. 1998).
Table 1: Superactive regions
selected, correlation coefficients between the investigated indicators
and the flare index, average value of indicator ![]() .
.
For 7 ARs (marked with a ``*'' in Table 1), which have been observed by TRACE, we also considered high resolution images at 171 Å or 195 Å in order to investigate their coronal configuration.
3 Data analysis
From each line-of-sight magnetogram sub-field we computed 5 parameters, three of which describe fractal and multifractal properties of the photospheric magnetic field and two which describe the behavior of the upper level of the solar atmosphere above the selected ARs. Then we investigated the correlation between these properties and the flare index computed over temporal windows of 50 h.
3.1 Fractal and multifractal indicators
To investigate the fractal properties of ARs, we estimated the generalized fractal dimension D8 by using the box-counting technique. The computation of the Contribution Diversity ![]() and Dimensional Diversity
and Dimensional Diversity ![]() allowed us to investigate multifractal properties. As already pointed
out in Sect. 1, the literature concerning fractal and multifractal
studies in solar physics is quite extensive; here we summarize the main
points.
allowed us to investigate multifractal properties. As already pointed
out in Sect. 1, the literature concerning fractal and multifractal
studies in solar physics is quite extensive; here we summarize the main
points.
The most common method of estimating the fractal dimension of an
object given its image is box counting. It consists of covering the
image with boxes of different sizes ![]() and then estimating the slope of the linear relation
and then estimating the slope of the linear relation
where
where q is a real number,
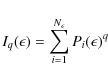
|
(4) |
and we have introduced the more compact notation
We choose D8 since it is less sensitive to spatial resolution and pixelization effects (Lawrence et al. 1996).
The strength of the measure ![]() is defined as
is defined as
where
The multifractal spectrum
![]() is defined as
is defined as
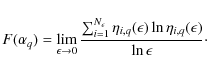
|
(7) |
It can be shown that, under the assumption
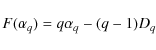
|
(8) |
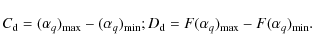
|
(9) |
Therefore, the contribution diversity and the dimensional diversity describe the variety of the concentration of the different structures in an image (spikes, filaments, clumpy structures) and of the their complexity. Following Conlon et al. (2008), the analysis was restricted to q>0, since numerical errors are larger for negative values of the exponent q.
![\begin{figure}
\par\mbox{\hspace*{1cm}\includegraphics[width=3cm,clip]{12044f1.p...
...s}\hspace*{0.25cm}
\includegraphics[width=3.8cm]{12044f9.ps} }
\par
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg37.png)
|
Figure 1:
Top: details of MDI magnetograms, acquired on 22 November 2000 04:51 UT ( left), 23 November 2000 11:20 UT ( center), 26 November 2000 19:11 UT ( right), showing the emergence phase of NOAA 9236. Middle: corresponding multifractal spectra. Bottom: corresponding distribution functions of total free energy. |
| Open with DEXTER | |
3.2 Volume and free magnetic energy of unstable magnetic discontinuities
For each magnetogram we performed a linear force-free field extrapolation to determine the 3D magnetic field configuration. We applied an extrapolation code based on the method introduced by Alissandrakis (1981), which assumes that the magnetic field is force-free not only in the corona but also in the lower levels and that it vanishes at infinity. In order to minimize the oscillatory behavior of the Fourier solutions, we put the original arrays of the data for the boundary in bigger arrays of double dimensions, before applying the extrapolation procedure. A consideration of the size of the integration box gives a resonant value of the force-free parameter. Below this value the periodicity effects inherent to the Alissandrakis method are reduced. Therefore, for each AR we fixed the force-free parameter just below the resonant value for the magnetogram with the largest field of view among the magnetograms of the same AR. Moreover, in order to investigate the sensitivity of our results to variation of this parameter, for 7 AR we also performed extrapolatons using the force-free parameters which best fit the coronal loops observed at 171 Å or 195 Å with TRACE.
Following the method used by Vlahos & Georgoulis (2004)
we applied a selection criterion based on the Parker angle in order to
identify potentially unstable regions inside each AR. In particular, we
considered as potentially unstable the location where the angular
difference between two adjacent magnetic field vectors was greater
than 30![]() .
Then, we computed the normalized total volume occupied by all the potentially unstable regions:
.
Then, we computed the normalized total volume occupied by all the potentially unstable regions:
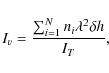
|
(10) |
where N is the number of the potentially unstable regions, ni is the number of adjacent locations inside each region,
We also measured the free magnetic energy Ei in each unstable region i consisting of a set of neighbouring grid points j where the instability criterion is met:
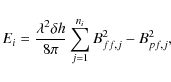
|
(11) |
with Bff,j and Bpf,j the magnetic field values deduced by the linear force-free field and the potential field, respectively. Note that this formula, which has been widely used in the literature (e.g. Jing et al. 2009; Bobra et al. 2008; Kusano et al. 2002), differs from the one reported in Vlahos & Georgoulis (2004) for reasons not known to these authors.
Considering the distribution function of the total free energy Ei in the selected discontinuities, we obtained a power law with a different power law index
![]() for each magnetogram. This indicator was estimated by a linear fit to
the logarithm of the total free energy distribution. Since the shapes
of the distribution functions evolve with time (see for instance
Figs. 1-3), we employed an automatic technique (McAteer et al. 2005) to determine the linearity ranges and perform the linear fits.
for each magnetogram. This indicator was estimated by a linear fit to
the logarithm of the total free energy distribution. Since the shapes
of the distribution functions evolve with time (see for instance
Figs. 1-3), we employed an automatic technique (McAteer et al. 2005) to determine the linearity ranges and perform the linear fits.
The difference between Iv and
![]() estimated
using force-free parameters obtained by the best fit of the observed
loops and using the resonant values are on average
estimated
using force-free parameters obtained by the best fit of the observed
loops and using the resonant values are on average ![]() for both quantities. These differences are lower than temporal variations measured for Iv and are within the error associated with the estimation of
for both quantities. These differences are lower than temporal variations measured for Iv and are within the error associated with the estimation of
![]() (see Sect. 4.1), thus showing that the choice of using as a
force-free parameter the magnetogram resonant value produces reasonable
results.
(see Sect. 4.1), thus showing that the choice of using as a
force-free parameter the magnetogram resonant value produces reasonable
results.
![\begin{figure}
\par\mbox{\hspace*{1cm}\includegraphics[width=3cm,clip]{12044f10....
...7.ps}\hspace*{0.25cm}
\includegraphics[width=3.8cm]{12044f18.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg44.png)
|
Figure 2:
Top: details of MDI magnetograms, acquired on 05 June 2000 00:00 UT ( left), 08 June 2000 04:48 UT ( center), 10 June 2000 16:00 UT ( right), showing the decay phase of NOAA 9026. Middle: corresponding multifractal spectra. Bottom: corresponding distribution functions of total free energy. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\hspace*{1cm}\includegraphics[width=3cm,clip]{12044f19....
...6.ps}\hspace*{0.25cm}
\includegraphics[width=3.8cm]{12044f27.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg45.png)
|
Figure 3:
Top: details of MDI magnetograms, acquired on 11 December 2001 06:27 UT ( left), 14 December 2001 09:36 UT ( center), 16 December 2001 09:36 UT ( right), showing the temporal evolution of NOAA 9733. Middle: corresponding multifractal spectra. Bottom: corresponding distribution functions of total free energy. |
| Open with DEXTER | |
4 Results
4.1 Temporal evolution of the indicators
We studied the temporal evolution of D8, ![]() ,
,
![]() ,
Iv and
,
Iv and
![]() for each superactive region. For some indicators, we found these variations to be dependent on the evolution of the ARs.
for each superactive region. For some indicators, we found these variations to be dependent on the evolution of the ARs.
![\begin{figure}
\par\mbox{\includegraphics[width=8.25cm,clip]{12044f28.ps}\hspace...
....ps} }
\par\mbox{\hspace*{4cm}{\bf (a)}\hspace*{8cm}{\bf (b)}}
\par
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg46.png)
|
Figure 4: Temporal variations of the estimated parameters for a) region NOAA 9236 and b) NOAA 9026 b). The squares in the last panel of b) indicate the Iv values deduced from the force-free field extrapolations performed using a best fit criterion with the loops observed by TRACE at that time. |
| Open with DEXTER | |
We found that for all the active regions characterized by an
emerging magnetic flux, the multifractal spectrum ``contracts'' and
gradually shifts toward higher values of both ![]() and
and
![]() .
As shown for instance in Fig. 1
for NOAA 9236, the MDI magnetograms taken on 22, 23 and
26 November 2000 (first row) show the emergence of flux in
photosphere, and the corresponding plots of multifractal spectra
(second row) show that the values of both
.
As shown for instance in Fig. 1
for NOAA 9236, the MDI magnetograms taken on 22, 23 and
26 November 2000 (first row) show the emergence of flux in
photosphere, and the corresponding plots of multifractal spectra
(second row) show that the values of both
![]() and
and ![]() increase, while the ranges of values spanned by these quantities gradually reduce. As already pointed out by Conlon et al. (2008),
who found similar results, this reflects the fact that magnetic flux
typically emerges fragmented in small-size features, which coalesce and
evolve into larger and more complex structures. On the contrary, during
the decay phase both
increase, while the ranges of values spanned by these quantities gradually reduce. As already pointed out by Conlon et al. (2008),
who found similar results, this reflects the fact that magnetic flux
typically emerges fragmented in small-size features, which coalesce and
evolve into larger and more complex structures. On the contrary, during
the decay phase both ![]() and
and
![]() decrease while the spectrum broadens, as illustrated in Fig. 2
for NOAA 9026. 1mm This probably reflects the fragmentation of the
magnetic field into less and less complex small-scale regions as
confirmed by the magnetograms shown in the first raw of Fig. 2.
decrease while the spectrum broadens, as illustrated in Fig. 2
for NOAA 9026. 1mm This probably reflects the fragmentation of the
magnetic field into less and less complex small-scale regions as
confirmed by the magnetograms shown in the first raw of Fig. 2.
For ARs in the emerging phase the fractal dimension D8 increases with time, while both multifractal indices ![]() and
and ![]() decrease, as shown for instance in Fig. 4a. The opposite is found for NOAA 9026 during its decay phase, as shown in Fig. 4b. In these plots t=0 corresponds to the time when the first flare was registered.
decrease, as shown for instance in Fig. 4a. The opposite is found for NOAA 9026 during its decay phase, as shown in Fig. 4b. In these plots t=0 corresponds to the time when the first flare was registered.
For regions observed around the maximum of their life, the evolution
of the multifractal spectrum is more complex. In general, we found that
the fractal dimension stays fairly constant, while larger variations of
multifractal indicators are observed at the emergence of new magnetic
flux. This is particularly evident, for instance, for NOAA 10030,
as shown in the appendix. Some cases also show that at the very
beginning of the decay phase, that is, during the hours after the
maximum of flux is measured, the fractal dimension continues to
increase and multifractal indicators to decrease. Figure 3
displays for instance the magnetograms and the corresponding
multifractal spectra of NOAA 9733 at the beginning of the
observations (left), at the moment in which the maximum total flux was
measured (center), and at the end of the observations (right).
Comparison of images in the left and middle columns shows that with the
emergence of new magnetic flux, both the number of compact larger
features and of fragmented smaller features increases. The former
result from the coalescence of ``old'' flux into larger and compact
features, whereas the latter are the signature of ``new'' emerged flux.
As a consequence, the multifractal spectrum broadens and
![]() ,
i.e. the fractal dimension of the largest scale structures,
decreases. The right column shows that, at the very beginning of the
decay phase, the small features coalesce into larger and more complex
regions, so that the spectrum ``contracts'' and shifts toward higher
values of both
,
i.e. the fractal dimension of the largest scale structures,
decreases. The right column shows that, at the very beginning of the
decay phase, the small features coalesce into larger and more complex
regions, so that the spectrum ``contracts'' and shifts toward higher
values of both
![]() and
and ![]() ,
although the total amount of magnetic flux is decreasing.
,
although the total amount of magnetic flux is decreasing.
On the other hand, the temporal evolution of Iv does not seem to be strictly correlated with the evolution of the magnetic flux in the photosphere. Although in some cases during the emerging phases Iv increases, as shown in Fig. 4a, and during the decaying phases it decreases, as shown in Fig. 4b, in other cases the amount of magnetic discontinuities changes independently from the magnetic flux observed in the photosphere. This result confirms that the coronal field extrapolated using the linear force-free approximation provides some independent information from the magnetic field above the level of the measurements. We also found that for most of the regions analyzed, Iv does not vary monotonically, but it is rather a discontinuous function of time. Square symbols in the plot of Iv in Fig. 4b represent the total unstable volume computed by using a force-free parameter derived from the comparison with TRACE data. The values obtained in this way are very close to the ones obtained when the force-free field parameter is fixed just below its resonant value.
The analysis of the temporal evolution of the distribution functions
of total free energy of unstable volumes shows that during the
emergence phase the peak of the distribution, as well as the linearity
range, shift gradually toward higher energy values, as shown for
instance in Figs. 1 and 3. On the contrary, temporal variations of the energy distribution of region NOAA 9026 (Fig. 2),
observed during the decay phase, do not seem to have a particular trend
with the evolution of the region. Variations with time of the slope of
the linear fits to the distributions (![]() indicator) are within the error bars and are not correlated with the evolution of the regions.
indicator) are within the error bars and are not correlated with the evolution of the regions.
4.2 Correlation with the flare index
In order to investigate the correlation of the magnetic field topology with the flare occurrence we reported the flare index and the other parameters in the same plots for each superactive region (see for instance Figs. 4a and b and Appendix A). We represented each single flare with a black bar whose height is proportional to the X-ray flare peak observed by GOES and the total of the flare index over 50 h with grey bars. We used the logarithmic scale to show the magnitude of different flares in the same plot.
We estimated for each AR the correlation coefficients between the considered indicators and the flare index computed over windows of 50 h. Results are reported in Table 1 (columns from 5 to 8).
In approximately 50% of the ARs we found that D8
is positively correlated with the flare index: 7 ARs have a
correlation coefficient larger than 0.5, with the highest value
of 0.88 for NOAA 10656. For the same ARs (except for
NOAA 10375) we obtained that ![]() and
and ![]() are anticorrelated with the flare index. The smallest correlation
coefficients between the multifractal parameters and the flare index
are -0.78 and -0.66 for NOAA 10365. For other regions the
correlation between fractal and multifractal indicators is almost null.
A comparison to total flux variation (see Appendix A) reveals
that most of these regions have been observed at about the maximum of
their evolution. The peculiar values found for NOAA 9733 are due
to the large decrease of the flare index at the beginning of the decay
phase, during which, as already pointed out in previous paragraph, D8 increases while
are anticorrelated with the flare index. The smallest correlation
coefficients between the multifractal parameters and the flare index
are -0.78 and -0.66 for NOAA 10365. For other regions the
correlation between fractal and multifractal indicators is almost null.
A comparison to total flux variation (see Appendix A) reveals
that most of these regions have been observed at about the maximum of
their evolution. The peculiar values found for NOAA 9733 are due
to the large decrease of the flare index at the beginning of the decay
phase, during which, as already pointed out in previous paragraph, D8 increases while ![]() and
and ![]() decrease.
decrease.
Figure 5 displayes the relation between the average fractal dimension D8 and the maximum measured for the flare index. In agreement with previous works (McAteer et al. 2005; Abramenko 2005b),
the plot suggests that more complex regions have a higher probability
of developing more intense and a larger number of flares. Nevertheless,
the large scatter of data does not allow us to derive an analytical
relation between D8 and the flare index. Note
that the correlation coefficient between these two quantities
is 0.7, while the correlation coefficients between the maximum
flare index and the average values of ![]() and
and ![]() are approximately -0.7. Interestingly, the correlation is 0.5 if D8 is averaged over the same 50 h time interval.
are approximately -0.7. Interestingly, the correlation is 0.5 if D8 is averaged over the same 50 h time interval.
From Table 1 we can see that there is a large scatter of correlation coefficients between flare indices computed over windows of 50 h and Iv. On the other hand, we noted that Iv shows more rapid variations than the fractal and multifractal parameters. Clear and strong increases of its value correspond to phases of particularly frequent and intense activity, as we can see around 100 h and 120 h from the beginning of our observation in NOAA 9236 and NOAA 9026, respectively (Figs. 4a and b)
As reported also by Vlahos & Georgoulis (2004) ![]() does
not show a particular trend with time, but it is interesting to notice
that the average value estimated during the observation time for our
superactive regions, except for NOAA 9733 and NOAA 10486, is
between -1.6 and -1.8 (see Table 1, last column).
does
not show a particular trend with time, but it is interesting to notice
that the average value estimated during the observation time for our
superactive regions, except for NOAA 9733 and NOAA 10486, is
between -1.6 and -1.8 (see Table 1, last column).
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{12044f30.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg49.png)
|
Figure 5: Maximum of the flare index versus average generalized fractal dimension D8 for the 14 ARs analyzed. |
| Open with DEXTER | |
5 Discussion and conclusions
We investigated the temporal evolution of the generalized fractal dimension, the contribution diversity, the dimensional diversity, the volume occupied by the potentially unstable regions and the power law index of the distribution function of the total free energy in 14 superactive regions. The first three quantities provide information about complexity of the magnetic field in the photosphere, while the other two provide information about magnetic field organization in the upper layers of the solar atmosphere. In particular, we investigated the variations of these indicators with the emergence of magnetic flux. With the exception of the fractal dimension, we have also employed these indicators for the first time for statistical studies aimed at the investigation of their correlation with flare productivity.
We found that fractal dimension and multifractal parameters are anticorrelated. During the emergence phase, the fractal dimension rapidly increases and multifractal parameters decrease. The opposite was observed during the decay phase. In the 'mature' phase, fractal dimension stays fairly constant, while larger variations have been observed for multifractal parameters. Movies reveal that these variations are usually due to the emergence of new magnetic flux. These findings are in agreement with results presented by Conlon et al. (2008), who also observed a rapid increase of multifractal parameters at the very beginning of the emergence phase. We do not find such an increase in our results, since we analyzed images taken after the observation of the first flare, that is, after the emergence of a large part of the magnetic flux. These results confirm the fact that magnetic flux emerges fragmented in the photosphere and then it evolves in more and more compact and complex regions. Moreover, the evolution of the magnetic field in the photosphere seems to influence the volume occupied by the magnetic discontinuities, that is the value of Iv and the distribution functions of the energy of unstable volumes, only in part. Of course, the more flux that emerges, the greater is the probability of formation of unstable regions. Nevertheless, the complexity of the magnetic field in the upper layers of the solar atmosphere can be largely increased by photospheric magnetic field dynamics (Choe & Cheng 2000), that fractal and multifractal studies do not properly take into account for.
We also analyzed the temporal evolution of the distribution
functions of the total energy of unstable volumes. We found that for
most of the observed regions, during the emergence phase the
distribution function peaks as well as the linearity range shift toward
higher energy values, while the slope of the linear fit (parameter ![]() )
does not vary significantly with the evolution of the region.
)
does not vary significantly with the evolution of the region.
In 6 ARs we found that the flare index is positively correlated with D8 and anticorrelated with ![]() and
and ![]() .
This indicates that in many cases the photospheric complexity is a
strong condition for flare production. On the other hand, the absence
of any correlation in the other ARs confirms that the evolution of the
photospheric magnetic field investigated by the fractal and
multifractal parameters might not clearly reflect the real complexity
of the AR in the upper levels of the solar atmosphere.
.
This indicates that in many cases the photospheric complexity is a
strong condition for flare production. On the other hand, the absence
of any correlation in the other ARs confirms that the evolution of the
photospheric magnetic field investigated by the fractal and
multifractal parameters might not clearly reflect the real complexity
of the AR in the upper levels of the solar atmosphere.
In agreement with previous works of McAteer et al. (2005) and Abramenko (2005b), we also found that more complex regions are more likely to develop flares. In particular, Abramenko (2005b) found that the power spectrum index of ARs magnetograms and the daily flare index are correlated and that their variation can be described by a power law. We do not find such a law in our data (see Fig. 5), most likely because our sample includes only superactive regions. Nevertheless, we also find good correlation between flare index and average fractal dimension of a region, and good anticorrelation between flare index and average multifractal indicators.
For Iv we did not find a significant correlation with the flare index computed over time windows of 50 h, but we noted a clear increase of this parameter during the phases when the ARs showed a burst of flares. This suggests that the presence of magnetic discontinuities plays an important role in the determination of the conditions useful for the occurrence of magnetic reconnection. Moreover, the fact that the flares occur more frequently while the volume of potentially unstable regions increases, indicates that the flare itself does not provide any mechanism to stop the formation of the instability regions. Therefore, we believe that the source of the current sheet formation should not be searched for only inside the discontinuities, but in the whole AR evolution.
Although we did not observe any significant variation with time of ![]() ,
we obtained average values of this indicator below the values obtained by Vlahos & Georgoulis (2004)
over two quiet ARs. This confirms the hypothesis of these authors
according to which the steeper the slope of the free energy
distribution function of unstable volumes of an AR, the higher is the
probability of flare production.
,
we obtained average values of this indicator below the values obtained by Vlahos & Georgoulis (2004)
over two quiet ARs. This confirms the hypothesis of these authors
according to which the steeper the slope of the free energy
distribution function of unstable volumes of an AR, the higher is the
probability of flare production.
We conclude that among the complexity parameters analyzed and for
the time resolution of the dataset, the generalized fractal
dimension ![]() and the potential unstable volume of magnetic discontinuities Iv
are the most suitable measurements to investigate the flare activity
over longer (50 h) and shorter (few hours) time intervals,
respectively. Moreover,
and the potential unstable volume of magnetic discontinuities Iv
are the most suitable measurements to investigate the flare activity
over longer (50 h) and shorter (few hours) time intervals,
respectively. Moreover, ![]() is less useful and is redundant if
is less useful and is redundant if ![]() is already estimated. This result is in contrast with results obtained in previous studies, such as Georgoulis (2005); Abramenko (2005a); Abramenko et al. (2008)
which reported variations in the degree of multifractality of ARs with
flare productivity. These discrepancies are likely due to the different
spatial and temporal resolution of our dataset and to the employment of
different multifractal estimators. In particular, Georgoulis (2005)
compared results obtained with different estimators and found that the
structure functions and their inertial-scale scaling exponents show
larger temporal variations than the spectrum of the generalized
dimension, that is, the variation of Dq (defined in Eq. (3)) with q, with flare occurrence. Since the multifractal spectrum is a function of Dq, our results confirm, through an analysis of a larger sample of data, results presented in Georgoulis (2005).
The different spatial and temporal resolution of the data employed in
this study can also contribute to explain the discrepancy of our
results.
is already estimated. This result is in contrast with results obtained in previous studies, such as Georgoulis (2005); Abramenko (2005a); Abramenko et al. (2008)
which reported variations in the degree of multifractality of ARs with
flare productivity. These discrepancies are likely due to the different
spatial and temporal resolution of our dataset and to the employment of
different multifractal estimators. In particular, Georgoulis (2005)
compared results obtained with different estimators and found that the
structure functions and their inertial-scale scaling exponents show
larger temporal variations than the spectrum of the generalized
dimension, that is, the variation of Dq (defined in Eq. (3)) with q, with flare occurrence. Since the multifractal spectrum is a function of Dq, our results confirm, through an analysis of a larger sample of data, results presented in Georgoulis (2005).
The different spatial and temporal resolution of the data employed in
this study can also contribute to explain the discrepancy of our
results.
A better spatial and temporal resolution is needed to investigate in detail our findings. Therefore, the analyses of MDI high resolution or HINODE/SOT data could provide a good test for our results. Larger samples of data and statistical techniques more sophisticated than the correlation, such as the one proposed by Barnes & Leka (2008), should be employed to evaluate the ability of complexity indicators to forecast flares.
AcknowledgementsThis work was supported by the European Commission through the SOLAIRE Network (MTRN-CT-2006-035484), by the Istituto Nazionale di Astrofisica (INAF), by the Agenzia Spaziale Italiana (contract ASI I/01510710, Studio Esplorazione Sistema Solare, sub-task 2210 Origine delle perturbazioni solari), by the Università degli Studi di Catania and by the Regione Lazio (progetto CVS). S.C also thanks I. Ermolli for useful discussions and support.
References
- Abramenko, V. I. 2005a, Sol. Phys., 228, 29 [NASA ADS] [CrossRef]
- Abramenko, V. I. 2005b, ApJ, 629, 1141 [NASA ADS] [CrossRef]
- Abramenko, V. I., & Longcope, D. W. 2005, ApJ, 619, 1160 [NASA ADS] [CrossRef]
- Abramenko, V. I., Yurchyshyn, V., & Wang, H. 2008, ApJ, 681, 1669 [NASA ADS] [CrossRef]
- Alissandrakis, C. E. 1981, A&A, 100, 197 [NASA ADS]
- Aschwanden, M. J., & Aschwanden, P. D. 2008a, ApJ, 674, 530 [NASA ADS] [CrossRef]
- Aschwanden, M. J., & Aschwanden, P. D. 2008b, ApJ, 674, 544 [NASA ADS] [CrossRef]
- Aschwanden, M. J., Nightingale, R. W., Tarbell, T. D., & Wolfson, C. J. 2000, ApJ, 535, 1027 [NASA ADS] [CrossRef]
- Balke, A. C., Schrijver, C. J., Zwaan, C., & Tarbell, T. D. 1993, Sol. Phys., 143, 215 [NASA ADS] [CrossRef]
- Barnes, G., & Leka, D. 2006, ApJ, 646, 1303 [NASA ADS] [CrossRef]
- Barnes, G., & Leka, D. 2008, ApJ, 688, L107 [NASA ADS] [CrossRef]
- Bélanger, E., Vincent, A., & Charbonneau, P. 2007, ApJ, 646, 1303
- Bobra, M. G., van Ballegooijen, A. A., & DeLuca, E. E. 2008, ApJ, 672, 1209 [NASA ADS] [CrossRef]
- Bushby, P. J., & Houghton, S. M. 2005, MNRAS, 362, 313 [NASA ADS] [CrossRef]
- Cattaneo, F., Emonet, T., & Weiss, N. 2003, ApJ, 588, 1183 [NASA ADS] [CrossRef]
- Chappell, D., & Scalo, J. 2001, ApJ, 551, 712 [NASA ADS] [CrossRef]
- Choe, G. S., & Cheng, C. Z. 2000, ApJ, 541, 449 [NASA ADS] [CrossRef]
- Conlon, P. A., Gallagher, P. T., McAteer, R. T. J., et al. 2008, Sol. Phys., 248, 297 [NASA ADS] [CrossRef]
- Criscuoli, S., Rast, M. P., Ermolli, I., & Centrone, M. 2007, A&A, 461, 331 [NASA ADS] [CrossRef] [EDP Sciences]
- Crouch, A. D., Charbonneau, P., & Thibault, K. 2007, ApJ, 662, 715 [NASA ADS] [CrossRef]
- Freeland, S. L., & Handy, B. N. 1998, Sol. Phys., 182, 497 [NASA ADS] [CrossRef]
- Georgoulis, M. K. 2005, Sol. Phys., 228, 5 [NASA ADS] [CrossRef]
- Georgoulis, M. K., & Rust, D. M. 2007, ApJ, 661, 109 [NASA ADS] [CrossRef]
- Halsey, T. C., Jensen, M. H., Kadanoff, L. P., Procaccia, I., & Shraiman, B. I. 1986, Phys. Rev. A, 33, 1141 [NASA ADS] [CrossRef]
- Hewett, R. J., Gallagher, P. T., McAteer, R. T. J., et al. 2008, Sol. Phys., 248, 311 [NASA ADS] [CrossRef]
- Jing, J., Chen, P. F., Wiegelmann, T., et al. 2009, ApJ, 696, 84 [NASA ADS] [CrossRef]
- Kusano, K., Maeshiro, T., Yokoyama, T., & Sakurai, T. 2002, ApJ, 577, 501 [NASA ADS] [CrossRef]
- Lawrence, J. K., Cadavid, A. C., & Ruzmaikin, A. A. 1995, Phys. Rev. E, 51, 316 [NASA ADS] [CrossRef]
- Lawrence, J. K., Cadavid, A. C., & Ruzmaikin, A. A. 1996, ApJ, 465, 425 [NASA ADS] [CrossRef]
- Lawrence, J. K., Cadavid, A. C., & Ruzmaikin, A. A. 1999, ApJ, 513, 506 [NASA ADS] [CrossRef]
- Leka, K. D., & Barnes, G. 2007, ApJ, 656, 1173 [NASA ADS] [CrossRef]
- Li, Y., Luhmann, J., Fisher, G., & Welsch, B. 2004, J. Atm. Solar-Terrestrial Phys., 66, 1261 [NASA ADS]
- Liu, Y., Norton, A. A., & Scherrer, P. H. 2007, Sol. Phys., 241, 185 [NASA ADS] [CrossRef]
- McAteer, R. T. J., Gallagher, P. T., & Ireland, J. 2005, ApJ, 631, 628 [NASA ADS] [CrossRef]
- Longcope, D. 2005, LRSP, 2, 7 [NASA ADS]
- Meunier, N. 1999, ApJ, 515, 801 [NASA ADS] [CrossRef]
- Meunier, N. 2004, A&A, 420, 333 [NASA ADS] [CrossRef] [EDP Sciences]
- Nesme-Ribes, E., Meunier, N., & Collin, B. 1996, A&A, 308, 2213
- Parker, E. N. 1988, ApJ, 330, 474 [NASA ADS] [CrossRef]
- Pietarila Graham, J., Danilovic, S., & Schüssler, M. 2009, ApJ, 693, 1728 [NASA ADS] [CrossRef]
- Romano, P., & Zuccarello, F. 2007, A&A, 474, 633 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I)
- Schrijver, C. J. 2007, ApJ, 655, 117 [NASA ADS] [CrossRef]
- Schrijver, C. J. 2009, AdSpR, 43, 739 [NASA ADS]
- Schrijver, C. J., Zwaan, C., Balke, A. C., Tarbell, T. D., & Lawrence, J. K. 1992, A&A, 253, 1 [NASA ADS]
- Song, H., Tan, C., Jing, J., et al. 2009, Sol. Phys., 254, 101 [NASA ADS] [CrossRef]
- Stein, R. F., & Nordlund, Å. 2006, ApJ, 642, 1246 [NASA ADS] [CrossRef]
- Stenflo, J. O., & Holzreuter, R. 2002, in SOLMAG 2002, proceedings of the Magnetic Coupling of the Solar Atmosphere Euroconference, ed. H. Sawaya-Lacoste, ESA SP, 505, 101
- Tandberg-Hanssen, E., & Emslie, G. 1988, The physics of solar flares, Cambridge Astrophys. Ser.
- Tao, L., Du, Y., Rosner, R., & Cattaneo, F. 1995, ApJ, 443, 434 [NASA ADS] [CrossRef]
- Ugarte-Urra, I., Warren, H. P., & Winebarger, A. R. 2007, ApJ, 662, 1293 [NASA ADS] [CrossRef]
- Vlahos, L., & Gergoulisa, M. K. 2004, ApJ, 603, L61 [NASA ADS] [CrossRef]
Online Material
Appendix A: Parameter evolution
In Figs. A.1-A.14 we report the evolution of the flare activity, total magnetic flux![\begin{figure}
\par\includegraphics[height=14cm]{12044f29.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg50.png)
|
Figure A.1:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f28.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg51.png)
|
Figure A.2:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f31.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg52.png)
|
Figure A.3:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f32.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg53.png)
|
Figure A.4:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f33.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg54.png)
|
Figure A.5:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f34.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg55.png)
|
Figure A.6:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f35.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg56.png)
|
Figure A.7:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f36.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg57.png)
|
Figure A.8:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f37.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg58.png)
|
Figure A.9:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f38.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg59.png)
|
Figure A.10:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f39.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg60.png)
|
Figure A.11:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f40.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg61.png)
|
Figure A.12:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f41.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg62.png)
|
Figure A.13:
Flare activity,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f42.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg63.png)
|
Figure A.14:
Flare activity,
|
| Open with DEXTER | |
Footnotes
- ... discontinuities
![[*]](/icons/foot_motif.png)
- Appendix A is only available in electronic form at http://www.aanda.org
All Tables
Table 1: Superactive regions
selected, correlation coefficients between the investigated indicators
and the flare index, average value of indicator ![]() .
.
All Figures
![\begin{figure}
\par\mbox{\hspace*{1cm}\includegraphics[width=3cm,clip]{12044f1.p...
...s}\hspace*{0.25cm}
\includegraphics[width=3.8cm]{12044f9.ps} }
\par
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg37.png)
|
Figure 1:
Top: details of MDI magnetograms, acquired on 22 November 2000 04:51 UT ( left), 23 November 2000 11:20 UT ( center), 26 November 2000 19:11 UT ( right), showing the emergence phase of NOAA 9236. Middle: corresponding multifractal spectra. Bottom: corresponding distribution functions of total free energy. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\hspace*{1cm}\includegraphics[width=3cm,clip]{12044f10....
...7.ps}\hspace*{0.25cm}
\includegraphics[width=3.8cm]{12044f18.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg44.png)
|
Figure 2:
Top: details of MDI magnetograms, acquired on 05 June 2000 00:00 UT ( left), 08 June 2000 04:48 UT ( center), 10 June 2000 16:00 UT ( right), showing the decay phase of NOAA 9026. Middle: corresponding multifractal spectra. Bottom: corresponding distribution functions of total free energy. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\hspace*{1cm}\includegraphics[width=3cm,clip]{12044f19....
...6.ps}\hspace*{0.25cm}
\includegraphics[width=3.8cm]{12044f27.ps} }\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg45.png)
|
Figure 3:
Top: details of MDI magnetograms, acquired on 11 December 2001 06:27 UT ( left), 14 December 2001 09:36 UT ( center), 16 December 2001 09:36 UT ( right), showing the temporal evolution of NOAA 9733. Middle: corresponding multifractal spectra. Bottom: corresponding distribution functions of total free energy. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.25cm,clip]{12044f28.ps}\hspace...
....ps} }
\par\mbox{\hspace*{4cm}{\bf (a)}\hspace*{8cm}{\bf (b)}}
\par
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg46.png)
|
Figure 4: Temporal variations of the estimated parameters for a) region NOAA 9236 and b) NOAA 9026 b). The squares in the last panel of b) indicate the Iv values deduced from the force-free field extrapolations performed using a best fit criterion with the loops observed by TRACE at that time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{12044f30.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg49.png)
|
Figure 5: Maximum of the flare index versus average generalized fractal dimension D8 for the 14 ARs analyzed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f29.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg50.png)
|
Figure A.1:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f28.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg51.png)
|
Figure A.2:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f31.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg52.png)
|
Figure A.3:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f32.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg53.png)
|
Figure A.4:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f33.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg54.png)
|
Figure A.5:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f34.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg55.png)
|
Figure A.6:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f35.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg56.png)
|
Figure A.7:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f36.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg57.png)
|
Figure A.8:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f37.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg58.png)
|
Figure A.9:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f38.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg59.png)
|
Figure A.10:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f39.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg60.png)
|
Figure A.11:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f40.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg61.png)
|
Figure A.12:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f41.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg62.png)
|
Figure A.13:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=14cm]{12044f42.ps}
\end{figure}](/articles/aa/full_html/2009/42/aa12044-09/Timg63.png)
|
Figure A.14:
Flare activity,
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.