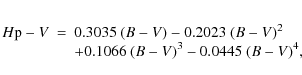| Issue |
A&A
Volume 506, Number 2, November I 2009
|
|
|---|---|---|
| Page(s) | 935 - 954 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912134 | |
| Published online | 27 August 2009 | |
A&A 506, 935-954 (2009)
Genetic inversion of sparse disk-integrated photometric data of asteroids: application to Hipparcos data
A. Cellino1,![]() - D. Hestroffer2
- P. Tanga3 - S. Mottola4
- A. Dell'Oro1
- D. Hestroffer2
- P. Tanga3 - S. Mottola4
- A. Dell'Oro1
1 - INAF, Astronomical Observatory of Torino, strada Osservatorio 20,
10025 Pino, Torinese, Italy
2 - IMCCE, Observatoire de Paris, 77 Av. Denfert Rochereau, 75014
Paris, France
3 - Laboratoire Cassiopée, Observatoire de la Côte d'Azur, BP 4229,
06304 Nice, France
4 - DLR, Institute of Planetary Research, Rutherfordstr. 2, 12489
Berlin, Germany
Received 23 March 2009 / Accepted 10 July 2009
Abstract
Context. The development of techniques for the
inversion of sparse disk-integrated photometric data of asteroids is a
very urgent task, due to the imminent commencements of large sky
surveys from both space (Gaia) and the ground (Pan-STARRS).
Aims. We developed a numerical algorithm for the
inversion of sparse photometric data of asteroids. An application to
real data collected in past by the Hipparcos satellite provided very
encouraging results.
Methods. The inversion method is based on the
application of a ``genetic'' algorithm approach. The objects are
assumed to have triaxial ellipsoid shape. However, it is shown by means
of simulations and applications to real data that this simplistic
choice does not cause any significant problems. The algorithm solves
for a number of unknown parameters, including the spin period, the
coordinates of the spin axis, the axial ratios of the ellipsoid, an
initial rotational phase corresponding to the first observation of a
given dataset, and the slope of a linear variation in the magnitude as
a function of solar phase. Additional parameters, describing some
possible albedo variegation of the surface, can also be introduced.
Results. The application of the inversion technique
to both simulations and a dataset of sparse photometric data obtained
some years ago by the Hipparcos satellite shows that the performance of
the algorithm is strongly encouraging, and the correct solution for the
rotational parameters is obtained in the majority of cases when a
reasonable number of observations are available.
Key words: minor planets, asteroids - techniques: photometric - methods: numerical
1 Introduction
Photometry has historically been one of the first observing techniques adopted to derive information about the physical properties of asteroids. In particular, a continuous periodic variation in the apparent brightness of these objects occurs as a consequence of their rotations and generally not spherical shapes (Russell 1906). Since the rotation periods are generally of the order of hours, continuous photometric measurements of an object over one or a few nights are usually sufficient to obtain what is generally called the lightcurve of an asteroid, namely a recording of its periodic brightness variation due to rotation.
The rotation period can then be derived from an analysis of the lightcurve. At the same time, the amplitude of the photometric variation also provides preliminary information about the overall shape of an object. Light curves obtained at different oppositions of the same object correspond to different observing circumstances, in particular in terms of orientation of the object's spin axis with respect to the direction of sight of the observer (the so-called aspect angle). As a consequence, the availability of light curves obtained at different apparitions (an apparition being the interval of time, usually some weeks, when an object is observable) makes it possible to determine the sky orientation of the spin axis (the asteroid ``pole''), and also gives a first-order approximation of an object's shape (Magnusson et al. 1989). In addition, the measurement of the light-curve maximum (or average) brightness from multiple observations during a single apparition is also useful. When observations are performed over a time span covering a sufficient range of different illumination conditions, described by the so-called phase angle (the angle between the directions to the Sun and to the observer as seen from the asteroid), it is possible to analyze the general variation in brightness observed for a given aspect angle, but at a variety of possible phase angles (``phase curve''). This information is an important input to the theories of scattering of sunlight by asteroidal surfaces, and, coupled with complementary polarimetric observations, provides information about some physical properties of asteroid surfaces (Kaasalainen et al. 2003; Muinonen et al. 2002).
According to the above considerations, it is clear that asteroid photometry can provide a wealth of useful physical information about these objects. It is also clear why observers have previously concentrated on obtaining full light curves of the objects, by means of continuous observations spanning over a time length sufficient to derive the period of the photometric variation. Based on these data, sophisticated methods of light-curve inversion have been developed to obtain estimates of not only the spin periods and poles, but also some fine details of the overall shapes of the objects (Kaasalainen et al. 2002, and references therein). These methods of light-curve inversion have been found to provide fairly accurate results as proven in the cases of objects visited in situ by space probes.
In the future, however, asteroid photometry will face new, exciting challenges. In particular, instead of dealing with data obtained in time-consuming observations aimed at obtaining full light curves, as in the past, some systematic sky surveys both from space (Gaia) and the ground (Pan-STARRS) will provide enormous data sets of sparse photometric data, namely photometric recordings obtained during systematic surveys of the entire sky, aimed at detecting all the objects transiting into the telescope field of view during the sky scanning process, to increasingly fainter limiting magnitudes. This means that any given asteroid will be observed many times, but every observation will only be a pure photometric snapshot covering a negligible fraction of the rotation period. The observations, however, will be repeated over several years, and the final result of these surveys will be a huge catalogue of sparse, instantaneous photometric recordings of tens of thousands of asteroids, most of them never photometrically observed before. A natural question thus arises, namely whether it will be possible to use these large catalogues of sparse data to derive information about the spin and shape properties of the objects, without having at disposal full light curves, but only single snapshots.
In this paper, we present the results of an analysis that we have been carrying out in the framework of the preparation of the pipeline of data reduction for the ESA Gaia mission. We show that our answer to the previous question is affirmative, i.e., yes, we expect to be able to successfully invert, using a suitable model, Gaia disk-integrated photometric snapshots of asteroids sparsely observed over a time span of five years. In the following sections, we present our approach to the problem of the inversion of sparse photometric data, we show the results of the inversion of a variety of simulated Gaia data, and finally we apply our inversion method to a data set of real asteroid photometric data acquired by the Hipparcos satellite, in a way similar, albeit on a smaller scale, to that expected for Gaia.
2 Asteroid photometry: a few basic concepts
The apparent magnitude of an asteroid observed at any given instant is a complicated function of many parameters. First, and obvious, it depends on the distance of the object from both the Sun and the Earth. Apart from the cases of newly discovered objects, these parameters are generally known to great accuracy, and can be easily accounted for, since the brightness trivially decreases as the square of these distances. In a more subtle way, the apparent magnitude observed at a given instant depends on the distance of the object from the Earth because of the need to apply also a light-time correction due to the finite speed of light. The resulting epoch correction, of the order of several minutes for main belt asteroids, is important and must be taken into account. The inversion of sparse photometric data is thus carried out using sets of magnitudes reduced to a unit distance from Sun and Earth, and corresponding light time-corrected epochs of observation.
In addition, the apparent magnitude of an object also depends on a number of physical parameters that are far less easily determined a priori. The determination of these parameters represents a major goal of any technique of photometry inversion. In particular, the amount of scattered sunlight received by the observer depends on both properties on macroscopic scales, such as the size and shape of the object, the macroscopic surface roughness, the presence of shadows cast by local terrain elevations, the presence of concavities (such as those associated with impact craters), as well as on properties of the surface on small and microscopic scales, such as the texture of the soil, the albedo of the particles present on the surface layer, the relative abundances of different kinds of minerals among the surface regolith particles, and the resulting complex refractive index of the surface material, to name just a few examples. It is difficult to differentiate between the effects of the different actors playing in this complex game. The main observable feature related to the light scattering properties of the surface, as well as to the varying defect of illumination at different phase angles, is the phase - brightness relation, which consists of an overall linear decrease in the magnitude with increasing solar phase, and a non-linear magnitude surge at very low phase angles. The so-called (H, G) system is presently adopted by the IAU to describe this general behaviour (Bowell et al. 1989).
In addition, the brightness of an object varies continuously because its rotation around its spin axis steadily produces a change in the illuminated fraction of the surface visible by the observer. The resulting light variation is intrinsically periodic, but the resulting cyclic brightness variation does not repeat perfectly over consecutive spin periods, because of the superposition of other, independent effects. In particular, during the time of a full rotation of the object, the orbital motion of both the Earth and the asteroid produces a small, steady change in the observing geometry. Superimposed on the periodic variation due to the rotation (the lightcurve), there is then also the effect of varying apparent brightness caused by the change in the phase angle (illumination conditions), as discussed above. This effect is well known to those who have ever attempted for a given asteroid to combine photometric data collected during consecutive nights into a single lightcurve. In the case of near-Earth objects, which can be observed over a wider interval of phase angles because of their greater proximity to Earth, during a single apparition the objects tend also to have a fairly rapid change in aspect angle, which in turn is responsible for a corresponding progressive magnitude variation because of the change in the average illuminated cross-section visible to the observer.
In spite of all these difficulties, the analysis of asteroid light curves has a long tradition of successful determinations of both the rotational properties (spin period and pole orientation) and the overall shapes of several asteroids, as confirmed by observations in situ by space probes and/or by radar data (Kaasalainen et al. 2002). This is encouraging, because it shows that the observed light curves of real asteroids can be used to infer a great deal of physical information about these objects. At the same time, this also suggests that the apparent brightness of an object at any given epoch may in principle be predictable, if one has at disposal some suitable model. This model, however, can rarely include in practice a full, detailed treatment of the whole variety of physical processes that should be taken into account by a rigorous and complete analytic theory. Apart from the intrinsic difficulty of developing a model of such complexity, because of limits to our knowledge of several processes responsible for the observed photometric features, one should recall that in practical situations one has only a limited amount of photometric observations that can be fitted by model predictions; it is then neither practical nor useful to increase unnecessarily the number of free model parameters. When analysing a limited amount of sparse photometric data, a reasonable approach is thus to introduce a photometric model based on the smallest possible number of parameters determining the overall photometric behaviour of an object, by attempt to merge the effects of many different physical effects into a limited number of simple functions of a few parameters.
We note that the general feasibility of the inversion of sets of photometric data obtained from sparse observations of convex-shape asteroids, in cases in which the data cover a sufficiently wide variety of observing circumstances, was first demonstrated in the pioneering work by Kaasalainen (2004), while later results were published by Durech et al. (2007). The possibility of inverting a set of photometric measurements including both sparsely and frequently sampled (light-curve) data, was shown by Durech et al. (2009). In the remainder of this paper, however, we describe our own approach to the inversion problem of a set of sparse (only) photometric data.
3 The photometry inversion problem: our approach
In our approach we make a number of assumptions. First, we assume that the body is in a simple rotation state and has a surface with optical properties that can be modelled by a simple geometric scattering law. Second, we assume that the objects have the shapes of triaxial ellipsoids. This assumption, which appears arbitrary and possibly inaccurate, has been applied widely in the past in several analyses, and specifically to the derivation of asteroid poles (see Magnusson et al. 1989, for a classical review of this subject). More generally, the meaning of our shape assumption is certainly not that we believe that real objects are perfect triaxial ellipsoids. To be clearer, we use the triaxial shape only as a model parameter to describe the object and perform our fit. In this way we can derive the rotational parameters, and, as a bonus, also an idea of the elongation of the body. Our purpose is therefore to determine the triaxial ellipsoid shape that most closely resembles the true shape of a given object. Coupled with a spin period, a pole direction, and a magnitude-phase relation, this shape may be used to fit a given set of sparse photometric snapshots taken at different epochs. This best-fit model ellipsoid may be more or less close to the true shape in different cases. Of course, because of its symmetry, a triaxial ellipsoid shape cannot be expected to fit very accurately objects with very irregular shapes, and/or concavities and/or albedo spots that produce strongly asymmetric light-curve maxima and minima, although we know that these cases do exist in the real world. On the other hand, however, we do not expect that our simple shape assumption can systematically lead to dramatic errors. A triaxial ellipsoid shape is intrinsically fairly flexible and convenient to reasonably fit a large variety of possible convex shapes, as also shown by Torppa et al. (2008). As another example, in the past, the shapes of fragments produced in laboratory data of catastrophic break-up processes have been conveniently expressed, for sake of simplicity, in terms of axial ratios of circumscribed triaxial ellipsoids (Capaccioni et al. 1984), and the resulting axial ratios have been used to infer general information about the shapes of fragments produced in collisional processes. Numerical models capable deriving more refined shapes from sets of photometric data do exist and have been successfully applied in many cases (Kaasalainen et al. 2002). We do not exclude the possibility of implementing them in some future development of our model, but for the moment we limit ourselves to triaxial ellipsoid shapes, because we wish to minimize the CPU time required, as explained below.
In particular, our choices are dictated mainly by one practical application that we have in mind, namely the reduction of future photometric data of asteroids obtained by the Gaia mission. Since Gaia will in general not produce an extremely large number of observations per object (the average expected number being of the order of 70), we wish to verify whether our simple model can be sufficient to obtain reasonably good inversions in most cases. Later, we could consider using complex inversion in cases that show peculiar photometric properties or that refuse to converge with our method. We also note that the need to minimize the CPU time requirements is accompanied by the need to produce an automated, standard procedure for working on large amounts of data in unattended runs.
An assessment of the true effectiveness of the triaxial ellipsoid approach must of course be made a posteriori by means of both numerical simulations and application to real photometric data. This is the main subject of this paper, as shown in the following sections.
Following our approach, we must invert a set of sparse photometric data using a model that contains the following unknown and adjustable parameters, to be determined by the inversion algorithm:
- the sidereal rotation period of the object: P (expressed in hours);
- the (J2000 ecliptic in our implementation) coordinates of
the asteroid pole:
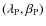 ;
;
- the axial ratios b/a and c/a of the triaxial ellipsoid shape;
- an initial rotational phase
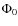 of the object corresponding to a given epoch, in our case chosen as the
epoch of the first observation in the available dataset;
of the object corresponding to a given epoch, in our case chosen as the
epoch of the first observation in the available dataset;
- the coefficient k of a linear relation of magnitude variation as a function of the phase angle.
We note that our method allows us to distinguish between
prograde and retrograde rotation, since we analyse photometric
snapshots taken at a number of precise epochs, and not simply
light-curve amplitude and maximum brightness, as in typical pole
determination models used in the past by different authors. As a
consequence, no ambiguity related to the sense of rotation affects our
pole
solutions. On the other hand, the ![]() ambiguity in the longitude of the pole that is present when the orbital
inclination is small, cannot be totally eliminated by our method, but
we see that this problem does not have a significant effect in many
practical applications.
Third, we assume that the (reduced to unit distance) magnitude of the
object varies linearly with phase angle. This assumption is known to be
quite realistic for observations obtained in the interval of phase
angles covered by future Gaia observations, namely between about 10 and
30 degrees for main-belt asteroids. Our assumption, however,
is stronger, namely that this linear slope does not change for
different aspect angles (different apparitions of the object). Fourth,
we carry out our analysis in terms of magnitude differences with
respect to a reference observation (usually, the one corresponding to
the first epoch in a given photometric dataset). In this way, we
automatically remove from the magnitude data any instrumental constants
that are not relevant to our
inversion purposes.
ambiguity in the longitude of the pole that is present when the orbital
inclination is small, cannot be totally eliminated by our method, but
we see that this problem does not have a significant effect in many
practical applications.
Third, we assume that the (reduced to unit distance) magnitude of the
object varies linearly with phase angle. This assumption is known to be
quite realistic for observations obtained in the interval of phase
angles covered by future Gaia observations, namely between about 10 and
30 degrees for main-belt asteroids. Our assumption, however,
is stronger, namely that this linear slope does not change for
different aspect angles (different apparitions of the object). Fourth,
we carry out our analysis in terms of magnitude differences with
respect to a reference observation (usually, the one corresponding to
the first epoch in a given photometric dataset). In this way, we
automatically remove from the magnitude data any instrumental constants
that are not relevant to our
inversion purposes.
Based on this model, it is easy to compute the photometric behaviour of any given object, provided a set of epochs of observation and corresponding observing circumstances. In particular, it is possible to use analytic functions to compute the apparent illuminated area of a triaxial ellipsoid object in different observing circumstances corresponding to different locations of the sub-Earth and sub-solar points (the points of the object's surface intersected by the two lines connecting the centre of the object to the Earth's and Sun's centers, respectively) at different epochs. In this respect, another advantage of the triaxial ellipsoid approximation is that one can write the equation that describes the object in a cartesian (x,y,z) frame, where the coordinate axes are aligned with the principal axes of inertia of the object. As a consequence, one can assume that the spin axis coincides with the z axis, and no complicated computation of the orientation of the inertia axes by means of a diagonalization of the inertia tensor is necessary, as would be the case when considering more complicated shapes. Of course, we also assume that the object is not in a tumbling rotation state.
Given the rotational phase of the object at a reference epoch,
corresponding to a given observing circumstance, we use the analytical
formulae from Pospieszalska-Surdej
& Surdej (1985) to compute the fraction of the
illuminated surface visible to the observer. In more detail, at a given
epoch the apparent illuminated cross-section of the supposedly triaxial
ellipsoid object, as seen by the observer, is characterized by four
angles: the phase angle ![]() ,
the rotation angle
,
the rotation angle ![]() ,
the aspect angle
,
the aspect angle ![]() ,
and the obliquity angle
,
and the obliquity angle ![]() .
The meaning of the phase angle, describing the illumination of the
surface by the Sun, has already been mentioned. The rotation angle
corresponds to the rotational phase of the object at the given epoch.
The aspect angle
.
The meaning of the phase angle, describing the illumination of the
surface by the Sun, has already been mentioned. The rotation angle
corresponds to the rotational phase of the object at the given epoch.
The aspect angle ![]() is the angle between the direction of the object's spin axis and the
direction to the observer. The obliquity angle
is the angle between the direction of the object's spin axis and the
direction to the observer. The obliquity angle ![]() is the angle between the plane containing the
observer, the object, and its spin axis, and the plane containing the
observer and the object, and perpendicular to the object-observer-Sun
plane. When
we know the above angles and the semi-axes a>b>c
that describe the triaxial ellipsoid shape of the object, the visible
illuminated surface S measurable by the observer is
given by
is the angle between the plane containing the
observer, the object, and its spin axis, and the plane containing the
observer and the object, and perpendicular to the object-observer-Sun
plane. When
we know the above angles and the semi-axes a>b>c
that describe the triaxial ellipsoid shape of the object, the visible
illuminated surface S measurable by the observer is
given by
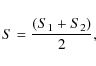 |
(1) |
where S1 and S2 are given by the following expressions
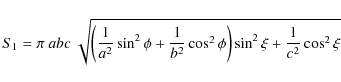 |
(2) |
and
 |
(3) |
where V11, V12, V22 are

In practice, since we compute only magnitude differences between observations obtained in different epochs, in the formulae above we fix a = 1, and we substitute b and c with the axial ratio parameters b/a and c/a.
From the computation of the visible illuminated surface at any chosen reference epoch, it is then possible to compute the resulting differences of apparent magnitude for observations at any other given epochs. This computation also includes the effect of the magnitude-phase variation, assumed to be simply linear, as explained above. On the other hand, no law of limb-darkening or other scattering model that differs from a purely geometric approach is included in this step. In other words, the effect of light scattering is only implicitly taken into account by the assumed linear relation of the magnitude as a function of the phase angle.
We note that we developed different versions of our inversion
algorithm, some of which include some additional parameters, such as a
coefficient taking into account the effect of an increase in lightcurve
amplitude as a function of phase angle (Zappala
et al. 1990), or the presence of some possible
albedo spots on the asteroid surface. The latter is particularly suited
to one specific case, namely that of (4) Vesta (see Sect. 5). In what
follows, however, we describe the results obtained using a standard
algorithm that takes into account only the set of seven unknown
parameters P, ![]() ,
,
![]() ,
b/a, c/a,
,
b/a, c/a,
![]() ,
and k listed above, without further complications.
The main reason is that we checked that the inclusion of further model
complications does not produce in general any significant improvement
in the final results of our inversion attempts, both in simulated cases
and in the case of real Hipparcos data. In particular, for instance,
the inclusion of one albedo spot in the model may occasionally produce
superior fits for a few individual objects, but at the cost of
introducing additional parameters that make the inversion algorithm
less stable and more time consuming without producing relevant
improvements in the vast majority of cases, according to our results.
,
and k listed above, without further complications.
The main reason is that we checked that the inclusion of further model
complications does not produce in general any significant improvement
in the final results of our inversion attempts, both in simulated cases
and in the case of real Hipparcos data. In particular, for instance,
the inclusion of one albedo spot in the model may occasionally produce
superior fits for a few individual objects, but at the cost of
introducing additional parameters that make the inversion algorithm
less stable and more time consuming without producing relevant
improvements in the vast majority of cases, according to our results.
The problem of photometric inversion therefore consists of
processing a given sample of photometric data, and being able to find a
set of model parameters that provides the best-fit to the data. The
goodness of the fit can be quantitatively evaluated by defining a
metric. Our choice was that of minimizing the parameter

where Oi and Ci are, respectively, the observed and computed magnitudes of the ith observation, wi is the assigned statistical weight of the ith observation (assumed to be the inverse of the nominal uncertainty in the measurement), and N is the number of photometric observations for a given object. More particularly, in computing the residuals we apply to the observed (or simulated) data statistical weights inversely proportional to their nominal error bars. Our
3.1 A ``genetic'' algorithm
The inversion algorithm that we developed is based on an
approach inspired by the mechanisms acting in the evolution of
biological organisms, and more generally on the concept of ``survival
of the fittest''. This kind of approach has been adopted by a variety
of scientific disciplines, because in many situations if offers a
number of advantages with respect to more conventional and
CPU-consuming numeric techniques. In our implementation, the basic idea
is to treat the possible solutions of the photometric inversion process
as individuals subject to a process of evolution. Each solution
consists of a set of possible values of the seven unknown physical
parameters described above. This set of parameters can be seen as the
``DNA'' of the solution. The strongest individuals in this framework
are those that are ``more adapted to their environment'', that is those
that produce a closer fit to the set of photometric data to be
inverted. At the very beginning, the numerical program produces a set
of a very large number ![]() of random individuals, namely
of random individuals, namely ![]() possible solutions generated by a completely random choice of the
solution parameters. In particular, after some tests we decided to
choose
possible solutions generated by a completely random choice of the
solution parameters. In particular, after some tests we decided to
choose ![]() .
The quality of the fit generated by each solution at this stage,
evaluated by means of the
.
The quality of the fit generated by each solution at this stage,
evaluated by means of the ![]() parameter defined above, is generally very low, as can be easily
expected for a completely random choice of the solution parameters. We
note, in this respect, that the required accuracy of the spin period,
for a photometric survey covering five years such as Gaia, is superior
to 1 second of time, to ``keep in phase'' the photometric data over a
time interval of a few years.
parameter defined above, is generally very low, as can be easily
expected for a completely random choice of the solution parameters. We
note, in this respect, that the required accuracy of the spin period,
for a photometric survey covering five years such as Gaia, is superior
to 1 second of time, to ``keep in phase'' the photometric data over a
time interval of a few years.
The 30 000 random solutions are sorted according to
their fit to the photometric dataset, and only the tightest ![]() solutions (those producing the
solutions (those producing the ![]() smallest
smallest ![]() residuals) are kept for the further steps of the procedure. The optimal
value of
residuals) are kept for the further steps of the procedure. The optimal
value of ![]() was found in practice to be between 50 and 100, based on the resulting
CPU execution times and accuracy of the results in a wide variety of
simulations. At this stage, the ``genetic loop'' is switched on. At
each step, one new ``baby'' solution is generated. This is randomly
achieved by means of one of two possible procedures. The first option
is to produce a coupling of two different ``parent'' solutions randomly
taken among the top-
was found in practice to be between 50 and 100, based on the resulting
CPU execution times and accuracy of the results in a wide variety of
simulations. At this stage, the ``genetic loop'' is switched on. At
each step, one new ``baby'' solution is generated. This is randomly
achieved by means of one of two possible procedures. The first option
is to produce a coupling of two different ``parent'' solutions randomly
taken among the top-
![]() list. In this case, the baby solution inherits its DNA from its
parents. In particular, each solution parameter of the baby is taken
randomly from the corresponding parameter of one of the two parents.
The second option is a random mutation of the DNA of one single
solution belonging to the top-
list. In this case, the baby solution inherits its DNA from its
parents. In particular, each solution parameter of the baby is taken
randomly from the corresponding parameter of one of the two parents.
The second option is a random mutation of the DNA of one single
solution belonging to the top-
![]() list. In this case, the newly born solution takes all its set of
physical parameters from a single parent solution, but one (or,
possibly, more than one, but with a lower probability) of its
parameters is
randomly changed. Independent of the procedure of its generation, the
residuals of the new baby solution are computed, in terms of the
list. In this case, the newly born solution takes all its set of
physical parameters from a single parent solution, but one (or,
possibly, more than one, but with a lower probability) of its
parameters is
randomly changed. Independent of the procedure of its generation, the
residuals of the new baby solution are computed, in terms of the ![]() parameter, and when this is sufficiently low to enter the top-
parameter, and when this is sufficiently low to enter the top-
![]() list, the new solution is retained in the position corresponding to its
ranking, while the previously worst solution of the list is dropped
from the list.
list, the new solution is retained in the position corresponding to its
ranking, while the previously worst solution of the list is dropped
from the list.
This procedure is repeated many times (between
300 000 and 1 000 000 in different
experiments), and at the end the best solution of the top-
![]() list represents the final solution of
the inversion attempt. Because of the random path in the ``evolution
tree'' followed by the algorithm, however, it is not necessarily true
that each genetic attempt always converges to a unique, and optimal,
solution. Several times, the evolution tree follows some ``dead
branch'' in the space of the parameters, and the resulting solution is
inadequate for fitting the observations. For this reason, the genetic
algorithm is applied some tens of times, (between 20 and 80 in
different experiments) to the same set of observations, and the best
solutions found in each attempt are retained and compared. Although the
differences between the resulting
list represents the final solution of
the inversion attempt. Because of the random path in the ``evolution
tree'' followed by the algorithm, however, it is not necessarily true
that each genetic attempt always converges to a unique, and optimal,
solution. Several times, the evolution tree follows some ``dead
branch'' in the space of the parameters, and the resulting solution is
inadequate for fitting the observations. For this reason, the genetic
algorithm is applied some tens of times, (between 20 and 80 in
different experiments) to the same set of observations, and the best
solutions found in each attempt are retained and compared. Although the
differences between the resulting ![]() values of different solutions may in several cases be quite small,
little more than 0.001 mag, the tightest
solution among those resulting from this procedure have always been
found so far to correspond to the correct solution in all the extensive
set of simulations performed up to now. The best solution
is usually found more than once among the different genetic attempts,
and this fact is exploited to derive, from the tiny differences among
the exact values of the parameters found for the best solution in
several attempts, the nominal uncertainty in each of the solution
parameters. We note that ``tiny'', here, means differences of the order
of a few 0.00001 h in period, of one
degree in pole location, of 0.01 in the axial ratios, or less, and of
0.001 in k. These differences correspond to
resulting
values of different solutions may in several cases be quite small,
little more than 0.001 mag, the tightest
solution among those resulting from this procedure have always been
found so far to correspond to the correct solution in all the extensive
set of simulations performed up to now. The best solution
is usually found more than once among the different genetic attempts,
and this fact is exploited to derive, from the tiny differences among
the exact values of the parameters found for the best solution in
several attempts, the nominal uncertainty in each of the solution
parameters. We note that ``tiny'', here, means differences of the order
of a few 0.00001 h in period, of one
degree in pole location, of 0.01 in the axial ratios, or less, and of
0.001 in k. These differences correspond to
resulting ![]() values differing by less than 0.001. In more detail, the number of
genetic attempts in the most recent applications of the algorithm is no
longer determined a priori, but is based on the criterion of ranging
between a minimum number of 20, up to a maximum corresponding to the
number of attempts needed to derive at least five times the same
optimal solution.
values differing by less than 0.001. In more detail, the number of
genetic attempts in the most recent applications of the algorithm is no
longer determined a priori, but is based on the criterion of ranging
between a minimum number of 20, up to a maximum corresponding to the
number of attempts needed to derive at least five times the same
optimal solution.
We give now a couple of small technical details. First, in
cases in which it is evident that after a large number of genetic steps
in a single inversion attempt the resulting solution does not evolve to
produce acceptable residuals, where the ![]() parameter remains above values of some tenths of magnitude (``dead
branch'' in the evolution), this particular genetic attempt is stopped
prematurely (usually after 600 000 steps) to save CPU
time. Second, we have seen that a means of accelerating considerably
the convergence of the genetic algorithm to the correct solution,
mainly for the rotation period of the object, consists of introducing
at each step a very small ``transcription error'' in the ``DNA'' of the
generated ``baby solution''. In practice, this is equivalent to
introduce a tiny random variation in all the solution parameters
inherited by the parent solution(s). This was empirically discovered in
our numerical experiments. Finally, we remark that the total CPU time
needed to perform a full inversion consisting of 50 genetic attempts,
depends on the number of single photometric observations to be
inverted. For the cases considered so far (a few tens of observations),
the corresponding time is of the order of thirty minutes using a
commercial, 2006 generation, 64-bit server. The numerical program is
currently written in FORTRAN 77, while a Java version has been
developed for the Gaia data analysis pipeline, and is now being tested.
parameter remains above values of some tenths of magnitude (``dead
branch'' in the evolution), this particular genetic attempt is stopped
prematurely (usually after 600 000 steps) to save CPU
time. Second, we have seen that a means of accelerating considerably
the convergence of the genetic algorithm to the correct solution,
mainly for the rotation period of the object, consists of introducing
at each step a very small ``transcription error'' in the ``DNA'' of the
generated ``baby solution''. In practice, this is equivalent to
introduce a tiny random variation in all the solution parameters
inherited by the parent solution(s). This was empirically discovered in
our numerical experiments. Finally, we remark that the total CPU time
needed to perform a full inversion consisting of 50 genetic attempts,
depends on the number of single photometric observations to be
inverted. For the cases considered so far (a few tens of observations),
the corresponding time is of the order of thirty minutes using a
commercial, 2006 generation, 64-bit server. The numerical program is
currently written in FORTRAN 77, while a Java version has been
developed for the Gaia data analysis pipeline, and is now being tested.
4 A simulation of the Gaia sky survey
The development of the photometric inversion algorithm based on a genetic approach has been possible only by the simultaneous development of simulation algorithms aimed at generating sets of simulated photometric data, to test the performances of the inversion algorithm, and to explore its applicability conditions, in terms of minimum amounts of observations and minimum photometric accuracy required to obtain a reasonable data inversion.
In principle, it is interesting to explore the general requirements in terms of different possible distributions of the data in time and sky locations, corresponding to a variety of possible asteroid photometric surveys. In practice, since the photometric inversion algorithm has been developed with a specific application in mind, namely the asteroid photometric dataset that will be produced by the Gaia space mission, most simulations have been done in such a way as to mimic specifically this particular situation.
In particular, disk-integrated photometry simulations represent an important part of more general simulation software developed to predict the observing circumstances and the corresponding signals that will be received in the focal plane during the planned Gaia survey of Solar System objects. This software was developed primarily by F. Mignard at the Observatory of Nice (France) and by one of us (PT).
4.1 Simple triaxial ellipsoid models
The implementation of disk-integrated photometry observations of simulated triaxial ellipsoid asteroids was done as part of the numerical simulator of the Gaia sky survey. The most general part of this software includes an accurate simulation of all the single detections of currently known asteroids by the Gaia satellite during a nominal mission lifetime of five years. In the simulations, it was assumed that the beginning of the survey will start on January 1, 2010. This is irrelevant, however, since from a statistical perspective different starting epochs are fully equivalent when large numbers of asteroids are taken into account as in the case of this simulation.
Having chosen a triaxial ellipsoid model for the shape of the simulated objects, the basic photometric algorithm used to compute the magnitudes is practically identical to that used by the inversion algorithm. In particular, as a first step, the magnitudes were computed by assuming a pure geometric scattering of sunlight (i.e., a scattered intensity proportional to the visible and illuminated asteroid cross-section). The only relevant difference between the Gaia photometry simulator and the photometric algorithm implemented in the inversion program is that in the Gaia survey simulator, the dependence of the asteroid magnitude upon the phase angle was described using the (H, G) system, whereas the inversion algorithm simply uses a linear variation in magnitude as a function of the phase angle. In practical terms, however, when dealing with main-belt asteroids these two options are largely equivalent, because for the range of phase angles covered by Gaia for these targets, the trend described by the (H, G) system is practically linear. As a first step, we decided to produce ideal photometric data unaffected by any observational error. This kind of test was aimed mainly at checking that the overall inversion algorithm works in an ideal situation, in which the simulated objects display magnitudes that correspond exactly to the photometric model assumed by the inversion algorithm. A failure to invert these data would imply that the overall genetic approach is seriously flawed.
The photometric simulator was then extensively used in a series of blind tests. In these tests, simulations of Gaia disk-integrated photometric measurements of a variety of different triaxial ellipsoid objects with orbits belonging mostly but not exclusively to the asteroid main belt were performed. In each simulation, a full set of sparse photometric data were generated, and used to feed the inversion algorithm, to test its ability to determine the physical parameters used in producing the simulated data. A wide variety of different rotation periods, pole coordinates, and shape parameters were generated in a large number of numerical experiments.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg1.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg25.png) |
Figure 1: Comparison of a set of simulated magnitudes collected by Gaia for a triaxial-ellipsoid object having the same orbit of the asteroid (3) Juno, and the corresponding magnitudes resulting from the obtained photometric inversion solution. Magnitudes are expressed in terms of differences with respect to the first observation, and are plotted against ecliptic longitude. Simulated and inversion solution data are displayed using different symbols. |
| Open with DEXTER | |
The results of this preliminary series of tests were highly positive. We show in Fig. 1 a typical example, referring to a simulation of an object with the same orbit as asteroid (3) Juno, and rotational properties corresponding to those known for the real object from light-curve data. Here, however, the simulated shape of the object was that of a triaxial ellipsoid with axial ratios b/a and c/a equal to 0.83 and 0.66, respectively. The total number of simulated Gaia observations for this object is N= 61. The figure displays the ecliptic longitude of each simulated detection of the object, and the corresponding magnitude, expressed in terms of the magnitude difference with respect to the first observation. Both the originally simulated data and those computed according to the inversion solution are displayed using different symbols. As can be seen, the fit to the simulated data is practically perfect in this ideal situation (perfect triaxial ellipsoid shape, no photometric errors), since, in quantitative terms, the (O-C) residuals are always below 0.001 mag for each observation. The corresponding solution of the inversion algorithm, namely the set of unknown rotational parameters, was also very accurate. The rotation period was precise to within 10-5 h, less than one degree in the pole coordinates, and less than 0.01 in the axial ratios. The fit displayed in Fig. 1 is fully representative of what has been found in a large number of simulations at the same (low) degree of complexity. Clearly, the inversion algorithm is definitely able to invert photometric data produced using the same algorithm of its ``photometric engine''.
We also note that we have seen, at least in a (still limited) number of tests devoted to simulate Gaia observations of near-Earth asteroids, that the inversion algorithm works fine also in cases of simulations of these objects. The only difference is that the residuals tend to increase because of the difference between the computed magnitudes at large phase angles, where the (H, G) system differs from a purely linear trend of the magnitude-phase relation.
For the next steps of our simulated tests, three main directions were possible, to produce more realistic simulated observations. The three main improvements concerned (1) the simulated shape of the objects; (2) the implementation of more refined scattering laws; and (3) the implementation of simulated photometric errors affecting the observations. It was also important to assess the minimum applicability conditions of the inversion algorithm in terms of number of available observations.
The first two points are described in the following subsection. In the rest of this section, we show some results of our exploration of the role played by the photometric errors of the observations, and by the number of available measurements. This is a necessary prerequisite to facing the challenge of analyzing true data, because it is in any case important to have at disposal an assessment of the minimum requirements of the inversion algorithm in terms of number and accuracy of the observational data. It is clear that we can qualitatively expect that the method should be successful in inverting very large numbers of extremely accurate observations, whereas we expect that the inversion of small numbers of very noisy observations to be almost unconstrained. It is important, however, to provide a quantitative estimate of this.
To study this problem, we developed simple software capable of introducing some Gaussian errors in given sets of simulated observations, and removing random numbers of data points from a given data set, to study the effects of varying numbers of observations and different error bars. Given a data set of observations with uncertainties below some given limit, the final goal is to be able to determine the minimum amount of data needed to make the inversion possible. As a first step of this analysis, we started from data corresponding to ideal triaxial ellipsoid shapes, the easiest conceivable situation.
As an example, Fig. 2 shows how the
apparent agreement between simulated and inverted data changes as a
consequence of applying photometric error to the simulated data. This
figure refers to a case identical to that shown in Fig. 1, but the difference
is that a random Gaussian error with a constant ![]() of 0.03 mag was added to each simulated observation. With
respect to the ideal case shown in Fig. 1 (no photometric
error), it can be seen that the situation slightly differs, and the
residuals are no longer null. They are shown more clearly in
Fig. 3,
where it is evident that these residuals behave as expected based on a
Gaussian error of 0.03 mag affecting the observations. In particular,
we find that the residuals, in this case, are caused entirely by the
errors in the simulated photometric data.
of 0.03 mag was added to each simulated observation. With
respect to the ideal case shown in Fig. 1 (no photometric
error), it can be seen that the situation slightly differs, and the
residuals are no longer null. They are shown more clearly in
Fig. 3,
where it is evident that these residuals behave as expected based on a
Gaussian error of 0.03 mag affecting the observations. In particular,
we find that the residuals, in this case, are caused entirely by the
errors in the simulated photometric data.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg2.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg26.png) |
Figure 2:
Same as Fig. 1,
but this time the simulated observations are affected by a simulated
Gaussian error having a |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg3.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg27.png) |
Figure 3: Same results shown in Fig. 2, but this time we plot directly the residuals O-C as a function of the ecliptic longitudes of the observations. |
| Open with DEXTER | |
Although it is not easy to realize this from inspection of Figs. 1 and 2, the points corresponding to the inversion solution are practically identical in the two plots, with differences of below 0.001 mag. The reason is that the inversion solution is practically coincident in the two cases, with and without photometric error. This means that, at least in a case like this, with 61 available observations affected by an error of the order of 0.03 mag, and for the chosen ellipsoid axial ratios and simulated asteroid orbit, the inversion algorithm is perfectly capable of finding the correct inversion solution.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg4.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg28.png) |
Figure 4:
Results of a set of simulations of triaxial ellipsoid objects, as a
function of the number of available observations for a given object,
and as a function of the error bars of the observations. Errors are
expressed in terms of the |
| Open with DEXTER | |
To obtain a clear understanding of the applicability conditions of the
inversion algorithm, we attempted inversions in varying numbers of
observations of a given object, and a varying superimposed photometric
error in the simulated observations. We always simulated Gaussian
errors and varied the corresponding ![]() .
The results of this exercise, valid for an object with a typical main
belt orbit, are summarized in Fig. 4. In this
figure, we indicate by means of different symbols the result of the
inversion attempt for different locations in the plane of number of
observations versus
.
The results of this exercise, valid for an object with a typical main
belt orbit, are summarized in Fig. 4. In this
figure, we indicate by means of different symbols the result of the
inversion attempt for different locations in the plane of number of
observations versus ![]() ,
the photometric error. We identify three possible cases: positive
tests, in which the best-fit solution of the inversion algorithm is the
correct one; negative tests, in which the correct solution cannot be
found; and marginally positive tests, in which the algorithm finds a
number of equivalent best-fit solutions, including but not limited to
the correct one, which turns out not to be that providing the best-fit
to the data.
,
the photometric error. We identify three possible cases: positive
tests, in which the best-fit solution of the inversion algorithm is the
correct one; negative tests, in which the correct solution cannot be
found; and marginally positive tests, in which the algorithm finds a
number of equivalent best-fit solutions, including but not limited to
the correct one, which turns out not to be that providing the best-fit
to the data.
Figure 4 suggests that the conditions of applicability of the inversion algorithm are not exceedingly restrictive. For Gaia observations affected by small photometric errors, even small numbers of data points, between 20 and 30, are found to be sufficient to perform a successful inversion. The minimum number of observations increases for an increasing photometric error, but we see that about 60 data points may be sufficient when the error bars are as large as 0.05 mag. We should interpret these numbers in terms of the expected performances of the Gaia survey. According to current estimates, four major sources of error should be taken into account for Gaia. These are the photon noise of the signal, the imperfect knowledge of the along-scan PSF of the objects, the effect of progressive radiation damage in the CCD detectors, and errors in sensitivity calibration. For faint sources, the readout noise may also be important. All of the above error sources are currently under scrutiny. In the case of asteroids, one should also consider the effect of the motion of the objects, which in some cases can remove them from the observing window before the end of a full transit on the Gaia focal plane. Based on current modeling of all the above effects, it seems that, to be conservative, for main belt asteroids as faint as V=20 mag, the photometric error during a single transit might reach in many cases values of the order of 0.05 mag. However, the photometric uncertainty decreases rapidly for increasing apparent brightness. For instance, the accuracy is increased by a factor of about 4 at V=18 and by a factor of 10 at V=16. We also recall that Gaia will observe any typical main belt asteroid on average 60-70 times. This should be taken into account when interpreting Fig. 4.
This means that we can expect that true Gaia observations will fulfill the inversion requirements in a very large number of cases. This should be true even if the results shown in Fig. 4 are an optimistic limit, taking into account that the simulations to whom this figure refers were simulations of ideal triaxial ellipsoids, whereas in the real world the situation may be worse because real shapes are not so regular. Even taking this into consideration, however, an extremely conservative estimate of at least 10 000 objects for which inversion is expected to be possible has been published in a previous analysis, considering a much brighter limit of apparent magnitude: V=18.5 (Cellino et al. 2006). Even taking into account all quoted difficulties, it is very likely that the true number will probably be much higher.
4.2 More realistic simulations
Since the limits to the realism of simulations based purely on perfectly triaxial ellipsoid shapes and geometric scattering are self-evident, we also performed a number of simulations of more realistic situations. In particular, we considered first perfect triaxial ellipsoids characterized by realistic light scattering properties, and subsequently we relaxed the triaxial ellipsoid shape assumption and simulated observations of a few ``real'' asteroids, taking their shapes from the results of radar and in situ imaging by space probes. While the observational circumstances of Gaia detections of any given object were given again by the Gaia simulator used for the tests described in the previous section, the corresponding magnitudes were produced in these cases by one of us (SM) using a completely different algorithm, adapted to treat the cases of complex shapes and more realistic light scattering properties. In particular, this algorithm computes the brightness as the sum of the contribution of a large number of different facets used to approximate the asteroid surface. Of course, using a different algorithm to compute simulated magnitudes, which completely differs from that used in the inversion algorithm, is also useful to strengthen our confidence in the reliability of our numerical approach.
In particular, we used the radar shape model of (6489) Golevka
from Hudson et al. (2000), the NEAR digital shape model of
(433) Eros from Thomas et al. (2002) and the convex model of
(15) Eunomia
obtained from ground-based lightcurve inversion (Nathues et al. 2005).
The models are represented as polyhedra with 4092, 22 540 and
2038 triangular facets, respectively. A pictorial view of the three
object models is shown in Fig. 5. For the
first two shape models, which contain concavities, mutual facet
occultation and/or shadowing must be taken into account. This was
achieved by means of ray-tracing techniques. The observed flux was
computed at each time step by determining for each facet the
illumination and viewing geometries, and by applying the Hapke
photometric scattering law (Hapke 1984,
and references therein) with parameters that are typical of ![]() -type
asteroids (Verbiscer &
Veverka 1995). Mutual illumination of the facets was not
taken into account, as this effect is negligible for low-albedo
objects.
-type
asteroids (Verbiscer &
Veverka 1995). Mutual illumination of the facets was not
taken into account, as this effect is negligible for low-albedo
objects.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg5.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg30.png) |
Figure 5: Three views for each of the realistic object models considered in our simulations. From top to bottom, the figure shows the models of Golevka, (433) Eros and (15) Eunomia, respectively. |
| Open with DEXTER | |
Table 1: Results of the photometric inversion of simulated ellipsoids and Eunomia-like shaped asteroids.
The first step was, however, to revert back to triaxial
ellipsoids, but computing the synthetic brightness at the epochs of
simulated Gaia observations by relaxing the simplifying assumption of
pure geometric scattering. This time, we completed the computations by
considering a Hapke photometric scattering law, as mentioned above.
This set of tests provided very encouraging results, as shown in
Table 1.
The correct solution was always found in a variety of situations. The
overall residuals of the single observations, expressed in terms of the
![]() parameter defined above, increased to typical values of
0.02 mag in the case of Hapke scattering, but the resulting
inversion solution was correct, with a very good accuracy in the
determination of the spin period, pole orientation, and shape,
comparable to the previous results obtained in the simpler case of
geometric scattering. The most important inaccuracy was found to affect
the coordinates of the pole, which turned out to be affected by errors
of the order of 5 degrees, fully acceptable in any respect.
parameter defined above, increased to typical values of
0.02 mag in the case of Hapke scattering, but the resulting
inversion solution was correct, with a very good accuracy in the
determination of the spin period, pole orientation, and shape,
comparable to the previous results obtained in the simpler case of
geometric scattering. The most important inaccuracy was found to affect
the coordinates of the pole, which turned out to be affected by errors
of the order of 5 degrees, fully acceptable in any respect.
We note that the precisions in the results listed in Table 1 always correspond to very small values. They were derived by considering the dispersion in the resulting parameter values found by different single genetic solutions. We recall that the genetic algorithm makes some tens of inversion attempts during a single run, and the same solution is generally obtained several times with some corresponding differences in the values of each resulting parameter. The resulting range is then adopted as the nominal precision of each solution parameter. We note that the ``real" accuracies of the solutions, that is the differences from the true solution, are also always very good. In the case of the spin period, for instance, the accuracy is of the order of a few 10-4 h in the worst cases listed in the table.
At this point, we studied two more complicated situations, by
developing simulations based on the Eunomia shape model. In particular,
we computed the apparent magnitudes of an Eunomia-like object moving
along the orbit of the real asteroid (4) Vesta (a typical main belt
asteroid, chosen by chance), corresponding to the simulated observing
circumstances for a five-year Gaia survey. We completed two separate
simulations, a simpler one based on magnitudes computed according to
simple geometric scattering, and one based on a Hapke scattering law
adopting the same set of Hapke parameters found to reproduce the
behaviour of ![]() -type
asteroids well (Verbiscer
& Veverka 1995), in particular the values
-type
asteroids well (Verbiscer
& Veverka 1995), in particular the values ![]() ,
g=-0.26, B0=1.2,
h=0.06,
,
g=-0.26, B0=1.2,
h=0.06, ![]() .
The
simulated pole was at an ecliptic longitude of
.
The
simulated pole was at an ecliptic longitude of ![]() and an ecliptic latitude of
and an ecliptic latitude of ![]() .
The simulated spin period was 19.15 h.
.
The simulated spin period was 19.15 h.
The results of these simulations are also listed in
Table 1,
and show, not unexpectedly, some differences. Using geometric
scattering, the simpler simulation gave a very good
inversion solution, although the average residuals increased, with an ![]() parameter about 0.02 mag. This is reasonable, since the
simulated shape did not correspond to a triaxial ellipsoid. In the case
of the most realistic simulation of Hapke scattering, the results of
the inversion show the presence of one additional solution of
practically the same rotation period but different pole coordinates,
which produces residuals fully equivalent to those of the correct
solution. This result is interesting. In principle, the existence of
equivalent pole solutions is not too surprising, since this is the
normal situation in asteroid pole determinations, as can be seen by
looking at the updated catalog of asteroid poles maintained at the
Poznan Observatory
parameter about 0.02 mag. This is reasonable, since the
simulated shape did not correspond to a triaxial ellipsoid. In the case
of the most realistic simulation of Hapke scattering, the results of
the inversion show the presence of one additional solution of
practically the same rotation period but different pole coordinates,
which produces residuals fully equivalent to those of the correct
solution. This result is interesting. In principle, the existence of
equivalent pole solutions is not too surprising, since this is the
normal situation in asteroid pole determinations, as can be seen by
looking at the updated catalog of asteroid poles maintained at the
Poznan Observatory![]() .
.
A photometrically-obtained pole ambiguity is normally assumed
to be related to the orbital parameters of the object, which determine
the observing circumstances (i.e., Sun, Earth, asteroid geometric
configuration) at different epochs. In principle, for instance, a pole
ambiguity cannot be eliminated in the ideal case of a perfectly
triaxial ellipsoid orbiting on a circular orbit that is coplanar with
the ecliptic. For this reason, we decided to perform a set of
simulations in which the same spin properties (period P=19.15 h,
pole coordinates (48.5,
51.0)) and the Eunomia shape
remained unchanged, but the orbit of the simulated asteroid was
altered. In particular, we chose a number of real orbits belonging to
asteroids representative of the wide variety of orbits that exist
in the main belt, including objects with eccentricity and inclination
ranging between practically zero up to the largest values encountered
in the belt. Also the range of main belt semi-major axis values was
properly sampled, and we included in our simulations also a typical
near-Earth orbit, corresponding to that of the asteroid (433) Eros.
This simulated orbit is particularly important, because the phase angle
at the epochs of the simulated Gaia observations in this case turns out
to be systematically higher (being on the average of the order of ![]() )
than in the cases of simulated main belt objects (for which the phase
angle ranges mostly between
)
than in the cases of simulated main belt objects (for which the phase
angle ranges mostly between ![]() and
and ![]() ).
In this situation, the assumed linearity of the phase-magnitude
relation may be a less
solid assumption, and it is interesting to check the performances of
the inversion algorithm in this situation, which is fully
representative of the future Gaia observations of near-Earth objects.
We are aware that a larger number of simulated near-Earth orbits would
be important to more detailed tests of the performances of our
inversion algorithm in situations that would be a priori more
challenging than those corresponding to main-belt asteroids, but we
postpone this to a separate analysis, taking into account that main
belt asteroids are far more numerous and constitute the major fraction
of the Gaia Solar System object catalogue. The set of orbital
semi-major axes, eccentricities, and inclinations of the simulated
objects are given in Table 2. For each
simulated object, a full set of Gaia detections and corresponding
observing circumstances were computed, while the magnitudes were
computed taking into account the more realistic case of Hapke
scattering law, as in previous simulations.
).
In this situation, the assumed linearity of the phase-magnitude
relation may be a less
solid assumption, and it is interesting to check the performances of
the inversion algorithm in this situation, which is fully
representative of the future Gaia observations of near-Earth objects.
We are aware that a larger number of simulated near-Earth orbits would
be important to more detailed tests of the performances of our
inversion algorithm in situations that would be a priori more
challenging than those corresponding to main-belt asteroids, but we
postpone this to a separate analysis, taking into account that main
belt asteroids are far more numerous and constitute the major fraction
of the Gaia Solar System object catalogue. The set of orbital
semi-major axes, eccentricities, and inclinations of the simulated
objects are given in Table 2. For each
simulated object, a full set of Gaia detections and corresponding
observing circumstances were computed, while the magnitudes were
computed taking into account the more realistic case of Hapke
scattering law, as in previous simulations.
Table 2: List of different orbits adopted in the simulations.
Table 3: Results of the photometric inversion of simulated Eunomia-like shaped asteroids on different asteroidal orbits.
The results of the inversion of these simulations is given in Table 3, in which we list for each simulated case not only the spin and shape solutions, as in Table 1, but also the value of the resulting slope k of the linear phase-magnitude relation. As can be seen, a non-negligible variation in the resulting solutions seems to be related to the orbital properties of the object. The parameters that are found to vary the most are the pole coordinates. With respect to the exact pole solution, we find differences of up to a dozen of degrees in pole longitude and up to 22 degrees in pole latitude. However, these cases are fairly exceptional, and we note that the maximum error is never reached simultaneously in both pole longitude and latitude, the overall accuracy in the pole determination being more than reasonable, or even excellent, in most cases. In a couple of cases, we identify a spurious pole solution, which in the case of the simulated orbit of asteroid (363) gives slightly better residuals than the correct solution. We note, however, that the case of the simulated (363) orbit corresponds to the minimum number of simulated observations (44) in our sample.
The spin period solution is always found with excellent accuracy, of the order of 10-4 h, although the resulting nominal uncertainties derived from the range of variation in the same solution over different attempts, are always underestimated, taking into account the correct spin period adopted in the simulations (19.15 h). The axial ratios exhibit some variability among the different simulations, but they are always very stable in each single case, and are in general reasonable triaxial approximations of the adopted Eunomia shape. The resulting slope of the phase-magnitude relation is also found to vary little among the different simulations, and always corresponds to realistic values.
The residuals are found to vary in a non-negligible way
depending on the orbital properties of the simulated object. In
general, the ![]() parameter is of the order of about 0.04 mag, but in the case
of the simulated near-Earth orbit of (433) Eros a value twice as large
is found. This demonstrates that, even in the presence of large
residuals, which might lead to the expectation that the inversion
solution has little sense, the derived solution tends to be instead
fairly accurate. This illustrates again the significance of our
approach to the problem of photometric inversion. The point is that our
algorithm is effective in identifying the triaxial ellipsoid solution
that most closely fits the data. In spite of its simplistic
assumptions, the triaxial ellipsoid solution is a good representation
of the spin properties and overall shape and scattering properties of
the objects, even if in many cases the residuals of the individual
measurements are fairly large.
parameter is of the order of about 0.04 mag, but in the case
of the simulated near-Earth orbit of (433) Eros a value twice as large
is found. This demonstrates that, even in the presence of large
residuals, which might lead to the expectation that the inversion
solution has little sense, the derived solution tends to be instead
fairly accurate. This illustrates again the significance of our
approach to the problem of photometric inversion. The point is that our
algorithm is effective in identifying the triaxial ellipsoid solution
that most closely fits the data. In spite of its simplistic
assumptions, the triaxial ellipsoid solution is a good representation
of the spin properties and overall shape and scattering properties of
the objects, even if in many cases the residuals of the individual
measurements are fairly large.
The Eunomia shape adopted in the above batch of simulations is certainly more realistic than ideal triaxial ellipsoids, yet it may still be exceedingly ``easy'', since it does not include the presence of concavities, which are known to exist among the real objects, and may have an important role in determining the photometric behaviour, which may be a challenge to photometric inversion attempts (Kaasalainen et al. 2002). For this reason, we performed a new series of simulations similar to those described above (same simulated orbits, pole coordinates, spin period, and Hapke scattering law), but this time considering a shape corresponding to that of asteroid (6489) Golevka. With respect to the previously simulated Eunomia shape, the Golevka shape does contain concavities, and we were obviously interested in checking the performances of the inversion algorithm in cases such as this.
Table 4: Results of the photometric inversion of simulated Golevka-like shaped asteroids on different asteroidal orbits.
The results of this exercise are summarized in Table 4. As can be seen, the performance of the inversion method is found again to be good. The discrepancies between the obtained solution and the true simulated case are still fairly small, of the same order as those obtained in the previous Eunomia simulation. Only in one case is a double solution found, and this occurs again in the case of one of the two simulated orbits (that of asteroid (24) Themis) that also gave a double solution in the case of the Eunomia simulations.
Table 5: Results of the photometric inversion of simulated Eros-like shaped asteroids on different asteroidal orbits.
Since the shape of (6489) Golevka constitutes only one single example of a complex object with concavities, we decided to perform another set of simulations by considering another exotic and irregular shape, that of the near-Earth object (433) Eros, well known after the in situ images taken by the Near-Shoemaker space probe. We note that the digitized shape of Eros, in addition to being strongly elongated and irregular, also includes concavities. In this respect, therefore, the Eros simulations are among the most extreme cases that one can conceivably perform to simulate complicated observational situations. Again, we considered the same variety of possible asteroidal orbits already simulated in the previous Eunomia and Golevka tests. The results of this new set of simulations are given in Table 5. As can be seen, the inversion solution is found again to be generally very good, in spite of the residuals of the individual observations being high. Taking into account the intrinsic complexity of the simulated shape and the variety of simulated orbits, we can conclude that the results of the inversion algorithm are more than satisfactory.
Interestingly, in the case of the Eros shape, no spurious solution is found for any of the simulated orbits, including the (24) orbit, that produced spurious solutions in the previous simulations. We propose that this is because the Eros shape is intrinsically very elongated, produces a much wider range of observed magnitudes, which may help in constraining in a firmer way the corresponding pole solution. As a matter of fact, we expect that the photometric inversion may become increasingly difficult as the object's shape approaches that of a spheroid, or even of a sphere, for which no solution can in principle be found. Therefore, very irregular shapes may counter-intuitively be found to be more easily inverted than more regular ones, in principle, although it is clear that the (O-C) residuals produced by a very irregular shape may be fairly large.
Table 6: Results of the photometric inversion of simulated Golevka-like shaped asteroids on two different asteroidal orbits.
The results of the Eunomia, Golevka, and Eros simulations
described above are encouraging, but an important limit is that they
were obtained by applying the inversion algorithm to simulated
photometric data without considering any superimposed photometric
error. For this reason, we performed a new series of simulations, in
which we again considered some of the cases previously described, but
this time we superimposed the nominal magnitude data of some realistic
photometric errors. In particular, we explored two cases chosen among
the previously shown simulations of two Golevka-shaped objects, moving
along the orbits of asteroids (319) and (363). The numbers of simulated
observations are 64 for the simulated (319) orbit, and 44 for the
simulated (363) orbit. To each simulated observation, we randomly added
a Gaussian photometric error with different values of ![]() .
In particular, we were interested in checking the extent to which the
presence of photometric errors of increasing importance could affect
the quality of the obtained inversion solution. For this reason, we
performed simulations with superimposed Gaussian errors with
.
In particular, we were interested in checking the extent to which the
presence of photometric errors of increasing importance could affect
the quality of the obtained inversion solution. For this reason, we
performed simulations with superimposed Gaussian errors with ![]() values of 0.01, 0.02, 0.03, 0.04, and 0.05 mag, respectively.
We note that errors
larger than 0.03 mag should be considered as pessimistic, since the
photometric accuracy of Gaia data is expected to be generally better,
or even much better, down to objects as faint as 18th mag
in visible light, some exceptions possibly being fast-moving objects
that might be measured only during a fraction of their transit across
the Gaia focal plane. On the other hand, we were interested in
assessing the performances of our inversion method in very challenging
situations, since we cannot exclude the unfortunate possibility that
for some reason the true photometric performances of Gaia might be
worse than predicted. The results of these simulations are listed in
Table 6.
values of 0.01, 0.02, 0.03, 0.04, and 0.05 mag, respectively.
We note that errors
larger than 0.03 mag should be considered as pessimistic, since the
photometric accuracy of Gaia data is expected to be generally better,
or even much better, down to objects as faint as 18th mag
in visible light, some exceptions possibly being fast-moving objects
that might be measured only during a fraction of their transit across
the Gaia focal plane. On the other hand, we were interested in
assessing the performances of our inversion method in very challenging
situations, since we cannot exclude the unfortunate possibility that
for some reason the true photometric performances of Gaia might be
worse than predicted. The results of these simulations are listed in
Table 6.
As can be seen, the inversion solutions tend to be stable and
quite accurate even when the superimposed errors reach high values.
Some problems become apparent in the case of the simulated (319) orbit,
but only when the ![]() of the Gaussian photometric error reaches values of 0.04 or
0.05 mag. In particular, two equivalent solutions are found in
these cases, differing mainly in terms of resulting ecliptic longitude
of the pole. When looking at Table 6, one
should recall that the indicated nominal uncertainties in the resulting
solution parameters are related to the range of variation in different
occurrences of the same solution in different genetic runs. Null values
of the resulting parameters may imply either that exactly the same
values were obtained in different cases, or, less frequently, that the
indicated solution was found only once before reaching a maximum number
of genetic attempts equal to 50. In particular, this is the case for
the second solution corresponding to the
of the Gaussian photometric error reaches values of 0.04 or
0.05 mag. In particular, two equivalent solutions are found in
these cases, differing mainly in terms of resulting ecliptic longitude
of the pole. When looking at Table 6, one
should recall that the indicated nominal uncertainties in the resulting
solution parameters are related to the range of variation in different
occurrences of the same solution in different genetic runs. Null values
of the resulting parameters may imply either that exactly the same
values were obtained in different cases, or, less frequently, that the
indicated solution was found only once before reaching a maximum number
of genetic attempts equal to 50. In particular, this is the case for
the second solution corresponding to the ![]() case for the simulated (319) orbit.
case for the simulated (319) orbit.
Of course, the real errors of the obtained solutions, in the case of our simulations, can be derived by comparing the values of the resulting parameters with those assumed in producing the simulated photometric data. This can be done in a straightforward way as far as the spin and pole solution are concerned. In particular, it is found that, in general terms, the performances of the inversion algorithm are very satisfactory, or even excellent, as can easily be seen by looking at the data listed in Tables 3, 4, and 6. As for the shape, a direct quantitative estimate of the error is less straightforward, just because the inversion algorithm infers the axial ratios of the triaxial ellipsoid shapes that most closely fit the simulated photometric data. In general terms, we assume that the resulting values are generally quite reasonable. Shapes such as those of Eunomia and Golevka are found to clearly provide different axial ratios, and the more elongated Eunomia shape, with respect to that of Golevka, has a reasonable counterpart in the resulting shape solutions. Finally, we also note that the resulting linear slopes of the magnitude-phase relation are reasonable, and close to the behavior of real asteroids, as expected at least in cases in which realistic Hapke light scattering laws are adopted to produce the simulated photometric data.
Of course, throughout this section we presented only the results of numerical simulations. In principle, nothing ensures us that the objects that exist in the real world behave so nicely as to be adequately simulated by means of our more or less simplified models. For this reason, an analysis of real asteroid data is crucial, and it is timely to present some results.
5 Application to Hipparcos data
5.1 The Hipparcos mission and instrument
The HIPPARCOS (HIgh-Precision PARallax COllecting Satellite) astrometric mission of the European Space Agency (ESA) consisted of a satellite hosting two main onboard experiments, named Hipparcos (the primary experiment based on the focal plane instruments) and Tycho (corresponding to data collected by the onboard star mapper). The satellite was operated from November 1989 to March 1993.
Similarly to Gaia, the Hipparcos observing strategy was based on a continuous scanning of the sky over slowly precessing great circles. The Hipparcos measurement principles and data processing are described in Hestroffer et al. (1998) and Perryman (1997), and consisted of observing the target as it crossed the field of view, and recording the photon flux as modulated by a periodic grid, leading to an accurate astrometric measurement. In addition to astrometric information, the total flux of the signal was also recorded, providing the magnitudes in the so-called broad-band Hp photometric system of Hipparcos.
Photometric data were also obtained in two bands (red and blue) in the Tycho experiment. The Tycho detector, however, was less sensitive, and produced data for only 6 asteroids compared to 48asteroids observed within the Hipparcos experiment. We thus restrict our analysis to the Hipparcos data only. In particular, we used photometric data from the Hipparcos annex for Solar System objects ``The Hipparcos solar system objects catalogues'' (Hestroffer et al. 1998; Perryman 1997). Some outlier-rejection filters were applied to minimize the number of possibly corrupted entries in the Hipparcos catalogue. These filters were rather liberal, however, and the effect was that in general terms it was easier to retain measurements of poor quality than to reject higher quality data, although we are not aware of any quantitative estimate of the amount of bad data points which might contaminate the catalogue.
5.2 The Hipparcos photometric system
No filters were present, and the Hipparcos Hp
photometric system consists of a broad passband centered roughly on the
same wavelength as the Johnson V. Conversion from Hp
magnitudes to the V band of the standard Johnson UBV
system was computed for asteroids by considering only the B-V
colour index (van Leeuwen
et al. 1997, and references therein):
although for very red stars the situation was more complicated. The Hipparcos Input Catalogue included V magnitudes and B-V colour indices, to be used in the above-mentioned transformation to the standard Johnson UBV system. The final Hipparcos photometric catalog includes B-V data that were generally obtained from ground-based observations, but in cases in which more accurate values were directly measured by Tycho. Since the Tycho B and V bands differed from the standard Johnson UBV system, a linear transformation from the Tycho system to the standard system was needed in these cases.
Because the true response curve of Hp varied with time during the mission, the Hp passband was re-calibrated as a function of wavelength and time, and all photometric measurements were reduced to a photometric reference epoch (January 1st, 1992). All photometric data were finally calibrated using a set of about 22 000 standard stars.
5.3 Hipparcos photometric observations of asteroids
Hipparcos observations of asteroids were designed to derive their
astrometric positions. The modulated signal was measured by a
photon-counting image dissector tube device, and both the mean level as
well as the amplitude of the modulated signal were used to produce a
calibrated magnitude, which we call ![]() and
and ![]() ,
respectively. The first,
,
respectively. The first, ![]() ,
was based on the recorded total flux and was intrinsically more
precise, but it was affected by errors due to background, either from a
``flat'' diffuse light in the field of view, or from the presence of a
nearby background object. The signal amplitude component
,
was based on the recorded total flux and was intrinsically more
precise, but it was affected by errors due to background, either from a
``flat'' diffuse light in the field of view, or from the presence of a
nearby background object. The signal amplitude component ![]() was
insensitive to background noise, but was influenced by the apparent
angular width of the object (resolved objects or binaries). This second
estimator was therefore more suited to deriving the
magnitudes of point-like sources, but was less accurate in the cases of
resolved sources (Hestroffer
2003; Hestroffer
& Mignard 1997).
was
insensitive to background noise, but was influenced by the apparent
angular width of the object (resolved objects or binaries). This second
estimator was therefore more suited to deriving the
magnitudes of point-like sources, but was less accurate in the cases of
resolved sources (Hestroffer
2003; Hestroffer
& Mignard 1997).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg6.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg249.png) |
Figure 6:
Difference |
| Open with DEXTER | |
In principle, the difference between the two magnitude estimators, shown as an example in Fig. 6 for the asteroid (15) Eunomia, might be used to derive information about the size and limb darkening of a given object, or, in case of strong differences, to identify problematic observations.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg7.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg250.png) |
Figure 7:
Accuracy of the Hipparcos |
| Open with DEXTER | |
In practical terms, however, data are intrinsically noisy, and in the
present analysis we use only the ![]() data published in the Hipparcos photometric catalogue. The nominal
photometric accuracy in the Hp photometric system
was mostly between 0.01 and 0.05 mag, with a global average of
0.028 mag. However, errors larger than 0.05 mag were not so
unusual for asteroids fainter than magnitude 7. Only a few transits of
objects fainter than magnitude 9 were measured (see Fig. 7).
data published in the Hipparcos photometric catalogue. The nominal
photometric accuracy in the Hp photometric system
was mostly between 0.01 and 0.05 mag, with a global average of
0.028 mag. However, errors larger than 0.05 mag were not so
unusual for asteroids fainter than magnitude 7. Only a few transits of
objects fainter than magnitude 9 were measured (see Fig. 7).
The number of asteroid transits recorded by Hipparcos varied
greatly among different objects, ranging from only 12
observations for (63) Ausonia to 112 transits for
both (39) Laetitia and
(471) Papagena. The average number of recorded transits was
55. The phase angle at each observation was always larger than ![]() .
In the catalogue, observation epochs are always
light-time corrected, and all apparent magnitudes were converted to
both unit distance to the satellite and the Sun.
.
In the catalogue, observation epochs are always
light-time corrected, and all apparent magnitudes were converted to
both unit distance to the satellite and the Sun.
All the spin periods of the asteroids observed by Hipparcos
are known from light-curve analyses, and in the majority of cases the
overall shape and the pole orientation are also known to good accuracy,
although often more than one possible pole solutions have been found by
different authors. Here, we refer in particular to the asteroid pole
database initially assembled by Magnusson
et al. (1989), and now maintained and regularly
updated by the team of the Poznan Observatory, as described by
Kryszczynska et al. (2007)![]() In some cases, some very
detailed shape and spin models are given by Durech
& Sidorin (2009). As for the spin periods, we refer
to the data available at the NASA PDS web site (Harris
et al. 2006). The availability of spin and shape
information for the asteroids of our sample allows us to validate the
performances of our photometric inversion method. In some cases, it is
in principle possible to favour one particular pole solution among a
set of different published values.
In some cases, some very
detailed shape and spin models are given by Durech
& Sidorin (2009). As for the spin periods, we refer
to the data available at the NASA PDS web site (Harris
et al. 2006). The availability of spin and shape
information for the asteroids of our sample allows us to validate the
performances of our photometric inversion method. In some cases, it is
in principle possible to favour one particular pole solution among a
set of different published values.
Table 7: The Hipparcos asteroid photometric dataset.
Table 8: Comparison of known spin periods and pole coordinates, and results from inversion of Hipparcos data.
A fundamental problem, however, becomes apparent when looking
at the summary of Hipparcos photometric observations displayed in
Table 7.
In this Table, for each object the total number of available
observations is listed, with the corresponding numbers of observations
affected by different nominal errors, from 0.01 mag up to
0.05 mag. It is easy to recognize that the situation is far
from being encouraging. The error bars of the measurements are very
rarely below 0.01 mag, and observations with errors below
0.02 mag are also infrequent. If we take at face value the
results shown in Fig. 4,
and we analyze the numbers of observations of superior quality than a
given accuracy for each object, it turns out that, among the 48
asteroids listed in Table 7, only 23
meet the requirements for a successful inversion. These cases are
indicated by bold characters in Table 7. In
general, Hipparcos objects have very few if any observations of high
accuracy, and the inversion requirements are achieved mostly in cases
in which a fairly high number of low-quality detections are available.
It should also be noted that the invertibility constraints shown in
Fig. 4
were derived from simulations of perfect triaxial ellipsoids with
geometric scattering, which was a very optimistic scenario. As a
consequence, it is a priori very likely that the true number of objects
in
the Hipparcos dataset for which we should hope to be able to achieve a
reliable photometric inversion could be far smaller than the set of 23
asteroids listed in bold in Table 7. One
should note, for instance, that in several cases (asteroids (10)
Hygiea, (20) Massalia, (42) Isis, and (704) Interamnia) the
above-mentioned invertibility conditions are only very marginally
satisfied. It is also not unreasonable to expect that at least in some
cases the magnitude data in the catalogue, corresponding to the nominal
![]() measurements,
might be affected by error bars even larger than the published values,
in cases in which background effects (such as the proximity of some
star, or a misidentification) might have played an important role (see,
for reference, Fig. 6).
Summarizing, we may say that Hipparcos photometric data of asteroids
are generally scarce, and of a quite low quality, thus they present
certainly a significant challenge to any inversion attempt.
measurements,
might be affected by error bars even larger than the published values,
in cases in which background effects (such as the proximity of some
star, or a misidentification) might have played an important role (see,
for reference, Fig. 6).
Summarizing, we may say that Hipparcos photometric data of asteroids
are generally scarce, and of a quite low quality, thus they present
certainly a significant challenge to any inversion attempt.
6 Photometric inversion results
In spite of the above-mentioned difficulties, we performed photometric
inversion attempts for all the objects of the Hipparcos dataset. The
results were analyzed in terms of ability to obtain the correct spin
rate, always taken from the NASA PDS web site![]() .
When this occurred, the resulting pole orientation and general triaxial
shape were also analyzed and compared with results obtained by other
authors and available at the web site of the Poznan Observatory (Kryszczynska 2009). We
summarize our main results in Table 8. The
table lists for each object both the period and pole available from
ground-based observations, and our corresponding inversion solution.
The best solutions were not always obtained by using all available
Hipparcos data. The number of observations used to obtain each solution
is also listed in Table 8. The
correspondence with the maximum error bar accepted in different cases
can be immediately understood by looking at the columns of
Table 7.
.
When this occurred, the resulting pole orientation and general triaxial
shape were also analyzed and compared with results obtained by other
authors and available at the web site of the Poznan Observatory (Kryszczynska 2009). We
summarize our main results in Table 8. The
table lists for each object both the period and pole available from
ground-based observations, and our corresponding inversion solution.
The best solutions were not always obtained by using all available
Hipparcos data. The number of observations used to obtain each solution
is also listed in Table 8. The
correspondence with the maximum error bar accepted in different cases
can be immediately understood by looking at the columns of
Table 7.
In the table, we note that we do not list for each object the nominal errors of the solution parameters. As we have seen in Sect. 4, the reason is that the nominal errors in the solutions, evaluated by looking at the variations of the results in different genetic procedures, are always very small, and unrealistic. For a more reliable estimate of the true uncertainties in the solution parameters, we refer to the results of simulations described in both Table 1, and Tables 3 to 6. In particular, the differences between the solution parameters and the true parameters used to perform the simulations should certainly be a more reliable estimate of the true uncertainties in the solution parameters.
In several inversion attempts, we were unable to find a unique solution. Several period solutions, associated with different pole coordinates, were found by the genetic algorithm to be equivalent in term of residuals. As a consequence, we did not include these cases in Table 8. In a few cases, more than one possible pole was associated with the same rotation period, and this is shown in the Table. This is also the usual situation encountered in the case of literature data. As a rule, more than one possible pole is listed by Kryszczynska (2009), and these different poles, or at least the most reliable ones are also listed in Table 8.
The results shown in Table 8 deserve some comments. First of all, we found that, among the 25 objects that were not expected to be inverted, namely the objects indicated in plain ink in Table 7, none but two of them produced a reasonable solution. Another case, that of (192) Nausikaa, was only marginally unacceptable, as we discuss below. The failure of the inversion algorithm for these most difficult cases is hardly surprising, since these objects were, in general terms, those for which only small numbers of poorly accurate observations were available.
Among the 23 objects for which we might have expected that an inversion solution could be possible based on the criteria visually displayed in Fig. 4 (the asteroids indicated in bold in Table 7), several situations are encountered. For the moment we disregard the cases of (1) Ceres and (4) Vesta, which are special and discussed separately below.
Some objects, including the asteroids (7), (8), (11), (18), (28), (29), (324), and (704) (eight objects) were not inverted. Moreover, only marginally acceptable solutions were obtained for (354) Eleonora, while in the cases of (2) Pallas, (10) Hygiea, and (42) Isis the results deserve some further comments, as we see below. For all of these objects, including some of the brightest and largest asteroids in the main belt, we understand that the failure or marginal success of our inversion attempt may be explained as the interplay of different effects, including the overall poor quality of the Hipparcos data and their scarcity. We also know that for at least some of these objects, the photometric behaviour is represented by complex lightcurves with more than two maxima and minima at some apparitions, which may even be diagnostic of possible albedo features and/or complex shapes. The hypothesis of a constant slope of the magnitude-phase relation at different aspect angles might also possibly fail in these cases.
We emphasize that we call a particular trial a failure if the method is unable to find the correct spin period as the nominal (best) solution of inversion, based on a set of ``genetic'' attempts, as explained in Sect. 3.1, or, as in the case of (42) Isis, there is a failure mostly in finding a plausible pole and shape solution. According to our criteria, a solution is good if it finds a rotation period that does not differ from that quoted in the literature by more than a few thousandths of an hour. This seems reasonable for several reasons. The first reason is that the effective operational lifetime of the Hipparcos satellite covered only about three years, a duration significantly shorter than the planned operational time of Gaia. As a consequence, we cannot expect the same accuracy in the period as we requested in our Gaia simulations presented in the previous sections. Moreover, period uncertainties of the order of a few seconds also seem not unrealistic in practical cases, as also indicated by the number of digits present in the rotational periods provided by the NASA PDS web site (Harris et al. 2006). We note that pole determination techniques based on the so-called epoch method have been applied to many asteroids of our dataset, and as a consequence the Poznan data-base often includes corresponding values of the sidereal period to several significant figures. If one looks at the data, however, it is easy to see that non-negligible differences exist in many cases in the periods derived by different authors. As a consequence, we believe that errors of up to a few seconds are still acceptable when assessing the success or failure of our inversion attempts.
In some of the above-mentioned cases labeled as failures, the inversion method identified the correct solution as one among a number of different possible inversion solutions for the spin period (for instance, as for the asteroids (18) Melpomene and (29) Amphitrite); in these cases, the correct solution was never that with nominally the smallest residuals, although the corresponding pole was found to be close to the most accurate values listed in the literature for these asteroids. Clearly, in cases such as these, one would not a priori have any possibility to choose the correct spin and pole solution when another one producing a slightly closer fit to the observations is present. However, these cases may also suggest that the failure of the method is largely the consequence of very noisy data. We found no obvious criterion to identify and remove particularly bad photometric measurements from the available samples, something that in principle might be possible, but we did not want in any case to make very detailed analyzes of single cases, since this was beyond the scope of our exercise.
In the following subsections, we provide some additional comments on single cases, and we present also the corresponding shape solution (axial ratios) found in our most successful inversion attempts.
6.1 (1) Ceres and (4) Vesta
The cases of the two big asteroids (1) Ceres and (4) Vesta are in some respects special. Both objects are known to have shapes that are close to those of oblate spheroids, because of their noticeable sizes and masses. In particular, (1) Ceres, with its diameter close to 1000 km, is now officially classified as a dwarf planet, according to the nomenclature approved at the General Assembly of the IAU in 2006. The spheroidal shapes of Ceres and Vesta were directly recorded by high-resolution HST images (Thomas et al. 2005,1997), and for Vesta it had also been previously predicted based on an analysis of available light curves (Cellino et al. 1987).
Nearly-spheroidal shapes are certainly challenging for photometric inversion, since the photometric variation of these objects tends to be very small, making the determination of the spin period and of the spin axis orientation more difficult. At least in the case of Vesta, there is also another major difficulty: the photometric variation of this asteroid is known to be caused mostly by the presence of a hemispheric-scale albedo variation, first detected by means of polarimetric variations. This large albedo spot was subsequently modeled by Cellino et al. (1987), using available lightcurves to produce a global solution for the pole and the flattening of the asteroid. The existence of this spot was later confirmed by HST observations (Thomas et al. 1997). The problem of a photometric variation dominated by a hemispheric albedo spot is that the resulting light curve tends to have only one maximum and one minimum per cycle. This clearly differs from the photometric variation caused purely by shape, since in this case the lightcurve tends to have two maxima and minima per cycle.
The known rotation period of Vesta is 5.342 h. The
generally accepted pole has ecliptic coordinates of
(326, +53). The Hipparcos photometric data set includes 58 observations
of Vesta. Among them, 48 have nominal error bars less than
0.01 mag. In this respect, Vesta is certainly one of the most
favourable cases among the objects listed in the catalog. Our
inversion, taking into account all the 58 observations, led to a
solution with a rotation period of 10.683 h, and pole
coordinates (350, +70). The
axial ratios were found to be b/a
= 0.91, c/a
= 0.53, with an evident exaggeration of the object's flatness with
respect to the c/a
= 0.81 value found by Thomas
et al. (1997). We interpret our result, with the
derived spin period being twice its correct value, as a nice proof of
the fact that our inversion algorithm correctly tries to derive the
period of an object exhibiting two maxima and minima per cycle, whereas
we do know that this is not the case for Vesta. Only for this asteroid,
we therefore developed a separate version of the algorithm, based on
the idea of fitting a hemispheric-scale albedo variegation, by assuming
that the magnitude depends on the visible illuminated cross-section,
but with a superimposed cyclic variation depending on the longitude of
the sub-Earth point (hereafter we should speak of ``sub-Hipparcos''
point, but we prefer to use the more conventional ``sub-Earth''
expression). In particular, we assumed that the magnitude V
corresponding to the visibility of an illuminated surface S
is given by:
where C is a constant that disappears when working in terms of magnitude differences with respect to a particular observation,
The result of this exercise was very positive. The genetic algorithm implementing the above expression for the magnitude gave the following solution: spin period P equal to 5.342 h, pole coordinates (345, 65), axial ratios b/a = 0.97, c/a = 0.69. The A parameter introduced above was found to take the reasonable value of 0.054, corresponding to a mild albedo difference. These results are in very good agreement with the corresponding correct properties of Vesta, and represent thus a success of our genetic fitting. On the other hand, we are aware that a hemispheric-scale albedo feature is special, and this case certainly cannot be generalized to the rest of the asteroid population. For this reason, we did not make any further attempt to take into account similar, or even more complicated albedo spots in our inversion attempts, even when failures of the normal algorithm might suggest that some albedo variegation could be present.
In the case of (1) Ceres, we obtained a spin period of 18.116 h, a pole solution (337, 85), and axial ratios b/a = 0.98 and c/a ranging between 0.63 and 0.76. Again, we have here the case of a fairly good inversion, since a pole solution (332, 70) is found in the literature, and the general spheroidal shape agrees with the results of direct imaging. The spin period, however, is about twice the correct spin period of 9.075 h known from lightcurve observations. We note that the overall photometric variation of this asteroid is characterized by a quite small lightcurve amplitude, because of its nearly perfect spheroidal shape. Again, we have to conclude that in the case of Ceres, as in the previously discussed case of Vesta, the photometric modulation displayed by the object must be caused mostly by albedo variegation of the surface, since the shape signature is very small. This finding, supported by our results, is known to have been confirmed by direct images of Ceres (Thomas et al. 2005).
6.2 (2) Pallas
The numbers of observations of (2) Pallas, with different
uncertainties, are always very close to the minimum limit for inversion
of perfect triaxial ellipsoids with pure geometric light scattering.
The overall shape of Pallas, the second largest asteroid in the main
belt, is only slightly elongated, and according to several authors its
axial ratio is ![]() (Kryszczynska 2009).
(Kryszczynska 2009).
When considering only the 43 Hipparcos measurements with nominal errors smaller than 0.02 mag, we found two possible solutions, as shown in Table 8. The solution with spin period P = 7.63075, pole coordinates (198, 56), has corresponding axial ratios of b/a = 0.89, and c/a = 0.86. The pole coordinates are in a fair agreement with the pole solution (193, 43) found by Torppa et al. (2003). The general shape is also quite reasonable. The rotation period, however, is incorrect by about eleven minutes, a discrepancy that is too high to be acceptable, although not dramatically far from the correct value. Moreover, a second solution, characterized by a spin period of about 11 h, but with retrograde rotation, and similar pole and shape of the previous solution, is also present and provides nearly identical residuals.
When trying to exploit a larger number of measurements, we find that, in the case of Pallas, the situation worsens. In particular, the inversion of the set of 60 observations with error bars within 0.04 mag produces a solution that is fairly equivalent to the previous one in terms of pole coordinates and axial ratios, but the rotation period is definitely worse. No spurious solution, however, is found in this case.
6.3 (3) Juno
The case of the other large asteroid (3) Juno is similar in some respects to the case of Pallas presented above, in that the number of photometric measurements, mainly at high levels of accuracy, is not high. In this case, however, the inversion solution is found to provide better results.
By running our inversion algorithm, we found two possible solutions, which are equivalent in terms of residuals. The first solution infers a rotation period P = 13.59130, pole coordinates (125,45), and axial ratios b/a = 0.86, c/a = 0.69. The second solution is the correct one: P = 7.20522, pole coordinates (282, -21) (retrograde rotation), axial ratios b/a = 0.76, c/a = 0.73. The pole is fully consistent with the (106, 34) solution quoted in the literature, apart from the opposite sign of rotation. We also note that for this asteroid, as in the previous case of (2) Pallas, we find an axial ratio b/c close to 1.
6.4 (5) Astraea
Our inversion of the entire data set of 81 measurements was successful,
and the solution given in Table 8 is
essentially correct. A difference of about 30 degrees between
the
resulting longitude of the pole and the pole solution obtained by
ground-based observations, is not really dramatic, especially when
considering the dispersion in the pole coordinates found by different
authors for most objects listed in the Poznan catalog. The axial ratios
corresponding to our solution are b/a
= 0.66, c/a
= 0.66 (another case of shape solution with ![]() ). However,
we note that another, nearly equivalent in terms of residuals, pole
solutions exists with pole longitude
). However,
we note that another, nearly equivalent in terms of residuals, pole
solutions exists with pole longitude ![]() ,
a little more than
,
a little more than ![]() apart in ecliptic longitude with respect to the best solution. This
second solution has a pole latitude varying between around 31 and
39 degrees, and is associated with correspondingly different
values of axial ratios, but with b = c.
apart in ecliptic longitude with respect to the best solution. This
second solution has a pole latitude varying between around 31 and
39 degrees, and is associated with correspondingly different
values of axial ratios, but with b = c.
6.5 (6) Hebe
The asteroid (6) Hebe is known to exhibit a complicated light curve with more than two maxima and two minima at some apparitions. On the basis of an extensive spectroscopic, photometric and polarimetric campaign, Migliorini et al. (1997) suggested that the surface of this object is probably uniform in composition, but large impact craters may be responsible for local inhomogeneity in albedo. For this asteroid, we have a large number of Hipparcos observations, but most of them have large associated error bars. We inverted the set of 85 photometric measurements with errors smaller than 0.03 mag, and we found a solution with P = 7.27290, and pole (45, 75). The axial ratios turned out to be b/a = 0.91, c/a = 0.21. This solution is questionable in many respects: the spin period is essentially correct, but the pole coordinates seem to have little to do with previous ground-based results, and the resulting shape also seems exceedingly elongated. Several other solutions are also found in different genetic attempts, giving slightly worse residuals, but corresponding practically to the same rotation period, but with different poles, as shown in Table 8. By using the data with uncertainties smaller than 0.02 mag (63 observations) leads to a solution characterized by a rotation period that is nearly exactly twice the correct value, but the corresponding pole is (338, 44), in perfect agreement with the previous determination by Torppa et al. (2003). The axial ratios of this solution are b/a = 0.85, and c/a = 0.76, corresponding to a reasonable, and not too elongated, shape. How can we interpret this? One speculative possibility is that some albedo variegation may be present. This variegation may be sufficient to lead to an inferred double spin period when the best data at our disposal are used, giving at the same time the correct pole and a reasonable shape. Adding a significant amount of measurements of lower quality leads to the effect of the albedo variegation disappearing, and the correct rotation period can be found, the drawback being that of a much decreased capability of deriving the correct pole and overall shape. Of course, these considerations are mostly qualitative.
6.6 (10) Hygiea
The Hipparcos photometric data set for (10) Hygiea, one of the largest asteroids located in the outer belt, is of quite poor quality. Taking at face value the invertibility criteria for perfect triaxial ellipsoids shown in Fig. 4, only the set of observations with error bars better than 0.04 mag, 46 measurements, might be marginally sufficient to attempt a successful inversion. We attempted this inversion, and as a result we found two solutions that are equivalent in terms of residuals. The first solution has P = 37.54308, pole (12, 71) (prograde rotation), axial ratios b/a = 0.74, c/a = 0.44 and is clearly incorrect. The second solution infers nearly the correct period (with retrograde rotation), but the corresponding pole has little to do with previous ground-based determinations, and the axial ratios are b/a = 0.77, c/a = 0.06. These values look absolutely unrealistic, since an asteroid of this size is certainly not disk-shaped.
It is clear that also for Hygiea the scarcity and low quality of Hipparcos photometric measurements are essential in obtaining a reasonable solution. The correct period and sense of rotation can be found, which is per se fairly encouraging in such a situation.
6.7 (15) Eunomia
Our inversion attempt was completely successful in this case. The axial ratios corresponding to our solution listed in Table 8 are b/a = 0.70, c/a = 0.55.
6.8 (20) Massalia
We took into account only the observations of (20) Massalia with accuracy better than 0.04 mag. The axial ratios associated with our solution listed in Table 8 are b/a = 0.84, c/a = 0.84. Our spin period is correct, but the sense of rotation is opposite to that of previous ground-based investigations. The resulting pole is in good agreement with the pole solutions listed by Kryszczynska (2009), apart from the inversion in the asteroid's sense of rotation. Our solution seems robust, although future observations will be useful to confirm the retrograde sense of rotation. We note also that this is another case in which the derived shape implies a b/c axial ratio close to 1.
6.9 (39) Laetitia
In the case of (39) Laetitia, we applied our inversion algorithm to the large data set of 109 observations of accuracy higher than 0.05 mag, and we were able to derive the correct spin and pole solution. We note, however, that a second possible pole solution was also found, with the same spin period.
We also attempted an inversion of the much smaller sample of measurements with nominal errors better than 0.02 mag, but in this case we were unable to find the correct solution.
6.10 (40) Harmonia
In the case of (40) Harmonia, the Hipparcos data set is also quite abundant, with a total of 103 observations. The difference between the results of our inversion attempt with respect to the similar case of (39) Laetitia discussed above, is that in this case the nominal accuracy of the data makes a real difference. In particular, we did not obtain a good solution when trying to invert the bigger sample of Hipparcos measurements having nominal accuracies better than 0.05 mag. But when we attempted the inversion of the much more limited sample of observations with nominal accuracies better than 0.03 mag, we obtained a solution which, apart from the sense of rotation, is in excellent agreement with the results of ground-based determinations. The resulting axial ratios were found to be b/a = c/a = 0.73.
6.11 (42) Isis
There are not many Hipparcos observations of asteroid (42) Isis. Using the sample of 40 observations with error bar below 0.03 mag, we obtained a spin period very close, although not identical to the value known from ground-based light curves. We note, however, that the sense of rotation of our inversion solution is found to be opposite to that found by light curve observations. The corresponding pole solution, however, has little to do with the different proposed pole solutions listed in the literature. The axial ratios turn out to be b/a = 0.77, c/a = 0.23, corresponding to a very elongated, and probably implausible, shape, taking into account also the moderate lightcurve amplitudes known for this asteroid. The situation does not improve when considering the larger sample of observations with nominal uncertainties of up to 0.04 mag. The scarcity of data for Isis could explain a priori the failure of our inversion attempt. On the other hand, since we are able to derive a rotation period that is at least nearly correct, the failure in this case may be only marginal.
6.12 (44) Nysa
Using the entire sample of available Hipparcos measurements of (44) Nysa, did not enable us to find a unique solution, but instead a number of equivalent solutions including one characterized by the correct spin period. When limiting ourselves to the sample of 41 observations with accuracies superior to 0.04 mag, however, without ambiguity, we obtained from inversion the correct solution for this asteroid. The resulting axial ratios were b/a = 0.41, and c/a = 0.32, corresponding to a significant, and probably overestimated, flattening.
6.13 (192) Nausikaa
For the asteroid (192) Nausikaa, the Hipparcos photometric catalog includes only a few observations, i.e., 32, and among them only 28 have nominal uncertainties smaller than 0.05 mag. A priori, therefore, this is a case that we should not expect to be able to invert successfully.
Our inversion attempt using all the 32 available measurements found more than one possible solution. The solution providing the best fit is characterized by an incorrect rotation period, but an almost correct solution for the period, with retrograde rotation, is also present, although slightly poorer in terms of residuals. We tried to limit the inversion attempt by considering only the 21 measurements with error bars smaller that 0.04 mag, and in this case we found two equivalent solutions: a spurious one, and another corresponding to the (practically correct) rotation period, and pole (95, -35). The axial ratios, however, are rather extreme in this case: b/a = 0.22, and c/a = 0.13. It is clear that the Hipparcos data for Nausikaa are very challenging, and it is encouraging that the correct rotation solution may be found in such an extreme case. That formally one of two best solutions provides the smallest residuals when considering only 21 observations indicates that the signature of the right solution, at least in some cases, may be found even when the number of available data points is very small.
6.14 (216) Kleopatra
The case of the asteroid (216) Kleopatra is in some respect similar to the case of (192) Nausikaa described above. In this case we also have at our disposal only a few photometric measurements: 21, implying that the inversion attempt is impossible. The result of our exercise, however, is surprisingly good. We found two equivalent solutions: one of them, with P = 5.38536 h and pole coordinates (226, 44) corresponds to the correct spin period, and to the pole solution (232, 37) found in the literature (Kryszczynska 2009). Moreover, the resulting overall shape solution, with axial ratios b/a = 0.42, c/a = 0.34, seems a fairly good approximation of the very elongated shape of this asteroid, as derived by radar and HST observations (Ostro et al. 2000; Hestroffer et al. 2002). This unexpected success of the inversion attempt might speculatively be an effect of the very elongated shape of the object, which may possibly produce a very strong signature of the correct spin period in the data.
6.15 (349) Dembowska
The inversion attempts for (349) Dembowska always found more than one solution, including the correct one. In particular, a spurious solution characterized by P = 4.6912 h, pole (200, 71), and axial ratios b/a = 0.78, c/a = 0.42, always appears, and is the best one when considering the full sample of measurements. We note that this solution for the rotation period is not poor, and only differs slightly from the values determined by means of ground-based observations. The pole solution, however, seems to have little to do with the most accurate ground-based determinations. In addition to the above solution, however, another solution is always found, which is also indistinguishable in terms of residuals when considering the sample of observations with error bars smaller than 0.04 mag. This solution has P = 4.7015 h, practically coincident with the correct spin period of this asteroid, and pole coordinates (137, -11), in excellent agreement with one of the two solutions given by Kryszczynska (2009), but with an inverse sense of rotation. The axial ratios are found to be, in this case, b/a = 0.75, and c/a = 0.74.
6.16 (354) Eleonora
We applied our inversion algorithm to the sample of 86 observations with error bars smaller than 0.05 mag. The axial ratios associated with our solution, listed in Table 8, are b/a = 0.68 and c/a = 0.64. Our solution is essentially correct in terms of the spin period, a difference of the order of 0.02 h being small in absolute terms, but certainly not negligible. The pole coordinates do not agree very well with the preferred solution by Kryszczynska (2009). In particular, the sense of rotation is opposite, but even taking into account this, the ecliptic longitude of the pole differs by about 30 degrees. The pole latitude, however, is in very good agreement with the preferred solution of Kryszczynska (2009).
6.17 (471) Papagena
Our inversion attempt using the larger sample of 94 observations of (471) Papagena with uncertainties below 0.05 mag produced the solution listed in Table 8. The associated axial ratios are b/a = 0.85, c/a = 0.39. This solution is essentially correct in terms of the spin period, although an error of the order of some thousandths of an hour is present. The pole solution is also in substantial agreement with one of the two main pole solutions reported in the literature.
7 Conclusions and future work
In this paper, we have presented a method designed to invert sets of sparsely acquired photometric data of asteroids, to derive the rotation period, spin axis orientation, and overall shape of the objects. We have first carried out an extensive set of blind tests using simulated data of increasing sophistication, and also applied the method to the catalog of Hipparcos photometric observations.
We have adopted a simple triaxial ellipsoid model for the object shapes, not because we believe that the true shapes of the objects are so simple, but because we need to develop a method with minimal CPU time requirements, with a goal of applying our algorithm to the inversion of the large dataset of disk-integrated observations of asteroids that will be produced by Gaia.
The results of our exercise seem to be encouraging. In the case of simulated data, we have been able to derive the correct solutions even for simulated objects with shapes quite far from our triaxial ellipsoid model, realistic scattering properties, and large superimposed photometric errors. In some cases, we find that some spurious solutions appear, but this is unsurprising because of the assumption of a triaxial ellipsoid shape.
The application of our inversion algorithm to the dataset of real observations obtained years ago by the Hipparcos satellite also provided reasonable results. We must take into account that, in absolute terms, the Hipparcos data are of quite poor quality, since in most cases only very limited numbers of observations are available for the small sample of objects observed by Hipparcos, and these observations are also affected by very large error bars. In this respect, our ability to successfully invert a significant fraction of these observations seems a good result.
We are aware that in some cases the success of the inversion seems to be more dependent on the nominal accuracy of the Hipparcos photometric measurements than on the number of available observations, whereas in other cases this is not true. This is certainly contradictory and in some respects disappointing, since we cannot state, based on the results of our analysis, that as a general rule for real objects the quality of the data, or their quantity, is more important. On the other hand, we tend to believe that, given the data at our disposal, we should be satisfied with what we are able to do.
We note that in principle our inversion algorithm might also be applied to other interesting cases that we have not considered in the present paper: in particular, it would be interesting to apply the method to a data set consisting of sparse photometric data such as those we have considered in this analysis, but complemented by the data from one or more full lightcurves. We did not analyse this kind of situation in the present paper, because we were mostly interested in preparing the data reduction pipeline of future Gaia data, for which in the vast majority of cases no light curve will be available. However, we are aware that in some cases supplementing sparse data with full light curves (properly calibrated to avoid problems withmagnitudes obtained by different instruments) might be useful, and we plan to explore some cases of this kind in the near future.
We are now at the beginning of a new era, in which large volumes of sparse photometric data will be obtained for asteroids by large sky surveys of the next generation. We may be confident that these data will be properly exploited in the next years, and will produce a wealth of results that are well beyond the practical limits of the older, classical observational work based on measurement of full light curves at different oppositions. The new era will be challenging, but we are ready to profit from it.
AcknowledgementsWe thank the Referee, Anna Marciniak, for her careful review and many comments and suggestions that led to a substantial improvement of this work. A.C. and A.D.O. work was partly supported by the Italian Space Agency (ASI), under Contract n. I/015/07/0. A.C. carried out most of this work while being Invited Researcher at the IMCCE of the Paris Observatory.
References
- Bowell, E., Hapke, B., Domingue, D., et al. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M. S. Matthews, 524
- Capaccioni, F., Cerroni, P., Coradini, M., et al. 1984, Nature, 308, 832 [NASA ADS] [CrossRef]
- Cellino, A., Zappala, V., di Martino, M., Farinella, P., & Paolicchi, P. 1987, Icarus, 70, 546 [NASA ADS] [CrossRef]
- Cellino, A., Delbò, M., Zappalà, V., Dell'Oro, A., & Tanga, P. 2006, Adv. Space Res., 38, 2000 [NASA ADS] [CrossRef]
- Durech, J., & Sidorin, V. 2009, Database of asteroid models from Inversion Techniques, http://astro.troja.mff.cuni.cz/projects/asteroids3D/
- Durech, J., Scheirich, P., Kaasalainen, M., et al. 2007, in IAU Symp. 236, ed. G. B. Valsecchi, D. Vokrouhlický, & A. Milani, 191
- Durech, J., Kaasalainen, M., Warner, B. D., et al. 2009, A&A, 493, 291 [NASA ADS] [CrossRef] [EDP Sciences]
- Hapke, B. 1984, Icarus, 59, 41 [NASA ADS] [CrossRef]
- Harris, A. W., Warner, B. D., & Pravec, P. 2006, NASA Planetary Data System, EAR-A-5-DDR-DERIVED-LIGHTCURVE-V8.0:LCREF_TAB, 56, 3
- Hestroffer, D. 2003, A&A, 403, 749 [NASA ADS] [CrossRef] [EDP Sciences]
- Hestroffer, D., & Mignard, F. 1997, A&A, 325, 1253 [NASA ADS]
- Hestroffer, D., Morando, B., Hog, E., et al. 1998, A&A, 334, 325 [NASA ADS]
- Hestroffer, D., Berthier, J., Descamps, P., et al. 2002, A&A, 392, 729 [NASA ADS] [CrossRef] [EDP Sciences]
- Kaasalainen, M. 2004, A&A, 422, L39 [NASA ADS] [CrossRef] [EDP Sciences]
- Kaasalainen, M., Mottola, S., & Fulchignoni, M. 2002, Asteroids III, 139
- Kaasalainen, S., Piironen, J., Kaasalainen, M., et al. 2003, Icarus, 161, 34 [NASA ADS] [CrossRef]
- Kryszczynska, A. 2009, Database of asteroid spin vector determinations, http://vesta.astro.amu.edu.pl/Science/Asteroids/
- Kryszczynska, A., La Spina, A., Paolicchi, P., et al. 2007, Icarus, 192, 223 [NASA ADS] [CrossRef]
- Magnusson, P., Barucci, M. A., Drummond, J. D., et al. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M. S. Matthews, 66
- Migliorini, F., Manara, A., Scaltriti, F., et al. 1997, Icarus, 128, 104 [NASA ADS] [CrossRef]
- Muinonen, K., Piironen, J., Shkuratov, Y. G., Ovcharenko, A., & Clark, B. E. 2002, Asteroids III, 123
- Nathues, A., Mottola, S., Kaasalainen, M., & Neukum, G. 2005, Icarus, 175, 452 [NASA ADS] [CrossRef]
- Ostro, S. J., Hudson, R. S., Nolan, M. C., et al. 2000, Science, 288, 836 [NASA ADS] [CrossRef]
- Perryman, M. A. C. 1997, The HIPPARCOS and TYCHO catalogues Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200
- Pospieszalska-Surdej, A., & Surdej, J. 1985, A&A, 149, 186 [NASA ADS]
- Russell, H. N. 1906, ApJ, 24, 1 [NASA ADS] [CrossRef]
- Seidelmann, P. K., Archinal, B. A., A'Hearn, M. F., et al. 2007, Cel. Mech. Dynam. Astr., 98, 155 [NASA ADS] [CrossRef]
- Thomas, P. C., Binzel, R. P., Gaffey, M. J., et al. 1997, Icarus, 128, 88 [NASA ADS] [CrossRef]
- Thomas, P. C., Parker, J. W., McFadden, L. A., et al. 2005, Nature, 437, 224 [NASA ADS] [CrossRef]
- Torppa, J., Kaasalainen, M., Michalowski, T., et al. 2003, Icarus, 164, 346 [NASA ADS] [CrossRef]
- Torppa, J., Hentunen, V.-P., Pääkkönen, P., Kehusmaa, P., & Muinonen, K. 2008, Icarus, 198, 91 [NASA ADS] [CrossRef]
- van Leeuwen, F., Evans, D. W., Grenon, M., et al. 1997, A&A, 323, L61 [NASA ADS]
- Verbiscer, A. J., & Veverka, J. 1995, Icarus, 115, 369 [NASA ADS] [CrossRef]
- Zappala, V., Cellino, A., Barucci, A. M., Fulchignoni, M., & Lupishko, D. F. 1990, A&A, 231, 548 [NASA ADS]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- A.C. thanks the IMCCE of the Paris Observatory and the Paris Observatory for kindly offering him three stages as invited researcher at IMCCE to work on this research.
- ... Observatory
![[*]](/icons/foot_motif.png)
- Publicly available at the web address http://vesta.astro.amu.edu.pl/Science/Asteroids/Spindata/spin.pdf
- ...Kryszczynska et al. (2007)
![[*]](/icons/foot_motif.png)
- The electronic version of the catalogue available in the web will be hereinafter quoted as Kryszczynska (2009), and includes also all bibliographic reference to the original papers in which pole solutions were published.
- ... site
![[*]](/icons/foot_motif.png)
- http://pds.jpl.nasa.gov/
All Tables
Table 1: Results of the photometric inversion of simulated ellipsoids and Eunomia-like shaped asteroids.
Table 2: List of different orbits adopted in the simulations.
Table 3: Results of the photometric inversion of simulated Eunomia-like shaped asteroids on different asteroidal orbits.
Table 4: Results of the photometric inversion of simulated Golevka-like shaped asteroids on different asteroidal orbits.
Table 5: Results of the photometric inversion of simulated Eros-like shaped asteroids on different asteroidal orbits.
Table 6: Results of the photometric inversion of simulated Golevka-like shaped asteroids on two different asteroidal orbits.
Table 7: The Hipparcos asteroid photometric dataset.
Table 8: Comparison of known spin periods and pole coordinates, and results from inversion of Hipparcos data.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg1.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg25.png) |
Figure 1: Comparison of a set of simulated magnitudes collected by Gaia for a triaxial-ellipsoid object having the same orbit of the asteroid (3) Juno, and the corresponding magnitudes resulting from the obtained photometric inversion solution. Magnitudes are expressed in terms of differences with respect to the first observation, and are plotted against ecliptic longitude. Simulated and inversion solution data are displayed using different symbols. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg2.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg26.png) |
Figure 2:
Same as Fig. 1,
but this time the simulated observations are affected by a simulated
Gaussian error having a |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg3.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg27.png) |
Figure 3: Same results shown in Fig. 2, but this time we plot directly the residuals O-C as a function of the ecliptic longitudes of the observations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg4.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg28.png) |
Figure 4:
Results of a set of simulations of triaxial ellipsoid objects, as a
function of the number of available observations for a given object,
and as a function of the error bars of the observations. Errors are
expressed in terms of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg5.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg30.png) |
Figure 5: Three views for each of the realistic object models considered in our simulations. From top to bottom, the figure shows the models of Golevka, (433) Eros and (15) Eunomia, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg6.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg249.png) |
Figure 6:
Difference |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12134fg7.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12134-09/Timg250.png) |
Figure 7:
Accuracy of the Hipparcos |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.