EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 506 / No 1 (October IV 2009) A&A, 506 1 (2009) 175-181 Full HTML
Issue
A&A
Volume 506, Number 1, October IV 2009
The CoRoT space mission: early results
Page(s) 175 - 181
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200911947
Published online 15 July 2009

The CoRoT space mission: early results

Impact of the physical processes in the modeling of HD 49933

L. Piau1 - S. Turck-Chièze1 - V. Duez1 - R. F. Stein2

1 - CEA-Saclay, DSM/IRFU/SAp, L'Orme des merisiers, Bâtiment 709, 91191 Gif-sur-Yvette, France
2 - Michigan State University, Department of Physics & Astronomy East Lansing, MI 48824-2320, USA

Received 25 February 2009 / Accepted 25 June 2009

Abstract
Context. On its asteroseismic side, the initial run of CoRoT was partly devoted to the solar like star HD 49933. The eigenmodes of this F dwarf have been observed with unprecedented accuracy.
Aims. We investigate quantitatively the impact of changes in the modeling parameters like mass and composition. More importantly we investigate how a sophisticated physics affects the seismological picture of HD 49933. We consider the effects of diffusion, rotation and the changes in convection efficiency.
Methods. We use the CESAM stellar evolution code coupled to the ADIPLS adiabatic pulsation package to build secular models and their associated oscillation frequencies. We also exploited the hydrodynamical code STAGGER to perform surface convection calculations. The seismic variables used in this work are: the large frequency separation, the derivative of the surface phase shift, and the eigenfrequencies $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.
Results. Mass and uncertainties on the composition have much larger impacts on the seismic variables we consider than the rotation. The derivative of the surface phase shift is a promising variable for the determination of the helium content. The seismological variables of HD 49933 are sensitive to the assumed solar composition and also to the presence of diffusion in the models.

Key words: stars: late-type - stars: oscillations - stars: interiors - stars: rotation - convection

1 Introduction

The accurate measurements of oscillation frequencies by CoRoT (Baglin et al. 2006) in nearby solar-like stars such as HD 49933 (Appourchaux et al. 2008) aims at constraining their internal dynamics. First, the global parameters of the star (age, mass, composition) must be determined. For this, the seismic data complement the information that already exists. Second, a comparison with sophisticated models is required. In this work we use an updated version of the CESAM stellar evolution code (Morel 1997). CESAM can take into account microscopic diffusion and the radiative accelerations of heavy elements. It also optionally includes the secular effects of rotation in the radiation zones (Mathis & Zahn 2004). The resulting mixing slightly changes the temperature profile of otherwise stably stratified regions and modifies the structure and evolution of the star (Maeder & Meynet 2000; Decressin et al. 2009).

Like helioseismology for the Sun, asteroseismology can constrain the helium fraction in solar analogs. In this respect stars slightly more massive than the Sun are especially interesting targets. Asteroseismology can also constrain convection: the depth of the outer convection zone depends on the efficiency of convective energy transport in the subsurface layers and in turn affects the seismic signal. In the current work, we compute the relation between the effective temperature and the specific entropy in the deep convection zone where the motions become adiabatic. To this purpose, we use the STAGGER hydrodynamical code (Stein & Nordlund 1998). This computation gives an idea of the magnitude of the change of the mixing length main parameter  $\alpha_{\rm mlt}$ with the effective temperature for stars having surface conditions close to the solar ones like HD 49933.

Although some of our models are in fair agreement with the current classical and seismological observations of HD 49933, our purpose is not to find the model that best fits them. We intend to estimate the influence of mass, composition and of different internal processes on the seismic indicators and the surface properties of HD 49933. Section 2 presents our secular models of HD 49933 and explores the impact of mass, composition, microscopic diffusion and rotation. Section 3 presents the effects of a modified surface convection efficiency and conclusion follows in Sect. 4.

2 Secular models of HD 49933

We build models of HD 49933 using the CESAM stellar evolution code (Morel 1997). The models are initiated on the zero age main sequence. We use the NACRE compilation of nuclear reaction rates (Angulo et al. 1999). The equation of state (OPAL2001) and high temperature opacities come from the OPAL group (Rogers et al. 1996; Iglesias & Rogers 1996). Below 5800 K we use the opacities of Ferguson et al. (2005). The equation of state and opacity tables were computed for the recent solar metal repartition advocated by Asplund et al. (2005). The atmosphere is buildt using the Hopf law (Mihalas 1978). It is connected to the envelope at the optical depth 20. Finally, the convection zone is fully homogeneous and modeled using mixing-length theory (hereafter MLT) in a formalism close to Böhm-Vitense (1958) (see Piau et al. 2005, for the exact description of the current MLT formalism). Our Sun calibrated value for the main MLT parameter is $\alpha_{\rm MLT}=1.587$.

Solano et al. (2005) find [Fe/H] = -0.37. If we assume the Asplund et al. (2005) solar surface composition (X=0.7392, Z=0.0122) and metal repartition then HD 49933 should currently exhibit X=0.7664, Z=5.4 $\times $ 10-3 provided the helium and metals surface abundances follow the typical Galactic enrichment law $\frac{\Delta Y}{\Delta Z}=3$ (Fernandes et al. 1998)[*]. The effective temperature found in the literature ranges from $T_{\rm eff}=6780$ $\pm$ 130 K (Bruntt et al. 2008) to $T_{\rm eff}=6700$ $\pm$ 65 K (Gillon & Magain 2006) but values as low as $T_{\rm eff}=6600$ $\pm$ 130 K have also been suggested (Lastennet et al. 2001). For a visual magnitude of $m_{\rm v}=5.77$, the HIPPARCOS parallax (33.7 $\pm$ 0.4 mas, van Leeuwen 2007) and bolometric correction ( $\rm BC=0.025$ $\pm$ 0.005, Bessell et al. 1998) suggest $\log (L/L_{\odot})=0.53$ $\pm$ 0.01. The following models have been calibrated in luminosity in the sense that we stop the evolution once they reach the observed luminosity. Unless explicitly mentioned all the models include overshooting of 0.2 pressure scale height (hereafter $H_{\rm p}$) that is typical of the expected mass range of the star (Claret 2007). We investigate the impact of the mass, the composition and the rotation on the seismic properties of the star. The oscillation frequencies are computed using the Aarhus adiabatic pulsation package ADIPLS (Christensen-Dalsgaard & Berthomieu 1991). We focus our attention on three seismic quantities: the large frequency separation ( $\Delta \nu = \nu_{\ell,n+1}-\nu_{\ell,n}$) that is sensitive to the global properties of the star such as mass and age, the lowest degree lowest and highest order modes frequency currently observed ( $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$) and the derivative of the surface phase shift with frequency ( $\beta ^{\star } (\nu )$) in order to address the helium ionization effects. We do not investigate the small separation or other seismic variables. To determine the averages of these quantities, we exclude frequencies below a cut off of 1 mHz in order to be in the asymptotic regime.

2.1 Mass effects

HD 49933 being a single star, its mass estimate relies on evolutionary tracks. It is therefore sensitive not only to the approach chosen in the modelling (e.g. description of diffusion, rotation mixing, overshooting ...) but also to the input parameters of the models such as the metallicity and the helium fraction. For these reasons it is interesting to address the influence of the mass on the seismic signature of this star. Mosser et al. (2005) suggested $M/M_{\odot} \approx 1.2$ and we explore the effect of mass variation around this value. No diffusion or rotation effects are taken into account in the models of this subsection. The convection overshooting in the core is $0.2~H_{\rm p}$, however the overshooting has a very moderate impact on the variables we consider here. As illustrated by the work of Goupil et al. (2009), overshooting mostly influences the small seismic separation which we have not considered here. As an indication of the overshooting impact, we provide a 1.17 $M_{\odot}$ model without overshooting on the last line of Table 1.

Table 1 shows the values of the large separation and the frequencies of the modes of degree $\ell =0$ and radial orders n=14 and n=27. These modes should respectively minimize and maximize the surface effects. The recent analysis of Benomar et al. (2009) suggests two slightly different observational solutions owing to the modes identification. The first mode identification, named $M_{\rm A}$ by Benomar et al., corresponds to the work of Appourchaux et al. (2008) $\Delta \nu = 85.92$ $\pm$ $0.43~\mu {\rm Hz}$, $\nu_{\ell=0,n=14}=1244.43$ $\pm$ $3.90~\mu{\rm Hz}$ and $\nu_{\ell=0,n=27}=2363.81$ $\pm$ $3.90~\mu{\rm Hz}$. The other mode identification, $M_{\rm B}$, provides $\Delta \nu = 85.81$ $\pm$ $0.29~\mu{\rm Hz}$, $\nu_{\ell=0,n=14}=1290.55$ $\pm$ $6.97~\mu{\rm Hz}$ and $\nu_{\ell=0,n=27}=2405.90$ $\pm$ $3.48~\mu{\rm Hz}$ ($2 \sigma $ error bars). The models in Table 1 all have the same composition: X=0.7664, Z=5.4 $\times $ 10-3. A 0.2 $H_{\rm p}$ core convection overshooting is included in all models except the one mentioned by $\dagger$ where there is no overshooting. The second part of the table displays the current seismic observations following the two possible mode identification $M_{\rm A}$ and $M_{\rm B}$ of Benomar et al. (2009). The best fit with seismic data is obtained for $1.17~M_{\odot}$. Within error bars, the large separation of this model agrees with identification $M_{\rm A}$ of Benomar et al. (2009) and is marginaly above their identification $M_{\rm B}$. The absolute frequencies of our model and of this second solution agree at low and high order. Figure 1 displays the difference in eigenfrequencies between our model and the two observational solutions for degree $\ell =0$, as a function of the radial order. The difference is always below  $40~\mu{\rm Hz}$. Note that in the solar case, predicted and observed eigenmodes frequencies agree at low frequencies but differ by ${\sim}20~\mu{\rm Hz}$ at high frequencies most likely because of surface effects (Turck-Chièze et al. 1997). The average difference between the model and the first and second observed solutions of Benomar et al. (2009) are respectively $-32.6~\mu{\rm Hz}$ and $12.2~\mu{\rm Hz}$. In both cases there is a clear trend in the model/observations difference with increasing frequency which might be due to the absence of subphotospheric turbulence and/or magnetic surface effects as in the solar case.

Table 1:   Mass effect on the large frequency separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.

 \begin{figure} \par\includegraphics[width=8cm,clip]{11947fg1.ps} \end{figure} Figure 1:

Differences between the observed eigenfrequencies and the model eigenfrequencies vs. the radial order for degree modes $\ell =0$. The model considered is model 3, losanges and stars respectively correspond to the $M_{\rm A}$ and $M_{\rm B}$ modes identifications of Benomar et al. (2009). We also indicated the $2 \sigma $ error bars from these authors.
Open with DEXTER

The large separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$ decreases rapidly with mass and with current modeling assumptions suggests a mass slightly below 1.2 $M_{\odot}$. The logarithmic derivative of the large separation with mass around $1.17~M_{\odot}$ is $\frac{\partial {\rm ln} \Delta \nu}{\partial {\rm ln} \Delta M}=2.6$ which means a significant dependence of $\Delta \nu$ on mass (see hereafter). If we extrapolate this result to the average large separation observed by Benomar et al. (2009) $85.92~\mu{\rm Hz}$, we find that the mass of HD 49933 should be $1.168~M_{\odot}$. We note that the effective temperature of our $1.17~M_{\odot}$ model is between 100 and 150 K below the current estimates but in agreement with the previous determination of Lastennet et al. (2001). We recall that this model was obtained assuming [Fe/H] = -0.37, the solar Asplund et al. (2005) metal repartition and $\frac{\Delta Y}{\Delta Z}=3$ as the metal vs. helium relation. In the next section we study the effects of composition.

2.2 Composition effects

As recent developments in solar physics have shown, helioseismological results are very sensitive to the solar composition and therefore stand as key indicators of it (Turck-Chièze et al. 2004; Bahcall et al. 2005). On the one hand the metals are the main contributors to the opacities in low mass stars (Turck-Chièze et al. 2009, 1993) which directly affects the structure and the seismic signal. On the other hand, because of the low effective temperature, the helium fraction is only accessible through seismology (Basu & Antia 1995). Yet the mass and the age of stars other than the Sun have to be known if one wants to constrain their metals or helium fractions (Basu et al. 2004). In the case of HD 49933 we can therefore only give qualitative indications on the composition.

We addressed the composition issue using the $1.17~M_{\odot}$ models, as the mass effects suggest this is the best fit for HD 49933. The A05 and GS98 respectively stand for Asplund et al. (2005) and Grevesse & Sauval (1998) solar metal repartitions. In both cases the assumed metallicity is [Fe/H] = -0.37 dex but in the former case this corresponds to a smaller absolute amount of metals other than iron (mostly oxygen and carbon) than in the later case. If we assume the A05 metal repartition then X=0.7664 and Z=5.4 $\times $ 10-3 (model 3) whereas if we assume the GS98 metal repartition X=0.7638, Z=8.02 $\times $ 10-3 (model 4). These are the current and initial convection zone compositions because no microscopic diffusion is taken into account in this subsection. As illustrated in Table 2 the metal repartition and helium abundance have significant impacts on  $\Delta \nu$ although smaller than the impact of mass (Sect. 2.1). Please note that the models in Table 2 all have the same mass: $1.17~M_{\odot}$. The main difference between A05 and GS98 metal repartition is the [O/Fe] ratio. The logarithmic derivative of the large separation with [O/Fe] is $\frac{\partial {\rm ln} \Delta \nu}{\partial {\rm ln} \Delta [{\rm O/Fe}]}=0.83$[*]. We mention that variations of the [O/Fe] ratio are observed in nearby stars, the scatter of [O/Fe] across the Galactic disk being the order of 0.2 dex (Edvardsson et al. 1993).

The decrease in the global metal content from GS98 to A05 creates a drop in opacity and therefore a somewhat higher effective temperature at a given luminosity. This corresponds to a smaller radius and a higher interior temperature and is consistent with a larger large separation as:

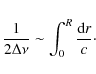
\begin{eqnarray*}\frac{1}{2 \Delta\nu} \sim \int_{0}^{R} \frac{{\rm d}r}{c}\cdot \end{eqnarray*}


Thus more metal rich models (GS98) suggest a mass higher than $1.17~M_{\odot}$. Quantitatively, going from the A05 to the GS98 composition lowers the large difference by ${\sim}8~\mu$Hz which is comparable to the mass effect between models 2 and 3 ( $0.03~M_{\odot}$ difference).

Table 2:   Composition effects on the large frequency separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.

 \begin{figure} \par\includegraphics[width=8cm,clip]{11947fg2.ps} \end{figure} Figure 2:

Losanges: $\beta ^{\star } (\nu )$ vs. $\nu $ for the model having $M_{\star}=1.17~M_{\odot}$ and X=0.7664, Y=0.2282 and Z=5.4 $\times $ 10-3 (model 3). Triangles: $\beta ^{\star } (\nu )$ vs. $\nu $ for the same mass but X=0.7529, Y=0.2417 and Z=5.3 $\times $ 10-3 (model 5).
Open with DEXTER

The region of the helium second ionization, located right below the photosphere, appears as a discontinuity to the internal waves. As such it creates an oscillatory pattern in the eigenmodes frequencies (Gough 1990) that has been used for some time to infer, for instance, the solar photosphere abundance in helium (Vorontsov et al. 1991). The oscillatory pattern is clearly visible in the second difference seismic variable $\delta_2 \nu_{\ell,n}= \nu_{\ell,n-1} -2\nu_{\ell,n} + \nu_{\ell,n+1}$ especially in stars slightly more massive than the Sun (Piau et al. 2005). While $\delta_2 \nu_{\ell,n}$ is probably easier to determine from the observations than the surface phase shift  $\alpha (\nu)$, this later variable and its derivatives are less sensitive to uncertainties in frequency determinations (Lopes et al. 1997).

Following Lopes et al. (1997) we compute $\beta (\nu)= \alpha (\nu) - \nu \frac{{\rm d} \alpha}{{\rm d} \nu}$ to extract the effect of helium in the cases of three stars: models 2, 3 and 5 (see Tables 1 and 2). $\beta (\nu)$ is estimated for the low degree modes $\ell=0,1,2$. Then it is corrected by a linear fit in order to obtain  $\beta ^{\star } (\nu )$ whose mean value is 0. $\beta ^{\star } (\nu )$ vs. $\nu $ is shown in Figs. 2 and 3. The differences between models 2 and 3 account for the effects of mass whereas the differences between the models 3 and 5 account for the effect of the helium fraction. Models 2 and 3 have an helium mass fraction of Y=0.2282. Because of a different $\frac{\Delta Y}{\Delta Z}$ law model 5 is richer in helium than the other models with Y=0.2417. Note that all our models have the same metallicity [Fe/H] = -0.37.

 \begin{figure} \par\includegraphics[width=8.4cm,clip]{11947fg3.ps} \end{figure} Figure 3:

$\beta ^{\star } (\nu )$ vs. $\nu $ for the model having $M_{\star}=1.2~M_{\odot}$, X=0.7664, Y=0.2282 and Z=5.4 $\times $ 10-3 (model 2).
Open with DEXTER

Figure 2 illustrates the strong dependence of the peaks of $\beta ^{\star } (\nu )$ and therefore $\beta (\nu)$ on the helium mass fraction. The increase of $\Delta Y$ = 0.0135 from models 3 to 5 increases the frequency of the first peak of  $\beta ^{\star } (\nu )$ above 1 mHz by $\approx$ $150~\mu{\rm Hz}$. The second peak of  $\beta ^{\star } (\nu )$ is shifted by $\approx$ $200~\mu{\rm Hz}$. However Fig. 3 shows that the position of the peaks in  $\beta ^{\star } (\nu )$ is also strongly related to the mass. Based on the differences from models 3 to 5, the logarithmic derivative of the large separation with the helium mass fraction is $\frac{\partial {\rm ln} \Delta \nu}{\partial {\rm ln} \Delta Y}=0.90$.

2.3 Diffusion effects

The consequences of microscopic diffusion in the enveloppes of solar-like stars are clearly observed. In the case of the Sun it has been known for some time that it improves the agreement between theoretical and observed sound speed profiles (Christensen-Dalsgaard et al. 1993) and it is a necessary process to explain the current photospheric helium abundance (Basu & Antia 1995). Besides this, diffusion is the best candidate to explain the 7Li abundance in Population II solar analogs (Piau 2008; Richard et al. 2005). Finally refined calculations by Turcotte et al. (1998) have shown that a significant change in surface composition through diffusion is expected between $1.1~M_{\odot}$ and $1.5~M_{\odot}$ (the typical mass range of HD 49933). We calculate the joint effects of microscopic diffusion (following the formalism of Burgers 1969) and radiative accelerations. We consider that the initial composition is the initial composition of our calibrated solar models including diffusion i.e. X=0.7195 and Y=0.2664 (Turck-Chièze et al. 2004).

Because diffusion takes the metals away from the surface, the diffusive models for a given mass and Z/X surface ratio are cooler than the non diffusive models with the same Z/X surface ratio. For instance a  $1.25~M_{\odot}$ non diffusive model with Z/X=1.15 $\times $ 10-2 and Y=0.2664 has an effective temperature of $T_{\rm eff}=6856$ K when it reaches the luminosity $\log (L/L_{\odot})=0.53$ at 1.12 Gyr. The corresponding $1.25~M_{\odot}$ diffusive model exhibits $T_{\rm eff}=6151$ K at the same luminosity which it reaches at 3.32 Gyr (see Table 3). Because of this effect, the diffusive models complying with the observed effective temperature of HD 49933 are more massive than the non diffusive ones. Table 3 shows that they lie around  $1.35~M_{\odot}$ while the non diffusive model with the correct effective temperature have masses around $1.2~M_{\odot}$. Regarding the seismic properties of diffusive models the same remark can be done. The diffusive model that best agrees with the observations is significantly more massive ( $1.3~M_{\odot}$) than the non diffusive one ( $1.17~M_{\odot}$). Being more massive than the non diffusive models, the diffusive models fitting the observations are also younger: the $1.3~M_{\odot}$ diffusive model is 1.79 Gyr whereas the $1.17~M_{\odot}$ non diffusive model is 3.59 Gyr.

As stated above, if we assume the Asplund et al. (2005) solar composition, then in HD 49933 we have Z/X=7.04 $\times $ 10-3. Table 3 shows that the diffusive models that meet this condition are too cool, or equivalently that the diffusive models in the right range of the effective temperature are too metal poor. The physical reason for this being that in the higher mass regime the outer convection zone becomes too shallow for convection to brake significantly the gravitational settling of the heavy elements. This drawback suggests that the microscopic diffusion (and radiative acceleration) effects are moderated by an additional mixing process in the radiation envelope below the outer convection zone. There is actually a strong evidence of such a mixing as, with $T_{\rm eff}=6780$ K HD 49933, nearly stands to the middle of the so-called lithium dip (Boesgaard & Tripicco 1986; Boesgaard & King 2002). The stars of the lithium dip show lithium and beryllium depletion which implies deep mixing in their radiation zones. A likely candidate to this is the shear turbulence induced by the angular momentum loss (Talon & Charbonnel 1998; Decressin et al. 2009). The occurence of such a process within HD 49933 would brake the microscopic diffusion. Similarly the tachocline mixing (Spiegel & Zahn 1992) in the transition region between convection and radiation zones brakes the metals and helium diffusion in the Sun (Turck-Chièze et al. 2004). The interplay between diffusion and this process - or another non standard mixing phenomenon - appears necessary to build the observed 7Li abundance in Population II (Piau 2008; Richard et al. 2005). In the next subsection we briefly address the effects of rotation and of the interaction between diffusion and rotation.

Table 3:   Microscopic diffusion and radiative acceleration effects on the large frequency separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.

2.4 Rotation effects

The power spectrum of HD 49933 suggests a surface rotation period of 3.4 days (Appourchaux et al. 2008). If, following Thévenin et al. (2006), we consider $R_{\star}/ R_{\odot}=1.43$ this leads to an equatorial velocity $V_{\rm eq}= 21.3~{\rm km~s}^{-1}$. This result is in agreement with direct estimates of $v \sin i$ (Solano et al. 2005; Mosser et al. 2005).

We have applied the theory of Mathis & Zahn (2004) for two $1.17~M_{\odot}$ models evolving without angular momentum loss and showing equatorial velocities $V_{\rm eq}=10~{\rm km~s}^{-1}$ (model 9) and $V_{\rm eq}=20~{\rm km~s}^{-1}$ (model 10) at 4.35 Gyr and 3.97 Gyr respectively. These ages correspond to $\log (L/L_{\odot})=0.53$. The Mathis & Zahn (2004) transport equations account for the modifications in temperature, mean molecular weight and gravitational potential induced by rotation. The meridional circulation is calculated as well. Table 4 provides information similar to the preceeding ones. The model 11 mentionned with $\dagger$ includes both rotation and microscopic diffusion. Its initial composition is X=0.7195, Y=0.2664 ( Z/X= 1.959 $\times $ 10-2). All the other models of the table have rotation but no microscopic diffusion effects and an initial composition X=0.7664, Z=5.4 $\times $ 10-3. The impact of rotation effects on the large frequency separation is hardly visible. The logarithmic derivative of the large separation with the equatorial velocity computed from models 9 and 10 is tiny $\frac{\partial {\rm ln} \Delta \nu}{\partial {\rm ln} V_{\rm eq}}=1.1$ $\times $ 10-3.

Thus the rotation effects seem negligible. However when tested in diffusive models they diminish the diffusion efficiency and therefore help improving the issue outlined in Sect. 2.3. The physics used in building models 7 and 11 is similar except for rotation. Table 4 shows that they nearly are identical except their difference in the surface Z/X ratio. Model 11 is not our best fit to the observational constrains but it is the most sophisticated secular model of this work as it includes both of the significant diffusion and rotation effects expected in HD 49933. Its large frequency separation and surface metallicity lie very close to the observations. Even tough model 11 is too cool, it points out that the mass of HD 49933 predicted by refined models is higher than the mass predicted by simple models (e.g. model 3).

Table 4:   Rotation and microscopic diffusion effects on the large frequency separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.

3 Surface convection of HD 49933

3.1 Dynamical models

We use the STAGGER code (Stein & Nordlund 1998) to investigate the convective and the radiative energy transfer from 500 km above the photosphere downto 2500 km below. The computational domain extends over 6000 by 6000 km horizontaly. The current grid has 63 points in each direction. We solve the fully compressible equations of hydrodynamics and use the same equation of state - OPAL - as in the CESAM calculations. As far as possible, we use the same opacities as well. Near and above the photosphere, the diffusion approximation for radiative energy transport breaks down and one has to solve the radiative energy transfer equation. We adopted the binning method to solve this equation (Nordlund 1982). This widely used method (see e.g. Ludwig et al. 2006) requires 1D atmosphere model structure as well as monochromatic opacities. For both we use the Kurucz data and programs (Castelli 2005a,b). Thus the opacities near and above the photosphere are not the OPAL opacities. The equation of state and opacity tables were computed for the composition X=0.7664, Z=5.4 $\times $ 10-3 (see Sect. 2.2).

We run STAGGER over the typical Kelvin-Helmholtz time-scale of the computational box that is 104 s. The effective temperature is computed using the surface radiative flux. The efficiency of the surface convection is a priori dependent on the total energy flux (i.e. the $T_{\rm eff}$) and the surface gravity. We considered three simulations: a reference one for the Sun (model A), a model where the specific entropy of the deep convection zone was slightly increased with respect to the Sun (model B) and a model where the surface gravity was slightly lowered (model C). Model B is obtained by increasing the internal energy entering the lower boundary of the domain by 2%. The gravity field in model B is kept to its solar surface value and constant throughout the simulation box. Model C is obtained by decreasing the surface gravity by 2% but the specific entropy of the deep convection zone keeps its solar value of model A.

Table 5 gives the surface conditions and the specific entropy in the deep convection zone (adiabatic regime) in the hydrodynamical models A-C and our stellar evolution code best fit model. The increase of the specific entropy in the adiabatic regime ( $s_{\rm ad}$) or the decrease of the surface gravity induce a decrease in the effective temperature. Around the solar surface conditions, the logarithmic derivative of  $s_{\rm ad}$ with  $T_{\rm eff}$ is $\frac{\partial {\rm ln} s_{\rm ad}}{\partial {\rm ln} \Delta T_{\rm eff}}=-0.225$ between models A and B.

If we extrapolate this to the case of HD 49933 ( $T_{\rm eff}=6780$ K) it provides $s_{\rm ad~HD~49933}= 1.8605$ $\times $ $10^9~{\rm erg~K^{-1}~g^{-1}}$. Our best fit model of HD 49933 (model 3 see Table 1) based on a solar calibrated value of  $\alpha_{\rm mlt}$ exhibits $s_{\rm ad}= 2.3370$ $\times $ $10^9~{\rm erg~K^{-1}~g^{-1}}$. This suggests that the efficiency of convection increases when going from the Sun to the HD 49933 surface effective temperature (decreasing  $s_{\rm ad}$ corresponds to increasing  $\alpha_{\rm mlt}$). However the effects of changing the surface gravity are not accounted for.

Table 5:   Surface gravity, effective temperature and deep convection zone specific entropy for the hydrodynamical surface convection models of HD 49933 and the best fit model, model 3, computed with CESAM.

3.2 The mixing length parameter

Our hydrodynamical models suggest that the efficiency of convection is higher in HD 49933 than in the Sun. This means that the $\alpha_{\rm mlt}$ adopted for HD 49933 should be larger. Table 6 estimates the effects of a modified $\alpha_{\rm mlt}$ on $\Delta \nu$, $\nu _{\ell =0,n=14}$ and $\rm\nu_{\ell=0,n=27}$ for $1.17~M_{\odot}$ models with X=0.7664 and Z=5.4 $\times $ 10-3. As for the other models, core convection overshooting over $0.2~H_{\rm p}$ is included. The specific entropies  $s_{\rm ad}$ of the deep convection zones in models 8, 3 and 9 are respectively: 2.2962 $\times $ $10^9~{\rm erg~K^{-1}~g^{-1}}$, 2.3370 $\times $ $10^9~{\rm erg~K^{-1}~g^{-1}}$ and 2.4371 $\times $ $10^9~{\rm erg~K^{-1}~g^{-1}}$. Our hydrodynamical models (Sect. 3.1) qualitatively predict a typical change ( $s_{\rm ad~HD~49933}-s_{\rm ad~Model~A}$) in  $s_{\rm ad}$ larger than what changes of 0.2 in  $\alpha_{\rm mlt}$ would induce. We conclude that a variation of 0.2 in  $\alpha_{\rm mlt}$ between the Sun and HD 49933 is plausible.

Table 6:   Convection efficiency effect on the large frequency separation, $\nu _{\ell =0,n=14}$ - $\nu _{\ell =0,n=27}$.

The trend in $\Delta \nu$ and frequency for an increasing efficiency of convection disagrees with the observations. Benomar et al. (2009) favored identification is $\Delta \nu = 85.92$ $\pm$ $0.43~\mu {\rm Hz}$, $\nu_{\ell=0,n=14}=1244.43$ $\pm$ $3.90~\mu{\rm Hz}$ and $\nu_{\ell=0,n=27}=2363.81$ $\pm$ $3.90~\mu{\rm Hz}$. For a model slightly below $1.2~M_{\odot}$ this is consistent with a smaller  $\alpha_{\rm mlt}$ throughout the evolution. The logarithmic derivative of the large separation with $\alpha_{\rm mlt}$ computed from models 8 and 9 is $\frac{\partial {\rm ln} \Delta \nu}{\partial {\rm ln} \alpha_{\rm mlt}}=0.213$.

4 Conclusion

In the context of the first CoRoT results, we build secular and dynamical models of the solar type star HD 49933. We use the CESAM stellar evolution code, the hydrodynamical code STAGGER and the Aarhus ADIPLS oscillation package to compute the eigenfrequencies. The purposes of this work are to calculate the impact of mass, composition, diffusion, rotation and convection on classical and seismological parameters. We do not aim at finding the best fit to the current observational constraints but to explore physical effects on the models. We focus on the (average) large frequency separation  $\Delta \nu$. In particular we give the logarithmic derivatives of  $\Delta \nu$ with mass, composition, rotation and  $\alpha_{\rm mlt}$ in order to compare quantitavely their seismic influences. Table 7 sums up the corresponding results.

Table 7:   Logarithmic derivatives of the large separation with various modeling parameters: mass, metal fraction, helium fraction, rotation and mixing length parameter.

We also investigate the derivative of the surface phase shift ( $\beta (\nu)$) that is sensitive to the helium content of the star. We finally give the frequencies of the modes of orders n=14, n=27 and degree $\ell =0$ as they respectively minimize and maximize the surface effects on oscillations. With one exception all the models include a core convection overshooting of 0.2 $H_{\rm p}$. In the case of the models with rotation the angular momentum loss is not taken into account. The results are as follows:

1.
Mass: 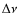$\Delta \nu$ is very sensitive to mass (Table 1). It is a factor 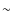$\sim$3 less sensitive to composition effects and a further factor 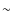$\sim$3 less sensitive to convection efficiency effects. The mass of HD 49933 has to be tighly constrained if one wants to tackle composition or convection efficiency issues.

2.
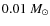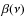Composition: the assumed solar composition strongly influences the absolute metal content of HD 49933 and therefore its seismic properties (Table 2). If using seismology, a mass estimate to better than a few $0.01~M_{\odot}$ will not be reliable as long as the solar composition is not settled. The derivative  $\beta (\nu)$ of the surface phase shift depends on the helium content (Table 2). 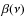However the $\beta (\nu)$ dependence on mass shows once more that mass should be precisely constrained.

3.
Diffusion: diffusion effects are expected to be more important in HD 49933 than in our Sun. The models taking diffusion into account suggest that HD 49933 is more massive than the models that do not take diffusion into account (Table 3). The diffusive models rise an issue: when having the correct effective temperature they are too metal poor, when having the right metallicity they are too cool.

4.
Rotation: the rotational effects appear negligible on both classical and seismological parameters describing HD 49933 except for the Z/X ratio (Table 4). This point is also observed for the Sun. The interplay between rotation and diffusion improves the situation of purely diffusive models by braking the gravitational settling of heavy elements.

5.
Outer convection: our hydrodynamical calculations suggest that the efficiency of convection in HD 49933 should be slightly higher than in the Sun. This contradicts the better agreement of small 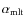$\alpha_{\rm mlt}$ models than large 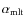$\alpha_{\rm mlt}$ models with the observed large frequency separation. The seismic observations of HD 49933 favor a decrease in the efficiency of convection with increasing mass.

6.
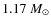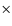Our best fit model has a mass of $1.17~M_{\odot}$. It includes neither diffusion or rotation. Its initial composition is X=0.7664 and Z=5.4 $\times $ 10-3. This mass estimate is unchanged if core overshooting is suppressed. It is also not sensitive to the two current possible mode identification.
This work points out the role of sophisticated physics in the seismological modeling of HD 49933. It stresses the need for an accurate mass and composition determination before the observational data can be used to constrain the internal dynamics. Moreover it shows that diffusive effects and their interplay with rotational effects significantly change the mass and age estimates of the star. Both diffusion and rotation effects have to be taken into account in HD 49933 to draw reliable conculsions. Thus there is a need for sophisticated modelling of this CoRot target. That is especially important as with respect to its temperature the star lies in the middle of the so-called lithium dip. Therefore the future modelling works should include the angular momentum loss as well as the possible rotationally induced shear turbulence in the upper radiation zone of the star. For the same reason it would be interesting to investigate the current surface abundance in lithium and beryllium from the observational point of view.

Acknowledgements
We thank the anonymous referee whose remarks helped to expand and improve the content of this article. L. Piau is member of the UMR7158. This work was supported by the French Centre National de la Recherche Scientifique, CNRS and the Centre National d'Etudes Spatiales, CNES.

References

Footnotes

...1998)[*]
It should be noted that the absolute Z/X=7.04 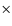$\times $ 10-3 we adopt is smaller than the one adopted in the study of Goupil et al. (2009) Z/X=0.0106. Unlike us these authors consider the solar metal abundance and mixture of Grevesse & Noels (1993).
...$\frac{\partial {\rm ln} \Delta \nu}{\partial {\rm ln} \Delta [{\rm O/Fe}]}=0.83$[*]
Asplund et al. (2005) provide [O/Fe] = 1.21 for the Sun and a variation of [O/Fe] of 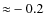${\approx}-0.2$ with respect to Grevesse & Sauval (1998) earlier work.

All Tables

Table 1:   Mass effect on the large frequency separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.

Table 2:   Composition effects on the large frequency separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.

Table 3:   Microscopic diffusion and radiative acceleration effects on the large frequency separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.

Table 4:   Rotation and microscopic diffusion effects on the large frequency separation, $\nu _{\ell =0,n=14}$ and $\nu _{\ell =0,n=27}$.

Table 5:   Surface gravity, effective temperature and deep convection zone specific entropy for the hydrodynamical surface convection models of HD 49933 and the best fit model, model 3, computed with CESAM.

Table 6:   Convection efficiency effect on the large frequency separation, $\nu _{\ell =0,n=14}$ - $\nu _{\ell =0,n=27}$.

Table 7:   Logarithmic derivatives of the large separation with various modeling parameters: mass, metal fraction, helium fraction, rotation and mixing length parameter.

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{11947fg1.ps} \end{figure} Figure 1:

Differences between the observed eigenfrequencies and the model eigenfrequencies vs. the radial order for degree modes $\ell =0$. The model considered is model 3, losanges and stars respectively correspond to the $M_{\rm A}$ and $M_{\rm B}$ modes identifications of Benomar et al. (2009). We also indicated the $2 \sigma $ error bars from these authors.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{11947fg2.ps} \end{figure} Figure 2:

Losanges: $\beta ^{\star } (\nu )$ vs. $\nu $ for the model having $M_{\star}=1.17~M_{\odot}$ and X=0.7664, Y=0.2282 and Z=5.4 $\times $ 10-3 (model 3). Triangles: $\beta ^{\star } (\nu )$ vs. $\nu $ for the same mass but X=0.7529, Y=0.2417 and Z=5.3 $\times $ 10-3 (model 5).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{11947fg3.ps} \end{figure} Figure 3:

$\beta ^{\star } (\nu )$ vs. $\nu $ for the model having $M_{\star}=1.2~M_{\odot}$, X=0.7664, Y=0.2282 and Z=5.4 $\times $ 10-3 (model 2).
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.