| Issue |
A&A
Volume 506, Number 1, October IV 2009
The CoRoT space mission: early results
|
|
|---|---|---|
| Page(s) | 391 - 398 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200911916 | |
| Published online | 02 July 2009 | |
The CoRoT space mission: early results
Planet formation by nucleated-instability: comparison with the two first CoRoT runs
Y. Alibert1,2 - F. Pont3 - I. Baraffe4 - C. Reylé1 - C. Mordasini5,2 - D. Queloz6 - W. Benz2 - S. Udry6
1 - Institut UTINAM, CNRS-UMR 6213, Observatoire de Besançon, BP 1615, 25010 Besançon Cedex, France
2 - Physikalisches Institut, University of Bern, Sidlerstrasse 5, 3012 Bern, Switzerland
3 - School of Physics, University of Exeter, Stocker Road, Exeter EX4 4QL, UK
4 - École normale supérieure de Lyon, CRAL (CNRS), Université de Lyon, 46 allée d'Italie, 69007 Lyon, France
5 -
Max-Planck Institute for Astronomy, Konigstuhl 17, 69117 Heidelberg, Germany
6 - Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Sauverny, Switzerland
Received 20 February 2009 / Accepted 1 July 2009
Abstract
Aims. We use extended planet formation models to analyse the results the two first runs of CoRoT, namely the initial one (IRa01) and the first long one (LRc01). We compare our calculations to the actual observations and discuss the possible origins of the differences between the two, not only in term of detection rate, but also regarding the magnitude of transiting planets parent stars.
Methods. We use a galactic population synthesis model in order to calculate the characteristics of stars in the field-of-view of CoRoT. In a second step, we calculate planet formation models to derive the population of planets expected around these stars. In a third step, using planet evolution models, we calculate the radius of planets predicted by the model and estimate the probability of transit detection and confirmation by radial-velocity follow-up.
Results. Our calculations show that the present day CoRoT detection rate, based only on IRa01 and LRc01, is a factor 5 lower than the one predicted assuming all target are dwarf stars. On the other hand, the two detection rates become similar if one assumes some contamination of CoRoT targets by giant stars, or some less optimistic determinations of the noise level, the limiting signal-to-noise ratio and radial velocity follow-up performances. However, in all the cases we have considered, the majority of transits are found around faint stars, in conflict with the actual CoRoT detections.
Key words: planetary systems - planetary systems: formation - planetary systems: protoplanetary disks - planets and satellites: formation
1 Introduction
Our understanding of planet formation relies on the comparison between theoretical models and actual detected planets. The majority of them have been discovered by radial velocity surveys, which introduce an observational bias toward massive planets located at short distance from their central star. As a consequence, population synthesis models of planet formation have focussed on the comparison with giant planets discovered with this technique (see Ida & Lin 2004a,b, 2005, 2008; Mordasini et al. 2009b).
However, the situation has changed during the recent years, as more and more planets are discovered by other methods, like transit, microlensing effect or direct imaging. Comparing population synthesis models with these latter planets is however difficult, since it requires the knowledge of the selection biases introduced by the different observational techniques, which themselves depend on the observation strategy. In this context, the first results provided by the CoRoT mission, and later on by Kepler, will allow constraining planet formation models, at least if the characteristics of the instruments and the observational strategy can be known with a sufficient precision.
The calculations presented in this paper constitute a follow-up of the population synthesis calculations presented in Mordasini et al. (2009a,b), in the sense that we compare them to the results obtained by CoRoT during the initial (IRa01) and first long run (LRc01) of the satellite. For this, our strategy is the following: we calculate in a first step the characteristics of stars observed by CoRoT in the IRa01 and LRc01 fields, using a stellar population synthesis model (also named galactic model in the following). For each of these stars, we calculate the expected population of planets, using the extended planet formation models developed in Alibert et al. (2005a), and used in Mordasini et al. (2009b) to compare to planets discovered by radial velocity surveys. This theoretical population depends in particular on the mass and metallicity of the star, which result from the galactic model. We then obtain the population of synthetic planets expected in the two fields of CoRoT considered in this work. Finally, we calculate for all of these synthetic star/planet systems, the probability to detect, and confirm by radial velocity, the transit.
The paper is organized as follows: we present in Sect. 2 the numerical tools we use in this work, namely the planet formation models, the characteristics of CoRoT targets (which themselves depends on the galactic model and the effective selection of the targets), the derivation of transit detection probability (including the calculation of planet's radii), and follow-up observations. We present our results in Sect. 3 and our conclusions in Sect. 4.
2 Numerical methods
2.1 Formation models
The models we use here are derived from the planet formation models presented in Alibert et al. (2005a). They take into account planet formation, planet migration and protoplanetary disk structure and evolution in a self-consistent way. These models follow the work by Pollack et al. (1996) with some notable additions. They consist in four different modules that calculate: 1) the disk structure and its time evolution; 2) the interaction of infalling planetesimals with the atmosphere of the planet; 3) the internal structure of the planet; and 4) the migration of the planet. These modules are now shortly described, more details and some tests are described in Alibert et al. (2005a).
- 1)
- The structure and evolution of the protoplanetary disk is calculated in the framework of the
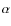 -disk model (Shakura & Sunyaev 1973), in a 1+1D approach. The vertical structure of the disk is computed in a first step, by solving the differential equations of hydrostatic equilibrium, energy conservation (which states that energy released by viscosity is
compensated for by energy losses by radiation), momentum conservation and (vertical) radiative transfer
in the diffusion approximation. In a second step, the standard diffusion equation, modified to take into account photoevaporation, is solved, leading to the determination of the radial structure. This module gives the boundary conditions at the location of the forming planet, and is used to calculate its migration. The disk of solids is finally treated in a very simplified way, since the surface density of solids only
evolves due to accretion and ejection by the forming planet. Our computational disk extends down to 0.1 AU, therefore,
planets whose inner boundary of the feeding zone enters the inner 0.1 AU cannot be followed in a fully consistent way. Instead,
we assume that these planets are halted by some unknown stopping mechanism in the inner parts of the disk.
In order to calculate the transit probability of these latter planets, we distribute them at random between 0.01 AU
and the place from where they cannot be computationally followed. In order to infer the influence of the way we use to distribute
planets in this part of the disk, we considered an uniform distribution and an uniform-in-log distribution of final planet semi-major
axis. The former distribution (used in the calculations presented here) translates in a probability of transit decreased by a factor 2 compared to the latest one. We plan in future work to use the observed distribution of semi-major axis derived from
an unbiased sample (e.g. from CORALIE) in order to remove this uncertainty in our calculations. We think however that the two distributions
considered in this paper adequately bracket the reality.
-disk model (Shakura & Sunyaev 1973), in a 1+1D approach. The vertical structure of the disk is computed in a first step, by solving the differential equations of hydrostatic equilibrium, energy conservation (which states that energy released by viscosity is
compensated for by energy losses by radiation), momentum conservation and (vertical) radiative transfer
in the diffusion approximation. In a second step, the standard diffusion equation, modified to take into account photoevaporation, is solved, leading to the determination of the radial structure. This module gives the boundary conditions at the location of the forming planet, and is used to calculate its migration. The disk of solids is finally treated in a very simplified way, since the surface density of solids only
evolves due to accretion and ejection by the forming planet. Our computational disk extends down to 0.1 AU, therefore,
planets whose inner boundary of the feeding zone enters the inner 0.1 AU cannot be followed in a fully consistent way. Instead,
we assume that these planets are halted by some unknown stopping mechanism in the inner parts of the disk.
In order to calculate the transit probability of these latter planets, we distribute them at random between 0.01 AU
and the place from where they cannot be computationally followed. In order to infer the influence of the way we use to distribute
planets in this part of the disk, we considered an uniform distribution and an uniform-in-log distribution of final planet semi-major
axis. The former distribution (used in the calculations presented here) translates in a probability of transit decreased by a factor 2 compared to the latest one. We plan in future work to use the observed distribution of semi-major axis derived from
an unbiased sample (e.g. from CORALIE) in order to remove this uncertainty in our calculations. We think however that the two distributions
considered in this paper adequately bracket the reality.
- 2)
- The interactions between infalling planetesimals and the envelope of the planet are calculated taking into account gas drag, mass ablation and disruption. This module gives the planets capture radius (i.e. the increase of the planets cross section due the presence of its envelope).
- 3)
- The internal structure of the forming planet is calculated by solving the standard internal structure equations, taking into account the core luminosity due to accretion of planetesimals, as well as core and envelope growth by accretion. The outer boundary conditions are the one given by the first module, since the planet is supposed to extend up to its Hill radius.
- 4)
- The migration of the forming planet is calculated as a function of the disk structure and the planet mass.
Although simplified in some aspects, these models allowed to calculate Jupiter and Saturn formation in the same protoplanetary disk, the planets obtained having bulk properties (e.g. mass, semi-major axis, mean metallicity,...) and atmospheric composition (in particular regarding volatile species like C, N, O, Ar, Kr, Xe) compatible with observations (see Alibert et al. 2005b).
In a population synthesis approach, the same models allowed to reproduce the distribution of (minimum) masses and semi-major
axis of giant extrasolar planets observed by radial velocity surveys with a precision larger than
10 m/s (see Mordasini et al. 2009a,b). In order to match both the Jupiter and Saturn properties, and the ones of extrasolar planets, the parameter ![]() must be set to 0.001, which we regard as our ``nominal'' model. We will also explore the outcome of formation models for
must be set to 0.001, which we regard as our ``nominal'' model. We will also explore the outcome of formation models for
![]() and
and
![]() .
Only the former value can also marginally account for the properties of extrasolar planets.
.
Only the former value can also marginally account for the properties of extrasolar planets.
In the present work, we have extended these models to calculate the formation of planets around stars of different mass.
All parameters are kept identical to the ones assumed in Mordasini et al. (2009a,b), with the exception of the disk masses
which are assumed to depend on the primary mass following the relation
![]() .
The determination of the
.
The determination of the
![]() exponent as been the subject of numerous observational studies. Based on H
exponent as been the subject of numerous observational studies. Based on H![]() line profiles, Muzerolle et al. (2003), and Natta et al. (2004) have inferred that the disk accretion rate roughly scales with the square of the primary mass. We have calculated, using our disk model, the dependance of this accretion rate, at the inner edge of our computational disk, and studied the influence of the
line profiles, Muzerolle et al. (2003), and Natta et al. (2004) have inferred that the disk accretion rate roughly scales with the square of the primary mass. We have calculated, using our disk model, the dependance of this accretion rate, at the inner edge of our computational disk, and studied the influence of the ![]() value. Our calculations show that
value. Our calculations show that
![]() allows to roughly reproduce the data from Muzerolle et al. (2003) and Natta et al. (2004)
(see Alibert et al., in prep.)
for more studies related to the effect of the
allows to roughly reproduce the data from Muzerolle et al. (2003) and Natta et al. (2004)
(see Alibert et al., in prep.)
for more studies related to the effect of the ![]() exponent). We note that our
exponent). We note that our ![]() exponent is close to the value
exponent is close to the value
![]() suggested by Klein et al. (2003) and Alexander and Armitage (2006).
suggested by Klein et al. (2003) and Alexander and Armitage (2006).
Note that in these models, we assume that around every star, one (and only one) planet embryo is present (``one-embryo-per-star approximation''). However, using this approximation, the theoretical detection probability for radial velocity surveys was similar to the real observed detection probability. Therefore, the ``one-embryo-per-star'' approximation should not be too far from reality, at least for massive planets.
2.2 Characteristics of CoRoT targets
2.2.1 Galactic model
The planet formation models we use in this work allow determining the population of expected planets, given the stellar mass and metallicity. In the case of CoRoT, it is therefore necessary to know the mass and metallicity function of dwarf stars in the different directions of observations (see Table 1 for characteristics of the runs considered here). For this, we used the Galaxy model developped in Besançon (e.g. Robin et al. 2003), which provides the characteristics of stars observed by CoRoT for the different observation directions. In particular, the model provides the mass, spectral type, luminosity class, radius and V magnitude for the stars expected in a given direction.
The model assumes that stars are created from gas following a star formation history and an initial mass function, and that stellar evolution follows theoretical evolutionary tracks. The comparison between the galactic model and observational data is presented in Robin et al. (2003). To reproduce the overall galaxy formation and evolution four populations of different ages and star formation history are considered, which we now describe.
The oldest population is the spheroid. For this population a single-burst star formation history ocurring early in the lifetime of the Galaxy is assumed, around 14 Gyr ago, from gas still in a spheroidal distribution. The initial mass function (IMF) and the density distribution of this population are constrained by remote star counts at high and medium Galactic latitudes (Robin et al. 2000). The mean metallicity of the spheroid is assumed to be -1.7 dex with an intrinsic dispersion of 0.5 dex.
Secondly, a population, called the thick disk, is formed of stars born about 11-12 Gyr ago in a short period of time as implied by recent metallicity determinations for this population. For the thick disk, star formation occurred from the gas already settled in the disk. The IMF, density distribution and local normalisation are constrained from star counts (Reylé & Robin 2001). The mean metallicity of the thick disc is assumed to be -0.7 dex with an intrinsic dispersion of 0.3 dex.
Table 1: Characteristics of runs considered in this work.
Thirdly, a bulge population is present in the center of the Galaxy and extends to about 2 kpc. Its age is of the order of 10 Gyr but is poorly constrained. This population has a triaxial distribution, as inferred from near-infrared star counts (Picaud et al. 2004). The mean metallicity is assumed solar with a dispersion of 0.5 dex.
Finally, the fourth population, the thin disk one, is computed as a result of a star formation rate (SFR) and an IMF. The thin disk population is evolved during 10 Gyr, following stellar evolutionary tracks. The IMF and SFR, as well as the characteristics of the thin disk (e.g. disk scale height, ...) are constrained against star counts (e.g. Haywood et al. 1997). In particular, the IMF is adjusted to agree with the most recent Hipparcos results, using the age-velocity dispersion relation from Gómez et al. (1997), and the local luminosity function from Jahreiß & Wielen (1997). The disk scale height is computed self-consistently using the potential via the Boltzmann equation, the local dynamical mass being taken from Crézé et al. (1998).
The evolutionary model fixes the distribution of stars within the parameter space of effective temperature, gravity, absolute magnitude, mass and age. From these parameters are finally derived the star radius which enters in the signal-to-noise ratio during transits, and finally the transit detection probability (see Sect. 2.3). Figure 1 shows the properties of dwarf stars in the two CoRoT fields considered here.
In the two fields considered here (IRa01 and LRc01), the fractions of thick disk stars are respectively 6.6% and 4%, considering only main sequence stars lower than 2 ![]() .
The two populations (thin and thick disk) differ in two aspects: the metallicity is lower for thick disk stars (a mean around 0 to 0.2 dex for the thin disk, and a mean around -0.7 for the thick disk), and no stars more massive than 1
.
The two populations (thin and thick disk) differ in two aspects: the metallicity is lower for thick disk stars (a mean around 0 to 0.2 dex for the thin disk, and a mean around -0.7 for the thick disk), and no stars more massive than 1 ![]() are present in the thick disk (this results from its age).
are present in the thick disk (this results from its age).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11916fg1.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg13.png) |
Figure 1: Characteristics of the stars in the IRa01 and LRc01 fields (solid and dashed curves respectively). The V magnitude, mass, metallicity and radius of the stars are derived from the galactic model. Only main sequence stars with V magnitude below 17 and mass between 0.1 and 2.0 solar masses are considered when computing the histograms. The total numbers of such stars, as derived from the galactic model, are 14 011 and 28 302 respectively in the IRa01 and LRc01 fields. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11916fg2.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg14.png) |
Figure 2: Fraction of dwarf stars, giant and sub-giant stars as a function of the V magnitude for IRa01 and LRc01. The thick curves give the number of dwarf stars per 0.2 V mag bin, whereas the thin curves give the number of giant and sub-giant stars per 0.2 V mag bin. The solid lines are for IRa01, and the dashed lines for LRc01. The cross-over is at lower magnitude for IRa01, compared to LRc01. This can be understood since, for a given magnitude, giants are located farther than dwarfs. In the case of IRa01, there are less giants due to the decrease of disk density with distance, so dwarf stars overcome giants for a lower magnitude. |
| Open with DEXTER | |
2.2.2 Target selection
For each of the CoRoT runs, a number of stars are selected and followed for transit detection, the number being around 9900 for the initial run (IRa01), and 11 300 for the first long run (LRc01), the two ones considered here. The selection algorithm is not clearly known to us, therefore we have considered two different possibilities.
In the ``ideal'' selection procedure, we assume that the source stars are the brightest main sequence ones. This is clearly an idealization, since separating dwarf and giant stars is not obvious, in particular for faint objects.
We have therefore also considered an alternative, ``non-ideal'', selection procedure, by allowing for a fraction of contaminating giant stars: for objects brighter than V = 14, we assume a 50% contamination by giant stars, whereas for objects fainter than V = 14, we assume that stars are chosen at random. The effective contamination rate by giants (more exactly stars with luminosity class equal to 3 or 4) at a given magnitude, therefore depends on the fraction of dwarf and giant stars at the given magnitude, as presented in Fig. 2. Finally, we assume that a fraction of stars (15%, corresponding to early-type and unresolved binary stars) cannot be used for planet detection. This fraction is similar to the one derived from the analysis of IRa01, where 5 stars, out of 27 candidates, were not usable for radial-velocity follow-up (Moutou et al. 2009).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11916fg3.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg15.png) |
Figure 3:
Mass versus semi-major axis diagram for synthetic planets. The black dots are results of planet formation models. The red dots are planets whose transit can be detected, assuming there is a transit. The red dots therefore do not take into account the inclination effect (and the associated probability of transit), nor the cut-off at DT/2. The blue dots indicate planets whose radial velocity motion can be detected
(assuming the orbital plan is aligned with the line-of-sight). Finally, the green open circles are planets that can be detected by CoRoT and confirmed with radial velocity follow-up, taking into account the inclination effect and the cut-off at DT/2. The red open circles are the four detections by CoRoT during IRa01 and LRc01. Upper left: case 1 (nominal model) (i.e. the model giving best fits with planets observed by radial velocity surveys,
with
|
| Open with DEXTER | |
2.3 Transit detection
We assume that transits are detected if the corresponding signal-to-noise ratio is greater than a limiting value ![]() ,
which is taken equal to 12. We have also considered a limiting value of 25, which may be closer to reality (Moutou et al. 2009). The noise evolves as a function of the V magnitude, as presented by Aigrain et al. (2009). We adopt for the sake of simplicity an approximate fit given by:
,
which is taken equal to 12. We have also considered a limiting value of 25, which may be closer to reality (Moutou et al. 2009). The noise evolves as a function of the V magnitude, as presented by Aigrain et al. (2009). We adopt for the sake of simplicity an approximate fit given by:
The total noise during the transit also depends on the transit duration, which itself depends on the impact parameter, the star and planet radius. The impact parameter is chosen at random with an uniform probability distribution, whereas the star radius,

where DT is the total duration of the run and P the orbital period. Finally, we assume that transit detection is not possible for periods larger than DT/2.
2.4 Planetary radii
The planetary radius enters in the determination of the signal-to-noise ratio, and on the possibility to detect transits. It depends in principle on many parameters, such as the planet bulk composition (total mass and mass of heavy elements inside it), the irradiation flux (which itself depends on the star age and spectral type, and on the planet semi-major axis), and finally on the planet age.
We use in this work the planetary evolution calculations developed by Baraffe et al. (2008), which include the effects of irradiation, the presence of solid core and heavy elements inside the planets (these values being derived from planet formation models), and the planet age. A more detailed description of the radius calculation can also be found in Leconte et al. (2009). For simplicity, the age of all planets is taken to be 5 Gyr, and the irradiation flux is the one received by a planet at 0.045 AU from a Sun-like star. We have checked that varying the age of the systems (from 2 to 5 Gyr) and including or not the effects of irradiation on the planet radius do not have a strong effect on the detection rate of planets.
2.5 Radial velocity follow-up
Radial Velocity follow-up is mandatory not only to confirm the planetary nature of transits, but also to derive the
mass and mean density of transiting planets. The precision that can be obtained by radial velocity is however difficult to estimate, since it depends on the stellar magnitude, stellar mass, and activity of the star in particular. We use in this work a conservative estimate of the radial velocity precision (
![]() )
that can be obtained as a function of the stellar magnitude:
)
that can be obtained as a function of the stellar magnitude:
![]() is increased by a factor
is increased by a factor ![]() per unit of V magnitude, and is normalized at
per unit of V magnitude, and is normalized at
![]() m/s at V = 13. We assume moreover that no radial velocity follow-up is possible for giant stars, and for stars more massive than 2 solar masses.
m/s at V = 13. We assume moreover that no radial velocity follow-up is possible for giant stars, and for stars more massive than 2 solar masses.
3 Results
3.1 Detection in the mass versus semi-major axis diagram
By combining the different numerical tools presented above, we can calculate the expected characteristics of transiting planets, in particular their mass and semi-major axis, as well as the V magnitude of the central stars. The upper left panel of Fig. 3 shows the predicted planet population, combining the IRa01 and LRc01 runs, together with the fraction of these planets that can be detected for transit and radial velocity follow-up. The synthetic planets are represented by black dots, whereas planets whose transit can be detected are represented in red. Note that these red dots only account for the possibility of transit thanks to a high enough signal-to-noise ratio, and to not include the geometry effect and the observational cut-off at DT/2 where DT is the duration of each run. Blue dots represent planets whose radial velocity effect can be measured, the radial velocity amplitude being computed assuming the angle between the line-of-sight and the orbital planet is equal to 0. Finally, green circles represent planets that can be detected by CoRoT, incuding all the effects, and red circles represent the four transiting planets COROT-1b to COROT-4b.
The synthetic transiting planets (green circle) and real observations occupy a similar area of the mass versus semi-major axis diagram, with however some differences. In particular, some synthetic planets are found at masses slightly lower than the actual detected planets, and some of them are found very close to their central star. However, note that, as mentioned at the beginning of this paper, the computational disk in our planet formation model extends down to 0.1 AU. At the time the inner boundary of a forming planet feeding zone enters the innermost 0.1 AU of the disk, the formation process
cannot be followed anymore (it would require the knowledge of thermodynamical conditions in the disk innermost parts). Since the size of forming
planets feeding zone depends on their mass (proportional to
![]() ), the place where planet formation cannot be
followed anymore depends on the planet mass, and is represented by the dashed lines in Fig. 3. When a planet enters the zone
between the vertical axis and the dashed line, we set a final semi-major axis at random (with a constant distribution fonction
), the place where planet formation cannot be
followed anymore depends on the planet mass, and is represented by the dashed lines in Fig. 3. When a planet enters the zone
between the vertical axis and the dashed line, we set a final semi-major axis at random (with a constant distribution fonction![]() ) between 0.01 AU and the dashed line, the planet mass being not modified. The difference in the periods of synthetic transits and actually observed transits can therefore originate from the afore-mentioned simplifications.
) between 0.01 AU and the dashed line, the planet mass being not modified. The difference in the periods of synthetic transits and actually observed transits can therefore originate from the afore-mentioned simplifications.
3.2 Detection rate and magnitude effect
In the nominal case (assuming an ideal selection of targets), 20 transits are predicted, and only four have been detected![]() . Moreover, 75% of the predicted transits are found around faint stars (V magnitude larger than 14), whereas all the observed transiting planets are around brighter stars (V magnitude lower than 14), see
Fig. 4. The theoretical repartition of V magnitude of transiting planet's star follows simply the fact that the large majority of targets are faint stars. While the number of transiting planets in the sub-sample of bright targets is consistant with observations, there is a serious difference for fainter stars.
. Moreover, 75% of the predicted transits are found around faint stars (V magnitude larger than 14), whereas all the observed transiting planets are around brighter stars (V magnitude lower than 14), see
Fig. 4. The theoretical repartition of V magnitude of transiting planet's star follows simply the fact that the large majority of targets are faint stars. While the number of transiting planets in the sub-sample of bright targets is consistant with observations, there is a serious difference for fainter stars.
In order to try to understand this difference, we have considered the same planet formation model, but assuming a ``non-ideal'' target selection (see Sect. 2.2.2). In this case (case 2), the number of transits is 7, consistent with the actual number of detected transits, half of them being found around brighter stars (V magnitude smaller than 14, see Fig. 5). If could seem surprising that the minimum mass of observed planets is lower in this non-ideal case (compared to case 1). However, only one such planet is predicted and is the result of statistical fluctuations (some other realisations of case 1 can also product such a synthetic observable planet).
Even if we still predict some transits around fainter stars, contamination allows to match in a better way the characteristics of synthetic and observed transits. However, predicting only transits around bright stars would require that the large majority of fainter stars are actually giant stars. We have also run a simulation with a limiting signal-to-noise ratio of 25 (Moutou et al. 2009), the effect being to reduce the number of detected and confrimed transits to 3, all of then being predicted around faint stars. Finally, another possibility would be that the estimation of noise or radial velocity follow-up accuracy are strongly different from expected, in the case of faint stars.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11916fg4.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg25.png) |
Figure 4: Semi-major axis versus V magnitude for models and observations. Small dots are results of models, circles are synthetic transits, and triangles are real observations. The theoretical model is the nominal one, the target selection is assumed to be ``ideal''. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11916fg5.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg26.png) |
Figure 5: Same as Fig. 4, but assuming a ``non-ideal'' target selection. |
| Open with DEXTER | |
3.3 Effect of migration
The parameters entering in our nominal planet formation model were adjusted in order to reproduce
the statistical properties of extrasolar planets (see Mordasini et al. 2009b). In particular, the type I migration
rate efficiency factor, ![]() was found to be low, between 0.01 and 0.001, the best fit model being 0.001.
was found to be low, between 0.01 and 0.001, the best fit model being 0.001.
In order to test the influence of type I migration rate on the population of synthetic transits, we have considered models
similar to case 2, but for
![]() (case 3) and
(case 3) and
![]() (case 4). The resulting mass versus
semi-major axis diagrams are shown in Fig. 3, and the statistics of transits are presented in Table 2.
Since we assume a ``non-ideal'' target selection, these two latter models must be compared to case 2 (upper right panel
in Fig. 3).
(case 4). The resulting mass versus
semi-major axis diagrams are shown in Fig. 3, and the statistics of transits are presented in Table 2.
Since we assume a ``non-ideal'' target selection, these two latter models must be compared to case 2 (upper right panel
in Fig. 3).
Comparing case 2 and case 3, the statistics of transits does not vary much, the main difference being the absence of a ``planet desert'' for planets between 3 and 10
![]() and between 0.1 AU and 0.5 AU. However, this part of the diagram is hardly accessible to CoRoT. Comparing case 2 and case 4, the number of synthetic transits is increased to 37, and a few Neptune mass planets are
predicted. In view of the actual number of transit discovered to date by CoRoT, high migration rates (case 4) seem to have to be rejected. We note that this conclusion is also consistent with results of comparison with planets detected by radial velocity surveys (see Mordasini et al. 2009b).
and between 0.1 AU and 0.5 AU. However, this part of the diagram is hardly accessible to CoRoT. Comparing case 2 and case 4, the number of synthetic transits is increased to 37, and a few Neptune mass planets are
predicted. In view of the actual number of transit discovered to date by CoRoT, high migration rates (case 4) seem to have to be rejected. We note that this conclusion is also consistent with results of comparison with planets detected by radial velocity surveys (see Mordasini et al. 2009b).
Table 2: Characteristics of the four cases considered, and statistics of results.
Radial velocity survey are presently detecting a large number of Hot-Neptune to Super-Earth planets, around maybe up to 30% of solar type stars harboring such objects (Mayor et al. 2009). This number constitutes a very important constrain for planet formation models, and in particular for migration of
low mass planets. Indeed, in order to match this number, the type I migration rate must be increased to values around
![]() .
However, such values are hardly compatible with results of RV surveys for giant planets, and it appears difficult to match both
kind of observations (Hot Neptune and gas giant planets) with a constant value of
.
However, such values are hardly compatible with results of RV surveys for giant planets, and it appears difficult to match both
kind of observations (Hot Neptune and gas giant planets) with a constant value of ![]() .
Indeed, recent hydrodynamical
simulations (e.g. Paardekooper & Mellema 2008; Kley & Crida 2008) show that the type I migration rate is a strong function of the planetary mass (which would imply a varying
.
Indeed, recent hydrodynamical
simulations (e.g. Paardekooper & Mellema 2008; Kley & Crida 2008) show that the type I migration rate is a strong function of the planetary mass (which would imply a varying ![]() ). Moreover, our calculations assume that only one embryo grow around a given star. Low mass planets appear to belong more likely to multi-planetary systems (Mayor & Udry 2008). Therefore, we expect that differences between models and observations will be higher for these planets. Finally, CoRoT should be able to see some of these Neptune mass planets, and it seems there is an incompatibility between results of
RV searches and results from CoRoT. This is very likely related to the global paucity of CoRoT results, the effect being increased
by the fact that Neptune mass planets are difficult to detect and confirm.
). Moreover, our calculations assume that only one embryo grow around a given star. Low mass planets appear to belong more likely to multi-planetary systems (Mayor & Udry 2008). Therefore, we expect that differences between models and observations will be higher for these planets. Finally, CoRoT should be able to see some of these Neptune mass planets, and it seems there is an incompatibility between results of
RV searches and results from CoRoT. This is very likely related to the global paucity of CoRoT results, the effect being increased
by the fact that Neptune mass planets are difficult to detect and confirm.
4 Discussion and conclusions
Our calculations show that the detection rate by CoRoT is low compared to the one expected from theoretical models. More importantly, our models predict that the majority of transits should be discovered around faint stars, this effect resulting only from geometry: the majority of stars observed by CoRoT are at magnitude larger than 14.
This discrepancy could have different origins, some of them being tested in the present calculation. This origin could of course be that planet formation models predict the presence of too many planets in regions close to the central star. Indeed, the fate of planets entering the innermost regions of protoplanetary disks is not presently well understood, since some (unknown) stopping mechanism are likely to be at work in these regions. The planet formation models we use here assume that all planets are stopped, which may be the origin of the high detection rates we obtain. However, these models have already been tested by reproducing some of the properties of Jupiter and Saturn (see Alibert et al. 2005b), and, in a population synthesis approach, some of the statistical characteristics of extrasolar planets around solar-like stars (Mordasini et al. 2009b). In particular, the detection rate obtained for radial velocity surveys is consistent with observations (see Mordasini et al. 2009b). Finally, explaining the magnitude effect (all transits have been discovered for stars with V magnitude lower than 14) from planet formation models seems very difficult. We note in passing that, if we retain only planets brighter than V = 14, the theoretical and observed detection rates are similar.
We therefore conclude that the lack of observed planets has likely an observational origin, which remains to be understood. Different hypotheses can be done, as for example: 1) an under-estimation of the noise for high magnitude stars; 2) an over-estimation of the radial velocity accuracy for the same stars; 3) a strong effect of target selection; 4) an other unknown effect. In particular, the fact that CoRoT is finding more planets orbiting bright stars may indicate that there could be a bottleneck at the RV follow-up stage. This could arise partly from the decrease in RV accuracy for faint stars, partly from the economics of observations scheduling. There may not have been adequate Doppler resources yet to really vet all of the transit candidates orbiting dim candidate stars. Understanding the origin of the low detection rate achieved to date by CoRoT is mandatory, in particular for the remaining lifetime of CoRoT and the future of space missions similar in concept to CoRoT, like Kepler or PLATO.
We have made tests in order to try to match the detection rate of the two first CoRoT runs, as well as the magnitude effect, in particular to test the three first hypotheses mentioned above. For the first one, the noise level had to be increased by a factor 5 compared to the one assumed in Sect. 2.3, for faint stars. In a similar way, the radial velocity accuracy must be increased up to 100 m/s for stars fainter than V = 14 in order to recover the observed detection rate. These two assumptions seem to be very unlikely. Regarding the effect of target selection, we have tested using the ``non-ideal'' target selection (see Sect. 2.2.2) that, in the framework of the galactic model, selecting stars at random for V > 14 does not allow to recover the detection rate, although it goes in the correct direction. However, note that there could be more giant stars in the actual CoRoT fields than predicted by the galactic model (whose aim is to reproduce the ``mean'' structure of the Galaxy, ignoring small scale sub-structures). Finally, still related to target selection, the fraction of binary stars for faint objects is unknown, and could also reduce the number of ``effective'' target stars, thus reducing the detection rate. The answer to these questions can only be given by observational characterization of CoRoT target stars.
References
- Aigrain, S., Pont, F., & Fressin, F. 2009, A&A, 506, 425 [CrossRef] [EDP Sciences] (In the text)
- Alibert, Y., Mordasini, C., Benz, W., et al. 2005a, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Alibert, Y., Mousis, O., Mordasini, C., et al. 2005b, ApJ, 626, L57 [NASA ADS] [CrossRef] (In the text)
- Alexander, R. D., & Armitage, P. J. 2006, ApJ, 639, L83 [NASA ADS] [CrossRef] (In the text)
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Crézé, M., Chereul, E., Bienaymé, O., et al. 1998, A&A, 329, 920 [NASA ADS] (In the text)
- Gómez, A. E., Grenier, S., Udry, S., et al. 1997, ESA SP-402: Hipparcos - Venice '97, 402, 621 [NASA ADS] (In the text)
- Haywood, M., Robin, A. C., & Crézé, M. 1997, A&A, 320, 428 [NASA ADS] (In the text)
- Ida, S., & Lin, D. N. C. 2004a, ApJ, 604, 388 [NASA ADS] [CrossRef] (In the text)
- Ida, S., & Lin, D. N. C. 2004b, ApJ, 616, 567 [NASA ADS] [CrossRef]
- Ida, S., & Lin, D. N. C. 2005, ApJ, 626, 1045 [NASA ADS] [CrossRef] (In the text)
- Ida, S., & Lin, D. N. C. 2008, ApJ, 673, 487 [NASA ADS] [CrossRef] (In the text)
- Jahreiß, H., & Wielen, R. 1997, ESA SP-402: Hipparcos - Venice '97, 402, 675 [NASA ADS] (In the text)
- Klein, R., Apai, D., Pascucci, I., Henning, T., & Waters, L. B. F. M. 2003, ApJ, 593, L57 [NASA ADS] [CrossRef] (In the text)
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Laughlin, G., Steinacker, A., & Adams, F. C. 2004, Apj, 608, 489 [NASA ADS] [CrossRef] (In the text)
- Leconte, J., Baraffe, I., Chabrier, G., Barman, T., & Levrard, B. 2009, A&A, 506, 385 [CrossRef] [EDP Sciences] (In the text)
- Mayor, M., Udry, S., Lovis, C., et al. 2009, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences]
- Menou, K., & Goodman, J. 2004, ApJ, 606, 520 [NASA ADS] [CrossRef] (In the text)
- Mordasini, C., Alibert, Y., & Benz, W. 2009a, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mordasini, C., Alibert, Y., Benz, W., et al. 2009b, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moutou, C., Pont, F., Bouchy, F., et al. 2009, A&A, 506, 321 [CrossRef] [EDP Sciences] (In the text)
- Muzerolle, J., Hillenbrand, L., Calvet, N., Briceno, C., & Hartmann 2003, ApJ, 592, 266 [NASA ADS] [CrossRef] (In the text)
- Natta, A., Testi, L., Muzerolle, J., et al. 2004, A&A, 424, 603 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Nelson, R. P., & Papaloizou, J. C. B. 2004, MNRAS, 350, 849 [NASA ADS] [CrossRef] (In the text)
- Paardekooper, S., & Mellema, G. 2008. A&A, 478, 245 (In the text)
- Picaud, S., & Robin, A. C. 2004, A&A, 428, 891 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] (In the text)
- Reylé, C., & Robin, A. C. 2001, A&A, 373, 886 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Robin A. C., Reylé C., & Crézé, M. 2000, A&A, 359, 103 [NASA ADS] (In the text)
- Robin A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523, Erratum 2004, A&A, 416, 157 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] (In the text)
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] (In the text)
- Ward, W. R. 1997, ApJ, 482, L211 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... fonction
![[*]](/icons/foot_motif.png)
- We have also tested a probability distribution constant in log of the semi-major axis, the resulting effect being to increase the number of detected transits by a factor around 2.
- ... detected
![[*]](/icons/foot_motif.png)
- If the final semi-major axis of close-in planets is assumed to follow a probability distribution uniform in log, this number becomes larger than 35.
All Tables
Table 1: Characteristics of runs considered in this work.
Table 2: Characteristics of the four cases considered, and statistics of results.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11916fg1.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg13.png) |
Figure 1: Characteristics of the stars in the IRa01 and LRc01 fields (solid and dashed curves respectively). The V magnitude, mass, metallicity and radius of the stars are derived from the galactic model. Only main sequence stars with V magnitude below 17 and mass between 0.1 and 2.0 solar masses are considered when computing the histograms. The total numbers of such stars, as derived from the galactic model, are 14 011 and 28 302 respectively in the IRa01 and LRc01 fields. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11916fg2.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg14.png) |
Figure 2: Fraction of dwarf stars, giant and sub-giant stars as a function of the V magnitude for IRa01 and LRc01. The thick curves give the number of dwarf stars per 0.2 V mag bin, whereas the thin curves give the number of giant and sub-giant stars per 0.2 V mag bin. The solid lines are for IRa01, and the dashed lines for LRc01. The cross-over is at lower magnitude for IRa01, compared to LRc01. This can be understood since, for a given magnitude, giants are located farther than dwarfs. In the case of IRa01, there are less giants due to the decrease of disk density with distance, so dwarf stars overcome giants for a lower magnitude. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11916fg3.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg15.png) |
Figure 3:
Mass versus semi-major axis diagram for synthetic planets. The black dots are results of planet formation models. The red dots are planets whose transit can be detected, assuming there is a transit. The red dots therefore do not take into account the inclination effect (and the associated probability of transit), nor the cut-off at DT/2. The blue dots indicate planets whose radial velocity motion can be detected
(assuming the orbital plan is aligned with the line-of-sight). Finally, the green open circles are planets that can be detected by CoRoT and confirmed with radial velocity follow-up, taking into account the inclination effect and the cut-off at DT/2. The red open circles are the four detections by CoRoT during IRa01 and LRc01. Upper left: case 1 (nominal model) (i.e. the model giving best fits with planets observed by radial velocity surveys,
with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11916fg4.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg25.png) |
Figure 4: Semi-major axis versus V magnitude for models and observations. Small dots are results of models, circles are synthetic transits, and triangles are real observations. The theoretical model is the nominal one, the target selection is assumed to be ``ideal''. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11916fg5.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11916-09/Timg26.png) |
Figure 5: Same as Fig. 4, but assuming a ``non-ideal'' target selection. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


